Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Mar 4;12(9):2423–2428. doi: 10.1021/acs.jpclett.1c00205

Grain Size Influences Activation Energy and Migration Pathways in MAPbBr3 Perovskite Solar Cells

Lucie McGovern 1, Isabel Koschany 1, Gianluca Grimaldi 1, Loreta A Muscarella 1, Bruno Ehrler 1,*
PMCID: PMC8041307  PMID: 33661008

Abstract

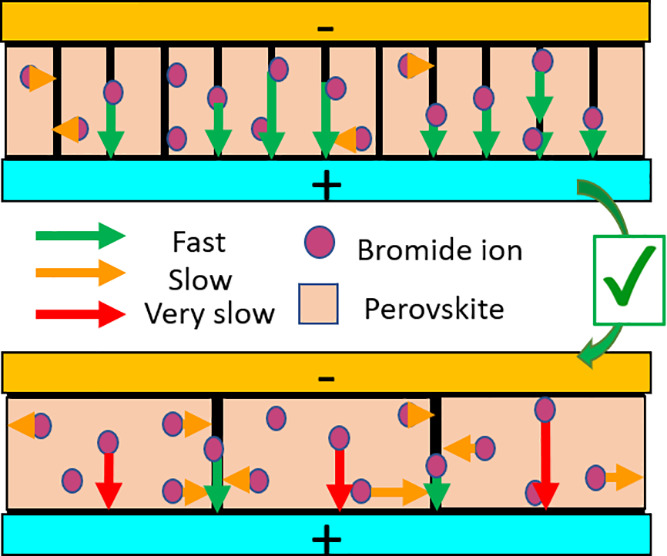
graphic file with name jz1c00205_0005.jpg

Ion migration in perovskite layers can significantly reduce the long-term stability of the devices. While perovskite composition engineering has proven an interesting tool to mitigate ion migration, many optoelectronic devices require a specific bandgap and thus require a specific perovskite composition. Here, we look at the effect of grain size to mitigate ion migration. We find that in MAPbBr3 solar cells prepared with grain sizes varying from 2 to 11 μm the activation energy for bromide ion migration increases from 0.17 to 0.28 eV. Moreover, we observe the appearance of a second bromide ion migration pathway for the devices with largest grain size, which we attribute to ion migration mediated by the bulk of the perovskite, as opposed to ion migration mediated by the grain boundaries. Together, these results suggest the beneficial nature of grain engineering for reduction of ion migration in perovskite solar cells.

Over the recent decade, the advancement of metal halide perovskite solar cells has shown remarkable results, with power conversion efficiencies (PCEs) reaching as high as 25.5% for single junctions and 29.2% for perovskite/silicon tandems.1 In terms of efficiency, this class of material has thus proven effective in solar cell devices. This high performance in terms of efficiency is, however, somewhat mitigated by the stability issue this technology currently exhibits, where a decrease of the PCE of devices over time is commonly observed. This stability loss can be linked to two types of degradation processes, caused by either intrinsic factors or extrinsic factors. Extrinsic factors include moisture, oxygen exposure, and heat and can rapidly degrade the PCE of devices. Though very detrimental to cell performance, these degradation-inducing factors can mostly be prevented, noticeably through passivation or encapsulation schemes of the perovskite layer.2−5 Of more problematic nature are the intrinsic factors of degradation. Indeed, contrary to most solar cell technologies, perovskite crystals are not formed by covalent bonds only, but instead exhibit dual covalent and ionic nature,6,7 bearing in mind that ionic bonds are weaker. A number of defects can thus readily occur in the perovskite lattice, including ion vacancies and ion interstitials.8 Within the solar cell stack, these charged ions can drift toward the electrode of reverse polarity, in a process called ion migration. Under operation, this migration can further change the charge and elemental distribution throughout the perovskite layer and is known to affect the long-term stability of devices.9−11

To achieve long-term stability in metal halide perovskite solar cells, it is thus necessary to understand the intrinsic degradation process that is ion migration, to find suitable ways of mitigating and eventually suppressing this feature altogether.

In devices, the ions migrate from their initial defect position in the lattice toward the perovskite interface with the transport layer and accumulate at that interface.12 However, there is still ongoing debate on how this migration proceeds in the film, namely, whether the process is mediated by the grain boundaries or rather by the bulk of the polycrystalline perovskite films. Some studies report an increased ion migration at grain boundaries, while others report the opposite effect: Studies reporting an enhancement of ion migration at grain boundaries include a range of atomic force microscopy techniques (c-AFM, KPFM, and BE-KPFM) showing the contact potential difference or the hysteresis percentage mapped locally;13−15 imaging techniques (SEM) visualizing the deterioration of the grain boundaries;14 elemental techniques (EDX) measuring the dynamic of the lead-to-halide ratio;14 and conductivity measurements comparing films of various grain size to extract an activation energy for the migration process.16 Studies reporting a reduction of ion migration at grain boundaries include PL techniques (PL microscopy and PLQY) tracking the ionic defect distribution rate17 and intensity-modulated photocurrent spectroscopy measurements (IMPS) comparing the ionic current responses in thin and thick cells.18

With this study, we thus aim to answer the following question: is increasing the grain size an effective way to mitigate ion migration? We choose MAPbBr3, a well-characterized perovskite in terms of ion migration.19−21 The major advantage of using this perovskite material is the possibility to synthesize films of varying grain size, without altering key physical or chemical properties of the film. To characterize and quantify ion migration, we use transient ion drift (TID), a capacitance-based technique which allows for determination of the nature of the mobile ions and quantification of their migration activation energy, diffusion coefficient, and number density.22−24 The combination of this measurement technique together with a perovskite recipe that allows for grain size variation without any modification of the perovskite composition allows us to determine the influence of grain boundaries on ion migration in perovskite solar cells.

To measure the influence of grain size on ion migration, we prepare solar cell devices with an active layer of polycrystalline MAPbBr3 perovskite, of which we modulate the grain size. The recipe for MAPbBr3 perovskite is adapted from ref (25). Its advantage is the possibility of varying the perovskite grain size without modifying any key chemical parameters: only the spin-coating time is varied, while all other parameters, including precursor content, solvent, antisolvent, and annealing conditions, remain unchanged. Optical microscopy (OM) images of the films are shown in Figure 1a,b, where we observe that the grain size is correlated to the spinning time of the solution, with short spinning times leading to larger grains. After a spinning duration of 5 s, the grains in the final film measure an average size of 11.3 ± 1.7 μm (Figure 1a), while 60 s of spinning leads to an average size of 1.7 ± 0.2 μm (Figure 1b). Grain size attribution by microscopy techniques such as OM and SEM might be misleading;25,26 we thus confirm our initial OM characterization with electron backscatter diffraction (EBSD). The EBSD images show an overlay of the image quality (brightness, IQ) with the inverse pole figure (color, IPF) along the z-axis (normal to the substrate, Figure 1c,d) and x-axis (parallel to the substrate, Figure 1e,f). The IPF relative to the x-axis shows a distribution of orientations along the [101] and the [111] directions, indicative of polycrystallinity. The grains and grain boundaries detected by EBSD correspond to those observed by OM, thereby confirming the grain size characterization by OM. We conclude that this recipe, when used at spinning times between 5 and 60 s, allows for about 1 order of magnitude in grain size variation.

Figure 1.

Figure 1

Open in a new tab

Top-view OM image of a MAPbBr3 perovskite film spin coated for (a) 5 s and (b) 60 s. The z orthogonal-direction top-view EBSD of the MAPbBr3 films spin coated for (c) 5 s and (d) 60 s. The x in-plane-direction top-view EBSD of the MAPbBr3 films spin coated for (e) 5 s and (f) 60 s. The inverse pole figure legend in the EBSD images shows the crystallization plane as a function of color. (g) Histogram of the average grain size as a function of spin coating time, with inset of the dark IV curves of the devices. (h) Cross-section SEM image showing the device layers: FTO, NiOx, MAPbBr3, C60, BCP, and gold. The device has a planar p–i–n architecture. The white scale bars presented from (a) to (f) all represent a 10 μm length.

The polydispersity in grain size is presented in the histogram in Figure 1g. The small grain regime is characterized by relatively sharp peaks of standard deviation ∼0.2 μm, whereas the size distribution is more pronounced in the big grain regime, with standard deviations of 0.6 and 1.7 μm respectively for the 5 and 11 μm samples.

Each of these active perovskite layers of MAPbBr3 is incorporated into a p–i–n solar cell architecture as shown in Figure 1h. Representative cross-section SEM pictures show uniform stacking of these successive layers. The thick perovskite film exhibits vertical grain boundaries—the same as those observed in top-view OM images. The bottom electrode is a FTO layer, covered by a hole transport layer of NiOx on top of which the MAPbBr3 perovskite is spin coated, finally the electron transport layer consists of C60 and BCP, and a gold electrode on top completes the device. The extraction layers are chosen specifically because they exhibit no direct ion migration, even though they may reduce the overall PCE of the devices. Dark IV curves of the devices (see the inset of Figure 1g) confirm good diode characteristics, a prerequisite for the TID measurements to study ion migration. Details about the solar cell characteristics are presented in section 1 of the Supporting Information.

TID is an electric spectroscopy technique for ion migration measurements used in perovskite solar cells.23,24 The measurement is based on two steps: first, the application of a filling voltage which will redistribute the ions within a device and, second, the interruption of this voltage pulse, which will lead to the ions drifting back to their initial position. We record the capacitance signal during this second step by applying a small alternating voltage VAC, which thus provides a direct measurement of the ion migration process.

For TID characterization, the first step is the selection of a relevant frequency at which to apply the alternating voltage—for this purpose we measure the impedance spectra of all devices. The two extreme situations are presented in Figure 2, where the impedance spectra of the devices with smallest and largest grain size are shown respectively in panels a and b. Both impedance spectra look very much alike and resemble earlier measurements of MAPbBr3.24 They can be decomposed into a low-frequency regime which is temperature-dependent and dominated by ion accumulation27 and a high-frequency regime which is characterized by a decrease of the capacitance signal due to the series resistance. In-between these two regimes lies an intermediate plateau regime, where the capacitance is determined by the depletion capacitance—this is suitable for TID measurements. We thus select the frequency of 104 Hz for the small alternating voltage VAC in the intermediate impedance regime.

Figure 2.

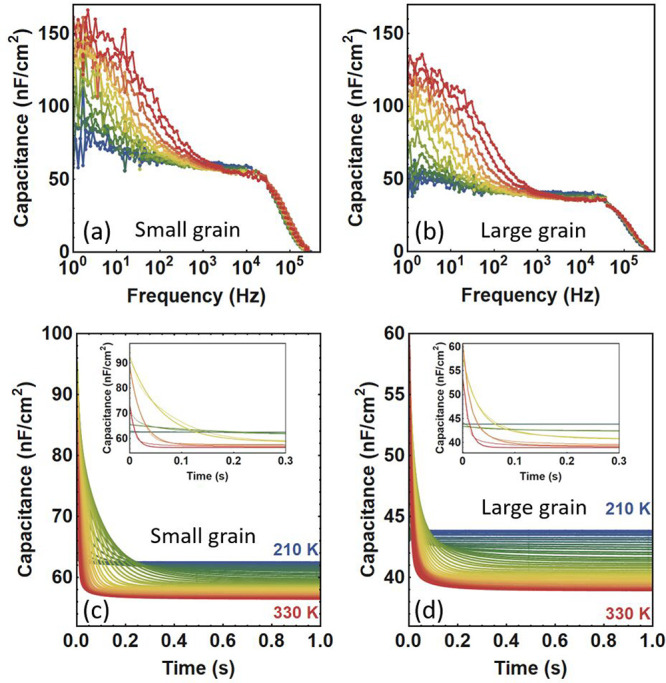
Figure 2

Open in a new tab

Impedance spectra of the devices with (a) 1.7 μm and (b) 11.3 μm grain size MAPbBr3 perovskite films, measured by using an AC voltage of 10 mV. TID traces after applying a voltage pulse of 1 V for 2 s to the devices with (c) 1.7 μm and (d) 11.3 μm grain size perovskite films, between 210 and 330 K in steps of 3 K. The insets in (c) and (d) show the fit to the data for five intermediate temperatures: 210, 240, 270, 300, and 330 K.

Figures 2c and 2d show the TID capacitance traces after applying a filling voltage of 1 V for 2 s to the devices with smallest and largest grain size, respectively. Interestingly, both TID traces show a negative slope in the whole temperature range considered, independent of the grain size. This is further confirmed in the TID traces taken after applying filling voltages of 0.75 or 1.1 V (see Supporting Information section S1). In TID of p-type semiconductors, a negative transient is attributed to anion migration. In the MAPbBr3 crystal structure, the only anion species is the bromide ion. The main ion migration process at play in the whole device range is thus bromide migration. This was previously observed for MAPbBr3 in our work comparing MAPbI3 and MAPbBr324 and is further confirmed here.

In this study, we use TID to quantify the ion migration activation energy Ea, the density of mobile ions Nion, and the diffusion coefficient D for each grain size. The fitting procedure is described in section 2 of the Supporting Information, where the insets in Figure 2c,d show the good correspondence of the fits with the data.

In the small grain regime (1–3 μm), the data can be accurately fitted with one exponential contribution, suggesting a single ion migration process. As the average grain size grows (>5 μm), the fit needs an additional exponential contribution to accurately represent the data (see Figure 3a). TID cannot directly point to the microscopic migration pathway; however, the presence of two separate peaks (with distinct Ea, Nion, and D) is a strong indication for the combination of two bromide migration processes in the perovskite film, where, for example, in addition to the grain boundary mediated pathway most often described, a bulk pathway would appear for films with larger grains. We expand on this idea below and for now refer to these migration pathways as peak A and peak B (respectively in purple and in orange in Figure 3).

Figure 3.

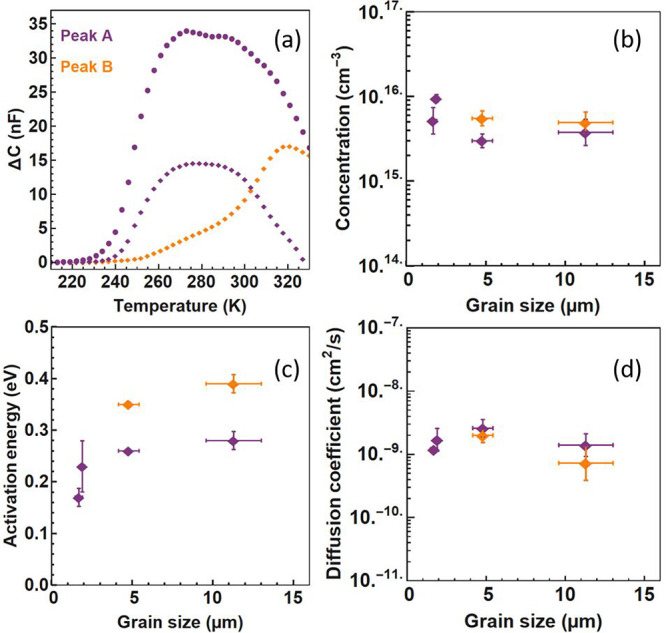
Figure 3

Open in a new tab

Effect of grain size on ion migration parameters: (a) Typical ΔC peak(s) found after fitting the TID traces for samples with 1.7 μm grain size (circle) and with 11 μm grain size (diamond). Peaks A and B are shown in purple and orange, respectively. (b) Concentration of mobile ions, (c) activation energy, and (d) diffusion coefficient, extracted by using equations in section S2 of the Supporting Information.

The density of mobile ions is on the order of 5 × 1015–1 × 1016 cm–3, as shown in Figure 3b. We note that this low density of mobile ions is in agreement with the assumption of ions incompletely screening the built-in voltage in perovskites.28 The total density of mobiles species from peaks A and B is rather constant with grain size: 5.2 × 1015, 9.5 × 1015, 8.5 × 1015, and 8.7 × 1015 cm–3 for the samples with 1.7, 1.9, 4.8, and 11.3 μm grain size, respectively. This is consistent with a model where the ion defect formation energy is independent of the grain size. This trend suggests that ion vacancies form in the bulk of the perovskite or at the interface with the transport layers.

We now look at the evolution of Ea as a function of grain size, as shown in Figure 3c. The activation energy describes the energy it takes for an ion to move to the neighboring unit cell. Ea of peak A first strongly increases with grain size, before reaching a saturation regime for grains larger than 5 μm. For peak B, which is only present for the larger grains, we notice a higher activation energy than peak A and a slight increase with grain size from 0.35 ± 0.01 to 0.39 ± 0.02 eV for films of average grain size 4.8 to 11.3 μm. The general trend is thus an increase in the activation energy with grain size, indicative of a stronger barrier to the migration process for larger grains. This increase is first rapid and then reaches a saturation regime for grains between 5 and 11 μm. We note that the defect formation energy (DFE) model developed by Meggiolaro et al.29 shows a similar evolution of the activation energy with grain size but that a difference of DFE would lead to a change in the density of mobile ions in grain interiors compared to grain boundaries, an explanation which is in contradiction with our observation.

The diffusion coefficient as a function of grain size is presented in Figure 3d. The values are on the order of 10–9 cm2 s–1, similar to previous observations for halide migration.24 These remain relatively constant with grain size, the lowest value being observed for peak B of the sample with largest grains, with (7.3 ± 4.6) × 10–10 cm2 s–1 and the highest value being observed for peak A of the sample with 4.8 μm grains, with (2.6 ± 0.8) × 10–9 cm2 s–1. Within the error this shows a relatively constant diffusion coefficient as compared to the clear increase in activation energy with grain size. Additional considerations regarding the diffusion coefficient and activation energy trends are added to section 2 of the Supporting Information.

We now combine all the previous observations into a possible model. We find the same total number of mobile ions (from peaks A and B combined) independent of the grain size, which means that these mobile ions do not arise from the grain boundary. On top of that the activation energy of peak A increases with grain size. Here it cannot be explained by a reduced number of mobile ions in grain interiors compared to grain boundaries: this observation instead suggests that the mobile bromide ions experience a migration pathway with higher activation energy in the bulk of the grain relative to grain boundaries. We speculate that ions migrate first from their original location in the grain interior to the grain boundary and then through a grain boundary channel toward the interface. The larger the grain size, the less grain boundaries are present, and the further away from a grain boundary an average ion will be positioned. The increase in activation energy of peak A with grain size is thus a representation of the longer average traveling distance to the grain boundary. The migration through the grain boundary channel is thus faster than the migration within the grain, in agreement with various experimental studies showing faster ion migration at the grain boundaries.13−16 For larger grains we find a new ion migration pathway labeled peak B. With larger grains, it is possible that some of the ions migrating within the grain become so far away from any grain boundary that an additional migration pattern arises, where the ions migrate directly from the grain interior to the interface. The implication there is that the migration from grain interior to interface is slower than the migration from grain interior to grain boundary but still takes place when the interface becomes closer than a grain boundary region. This model is also consistent with a relatively constant activation energy and diffusion coefficient for peak B. The illustrative scheme of this model is presented in Figure 4a,b. We thus assign peak A as grain-boundary-mediated bromide migration and peak B as grain-interior-mediated bromide migration.

Figure 4.

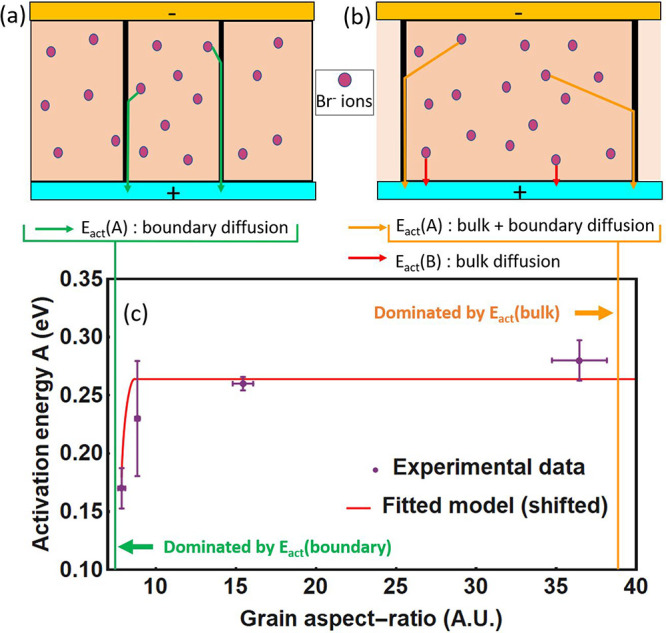
Figure 4

Open in a new tab

Model of ion migration in grains with different lateral size. Schematic of the proposed ion migration, where (a) in small grain sizes most ions first migrate to the grain boundary before they migrate to the interface via the boundary and (b) for larger grain sizes a second pathway appears where the ions migrate to the interface directly. (c) Fit to the experimental data of a geometrical model for the activation energy of ion diffusion (section S4 in the Supporting Information).

The observed trend can be approximately captured by a geometrical model for the motion of ions, in which, for simplicity, we consider the motion of ions along the fastest path to the electrode (section 3 of the Supporting Information). Figure 4c shows the effective activation energy as a function of grain size, obtained by computing the fraction of the path occurring inside the grain and optimizing the value of the activation energies for bulk and grain boundaries diffusion. We obtain activation energies of 0.18 and 0.50 eV for ion diffusion along the grain boundaries and in the bulk. Despite the approximate nature of the model, leading to a large shift in the onset of the activation energy change as a function of grain size, it captures the experimentally observed increase in activation energy for larger grains.

We note that PL microscopy, PLQY, and IMPS studies17,18 suggest that ions migrate from the inside of a grain to a grain boundary and then become trapped at the grain boundary. These works all have in common that they study ion migration along the in-plane direction by diffusion. Here, the ions may be initially trapped at the grain boundary, but they are then allowed to drift through the grain boundary channel in the normal direction, leading them to the interface of reverse polarity.

The grain size of a perovskite film can also affect the electronic trap states. By applying a short voltage pulse of 20 ms instead of 2 s to measure only the contribution of trap states to the capacitance signal, we see changes in the trap state population and energy. We find one dominant electronic trap, which is shallower for the largest grain size sample (ET = 192 meV) compared to the smallest grain size (ET = 300 meV). The density of trap states scales with the number of grain boundaries present, suggesting that the grain boundaries play a major role in trap state formation. These initial findings shown in section S4 of the Supporting Information warrant further investigation.

We studied bromide ion migration in MAPbBr3 perovskite solar cells where we find that the grain size mainly affects the activation energy, while the density of mobile ions and their diffusion coefficient remain relatively constant with grain size. This is a first indication that crystallinity is indeed an effective tool to mitigate ion migration. The quantification of the density of mobile ions and diffusion coefficient are further useful in understanding how the migration pathway is affected by grain size. Ion migration is reduced in cells with larger grains not due to a lower density of mobile ions, but rather due to a higher energy of the transition state for the hopping process in the grain interior compared to that transition state at the grain boundary. Together, our results suggest that for smaller grains there is only one migration process mediated by the grain boundaries and that for larger grains a process mediated by the grain bulk becomes significant. Crystallinity is thus an effective tool to reduce ion migration, proving itself as an interesting strategy for long-term stability of devices.

Acknowledgments

We thank Sven Askes for carefully reading and commenting on the manuscript. This work is part of the Dutch Research Council (NWO) and was performed at the research institute AMOLF. The work of L.M. and L.A.M. was supported by NWO Vidi Grant 016.Vidi.179.005, and the work of G.G. was supported by the EPSRC International Centre to Centre Grant EP/S030638/1.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.1c00205.

  • Device fabrication and characterization; capacitance measurements; model of ion migration pathways; trap states (PDF)

The authors declare no competing financial interest.

Supplementary Material

jz1c00205_si_001.pdf (748.3KB, pdf)

References

  1. Best Research-Cell Efficiency Chart|Photovoltaic Research|NREL https://www.nrel.gov/pv/cell-efficiency.html (accessed 2020-10-09).
  2. Park C.; Ko H.; Sin D. H.; Song K. C.; Cho K. Organometal Halide Perovskite Solar Cells with Improved Thermal Stability via Grain Boundary Passivation Using a Molecular Additive. Adv. Funct. Mater. 2017, 27 (42), 1703546. 10.1002/adfm.201703546. [DOI] [Google Scholar]
  3. Idígoras J.; Aparicio F. J.; Contreras-Bernal L.; Ramos-Terrón S.; Alcaire M.; Sánchez-Valencia J. R.; Borras A.; Barranco Á.; Anta J. A. Enhancing Moisture and Water Resistance in Perovskite Solar Cells by Encapsulation with Ultrathin Plasma Polymers. ACS Appl. Mater. Interfaces 2018, 10 (14), 11587–11594. 10.1021/acsami.7b17824. [DOI] [PubMed] [Google Scholar]
  4. Cheacharoen R.; Boyd C. C.; Burkhard G. F.; Leijtens T.; Raiford J. A.; Bush K. A.; Bent S. F.; McGehee M. D. Encapsulating Perovskite Solar Cells to Withstand Damp Heat and Thermal Cycling. Sustain. Energy Fuels 2018, 2 (11), 2398–2406. 10.1039/C8SE00250A. [DOI] [Google Scholar]
  5. Ma S.; Bai Y.; Wang H.; Zai H.; Wu J.; Li L.; Xiang S.; Liu N.; Liu L.; Zhu C.; et al. 1000 h Operational Lifetime Perovskite Solar Cells by Ambient Melting Encapsulation. Adv. Energy Mater. 2020, 10 (9), 1902472. 10.1002/aenm.201902472. [DOI] [Google Scholar]
  6. Brivio F.; Walker A. B.; Walsh A. Structural and Electronic Properties of Hybrid Perovskites for High-Efficiency Thin-Film Photovoltaics from First-Principles. APL Mater. 2013, 1 (4), 042111. 10.1063/1.4824147. [DOI] [Google Scholar]
  7. Yin W. J.; Shi T.; Yan Y. Unusual Defect Physics in CH3NH3PbI3 Perovskite Solar Cell Absorber. Appl. Phys. Lett. 2014, 104 (6), 063903. 10.1063/1.4864778. [DOI] [Google Scholar]
  8. Eames C.; Frost J. M.; Barnes P. R. F.; O’Regan B. C.; Walsh A.; Islam M. S. Ionic Transport in Hybrid Lead Iodide Perovskite Solar Cells. Nat. Commun. 2015, 6 (1), 1–8. 10.1038/ncomms8497. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Domanski K.; Roose B.; Matsui T.; Saliba M.; Turren-Cruz S. H.; Correa-Baena J. P.; Carmona C. R.; Richardson G.; Foster J. M.; De Angelis F.; et al. Migration of Cations Induces Reversible Performance Losses over Day/Night Cycling in Perovskite Solar Cells. Energy Environ. Sci. 2017, 10 (2), 604–613. 10.1039/C6EE03352K. [DOI] [Google Scholar]
  10. Bae S.; Kim S.; Lee S. W.; Cho K. J.; Park S.; Lee S.; Kang Y.; Lee H. S.; Kim D. Electric-Field-Induced Degradation of Methylammonium Lead Iodide Perovskite Solar Cells. J. Phys. Chem. Lett. 2016, 7 (16), 3091–3096. 10.1021/acs.jpclett.6b01176. [DOI] [PubMed] [Google Scholar]
  11. Khenkin M. V.; Anoop K. M.; Katz E. A.; Visoly-Fisher I. Bias-Dependent Degradation of Various Solar Cells: Lessons for Stability of Perovskite Photovoltaics. Energy Environ. Sci. 2019, 12 (2), 550–558. 10.1039/C8EE03475C. [DOI] [Google Scholar]
  12. Weber S. A. L.; Hermes I. M.; Turren-Cruz S. H.; Gort C.; Bergmann V. W.; Gilson L.; Hagfeldt A.; Graetzel M.; Tress W.; Berger R. How the Formation of Interfacial Charge Causes Hysteresis in Perovskite Solar Cells. Energy Environ. Sci. 2018, 11 (9), 2404–2413. 10.1039/C8EE01447G. [DOI] [Google Scholar]
  13. Yun J. S.; Ho-Baillie A.; Huang S.; Woo S. H.; Heo Y.; Seidel J.; Huang F.; Cheng Y. B.; Green M. A. Benefit of Grain Boundaries in Organic-Inorganic Halide Planar Perovskite Solar Cells. J. Phys. Chem. Lett. 2015, 6 (5), 875–880. 10.1021/acs.jpclett.5b00182. [DOI] [PubMed] [Google Scholar]
  14. Shao Y.; Fang Y.; Li T.; Wang Q.; Dong Q.; Deng Y.; Yuan Y.; Wei H.; Wang M.; Gruverman A.; et al. Grain Boundary Dominated Ion Migration in Polycrystalline Organic-Inorganic Halide Perovskite Films. Energy Environ. Sci. 2016, 9 (5), 1752–1759. 10.1039/C6EE00413J. [DOI] [Google Scholar]
  15. Yang B.; Brown C. C.; Huang J.; Collins L.; Sang X.; Unocic R. R.; Jesse S.; Kalinin S. V.; Belianinov A.; Jakowski J.; et al. Enhancing Ion Migration in Grain Boundaries of Hybrid Organic-Inorganic Perovskites by Chlorine. Adv. Funct. Mater. 2017, 27 (26), 1700749. 10.1002/adfm.201700749. [DOI] [Google Scholar]
  16. Xing J.; Wang Q.; Dong Q.; Yuan Y.; Fang Y.; Huang J. Ultrafast Ion Migration in Hybrid Perovskite Polycrystalline Thin Films under Light and Suppression in Single Crystals. Phys. Chem. Chem. Phys. 2016, 18 (44), 30484–30490. 10.1039/C6CP06496E. [DOI] [PubMed] [Google Scholar]
  17. Phung N.; Al-Ashouri A.; Meloni S.; Mattoni A.; Albrecht S.; Unger E. L.; Merdasa A.; Abate A. The Role of Grain Boundaries on Ionic Defect Migration in Metal Halide Perovskites. Adv. Energy Mater. 2020, 10 (20), 1903735. 10.1002/aenm.201903735. [DOI] [Google Scholar]
  18. Correa-Baena J.-P.; Anaya M.; Lozano G.; Tress W.; Domanski K.; Saliba M.; Matsui T.; Jacobsson T. J.; Calvo M. E.; Abate A.; et al. Unbroken Perovskite: Interplay of Morphology, Electro-Optical Properties, and Ionic Movement. Adv. Mater. 2016, 28 (25), 5031–5037. 10.1002/adma.201600624. [DOI] [PubMed] [Google Scholar]
  19. McGovern L.; Futscher M. H.; Muscarella L. A.; Ehrler B. Understanding the Stability of MAPbBr3versus MAPbI3: Suppression of Methylammonium Migration and Reduction of Halide Migration. J. Phys. Chem. Lett. 2020, 11 (17), 7127–7132. 10.1021/acs.jpclett.0c01822. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Oranskaia A.; Yin J.; Bakr O. M.; Brédas J.-L.; Mohammed O. F. Halogen Migration in Hybrid Perovskites: The Organic Cation Matters. J. Phys. Chem. Lett. 2018, 9, 59. 10.1021/acs.jpclett.8b02522. [DOI] [PubMed] [Google Scholar]
  21. Mahapatra A.; Parikh N.; Kumari H.; Pandey M. K.; Kumar M.; Prochowicz D.; Kalam A.; Tavakoli M. M.; Yadav P. Reducing Ion Migration in Methylammonium Lead Tri-Bromide Single Crystal via Lead Sulfate Passivation. J. Appl. Phys. 2020, 127 (18), 185501. 10.1063/5.0005369. [DOI] [Google Scholar]
  22. Futscher M. H.; Gangishetty M. K.; Congreve D. N.; Ehrler B. Quantifying Mobile Ions and Electronic Defects in Perovskite-Based Devices with Temperature-Dependent Capacitance Measurements: Frequency vs Time Domain. J. Chem. Phys. 2020, 152 (4), 044202. 10.1063/1.5132754. [DOI] [PubMed] [Google Scholar]
  23. Futscher M. H.; Lee J. M.; McGovern L.; Muscarella L. A.; Wang T.; Haider M. I.; Fakharuddin A.; Schmidt-Mende L.; Ehrler B. Quantification of Ion Migration in CH3NH3PbI3 Perovskite Solar Cells by Transient Capacitance Measurements. Mater. Mater. Horiz. 2019, 6 (7), 1497–1503. 10.1039/C9MH00445A. [DOI] [Google Scholar]
  24. McGovern L.; Futscher M. H.; Muscarella L. A.; Ehrler B. Understanding the Stability of MAPbBr3 versus MAPbI3: Suppression of Methylammonium Migration and Reduction of Halide Migration. J. Phys. Chem. Lett. 2020, 11 (17), 7127–7132. 10.1021/acs.jpclett.0c01822. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Adhyaksa G. W. P.; Brittman S.; Abolins H.; Lof A.; Li X.; Keelor J. D.; Luo Y.; Duevski T.; Heeren R. M. A.; Ellis S. R.; Fenning D. P.; Garnett E. C. Understanding Detrimental and Beneficial Grain Boundary Effects in Halide Perovskites. Adv. Mater. 2018, 30 (52), 1804792. 10.1002/adma.201804792. [DOI] [PubMed] [Google Scholar]
  26. Gao N.; Wang S. C.; Ubhi H. S.; Starink M. J. A Comparison of Grain Size Determination by Light Microscopy and EBSD Analysis. J. Mater. Sci. 2005, 40 (18), 4971–4974. 10.1007/s10853-005-3867-6. [DOI] [Google Scholar]
  27. Almora O.; Aranda C.; Mas-Marzá E.; Garcia-Belmonte G. On Mott-Schottky Analysis Interpretation of Capacitance Measurements in Organometal Perovskite Solar Cells. Appl. Phys. Lett. 2016, 109 (17), 173903. 10.1063/1.4966127. [DOI] [Google Scholar]
  28. Bertoluzzi L.; Boyd C. C.; Rolston N.; Xu J.; Prasanna R.; O’Regan B. C.; McGehee M. D. Mobile Ion Concentration Measurement and Open-Access Band Diagram Simulation Platform for Halide Perovskite Solar Cells. Joule 2020, 4 (1), 109–127. 10.1016/j.joule.2019.10.003. [DOI] [Google Scholar]
  29. Meggiolaro D.; Mosconi E.; De Angelis F. Formation of Surface Defects Dominates Ion Migration in Lead-Halide Perovskites. ACS Energy Lett. 2019, 4 (3), 779–785. 10.1021/acsenergylett.9b00247. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz1c00205_si_001.pdf (748.3KB, pdf)

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES