Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Mar 24;12(12):3182–3186. doi: 10.1021/acs.jpclett.1c00512

Disentangling Nano- and Macroscopic Viscosities of Aqueous Polymer Solutions Using a Fluorescent Molecular Rotor

Marius R Bittermann †,§,*, Marion Grzelka †, Sander Woutersen ‡, Albert M Brouwer ‡, Daniel Bonn †
PMCID: PMC8041377  PMID: 33759527

Abstract

graphic file with name jz1c00512_0006.jpg

The macroscopic viscosity of polymer solutions in general differs strongly from the viscosity at the nanometer scale, and the relation between the two can be complicated. To investigate this relation, we use a fluorescent molecular rotor that probes the local viscosity of its molecular environment. For a range of chain lengths and concentrations, the dependence of the fluorescence on the macroscopic viscosity is well described by the classical Förster–Hoffmann (FH) equation, but the value of the FH exponent depends on the polymer chain length. We show that all data can be collapsed onto a master curve by plotting the fluorescence versus polymer concentration, which we explain in terms of the characteristic mesh size of the polymer solution. Using known scaling laws for polymers then allows us to quantitatively explain the relation between the FH exponent and the polymer chain length, allowing us to link the nano- to the macroviscosity.

Polymer melts and solutions are omnipresent in everyday life; for instance, in food and cosmetic products polymers are often added as thickening agents since small amounts allow researchers to significantly increase the macroscopic viscosity. However, at the scale of the polymer molecules themselves, the viscosity that molecules or probe particles experience can be very different from the macroscopic one. Brochard-Wyart and de Gennes already asked the question of how to measure and describe the viscosity at small scales in such systems, and they asserted that flows around small colloidal particles or in thin films, capillaries, etc., cannot be understood in terms of the macroscopic polymer viscosity.1 This takes all of its importance when one realizes that our cells contain biopolymers, and many different types of molecules have to be transported in this crowded environment. Microrheology is a much-used technique for the study of the viscoelastic properties of cells and complex fluids and relies precisely on the measurement of the Brownian motion of small colloidal probes, generally assuming that what they probe are the macroscopic mechanical properties. There is consequently a strong need to understand the viscosity of simple model systems at the scale of individual molecules. We pursue this here with molecular rotors, whose fluorescence depends on the viscosity of the suspending medium. Such molecular rotors are widely used probes for local viscosities in condensed matter.2−10 Generically, intramolecular twisting upon photoexcitation enables rapid nonemissive relaxation,11−14 but when the twisting is hindered by a high degree of molecular crowding, the energy dissipation mechanism is disabled; this then leads to fluorescence emission from the excited state. The central question we ask here is what happens to the fluorescence of molecular rotors in systems, in which the local nanoscopic viscosity is different from the macroscopic viscosity. Arguably the best known and characterized complex fluids are aqueous polymer solutions for which it is known that the viscosity reported by conventional macroscopic rheology can be completely different from the nanoscopic viscosity sensed by molecular probes.15−27

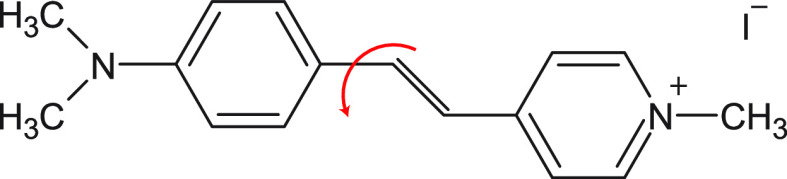
We study the fluorescence of the water-soluble hemicyane molecular rotor trans-4-[4-(dimethylamino)styryl]-1-methylpyridinium iodide (4-DASPI)28−32 (Figure 1) in aqueous poly(ethylene oxide) (PEO) solutions, covering a broad range of concentrations and four orders of magnitude in molecular weight. Our systematic study shows that the local viscosity reported by the molecular rotor is determined by the polymer concentration rather than by the macroscopic viscosity of the solutions. Polymer scaling laws prescribe the relation between the total number of monomers and the polymer correlation length, allowing for a nanoscale interpretation of the fluorescence of the molecular rotor in semidilute polymer solutions. The usual Förster–Hoffmann equation relates the fluorescence to the macroscopic viscosity, and we show here a correlation between the fluorescence and the polymer chain length. This then enables us to use the environment-sensitive molecular rotor to not only measure correlation lengths but also to predict the molecular weight of the polymers from the fluorescence data.

Figure 1.

Figure 1

Open in a new tab

Chemical structure of the molecular rotor 4-DASPI. The red arrow indicates intramolecular rotation.28

Stock solutions of PEO (Sigma-Aldrich) with average molecular weights M (documented as Mn for M < 105 and Mv for M > 105 g mol–1) in the range of [4 × 102 to 2 × 106] g mol–1 in ultrapure water were prepared by gently stirring the mixtures over a week to guarantee complete dissolution. The solutions were then further diluted to cover a wide range of polymer concentrations c (in percentage by weight) and viscosities η. We focus on the semidilute regime as the viscosities are high enough to be distinguishable by molecular rotors and scaling laws are well-established33 and verified in this regime.34,35 The semidilute regime of polymer solutions starts above the overlap concentration, which we estimate as 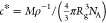Inline graphic,19 where ρ is the solution density, Rg = 0.02M0.58 is the radius of gyration, and NA is Avogadro’s number.36Table 1 lists the calculated c* values for our solutions. 4-DASPI (Sigma-Aldrich, 98% purity, Figure 1) in ultrapure water was added to the polymer solutions to produce molar concentrations of ≈10 μM. These concentrations guarantee sufficient fluorescence intensity while excluding possible inner filter effects. Macroscopic viscosities were obtained from rheological measurements performed on an Anton Paar MCR 302 rheometer using a cone–plate geometry (diameter 50 mm, angle 1°) at ambient temperature and included preshear and rest periods to establish reproducible and controllable initial states of all samples. To account for non-Newtonian behavior observed in the high molecular weight samples (9 × 105 and 2 × 106 g mol–1),34 we extracted viscosities at low-shear rates in the Newtonian plateau of these samples (see Supporting Information, Figure S1). Prior to each fluorescence measurement, UV–vis absorption spectra were recorded using an HP/Agilent 8453 spectrometer. Fluorescence emission spectra were measured using a SPEX Fluorolog 3-22 fluorimeter, equipped with double grating monochromators. To avoid spectral contamination by incident light, the fluorescence emission spectra were recorded by a photomultiplier at a viewing angle of 90°. All polymer solutions were excited at 488 nm, and the emitted light, corrected for both spectral sensitivity of the detection system and intensity fluctuations of the lamp, was collected between 510 and 700 nm. Absorption spectra were background-corrected and fluorescence intensity compensated for light attenuation using the relation I = Iraw/(1 – 10–A) with A the absorbance at the excitation wavelength and Iraw the uncorrected fluorescence intensity at its peak wavelength close to 600 nm. All spectra shown in this work were smoothed to increase readability.

Table 1. Characteristics of the Poly(ethylene oxide) Solutions Studied.

M [g mol–1] c* [wt %] c [wt %]
4 × 102 36.7 [40–100]
6 × 103 7.9 [8–50]
2 × 104 3.3 [4–30]
2 × 105 0.6 [0.8–4]
9 × 105 0.2 [0.2–1]
2 × 106 0.1 [0.1–1]
Open in a new tab

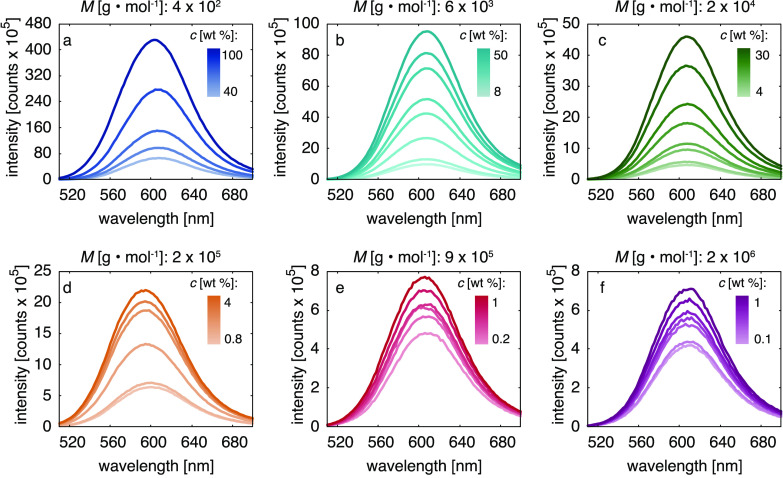
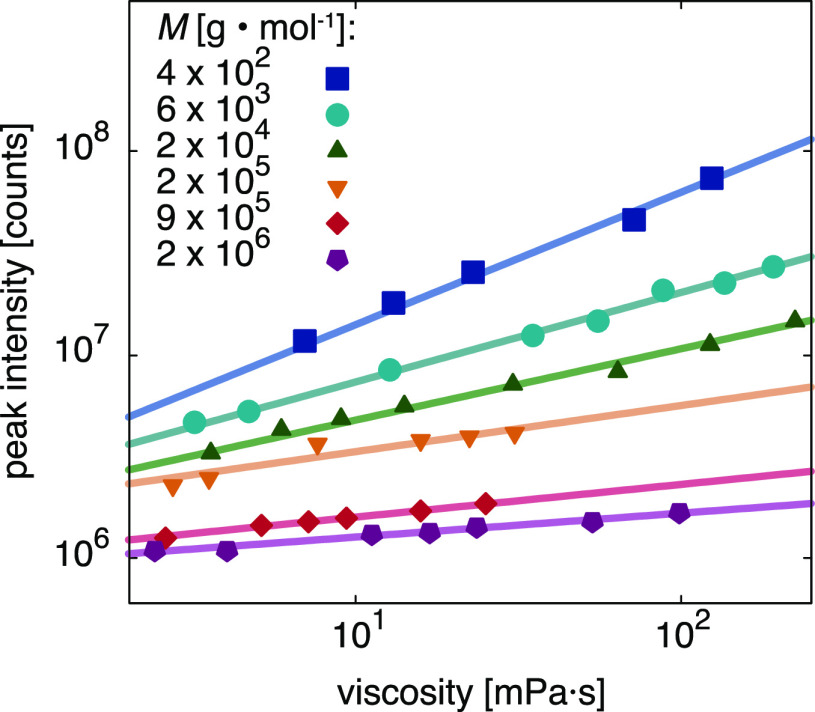
Absorption and fluorescence emission spectra of 4-DASPI in aqueous PEO solutions are presented in Figure S2 and Figure 2, respectively. The hemicyanine dye is known to exhibit an absorption maximum at 452 nm in water,28 which we also find for solutions of low polymer concentrations. A moderate redshift at higher concentrations is due to solvatochromism. We found the influence of polarity effects on the fluorescence to be negligible in these systems (see Supporting Information, Figure S3). As shown in Figure 2, the fluorescence intensity increases with polymer concentration for all molecular weights, in a way that is more pronounced for lower molecular weights. The increase in fluorescence intensity is primarily due to an increase in solvent viscosity, preventing the formation of 4-DASPI’s twisted intramolecular charge-transfer state.11−14 Plotting the absorption-corrected fluorescence intensity at its peak versus the macroscopic viscosity ηmacro (Figure 3) reveals a different power law behavior for all molecular weights. The conclusion is that the fluorescence is not only sensitive to the macroviscosity (that we fit with the Förster–Hoffmann equation relation11,13,14) but also to the polymer molecular weight. The Förster–Hoffmann fits

graphic file with name jz1c00512_m002.jpg 1

have k and x which are solvent- and dye-dependent parameters,37 and the slope x varies with the molecular weight.38

Figure 2.

Figure 2

Open in a new tab

(a–f) Fluorescence emission spectra of 4-DASPI in aqueous PEO solutions of different molecular weights M and concentrations c. At constant dye concentration all samples show a gradual increase in fluorescence intensity with polymer concentration and, thus, solution viscosity. The effect is more pronounced for the lower molecular weight samples (a–c) than for the higher ones (d–f). The corresponding UV–vis absorption spectra can be found in Figure S2.

Figure 3.

Figure 3

Open in a new tab

Fluorescence peak intensity versus viscosity of 4-DASPI in aqueous PEO solutions of different molecular weights M and concentrations c. Viscosities were obtained from conventional macroscopic rheological measurements. Lines are obtained by fitting eq 1 to the experimental data.

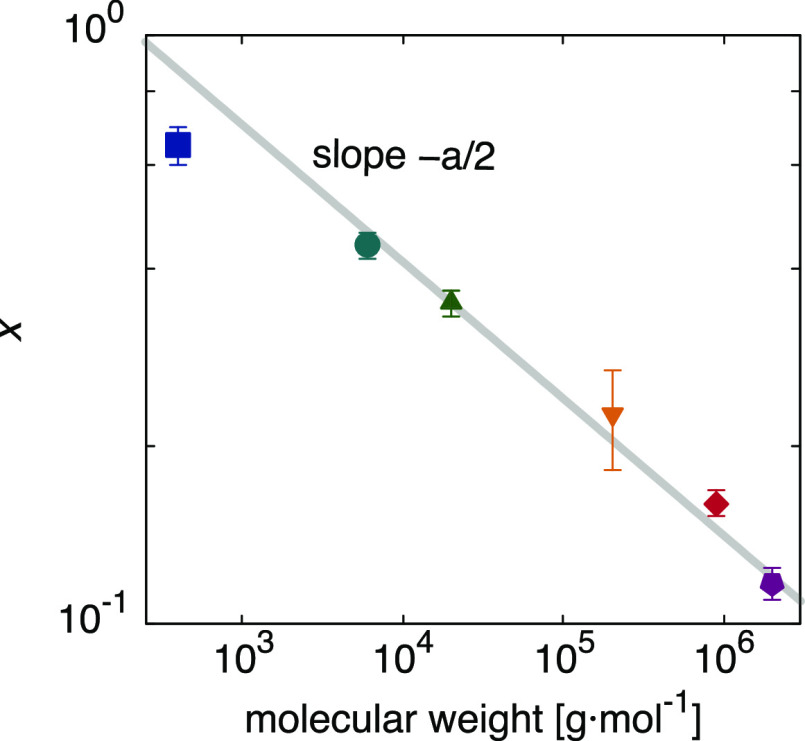
We find that, as the molecular weight increases from 4 × 102 to 2 × 106 g mol–1, x decreases from 0.65 ± 0.05 to 0.12 ± 0.01 (Figure 3). Our upper value agrees well with the theoretical value11 of 2/3, which has also been reported for 4-DASPI in water/glycerol mixtures.30 This means that for the smallest molecular weight, the solution behaves like a simple homogeneous fluid, but for polymers that are much larger than the probe size, the probe “feels” an effective viscosity that is between that of the solvent and the macroscopic viscosity.

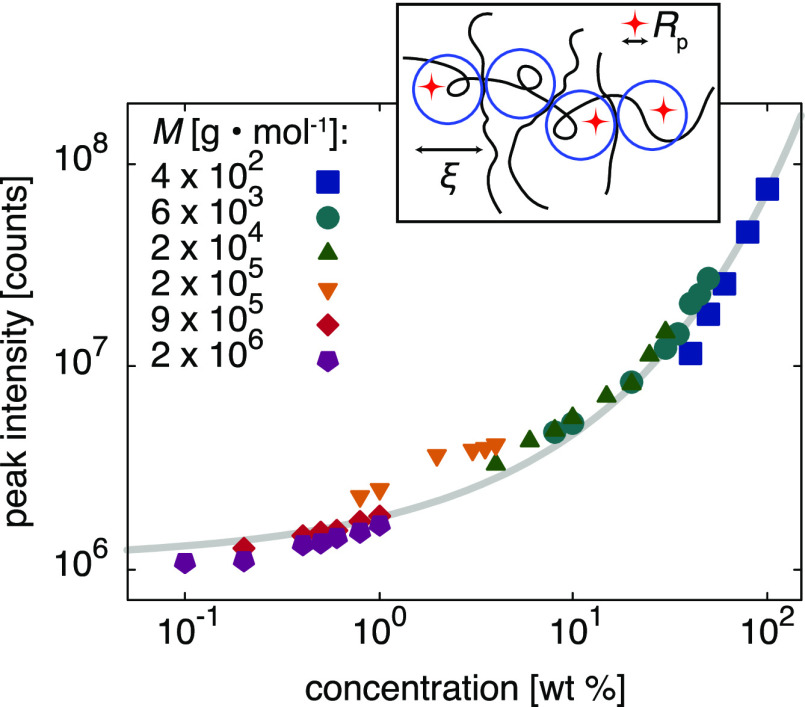
By plotting the fluorescence intensity as a function of polymer concentration c (Figure 4), we find all data points to collapse onto a single master curve. This indicates that the local viscosity reported by 4-DASPI scales with the total number of monomers rather than with the macroscopic viscosity of the solutions. Our measurements are in the semidilute regime, which de Gennes described as a network of polymer chains with a characteristic mesh size ξ, corresponding to the screening distance of excluded volume interactions.33 The correlation length or “blob” size is independent of the molecular weight and thus varies only with the polymer concentration, ξ ∝ cγ, where γ is a solvent-dependent parameter.33 It is therefore tempting to see whether the rotors probe the fluid properties at this nanoscopic length scale. De Gennes indeed postulated that the nanoscopic viscosity ηnano experienced by a nanoprobe of radius Rp is a function depending only on Rp/ξ,33 which was subsequently verified experimentally.16 This is also in line with our measurements; Figure 4 shows that the data can be fitted using the stretched exponential suggested by polymer theory1,20−22,39 and experiments:15,23,40

graphic file with name jz1c00512_m003.jpg 2

where I0 = 1.10 × 106 counts is the measured fluorescence intensity of 4-DASPI in pure water and b and a are fitting parameters (b = 0.49 ± 0.03 and a = 0.46 ± 0.01 for the fit of Figure 4). This nanoscopic interpretation has some interesting implications. Given the proportionality c ∝ ξ1/γ and the independence of ξ on the molecular weight, molecular rotors not only probe local viscosities within polymer solutions but also yield direct information on the characteristic length scales of the semidilute polymer solutions, ξ (Figure 4, inset). From a molecular viewpoint, we conclude that an increase in the total number of PEO monomers results in a decrease of the correlation length or “blob” size and thus exposes the molecular rotor to a higher degree of confinement on a nanoscopic scale. This confinement then restricts the formation of 4-DASPI’s twisted intramolecular charge-transfer state and increases the fluorescence.

Figure 4.

Figure 4

Open in a new tab

Fluorescence peak intensity versus polymer concentration of 4-DASPI in aqueous PEO solutions of different molecular weights M and concentrations c. The data fall onto a master curve, which is fitted by eq 2 (gray line). The inset shows an illustration of the partition of 4-DASPI probe molecules of size Rp (red stars) within PEO “blobs” of size ξ (blue circles).

The remaining question is then how to connect the Förster–Hoffmann eq 1 to our molecular picture and relate the fluorescence intensity to both the macro and the nanoscopic viscosity. To do so, we first express c in the stretched exponential in terms of the macroscopic viscosity using the scaling law ηmacro ∝ Mαcβ.35 Using α = 1 and β = 2 in the range of our semidilute PEO solutions34,35 (see Supporting Information, Figure S4), we find

graphic file with name jz1c00512_m004.jpg 3

where c1 and c2 are constants (see Supporting Information). Equation 3 indeed has the shape of Förster–Hoffmann’s eq 1 and indicates that the slope x is related to the molecular weight by a power law, x ∝ M–a/2. Compared with our measurements (Figure 5), we find a good agreement with this theoretical prediction, providing strong evidence for our molecular picture.

Figure 5.

Figure 5

Open in a new tab

Förster–Hoffmann parameter x as a function of the molecular weight M. The gray line is the predicted slope from eq 3.

In conclusion, considering a molecular interpretation of the molecular rotors residing in “blobs” of polymers in the semidilute regime, we disentangled the effect of polymer molecular weight and monomer concentration on the fluorescence. We also derived a quantitative relation between the exponent of the empirical Förster–Hoffmann power law and well-established scaling laws for the viscosity in polymer solutions. Our observations contribute to the understanding of molecular rotors in systems exhibiting large deviations between macroscopic and nanoscopic viscosities, and they allow us to better understand the small-scale viscosity experienced by molecules in crowded systems such as polymer solutions.

Acknowledgments

This work was supported by The Netherlands Organization for Scientific Research (NWO) and Top Institute Food and Nutrition (TiFN).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.1c00512.

  • Rheological measurements, UV–vis spectroscopy, effect of polarity, scaling laws for the viscosity of PEO solutions, derivation of Förster–Hoffmann’s relation from the stretched exponential (PDF)

The authors declare no competing financial interest.

Supplementary Material

jz1c00512_si_001.pdf (1.3MB, pdf)

References

  1. Brochard-Wyart F.; De Gennes P. Viscosity at Small Scales in Polymer Melts. Eur. Phys. J. E: Soft Matter Biol. Phys. 2000, 1, 93–97. 10.1007/s101890050011. [DOI] [Google Scholar]
  2. Kuimova M. K.; Yahioglu G.; Levitt J. A.; Suhling K. Molecular Rotor Measures Viscosity of Live Cells via Fluorescence Lifetime Imaging. J. Am. Chem. Soc. 2008, 130, 6672–6673. 10.1021/ja800570d. [DOI] [PubMed] [Google Scholar]
  3. Kuimova M. K. Mapping Viscosity in Cells Using Molecular Rotors. Phys. Chem. Chem. Phys. 2012, 14, 12671. 10.1039/c2cp41674c. [DOI] [PubMed] [Google Scholar]
  4. Hosny N. A.; Mohamedi G.; Rademeyer P.; Owen J.; Wu Y.; Tang M.-X.; Eckersley R. J.; Stride E.; Kuimova M. K. Mapping Microbubble Viscosity Using Fluorescence Lifetime Imaging of Molecular Rotors. Proc. Natl. Acad. Sci. U. S. A. 2013, 110, 9225–9230. 10.1073/pnas.1301479110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Levitt J. A.; Kuimova M. K.; Yahioglu G.; Chung P.-H.; Suhling K.; Phillips D. Membrane-Bound Molecular Rotors Measure Viscosity in Live Cells via Fluorescence Lifetime Imaging. J. Phys. Chem. C 2009, 113, 11634–11642. 10.1021/jp9013493. [DOI] [Google Scholar]
  6. Suhina T.; Weber B.; Carpentier C. E.; Lorincz K.; Schall P.; Bonn D.; Brouwer A. M. Fluorescence Microscopy Visualization of Contacts Between Objects. Angew. Chem., Int. Ed. 2015, 54, 3688–3691. 10.1002/anie.201410240. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Pan Z.; de Cagny H.; Weber B.; Bonn D. S-Shaped Flow Curves of Shear Thickening Suspensions: Direct Observation of Frictional Rheology. Phys. Rev. E 2015, 92, 032202. 10.1103/PhysRevE.92.032202. [DOI] [PubMed] [Google Scholar]
  8. Sutharsan J.; Lichlyter D.; Wright N. E.; Dakanali M.; Haidekker M. A.; Theodorakis E. A. Molecular Rotors: Synthesis and Evaluation as Viscosity Sensors. Tetrahedron 2010, 66, 2582–2588. 10.1016/j.tet.2010.01.093. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Kashirina A. S.; López-Duarte I.; Kubánková M.; Gulin A. A.; Dudenkova V. V.; Rodimova S. A.; Torgomyan H. G.; Zagaynova E. V.; Meleshina A. V.; Kuimova M. K. Monitoring Membrane Viscosity in Differentiating Stem Cells Using BODIPY-Based Molecular Rotors and FLIM. Sci. Rep. 2020, 10, 14063. 10.1038/s41598-020-70972-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Ghosh R.; Kushwaha A.; Das D. Conformational Control of Ultrafast Molecular Rotor Property: Tuning Viscosity Sensing Efficiency by Twist Angle Variation. J. Phys. Chem. B 2017, 121, 8786–8794. 10.1021/acs.jpcb.7b05947. [DOI] [PubMed] [Google Scholar]
  11. Förster T.; Hoffmann G. Die Viskositätsabhängigkeit der Fluoreszenzquantenausbeuten einiger Farbstoffsysteme. Z. Phys. Chem. 1971, 75, 63–76. 10.1524/zpch.1971.75.1_2.063. [DOI] [Google Scholar]
  12. Loutfy R. O.; Arnold B. A. Effect of Viscosity and Temperature on Torsional Relaxation of Molecular Rotors. J. Phys. Chem. 1982, 86, 4205–4211. 10.1021/j100218a023. [DOI] [Google Scholar]
  13. Haidekker M. A.; Theodorakis E. A. Molecular Rotors—Fluorescent Biosensors for Viscosity and Flow. Org. Biomol. Chem. 2007, 5, 1669–1678. 10.1039/B618415D. [DOI] [PubMed] [Google Scholar]
  14. Haidekker M. A.; Theodorakis E. A. Environment-Sensitive Behavior of Fluorescent Molecular Rotors. J. Biol. Eng. 2010, 4, 11. 10.1186/1754-1611-4-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Rodbard D.; Chrambach A. Estimation of Molecular Radius, Free Mobility, and Valence Using Polyacrylamide Gel Electrophoresis. Anal. Biochem. 1971, 40, 95–134. 10.1016/0003-2697(71)90086-8. [DOI] [PubMed] [Google Scholar]
  16. Langevin D.; Rondelez F. Sedimentation of Large Colloidal Particles Through Semidilute Polymer Solutions. Polymer 1978, 19, 875–882. 10.1016/0032-3861(78)90191-X. [DOI] [Google Scholar]
  17. Tong P.; Ye X.; Ackerson B. J.; Fetters L. J. Sedimentation of Colloidal Particles Through a Polymer Solution. Phys. Rev. Lett. 1997, 79, 2363–2366. 10.1103/PhysRevLett.79.2363. [DOI] [Google Scholar]
  18. Kalwarczyk T.; Sozanski K.; Ochab-Marcinek A.; Szymanski J.; Tabaka M.; Hou S.; Holyst R. Motion of Nanoprobes in Complex Liquids Within the Framework of the Length-Scale Dependent Viscosity Model. Adv. Colloid Interface Sci. 2015, 223, 55–63. 10.1016/j.cis.2015.06.007. [DOI] [PubMed] [Google Scholar]
  19. Holyst R.; Bielejewska A.; Szymański J.; Wilk A.; Patkowski A.; Gapiński J.; Żywociński A.; Kalwarczyk T.; Kalwarczyk E.; Tabaka M.; et al. Scaling Form of Viscosity at All Length-Scales in Poly(ethylene glycol) Solutions Studied by Fluorescence Correlation Spectroscopy and Capillary Electrophoresis. Phys. Chem. Chem. Phys. 2009, 11, 9025. 10.1039/b908386c. [DOI] [PubMed] [Google Scholar]
  20. Odijk T. Depletion Theory of Protein Transport in Semi-Dilute Polymer Solutions. Biophys. J. 2000, 79, 2314–2321. 10.1016/S0006-3495(00)76477-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Cukier R. I. Diffusion of Brownian Spheres in Semidilute Polymer Solutions. Macromolecules 1984, 17, 252–255. 10.1021/ma00132a023. [DOI] [Google Scholar]
  22. Amsden B. Modeling Solute Diffusion in Aqueous Polymer Solutions. Polymer 2002, 43, 1623–1630. 10.1016/S0032-3861(01)00749-2. [DOI] [Google Scholar]
  23. Ogston A. G.; Preston B. N.; Wells J. D.; Snowden J. M. On The Transport of Compact Particles Through Solutions of Chain-Polymers. Proc. R. Soc. Lond. A 1973, 333, 297–316. 10.1098/rspa.1973.0064. [DOI] [Google Scholar]
  24. Radko S.; Chrambach A. Mechanisms of Retardation of Rigid Spherical Particles with 3 to 1,085 nm Radius in Capillary Electrophoresis, Using Buffered Polyacrylamide (Molecular Weight 5 × 106) Solutions. Electrophoresis 1996, 17, 1094–102. 10.1002/elps.1150170619. [DOI] [PubMed] [Google Scholar]
  25. Radko S. P.; Chrambach A. Electrophoresis of Proteins in Semidilute Polyethylene Glycol Solutions: Mechanism of Retardation. Biopolymers 1997, 42, 183–189. . [DOI] [PubMed] [Google Scholar]
  26. Michelman-Ribeiro A.; Horkay F.; Nossal R.; Boukari H. Probe Diffusion in Aqueous Poly(vinyl alcohol) Solutions Studied by Fluorescence Correlation Spectroscopy. Biomacromolecules 2007, 8, 1595–1600. 10.1021/bm061195r. [DOI] [PubMed] [Google Scholar]
  27. Jagesar D. C.; Fazio S. M.; Taybi J.; Eiser E.; Gatti F. G.; Leigh D. A.; Brouwer A. M. Photoinduced Shuttling Dynamics of Rotaxanes in Viscous Polymer Solutions. Adv. Funct. Mater. 2009, 19, 3440–3449. 10.1002/adfm.200900668. [DOI] [Google Scholar]
  28. Kim J.; Lee M. Excited-State Photophysics and Dynamics of a Hemicyanine Dye in AOT Reverse Micelles. J. Phys. Chem. A 1999, 103, 3378–3382. 10.1021/jp984167e. [DOI] [Google Scholar]
  29. Strehmel B.; Seifert H.; Rettig W. Photophysical Properties of Fluorescence Probes. 2. A Model of Multiple Fluorescence for Stilbazolium Dyes Studied by Global Analysis and Quantum Chemical Calculations. J. Phys. Chem. B 1997, 101, 2232–2243. 10.1021/jp962835v. [DOI] [Google Scholar]
  30. Jee A.-Y.; Bae E.; Lee M. Internal Motion of an Electronically Excited Molecule in Viscoelastic Media. J. Chem. Phys. 2010, 133, 014507. 10.1063/1.3454724. [DOI] [PubMed] [Google Scholar]
  31. Jee A.-Y.; Lee H.; Lee Y.; Lee M. Determination of the Elastic Modulus of Poly(ethylene oxide) Using a Photoisomerizing Dye. Chem. Phys. 2013, 422, 246–250. 10.1016/j.chemphys.2012.12.028. [DOI] [Google Scholar]
  32. Kim J.; Lee M.; Yang J.-H.; Choy J.-H. Photophysical Properties of Hemicyanine Dyes Intercalated in Na-Fluorine Mica. J. Phys. Chem. A 2000, 104, 1388–1392. 10.1021/jp9927855. [DOI] [Google Scholar]
  33. De Gennes P.Scaling Concepts in Polymer Physics; Cornell University Press: 1979. [Google Scholar]
  34. Ebagninin K. W.; Benchabane A.; Bekkour K. Rheological Characterization of Poly(ethylene oxide) Solutions of Different Molecular Weights. J. Colloid Interface Sci. 2009, 336, 360–367. 10.1016/j.jcis.2009.03.014. [DOI] [PubMed] [Google Scholar]
  35. Rubinstein M.; Colby R.. Polymer Physics; Oxford University Press: 2003. [Google Scholar]
  36. Devanand K.; Selser J. C. Asymptotic Behavior and Long-Range Interactions in Aqueous Solutions of Poly(ethylene oxide). Macromolecules 1991, 24, 5943–5947. 10.1021/ma00022a008. [DOI] [Google Scholar]
  37. Howell S.; Dakanali M.; Theodorakis E. A.; Haidekker M. A. Intrinsic and Extrinsic Temperature-Dependency of Viscosity-Sensitive Fluorescent Molecular Rotors. J. Fluoresc. 2012, 22, 457–465. 10.1007/s10895-011-0979-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Polita A.; Toliautas S.; Žvirblis R.; Vyšniauskas A. The Effect of Solvent Polarity and Macromolecular Crowding on the Viscosity Sensitivity of a Molecular Rotor BODIPY-C10. Phys. Chem. Chem. Phys. 2020, 22, 8296–8303. 10.1039/C9CP06865A. [DOI] [PubMed] [Google Scholar]
  39. Altenberger A. R.; Tirrell M. On The Theory of Self-Diffusion in a Polymer Gel. J. Chem. Phys. 1984, 80, 2208–2213. 10.1063/1.446910. [DOI] [Google Scholar]
  40. Laurent T. C.; Pietruszkiewicz A. The Effect of Hyaluronic Acid on the Sedimentation Rate of Other Substances. Biochim. Biophys. Acta 1961, 49, 258–264. 10.1016/0006-3002(61)90125-1. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz1c00512_si_001.pdf (1.3MB, pdf)

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES