A Detailed Experimental and Monte Carlo Analysis of Gold Nanoparticle Dose Enhancement using 6 MV and 18 MV External Beam Energies in a Macroscopic Scale

Abstract

Dose enhancement due to gold nanoparticles (GNPs) has been quantified experimentally and through Monte Carlo simulations for external beam radiation therapy energies of 6 and 18 MV. The highest enhancement was observed for the 18 MV beam at the highest GNP concentration tested, amounting to a DEF of 1.02. DEF is shown to increase with increasing concentration of gold and increasing energy in the megavoltage energy range. The largest difference in measured vs. simulated DEF across all data sets was 0.3%, showing good agreement.

I. Introduction

External beam radiation therapy currently stands as the most common treatment modality used in radiotherapy. This modality utilizes high energy photons to deliver a prescribed dose to a tumor while sparing surrounding normal tissue. However, even with the most up-to-date advancements in the field of radiation therapy, improvements to normal tissue sparing and dose enhancement to a tumor are still needed.

The use of gold nanoparticles to achieve better normal tissue sparing and dose enhancement together seems promising, due to the high atomic number of gold and the fact that nanoparticles can more easily penetrate the tumor vasculature. Following the work of Hainfeld et al.^1–3, considerable interest in the use of gold nanoparticles and other heavy metals to enhance dose delivered to tumors and normal tissue sparing has gained much interest. After these initial studies, there have been many other experimental and Monte Carlo studies produced on GNP dose enhancement, reporting a large amount of dose enhancement using gold nanoparticles primarily at lower energies. ^4–21 In the case of external beam radiation therapy, the photoelectric effect and pair production play a heavy role in increasing the radio-sensitivity of tumor cells, since both of these processes depend on the atomic number (Z) of a material. For lower energy photon beams, the photoelectric cross section of gold is primarily responsible for creating secondary products, increasing dose to a tumor as Z is increased and energy decreased. At the higher photon energies, pair production is primarily responsible for dose enhancing effects as Z is increased and energy increased above 10 MeV. While the photoelectric effect dominates at very low photon energies, such as those energies used in brachytherapy, pair production dominates at higher therapeutic energies, above 10 MeV, and therefore is responsible for producing higher DEFs in the therapeutic range.

The dose enhancing effects of external beam radiation therapy have been explored extensively with the use of both Monte Carlo and experimental methods. ^{15,19,20,22–28} Kakade et al.²⁴ utilized EGSnrc Monte Carlo code to estimate the dose enhancement through the introduction of GNPs inside a polymer gel dosimeter containing 7 (0.7% gold by mass) and 18 mg/g (1.8% gold by mass) of gold in the gel. The gel and GNP volume was irradiated by x-ray beams of 100 kVp, 150 kVp, 6 MV, and 15 MV. In this particular study, very high DEFs were reported for the lower energy x-rays, but no significant dose enhancement was found for the higher energy photon beams of 6 MV and 15 MV. Abolfazli et al.²⁵ studied the radiation dose enhancing effect of 6 MV and 18 MV external beam energies on melanoma tumors injected with 50 nm GNPs with a concentration of 5 mg/mL (0.5% gold by mass) applied to the tumor growing in the left leg of 7 to 8 mice in 4 control and treatment groups of C57BL/6 mice. Authors of this study found that local dose enhancement can be achieved for both 6 MV and 18 MV photon beams with more treatment benefit seen for the 18 MV beam. Mesbahi et al.²⁶ used MCNPX to study the effect of using different energies, including external beam energies of 6 MV and 18 MV on a volume of GNPs containing 7 mg/g gold vs 18 mg/g of gold and found that 90 keV is the optimum energy to produce the most dose enhancement to a tumor. The DEF for 6 MV and 18 MV external beam energies were 1.01 and 1.02, respectively. Authors of this study also observed a small increase in DEF with larger diameter GNPs at significantly low photon energies. Amato et al. used Geant4 to investigate gold nanoparticle dose enhancement under 6 MV external beam irradiation and obtained a DEF of 1.016 for a GNP concentration of 1% by weight.²⁸ The DEF from GNPs has also been calculated using analytical methods as shown in Roeske et al..¹⁵ Many of these studies, however, do not take into consideration optimal GNP features, such as size, concentration and surface coating that present the least cytotoxic effect, which is important to investigate for future clinical use. The present study utilizes realistic, safe concentrations of non-cytotoxic GNPs by coating the GNPs with polyethylene glycol (PEG), to give the most accurate predictions of dose enhancement as they would be seen in future clinical practice.

It has been shown that polyethylene glycol (PEG) coating on GNPs are safe in vivo for studies conducted in vitro and in mice.^29,30 More importantly, the coating of GNPs with polyethylene glycol (PEG) or bovine serum albumin (BSA) has been shown to increase the likelihood of each nanoparticle reaching the tumor, since both of these organic molecules help GNPs avoid the reticuloendothelial system uptake and increase circulation time in blood. A recent study conducted by Kim et al. found that PEG-coated GNPs had a much longer blood circulation time (>4h) than non-PEG-coated GNPs.³¹ It was also found by Dorsey et al. that PEG coated GNPs can accumulate in mouse sarcoma flank tumors to a concentration 10 times that of muscle and 50 times that of brain.³² Puvanakrishnan et al. investigated the effect of PEG-coated gold nanoshells and gold nanorods for their tumor targeting efficiency on mice with subcutaneous tumors. The nanoparticles were injected via IV in single and multiple doses of gold nanoshells and gold nanorods. Particle accumulation in tumors for three consecutive doses was increased by 2 for gold nanoshells and 2.45 for gold nanorods compared with a single dose. In the case of five consecutive doses, particle accumulation increased by 3 fold for gold nanoshells and by 1.6 for gold nanorods in comparison with a single dose. Uptake of smaller PEG-coated gold nanorods was 12 times more compared to the uptake of larger PEG-coated gold nanoshells, which compare well in terms of surface area with gold nanospheres, in the tumor after 24 hours.³³

Despite many types of studies being conducted on gold nanoparticle dose enhancement in radiation therapy, there still exists a knowledge gap between Monte Carlo simulation and in vitro/in vivo studies. This discrepancy could be due to the gold nanoparticle solution or radiation source not being accurately represented or modeled accurately in Monte Carlo studies or it could equally be due to differences in biological factors, such as cellular uptake of the GNPs. Due to these reasons, the development of methods to physically measure and characterize gold nanoparticle dose enhancement coming directly from the increase in absorbed dose become useful tools. There are in fact also some starting points to measuring direct and indirect damage to DNA and cellular repair modeling, such as in Sakata et al.³⁴, but further work still needs to be done in this context. Physical dose enhancement measurements of absorbed dose are utilized to validate Monte Carlo simulations against experimental measurements and vice versa in this study, a need that this study fulfills. These measurements and simulations can be easily implemented and utilized for future in vitro and in vivo studies. Any discrepancies between Monte Carlo simulations and physical dose enhancement measurements would reveal any problems with the assumed properties of GNP solution or errors in a simulation or measurement set-up, which could prove to be a useful guide for further in vitro or in vivo studies. Another useful point to mention is that Monte Carlo codes also model the physical and physio-chemical and chemical stages of interactions up to 1 microsecond only, so this could represent a current discrepancy between simulation and in vitro and in vivo experiments as well. Also, to our knowledge, limited to no information is available on direct Monte Carlo comparison with experimental dose enhancement from clinically relevant GNP concentrations and surface coatings, such as PEG. Finally, information in the literature on how GNP size affects the physical dose enhancement/DEF is often conflicting, with some studies claiming that there is a significant GNP size effect²⁷ and others²⁶ claiming there is none. In the present study, we predict dose enhancement from different solutions containing different sizes of GNPs and concentrations of gold in solution using Monte Carlo methods with MCNP6.2 and evaluate this dose enhancement experimentally for 6 MV and 18 MV external beam photon energies.

For large energies, like 18 MV, it is also increasingly difficult for tumors themselves to be fully in charged particle equilibrium (CPE). In this study, we also compute the DEF from GNPs in CPE using MCNP6.2 and compare these DEFs with experimental conditions not fully in CPE. This represents one of the great values of simple MC models. This method can be utilized to more accurately verify and predict GNP DEF values, especially for future in vitro and in vivo studies. Also as described, the Monte Carlo simulations and experimental methods utilized in this paper are also easily reproducible, making this method easily to replicate for future experiments and simulations.

II. Materials and Methods

A. GNP Synthesis and Functionalization with Polyethylene Glycol (PEG)

GNPs in this study were synthesized using a standard citrate reduction method.³⁵ 7.87 mL of gold chloride salt (HAuCl₄) stock solution at a concentration of 28 mM was mixed with 6.53 mL of water to make a 14.4 mL solution. The mixture was dispensed in to 12 individual Eppendorf tubes and centrifuged for 1 hour at 14,000 × g in a microcentrifuge to remove any aggregates. 900 μL of supernatant was reserved and any aggregates were discarded. Next, 94.2 mg of sodium citrate dihydrate was added to 10 mL of water to make a 1% w/v sodium citrate solution. 600 mL of ultrapure water and 12 mL of the HAuCl₄ solution were added to a 1 L glass bottle. The solution in the 1 L bottle was brought to a boil while rapidly stirring and an appropriate volume of the sodium citrate solution was added (8 mL to produce 30 nm diameter GNPs and 4 mL to produce 100 nm diameter GNPs). After 10 minutes of boiling, the 1 L bottle containing the solution was removed from the heat. After the two batches of 30 nm and 100 nm GNPs, respectively, were synthesized, they were functionalized with poly-ethylene glycol (PEG) by dissolving 10 mg of carboxy-PEG-thiol of molecular weight 5000 in 1 mL ultrapure water. To achieve a final PEG concentration of about 0.0036 mg/mL³⁶, which is ideal for achieving optimal capping density of the PEG to the GNPs, approximately 2.348 mL of PEG solution was added to about 650 mL of the GNP solution after it was first synthesized. The solution was stirred vigorously at room temperature for 2 hours to ensure full reaction.

The GNPs were characterized using scanning electron microscopy (SEM), using a ZEISS FIB-SEM Crossbeam at the University of Texas at San Antonio Kleberg Microscopy Center. GNPs were then concentrated by aliquoting the GNP solution in 15 mL centrifuge tubes and centrifuging at 4,000 rpm for 25 minutes. After the initial centrifugation, 14 mL supernatant was removed. The remaining 1 mL was re-suspended and centrifuged again at the same rpm and time. The supernatant was again removed from each centrifuge tube and the remaining GNP solution in each tube was combined in to one tube and centrifuged a second time to concentrate the GNP solution to the desired concentration to use in experiment. Two different batches of GNP solution were separated out and concentrated to a high concentration (1.3% gold by mass) and low concentration (1% gold by mass), respectively, for both 30 nm and 100 nm GNPs. Mass percent of gold in each solution was determined by weighing a fixed volume of the solution on an analytical balance.

B. External Beam Verification

For accurate prediction of external beam radiation dose enhancement due to GNPs, a simple model of the treatment head for a Varian Clinac 23EX linear accelerator at the University of Texas Health MD Anderson Mays Cancer Center in San Antonio was implemented as in Gray et al..³⁷ The energy source, containing the appropriate energy spectrum and angular spectrum of primary photons for 6 MV and 18 MV energies, respectively, was modeled approximately 100 cm from the surface of a water phantom. Primary X- and Y- collimators and MLC leaf banks were modeled below the source according to blueprints made available by the manufacturer containing approximate dimensions and materials of the parts making up the head of the linear accelerator. A water phantom of volume 30 × 30 × 50 cm³, containing small 0.5 × 0.5 × 0.5 cm³ cells down the length of and across the phantom in x- and y-directions to tally percent-depth dose (PDD) and crossline and inline profiles, respectively, was modeled inside the water phantom. Dose to each small cell was tallied and PDD and beam profiles obtained from these simulations were compared against experimentally measured PDDs and profiles. All measurements of PDD and beam profiles were performed using a water tank (PTW, Freiberg, Germany) with water surface 100 cm source-to-surface distance (SSD). Measurements of PDD, crossline and inline profiles were measured using a PTW 31010, 0.125 cc ion chamber placed inside the water phantom, below the central axis of the photon beam. A second reference ion chamber (PTW 31010) was mounted above the water phantom, at the corner of the radiation field, to account for output variations in the photon beam. Charge measurements from the two ion chambers were recorded and utilized to determine the PDD and profiles of this linac. Field size was set to 10 × 10 cm² and profile depth of measurement was 10 cm.

C. Experimental DEF Measurement

To experimentally verify GNP dose enhancement, an acrylic measurement apparatus, similar to that in Bassiri et al.38, was designed for taking external beam measurements. The apparatus is made up of two slabs of acrylic, each approximately 1.3 cm in height, with a hole of approximately 0.5 cm radius, drilled in the center of both pieces of acrylic to house the GNP solution. EBT3 film was sandwiched in between both slabs of acrylic to measure the dose delivered to each solution at each energy, 6 MV and 18 MV. The first slab of acrylic contained 500 μL of GNP solution and the second slab, below the EBT3 film contained approximately 250 μL of GNP solution, making a total volume of 750 μL. Bolus of appropriate height for the depth of maximum dose (D_max) to occur directly in solution was placed on top of the measurement volume and the apparatus was centered 100 cm SSD from the exit of the head of the linear accelerator to the top of the bolus. Solid water backscatter 10 cm high was placed below the dose measurement apparatus. Four groups of measurements, consisting of 14 measurements each of GNP solution and water, to obtain a viable statistical uncertainty, were performed. The four different measurements performed were (a) 18 MV, 30 nm GNPs at 1.3% gold by mass, (b) 18 MV, 30 nm GNPs at 1% gold by mass, (c) 18 MV, 100 nm GNPs at 1% gold by mass and (d) 6 MV, 30 nm GNPs at 1.3% gold by mass. The Varian Clinac 23 EX was operated at a dose rate of 600 MU/min for all measurements. All measurements were taken at a field size of 10 × 10 cm². DEF was calculated as described in detail in our previous work³⁸; it is defined as the ratio of the dose to the film immersed in GNP solution to the dose to the film immersed in water.

$$DEF=\frac{D_{GNP}}{D_{water}}$$

D. Monte Carlo Simulations

MCNP6.2 Monte Carlo code (Los Alamos National Laboratory, Los Alamos NM) was utilized to carry out simulations of the measurement set-up. The acrylic apparatus was placed 100 cm SSD from the source. A simple beam model is used as described in detail in Gray et al.³⁷ Briefly, the energy spectra and angular spectra of the 6 MV and 18 MV beams are modeled based on data from the literature, and verified via experimental measurements of percent depth dose curves as well as crossline and inline beam profiles. The repeating structures capability of MCNP6.2 was utilized to model the GNP solution accurately as an array of homogenously distributed GNPs in surrounding water. The spacing of GNPs in the array was determined by calculating the concentration of GNPs from the measured mass percent of gold in each solution and finding the number of GNPs per cubic centimeter in solution. From this information, the side length of a cell in the array housing a single GNP was determined. The GNP solution occupied a total volume of 750 μL (0.750 cm³) as shown in Figure 1. For a solution with 1% GNPs by mass and a GNP diameter of 30 nm, the total number of GNPs in the simulation was approximately 2.775 × 10¹³. For a solution with 1% GNPs by mass and a GNP diameter of 100 nm, the total number of GNPs in the simulation was approximately 7.493 × 10¹¹. For a solution with 1.3% GNPs by mass and a GNP diameter of 30 nm, the total number of GNPs in the simulation was approximately 3.618 × 10¹³. Finally, for a solution with 1.3% GNPs by mass and a GNP diameter of 100 nm, the total number of GNPs in the simulation was approximately 9.741 × 10¹¹. The side length of a single cell making up the array is 0.150 μm (3.67E-03 μm³ voxel size) for 1% gold by mass containing 30 nm GNPs, 0.138 μm (2.63E-03 μm³ voxel size) for 1.3% gold by mass containing 30 nm GNPs and 0.502 μm (1.27E-01 μm³) for 1% gold by mass containing 100 nm GNPs. The rpp card, which constructs a right parallelepiped surface in MCNP was utilized to create a single cell of the array. The array was then ultimately constructed from the single right parallelpiped containing a single GNP by the application of the universe and fill cards to fill in the containing volume of the array with multiple adjacent right parallelepipeds containing a single GNP.³⁷ Right parallelpiped size can be simulated down to dimensions on the order of 10⁻⁵ in MCNP. This set-up is shown in Figure 2A. DEF was calculated as the ratio of the dose delivered to the GNP solution volume to the dose delivered to an equivalent volume of pure water.

Figure 1.

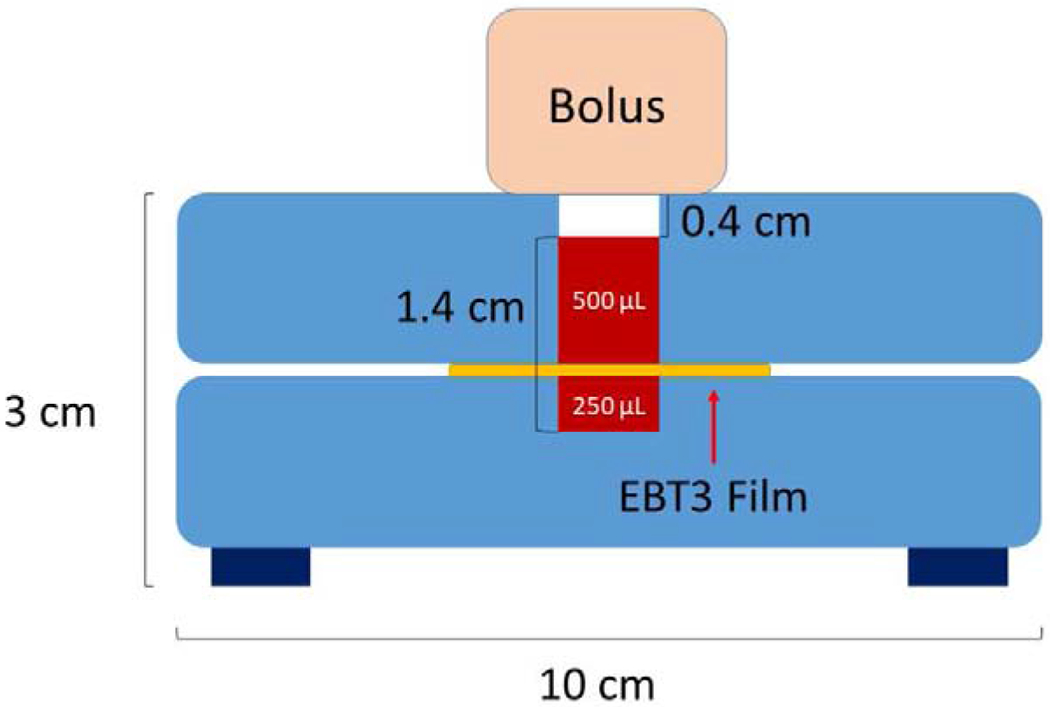
Diagram of acrylic measurement apparatus for external beam DEF measurements. The regions labeled 500 μL and 250 μL are filled with GNP solution. The EBT3 film is sandwiched between the two layers of GNP solution.

Figure 2.

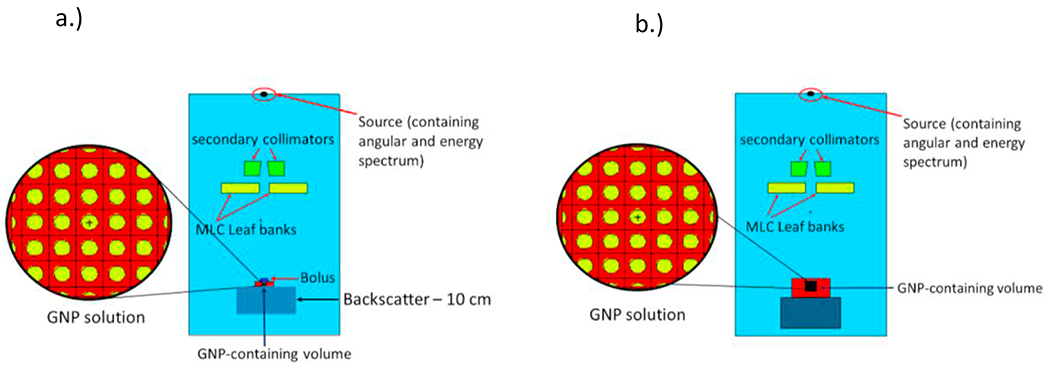
MCNP geometry for a) the experimental set-up and b) the electronic equilibrium set-up.

Since dimensions of the measurement apparatus are not conducive to complete electronic equilibrium conditions, a second set of simulations were designed to predict the dose enhancement in complete electronic equilibrium. For this particular set of simulations, the same treatment head model described above³⁷ was utilized as the radiation source and the GNP-containing volumes were modeled as cubes of side length appropriate for electronic equilibrium conditions for each energy (6 MV and 18 MV). Depth of D_max was designed to occur in the center of the GNP-containing volume, at a depth of 3.5 cm for 18 MV and a depth of 1.5 cm for 6 MV. The GNP-containing solution was modeled with volume 6 × 6 × 6 cm³ for the 18 MV beam and 2 × 2 × 2 cm³ for 6 MV beam. Side lengths of each volume were calculated to accommodate for the secondary electron energy loss of 2 MeV/cm, according to the average energy of each photon source. This simulation type is shown in Figure 2B. For each simulation, 3 × 10⁹ particles were simulated using a computational cluster containing 3580 total CPU cores. Average computing time for the simulations containing the actual measurement set-up was about 1600000 minutes across 255 compute nodes. Average computing time for the simulations containing the electronic equilibrium set-up was about 1400000 minutes across 255 compute nodes. The threshold of production of secondary particles was set to 20 eV, as this cutoff energy allowed for incorporation of the maximum number of secondary particles to be transported and deposit their energy, which was tabulated in each simulation.

III. Results

A. GNP Synthesis and Characterization

Figure 3 shows the 30 nm diameter GNPs deposited on a 2D surface. The GNPs are on average 29.8 ± 2.8 nm in diameter. The UV-vis absorption spectrum (optical density vs. wavelength) of the citrate-capped GNPs directly after synthesis compared with that of the same GNPs after functionalization with PEG showed a 6-10 nm red shift (shift in the absorption spectrum to the right). After PEGylation, the wavelength at maximum absorbance increased from 577 nm to 588 nm for the 100 nm GNPs and from 523 nm to 530 nm for the 30 nm GNPs.

Figure 3.

SEM image of gold nanoparticles.

B. External Beam Verification

Figures 4 and 5 show PDD and beam profiles for the 6 MV and 18 MV beam verification in a 10 × 10 cm² field size at a depth of 10 cm. Error bars lie within the depicted points.

Figure 4.

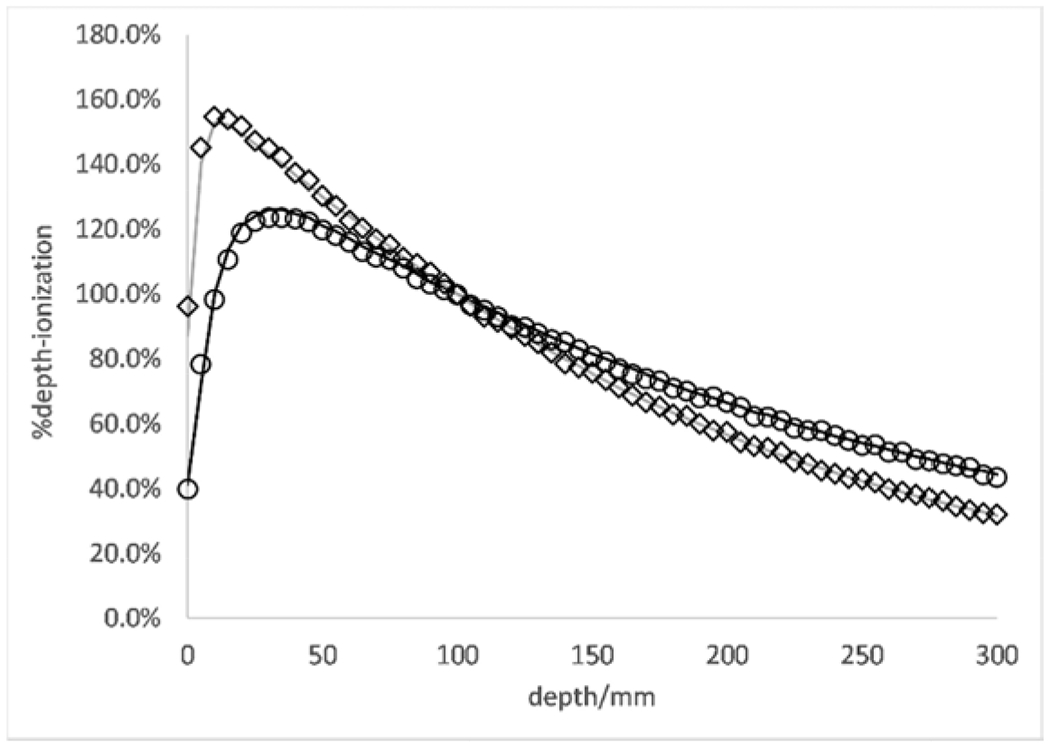
PDD curves for 6 MV (diamonds -- MCNP calculated; gray line -- measured) and 18 MV (circles -- MCNP calculated; black solid line -- measured) energies at a 10×10 cm² field size and 10 cm depth in water phantom.

Figure 5.

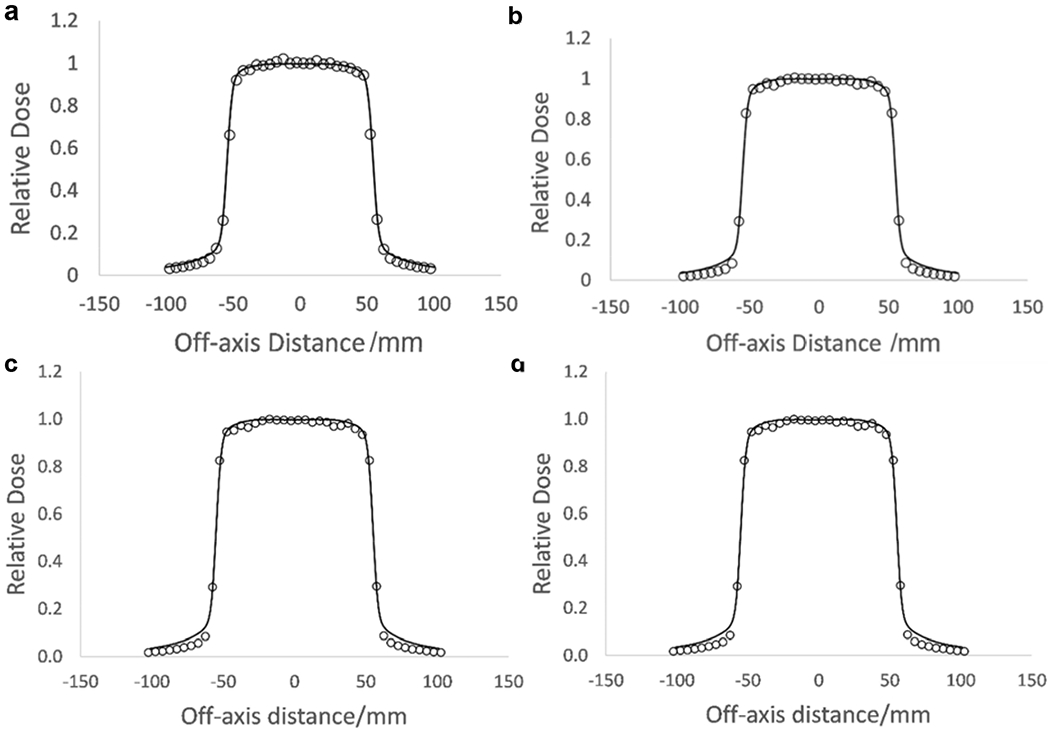
MCNP verified beam profiles for 6 MV and 18 MV energies at 10 cm depth, 10×10 cm² field size. a.) Inline profile for 6 MV. b.) Crossline profile for 6 MV. c.) Inline profile for 18 MV. d.) Crossline profile for 18 MV (circles -- MCNP calculated; black solid line -- measured).

Simulated and measured PDD curves were normalized to the measured values at a depth of 10 cm. There is an average 1.02% difference between measured and Monte Carlo generated PDDs for 18 MV. There is a fractional difference of 0.02-0.03 for the low dose region of the profiles and a fractional difference of 0.005 – 0.01 for the high dose low-gradient region for the 18 MV beam Inline and Crossline profiles. There is an average 1.07% difference between measured and Monte Carlo generated PDDs and a fractional difference of 0.01-0.03 between measured and simulated values in the high-dose low gradient region and a difference of 0.03-0.05 for the low dose region for Inline and Crossline profiles for 6 MV.

C. Experimental Measurement Compared with Monte Carlo Results

Tables 1 and 2 below show the comparison between measured and Monte Carlo DEFs, and comparison between Monte Carlo DEFs for simulations of the experimental setup and simulations in electronic equilibrium, respectively. A gold mass percentage of 1.3% for GNPs of 30 nm in diameter shows the highest DEF for both Monte Carlo and measured results. The 100 nm diameter GNPs showed an almost equivalent DEF to 30 nm GNPs at the same concentration (1% gold by mass). Since the measured DEF at 6 MV for the sample with the highest percentage of gold by mass (30 nm GNPs at 1.3% gold by mass) indicated no dose enhancement, no other samples with lower mass percentage of gold were measured at the 6 MV energy. The Monte Carlo simulations in full electronic equilibrium conditions showed very little difference in DEF when compared against results of the Monte Carlo simulations of the dose measurement apparatus. The highest concentration of gold (1.3% gold by mass) at 18 MV energy showed the largest difference between the two different types of simulations.

Table 1:

Simulation of Dose Measurement Apparatus vs Measured DEFs

18 MV
30 nm GNP diameter
Mass% Gold	Measured DEF	Monte Carlo DEF
1.3	1.0204± 0.0108	1.0215 ± 0.0013
1	1.0097 ± 0.0071	1.0094 ± 0.0009
100 nm GNP diameter
Mass% Gold	Measured DEF	Monte Carlo DEF
1	1.0099 ± 0.0054	1.0104 ± 0.0008
6 MV
30 nm GNP diameter
Mass% Gold	Measured DEF	Monte Carlo DEF
1.3	0.9979 ± 0.0044	1.0001 ± 0.0022

Table 2:

Monte Carlo Comparison: Simulated Measurement Apparatus vs Electronic Equilibrium Simulations

18 MV
30 nm GNP diameter
Mass% Gold	Monte Carlo DEF – Experimental Geometry	Monte Carlo DEF – Electronic Equilibrium	Percent Difference between means
1.3	1.0215 ± 0.0013	1.0203 ± 0.0004	0.12%
1	1.0094 ± 0.0009	1.0095 ± 0.0004	0.009%
100 nm GNP diameter
Mass% Gold	Monte Carlo DEF – Experimental Geometry	Monte Carlo DEF – Electronic Equilibrium	Percent Difference between means
1	1.0104 ± 0.0008	1.0111 ± 0.0004	0.07%
6 MV
30 nm GNP diameter
Mass% Gold	Monte Carlo DEF – Experimental Geometry	Monte Carlo DEF – Electronic Equilibrium	Percent Difference between means
1.3	1.0001 ± 0.0022	1.0004 ± 0.0019	0.03%

IV. Discussion

In this work, we present i. A novel method of measuring accurately the DEF for GNPs with very small spatial resolutions ranging from 0.138 × 0.138 × 0.138 μm³ to 0.502 × 0.502 × 0.502 pm using Monte Carlo methods and taking advantage of new features offered by MCNP version 6.2, ii. A novel and accurate method to measure the dose enhancement effect from different sizes and concentrations of GNPs using Monte Carlo methods at external beam energies, iii. An accurate picture of what the DEF from physical absorbed dose should look like for external beam energies, using simulations with the GNP solution in electronic equilibrium, which is difficult to achieve at external beam energies, and iv. A characterization method for measuring and estimating GNP dose enhancement for future in vitro and in vivo studies using external beam energies. A novel aspect of this work is the experimental method for measuring nanoparticle-induced macroscopic dose enhancement to a volume, which is based on commonly used EBT3 film, making it easily adoptable by other groups. A second novel aspect is in the side-by-side comparison between experiment and Monte Carlo simulations, which include the actual experimental geometry, measured beam parameters, and explicit modeling of the GNPs as nanosized spheres of gold. A third novel aspect is the direct experimental and computational comparison of two samples containing the same mass percentage of gold achieved with two different nanoparticle sizes at 18 MV energy. Lastly, the distinguishing aspects of the Monte Carlo model that presents a more accurate and detailed depiction of GNP dose enhancement effect are taking advantage of new features presented in MCNP version 6.2 by using a lower cutoff energy to catch dose deposited by secondary particles.

We show that generally, as the mass percent of gold in solution increases, the measured and computed DEF increases in the case of an 18 MV beam using 30 nm diameter GNPs. Monte Carlo results agree with measured results to within 0.3%, with the Monte Carlo results slightly overestimating the measured results between data sets. Uncertainties for each measurement and simulation at least overlap error bars or overlap the mean value itself of the corresponding simulation or measurement, showing good agreement between both measurements and simulation. The highest measured DEF was 1.0204 (2.04% dose enhancement). This value was measured for the 18 MV beam with the highest concentration of gold in solution tested (1.3% by mass). For the 6 MV beam with the same concentration of gold, the measured DEF was only 0.9979 (0% dose enhancement). This result is due to the increased amount of Compton effect present at 6 MV, which does not depend directly on the atomic number of the interacting medium, taking place when photons from the 6 MV beam interact with the GNPs in solution. The Compton effect is a function of the particle nature of light and occurs when a photon interacts with an outer shell electron and is scattered through some angle ejecting the electron who has an energy related to the scattering angle. The Compton effect dominates between 30 keV and 25 MeV, but decreases with an increase in energy, so it is very prevalent at 6 MV energy. The interaction probability per unit mass is proportional to Z/A, which is constant for everything but hydrogen, therefore, no dose enhancement effect is present for 6 MV due to the increased presence of Compton effect at this energy. Due to the increased amount of the pair production effect in an 18 MV beam when photons interact with the GNP solution, the DEFs are higher for 18 MV, since this effect directly depends on the atomic number of the medium the photons are interacting with. Results of this study indicate that dose enhancement can be predicted at a minimum GNP concentration of about 1% at 18 MV or higher energy. The concentrations of PEGylated GNPs used in this study are relatively non-cytotoxic, so they can potentially be utilized in future in vitro and in vivo applications as well as future clinical applications.^39–41 We note that although PEGylated GNPs were used in the dose measurement experiments, the PEG layer was not explicitly modeled in the simulations. Because our experimental and Monte Carlo results for DEF are in good agreement, we predict that the PEG layer will not significantly affect the DEF. This is consistent with the fact that PEG does not contain any high-Z elements which would enhance the dose. However, future specific studies that actually model the PEG layer with the GNPs macroscopically as well as microscopically are needed in order to determine the exact effect of PEG with GNPs on DEF.

Monte Carlo simulations of physical DEF which model the dose measurement apparatus show that this DEF measurement technique is an accurate representation of the macroscopic evaluation of the physical dose enhancement due to GNPs due to comparison with simulations in full electronic equilibrium conditions. Furthermore, we show that the method utilized to model the accelerator beam head and GNP solution using MCNP6.2 is accurate in reporting the correct physical DEF from GNPs, as the measured DEF matches the simulated Monte Carlo results to a 0.3% agreement at most. We note that in the real GNP solution, the spatial distribution of GNPs is random, not lattice-like as in our simulation. In addition, it could have some inhomogeneity due to aggregation of the GNPs. However, these differences do not appear to have a substantial effect on the macroscopic scale for DEF, as evidenced by the good agreement between simulation and experiment. Further studies on microscopic DEF are needed to determine any significant effect of the PEG layer on DEF. Zabihzadeh et al. studied the change in DEF calculated using Monte Carlo methods between cases in which the GNPs are arranged in an inhomogenous vs homogenous distribution.⁴² In this particular study, the authors report a larger percent difference in in-tumor average DEFs at lower energies when compared with those of higher energies in the kilovoltage range. Since an inhomogenous distribution of GNPs is a slightly more accurate representation of the GNP distribution inside an actual tumor, further studies on the effect of modeling the GNP distribution homogenously vs inhomogenously in the megavoltage energy range could potentially be useful. However, due to limitations of MCNP for modeling an accurate inhomogenous distribution of GNPs and the fact that the extremely small lattice size (due to the larger concentration of GNPs needed to produce dose enhancement at megavoltage energies) in this study limits the placement of GNPs in an inhomogenous distribution and therefore would predict similar dose enhancements to the homogenously distributed GNP case, we did not study this effect in the present study. Comparison of Monte Carlo simulated and measured DEFs for 100 nm GNPs vs 30 nm GNPs at the same mass percent show similar results for DEF, with only a maximum 0.05% difference between reported DEF values. This indicates that the DEF on a macroscopic scale depends on the mass percent of gold.

Our Monte Carlo results are consistent with Mesbahi et al.²⁶, who utilized MCNP to model a full linear accelerator head to determine DEFs for both 6 MV and 18 MV energies. Mesbahi et al. reported a DEF of 1.01 for 6 MV at concentrations of gold close to those used in the present study. Results for the 18 MV case were also similar to those in the present study, with Mesbahi et al. reporting a DEF of 1.02 at a similar concentration of GNPs. Spatial resolution used in MCNP by Mesbahi et al. was on the micrometer scale, with similar concentrations of GNPs to the present study. Comparing the DEFs tabulated in Mesbahi et al., reveals that the DEF shows a slight increase along with GNP size across multiple energy ranges, however the effect on DEF is negligible in most cases. It should be noted that in order to demonstrate dose enhancement does or does not take place in these cases, Monte Carlo simulations should be performed on the microscopic scale, such as in McMahon et al.⁴³, described later in this discussion. So in essence, Mesbahi et al. reports that the effect of GNP concentration on dose enhancement is very pronounced compared with any size effect. This result is consistent with the findings of the present study as well. More recently, Kakade et al.²⁴ used EGSnrc Monte Carlo code to estimate DEF inside a polymer gel dosimeter containing different concentrations of gold at 7 mg/g and 18 mg/g of gold when irradiated by x-rays of energy 100 kVp, 150 kVp, 6 MV and 15 MV. Authors of this study report the highest DEF occurring for the higher gold concentration at lower energies; however, at the higher energies of 6 MV and 15 MV, lower dose enhancement was reported, due to the higher probability of Compton effect for both of these energies. The DEF for these cases were both 1.01. This value is in approximate agreement with the present study, as we report a similar, close DEF for 6 MV. Concentration of GNPs in Kakade et al. were within the same order of magnitude as in the present study, however spatial resolution was not reported. When the energy is increased to 18 MV, as in the present study, we show DEF increases to approximately 1.02, which is also consistent with Kakade et al., since an increase in energy from 15 MV to 18 MV produces a higher DEF at the higher energy due to increased pair production at 18 MV. Cho et al.⁴⁴ carried out a Monte Carlo study using the EGS-based Monte Carlo code based on preclinical results from Hainfeld et al.⁴⁵ to determine the dose enhancement for the addition of GNPs to a tumor. Polyenergetic photon beams (140 kVp, 4 and 6 MV) and GNP concentration in water using a macroscopic approach were both varied. Cho et al. found that the dose enhancement with GNP irradiated by the 140 kVp photon beam was at least a factor of 2 for gold concentration equal to 7 mg-Au/g-water. He found that the DEF was 1.007 for 6 MV beam at a gold concentration of 7 mg Au/g water, which increased to a DEF of 1.015 for a gold concentration of 18 mg Au/g water in a 2.4 × 2.4 × 3.5 cm³ volume of solution, which is slightly larger than, but close to the solution volume used for the electronic equilibrium case simulations used in the present study. Therefore, the present study is comparable (with a DEF of 1.0111) with those reported by Cho et al., as we used a gold concentration of 13 mg/g, in between the two concentrations used by Cho et al.. Cho et al. also found that dose enhancement increased with gold concentration when the photon beam energy was constant. This result is also synonymous with results found in the present study. In the present study, for 18 MV, 30 nm GNP diameter, the DEF generally increases with increasing gold concentration in water. No voxel size for spatial resolution of GNPs were reported in Cho et al., however.

Past studies investigating the effects of high energy photons on the DEF microscopically show even greater DEF values immediately surrounding a single GNP. These microscopic studies, compared with macroscopic studies, such as the present study, normally predict much higher dose enhancement closer to a single nanoparticle, since the region of interest is smaller compared with that of a macroscopic study, such as the present one, where the spacing of the GNPs are much larger than the GNP diameter themselves, allowing the dose to be spread over a greater surrounding volume of water. Microscopic DEF studies for single GNPs are however important to review, since they provide insight in to underlying contributing factors to dose enhancement. They are also of importance for determining local effects of external beam radiation and the effect of GNP size on dose enhancement as well as determining the range of secondary products from the surface of the GNPs.^{12,43,46–48} Of these studies most relevant to the present study, McMahon et al⁴³ studied microdosimetric DEFs for higher energy photon beams of 6 MV and 15 MV. Particle shower calculations using Geant4 Monte Carlo kit were carried out for both energies and fully showered spectra were used as input into nanoscale simulations of 2 nm GNPs, allowing for full effects of secondary photons and electrons to be incorporated in reasonable time scales. This study reports maximum dose deposited around a single 2 nm GNP up to a distance of 300 nm, where a dose of 0.1 Gy is reported for dose deposited in water per ionization. This author also reports that single ionizations in a GNP have the potential to deposit very high doses in the surrounding water volume due to the cascade of low-energy secondary electrons generated following an ionizing event in gold. Jones et al. used EGSnrc and NOREC to quantify the radial dose distribution around a single GNP and found that microscopic dose increases up to a factor of 10 for 6 MV energies up to a distance of 1 μm from the surface of the GNP. At lower energies, Auger electrons contribute more to localized dose enhancement, but do not contribute significantly to local dose enhancement as much at higher energies.⁴⁹ Leung et al. used Geant4 to simulate the microscopic dose enhancement and behavior of secondary electrons around GNPs 2, 50, and 100 nm in diameter at a range of energies; for 6 MV irradiation they predicted microscopic DEFs up to a factor of 10; however, enhancements were much higher for lower-energy sources.⁵⁰ Berbeco et al. carried out Monte Carlo simulations using to study the microscopic dose enhancement due to GNPs under 6 MV irradiation in an endothelial cell model.⁵¹ They found microscopic DEFs of up to 2.2 in a single cell volume for local GNP concentrations of up to 50 mg/g. While these studies focus on the microscopic dose enhancement surrounding single GNPs and are aimed at characterizing potential therapeutic efficacy of a radiotherapy treatment using GNPs, for example, the present study focuses solely on the macroscopic dose enhancement from solutions of GNPs, which is useful to define a common experimental methodology to quantify the dose in the presence of GNPs in a medium. These two methods are in synergy and should be used together in determining optimal dose enhancing parameters in future in vitro and in vivo studies. The DEFs are normally much smaller overall for macroscopic studies, due to the fact that there is a larger volume of water surrounding the GNPs, so the dose from secondary electrons is spread out over a larger area overall compared with dose from secondary electrons in microscopic studies. Though it can be widely recognized that approaches adopted by McMahon and similar studies to simulate dose enhancement due to high-Z NPs is more accurate than the approach adopted in the present study, the Monte Carlo set-up in the present study stands as adequate to develop an experimental, dosimetric procedure to quantify physical dose due to a distribution of different sizes and concentrations of GNPs in a biological medium. Macroscopic dose enhancing effects of GNPs in this study could be used as a reference parameter when investigating dose-enhancement with radiobiological experiments and for nanoscale Monte Carlo simulations. Through macroscopic studies, such as the present study, combined with other current and future microscopic studies on dose enhancement, we gain insight into what the collective dose enhancing effects are for realistic concentrations of non-cytotoxic (PEGylated) GNPs once they become utilized clinically, what concentrations and sizes of GNPs would produce the greatest dose enhancing effect overall to a tumor, and most importantly, what energies to utilize in combination with other factors to maximize the effect of dose enhancement from GNPs in future in vitro and in vivo studies as well as for future practice. Especially in megavoltage radiotherapy, a microscopic study characterizing indirect and direct damage of radiation is important. Indirect damage of radiation is significant in the megavoltage energy range especially, and should be studied in more detail in future studies.

V. Conclusions

We have successfully shown that experimental GNP dose enhancement for external beam radiotherapy energies, a low energy and a high energy, can be accurately measured and simulated using a simple clinical set-up. DEFs simulated in the smaller, experimental volume correspond well with DEF simulated in electronic equilibrium conditions. DEFs obtained from Monte Carlo simulations containing GNPs modeled as an array are also within reasonable accuracy of measured DEFs. DEF was found to depend on the total mass percentage of gold present, not on the GNP size. This method of measurement and verification of physical GNP dose enhancement serves as a benchmark and guide for future in vitro and in vivo studies. Future work should look beyond the macroscopic to the microdosimetric nanoparticle-induced dose enhancement in order to gain more insight into the radiobiological effects of GNP dose enhancement with the same concentration and sizes of GNPs used in the present study.

Highlights.

• External beam radiation dose enhancement due to Au nanoparticles is characterized.

• Dose enhancement factor (DEF) is measured experimentally for 6 and 18 MV beams.

• DEF is calculated from MC simulations and is within ≤ 0.3% of experimental values.

• Simulations are performed for experimental and electronic equilibrium geometries.

• Effects of nanoparticle size and concentration and beam energy are assessed.