Abstract
Evidence suggests that emerging infectious diseases, such as COVID-19, originate from wildlife species, and that land-use change is an important pathway for pathogen transmission to humans. We first focus on zoonotic disease spillover and the rate at which primary human cases appear, demonstrating that a potential outbreak is directly related to the area of wildlife habitat. We then develop a model of the costs and benefits of land conversion that includes the effect of habitat size on the risk of disease outbreak. Our model and numerical simulations show that incorporating this risk requires more wildlife habitat conservation in the long run, and how much more should be conserved will depend on the initial habitat size. If the area is too small, then no conversion should take place. Any policy to control habitat loss, such as a tax imposed on the rents from converted land, should also vary with habitat area.
Keywords: COVID-19, Disease, Habitat conversion, Land use, Risk, Wildlife, Zoonosis
1. Introduction
Scientific consensus suggests that COVID-19 was transmitted to humans from wildlife (Rodriguez-Morales et al., 2020; Zhang et al., 2020). Any such disease that is transferred from animals to humans through direct contact or though food, water, and the environment is commonly referred to as a zoonosis. Nearly two thirds of emerging infectious diseases are zoonotic, and three-quarters of them originate in wildlife (Jones et al., 2008; Cunningham et al., 2017). Consequently, COVID-19 could be one of possibly many newly emerging zoonotic diseases that originate from a wild species.
There is growing evidence that land-use change is an important pathway for the transmission of zoonotic diseases from wildlife to humans (Cunningham et al., 2017; Faust et al., 2018; Gibb et al., 2020a and 2020b; Johnson et al., 2020; Shah et al., 2019; White and Razgour, 2020; Zohdy et al., 2019). Human activities that alter the landscape, such as land conversion and habitat fragmentation, increase the probability of animal–human interactions and thus disease transmission (Johnson et al., 2020). As noted by Zohdy et al. (2019, p. 399), “human land alteration continues to shift existing landscapes into island-like habitats with reduced area, increased isolation, and increased ratios of edge habitat to total area.” Studies also show that “deforestation resulting in crop monocultures is particularly problematic for elevating infection risks in susceptible nearby populations” (Shah et al., 2019, p.7). All of these effects of wildlife habitat loss and fragmentation increase interactions between wildlife and humans, and thus the risk of spillover of zoonotic disease (Borremans et al., 2019; Faust et al., 2018; Gibbs et al., 2020b; Johnson et al., 2020; White and Razgour 2020; Wilkinson et al., 2018; Zohdy et al., 2019). Even diseases transmitted by bats – the suspected wildlife source of COVID-19 – are associated with increased habitat loss and human-wildlife interactions (Olival et al., 2017). As the biologist Thomas Lovejoy has noted, “This pandemic is the consequence of our persistent and excessive intrusion in nature.“1
Only recently have models of infectious disease began incorporating land conversion leading to the possible spillover of disease and pathogens from wildlife to humans (Faust et al., 2018; Wilkinson et al., 2018). Economists are beginning to approach these issues by examining the pathways through which human interactions with the environment spread zoonotic diseases (Albers et al., 2020), exploring the role of animal farming and meat consumption in the emergence and amplification of infectious diseases (Espinosa et al., 2020), and modeling the relation between biodiversity loss and zoonotic pandemic risks (Augeraud-Véron et al., 2021).
The following paper develops an economic model of the costs and benefits of habitat conversion that also includes the risk of a zoonosis disease outbreak due to transmission from wildlife to humans. To do this, the paper focuses on a specific region with an initially given wildlife habitat area and human population. The paper therefore develops a model of optimal habitat conversion that also includes the risk of an initial zoonosis disease outbreak due to transmission from wildlife to humans in the same region that the habitat conversion takes place. Thus, the planner must take into account both the normal cost and benefits associated with converting wildlife habitat (e.g. benefits of conversion to agriculture or the ecosystem benefits associated with preserving wildlife habitat) as well as the risk that smaller habitat will increase the risk of establishing primary cases of infection in the human population and the disutility if this disease outbreak occurs.
The model is developed in two stages. Using basic principles of dynamic models of a zoonosis disease spillover to humans (Begon et al., 2002; Davis et al., 2005; Lloyd-Smith et al., 2009), we first establish how wildlife-human transmission can be affected by the size of the habitat area occupied by the wildlife population carrying the pathogen. It follows that declining habitat area increases the rate of contact between humans and infected wildlife, influences the expected occurrence of a primary case of infection among humans, and thus determines whether a disease outbreak among humans occurs. Consequently, efficient and optimal conversion of the habitat must take into account any impacts on the risks of an outbreak occurring.
To illustrate this, we next develop a model of converting wildlife habitat into land that is valued as an input into commercially marketed activities while the remaining habitat yields wider environmental benefits (e.g. biodiversity, recreation and tourism values and a wide range of ecosystem services). Our approach is related to models of optimal habitat conversion among competing uses, such as conservation as opposed to development (Barbier, 2011; Barbier and Burgess 1997; Bulte and Horan 2003; Hartwick et al., 2001; Skonhoft, 1999). However, we extend such an approach so that allocating natural habitat across competing uses must also take into account the potential risk of a zoonosis disease outbreak as wildlife habitat declines. If the social disutility from a disease outbreak caused by wildlife habitat loss is extremely high compared to the benefits from conversion, then no conversion should take place and the initial wildlife habitat area should be preserved indefinitely. But even if some habitat conversion is optimal, the decision to convert must include a risk premium for the threat of an outbreak, which is impacted by the size of the remaining habitat area, the adverse impact of loss of habitat on the likelihood of the disease outbreak, and the negative value associated with an increase in the risk that a zoonosis disease outbreak occurs. Compared to this case where no account is taken of the impact of wildlife habitat loss on the risk of disease outbreak, more wildlife habitat will therefore be conserved.
These outcomes are captured in a numerical simulation. The scenarios confirm that accounting for the impact of wildlife habitat loss on the risk of disease outbreak ensures that more wildlife habitat will be conserved in the long run. However, because this risk is inversely impacted by habitat size, proportionately more of the habitat is conserved if the initial habitat area is smaller. If the area is too small, then no conversion should take place. We also show that any policy to control habitat conversion, such as a tax imposed on the rents from converted land, should vary with habitat area.
Our theoretical and numerical results have important policy implications. As long as there is significant risk of a zoonosis disease outbreak due to wildlife habitat loss, then more habitat needs to be conserved than in the case where that risk is insignificant or does not exist. How much more should be conserved will depend on the size of the habitat area, which confirms the concern that many zoonosis disease experts have over how land conversion is leading to the fragmentation of larger wildlife habitats into island-like habitats with reduced area, increased isolation, and increased ratios of edge habitat to other areas occupied by humans (Borremans et al., 2019; Faust et al., 2018; Johnson et al., 2020; White and Razgour 2020; Wilkinson et al., 2018; Zohdy et al., 2019). Control and regulation of converting wildlife habitat is essential, if there is a significant risk of zoonosis disease outbreak.
2. Zoonosis disease outbreak
We begin by developing a general model of a zoonosis disease transmission from wildlife to humans, which incorporate the basic dynamics of the process that could lead to the potential establishment of a large number of primary cases among humans (Begon et al., 2002; Davis et al., 2005; Lloyd-Smith et al., 2009). We therefore focus on the relationship between transmission from a wildlife reservoir to a human population and the rate at which primary human cases appear, which in the context of this model is what is meant as a zoonotic disease outbreak. We then show how such a potential outbreak is directly related to the area of wildlife habitat. Our context is the risk of a single zoonosis disease spillover from wildlife to humans. As pointed out by Lo Iacono et al. (2016), single spillover events are most likely the cause of the global SARS outbreak, the swine influenza pandemic, and the Ebola epidemic, and as noted in the Introduction, the most likely cause of the COVID-19 pandemic.
Let N be a human population of fixed size located in a region containing a wildlife habitat. In this population, there are a number of individuals susceptible to infection by a zoonosis disease spillover from a wildlife reservoir. In the case of a zoonosis, which is a disease that can be transmitted from animals to humans, the source of the initial infection of the human population is a wildlife reservoir. This reservoir is the population of wildlife W, some of which are carrying the pathogen that can infect the neighboring human population.
Following Davis et al. (2005) and Lloyd-Smith et al. (2009), the force of the infection of the zoonosis on humans is a per capita rate determined multiplicatively by three factors: i) the number of contacts between humans and the wildlife population over some time period, ii) the probability that the contact is with an infected wildlife; and iii) the probability that transmission actually occurs given that contact has occurred.
Davis et al. (2005) assume that contacts between humans and infected wildlife increase with the abundance of the wildlife population, in terms of numbers or density. Here, we assume the latter. Denoting A as the size of the habitat area occupied by the wildlife population carrying the pathogen, then the rate of contact between humans and an infected animal is likely to increase proportionately with the wildlife population density, i.e. . The probability that the contact is with an infected wildlife is thought to be a function of the size of the wildlife population (Begon et al., 2002; Davis et al., 2005; Lo Iacono et al., 2016); consequently, we denote the likelihood of such contact as . A common assumption is that the number of infected wildlife is constant, or if increasing, the rate is less than the increase in the wildlife population W (Begon et al., 2002). If this is the case, then the likelihood that contact is with an infected wildlife ω declines with W. For simplicity, we specify this probability as .
Thus, the force of an infection on humans from the zoonosis is
| (1) |
where the parameter β is the transmission coefficient, which in this context represents the transmission from a wildlife reservoir to a human population (Davis et al., 2005). It is the rate at which primary human cases appear. As equation (1) indicates, the force of infection and thus the transmission of the disease from wildlife to humans declines with the size of the wildlife habitat.
For any zoonotic disease that spills over from wildlife, there is a relationship between wildlife-human transmission and the rate at which primary human cases appear (Davis et al., 2005). This relationship determines in turn the number of primary cases X of this disease that emerge initially in the human population. However, at this stage, the pathogen may die out quickly because of “stuttering transmission” from the initial person or persons infected and other susceptible humans, or alternatively, there can be “sustained transmission” between the first person or persons infected and other humans so that a large pool of X is created (Lloyd-Smith et al., 2009; Lo Iaocono et al., 2016). Both of these outcomes, which do depend on the transmission from wildlife to humans, occur before the “final stage” of human-to-human transmission, “when a pathogen gains the ability to transmit effectively between humans and no longer requires zoonotic transmission” (Lo Iacono et al., 2016, p. 2).
In the first case of “stuttering transmission”, the rate at which primary human cases occur is relatively small, and so eventually the number of primary cases disappear. Examples of this type of zoonotic disease are monkey pox virus, leishmaniasis and Lassa fever. In the second case of “sustained transmission”, the rate at which primary human cases appear is relatively large, and the number of primary cases can grow to be quite sizable. Examples of this type of pathogen include Yersinia pestis (plague), pandemic influenza (including swine flu and SARS), Ebola, HIV-1, and of course now COVID-19. But there is also a third type of zoonosis, in which transmission from wildlife to humans occur to create primary infections but there is no human-to-human transmission involved (Lloyd-Smith et al., 2009). Examples include the West Nile virus, malaria and other mosquito-carrying pathogens, Lyme or other tick-borne diseases and brucellosis.
We start by modeling the first two cases, where the relationship between transmission of the pathogen from wildlife to a human population and the rate at which primary human cases appear is also influenced by contact between the initial person or persons infected and other humans.
From equation (1), suppose that initially the entire population is susceptible to the new disease and at least one individual is infected at expected occurrence , where are the sufficient number of susceptible individuals that allow this to happen. It follows that is very small and . This means that all the contacts of the person or persons initially infected by the zoonosis are with susceptible people. If this initial pool , while still infected, has κ expected number of contacts with others and the probability that the contact results in transmission is α, then the pathogen is passed to susceptible individuals per unit of time. A common assumption is that the average duration of infection can be represented as , where is the rate of recovery of an individual from the infection. It follows that the basic rate at which primary cases appear in the human population is
| (2) |
where we make use of that fact that, for a large population, . The parameter φ can be interpreted as a modified transmission coefficient, in that it represents the transmission of the disease from the wildlife reservoir to the initially infected person or persons and then to other susceptible humans that together comprise the entire pool of primary cases. The rate at which primary cases occur varies inversely with the size of the remaining wildlife habitat A. A smaller habitat size increases the expected occurrence of initial infection among humans, and this is likely to result in more primary cases appearing in the population through a higher .
In the third case, transmission from wildlife to humans creates primary infections but without any human-to-human transmission occurring. Now a large share of the human population is potentially susceptible to infection via wildlife contact, and represents that share. The rate at which primary cases appear is
| (3) |
Using a dot over a variable to denote the change in that variable with respect to time, whether there is an increase or decline in the number of primary cases can now be denoted as
| (4) |
where is determined by either (2) or (3) depending on the type of zoonotic disease. As is clear from (4), how many primary cases are established among humans depends on the rate at which primary cases emerge. It has a threshold value , in that if the number of primary cases increases at rate until a maximum number of primary cases is reached.2 In comparison, if then no additional primary cases are created, and if the disease will eventually die out among humans. Consequently, if , a smaller wildlife habitat area A will cause to fall, and if A continues to decline, it is more likely that the threshold value is exceeded and thus a disease outbreak among humans occurs.
Conditions (2)–(4) allow the threshold value for K 0 to be expressed in terms of the area of natural habitat A. That is, implies that , which will henceforth be denoted as a habitat of size . Consequently, whether or not any zoonosis spillover results in a sustained number of primary cases among the human population depends on
| (5) |
It follows from (5) that a zoonosis spillover will result in a disease outbreak in humans if wildlife habitat area falls below the threshold size . From (4), primary cases among humans will increase until the maximum number is reached. For zoonotic diseases that do involve human-to-human transmission, only primary cases of infections are created (see equation (3)). However, for other zoonotic diseases, the establishment of primary cases through wildlife-human transmission is not the end of the story. Instead, some pathogens could enter into the “final stage” where only transmission among humans occurs (La Lo Iacono et al., 2016). Once this stage is reached, and disease transmission takes place solely through human-to-human contact, standard disease models that employ the basic reproductive rate R 0 apply and can determine how the creation of secondary from primary human cases causes any additional spread of the infection among the population (Cobey, 2020; Diekmann and Heesterbeek 2000; Hethcote 2009; van den Driessche 2017).3
In sum, the relationship between transmission from a wildlife reservoir to a human population and the rate at which primary human cases appear can influence whether a zoonotic disease outbreak occurs. Moreover, such a potential outbreak is directly related to the area of wildlife habitat. It follows that efficient and optimal conversion of the habitat should take into account any impacts on the risks of an outbreak occurring. As we shall see next, this is especially important when the threshold habitat size A z that might trigger such an outbreak is unknown, which is often the case.
3. Habitat conversion and the risk of disease outbreak
Most habitat loss occurs through its conversion into land that is valued as an input into commercially marketed activities, such as agriculture, forestry, mining, residential and commercial real estate, and so forth. This implies that any remaining habitat has potential value as a “reserve” to be converted for commercial land. At the same time, wildlife habitat yields many additional benefits, such as biodiversity, recreation and tourism values and a wide range of ecosystem services. However, allocating natural habitat across these competing uses must also take into account the potential risk of a zoonosis disease outbreak as wildlife habitat declines.
As condition (5) indicates, this risk is a real threat due to habitat conversion. Such conversion ensures that any given wildlife habitat area could decline over time and could eventually converge to its threshold habitat size A z. If that happens, then as (5) shows there might be some future time period t z in which . The following model takes into account this risk, along with the competing land uses for wildlife habitat.
Let the initial wildlife habitat area be denoted as . Define as the cumulative amount of habitat converted by economic activity up to time t. The remaining area at time t is therefore , and it follows that
| (6) |
We represent the two competing economic uses for habitat as follows. Conversion of habitat yields land for commercially marketed activities, such as agriculture, real estate, forestry, mining, etc. At any time t, land rents obtained from this converted habitat are , whereas the ecosystem, biodiversity and other environmental benefits of the remaining habitat are . The functions and are strictly concave. The costs of converting wildlife habitat to developed land are , and are strictly convex for . Consequently, the net benefit flow from allocating wildlife habitat between these two uses at time t is .
Although there may be awareness that loss of wildlife habitat could potentially cause a zoonosis disease outbreak if the area falls to A z, it is unlikely that this threshold level of habitat is known in advance. Since A z is unknown, then the time of the disease outbreak occurring t z is a random variable. Nonetheless, the likelihood of an outbreak can be characterized by a hazard rate function that specifies the probability that the disease outbreak occurs at any time t, given that it has not yet occurred at that time. But as long as habitat conversion takes place at time t, then will be declining and the likelihood of an outbreak rises. This suggests that the likelihood of the disease outbreak occurring at any time t, given that it has not yet happened, increases as falls. Finally, if the disease outbreak does occur because converges to A z, there will be considerable social disutility of absolute value associated with this outbreak. For analytical convenience, we assume that this social disutility is invariant with respect to time, and is net of any benefits associated with the remaining habitat.
Let be the probability of a zoonosis disease outbreak occurring by time t, and is the associated probability density function. It follows that the hazard rate function denoting the likelihood of the outbreak occurring at time t given that it has not yet happened can be specified as . Rearranging yields
| (7) |
It follows that the probability that the outbreak will occur at t is . Finally, the likelihood of the disease outbreak occurring as represented by in (7) depends inversely on the size of the remaining wildlife habitat area . Consequently,
| (8) |
Expected social welfare up to the unknown time of the outbreak t z is
| (9) |
Choosing optimal conversion to maximize (9) is a stochastic problem. However, it can be transformed into an analogous deterministic problem by adapting the approach of Kamien and Schwartz (1991, pp. 62–63 and 190–194).
As is the probability of a zoonosis disease outbreak not occurring by time t, the expected discounted social welfare for the case when the disease outbreak has not yet occurred over some time period [0,T] is
| (10) |
where is the welfare gained from the remaining of natural habitat if there is no disease outbreak by time T.
If the disease outbreak does occur at some time then expected disutility from the outbreak is , where and thus . Integrating by parts this expression yields
| (11) |
Putting (10) and (11) together, using and allowing , (9) becomes
| (12) |
Discounted social welfare as represented by (12) can be maximized with respect to choice of subject to (6) and (7) and the standard transversality conditions. Note, however, that if the social disutility from a disease outbreak is extremely high relative to the benefits from habitat conversion, then and the wildlife habitat should be conserved indefinitely at its initial size A 0.
The current - value Hamiltonian of the problem is
| (13) |
The co-state variable is the shadow value of an additional unit of the remaining wildlife habitat, conditional on the outbreak not yet occurring at time t. Differentiating yields . The co-state variable γ2 is defined as , where is the value of the remaining wildlife habitat at time t corresponding to the optimal solution J∗ of (12). As an additional unit of Γ represents an increase in the risk that an outbreak occurs, then γ2 is the negative of the expected present value at time t of the remaining optimally managed habitat, given that the outbreak has not yet happened.
The first-order conditions for maximization are
| (14) |
| (15) |
| (16) |
Rearranging (16) yields
| (17) |
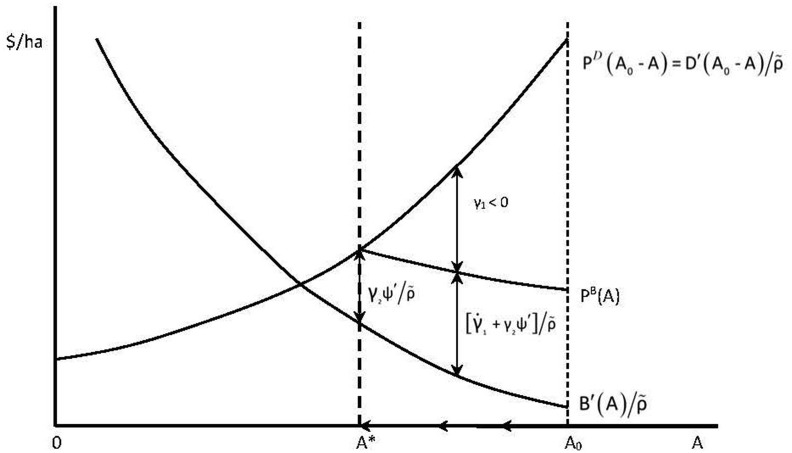
Condition (17) is negative, as by definition . Any change in the costate variable over time must be less than the net benefit of holding onto wildlife habitat at time t as represented by . Both of the values on the right-hand side of (17) are adjusted by the effective discount rate , which includes the risk premium for the threat of an outbreak . Note that this premium indicates that the effective discount rate rises as more habitat is converted over time. Thus, (17) implies that but gets progressively smaller and converges toward zero for along the optimal path.
| (18) |
Condition (18) states that, along the optimal path, the returns from the two competing uses of the wildlife habitat must be equal. The net marginal rents from development are balanced by the marginal benefits of holding onto the wildlife habitat . These benefits include the impact on the likelihood of a zoonosis disease outbreak of the size of the remaining habitat . The latter impact is positive, implying that one would want to hold onto more wildlife habitat because it reduces the risk of an outbreak occurring. This additional benefit of holding onto wildlife habitat suggests that, along the optimal path, more wildlife habitat should be preserved compared to the case where there is no impact of habitat loss on the likelihood of the disease outbreak, i.e. condition (8) does not apply and
Condition (18) can be expressed in terms of capitalized land values at any time t along the optimal path:
| (19) |
The difference between the capitalized marginal value of converted land and the capitalized value of remaining wildlife habitat is the marginal cost of converting habitat . Note that both capitalized values are lowered by the risk premium due to the threat of a disease outbreak . In addition, the capitalized value of remaining wildlife habitat reflects the impact of conversion and thus the loss of habitat on increasing the likelihood of an outbreak . Each capitalized land use value can also be denoted as respective “prices” of the two types of land, or and respectively. The result is that the difference in land prices between converted and remaining habitat is smaller compared to the case where habitat size does not impact the risk of an outbreak and thus .
The optimal path of habitat conversion must therefore satisfy (6), (7), (17) and (19), as well as the transversality conditions subject to the outbreak not occurring by this limit. A steady state for wildlife habitat is obtained by setting . Suppose that this steady state A∗ occurs at some time , subject to this outbreak not yet happening. It follows from (6), (14) that and , and the hazard rate specified in (8) is constant . Thus A∗ is uniquely determined by the equation
| (20) |
where and . Provided that and , then and at least some habitat conversion will take place initially.
Suppose that initial wildlife habitat area is large . Developed land converted from habitat is relatively scarce compared to wildlife habitat, and thus in (19), the marginal land rents are relatively large. Abundant wildlife habitat in turn also means that its marginal environmental benefits are low, and more importantly, so is the risk premium associated with the threat of a disease outbreak and the marginal change in this risk due to declining habitat . Consequently, the gap between capitalized values, and thus land prices and , is initially wide and optimal habitat conversion should start out high.
However, as wildlife habitat conversion proceeds along the transition path to the steady state defined by (20), marginal rents from converted habitat start to fall, whereas the loss of habitat means that will rise. Consequently, optimal habitat conversion is initially large but falls over time, as the difference in land capitalized land values begins to disappear. From (14), along the transition path, the marginal value of an additional unit of habitat is negative but rising over time, i.e. and . The implication is that, given that , along the optimal path until the steady state (20) is reached, declines, continues rising and is falling.4 This outcome for the optimal wildlife habitat conversion path with a risk of disease outbreak is depicted in Fig. 1 .
Fig. 1.
Optimal wildlife habitat conversion with the risk of disease outbreak.
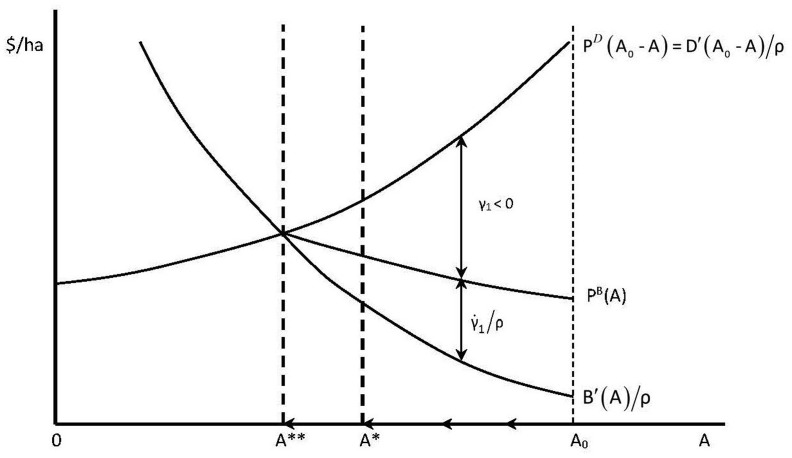
It is instructive to compare this outcome to the case where there is no risk of disease outbreak if conversion of wildlife habitat takes place, i.e. . Conditions (19) and (20) become
| (21) |
| (22) |
Provided that and , then and at least some habitat conversion will take place initially. If the wildlife habitat is initially large so that , then optimal conversion will start large, decline over time, and converge to zero at the steady state defined by (22). Along this transition path, the marginal value of an additional unit of habitat is negative but rising over time, i.e. and .5 However, since there is no risk premium associated with habitat conversion as , more habitat will be converted in the long run, i.e. . This outcome is depicted in Fig. 2 .
Fig. 2.
Optimal wildlife habitat conversion with no risk of disease outbreak.
To summarize, even though wildlife habitat may have considerable value if it is converted for land used in commercially marketed activities, such as agriculture, forestry, mining, residential and commercial real estate, and so forth, converting habitat for such uses should take into account the potential risk of a zoonosis disease outbreak as wildlife habitat declines. If the social disutility from a disease outbreak caused by wildlife habitat loss is extremely high compared to the benefits from conversion, then no conversion should take place and the initial wildlife habitat area A 0 should be preserved indefinitely (see (12)). However, even if some habitat conversion is optimal, the decision to convert must include a risk premium for the threat of an outbreak , which is impacted by the size of the remaining habitat area, the adverse impact of loss of habitat on the likelihood of the disease outbreak , and the negative value associated with an increase in the risk that an zoonosis disease outbreak occurs . Compared to this case where no account is taken of the impact of wildlife habitat loss on the risk of disease outbreak, more wildlife habitat will therefore be conserved, i.e. .
4. Numerical results
Comparison of outcomes (19) and (20) with conditions (21) and (22) provides additional insights into how the risk of disease outbreak impacts optimal wildlife habitat in the long run. The comparison focuses on how these long-run outcomes differ if the initial size of the wildlife habitat varies, and the resulting divergence in the marginal rents from converted habitat. The latter allows calculation of a possible tax on these rents. Our approach to this analysis is through numerical simulation, as the general expressions (19)–(22) are not very tractable. The Appendix specifies the functional forms and key relationships underlying this simulation.
Table 1 reports the key numerical results from the simulation of the long-run wildlife habitat size where there is a risk of a disease outbreak A∗ as opposed to the outcome A∗∗ where there is no such risk. The simulation is conducted for several different levels of initial habitat area A 0, specified in square kilometers (km2). The largest initial area is 30,000 km2 (about the size of Belgium) and the smallest is 500 km2 (around the land area of Guam).
Table 1.
Effects of the risk of a disease outbreak on long-run wildlife habitat.
| Parameter values: σz = 10,000 ρ = 0.04 ψ0 = 0.01 a (A0) = a bD (A0) = bD 1 – bBA0 = 0 for A0 = 2500 | |||||||
|---|---|---|---|---|---|---|---|
|
Scenario Estimates | |||||||
| Initial habitat (km2), A0 | Final habitat, without risk, A∗∗ | Final habitat with risk, A∗ | Ratio A∗/A∗∗ | Marginal rents from converted habitat D′ (A0-A∗∗) | Marginal rents from converted habitat D′ (A0-A∗) | Tax adjustment 1 + τ | Tax rate τ |
| 500 | 83 | 497 | 6.0 | 0.87 | 1.00 | 1.15 | 15.3% |
| 1000 | 175 | 857 | 4.9 | 0.82 | 0.97 | 1.18 | 17.6% |
| 2500 | 500 | 2000 | 4.0 | 0.80 | 0.95 | 1.19 | 18.8% |
| 4000 | 863 | 3209 | 3.7 | 0.78 | 0.95 | 1.21 | 20.6% |
| 10,000 | 2233 | 7920 | 3.5 | 0.78 | 0.94 | 1.21 | 21.1% |
| 15,000 | 3462 | 11,990 | 3.5 | 0.77 | 0.94 | 1.22 | 22.2% |
| 30,000 | 7358 | 24,554 | 3.3 | 0.75 | 0.94 | 1.25 | 24.7% |
Notes: Marginal rents are in $1000 per km2.
To give an indication of the comparative size of each initial habitat area A 0, they can be related to the approximate land size of selected countries. For example, the land area of Guam is 544 km2, São Tomé and Principe 964 km2, Luxembourg 2586 km2, Cape Verde 4033 km2, Lebanon 10,230 km2, Timor-Leste 14,919 km2 and Belgium 30,278 km2.
The results of the numerical simulation confirm that incorporating the impacts of wildlife habitat conversion on the risk of a disease outbreak leads to more habitat conservation in the long run (see Table 1 ). Moreover, the difference between A∗ and A∗∗is greater for a smaller initial habitat size. When A 0 is 15,000 to 30,000 km2, A∗ is 3.5 to 3.3 times A∗∗. However, when initial habitat size is only 2500 km2 (ca. the land area of Luxembourg) the ratio of A∗ to A∗∗rises to four, and when A 0 is only 500 km2, the ratio is six. This outcome is directly related to the risk premium for the threat of an outbreak , which is adversely impacted by the size of the remaining habitat area, as well as the negative value associated with an increase in the risk that a zoonosis disease outbreak occurs . When initial habitat area is already small, these effects mean that the likelihood of a disease outbreak is already great, and so even less conversion should take place compared to the case when there is no such risk.
In fact, the simulation results suggest that, when initial wildlife habitat area is only 500 km2, very little conversion should be allowed, as A∗ is 497 km2. Based on the given parameter values, the simulation implies that 500 km2 is a threshold level of wildlife habitat size. For any initial wildlife habitat area A 0 below this threshold, the social disutility from a disease outbreak caused by habitat loss is too high relative to the benefits from conversion. Instead, the wildlife habitat should be conserved indefinitely at its initial size A 0, as condition (12) indicates.
The simulation also allows estimation of a possible tax imposed on the marginal rents from converted habitat in the long run to account for the additional risk of a disease outbreak. As more habitat is converted in the long run when there is no risk of a disease outbreak, marginal converted land rents will be lower compared to the rents when there is a risk. As can be seen from Table 1, this difference in rents varies depending on initial wildlife habitat area. Consequently, the tax rate also varies with A 0. When initial wildlife habitat is 10,000 to 30,000 km2, the tax rate is 21–25%. However, for A 0 of 2500 km2, the rate is almost 19%, and for 500 km2 it falls to 15%.
In sum, the simulation scenarios confirm that taking into account the impact of wildlife habitat loss on the risk of disease outbreak ensures that more wildlife habitat will be conserved in the long run, i.e. . However, because this risk rises inversely with habitat size, this difference between A∗ and A∗∗ increases significantly for smaller initial wildlife habitat. If the area is too small, then no conversion should take place. Based on the parameters of this simulation, this threshold size is around 500 km2. Equally, the tax rate imposed on marginal rents from converted land also falls with diminished habitat size. Of course, these numerical results are sensitive to the parameters chosen, which in this instance appear to suggest a high impact of habitat loss on the likelihood of disease outbreak. But the general results should hold regardless of the parameter values chosen: the risk of disease outbreak requires more wildlife habitat conservation in the long run, and how much more should be conserved will depend on the size of the habitat area. It follows that any tax rate imposed on the rents from converted land should also depend on habitat area.
5. Further research
For analytical convenience, we have focused here on habitat conversion and its effect on the likelihood of a zoonotic disease transmission and outbreak. Other human-wildlife interactions, such as hunting and capturing wildlife for trade and meat production, are not explicitly modelled even though they are important transmission channels (Borsky et al., 2020; Espinosa et al., 2020). As Borsky et al. (2020) show, making trade requirements more stringent leads to a decrease in the number of animals traded, and as a result, the number of zoonotic diseases that are transmitted. However, reduced habitat area could limit the effectiveness of such trade restrictions, as habitat conversion could instead lead to greater hunting or capturing intensity, and therefore also impact the risk of a zoonotic disease outbreak. Similarly, wildlife populations and the number of wildlife infected with a potentially zoonotic disease transmitted to humans could vary non-linearly with changes in wildlife habitat, due to a range of local ecological factors (Gibb et al., 2020b). This could also influence greatly how habitat conversion impacts the transmission of disease from wildlife to humans, and thus the risk of a disease outbreak.
The model of this paper examines the risk of an initial disease outbreak among the neighboring human population from the conversion of wildlife habitat in the region. It does not include the probability that the disease outbreak could lead to a pandemic, which is by definition a global phenomenon involving disease spread to multiple regions and populations. In addition, as the emphasis is on an initial disease outbreak, the model here considers only the disutility associated with this event possibly happening at some time in the future. Intuitively, this disutility reflects the dislike of a disease outbreak occurring among the population, and does not include aversion as to how severe or deadly it might become once the disease spreads among the human population of the region. A more complete model might include these additional features to determine optimal habitat conversion, and possibly include it in a general equilibrium framework (Augeraud-Véron et al., 2021).
Similarly, as the recent zoonosis disease outbreaks have shown - the global SARS outbreak, the swine influenza pandemic, the Ebola crisis, and now the COVID-19 pandemic – local land-use change as a cause of potential new zoonosis is a global concern (Córdoba-Aguilar et al., 2021; Gibb et al., 2020a). In an analysis of 6801 ecological assemblages and 376 host species worldwide, Gibb et al. (2020b, p. 398) find that “known wildlife hosts of human-shared pathogens and parasites overall comprise a greater proportion of local species richness (18–72% higher) and total abundance (21–144% higher) in sites under substantial human use (secondary, agricultural and urban ecosystems) compared with nearby undisturbed habitats.” The implication is that policies to control land conversion in one region to reduce the risk of disease outbreak locally could also reduce disease spread to multiple regions and populations. These potential multi-regional and global benefits of reducing zoonosis risk from a country or region need to be considered in the design of both domestic and global policies to control land conversion in a region. For example, Dobson et al. (2020) estimate that direct forest-protection payments to host countries to reduce deforestation totaling $9.6 billion per year could achieve a 40% reduction in areas at highest risk for virus spillover. However, they also maintain that the same outcome could be achieved for only $1.5 billion annually if countries adopt domestic policies that remove subsidies favoring deforestation, restricting private land clearing, and supporting territorial rights of indigenous peoples. Others suggest the need for more adaptive, ecosystem-based interventions to help manage zoonotic hazards and risks across multiple policy jurisdictions, and developing early-warning surveillance and control measures for particular global “hot spot” locations and reservoirs threatened by land-use change (Córdoba-Aguilar et al., 2021; Gibb et al., 2020a; White and Razgour 2020).
Finally, models of infectious disease that incorporate the impact of land conversion on the spillover of a zoonotic disease from wildlife to humans are beginning to allow for spatial aspects of this spillover effect (Albers et al., 2020; Faust et al., 2018; Wilkinson et al., 2018). This is especially important to analyze the consequences of habitat fragmentation across landscapes for the risk of a zoonotic disease outbreak. Future research could involve extensions of the model developed in this paper to explore further the spatial spillover effects of habitat fragmentation and increased ratios of edge habitat to other areas occupied by humans (Borremans et al., 2019). In a spatially explicit model of habitat conversion with a risk of zoonotic disease outbreak, optimization would not only have to determine the time path of the overall quantity of land conversion but also the optimal locations for habitat conversion. Such modeling approaches should also be extended to evaluate how future climate and land change scenarios may affect geographic trends in zoonotic hazard for multiple zoonoses (Gibb et al., 2020a).
6. Conclusion
Increasing evidence suggests that emerging infectious diseases, such as COVID-19, originate from wildlife species, and that land-use change is an important pathway for the transmission of zoonotic diseases from wildlife to humans (Cunningham et al., 2017; Faust et al., 2018; Gibb et al. 2020a, 2020b; Johnson et al., 2020; Olival et al., 2017; Shah et al., 2019; White and Razgour 2020; Zohdy et al., 2019). To explore the problem further, this paper develops an economic model of the costs and benefits of habitat conversion that also includes the risk of a zoonosis disease outbreak due to transmission from wildlife to humans. Several results emerge from our theoretical and numerical analysis.
First, we demonstrate that a smaller wildlife habitat leads to more contact between humans and wildlife carrying the pathogen, increases the rate at which primary cases emerge among humans, and thus ensures that an outbreak is more likely. Both the model and the simulation scenarios of this paper confirm that taking into account the impact of wildlife habitat loss on the risk of disease outbreak ensures that more wildlife habitat should be conserved in the long run, compared to when this risk is ignored. Consequently, efficient and optimal conversion of the habitat must take into account any impacts on the risks of an outbreak occurring.
Second, the risk of a zoonotic disease outbreak requires more wildlife habitat conservation, and how much more should be conserved will depend on the size of the habitat area. Because the risk varies inversely with habitat size, less conversion occurs if the initial habitat size is smaller as opposed to larger. If the area is too small, then no conversion should take place, because the risk of disease outbreak is too great. For example, based on the parameters of the simulation conducted in this paper, this threshold size is around 500 km2. Actual threshold values will depend greatly on the economic and natural conditions in a country or region, and need to be studied carefully.
Third, any policy to control habitat conversion, such as a tax imposed on the rents from converted land, should also vary with habitat area. As more habitat is converted in the long run when there is no risk of a disease outbreak, marginal converted land rents will be lower compared to the rents when there is a risk. However, this difference in rents declines if a region contains a smaller initial habitat area, and so the tax rate imposed on marginal rents from converted land also falls with diminished habitat size.
Several policy implications emerge from these outcomes. Our analysis confirms the concern of wildlife disease experts that land conversion and fragmentation of larger wildlife habitats poses a risk of zoonotic disease transmission to humans (Borremans et al., 2019; Faust et al., 2018; Gibbs et al., 2020b; Johnson et al., 2020; Olival et al., 2017; Wilkinson et al., 2018; Zohdy et al., 2019). Control and regulation of converting wildlife habitat is essential, if there is a significant risk of zoonosis disease outbreak. If the social disutility from a disease outbreak caused by wildlife habitat loss is extremely high compared to the benefits from conversion, then no conversion should take place and the initial wildlife habitat area should be preserved indefinitely. In the case where some conversion is optimal, any policy to control excess habitat conversion, such as a tax imposed on the rents from converted land, should vary with habitat area. Other policies to reduce conversion, whether it is restricting agriculture and other land-converting commercial activities, designating large contiguous habitat reserves or limiting human access to wildlife habitat, may also need to be adjusted to account for the size of the wildlife area protected. Based on our analysis, the general rule appears to be: the smaller and more isolated the wildlife area, the greater and more stringent the restrictions imposed.
Finally, the analysis of this paper also points to some important empirical issues. As is shown here, determining how much wildlife habitat to conserve depends on how habitat conversion influences the risk of a zoonosis outbreak. In the model of this paper, we identify three key effects. The decision to convert must include a risk premium for the threat of an outbreak, which is impacted by the size of the remaining habitat area, the adverse impact of loss of habitat on the likelihood of the disease outbreak, and the negative value associated with an increase in the risk that a zoonotic disease outbreak occurs. Estimating these three influences is critical to determining the optimal amount of wildlife habitat conversion, or indeed if any habitat loss should take place at all. More research is needed to improve our understanding of these effects, as well as quantifying them.
Clearly, exploring the policy and empirical implications of our analysis is urgent, if we are to avoid the risk of another major zoonotic pandemic such as COVID-19.
Declaration of competing interest
The author declares no conflict of interest. There are also no funding sources associated with this paper that need to be disclosed.
Footnotes
Quoted in Phoebe Weston, “‘We did it to ourselves’: scientist says intrusion into nature led to the pandemic.” The Guardian 25 April 2020. https://www.theguardian.com/world/2020/apr/25/ourselves-scientist-says-human-intrusion-nature-pandemic-aoe?CMP=share_btn_link.
As is clear from the earlier discussion and (2) and (3), can vary significantly depending on the epidemiological characteristics of the disease, including the force of infection through contact with wildlife and the susceptibility of the human population to the pathogen.
The basic reproduction rate R0 of a disease is the expected number of secondary cases per primary case in a population of individuals susceptible to the new disease (Cobey 2020; van den Driessche 2017). Thus, R0 is the initial growth rate of the disease in the human population through human-to-human transmission. In our model, the number of primary cases created through wildlife-human transmission is the initial infected members of the population, i.e. . If R0 is sufficiently large, the number of infected individuals in the population will grow rapidly through human-to-human transmission, which seems to be the case with many recent epidemics from zoonosis, such as SARS, swine flu, Ebola, and now COVID-19.
From (14), , which implies that (6) can be written as and confirms that, as the shadow value of the wildlife habitat becomes less negative over time, optimal conversion falls. The slope of the optimal path is for . Although initially the wildlife habitat is very large, as land conversion proceeds and A falls, the shadow value of the habitat becomes less negative.
As before , and . The slope of the optimal path is now for , which suggests a similar outcome. Although initially the wildlife habitat is very large, as land conversion proceeds and A falls, the shadow value of the habitat becomes less negative.
Appendix.
The numerical simulation of how the risk of disease outbreak impacts wildlife habitat conservation in the long run is based on the following functional forms and key relationships.
Functional forms
| (A.1) |
| (A.2) |
| (A.3) |
To ensure, concavity of and , b D and b B must adjust with the size of A 0. We additionally specify that . Note that the parameter a also adjusts with A 0. We calibrate a for and adjust it accordingly for different initial habitat size.
Equilibrium for optimal wildlife habitat with no risk of disease outbreak
Steady state A∗∗ is found by
This implies from (A.1) and (A.2)
| (A.4) |
Equilibrium for optimal wildlife habitat with risk of disease habitat.
Steady state A∗ is found by
where and .
| (A.5) |
From (A.1), (A.2) and (A.3).
, and . Thus substituting these expressions into (5) and rearranging yields the quadratic expression.
, which has the solution.
. (6) This solution is determined by the parameters .
References
- Albers H.J., Lee K.D., Rushlow J.R., Zambrana-Torsello C. Disease risk from human-environment interactions: environment and development economics for joint conservation-health policy. Environ. Resour. Econ. 2020;76:929–944. doi: 10.1007/s10640-020-00449-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Augeraud-Véron E., Fabbri G., Schubert K. Prevention and mitigation of epidemics: biodiversity conservation and confinement policies. J. Math. Econ. 2021;93:102484. [Google Scholar]
- Barbier E.B. Cambridge University Press; Cambridge and New York: 2011. Capitalizing on Nature: Ecosystems as Natural Assets. [Google Scholar]
- Barbier E.B., Burgess J.C. The economics of tropical forest land use options. Land Econ. 1997;73:174–195. [Google Scholar]
- Begon M., Bennett M., Bowers R.G., French N.P., Hazel S.M., Turner J. A clarification of transmission terms in host-microparasite models: numbers, densities and area. Epidemiol. Infect. 2002;129:147–153. doi: 10.1017/s0950268802007148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borremans B., Faust C., Manlove K.R., Sokolow S.H., Lloyd-Smith J.O. Cross-species pathogen spillover across ecosystem boundaries: mechanisms and theory. Philos. Trans. Roy. Soc. B. 2019;374(1782):20180344. doi: 10.1098/rstb.2018.0344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borsky S., Hennighausen H., Leiter A., Williges K. CITES and the zoonotic disease content in international wildlife trade. Environ. Resour. Econ. 2020;76:1001–1017. doi: 10.1007/s10640-020-00456-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bulte E.H., Horan R.D. Habitat conservation, wildlife extraction and agricultural expansion. J. Environ. Econ. Manag. 2003;45:109–127. [Google Scholar]
- Cobey S. Modeling infectious disease dynamics. Science. 2020;368(6492):713–714. doi: 10.1126/science.abb5659. [DOI] [PubMed] [Google Scholar]
- Córdoba-Aguilar A., Ibarra-Cedeña C.N., Castro-Arellano I., Suzan G. Tackling zoonoses in a crowded world: lessons to be learned from the COVID-19 pandemic. Acta Trop. 2021;214:105780. doi: 10.1016/j.actatropica.2020.105780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cunningham A.A., Daszak P., Wood J.L.N. One Health, emerging infectious diseases and wildlife: two decades of progress? Philos. Trans. Roy. Soc. B. 2017;372:20160167. doi: 10.1098/rstb.2016.0167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis S., Calvet E., Leirs H. Fluctuating rodent populations and risk to humans from rodent-borne zoonoses. Vector Borne Zoonotic Dis. 2005;5(4):305–314. doi: 10.1089/vbz.2005.5.305. [DOI] [PubMed] [Google Scholar]
- Diekmann O., Heesterbeek J.A.P. John Wiley; Chichester, U.K: 2000. Mathematical Epidemiology of Infectious Diseases: Model Building, Analysis and Interpretation. [Google Scholar]
- Dobson A.P., Pimm S.L., Hannah L., Kaufman L., Ahumada J.A., Ando A.W., Bernstein A., Busch J., Daszak P., Engelmann J., Kinnaird M.F., Li B.V., Loch-Temzelides T., Lovejoy T., Nowak K., Roehrdanz P.R., Vale M.M. Ecology and economics for pandemic prevention. Science. 2020;369:379–381. doi: 10.1126/science.abc3189. [DOI] [PubMed] [Google Scholar]
- Espinosa R., Tago D., Treisch N. Infectious diseases and meat production. Environ. Resour. Econ. 2020;76:1019–1044. doi: 10.1007/s10640-020-00484-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faust C.L., McCallum H.I., Bloomfield L.S.P., Gottdenker N.L., Gillespie T.R., Torney C.J., Dobson A.P., Plowright R.K. Pathogen spillover during land conversion. Ecol. Lett. 2018;21(4):471–483. doi: 10.1111/ele.12904. [DOI] [PubMed] [Google Scholar]
- Gibb R., Franklinos L.H.V., Redding D.W., Jones K.E. Ecosystem perspectives are needed to manage zoonotic risks in a changing climate. BMJ. 2020;371:m3389. doi: 10.1136/bmj.m3389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gibb R., Redding D.W., Chin K.Q., Donnelly C.A., Blackburn T.M., Newbold T., Jones K.E. Zoonotic host diversity increases in human-dominated ecosystems. Nature. 2020;584:398–402. doi: 10.1038/s41586-020-2562-8. [DOI] [PubMed] [Google Scholar]
- Hartwick J., van Long N., Tian H. Deforestation and development in a small open economy. J. Environ. Econ. Manag. 2001;41:235–251. [Google Scholar]
- Hethcote H.W. The basic epidemiology models: models, expression for R0, parameter estimation, and applications. Math. Understand. Infect. Disease Dynam. 2009;16:1–61. [Google Scholar]
- Johnson C.K., Hitchens P.L., Pandit P.S., Rushmore J., Evans T.S., Young C.C.W., Doyle M.M. Global shifts in mammalian population trends reveal key predictors of virus spillover risk. Proceed. Roy. Soc. B. 2020;287(1924):20192736. doi: 10.1098/rspb.2019.2736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones K.E., Patel N.G., Levy M.A., Storeygard A., Balk D., Gittleman J.L., Daszak P. Global trends in emerging infectious diseases. Nature. 2008;451(7181):990–993. doi: 10.1038/nature06536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kamien M.L., Schwartz N.L. second ed. Elsevier; Amsterdam: 1991. Dynamic Optimization: the Calculus of Variations and Optimal Control in Economics and Management. [Google Scholar]
- Lloyd-Smith J.O., George D., Pepin K.M., Pitzer V.E., Pulliam J.R.C., Dobson A.P., et al. Epidemic dynamics at the human-animal interface. Science. 2009;326(5958):1362–1367. doi: 10.1126/science.1177345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lo Iacono G., Cunningham A.A., Fichet-Calvet E., Garry R.F., Grant D.S., Leach M., et al. A unified framework for the infection dynamics of zoonotic spillover and spread. PLoS Neglected Trop. Dis. 2016;10(9) doi: 10.1371/journal.pntd.0004957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olival K.J., Hosseini P.R., Zambrana-Torrelio C., Ross N., Bogich T.L., Daszak P. Host and viral traits predict zoonotic spillover from mammals. Nature. 2017;546(7660):646–650. doi: 10.1038/nature22975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodriguea-Morales A.J., Katterine Bonilla-Aldana D., Balbin-Ramon G.J., Rabaan A.A., Sah R., Paniz-Mondolfi A., Pagliano P., Esposito S. History is repeating itself: probably zoonotic spillover as the cause of the 2019 novel Coronavirus epidemic. Infezioni Med. Le. 2020;1:3–5. https://pubmed.ncbi.nlm.nih.gov/32009128/ [PubMed] [Google Scholar]
- Shah H.A., Huxley P., Elmes J., Murray K.A. Agricultural land-uses consistently exacerbate infectious disease risks in Southeast Asia. Nat. Commun. 2019;10:4299. doi: 10.1038/s41467-019-12333-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skonhoft A. On the optimal exploitation of terrestrial animal species. Environ. Resour. Econ. 1999;13:45–57. [Google Scholar]
- van den Driessche P. Reproduction numbers of infectious disease models. Infect. Disease Modell. 2017;2:288–303. doi: 10.1016/j.idm.2017.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- White R.J., Razgour O. Emerging zoonotic diseases originating in mammals: a systematic review of effects of anthropogenic land-use change. Mamm Rev. 2020;50:336–352. doi: 10.1111/mam.12201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilkinson D.A., Marshall J.C., French N.P., Hayman D.T.S. Habitat fragmentation, biodiversity loss and the risk of novel infectious disease emergence. J. R. Soc. Interface. 2018;15(149):20180403. doi: 10.1098/rsif.2018.0403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang T., Wu Q., Zhang Z. Probable pangolin origin of SARS-CoV-2 associated with the COVID-19 outbreak. Curr. Biol. 2020;30:1346–1351.e2. doi: 10.1016/j.cub.2020.03.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zohdy S., Schwartz T.S., Oaks J.R. The coevolution effect as a driver of spillover. Trends Parasitol. 2019;35(6):399–408. doi: 10.1016/j.pt.2019.03.010. [DOI] [PubMed] [Google Scholar]