Abstract
Protection of the healthcare workforce is of paramount importance for the care of patients in the setting of a pandemic such as coronavirus disease 2019 (COVID-19). Healthcare workers are at increased risk of becoming infected. The ideal organisational strategy to protect the workforce in a situation in which social distancing cannot be maintained remains to be determined. In this study, we have mathematically modelled strategies for the employment of the hospital workforce with the goal of simulating the health and productivity of the workers. The models were designed to determine if desynchronization of medical teams by dichotomizing the workers may protect the workforce. Our studies model workforce productivity and the efficiency of home office applied to the case of COVID-19. The results reveal that a desynchronization strategy in which two medical teams work alternating for 7 days increases the available workforce.
Keywords: Epidemiology, Mathematical modelling, Desynchronization strategy, Master equations, Differential equations
1. Introduction
During the spread of worldwide pandemics, protecting and supporting caregivers to maintain the workforce in hospitals is a crucial and challenging task. Under such extraordinary situations, the efficiency of the healthcare workforce is threatened by several factors including: 1) infected patients, 2) infected co-workers and 3) infected persons outside the hospital. This is of high importance in the current coronavirus disease 2019 pandemic (COVID-19) given that the virus may be transmitted by asymptomatic persons and the long incubation period averaging 5 days (Guan et al., 2020, Zhou et al., 2020, Lauer et al., 2020). Unlike for most other professions, social distancing is typically not possible in medical teams where healthcare workers are required to work in close contact with patients and coworkers. Currently, little is known about which work organizational strategies in the hospital are most suitable for protecting the healthcare workforce. Potential strategies may include prolonging duty hours and thereby limiting interactions between coworkers or complete desynchronization of the workforce in which teams are dichotomized and each half of the team work alternate weeks.
In this report, we perform simulations of biophysical models of coronavirus epidemics of COVID-19 in a healthcare working team, and discuss the efficiency of different work strategies during the viral outbreak.
Different types of mathematical models have been used to study epidemiology. In the classical Susceptible-Infectious-Recovered (SIR) model, a susceptible worker (S) can be infected (I), and the infected person can recover (R), without the risk of reinfection. Variants of this model are the Susceptible-Infectious-Susceptible (SIS) and Susceptible-Exposed-Infectious-Recovered (SEIR) models (Getz et al., 2018) and the Susceptible-Infected-Recovered-Deceased (SIRD) models (Sinha et al., 2020). The SEIR model in which the recovered patients are susceptible again, has already been used for modeling purposes during the COVID-19 outbreak (Rocklöv et al., 2020). Also, SEIR models have been used to model control of expansion in the context of the COVID-19 and have been extended to include patients age and asymptomatic cases (Pan et al., 2019, Prem et al., 2020). Furthermore, SEIR models have been applied in this context by including persons in quarantine (QSEIR model) (Liu et al., 2020, Peak et al., 2020). A model based on Microscopic Markov Chain approach have been proposed to study the effect of confinement (Arenas et al., 2020).
Further extensions have recently been proposed to better model COVID-19 transmission dynamics. Mobility data from the United States have been used to create social-distance metrics and combined with epidemiological models to assess infection rates (Badr et al., 2020). Recent work has analyzed the impact of population heterogeneity in epidemic waves (Neipel et al., 2020). Models of the transmission dynamics in Switzerland have been developed to study the effect of the implementation of non-pharmaceutical interventions (NPIs) on time-varying reproduction number (Joseph et al., 2020) as well as to explore counterfactual scenarios of earlier and later implementation of NPIs (Althaus et al., 2020). Optimization of resource sharing of multiple hospitals has been studied to optimize the use of ICU beds (Lacasa et al., 2020). However, the question on how to organize healthcare units during pandemics remains unclear.
Here, we put forward SIS and SIR models by dividing the infectious persons into a latent and infected state in order to account for the potentially long asymptomatic phase of COVID-19. Next, have developed a family of time-dependent compartmental models with and without reinfection by adapting the SAIR model (Althaus et al., 2010, Leung et al., 2018, Kahn et al., 2019). We added a variable to account for work W and built mathematical models for COVID-19 described by ordinary differential equations (ODE). The family of models is denoted Susceptible-Latent-Infected-Recovered-Susceptible-Work (SLIRSW) model. In our SLIRSW models, the workers can be healthy and susceptible to infection, S, infected in the incubation period, L, infected presenting symptoms, I, and after recovery temporarily immune to new infections, R. Eventually the recovered workers lose their immunity and become susceptible again. Additionally, the models are adapted to account for work, W, done by the non-infected workers. There are two limiting cases of particular interest: when the recovered do not gain immunity (SLIW) and when the immunity is permanent (SLIRW).
To investigate the possible scenarios for workforce organization, we use ODEs describing the dynamics of the models including time-dependent parameters in which the rate changes based on their location, that is, in-hospital compared with home office. Deterministic models may not be accurate to describe the dynamics when small populations are present (McKane et al., 2005). In the context of COVID-19, stochastic epidemiology models have been used to study confinement strategies (Bittihn et al., 2020).
For this reason, we studied the limitations of the deterministic model by reformulating them in terms of a master equation (Gillespie, 1977), and we determined the range of parameters where stochastic models were necessary. Later, the stochastic models are used to investigate space separation of the workers.
The rest of the report is organized as follows: we formulate mathematical models to investigate organizational strategies of the hospital workforce and their effect on productivity during a pandemic (Section 2, and present the results of simulations (Section 3). Finally, our results are summarized and discussed (Section 4).
2. Models
In this section we present the mathematical models used to explore the different strategies to organize healthcare workers.
Our goal is to create a model to study the pandemic from its beginning, where the number of infected workers is 0, to later time points where the population becomes immune, or when the virus becomes endemic. Therefore we are studying both, the steady state and the transient dynamics.
2.1. Sketch of the models
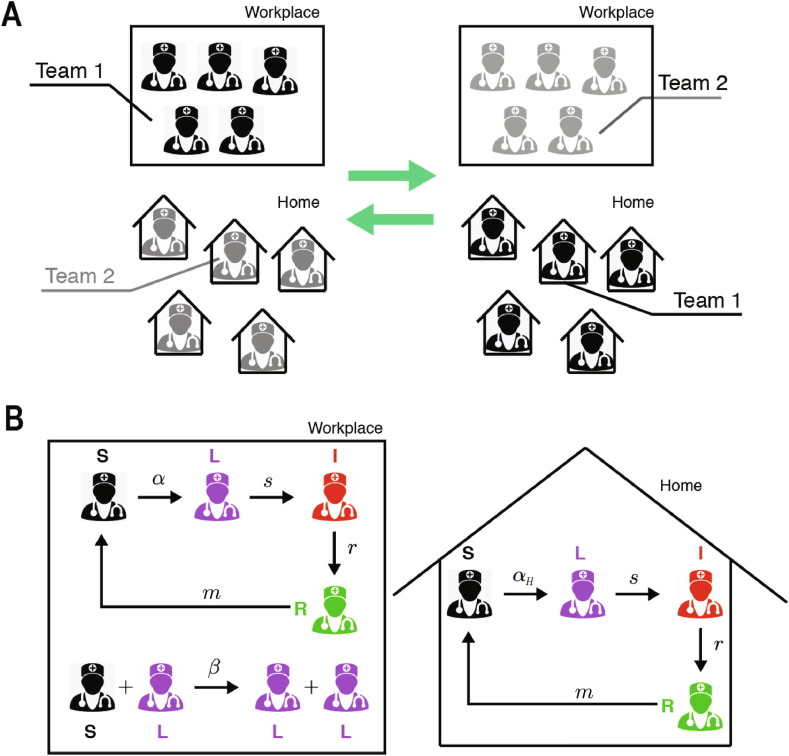
In the normal/control strategy, the SLIRSW model describes the transmission dynamics among one group of healthcare workers that follows their usual schedule at the hospital. In that scenario, workers can be infected by coworkers and by the general population. This model is described in detail in Section 2.2.1. This normal strategy is compared with a desynchronized model, in which the healthcare workers are divided into two non-interacting teams of equal size. At any time, one team is at the workplace and the other team stays at home. A dichotomous work switch is implemented as follows (Fig. 1 A): during the first week Team 1 stays at the workplace and Team 2 at home; during the second week Team 1 stays at home and Team 2 at the workplace; next the teams continue alternating their location at the end of each week. When at the workplace, each healthy susceptible worker can become latent at an infection rate that is larger than when staying at home. Latent workers develop the infection at the workplace, at the same rate as at home. Infection of a susceptible by a latent worker can only occur in the workplace. We also assume that infected workers recover at the same rate at the workplace than at home, becoming recovered and immune and eventually losing their immunity. This model is described in detail in Section 2.2.1. Fig. 1 shows the SLIRSW model with compartmentalization.
Fig. 1.
Sketch of the Susceptible-Latent-Infected-Recovered-Susceptible-Work model (SLIRSW). (A) Scheme of work shifts between two teams changing their location in the workplace and at home once per week. (B) Infection dynamics at the workplace and home. See Section 2.2 for further details. Image of the doctor adapted from Kissclipart (2020).
2.2. Mathematical formulation
In this section we present the mathematical details of the SLIRSW model.
2.2.1. Normal strategy: One group of healthcare workers
In the normal strategy, our infection model describes the evolution in time t of the number S of healthy workers susceptible to be infected, the number, L, of infected workers in a latent state, the number, I, of infected workers presenting symptoms and therefore isolated, and the number R of recovered workers who gained temporal immunity and can not be infected. The dynamics of each population are described by the following system of ODEs:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
where is the infection rate coming from the general population –e.g. infected persons in the city where the hospital is located–, resulting in an infected worker in a latent state, is the infection rate when the person is infected by a co-worker, s is the inverse of the incubation period, or the activation rate, at which a patient in a latent state starts presenting symptoms. r is the recovery rate, where an infected patient recovers and becomes healthy, and m is the loss of immunity rate at which a recovered patient becomes susceptible.
By considering to be constant, we assume that there is a roughly constant fraction of infected individuals among the general population that becomes infected and can infect the healthcare workers. Although more complex infection rate functions that introduce an infection curve could be considered, we use a constant force of infection for simplicity to represent infections from the general population. One interpretation of this approximation is to consider it as a worst-case approximation when the infection rate is fixed at its highest during the whole epidemic. This worst-case approximation would produce a lower bound on the number of healthy workers.
W is a function that keeps track of the work output of the workers, for simplicity we assume its growth is proportional to the number of available workers. For simplicity, we consider the death rate negligible and we do not consider recoveries coming from latent patients. In our simulations reported below, we set the initial condition to , and , thereby representing a large unit with 300 workers.
As a function of m, there are two limiting cases of this model. When , the immunity gained is permanent, we denote this model as SLIRW. When , the time to go from R to S tends to 0, we will refer to this model as SLIW.
2.2.2. Desynchronization strategy: Two groups of healthcare workers
Our main goal is to identify strategies to protect healthcare workers. The first organizational strategy we present is a desynchronization strategy that we compare with the normal strategy presented in Section 2.2.1. The desynchronization strategy consists of the division of the workers into two groups, one group works for one week in the hospital while the other works at home, and the week after the two groups swap their roles. Accordingly, we model it as two groups of healthy persons susceptible to be infected, and , two groups of infected persons in a latent state, and , two groups of infected persons presenting symptoms, and , and two groups of recovered and . The dynamics of each population are described by the following system of ODEs.
| (6) |
| (7) |
| (8) |
| (9) |
for the first group and
| (10) |
| (11) |
| (12) |
| (13) |
for the second group. The rate of change of the work output obeys
| (14) |
For this model, the parameters that are purely related to the disease, and m remain the same, while the parameters that determine the epidemiological spreading vary. Accordingly, we simulate our model for the first seven days with because the workers are not in contact with the other co-workers when they do home office. Additionally we define as the value () takes during the home office of group 1 (group 2). We consider because we assume that the probability of becoming infected by the general population is higher when working at the hospital. Every seven days, we switched the group’s roles, by exchanging their parameter values. We assume that the productivity decreases during home office, therefore we choose and during the odd weeks and and during the even weeks. Then, and can be written as
Our model assumes that remains constant when the desynchronization strategy is applied. The rational for this assumption is that with half of the workers in the same space, the time for them to interact would double. However, some procedures (e.g. surgical interventions) would require the workers to interact, increasing the value of . The current lack of data does not allow us to estimate during desynchronization, and the assessment of the true value is yet an open question.
In our simulations reported below, we set the initial condition to , and .
Based on the available data of COVID-19, we choose , because the average duration of the incubation period is 5 days (Guan et al., 2020, Zhou et al., 2020, Lauer et al., 2020), and because the average recovery time is 14 days (Rhee et al., 2020, Gandhi et al., 2020).
2.2.3. Spatial divisions
Another strategy we consider, in addition to desynchronization, is the possibility of dividing the space in the hospital into spatial compartments.
In order to model space division, we divide our variables , in non-interacting compartments, with and N is the number of compartments. Since the space is divided by N where N is the number of compartments, we assume the rate is multiplied by N, that is, .
With these extensions, the equations describing the model read
| (15) |
| (16) |
| (17) |
| (18) |
for the first group and
| (19) |
| (20) |
| (21) |
| (22) |
for the second group, where the case describes our previous model.
2.3. Stochastic model
In this section, we present a stochastic formulation of our model in terms of a Master equation, which we use to study smaller units, e.g. 75 workers instead of 300. Here, due to the small size, stochastic effects can become dominant.
We consider the susceptible, S, latent, L, infected showing symptoms I, and recovered R, coupled with the following reactions
-
•
S can be infected by a non-co-worker resulting into a L with a rate . See Table 1 .
-
•
S can be infected by a co-workers resulting into a L with a rate . See Table 1.
-
•
A latent infected worker L can start presenting symptoms and be sent to quarantine at rate . See Table 1.
-
•
An infected worker I can recover and become R at rate . See Table 1.
-
•
A recovered worker R can lose their immunity and become S at rate . See Table 1.
Table 1.
Transition rates and state changes describing the model.
| Transition rate | State change | Description |
|---|---|---|
The SLIW and SLIRW models are reformulated in terms of the following Master Equation
| (23) |
Where is the probability of being at state X at time t, where in the control model and in the desynchronized model. The transition rates, , and the state changes, , are described in Table 1.
The Work done, W, is described as the ODE of the deterministic models, Eq. (14).
Analogously, for spatial desynchronization the master equation reads
| (24) |
where , and the transition rates are described by the Table 1.
The Master equations are investigated by using the Gillespie stochastic simulation algorithm (Gillespie, 1977).
3. Results
3.1. Desynchronization increases the available workforce during the peak of infected healthcare workers
In this section we performed numerical simulations of our dynamical systems model to study the effect of the desynchronization. Our strategy consists of comparing simulations of the model with desynchronization and the model without desynchronization in terms of number of healthy workers, and amount of work done.
3.1.1. Simulations of the SLIW model
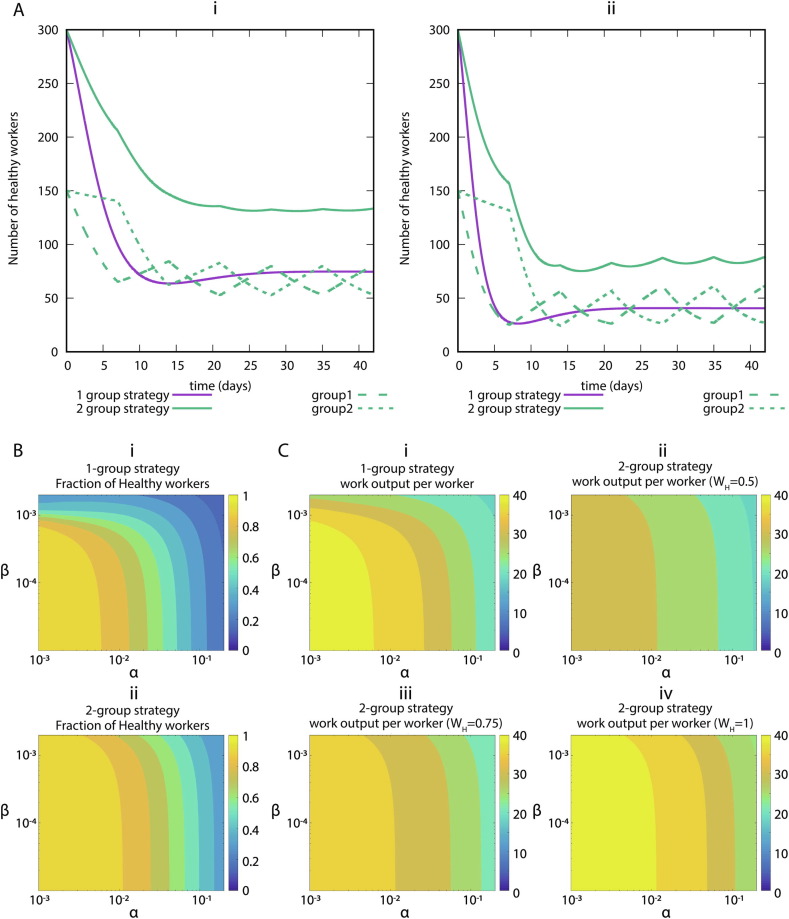
First, we study the effect of the infection rates on the health of the workers. In Fig. 2 we show the simulations of our systems of ODEs with two representative sets of parameters, low infection rate (Fig. 2Ai) and high infection rate (Fig. 2Aii). Regardless of the values, we observe that the strategy of dividing the workers into two groups decreases the number of infected workers, thus increasing the available workforce. In Fig. 2B we show the number of workers as a function of the infection rates. We observe that with the desynchronization strategy the number of healthy workers is higher than with the normal strategy. So far, we have observed that the desynchronization strategy increases the number of healthy workers. Because a desynchronization strategy includes decreased productivity of home office, we next determined the overall economic impact of this strategy. Therefore, we simulate our model for 6 weeks and we represent the value of W divided by the total number of workers as a function of and , for different values of home office efficiency (Fig. 2C). We observe that if the productivity decreases by 50 during the home office week, the normal strategy performs better than the desynchronization strategy. For higher values (75 or 100) of the home office productivity, the desynchronization strategy outperforms the normal strategy for high infection rates.
Fig. 2.
SLIW model simulations. (A) Representative examples of infection rates of healthcare workers with and without desynchronization. Number of healthy workers (S + R) as a function of time for two sets of parameters values. (i) Assumption: low infection rate: . (ii) Assumption: high infection rate: . All rates are in units of day−1. (B) Impact of infection rates on healthcare workers availability. Number of healthy workers as a function of the infection rates. (i) Normal strategy. (ii) Desynchronization strategy . The rates , and in units of day−1. (C) Impact of infection rates on the productivity. Value of the work output at the end of the simulation (6 weeks) divided by the total number of workers for the normal strategy (Strategy 1), and different values of the home office productivity with the desynchronized strategy (Strategy 2). (i) Strategy 1, (ii) Strategy 2, with productivity at home , (iii) Strategy 2, productivity at home , (iv) Strategy 2, productivity at home . The rates , and in units of day−1. The color levels of the heatmaps were discretized to make the comparisons easier.
3.1.2. Simulations of the SLIRW model
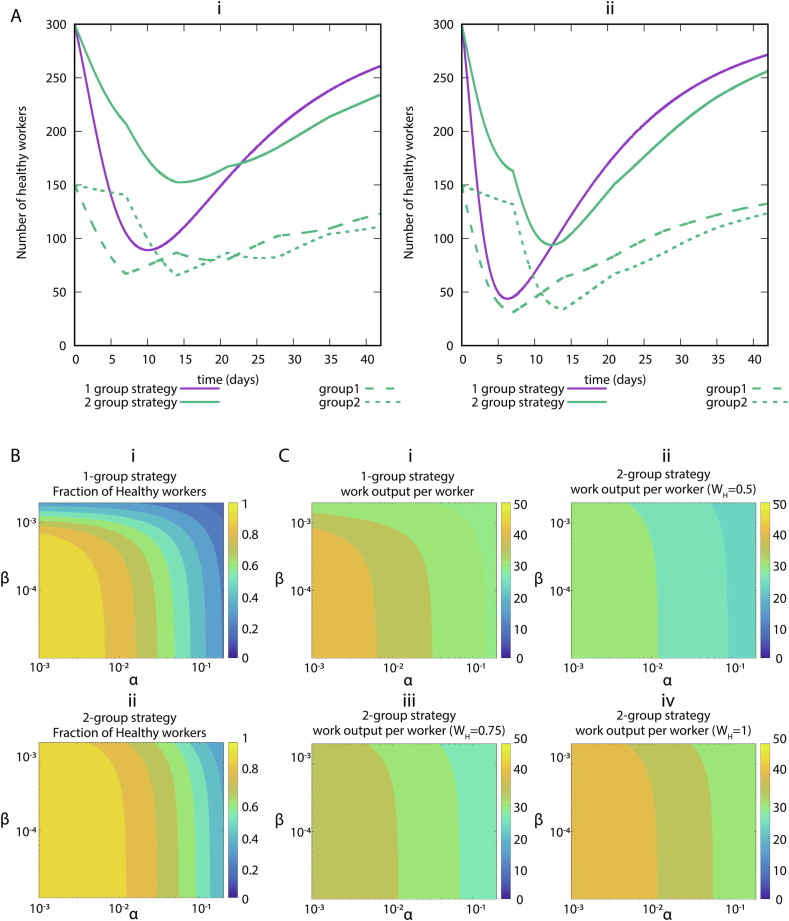
Next, we study the effect of the infection rates in a model that does not allow for reinfection. In Fig. 3 A we show the simulations of our systems of ODE with two representative sets of parameters. Regardless of the values, we observe that the strategy of dividing the workers into two groups increases the number of healthy workers when the maximum of infected healthcare workers is reached. In Fig. 3B we show the number of minimum healthy workers as a function of the infection rates during a 6-week simulation.
Fig. 3.
SLIRW model simulations. (A) Representative examples of infection rates of healthcare workers with and without desynchronization (SLIRW). Number of healthy workers (S + R) as a function of time. (i) Assumption: low infection rate: . (ii) Assumption: high infection rate: . All rates are in units of day-1. (B). Impact of infection rates on healthcare workers availability during the peak of infected healthcare workers. Minimum fraction of healthy workers during a simulation as a function of the infection rates. (i) Normal strategy. (ii) Desynchronization strategy stands for during the odd weeks and during the even weeks, idem for . The rates and in units of day−1. (C). Impact of infection rates on the productivity. Value of divided by the total number of workers at the end of the simulation for the normal strategy (Strategy 1), and different values of the home office productivity with the desynchronized strategy. (i) Strategy 1, (ii) Strategy 2, =0.5, (iii) Strategy 2, =0.75, (iv) Strategy 2, =1. The rates , and in units of day−1. The color levels of the heatmaps were discretized to make the comparisons easier.
So far, we have observed that the desynchronization strategy also increases the number of healthy workers in the situation without reinfection. To determine the economic impact, we simulate our model for 6 weeks and we represent the value of W as a function and , for different values of home office efficiency (Fig. 3C). The desynchronization strategy outperforms the normal strategy for high values of home office efficiency. However, to achieve the same amount of work done, the desynchronization strategy requires higher values of home office productivity than in the SLIW model.
3.1.3. Simulations of the SLIRSW models
In this section, we study the remaining scenario, where the worker gains immunity after recovery, which is however not permanent. We consider that this immunity is lost at a rate m which can vary from 0 (SLIRW model) to (SLIW model).
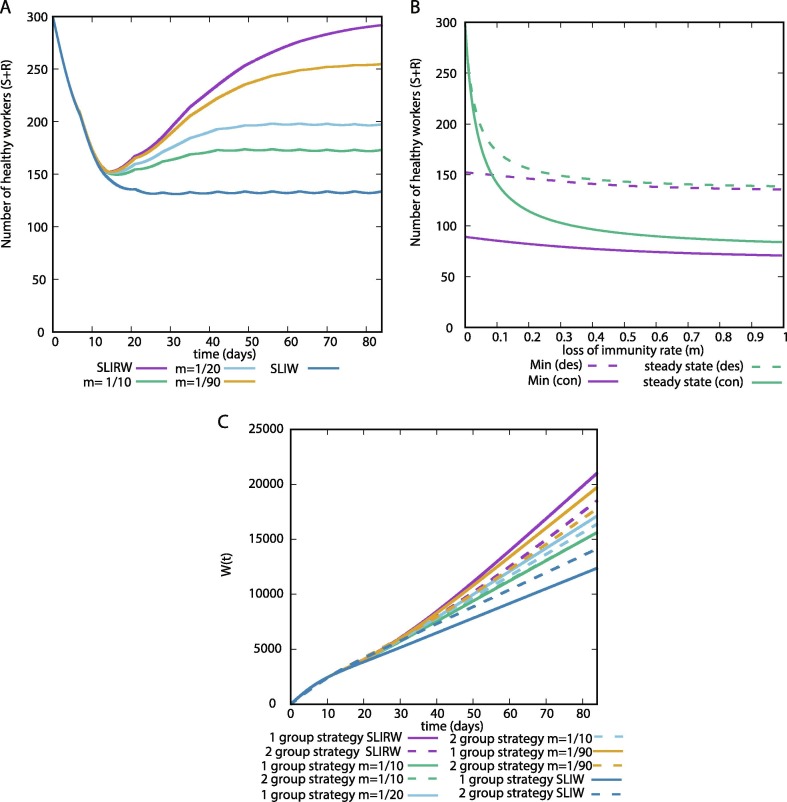
In Fig. 4 A we illustrate a 12 week simulation of the number of healthy workers for different values of m. They showed similar dynamics before the peak of infected healthcare workers, all of them reaching a similar minimum value. Thereafter, each condition tends to a different steady state, which decreases with the value of m.
Fig. 4.
(A) Representative examples of the number of healthy healthcare workers with desynchronization (SLIRSW) for different values of m. (B) Minimum value of during a 12 week simulation, and steady state approximated as the final value of a simulation for a large time period (300 weeks). (des) Desynchronization or 2 group strategy, (con) control or 1 group strategy. (C) as a function of time for different values of m. , and .
In Fig. 4B we show how the minimum value and the steady state vary as a function of the parameter m. We do not observe remarkable differences in the minimum value, and desynchronization reduces the number of maximum infected workers for all values of m. The steady state increases for values close to 0. Therefore, if the immunity is preserved for a long time, the system tends to the SLIRW results.
In Fig. 4C we show the for multiple values of m. During the first weeks we do not observe differences. After that, the lower the value of m, the higher the value of . This effect is due to the fraction of non–healthy workers after reaching the peak of infected healthcare workers (Fig. 4A). In this scenario, we observe that the desynchronization strategy is beneficial for high values of m and only detrimental for low values of m for long periods of observation.
In summary, our results show that the effect of desynchronization can be helpful to protect healthcare workers for all values of m, and the dynamics for all values of m are in between the extreme cases SLIW and SLIRW.
3.1.4. Impact of home productivity on the performance of the two strategies for the limiting cases
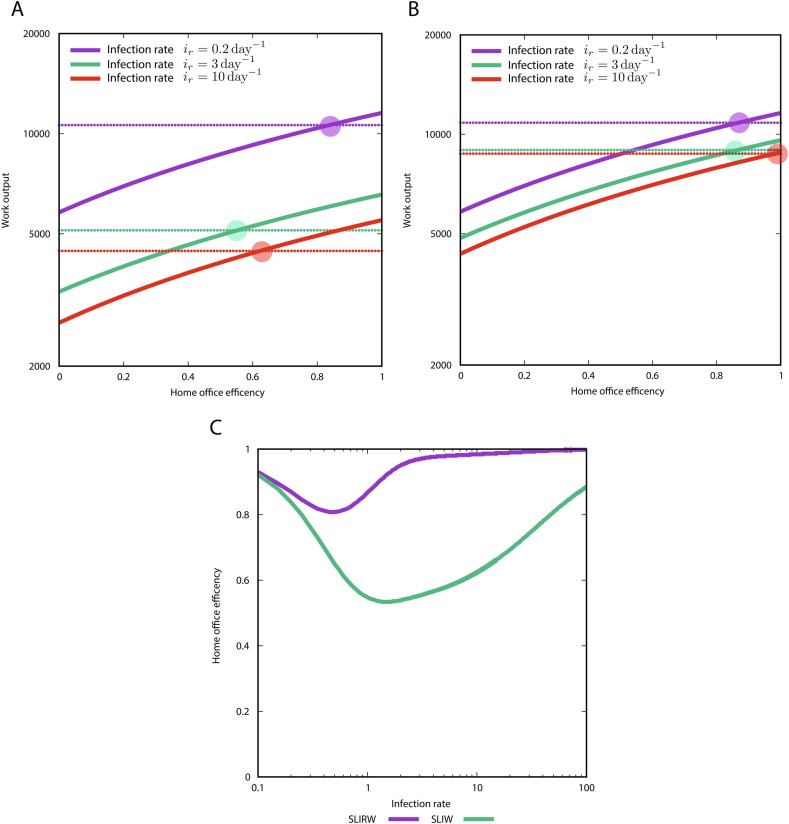
Next, we compared the SLIW and SLIRW. To this end, we defined as the infection rate and we computed the value of W as a function of the home office efficiency for different values of the infection rate, by choosing and (Fig. 5 ). We observe that the SLIW model requires a lower home office efficiency than the SLIRW model (Fig. 5A,B). Next, we computed the minimal value of home office efficiency needed to not have loss in work using the desynchronization strategy (Fig. 5C).
Fig. 5.
Value of W (work done) at the end of the simulation as a function of the home office efficiency for different infection rates, where , and . The dashed threshold is the productivity with the 1 group strategy. (A) SLIW model. (B) SLIRW model. (C) Value of home office efficiency needed to be as productive as the normal strategy, as a function of infection rates.
Note that we have fixed a ratio of to compare the SLIW and the SLIRW model, and a different value could change the quantitative behavior of what we observed in Fig. 5. However, this selection is a representative value of the qualitative dynamics which allows for the understanding of the difference between the extreme cases.
3.1.5. For small values of and high values the stochasticity is dominant
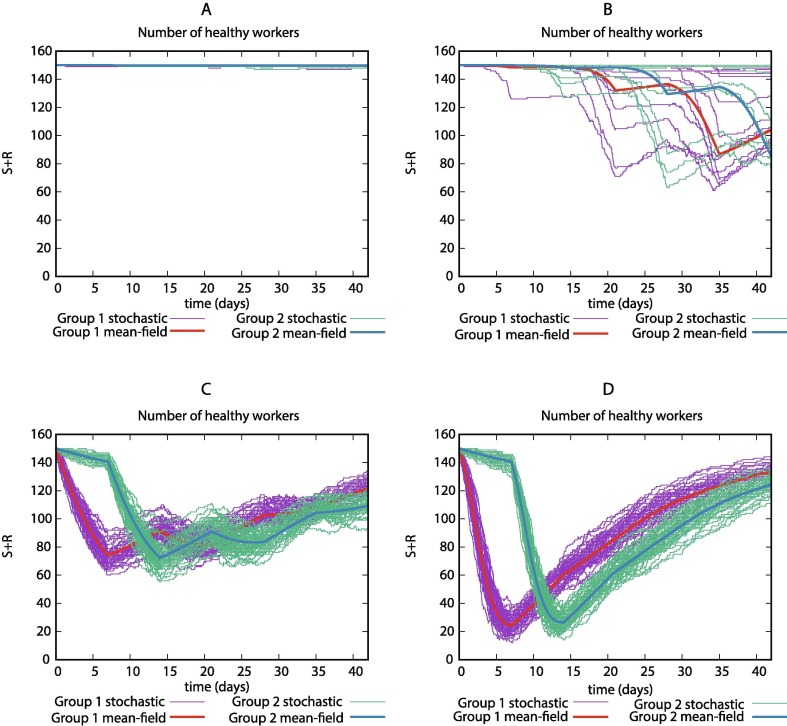
Our deterministic model allowed us to identify differences between the normal and the desynchronization strategy. However, it remains unclear if some features could be hidden because of stochasticity. In this section, we study the stochastic effects on our model by performing Gillespie simulations.
In Fig. 6 A, we show that for low levels of and low values of , the stochasticity does not play an important role due to the low number of infections. For high values of , regardless the value of , stochasticity does not play an important role, in that situation, stochastic simulations are oscillating around the mean-field dynamics (6C, D). However, we found that for low rates of and high rates of , the stochastic effects are dominant (6B). This result led us to study them further as shown below.
Fig. 6.
Number of non-infected workers during a 6-week simulation in the deterministic system and 50 Gillespie simulations for different values of and using the SLIWR model. Parameter values: (A) . (B) . (C) . (D) .
3.2. Spatial desynchronization introduces a purely stochastic protective mechanism
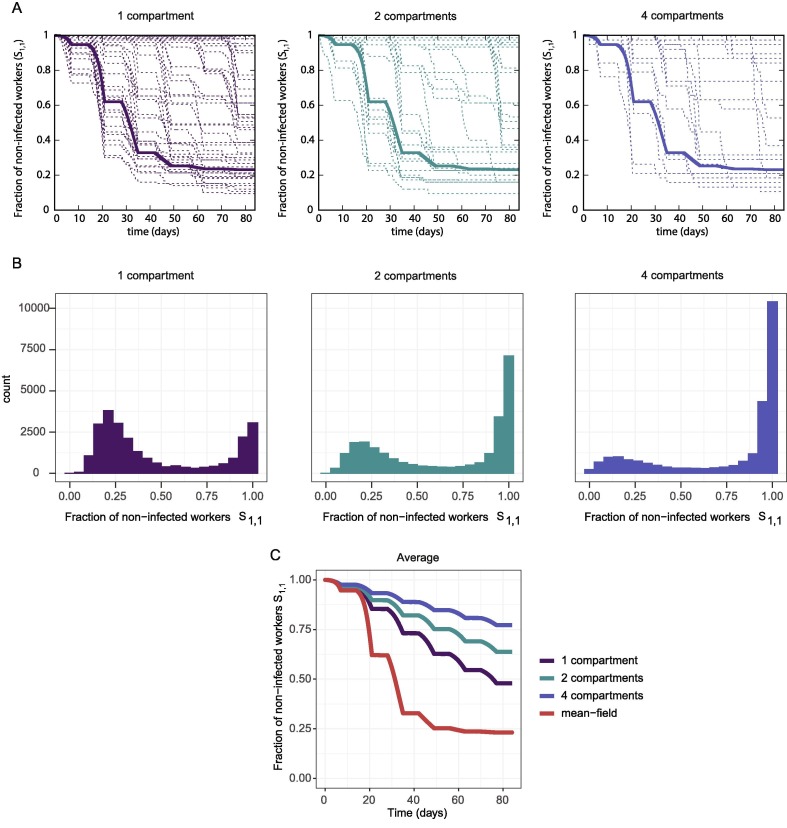
In this section we explore the effect of dividing the work space by reducing the number of persons working in a team. The workers are assigned to one small team and are never in contact with workers from other teams. In doing so, we simulate the stochastic model with spatial compartmentalization described in Section 2.3.
In Fig. 7 A,B we observe that several stochastic trajectories remain unchanged (i.e. at 1), indicating that all individuals stay non-infected in those simulations. The number of non-infected trajectories increases with the number of compartments, while the mean field dynamics remain the same. In Fig. 7C we observe that, on average, an increase in the number of compartments is translated into a higher number of healthy workers. Note that the changes in the number of compartments come with an increase in resulting in the ODE system giving the same result (Fig. 7A). Therefore, the spatial division incorporates a purely stochastic protective mechanism to our system.
Fig. 7.
(A) Mean-field dynamics (thick line) and 100 gillespie simulations (thin lines) of one group of workers during a 12-week simulation of the stochastic model with spatial separation, for 150 workers (1 compartment), 75 workers (2 compartments), and 38 workers (4 compartments). (B) Distribution of at the end of a 12-week simulation, computed using 25000 gillespie simulations of the stochastic model with spatial separation, for 150 workers (1 compartment), 75 workers (2 compartments), and 38 workers (4 compartments). (C) Average of for 150 workers (1 compartment), 75 workers (2 compartments), and 38 workers (4 compartments). Parameters: (1 compartment), (2 compartments), (4 compartments).
This protective mechanism points to possible problems with the interpretation of certain regions of Fig. 2B,C and Fig. 3B,C. Specifically, the upper left region of the heatmaps (high , low ). In that regime, the mean-field dynamics possibly overestimate the number of infected workers.
4. Discussion
Given the urgent need to protect caretakers, we present here modelling approaches that address the impact of desynchronization of healthcare workforces. We have developed a family of time-dependent compartmental models (SLIRSW) with and without reinfection by adapting the SAIR model of Althaus et al., 2010, Leung et al., 2018, Kahn et al., 2019. A time-dependent compartmental model was included to account for the desynchronization of healthcare teams. In addition to the availability of healthcare workers, we modelled productivity by incorporating different levels of work performed at home office.
First, we studied the limiting case where workers turn susceptible again immediately after recovery (SLIW model), which showed that the desynchronization strategy is associated with an increase in the number of healthy workers compared to no desynchronization. This effect is present with both high and low levels of infection rates (Fig. 2).
Next, we incorporated productivity of the workers in the period of home office. In practice, productivity of home office may depend on the tasks that may be done outside the hospital such as writing reports. We have determined the overall productivity as a function of infection rates and home office efficiency. Figs. 2 and 5 show that, for our case study model of COVID-19, a decrease of productivity to 50 during home office (only half of the time can be used for productive work) does not imply a substantial decrease of the overall productivity. However, if the productivity at home office is above 75, overall productivity is increased with a desynchronization strategy for high infection rates.
Second, we studied the case, in which the workers gain permanent immunity to the disease after recovering (SLIRW model). In this SLIRW model, the protective effect of desynchronization reduces over time (Fig. 3). In this situation, however, the number of healthy workers with desynchronization increases, especially during the peak of infected healthcare workers (Fig. 3). This observation is potentially the consequence of workers being immune to the infection thereby not requiring a desynchronization anymore. The protection of the healthcare workforce (Fig. 3B) and productivity (Fig. 3C) also depends on the infection rate in the SLIRW model.
Third, we studied an intermediate scenario in which the worker gains immunity after recovery, which can be lost after some time. We quantified the effect of the protective measure (Fig. 4), which is between the two extreme cases of SLIW and SLIRW.
Next, we aimed to determine the ideal level of productivity for each model (Fig. 5). The ideal home office productivity strongly depends on infection rates in the model with reinfection (SLIW). In this model productivity is required to be around 60 for infection rates 3 and 10. In the model without reinfection (SLIRW), which is rather the case with COVID-19, the home office productivity needs to be higher in order to keep overall productivity similar between the one and two group strategy.
However, the way the model was designed, we artificially included a handicap to the desynchronization strategy. As long as it remains unclear if reinfection is possible, the desynchronization strategy would be maintained. Such strategy would be stopped for recovered workers if reinfection does not occur because of immunity. A possible future direction would be the study of optimization strategies to manage healthcare workers with adaptive strategies that analyze the temporal immunity of the recovered workers.
Next, we reformulated the model in terms of a master equation to study the effect of the intrinsic noise. In Fig. 6 we showed that for low levels of and high levels of , the stochastic effects can be dominant, and therefore, in that regime a deterministic model would not be an accurate approximation of the process.
The stochasticity was of special importance in our next in silico experiment, where we studied spatial separation, due to the low number of individuals in each compartment. We have shown (Fig. 7) that for low levels of , the spatial separation reduces the spread of the disease among the workers. We investigated the origin of this effect by studying the distribution of the number of infected workers, and we have shown that most of the simulations had no infections (Fig. 7A,B), reducing considerably the average number of infected workers (Fig. 7C). This stochastic protective measure is a discrete effect similar to ones previously reported in biology (Bittihn et al., 2020, Sánchez-Taltavull et al., 2016).
Thus, we have determined the impact of a pandemic in the number of available healthcare workers for the different possible infection rates. It is important to note the different regimes. Low and low would correspond to an infectious disease that it is slowly spread among the healthcare workers, and few or no measures would be necessary. High and high would correspond to an infectious disease that spread rapidly and the desynchronization could help to keep the healthcare workforce available. High and low represent an epidemic with high case numbers among the general population but to which healthcare workers remain relatively well protected and avoid transmission amongst themselves. This would be the case in which high social distancing measures are applied in the hospital. Low and high would represent the opposite scenario - an epidemic that does not significantly reach the general population but spreads mainly in hospital settings – which has been seen in other outburst like MERS (Hastings et al., 2016).
An important limitation of our model, is that it assumes the infections coming from the general population to be constant. A possible future direction would be to build a more complex model in which the hospital dynamics are coupled to an epidemiological model of the general population (e.g. a city where the hospital is), and the pandemic in the general population and the hospital co-evolves.
Recent models have revealed that the efficiency of desynchronization strategies is dependent on the frequency of rotations (Ely et al., 2020, Lim et al., 2020). Our study extends these models by incorporation assumptions on work efficiency and reinfection rates.
Our model has limitations that can be addressed in multiple ways. Another extension would be to add asymptomatic patients to the model, that is, patients that pass the infection without presenting symptoms. Furthermore, the model does neither address at what costs such a desynchronization strategy would come. Given that a complete set of workers is always present, there might be losses of acquired experience for the group absent. Furthermore, these models neither address the impact of length of duty shifts nor the impact of potentially impaired communication as a consequence of decreased interactions between healthcare workers.
In summary, our model is a starting point to study how to protect healthcare workers while determining economic impact during a pandemic outbreak.
CRediT authorship contribution statement
Daniel Sánchez-Taltavull: Conceptualization, Methodology, Software, Formal analysis, Writing - original draft, Writing - review & editing, Visualization, Funding acquisition. Violeta Castelo-Szekely: Methodology, Validation, Software, Formal analysis, Writing - review & editing, Visualization. Daniel Candinas: Conceptualization, Writing - original draft, Supervision. Edgar Roldán: Conceptualization, Methodology, Formal analysis, Writing - original draft, Writing - review & editing, Visualization. Guido Beldi: Conceptualization, Methodology, Resources, Writing - original draft, Writing - review & editing, Supervision, Project administration, Funding acquisition.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgment
We would like to thank the Swiss National Science foundation (Grant No. 196059) and the Bern Center for Precision Medicine for funding.
References
- Althaus C.L., Heijne J.C., Roellin A., Low N. Transmission dynamics of chlamydia trachomatis affect the impact of screening programmes. Epidemics. 2010;2(3):123–131. doi: 10.1016/j.epidem.2010.04.002. [DOI] [PubMed] [Google Scholar]
- Althaus C.L., Probst D., Hauser A., Riou J.L. 2020. Time is of the essence: containment of the sars-cov-2 epidemic in switzerland from february to may 2020. MedRxiv.
- Arenas A., Cota W., Gomez-Gardenes J., Gómez S., Granell C., Matamalas J. T., Soriano-Panos D., Steinegger B. 2020. A mathematical model for the spatiotemporal epidemic spreading of covid19. MedRxiv
- Badr H.S., Du H., Marshall M., Dong E., Squire M.M., Gardner L.M. Association between mobility patterns and covid-19 transmission in the usa: a mathematical modelling study. The Lancet Infectious Diseases. 2020;20(11):1247–1254. doi: 10.1016/S1473-3099(20)30553-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bittihn P. Golestanian R. 2020. Containment strategy for an epidemic based on uctuations in the sir model. arXiv preprint arXiv:2003.08784.
- Ely J., Galeotti A., Steiner J. 2021. Rotation as contagion mitigation. Management Science.
- Gandhi R. T., Lynch J. B., del Rio C. 2020. Mild or moderate covid-19. New England Journal of Medicine. [DOI] [PubMed]
- Getz W.M., Salter R., Muellerklein O., Yoon H.S., Tallam K. Modeling epidemics: A primer and numerus model builder implementation. Epidemics. 2018;25:9–19. doi: 10.1016/j.epidem.2018.06.001. [DOI] [PubMed] [Google Scholar]
- Gillespie D.T. Exact stochastic simulation of coupled chemical reactions. The Journal of Physical Chemistry. 1977;81(25):2340–2361. [Google Scholar]
- Guan W.-J., Ni Z.-Y., Hu Y., Liang W.-H., Ou C.-Q., He J.-X., Liu L., Shan H., Lei C.-L., Hui D.S., et al. Clinical characteristics of coronavirus disease 2019 in china. New England Journal of Medicine. 2020;382(18):1708–1720. doi: 10.1056/NEJMoa2002032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hastings D. L., Tokars J. I., Aziz I. Z. A. A., Alkhaldi K. Z., Bensadek A. T., Alraddadi B. M., Jokhdar H., Jernigan J. A., Garout M. A., Tomczyk S. M., et al. 2016. Outbreak of middle east respiratory syndrome at tertiary care hospital, jeddah, saudi arabia, 2014. Emerging infectious diseases, 22 (5), 794. [DOI] [PMC free article] [PubMed]
- Joseph L.C., Javier P.-S., Andrew A.S., Andrea R., Jacques F. Assessing the impact of non-pharmaceutical interventions on sars-cov-2 transmission in switzerland. Swiss Medical Weekly 150 (ARTICLE) 2020 doi: 10.4414/smw.2020.20295. [DOI] [PubMed] [Google Scholar]
- Kahn R., Hitchings M., Wang R., Bellan S.E., Lipsitch M. Analyzing vaccine trials in epidemics with mild and asymptomatic infection. American Journal of Epidemiology. 2019;188(2):467–474. doi: 10.1093/aje/kwy239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kissclipart, March 2020. URL:https://www.kissclipart.com/doctor-icon-free-clipart-computer-icons-physician-jdrmeo.
- Lacasa L., Challen R., Brooks-Pollock E., Danon L. A flexible method for optimising sharing of healthcare resources and demand in the context of the covid-19 pandemic. Plos one. 2020;15(10) doi: 10.1371/journal.pone.0241027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lauer S.A., Grantz K.H., Bi Q., Jones F.K., Zheng Q., Meredith H.R., Azman A.S., Reich N.G., Lessler J. The incubation period of coronavirus disease 2019 (covid-19) from publicly reported confirmed cases: estimation and application. Annals of Internal Medicine. 2020;172(9):577–582. doi: 10.7326/M20-0504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leung K.Y., Trapman P., Britton T. Who is the infector? Epidemic models with symptomatic and asymptomatic cases. Mathematical Biosciences. 2018;301:190–198. doi: 10.1016/j.mbs.2018.04.002. [DOI] [PubMed] [Google Scholar]
- Lim C. Y., Bohn M. K., Lippi G., Ferrari M., Loh T. P., Yuen K.-Y., Adeli K., Horvath A. R., et al. 2020. Sta rostering, split team arrangement, social distancing (physical distancing) and use of personal protective equipment to minimize risk of workplace transmission during the covid-19 pandemic: A simulation study. Clinical biochemistry. [DOI] [PMC free article] [PubMed]
- Liu X., Hewings G.J., Qin M., Xiang X., Zheng S., Li X., Wang S., Modelling the situation of covid-19 and effects of different containment strategies in china with dynamic differential equations and parameters estimation, Available at SSRN 3551359, 2020.
- McKane A.J., Newman T.J. Predator-prey cycles from resonant amplification of demographic stochasticity. Physical Review Letters. 2005;94(21) doi: 10.1103/PhysRevLett.94.218102. [DOI] [PubMed] [Google Scholar]
- Neipel J., Bauermann J., Bo S., Harmon T., Jülicher F. Power-law population heterogeneity governs epidemic waves. PloS one. 2020;15(10) doi: 10.1371/journal.pone.0239678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pan J., Yao Y., Liu Z., Li M., Wang Y., Dong W., Kan H., Wang W. 2020. Eectiveness of control strategies for coronavirus disease 2019: a seir dynamic modeling study. medRxiv.
- Peak C. M., Kahn R., Grad Y. H., Childs L. M., Li R., Lipsitch M., Buckee C. O. 2020. Individual quarantine versus active monitoring of contacts for the mitigation of covid-19: a modelling study. The Lancet Infectious Diseases. [DOI] [PMC free article] [PubMed]
- Prem K., Liu Y., Russell T. W., Kucharski A. J., Eggo R. M., Davies N., Flasche S., Cliord S., Pearson C. A., Munday J. D., et al. 2020. The eect of control strategies to reduce social mixing on outcomes of the covid-19 epidemic in wuhan, china: a modelling study. The Lancet Public Health. [DOI] [PMC free article] [PubMed]
- Rhee C., Kanjilal S., Baker M., Klompas M. 2020. Duration of severe acute respiratory syndrome coronavirus 2 (sars-cov-2) infectivity: When is it safe to discontinue isolation? Clinical infectious diseases. [DOI] [PMC free article] [PubMed]
- Rocklöv J., Sjödin H., Wilder-Smith A. 2020. Covid-19 outbreak on the diamond princess cruise ship: estimating the epidemic potential and effectiveness of public health countermeasures. Journal of travel medicine, 27 (3), taaa030. [DOI] [PMC free article] [PubMed]
- Sánchez-Taltavull D. Optimal architecture of differentiation cascades with asymmetric and symmetric stem cell division. Journal of Theoretical Biology. 2016;407:106–117. doi: 10.1016/j.jtbi.2016.07.029. [DOI] [PubMed] [Google Scholar]
- Sinha S., Nath D., Roy S. 2020. Mass testing and proactiveness aect epidemic spreading. arXiv preprint arXiv:2008.10387.
- Zhou F., Yu T., Du R., Fan G., Liu Y., Liu Z., Xiang J., Wang Y., Song B., Gu X., et al. 2020. Clinical course and risk factors for mortality of adult inpatients with covid-19 in wuhan, china: a retrospective cohort study. The lancet. [DOI] [PMC free article] [PubMed]