Abstract
Electrochemical systems function via interconversion of electric charge and chemical species and represent promising technologies for our cleaner, more sustainable future. However, their development time is fundamentally limited by our ability to identify new materials and understand their electrochemical response. To shorten this time frame, we need to switch from the trial-and-error approach of finding useful materials to a more selective process by leveraging model predictions. Machine learning (ML) offers data-driven predictions and can be helpful. Herein we ask if ML can revolutionize the development cycle from decades to a few years. We outline the necessary characteristics of such ML implementations. Instead of enumerating various ML algorithms, we discuss scientific questions about the electrochemical systems to which ML can contribute.
Clean energy, pure water, reduced air pollution, and sustainable fuels are some of the most urgent global challenges that must be answered within the next few decades.1 Electrochemical systems are promising technologies for many of these quests.2,3 These devices function via interconversion of electric charge and chemical species. In turn, they intrinsically offer a direct control over the desired chemical transformation by externally modulating electricity. For example, the chemical energy stored in a battery can be converted to electricity on demand. Another example is electrochemical conversion of CO2 to useful fuels, where the amount and selectivity can be controlled by the electrochemical driving force. However, the successful implementations of electrochemical systems are rather limited, as we lack the material systems that exhibit the desired performance and longevity for these applications. These materials typically perform multiple functions, and the challenge is to find not only materials with appropriate functionalities but also the ones exhibiting these functions efficiently. To further complicate this process, the electrochemical systems contain multiple material phases—electrode and electrolyte in the simplest form—and the overall functionality strongly relates to how these phases interact with each other (in addition to their individual behavior). Accordingly, the development times have been historically very long, e.g., the first commercial Li-ion battery took about two decades, and all subsequent chemistries have required a decade or longer for the lab-to-market transition.4 Traditionally, this development has been through trial and error for discovering promising materials and subsequently a sequential process of understanding their individual and joint electrochemical responses. We must shorten this time frame to come up with feasible solutions to the aforementioned global challenges.
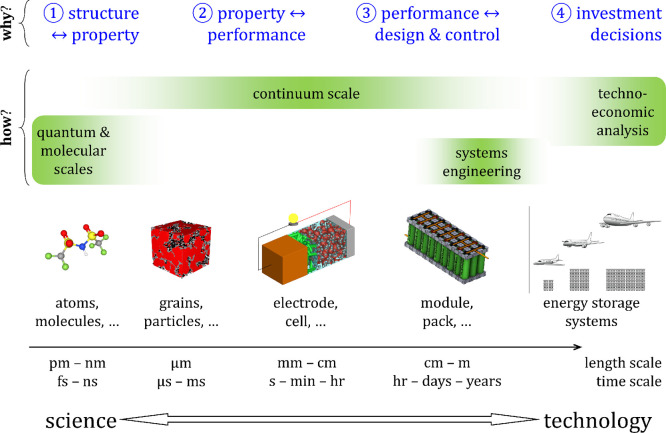
One can condense the development cycle for any electrochemical system into answering the four essential why questions identified in Figure 1:
-
1.
Relationship between structure and relevant property, e.g., how the molecular structure of an electrolyte relates to properties describing ion transport. Here structure can be the atomic/molecular structure, the crystal structure of bulk phases, or the porous structure of electrodes. Equivalently, the relevant properties differ.
-
2.
Property ↔ performance relationship describes how different properties (and, in turn, the corresponding processes) come together to define an observable electrochemical response.
-
3.
Design and control deal with how to scale up to commercial systems and their operation. For example, how to combine cells to make a battery pack and modulate its operation.
-
4.
Comparing viability of different electrochemical systems for a given task: a battery designed for electric vehicles is not suitable for electric aircraft or storing energy on the grid.
Figure 1.
Research, development, and deployment tasks in any electrochemical system involve fundamentally four why questions. Each implicitly identifies the length and time scales of interest, thus specifying how to answer these questions using experiments and modeling as the tools. The sub-figures in the bottom panel are drawn as modules of energy storage systems and can be used to represent equivalent examples of other electrochemical systems. [Reprinted with permission from ref (5). Copyright 2020 The Electrochemical Society.]
These four questions are valid across any electrochemical system, since the fundamental interactions, such as ion transport, reactions, porous electrodes, etc., are the common denominator.6 Given the authors’ primary research focus, batteries are used as tangible examples illustrating the concepts, but one can easily find equivalent specific examples for any electrochemical system of interest. Of these four questions, the smaller scale questions, ① and ②, represent the electrochemical sciences and prolong the development process. Any new material comes with its own peculiarities, and its behavior has to be understood sufficiently for commercialization. Electrochemical sciences examine these smaller scale phenomena that are strongly material dependent and prohibit us from naively assuming similarities to previously explored materials (larger scales are comparatively material agnostic).
Physics-based analysis has increasingly become commonplace to quantitatively describe structure ↔ property and/or property ↔ performance relationships and facilitate predictability across scales.7−16 Such model predictions decrease the experimental efforts as well as identify the rate-limiting processes to guide material development, thus rationalizing the otherwise empirical development scheme. An implicit assumption in these physics-based models is that the physics of the material response is accurately known. While the fundamental laws governing material behavior, e.g., conservation of mass, energy balance, etc., are unambiguously known, multiple processes simultaneously contribute to each of these; for example, reactions and transport both contribute to species balance. Furthermore, one has to sufficiently characterize these processes (in terms of relevant constitutive relations and corresponding material properties).
Machine learning (ML), on the other hand, is a type of data-driven modeling that makes predictions without knowing the underlying physics. The data-driven nature of ML substitutes knowledge of the underlying physical mechanisms with many observations of system behavior. This has revolutionized many domains in the past decade,17,18 especially where large datasets are available. Successful ML applications typically rely on abundant data, be it speech patterns to train personal assistants (e.g., Apple’s “Siri”), purchase history to predict consumer preferences (e.g., Amazon), or video data to train self-driving cars (e.g., Comma’s “openpilot”).
This success of ML in the technology sector might lead one to expect a similar shift in the sciences.19,20 However, breakthroughs in science have traditionally relied on our ability to understand, reason, and formalize underlying physical mechanisms. The data-based character of ML appears insufficient to answer such scientific questions. Accordingly, the time scale and nature of the ML revolution in sciences will be different. This dichotomy between the physics-based nature of scientific discoveries and data-driven nature of ML has cornered its visible scientific applications to the data-heavy end of the spectrum, such as automated experiments21 and data-driven predictions for battery aging.22
The electrochemical sciences are meant to offer rational guidelines for designing electrochemical systems. The predictability of the material response is essential to the rational design. Both data-driven and physics-based approaches facilitate predictability and offer complementary information. Accordingly, the choice of analysis is driven by the questions the investigator chooses to ask (a secondary criterion is the efforts required in pursuing each approach). For example, consider making a high-performing Li-ion porous electrode using prescribed materials, such as nickel manganese cobalt oxide (NMC). A data-driven solution is to make multiple porous electrodes—each with different material compositions (active material : carbon : binder weight fractions), porosities, and thicknesses—and carry out electrochemical measurements of the resulting performance across (dis)charge rates of interest. Once such a dataset of controlled factors (compositions, porosities, and thicknesses) and corresponding outcomes (e.g., energy and power) is available, data analysis identifies an optimally performing electrode. Such an approach identifies the optimal electrode within the design space studied, but it does not offer any insight into why this electrode configuration is the optimal one. Therefore, if one were to change the active material to a different chemistry or even just change the particle morphology, the previously generated dataset would lose nearly all usefulness. The physics-based understanding of the porous electrode performance answers the why question by relying on intrinsic material properties (e.g., diffusivities, reaction rate constants, etc.) and predicting the performance differences across a variety of electrodes having different geometrical arrangements. The underlying cause for the resultant performance is precisely identified in this approach, and any ambiguity is related to inaccurate properties or incomplete physics.
Alternatively, if we combine both approaches, we would use the measured performance (data) and the physics rules to characterize the geometrical properties of the electrodes.23 This amounts to creating a structure–property–performance mapping—a generalized thought across many material systems (Figure 1)—that provides more, as well as quantitatively precise, information (e.g., uncertainty bounds) than either of the approaches alone and answers the following questions:
What electrode specifications lead to better performance?
Why a particular electrode specification leads to better performance?
How to translate the understanding developed by studying a particular set of electrode materials to other materials?
Thus, instead of the either-or fallacy, we should explore combinations of physics- and data-driven predictions to unlock the true potential of ML for sciences. A judicious combination of data-driven and physics-based approaches can speed up scientific discoveries by translating mechanistic information across systems using physics (i.e., causation) and substituting unknown or complex physics via data (i.e., correlation). With the help of physics, one can partially relax the data overhead since the physics-constrained behavior can be approximated using a limited dataset. This is particularly suited for ML applications in sciences19 where the observed response satisfies fundamental laws such as energy conservation, entropy generation, charge neutrality, etc. The goal is to improve predictive accuracy while minimizing efforts. This approach also aids in the development of transferable functions. In a conventional physics-based analysis, the accuracy is improved by progressively introducing advanced constitutive relations, while the fundamental laws remain unchanged (for example, replacing dilute solution theory with concentrated electrolyte transport). In a typical data-driven model, the accuracy is improved by adding data points. If sufficient data is available, the underlying physics can be approximated, and if the physics is accurately known, the observed behavior can be explained. However, either approach becomes prohibitively expensive as more accuracy is desired. If pursued alone, accuracy and efforts scale positively for each approach. For scientific discoveries, neither sufficient data nor accurate physics is known, and a suitable combination of the two approaches is an efficient path forward to simultaneously improve accuracy and reduce efforts. The subsequent electrochemical examples will illustrate these ideas. The examples are presented in the order of increasing length and time scales in Figure 1.
Predicting Material Properties
For Li intercalation materials such as NMC, the thermodynamic energy storage response is prescribed as voltage for different extents of intercalated Li.24 Density Function Theory (DFT) calculations can, in principle, provide this information. However, the task becomes computationally prohibitive if one wishes to compute the open-circuit voltage for all possible combinations of Ni, Mn, and Co contents over multiple Li intercalation states.25 The problem becomes even less tractable in the presence of additional dopants/impurity atoms. Herein, ML surrogates offers a reasonable solution. Based on selected DFT calculations, an ML model can be developed that accurately predicts the inter-species interactions and honors the requisite geometrical symmetries and invariances.26 Using these ML potentials, one can accurately explore the open-circuit voltage over a quaternary composition space of Li, Ni, Mn, and Co. This approach effectively changes how we answer the first question in Figure 1.
ML potentials have vastly improved in accuracy and reliability27,28 and are approaching the accuracy of ab initio methods at a minuscule fraction of the computational cost. Such computational improvements relate to the choice of regression (i.e., approximation of the underlying trends) as well as featurization of the structure information.29,30 The featurizations are also necessary and effective for unsupervised learning in materials classification and inference.31 Additionally, these techniques have been shown to accurately and efficiently expand to many-component systems,32 enabling design searches that were not possible previously. In a recent work, featurization using atom-centered symmetry functions and neural network as the regressor are used to generate the voltage profile and lattice structure dynamics as a function of Li intercalation states for any arbitrary NMC composition, marking the first step toward a computationally feasible optimization workflow for relevant performance properties of cathode material24 and anode materials.33 The ML potentials are seeing incredible progress34 toward increasing the generalizability, extrapolation capabilities, and principled selection of feautrization and hyperparameters.31 Such progress can lead to mapping high-fidelity multi-component (n > 5) phase diagrams to discover new battery electrode and electrolyte materials in the coming years.
Rational Electrode Manufacturing
A philosophically equivalent question arises while defining the mapping from porous electrode structure (mesostructure) to corresponding effective properties such as tortuosity factor. As the mesostructure is set during the electrode manufacturing stage, one can go a step further and correlate electrode manufacturing to mesostructure properties. For the same electrode materials, the mesostructure properties describe the variations in the electrochemical performance. While the physical modeling of the manufacturing processes has received some attention,35−37 the data-driven approaches38 are just emerging. We essentially face two interrelated challenges: unraveling the influence of manufacturing parameters (e.g., recipe, calendering pressure) and determining the role of different processing steps on the final electrode mesostructure.
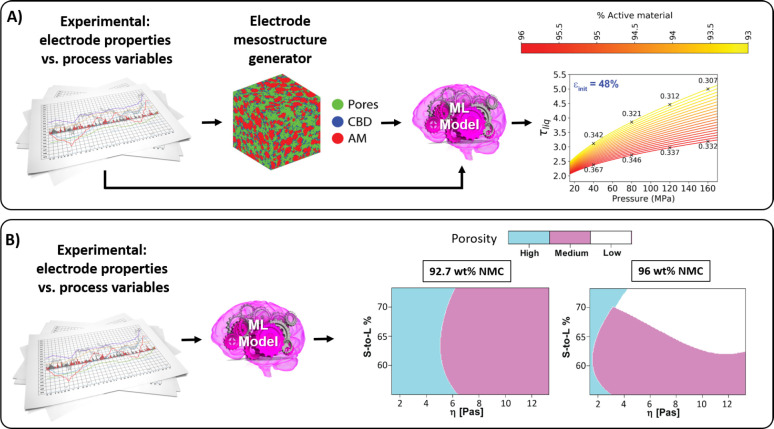
Classically, physical models can be used to simulate each process step and combine them through sequential multiscale coupling.15 For example, calculated electrode slurries40 can be used in the simulation of their drying,35 and the dried electrode mesostructures can be used as inputs for calendering simulations.41 The resulting geometrical arrangement the electrodes can then be used in electrochemical performance simulators to establish the manufacturing–mesostructure–performance links.36 ML models are efficient tools in ensuring the experimental validity of such involved multiscale computational models. For instance, ML models have been used to correctly parameterize force fields used in the coarse-grained simulation of electrode slurries.40 They ensured a proper matching of calculated and experimental properties (e.g., viscosity vs applied shear rate) with about 20 times reduction in efforts—from 6 months to 8 days—compared to manual parameterization.40 ML can be also used in combination with surrogate models to bypass these expensive physical simulations, which usually solve the dynamics of a very significant number of particles37,40), and to accelerate the manufacturing parameters’ optimization. For instance, a surrogate modeling approach informed with experimental data to predict electrode mesostructures in three dimensions and their properties has been recently proposed.39 The experimental data and the surrogate model results are used to successfully train a ML model to be able to predict the influence of calendering conditions on the electrode properties, such as the tortuosity factor (Figure 2a).
Figure 2.
(a) Example of a workflow coupling experimental data, a surrogate electrode mesostructure predictor, and ML (Sure Independent Screening and Sparsifying Operator) to predict the impact of electrode composition, initial porosity, and calendered pressure on the electrode tortuosity factor. [Reprinted with permission from ref (39). Copyright 2020 Elsevier.] (b) Example of a classification machine learning algorithm (Support Vector Machine) able to predict the impact of the percentage of NMC active material, solid-to-liquid ratio, and viscosity of the slurry on the final porosity of a lithium ion battery positive electrode. [Reprinted with permission from ref (38). Copyright 2019 Wiley-VCH GmbH.]
Another way to approach these problems is to apply ML directly to experimental data. This works only if accurate experimental measurements are available for electrodes prepared under different conditions—composition, solid-to-liquid ratio, etc. ML has been employed to map electrode properties, e.g., porosity as a function of the manufacturing conditions, as shown in Figure 2b.38 Once such a mapping is generated, it is used to identify optimal conditions for electrode manufacturing.
Accurate 3D Mesostructures
Instead of sequentially building mesostructure ↔ effective properties and effective properties ↔ electrochemical performance relationships, if detailed mesostructure information is available, one may directly simulate electrochemical interactions at the pore scale. X-ray computed tomography (XCT) and other advances in 3D imaging allow us to study the composition and structure of critical materials as manufactured, rather than using idealized representations. The use of such realistic geometries is directly related to higher fidelity predictions of the electrochemical responses of these materials. However, many challenges are prevalent in obtaining accurate 3D mesostructures, including image segmentation (i.e., assigning correct material phase to each voxel) and the effort required for 3D imaging, resulting in limited datasets.
Convolutional neural networks (CNNs) are particularly suited for image segmentation using supervised learning methods. Unlike 2D image analysis in other fields, electrodes are 3D and require appropriate customization to typical CNN algorithms.42,44Figure 3a–c shows a recent application of CNN-based image segmentation for graphite anode materials. In this and other cases,44 CNNs are shown to produce more convincing segmentations than several conventional segmentation approaches. Amazingly, CNNs can even generate segmentations that are, in a sense, more reliable than the training data used to produce them, as they apply their learned rules consistently over the whole volume, which can be difficult for a human when manually segmenting billion-voxel volumes. Crucially, the segmentations are based on features resulting from 3D convolutions, meaning that non-trivial (i.e., not “thresholded”) segmentations result and imaging artifacts (such as varying brightness) can be overcome. The training itself is the computationally intensive step for CNNs, but once trained, inferences are very fast (orders of magnitude faster than manual segmentation) and repeatable. Such CNNs are specific to particle morphology, i.e., segmenting graphite vs NMC electrodes. In other words, a CNN trained on one electrode can be used to convincingly segment many electrode samples of the same type, but likely not a different particle morphology without additional training.
Figure 3.
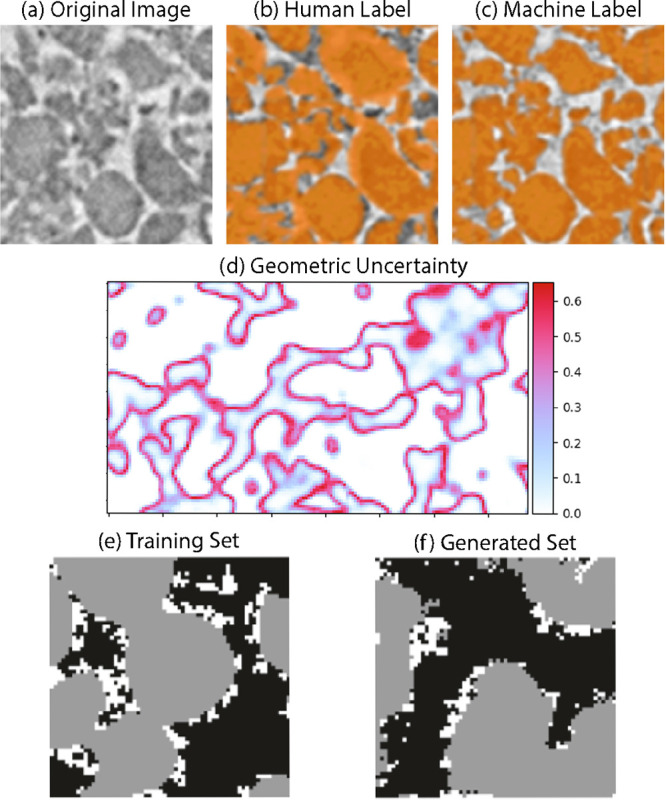
(a–c) Comparison between human (b) and CNN (c) segmentations of 3D XCT images. (d) Bayesian CNNs used to quantify the uncertainty in image segmentations.42 (e, f) Application of GANs to create unique, yet realistic, mesostructures.43
Since training data derived from real images is never perfect, it is important to characterize associated uncertainties. An emerging direction is to combine Bayesian inference with CNNs to quantify uncertainties. By probing the trained variances in the weights of such networks, uncertainty maps can be generated (Figure 3d). 3D image uncertainties can then be propagated to subsequent physics calculations, for example, porosity, effective property, and electrochemical predictions (unpublished results). In addition, following segmentation, Generative Adversarial Networks (GANs) are now being developed to learn the phase arrangement in segmented data and generate mesostructure realizations with customized properties in volumes larger than could be obtained from imaging alone (Figure 3e,f).43
Estimating Properties from Experiments
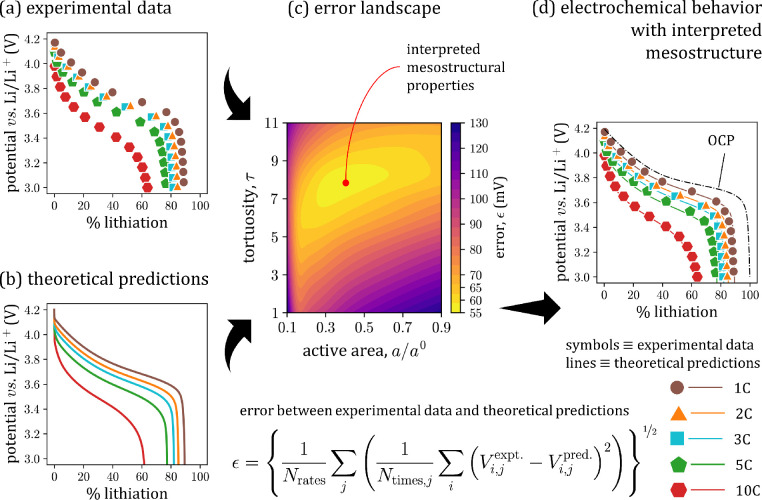
Typically the effective mesostructure properties ↔ electrochemical performance mapping is used to explore how performance varies with effective properties. This mapping can be inverted to characterize effective properties if appropriate performance measurements are available. As shown in Figure 4, first physics-based performance calculations are carried out for multiple effective property combinations. Once such a dataset is available, the data-driven modeling is used to generate such mappings. Subsequently, it is used to estimate mesostructure properties from performance measurements.23 The data-driven modeling avoids explicitly solving the governing equations for all possible combinations of property values, which is prohibitively expensive.
Figure 4.
(a) Measured electrode performance is interpreted using (b) physics-based electrochemical description. (c) The difference between the two is mapped in terms of mesostructure properties using data-driven modeling. The most representative properties are retrieved using this error landscape. (d) Experiments and predictions using interpreted mesostructure properties are shown to illustrate reliability of analysis. [Used with permission from Mistry et al., ref (23).]
For example, consider identifying mesostructure properties, e.g., tortuosity factor, from the electrochemical performance of porous electrodes, as shown in Figure 4. Not every mesostructure property ↔ electrochemical performance mapping can be inverted, and accordingly one must ensure that the mapping is sensitive to every property one wishes to estimate. Figure 4c is an example mapping generated for a given experimental dataset (Figure 4a) and physics-based porous electrode theory responses (Figure 4b) based on a select few property combinations. Herein the sensitivity to each property is achieved by comparing performance at multiple currents (C-rates). The accuracy of such an approach is presented in Figure 4d by comparing measurements against the physics-based predictions using the estimated mesostructure properties.
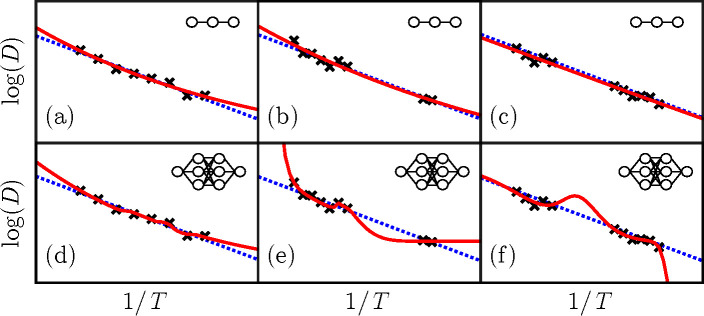
In essence, ML builds reduced order (or surrogate) models from data. The model building is an iterative process where the reliable approximation of the datasets is not known beforehand (refer to “Model Parameters and Data Accuracy” in the Supporting Information). If pursued as a purely data-driven problem, the usefulness of such models is limited. The fidelity of ML predictions is constrained by (i) the quality and quantity of the training data and (ii) the appropriateness of the function representation. It is implicitly assumed that, given sufficient data and suitable function, the necessary trends can be learned efficiently. It is possible that the chosen representation is effort-intensive to learn, and either a customized learning approach (to find model coefficients faster) or a different representation (to speed up learning) is required for a practical ML implementation. To illustrate these nuances, consider having a set of discrete measurements of diffusivity, D, at different temperatures, T. This discrete information needs to be converted into a continuous function for further analysis, such as obtaining activation energies from the slope or using the D = D(T) property relation in a temperature-dependent analysis. In essence, machine learning builds reduced order (or surrogate) models from data.
Figure 5 shows three different datasets in each of the columns, and two different Neural Network (NN) representations are used to learn the underlying trends (each row respectively). The datapoints contain inaccuracies (noise in the measurements). The learning ensures that the model predicts the training data accurately, while a similar accuracy is not necessarily guaranteed for predicting datapoints not part of the training set. For example, Figure 5e,f shows that predicted trends exhibit drastic changes away from the training datapoints. Note that not just extrapolation but also interpolation in between the two data clusters are questionable.
Figure 5.
Data-dependent characteristics of ML are illustrated by learning D(T) relation from discrete datapoints using two NN representations (with Sigmoid activation functions) shown in the insets. Columns represent different data complexity, while rows express model complexity. The solid red line is the trained model in each plot.
Approaching this as a data-driven modeling question, testing the model accuracy on a dataset not used for training can help expose and manage artifacts. The model complexity is intrinsically tied to the accuracy of the dataset. Compare Figure 5, panels b and e, having identical datapoints: the simpler representation in (b) is reliable if the data contains inaccuracies, while the more complex representation in (e) is meaningful if the datapoints are reliable. (“Model Parameters and Data Accuracy” in the Supporting Information further discusses the connection between model complexity and data reliability; model complexity often scales with the number of model parameters.) Alternatively, the physics can guide through this impasse. The slope of log(D) vs 1/T in Figure 5 represents activation energy and is typically a positive and a slowly varying property (if at all). Accordingly, the trends in Figure 5e,f are likely unphysical. These qualifications are easier to make from Figure 5 where a one-dimensional dataset is explored, but become quite difficult to identify when higher dimensional datasets are studied.
Appropriately pre-processing datasets using physical symmetries or geometrical invariances (known as feature engineering), for example, training log(D) vs 1/T, instead of D vs T, helps considerably with building data-driven models. Since any ML implementation relies on data, data generation and curation are crucial steps. If data is generated through experiments, one must ensure repeatability and reproducibility of measurements. Such precautions minimize systematic errors so that the remaining variability is a true random error and analyzed statistically. Instead, if data is generated using physics-based calculations, the accuracy of computed trends in deterministic simulations and reliability of statistics in stochastic simulations must be ensured. Essentially, one should be mindful of the confidence in the raw data and how the uncertainty propagates to predictions. One must also be wary of over-fit models (often nicer-looking fits of the data) that may not be useful or predictive outside of the scope in which they are fit.
Typically, the datasets are not as simple as D = D (T) so that one can visually assess the reliability of the data-driven model. In addition to rigorous verification of model accuracy, we should also focus on interpreting these approximations. Either our intuition needs to evolve to comprehend the information flow or we need to visually express the data-driven models for human interpretation. The interpretation is essential to generating insights from data, identifying limiting mechanisms, and making decisions. When combined with physics, the overall analysis scheme offers both more accurate correlations and clearer causality.45 Most of the examples discussed so far train ML on explicit physics-based calculations (physics-informed mappings). An alternative is to modify the training process to explicitly follow physics-based governing equations46−48 (which should be referred to as physics-encoded mappings).
Materials discovery49−52 is a promising ML application. Atomic- or molecular-scale calculations are performed over a wide range of compounds to map atomic/molecular variations to macroscopically relevant properties. For example, electrolytes with different solvent molecules can be analyzed to map molecular structure to ionic conductivity.53 Such structure-to-property maps (① in Figure 1) reliably compute properties for new structures without having to do explicit physics-based calculations once the map is built. For target property values, these maps can be used in an inverse fashion to identify essential structural attributes for the property targets.54
A seemingly different but philosophically equivalent application is the calculation of effective properties from 3D mesostructures. The traditional approach is to solve 3D species conservation equations. ML can speed this up by mapping 3D mesostructures to corresponding effective properties.39,55 Afterward, new 3D mesostructures of a similar type do not require 3D physics calculations since the physics is implicitly captured in the mapping. Taking this idea a step further, ML can streamline electrode manufacturing–mesostructure–effective properties–electrochemical performance mapping in a physically consistent fashion (Figure 1). Such a mapping allows one to track the influence of a processing step on performance and, in turn, rationally design porous electrodes for the target performance. Present-day electrode processing controls the bulk specifications such as composition and porosity, but with advances in 3D printing, in the future, we should be able to explicitly control electrode arrangement by leveraging the aforementioned structure–property–performance mapping.
An alternative to building such structure ↔ property and property ↔ performance mappings (① and ② in Figure 1) is to simultaneously resolve all scales using a suitable physics-based approach. A new paradigm of exascale computing has been introduced recently that aims to build computing solutions catering to such expensive problems.56 Exascale computing is ideally suited for simultaneously resolving multiple length scales, such as performing DFT or ab initio calculations for length and time scales approaching continuum behavior or simulating electrochemical interactions of large 3D porous electrodes (∼100 μm thick and ∼1000 × 1000 μm2 cross-section) with pore-scale resolution. Alternatively, an appropriate combination of ML and physics-based simulations may offer a computationally less expensive solution where physics-based simulations work at different scales and these scales are coupled through ML. For example, as discussed earlier, the force fields from a DFT simulation can be machine learned and separately used in Molecular Dynamics or Monte Carlo simulations. Such a solution essentially replaces the hardware (e.g., exascale computing) requirements with specialized software development.
As these physics-based simulations produce larger and larger datasets, their interpretation becomes challenging. ML can parse through these datasets to identify relevant information that should be visualized by the researchers. Consider a 3D simulation of an intercalating porous electrode13,36 where multiple small-scale entities jointly reproduce a macroscopic response. Given the sheer number of such entities, it is infeasible (and unnecessary) to visually track each of them. Rather the interest is in visualizing norms and outliers. For this electrode, the representative particles are the ones whose lithiation follows the macroscopic response (the norms) and those severely lagging or leading (i.e., outliers). Unsupervised learning is suitable to parse through the simulation data and identify such representative events.31,57,58 Alternatively, the dimensionality of the data can be reduced to correlate the most essential features.59
An operational constraint in executing such a multiscale investigative scheme is the development time of the physics-based simulation for mesoscale interactions. Smaller (quantum, atomic, molecular) and larger (porous electrode and above) scales have relatively mature computational methods, while the interactions at intermediate scales (mesoscale) range widely, and consequently many methods exist, e.g., phase-field modeling, discrete element method, kinetic Monte Carlo, etc., each suitable for a specific set of interactions, with no off-the-shelf simulation tool that can be directly applied to any new material system. ML can speed up this development by (at least partially) eliminating the overhead for manually learning a new method. Not only can it sift through literature to suggest solutions for a new problem, but it can iterate through multiple simulations and automatically identify meaningful conditions. The hope is to let the researcher focus on understanding mechanisms and automate the tools used to probe these mechanisms. A philosophically similar example is Sony’s recently proposed music creation paradigm which allows the artist to focus on creating the music without having to worry about the required instruments.60The hope is to let the researcher focus on understanding mechanisms and automate the tools used to probe these mechanisms.
While ML offers a new toolset for scientific discoveries, not all ML can revolutionize electrochemical sciences. Any meaningful ML implementation needs to help identify promising materials or pinpoint mechanisms limiting material behavior so that the development cycle for the electrochemical systems can be shortened. Hence, we should focus on adopting and developing ML that provides more insights than before or allows us to pursue questions that have remained unanswered due to effort-intensive existing approaches.
Acknowledgments
A.M. gratefully acknowledges support from Argonne National Laboratory. Argonne National Laboratory is operated for the U.S. Department of Energy Office of Science by UChicago Argonne, LLC, under contract number DE-AC02-06CH11357. A.M. also appreciates inputs from Alex P. Cocco, Ananya R. Balakrishna, Ankit Verma, Arjun Bhasin, Daniel Juarez-Robles, Darren Law, Koffi Pierre Yao, Taylor R. Juaran, and Yuliya Preger that helped streamline the discussions in this Perspective. A.A.F. acknowledges the European Union’s Horizon 2020 Research and Innovation Programme for the funding support through the European Research Council (grant agreement 772873, “ARTISTIC” project: https://www.erc-artistic.eu). A.A.F. also acknowledges his ARTISTIC project team for their hard work and the Institut Universitaire de France for support. S.J.C. is supported by the EPSRC Faraday Institution Multi-Scale Modeling project (https://faraday.ac.uk/, EP/S003053/1, grant number FIRG003). S.A.R. is supported by the Laboratory Directed Research and Development program at Sandia National Laboratories, a multimission laboratory managed and operated by National Technology and Engineering Solutions of Sandia, LLC., a wholly owned subsidiary of Honeywell International, Inc., for the U.S. Department of Energy’s National Nuclear Security Administration under contract DE-NA-0003525. This paper describes objective technical results and analysis. S.A.R. also acknowledges excellent discussions and technical contributions to Figure 3 from Carianne Martinez, Tyler LaBonte, Kevin Potter, and Matthew Smith. V.V. acknowledges support from the Advanced Research Projects Agency-Energy (ARPA-E), U.S. Department of Energy, under Award Number DE-AR0001211. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof.
Biographies
Aashutosh Mistry is a Postdoctoral Appointee in the Chemical Sciences and Engineering Division at Argonne National Laboratory (https://www.anl.gov/profile/aashutosh-mistry). He has received many awards including the MRS Graduate Student Award and the ECS Summer Fellowship. His research interest is understanding mechanisms that limit electrochemical systems. He combines physics-based analysis, data-driven predictions, and controlled experiments to probe such mechanisms.
Alejandro A. Franco is a Full Professor at Université de Picardie Jules Verne in Amiens, France, and ERC Consolidator Grantee (https://www.modeling-electrochemistry.com/). His research interests are in multiscale modeling and ML techniques for the optimization of electrochemical energy devices. Alejandro’s team has recently developed a digital twin prototype of the manufacturing process of lithium ion batteries, involving physical models at different scales and ML models.
Samuel J. Cooper is a Senior Lecturer in energy science and materials design at the Dyson School of Design Engineering at Imperial College London (http://www.imperial.ac.uk/people/samuel.cooper). His research interests include the use of simulation and machine learning to characterise and design electrode materials. Sam’s team has recently developed methods for reconstructing and optimizing microstructure using DC-GANs, as well as ML models for grid-scale load prediction.
Scott A. Roberts is a Principal Research and Development Chemical Engineer in the Engineering Sciences Center at Sandia National Laboratories (https://www.sandia.gov/-sarober/). His research interests are in coupled multiphysics simulations using high-performance computing, and he has won a R&D 100 award for this work. Scott has recently developed ML-enabled image-based simulation technologies, applying them to multiphysics simulations of battery electrodes.
Venkatasubramanian Viswanathan is an Associate Professor of Mechanical Engineering at Carnegie Mellon University (http://www.andrew.cmu.edu/user/venkatv/). He is a recipient of numerous awards, including the MIT Technology Review Innovators Under 35, Alfred P. Sloan Fellowship, Office of Naval Research Young Investigator Award, and National Science Foundation CAREER award. His research interests lie in inventing and optimizing new materials for electrifying transportation, aviation, and chemicals production.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsenergylett.1c00194.
Model Parameters and Data Accuracy: connection between data (how many data points and how accurate) and parameters in the ML approximation; and ML Applications - an Extended List: additional references, categorized as per the underlying why questions, common literature, and interesting non-electrochemical works (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- United Nations Sustainable Development Goals. https://sdgs.un.org/goals [accessed Jan 25, 2021].
- Kenis P. J. A. Electrochemistry for a Sustainable World. Electrochem. Soc. Interface 2020, 29, 41–42. 10.1149/2.F05203IF. [DOI] [Google Scholar]
- Trahey L.; et al. Energy storage emerging: A perspective from the Joint Center for Energy Storage Research. Proc. Natl. Acad. Sci. U. S. A. 2020, 117, 12550–12557. 10.1073/pnas.1821672117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Armand M.; Tarascon J.-M. Building better batteries. Nature 2008, 451, 652–657. 10.1038/451652a. [DOI] [PubMed] [Google Scholar]
- Howey D. A.; Roberts S. A.; Viswanathan V.; Mistry A.; Beuse M.; Khoo E.; DeCaluwe S. C.; Sulzer V. Making a Case for Battery Modeling. Electrochemical Society Interface 2020, 29 (4), 28–32. 10.1149/2.F03204IF. [DOI] [Google Scholar]
- Newman J.; Thomas-Alyea K. E.. Electrochemical systems; John Wiley & Sons, 2012. [Google Scholar]
- Newman J.; Tiedemann W. Porous-electrode theory with battery applications. AIChE J. 1975, 21, 25–41. 10.1002/aic.690210103. [DOI] [Google Scholar]
- Monroe C.; Newman J. The Impact of Elastic Deformation on Deposition Kinetics at Lithium/Polymer Interfaces. J. Electrochem. Soc. 2005, 152, A396. 10.1149/1.1850854. [DOI] [Google Scholar]
- Kumaresan K.; Mikhaylik Y.; White R. E. A Mathematical Model for a Lithium-Sulfur Cell. J. Electrochem. Soc. 2008, 155, A576. 10.1149/1.2937304. [DOI] [Google Scholar]
- Ahmad Z.; Viswanathan V. Stability of Electrodeposition at Solid-Solid Interfaces and Implications for Metal Anodes. Phys. Rev. Lett. 2017, 119, 056003. 10.1103/PhysRevLett.119.056003. [DOI] [PubMed] [Google Scholar]
- Cooper S. J.; Bertei A.; Finegan D. P.; Brandon N. P. Simulated impedance of diffusion in porous media. Electrochim. Acta 2017, 251, 681–689. 10.1016/j.electacta.2017.07.152. [DOI] [Google Scholar]
- Mistry A.; Fear C.; Carter R.; Love C. T.; Mukherjee P. P. Electrolyte Confinement Alters Lithium Electrodeposition. ACS Energy Letters 2019, 4, 156–162. 10.1021/acsenergylett.8b02003. [DOI] [Google Scholar]
- Ferraro M. E.; Trembacki B. L.; Brunini V. E.; Noble D. R.; Roberts S. A. Electrode Mesoscale as a Collection of Particles: Coupled Electrochemical and Mechanical Analysis of NMC Cathodes. J. Electrochem. Soc. 2020, 167, 013543. 10.1149/1945-7111/ab632b. [DOI] [Google Scholar]
- Mistry A.; Usseglio-Viretta F. L. E.; Colclasure A.; Smith K.; Mukherjee P. P. Fingerprinting Redox Heterogeneity in Electrodes during Extreme Fast Charging. J. Electrochem. Soc. 2020, 167, 090542. 10.1149/1945-7111/ab8fd7. [DOI] [Google Scholar]
- Franco A. A.; Rucci A.; Brandell D.; Frayret C.; Gaberscek M.; Jankowski P.; Johansson P. Boosting Rechargeable Batteries R&D by Multiscale Modeling: Myth or Reality?. Chem. Rev. 2019, 119, 4569–4627. 10.1021/acs.chemrev.8b00239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bai P.; Cogswell D. A.; Bazant M. Z. Suppression of Phase Separation in LiFePO4 Nanoparticles During Battery Discharge. Nano Lett. 2011, 11, 4890–4896. 10.1021/nl202764f. [DOI] [PubMed] [Google Scholar]
- Artificial Intelligence: the Future of Humankind; Giibs N., Ed.; Time Inc. Books, 2017. [Google Scholar]
- Park A.Machines Treating Patients? It’s Already Happening. Time, March 31, 2019. https://time.com/5556339/artificial-intelligence-robots-medicine/ [Google Scholar]
- Stevens R.; Taylor V.; Nichols J.; MacCabe A. B.; Yelick K.; Brown D.. AI for Science, February 2020. https://www.anl.gov/ai-for-science-report [accessed Sep 6, 2020].
- Aykol M.; Herring P.; Anapolsky A. Machine learning for continuous innovation in battery technologies. Nature Reviews Materials 2020, 5, 725–727. 10.1038/s41578-020-0216-y. [DOI] [Google Scholar]
- MacLeod B. P.; et al. Self-driving laboratory for accelerated discovery of thin-film materials. Science Advances 2020, 6, eaaz8867. 10.1126/sciadv.aaz8867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Attia P. M.; Grover A.; Jin N.; Severson K. A.; Markov T. M.; Liao Y.-H.; Chen M. H.; Cheong B.; Perkins N.; Yang Z.; et al. Closed-loop optimization of fast-charging protocols for batteries with machine learning. Nature 2020, 578, 397–402. 10.1038/s41586-020-1994-5. [DOI] [PubMed] [Google Scholar]
- Mistry A.; Trask S.; Dunlop A.; Jeka G.; Polzin B.; Mukherjee P. P.; Srinivasan V.. Quantifying Negative Effects of Carbon-binder Networks from Electrochemical Performance of Porous Li-ion Electrodes, 2021, under review.
- Houchins G.; Viswanathan V. Towards Ultra Low Cobalt Cathodes: A High Fidelity Computational Phase Search of Layered Li-Ni-Mn-Co Oxides. J. Electrochem. Soc. 2020, 167, 070506. 10.1149/2.0062007JES. [DOI] [Google Scholar]
- Min K.; Kim K.; Jung C.; Seo S.-W.; Song Y. Y.; Lee H. S.; Shin J.; Cho E. A comparative study of structural changes in lithium nickel cobalt manganese oxide as a function of Ni content during delithiation process. J. Power Sources 2016, 315, 111–119. 10.1016/j.jpowsour.2016.03.017. [DOI] [Google Scholar]
- Bartók A. P.; Kondor R.; Csányi G. On representing chemical environments. Phys. Rev. B: Condens. Matter Mater. Phys. 2013, 87, 184115. 10.1103/PhysRevB.87.184115. [DOI] [Google Scholar]
- Behler J. Perspective: Machine learning potentials for atomistic simulations. J. Chem. Phys. 2016, 145, 170901. 10.1063/1.4966192. [DOI] [PubMed] [Google Scholar]
- Nguyen T. T.; Székely E.; Imbalzano G.; Behler J.; Csányi G.; Ceriotti M.; Götz A. W.; Paesani F. Comparison of permutationally invariant polynomials, neural networks, and Gaussian approximation potentials in representing water interactions through many-body expansions. J. Chem. Phys. 2018, 148, 241725. 10.1063/1.5024577. [DOI] [PubMed] [Google Scholar]
- Bartók A. P.; Kondor R.; Csányi G. On representing chemical environments. Phys. Rev. B 2013, 87, 184115. 10.1103/PhysRevB.87.184115. [DOI] [Google Scholar]
- Himanen L.; Jäger M. O.; Morooka E. V.; Canova F. F.; Ranawat Y. S.; Gao D. Z.; Rinke P.; Foster A. S. DScribe: Library of descriptors for machine learning in materials science. Comput. Phys. Commun. 2020, 247, 106949. 10.1016/j.cpc.2019.106949. [DOI] [Google Scholar]
- Ceriotti M. Unsupervised machine learning in atomistic simulations, between predictions and understanding. J. Chem. Phys. 2019, 150, 150901. 10.1063/1.5091842. [DOI] [PubMed] [Google Scholar]
- Artrith N.; Urban A.; Ceder G. Efficient and accurate machine-learning interpolation of atomic energies in compositions with many species. Phys. Rev. B: Condens. Matter Mater. Phys. 2017, 96, 014112. 10.1103/PhysRevB.96.014112. [DOI] [Google Scholar]
- Babar M.; Parks H. L.; Houchins G.; Viswanathan V. An accurate machine learning calculator for the lithium-graphite system. Journal of Physics: Energy 2021, 3, 014005. 10.1088/2515-7655/abc96f. [DOI] [Google Scholar]
- Smith J. S.; Isayev O.; Roitberg A. E. ANI-1: an extensible neural network potential with DFT accuracy at force field computational cost. Chemical Science 2017, 8, 3192–3203. 10.1039/C6SC05720A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ngandjong A. C.; Rucci A.; Maiza M.; Shukla G.; Vazquez-Arenas J.; Franco A. A. Multiscale Simulation Platform Linking Lithium Ion Battery Electrode Fabrication Process with Performance at the Cell Level. J. Phys. Chem. Lett. 2017, 8, 5966–5972. 10.1021/acs.jpclett.7b02647. [DOI] [PubMed] [Google Scholar]
- Chouchane M.; Rucci A.; Lombardo T.; Ngandjong A. C.; Franco A. A. Lithium ion battery electrodes predicted from manufacturing simulations: Assessing the impact of the carbon-binder spatial location on the electrochemical performance. J. Power Sources 2019, 444, 227285. 10.1016/j.jpowsour.2019.227285. [DOI] [Google Scholar]
- Srivastava I.; Bolintineanu D. S.; Lechman J. B.; Roberts S. A. Controlling Binder Adhesion to Impact Electrode Mesostructures and Transport. ACS Appl. Mater. Interfaces 2020, 12, 34919–34930. 10.1021/acsami.0c08251. [DOI] [PubMed] [Google Scholar]
- Cunha R. P.; Lombardo T.; Primo E. N.; Franco A. A. Artificial Intelligence Investigation of NMC Cathode Manufacturing Parameters Interdependencies. Batteries & Supercaps 2020, 3, 60–67. 10.1002/batt.201900135. [DOI] [Google Scholar]
- Duquesnoy M.; Lombardo T.; Chouchane M.; Primo E. N.; Franco A. A. Data-driven assessment of electrode calendering process by combining experimental results, in silico mesostructures generation and machine learning. J. Power Sources 2020, 480, 229103. 10.1016/j.jpowsour.2020.229103. [DOI] [Google Scholar]
- Lombardo T.; Hoock J.-B.; Primo E. N.; Ngandjong A. C.; Duquesnoy M.; Franco A. A. Accelerated Optimization Methods for Force-Field Parametrization in Battery Electrode Manufacturing Modeling. Batteries & Supercaps 2020, 3, 721–730. 10.1002/batt.202000049. [DOI] [Google Scholar]
- Ngandjong A. C.; Lombardo T.; Primo E. N.; Chouchane M.; Shodiev A.; Arcelus O.; Franco A. A. Investigating electrode calendering and its impact on electrochemical performance by means of a new discrete element method model: Towards a digital twin of Li-Ion battery manufacturing. J. Power Sources 2021, 485, 229320. 10.1016/j.jpowsour.2020.229320. [DOI] [Google Scholar]
- LaBonte T.; Martinez C.; Roberts S. A.. We Know Where We Don’t Know: 3D Bayesian CNNs for Credible Geometric Uncertainty. arXiv Preprint 2019, arXiv: 1910.10793. https://arxiv.org/abs/1910.10793.
- Gayon-Lombardo A.; Mosser L.; Brandon N. P.; Cooper S. J. Pores for thought: generative adversarial networks for stochastic reconstruction of 3D multi-phase electrode microstructures with periodic boundaries. npj Computational Materials 2020, 6, 82. 10.1038/s41524-020-0340-7. [DOI] [Google Scholar]
- Jiang Z.; Li J.; Yang Y.; Mu L.; Wei C.; Yu X.; Pianetta P.; Zhao K.; Cloetens P.; Lin F.; Liu Y. Machine-learning-revealed statistics of the particle-carbon/binder detachment in lithium-ion battery cathodes. Nat. Commun. 2020, 11, 2310. 10.1038/s41467-020-16233-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schölkopf B.Causality for machine learning. arXiv Preprint 2019, arXiv 1911.10500. https://arxiv.org/abs/1911.10500.
- Raissi M.; Perdikaris P.; Karniadakis G. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. 10.1016/j.jcp.2018.10.045. [DOI] [Google Scholar]
- Weinan E. A proposal on machine learning via dynamical systems. Communications in Mathematics and Statistics 2017, 5, 1–11. 10.1007/s40304-017-0103-z. [DOI] [Google Scholar]
- Ruthotto L.; Haber E. Deep neural networks motivated by partial differential equations. Journal of Mathematical Imaging and Vision 2020, 62, 352–364. 10.1007/s10851-019-00903-1. [DOI] [Google Scholar]
- Allahyari Z.; Oganov A. R. Coevolutionary search for optimal materials in the space of all possible compounds. npj Computational Materials 2020, 6, 55. 10.1038/s41524-020-0322-9. [DOI] [Google Scholar]
- Alshehri A. S.; Gani R.; You F. Deep Learning and Knowledge-Based Methods for Computer-Aided Molecular Design - Toward a Unified Approach: State-of-the-Art and Future Directions. Comput. Chem. Eng. 2020, 141, 107005. 10.1016/j.compchemeng.2020.107005. [DOI] [Google Scholar]
- Sanchez-Lengeling B.; Aspuru-Guzik A. Inverse molecular design using machine learning: Generative models for matter engineering. Science 2018, 361, 360–365. 10.1126/science.aat2663. [DOI] [PubMed] [Google Scholar]
- Ahmad Z.; Xie T.; Maheshwari C.; Grossman J. C.; Viswanathan V. Machine Learning Enabled Computational Screening of Inorganic Solid Electrolytes for Suppression of Dendrite Formation in Lithium Metal Anodes. ACS Cent. Sci. 2018, 4, 996–1006. 10.1021/acscentsci.8b00229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qiao B.; Mohapatra S.; Lopez J.; Leverick G. M.; Tatara R.; Shibuya Y.; Jiang Y.; France-Lanord A.; Grossman J. C.; Gómez-Bombarelli R.; Johnson J. A.; Shao-Horn Y. Quantitative Mapping of Molecular Substituents to Macroscopic Properties Enables Predictive Design of Oligoethylene Glycol-Based Lithium Electrolytes. ACS Cent. Sci. 2020, 6, 1115–1128. 10.1021/acscentsci.0c00475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simonyan K.; Vedaldi A.; Zisserman A.. Deep Inside Convolutional Networks: Visualising Image Classification Models and Saliency Maps. arXiv Preprint, 2014, arXiv:1312.6034. https://arxiv.org/abs/1312.6034.
- Mistry A.; Mukherjee P. P. Deconstructing electrode pore network to learn transport distortion. Phys. Fluids 2019, 31, 122005. 10.1063/1.5124099. [DOI] [Google Scholar]
- Alexander F.; et al. Exascale applications: skin in the game. Philos. Trans. R. Soc., A 2020, 378, 20190056. 10.1098/rsta.2019.0056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie T.; France-Lanord A.; Wang Y.; Shao-Horn Y.; Grossman J. C. Graph dynamical networks for unsupervised learning of atomic scale dynamics in materials. Nat. Commun. 2019, 10, 2667. 10.1038/s41467-019-10663-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kahle L.; Musaelian A.; Marzari N.; Kozinsky B. Unsupervised landmark analysis for jump detection in molecular dynamics simulations. Phys. Rev. Materials 2019, 3, 055404. 10.1103/PhysRevMaterials.3.055404. [DOI] [Google Scholar]
- Hinton G. E.; Salakhutdinov R. R. Reducing the Dimensionality of Data with Neural Networks. Science 2006, 313, 504–507. 10.1126/science.1127647. [DOI] [PubMed] [Google Scholar]
- Flow Machines: AI Assisted Music. https://www.flow-machines.com/ [accessed Nov 2, 2020].
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.