Automated Analysis of Alignment in Long-Leg Radiographs by Using a Fully Automated Support System Based on Artificial Intelligence

Abstract

Purpose

To develop and validate a deep learning–based method for automatic quantitative analysis of lower-extremity alignment.

Materials and Methods

In this retrospective study, bilateral long-leg radiographs (LLRs) from 255 patients that were obtained between January and September of 2018 were included. For training data (n = 109), a U-Net convolutional neural network was trained to segment the femur and tibia versus manual segmentation. For validation data (n = 40), model parameters were optimized. Following identification of anatomic landmarks, anatomic and mechanical axes were identified and used to quantify alignment through the hip-knee-ankle angle (HKAA) and femoral anatomic-mechanical angle (AMA). For testing data (n = 106), algorithm-based angle measurements were compared with reference measurements by two radiologists. Angles and time for 30 random radiographs were compared by using repeated-measures analysis of variance and one-way analysis of variance, whereas correlations were quantified by using Pearson r and intraclass correlation coefficients.

Results

Bilateral LLRs of 255 patients (mean age, 26 years ± 23 [standard deviation]; range, 0–88 years; 157 male patients) were included. Mean Sørensen-Dice coefficients for segmentation were 0.97 ± 0.09 for the femur and 0.96 ± 0.11 for the tibia. Mean HKAAs and AMAs as measured by the readers and the algorithm ranged from 0.05° to 0.11° (P = .5) and from 4.82° to 5.43° (P < .001). Interreader correlation coefficients ranged from 0.918 to 0.995 (r range, P < .001), and agreement was almost perfect (intraclass correlation coefficient range, 0.87–0.99). Automatic analysis was faster than the two radiologists’ manual measurements (3 vs 36 vs 35 seconds, P < .001).

Conclusion

Fully automated analysis of LLRs yielded accurate results across a wide range of clinical and pathologic indications and is fast enough to enhance and accelerate clinical workflows.

Supplemental material is available for this article.

© RSNA, 2020

See also commentary by Andreisek in this issue.

Summary

Fully automatic analysis of long-leg radiographs was reliable and fast, was as accurate as clinical radiologists’ manual assessment, and was also feasible in a clinical environment.

Key Points

• ■ Radiologists’ manual reference measurements of lower-extremity alignment (ie, the hip-knee-ankle angle [HKAA] and femoral anatomic-mechanical angle [AMA]) were strongly correlated with automatic measurements (HKAA: r = 0.994–0.995; AMA: r = 0.918–0.993 [P < .001]) and displayed almost perfect interreader agreement (intraclass coefficients: HKAA, 0.99; AMA, 0.87–0.89).

• ■ Automatic assessment was completed within 3–7 seconds, depending on computational power, compared with 35–164 seconds by radiologists’ manual measurements (P < .001).

Introduction

Radiographic evaluation of the lower extremities based on long-leg radiographs (LLRs) is performed in various degenerative, congenital, and posttraumatic clinical contexts to assess alignment, joint orientation, and leg length. Malalignment is considered a major contributing factor to knee osteoarthritis (1,2), whereas pediatric lower-limb deformities interfere with normal gait and motoric development and predispose individuals to premature degeneration (3). As corrective osteotomy and total knee arthroplasty are planned on LLRs (4,5), their exact radiographic evaluation is a prerequisite for accurate surgical management.

In clinical practice, LLRs are routinely acquired using digital radiography of both lower extremities while the patient is in a weight-bearing, upright, standing position. Alignment is usually quantified by defining distinct anatomic landmarks (4). Traditionally, the hip-knee-ankle angle (HKAA) as the medial angle between the femoral and tibial mechanical axes is used as a well-validated measure of overall alignment (6–8). Although the tibial mechanical and anatomic axes are usually identical (4), this is not true for the femur. Femoral mechanical and anatomic axes deviate by a mean 6°, whereas larger ranges of 2.5°–8.8° have also been reported (9). The femoral anatomic-mechanical angle (AMA) as an orientational measure of femoral alignment is central in assessing femoral deformities (4) and in achieving optimal coronal alignment after total knee arthroplasty (9,10).

Although lower-extremity assessment based on LLRs is highly standardized, widely available, and commonly performed in clinical practice and related research, its use is still debated regarding accuracy and reproducibility. Measurement accuracy is affected by loading (11), flexion (12), rotation (13), image quality (4), software assistance (14,15), and reader experience (16,17). Consequently, inter- and intrareader reliability is variable with excellent (5,18) and poor-to-moderate reliability (16,17,19).

In this era of much-sought standardization of image analysis, there is an as yet unmet clinical need for standardized and reproducible automatic analysis of alignment based on LLRs. Recent advances in machine learning may provide the suitable technical framework (20,21). Hence, this study aimed to develop, train, and validate a deep learning–based diagnostic support system to automatically analyze lower-extremity alignment by quantification of HKAA and AMA in a clinical study sample and in reference to manual reference measurements. Our hypotheses were that LLRs may be automatically and quantitatively evaluated by using this algorithm and that the measurements thus obtained would be as equally precise and accurate as manual reference measurements at a fraction of the associated time demand.

Materials and Methods

Study Design

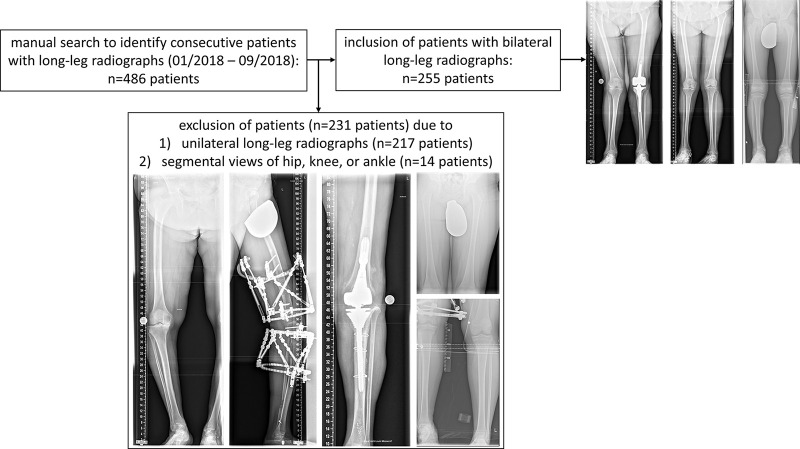
This retrospective study was conducted in accordance with local data-protection regulations. Following approval by the local ethical committee (Reference No. 028/19), the requirement to obtain individual informed consent was waived. Included patients underwent LLR at our institution between January 2018 and September 2018. During that period, a total of 486 patients underwent weight-bearing bilateral LLR in their lower extremities. For methodologic coherence, 231 of these patients were excluded because only one lower extremity had been imaged (n = 217) or only segmental views of the hips, knees, or ankles were available (n = 14) (Fig 1). No further exclusion criteria were defined and, accordingly, radiographs with an incorrect orientation (eg, off-center patellae, suboptimal image quality, or ill-positioned gonad shields or scales) were not excluded. Similarly, patients with orthopedic hardware, skeletal dysplasia, or other skeletal abnormalities or unusual lower-extremity shapes were included to assess the algorithm’s performance across a wide spectrum of indications, age groups, and morphologic characteristics in the clinical routine.

Figure 1:

Flowchart to indicate patient numbers after manual search of the database and after application of inclusion and exclusion criteria.

Overall, 255 patients with 255 bilateral LLRs were included. To realize strict separation of training, validation, and testing data, patients were randomly assigned to the training set (n = 109; 42.7%), validation set (n = 40; 15.7%), and test set (n = 106; 41.6%). The training set was used to train the neural network on image segmentation and algorithm-based postprocessing, whereas the validation set was used to determine optimal model-framework conditions. The yet-unseen test set was subject to the optimized image-segmentation model followed by quantitative postprocessing routines.

Radiograph Acquisition

LLRs were obtained by using two state-of-the-art digital radiographic systems: Philips Digital Diagnost (version 4.1.9, Philips Healthcare) and Siemens Ysio Max (version VF10F, Siemens Healthineers), both equipped with standard x-ray tubes, high-frequency inverter-type x-ray generators, and digital flat-panel detectors (size, 43 × 43 cm). Acquisition protocols were standardized, and each patient was placed on a weight-bearing platform with the patella oriented anteriorly against a motorized vertical detector stand at a source-to-image distance of 300 cm. Depending on patient size, a series of two or three separate overlapping radiographs were acquired and automatically stitched.

Manual Reference Measurements

Each of two clinical radiologists (M.P. and F.M., radiologists-in-training, both with 3 years of experience) performed manual reference measurements on the 106 bilateral LLRs within the test set.

For the unassisted reference measurements, HKAA was determined by using the in-house picture archiving and communication system (iSite, Philips Healthcare) and its standard image-analysis toolbox (ie, centerline, ruler, circle, and angle measures). The following anatomic landmarks were identified by both readers: the center of femoral head, femoral intercondylar point (apex of femoral notch), tibial interspinous point (midpoint of the tibial spines), and tibial midplafond point (midpoint of the outer edges of the malleoli along the tibial plafond). The line along the center of the femoral head and the femoral intercondylar point was defined as the femoral mechanical axis. The line along the tibial interspinous point and the tibial midplafond point was defined as the tibial mechanical axis. The HKAA was measured at the intersection of both mechanical axes on the medial side and given as deviation from straight alignment (180°) (6–8). Accordingly, negative angles indicated varus alignment, whereas positive angles indicated valgus alignment. In healthy adults, the HKAA ranges from 1.0°–1.5° varus (7,8,22), even though it is variable during childhood (6).

For the software-assisted reference measurements, femoral AMA was determined by using a dedicated U.S. Food and Drug Administration–approved and landmark-based software package (mediCAD Classic, Knee 2D, version 6.0; Hectec) that features digital analysis of alignment and joint orientation. Centers of the femoral head, apices of the greater trochanter, medial and lateral femoral condyles and epicondyles, the talus, and the ankle joint line were marked as indicated by the software. Among other angles and measures (14), the software issues the AMA as the angle between the anatomic and mechanical femoral axes, whereas it does not issue the HKAA. Secondary correction of marked points was not possible.

For methodologic coherence, the radiologic reference measurements were performed in well-controlled study conditions by using diagnostic monitors and dedicated workstations with both radiologists blinded to demographic and clinical information. For each radiologist, time demand for bilateral HKAA and AMA measurements was determined on 30 randomly chosen LLRs.

Manual Segmentation

The femoral and tibial bone contours of the bilateral LLRs of the training and validation data were manually segmented as ground truth. M.P. performed the segmentations by using ITK-SNAP 3.8 software (semiautomatic segmentation; Cognitica) (23). Consequently, 298 lower extremities consisting of one femur and tibia each were included from 149 datasets. Segmentation outlines were reviewed by D.T. and S.N. (clinical radiologists, both with 8 years of experience) and modified, if necessary.

Training of Automated Segmentation based on the Neural Network

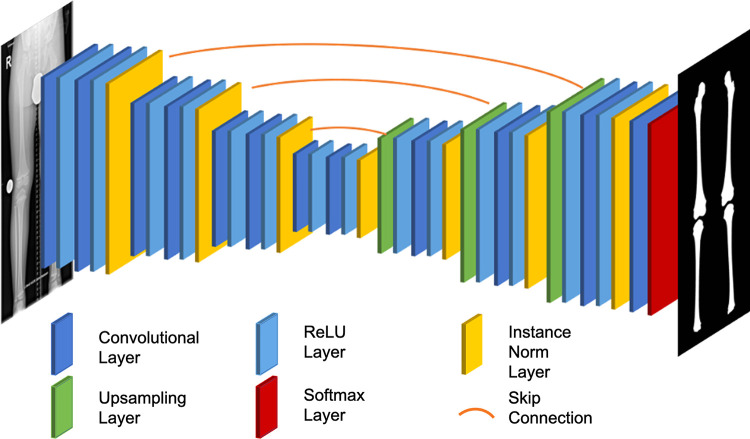
For automatic segmentation of the femoral and tibial bone contours, we used a U-Net convolutional neural network as suggested by others (24). More specifically, the network architecture had a depth of 6, starting at 16 filters per convolution and doubling with each downsampling layer. Moreover, instance normalization and bilinear upsampling followed by a 1 × 1 convolution in the decoder was used. Figure 2 gives details of the network topologic characteristics.

Figure 2:

Graphic view of the neural network topologic characteristics of the deep learning model applied to realize segmentation of femoral and tibial bone contours (right) from bilateral long-leg radiographs (left). By using a U-Net convolutional neural network architecture, the global information contained in the radiograph was compressed to a more compact representation. Fine-grained details were then fed back during upsampling by using skip connections. Upsampling was performed by using bilinear interpolation, and the rectified linear unit (ReLU) was used as an activation function. Normalization layers used instance normalization because of the small batch size.

Images were preprocessed by coarsely splitting each bilateral LLR into right and left images. To standardize inputs, each of the split images was resized to a resolution of 1024 × 256 pixels and rescaled to intensity values ranging from −1 to + 1. Training proceeded by feeding the images of the training set into the neural network; calculating the loss function by comparison with the ground truth segmentation; and calculating weight updates by employing gradient descent with Adam, a widely used algorithm for gradient-based optimization of objective functions (25), and a learning rate of 0.001. We used the focal loss as proposed by Lin et al (26) to increase stability and account for imbalances between foreground and background classes and the softmax classifier to determine the most likely class for each pixel (ie, tibial bone, femoral bone, or background) (27). To avoid overfitting (model correspondence too close with that of the training set), data augmentation in line with standard procedures was used (28). To this end, images were randomly mirrored along the craniocaudal axis, rotated by an angle randomly chosen from the interval (−10°, 10°), and randomly zoomed by a factor ranging from 0.8 to 1.2, with subsequent cropping to the original image size of 1024 × 256 pixels. Training was performed on a state-of-the-art graphics processing unit (GeForce RTX 2080 Ti; NVIDIA) with a batch size of 1.

Automatic Determination of Lower-Extremity Alignment

Femoral and tibial anatomic and mechanical axes were automatically determined based on the segmentation masks. First, the center of the femoral head was determined by fitting a circle to the mediocranial aspect of the segmentation outline of the femoral head. Second, anatomic axes were identified by performing least-squares fitting on the bone-shaft contours. Third, joint-surface lines of the knee and ankle joints were determined by fitting straight lines to the articulating joint surfaces of the segmentation outlines. Fourth, the knee-joint center was defined as the mean of the center points along the joint-surface lines of the femoral condyles and the tibial plateau, whereas the center of the ankle was defined as the center of the distal tibial joint-surface line after eliminating both malleoli from the segmentation outlines. The anatomic reference points and axes were then used to automatically calculate the HKAA and AMA. Figure 3 gives an overview of the successive image postprocessing steps.

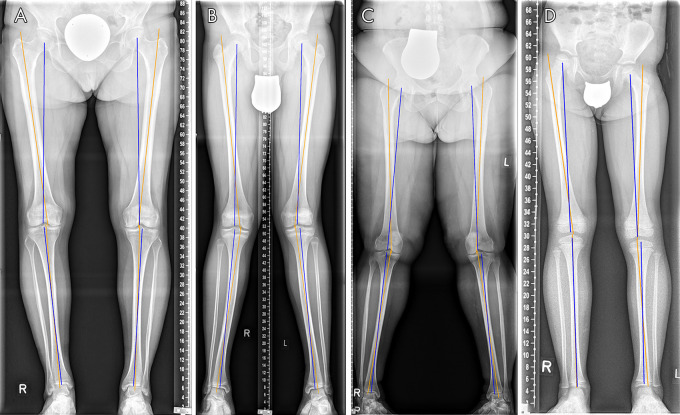
Figure 3:

Original and processed bilateral long-leg radiographs in a 16-year-old male patient after guided correction of both lower extremities by means of temporary femoral hemiepiphysiodesis. A, Original bilateral long-leg radiograph. B, Exemplary display of the manual reference measurements. For illustrative purposes, the femoral anatomic-mechanical angle (AMA) for the right lower extremity (dashed line) and the hip-knee-ankle angle (HKAA) for the left lower extremity (solid line) were determined by using the in-house picture archiving and communication system. C, Automatically determined segmentation outlines of the femoral (red) and tibial (green) bones. D, Automatically determined anatomic landmarks (the apical circumference of the femoral head [yellow], the center of the femoral head [blue], the centers along the tibial and femoral joint surfaces around the knee joint [orange and green], and the center of the distal tibia [red]). E, Automatically determined mechanical (blue) and anatomic (orange) axes of the femur and tibia. These were used to automatically determine the AMA (right, 4.76°; left, 4.41°) and the HKAA (right, 4.40°; left, 0.57° [both varus]).

A detailed description of the algorithm is available in Appendix E1 (supplement), and the entire algorithm is publicly available on GitHub (https://github.com/MSK-Rad/whole-leg-radiographs/tree/v0.1.0).

The total time demand for complete postprocessing of a single bilateral LLR was determined on a dedicated workstation with a state-of-the-art graphics processing unit (Intel Core i7–9700K at 3.60 GHz, Intel; GeForce RTX 2080 Ti, NVIDIA) and on a consumer-grade laptop (Intel Core i5–8259U at 2.3 GHz, Intel; no dedicated graphics processing unit) and compared with manual reference measurements.

Statistical Analysis

Statistical analyses were performed by J.S., D.T., and S.N. by using the Python libraries statsmodels and NumPy, GraphPad Prism software (version 8.4), and R software (version 4.0.2; R Foundation for Statistical Computing). The diagnostic performance of the algorithm-based image analysis was compared against the manual measurements. A priori, the normal distribution of HKAA and AMA values was assessed by using the D’Agostino and Pearson omnibus normality test. Although normality was confirmed in each group for HKAA (ie, radiologist 1 vs radiologist 2 vs artificial intelligence algorithm) (P > .05), normality was not ascertained for the AMA (P ≤ .003). Consequently, groupwise comparisons of the HKAA were performed by using repeated-measures analysis of variance, whereas groupwise comparisons of AMA were performed based on the Friedman test as the former’s nonparametric equivalent. Measurement times were compared by using one-way analysis of variance. Correspondence of manual and automatic segmentation outlines (in the validation set) was quantified by using the Sørensen-Dice coefficient. Interreader agreement was quantified by using the intraclass correlation coefficient. Significance was indicated by a P value less than or equal to .05.

Results

Patient Characteristics

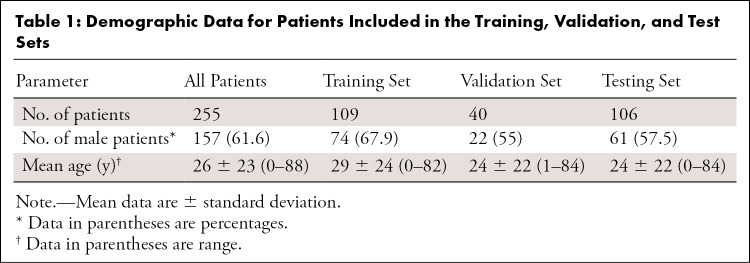
Overall, bilateral LLRs of 255 patients from all age groups (mean age, 26 years ± 23 [standard deviation]; range, 0–88 years; 157 male patients) were included. Consequently, bilateral LLRs were randomly divided into training (n = 109), validation (n = 40), and test (n = 106) data (Table 1). Orthopedic hardware was present in 38% (41 of 109), 28% (11 of 40), and 34% (36 of 106) of the training, validation, and test datasets. Unusual morphologic characteristics, defined as moderate-to-severe leg length discrepancy (>2 cm), substantial bone defects, excessive varus or valgus morphotypes with anatomic axis deviations of at least 10° valgus or less than 0° varus, bone tumors or tumorlike lesions, and skeletal dysplasia (ie, grossly abnormal bone shapes) were present in 37% (40 of 109), 45% (18 of 40), and 36% (38 of 106) of the training, validation, and test datasets, respectively.

Table 1:

Demographic Data for Patients Included in the Training, Validation, and Test Sets

Segmentation Performance

Correspondence between automatic and manual segmentations were evaluated on the validation set, as manual segmentations were not available for the test set. Mean Sørensen-Dice coefficients of 0.97 ± 0.09 for femora and 0.96 ± 0.11 for tibias were determined, indicating excellent correspondence between manual and automatic segmentations.

Interreader Agreement and Comparisons with Artificial Intelligence Algorithm

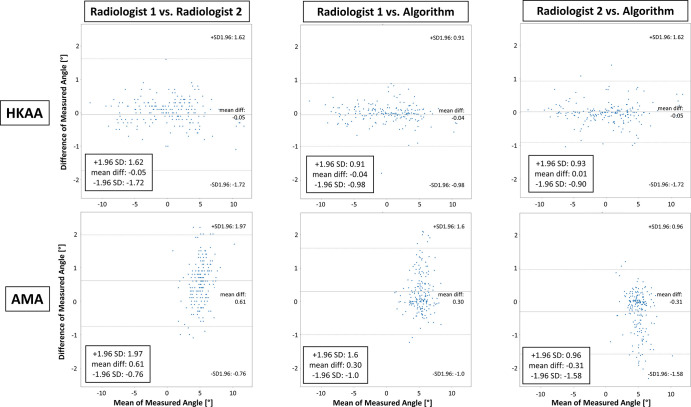
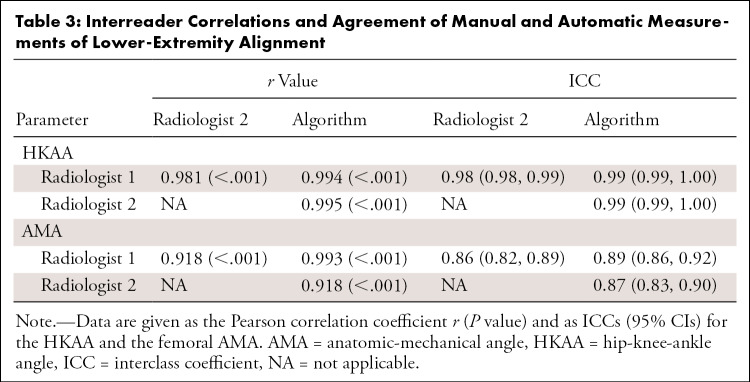
On the test set, quantitative evaluation of alignment revealed high interreader agreement. Table 2 and Figure E1 (supplement) show quantitative details of the HKAA and AMA measurements. No differences were found for the HKAA (radiologist 1, 0.05° ± 4.41; radiologist 2, 0.11° ± 4.44; artificial intelligence algorithm, 0.10° ± 4.32; P = .5), whereas significant differences were found for the AMA (radiologist 1, 5.43° ± 1.43; radiologist 2, 4.82° ± 1.20; artificial intelligence algorithm, 5.13° ± 1.36; P < .001). Mean interreader differences and differences of measured angles as a function of their means are given in Figure 4. For the HKAA, mean differences ranged from −0.05° (radiologist 1 vs radiologist 2) to 0.01° (radiologist 2 vs artificial intelligence algorithm), whereas for the AMA, mean differences ranged from −0.31° (radiologist 2 vs artificial intelligence algorithm) to 0.61° (radiologist 1 vs radiologist 2). Interreader correlations were strong and highly significant, both for the HKAA and the AMA, with correlation coefficients ranging from 0.981 to 0.995 and from 0.918 to 0.993, respectively (P < .001 each) (Table 3). Similarly, intraclass correlation coefficient scores ranged from 0.98 to 0.99 for the HKAA and from 0.86 to 0.89 for the AMA, indicating almost perfect agreement between readers and methods (Table 3).

Table 2:

Details of Manual and Automatic Measurements of Lower-Extremity Alignment

Figure 4:

Comparative evaluation of manual and automatic assessment of lower extremity alignment based on the hip-knee-ankle angle (HKAA) and the femoral anatomic-mechanical-angle (AMA). Bland-Altman plots display the agreement of both radiologists’ manual reference measurements (radiologist 1 and radiologist 2) and the algorithm-based measurements of both measures. Upper and lower rows detail pairwise comparisons for the HKAA and AMA, respectively, between both radiologists (left column), radiologist 1 and the algorithm (middle column), and radiologist 2 and the algorithm (right column). Note that differences of measured angles are more strongly discretized because of the finite accuracy with which the HKAA and AMA were measured manually. diff = difference, SD = standard deviation.

Table 3:

Interreader Correlations and Agreement of Manual and Automatic Measurements of Lower-Extremity Alignment

Algorithm-based Assessment of Alignment

Figures 5 and 6 show algorithm-based assessment of alignment in example cases with a wide variety of clinical indications, both without (Fig 5) and with orthopedic hardware components (Fig 6). Algorithm-based quantification of alignment proved robust in the presence of bone screws and plates, intramedullary nails, prostheses, ill-positioned protective radiographic shielding equipment, scales, open epiphysial plates, incomplete bone maturation, or eccentric joint positions. Yet segmentation accuracy was adversely affected by orthopedic hardware, extremity configuration, joint degeneration, bone and soft-tissue structure, and image quality (Figs E2 E3 [supplement]).

Figure 5:

Algorithm-based quantitative analysis of lower-extremity alignment in representative patients reflective of the spectrum of clinical indications. A, Female adult patient with bilateral medial compartmental osteoarthritis of the knee joints. B, Male adolescent patient with bilateral valgus deformity. C, Female adult patient with valgus deformity and morbid obesity. D, Female child with dysplasia of the right hip, pelvic obliquity, and leg-length discrepancy. Although the algorithm-based identification of the mechanical (blue) and anatomic axes (orange) was robust and not affected by joint degeneration, A, incomplete bone maturation, B, D, eccentric projection of both patellae, B, C, excess skin folds, C, displaced gonad shields, C, or open epiphysial plates, D, segmentation outlines were rendered focally imprecise. Corresponding original radiographs and segmentation outlines are detailed in Figure E2 (supplement). Units of scales, if present, are centimeters.

Figure 6:

Algorithm-based quantitative analysis of lower-extremity alignment in representative patients reflective of the spectrum of clinical indications. A, Male adolescent patient after guided correction of bone growth through bilateral temporary femoral hemiepiphysiodesis plates, medial malleolar screws, and subtalar arthroereisis. B, Female adult patient after uncemented total hip and knee replacement of the right lower extremity and advanced medial osteoarthritis of the left lower extremity. C, Male adult patient after femoral osteotomy and intramedullary osteosynthesis to induce callus distraction in the shortened femur. D, Female adult patient after posttraumatic surgical reconstruction of the proximal and distal tibia with a range of metallic osteosynthetic materials (ie, bone screws, bone plates, and metallic remnants) still visible. Although the algorithm-based quantification of lower-extremity alignment is robust despite orthopedic hardware, A–D, or the radiographic reference equipment, B, segmentation outlines are focally imprecise. Corresponding original radiographs and segmentation outlines are detailed in Figure E3 (supplement). Otherwise, image details are as described in Figure 5.

Measurement Times

The time demand was significantly different between readers and the artificial intelligence algorithm. Complete postprocessing of a single bilateral LLR took 3 seconds on a dedicated workstation and 7 seconds on a consumer-grade laptop, whereas manual reference measurements took longer (radiologist 1 and radiologist 2: HKAA, 36 seconds ± 6 and 35 seconds ± 6, respectively [P < .001]; AMA, 164 seconds ± 72 and 126 seconds ± 10, respectively [P < .001]).

External Validation of the Algorithm’s Performance

The algorithm’s performance was assessed on consecutive LLRs from an external institution (n = 50). Overall, the mean HKAA and AMA values were largely comparable between the readers and methods, suggesting that the algorithm performs equally well on external data (Appendix E1[supplement]).

Discussion

In this study we aimed to develop an algorithm for the automatic assessment of lower-extremity alignment. The most important findings of this study are that the fully automated and algorithm-based analysis of lower-extremity alignment proposed herein yields accurate and reliable measurements across a wide range of morphologic configurations, irrespective of the presence of orthopedic hardware, and that these measurements are performed within a fraction of the time that is usually needed for manual measurements, suggesting that this algorithm is suitable for integration into clinical workflows.

Machine learning is an important technologic field that may impact musculoskeletal radiologists and their referring health care providers by improving image quality, workflow efficiency, and possibly diagnostic accuracy or reproducibility (21). With ever-growing increases in the use of diagnostic medical imaging at large (29) and demands for quantification of findings (21), machine learning techniques must be integrated into clinical workflows, ideally relieving the radiologists from tedious work while increasing precision and efficiency and reducing subjectivity and variability secondary to fatigue or differences in reader experience. The automatic analysis of LLRs lends itself to such clinical use. Recently, computer-aided quantification of leg-length discrepancy in a pediatric population was presented by Zheng et al (30). By using a standard network architecture that determines bone lengths based on automatically obtained segmentation outlines, leg lengths were automatically determined in 1 second. Even though this algorithm achieved a Sørensen-Dice coefficient of 0.94, indicating high concordance between manual and automatic segmentation outlines, its unsupervised clinical application is questionable because patients with unusual extremity shapes, orthopedic hardware, and scales were excluded (31% of all initially included patients). Still, 5% of automatic segmentations were considered improper (30), thereby highlighting the challenge of balancing robustness with precision and performance. However, as a tool that assists in the radiologic workflow by image pre-evaluation for the radiologist to be confirmed, such algorithms might become indispensable for future high-throughput handling of large image volumes.

In our study, mean Sørensen-Dice coefficients were slightly higher at 0.97 for the femur and 0.96 for the tibia; more importantly, these levels of concordance were achieved without using such wide-ranging exclusion criteria as the ones in the work by Zheng et al (30). We therefore consider our algorithm to be of true clinical value because of its exposure to a wide spectrum of clinical-pathologic indications that demonstrated its performance.

With our algorithm, automatic segmentation was not perfect and was challenged by orthopedic hardware, extremity shape and position, joint degeneration, bone texture and structure, and image quality. Nonetheless, quantification of alignment in terms of the HKAA and AMA proved fairly robust, most likely because segmentation inaccuracies were slight and primarily present in underrepresented configurations (eg, prostheses), anatomic and mechanical axes were still accurately identified if large parts of the femur and tibia were correct, and the long distances between the anatomic landmarks limited the relevance of ill-placed coordinates and resultant quantification errors. Yet more refined quantification of joint-level metrics relevant in the analysis of the deformity underlying the malalignment of the extremity, such as the mechanical lateral distal femoral angle, among others (4), necessitates improved segmentation robustness and accuracy. This may be realized by implementing active shape models, increasing data diversity, and controlling image quality. Active shape models are a priori–defined bone-shape models that are iteratively deformed to fit any bone shape (31) and increase the chances of plausible segmentation (32). Because machine learning depends on sufficiently variable data to generalize well, more diverse training data with as-yet inaccurate segmentations (ie, joint degeneration or orthopedic hardware) may enhance segmentation performance. Control of image quality in terms of technical parameters (resolution and contrast) and extremity position (patella and extremity position) may also optimize performance. Although technically problematic images characterized by inaccurate digital stitching, underexposure, or increased noise may be identified easily, quality control and measurement accuracy in a busy radiologic practice may be more challenging with aberrant extremity positions and rotations. Avoiding erroneous quantification (13) by repeating radiography necessarily has to be balanced against increased radiation exposure. Future approaches that identify the patella relative to the femur may help realize consistent extremity position and image quality. As expected, manual reference measurements were time-consuming and required up to more than 2 minutes per measurement. For this study alone, each radiologist spent more than 1 hour (unassisted) and 3.5–5 hours (software assisted) on relatively simple measurements. Ideal study conditions may have decreased interreader variability as compared with studies that derive reference measurements from clinical-routine radiologic reports. Surprisingly, interreader agreement was lower in software-assisted measurements than in unassisted measurements. First, relatively short femoral distances render ill-placed coordinates more relevant. Second, defining the femoral-shaft axis manually may be prone to variability, even when assisted, especially in bowed configurations. It is against this background that the significant groupwise differences of AMA measurements must be considered, even though, by and large, AMA measurements were consistent between readers. Consequently, the substantial user input necessary to quantify the AMA brings about considerable residual variability (15,33).

External validation of the algorithm’s performance demonstrated its generalizability, thereby underscoring the algorithm’s potential clinical applicability in other institutions. Nonetheless, it requires more comprehensive validation and training for clinical use so that the algorithm prospectively improves radiologists’ workflow efficiency and productivity. Its implementation may involve forwarding acquired images (LLRs) to a dedicated central platform where they undergo analysis (automatic quantification of alignment) and feeding the annotated results back to the radiologist for final checking and signing.

This study had limitations. First, unilateral LLRs were excluded for the sake of methodologic coherence, thereby limiting data diversity. The entire dataset was secondarily tilted to the younger population because local patient management is heavily centered on unilateral LLRs. Because of their a priori exclusion, older patients after joint replacement or internal fixation were underrepresented. Second, the algorithm did not consider additional joint-level metrics for enhanced assessment of the deformity underlying lower-extremity malalignment, which requires improved segmentations. Third, reproducibility of the manual reference measurements (ie, test-retest reliability) was not assessed.

In conclusion, fully automated analysis of LLRs yields accurate results across a wide range of clinical and pathologic indications and is fast enough to enhance and accelerate clinical workflows.