Ring-opening polymerization of ε-caprolactone initiated by tin(II) octoate/n-hexanol: DSC isoconversional kinetics analysis and polymer synthesis

ABSTRACT

The kinetics of ring-opening polymerization (ROP) of ε-caprolactone (ε-CL) initiated by 1.0, 1.5 and 2.0 mol% of stannous(II) octoate/n-hexanol (Sn(Oct)₂/n-HexOH) wase successfully studied by non-isothermal differential scanning calorimetry (DSC) at heating rates of 5, 10, 15 and 20 °C/min. The DSC polymerization kinetic parameters of ε-CL were calculated using differential (Friedman) and integral isoconversional methods (Kissinger-Akahira-Sunose, KAS). The average activation energy (E_a) values obtained from Friedman and KAS methods were in the range of 64.9–70.5 kJ/mol and 64.9–80.4 kJ/mol, respectively. The values of frequency factor (A) were determined from model fitting method using Avrami-Erofeev reaction model. The average values of A for the ROP of ε-CL initiated by 1.0, 1.5 and 2.0 mol% of Sn(Oct)₂/n-HexOH (1:2) were 7.3x10⁷, 2.8x10⁶ and 1.2x10⁶ min⁻¹, respectively. From kinetics studied, the polymerization rate of ε-CL increased with increasing initiator concentration. The performance of Sn(Oct)₂/n-HexOH in the synthesis of poly(ε-caprolactone) (PCL) was investigated by bulk polymerization at temperatures of 140, 160 and 180 °C. Sn(Oct)₂/n-HexOH (1:2) could produce high number average molecular weight ($\overline{M_{\mathrm{n}}}$= 9.0 × 10⁴ g/mol) and %yield (89%) of PCL in a short period of time at Sn(Oct)₂ concentration of 0.1 mol% and temperature of 160°C. The mechanism of the ROP of ε-CL with Sn(Oct)₂/n-HexOH was proposed through the coordination-insertion mechanism.

Introduction

Poly(ε-caprolactone) (PCL) is very attractive polyester due to its versatile properties such as biodegradability, biocompatibility and capable blend with various polymers. PCL is widely interesting in industrial and academic research because of its important applications in packaging, agriculture and biomedical field [1–3]. PCL is frequently used in medical and pharmaceutical applications such as drug delivery systems, suture and scaffold for tissue engineering due to the nontoxic products from degradation process can be eliminated or resorbable by the human body [4–6].

Recently, the ring-opening polymerization (ROP) of ε-caprolactone (ε-CL) is considered as an potential route to obtain the biodegradable PCL with controlled properties. For this manner, effective metal-containing initiators are required to achieve the control ROP of ε-CL. Tin(II) bis(2-ethyl hexanoate) or tin(II) octoate (Sn(Oct)₂), a well-known initiating system, is traditionally utilized in the ROP of cyclic esters [6–11]. In ROP of cyclic esters, Sn(Oct)₂ can be converted into tin alkoxide (Sn(OR)₂), the actual initiator, by reaction with alcohol (R′OH) prior to initiate polymerization [9]. After formation of Sn(OR)₂, the ROP of cyclic esters with this Sn(OR)₂ proceeds by the coordination-insertion mechanism [10,11]. The understanding of this mechanism has impacted the attention of many researchers until now.

Long time ago, the thermal stimulated reactions have been effectively studied by thermoanalytical techniques, especially differential scanning calorimetry (DSC) [12–23]. In the recent years, isoconversional methods such as differential and integral methods, have been used to determine the values of effective activation energy (E_a) as a function of conversion (α) at which an equivalent stage of reaction occurs for various heating rates [12,13]. For the integral isoconversional methods such as Kissinger-Akahira-Sunnose (KAS) [14,15] and Ozawa-Flynn-Wall (OFW) [22,23], the more accurate methods, require the mathematics approximation of the temperature integral for calculation of E_a. Recently, an attempt to use DSC for investigating the kinetics of L-lactide (LL) polymerization with Sn(Oct)₂ catalyst was reported in literature [24]. The experiments were conducted under isothermal mode at constant temperature of 180–220°C. The E_a and pre-exponential factor (A) were calculated using model of reversible lactide polymerization. Li and co-workers [19] also investigated the ROP of ε-CL initiated by titanium(IV) alkoxide (Ti[O(CH₂)₄OCH = CH₂]₄) by DSC technique. The obtained E_a values for this reaction were in the range of 75–86 kJ/mol. From our previous works, the non-isothermal DSC technique was successfully used to study the kinetics of the ROP of ε-CL initiated by different metal-containing initiators such as tributyltin(IV) alkoxides, tin(II) n-butyl L-lactate, tin(II) chloride, dibutyltin(IV) dichloride and tributyltin(IV) chloride [16–18].

Therefore, the objective of this work is to investigate the ROP of ε-CL with Sn(Oct)₂/n-hexanol (n-HexOH) initiating system by non-isothermal DSC. The non-isothermal kinetics of this reaction is studied for the first time by isoconversional methods. The effect of Sn(Oct)₂/n-HexOH concentration on the ROP of ε-CL is also discussed. The catalysis effect of this Sn(Oct)₂/n-HexOH on the synthesis of high molecular weight PCL is investigated by bulk polymerization. Furthermore, the mechanistic aspect for the ROP of ε-CL will be studied and described.

Materials and methods

Materials

ε-Caprolactone (ε-CL) (Acros Organics, 99%) was purified by fractional distillation under reduced pressure. Tin(II) octoate (Sn(Oct₂)) (Sigma-Aldrich, 95%) was purified by vacuum distillation before used. n-Hexanol (n-HexOH) (Scharlau, 99%) were dried over sodium metal and purified by distillation before used. Chloroform (Carlo Erba, 99%) and methanol (Carlo Erba, 99%) were used as received.

Methods

Non-isothermal DSC polymerization

Kinetics of the ROP of ε-CL initiated by 1.0, 1.5 and 2.0 mol% of Sn(Oct)₂/n-HexOH (1:2) were investigated by Perkin-Elmer DSC-7 under non-isothermal condition. The 2 g of ε-CL with Sn(Oct)₂/n-HexOH (1:2) was weighed in a dry vial and stirred vigorously for 10 min. For each experiment, about 5–10 mg of reaction mixture was accurately weighed into an aluminum DSC pan. The samples were heated from 20 to 260 °C at heating rates of 5, 10, 15, and 20 °C/min under a flowing nitrogen atmosphere of 20 mL/min without sample mass lost. The obtained data was analyzed and processed by Pyris DSC-7 software.

Theoretical consideration for non-isothermal DSC kinetics analysis

Normally, the ROP of cyclic ester monomer is exothermic reaction similar to other polymerization reaction. Therefore, the kinetic of ROP can be alternatively investigated by measuring the heat released from polymerization using non-isothermal differential scanning calorimetry (DSC) technique. Under non-isothermal condition, the overall rate of reaction can be determined from Equation (1) [12].

$$\beta \frac{\mathrm{d}\alpha }{\mathrm{d}T}=Aexp\left(-\frac{E_a}{RT}\right)f(\alpha )$$ (1)

where β is heating rate, dα/dT is polymerization rate, A is frequency factor, E_a is activation energy, R is universal gas constant, T is temperature, α is the fraction of monomer conversion determined from ratio of the released heat at any time and heat of polymerization [17] and f(α) is the rection model or the conversion function. The values of E_a and A can be determined by the peak methods or the isoconversional methods [18]. The dependency of E_a values with monomer conversion obtained from isoconversional methods can be used to investigate the complexity of polymerization such as the single or the multiple reactions [12]. The differential isoconversional method of Friedman [20] allows E_a to be determined at each given conversion degree as shown in Equation (2).

$$ln{\left(\frac{\mathrm{d}\alpha }{\mathrm{d}t}\right)}_{\alpha ,i}=ln\left(A_{\alpha }f(\alpha )\right)-\frac{E_{a,\alpha }}{R{T}_{\alpha ,i}}$$ (2)

where the subscript i denotes the ordinal number of a non-isothermal experiment conducted at the heating rate β_i and the subscript α denotes the quantities evaluated at a specific conversion degree. For integral isoconversional method, Kissinger-Akahira-Sunose (KAS) is one of the accurate methods to determine the values of E_a under non-isothermal condition using Murray and White mathematic approximation [13]. The KAS isoconversional method shows the linear relationship between ln(β/T²) and 1/T as shown in Equation (3). From KAS plots, the values of E_a at each monomer conversion can be determined from the slope of these plots.

$$ln\left(\frac{\beta }{T^2}\right)=ln\left(\frac{-RA{f}^{\prime }\left(\alpha \right)}{E_{\alpha }}\right)-\frac{E_{\alpha }}{RT}$$ (3)

When replacing the E_a values obtained at different monomer conversions from Friedman isoconversional method into the compensation effect as shown in Equation (4) [12], the value of A from Equation (2) can be determined.

$$lnA=a{E}_a+b$$ (4)

where a and b are compensation parameters that can be obtained from the linear least-squares best-fit technique with the knowledge of E_i and lnA_i shown in Equation (5). When replacement the reaction models (f_i(α)) at each heating rate into Equation (5), The values of E_i and lnA_i can be determined.

$$ln\left(\frac{\beta (\mathrm{d}\alpha /\mathrm{d}T)}{f_{\mathrm{i}}(\alpha )}\right)=-\frac{E_{\mathrm{i}}}{RT}+ln{A}_{\mathrm{i}}$$ (5)

The values of E_i and lnA_i can be extracted from slope and intercept of the linear plots between ln[dα/dT)/f_i(α)] and 1/T under suitable f_i(α) (highest R² values in the α = 0.2–0.8). When the E_i value shown in Equation (6) is replaced by E₀ which is the average value of E_a obtained from Friedman method combination with a and b values, lnA₀ can be determined [12,18]. Thus, the reaction model (f(α)) can be determined by substituting the E₀ and A₀ into Equation (1) resulting in Equation (6).

$$f(\alpha )={\left(\frac{\mathrm{d}\alpha }{\mathrm{d}t}\right)}_{\alpha ,h}{\left[A_{0}exp{\left(-\frac{E_0}{RT}\right)}_{\alpha ,h}\right]}^{-1}$$ (6)

Synthesis of poly(ε-caprolactone) by bulk polymerization

The ROP of ε-CL with Sn(Oct)₂/n-HexOH (1:2) initiating system were carried out in round-bottomed flask with ground-glass joints and magnetic stirring. To investigate the effectiveness of the Sn(Oct)₂/n-HexOH, ε-CL (4 g) with 0.1, 0.2, 0.3, 0.4 and 0.5 mol% of Sn(Oct)₂/n-HexOH (1:2) were weighted accurately into the reaction flask in a controlled atmosphere glove box under nitrogen gas at room temperature. The flasks were immersed in a pre-heated silicone oil bath at a constant temperatures 140, 160 and 180 °C for 1 h. At the end of polymerization, the flasks were cooled down to room temperature. The crude PCLs were purified by dissolving in chloroform and re-precipitating in cold methanol before drying in a vacuum oven at 45 °C until the constant weight. The chemical structure and the %conversion of the obtained PCLs were characterized by proton nuclear magnetic resonance spectroscopy (¹H-NMR) (Bruker Avance 400). The molecular weight averages and polydispersity (PDI) of the purified PCLs were determined by Water e2695 gel permeation chromatography (GPC) at 40°C with refractive index and viscosity detector. Tetrahydrofuran (THF) was used as an eluent with a flow rate of 1.0 mL/min.

Results and discussion

Non-isothermal DSC kinetic analysis for the ROP of ε-caprolactone initiated by tin(II) octoate/n-hexanol

The polymerization measurement under non-isothermal DSC condition provides good kinetic information under different heating rates in a short period of time. For non-isothermal DSC polymerization, the reaction mixtures of ε-CL with 1.0, 1.5 and 2.0 mol% of Sn(Oct)₂/n-HexOH (1:2) are heated from 20 to 300°C at heating rates of 5, 10, 15 and 20°C/min. Non-isothermal DSC curves for the ROP of ε-CL initiated by 1.0, 1.5 and 2.0 mol% of Sn(Oct)₂/n-HexOH (1:2) in the temperature ranges between 100 and 260°C at various heating rates are displayed in Figure 1. From Figure 1(a–c), it is found that the polymerization exotherms shift to higher temperature range as heating rate increases similar to literatures [17,24,25]. At high heating rate, the curves showed wider and sharper exotherms which are related to the high polymerization rate [16]. From Figure 1(d), the polymerization exotherms obtained from ROP of ε-CL with 1.0 mol% of Sn(Oct)₂/n-HexOH (1:2) system are observed at higher temperature range than 1.5 and 2.0 mol%, respectively. This indicates that the initiator concentration affects the polymerization temperature.

Figure 1.

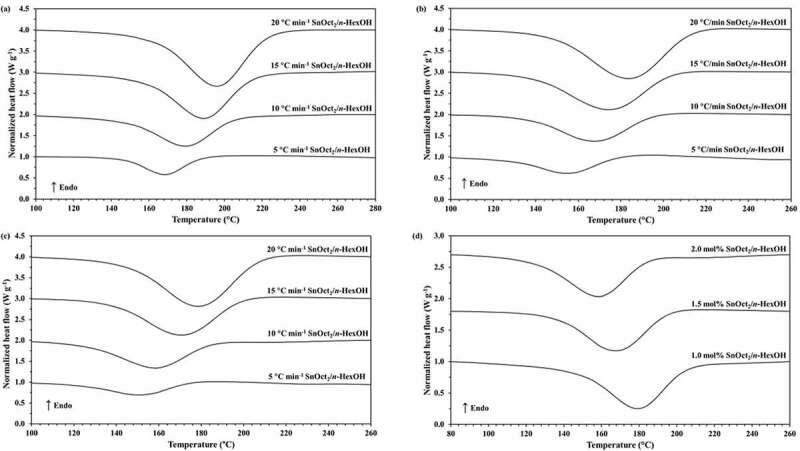
Non-isothermal DSC curves for the ROP of ε-CL initiated by SnOct₂/n-HexOH (1:2): (a) 1.0, (b) 1.5, (c) 2.0 mol% at heating rates of 5, 10, 15 and 20°C/min and (d) non-isothermal DSC curve for the ROP of ε-CL initiated by 1.0, 1.5 and 2.0 mol% Sn(Oct₂)/n-HexOH (1:2) at a heating rate of 10°C/min

From the obtained results in Figure 1, the values of monomer conversion (α) and polymerization rate (dα/dt) can be determined and the plots of monomer conversion and polymerization rate for the ROP of ε-CL initiated by 1.0, 1.5 and 2.0 mol% Sn(Oct)₂/n-HexOH (1:2) against temperature are depicted in Figures 2–3. From Figure 2, it is found that as heating rate increases, the monomer conversion approaches 1 at higher temperature. The monomer conversion for the ROP of ε-CL initiated by 2.0 mol% Sn(Oct)₂/n-HexOH (1:2) reaches 1.0 at lower temperature range than 1.5 and 1.0 mol% Sn(Oct)₂/n-HexOH, respectively. From Figure 3, it is found that the polymerization rate of ε-CL with 2.0 mol% of Sn(Oct)₂/n-HexOH increases to maximum at lower temperature range than 1.5 and 1.0 mol%, respectively. This indicates that the polymerization rate of ε-CL increases with increasing initiator concentration.

Figure 2.

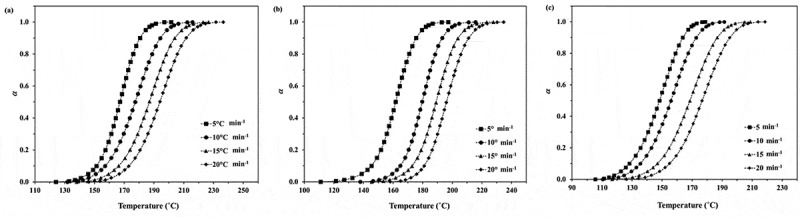
Plots of monomer conversion against temperature for the ROP of ε-CL initiated by (a) 1.0, (b) 1.5 and (c) 2.0 mol% of Sn(Oct)₂/n-HexOH (1:2) at heating rates of 5, 10, 15, and 20°C min⁻¹

Figure 3.

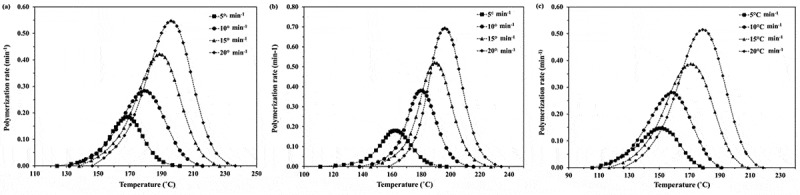
Plots of polymerization rate against temperature for the ROP of ε-CL initiated by (a) 1.0, (b) 1.5 and (c) 2.0 mol% of Sn(Oct)₂/n-HexOH (1:2) at heating rates of 5, 10, 15, and 20°C min⁻¹

From the obtained results, the values of activation energy (E_a) can be effectively determined by the isoconverisonal methods. The assumption in the isoconversional method is that the effective activation energy solely depends on conversion and not on temperature. In this work, the values of E_a for the whole stage of ε-CL polymerization are investigated from Friedman (Equation (2)) and KAS isoconversional method (Equation (3)). The example of KAS plots for the ROP of ε-CL initiated by 1.0, 1.5 and 2.0 mol% of Sn(Oct)₂/n-HexOH (1:2) are presented in Figure 4 and the plots of E_a against monomer conversion are illustrated in Figure 5.

Figure 4.

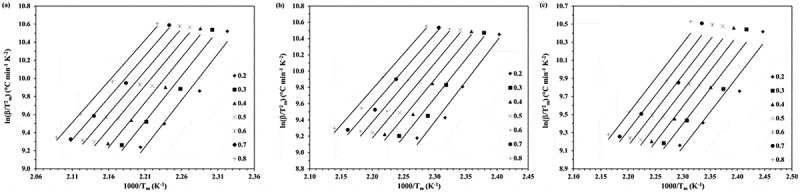
The KAS plots for the ROP of ε-CL initiated by (a) 1.0, (b) 1.5 and (c) 2.0 mol% of Sn(Oct)₂/n-HexOH (1:2)

Figure 5.

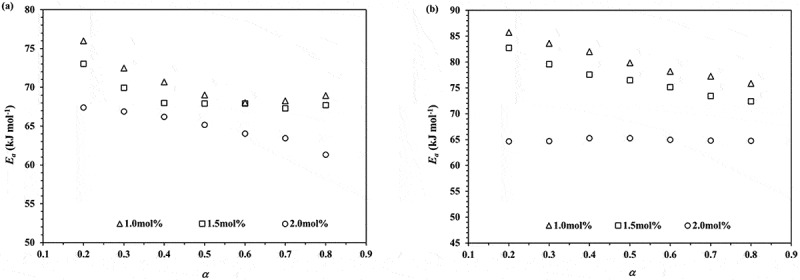
Plots of E_a against monomer conversion obtained from the ROP of ε-CL initiated by 1.0, 1.5 and 2.0 mol% of Sn(Oct)₂/n-HexOH (1:2): (a) Friedman and (b) KAS isoconversional method

From Figure 5, the average E_a values for the ROP of ε-CL initiated by 1.0, 1.5 and 2.0 mol% of Sn(Oct)₂/n-HexOH (1:2) obtained from the Friedman isoconversional method are 70.49 ± 2.89, 68.83 ± 2.04 and 64.93 ± 2.15 kJ/mol, respectively. From KAS isoconversional method, the average E_a values are found to be 80.63 ± 3.57, 76.77 ± 3.59 and 64.94 ± 0.27 kJ/mol, respectively. The KAS isoconversional method is more accurate method in the determination of E_a and can be used to evaluate a single or a multiple step reaction process [9,10]. The values of E_a obtained from 2.0 mol% Sn(Oct)₂/n-HexOH seem to be more constant for the whole stage of polymerization and are lower than 1.5 and 1.0 mol% Sn(Oct)₂/n-HexOH, respectively. The higher rate of polymerization obtained from 2.0 mol% of Sn(Oct)₂/n-HexOH is related to the higher amount of true initiator presented in reaction mixture. As described in literature [10], Sn(Oct)₂ is not a true active specie. Sn(Oct)₂ will react with n-HexOH and convert to tin(II) n-hexoxide (Sn(OnHex)₂) before initiates polymerization of ε-CL. This will be further described in the study of polymer mechanism. To support these findings, the values of frequency factor (A) are also calculated by Equation (2). It is important that the f(α) is required before calculating the A values for the ROP of ε-CL. Thus, Equation (4) can be used to determine the compensation parameter (a and b) with the learning of E_i and lnA_i. From the obtained f(α) at different monomer conversions and heating rates, the best-fitting model can be investigated by comparing the obtained values of f(α) with the theoretical f(α) values shown in Table 1 [12].

Table 1.

Ideal reaction mechanism and kinetics model for solid state reaction [12,18,26]

Model	Symbol	f(α)	Model description
Reaction model	A1 (F1)	(1-α)	Unimolecular decay law (instantaneous nucleation and unidimensional growth)
Nucleation models	A2	2(1-α)[-ln(1-α)]1/2	Avrami-Erofeev (random instant nucleation and 2D growth)
	A3	3(1-α)[-ln(1-α)]2/3	Avrami-Erofeev (random instant nucleation and 3D growth)
	P2	2α1/2	Power law (nuclei growth is a constant)
	P3	3α2/3	Power law (nuclei growth is a constant)
Geometricalcontraction models	R2	2(1-α)1/2	Phase boundary control reaction (contraction area, i.e., bidimensional shape)
	R3	3(1-α)2/3	Phase boundary control reaction (contraction area, i.e., tridimensional shape)
Diffusion models	D1	1/(2α)	1D diffusion (disk particle shape)
	D2	1/[-ln(1-α)]	2D diffusion (cylinder particle shape)

From model fitting method, the E_i and lnA_i values can be determined from the slope and the intercept of the plots between ln[(dα/dt)/fi(α)] and 1/T at different heating rates using apparent model that gives the best linearity for α ranges of 0.2–0.8. The apparent reaction model, namely Avrami-Erofeev nucleation model (f(α) = m(1-α)^m[-ln(1-α)]^m−1/m; m = 1.5 and 2.0) is used to determine compensation parameter [10,21]. From the results, it was found that the Avrami-Erofeev nucleation and growth model (A2) with m = 1.5 yields the best linearity (R² > 0.99) of plots of ln[dα/dt)/f_i(α)] against 1/T for the ROP of ε-CL with Sn(Oct)₂/n-HexOH (1:2) as depicted in Figure 6. The average values of E_i and lnA_i for the ROP of ε-CL with 1.0 mol% Sn(Oct)₂/n-HexOH are 118.2 kJ/mol and 30.8. For 1.5 mol% of Sn(Oct)₂/n-HexOH, the average values of E_i and lnA_i are 105.5 kJ/mol and 28.4. For 2.0 mol% of Sn(Oct)₂/n-HexOH, the average values of E_i and lnA_i are 103.7 kJ/mol and 28.2. The determined compensation parameters for the ROP of ε-CL with Sn(Oct)₂/n-HexOH (1:2) are summarized in Table 2.

Figure 6.

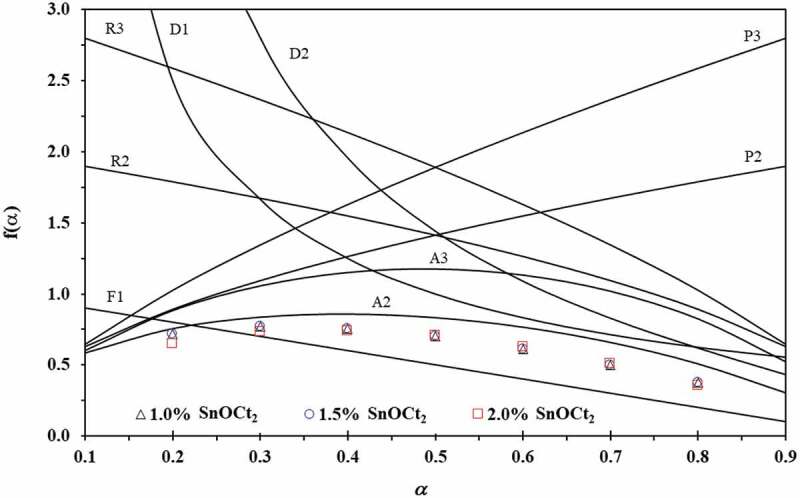
Plots of f(α) against α for the reaction models shown in Table 1 (line) and the experimental plots of f(α) against α for the ROP of ε-CL initiated by 1.0, 1.5 and 2.0 mol% of Sn(Oct)₂/n-HexOH (1:2) at a heating rate of 5 °C min⁻¹ (dot)

Table 2.

Compensation parameters for f(α) = m(1-α)^m[-ln(1-α)]^m−1/m (m = 1.5 and 2.0) for the ROP of ε-CL with Sn(Oct)₂/n-HexOH (1:2) at different heating rates

Initiating systems	Heating rate (°C min−1)	a	b	lnA0
2.0 mol% Sn(Oct)2/n-HexOH (1:2)	5	0.279	−1.77	17.9
	10	0.275	−1.35	18.0
	15	0.269	−0.96	18.0
	20	0.275	−1.35	18.0
1.5 mol% Sn(Oct)2/n-HexOH (1:2)	5	0.289	−1.86	18.0
	10	0.282	−1.32	18.1
	15	0.278	−1.00	18.2
	20	0.273	−0.75	18.0
1.0% Sn(Oct)2/n-HexOH (1:2)	5	0.294	−2.06	17.0
	10	0.289	−1.37	17.4
	15	0.281	−1.00	17.2
	20	0.276	−0.74	17.2

From Table 2, the reaction model can be reconstructed based on Equation (6) by using E₀ and A₀ obtained from all Sn(Oct)₂/n-HexOH. The example plots of f(α) against α for the ROP of ε-CL with all Sn(Oct)₂/n-HexOH initiators at a heating rate of 5 °C/min compare to theoretical models are shown in Figure 6. From the results, it is found that the reconstructed model for the ROP of ε-CL initiated by Sn(Oct)₂/n-HexOH approach to A2 model. Therefore, the A2 model will be used in Equation (5) to determine the values of A. The average values of A for the ROP of ε-CL with 1.0, 1.5 and 2.0 mol% of Sn(Oct)₂/n-HexOH are 7.3x10⁷, 2.8x10⁶ and 1.2x10⁶ min⁻¹, respectively. From the obtained kinetics results, it clearly demonstrates that the concentration of Sn(Oct)₂/n-HexOH affects the kinetics of polymerization. The reactivity of 2.0 mol% Sn(Oct)₂/n-HexOH in the ROP of ε-CL is higher than 1.5 and 1.0 mol% Sn(Oct)₂/n-HexOH, respectively.

Polymerization mechanism and synthesis of poly(ε-caprolactone) via bulk polymerization

The polymerization of ε-CL with Sn(Oct)₂/n-HexOH is proposed through coordination mechanism as depicted in Scheme 1. In the first step, tin(II) alkoxide as Sn(On-Hex)₂ is formed by the exchange reactions between Sn(Oct)₂ and n-HexOH [9–11]. After formation of true Sn(On-Hex)₂ initiator, the initiation step is started by the coordination of carbonyl oxygen of ε-CL with tin atom. After that, the nucleophilic attack of – On-Hex group to carbonyl carbon of ε-CL resulting in the acyl-oxygen bond cleavage of ε-CL ring. From this process, the propagating species (-SnO-) is formed and the propagation step proceeds by the insertion of ε-CL into reactive Sn-O bond presented in these active species.

Scheme 1.

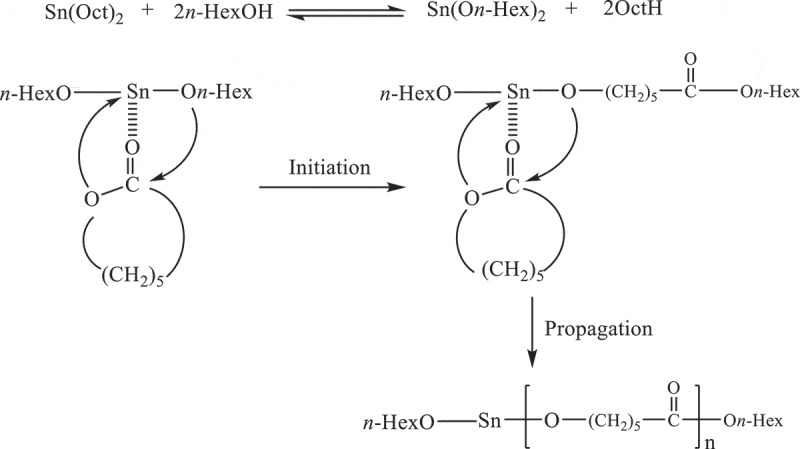
The proposed mechanism of ROP of ε-CL initiated with Sn(Oct)₂/n-HexOH

To confirmed the efficiency of Sn(Oct)₂/n-HexOH in the synthesis of PCLs, the bulk polymerizations of ε-CL with Sn(Oct)₂/n-HexOH are conducted at 140, 160 and 180°C for 1 h. After complete polymerization time, the obtained crude PCLs are dissolved in CHCl₃ and re-precipitation in cold methanol. The molecular weight averages and polydispersity index (PDI) are determined by GPC technique and the results are summarized in Table 3. From Table 3, it is found that Sn(Oct)₂/n-HexOH can control the molecular weight of PCL by adjusting their concentration. The molecular weight of PCL increases with decreasing of Sn(Oct)₂/n-HexOH concentration. The highest molecular weight of PCL ($\overline{M_{\mathrm{n}}}$of 9.0 × 10⁴ g/mol) is obtained at 0.1 mol% of Sn(Oct)₂/n-HexOH and temperature of 160°C. Furthermore, the %yield of all synthesized PCLs are higher than 78%. Based on the obtained results, Sn(Oct)₂/n-HexOH acts as highly efficient initiator in the synthesis of high molecular weight PCL.

Table 3.

Number average molecular weight ($\overline{M_{\mathrm{n}}}$), weight average molecular weight ($\overline{M_{\mathrm{w}}}$), polydispersity index (PDI) and %yield of PCLs from bulk polymerization of ε-CL initiated by Sn(Oct)₂/n-HexOH at 140, 160 and 180 °C for 1 h

Model	Symbol	f(α)	Model description
Reaction model	A1 (F1)	(1-α)	Unimolecular decay law (instantaneous nucleation and unidimensional growth)
Nucleation models	A2	2(1-α)[-ln(1-α)]1/2	Avrami-Erofeev (random instant nucleation and 2D growth)
	A3	3(1-α)[-ln(1-α)]2/3	Avrami-Erofeev (random instant nucleation and 3D growth)
	P2	2α1/2	Power law (nuclei growth is a constant)
	P3	3α2/3	Power law (nuclei growth is a constant)
Geometricalcontraction models	R2	2(1-α)1/2	Phase boundary control reaction (contraction area, i.e., bidimensional shape)
	R3	3(1-α)2/3	Phase boundary control reaction (contraction area, i.e., tridimensional shape)
Diffusion models	D1	1/(2α)	1D diffusion (disk particle shape)
	D2	1/[-ln(1-α)]	2D diffusion (cylinder particle shape)

Conclusions

The kinetics of the ROP of ε-CL initiated by 1.0, 1.5 and 2.0 mol% of Sn(Oct)₂/n-HexOH (1:2) was successfully studied by non-isothermal DSC technique. The isoconversional and model fitting methods were applied to determine the E_a and A values for the ROP of ε-CL with Sn(Oct)₂/n-HexOH. From Friedman and KAS isoconversional kinetics analysis, the E_a values for the ROP of ε-CL with 2.0 mol% of Sn(Oct)₂/n-HexOH were lower than 1.5 and 1.0 mol%, respectively. The average values of A for the ROP of ε-CL initiated by 1.0, 1.5 and 2.0 mol% of Sn(Oct)₂/n-HexOH are 7.3x10⁷, 2.8x10⁶ and 1.2x10⁶min⁻¹, respectively. The reactivity of Sn(Oct)₂/n-HexOH in the ROP of ε-CL was increased with increasing their concentration. From polymer synthesis via bulk polymerization, the molecular weight of PCL was controlled by Sn(Oct)₂/n-HexOH concentration. Sn(Oct)₂/n-HexOH could produce high molecular weight PCL with high %yield in 1 h. The mechanism of the ROP of ε-CL with Sn(Oct)₂/n-HexOH was proposed through the coordination-insertion mechanism. The results from this work may be applied to study the catalytic performance of others initiator in the ROP of cyclic esters.

Funding Statement

This work was supported by the University of Phayao [R020058216005].

Disclosure statement

No potential conflict of interest was reported by the authors.