Abstract
In this work, we present a methodology to identify COVID-19 spreaders using the analysis of the relationship between socio-cultural and economic characteristics with the number of infections and deaths caused by the COVID-19 virus in different countries. For this, we analyze the information of each country using the complex networks approach, specifically by analyzing the spreaders countries based on the separator set in 5-layer multiplex networks. The results show that, we obtain a classification of the countries based on their numerical values in socioeconomics, population, Gross Domestic Product (GDP), health and air connections; where, in the spreader set there are those countries that have high, medium or low values in the different characteristics; however, the aspect that all the countries belonging to the separator set share is a high value in air connections.
Keywords: Complex networks, complex systems, COVID-19, multiplex networks, optimization, social networks
I. Introduction
In the current year (2020), the world has faced a disease caused by SARS-CoV-2, known as COVID-19. This virus began to spread in Wuhan China on December 31, 2019 [1] and, because the virus has spread rapidly throughout the world, it has been determined as a pandemic by the World Health Organization (WHO) in January 2020 [2].
COVID-19 is classified as a virus composed of single-stranded RNA strands, and the symptoms of the disease caused by COVID-19 are headache, dry cough, malaise, fever, and respiratory failure [3]. However, cases of asymptomatic people against the virus have been identified, which implies a real challenge for health institutions.
As of March 31, 2020, the United States has become the epicenter of the pandemic, followed by Italy, Spain, China, and Germany with 186,265, 105,792, 95,923, 82,278, and 71,690 confirmed cases, respectively [4]. These five countries represent 63.4% of the total confirmed cases worldwide. The recovery percentages of this new pandemic are led by China, Spain, Germany, Italy, and Iran with 42.8, 10.8, 9.1, 8.8, and 8.2% of cases. It is essential to mention that in Europe and America, the spread of COVID-19 throughout the world can be attributed to differences in health infrastructure, air travel, human development, and other socio-cultural and economic factors [5]–[7].
Therefore, in this work, we analyze the effect of socio-cultural and economic factors, air travels, human development on both spreading and growth of COVID-19 in each country, using the Vertex Separator Problem (VSP) [8] in multiplex complex networks. Here, it is essential to mention that the data for each topic was obtained from the websites of the European Union (EU) [9], the World Health Organization (WHO) [4], the World Bank (WB) [10], the International Monetary Foundation (IMF) [11] and Transparency International (TI) [12] until May 15, 2020.
On the other hand, a complex network is a network with non-trivial topological characteristics that do not occur in simple networks, such as degree distributions, hierarchical structures, community structures, and high local cohesiveness (measured through the clustering coefficients) [13].
The identification and quantification of influential nodes in complex networks is an essential activity in several application fields, such as the spread and control of diseases [14], the identification of the most influential members of a criminal group [15], to know how impactful are the academic publications [16], to predict future relationships [17]–[19], among others [20], [21].
Currently, there are several measures to identify influential or spreaders nodes in complex networks, where the most classic and important are:
-
•
Closeness Centrality (CC) [22]: Classifies the importance based on the inverse sum of the shortest distances to all other nodes from a central node, measuring the global structure.
-
•
Degree centrality (DC) [23]: Classifies each node based on its degree; therefore, the more connections a particular node has, the more important it is considered.
-
•
Betweenies Centrality (BC) [22]: Classifies the nodes by the number of the shortest paths between any other pair of nodes that cross through it.
In recent years, the study of complex networks and specifically of multilayer networks has been emphasized; this is thanks to the fact that most real systems have structures with multiple types of links or interactions between nodes; for example: Multimodal transport systems, biological systems, social networks and numerous modes of communication [24].
Multiplex networks are a particular class of multilayer networks, which were introduced to better model complex real-world systems [25], [26]. The main characteristic of multiplex networks is that all the nodes in each layer are replicated in other layers, and there is a direct link between each replica node to denote the relationship.
Formally, let 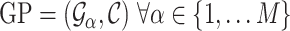 , be a multiplex network where:
, be a multiplex network where:
-
•
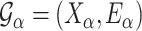 , is a monoplex network called layer
, is a monoplex network called layer 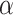 , where
, where 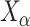 and
and 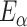 are the set of nodes1 and the links in layer
are the set of nodes1 and the links in layer 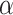 , respectively.
, respectively. -
•
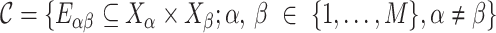 ; is the set of interconnections between nodes in different layers. The elements of
; is the set of interconnections between nodes in different layers. The elements of 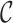 are called cross layers and the elements of each
are called cross layers and the elements of each 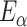 are called intralayer connections of GP.
are called intralayer connections of GP.
The present work is organized as follows: In Related work, we show the main works indicated in the specific literature from previous years related to COVID-19, complex networks, spreaders nodes, and robustness in multiplex networks. In Materials and methods, we describe the main characteristics and the modeling process for monoplex and multiplex networks. In Results, we show the study of the numerical results. In Limitations of the study and discussion, we present the main characteristics and limitations of the work and finally, in Conclusions, we describe the summary of the work.
II. Related Work
As mentioned above, the world is facing a pandemic caused by COVID-19 and, the analysis developed in this work shows that there is different behavior in the development of the disease in different countries. The identification of most spreader nodes in complex systems has led to the development of different methodologies; which are based on the calculation of the structural information of the network or the analogies of statistical physics or mathematical models.
At this point, it is essential to mention that we use the multiplex network approach since there are at least five types of complex systems to analyze (for more information, see Materials and Methods); therefore, we present the main works denoted in the specific literature related to multiplex networks, robustness, spreaders nodes, and COVID-19.
For the methodologies to identify spreaders nodes in networks based on structural information, the most representative works are:
-
•
Zhao et al. [27], present an index to calculate the influence of a node based on the number of communities to which it belongs.
-
•
Berahmand et al. [28], propose a local approach based on the detection and expansion of central nodes. The proposed algorithm can detect all the communities of the graph in a network using local information and identify several functions of the nodes.
-
•
Berahmand et al. [29], propose a new measure of semi-local centrality that can assign higher ranges or structural holes as better diffusers in the network; therefore, the proposed centrality avoids the selection of separators that are very close to each other.
-
•
Berahmand et al. [30], demonstrate that, in data sets with a rich-club, it is better to use degree centrality to find influential nodes because it has linear time complexity and uses local information.
-
•
Berahmand et al. [31], propose a new local classification measure to identify the influence of a node, using the propagation capacity of the nodes based on their essential location parameters, such as the degree of the node, the degree of its neighbors, the standard links between a node and its neighbors and the inverse clustering coefficient.
-
•
Wang et al. [32], study the identification of influential spreaders in complex networks based on several centrality indices.
-
•
His et al. [33] and Han et al. [34] propose some node classification algorithms based on the identification of structural holes. A structural hole is known as the phenomenon that occurs when a node connected to multiple local bridges (multiple communities) is removed, and space is produced.
-
•
Li et al. [35], present a classified neighbor algorithm to quantify the nodal propagation capacity. The results show that the proposed algorithm can effectively control the outbreak of epidemics in many real-world systems.
-
•
Wang et al. [36], propose a measure of influence to quantify the propagation capacity of nodes in complex networks.
-
•
Yan et al. [37], propose a method that takes into account several aspects of node properties, including local topological characteristics, central location, propagation characteristics, and ownership of neighboring nodes.
Most of these strategies are based on the global characteristics of the networks, such as: PageRank [38], LeaderRank [39], Excentricity Centrality [40], ClusterRank [41], K-shell [42], Eigenvector Centrality [43] and Katz Centrality [44].
For statistical physics-based methods, most papers use the percolation model [45]–[47], which is known as the time when the giant component (GC) is formed; for example:
-
•
Radicci et al. [48], present a methodology based on the filtration of links, finding the relationships that make a node more influential or spreader.
-
•
Fei et al. [49], present a methodology based on the inverse square law, where the sum of the attraction between any pair of nodes is used to classify the influence of each node.
-
•
Marone and Makse [46], present a model of immunization of a network against epidemics and argue that the most influential or spreader nodes can be mapped in the optimal filtration.
On the other hand, several optimization models have been presented, where the most representative works are:
-
•
Cheng et al. [50], propose a methodology based on the Influence Maximization Problem (IMP) [51], which identifies a set of nodes that maximizes the influence effect on the network.
Finally, there are some optimization methods to solve the network percolation problem [45], [52], and recently, Montes-Orozco et al. [53] proposed a methodology based on inverse percolation that causes a rupture of the GC in monoplex and multiplex networks.
The main advantage of optimization models is that they can guarantee the optimal solution to the problem. However, some methodologies depend on the topology of the network.
Furthermore, if the nodes are removed randomly, the effect on the transmission is very slight; but, if the deleted nodes are chosen carefully, they can cause the system to colapse. Therefore, finding the elements that are important to network connectivity is of great importance.
Specifically for COVID-19, several mathematical and statistical models have been used in order to predict the behavior of the pandemic and even to evaluate its economic costs. Yuan et al. [54], present a model denoted as iSEIR to chart the pandemic path in Wuhan China, and thus they could precede the date of maximum contagion. Messina et al. [55], developed a network-based model to define the molecular aspects of pathogenic phenotypes in coronavirus infections. Liang et al. [56], developed a mathematical model to predict the propagation rates of three cases of pneumonia: COVID-19, SARS, and MERS.
On the other hand, Chin et al. [57], propose a methodology to identify spatial superspreaders with daily passenger data from public transport in Singapore. Chatterjee et al. [58], developed a stochastic mathematical model to predict the number of infections in India. Cao et al. [59], present an analysis based on several mathematical models to assess the prevention actions that were carried out in Wuhan, and they include that the actions had a crucial effect on the spread of the pandemic.
Finally, Bragazzi et al. [60], and Pham et al. [61], discuss extensively computational techniques and information technologies, artificial intelligence, and Big Data can help manage the enormous amount of data derived from the present pandemic.
III. Materials and Methods
In this section, we present the way of model the multiplex networks, and the methodology to analyze and identify the most spreader countries of COVID-19. This study is divided into four phases, which are:
-
1)
Data collection: In this phase, we build the data set through a statistical analysis applied to the information obtained from the IMF, WB, WHO and IT.
-
2)
Construction of networks: In this phase, based on the similarity of the characteristics for each country, we model the monoplex and multiplex networks.
-
3)
Analysis of spreader nodes: For the modeled networks, we use an adaptation of the VSP to identify spreaders countries in multiplex networks.
-
4)
Analysis of results: In this phase, we show the study of the countries that are classified as spreaders, which cause the rupture of the multiplex networks.
A. Materials
As mentioned above, to model the networks used in this work, we use the information about COVID-19 available on the websites of the European Union (EU) and World Health Organization (WHO); while for the socio-cultural and economic data we use the information available on the websites of the World Bank (WB), the International Monetary Foundation (IMF) and Transparency International (TI).
The information of COVID-19 (infections and deaths), includes the period from 12/31/19 to 05/15/20 and the indicators used to define the socio-cultural-economic characteristics, are: projected real Gross Domestic Product (GDP) (2020), projected consumer prices (2020), special drawing rights (millions), quota (millions), human development index (HDI) (2009-2018), corruption perception index (2018), Gross national income (GNI) per capita, GNI per capita rank minus HDI rank, country population (population/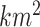 ), real population density (hectares by person), Gini Coefficient, current health expenditure (% of GDP 2000-2016) and air travels (2019-2020).
), real population density (hectares by person), Gini Coefficient, current health expenditure (% of GDP 2000-2016) and air travels (2019-2020).
Specifically, in this work, we modeled two 5-layer multiplex networks; where each layer represents the relationship between each pair of countries 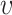 as follows:
as follows:
-
•
Layer 1 (L1), for Human Development Index and its components.
-
•
Layer 2 (L2), for Human Development Index Trends, 1990-2018.
-
•
Layer 3 (L3), for the Inequality-adjusted Human Development Index.
-
•
Layer 4 (L4), for the air travels (inbound and outbound) between each country.
-
•
Layer 5 (L5), L5.1 for the number of infections and deaths network, and L5.2 for the GDP and health network.
These relationships are given by the number of characteristics in which the countries are similar, and their quantification is obtained as follows:
-
•
The Mahalanobis distance between each pair of countries is calculated.
-
•
The median of the Mahalanobis distances is calculated.
-
•
For each pair of countries with a distance less than the median, a link is added.
Here, it is essential to emphasize that, although GDP is frequently used to compare international economies or the air travels are used to analyze the population movement; the idea of modeling five different types of layers is to be able to carry out a classification based on a multi-criteria analysis that allows a stable assessment of the different elements included, thus streamlining the decision-making process.
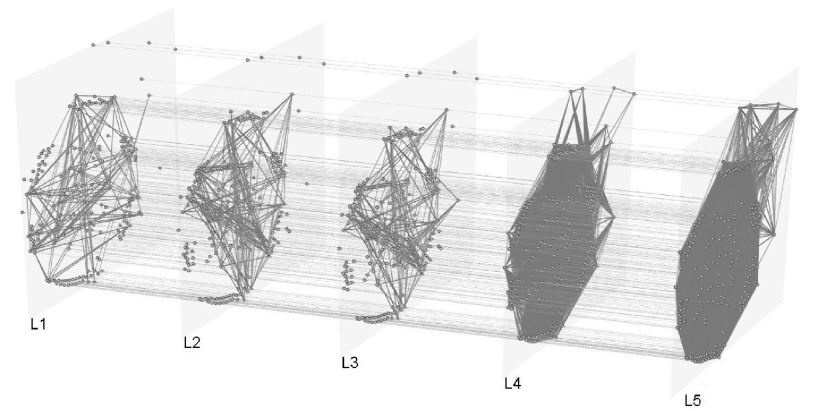
Now, we present Figures 1 and 2, that show graphically the two 5-layer multiplex networks, denoted as infection and GDP, respectively.
FIGURE 1.
Graph of the infection multiplex network.
FIGURE 2.
Graph of the GDP multiplex network.
In this study, each node represents a country, which belongs to all the layers of the multiplex network, where each interlayer link indicates that the two countries are similar in most of the characteristics analyzed, and the intralayer links indicate the identity relationship (main characteristic of multiplex networks).
Then, with the modeled networks, using the approach of VSP in multiplex networks, we develop an analysis about the influence of the countries and the propagation of COVID-19 using the information of the relationship of the main socio-cultural and economic characteristics, the number of flights, as well as the number of infections and deaths caused by COVID-19.
B. Methods
In this work, the VSP is used to identify the spreaders countries. The approach of VSP is based on the robustness in networks finding the nodes that cause the rupture of the GC. In the case of multiplex networks, the GC is denoted as the Mutually Connected Giant Component (MCGC) defined in [62]:
Each node 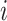 is in the MCGC if it has at least one neighbor
is in the MCGC if it has at least one neighbor 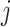 that belongs to the MCGC and if all its replica nodes in each interdependent network are also in the MCGC.
that belongs to the MCGC and if all its replica nodes in each interdependent network are also in the MCGC.
From this definition, Bianconi et al.
[62] deduce that if a node 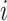 in a particular layer of a multiplex network is in an MCGC, then all its replica nodes in all layers are in the MCGC.
in a particular layer of a multiplex network is in an MCGC, then all its replica nodes in all layers are in the MCGC.
On the other hand, the VSP [53] consists of finding a minimum set of C nodes that, when their links are removed from the network, produce a disconnection from the multiplex network into at least two connected components (A, B), such that 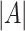 and
and 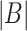 are maximized. Then, the adaptation of VSP can be summarized as:
are maximized. Then, the adaptation of VSP can be summarized as:
-
•
Instance: A MCGC of a multiplex network
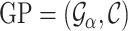 .
. -
•
Problem: Find a partition of nodes belonging to the MCGC of GP that results into three disjoint sets
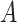 ,
, 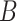 and
and 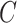 ,
, 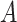 and
and 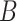 nonempty, such that:
nonempty, such that:
There are no interlayer or intralayer links between the elements belonging to each set
,
or
.
are maximized.
is minimized.
It is essential to mention that we can quantify the robustness and the number of spreaders in the networks by analyzing the percentage of nodes that belong to the separator set 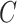 (set of spreaders). For example, a high percentage (more than 70%) of nodes in
(set of spreaders). For example, a high percentage (more than 70%) of nodes in 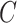 indicates that the network is robust (there are a high number of spreader countries). In contrast, a low percentage (less than 30%) indicates that the network is not very robust (there are a low number of spreader countries).
indicates that the network is robust (there are a high number of spreader countries). In contrast, a low percentage (less than 30%) indicates that the network is not very robust (there are a low number of spreader countries).
Because the original VSP is considered as NP-Hard [8], [63], the adaptation from multiplex networks, is NP-Hard too [64], [65]; therefore, we can solve the adaptation of VSP using a heuristic method.
In this work, we used a simulated annealing algorithm (SA) [66] developed in C language. SA is a technique based on local search, and it is necessary to establish the structure of neighborhoods. In the development of this work, two neighborhoods were used: Hamming distance 12 and Hamming distance 2. Then, the first type of neighborhood is added or deleted one node of the current solution with the following steps:
-
1)
A random number between 0 and 1 is generated.
-
2)
If random ≤ 0.5, one node is removed, otherwise one node is added.
-
3)
To remove an element, it is chosen randomly, giving the same probability to each element that belongs to the current solution.
-
4)
To add an element, it is chosen randomly, giving the same probability to each element that not belongs to the current solution.
For the other neighborhood, two nodes are removed, or two nodes are added, and if it is the case that two nodes can not be removed or added, one is deleted, and a different one is added. With this, the distance of Hamming 2 is maintained.
By last, the algorithm finished when the best solution it is not updated when 50 temperature updates have elapsed or 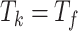 .
.
SA requires 4 control parameters and, in order to obtain a good performance it is important to find the effective parameter settings for the technique. Then, using the Differential Evolution algorithm (DE) [67]; we obtain the following values (for more information, see [68]):
-
•
Initial temperature
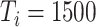 .
. -
•
Final temperature
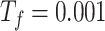 .
. -
•
Cooling program
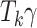 , with
, with 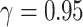 .
. -
•
Times that a new neighbor is generated
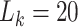 .
.
IV. Results
In this section, we show the results and discussion on the main structural metrics of the modeled networks and the countries that cause the spread of COVID-19.
A. Structural Metrics
In order to facilitate the understanding of the results of the networks structural metrics, we briefly introduce some fundamental concepts:
-
•Clustering coefficient [69]. It quantifies how much a node is interconnected with its neighbors; where, two nodes are neighbors if exist a link that join them, and for non-directed graphs, it is calculated in the following way:
where,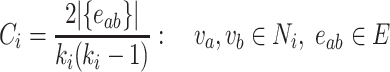
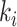 is the degree of the node
is the degree of the node 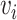 ;
; 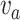 and
and 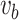 belong to the neighborhood for the node
belong to the neighborhood for the node 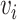 (
(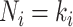 ) and;
) and; 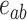 is a subset of the total number of links (
is a subset of the total number of links (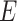 ) that connect any pair of nodes
) that connect any pair of nodes 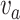 ,
, 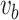 .
.It is essential to mention that, the higher the number of triangles, the greater is the clustering coefficient value.
-
•
Average degree [70]. The degree of a node is the number of links connected to it. Then, the average degree is calculated with the degrees of all the nodes of the network.
-
•
Diameter of the network [71]. It is given by the longest route of all the shortest paths between any pair of nodes.
-
•
Average path length [72]. Defines the average number of steps that must be traveled through the shortest path for all possible pairs of nodes.
In Table 1, we present the numerical values for the average, variance and the low and high limits for each structural metric and the closeness and betweenies centralities with 95% level of certainty (for each layer).
TABLE 1. Structural Metrics of Layers.
| ID | Degree | Clust. C. | Triangles | Closeness C. | Betweenies C. | Diam. | Path L. | |
|---|---|---|---|---|---|---|---|---|
| L1 | Av. | 35.630 | 0.933 | 822.361 | 0.812 | 0.832 | 2 | 1.042 |
| Var. | 421.636 | 0.012 | 335328.341 | 0.042 | 0.047 | |||
| Low L. | 34.178 | 0.921 | 741.032 | 0.742 | 0.815 | |||
| High L. | 40.083 | 0.945 | 921.225 | 0.842 | 0.845 | |||
| L2 | Av. | 38.761 | 0.215 | 823.263 | 0.815 | 0.842 | 3 | 1.099 |
| Var. | 422.462 | 0.092 | 383342.402 | 0.0624 | 0.049 | |||
| Low L. | 33.712 | 0.159 | 729.631 | 0.763 | 0.832 | |||
| High L. | 43.826 | 0.271 | 916.831 | 0.831 | 0.853 | |||
| L3 | Av. | 37.405 | 0.946 | 837.774 | 0.824 | 0.856 | 4 | 1.322 |
| Var. | 423.726 | 0.015 | 395358.351 | 0.064 | 0.051 | |||
| Low L. | 34.515 | 0.929 | 749.520 | 0.789 | 0.824 | |||
| High L. | 40.294 | 0.964 | 926.028 | 0.860 | 0.888 | |||
| L4 | Av. | 190.342 | 0.992 | 20129.969 | 0.971 | 0.985 | 2 | 1.056 |
| Var. | 4.841 | 0.001 | 4842.545 | 0.001 | 0.002 | |||
| Low L. | 186.893 | 0.989 | 20120.201 | 0.970 | 0.984 | |||
| High L. | 193.257 | 0.994 | 20139.736 | 0.973 | 0.986 | |||
| L5.1 | Av. | 3.437 | 0.191 | 5.964 | 0.203 | 0.203 | 1 | 1 |
| Var. | 10.066 | 0.145 | 217.914 | 0.029 | 0.029 | |||
| Low L. | 2.991 | 0.138 | 3.892 | 0.146 | 0.146 | |||
| High L. | 3.882 | 0.245 | 8.036 | 0.260 | 0.260 | |||
| L5.2 | Av. | 54.869 | 0.654 | 1239.767 | 0.549 | 0.634 | 3 | 1.86 |
| Var. | 883.359 | 0.022 | 883668.239 | 0.020 | 0.028 | |||
| Low L. | 50.697 | 0.633 | 1107.825 | 0.529 | 0.610 | |||
| High L. | 59.040 | 0.675 | 1371.709 | 0.569 | 0.657 | |||
Based on the information presented in Table 1, we can see that L1 to L4 and L5.2, have characteristics of the small-world model [73], while the layer 5.1 has characteristics of the scale-free model [74].
For example, L3 has a clustering coefficient of 0.952 and an average path length of 1.32, while L5.1 has 0.191 and 1, respectively. On the other hand, for closeness and betweenies centralities, L1 to L4 and L5.2 have high values, while L5.1 has low values.
B. Identification of Spreaders of COVID-19
In Table 2, we present the numerical values obtained by applying the adaptation of VSP to the MCGC of Infections and GDP networks. In the first column, we show the identifier for each network; in the second column, we present the values for  , and; in the third column, we show the values for
, and; in the third column, we show the values for 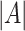 and
and 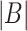 .
.
TABLE 2. Cardinality of Components 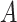 ,
, 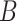 and
and 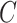 .
.
| Network | |C| | |A| and |B| | Isolated components |
|---|---|---|---|
| Infection | 108 | 42 and 43 | 3 |
| GDP and health | 111 | 36, 26 and 11 | 12 |
It is essential to mention that, in both networks, the MCGC is the total of the nodes (195 countries). On the other hand, we must remember that if  has a value higher than 70% of the total nodes of the MCGC, it is considered robust (there are many spreader nodes). On the other hand, when
has a value higher than 70% of the total nodes of the MCGC, it is considered robust (there are many spreader nodes). On the other hand, when  has a value lower than 30%, the network is not very robust (there are few spreader nodes).
has a value lower than 30%, the network is not very robust (there are few spreader nodes).
According to the results shown in Table 2, we can verify that applying the adaptation of VSP; we can find the set of nodes that cause the rupture of the MCGC for the 5-layer multiplex networks, since the sum of 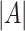 ,
, 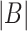 ,
,  and the isolated components (nodes without connections to other nodes) is equivalent to the total number of nodes that belong to the MCGC.
and the isolated components (nodes without connections to other nodes) is equivalent to the total number of nodes that belong to the MCGC.
Furthermore, we can assure that the networks are not robust and that there are many spreader nodes; therefore, we can deduce that the elimination of the links of the countries that are in the separator set, the pandemic caused by COVID-19 can be controlled, since in both networks  is 54% and 56% of the total nodes belonging to the MCGC, respectively.
is 54% and 56% of the total nodes belonging to the MCGC, respectively.
Then, in order to analyze the countries that cause the rupture of the MCGC in the networks, we perform an analysis of the types of countries that cause the spread of COVID-19.
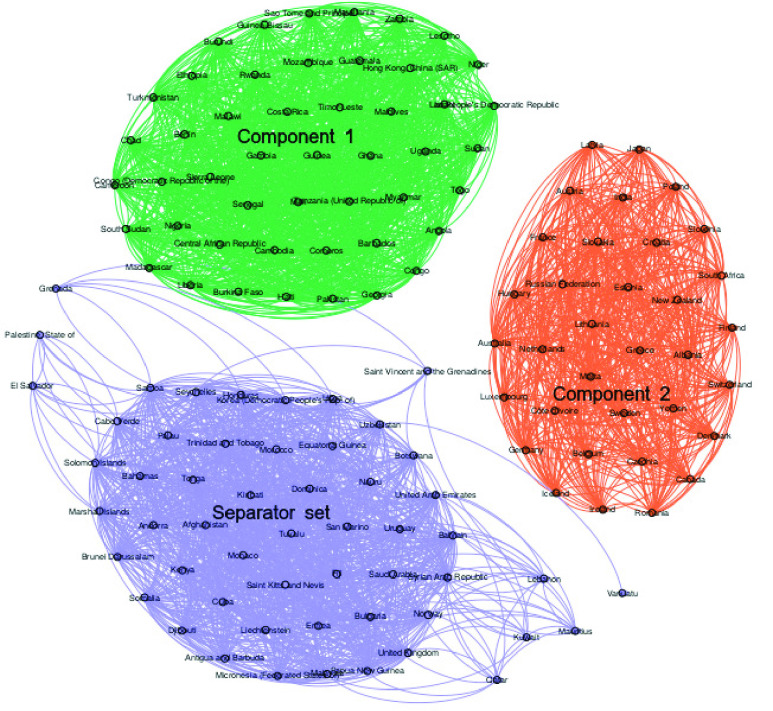
Now, we present Table 3 and Figure 3), which show the countries that belong to each set after the rupture of the MCGC for the infection network.
TABLE 3. Sets of Countries After the Rupture of the MCGC (Infection Network).
| Infection network | |
|---|---|
| Separator set | Norway, Ireland, Hong Kong, Australia, Sweden, Singapore, Netherlands, Denmark, United Kingdom, Liechestein, Austria, Luxembourg, India, Israel, France, Lithuania, Andorra, Qatar, Chile, Croatia, Argentina, Kazahstan, Romania, Kuwait, Bahamas, Malaysia, Serbia, Trinidad and Tobago, Iran, Mauritius, Panama, Georgia, Sri Lanka, Cuba, Saint Kitts and Nevis, Antigua y Barbuda, Mexico, Armenia, Algeria, Nicaragua, North Macedonia, Peru, Tunisia, Mongolia, Lebanon, Jamaica, Venezuela, Suriname, Belize, Maldives, Tonga, Turkmenistan, Uzbekistan, Libya, Samoa, South Africa, Gabon, Egypt, Marshall Islands, Viet Nam, Iraq, Morocco, Kyrgyzstan, Mozambique, Tjikistan, Cabo Verde. |
| Component1 | Brazil, Bangladesh, Colombia, Thailand, Philippines, Guyana, Indonesia, Uruguay, Dominica, Palau, Brunei Darussalam, Kribati, Botswanna, Bahrain, Fiji, Central Africa Republic, United Arab Emirates, Honduras, Azerbaijan, Dominican Republic, Palestine, Moldova, Saint Vincent and the Grenadines, Grenada, Saint Lucia, Paraguay, Ecuador, Ukraine, El Salvador, United States, Cyprus, Bosnia and Herzegovina, Spain, Oman, Italy, Korea, China. |
| Component 2 | Congo, Ghana, Belarus, Rwanda, Niger, Togo, Barbados, Senegal, Sudan, Mali, Nepal, Ethiopia, Costa Rica, Belgium, Germany, Hungary, New Zealand, Russian Federation, Estonia, Switzerland, Montenegro, Slovakia, Finland, Slovenia, Malta, Latvia, Yemen, North Macedonia, Algeria, Sweden, Albani, Czechia, Canada. |
FIGURE 3.
Graph of the sets of countries after the rupture of the MCGC (infection network).
It is important to mention that Figure 3 presents the connections that the nodes belonging to each set have in the five layers.
Based on the information presented in Figure 3 and Table 3, we can see that in Component 1, there are countries as Brazil, China, Italy (among others) with a high human development index; however, these countries present high percentage in contagion and deaths. On the other hand, in Component 2, there are countries as Congo, Niger, Montenegro (among others) with a low percentage of contagion, and low human development index; therefore, the characteristic that both types of countries share is the low number of air travels.
For the separator set, there are countries with different values of characteristics (for more information, see the URLs presented in Annex) according to the percentage of the population who infect or died by day, an average of the projected real GDP, average consumer prices, human development index, the average of the Corruption perception index, average current health expenditure (% of GDP), average population and number of air travels.
For example, in the socioeconomics and population characteristics: Norway, Ireland, Hong Kong, Sweden (among others) have high values in Human development index (HDI), life expectancy at birth, expected years of schooling, percentage of infected by day and the rate of deaths by day; while Iran, Mauritius, Panama, Georgia, Sri Lanka (among others) have average values and Viet Nam, Iraq, Morocco, Kyrgyzstan, Tajikistan, Cabo Verde (among others) have low values.
Based on the information about the number of infections and deaths, we can see that some countries as the United States, Italy, and China, which are considered the countries with the most diseases and deaths, are not in the set of the most spreaders. On the other hand, some countries that are in the spreaders set are: Norway, Ireland, and Denmark that present a high percentage of contagion; Mexico, Venezuela, and Egypt with an average percentage and countries like India, Nicaragua, and Mozambique have a low percentage.
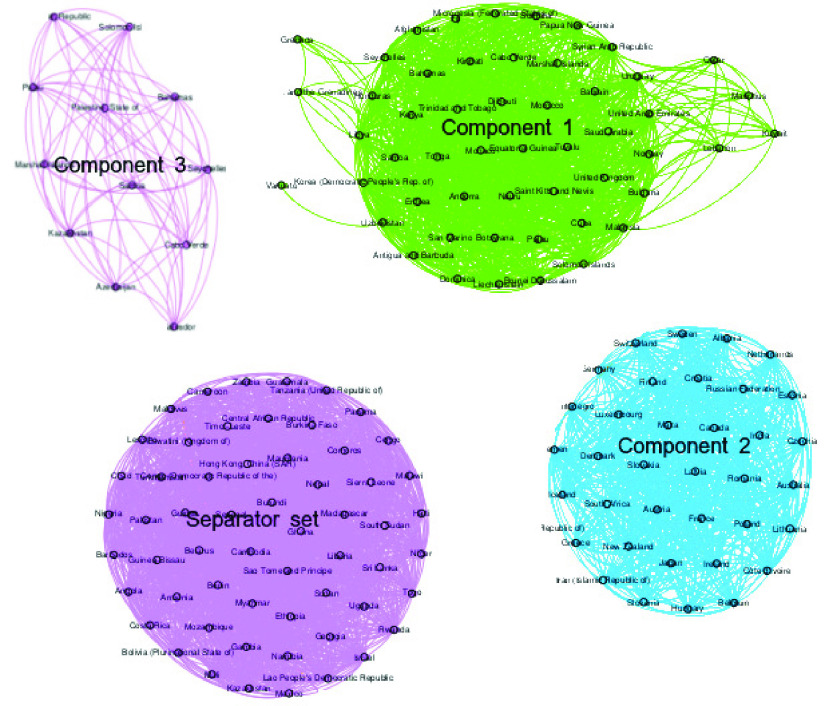
Now, to analyze the relationship between the GDP and the spread of COVID-19, we present Figure 4 and Table 4, which perform the sets of countries after the rupture of the MCGC in GDP and health network.
FIGURE 4.
Graph of the sets of countries after the rupture of the MCGC (GDP network).
TABLE 4. Sets of Countries After the Rupture of the MCGC (GDP and Health Network).
| GDP and health network | |
|---|---|
| Separator set | Norway, Switzerland, Ireland, Germany, Hong Kong, Iceland, Sweden, Finland, New Zealand, United States, Belgium, Liechtenstein, Austria, Luxembourg, Israel, Korea, Spain, Malta, Italy, Cyprus, Greece, Poland, Lithuania, United Arab Emirates, Saudi Arabia, Slovakia, Bahrain, Croatia, Oman, Russian Federation, Belarus, Kazahstan, Bulgaria, Kuwait, Bahamas, Seychelles, Serbia, Trinidad and Tobago, Mauritius, Albania, Costa Rica, Sri Lanka, Saint Kitts and Nevis, Antigua and Barbuda, Bosnia and Herzegovina, Mexico, Colombia, Armenia, Algerian, North Macedonia, China, Ecuador, Azerbaijan, Ukraine, Dominician Republic, Tunisia, Mongolia, Lebanon, Botswana, Jamaica, Venezuela, Dominica, Jordan, Tonga, Philippines, Turkmenistan, Uzbekistan, ybia, Samoa, Marshall Islands, Palestine, Guyana, Tajikistan, Cabo Verde, Namibia, Timor-Leste, Honduras, Bhutan, Bangladesh, Micronesia, Sao Tome and Principe, Lao People’s Democratic Republic, Vanuatu, Cambodia, Kenya, Nepal, Pakistan, Nigeria, Benin, Lesotho, Cote d’Ivoire, Togo, Haiti, Afghanistan, Dijbouti, Gambia, Guinea, Liberia, Mozambique, Sierra Leone, Burkina Faso, Eritrea, Mali, Burundi, Central African Republic, Niger, Monaco, Nauru, San Marino, Somalia, Tuvalu. |
| Component1 | Moldova, Nicaragua, El Salvador, Palau, Brunei, Darussalam, Fiji, Malaysia, Cuba, Nigeria, Papua New Guinea, Tonga, United Kingdom, Uruguay, Ecuador, Equatorial Guinea, Qatar, Democratic People’s Rep. of Korea, Syrian Arab Republic, Congo, Morocco, Denmark, Canada, Montenegro, Iran, Hungary, Japan, India, Romania, Czechia, Slovenia, France, Netherlands, Yemen, |
It is important to mention that Figure 4 presents the connections that the nodes belonging to each set have in the 5 layers.
As in the previous case, based on the information presented in Figure 4 and Table 4, we can see that in each set (separator, component 1 and component 2), there are countries with different values in the characteristics.
For example, in components 2 and 3, there are countries such as Ghana, Nepal, Uganda, Egypt (among others) with low human development index, and the high percentage of contagion and deaths.
For the socioeconomics, GDP and health characteristics, in the separator set (spreaders), are countries as Norway, Switzerland, Germany (among others) that have high values in Human development index (HDI), life expectancy at birth, expected years of schooling, percentage of infected and deaths by day; countries as Costa Rica, Mexico, Colombia, Armenia (among others) that have average values and countries like Nauru, San Marino, Somalia, Tuvalu (among others) have low values.
Based in the information about the flow in air travels, we can affirm that the countries in the separator set for both infection and GDP networks have an increase in the rate of contagion since in addition to being those countries where there is a higher flow in air travels (inbound and outbound), economies are based on business and transactions with other countries (which are in the same situation).
Finally, based on the results shown in Table 3 and Table 4, we can see that in order to mitigate a second outbreak of COVID-19 in the world, the countries that are in the union of both separator sets must reinforce their sanitary measures (in the area). On the other hand, the countries that are at the intersection of the two separator sets, in addition to strengthening their sanitary measures, must regulate the airflow in order to contain the spread of the disease.
V. Limitations of the Study and Discussion
The analysis developed in this work, is based on the modeling of two multiplex networks, which consist of 5 layers; where each layer shows the similarities of the countries for the different types of characteristics.
The idea of model five different types of layers is to be able to obtain an identification of the spreader nodes, based on a multi-criteria analysis that reduces the disadvantages of using only one set of nodes; thus, the technique is capable of identifying those countries that, based on different characteristics, are the most spreaders of COVID-19.
We apply the multiplex network approach using the adaptation of the Vertex Separator Problem, in order to identify those countries that, when their links are eliminated from all the layers of the network, cause the rupture of the system and, therefore, contain the spreaders countries of COVID-19.
The main advantage of this approach is that it allows information from various fields to be combined, such as economic, health, and transportation. Thus, with this approach, we can quantify the relationship between the different countries and model the networks that help to understand the dynamics of the system to be analyzed (in this case, the spread of COVID-19).
It is important to mention that, in this work, we are quantifying the dynamics of behavior of COVID-19 with the information available until May 15, 2020.
Therefore, a limitation of the study is that the drastic change of one or more variables causes the dynamics of the system to change. Then, because the information about COVID-19 is updated every day, the set of spreader countries that we find can be maintained if the behavior of the variables is maintained; otherwise, we must re-model the networks to carry out a new analysis.
Although we are schematizing the dynamics of the spread behavior of COVID-19, the analysis is susceptible to the existence of those elements that drastically alter one or more layers of the entire multiplex network. However, as long as the behavioral trends are maintained (values within the 95% level of certainty show in Table 1), the set of spreader countries found, will not change.
VI. Conclusions
In this work, we present an analysis of the countries that are spreaders of COVID-19, based on the main socio-cultural, economic, and connection characteristics, such as GDP, life expectancy, number of air travel, and budget for health, among others.
The results show that the methodology, can cause the rupture of the 5-layer multiplex network and help identify the spreader countries and obtains a classification of the countries based on their characteristics, where, in the spreaders set, the countries have high, medium or low values in the different socio-cultural and economic aspects; however, the characteristic that everyone shares are the high value in air connections.
On the other hand, we can affirm that to mitigate a second outbreak of COVID-19 in the world, the countries that are in the union of both separator sets must reinforce their sanitary measures; in contrast, the countries that are at the intersection of the two separate sets, in addition to improving their sanitary measures, must regulate airflow to contain the spread of the disease.
Based on the information collected and modeled (until May 15, 2020), we can affirm that, by changing the relationships of the air flow, the risk of a second outbreak of COVID 19 can be minimized; however, we cannot quantify how much it can help.
Finally, in order to study and analyze the behavior of the propagation of COVID-19, we are currently developing a simulation system, which is based on prediction models of COVID-19 in 165 countries, and the approach presented in this work.
Annex
Now, we present the URLs for the information used to model the six networks used as layers for the two 5-layer multiplex networks.
-
•
Information about Human Development Index: https://drive.google.com/file/d/136y0449h4sfM86Ye-qeOrL8x kx9ixFAE/view?usp=sharing
-
•
Information about deaths and infections: https://drive.google.com/file/d/1PqwJB-F3Y9WWFhVRwBUDydO CkqvT7ECn/view?usp=sharing
-
•
Information about air travels: https://drive.google.com/file/d/18PA8JMnzxueXLU1MzjkEya3htBe4hrBw/ view?usp=sharing
-
•
Information about GDP: https://drive.google.com/file/d/1HhAEpN-WzEBJXAzJeNbF5iSNm8S2xi1Q/view? usp=sharing
Biographies

Edwin Montes-Orozco was born in Mexico City, Mexico, in August 1992. He received the master’s degree in optimization from Universidad Autónoma Metropolitana-Azcapotzalco. He is currently pursuing the Ph.D. degree in information sciences and technologies with the Universidad Autónoma Metropolitana-Iztapalapa. His research interests include matheuristics and hybrid algorithms for combinatorial optimization, social networks, and complex systems.

Roman-Anselmo Mora-Gutiérrez was born in Mexico City, Mexico, in August 1983. He received the Ph.D. degree in engineering (operation research) from the Universidad Nacional Autonoma de Mexico. He is currently a Professor with the System Department, Universidad Autonoma Metropolitana-Azcapotzalco. His research interests include social metaheuristic methods, stochastic processes, pattern recognition, and comparative philology.

Sergio-Gerardo De-Los-Cobos-Silva was born in March 1958. He received the Ph.D. degree in engineering (operation research) from the Universidad Nacional Autonoma de Mexico. He is a Titular Professor with the Department of Electrical Engineering, Universidad Autonoma Metropolitana-Iztapalapa, Mexico City. His research interests include social metaheuristic methods, stochastic processes, probability, and statistics.

Eric-Alfredo Rincón-García was born in November 1976. He received the Ph.D. degree in engineering from Universidad Nacional Autonoma de Mexico. He is currently a Professor with the Department of Electrical Engineering, Autonoma Metropolitana-Iztapalapa, Mexico City. His principal areas of research are in heuristic methods for combinatorial optimization and zone design.

Gilberto-Sinuhe Torres-Cockrell was born in Mexico City, Mexico, in September 1982. He received the master’s degree in engineering (optimization) from Universidad Autónoma Metropolitana-Azcapotzalco, Mexico City, where he is currently pursuing the Ph.D. degree in information sciences and technologies. His research interests include common metaheuristic methods for combinatorial optimization, stochastic processes, pattern recognition, and comparative philology.

Jorge Juárez-Gómez was born in Mexico City, Mexico, in May 1985. He received the Ph.D. degree in science (chemistry) from Universidad Autónoma Metropolitana Iztapalapa. He specializes in analytical chemistry and data analysis and belongs to the Sistema Nacional de Investigadores (SNI) level 1.

Bibiana Obregón-Quintana received the Ph.D. degree in engineering (operation research) from Universidad Nacional Autonoma de Mexico (UNAM). She is currently a Professor with the Department of Mathematics, Science Faculty, UNAM. Her research interests are based on operation research and complex networks.

Pedro Lara-Velázquez was born in March 1971. He received the Ph.D. degree in engineering (operation research) from Universidad Nacional Autonoma de Mexico. He is currently a Titular Professor with the Department of Electrical Engineering, Universidad Autonoma Metropolitana-Iztapalapa, Mexico City. His research interests include social metaheuristic methods, stochastic processes, and pattern recognition.

Miguel-ángel Gutierrez-Andrade was born in August 1953. He received the Ph.D. degree in engineering (operation research) from the Universidad Nacional Autonoma de Mexico. He is currently a Titular Professor with the Department of Electrical Engineering, Universidad Autonoma Metropolitana-Iztapalapa, Mexico City. His research interests are heuristics methods, combinatorial optimization, and soft computing.
Funding Statement
This work was supported by the Mexican National Council for Science and Technology and Universidad Autónoma Metropolitana.
Footnotes
It is important to mention that in multiplex networks, each node belongs to all the 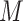 layers.
layers.
Hamming distance is defined as the number of elements that have to be changed to transform a solution into another valid solution.
References
- [1].WHO. (2020). Timeline Covid-19. [Online]. Available: https://www.who.int/news-room/detail/27-04-2020-who-timeline-covid-19
- [2].Sohrabi C., Alsafi Z., O’Neill N., Khan M., Kerwan A., Al-Jabir A., Iosifidis C., and Agha R., “World health organization declares global emergency: A review of the 2019 novel coronavirus (COVID-19),” Int. J. Surgery, vol. 76, pp. 71–76, Apr. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Coronavirus Disease (COVID-2019) Situation Reports, World Health Org., Geneva, Switzerland, 2020. [Google Scholar]
- [4].WHO. (2020). Covid-19 Dashboard. [Online]. Available: https://www.who.int/
- [5].Douglas M., Katikireddi S. V., Taulbut M., McKee M., and McCartney G., “Mitigating the wider health effects of COVID-19 pandemic response,” BMJ, vol. 27, p. m1557, Apr. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Gilbert M., Pullano G., Pinotti F., Valdano E., Poletto C., Boálle P.-Y., D’Ortenzio E., Yazdanpanah Y., Eholie S. P., Altmann M., Gutierrez B., Kraemer M. U. G., and Colizza V., “Preparedness and vulnerability of African countries against importations of COVID-19: A modelling study,” Lancet, vol. 395, no. , pp. 871–877, Mar. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Tuite A. R., Ng V., Rees E., and Fisman D., “Estimation of COVID-19 outbreak size in italy,” Lancet Infectious Diseases, vol. 20, no. 5, p. 537, May 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
-
[8].Müller R. and Wagner D., “
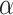 vertex separator is NP-hard even for 3-regular graphs,” Computing, vol. 46, no. 4, pp. 343–353, Dec.
1991. [Google Scholar]
vertex separator is NP-hard even for 3-regular graphs,” Computing, vol. 46, no. 4, pp. 343–353, Dec.
1991. [Google Scholar] - [9].(2020). Eu Global Response to COVID-19. [Online]. Available: https://ec.europa.eu/international-partnerships/topics/eu-global-response-covid-19_en
- [10].(2020). World Bank Group and COVID-19. [Online]. Available: https://www.worldbank.org/en/who-we-are/news/coronavirus-covid19
- [11].(2020). International Monetary Fundation Data. [Online]. Available: https://www.imf.org/en/Data
- [12].(2020). Transparency International (Countries). [Online]. Available: https://www.transparency.org/en/countries/
- [13].D’Agostino G. and Scala A., Networks of Networks: The Last Frontier of Complexity, vol. 340. Berlin, Germany: Springer, 2014. [Google Scholar]
- [14].Wang W., Tang M., Zhang H.-F., Gao H., Do Y., and Liu Z.-H., “Epidemic spreading on complex networks with general degree and weight distributions,” Phys. Rev. E, Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top., vol. 90, no. 4, Oct. 2014, Art. no. 042803. [DOI] [PubMed] [Google Scholar]
- [15].Alzaabi M., Taha K., and Martin T. A., “CISRI: A crime investigation system using the relative importance of information spreaders in networks depicting criminals communications,” IEEE Trans. Inf. Forensics Security, vol. 10, no. 10, pp. 2196–2211, Oct. 2015. [Google Scholar]
- [16].Sarli C. C. and Carpenter C. R., “Measuring academic productivity and changing definitions of scientific impact,” Missouri Med., vol. 111, no. 5, p. 399, 2014. [PMC free article] [PubMed] [Google Scholar]
- [17].Ma L.-L., Ma C., Zhang H.-F., and Wang B.-H., “Identifying influential spreaders in complex networks based on gravity formula,” Phys. A, Stat. Mech. Appl., vol. 451, pp. 205–212, Jun. 2016. [Google Scholar]
- [18].Tan S.-Y., Wu J., Lü L., Li M.-J., and Lu X., “Efficient network disintegration under incomplete information: The comic effect of link prediction,” Sci. Rep., vol. 6, no. 1, p. 22916, Mar. 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Wahid-Ul-Ashraf A., Budka M., and Musial-Gabrys K., “Newton’s gravitational law for link prediction in social networks,” in Proc. Int. Conf. Complex Netw. Appl. Cham, Switzerland: Springer, 2017, pp. 93–104. [Google Scholar]
- [20].Liu Y., Tang M., Zhou T., and Do Y., “Core-like groups result in invalidation of identifying super-spreader by k-shell decomposition,” Sci. Rep., vol. 5, no. 1, Sep. 2015, Art. no. 9602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Lü L., Chen D., Ren X.-L., Zhang Q.-M., Zhang Y.-C., and Zhou T., “Vital nodes identification in complex networks,” Phys. Rep., vol. 650, pp. 1–63, Sep. 2016. [Google Scholar]
- [22].Freeman L. C., “Centrality in social networks conceptual clarification,” Social Netw., vol. 1, no. 3, pp. 215–239, Jan. 1978. [Google Scholar]
- [23].Bonacich P. and Lloyd P., “Eigenvector-like measures of centrality for asymmetric relations,” Social Netw., vol. 23, no. 3, pp. 191–201, Jul. 2001. [Google Scholar]
- [24].Cozzo E., Kivelä M., De Domenico M., Solé A., Arenas A., Gómez S., Porter M. A., and Moreno Y., “Structure of triadic relations in multiplex networks,” 2013, arXiv:1307.6780. [Online]. Available: http://arxiv.org/abs/1307.6780
- [25].Mucha P. J., Richardson T., Macon K., Porter M. A., and Onnela J.-P., “Community structure in time-dependent, multiscale, and multiplex networks,” Science, vol. 328, no. 5980, pp. 876–878, May 2010. [DOI] [PubMed] [Google Scholar]
- [26].Lee K.-M., Min B., and Goh K.-I., “Towards real-world complexity: An introduction to multiplex networks,” Eur. Phys. J. B, vol. 88, no. 2, p. 48, Feb. 2015. [Google Scholar]
- [27].Zhao Z. Y., Yu H., Zhu Z. L., and Wang X. F., “Identifying influential spreaders based on network community structure,” Chin. J. Comput., vol. 37, pp. 753–766, Apr. 2014. [Google Scholar]
- [28].Berahmand K., Bouyer A., and Vasighi M., “Community detection in complex networks by detecting and expanding core nodes through extended local similarity of nodes,” IEEE Trans. Comput. Social Syst., vol. 5, no. 4, pp. 1021–1033, Dec. 2018. [Google Scholar]
- [29].Berahmand K., Bouyer A., and Samadi N., “A new centrality measure based on the negative and positive effects of clustering coefficient for identifying influential spreaders in complex networks,” Chaos, Solitons Fractals, vol. 110, pp. 41–54, May 2018. [Google Scholar]
- [30].Berahmand K., Samadi N., and Sheikholeslami S. M., “Effect of rich-club on diffusion in complex networks,” Int. J. Modern Phys. B, vol. 32, no. 12, May 2018, Art. no. 1850142. [Google Scholar]
- [31].Berahmand K., Bouyer A., and Samadi N., “A new local and multidimensional ranking measure to detect spreaders in social networks,” Computing, vol. 101, no. 11, pp. 1711–1733, Nov. 2019. [Google Scholar]
- [32].Wang J., Li C., and Xia C., “Improved centrality indicators to characterize the nodal spreading capability in complex networks,” Appl. Math. Comput., vol. 334, pp. 388–400, Oct. 2018. [Google Scholar]
- [33].Xiao-Ping S. and Yu-Rong S., “Leveraging neighborhood ‘structural holes’ to identifying key spreaders in social networks,” Acta Phys. Sinica, vol. 64, no. 2, 2015, Art. no. 020101. [Google Scholar]
- [34].Hu P. and Mei T., “Ranking influential nodes in complex networks with structural holes,” Phys. A, Stat. Mech. Appl., vol. 490, pp. 624–631, Jan. 2018. [Google Scholar]
- [35].Li C., Wang L., Sun S., and Xia C., “Identification of influential spreaders based on classified neighbors in real-world complex networks,” Appl. Math. Comput., vol. 320, pp. 512–523, Mar. 2018. [Google Scholar]
- [36].Wang J., Hou X., Li K., and Ding Y., “A novel weight neighborhood centrality algorithm for identifying influential spreaders in complex networks,” Phys. A, Stat. Mech. Appl., vol. 475, pp. 88–105, Jun. 2017. [Google Scholar]
- [37].Yan X.-L., “Identifying influential spreaders in complex networks based on entropy weight method and gravity law,” Chin. Phys. B, vol. 29, no. 4, 2020, Art. no. 048902. [Google Scholar]
- [38].Page L., Brin S., Motwani R., and Winograd T., “The PageRank citation ranking: Bringing order to the Web,” Stanford InfoLab, Stanford, CA USA, Tech. Rep. 1999-66, Nov. 1999. [Online]. Available: http://ilpubs.stanford.edu:8090/422/ [Google Scholar]
- [39].Lü L., Zhang Y.-C., Yeung C. H., and Zhou T., “Leaders in social networks, the delicious case,” PLoS ONE, vol. 6, no. 6, Jun. 2011, Art. no. e21202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Hage P. and Harary F., “Eccentricity and centrality in networks,” Social Netw., vol. 17, no. 1, pp. 57–63, Jan. 1995. [Google Scholar]
- [41].Chen D.-B., Gao H., Lü L., and Zhou T., “Identifying influential nodes in large-scale directed networks: The role of clustering,” PLoS ONE, vol. 8, no. 10, Oct. 2013, Art. no. e77455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Liu Y., Tang M., Zhou T., and Do Y., “Improving the accuracy of the k-shell method by removing redundant links: From a perspective of spreading dynamics,” Sci. Rep., vol. 5, no. 1, Oct. 2015, Art. no. 13172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Lohmann G., Margulies D. S., Horstmann A., Pleger B., Lepsien J., Goldhahn D., Schloegl H., Stumvoll M., Villringer A., and Turner R., “Eigenvector centrality mapping for analyzing connectivity patterns in fMRI data of the human brain,” PLoS ONE, vol. 5, no. 4, Apr. 2010, Art. no. e10232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Katz L., “A new status index derived from sociometric analysis,” Psychometrika, vol. 18, no. 1, pp. 39–43, Mar. 1953. [Google Scholar]
- [45].Chalupa J., Leath P. L., and Reich G. R., “Bootstrap percolation on a bethe lattice,” J. Phys. C, Solid State Phys., vol. 12, no. 1, pp. 31–35, Jan. 1979. [Google Scholar]
- [46].Morone F. and Makse H. A., “Influence maximization in complex networks through optimal percolation,” Nature, vol. 524, no. 7563, p. 65, 2015. [DOI] [PubMed] [Google Scholar]
- [47].Kitsak M., “Identification of influential spreaders in complex networks,” Nature Phys., vol. 6, no. 11, p. 888, 2010. [Google Scholar]
- [48].Radicchi F. and Castellano C., “Leveraging percolation theory to single out influential spreaders in networks,” Phys. Rev. E, Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top., vol. 93, no. 6, Jun. 2016, Art. no. 062314. [DOI] [PubMed] [Google Scholar]
- [49].Fei L., Zhang Q., and Deng Y., “Identifying influential nodes in complex networks based on the inverse-square law,” Phys. A, Stat. Mech. Appl., vol. 512, pp. 1044–1059, Dec. 2018. [Google Scholar]
- [50].He X. and Kempe D., “Robust influence maximization,” in Proc. 22nd ACM SIGKDD Int. Conf. Knowl. Discovery Data Mining, Aug. 2016, pp. 795–804. [Google Scholar]
- [51].Chen W., “Efficient influence maximization in social networks,” in Proc. 15th ACM SIGKDD Int. Conf. Knowl. Discovery Data Mining, 2009, pp. 199–208. [Google Scholar]
- [52].Gao J., Zhou T., and Hu Y., “Bootstrap percolation on spatial networks,” Sci. Rep., vol. 5, no. 1, Dec. 2015, Art. no. 14662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Montes-Orozco E., Mora-Gutiérrez R. A., Obregón-Quintana B., de-los-Cobos-Silva S. G., Rincón-García E. A., Gutiérrez-Andrade M. A., and Lara-Velázquez P., “Methodology to quantify the robustness in complex networks,” Computing, to be published.
- [54].Yuan G. X., “The framework for the prediction of the critical turning period for outbreak of COVID-19 spread in China based on the ISEIR model,” in Proc. SSRN, Apr. 2020, pp. 1–4. [Google Scholar]
- [55].Messina F., “COVID-19: Viral–host interactome analyzed by network based-approach model to study pathogenesis of SARS-CoV-2 infection,” bioRxiv, vol. 18, pp. 1–10, Dec. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Liang K., “Mathematical model of infection kinetics and its analysis for COVID-19, SARS and MERS,” Infection, Genet. Evol., vol. 82, Aug. 2020, Art. no. 104306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Chien Benny Chin W. and Bouffanais R., “Spatial super-spreaders and super-susceptibles in human movement networks,” 2020, arXiv:2005.05063. [Online]. Available: http://arxiv.org/abs/2005.05063 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Chatterjee K., Chatterjee K., Kumar A., and Shankar S., “Healthcare impact of COVID-19 epidemic in india: A stochastic mathematical model,” Med. J. Armed Forces India, vol. 76, no. 2, pp. 147–155, Apr. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].Cao J., “Mathematical modeling and epidemic prediction of covid-19 and its significance to epidemic prevention and control measures,” J. Biomed. Res. Innov., vol. 1, no. 1, pp. 1–19, 2020. [Google Scholar]
- [60].Bragazzi N. L., Dai H., Damiani G., Behzadifar M., Martini M., and Wu J., “How big data and artificial intelligence can help better manage the COVID-19 pandemic,” Int. J. Environ. Res. Public Health, vol. 17, no. 9, p. 3176, May 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [61].Pham Q.-V., Nguyen D. C., Huynh-The T., Hwang W.-J., and Pathirana P., “Artificial intelligence (AI) and big data for coronavirus (COVID-19) pandemic: A survey on the state-of-the-arts,” Tech. Rep., Apr. 2020, doi: 10.13140/RG.2.2.23518.38727. [DOI] [PMC free article] [PubMed]
- [62].Bianconi G. and Radicchi F., “Percolation in real multiplex networks,” Phys. Rev. E, Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top., vol. 94, no. 6, Dec. 2016, Art. no. 060301. [DOI] [PubMed] [Google Scholar]
- [63].Rendl F. and Sotirov R., “The min-cut and vertex separator problem,” Comput. Optim. Appl., vol. 69, no. 1, pp. 159–187, Jan. 2018. [Google Scholar]
- [64].Dréo J., Pétrowski A., Siarry P., and Taillard E., Metaheuristics for Hard Optimization: Methods Case Students. Berlin, Germany: Springer-Verlag, 2006. [Google Scholar]
- [65].Garey M. R., Johnson D. S., and Sethi R., “The complexity of flowshop and jobshop scheduling,” Math. Oper. Res., vol. 1, no. 2, pp. 117–129, May 1976. [Google Scholar]
- [66].Kirkpatrick S., Gelatt C. D., and Vecchi M. P., “Optimization by simulated annealing,” Science, vol. 220, no. 4598, pp. 671–680, 1983. [DOI] [PubMed] [Google Scholar]
- [67].Storn R. and Price K., “Differential evolution–A simple and efficient heuristic for global optimization over continuous spaces,” J. Global Optim., vol. 11, no. 4, pp. 341–359, 1997. [Google Scholar]
- [68].Montes-Orozco E., Mora-Gutiérrez R. A., Obregón-Quintana B., de-los-Cobos-Silva S. G., Rincón-García E. A., Lara-Velázquez P., and Gutiérrez-Andrade M. Á., “Mexican university ranking based on maximal clique,” in Educational Networking. Cham, Switzerland: Springer, 2020, pp. 327–395. [Google Scholar]
- [69].Watts D. J. and Strogatz S. H., “Collective dynamics ‘small-world’ networks,” Nature, vol. 393, no. 6684, p. 440, 1998. [DOI] [PubMed] [Google Scholar]
- [70].Erdos P. and Rényi A., “On the evolution of random graphs,” Math. Inst. Hungarian Acad. Sci., vol. 5, no. 1, pp. 17–60, 1960. [Google Scholar]
- [71].Albert R., Jeong H., and Barabási A.-L., “Error and attack tolerance of complex networks,” Nature, vol. 406, no. 6794, p. 378, 2000. [DOI] [PubMed] [Google Scholar]
- [72].Albert R. and Barabási A.-L., “Statistical mechanics of complex networks,” Rev. Mod. Phys., vol. 74, p. 47, Jan. 2002. [Google Scholar]
- [73].Watts D. J. and Strogatz S. H., “Collective dynamics o ‘small-world’ networks,” Nature, vol. 393, no. 6684, p. 440, 1998. [DOI] [PubMed] [Google Scholar]
- [74].Barabási A.-L. and Bonabeau E., “Scale-free networks,” Sci. Amer., vol. 288, no. 5, pp. 60–69, 2003. [DOI] [PubMed] [Google Scholar]