Abstract
Head motion during MRI acquisition presents significant challenges for neuroimaging analyses. In this work, we present a retrospective motion correction framework built on a Fourier domain motion simulation model combined with established 3D convolutional neural network (CNN) architectures. Quantitative evaluation metrics were used to validate the method on three separate multi-site datasets. The 3D CNN was trained using motion-free images that were corrupted using simulated artifacts. CNN based correction successfully diminished the severity of artifacts on real motion affected data on a separate test dataset as measured by significant improvements in image quality metrics compared to a minimal motion reference image. On the test set of 13 image pairs, the mean peak signal-to-noise-ratio was improved from 31.7 to 33.3 dB. Furthermore, improvements in cortical surface reconstruction quality were demonstrated using a blinded manual quality assessment on the Parkinson’s Progression Markers Initiative (PPMI) dataset. Upon applying the correction algorithm, out of a total of 617 images, the number of quality control failures was reduced from 61 to 38. On this same dataset, we investigated whether motion correction resulted in a more statistically significant relationship between cortical thickness and Parkinson’s disease. Before correction, significant cortical thinning was found to be restricted to limited regions within the temporal and frontal lobes. After correction, there was found to be more widespread and significant cortical thinning bilaterally across the temporal lobes and frontal cortex. Our results highlight the utility of image domain motion correction for use in studies with a high prevalence of motion artifacts, such as studies of movement disorders as well as infant and pediatric subjects.
Keywords: Motion Artifact, T1, Image Quality, Cortical Surface, Cortical Thickness, Parkinson’s Disease
1. Introduction
Head motion during MRI scanning results in serious confounding effects for subsequent neuroimaging analyses. Subject motion during acquisition results in blurring as well as ghost artifacts of the image in the phase-encoding directions. Quasiperiodic motion e.g. due to physiological activity e.g. respiration, results in coherent ghosting artifacts, whereas random motion, manifests as multiple displaced replicas of the image, or stripes (Zaitsev et al., 2015). Such neuroimaging confounds become more of a concern in imaging studies of infants, children (Yoshida et al., 2013), adolescents (Satterthwaite et al., 2012) or participants with psychological disorders as they may be less compliant during the imaging session. Consequently, a significant proportion (10-40%) of the initially acquired samples have to be excluded in the analysis stage (Engelhardt et al., 2015; Kim et al., 2016; Moradi et al., 2017). Even after exclusion of images with visually-recognized motion artifact through a standard image quality control procedure, the confounding effects of subtle artifacts in the remaining data may be substantial and sufficient to bias results from morphometric studies (Reuter et al., 2015).
Prospective motion correction, which involves online pulse sequence modification, has huge potential but is yet to be fully validated for routine use within the clinic and requires either expensive additional hardware or pulse-sequence modifications which can increase scan duration (Stucht et al., 2015; Tisdall et al., 2012; White et al., 2010). Where the motion trajectory is unknown e.g. in the absence of online monitoring using navigators or optical methods, the problem is extremely challenging due to its ill-posed nature. In the absence of online motion monitoring, retrospective methods represent the only available option apart from discarding the affected data entirely. Examples of retrospective correction methods include autofocusing methods which are based on optimization of image quality metrics (Atkinson et al., 1997; Haskell et al., 2018; Loktyushin et al., 2013), iterative estimation of phase-correction (Hedley et al., 1991) or more recently on compressed-sensing theory (Yang et al.) or parallel-imaging reconstruction (Cordero-Grande et al., 2018). These techniques are in general computationally expensive and require the raw frequency domain (k-space) data, which is seldom available for large-scale open datasets. For this reason, performing a magnitude image domain motion correction based on deep learning is likely to be valuable for some clinical or research applications.
Deep learning approaches, specifically convolutional neural network (CNN) models, have emerged as a potential solution for retrospective motion correction. Regression CNNs can be trained using motion-corrupted images as input data and the same individual’s motion-free images as the ground truth. It is however impractical to acquire large numbers of such coupled data for training deep neural networks. To overcome this problem, adding realistic motion simulation to clean images has been considered as a practical solution and it has been hypothesized that training a CNN with the combination of clean images and motion simulated data would be able to correct real motion artifact corrupted images (Duffy et al., 2018; Loktyushin et al., 2015).
There have been only a few attempts using deep learning for motion detection (Küstner et al., 2018; Meding et al.; Oksuz et al., 2018) or motion correction in MR images (Duffy et al., 2018; Kustner et al., 2019; Küstner et al., 2018; Loktyushin et al., 2015; Meding et al.; Pawar et al., 2018). Preliminary studies have been based on 2D CNNs for artifact correction (Kustner et al., 2019; Loktyushin et al., 2015; Pawar et al., 2018). However, such 2D approaches are limited in their effectiveness as they do not take advantage of the continuity of the image or artifacts across all three dimensions in 3D MR images (Dolz et al., 2018; Fu et al., 2019; Kamnitsas et al., 2017; Payan & Montana, 2015; Pham et al., 2017; Shabanian et al., 2019; Trivizakis et al., 2018). Most studies have attempted to simulate motion in the image domain, and then combine it piecewise in the Fourier domain (Johnson & Drangova, 2019; Pawar et al., 2018), an approach that is computationally expensive and therefore limited to unrealistic motion trajectories. Importantly, the Fourier domain approach generalizes to deep learning based reconstruction, which is currently the state-of-the-art for under-sampled k-space reconstruction (Hammernik et al., 2018). Here, we extend our previous method (Duffy et al., 2018) based on 3D motion simulation in the Fourier domain, to encompass a more general 3D simulation framework that includes translational and rotational motion as well as different motion sampling strategies. In addition, we perform a systematic evaluation which includes testing on: (1) images with simulated motion for validation, (2) a set of images with various degrees of motion but no ground truth. (3) A dataset with real motion artifact which included minimal motion rescans from the same imaging session. Crucially, our preliminary study and other studies have thus far not addressed the critical question of whether correction of motion corrupted data recuperates data quality enough for them to be included in research applications. Therefore in addition, we also examined whether the proposed technique improves cortical surface reconstructions and the estimation of cortical thickness in patients with Parkinson’s disease (PD).
2. Methods
2.1. Framework
The proposed study framework is illustrated in Fig. 1 and consisted of 5 stages: (1) Training of the regression CNN using simulated data. (2) Testing using unseen simulated data using the structural similarity index (SSIM) and peak signal-to-noise ratio (pSNR) as evaluation metrics. (3) Testing on real motion corrupted volumes using a manual quality control score as the evaluation metric and using SSIM and pSNR where a minimal motion “ground-truth” reference image was available. (4) Testing for possible improvements in cortical reconstruction quality based on a blinded manual quality control. (5) Testing whether the proposed motion correction was able to better identify brain morphological changes in patients with Parkinson’s disease.
Figure 1: Summary of the proposed study framework outlining the 5 different stages of model development and testing.
(1) Training the 3D CNN to learn the clean data from motion corrupted data. The model was trained patch-wise in native space using 128×128×128 patches. Preprocessing included intensity normalization and cropping of the input image. (2) Testing on unseen validation dataset using different levels of motion severity and SSIM and pSNR as evaluation metrics. (3) Testing on real motion artifact affected data was carried out using a manual QC evaluation where no ground-truth was available and SSIM/pSNR where a minimal motion paired “ground-truth” was available. (4) Cortical reconstruction quality improvement was assessed using a manual quality control. (5) Examining whether motion correction was able to better identify morphological changes in Parkinson’s disease.
2.2. Datasets
Three-dimensional T1-weighted MRI volumes from the Autism Brain Imaging Data Exchange I (ABIDE I, n=864) dataset (Di Martino et al., 2014) were used for training of the regression CNN. These data included 737 male and 127 female subjects between the ages of 6 and 64 years of age that were deemed to be artifact-free by our in-house quality control protocol. This QC protocol involved excluding images with any issues relating to image quality or artifacts including but not limited to: low signal-to-noise ratio, head coverage, susceptibility artifacts, flow artifacts, and ringing artifacts. An additional (n=46) subjects from ABIDE I, with artifact free images were held out as a simulated motion validation set. Finally, for testing (n=10) separate subjects from the ABIDE dataset that contained mild to moderate motion artifacts were used. The in-plane voxel size as well as the slice thickness varied between 1-1.3 mm. Further sequence parameter information for ABIDE dataset is available from: http://fcon_1000.projects.nitrc.org/indi/abide. Supplementary Tables 1 and 2 include the demographic information for each dataset and experiment.
In addition, the Alzheimer’s Disease Neuroimaging Initiative (ADNI) dataset (adni.loni.usc.edu, www.adni-info.org) alongside the Parkinson’s Progression Markers Initiative (PPMI) (www.ppmi-info.org) dataset were used as test datasets. The ADNI was launched in 2003 as a public-private partnership, led by Principal Investigator Michael W. Weiner, MD. The goal of ADNI has been to test whether imaging, other markers, clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early Alzheimer’s disease (AD). The mission of PPMI is to help identify biomarkers of Parkinson’s disease progression.
The imaging parameters for the ADNI dataset were as follows: TR: 6-8 ms, TE: 2-4 ms, in-plane voxel size: 1-1.25 mm, slice thickness: 1.2 mm. The PPMI dataset contained 3D sagittal T1 weighted images acquired with the following parameters: TR: 5-11 ms, TE: 2-6 ms, in-plane voxel size: 1×1 mm2 and slice thickness 1-1.5 mm. Thirteen subjects from the ADNI dataset were identified with paired T1-weighted volumes from the same imaging session, where one scan included observable motion artifacts and the other was deemed to be artifact free. This minimal-motion image was used as a ground-truth reference image. For the investigation into cortical surface reconstruction quality we used (N=617) images from the PPMI dataset. After excluding surfaces that failed QC, this same dataset was used to investigate how cortical thickness was associated with PD in this dataset before and after correction. For this analysis (n=556, 317 males and 239 females) subjects from the PD and Control groups between the ages of 31 and 83 years were included.
2.3. Motion artifact simulation
2.3.1. Overall Framework
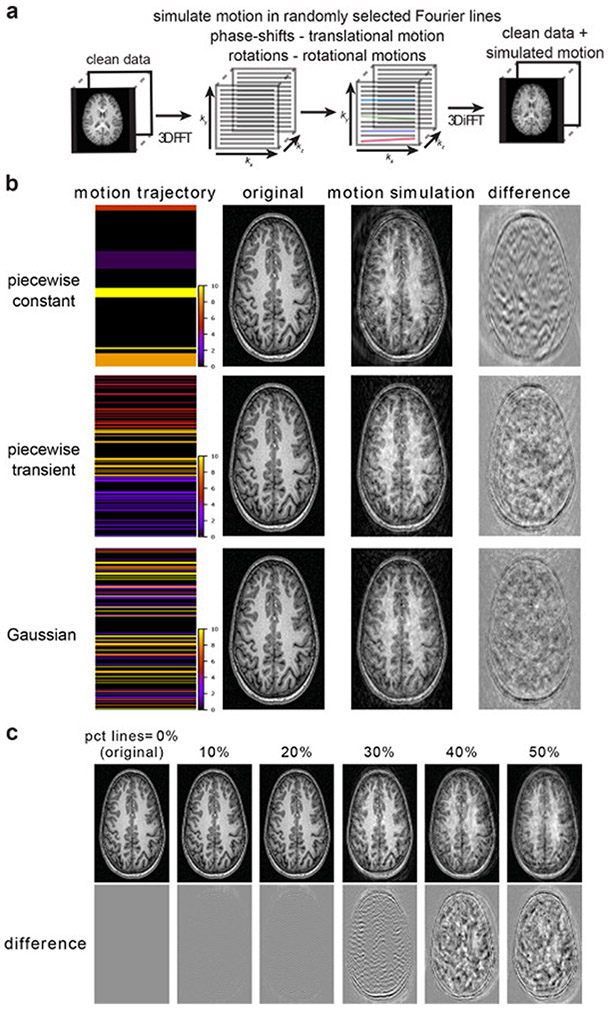
The simulated head motion including translations and rotations were generated in the frequency domain and inversely Fourier transformed to the image domain. As T1-weighted MP-RAGE acquisitions are typically 3D volume acquisitions, in our simulations we assumed a densely sampled line-by-line cartesian trajectory with a single frequency encoding dimension and 2 phase encoding directions. Because head motions are slow relative to the frequency encoding sampling interval, we assume their variations to be negligible within each frequency encoding line: i.e. the same motion parameter vector was used at each frequency encoding line. The frequency encoding direction was randomly selected to be one of the 3 dimensions (x,y,z), while the other 2 dimensions were assumed to be phase-encoding. Artifacts were simulated by applying translations and rotations to a random sampling of p phase-encoding lines in the Fourier transformed magnitude image (Fig. 2a).
Figure 2: Schematic of motion artifact simulation along with example images for different simulation parameters.
(a) Schematic of motion artifact simulation, which involves a 3D FFT followed by corruption of lines in the Fourier domain. Phase shifts are used to mimic translational motion and rotations (also in the Fourier domain) to simulate head rotation. (b) Different sampling schemes with image examples. Three sampling schemes were tested: Gaussian, piecewise transient and piecewise constant. For the Gaussian model, artifacts were less coherent compared to the piecewise constant or piecewise transient models where ghosting was more evident. The colorbar indicates the motion magnitude (in voxels) applied in the Fourier domain. (c) Examples of different motion severities for the piecewise constant model, generated by varying the percentage of motion affected Fourier lines. Upper panel – example images. Lower panel – Difference between the corrupted image and ground truth motion free image.
2.3.2. Motion Types
Each point in the Fourier domain was described by a motion parameter vector with 3 directional translations (x,y,z) and 3 rotations with respect to each of the x, y, and z axes. Translational motion was simulated by a pointwise multiplication with a linear phase term in the Fourier domain e.g. translation in the x direction is given by: exp(−2ikxθt), where kx is the Fourier line and θt is the magnitude of translation in voxels. Rotations about the center of an image are equivalent to rotations in Fourier space around the zero-frequency component. However, once points in the Fourier domain are rotated, they no longer lie on a uniform grid requiring non-uniform FFT (NUFFT) methods to transform the data back to the image domain. Here, in order to simulate rotational motion, we first rotated the Fourier domain coordinates and then used the fast and efficient multithreaded FINUFFT software library (Barnett et al., 2018) for computing the type-1 (Greengard & Lee, 2004) NUFFT, a method for evaluating a set of Fourier series coefficients at specified arbitrary locations. The 3D type-1 NUFFT evaluates the function:
for the points k1, k2, k3 on a uniform grid, where cj are the complex signal strengths at the transformed non-uniform locations, xj in the frequency domain. The FINUFFT library evaluates the NUFFT using the “exponential of semicircle” spreading kernel, which is faster than gridding using the more commonly used Kaiser-Bessel kernel (Barnett et al., 2018). Performing this NUFFT on an image of size 128×128×128 took around 1.2 s on a 3.6 GHz Intel Core i7-6850K CPU which made it possible for it to be carried out online during training.
2.3.3. Sampling Strategies
Three different sampling schemes for simulating motion across successive phase encoding lines were compared and are illustrated in Fig. 2b: (1) Where the (translation and rotation) motion parameters at each corrupted line were sampled independently from a Gaussian distribution. (2) A piecewise transient approach, where the motion corrupted lines were transient within each segment. This approach was similar to the piecewise constant approach except the segments were not contiguous, resulting in transient motions within each segment. (3) A piecewise constant approach, where the frequency domain was divided into segments with each segment being assigned the same translation and rotation vectors. This method was used to apply the same motion to grouped sampling intervals. For example, given k segments and p Fourier lines to be corrupted, then each corrupted line was randomly assigned to be in one of the k motion segments. The SD of the Gaussian distributions was set equal to 5, 10 or 20 voxels for translation and 3 degrees for rotation and the number of segments (k) was chosen from a uniform distribution. Three different ranges of k were investigated: 1-4, 1-8, and 1-16. Both methods (2) and (3) enabled the simulation of coherent ghosting artifacts, which was not the case for method (1) because the motion parameter vector was uncorrelated between adjacent corrupted lines. Fig. 2c shows examples of image generated by corrupting the same image with 0, 10, 20, 30, 40 and 50% of phase-encoding lines.
Corrupting 50% of the total number of phase-encoding lines resulted in more severely affected images than images that we aimed to correct, therefore this provided a useful upper bound on p. Artifacts generated using the piecewise constant or piecewise transient methods resulted in adjacent corrupted phase encoding lines being highly correlated and therefore generated coherent ghosting artifacts that were more realistic compared to where adjacent corrupted lines were drawn randomly from a Gaussian distribution (Fig. 2c). We hypothesized that training the model with these more coherent artifacts would produce better results.
We opted to preserve the center k-space lines. The central 7% (0-3.5% on each side of the center) were preserved as applying transformations to these lines led to displacement of the lowest frequencies and thus excessive distortion of the image. In contrast to this, corrupting a band of the frequencies higher than 3.5% from the center did not yield the same issue (Fig. S1). Ghosting of the bright fat tissue outside of the skull is a common problem for structural MRI data (Mortamet et al., 2009) that we were able to preserve in our simulations by performing corruption of the Fourier domain without brain masking and prior to cropping the images.
As illustrated in Fig. 2c, changing the distribution of p enabled us to simulate different levels of motion severity and subsequently allowed the CNN model to learn the variety of motion severity. We thus constructed and evaluated 4 different training-sets where we sampled various ranges of p phase-encoding lines using a uniform distribution ranging from: 0-20, 0-30, 0-40% of the total number of lines in each phase-encoding direction. Source code for the motion simulation is available at https://github.com/bduffy0/motion-correction.
2.4. Image preprocessing:
Online preprocessing during CNN training consisted of motion simulation, cropping and histogram intensity normalization based on the median signal intensity of the brain extracted image (Nyul et al., 2000) respectively. Brain masking was carried out to ensure that the intensity normalization performed well and loss masking using this mask was employed to ensure background artifacts did not contribute to the CNN loss function. Brain masks were generated using the Human Connectome project (HCP) pre-FreeSurfer preprocessing pipeline (Glasser et al., 2013), which was found to perform well on both motion-free and motion-corrupted images.
2.5. CNN training and inference:
CNNs were trained using NiftyNet version v0.6 (Gibson et al., 2018) and TensorFlow v.1.15 (Abadi et al., 2016). After initial experimentation with different architectures, a memory-efficient modified 18-convolutional layer No New-Net architecture (Isensee et al., 2018) was found to perform the best. The No New-Net architecture is a modification of the original U-Net architecture (Çiçek et al., 2016; Milletari et al., 2016; Ronneberger et al., 2015) except with trilinear upsampling instead of transpose convolutional upsampling, leaky ReLUs, and a reduction in the number of features before the upsampling layer using a 3×3 convolution layer (Isensee et al., 2018). Transpose convolution has been shown in certain situations to generate artifacts (Odena et al., 2016), therefore the No New-Net architecture which employs trilinear upsampling was favored over the standard U-net architecture. Preliminary experiments suggested that instance normalization was inferior to batch normalization, therefore contrary to Isensee et al. we opted to use the latter with a decay parameter of 0.9.
In preliminary experiments this improved UNet architecture was compared against a HighRes3dNet architecture (Li et al., 2017) as well as a GAN model (Goodfellow et al., 2014) using the same U-Net architecture as the generator with the adversarial loss term weighted by 1x10−4. Diagrams of these architectures are shown in Fig. S2.
The input to the CNN consisted of patches of size 128×128×128 and the regression CNN produced motion corrected output patches of 128×128×128 (Fig. S2). We trained the network patch-wise in native space because training the network with the full uncropped images would (depending on the image size) not always fit into GPU memory. In general, patch-wise training provides less context and is not as computationally efficient at inference time as using the full 3D volume. However, taking advantage of the full 3D volume would require larger architectures with larger receptive fields and in addition, using patches provides further augmentation of the training dataset which can prevent overfitting. Inference was also carried out using 128×128×128 patches. In order to reduce border effects (Li et al., 2017), each output patch was overlapped by 40 voxels in all dimensions, using the mean of the output at each overlapping voxel. Inference time per patch was approximately 170 ms, therefore for an image of size 256×256×128 the total inference time was around 45 s.
The CNN was trained using an Adam optimizer (Kingma & Ba, 2014), an L1 loss function and a batch size of 2 per GPU. The training data was augmented during training using random rotations with angles chosen uniformly between −10 and 10 degrees and random scaling between −5% and 5%. Networks were trained on two GPUs, averaging the gradient at each iteration. NiftyNet draws samples from a queue to avoid IO bottlenecks. A queue length of 150 was adopted with 30 samples per volume. Each network was trained for 80k iterations which took around 48h on two Nvidia GTX1080Ti GPUs.
2.6. Evaluation on simulated data
Unseen good quality images from the ABIDE I dataset were used to test the generalizability of the model to different levels of simulated motion severity. Different levels of simulated severity were tested by corrupting different percentages of Fourier lines. The image quality was assessed relative to the ground-truth using the structural similarity index (SSIM) (Wang et al., 2004) and peak signal-to-noise ratio.
2.7. Evaluation on real motion artifact affected data
Two independent T1-weighted test datasets were used, one from the ABIDE dataset, which was used for the investigation into different sampling schemes and hyperparameter optimization and another from the ADNI dataset for performance evaluation. The details of each dataset are provided below.
2.7.1. ABIDE dataset
A subset of images (n=10) from the ABIDE dataset with various degrees of motion severity but no ground-truth was used for investigating the performance of different motion sampling schemes and simulation parameters. The image quality was assessed manually on a scale of 1-5 (poorest to best) by an operator blinded to the group identity. The image was scored 1 if the entire volume was moderately or severely corrupted with artifacts, 2-3 if there were moderate to mild artifacts distributed across the 3D volume, 4 if there were artifacts that were only observable locally and 5 if there were no detectable artifacts.
2.7.2. ADNI dataset
The second test set was from the ADNI dataset which consisted of (n=13) pairs of images with real motion artifact and their rescans without observable motion from the same imaging session. This was used for quantitative evaluation as the minimal-motion images served as a “ground-truth” for comparison. In order to produce reliable similarity measurements, each image was bias-field corrected using N4 (Sled et al., 1998; Tustison et al., 2010), followed by non-linear registration to its corresponding ground-truth image using FSL’s FNIRT, followed by intensity normalization (Nyul et al., 2000). The image quality before and after correction was assessed using SSIM and pSNR.
2.8. Cortical reconstruction and quality control
Cortical reconstruction and volumetric segmentation on the PPMI dataset was performed with the FreeSurfer image analysis suite v6 (http://surfer.nmr.mgh.harvard.edu/) (Fischl & Dale, 2000). Specifically, the T1w images along with their corresponding brain masks generated from the HCP preFreeSurfer preprocessing pipeline were fed into the HCP FreeSurfer pipeline (Glasser et al., 2013). Quality control (QC) was performed manually on the FreeSurfer surface reconstructions. The cortical surface quality was assessed by manually scoring the quality of the pial and white matter surfaces by overlaying these on the T1w images in the axial view. QC on the cortical surfaces was performed by an operator blinded to the group identity i.e. corrected or uncorrected. Images were scored ‘pass’ – no visually identified widespread or localized errors, ‘questionable’ – less than 3 focal defects or ‘fail’ – 3 or more focal defects and/or a single significant error. Examples of focal defects included: localized inclusion of non-brain tissue (for example dura mater) within the pial surface, the pial surface being located within brain tissue or inaccurate localization of the gray/white matter surface.
2.9. Relationship between cortical thickness and Parkinson’s Disease
After excluding subjects that failed the surface quality control, in total there were n=247 control subjects and n=309 participants with PD. Or if “questionable” quality surfaces were also excluded, there were n=238 controls and n=300 participants with PD. Using these data, a region-of-interest (ROI) analysis was performed based on the mean cortical thickness of the regions in the Desikan-Killiany (DK) Atlas (Desikan et al., 2006). Using the Python StatsModels module (http://www.statsmodels.org), a general linear model was employed with cortical thickness as the dependent variable and group as the independent variable, covarying for age and sex.
2.10. Testing on Brain Tumor Data
The ability of algorithm to generalize to images that contained conspicuous pathology was also assessed visually. For this, five images from the BRATs dataset (Menze et al., 2014) were used, and the regions within and surrounding the tumor were evaluated for any potential distortions or artifacts introduced by applying the algorithm.
3. Results
3.1. Image domain vs. Fourier domain Simulation
Initially, we compared performing the motion simulation in the image domain to the Fourier domain. As to be expected, using the same motion parameters resulted in an almost identical image regardless of whether the image or the Fourier domain was used for simulation (Fig. S3). The advantage of carrying out the simulation in the Fourier domain was therefore predominantly related to run-time. The run-time of the image domain simulation, as to be expected, scales linearly with the number of discrete motion steps. This is in contrast to performing the simulation in the frequency domain which was constant with respect to the number of motion steps (Fig. S3). Videos displaying example images from multiple different slices for the image and frequency domain methods have been provided in Supplementary videos 1 and 2 respectively.
3.2. Neural network architecture
In preliminary experiments, we evaluated 3 different CNN architectures, based on a manual QC score on the 10 ABIDE test set images. Visually as well as based on this QC, the U-Net style architecture significantly outperformed the HighRes3DNet architecture (p=0.04, paired t-test). The U-Net GAN architecture did not perform as well as the corresponding architecture without adversarial loss, although the difference was not significant (Fig. S4). For this reason, only the U-Net style architecture was considered from hereon.
3.3. Simulated validation data
In order to test the generalizability of different models to different levels of motion artifact severity, a simulated validation set was employed. On these images, the model significantly improved the image quality both visually and quantitatively as evaluated by the image quality metrics: SSIM and pSNR, relative to the ground truth (Fig. 3ab). The ability of the CNN model to generalize to different motion severities was investigated by comparing the image similarity metrics on the heldout validation set before and after motion correction.
Figure 3: On the validation dataset CNN models trained with different severity levels (0-20, 0-30 and 0-40) significantly improved both data quality metrics at all levels of motion severity.
(a) Example images before and after correction with the 0-30 model. The corresponding difference image compared to the ground-truth is shown below each image. The ground-truth image is indicated by simulated severity = 0% before correction. (b) Similarity metrics relative to the ground-truth before correction and for different models trained on different severity ranges. Upper panel – structural similarity index (SSIM). Lower panel – pSNR. pSNR is not defined for the before correction 0% corruption case where the images are identical. * represents statistically significant differences at a significance level of p<0.05 (paired t-test). (n=46)
For these experiments, we used the piecewise constant scheme trained on a variety of different severity ranges: 0-20%, 0-30% and 0-40% of corrupted k-space lines. Each of these models was able to generalize well across the 0-50% range of simulated severities in the validation set. As expected, the 0-20 model did not perform as well as the other two models on the more severe 40% and 50% corrupted validation images. Despite this, all models significantly improved the image quality at every severity level according to the SSIM measurements and every severity level except for the 10% and 20% levels based on pSNR (Fig. 3ab). Even where the image was uncorrupted (severity = 0%), applying the CNN model did not result in a statistically significant loss in image quality for any of the three models as measured by SSIM.
After having validated the method on this simulated validation set, we then tested on real motion artifact affected data. First, the simulation parameters were optimized using manual scoring as the evaluation metric on the ABIDE test data, then we assessed the ability of the algorithm to generalize to new datasets.
3.4. Real motion-artifact affected data for optimization of training parameters
1. Manual quality control assessment:
The performance of each training parameter set was assessed using a manual quality control procedure across a set of n=10 images. Both visually and according to the manual QC scores, all motion simulation approaches significantly improved the motion-artifact affected image quality (p<0.05, Fig. 4a). As hypothesized, for the same simulation severity range, the piecewise constant and piecewise transient approaches outperformed the uncorrelated Gaussian model, where the simulation parameters for different k-space lines were drawn independently from a Gaussian distribution. (Fig. 4a). The piecewise constant approach without rotations, was found to perform approximately equally as well as the model which combined translations with rotations (using the nufft).
Figure 4: Motion correction visually and quantitatively improves the image quality of real motion artifact affected data.

Models trained with coherent motion, the piecewise transient and piecewise constant outperformed that trained with samples drawn independently from a Gaussian distribution. Upper panels – Example images. Lower panels – Quality score as assessed manually on a scale between 1-5. (a) Original and corrected results from models trained using different motion simulation approaches. From left-to-right: Gaussian, piecewise transient, piecewise constant, piecewise constant-nufft (with rotations) (b) Model performance on different motion serveries for the piecewise constant model, trained using increasing levels of simulated severity from left-to-right: 0-20, 0-30, 0-40 % of phase-encoding lines. Error bars indicate the standard deviation across n=10 images.
After having investigated different sampling strategies, we then assessed how artifact severity affected model performance on the piecewise constant model. Visually, some ghosting artifacts were still evident on the model trained with the least severe (0-20) range of simulated motion (Fig. 4b). The 0-30 model visually and quantitatively outperformed the 0-20 model (p<0.05, Fig. 4b). Training at the more severe 0-40% range did not result in additional improvements, therefore the 0-30 piecewise constant model was used for subsequent experiments to avoid unnecessary smoothing of the data that could be caused by training with excessively corrupted images. In addition, for the same model, the magnitude of translation of 10 voxels (≈ 10 mm) standard deviation outperformed that of using 5 voxels as well as 20 voxels (Fig. S5). Furthermore, a range of 1-4 motion segments (k) did not perform as well as 1-8 or 1-16 (Fig. S6). The optimal model with 0-30% k-space lines corrupted, a translation = 10 voxels (S.D.) and 1-8 segments, was hereafter used for evaluation of the motion correction method. Additional examples including multiple axial image slices have been provided in Supplementary videos 3 and 4.
2. Evaluation on scans with motion and rescans with minimal motion.
On the separate ADNI test dataset (n=13), the CNN model visually removed blurring as well as ringing artifacts (Fig. 5). At the same time the image quality was significantly improved as assessed by both image quality metrics, SSIM and pSNR calculated with respect to the minimal motion reference images (Table. 1). SSIM was improved in 9 of the 13 images, and pSNR in 10 of 13. The mean of each performance metric was significantly improved as assessed by a paired t-test (p=0.021, p=0.047 for SSIM and pSNR respectively) suggesting artifact correction generalized well to new datasets.
Figure 5: Example images from five different subjects from the ADNI dataset before and after motion correction compared to a minimal motion reference image.

Left column: minimal motion reference image. Middle column: motion affected image. Right column: Motion affected image after motion correction.
Table 1: Image similarity metrics relative to a minimal motion reference image from the ADNI dataset.
SSIM and pSNR were all significantly improved after motion correction for n=13 paired subjects from the ADNI dataset. Data is displayed as mean ± S.E.M
| SSIM | pSNR | |
|---|---|---|
| Before motion correction | 0.985±0.002 | 31.73±1.00 |
| After motion correction | 0.988±0.001 | 33.34±0.79 |
3.5. Improvements in surface reconstruction quality
T1-weighted structural datasets that passed the image QC and were mildly affected by motion artifacts frequently failed the surface reconstruction quality control protocol. After performing the motion correction, these QC failures due to motion were significantly reduced in number. Quantitatively, 536 of 617 (87%) of the images passed the surface reconstruction quality control before motion correction (Fig. 6a), which was increased to 553 (90%) after motion correction. The number of QC failures was reduced by 38% from 61 to 38. Surface reconstructions that were deemed to be of questionable quality were often related to subtle motion artifacts and low signal-to-noise ratio in the temporal lobes that resulted in failure of the surface reconstruction algorithm to estimate the true cortical surface. Many of these subtle errors were alleviated by the motion correction procedure (Fig. 6b). Surface reconstructions that failed QC due to the number or errors or severity of such errors were most commonly related to images exhibiting blurring, ghosting artifacts and low SNR. These were often dramatically improved by the motion correction procedure as indicated by the examples in Fig. 6c.
Figure 6: Motion correction improves the cortical reconstruction quality as indicated by a manual QC procedure.
(a) Proportions and number of images in each category: pass, questionable and fail. (b) Examples of cortical reconstructions that were deemed to be of questionable quality before motion correction but passed QC after correcting the image and re-running the reconstruction pipeline. (c) Examples of cortical reconstructions that failed QC before motion correction but passed QC after correcting the image and re-running the reconstruction pipeline. The orange arrowheads indicate specific areas of QC failures.
3.6. Relationship between cortical thickness and Parkinson’s Disease
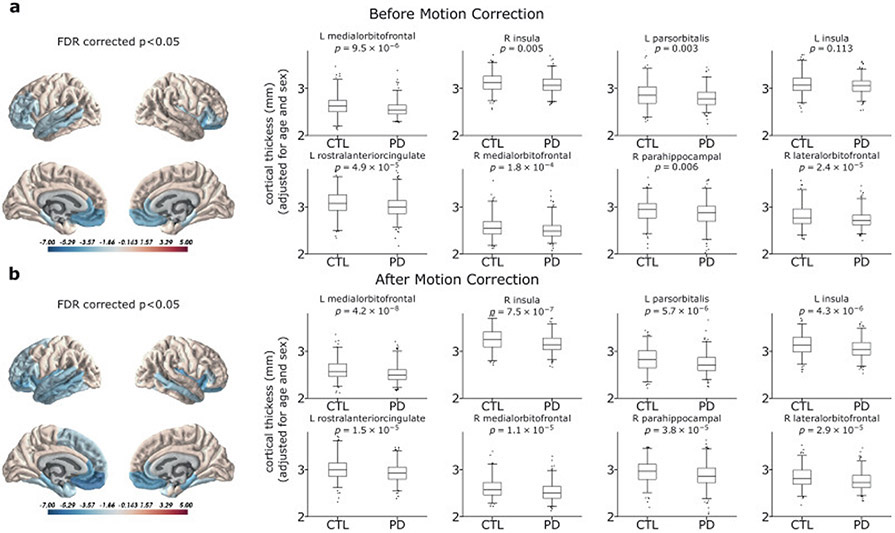
After excluding the data from subjects which failed the surface reconstruction quality control, but including “questionable” quality surfaces, an ROI-based GLM analysis was carried out using the DK atlas with age and sex as covariates. Before motion correction, significant decreases in cortical thickness were limited to the orbital frontal cortices of both cerebral hemispheres, the left inferior frontal gyrus, middle and superior temporal gyrus, the right temporal pole and insula as well as bilaterally across the anterior cingulate and parahippocampal gyri (Fig. 7a). After motion correction, in addition to the regions that were significant before correction, reductions in cortical thickness were more widespread and bilateral and included the left inferior temporal gyrus, the right middle temporal gyrus, the superior frontal gyrus as well as the right supramarginal gyrus (Fig. 7b). In addition, bilaterally the insula, entorhinal and fusiform gyrus also were significantly thinner in participants with PD at the p < 0.05 FDR corrected threshold. The regression statistics for each ROI are shown in Supplementary Table 3.
Figure 7: Cortical thinning in Parkinson’s disease is more significant and more widespread after motion correction compared to before correction.
Left column: T-statistic maps at FDR corrected p<0.05 threshold, indicating significant differences in cortical thickness between PD subjects and controls. Blue regions indicate significantly reduced thickness. Right column: Cortical thickness (adjusted for age and sex) vs. group for the 8 most significantly different regions identified after motion correction. P-values are shown before correction for multiple comparisons. (a) Before applying motion correction, decreases in cortical thickness were limited to the orbital frontal cortices, the left inferior frontal gyrus, middle and superior temporal gyri, the right temporal pole, right insula as well as the left and right anterior cingulate and parahippocampal gyri. (b) After motion correction, there were more significant and more widespread decreases in cortical thickness across both temporal lobes as well as the superior frontal gyrus. (CTL: n=247, PD: n=309)
Upon analyzing cortical surface representations, another possibility might be to exclude questionable surface reconstructions. Given this choice (i.e. only surface reconstructions that scored “pass” on the QC were included) without applying the correction, the regions of cortical thinning in the PD group were slightly more widespread. For example, as illustrated in Fig. 8, the right middle temporal gyrus also exhibited significant thinning, which was not the case where questionable data were included, suggesting that borderline group differences could be obscured by including lower quality surface reconstructions. Excluding questionable quality surfaces after motion correction, resulted in a pattern of cortical thinning that was consistent with that in which they were included, with the exception of the right temporal pole, and left frontal pole, which were close to but did not exceed the significance threshold. The regression statistics for each region including only the cases that passed QC are shown in Supplementary Table 4.
Figure 8: T-statistic maps and box plots indicating regions of significant cortical thinning in PD vs. Controls upon only including cortical reconstructions that passed QC i.e. after excluding questionable surfaces in addition to those that failed QC.
Left column: T-statistic maps at FDR corrected p<0.05 threshold, indicating significant differences in cortical thickness between PD subjects and controls. Blue regions indicate significantly reduced thickness. Right column: Cortical thickness (adjusted for age and sex) vs. group for the 8 most significantly different regions identified after motion correction. P-values are shown before correction for multiple comparisons. (CTL: n=238, PD: n=300)
Finally, given that the model was trained on scans without obvious structural abnormalities, the ability of algorithm to generalize to images that contained lesions was investigated. Five images from the BRATs dataset are shown before and after correction alongside their ground-truth tumor segmentation in Fig. S7. On these examples, there was no evidence that the correction algorithm obscured or distorted the appearance of large or small hyper- or hypointense lesions. However, on some images within the ADNI dataset, we observed that hypointense white matter lesions resembling motion artifacts and in proximity to real motion artifacts had the potential to be further obscured by the correction algorithm (Fig. S8).
4. Discussion
Here, we have developed an image domain retrospective motion correction framework based on a Fourier domain motion simulation model combined with various state-of-the-art 3D neural network architectures (U-Net style CNN, HighRes3DNet, GAN). To validate the method, we performed a systematic qualitative and quantitative evaluation on simulated and real motion artifact-affected images from three separate multi-site datasets. To validate the method, we performed a systematic qualitative and quantitative evaluation on simulated and real motion artifact-affected images. Results from this study suggested that training the model using a database of motion-free images as a ground truth and adding simulated motion enabled the network to generalize well to both unseen validation images with a broad range of unseen simulated motion artifacts, as well as real motion artifact-affected data. These results demonstrated the ability of CNN models trained using simulated data to correct for real motion artifacts as well as improve the quality of cortical surface reconstructions. In this way it was possible to uncover Parkinson’s disease group differences that would otherwise be masked by including cortical surface reconstructions of questionable quality, highlighting the potential utility for clinical and research studies.
It has been well established that Parkinson’s Disease is associated with widespread bilateral cortical thinning across the frontal and temporal cortex (Mak et al., 2015). Before applying motion correction, we found decreases in cortical thickness to be limited to the orbital frontal cortices, the left inferior frontal gyrus, middle and superior temporal gyri, the right temporal pole, right insula as well as the left and right anterior cingulate and parahippocampal gyri. After the CNN-based correction, there was found to be more significant bilateral cortical thinning across the temporal lobe as well as the superior frontal gyrus, right supramarginal gyrus, insula, entorhinal and fusiform gyrus. This is broadly in line with other investigations which have found widespread cortical thinning in patients with PD compared to controls. Specifically, several studies have identified the orbital frontal cortex (Lyoo et al., 2010; Tinaz et al., 2011; Wilson et al., 2019) as a region that is vulnerable even in the case of mild PD. In addition to this, the temporal lobe (Lyoo et al., 2010; Madhyastha et al., 2015; Pereira et al., 2012; Uribe et al., 2016) has also been frequently identified as a region that is at risk in PD. Finally, the cingulate gyrus has been implicated in more moderate to severe PD (Pagonabarraga et al., 2013; Wilson et al., 2019).
In any study, researchers face a challenging decision regarding whether or not to include questionable quality surface reconstructions. Here, instead of discarding these data from the analysis, we used deep learning to improve the quality of the artifact affected data, in order to maintain a larger sample size. Notably, around 10% of the PPMI data were deemed to have a poor-quality surface reconstruction. However, after motion correction, this significantly decreased to around 6%. Whilst it is well accepted that PD leads to widespread cortical thinning, there is still some uncertainty regarding the exact pattern of these changes. For this reason, we also investigated how the significance of the detected regions changed upon excluding the questionable quality surfaces. Before motion correction, excluding these questionable quality surfaces led to a more widespread bilateral pattern of cortical thinning across the temporal lobe that more closely resembled the pattern after correction. Moreover, excluding questionable quality surfaces after motion correction in general resulted in a reduced number of statistically significant regions i.e. the right temporal pole was no longer significant, likely due to the reduced statistical power. As to be expected, there exhibited a high correspondence between the thinning patterns before and after correction upon examining only the subset of surfaces that passed QC. However, it is also worth noting that subtle inaccuracies in the cortical surface reconstruction that were not significant or obvious enough to be revealed in the surface QC score might preclude a perfect agreement. While there was no evidence of hallucinations, in specific cases, white matter lesions that resembled motion artifacts had the potential to be further obscured by the correction procedure. Such limitations will be important to address in future studies, potentially by including corresponding cases in the training dataset. Another limitation relates to the inability to correct artifacts in different imaging sequences or other kinds of imaging artifacts, for example those that are hardware or physiology related. In addition, the algorithm requires a GPU for inference and would be prohibitively expensive on current CPUs.
Whilst the correction procedure was able to correct mild to moderately affected images, more severe cases with highly coherent artifacts were beyond its capabilities. It is possible that recent developments in artifact correction techniques that address the issue at the reconstruction stage will prove to be more powerful in this regard (Cordero-Grande et al., 2018; Cordero- Grande et al., 2020). However it also likely that a retrospective deep learning approach will provide a powerful tool for data that cannot be fixed at the acquisition or reconstruction stage. Indeed, one of the major strengths in the proposed approach is that it does not require availability of raw k-space data and could be used if the original complex data is unavailable. Furthermore, we have demonstrated that carrying out the simulation in the Fourier domain is more advantageous than performing it in the image domain as this way it can be performed online during training for any number of motion steps. CNNs can easily be adapted to operate on complex data (Zhu et al., 2018) and the Fourier domain simulation could therefore be combined with iterative or k-space-based reconstruction for potentially improved results. Furthermore, given an appropriate forward model, future work could explore a similar approach to correct for other commonly occurring artifact types, such as, RF spikes, field inhomogeneities, aliasing or low SNR/CNR.
It is likely that including any number of real motion artifact affected data in training of CNNs would improve the performance of the model enabling the model to generalize to patterns of artifacts that are not fully characterized by the simulation. However, generating paired data with and without motion artifacts is challenging as even if a subject is imaged during the same session, there may be intensity differences between scans that are unrelated to the motion. Further improvements in the method could be yielded by using real k-space trajectories, although this is complicated by the widespread use of under sampled and parallel imaging reconstructions and the wide range of trajectories used in structural MRI acquisitions.
In summary, our method has the potential to improve performance of image post processing such as cortical reconstruction, eventually increasing the statistical power as demonstrated in the analysis of Parkinson’s disease compared to healthy controls. In the image quality control procedure, scoring the severity of the given artifact is a crucial step towards the decision-making whether excluding the artifactual image or not in the subsequent image analysis. Instead of predicting a corrected image, the proposed simulation method could be adapted to train a model for estimating a motion severity score as the CNN output. This could be used as a score for quality control or as a nuisance covariate in subsequent statistical analyses (Iglesias et al., 2017). There is excellent potential for future work to adapt the method for use in image reconstruction.
Supplementary Material
5. Acknowledgements
This study was Supported by the National Institutes of Health grants (P41EB015922, R01EB028297) and the BrightFocus Foundation (A2019052S).
PPMI data was obtained from the Parkinson’s Progression Markers Initiative (PPMI) database (www.ppmi-info.org/data). For up-to-date information on the study, visit www.ppmi-info.org. PPMI – a public-private partnership – is funded by the Michael J. Fox Foundation for Parkinson’s Research and funding partners, including Abbvie, Avid Radiopharmaceuticals, Biogen Idec, Bristol-Myers Squibb, Covance, GE healthcare, Genentech, GlaxoSmithKline, Lilly, Lundbeck, Merck, Meso Scale Discovery, Pfizer, Piramal, Roche, Servier, and UCB found at www.ppmi-info.org/fundingpartners.
Data collection and sharing for the ADNI dataset was funded by the Alzheimer's Disease Neuroimaging Initiative (ADNI) (National Institutes of Health Grant U01 AG024904) and DOD ADNI (Department of Defense award number W81XWH-12-2-0012). ADNI is funded by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, and through generous contributions from the following: AbbVie, Alzheimer’s Association; Alzheimer’s Drug Discovery Foundation; Araclon Biotech; BioClinica, Inc.; Biogen; Bristol-Myers Squibb Company; CereSpir, Inc.;Cogstate; Eisai Inc.; Elan Pharmaceuticals, Inc.; Eli Lilly and Company; EuroImmun; F. Hoffmann-La Roche Ltd and its affiliated company Genentech, Inc.; Fujirebio; GE Healthcare; IXICO Ltd.; Janssen Alzheimer Immunotherapy Research & Development, LLC.; Johnson & Johnson Pharmaceutical Research & Development LLC.; Lumosity; Lundbeck; Merck & Co., Inc.; Meso Scale Diagnostics, LLC.; NeuroRx Research; Neurotrack Technologies; Novartis Pharmaceuticals Corporation; Pfizer Inc.; Piramal Imaging; Servier; Takeda Pharmaceutical Company; and Transition Therapeutics. The Canadian Institutes of Health Research is providing funds to support ADNI clinical sites in Canada. Private sector contributions are facilitated by the Foundation for the National Institutes of Health (www.fnih.org). The grantee organization is the Northern California Institute for Research and Education, and the study is coordinated by the Alzheimer’s Therapeutic Research Institute at the University of Southern California. ADNI data are disseminated by the Laboratory for Neuro Imaging at the University of Southern California.
Abbreviations:
- CNN
convolutional neural network
- ROI
region of interest
- NUFFT
non-uniform fast Fourier transform
- PD
Parkinson’s disease
- PPMI
Parkinson’s Progression Markers Initiative
- pSNR
peak signal-to-noise ratio
- QC
quality control
- SSIM
structural similarity index
- SD
standard deviation
Appendix
*Data used in preparation of this article were obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (adni.loni.usc.edu). As such, the investigators within the ADNI contributed to the design and implementation of ADNI and/or provided data but did not participate in analysis or writing of this report. A complete listing of ADNI investigators can be found at: http://adni.loni.usc.edu/wp-content/uploads/how_to_apply/ADNI_Acknowledgement_List.pdf
6. References
- Abadi M, Agarwal A, Barham P, Brevdo E, Chen Z, Citro C, Corrado GS, Davis A, Dean J, Devin M, Ghemawat S, Goodfellow I, Harp A, Irving G, Isard M, Jia Y, Jozefowicz R, Kaiser L, Kudlur M, Levenberg J, Mane D, Monga R, Moore S, Murray D, Olah C, Schuster M, Shlens J, Steiner B, Sutskever I, Talwar K, Tucker P, Vanhoucke V, Vasudevan V, Viegas F, Vinyals O, Warden P, Wattenberg M, Wicke M, Yu Y, Zheng X 2016. TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. [Google Scholar]
- Atkinson D, Hill DLG, Stoyle PNR, Summers PE, Keevil SF 1997. Automatic correction of motion artifacts in magnetic resonance images using an entropy focus criterion. IEEE Transactions on Medical Imaging, 16(6), 903–910. [DOI] [PubMed] [Google Scholar]
- Barnett AH, Magland JF, Klinteberg L.a. 2018. A parallel non-uniform fast Fourier transform library based on an" exponential of semicircle" kernel. arXivpreprint arXiv: 1808.06736. [Google Scholar]
- Çiçek Ö, Abdulkadir A, Lienkamp SS, Brox T, Ronneberger O 2016. 3D U-Net: learning dense volumetric segmentation from sparse annotation. International conference on medical image computing and computer-assisted intervention. Springer, pp. 424–432. [Google Scholar]
- Cordero-Grande L, Hughes EJ, Hutter J, Price AN, Hajnal JV 2018. Three-dimensional motion corrected sensitivity encoding reconstruction for multi-shot multi-slice MRI: Application to neonatal brain imaging. Magnetic Resonance in Medicine, 79(3), 1365–1376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cordero- Grande L, Ferrazzi G, Teixeira RPA, O'Muircheartaigh J, Price AN, Hajnal JV 2020. Motion- corrected MRI with DISORDER: Distributed and incoherent sample orders for reconstruction deblurring using encoding redundancy. Magnetic Resonance in Medicine, 84(2). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desikan RS, Segonne F, Fischl B, Quinn BT, Dickerson BC, Blacker D, Buckner RL, Dale AM, Maguire RP, Hyman BT, Albert MS, Killiany RJ 2006. An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. NeuroImage, 31(3), 968–980. [DOI] [PubMed] [Google Scholar]
- Di Martino A, Yan CG, Li Q, Denio E, Castellanos FX, Alaerts K, Anderson JS, Assaf M, Bookheimer SY, Dapretto M, Deen B, Delmonte S, Dinstein I, Ertl-Wagner B, Fair DA, Gallagher L, Kennedy DP, Keown CL, Keysers C, Lainhart JE, Lord C, Luna B, Menon V, Minshew NJ, Monk CS, Mueller S, Müller RA, Nebel MB, Nigg JT, O'Hearn K, Pelphrey KA, Peltier SJ, Rudie JD, Sunaert S, Thioux M, Tyszka JM, Uddin LQ, Verhoeven JS, Wenderoth N, Wiggins JL, Mostofsky SH, Milham MP 2014. The autism brain imaging data exchange: towards a large-scale evaluation of the intrinsic brain architecture in autism. Molecular Psychiatry, 19(6), 659–667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dolz J, Desrosiers C, Ayed IB 2018. 3D fully convolutional networks for subcortical segmentation in MRI: A large-scale study. NeuroImage, 170, 456–470. [DOI] [PubMed] [Google Scholar]
- Duffy BA, Zhang W, Tang H, Zhao L, Law M, Toga AW, Kim H 2018. Retrospective correction of motion artifact affected structural MRI images using deep learning of simulated motion 1st Conference on Medical Imaging with Deep Learning. [Google Scholar]
- Engelhardt E, Inder TE, Alexopoulos D, Dierker DL, Hill J, Van Essen D, Neil JJ 2015. Regional impairments of cortical folding in premature infants. Annals of Neurology. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B, Dale AM 2000. Measuring the thickness of the human cerebral cortex from magnetic resonance images. Proceedings of the National Academy of Sciences of the United States of America, 97(20), 11050–11055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu J, Yang Y, Singhrao K, Ruan D, Chu FI, Low DA, Lewis JH 2019. Deep learning approaches using 2D and 3D convolutional neural networks for generating male pelvic synthetic computed tomography from magnetic resonance imaging. Medical Physics, 46(9), 3788–3798. [DOI] [PubMed] [Google Scholar]
- Gibson E, Li W, Sudre C, Fidon L, Shakir DI, Wang G, Eaton-Rosen Z, Gray R, Doel T, Hu Y, Whyntie T, Nachev P, Modat M, Barratt DC, Ourselin S, Cardoso MJ, Vercauteren T 2018. NiftyNet: a deep-learning platform for medical imaging. Computer Methods and Programs in Biomedicine, 158, 113–122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glasser MF, Sotiropoulos SN, Wilson JA, Coalson TS, Fischl B, Andersson JL, Xu J, Jbabdi S, Webster M, Polimeni JR, Van Essen DC, Jenkinson M, Consortium WU-MH 2013. The minimal preprocessing pipelines for the Human Connectome Project. NeuroImage, 80, 105–124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodfellow I, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, Courville A, Bengio Y 2014. Generative adversarial nets. Advances in neural information processing systems. pp. 2672–2680. [Google Scholar]
- Greengard L, Lee J-Y 2004. Accelerating the nonuniform fast Fourier transform. SIAM review, 46(3), 443–454. [Google Scholar]
- Hammernik K, Klatzer T, Kobler E, Recht MP, Sodickson DK, Pock T, Knoll F 2018. Learning a variational network for reconstruction of accelerated MRI data. Magnetic resonance in medicine, 79(6), 3055–3071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haskell MW, Cauley SF, Wald LL 2018. TArgeted Motion Estimation and Reduction (TAMER): Data Consistency Based Motion Mitigation for MRI Using a Reduced Model Joint Optimization. IEEE transactions on medical imaging, 37(5), 1253–1265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hedley M, Yan H, Rosenfeld D 1991. An improved algorithm for 2-D translational motion artifact correction. IEEE Transactions on Medical Imaging, 10(4), 548–553. [DOI] [PubMed] [Google Scholar]
- Iglesias JE, Lerma-Usabiaga G, Garcia-Peraza-Herrera LC, Martinez S, Paz-Alonso PM 2017. Retrospective Head Motion Estimation in Structural Brain MRI with 3D CNNs, Springer, Cham, pp. 314–322. [Google Scholar]
- Isensee F, Kickingereder P, Wick W, Bendszus M, Maier-Hein KH 2018. No new-net. International MICCAI Brainlesion Workshop. Springer. pp. 234–244. [Google Scholar]
- Johnson PM, Drangova M 2019. Conditional generative adversarial network for 3D rigid-body motion correction in MRI. Magn Reson Med, 82(3), 901–910. [DOI] [PubMed] [Google Scholar]
- Kamnitsas K, Ledig C, Newcombe VF, Simpson JP, Kane AD, Menon DK, Rueckert D, Glocker B 2017. Efficient multi-scale 3D CNN with fully connected CRF for accurate brain lesion segmentation. Medical image analysis, 36, 61–78. [DOI] [PubMed] [Google Scholar]
- Kim H, Lepage C, Maheshwary R, Jeon S, Evans AC, Hess CP, Barkovich AJ, Xu D 2016. NEOCIVET: Towards accurate morphometry of neonatal gyrification and clinical applications in preterm newborns. NeuroImage, 138, 28–42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kingma DP, Ba J 2014. Adam: A Method for Stochastic Optimization. [Google Scholar]
- Kustner T, Armanious K, Yang J, Yang B, Schick F, Gatidis S 2019. Retrospective correction of motion-affected MR images using deep learning frameworks. Magn Reson Med, 82(4), 1527–1540. [DOI] [PubMed] [Google Scholar]
- Küstner T, Liebgott A, Mauch L, Martirosian P, Bamberg F, Nikolaou K, Yang B, Schick F, Gatidis S 2018. Automated reference-free detection of motion artifacts in magnetic resonance images. Magnetic Resonance Materials in Physics, Biology and Medicine, 31(2), 243–256. [DOI] [PubMed] [Google Scholar]
- Li W, Wang G, Fidon L, Ourselin S, Cardoso MJ, Vercauteren T 2017. On the Compactness, Efficiency, and Representation of 3D Convolutional Networks: Brain Parcellation as a Pretext Task. Cham. Springer International Publishing. pp. 348–360. [Google Scholar]
- Loktyushin A, Nickisch H, Pohmann R, Schölkopf B 2013. Blind retrospective motion correction of MR images. Magnetic Resonance in Medicine, 70(6), 1608–1618. [DOI] [PubMed] [Google Scholar]
- Loktyushin A, Schuler C, Scheffler K, Schölkopf B 2015. Retrospective Motion Correction of Magnitude-Input MR Images, Springer, Cham, pp. 3–12. [Google Scholar]
- Lyoo CH, Ryu YH, Lee MS 2010. Topographical distribution of cerebral cortical thinning in patients with mild Parkinson's disease without dementia. Mov Disord, 25(4), 496–9. [DOI] [PubMed] [Google Scholar]
- Madhyastha TM, Askren MK, Boord P, Zhang J, Leverenz JB, Grabowski TJ 2015. Cerebral perfusion and cortical thickness indicate cortical involvement in mild Parkinson's disease. Mov Disord, 30(14), 1893–900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mak E, Su L, Williams GB, Firbank MJ, Lawson RA, Yarnall AJ, Duncan GW, Owen AM, Khoo TK, Brooks DJ, Rowe JB, Barker RA, Burn DJ, O'Brien JT 2015. Baseline and longitudinal grey matter changes in newly diagnosed Parkinson's disease: ICICLE-PD study. Brain, 138(Pt 10), 2974–86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meding K, Loktyushin A, Hirsch M Automatic detection of motion artifacts in MR images using CNNS. 2017/March//. IEEE. pp. 811–815. [Google Scholar]
- Menze BH, Jakab A, Bauer S, Kalpathy-Cramer J, Farahani K, Kirby J, Burren Y, Porz N, Slotboom J, Wiest R 2014. The multimodal brain tumor image segmentation benchmark (BRATS). IEEE transactions on medical imaging, 34(10), 1993–2024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milletari F, Navab N, Ahmadi S-A 2016. V-net: Fully convolutional neural networks for volumetric medical image segmentation. 2016 fourth international conference on 3D vision (3DV). IEEE. pp. 565–571. [Google Scholar]
- Moradi E, Khundrakpam B, Lewis JD, Evans AC, Tohka J 2017. Predicting symptom severity in autism spectrum disorder based on cortical thickness measures in agglomerative data. NeuroImage, 144, 128–141. [DOI] [PubMed] [Google Scholar]
- Mortamet B, Bernstein MA, Jack CR Jr., Gunter JL, Ward C, Britson PJ, Meuli R, Thiran JP, Krueger G, Alzheimer's Disease Neuroimaging I 2009. Automatic quality assessment in structural brain magnetic resonance imaging. Magn Reson Med, 62(2), 365–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nyul LG, Udupa JK, Xuan Z 2000. New variants of a method of MRI scale standardization. IEEE Transactions on Medical Imaging, 19(2), 143–150. [DOI] [PubMed] [Google Scholar]
- Odena A, Dumoulin V, Olah C 2016. Deconvolution and checkerboard artifacts. Distill, 1(10), e3. [Google Scholar]
- Oksuz I, Ruijsink B, Puyol-Antón E, Bustin A, Cruz G, Prieto C, Rueckert D, Schnabel JA, King AP 2018. Deep learning using K-space based data augmentation for automated cardiac MR motion artefact detection. International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer. pp. 250–258. [Google Scholar]
- Pagonabarraga J, Corcuera-Solano I, Vives-Gilabert Y, Llebaria G, Garcia-Sanchez C, Pascual-Sedano B, Delfino M, Kulisevsky J, Gomez-Anson B 2013. Pattern of regional cortical thinning associated with cognitive deterioration in Parkinson's disease. PLoS One, 8(1), e54980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pawar K, Chen Z, Shah NJ, Egan GF 2018. Moconet: Motion correction in 3D MPRAGE images using a convolutional neural network approach. arXiv preprint arXiv:1807.10831. [Google Scholar]
- Payan A, Montana G 2015. Predicting Alzheimer's disease: a neuroimaging study with 3D convolutional neural networks. arXiv preprint arXiv:1502.02506. [Google Scholar]
- Pereira JB, Ibarretxe-Bilbao N, Marti MJ, Compta Y, Junque C, Bargallo N, Tolosa E 2012. Assessment of cortical degeneration in patients with Parkinson's disease by voxel-based morphometry, cortical folding, and cortical thickness. Hum Brain Mapp, 33(11), 2521–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pham C-H, Ducournau A, Fablet R, Rousseau F 2017. Brain MRI super-resolution using deep 3D convolutional networks. 2017 IEEE 14th International Symposium on Biomedical Imaging (ISBI 2017). IEEE. pp. 197–200. [Google Scholar]
- Reuter M, Tisdall MD, Qureshi A, Buckner RL, van der Kouwe AJW, Fischl B 2015. Head motion during MRI acquisition reduces gray matter volume and thickness estimates. NeuroImage, 107, 107–115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ronneberger O, Fischer P, Brox T 2015. U-net: Convolutional networks for biomedical image segmentation. International Conference on Medical image computing and computer-assisted intervention. Springer. pp. 234–241. [Google Scholar]
- Satterthwaite TD, Wolf DH, Loughead J, Ruparel K, Elliott MA, Hakonarson H, Gur RC, Gur RE 2012. Impact of in-scanner head motion on multiple measures of functional connectivity: relevance for studies of neurodevelopment in youth. NeuroImage, 60(1), 623–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shabanian M, Eckstein EC, Chen H, DeVincenzo JP 2019. Classification of Neurodevelopmental Age in Normal Infants Using 3D-CNN based on Brain MRI. 2019 IEEE International Conference on Bioinformatics and Biomedicine (BIBM). IEEE. pp. 2373–2378. [Google Scholar]
- Sled JG, Zijdenbos AP, Evans AC 1998. A nonparametric method for automatic correction of intensity nonuniformity in MRI data. IEEE transactions on medical imaging, 17(1), 87–97. [DOI] [PubMed] [Google Scholar]
- Stucht D, Danishad KA, Schulze P, Godenschweger F, Zaitsev M, Speck O 2015. Highest Resolution In Vivo Human Brain MRI Using Prospective Motion Correction. PLOS ONE, 10(7), e0133921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tinaz S, Courtney MG, Stern CE 2011. Focal cortical and subcortical atrophy in early Parkinson's disease. Mov Disord, 26(3), 436–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tisdall MD, Hess AT, Reuter M, Meintjes EM, Fischl B, van der Kouwe AJW 2012. Volumetric navigators for prospective motion correction and selective reacquisition in neuroanatomical MRI. Magnetic resonance in medicine, 68(2), 389–399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trivizakis E, Manikis GC, Nikiforaki K, Drevelegas K, Constantinides M, Drevelegas A, Marias K 2018. Extending 2-D convolutional neural networks to 3-D for advancing deep learning cancer classification with application to MRI liver tumor differentiation. IEEE journal of biomedical and health informatics, 23(3), 923–930. [DOI] [PubMed] [Google Scholar]
- Tustison NJ, Avants BB, Cook PA, Zheng Y, Egan A, Yushkevich PA, Gee JC 2010. N4ITK: improved N3 bias correction. IEEE transactions on medical imaging, 29(6), 1310–1320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uribe C, Segura B, Baggio HC, Abos A, Marti MJ, Valldeoriola F, Compta Y, Bargallo N, Junque C 2016. Patterns of cortical thinning in nondemented Parkinson's disease patients. Mov Disord, 31(5), 699–708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Z, Bovik AC, Sheikh HR, Simoncelli EP 2004. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Transactions on Image Processing, 13(4), 600–612. [DOI] [PubMed] [Google Scholar]
- White N, Roddey C, Shankaranarayanan A, Han E, Rettmann D, Santos J, Kuperman J, Dale A 2010. PROMO: Real-time prospective motion correction in MRI using image-based tracking. Magnetic Resonance in Medicine. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson H, Niccolini F, Pellicano C, Politis M 2019. Cortical thinning across Parkinson's disease stages and clinical correlates. J Neurol Sci, 398, 31–38. [DOI] [PubMed] [Google Scholar]
- Yang Z, Zhang C, Xie L Sparse MRI for motion correction. 2013/April//. IEEE. pp. 962–965. [Google Scholar]
- Yoshida S, Oishi K, Faria AV, Mori S 2013. Diffusion tensor imaging of normal brain development. Pediatric radiology, 43(1), 15–27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zaitsev M, Maclaren J, Herbst M 2015. Motion artifacts in MRI: A complex problem with many partial solutions. Journal of Magnetic Resonance Imaging, 42(4), 887–901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu B, Liu JZ, Cauley SF, Rosen BR, Rosen MS 2018. Image reconstruction by domain-transform manifold learning. Nature. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.