Implementing and Assessing an Alchemical Method for Calculating Protein–Protein Binding Free Energy

Abstract

Protein–protein binding is fundamental to most biological processes. It is important to be able to use computation to accurately estimate the change in protein–protein binding free energy due to mutations in order to answer biological questions that would be experimentally challenging, laborious, or time-consuming. Although nonrigorous free-energy methods are faster, rigorous alchemical molecular dynamics-based methods are considerably more accurate and are becoming more feasible with the advancement of computer hardware and molecular simulation software. Even with sufficient computational resources, there are still major challenges to using alchemical free-energy methods for protein–protein complexes, such as generating hybrid structures and topologies, maintaining a neutral net charge of the system when there is a charge-changing mutation, and setting up the simulation. In the current study, we have used the pmx package to generate hybrid structures and topologies, and a double-system/single-box approach to maintain the net charge of the system. To test the approach, we predicted relative binding affinities for two protein–protein complexes using a nonequilibrium alchemical method based on the Crooks fluctuation theorem and compared the results with experimental values. The method correctly identified stabilizing from destabilizing mutations for a small protein–protein complex, and a larger, more challenging antibody complex. Strong correlations were obtained between predicted and experimental relative binding affinities for both protein–protein systems.

Graphical Abstract

INTRODUCTION

Protein–protein binding is an essential phenomenon in molecular biology and directly mediates most functions in cells such as cellular metabolism, signal transduction, and coagulation among many other biological processes.^1,2 Mutations of the amino acids in protein–protein complexes can modulate or even disrupt protein–protein interactions by changing the associated binding free energy (ΔG) of the protein–protein complexes. The binding free energy of the protein–protein complexes determines the stability of association and the conditions for protein–protein complex formation.³ It is important to be able to quantify the stabilities of protein complexes and how they can be modified by amino acid mutations and how they are affected by evolution.

Many techniques have been employed to determine the change in the protein–protein binding free energy due to a mutation (i.e., relative binding affinity, ΔΔG). Experimental biophysical and biochemical methods are routinely used, but these methods are laborious, expensive, and time-consuming and are limited by technical challenges.^4-7 By contrast, computational methods can be relatively inexpensive, and the accuracy of such methods has been improved with the advancement of computational resources and better force fields.^8-10 Computational methods for estimating ΔΔG values can be broadly classified as either nonrigorous or rigorous.¹¹

Nonrigorous free-energy methods typically use a single, static all-atom structure of the protein complex. These methods typically have energy functions that are trained using experimentally measured binding affinities or changes in affinities.^12,13 Many such semiempirical approaches have been developed that combine molecular mechanics and various optimized energy terms from available experimental data.¹⁴ For example, BeAtMuSiC and mCSM use coarse-grained statistical potentials derived from known 3-D structures of proteins and machine learning.^15,16 FoldX uses empirical force field trained by experimentally measured binding free energies or changes in affinities.^12,13 The other so-called docking/scoring algorithms can predict binding affinities based on predicted binding poses and putative binding interactions between protein–protein complexes.^17-19

Rigorous free-energy approaches are based on the principles of statistical mechanics and use molecular simulations to explore the conformational space.²⁰ These methods typically provide more accurate ΔΔG predictions, compared to nonrigorous. One reason for this is that they inherently consider the conformational flexibility of the proteins and hence the entropic contribution. In recent years, rigorous approaches have made tremendous efficiency and theoretical advancements.^11,20 Rigorous free-energy calculation approaches are typically classified into three categories: endpoint methods, physical path sampling, and alchemical transformation.²⁰ Endpoint methods typically use molecular mechanics force fields with implicit solvent models such as molecular mechanics-generalized Born surface area (MMGB/SA) and molecular mechanics Poisson–Boltzmann surface area (MMPB/SA).^21,22 These methods are computationally less expensive than other rigorous approaches since simulations are only performed for two states; however, their accuracy is system-dependent and sensitive to simulation protocols such as sampling strategy and entropy calculation. For path sampling approaches, the physical unbinding and/or binding pathway of the protein with respect to its partner is sampled to obtain the underlying free-energy profile connecting bound and unbound states.^23-25 This category of methods can be very accurate but requires exhaustive conformational sampling along the pathway making it computationally expensive. Finally, alchemical methods exploit unphysical pathways by morphing, creating, and annihilating atoms.^26-29 These methods use molecular mechanics force fields as an energy function and the sampling of the correct thermodynamic ensemble is maintained by thermostatted and barostatted dynamics. The primary advantage is that the alchemical pathway does not need to be correlated with the physical binding process. This is particularly advantageous when considering relative binding affinity calculations due to single amino acid mutations (such as the current study). In this case, one needs to only calculate the free-energy change due to alchemically mutating the amino acid to another type in both the bound and unbound states.

Rigorous molecular dynamics (MD)-based alchemical free-energy calculation can be performed using equilibrium (e.g., free-energy perturbation,³⁰ thermodynamics integration³¹) or nonequilibrium (e.g., the Jarzynski equality,^32,33 Crooks fluctuation theorem³⁴) methods. The initial simulation setup is the same for both equilibrium and nonequilibrium methods, but the protocols used during the simulations and postanalyses are different. The Hamiltonian H is coupled to a parameter λ that navigates the system from wild-type (λ = 0) to mutant (λ = 1). While such alchemical methods can be very accurate, they can also be computationally expensive since sufficient sampling is required to overcome the energetic and entropic barriers. In addition, the initial setup is not user-friendly, particularly when there is a change in the net charge of the system.^29,35,36 Specifically, the setup requires the topology of the protein system to ensure that all bonded and nonbonded interactions are correctly switched from λ = 0 to 1.

To enable more user-friendly alchemical free-energy calculations, de Groot et al. developed a package called pmx that automatically generates hybrid protein structures and topologies using force field-specific pregenerated mutation libraries.^37-39 Moreover, to maintain the net charge of the system during alchemical transformation, they developed an approach that uses two protein systems in a single simulation box (double-system/single-box).^37,40 Their approach of using pmx-generated topologies with a double-system/single-box approach was previously used to predict protein folding ΔΔG values due to mutations.^37,38 Prior to the development of the pmx package, de Groot et al. used the hybrid topology approach to calculate binding free energies for ubiquitin in complex with different protein substrates using a fast-growth thermodynamic integration approach with the Crooks–Gaussian intersection (CGI) method.⁴¹ The main purpose of their study was to analyze ubiquitin conformations due to point mutations and predict the sign of ΔΔG for binding different substrates. They studied 11 mutations and obtained a Pearson correlation coefficient of 0.70 (p = 0.016). However, they have not explored the transition time per snapshot for nonequilibrium simulations. Later, the same group tested pmx with double-system/single-box approach to predict ΔΔG binding free energies for the protein–protein complex of α-chymotrypsin with its inhibitor Turkey Ovomucoid third domain with nine observed mutations of site L18 of Turkey Ovomucoid third domain.⁴⁰ The correlation coefficient between predicted and experimental ΔΔG was 0.80. Although promising, this protein–protein complex is small, all nine mutations occurred at the same amino acid site and were noncharge mutations.

Here, we tested the performance of using pmx with a double-system/single-box approach in a systematic manner using two protein–protein complexes of different sizes with a wide range of experimental ΔΔG values. For each system, we selected eight mutations from different sites with a broad range of experimental ΔΔG values. We estimated ΔΔG values using pmx hybrid topologies with a double-system/single-box approach and the nonequilibrium CGI method. Predicted ΔΔG values were compared with experimental values. In contrast to previous studies by de Groot et al., we optimized the transition times for the most stabilizing and the most destabilizing mutations of each protein–protein system. Higher correlation was found for smaller protein–protein complex as well as the larger, more complex, antigen-antibody system. Our results suggest that there is still room for improvement in rigorous binding free-energy methods to reduce computational cost, especially for large, complex protein–protein systems.

METHODS

Test System Selection.

We selected two protein–protein complexes from the SKEMPI database⁴² as test systems for this study. We chose the relatively small Barnase (110 aa)–Barstar (89 aa) complex (Protein Data Bank (PDB) ID: 1BRS)⁴³ and the larger, more challenging, antigen–antibody complex of lysozyme (129 aa)–HY/HEL-10 FAB (429 aa) (PDB ID: 3HFM).⁴⁴ 1BRS has total 30 mutations, and 3HFM has 67 mutations reported with their binding constants (K_d) in SKEMPI database. We wanted to shortlist eight mutations from each system based on ΔΔG values. In order to do that we first calculated ΔG values for wild-type and mutant using the reported K_d and reported temperature (T) with eq 1

$$\Delta G=-RT\text{ln}{K}_{\mathrm{d}}$$ (1)

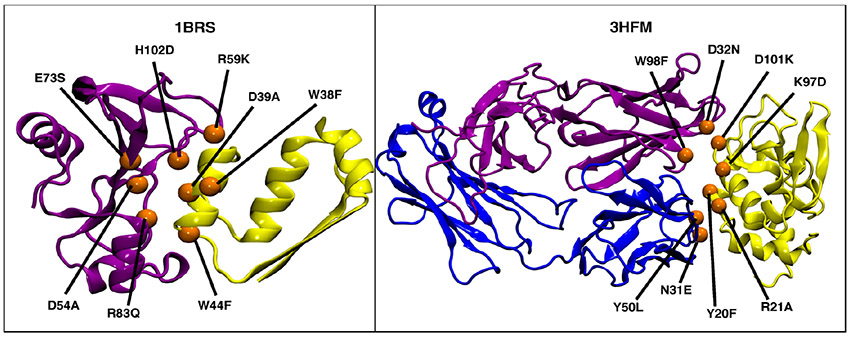
The ΔΔG values were calculated by taking the difference between ΔG of the mutant and ΔG of wild-type. The average ΔΔG value was used when multiple ΔΔG values for a single mutation were in the database (Supporting Information Table S1). We chose these systems and mutations based on several criteria: (i) ΔΔG values should vary in sign—important since mutations with negative (stabilizing) values are often more difficult to predict compared to positive (destabilizing) values; (ii) there should be a small number of missing residues in the 3-D structure of the protein complexes; (iii) chosen mutations should be nonalanine-scanning point mutations at differing amino acid sites; and (iv) reported mutations should be on multiple chains (Figure 1, Supporting Information Table S1).

Figure 1.

3-D structures of the test systems used in the current study with the eight selected mutations shown as orange spheres. Left: Barnase (purple)–Barstar (yellow) protein complex (PDB ID: 1BRS); Right: lysozyme–HY (yellow) HEL-10 FAB (purple and blue) antigen–antibody complex (PDB ID: 3HFM).

Preparation of Protein–Protein Complexes.

The 3-D structures of protein–protein complexes were downloaded from the PDB server (https://www.rcsb.org) and edited to preserve only the coordinates of the two or three interacting chains listed in the SKEMPI database.⁴² All missing residues and atoms were then added using MODELLER software.⁴⁵ Mutants were generated using the BuildModel command from FoldX software.^12,13 This process provided nine input structures for each protein complex (a wild-type and eight mutant forms) to carry out alchemical free-energy calculations.

Construction of Hybrid Residues.

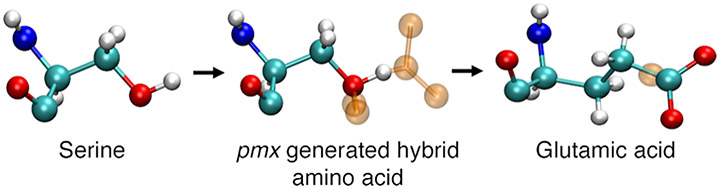
Alchemical binding free-energy calculations require the construction of a non-physical pathway of intermediate states connecting the wild-type amino acid (λ = 0) to its mutant form (λ = 1). The pmx webserver^37,38 allows automatic generation of these intermediate states by producing hybrid amino acid states representing a mixture of wild-type and mutant form (see Figure 2). Both wild-type and mutant complex structure files were uploaded to the pmx webserver. The pdb2gmx option to add hydrogen atoms, and the Amber99SB*ILDN modified force field options were selected. The pmx webserver output consisted of hybrid structure and topology files compatible with GROMACS to perform the alchemical MD simulations.

Figure 2.

Example of a pmx-generated hybrid amino acid structure for serine (λ = 0) to glutamic acid (λ = 1). Dummy atoms are shown as transparent orange spheres.

Free-Energy Calculation and the Thermodynamic Cycle.

To estimate relative binding free-energy values (ΔΔG), we alchemically morphed the wild-type amino acids to their mutated forms (Figure 2). This process was replicated for both the bound and unbound states as indicated by horizontal arrows in the thermodynamic cycle shown in Figure 3. We can efficiently obtain ΔG₁ and ΔG₃ values with high accuracy using this approach.^46-48 By contrast, to carry out binding/unbinding simulations (vertical arrows in Figure 3), to calculate ΔG₂ and ΔG₄ values would be considerably more challenging and computationally expensive.

Figure 3.

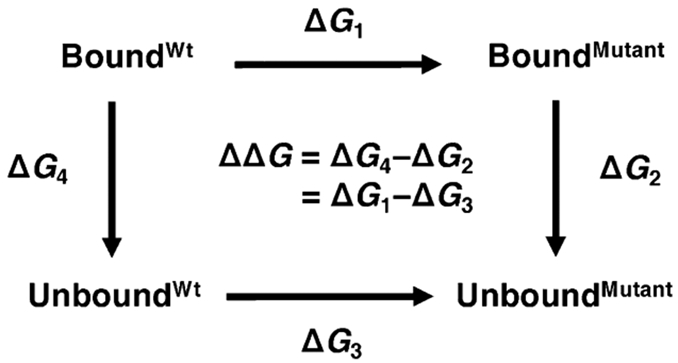
Schematic representation of the thermodynamic cycle used to calculate relative binding free energies due to mutation (ΔΔG = ΔG₁ – ΔG₃). Horizontal arrows indicate the non-physical pathways used in the current study where the amino acid was alchemically morphed from wild-type to its mutant form for both bound and unbound states.

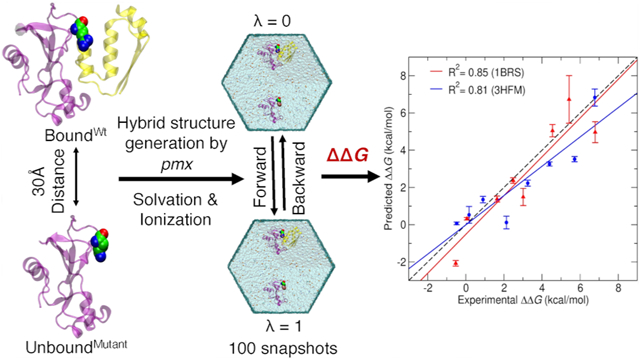
To estimate ΔG₁ and ΔG₃ (two horizontal arrows in Figure 3), we used the double-system/single-box approach developed by Gapsys et al.⁴⁰ Following this approach, we placed Bound^Wt protein complex and Unbound^Mutant protein in a single simulation box (λ = 0, Figure 4A) and similarly we placed Bound^Mutant protein complex and Unbound^Mutant protein in a second simulation box (λ = 1, Figure 4A). Figure 4B represents the series of steps involved for setting up the system for MD simulations and alchemical free-energy calculations. The distance between the two protein systems in each simulation box was maintained at 30 Å (Figure 4B) by applying position restraints on a single backbone atom close to the center of mass of each protein system. This separation distance was chosen to be larger than the short-range electrostatics cutoff to ensure that the two protein systems in a single simulation box did not interact with each other. Alchemical transformation from λ = 0 to 1 is termed “forward”, where Bound^Wt was transformed into Bound^Mutant and simultaneously Unbound^Mutant was transformed into Unbound^Wt, that is, “backward” λ = 1 to 0. Two independent simulations (forward and backward) were thus performed to calculate the ΔΔG value for each mutation. Use of the double-system/single-box approach enabled us to maintain charge neutrality of the simulation system, even when an alchemical transformation involved a charge change between the wild-type and a mutant state, for example, R83Q.

Figure 4.

Double-system/single-box simulation setup. (A) Each colored cylinder represents a simulation box. During the forward alchemical transition, double systems consisting of Bound^Wt and Unbound^Mutant (blue cylinder, λ = 0) are morphed into Bound^Mutant and Unbound^Wt (λ = 1) states, respectively. Similarly, backward alchemical transition (λ = 1 to λ = 0) takes place in the red cylinder. (B) Schematic representation of the steps involved for setting up one of the double-system/single-box simulations for a mutation of 1BRS protein complex.

MD Simulations and Alchemical Free-Energy Calculations.

All MD simulations were carried out with the GROMACS-2018.3⁴⁹ MD simulation package using the Amber99SB*ILDN force field and the TIP3P water model.⁵⁰ The pmx-generated hybrid structures and modified force field files were used as an input. For each mutation, we prepared two simulation boxes (λ = 0 and λ = 1, Figure 4A) to carry out forward and backward transitions using the steps shown in Figure 4B. Both the states were solvated using dodecahedron water boxes. Na⁺ and Cl⁻ ions were added at a 0.15 M concentration to neutralize the net charge. Both the simulation boxes were then energy-minimized for 10,000 steps using the steepest descent algorithm. Subsequent NVT followed by NPT ensemble simulations were performed for 500 ps for each simulation box. Note that in the scripts provided by pmx, NVT equilibration simulations were not performed; however, we included them in our study to reduce the system instability we observed. During the MD simulation, constant pressure and temperature were maintained using Parrinello–Rahmans⁵¹ pressure coupling at 1 atm and v-rescale temperature⁵² coupling at 300 K. A 2 fs time step was used and each snapshot was saved at every 10 ps. Final production MD simulations were then performed for 40 ns to ensure sufficient sampling under NPT conditions. To prevent the diffusion of the proteins and maintain a 30 Å distance between the two protein systems, backbone carbons close to the center of mass were harmonically restrained with a force constant of 1000 kJ/mol nm². Choice of backbone C atoms used to apply position restraints for 1BRS was made based on the bound and unbound forms: (i) site A40 of bound-state Barstar; (ii) site A74 of unbound Barnase; and (iii) site L20 of unbound Barstar. While for 3HFM, (i) site Q37 of the bound-state light chain; (ii) site H41 of unbound state of the light chain; and (iii) site L56 of the antigen. The light chain is always bound to the heavy chain regardless of whether the antigen is bound or unbound. These positional restraints affect only the translational degrees of freedom of the proteins, not the overall structure or orientation of the proteins. The contribution of the positional restraints to the estimation of ΔG will be the same for the bound and unbound form of the proteins and thus the bias cancels out when calculating ΔΔG, as is the case for the current study.

After the equilibrium MD simulations, fast-growth nonequilibrium alchemical simulations were performed to estimate the ΔΔG. From each equilibrated MD simulation, the first 10 ns of the trajectory was discarded, and the last 30 ns was used to generate 100 snapshots (i.e., every 300 ps). Each snapshot was used to initialize a nonequilibrium simulation with a transition time of 5 ns for 1BRS and 8 ns for 3HFM (see the Supporting Information) where λ was continuously changed from 0 to 1 or from 1 to 0. The speed of λ value change was set 2 × 10⁻⁷/fs for all forward and backward transitions. The derivatives of the Hamiltonian with respect to λ were recorded at every step and free energies were calculated from the work (W) distributions obtained from integration according to eq 2.

$$W={\int }_{\lambda =0}^{\lambda =1}\frac{\delta H}{\delta \lambda }\mathrm{d}\lambda$$ (2)

ΔΔG was estimated by calculating the intersection of the forward and backward work distributions according to the CGI method as described in Goette and Grubmüller.⁵³ The scripts used for analysis and calculations of ΔΔG were obtained from the pmx package.

RESULTS AND DISCUSSION

The purpose of our study is to test the accuracy of using pmx hybrid topologies and alchemical free-energy calculations with the double-system/single-box approach developed by Gapsys et al. to estimate relative binding affinities of protein–protein complexes. The pmx package allows for automated generation of the necessary hybrid topologies that are otherwise challenging to generate, and the double-system/single-box approach is a simple approach to maintain a neutral charge even when a mutation changes the protein charge. We tested this approach on two protein–protein systems of varying sizes (1BRS and 3HFM). For each system, we selected eight distinct mutations with experimental ΔΔG values reported in the literature using the criteria listed under the Methods section.

For alchemical nonequilibrium free-energy calculations using the fast growth method,^39,54,55 the transition time from λ = 0 to 1 or λ = 1 to 0 significantly influences the accuracy of ΔΔG prediction. Short transition times lead the system far away from the equilibrium leading to a heavily biased estimate, while long transition times are less biased but more computationally costly, so the right balance is required.³⁹ To develop our simulation protocol, we initially chose two mutations from the 1BRS and 3HFM as test cases. These cases represent the most stabilizing (1BRS:D54A, ΔΔG = −0.53 kcal/mol; 3HFM:Y20F, ΔΔG = −0.48 kcal/mol) and destabilizing (1BRS:D39A, ΔΔG = 6.79 kcal/mol; 3HFM:K97D, ΔΔG = 6.77 kcal/mol) charge-changing mutations from the list of eight selected mutations (See Tables 1 & 2). To determine a reasonable transition time for our production simulations, we calculated ΔΔG values for both the test case mutations of 1BRS and 3HFM using 100 snapshots with a range of transition times from 1 to 7 ns for 1BRS and 1 to 10 ns for 3HFM. Supporting Information Figure 1 shows that transition times of 5 ns for 1BRS and 8 ns for 3HFM were sufficient to accurately estimate the free energies for these challenging mutations.

Table 1.

Predicted Relative Binding Free Energy of Each Mutation of 1BRS at Different Transition Times between 1 to 5 ns for 100 Independent Transitions^a

	ΔΔG (kcal/mol)
mutations (1BRS)	experimental	1 ns	2 ns	3 ns	4 ns	5 ns	6 ns	7 ns
D54A	−0.53	17.71	15.77	11.94	4.92	−2.07	−2.46	−1.89
W44F	0.06 ± 0.2	0.48	0.23	0.41	0.61	0.32
W38F	1.64 ± 0.2	0.94	1.14	1.13	1.02	1.38
R59K	2.49	7.91	10.16	7.03	3.84	2.37
E73S	3.01 ± 0.2	−27.01	−19.31	−5.3	−1.30	1.49
H102D	4.55	12.39	10.98	9.86	7.87	5.05
R83Q	5.42 ± 0.2	−2.39	13.59	15.18	9.35	6.73
D39A	6.79	8.93	10.45	9.45	7.60	4.97	5.42	4.65

^aEstimated ΔΔG values of all eight mutations of the 1BRS system for 100 independent transitions. The predicted ΔΔG values were compared with the corresponding experimental data. ΔΔG values beyond 5 ns of transition time are for test mutations D54A and D39A as a part of the convergence study.

Table 2.

Predicted Relative Binding Free Energy of Each Mutation of 3HFM at Different Transition Times between 1 to 8 ns for 100 Independent Transitions^a

	ΔΔG (kcal/mol)
mutations (3HFM)	experimental	1 ns	2 ns	3 ns	4 ns	5 ns	6 ns	7 ns	8 ns	9 ns	10 ns
Y20F	−0.48	−7.53	−6.34	−3.45	−2.95	−0.34	−1.02	−0.83	0.07	−0.69	−0.98
D32N	0.17 ± 0.3	−3.47	−5.67	−2.99	−1.32	−1.59	−1.98	−1.14	0.53
R21A	0.90	5.82	7.54	4.56	3.98	1.23	2.34	1.74	1.35
D101K	2.13	16.98	13.27	7.43	3.59	−0.46	−1.27	0.87	0.12
W98F	3.25 ± 0.16	7.49	5.89	6.78	2.35	−0.16	−0.87	0.46	2.23
Y50L	4.39 ± 0.12	9.65	6.37	2.36	1.33	0.10	1.37	2.89	3.26
N31E	5.71 ± 0.13	13.28	8.73	9.67	4.78	−1.26	0.56	2.34	3.52
K97D	6.77 ± 0.14	10.25	10.47	7.09	5.36	9.00	7.20	8.33	6.83	7.86	8.24

^aEstimated ΔΔG values of all eight mutations of the 3HFM system for 100 independent transitions. The predicted ΔΔG values were compared with the corresponding experimental data. ΔΔG values beyond 8 ns of transition time are for test mutations Y20F and K97D as a part of the convergence study.

ΔΔG values of the remaining six mutations of 1BRS and 3HFM were estimated using the optimized simulation protocol and the transition time established through test case mutations. The predicted ΔΔG values were within ±2 kcal/mol of experimental ΔΔG values for optimized transition times for both protein–protein systems. In addition, experimental ΔΔG errors are within ±0.2 kcal/mol for both the test systems.

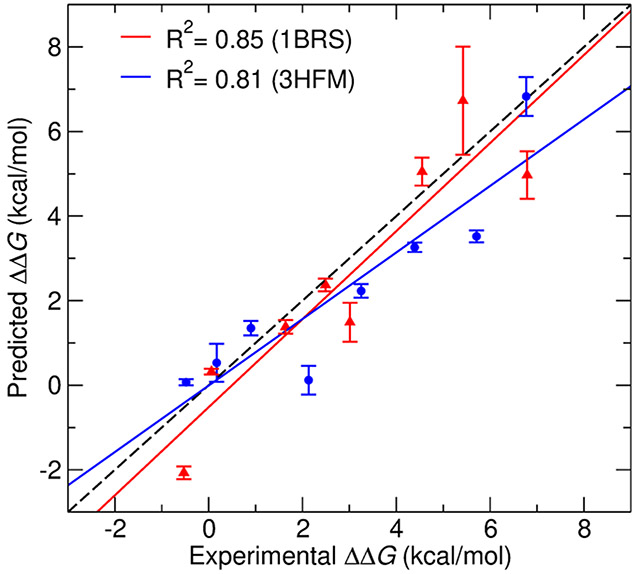
Figure 5 shows the correlation between the predicted and experimental ΔΔG values for all mutations from both the test systems. The calculated ΔΔG values correlate well with experimental data (R² = 0.85) for a smaller system of 1BRS and (R² = 0.81) for the larger, antigen–antibody complex 3HFM. The noncharge mutations from the 1BRS system such as W44F and W38F have the predicted ΔΔG values within the range of ±0.5 kcal/mol of experimental ΔΔG values. The convergence time for these mutations was within 1–2 ns transition time/snapshot. In the case of 3HFM, the noncharge mutations Y20F, W98F, and Y50L have higher accuracy, within range of ±1 kcal/mol of experimental ΔΔG values compared to other charge-changing mutations. Conversely, the charge-changing mutations are challenging to achieve convergence in free-energy calculations with short transition time. Longer transition times are likely needed in these cases to allow for sufficient conformational sampling. All the charge-changing mutations of the 1BRS system converged at around a 5 ns transition time with relatively high accuracy (±2 kcal/mol of experimental ΔΔG). However, in 3HFM, the charge-changing mutations show convergence at around 8 ns transition time with an accuracy of ±2.5 kcal/mol of experimental ΔΔG.

Figure 5.

Correlation between predicted and experimental ΔΔG values for 1BRS (red) and 3HFM (blue) systems. The dashed black line shows perfect correlation.

Both the test systems in this study were previously used by our laboratory to predict ΔΔG values for the same eight mutations using the nonrigorous methods FoldX and MD + FoldX and rigorous coarse-grained umbrella sampling MD simulations.⁵⁶ The pmx with a double-system/single-box approach significantly outperforms the accuracy our previous FoldX^12,13 (1BRS:R² = 0.59, 3HFM:R² = −0.005), MD + FoldX^57-59 (1BRS:R² = 0.62, 3HFM:R²= 0.04), and coarse-grained umbrella sampling (1BRS:R² = 0.85, 3HFM:R² = 0.35) estimates in both the complexes. There is an especially large improvement in the accuracy of predicted ΔΔG values for the antigen–antibody complex, 3HFM, with all-atom pmx with a double-system/single-box approach.

In this study, we used 100 snapshots per mutation to initiate the alchemical transitions and each snapshot was simulated for 5 ns. This means that 500 ns total simulation time was used to estimate ΔΔG for both forward and backward directions. The equilibration simulation required ~4500 CPUh for one mutation for the 1BRS system while in the case of 3HFM, it required ~85,300 CPUh. With pmx with a double-system/single-box approach, the alchemical nonequilibrium simulation time is the major contributing factor to estimate the computational cost for the calculation of one ΔΔG. In the 1BRS system, nonequilibrium simulations required ~45,000 CPUh for 100 transitions per ΔΔG prediction, however almost 30 times more CPUh (~1,364,800) required in the case of the 3HFM system. It should also be noted that nonequilibrium alchemical transition is trivially parallelizable in that each of the 100 transitions can be run independently without relying on the completion of the previous simulation.

In order to obtain accurate binding free-energy values for protein–protein complex, exhaustive conformational sampling is required in order to sufficiently explore conformational space. Larger protein–protein complexes, such as antigen–antibody complex 3HFM studied here, require longer simulations to obtain convergence compared to smaller protein–protein complexes such as 1BRS.^60-62 In our study, we first optimized the protocol to calculate ΔΔG values for the most stabilizing and the most destabilizing mutations of 1BRS and 3HFM systems and then applied the same protocol to rest of the mutations. We note that the accuracy of the nonequilibrium method could possibly be improved³⁹ via (i) longer equilibrium simulations to generate snapshots with more distant conformations, (ii) increasing the transition time per snapshot, and (iii) increasing number of independent transitions. We observed that in the case of 3HFM, the accuracy of ΔΔG values was improved with increasing the transition time per snapshot.

Future work could involve using the alchemical double-system/single-box method but with coarse-grained protein models. Based on results from our previous study,⁵⁶ this may significantly reduce computational cost and still retain similar accuracy. However, coarse-grained hybrid topologies of the proteins have not yet been developed. Another approach to reducing computational cost could be use of a dual-resolution water model where water around the protein is atomistic and the rest of the water molecules coarse-grained.^63-65

CONCLUSIONS

In this study, we have estimated protein–protein relative binding affinities due to single amino acid mutations using pmx hybrid topologies with a double-system/single-box approach. Nonequilibrium alchemical methods were used to generate ΔΔG estimates for one small and one large protein–protein complex, and results were compared with experimental values. We obtained a significantly higher correlation between predicted and experimental ΔΔG values for the small complex as well as the larger one. We were able to successfully distinguish stabilizing mutations from nonstabilizing mutations for all mutations in small complex and the large antigen–antibody complex. The accuracy of the predictions for the large complex is improved compared to previously tested rigorous and nonrigorous methods. Our results suggest that there are still potential areas for improvement in the reduction of computational cost for binding free-energy calculations, especially for larger protein–protein complexes. Future work could also be devoted to estimating binding free energies due to multiple mutations.