Deep learning-based inverse mapping for fluence map prediction

Abstract

We developed a fluence map prediction method that directly generates fluence maps for a given desired dose distribution without optimization for volumetric modulated arc therapy (VMAT) planning. The prediction consists of two steps. First, projections of the desired dose are calculated and then inversely mapped to fluence maps in the phantom geometry by a deep neural network (DNN). Second, a plan scaling technique is applied to scale fluence maps from phantom to patient geometry. We evaluated the performance of the proposed fluence map prediction method for 102 head and neck (H&N) and 14 prostate cancer VMAT plans by comparing the patient doses calculated from the predicted fluence maps with the given desired dose distributions. The mean dose differences were 1.42%±0.37%, 1.53%±0.44% and 1.25%±0.44% for the planning target volume (PTV), the region from the PTV boundary to the 50% isodose line, and the region from the 50% to the 20% isodose line, respectively. The gamma passing rate was 98.06%±2.64% with the 3 mm/3% criterion. The prediction time for a single VMAT plan was less than one second. In conclusion, we developed an inverse mapping-based method that predicts fluence maps for desired dose distributions with high accuracy. Our method is effectively an optimization-free inverse planning approach, which was orders of magnitude faster than fluence map optimization (FMO). Combining the proposed method with leaf sequencing has the potential to dramatically speed up VMAT treatment planning.

1. Introduction

Inverse planning that uses optimization to obtain machine parameters from the desired dose distribution is the central component of treatment planning in the era of intensity modulated radiation therapy (IMRT). Planners rely on their clinical experience or institutional practice to set metrics for the desired dose distribution as the optimization goals. These goals typically include point doses (maximum, minimum, or mean dose), dose-volume points and desired isodose lines. Planners can also use tools like knowledge-based planning (KBP) to mimic high quality historical plans (Appenzoller et al., 2012, Yuan et al., 2012) or multi-criteria optimization (MCO) to navigate the Pareto surface and explore trade-offs (Schlaefer et al., 2013, Teichert et al., 2019, Craft et al., 2012a, Craft et al., 2012b). No matter which approach is used for planning, the desired clinical goals are often expressed in point doses and dose-volume constraints for regions of interest (ROIs) and subsequently achieved by iterative optimization methods. Such methods include fluence map optimization (FMO) (Shepard et al., 2000, Lu, 2010), which essentially optimizes the weights of beamlets (fluence map intensity), and direct machine parameter optimization (DMPO), which further generates machine parameters for plan delivery (Papp and Unkelbach, 2014). FMO is typically a large-scale optimization problem involving a huge dose influence matrix (Lu, 2010), and its complexity increases as the number of beams increases, especially in volumetric modulated arc therapy (VMAT). FMO and other iterative optimization methods have the merits of constructing deliverable dose distributions and balancing dosimetric trade-offs, but the time-consuming process discourages planners from sufficiently tuning the plan towards clinical optimality and hinders the application of time-sensitive tasks like online adaptive planning.

Although optimization (especially FMO) is the work horse of clinical treatment planning, we never cease efforts to find the direct link from patient geometry (ROI distribution) to desired dose distribution because the desired dose distribution, as a concrete optimization objective, can reduce the trial-and-error of tuning the objectives during treatment planning. Recent successful applications of deep learning (DL) in the field of treatment planning have accomplished what was previously impossible. In contrast to the KBP methods that use one-dimensional statistics of the geometry of ROIs as inputs and one-dimensional statistics of the dose as outputs (Yuan et al., 2012, Appenzoller et al., 2012), a convolutional neural network (CNN) can map the three-dimensional (3D) geometry of ROIs to population-based 3D dose distributions for various disease sites, including the prostate (Nguyen et al., 2019c), lung (Barragán-Montero et al., 2019) and head and neck (H&N) (Nguyen et al., 2019b, Babier et al., 2020). More advanced models that can generate a set of doses with different objectives (Ma et al., 2019) or trade-offs (Nguyen et al., 2019a) have also been proposed. With predicting dose distributions from ROI distributions becoming a thriving field, researchers then have focused on using dose mimicking objectives to obtain deliverable plans from the predicted dose distributions. For example, dosimetric information like dose-volume points has been extracted from the predicted 3D dose and set as optimization objectives for FMO in an in-house developed software (Babier et al., 2018, Babier et al., 2020) and for FMO in a commercial treatment planning system (TPS) (McIntosh et al., 2017).

Three-dimensional dose distribution d is linked to fluence maps w by dose influence matrix D, which describes a linear mapping from w to d. The DL-based dose prediction models can generate the desired volumetric dose distribution d accurately, but the information in d has been lost by the methods (Babier et al., 2020, McIntosh et al., 2017) mentioned above, which reduced the spatial information of d to dose-volume points (as optimization goals), and then relied on the optimization algorithms to restore dose distribution d and to obtain fluence map w. Ideally, the fluence map w could be inversely mapped from the desired dose distribution d directly since they are linked by dose influence matrix D. We propose to utilize the complete information of the dose d by inversely mapping it to fluence map w in a single-shot inference calculation with no iterative optimization. The inference calculation is much faster than iterative FMO in mimicking the desired dose d, even with a dose influence matrix generated off-line for FMO.

The task of finding a desired dose d with balanced dosimetric trade-offs was undertaken by FMO before, but can be accomplished by the deep-learning based dose prediction methods using the ROI distribution as the input. This paper focuses on a method that takes the dose d with desired trade-offs as the input and converts it to fluence map w, which are machine-related parameters for plan delivery. So the combination of dose prediction methods and this work (fluence map prediction) form a new scheme that can jointly fulfill the function of FMO (determining d and w) in a sequential order. Since the new scheme involves no iterative operation, it will be much faster than FMO. The speed-up is essential for interactive tuning and on-line/real-time adaptive planning. A related work by (Lee et al., 2019) used the beam dose to predict the fluence map of the corresponding beam in prostate IMRT plans by deep neural network (DNN), but this is rather impractical as directly extracting a single-beam dose from the total dose is almost impossible. If it were available, the fluence map could then be obtained by deconvoluting the beam dose at the isocenter plane with a scatter kernel (Lu and Chen, 2010).

The rest of paper is organized as follows. In the Methods and Materials section, we describe the mathematical structure and realization of the proposed method. Section 2.1 covers formulas and terminologies and briefly introduces the two steps for fluence map prediction. Sections 2.2 and 2.3 detail these steps separately: first, inverse mapping in the phantom geometry (2.2), and second, plan scaling (2.3). Section 2.4 describes data collection and processing in the phantom geometry for DNN training. Section 2.5 presents the DNN design for learning the inverse mapping. In the Results section, we evaluate the speed and accuracy of the fluence map prediction. In the Discussion section, we highlight the strengths and weaknesses of this work, and explore the goals of future research.

2. Materials & Methods

2.1. Overall workflow

The physical interpretation of the map w ↦ d = D × w is the forward dose calculation. D_ij represents the dose delivered by unit-intensity beamlet j to voxel i. When voxel i is on the ray-tracing line of beamlet j, D_ij is the primary dose (ray-tracing dose); when voxel i is not on the ray-tracing line of beamlet j, D_ij is the scatter dose. We denote the primary dose influence matrix as $\tilde{D}$, which contains only the ray-tracing dose. ${\tilde{D}}_{ij}=0$ if the voxel i is not on the beamlet j ray-tracing line because the contribution of the scatter dose is excluded. Let us consider a beam with a finite field size irradiating vertically to the center of a semiinfinite water phantom. The values of ${\tilde{D}}_{ij}$ (no scatter) along the central beamlet j are proportional to the percentage depth dose curve of the same beam setup (source surface distance and energy) but with an infinitely small field size.

Given that deep learning can predict volumetric dose distributions, we assume that dose d is known. The central topic of this paper is to solve the mapping f_d from dose d to fluence map w:

$$f_d:d=Dw\mapsto w$$ (1)

Iterative FMO could solve this mapping, but iterative FMO takes too long for time-sensitive tasks like interactive tuning and online/real-time adaptive planning in clinical setting. We defined projections of dose as the sum of the doses weighted by ${\tilde{D}}_{ij}$ along the beamlet ray-tracing lines: $P={\tilde{D}}^{T}d={\tilde{D}}^{T}Dw$. The mapping d → P is the attenuated Radon transform. Analogous to tomographic reconstruction, when the angular samples are fine enough, we could fully reconstruct d from projection data P, i.e. the inverse mapping P → d is well-defined (Natterer, 2001). In this circumstance, P and d are equivalent, so learning the mapping f_d is equivalent to learning the mapping f_P from projections of dose P to fluence maps w:

$$f_P:P={\tilde{D}}^{T}Dw\mapsto w$$ (2)

In the next section, we will use a DNN to approximate f_P. Given the equivalence between f_P and f_d, we no longer need optimization to solve f_d. This is how the proposed inverse mapping method could realize inverse planning without optimization.

Note that w ↦ d ↦ P depends on D, which is further determined by electron density distribution of patient body. The same dependence on density distribution holds for f_d and f_P. A DNN that learns the f_P of one patient thus cannot work for another. To address this issue, we proposed the concept of ROI-specific phantom geometry and phantom plans. The dose distribution of a photon rotational therapy plan depends on the geometrical distribution of the planning target volumes (PTVs) and the organs at risk (OARs) and how those ROIs are weighted. The ROI-specific phantom geometry has the same isocenter and geometrical distribution of ROIs as the patient geometry but different electron density distribution and external contours. In the patient geometry, the external contour is the boundary of the body, and the density distribution is acquired from the simulation CT. The phantom geometry, on the other hand, is formed by replacing the body with a homogeneous water-equivalent cylindrical phantom while keeping the isocenter and all ROIs in the same geometrical positions as in the patient geometry. The dose influence matrices of patient geometry D_pt and phantom geometry D_pham are thus different. We use the subscript pt and phan to indicate values corresponding to patient and phantom geometry, respectively. To achieve the same dose to PTVs and OARs for the two geometries, the fluence maps of the phantom plan (w_phan) and the patient plan (w_pt) should be different.

We propose a two-step method to predict the fluence maps: inverse mapping and plan scaling (figure 1). We assume that the desired dose distribution of phantom plan d_phan is known, and we start from its projections P_phan, calculated by non-voxel-based broad beam (NVBB) framework (Lu, 2010), where $\tilde{D}$ is generated on-the-fly other than offline pre-calculation. In the first step, a DNN is used as an inverse function to map the projection of desired dose P_phan to fluence map w_phan in the phantom geometry. The DNN learns the mapping f_P for the phantom geometry, P_phan → w_phan, from the paired training data (P_phan, w_phan) in phantom plans. In the second step, the fluence map w_phan is scaled to the real patient geometry by a plan scaling technique, which will be detailed in 2.3. We trained and tested this prediction method, mapping followed by scaling, on radiotherapy plans for patients with H&N and prostate cancer treated at UT Southwestern Medical Center (UTSW).

Figure 1.

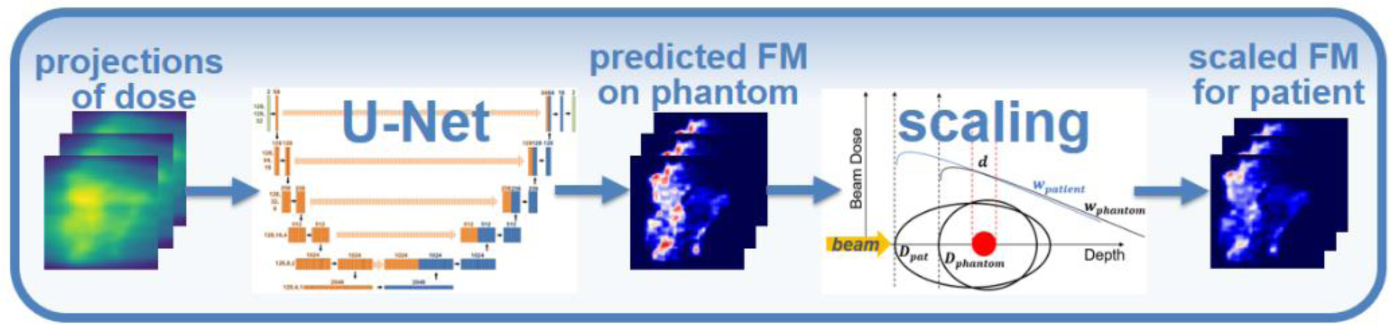
Workflow of the proposed fluence map prediction method. The leftmost figure represents the projections of dose in phantom geometry.

2.2. Inverse mapping from projections of dose to fluence maps

Before discussing the properties of $f_P:P={\tilde{D}}^{T}Dw\mapsto w$, we would like to make an analogy between inverse planning and image reconstruction. Suppose we want to use CT to measure the patient density distribution with a vectorized form y. CT acquisition is described by the system matrix A (Radon transform) and the acquired sinogram b as b = Ay. With the filtered back projection (FBP) A^†, the reconstructed image can be expressed as x = A^†b = A^†Ay. In the case of sparse view CT or other scenarios with under-sampled measurements, the system matrix A doesn’t have a full rank, so x ≠ y (Hyun et al., 2020), and reconstructed image x has artifacts and noise. To reconstruct images with minimal artifacts and noise, optimizations are typically applied to solve b → y, including a data fidelity term ||Ax − b|| and another term like total variation that utilizes our prior knowledge of x.

$$\text{Image }y\stackrel{\mathit{\text{Radon}}}{\to }\text{sinogram }b=Ay\stackrel{\mathit{\text{FBP}}}{\to }\text{Recon Image }x=A^{†}Ay$$ (3)

The optimization performed in inverse planning has a mathematical structure similar to that in image reconstruction. To obtain a deliverable fluence map from the desired dose distribution, optimization includes a dosimetric term ||Dw − d|| and another term on the degree of modulation of w that accounts for the deliverability constraint on w. Optimization solves f_d: d → w in (1), which is the inverse of the first half of (4).

$$\text{Fluence\hspace{0.17em}}w\stackrel{\mathit{\text{Attenuated\hspace{0.17em}}}BPw/\mathit{\text{scatter}}}{\to }\text{Dose\hspace{0.17em}}d=Dw\stackrel{\mathit{\text{Attenuated Radon}}}{\to }\text{Projection\hspace{0.17em}}P={\tilde{D}}^{T}Dw$$ (4)

Forward dose calculation for d can be viewed as a simple (unfiltered) back projection with attenuation and scatter of radiation beams or as attenuated filtered back projection, in which scatter is modeled by a convolution filter applied to the fluence (Holmes and Mackie, 1994, Lu and Chen, 2010). The projection calculation for P is an attenuated Radon transform. Comparing (3) to (4), we find that the CT acquisition/image reconstruction and the dose calculation/projection calculation have the same structure. We will break down the analogy into three levels. The first two levels are well known, and the third level is novel. In the first level, y, d and x are 3D volumes (in the image domain), and w, b and P are beam eye view (BEV) projections (in the projection domain). Dose calculation w → d and image reconstruction b → x are all back projection operations, but the former is a physical process, and the latter is a mathematical operation (Holmes and Mackie, 1994). Similarly, although CT acquisition y → b and dose projection d → P are Radon transforms, the former is a physical operation, and the latter is a mathematical operation whose results cannot be physically measured. In the second level of the analogy, optimization-based reconstruction algorithms solve b → y (first half of (3)), while fluence map optimization algorithms in inverse planning solve d → w (first half of (4)). In the third level, various DL models have been proposed to learn the mapping x → y (inverse of (3)), that is from low-quality images (with noise and artifacts due to under-sampled measurement) to high-quality images (Jin et al., 2017), which has proven a competent rival for optimization in the field of image reconstruction. It is not surprising that the same mapping exists in our inverse planning problem, given their similar mathematical structures. In section 2.4, we will use a DNN to learn the mapping f_P: P ↦ w (inverse of (4)) in (2). Since f_P is equivalent to f_d, a fluence map optimization that solves f_d: d → w in (1) is no longer needed.

Note that the matrix ${\tilde{D}}^{T}D$ is square, but it may have rank deficiency so that the mapping $w\mapsto P={\tilde{D}}^{T}D\times w$ is a many-to-one mapping. Therefore, f_P: P ↦ w is a one-to-many mapping and, thus, not learnable. The many possible w tend to have similar general profiles but very different smoothness (modulations). This is explained by the fluence convolution broad beam (FCBB) theory (Lu and Chen, 2010), in which scatter is modeled by convolving the fluence map with a scatter kernel followed by calculating the ray-tracing dose of the smeared fluence maps. For those fluence maps corresponding to the same dose d, their original forms are different in terms of smoothness, but their smeared forms after convolution are similar. Only one of the possible candidates of w that corresponds to the desired d and satisfies deliverability constraints is obtained by the optimizer in the TPS. Therefore, although f_P: P ↦ w is one-to-many, what we really want the DNN to learn is the pseudo-inverse f_P that satisfies $f_P\circ {\tilde{D}}^{T}D=I$ (identity map) for clinical plan fluence maps w. In section 2.4, a DNN will be trained by paired data (P, w) extracted from clinical plans so that the co-domain of the mapping learned consists of only clinically deliverable fluence maps. By this data-driven method, we will not only circumvent the one-to-many mapping problem, but also obtain the deliverable fluence maps w used clinically.

The mapping f_P: P ↦ w learned by DNN satisfies $f_P\circ {\tilde{D}}^{T}D=I$ for clinical plan fluence map, where ${\tilde{D}}^{T}D$ is the attenuated back projection followed by attenuated Radon transform. Its analogy in CT reconstruction, A^†A (Radon transform followed by FBP), is purely dependent on the CT data acquisition protocol (configuration of scanning beam), so we could use paired data from different patients to learn the map x → y because its inverse A^†A is patient-independent (Hyun et al., 2020). However, aside from the configuration of (treatment) beam, ${\tilde{D}}^{T}D$ is also dependent on the patient density distribution, so ${\tilde{D}}^{T}D$ is patient-specific, as is f_P: P ↦ w. If we still use data in clinical plans belonging to various patients for training, the DNN will fail to converge because the training data are not consistent. Because it’s unrealistic to train a DNN to learn f_P for each patient, we scaled all the clinical plans from patient geometry to phantom geometry (see section 2.3) and used paired data ($P_{\mathit{\text{phan}}}={\tilde{D}}_{\mathit{\text{phan}}}^T{D}_{\mathit{\text{phan}}}{w}_{\mathit{\text{phan}}},w_{\mathit{\text{phan}}}$) in phantom plans for training. The trained DNN learned f_P of a standard cylindrical phantom. Given the equivalence between f_P and f_d, the DNN works as an optimizer in phantom geometry.

We have explained why we used a data-driven method to learn the inverse mapping and why we need the DNN to learn it under phantom geometry. When we applied this method, we assumed that the desired dose distribution in phantom plan d_phan is known. The trained DNN, which learned the f_P of the phantom, will map the projections of dose P_phan to fluence maps w_phan for the phantom geometry directly. The next section will describe the plan scaling technique used to obtain the fluence maps w_pt for the patient geometry.

2.3. Fluence Map Scaling

In this section, we will describe a technique for scaling plans across different geometries. Specifically, by scaling fluence maps from one geometry to another (with different external contours and density distributions), we can achieve the same dose for the targets and even overlap regions of the two geometries. The scaling operation is realized by tissue phantom ratio (TPR) curve matching (figure 2).

Figure 2.

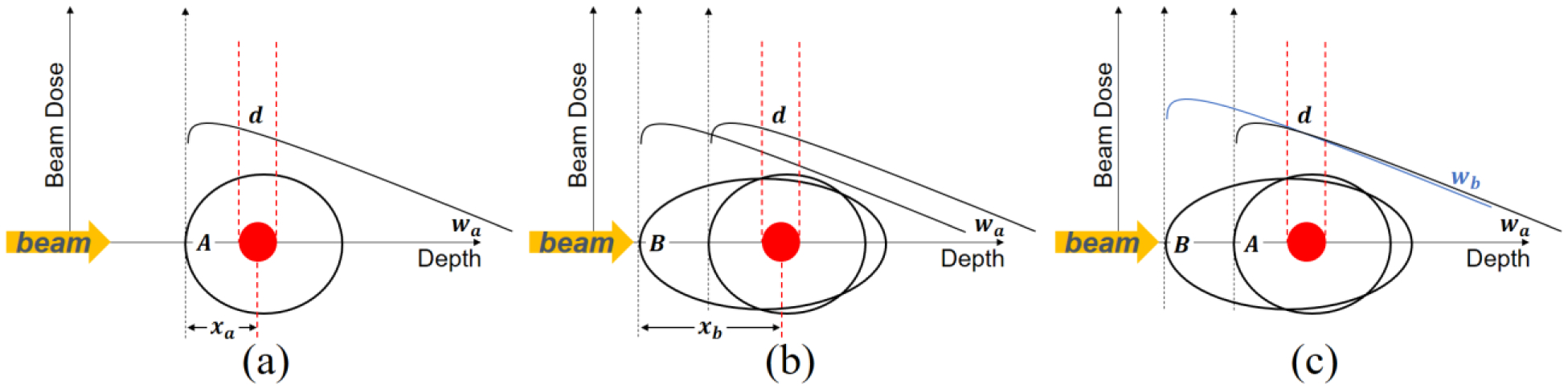
Plan scaling via tissue phantom ratio (TPR) curve matching.

Suppose a photon rotational therapy plan consisting of dose distribution and fluence maps from all beam angles is known for the phantom geometry. Their information is presented in figure 2(a). The black open circle is the external contour of the phantom and the red circle is the target volume. The black curve shows the dose distribution of one beamlet as a function of depth. We denote the intensity of that beamlet as w_a and the beamlet dose to target as d. We aim to obtain a plan for patient geometry such that the dose distribution in the target volume and other overlapping regions is the same as that in the phantom geometry. This cannot be achieved by simply shooting the fluence maps for phantom geometry on patient geometry, as revealed in figure 2(b), where the black ellipse indicates the contour of the patient body. We denote the radio-depth along the path of that beamlet to the target center plane as x_a and x_b, in phantom and patient respectively. The mismatching of two black curves in figure 2(b) illustrates that the target will be under-dosed due to the greater radio-depth if the beamlet in the phantom plan is used on the patient geometry directly. Assuming the treatment isocenter is placed on the target center, the scaling method is to scale the intensity of fluence maps per beamlet (per angle and per fluence map pixel) by

$$w_b=w_a\times \frac{TPR\left(fz=0,\mathit{\text{depth}}=x_a\right)}{TPR\left(fz=0,\mathit{\text{depth}}=x_b\right)}.$$ (5)

TPR stands for the dose delivered by a uniform square field to isocenter in fixed 100cm SAD (source axis distance) setup. It is a function of fz (field size) and radiological depth of isocenter. The scaling process for one beamlet is rendered in figure 2(c). Guaranteed by (5), the dose to target center (w_a × TPR(fz = 0, depth = x_a)) delivered by the beamlet for phantom geometry is the same as the dose (w_b × TPR(fz = 0, depth = x_b)) by the beamlet for patient geometry. Since all beamlets deliver the same dose to the center plane in both geometries, the total doses, as a linear combination of beamlet doses, in two geometries are the same in the target volume. The dose distributions in the overlapping region are also nearly the same because the photon TPR curves are linear to be matched well, except for the surface buildup region.

This technique scales the known fluence maps in plans for geometry A to geometry B so that the scaled fluence maps can deliver the same dose to geometry B. In the previous section, the projections of the desired dose in the phantom plan are mapped by the DNN to fluence maps for the phantom geometry. Then, the output w_phan of the DNN is scaled to w_pt so that it delivers the desired dose in the patient geometry. What’s more, we use this technique in the next section to scale all clinical patient plans to the phantom geometry, a cylindrical phantom with radius of 15 cm, to obtain paired data (P_phan, w_phan) for training the DNN.

2.4. Data collection and preprocessing

We extracted 443 VMAT plans for H&N cancer patients and 14 VMAT plans for prostate cancer patients treated at UTSW since 2017 from the Eclipse TPS. All the selected VMAT plans were 6MV coplanar full-arc plans with a single isocenter to ensure data consistency. All VMAT plans had up to 5 arcs. The continuous delivery of each arc has been discretized in the plan DICOM file to a list of control points (181 at most) with their individual gantry angles, aperture shapes and intensities in monitor units (MU).

We further processed these extracted clinical plans to make the format of the fluence maps w_pt consistent. Regardless of how many control points each arc had in the clinical plan, we interpolated each arc to 64 control points ranging from 2.8° to 357.2° with a spacing of 5.6° approximately (360°/64). We calculated the intensity map of each control point by multiplying the binary aperture with its weight, ignoring effects of leaf transmission, tongue and groove, field inhomogeneity, etc. Since all arcs have been interpolated and discretized to beams from the same 64 directions, we can add the arcs together by adding the intensity maps of beams from the same angle together. Each VMAT plan is thus discretized as 64 coplanar isocentric beams. The patient plans in figure 3(d) are the 64-beam “single-arc” plans interpolated from clinical multi-arc VMAT plans.

Figure 3.

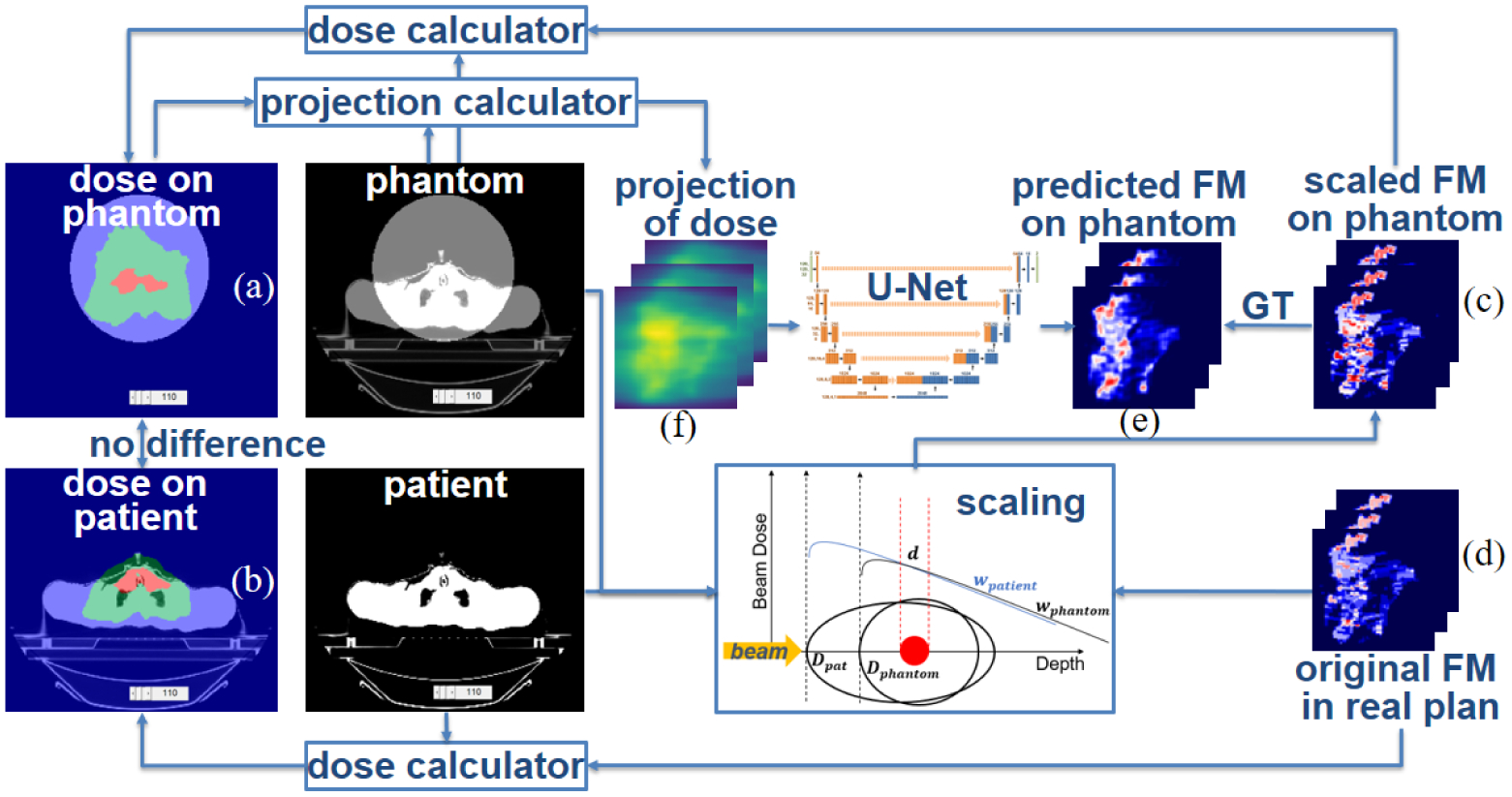
Data preparation and DNN training.

We aimed to use a DNN to learn the map f_P for the phantom geometry, P_phan ↦ w_phan, the inverse of ${\tilde{D}}_{\mathit{\text{phan}}}^T{D}_{\mathit{\text{phan}}}$. The map f_P is determined only by the beam configuration, so the phantom geometry should be independent of the disease site and the ROI distribution. In other words, a DNN that effectively learns f_P will work for all sites. To best support this argument, we should have designed many non-clinical ROI distributions like the C-shaped target in TG119 (Ezzell et al., 2009), placed them in a phantom and optimized the phantom plans. Then, we should have trained the DNN on data from these non-clinical phantom plans and tested the DNN on clinical plans of various sites to fully validate that the mapping that the DNN learned is likely to be the real f_P working in the space of all possible projections of doses $\left\{P\right\}\subset R_{0+}^m$, not just in the site-related subspace of {P}. However, in this paper, we used clinical plans (phantom plans scaled from patient plans) to train the DNN for two reasons: reducing workload and conservative estimation of the DNN’s generalizability. To show that f_P we learned is site-independent, we split the data selectively. The training and validation sets consist of only phantom plans scaled from H&N cancer patient plans, while the test set has both H&N and prostate plans. With this split, we will demonstrate that a DNN model trained solely on H&N data can work for unseen prostate data.

For each plan, the dose to patient d_pt (figure 3(b)) is calculated by the FCBB dose calculation algorithm (Lu and Chen, 2010) from the fluence maps w_pt (figure 3(d)) in the clinical plans. Although the clinical plans were delivered by various machines, we used one set of commission data to calculate the dose in the training data for consistency. We scaled the fluence maps from the patient geometry to the phantom geometry and used the scaled fluence maps w_phan (figure 3(c)) to calculate the dose on phantom d_phan (figure 3(a)). Details of this procedure are covered in table 1. Weighted projections of the dose in phantom plan P_phan (figure 3(f)) are calculated and used as the input of U-Net, which is trained to learn the inverse mapping f_P from projections of dose P_phan to fluence maps w_phan in the phantom geometry.

Table 1.

Scaling plans from patient to phantom geometry before the DNN implements inverse mapping.

Procedure 1. Scale clinical plans from patient geometry to phantom geometry

Input: Fluence maps in patient plan wpt, dose distribution in patient geometry dpt = Dptwpt

Output: Dose influence matrix Dphan, dose distribution dphan and fluence maps wphan in phantom geometry

Steps:

1. Generate a cylindrical water phantom whose axis passes treatment isocenter and calculate Dphan

2. Obtain composite PTV which is the summation of all planning target volumes

3. Calculate middle radio-depth of composite PTV from each beamlet’s eye view in patient geometry xpt and in phantom geometry xphan

4. Scale fluence map from patient geometry to phantom geometry per bixel $$w_{\mathit{\text{phan}}}=w_{pt}\times \frac{TPR\left(fz=0,z=x_{pt}\right)}{TPR\left(fz=0,z=x_{\mathit{\text{phan}}}\right)}$$

5. Calculate dose in phantom geometry dphan = Dphanwphan

2.5. Design Principles and Network Structure

In this section, we will introduce the structure of the DNN that learned the inverse map f_P: P_phan ↦ w_phan. We adopted the U-Net (Ronneberger et al., 2015) as the backbone because it was designed to learn the mapping between paired images defined in the same reference frame. We also made necessary adaptations to the data format and the network structure to account for the unique physical characteristics of projection images.

Figure 4 shows stacked 2D BEV projections of doses from various beam angles. Although the stacked 2D projection images form a volume (projection volume), the physical meaning of each axis differs from that of conventional 3D volumes in the Cartesian coordinate system: its three axes represent the superior-inferior direction, the left-right direction in BEV, and the beam angles, respectively. The array size of the projection volume is 128×128×64, and the resolution is 3.125 mm × 3.125 mm ×5.6°, which corresponds to a 40 cm × 40 cm field and full 360° arc. We used projection volumes formed by the projections of dose and the fluence maps as the model input and the ground truth (GT) for the model output, respectively.

Figure 4.

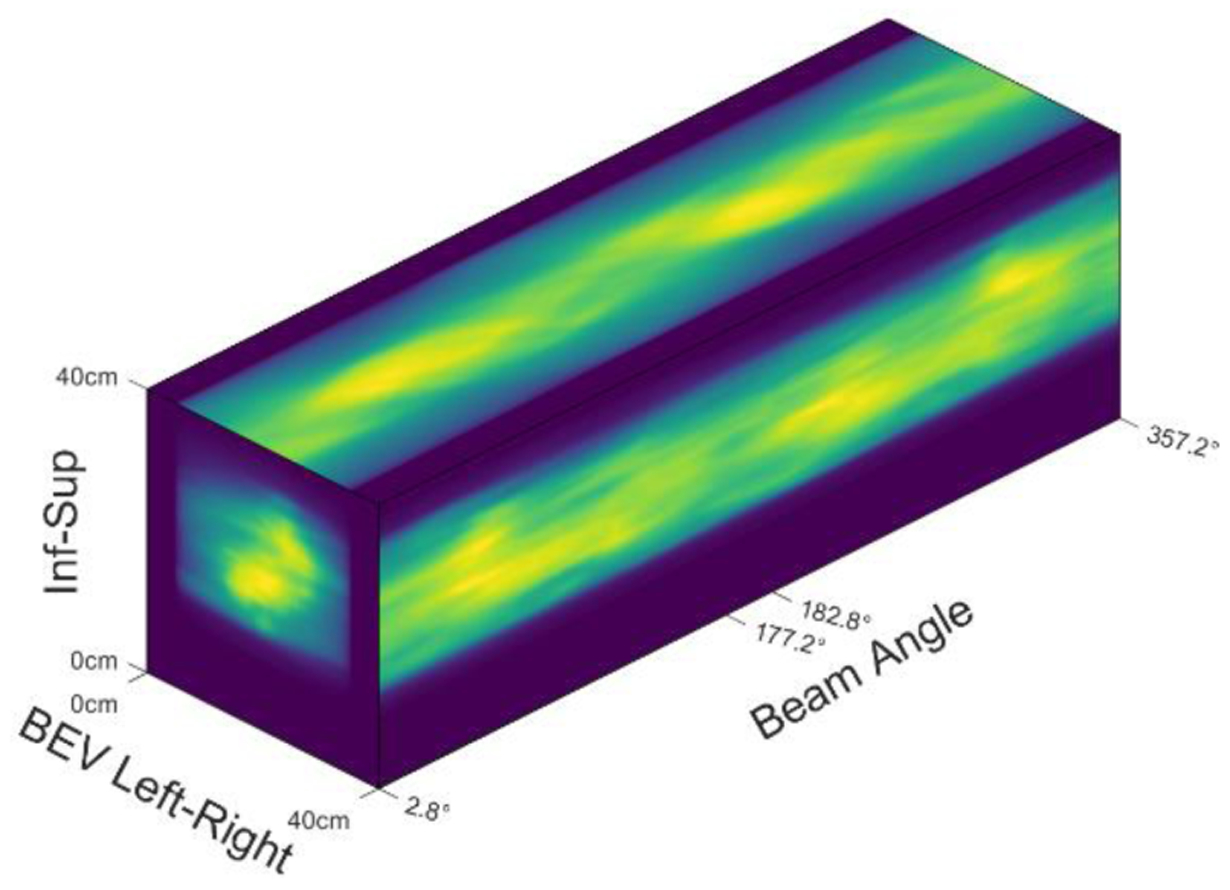
Projection Volume.

Convolutional neural networks can process conventional 3D images because the 3D convolution operation can capture the underlying locality in all three directions (superior-inferior, left-right, anterior-posterior). To validate the use of 3D convolution on the projection volume, we have to prove that locality exists in the projection volume as well. Planes formed by the superior-inferior and BEV left-right directions render the 2D projections, where locality obviously exists. Sinogram-like images show up on the planes formed by the BEV left-right and beam angle directions, as shown in the top view of figure 4. Because beam angle spacing is as little as 5.6°, sinogram-like images are smooth enough to preserve locality. We also observed that locality exists on two BEV projections from opposite angles but is not preserved in the projection volume because projections from opposite beam angles are far away on the axis of the beam angle. To fully utilize the locality, we cut the projection volume into two pieces and put these two pieces into two channels, as shown on the left side of figure 5. The first channel stores the projections from 2.8° to 177.2°, and the second channel stores projections from the opposite beam angles. Note that projections from the opposite BEV are laterally flipped, so we flipped the second channel along the BEV left-right direction, as shown on the right side of figure 5. Voxels in the same position in two channels carry the information from the same beamlet’s eye views from opposite directions.

Figure 5.

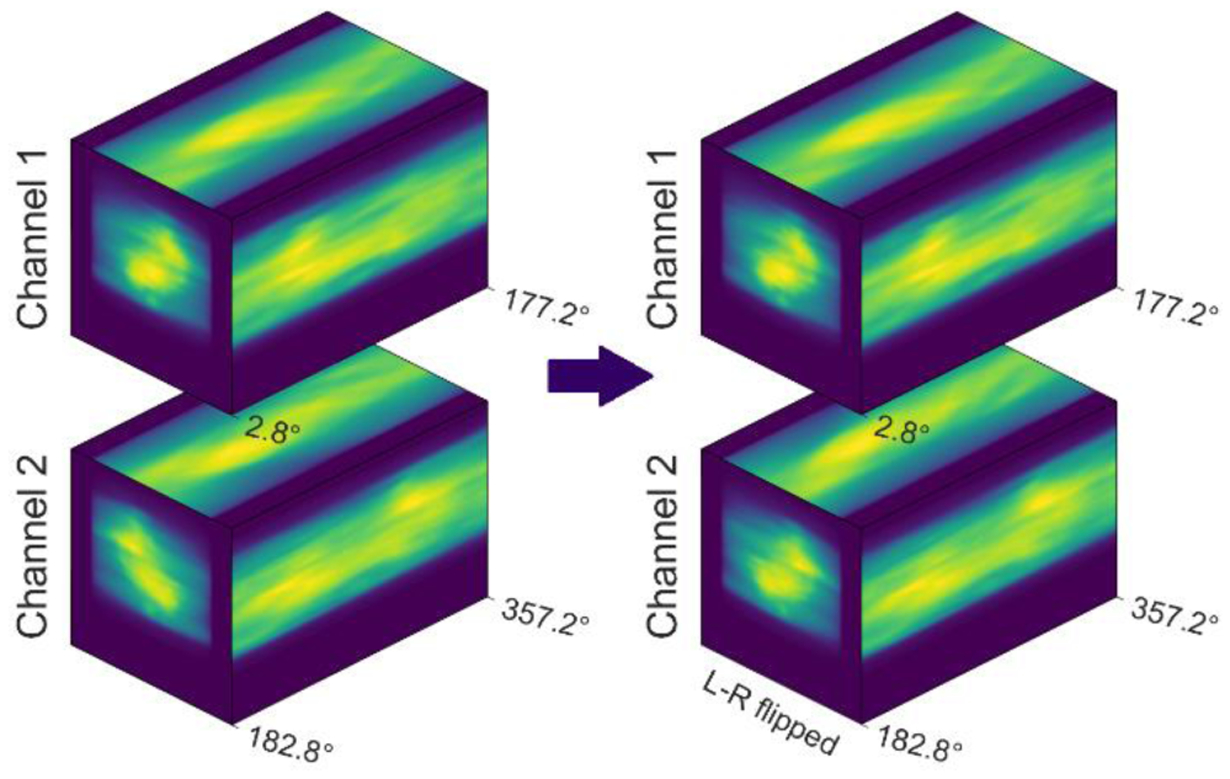
Input of the DNN.

The input and output of the U-Net are projections of the dose P (figure 3(f) & figure 5 right) and the fluence maps w (figure 3(e)) in the phantom plan, respectively, both of which are reformatted into two channels, as mentioned above. The network structure is shown in figure 6. Downwards, upwards and right arrows represent down-sampling, up-sampling and convolution layers, respectively. As with a conventional 3D U-Net, each layer is composed of a normalization layer (GroupNorm, (Wu and He, 2018)), a non-linear activation layer (ReLU), a padding layer and a convolution layer. We made two modifications to account for the geometry of beam delivery. First, we zero-padded the superior-inferior and left-right directions and wrap-padded the beam angle axis because of its periodic boundary condition. For the same reason, we randomly translated and flipped the image along the superior-inferior direction while rotating along the beam angle axis for data augmentation. Second, we never down-sampled data along the superior-inferior axis because the data we used are from coplanar plans, where the dose distribution on one axial slice is independent of that on distant slices.

Figure 6:

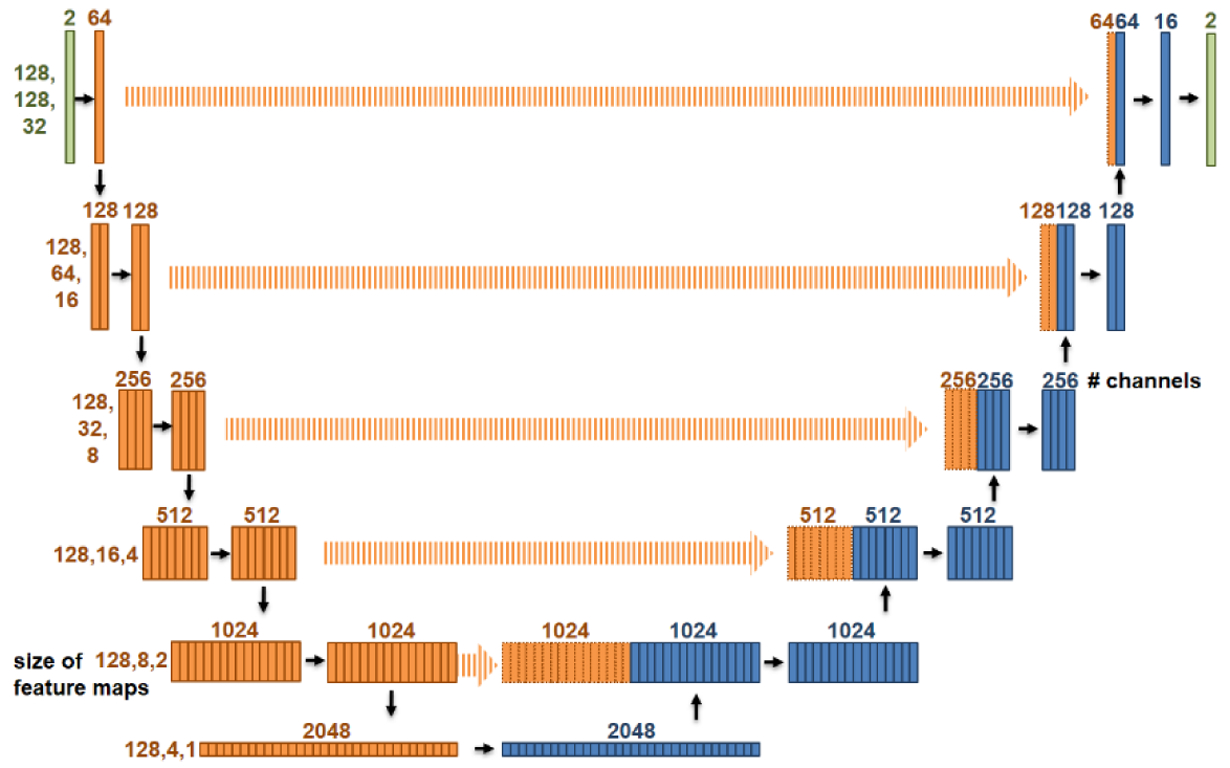
Network structure, a modified U-Net.

The model requires about 10GB GPU memory for training and 6GB GPU memory for inference. The number of fitting parameters in DNN is 97815026 (~10⁸), which corresponds to about 372MB of storage. The mapping DNN learned, f_P, is a pseudo-inverse that satisfies $f_P\circ {\tilde{D}}^{T}D=I$ (identity map) for clinical fluence maps. The number of elements in ${\tilde{D}}^{T}D$ is the square of number of beamlets. In our case, it is (128×128×64)² =10¹². In comparison, the DNN model used 10⁸ parameters to model f_P, which is a quite condensed representation.

3. Results

3.1. DNN training and evaluation

The 443 H&N plans were split into a training set (292), a validation set (49), and a test set (102). The 14 prostate plans were saved as a test set only. Different plans (original/adaptive/boost) for the same patient tend to be similar, so they were assigned to the same set to avoid data leakage. The clinical plans in patient geometry were converted to scaled plans in a cylindrical phantom. Projections of dose in the phantom plans (figure 3(f)) were the inputs of the DNN. The scaled fluence maps in the phantom plan (figure 3(c)) were used as the GT for the U-Net output (figure 3(e)). The U-Net was trained for 200 epochs with the Adam optimizer and a learning rate of 0.0001. The loss function was defined as the mean squared error (MSE). Data augmentation included random flipping and translation along the superior-inferior direction and random rolling along the beam angle axis.

It took 7 minutes to train one epoch on a workstation with an Nvidia GeForce RTX 2080 Ti GPU. The total training time was 24 hours. Inference time, the time needed for forward propagation of the network, was 0.25 second for each case regardless of plan complexity. Figure 7 shows the training loss and validation loss as a function of epochs. The training process was stopped not because of overfitting but because of the slow dropping speed of the validation loss. The model with the best validation loss was chosen. In the evaluation mode, the MSE (mean ± standard deviation) of the DNN model on the training set, validation set, and test set were 0.009±0.005, 0.013±0.009 and 0.012±0.010, respectively. Visual comparisons (figure 9, orange arrow) between the predicted and the GT fluence maps are shown in figure 8. Each row represents one channel. From left to right, each column shows one pair (out of 32 pairs) of opposite BEV images for the input projections of dose, GT, predicted fluence maps and their difference. The predicted fluence maps are similar to GT fluence maps in general profile, and are smoother than GT whose values are discrete, showing a similar pattern as FMO results.

Figure 7.

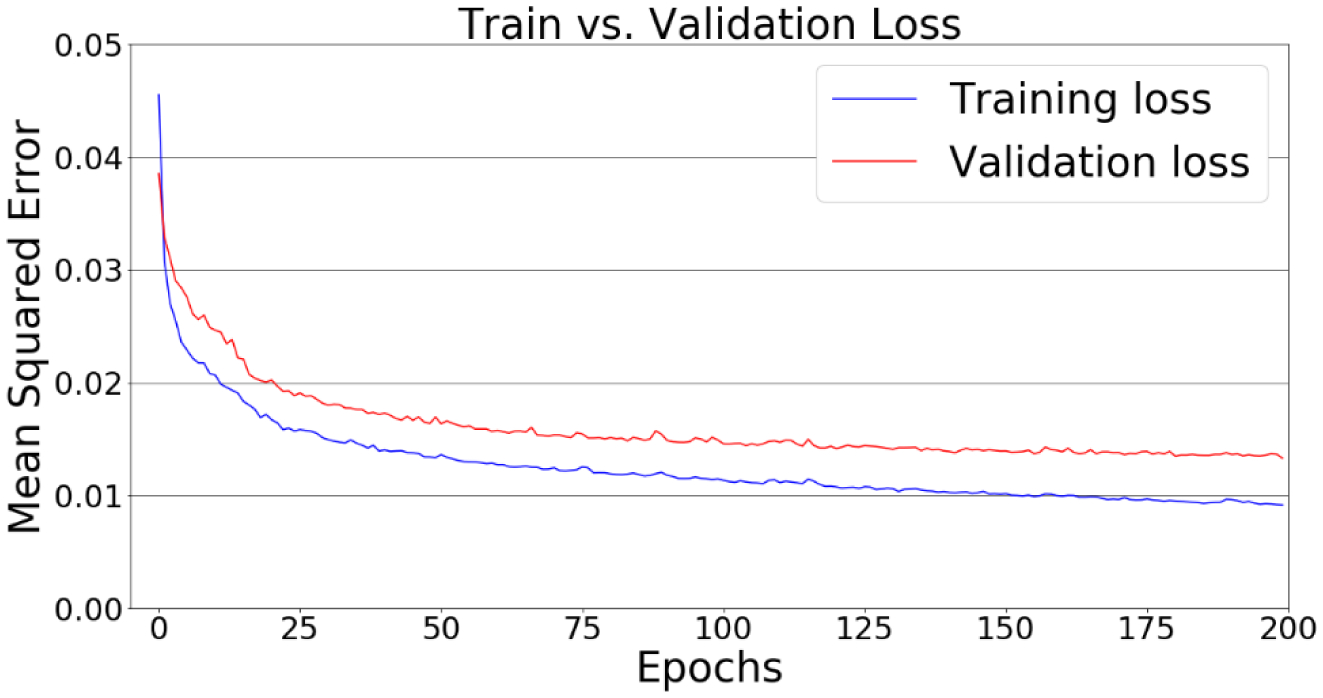
Loss curves of the training and validation sets.

Figure 9.

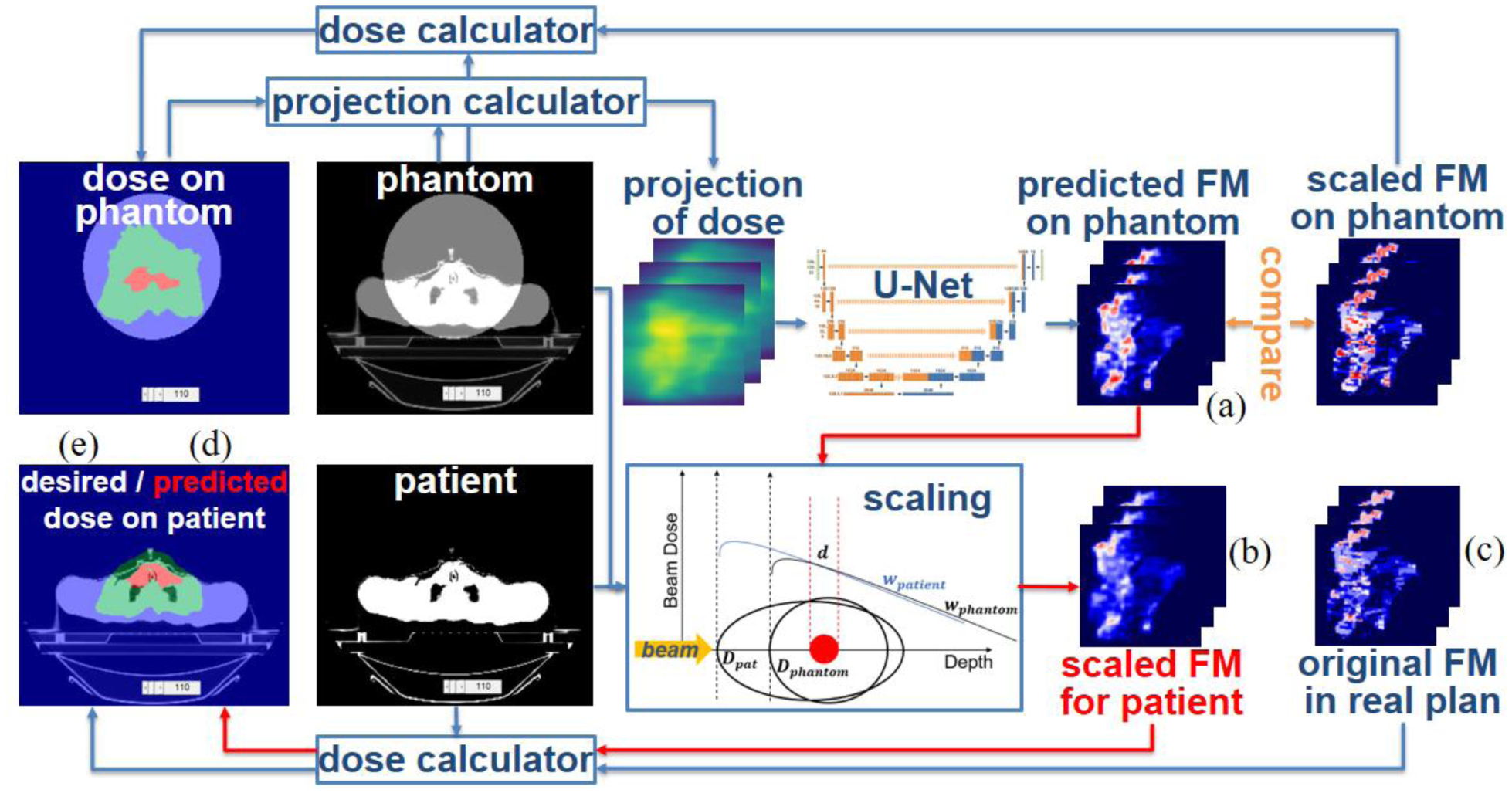
Dosimetric evaluation of the proposed fluence map prediction method.

Figure 8.

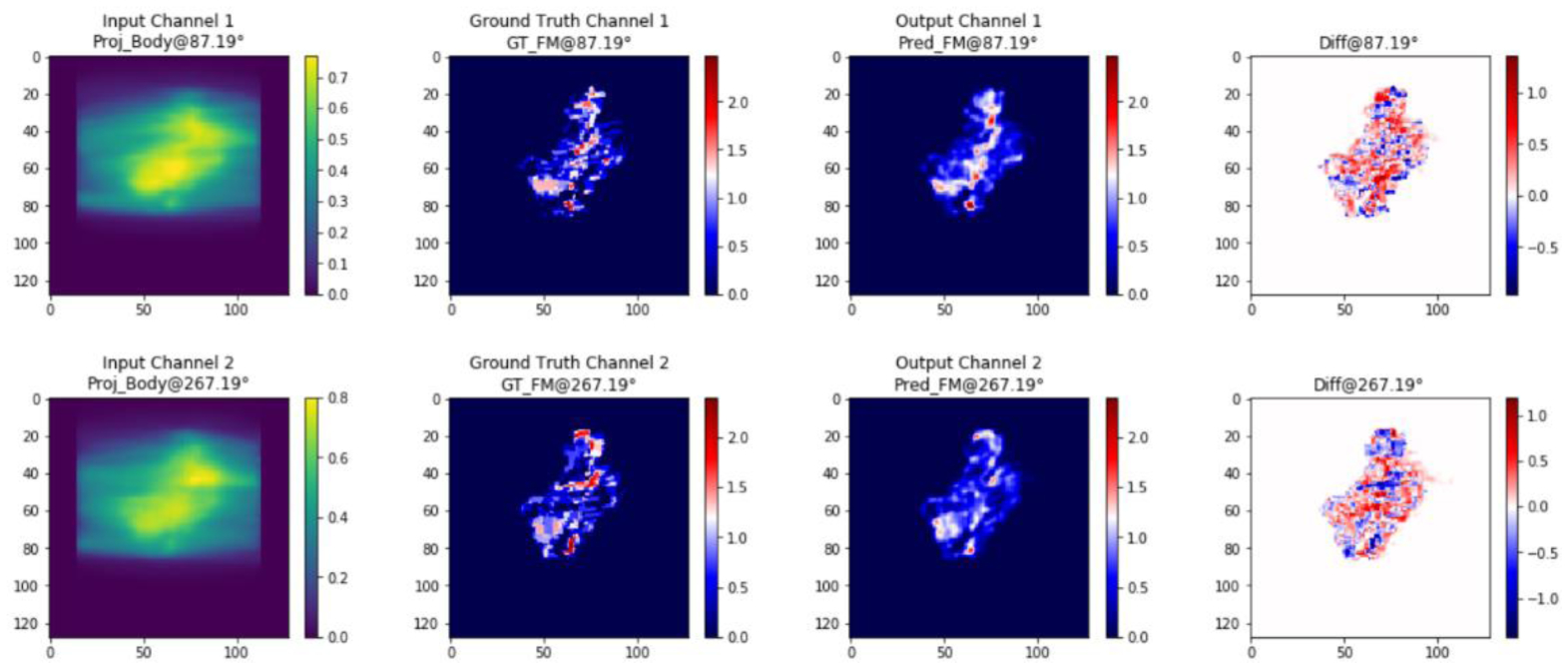
Input, GT, output and their difference. Each row represents one channel. From left to right, each column shows one pair (out of 32 pairs) of opposite BEV images for the input projections of dose, GT, predicted fluence maps and their difference.

3.2. Dosimetric evaluation of the fluence map prediction workflow

Fluence maps predicted on the cylindrical phantom ${\stackrel{⃛}{w}}_{\mathit{\text{phan}}}$ (figure 9(a)) were then scaled back to the patient geometry ${\stackrel{⃛}{w}}_{pt}$, as shown in figure 9(b) and step 1 of table 2. To evaluate the performance of the whole workflow, we calculated the 3D doses from ${\stackrel{⃛}{w}}_{pt}$ (predicted dose ${\stackrel{⃛}{d}}_{pt}$), as shown in figure 9(d) and step 2 of table 2, and compared the predicted doses ${\stackrel{⃛}{d}}_{pt}$ with the desired doses in clinical plans (desired dose d_pt, figure 9(e)) calculated from w_pt (figure 9(c)). We evaluated the difference between ${\stackrel{⃛}{d}}_{pt}$ and d_pt on 102 H&N plans and 14 prostate plans in the test set. For convenience, we refer to the composite PTV as the PTV hereafter. The mean and standard deviation of the relative difference in median dose (D50) in the PTV between the predicted dose ${\stackrel{⃛}{d}}_{pt}$ and the desired dose d_pt were −0.83±1.08% for the H&N plans and 1.06±0.70% for the prostate plans. Then, we normalized the predicted doses ${\stackrel{⃛}{d}}_{pt}$ by the D50 of the corresponding desired doses d_pt in the PTV and obtained ${\widehat{\stackrel{⃛}{d}}}_{pt}$ (table 2, step 3). We evaluated the differences between the normalized predicted dose ${\widehat{\stackrel{⃛}{d}}}_{pt}$ and the desired dose d_pt in terms of four metrics: dose-volume points, dose volume histogram (DVH) curves, dose per voxel and gamma passing rate.

Table 2.

Scaling fluence maps predicted by DNN from phantom to patient geometry and further processing.

Procedure 2. Scale predicted phantom plans back to patient geometry

Input: All the variables we obtained in procedure 1: Dpt, Dphan, wpt, wphan, dpt, dphan, Pphan, xpt, xphan, composite PTV. The fluence map ${\stackrel{⃛}{w}}_{\mathit{\text{phan}}}$ (figure 9(a)) obtained by DNN from Pphan

Output: Scaled fluence map ${\stackrel{⃛}{w}}_{pt}$ for patient geometry (figure 9(b)), predicted dose ${\stackrel{⃛}{d}}_{pt}$ in patient geometry (figure 9(d)) and normalized predicted dose ${\widehat{\stackrel{⃛}{d}}}_{pt}$ in patient geometry

Steps:

1. Scale the fluence map predicted by DNN ${\stackrel{⃛}{w}}_{\mathit{\text{phan}}}$ back to patient geometry ${\stackrel{⃛}{w}}_{pt}$ $${\stackrel{⃛}{w}}_{pt}={\stackrel{⃛}{w}}_{\mathit{\text{phan}}}\times \frac{TPR\left(fz=0,z=x_{\mathit{\text{phan}}}\right)}{TPR\left(fz=0,z=x_{pt}\right)}$$

2. Calculate predicted dose in patient geometry ${\stackrel{⃛}{d}}_{pt}=D_{pt}{\stackrel{⃛}{w}}_{pt}$

3. Normalize predicted dose by composite PTV’s D50 of dpt: ${\widehat{\stackrel{⃛}{d}}}_{pt}={\stackrel{⃛}{d}}_{pt}\times \frac{\mathit{\text{PTV\hspace{0.17em}}}{D}_{50}\mathit{\text{of\hspace{0.17em}}}{d}_{pt}}{\mathit{\text{PTV\hspace{0.17em}}}{D}_{50}\mathit{\text{of\hspace{0.17em}}}{\stackrel{⃛}{d}}_{pt}}$

Dose-Volume Points.

Table 3 shows the relative differences in the PTV D95, D90, V105, V110 and V115, defined by $\left(\frac{Q\mathit{\text{ predicted-Q desired}}}{Q\mathit{\text{ desired }}}\right)\times 100$, where Q is a query dose-volume point. The statistics of the differences are shown in boxplots in figure 10. The mean differences of D95 and D90 are systematically lower than 0%, meaning that the normalized prediction ${\widehat{\stackrel{⃛}{d}}}_{pt}$ had slightly inferior homogeneity than the desired dose d_pt. This is reasonable because it was hard for the U-Net to perfectly restore the sharp gradient of the fluence maps (leaf edges) from smooth projections of dose. The relative differences in V105, V110 and V115 centered at zeros, so there’s no systematic error in hotspot. Large variations (outliers) exist because the values of the denominator (V105, V110 and V115 of the desired plans) were small, at the order of 5%, 1% and 0.1% respectively.

Table 3.

Differences (mean ± standard deviation) of PTV dose in dose-volume points.

Dose-volume pts	D95	D90	V105	V110	V115
102 H&N cases	−1.06±1.30%	−0.61±1.11%	11.93±23.39%	2.44±20.31%	−2.07±12.73%
14 prostate cases	−0.45±0.81%	−0.18±0.54%	−10.58±14.21%	−10.06±10.56%	−2.38±7.68%

Figure 10.

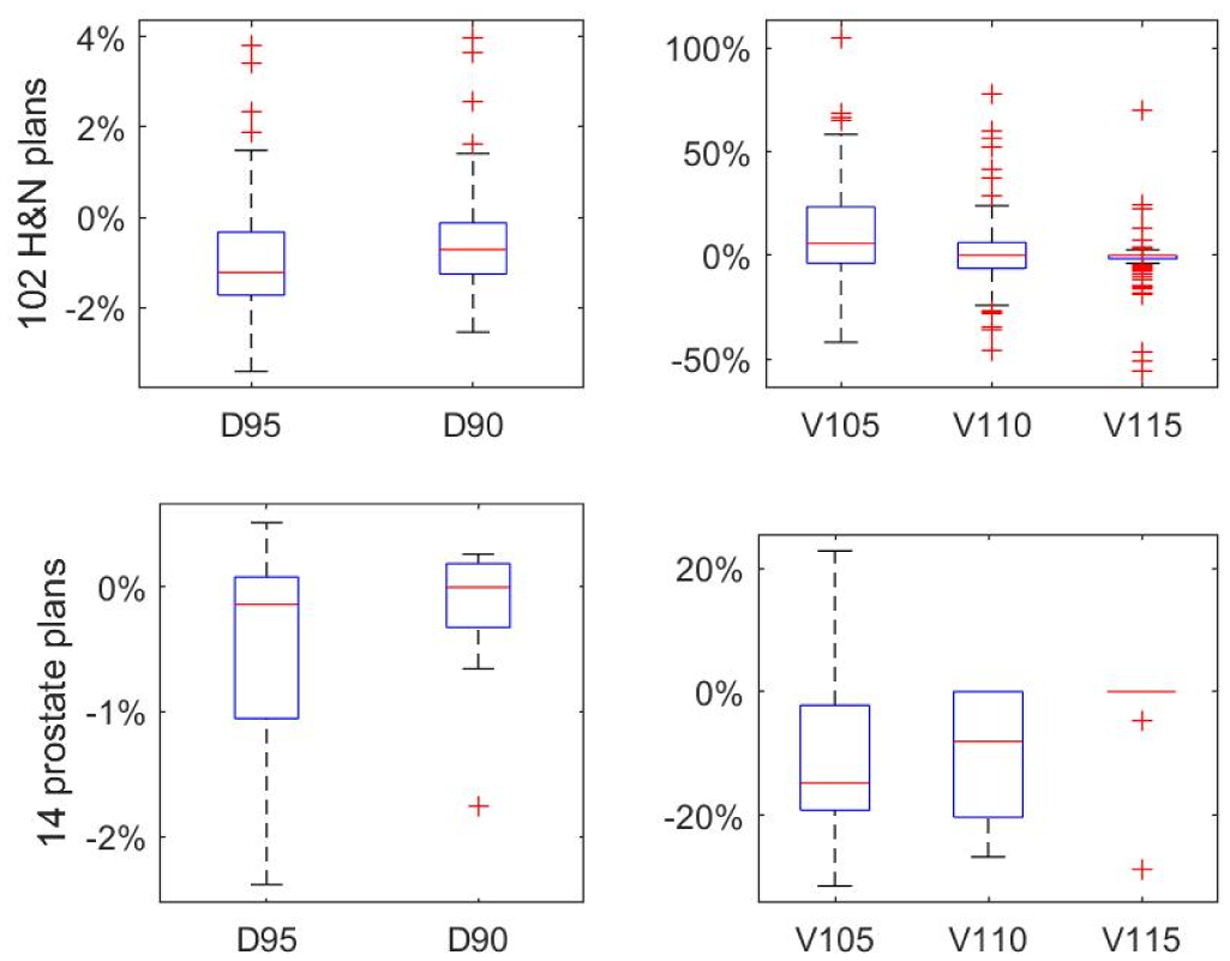
Boxplots of difference of dose-volume points.

Table 4 shows the OAR dose differences as percentages relative to PTV D50 of the desired dose d_pt. For H&N plans, we calculated the mean and standard deviation of dose differences in parotid glands (both sides), spinal cord, mandible, brain stem and masseter muscles (both sides). For prostate plans, we did in rectum and bladder. The mean relative difference in all OARs were less than 1% for both D50 and D2, so there’s no systematic under-dose or over-dose in OARs. The standard deviations, which reflect the scale of the difference between ${\widehat{\stackrel{⃛}{d}}}_{pt}$ and d_pt, are all less than 1.52%.

Table 4.

Differences (mean ± standard deviation) of OAR dose in dose-volume points.

Metric	Parotid	Spinal Cord	Mandible	Brain Stem	Masseter	Esophagus	Rectum	Bladder
D50	0.08±0.91%	−0.27±0.80%	−0.11 ±0.84%	−0.18±0.76%	−0.34±0.87%	−0.01±1.11%	−0.00±0.76%	−0.04±0.52%
D2	−0.45±1.39%	0.17±0.98%	−0.00±1.30%	−0.15±1.16%	0.04±1.16%	−0.36±1.52%	−0.36±0.75%	−0.58±0.77%

DVH Curves.

Figure 11 shows the DVH of a plan randomly selected from the H&N test set. The solid lines are DVHs of the desired dose d_pt, and the dashed lines are DVHs of the normalized predicted dose ${\widehat{\stackrel{⃛}{d}}}_{pt}$. Since the goal of this work is to predict the fluence maps that can deliver the input desired dose, we expect the two sets of curves to be as close as possible without either being superior to the other. Homogeneity in the target volumes (PTV56Gy33fx, PTV59.4Gy33fx, PTV66Gy33fx, PTV70Gy33fx) of the normalized predicted dose was slightly worse than the desired dose, as indicated by dashed curves’ extended tails in both low and high dose directions. The sparing of OARs was generally similar or comparable.

Figure 11.

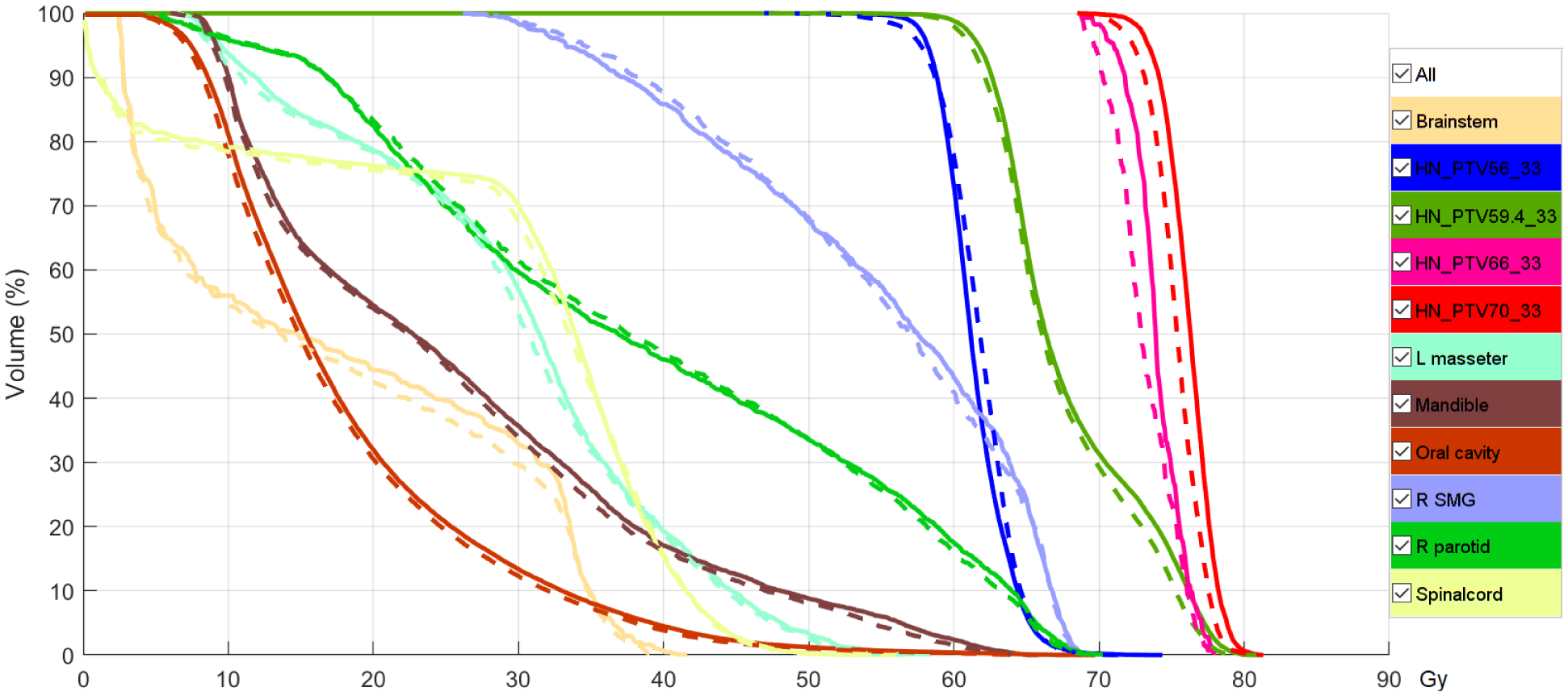
Dose volume histogram of a plan from the test set. Solid curves are for GT dose and dashed lines are for the predicted dose after normalization.

Voxel dose difference.

To compare difference in dose at the voxel level, we calculated the relative dose difference per voxel by $\left(\frac{\left|{\widehat{\stackrel{⃛}{d}}}_{pt}-d_{pt}\right|}{\mathit{\text{Prescription Dose}}}\right)\times 100$ and used PTV D50 as the prescription dose. We defined three ROIs for the comparison—the region inside the PTV, between the PTV boundary and the 50% isodose surface and between the 20%~50% isodose surface—to study the differences in high, intermediate and low dose regions, respectively. The mean and maximum differences were calculated for each ROI. In calculating the maximum difference, we excluded 2% outliers for numerical stability. The average and standard deviation of the mean and max dose differences for 102 H&N plans and 14 prostate plans are shown in table 5. The mean dose difference for every ROI was within 2%.

Table 5.

Differences (mean ± standard deviation) in voxel dose in 3 ROIs.

102 H&N cases	Mean difference	Max difference
Inside PTV	1.42±0.37%	4.40±1.09%
PTV→50% isodose	1.53±0.44%	4.82±1.38%
50%→20% isodose	1.25±0.44%	3.97±1.49%
102 prostate cases	Mean difference	Max difference
Inside PTV	1.09±0.28%	3.51±0.89%
PTV→50% isodose	1.23±0.22%	4.73±0.86%
50%→20% isodose	0.91±0.30%	2.94±0.97%

Gamma analysis.

We calculated the gamma passing rates between ${\widehat{\stackrel{⃛}{d}}}_{pt}$ and d_pt for the 2%/2mm, 3%/3mm and 5%/5mm criteria, excluding the low dose regions below 10% or 20% of the prescription dose. Results are shown in table 6. The similarity is clinically satisfiable for both sites.

Table 6.

Gamma passing rates (mean ± standard deviation).

102 H&N cases	2% 2mm	3% 3mm	5% 5mm
>10% Rx dose	93.37±5.86%	98.06±2.64%	99.75±0.61%
>20% Rx dose	92.76±6.30%	97.81±2.95%	99.72±0.68%
14 prostate cases	2% 2mm	3% 3mm	5% 5mm
>10% Rx dose	95.70±4.27%	99.06±1.75%	99.91±0.27%
>20% Rx dose	95.73±5.53%	98.92±2.27%	99.88±0.36%

3.3. Evaluation of speed

The proposed method took 0.5 second to generate fluence maps for a given desired dose distribution, regardless of plan complexity. Calculating projections of dose took 0.25 second, DNN mapping (forward propagation) took 0.25 second and the plan scaling was instantaneous because the operation is just multiplying the vector of fluence map with the vector of scaling factor (ratio of TPR) calculated offline. Even online calculation of scaling factor took less than one second. Projection calculation and plan scaling were accomplished by the NVBB framework (Lu, 2010).

For comparison, we set the desired dose distribution as voxelized objectives for the NVBB fluence map optimizer (Lu, 2010). Both the FMO and the proposed method used the same beam configuration (64 uniformly distributed beams). FMO’s running time varied with the complexity of the plan, with an average of 20 seconds on the same workstation. As revealed in NVBB paper (Lu, 2010), it would take longer to run the optimization using voxel-based beamlet superposition framework, even with a dose influence matrix calculated off-line. Therefore, the proposed method was faster than the FMO by orders of magnitude.

4. Discussion

In this paper, we assumed that the desired dose distribution in the phantom geometry d_phan was known, from which the corresponding fluence maps w_pt of a VMAT plan were predicted by the proposed method in two steps. In the first step, a DNN mapped projections of dose P_phan to fluence maps in phantom geometry w_phan. In the second step, a plan scaling technique scaled the fluence maps from phantom geometry w_phan to patient geometry w_pt. Fluence maps from 64 angles in a VMAT plan were predicted in less than one second, much faster than FMO, which uses the desired dose distribution as a voxelized objective. This method focused on coplanar VMAT for two reasons. First, VMAT plan optimization is more time-consuming than IMRT plan optimization, so we have a more urgent need to speed up optimization for VMAT. Second, this work proposed to use a DNN to learn the mapping f_P, which satisfies $f_P\circ {\tilde{D}}^{T}D=I$. Aside from dependence on density distribution, which has been resolved by the introduction of phantom geometry, f_P is also determined by beam configuration. The proposed method could be applied for VMAT because the beam configurations for all coplanar VMAT plans are the same, a continuous arc. The difference in angular sampling rate has been addressed by interpolation. However, IMRT has various and infinite beam configurations in terms of number of beams, beam angles and couch angles. It requires DNNs to be trained specifically for each beam configuration, which is not suitable for clinical application.

Our fluence map prediction work relied on the very strong condition that volumetric dose distribution d is available as input, because DL-based methods have shown their capability to generate d_pt from contours for multiple sites. The advent of deep learning allows us to obtain complete information about the desired dose and gives us the opportunity to use the inverse mapping method in this paper. Previously, we could only estimate the desired dose in forms like DVH curves, whose information is incomplete. The lack of full information about dose d made the inverse planning problem underdetermined, so inverse mapping was not applicable, and optimization was the only option. Additionally, the condition that phantom dose is available is equivalent to the condition that patient dose is available, rather than stronger. Let us suppose that d_pt and w_pt are known. We can always use plan scaling (which requires that w_pt is known!) to obtain d_phan and w_phan. The scaling method proved that d_pt and d_phan have a one-to-one correspondence. In case where the phantom is smaller than the patient, the phantom dose d_phan is obtained by cropping the patient dose d_pt according to the shape of the phantom. In case where the phantom is larger than the patient, in regions inside the phantom and outside the patient, the phantom dose d_phan can be viewed as an analytical continuation of the patient dose d_pt, which means that the content of the information in d_phan and d_pt are the same. This observation illustrates that the dose distribution delivered by rotational therapy has a nature (analytical continuation) similar to a complex analytical function. We will discuss more detailed observations about plan scaling will be discussed in a future paper. Since inverse planning is more complicated than CT reconstruction, in that ${\tilde{D}}^{T}D$ has an additional patient density-dependent attenuation part that A^†A does not have, there is no universal map f_P for all patients. Taking a detour through a phantom is the price we have to pay to overcome the extra complexity. Hopefully, d_pt and d_phan have equivalent and the same amount of information. We will discuss how to obtain d_phan in a separate paper.

Our future research goal is to add leaf sequencing after fluence map prediction to generate a deliverable clinical VMAT plan. This process is similar to two-step VMAT optimization, FMO followed by leaf sequencing and DMPO (Bzdusek et al., 2009). Our proposed method could replace FMO, given its high prediction accuracy and ultrafast speed. Existing leaf sequencing methods (Shepard et al., 2010, Luan et al., 2008, Wang et al., 2008, Bzdusek et al., 2009, Craft et al., 2012a) are available for segmenting our predicted fluence maps into multiple arcs. The angular grid in our method was 64 equi-spaced beams because of GPU memory limitations. Finer arc sampling would only require a slight adjustment of the network structure and retraining on a GPU with larger memory. Since projections of dose (input of DNN) are continuous as the gantry angle rotates, neighboring fluence maps (output of DNN) are similar; fluence maps predicted by the proposed method are easy to segment.

The DNN used in the first step learned the inverse map f_P of the phantom geometry, P_phan ↦ w_phan, from projections of dose to fluence maps. Our trained DNN is flexible and generalizable; it could be directly applied to 6MV coplanar full-arc VMAT plans for all sites by any machine/institute without retraining or fine tuning the model. This argument is validated by the following three considerations. First, we have shown that our trained model works for both H&N and prostate sites even though it was trained only by H&N data. It’s not surprising that the model can handle unseen sites because the mapping that the DNN learned is the inverse of ${\tilde{D}}_{\mathit{\text{phan}}}^T{D}_{\mathit{\text{phan}}}$, which is independent of ROI distribution and thus unrelated to the treatment site. Second, inter-institute variation in VMAT planning processes is minimal. No template is needed, and planning is fully automated. In contrast, a template (number of beams, beam angle, energy, etc.) is usually needed for IMRT planning, which gives rise to large inter-institute variation. Our model works for coplanar full-arc VMAT plans, which don’t involve gantry angle selection at all. Third, the dose in the training data is calculated by one set of commission data TPR_model, which may not be identical to the commission data of another specific machine TPR_match. That difference can be handled in the plan scaling step by using TPR_model in the numerator and TPR_match in the denominator of (5). More details will be given in a future paper on plan scaling.

We used a data-driven method to approximate f_P: P_phan ↦ w_phan by a DNN, whose operation is inverse to ${\tilde{D}}_{\mathit{\text{phan}}}^T{D}_{\mathit{\text{phan}}}$. The possibility of using a mathematical method is discussed below. First, the matrix inverse of ${\tilde{D}}_{\mathit{\text{phan}}}^T{D}_{\mathit{\text{phan}}}$ doesn’t exist because D_phan has a low rank. Other than solving the inverse matrix, we can also approach the problem by solving a linear equation $P=\left({\tilde{D}}_{\mathit{\text{phan}}}^T{D}_{\mathit{\text{phan}}}\right)\times w$. The projection of dose is known, and w is unknown. The size of D^TD equals the number of beamlets, which is on the order of 10⁶~10⁷ in VMAT plans, which typically have more than 100 beam angles and resolution higher than 100×100. Gaussian elimination doesn’t work because it has a complexity of O(n³), and ${\tilde{D}}_{\mathit{\text{phan}}}^T{D}_{\mathit{\text{phan}}}$ is low-rank. The conjugate gradient method has a complexity of O(n), but it’s essentially an iterative optimization method that uses a quadratic objective function. It cannot account for machine constraints (smoothness of w), and as such, we still have to resort to iterative optimization in the TPS. Cholesky decomposition, which decomposes ${\tilde{D}}_{\mathit{\text{phan}}}^T{D}_{\mathit{\text{phan}}}$ as a product of a lower triangle matrix and its transpose, is a method worth further investigation, but its application to this task is questionable because D_phan has a low rank. Overall, the data-driven method (deep learning) is more reliable for solving f_P than these other methods.

We proposed a plan scaling technique that is accurate for two reasons. First, the TPR curves of photon beams are linear, so any two curves can be matched by shifting and scaling, which is a unique feature of photon beams. Second, dose to target is delivered by beams from all directions in rotational therapy. Any error (imperfect match of the TPR curves) introduced by scaling from one direction will be cancelled out by other directions. The scaling method also demonstrates that the ROI distribution dominates the quality of photon rotational therapy plans. The dose distribution in the PTV, PTV margins and neighboring OARs are independent of the shape and size of the external boundary of the body (or phantom), so the scaling technique can be applied to either of the two geometries. The implementation and application of plan scaling and the nature of doses of rotational therapy will be further studied in a future work.

5. Conclusion

We developed a method to predict the fluence maps from the desired volumetric dose distribution in two steps. Projections were calculated from the desired dose and then mapped to fluence maps in a phantom geometry by a DNN that learned the inverse mapping between them to skip optimization. Then, the fluence maps were scaled from the phantom geometry to real patient geometry. Because it contains the volumetric information of prescriptions and trade-offs, the desired dose distribution can be viewed as a complete-information dosimetric objective. Taking the desired dose distribution as input, the proposed method predicted fluence maps in less than one second without optimization, which would allow dramatically faster VMAT planning and, ultimately, interactive plan tuning and online adaptive planning.

Symbols.

d Vectorized dose distribution with N voxels. d_i is dose in voxel i. The space of dose vectors is a subspace of N dimensional non-negative real-valued vector space. $\left\{d\right\}\subset R_{0+}^N$

w Vectorized fluence maps with M beamlets. w_j is intensity of beamlet j. Vectorized fluence maps belong to M dimensional non-negative real vector space. $w\in R_{0+}^M$

D Dose influence matrix with N rows and M columns. Each entry D_ij is the full dose delivered to voxel i by beamlet j, including contributions of primary dose and scatter dose.

$\tilde{D}$ Approximate dose influence matrix involving only primary dose. ${\tilde{D}}_{ij}=0$ if voxel i is not on the ray-tracing line of beamlet j.

P Vectorized projections of dose, calculated by weighted summation of dose along beamlet ray-tracing lines. $P={\tilde{D}}^T\times d.\left\{P\right\}\subset R_{0+}^M$