Validation of multivariable lung cancer risk prediction models for the personalized assignment of optimal screening frequency: a retrospective analysis of data from the German Lung Cancer Screening Intervention Trial (LUSI)

Abstract

Background

Current guidelines for lung cancer screening via low-dose computed tomography recommend annual screening for all candidates meeting basic eligibility criteria. However, lung cancer risk of eligible screening participants can vary widely, and further risk stratification could be used to individually optimize screening intervals in view of expected benefits, possible harms and financial costs. To this effect, models have been developed in the US National Lung Screening Trial based on self-reported lung cancer risk factors and imaging data. We evaluated these models using data from an independent screening trial in Germany.

Methods

We examined the Polynomial model by Schreuder et al., the Lung Cancer Risk Assessment Tool extended by CT characteristics (LCRAT + CT) by Robbins et al., and a criterion of presence vs. absence of pulmonary nodules ≥4 mm (Patz et al.), applied to sub-sets of screening participants according to eligibility criteria. Discrimination was evaluated via the receiver operating characteristic curve. Delayed diagnoses and false positive results were calculated at various thresholds of predicted risk. Model calibration was assessed by comparing mean predicted risk versus observed incidence.

Results

One thousand five hundred and six participants were eligible for the validation of the LCRAT + CT model, and 1,889 for the validation of the Polynomial model and Patz criterion, yielding areas under the receiver operating characteristic curve of 0.73 (95% CI: 0.63, 0.82), 0.75 (0.67, 0.83), and 0.56 (0.53, 0.72) respectively. Skipping 50% annual screenings (participants within the 5 lowest risk deciles by LCRAT + CT in any round or by the Polynomial model; baseline screening round), would have avoided 75% (21.9%, 98.7%) and 40% (21.8%, 61.1%) false positive screen tests and delayed 10% (1.8%, 33.1%) or no (0%, 32.1%) diagnoses, respectively. Using the Patz criterion, referring 63.2% (61.0% to 65.4%) of participants to biennial screening would have avoided 4% (0.2% to 22.3%) of false positive screen tests but delayed 55% (24.6% to 81.9%) diagnoses.

Conclusions

In this German trial, the LCRAT + CT and Polynomial models showed useful discrimination of screening participants for one-year lung cancer risk following CT examination. Our results illustrate the remaining heterogeneity in risk within screening-eligible subjects and the trade-off between a low-frequency screening approach and delayed detection.

Introduction

While it is now well-documented that low-dose computed tomography (LDCT) can significantly reduce lung cancer related mortality (1-5), each LDCT screening appointment represents financial costs and exposes patients to potentially harmful ionizing radiation as well as to the risks of receiving false-positive screen tests and overdiagnosis (6). A substantial amount of research is being directed at defining eligibility criteria for lung cancer (LC) screening with the purpose of optimizing the net clinical benefit of early detection and of increasing cost efficiency. Expert organizations in North America (7,8) and Europe (9) recommend annual screening, with eligibility criteria similar to those used previously in the US National Lung Cancer Screening Trial (NLST) (10), i.e., based on lower and upper limits for age, minimum lifetime cumulative smoking exposure (pack-years) and, for ex-smokers, maximum time since quitting. Compared to the latter eligibility criteria, using more detailed models for the prediction of individuals’ LC risk may further improve net benefit and cost-efficiency of LC screening (11-14).

A complementary line of research is the modification of screening intervals for individuals based on their estimated personalized LC risk, such that individuals with comparatively low risk could have their screening intervals extended beyond one year. Using data from the NLST, Patz et al. (10) showed that the average risk for LC detection at the first annual follow-up screen (“T₁”) was 0.35% for screening participants showing no pulmonary nodules of at least 4 mm in largest diameter at their initial screen (time “T₀”) (N=19,066, 73%), whereas the same risk was estimated at 1.02% among all screening participants (N=26,231). Similar results were found in the Dutch-Belgian NELSON trial (15). More recently, statistical models were developed that integrate the presence and more detailed characteristics of pulmonary nodules (16) or other radiologic indicators of pulmonary health (emphysema, consolidation) (16,17), as observed by LDCT, with general LC risk factors. Schreuder et al. (16) developed a polynomial model with linear and 2^nd-degree terms for a total of 11 selected risk factors, including age, sex, smoking history, personal and family history of cancer, and LDCT scan findings at the initial prevalence screen such as pulmonary nodules and emphysema (“Polynomial model”). A different model was developed for use among individuals with a negative LDCT screen (no nodules ≥4 mm) by Robbins et al. (17). It extends a pre-existing lung cancer risk prediction model [“Lung Cancer Risk Assessment Tool” (LCRAT)] (18) based on age, smoking history, family history of lung cancer, BMI and education level, by adding LDCT data on pulmonary emphysema and consolidation (“LCRAT + CT”). Compared to LDCT imaging data only, these models considerably improved discrimination of screening participants by their likelihood of receiving a LC diagnosis either at, or in the year following, the next screening appointment. Based on the Polynomial or LCRAT + CT models it was further estimated that, in the NLST, up to about 45% of annual screenings in the second round, and 58% of all annual follow-up (“incidence”) screenings could have been skipped at the cost of a delayed diagnosis for a comparatively small proportion of 10% to 24% of screen-detected cancers (16,17).

While promising, both models—LCRAT+CT and Polynomial—were developed and tested exclusively on the basis of NLST data, and so far these have not been externally validated on independent screening data. We here present findings of an external validation of these two models using data from the five annual rounds of LDCT screening in the German Lung Cancer Screening Intervention (LUSI) trial [International Standard Randomized Controlled Trial Number (ISRCTN):30604390] (19-21). In particular, we examine their risk discrimination ability and estimate the number of LC diagnoses that would have been delayed had annual incidence screenings been skipped by one year for participants below various LC risk thresholds.

We present the following article in accordance with the Transparent Reporting of a multivariable prediction model for Individual Prognosis or Diagnosis (TRIPOD) (22) reporting checklist (available at http://dx.doi.org/10.21037/tlcr-20-1173).

Methods

LUSI trial

The German Lung Cancer Screening Intervention (LUSI) is a registered randomized trial (ISRCTN: 30604390) with a recruitment phase between October 2007 and April 2011, active screening between October 2007 and April 2016 and ongoing follow-up. It recruited a total of 4052 men and women using population registries in Heidelberg (Germany) and surroundings, who were 50–69 years of age with a history of heavy smoking (≥25 years of smoking of ≥15 cigarettes per day, or ≥30 years smoking of ≥10 cigarettes per day; ≤10 years since smoking cessation). Participants were randomized into a screening intervention arm (N=2,029), comprising five annual LDCT screenings, and a control arm (N=2,023) with no intervention.

In the screening arm (N=2,029), participants were kept under regular annual screening, invited for short-term follow-up, or recommended immediate diagnostic work-up, depending on the size and/or growth of their observed nodules (Supplementary File, Table S2). For immediate work-up, participants were referred to a cooperating pulmonologist who then decided about further diagnostic procedures or treatments. Study design, image acquisition, reading and evaluation of CT images, management of pulmonary nodules and additional diagnostic work-up (in case of suspicions) have been described in detail previously (20,21).

LUSI is a registered clinical research study with ISRCTN 30604390 (19). Ethical approval was provided by the University of Heidelberg Medical Ethics Committee (073/2001) and by the radiation protection authority (BfS, 22462/2, 2006-045). The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). All participants enrolled provided written informed consent.

Participant selection for model validation

For the validation of the LCRAT + CT and Polynomial models, we analysed data from the LDCT arm only, focusing on participants of the LUSI, additionally fulfilling the eligibility criteria used for original model development. For the LCRAT + CT model (17), this included participants with at least one negative LDCT scan as of NLST criteria (absence of nodules ≥4 mm in longest diameter) and who were at risk for lung cancer detection at the next screening appointment (N=1,194 at time point T₀ of the initial “prevalence” screen, and 1,220, 1,262 and 1,228 at the three following incidence screens, at time points T₁-T₃), that is, subjects without a previous lung cancer diagnosis for whom an LDCT scan was performed at the next screening interval, and excluding interval cancers occurring in between screening appointments (N=1 in the year between T₂ and T₃ and N=1 in the year between T₃ and T₄) (Figure S1A).

For the validation of the Polynomial model (16), we selected participants with available LDCT scan images at the first screening appointment (baseline screen) and at risk for lung cancer detection at the second annual screening appointment (N=1,889), that is, excluding all interval cancers occurring in the year between T₀-T₁ (N=1, Figure S1B). Additionally, we applied the Polynomial model to data from eligible subjects at the incidence screening rounds T₁-T₄ (Figure S1B), estimating risk on the basis of CT images obtained during annual follow-up (incidence) screens to predict lung cancer diagnoses in subsequent years.

For comparison between the models, we also applied the LCRAT + CT model and the Polynomial model to the data set of subjects not showing any nodules ≥4 mm (i.e., following the criteria for which LCRAT + CT was developed; Figure S1A).

In all analyses, LDCT scan results were classified according to the nodule management protocol of the LUSI trial (Supplemental File, Table S3). Positive scans were those triggering immediate referral for further diagnostic workup. For purposes of the present analyses, LDCT scan evaluations that triggered 3- or 6-months follow-up appointments are referred to as “indeterminate”.

Description of the selected risk prediction models

The Polynomial model (16) uses information available at the first screening appointment (T₀) to predict the risk for lung cancer in the year (T₁, T₂), that is, the risk for lung cancer to be detected at the first follow-up screening appointment (T₁), or else diagnosed outside screening in the year (T₁, T₂). The Polynomial model includes linear and/or 2^nd-degree terms for a total of 11 selected risk factors including age, sex, smoking history, personal and family history of cancer, and LDCT scan findings at the initial prevalence screen such as pulmonary nodules and emphysema (Table S3).

The LCRAT + CT model estimates the risk of lung cancer detection at the next annual screening appointment (next-screen risk) at the time of any negative screening appointment by NLST criteria, by updating the 1-year lung cancer risk estimates obtained by the LCRAT model (17). By combining these two sets of predictors, the final model is based on age, smoking history, family history of lung cancer, BMI and education level, and on LDCT imaging findings about the presence of pulmonary emphysema and consolidation (Table S3). The current version of LCRAT + CT does not predict risk for individuals with nodules larger than 4mm in diameter.

Statistical methods

We applied the scores of the LCRAT + CT and Polynomial models (Table S3), as well as the Patz criterion (negative LDCT scan according to NLST criteria) on data from eligible subjects as described in the previous section.

For a few model variables, data were missing in the LUSI study. We handled these as follows: for the LCRAT + CT model, race (for which our study collected no information) was assumed Caucasian and the number of parents with lung cancer was assumed to be zero for all participants; reflecting the predominant demographic composition and the low prevalence of the disease in the German population. History of emphysema and COPD (not explicitly asked in our recruitment or assessment questionnaires) was replaced by history of chronic bronchitis; missing values (in <2% of participants for all variables) for education, BMI, smoking duration and time since quitting smoking were imputed by the median value recorded from participants within the same sex and age groups, and within the same smoking status group if applicable. For details about the conversion of variable “education” from the US system to the German system please see the Supplementary Methods section. For the Polynomial model, previous diagnosis of COPD was replaced by previous diagnosis of chronic bronchitis; participants without nodules were assigned values of zero for all nodule-related characteristics. Participants showing nodules, but for which nodule characteristics were missing (longest or perpendicular diameter, non-solid/solid, location, spiculation and/or nodule count were removed from the analysis (N=0 at T₀ and N=88 T₁ to T₄).

We evaluated discrimination via receiver operating characteristic (ROC) analysis. 95% confidence intervals (CI) for the area under the ROC curve (AUC) were calculated via stratified bootstrap (B =10,000). The method by DeLong et al. (23) was used for testing the difference (inferiority) in AUC values from two models applied to the same data. Additionally, for all models, we calculated the numbers of participants who would have been candidates for skipping the next screening appointment, using the deciles of predicted risk as thresholds. In addition, we calculated percentages and 95% confidence intervals (95% CI) of participants who would have had a delayed diagnosis if the screening round was skipped and the percentages of false positive or indeterminate screen tests that would have been either avoided or otherwise delayed. Confidence intervals for the proportions of delayed diagnoses were calculated with the Wilson score interval with continuity correction (24).

Using the deciles of predicted risk as risk thresholds, the discrimination ability of the models was evaluated based on their sensitivity, specificity, positive and negative predictive values, as well as positive and negative likelihood ratios. Exact binomial 95% confidence limits were calculated for sensitivity, specificity, and positive and negative predictive values. Approximate 95% confidence intervals were calculated for positive and negative likelihood ratios.

Calibration in-the-large (25) was evaluated by comparing the mean predicted risk from the LCRAT, LCRAT+CT and Polynomial models to the observed incidence within the population of eligible subjects, either by screening round or differentiating between prevalence and incidence rounds. Additionally, the models’ calibration was evaluated via Brier Scores and Spiegelhalter Z-test (26) (27) (28). Briefly, the Brier score is used for comparing the calibration of two prediction models (26), whereas the Spiegelhalter’s z-statistic is used for testing the null hypothesis of perfect calibration. Lower values of the Brier score indicate better calibration, while the null hypothesis of the Spiegelhalter’s test is rejected at the significance level α if the absolute value of the z-score is larger than the α-quantile of the standard normal distribution (26).

Statistical analyses were performed using R, version 3.4.4 (29) and the lcrisk (30), DescTools (31), rms (32), and pROC packages (33).

Results

There were 1,506 participants eligible for the validation of the LCRAT + CT model. Some of them were eligible at multiple rounds, given that they remained at risk for lung cancer detection: 1,194 at the initial “prevalence” screen (T₀), and 1,220, 1,262 and 1,228 participants at the three following incidence screens (T₁-T₃) (Figure S1A). These had a median age of 56.80 years (range, 50.30, 71.80) at first screening participation, were all long-term smokers, and 960 were males (63.7%). For 24 of these eligible participants, lung cancer was detected via LDCT at any of the three follow-up screening rounds. 20 of these detections occurred at the annual screening appointment following a negative screening result and were thus included in the LCRAT + CT validation (Table S4, Figure S1A). All 1889 participants eligible for the validation of the Polynomial model (Figure S1B) were long-term smokers with a median age of 56.80 years (range, 50.30, 71.90) at first screening participation, and 1238 of them were males (65.5%) (Table S4). Eleven (11) out of these eligible participants received a lung cancer diagnosis either as a result of further work-up triggered by positive LDCT findings at T₁, or by other means outside the screening protocol in the year after T₁ (Table S4).

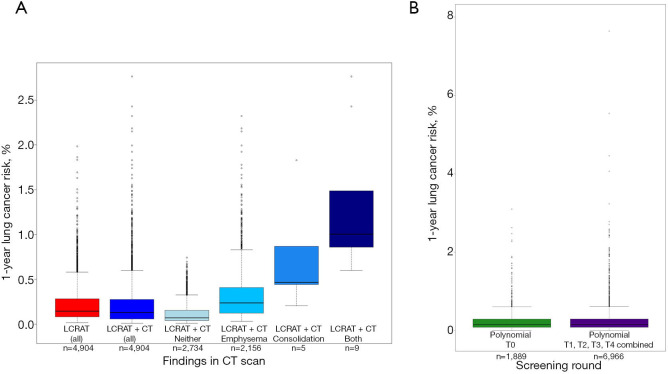
Estimates from both models varied widely across participants, covering a range of 0.009% to 2.76% risk for LC detection at the next annual screening appointment according to LCRAT + CT (Figure 1A), and of <0.001% to 8.34% risk for LC diagnosis (detected by screening or diagnosed outside screening) in the year [T_1, T₂) according to the Polynomial model (Figure 1B). For the LCRAT+CT model, highest model risks were estimated whenever eligible participants showed LDCT-based indications for both consolidation and emphysema (N=9, 0.60% of eligible participants, contributing with 9 estimated risk values in rounds T₀-T₃), consolidation without emphysema (N=5, 0.33% of eligible participants, contributing with 5 estimated risk values in rounds T₀-T₃), and to a lesser degree, emphysema (N=786, 52.2% of eligible participants, contributing to 2,156 estimated risk values in rounds T₀-T₃). For the Polynomial model, highest risks were observed especially for older participants with more pack-years, higher counts of nodules per LDCT scan, nodules present in the upper lobes of the lung, and nodules showing border spiculation.

Figure 1.

Distribution of predicted risks from the selected models: (A) LCRAT and LCRAT + CT, and (B) polynomial model.

When analyzing data from T₀ to T₃, LCRAT + CT achieved an AUC of 0.73 (95% CI: 0.63, 0.82) for the discrimination of participants with lung cancer detected at the next screening appointment from those with non-suspicious screening findings. For comparison, the original LCRAT model without CT data (18) showed a lower AUC of 0.68 (0.57, 0.78) (Figure S2A), although the difference in AUC compared to the combined LCRAT+CT model was not statistically significant (Z=−1.44, P=0.08). For the Polynomial model, analyses of data from the baseline (prevalence) screen yielded an AUC of 0.75 (95% CI: 0.67, 0.83) (Figure S2B) for the discrimination of participants who in the following year had LC diagnosis either through screening or independently of screening, from those who remained cancer-free. Applied to the combined data from the incidence screening rounds (T₁-T₄) the Polynomial model showed an AUC of 0.74 (0.65, 0.82). Finally, the dichotomous Patz criterion applied to baseline screen data produced a lower AUC of 0.56 (95% CI: 0.53, 0.72) (Figure S2C). To compare between the models, applying them both to individuals presenting no nodules ≥4 mm in diameter, the discrimination by the Polynomial model [AUC =0.76 (0.66, 0.87) at T_0, AUC =0.72 (0.62, 0.81) in T₀-T₃] was of comparable magnitude as that found for LCRAT + CT [AUC of 0.73 (95% CI: 0.63, 0.82)] (Figure S2D)

Using the LCRAT + CT estimates, we see that among screen-negative participants of the LUSI trial (as of NLST criteria), skipping about 40% to 50% of annual screenings, that is, for participants with estimated risks below 0.1% and 0.13% respectively, would have avoided or delayed 1 [25% (1.3%, 78.1%)] to 3 [75% (21.9%, 98.7%)] false positive screening tests and 3 [42.9% (11.8%, 79.8%)] indeterminate nodule findings, at the cost of 1 [5% (0.3%, 26.9%)] to 2 [10% (1.8%, 33.1%)] delayed LC detections (Table 1). Compared to LCRAT + CT, if the LCRAT model was used without CT information, at equal proportions of annual screenings skipped, there were generally higher numbers of LC detections delayed (Figure 2), combined with slightly higher numbers of false-positive or indeterminate screening tests (data not shown).

Table 1. Potential effect of risk thresholds from the LCRAT and LCRAT+CT models in eligible participants of the LUSI trial.

Percentile of risk	LCRAT + CT next-scan risk	Candidates for Longer Interval, N (%; 95% CI)	Delayed cancer detections, N (%; 95% CI)	False positives avoided/delayed, N (%; 95% CI)	Indeterminates avoided/delayed, N (%; 95% CI)	Sens (%; 95% CI)	Spec (%; 95% CI)	PPV (PPV; 95% CI)	NPV (NPV; 95% CI)	PLR (PLR; 95% CI)	NLR (NLR; 95% CI)
10th	r ≤0.03%	491 [10]	1 (5; 0.3, 26.9)	0 (0; 0, 60.4)	1 (14.3; 0.8, 58)	0.95 (0.75, 1.00)	0.10 (0.09, 0.11)	0.00 (0.00, 0.01)	1.00 (0.99, 1.00)	1.06 (0.95, 1.17)	0.50 (0.07, 3.37)
20th	r ≤0.05%	981 [20]	1 (5; 0.3, 26.9)	0 (0; 0, 60.4)	3 (42.9; 11.8, 79.8)	0.95 (0.75, 1.00)	0.20 (0.19, 0.21)	0.00 (0.00, 0.01)	1.00 (0.99, 1.00)	1.19 (1.07, 1.32)	0.25 (0.04, 1.68)
30th	r ≤0.07%	1,471 [30]	1 (5; 0.3, 26.9)	0 (0; 0, 60.4)	3 (42.9; 11.8, 79.8)	0.95 (0.75, 1.00)	0.30 (0.29, 0.31)	0.01 (0.00, 0.01)	1.00 (1.00, 1.00)	1.36 (1.23, 1.51)	0.17 (0.02, 1.12)
40th	r ≤0.1%	1,962 [40]	1 (5; 0.3, 26.9)	1 (25; 1.3, 78.1)	3 (42.9; 11.8, 79.8)	0.95 (0.75, 1.00)	0.40 (0.39, 0.42)	0.01 (0.00, 0.01)	1.00 (1.00, 1.00)	1.59 (1.43, 1.76)	0.12 (0.02, 0.84)
50th	r ≤0.13%	2,452 [50]	2 (10; 1.8, 33.1)	3 (75; 21.9, 98.7)	3 (42.9; 11.8, 79.8)	0.90 (0.68, 0.99)	0.50 (0.49, 0.52)	0.01 (0.00, 0.01)	1.00 (1.00, 1.00)	1.81 (1.56, 2.10)	0.20 (0.05, 0.74)
60th	r ≤0.17%	2,942 [60]	5 (25; 9.6, 49.4)	3 (75; 21.9, 98.7)	4 (57.1; 20.2, 88.2)	0.75 (0.51, 0.91)	0.60 (0.59, 0.62)	0.01 (0.00, 0.01)	1.00 (1.00, 1.00)	1.88 (1.46, 2.43)	0.42 (0.19, 0.89)
70th	r ≤0.23%	3,433 [70]	7 (35; 16.3, 59.1)	3 (75; 21.9, 98.7)	4 (57.1; 20.2, 88.2)	0.65 (0.41, 0.85)	0.70 (0.69, 0.71)	0.01 (0.00, 0.02)	1.00 (1.00, 1.00)	2.18 (1.57, 3.01)	0.50 (0.27, 0.91)
80th	r ≤0.32%	3,923 [80]	12 (60; 36.4, 80)	3 (75; 21.9, 98.7)	5 (71.4; 30.3, 94.9)	0.40 (0.19, 0.64)	0.80 (0.79, 0.81)	0.01 (0.00, 0.02)	1.00 (0.99, 1.00)	2.01 (1.17, 3.44)	0.75 (0.52, 1.07)
90th	r ≤0.48%	4,413 [90]	16 (80; 55.7, 93.4)	4 (100; 39.6, 97.6)	6 (85.7; 42, 99.2)	0.20 (0.06, 0.44)	0.90 (0.89, 0.91)	0.01 (0.00, 0.02)	1.00 (0.99, 1.00)	2.01 (0.83, 4.84)	0.89 (0.71, 1.11)
100th	r ≤2.76%	4,904 [100]	20 (100; 80, 99.5)	4 (100; 39.6, 97.6)	7 (100; 56.1, 98.7)

LCRAT, Lung Cancer risk Assessment Tool; Sens, sensitivity; Spec, specificity; PPV, positive predictive value; NPV, negative predictive value; PLR, positive likelihood ratio; NLR, negative likelihood ratio.

Figure 2.

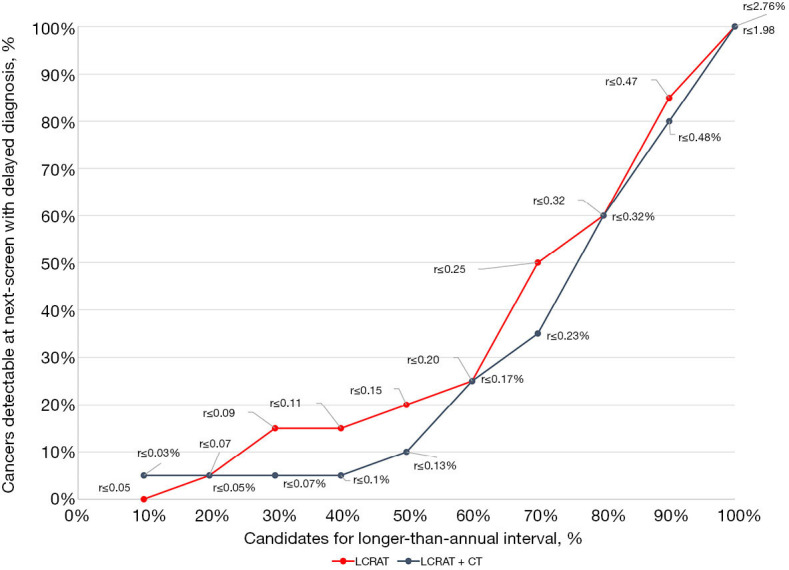
Potential effect of risk thresholds from the LCRAT and LCRAT + CT models in eligible participants of the LUSI trial.

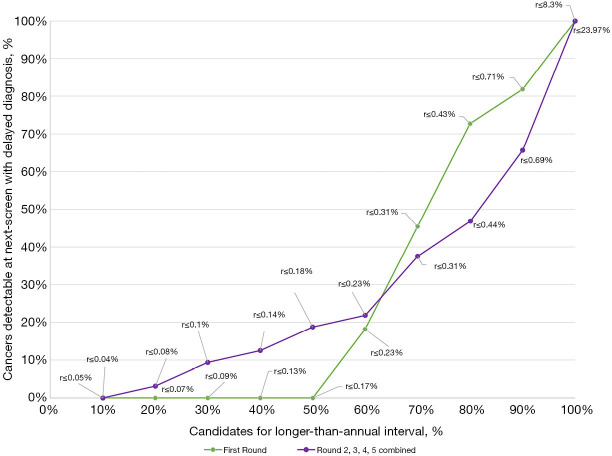
Using the Polynomial model, skipping the second round (T₁) for 40% to 50% of participants, that is, those with model risks below 0.13% and 0.17% at T₀, would have avoided or delayed 10 [40% (21.8%, 61.1%)] false positive screening tests and between 144 [38.8% (33.9%, 44%)] and 173 [46.6% (41.5%, 51.8%)] indeterminate screenings without delaying any diagnosis (0 (0%, 32.1%)) (Table 2, Figure 3). For comparison, applying the Patz criterion indicates that if all participants [N=1,194; 63.2% (95% CI: 61%, 65.4%)] with a negative T₀ scan would have skipped T_1, 1 [4% (0.2%, 22.3%)] false positive screen tests and 3 [0.8% (0.2%, 2.5%)] indeterminate scans could have been avoided, and 6 [54.5% (24.6%, 81.9%)] cancer diagnoses would have been delayed. For, both, the LCRAT + CT and Polynomial models (as applied to their respective eligible sub-sets) we found no statistically significant associations between predicted model risks and tumor stage for LC detected upon next annual screening, although this analysis was hampered by small overall case-numbers (results not shown).

Table 2. Potential effect of risk thresholds from the polynomial model in eligible participants of the LUSI trial.

Percentile of risk	Polynomial risk	Candidates for Longer Interval, N (%; 95% CI)	Delayed cancer detections, N (%; 95% CI)	False positives avoided/delayed, N (%; 95% CI)	Indeterminates avoided/delayed, N (%; 95% CI)	Sens (%; 95% CI)	Spec (%; 95% CI)	PPV (PPV; 95% CI)	NPV (NPV; 95% CI)	PLR (PLR; 95% CI)	NLR (NLR; 95% CI)
T0
10th	r ≤0.04%	189 (10)	0 (0; 0, 32.1)	8 (32; 15.7, 53.6)	83 (22.4; 18.3, 27)	1.00 (0.72, 1.00)	0.10 (0.09, 0.12)	0.01 (0.00, 0.01)	1.00 (0.98, 1.00)	1.11 (1.10, 1.13)	0.00 (0.00, NaN)
20th	r ≤0.07%	378 (20)	0 (0; 0, 32.1)	9 (36; 18.7, 57.4)	108 (29.1; 24.6, 34.1)	1.00 (0.72, 1.00)	0.20 (0.18, 0.22)	0.01 (0.00, 0.01)	1.00 (0.99, 1.00)	1.25 (1.22, 1.28)	0.00 (0.00, NaN)
30th	r ≤0.09%	567 (30)	0 (0; 0, 32.1)	9 (36; 18.7, 57.4)	128 (34.5; 29.7, 39.6)	1.00 (0.72, 1.00)	0.30 (0.28, 0.32)	0.01 (0.00, 0.01)	1.00 (0.99, 1.00)	1.43 (1.39, 1.48)	0.00 (0.00, NaN)
40th	r ≤0.13%	756 (40)	0 (0; 0, 32.1)	10 (40; 21.8, 61.1)	144 (38.8; 33.9, 44)	1.00 (0.72, 1.00)	0.40 (0.38, 0.43)	0.01 (0.00, 0.02)	1.00 (1.00, 1.00)	1.67 (1.61, 1.74)	0.00 (0.00, NaN)
50th	r ≤0.17%	945 (50)	0 (0; 0, 32.1)	10 (40; 21.8, 61.1)	173 (46.6; 41.5, 51.8)	1.00 (0.72, 1.00)	0.50 (0.48, 0.53)	0.01 (0.01, 0.02)	1.00 (1.00, 1.00)	2.01 (1.92, 2.10)	0.00 (0.00, NaN)
60th	r ≤0.23%	1,133 (60)	2 (18.2; 3.2, 52.2)	11 (44; 25, 64.7)	195 (52.6; 47.3, 57.7)	0.82 (0.48, 0.98)	0.60 (0.58, 0.62)	0.01 (0.01, 0.02)	1.00 (0.99, 1.00)	2.06 (1.55, 2.73)	0.30 (0.09, 1.06)
70th	r ≤0.31%	1,322 (70)	5 (45.5; 18.1, 75.4)	14 (56; 35.3, 75)	237 (63.9; 58.7, 68.7)	0.55 (0.23, 0.83)	0.70 (0.68, 0.72)	0.01 (0.00, 0.02)	1.00 (0.99, 1.00)	1.83 (1.06, 3.15)	0.65 (0.34, 1.24)
80th	r ≤0.43%	1,511 (80)	8 (72.7; 39.3, 92.7)	17 (68; 46.4, 84.3)	267 (72; 67.1, 76.4)	0.27 (0.06, 0.61)	0.80 (0.78, 0.82)	0.01 (0.00, 0.02)	0.99 (0.99, 1.00)	1.37 (0.52, 3.60)	0.91 (0.63, 1.31)
90th	r ≤0.71%	1,700 (90)	9 (81.8; 47.8, 96.8)	20 (80; 58.7, 92.4)	314 (84.6; 80.5, 88.1)	0.18 (0.02, 0.52)	0.90 (0.89, 0.91)	0.01 (0.00, 0.04)	0.99 (0.99, 1.00)	1.83 (0.52, 6.44)	0.91 (0.69, 1.20)
100th	r ≤8.3%	1,889 (100)	11 (100; 67.9, 99.2)	25 (100; 83.4, 99.6)	371 (100; 98.7, 100)
T1-T4
10th	r ≤0.05%	699 (10)	0 (0; 0.3, 13.3)	13 (16.2; 9.3, 26.6)	16 (7; 4.2, 11.4)	1.00 (0.89, 1.00)	0.10 (0.09, 0.11)	0.01 (0.00, 0.01)	1.00 (0.99, 1.00)	1.11 (1.10, 1.12)	0.00 (0.00, NaN)
20th	r ≤0.08%	1,395 (20)	1 (3.1; 0.2, 18)	14 (17.5; 10.2, 28)	26 (11.4; 7.7, 16.4)	0.97 (0.84, 1.00)	0.20 (0.19, 0.21)	0.01 (0.00, 0.01)	1.00 (1.00, 1.00)	1.21 (1.14, 1.29)	0.16 (0.02, 1.07)
30th	r ≤0.1%	2,090 (30)	3 (9.4; 2.5, 26.2)	15 (18.8; 11.2, 29.4)	31 (13.6; 9.6, 18.9)	0.91 (0.75, 0.98)	0.30 (0.29, 0.31)	0.01 (0.00, 0.01)	1.00 (1.00, 1.00)	1.30 (1.16, 1.45)	0.31 (0.11, 0.92)
40th	r ≤0.14%	2,787 (40)	4 (12.5; 4.1, 29.9)	15 (18.8; 11.2, 29.4)	41 (18; 13.3, 23.7)	0.88 (0.71, 0.96)	0.40 (0.39, 0.41)	0.01 (0.00, 0.01)	1.00 (1.00, 1.00)	1.46 (1.28, 1.67)	0.31 (0.12, 0.78)
50th	r ≤0.18%	3,483 (50)	6 (18.8; 7.9, 37)	17 (21.2; 13.2, 32.1)	58 (25.4; 20, 31.7)	0.81 (0.64, 0.93)	0.50 (0.49, 0.51)	0.01 (0.00, 0.01)	1.00 (1.00, 1.00)	1.63 (1.38, 1.93)	0.37 (0.18, 0.77)
60th	r ≤0.23%	4,181 (60)	7 (21.9; 9.9, 40.4)	20 (25; 16.3, 36.2)	76 (33.3; 27.3, 39.9)	0.78 (0.60, 0.91)	0.60 (0.59, 0.61)	0.01 (0.01, 0.01)	1.00 (1.00, 1.00)	1.96 (1.63, 2.36)	0.36 (0.19, 0.70)
70th	r ≤0.31%	4,876 (70)	12 (37.5; 21.7, 56.3)	25 (31.2; 21.6, 42.7)	110 (48.2; 41.6, 54.9)	0.62 (0.44, 0.79)	0.70 (0.69, 0.71)	0.01 (0.01, 0.01)	1.00 (1.00, 1.00)	2.09 (1.60, 2.74)	0.53 (0.34, 0.84)
80th	r ≤0.44%	5,576 (80)	15 (46.9; 29.5, 65)	36 (45; 34, 56.5)	134 (58.8; 52.1, 65.2)	0.53 (0.35, 0.71)	0.80 (0.79, 0.81)	0.01 (0.01, 0.02)	1.00 (1.00, 1.00)	2.68 (1.93, 3.73)	0.58 (0.40, 0.85)
90th	r ≤0.69%	6,269 (90)	21 (65.6; 46.8, 80.8)	46 (57.5; 46, 68.3)	162 (71.1; 64.6, 76.8)	0.34 (0.19, 0.53)	0.90 (0.89, 0.91)	0.02 (0.01, 0.03)	1.00 (0.99, 1.00)	3.47 (2.14, 5.64)	0.73 (0.57, 0.94)
100th	r ≤23.97%	6,966 (100)	32 (100; 86.7, 99.7)	80 (100; 94.3, 99.9)	228 (100; 97.9, 100)

Sens, sensitivity; Spec, specificity; PPV, positive predictive value; NPV, negative predictive value; PLR, positive likelihood ratio; NLR, negative likelihood ratio.

Figure 3.

Potential effect of risk thresholds from the polynomial model in eligible participants of the LUSI trial.

In the combined data from T₁ to T₄, the Polynomial model predicted 15 [18.8% (11.2%, 29.4%)] to 17 [21.2% (13.2%, 32.1%)] avoided false positive screen tests and 41 [18% (13.3%, 23.7%)] to 58 [25.4% (20%, 31.7%)] avoided indeterminate findings at the cost of delaying 4 [12.5% (4.1%, 29.9%)] to 6 [18.8% (7.9%, 37%)] LC detections, by skipping 40% to 50% next-round screenings (those of participants with risks below 0.14% and 0.18%) (Table 2). Using the subjects who were eligible for the LCRAT + CT model (i.e., those presenting no pulmonary nodules ≥4 mm), we observed that the Polynomial model predicted 0 [0% (0%, 69%)] avoided false positives and 2 [33.3% (6%, 75.9%)] avoided indeterminant results. This was at the cost of delaying 3 [13.6% (3.6%, 36%)] lung cancer detections by skipping 50% of screenings (i.e., if those with a risk below 0.14% were recommended to skip the screening) (Table S5, Figure S3).

In terms of calibration in-the-large, all models produced absolute risk estimates that were, on average, considerably lower than the observed lung cancer prevalence. Brier scores for the LCRAT, LCRAT + CT and Polynomial models were not significantly different from one another, thus indicating a similar calibration for the three models. For LCRAT and LCRAT + CT, the null hypothesis of calibration was rejected at α=0.05 when applied to the combined data of screening rounds T₀ (prevalence round) to T₃ (3^rd incidence screening) (P=0.004 for LCRAT, P=0.002 for LCRAT + CT), and also when applied to the data only from the incidence rounds T₁ to T₃ (P=0.049 for LCRAT and P=0.036 for LCRAT + CT). Likewise, the same hypothesis was rejected at α=0.05 when applied to the estimated risks from the Polynomial model from T₀ (P=0.032) and T₁ to T₄ (0.048) (Tables S6,S7).

Discussion

Using data from the German Lung cancer Screening Intervention (LUSI) trial, we performed an external validation of the criterion suggested by Patz et al. (10) and two risk prediction models by Robbins et al. (17) (LCRAT + CT) and Schreuder et al. (16) (Polynomial model). These models were recently developed on the basis of data from the NLST trial and are intended for the identification of candidates for longer lung cancer screening intervals.

In this study population, the LCRAT + CT (AUC =0.73 among negative screens, all rounds combined) and the Polynomial model (AUC =0.75 – baseline screening round) proved useful for discriminating participants at higher vs. lower risks of having LC detected at, or in the year following, their next annual screening appointment. In comparison, the criterion by Patz, based solely on the presence or absence of pulmonary nodules ≥4 mm, showed a lower discrimination ability (AUC =0.56). Our results are indicative of the improvement in discrimination attributed to the use of CT-based findings. The LCRAT model, designed to be used in the absence of screening (AUC =0.68) appeared somewhat inferior to the combination of LCRAT plus CT characteristics (LCRAT + CT), although this difference in performance did not reach statistical significance, possibly due to the small sample size of our study. Both the Polynomial and LCRAT + CT models showed Lorenz curves (Figures 2,3) indicating that, in populations similar to that of the LUSI trial, individuals for whom biennial screening would represent delayed diagnosis are very unevenly distributed across lung cancer risk groups. For example, only 10% of all delayed diagnoses would be found among the 50% of participants with lowest risks estimated by the LCRAT + CT model (Figure 2), and likewise, only 20% of delayed diagnoses would be found among 60% of participants with lowest risks estimated by the Polynomial model. Globally, these findings are similar to those by Robbins et al. (17), as well as by Schreuder et al. (16), in terms of general model capacity to discriminate of individuals at substantially different risks of having LC detected upon a next annual screening. Our findings thus support the proposal (34) that detailed risk models which integrate both subject characteristics and LDCT traits can be useful for identifying participants who should be advised to have their next CT screening over shorter or longer time intervals. In contrast, a simple criterion based on the presence or absence of nodules of a given size does not provide sufficient discrimination to support these decisions.

With regard to model calibration, our findings indicated underestimation of absolute LC risks by both the LCRAT + CT and Polynomial models in this German screening population. In addition, we observed that, when selecting candidates for longer screening intervals, corresponding to a given proportion of LC diagnoses that one may consider acceptable to be delayed, different absolute thresholds would need to be set for the two models. For example, in order to maintain the proportion of delayed diagnosis at roughly 10%, candidates for biennial screening would be those with estimated LC risks below 0.20% from the Polynomial model, but below 0.13% from the LCRAT + CT model. In part, these differences may be explained by the fact that the two models differ with regard to the risk they purport to estimate, predictor variables used, and the sub-populations of screening participants to which the models apply, which complicates any direct comparison. A direct comparison of equivalent risk cut-points between LUSI and the NLST study, as reported by Robbins (17) or Schreuder (16), is also complicated, as the LUSI trial included a larger proportion of participants with lower model risks, due to less stringent eligibility criteria used in the LUSI study (age 50–69, ≥15 cigarettes/day for 25 years; or ≥10 cig/d for at least 30 y; if former smokers, quitting time ≤10 y) relative to those of NLST (age 55–74, ≥30 pack-years of smoking, maximum of 15 years since quitting).

Our analyses have some limitations: Their retrospective nature did not allow for the investigation of actual harms or benefits from skipping a screening appointment (e.g., leading to uncertainty about numbers of false-positive test results that might be permanently avoided or just postponed by 1 year), and the small study size and case numbers led to wide confidence intervals for all our estimates and did not allow for a precise investigation of absolute risk calibration. A more minor limitation is that a subset of variables used in LCRAT + CT or polynomial models were missing in our dataset, though some of these variables would have contributed only minimal additional discrimination due to their low incidence even in the population eligible for screening. Nonetheless, our study provides a first evaluation of the selected risk prediction models on an independent dataset, using data from a longer time span compared to that of NLST (5 screening rounds compared to 3 from NLST), and confirming the potential of risk stratification by risk models integrating CT characteristics.

In conclusion, our study confirms the utility of the LCRAT + CT and Polynomial models in terms of discrimination ability, in view of defining individually more optimized screening intervals for participants in LC screening programs. A point worth noticing is the good discrimination performance achieved by the Polynomial model in data from later screening rounds, even though it was originally developed for its application on data from the first (prevalence) screening round. This suggests the model could also support decision making at later points in the screening process. Our findings provide some confirmation that, compared to general patient characteristics only (e.g., as in the LCRAT model), or to a simple criterion based on the presence/absence of pulmonary nodules, discrimination may be improved by incorporating additional risk indicators of pulmonary health derived from CT images. However, our findings suggest that, before application to populations different from that of the NLST, in which the two models were developed, the LCRAT + CT and Polynomial models might need to be re-calibrated for the specific screening population targeted.

For future screening programs, more reflection will be needed about how risk-based approaches may be used both to identify individuals for initial lung cancer screening, and then to determine optimized time points for follow-up screenings. Quantitative modeling studies have shown that, for equivalent numbers of individuals to be screened, using minimal-risk criteria based on LC risk prediction models such as LCRAT (13) or the PLCO_M2012 (11) will prevent more lung cancer deaths and lead to more life years gained than strategies based on current eligibility criteria (i.e., using lower and upper age limits, lifetime pack-years of smoking and maximum time since smoking cessation) (11-13). Conceivably, future screening strategies could use a general-population lung cancer risk model such as LCRAT or PLCO_M2012 to first identify individuals for whom at least a lower-intensity screening regimen with longer (e.g., 2-year) intervals would be recommended. In a next step, an augmented model integrating further risk indicators from the last CT scan, such as LCRAT + CT, could be used to identify those screening participants who would benefit most from more frequent (e.g., annual instead of biennial) screening. Further work is still needed, however, to determine risk thresholds that would guarantee a minimal expected net clinical benefit (as defined by expected gains in life years gained minus a well-motivated, weighted score of expected harms due to false-positive screen tests, overdiagnosis and radiation exposures), or that can be motivated by major improvements in financial cost efficiency. Finally, once these thresholds will be defined, it is recommended that models be systematically evaluated in context of actual screening programs, to ensure proper calibration of their risk predictions.

Supplementary

The article’s supplementary files as

Disclaimer: Where authors are identified as personnel of the International Agency for Research on Cancer/World Health Organization, the authors alone are responsible for the views expressed in this article and they do not necessarily represent the decisions, policy or views of the International Agency for Research on Cancer/World Health Organization.

Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. LUSI is a registered clinical research study with ISRCTN 30604390. Ethical approval was provided by the University of Heidelberg Medical Ethics Committee (073/2001) and by the radiation protection authority (BfS, 22462/2, 2006-045). The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). All participants enrolled provided written informed consent.