Impact of bubble coalescence in the determination of bubble sizes using a pulsed US technique: Part 1 – Argon bubbles in water

Highlights

• •An experimental method for determination of bubble sizes is thoroughly studied.
• •If conditions are not optimized, bubble coalescence leads to too big sizes.
• •The presence of a standing wave enhances coalescence.
• •Conditions for measurement of the ambient size of cavitation bubbles are determined.
• •An ambient radius of 2.9–3.0 µm is derived for Ar-saturated water at 362 kHz.

Abstract

A powerful experimental approach to measure the size distribution of bubbles active in sonoluminescence and/or sonochemistry is a technique based on pulsed ultrasound and sonoluminescence emission. While it is an accepted technique, it is still lacking an understanding of the effect of various experimental parameters, including the duration of the pulse on-time, the nature of the dissolved gas, the presence of a gas flow rate, etc. The present work, focusing on Ar-saturated water sonicated at 362 kHz, shows that increasing the pulse on-time leads to the measurement of coalesced bubbles. Reducing the on-time to a minimum and/or adding sodium dodecyl sulfate to water allows to reducing coalescence so that natural active cavitation bubble sizes can be measured. A radius of 2.9–3.0 µm is obtained in Ar-saturated water at 362 kHz. The effects of acoustic power and possible formation of a standing-wave on coalescence and measured bubble sizes are discussed.

1. Introduction

Ultrasound and sonochemistry find applications in many domains ranging from materials synthesis to food processing and medical applications. In many cases, the efficiency of the treatment, the yield, or the properties of the obtained products highly depend upon the cavitation efficiency, determined by the number and the size of the active bubbles, and by their content [1], [2]. Thus, it is of importance to estimate reliably the bubble sizes, in particular the distribution of bubble ambient radii (i.e., bubble radii at zero acoustic pressure) that correspond to the bubble gas contents and are necessary for all modelling of bubble behavior. One of the main difficulties in this determination is that bubble sizes are far from being monodisperse, with bubbles too small to be active and at the other end too big bubbles resulting from coalescence of smaller ones. Only a certain size interval is of interest for sonochemistry, namely that of cavitation bubbles.

Direct experimental determinations were based on techniques like acoustic scattering [3], laser diffraction [4], [5], [6], X-ray imaging [7] or direct observation of bubbles by a long distance microscope coupled to a camera. The latter method was initially based on a direct high-speed imaging of all visible bubbles [8]. It was recently further developed by coupling it to a statistical approach giving access to the distribution of equilibrium radii [9]. These reliable largely validated methods are however limited to low frequencies due to technical limitations (an increase in frequency leads to a decrease in bubble size and to shorter oscillation periods). For instance, Reuter et al. [9] indicated that due to the optical resolution, only bubbles larger than 10.5 µm are accessible to the measurement, or equilibrium radii larger than 2.2 µm with their statistical approach. Besides, in most cases, direct observations focus on all present bubbles, not just on cavitation bubbles, which explains the reported large size intervals. One remarkable work is to be highlighted, where maximum expansion radii of sonoluminescing bubbles could be determined at low frequency, in the particular, highly luminous case of Xe-saturated phosphoric acid [10].

To overcome these limitations and increase the accessible frequency interval, indirect methods were developed. The first one was based on the measurement of the void rate (i.e., the total volume of bubbles) after the end of the ultrasonic irradiation using an electromagnetic method [11], [12], [13], [14] and was applied to air-saturated water sonicated at frequencies of 300 and 1100 kHz. It was shown for instance that at 344 kHz most bubbles had an equilibrium radius below 3.5 µm [13]. It also underlined that coalescence of bubbles can perturb the measurement and lead to a shift of the determined bubble size distribution towards bigger sizes [12]. A second method also relied on the measurement of the time needed by bubbles to dissolve – this time being related to the bubble size – and followed the scattering intensity of bubbles vs. time with an acoustic method [15]. It demonstrated the feasibility of measurement of bubble size distributions at frequencies as high as 5 MHz in a focused configuration. In the third method [16] the chosen monitoring technique was the measurement of emitted light (of sonochemiluminescence, SCL or of sonoluminescence, SL) intensity. The latter choice presents the advantage of allowing to restricting the population of studied bubbles to (SCL or SL) active bubbles. This is why we’ll focus on it.

In the latter method, a solution is irradiated during a constant on-time (t_on) during which a certain active bubble population is formed that could be monitored by SL or SCL intensity. In the following off-time (t_off), no US is emitted and bubbles are allowed to dissolve. By varying the off-time in a large interval, the time needed for bubbles to completely dissolve was measured, from which bubble sizes could be determined. This method also produced valuable results, giving for instance the general trend of decrease in size with an increase in frequency of SCL bubbles [17]. It could thus a priori be used to gain further knowledge on bubble sizes and particularly at high frequency, which would be useful for various applications, such as therapeutic or diagnostic medicine [15], [18]. A prerequisite would be to further validate the method for a better understanding of this technique. In particular the influence of various experimental parameters on the bubble size determination needs to be well understood. Indeed, previous works arbitrarily fixed an US on-time of 4 or 6 ms and mostly studied pre-saturated solutions. However, it was reported that the bubble size highly depended on the on-time duration [19], which was assumed to reflect the existence of bubble clusters where bubbles experience a different acoustic pressure and thus have different sizes. Some reported results provide a hint that in some experimental conditions, interaction between bubbles may occur (contrary to the founding hypothesis) and lead to the measurement of the size of a coalesced bubble, similar to what was observed by Labouret and Frohly [11], [12] with their electromagnetic technique. For instance, a size distribution of 2.8–3.7 µm was reported for air-saturated water sonicated at 515 kHz, and a smaller size range (0.9–1.7 µm) for an aqueous solution containing 1.5 mM sodium dodecyl sulfate (SDS) [16] – SDS is known to limit bubble coalescence [20], [21], this discrepancy may indicate that coalesced bubbles were measured in water. Our hypothesis is also in line with the observation of Iida et al. [22] who measured the bubble size distribution (of all present bubbles) by laser diffraction in air-saturated water under pulsed US at 443 kHz and observed that an increase in t_on shifted the distribution towards larger sizes, due to bubble coalescence during t_on. Xu et al. [15] also observed similar results under high intensity focused US (HIFU, 1.2 MHz and 5 MHz). It thus appears necessary to further investigate possible phenomena taking place under pulsed US.

The Part 1 of the present study focuses on Ar saturated water and investigates in detail the impact of pulse on-time on bubble size distribution at 362 kHz, whereby the sonication on-time was varied between 0.5 ms and 8 ms. It also considers the effect of a continuous Ar gas flow, in line with the recent observation of different bubble sizes in NaCl solutions pre-saturated with He or Ar or continuously sparged with these gases [23].

2. Materials & methods

Milli-Q water was used in all experiments. Ar gas was purchased from Air Liquide and had a purity of 99.999%. Sodium dodecyl sulfate (SDS) from VWR was of analytical grade.

The experimental set-up and methods were described in detail elsewhere [16], [23]. In short, 250 mL of water or 0.1 mM SDS aqueous solution (corresponding to a liquid height of approximately 7.3 cm) was placed in a glass sonochemical reactor, at the bottom of which a 362 kHz transducer (ELAC Nautik, 25 cm²) was clamped. The input signal was provided by a high-frequency generator (T&C Power Conversion, Inc.) used as an amplifier for a Tektronix AFG320 function generator triggered by an external pulse generator (Stanford Research Systems, inc, model DG535). The solution was pre-saturated with Ar for 30 min at a gas flow rate of 100 mL/min. In the experiments on the effect of the gas flow rate, a constant gas flow was kept during measurements, with the gas inlet occurring approximately in the middle of the solution volume. In some experiments, a film was placed on the liquid surface to prevent surface vibration of the solution.

The absorbed acoustic power was determined calorimetrically. The temperature of the solution was kept at 10 °C using a Huber Unistat Tango thermo-cryostat.

The intensity of sonoluminescence (SL) was measured with a photomultiplier tube (PMT) (Hamamatsu R1463) placed, unless otherwise specified, on the side of the glass cylinder. For each t_on, the evolution of SL intensity, I_SL, was recorded for a large interval of t_off, with the measurement being performed from high to low t_off (see Fig. 1SI in Supporting Information). The time interval where SL strongly increased was determined from the I_SL vs t_off plots. Here, we considered the time at which SL starts to increase, the time corresponding to the middle of the increase, and that at the end of the increase. Corresponding bubble sizes (respectively, R_max, R_middle and R_min) were then calculated using Epstein and Plesset equation [24]:

$$\left(\frac{D{C}_s}{{\rho }_g{R}_0^2}\right)t=\frac{1}{3}\left(\frac{\mathit{RT}{\rho }_g{R}_0}{2M\gamma }+1\right)$$

Fig. 1.

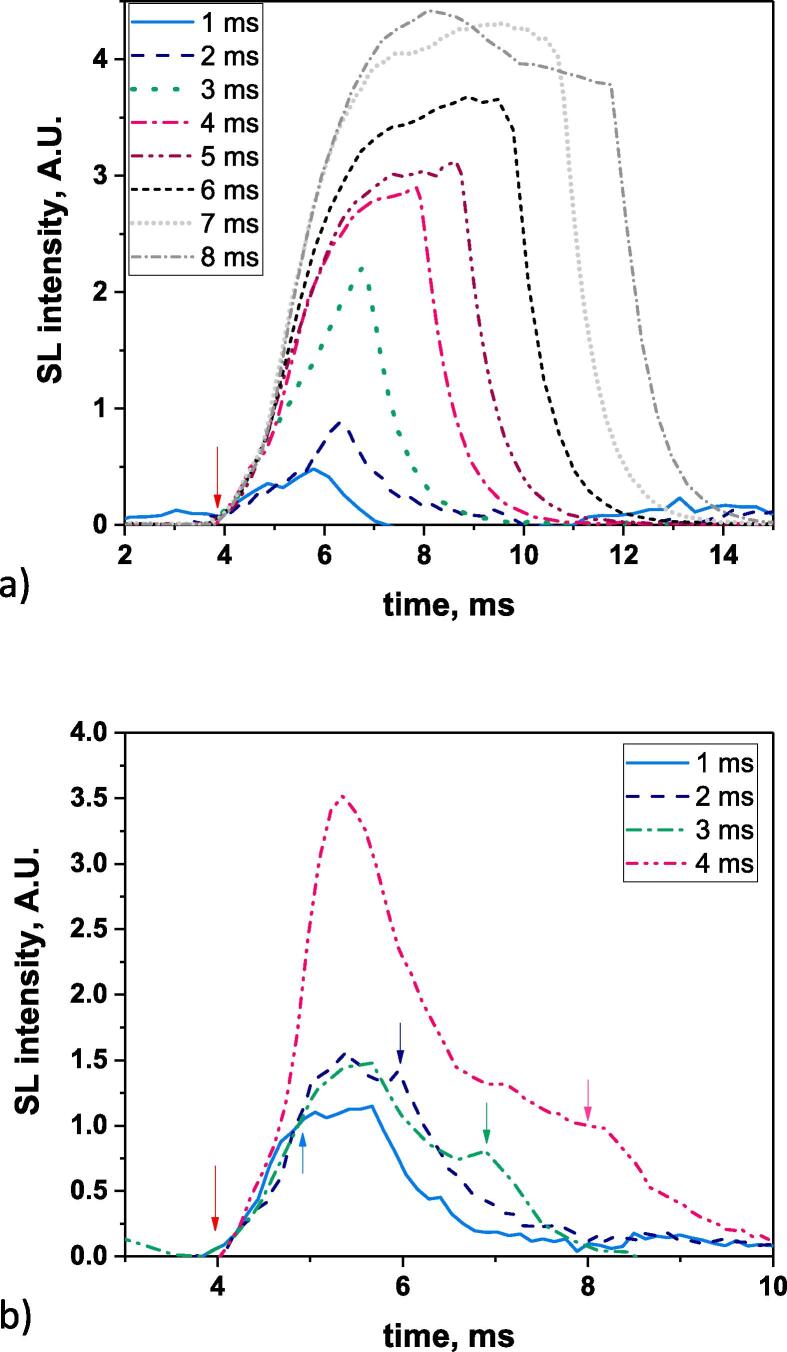
Evolution of the SL intensity during t_on, for various t_on values, Ar-saturated water, 362 kHz, 10 °C, a) P_ac = 48 W, (V_PMT = 600 V for 3–8 ms, 1000 V for 1–2 ms), b) P_ac = 4.4 W (V_PMT = 1000 V) (curves obtained at higher t_on are presented in Fig. 2SI in Supporting Information) (for each curve, the second arrow indicates the end of the US pulse).

where D is Ar diffusion coefficient, C_s is its saturation concentration in solution, ρ_g is the gas density in the bubble, R₀ is the initial bubble radius (here R_max, R_middle and R_min), t is the total dissolution time (corresponding to the measured t_off), M is Ar molecular weight, γ is the surface tension of the liquid, R is the universal gas constant, and T is the temperature of the liquid. Used values can be found in [23]. Bubble sizes are given with an uncertainty of ± 0.1 µm.

3. Results & discussion

3.1. Effect of t_on on the determined bubble size

Fig. 1a presents the evolution of the SL intensity during t_on for various t_on in the range 1–8 ms, for Ar-saturated water sonicated at 362 kHz at an acoustic power (P_ac) of 48 W. Similar to what was reported in the literature for air-saturated water [25], the shape of the SL intensity depends on t_on: for a short on-time (1–3 ms) the SL intensity steadily increases; if t_on lasts 4–6 ms the SL intensity then reaches a plateau. This plateau is followed by a decrease in intensity for longer on-times. These observations have been explained by an initial increase in the number of active bubbles followed by the reaching of an apparent steady-state bubble population. Interactions between bubbles then happen that decrease the number of active bubbles (and the SL intensity) [25]. Previous works chose an on-time corresponding to a reached steady-state population (4–6 ms). This choice also had the advantage to increase the measured SL intensity compared to shorter t_on.

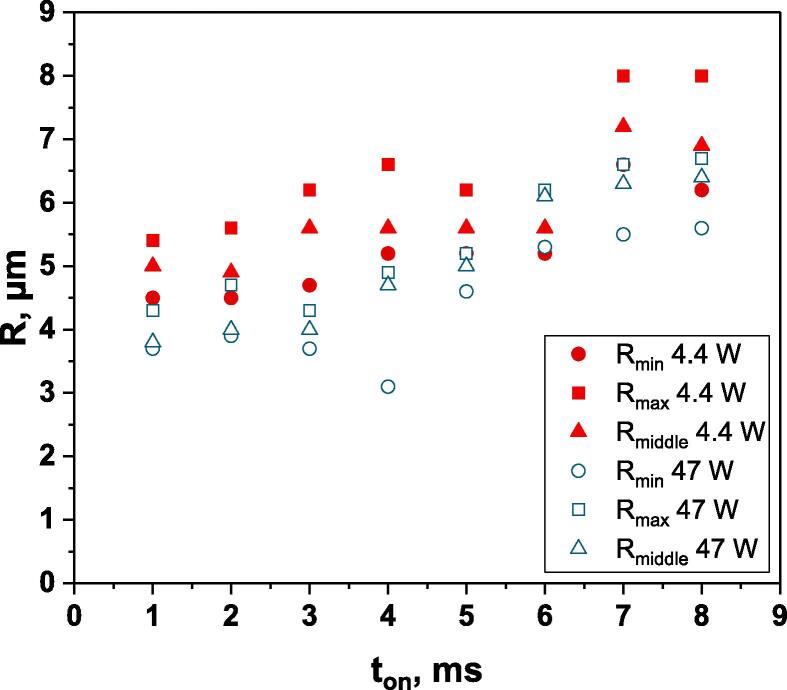
Calculated bubble sizes for water saturated with Ar (at P_ac = 48 W) at various on-times are plotted in Fig. 2 (blue empty symbols). As expected [26], they are all smaller than Minnaert resonance size (9.8 µm at 362 kHz) [27], due to the latter model not taking into account the strong nonlinearity of bubble collapse. It can be seen that the obtained values strongly depend on the on-time. For t_on = 1–3 ms, a mean radius of 3.8–4.0 µm is calculated, increasing to 5.0–5.2 µm for 4–5 ms and further to 6.2–6.8 µm for 6–8 ms. This discrepancy in the obtained bubble sizes indicates that t_on duration strongly impacts the measurement. This fact may be traced back to one of the founding hypotheses of the method that may be valid only for short on-times, namely that the sole phenomenon occurring during t_on would be the growth of bubbles (by gas diffusion and coalescence) to their active size and the growth of the active bubble population.

Fig. 2.

Bubble sizes calculated for different on-times; Ar-saturated water, 362 kHz, 10 °C, P_ac = 48 W (empty symbols) or 4.4 W (full symbols).

Indeed, longer the t_on, more time is available for bubbles to interact and possibly coalesce during t_on, leading to the formation of bigger bubbles, the dissolution of which (and thus the size of which) is then monitored. This hypothesis is in good agreement with the evolution of the calculated bubble sizes. Considering the mean value obtained for t_on = 1–3 ms, 3.8 µm, as the initial bubble size, the coalescence of two such bubbles would end in a bubble of volume $2\times \frac{4}{3}\pi {\times 3.8}^3$ and thus radius $\sqrt[3]{2}\times 3.8=4.8$ µm. Values obtained for longer t_on (6–8 ms) would correspond to bubbles formed from the coalescence of 3 (5.5 µm), 4 (6.0 µm), 5 (6.5 µm) bubbles of initial size 3.8 µm.

Similar measurements were performed for a low acoustic power of 4.4 W. The evolution of the SL intensity during t_on is depicted in Fig. 1b. For t_on = 4 ms, the SL intensity strongly increases during 2 ms, followed by a fast decrease. The intensity reached at 4.4 W is as high as that observed at 47 W. The increase in SL intensity is also observed to stop before the end of t_on for t_on = 2–3 ms, and shows a second local maximum at the end of the US pulse. For t_on = 1 ms, the trend is different and the SL intensity increases during 1.2 ms then stays constant during 0.6 ms, indicating the presence of SL bubbles after the end of the set US pulse, probably due to some instrumental effect leading to an on-time longer than 1 ms (see Fig. 3SI in Supporting Information).

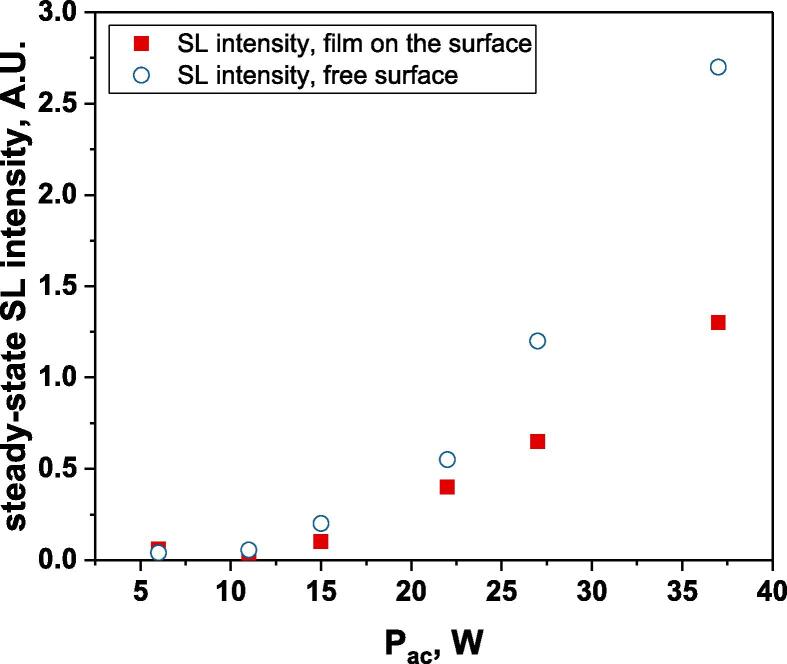
Fig. 3.

Evolution of the steady-state SL intensity with P_ac, for a free surface (empty symbols) and a surface blocked by a film (full symbols); Ar-saturated water, 362 kHz.

Calculated bubble sizes (Fig. 2, red symbols) are increasing with t_on, as observed for a high acoustic power. Considering the mean sizes (a similar reasoning holds for R_min and R_max), they can be regrouped into three sizes:

• -4.9 μm for t_on 1–2 ms, corresponding to the coalescence of 2 bubbles of 3.8 µm (taking the same reference as for 47 W): 3.8 × $\sqrt[3]{2}$ = 4.8 μm
• -5.6 μm for t_on 3–6 ms : coalescence of 3 bubbles 3.8 × $\sqrt[3]{3}$ = 5.5 μm
• -7.0 μm for t_on 7–8 ms : coalescence of 6 bubbles 3.8 × $\sqrt[3]{6}$ = 6.9 μm

Surprisingly, bubble sizes calculated for 4.4 W are larger than those determined for 47 W, except for 6 ms where they are similar. This trend is in disagreement with previously published results on air-saturated water sonicated at 1056 kHz (with t_on = 4 ms) [17], showing an increase in size up to 10 W acoustic power, followed by a constant bubble size. This fact indicates a larger extent of coalescence at lower acoustic powers that may be linked to the formation of a standing wave at low P_ac where the water surface is not deformed [28]: indeed, if a standing wave forms, active bubbles gather at the pressure antinodes, which makes them closer to another and thus more prompt to interact – a priori both during t_on and t_off. This larger extent of coalescence would explain the faster increase in SL intensity during t_on for 47 W compared to 4.4 W (see for instance the intense 4 ms case). In order to validate this assumption, the effect of the formation of a standing wave on bubble coalescence under pulsed US was investigated. It is to be noted that coalescence is also expected at high acoustic powers, in particular due to increased secondary Bjerkness forces [29] that are proportional to the square of the acoustic pressure. Thus, P_ac = 48 W is not necessarily the optimal case, and there may be acoustic powers in between for which the coalescence would be lower. However, this study is beyond the purpose of the current one.

3.2. Does the formation of a standing wave favor coalescence of bubbles?

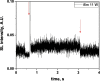
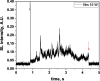
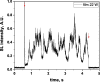
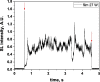
Two configurations were compared for the pulsed sonication of Ar-saturated water: with a free water surface and with the water surface covered by a film, to minimize surface vibrations, leading to the formation of a standing wave [30]. The evolution of the SL intensity in the first seconds of sonication was monitored for acoustic powers of 6, 11, 15, 22, 27 and 37 W and is depicted in Table 1.

Table 1.

Evolution of the SL intensity in the first seconds of sonication for a free surface and a surface covered by a film; P_ac = 6, 11, 15, 22, 27, 37 W. Red arrows indicate beginning and end of sonication.

Pac, W	Free surface	Reflecting surface (film)
6
11
15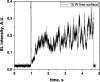
22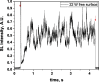
27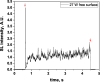
37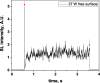

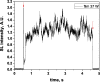An intense initial peak of SL is seen in all cases and corresponds more or less to what is observed in pulsed US during t_on (on the ms scale). The system then develops to a more stationary one. For all acoustic powers, this initial peak is more intense in the free surface configuration as can be observed for 27 W and 37 W (other cases are zoomed in for readability) which indicates the formation of a larger number of SL bubbles in the first ms of sonication in the free surface geometry. The evolution of the steady-state SL intensity with P_ac is plotted in Fig. 3 for the two surface conditions:

At very low acoustic powers (6 & 11 W) the solution surface remains stable even in the absence of a film, so that measurements in the two configurations are very similar. The higher value obtained at 6 W in the presence of a film compared to the same geometry at 11 W and the same power with a free surface may result from some instability of the signal generator at very low power. For acoustic powers ≥ 15 W the vibration of the solution surface was observed in the absence of the film. Similar to its initial value, the steady-state SL intensity is then higher for the free surface compared to that observed with a film, indicating that the SL bubble number is decreased when a standing wave forms due to more interaction between bubbles and in particular due to more coalescence. Another interesting observation is the large variation in SL intensity for P_ac ≥ 15 W, indicating a large time-variation in the number of SL bubbles. Indeed, the increase in acoustic power leads to an increase in the population of bubbles. The latter leads to more interactions between bubbles, more splitting and coalescence and therefore a higher variation in the bubble number. This variation is enhanced when the surface is covered with a film, i.e., in the presence of a standing wave, confirming that the latter favors bubble–bubble interactions. At higher acoustic powers (27, 37 W) a similar variation in the bubble number is observed but is proportionally less important due to the higher total active bubble number.

To further investigate the effect of the standing wave, bubble sizes were determined for the lowest (6 W) and the highest (37 W) acoustic powers in the free and blocked surface configurations, for t_on = 1 ms and 4 ms. As previously observed, light emission often occurs for a longer duration than t_on: for instance for t_on = 4 ms and P_ac = 37 W light emission is measured during 6 ms (see Table 1SI in Supporting Information). This light emission after the end on the US pulse indicates bubble–bubble interactions leading to the formation of bubbles having the right size to sonoluminescence. Some instrumental artefact also emphasizes it for t_on = 1 ms, where hydrophone measurements (Fig. 3SI in Supporting Information) revealed the presence of an acoustic pressure after the end of the pulse delivered by the function generator, which explains why the SL intensity continues increasing after t_on, as seen for t_on = 1 ms.

A different trend is observed at low acoustic power (6 W): for t_on = 4 ms, the SL intensity evolution during t_on is not regular (Fig. 4SI): it strongly decreases after ~ 1 ms, then increases again after 2.5 ms. This behavior indicates strong coalescence and confirms that the standing wave formation favors bubble interaction. Obviously, too big bubble sizes are expected to be calculated in this case.

Fig. 4.

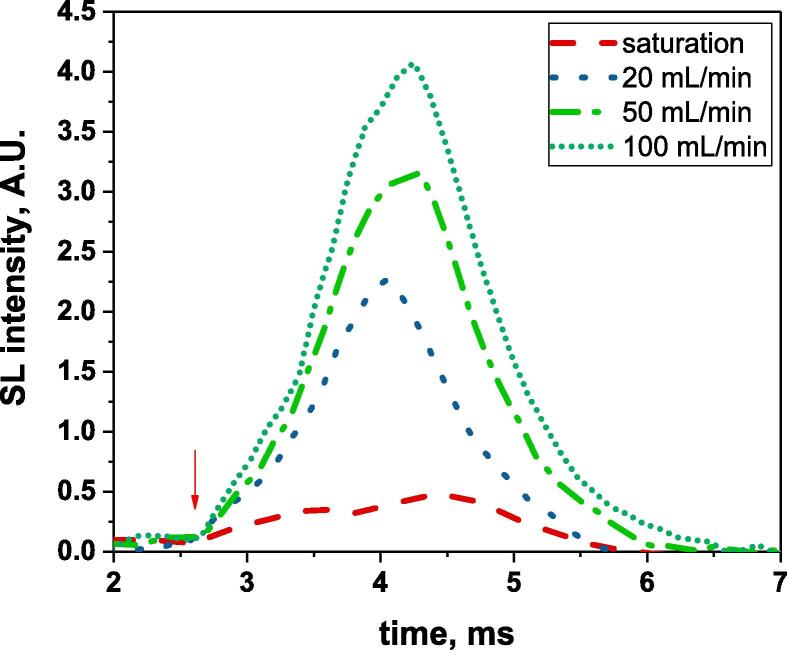
Evolution of the SL intensity in water during t_on for different Ar gas flow rates, t_on = 1 ms, P_ac = 47 W, V_PMT = 1000 V, t_off corresponding to the SL plateau; the red arrow indicates the beginning of the US pulse. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Calculated bubble radii for the different conditions are summarized in Table 2.

Table 2.

Calculated bubble radii for a free and blocked surface, at P_ac 37 and 6 W, for t_on = 1 & 4 ms; Ar-saturated water.

	Calculated radii, for Pac = 37 W, µm	Calculated radii for Pac = 6 W, µm
Free surface, ton = 1 ms	2.9–3.4 3.8	3.9 4.3 4.6 4.7 4.9
Free surface, ton = 4 ms	3.7	Not observed
Surface blocked by a film, ton = 1 ms	2.9–4.3 5.0–5.2	2.9–5.2
Surface blocked by a film, ton = 4 ms	4.3	2.9–4.3

In most cases, large size distributions and/or several size distributions are observed. Smaller sizes are obtained in the absence of a standing wave, i.e., for higher P_ac and a free surface, confirming the role of coalescence induced by the standing wave. Similarly, a smaller t_on reduces coalescence extent, so that smaller bubble sizes can be obtained.

All obtained values plead in favor of an initial bubble radius around 2.9 µm. Other sizes can be explained by coalescence of bubbles (2 for 3.7 µm, 3 for 4.2–4.3 µm, 4 for 4.6 µm, 5 for 5.0 µm, 6 for 5.3 µm). The large intervals of bubble sizes observed e.g. for t_on = 1 ms and a blocked surface can be explained by coalescence happening at different times during t_off. In this example, R_min corresponds to R₀ and R_max to the radius of a bubble issued from the coalescence of 6 R₀-bubbles.

It is to be noted that previously reported bubble sizes (for instance for Ar [19], [23]) having been measured with a large on-time (of 5.8 and 4 ms for the cited references), they correspond to coalesced bubbles.

3.3. Confirming Ar initial bubble size by further decreasing the extent of coalescence

To confirm that 2.9 µm can be considered as the initial bubble size for Ar-saturated water sonicated at 362 kHz, the extent of coalescence was further decreased by adding 1.5 mM SDS to water. The SDS concentration was chosen according to Sunartio’s [31] study that showed minimum coalescence in air-saturated water for 1–2 mM at 358 kHz. Bubble sizes were determined and compared for the two solutions (water and SDS) at t_on as low as possible (1 ms and 0.5 ms), in the free surface configuration, thus in conditions limiting coalescence. Measurements were performed at P_ac = 37 and 6 W for comparison. Obtained bubble sizes are summarized in Table 3.

Table 3.

Bubble sizes determined for Ar-saturated water and SDS 1.5 mM solution sonicated at 362 kHz in a free surface configuration for P_ac = 6 & 37 W. (The SL intensity was too low at P_ac = 37 W and t_on = 0.5 ms.).

		ton = 1 ms	ton = 0.5 ms
Pac = 37 W	H2O	3.8–4.0 µm	–
	SDS	3.1 µm 3.4 µm 4.0 µm	3.0 µm 3.8 µm
Pac = 6 W	H2O	4.0 µm	4.0 µm 3.4 µm
	SDS	4.0 µm 3.4 µm 3.2 µm	4.1 µm 3.7 µm 3.0 µm

Small differences are observed in comparison with results from Table 2: in particular the smallest size of 2.9 µm is not observed here. This difference is attributed to the fact that the PMT was placed at a slightly different height. Indeed, in the dissolved gas concentrations corresponding to saturation (and pulsed US hardly degas especially with a very short on-time) most active bubbles concentrate near the liquid surface [32], and the further from the surface, the less active bubbles are present. The probability of interaction and coalescence is therefore much higher at the top of the reactor. Measuring from the side close to the bottom of the reactor focuses on a zone with a lower density of bubbles. To illustrate this difference, Fig. 5SI presents bubble sizes obtained in Ar-saturated water when measuring with the PMT placed above the reactor, thus looking at the water surface: the obtained size distribution ranges from 4 to 7 µm, supporting the assumption mentioned above.

Fig. 5.

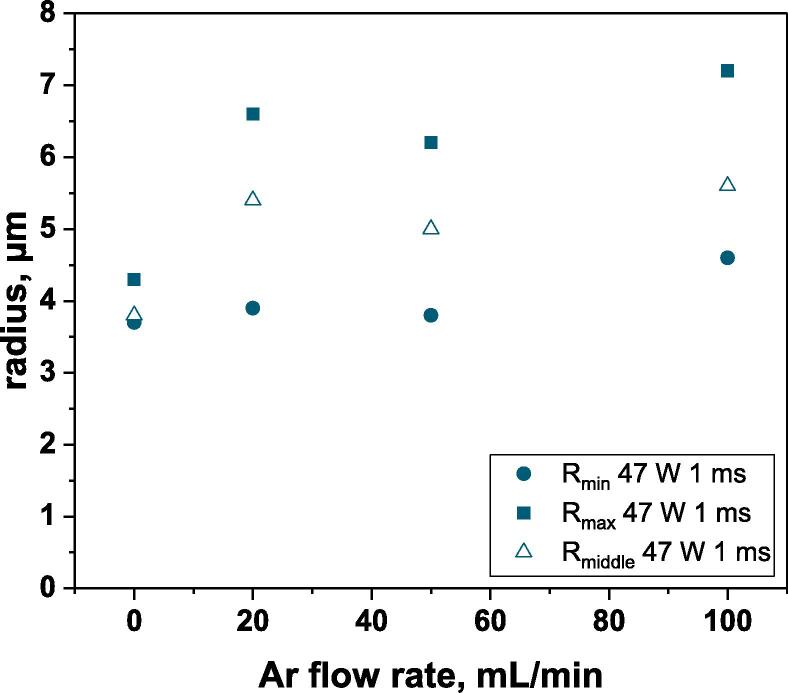
Bubble sizes vs. Ar flow rate in water; t_on = 1 ms, 362 kHz, 10 °C, P_ac = 47 W.

In spite of this difference, it can be noticed in Table 3 that as expected [20], [21], less coalescence is observed in the presence of SDS, allowing to observing the dissolution of ‘natural’ bubbles (and not only of coalesced bubbles). In the presence of SDS, a size around 3.0 µm is obtained in all cases, for both acoustic powers and t_on = 0.5 & 1 ms, contrary to the water case. This size is in perfect agreement with the 2.9 µm reported in Table 2. Interestingly some coalescence still happens with SDS and the dissolution of bigger (coalesced) bubbles is observed. Considering the minimum radius obtained with SDS, 3.0 µm, the other values can be derived from bubble coalescence: the coalescence of 2 3.0 µm bubbles leads to a radius of 3.0 × $\sqrt[3]{2}$ = 3.8 µm, that of 3 bubbles to 3.0 × $\sqrt[3]{3}$ = 4.3 µm.

3.4. Effect of a continuous gas flow

A previous study, on the impact of NaCl concentration on bubble sizes under a continuous gas (Ar, He) flow [23], showed that smaller bubble sizes were obtained compared to gas-saturated solutions. This difference was attributed to numerous cavitation nuclei being introduced by the gas flow, which modified the number of cavitation bubbles and their interactions. However, measurements were performed with an on-time of 4 ms, so that the size range may have been biased due to coalescence occurring during t_on. To further investigate the effect of a continuous gas flow on the bubble size, we compared bubble sizes obtained in the Ar-water system at different gas flow rates for the small on-time of 1 ms, P_ac = 47 W and a free water surface to limit coalescence. For the different tested gas flow rates, the evolution of the SL intensity during t_on shows a continuous increase that goes beyond the end of the US pulse (Fig. 4). No plateau is reached.

At t_off corresponding to the SL plateau (in the SL intensity vs. t_off plot), the reached SL intensity increases with the gas flow rate, indicating an increasing number of sonoluminescing bubbles, either due to the higher number of cavitation nuclei or to the more pronounced coalescence (growing bubbles to their active size). Such an impact is only valid for pulsed US, it cannot be extrapolated to steady-state sonication since continuous sonication modifies the dissolved gas content, in a way that depends on acoustic power and gas flow rate [33], [34], and since as seen above at sonication times longer than t_on = 1 ms, interactions and bubble coalescence do take place that modify the active bubble population.

Bubble sizes obtained for Ar flow rates of 0, 20, 50 and 100 mL/min are plotted in Fig. 5. When experimental conditions are chosen to limit coalescence (with t_on = 1 ms, a free water surface and a high P_ac) the presence of a gas flow clearly increases the determined bubble sizes, and in particular maximum radii, whatever the gas flow rate value. For instance, if a reference size of 2.9 µm is considered, maximum radii corresponding to the coalescence of 10–14 bubbles are obtained under a continuous gas flow. The minimum size remains close to the saturation case as long as the flow rate is not too high. A similar size range (from around 3.0 µm to 6 µm) was obtained previously [23] with t_on = 4 ms and an Ar flow rate of 67 mL/min, indicating that coalescence induced by the gas flow rate (during t_on and t_off) may be predominant compared to that during t_on. This observation cannot however be extrapolated to other gases or solutions, due to huge differences in dissolved gas concentrations and thus numbers of active bubbles.

4. Conclusion

While the theoretical ambient radius of SL active bubbles is expected to be determined by a limited number of parameters (like the US frequency, the liquid nature and temperature, the dissolved gas nature and concentration or the acoustic pressure), more parameters appear to impact its experimental determination and great care should be taken in choosing experimental conditions for it. Coalescence of bubbles is observed under pulsed US, both during the pulse off- and on-times. Increasing the on-time leads to an increase in the extent of coalescence, and consequently to the measurement of the dissolution time of coalesced bubbles instead of active bubbles. Also the formation of a standing-wave, due either to a low acoustic power or to the presence of a reflecting surface on the water one, enhances interactions between bubbles and coalescence. If such conditions are avoided (at higher acoustic power and in a free surface configuration), with a proper geometry of measurement (placing the PMT on the side of the reactor, close to its bottom, to focus on a zone of lower bubble density), and decreasing the on-time to a value as low as possible (of the order of 1 ms or less for Ar) measurement of the natural active bubble size can be achieved. It indicates an equilibrium radius around 2.9–3.0 µm for Ar-saturated water sonicated at 362 kHz, as was confirmed by measurements in the presence of the coalescence inhibiter SDS.

A continuous gas flow enhances coalescence during t_off. In conditions that otherwise limit coalescence, the measured bubble sizes increase with the Ar flow rate, indicating that the global bubble population is shifted towards higher sizes. It is noteworthy, however, that the determined minimum bubble sizes in the presence of a gas flow coincide with that obtained under saturation, indicating that the active bubbles would have a similar size in both cases, at least for the water-Ar system.

Funding

This work was supported by the program for scientific mobility of the French Embassy in Australia (833171 E, 2014) and by the University of Melbourne (PRC0988 UCAB, 2015).

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article: