Metabolite Structure Assignment Using in silico NMR Techniques.

Abstract

A major challenge for Metabolomic analysis is to obtain an unambiguous identification of the metabolites detected in a sample. Among metabolomics techniques, NMR spectroscopy is a sophisticated, powerful and generally applicable spectroscopic tool that can be used to ascertain the correct structure of newly isolated biogenic molecules. However, accurate structure prediction using computational NMR techniques depends on how much of the relevant conformational space of a particular compound is considered. It is intrinsically challenging to calculate NMR chemical shifts using high level DFT when the conformational space of a metabolite is extensive. In this work, we developed NMR chemical shift calculation protocols using a machine learning model in conjunction with standard DFT methods. The pipeline encompasses the following steps: (1) conformation generation using a force field (FF) based method, (2) filtering the FF generated conformations using the ASE-ANI machine learning model, (3) clustering of the optimized conformations based on structural similarity to identify chemically unique conformations, (4) DFT structural optimization of the unique conformations and (5) DFT NMR chemical shift calculation. This protocol can calculate the NMR chemical shifts of a set of molecules using any available combination of DFT theory, solvent model, and NMR-active nuclei, using both user-selected reference compounds and/or linear regression methods. Our protocol reduces the overall computational time by 2 orders of magnitude (see Figure 1) over methods that optimize the conformations using fully ab initio methods, while still producing good agreement with experimental observations. The complete protocol is designed in such a manner that makes the computation of chemical shifts tractable for a large number of conformationally flexible metabolites.

Graphical Abstract

INTRODUCTION

Metabolites are the intermediate or end products of metabolic reactions that occur within cells, through interactions with the microbiome, or through exposures to the environment and are often dysregulated with diseases such as cancer.^1–6 Metabolomics is an “omics” technology that investigates the structure and activity of biogenic small molecules or metabolites and attempts to relate their concentrations to specific phenotypes or disease.^7–11 It involves the measurement of endogenous and exogenous molecules, that are the substrates and products of a range of biological transformations. With the latest advances in high-throughput technologies, the capabilities of the metabolomics field has been markedly enhanced.^12–14 The measurement of metabolites provides fundamental insights into biochemical pathways. For example, metabolites associated with the human diet can serve as a diagnostic marker for a wide range of biological conditions.^15,16

Metabolomics can involve non-targeted screening where thousands of unknowns are profiled and the relative difference between two conditions is measured.^14,17–19 This non-targeted screening is useful in identifying new metabolites that can be present in a disease, specific genetic or environmental conditions, or in a newly engineered metabolic pathway. The primary drawback to non-targeted analysis is the challenge in confident identification of features and quantification of metabolites.

On the other hand, targeted analysis deals with a relatively small and specific number of known metabolites.^20,21 These metabolites are chemically characterized and biochemically annotated and have an hypothesized biological importance even before data acquisition is performed. A targeted study can only be performed if an authentic chemical standard of the metabolite is available. Quantification of the metabolite is performed through the use of internal standards to construct calibration curves for each metabolite under investigation. Semi-targeted methods fall in between untargeted and targeted approaches. This approach aims to quantify hundreds of metabolites whose chemical class is known before data acquisition.^8,22,23 In summary, targeted experiments provide deeper insights by examining a particular hypothesis because the absolute concentrations of the molecules is measured but they may miss important factors that a non-targeted study would capture.²⁰

Liquid chromatography-mass spectrometry (LC-MS) is very sensitive and the most common technology for metabolomics today, but challenges remain in compound identification.^14,24 Technology such as Fourier-transform-ion-cyclotron-resonance–mass-spectrometry (FTICR–MS)²⁵ and Orbitrap mass analyzers²⁶ can provide exceptionally high mass resolution to measure the empirical formula for thousands of metabolites in a sample. However, the empirical formula alone is not sufficient for the confident identification of a chemical structure, especially as the molecular weight increases. LC-MS/MS can be used to match reference databases for a more definitive match, but when a compound is not in a database, the identity of the unknown feature remains uncertain.

Nuclear Magnetic Resonance (NMR) spectroscopy provides a good complement to MS-based metabolomic methods.^10,27–31 Because of its ability to record atom-specific interactions, NMR is capable of providing sufficient information for the elucidation of the molecular structure of an unknown substance.^32,33 NMR technologies can be directly coupled through solid phase extraction to complement LC-MS data in unknown metabolites.^34,35 This is especially important in metabolomics research where experiments using ultra-sensitive mass spectroscopy instruments can detect differential mass signals, but in many cases even tandem MS approaches are unable to provide enough information for a de-novo characterization of a newly isolated metabolite.¹⁴

Although NMR and MS are complementary, they are still difficult to merge to fully leverage the information content available in both techniques. Brüschweiler and co-workers has developed a very promising approach towards this end called SUMMIT MS/NMR (Structure of Unknown Metabolomic Mixture components by MS/NMR).³⁶ The basic concept of SUMMIT is quite simple: First, NMR and high-resolution MS spectra are measured for the same metabolomic mixture. For a given unknown feature in the MS data, the empirical formula is determined through the isotopic fine structure. The ChemSpider³⁷ database is then used to enumerate all known chemical structures consistent with that empirical formula. The ChemSpider-derived structures are used to compute the NMR chemical shifts, which are then compared with the experimental NMR spectra. The overall SUMMIT concept is simple and powerful, but there are some major obstacles to practical implementation. As the molecular weight of the unknown feature increases, the numbers of possible structures increase dramatically and can reach several hundred (or more) candidate structures. The large number of candidate structures necessitates using a level of theory in computing NMR chemical shifts that may compromise the ability to make accurate comparisons. If methods can be improved to more rapidly use high-level and accurate computational methods of NMR chemical shifts, the implementation of SUMMIT-like approaches would be easier and more accurate.

To supplement the impressive array of experimental technologies used in metabolomics research researchers have been turning towards the potential of computational approaches to build a bridge between spectroscopic insights and molecular structure. Because of this promise in silico techniques have begun to have a significant impact on metabolomics studies.^38–44 Grimme et al. have developed QM based protocol to compute spin-spin coupled ¹H NMR spectra.⁴⁵ The protocol is based on four steps, (1) generation of a conformer/rotamer ensemble (CRE) using the fast tight-binding method GFN-xTB and a newly developed search algorithm, (2) computation of the relative free energies and (3) NMR parameters, and (4) solving the spin Hamiltonian. They achieved good agreement between computed and experimental of NMR parameters. But this method is currently limited to ¹H NMR spectra. The efficiency of a given in silico technique primarily depends on two factors: (a) a stream-lined computational workflow and (b) the available computational power to carry out the computational workflow. Of the available in silico techniques modern quantum mechanical (QM) methods have the ability to provide highly accurate results in terms of molecular structure and energetics, but it comes at a steep computational cost. Because of the steep costs involved it remains a challenge to develop an efficient method to accurately predict the structure of metabolites.^46,47 Force field (FF) based methods are computationally inexpensive, but their accuracy can vary depending on the parametrization. Machine Learning methods (ML) can achieve a balance between computation cost and accuracy, and this remains an active area of research.^48,49 Calculations of NMR chemical shifts have become quite accurate^50,51 and, in principle, have reached a point where they can be useful in many metabolomics applications. In our NMR based approach we developed a protocol that takes the best aspects of FF, ML and QM based methods linked together in a workflow in order to obtain accurate structural predictions of metabolites. To test the efficiency and reliability of our NMR calculation protocol, we studied 10 metabolites with NMR data from the BMRB⁵² data bank, with atom counts ranging from 20 to 65. The calculated chemical shift values are in good agreement with experiment, supporting the reliability of our protocol. The newly developed high-throughput workflow (relative to extant workflows) has the potential to calculate the NMR chemical shifts of a large numbers of metabolites and can be used as a valuable tool for structure assignment of unknown compounds.

METHODS

The approach we use has a number of distinct steps. First, we perform a conformational search to generate candidate structures followed by a QM based ML model for energy minimization. The remaining structures are then clustered to identify minimum energy regions and examples are taken from each cluster and energy minimized using computationally expensive standard QM methods. This last step involves NMR shift computation, Boltzmann weighting and comparison with experiment. The details for each of these steps are individually discussed below.

Conformation generation.

We generated the conformations of our metabolites using Schrodinger’s MacroModel tool.⁵³ MacroModel is force field-based and is a widely used conformation generation tool for small organic molecules.⁵⁴ The software allows the use of several molecular mechanics force fields and supports several methods of conformational searching. To generate the conformations, we used the Monte Carlo multiple minimum method, which is a stochastic approach that uses torsional sampling.⁵⁵ We used the default setting presented by MacroModel for the conformational search. An important setting in any conformational search is the energy window between a given conformation and the most stable conformer, which is set to 5.02 kcal mol⁻¹ in MacroModel. We did not explore multiple settings for the conformational search step. Other commercial or open source conformational search tools can be used, but we have not explored all the options in detail given the performance of the MacroModel option (vide infra).

Filtering the conformation.

The MacroModel generated conformations were then geometry optimized using the ASE_ANI machine learning model.^56,57 This model yields CCSD(T)/CBS accuracy for molecular properties but is literally billions of times faster than the standard CCSD(T)/CBS method. We further computed frequencies after a successful geometry optimization to confirm we obtained a local minimum with all nonimaginary frequencies.

Clustering.

From the ASE_ANI minimization step we did not obtain a greatly reduced set of unique energy minima (see Table 1), which we hypothesize has to do with errors in the gradients computed by this method which affects the energy minimization algorithm. However, from visual inspection of the resultant conformers we observed that ASE_ANI gave families of conformations which we could extract using clustering algorithms. Hence, we performed structural similarity based (RMSD) clustering using Schrodinger Maestro.⁵³ All the ASE_ANI optimized conformations were clustered by requesting 2 or more clusters until visually we clearly discriminated the obtained clusters (see Table 1 and Figure 4). Finally, one representative conformation from each cluster was then subjected to standard DFT geometry optimization.

Table 1.

BMRB ID, No. of atoms, No. of rotatable bonds, Force-field generated conformation, ANI optimized conformations, and No. of Cluster are reported.

No	Metabolites	BMRB ID	No. of atoms	No. of rotatable bonds	Conf. Nos. (FF)	ANI Optimized Conf. Nos.	Number of clusters
1	L- citrulline	bmse000032	25	6	171	171	15
2	O-succinyl-L-homoserine	bmse000058	28	8	501	485	25
3	4-hydroxyphenethyl-alcohol	bmse000173	20	4	32	30	5
4	N-acetyl-D-glucosamine	bmse000231	30	6	112	93	10
5	N-acetylneuraminic-acid	bmse000057	40	10	245	236	20
6	Salicylate	bmse000252	16	2	2	2	2
7	Kanamycin	bmse000201	69	17	207	207	20
8	Methyl-N-acetyl-alpha-D-glucosaminide	bmse000196	33	6	104	102	10
9	Pantothenate	bmse000287	32	8	380	378	25
10	Choline	bmse000285	21	3	7	7	7

Figure 4.

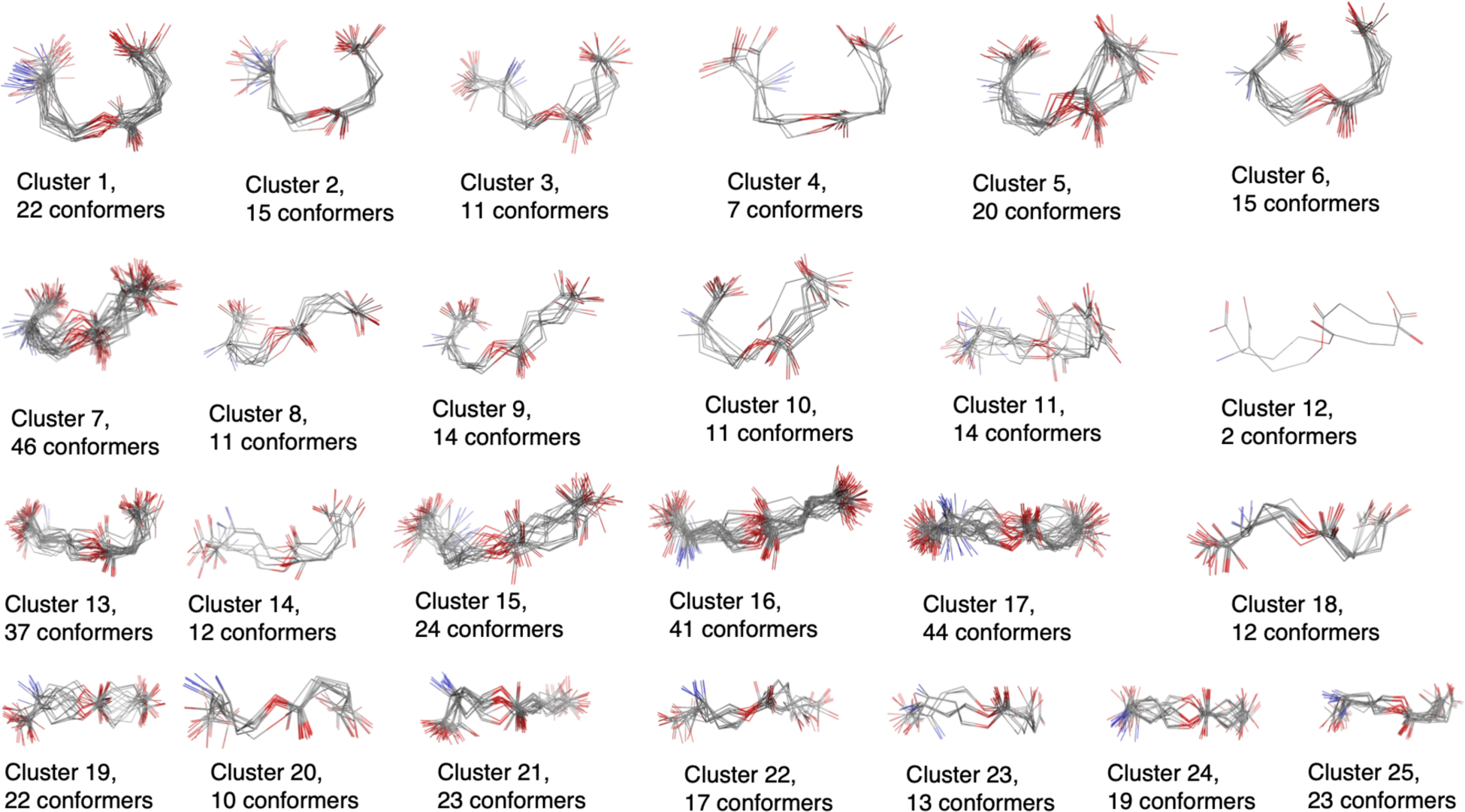
Clusters of O-succinyl-L-homoserine as example. A total of 485 ANI optimized conformers are clustered into 25 distinct regions.

QM Optimization.

In order to perform the necessary DFT geometry optimizations, parallel processing on a high performance computing (HPC) cluster was employed. Geometry optimization was performed for all the structurally distinct conformations obtained from our clustering analysis. The M06–2X DFT functional and the 6–31+G (d, p) basis set were used for geometry optimization.^58,59 We further checked for the absence of imaginary frequencies to confirm a local minima. All the calculations were performed using Gaussian 16.⁶⁰ The effect of solvation was evaluated implicitly using the integrated equation formalism polarized continuum model (IEFPCM).⁶¹ D₂O was chosen as the solvent since all the experimental NMR data we compared to were obtained in D₂O as solvent. Substrate solvation cavities were modeled by united-atomic radii (i.e UA0)⁶² for the geometry optimization/frequency calculation and individual atomic radii (i.e, Bondi).⁶³

NMR Chemical Shift and Boltzmann averaging.

Finally, we computed the ¹H and ¹³C NMR chemical shifts of all nuclei using the B3LYP functional and the 6–311G+(2d, p) basis set.⁶⁴ The NMR shielding tensor is calculated using the GIAO (gauge-independent (or including) atomic orbitals) method⁶⁵ implemented in Gaussian 16. The resultant shielding tensors were converted to referenced NMR chemical shifts using a linear regression scaling parameter as defined by equation 1

$$\delta =\frac{\sigma -\mathit{\text{ intercept }}}{\mathit{\text{ slope }}}$$ (1)

Where δ is the referenced chemical shift and σ is the computed NMR shielding tensor. The values of the scaling parameter (slope and intercept) were obtained from Tantilo et al.⁵⁰ The Boltzmann averaging is performed with all the computed chemical shifts using eq. 2.

$$\text{Percentage }(\text{mole fraction}){\text{of the i}}^{\text{th}}\text{component of n species}\text{in equilibrium }=\frac{e^{\left(-\frac{\Delta E_i}{RT}\right)}}{{{\sum }_{i=1}^{n}e}^{\left(-\frac{\Delta E_i}{RT}\right)}}$$ (2)

Where ΔE_i is the energy difference between the i^th conformer and the most stable conformer.

RESULTS AND DISCUSSION

Our computational workflow is illustrated in Figure 2. In this validation effort we examined 10 metabolites whose structures are given in Figure 3. The number of atoms ranged between 20–65 and the number of rotatable bonds ranged between 2 and 17 giving us a range of conformational flexibilities.

Figure 2.

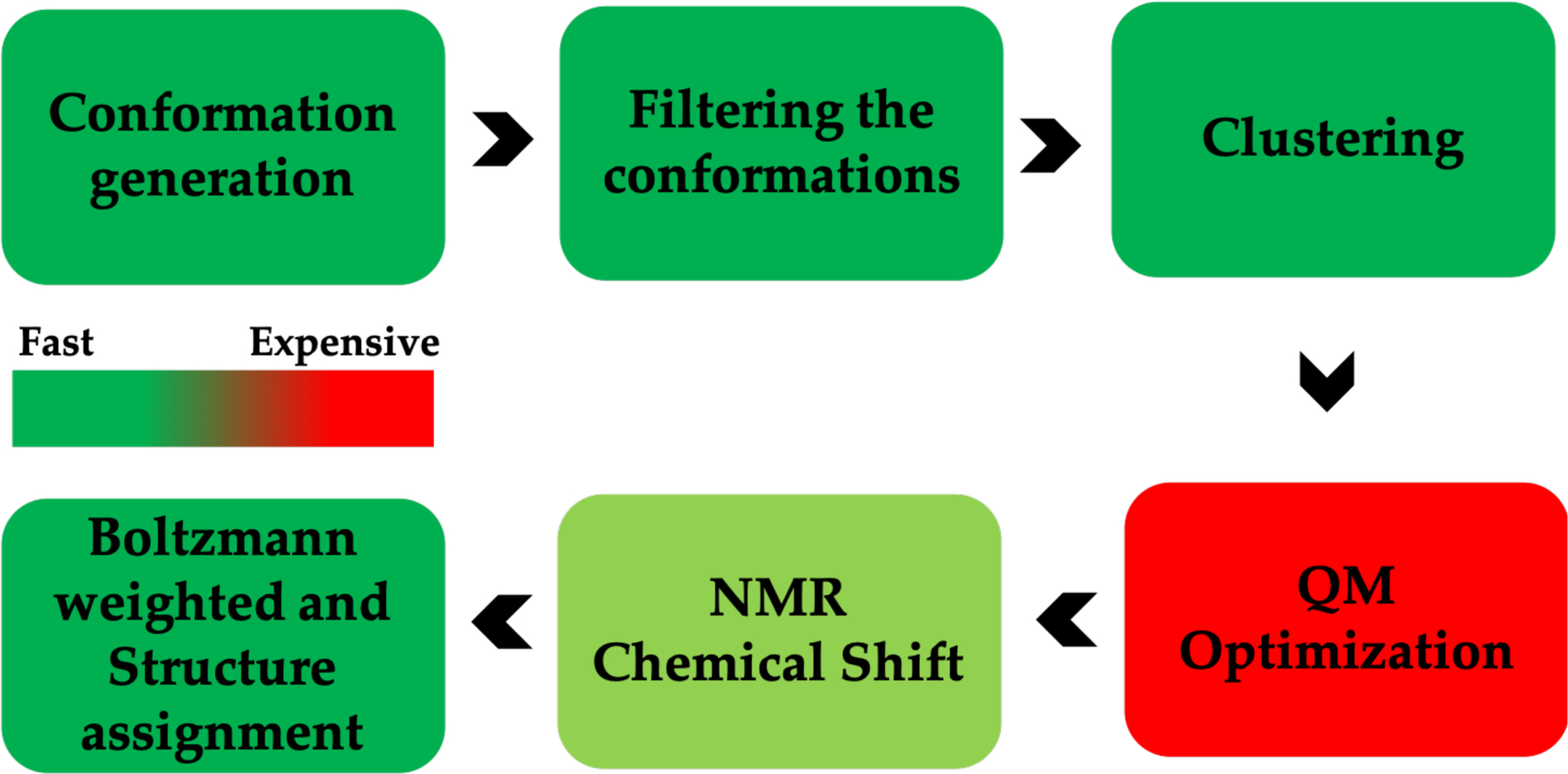
NMR Chemical shift calculation workflow.

Figure 3.

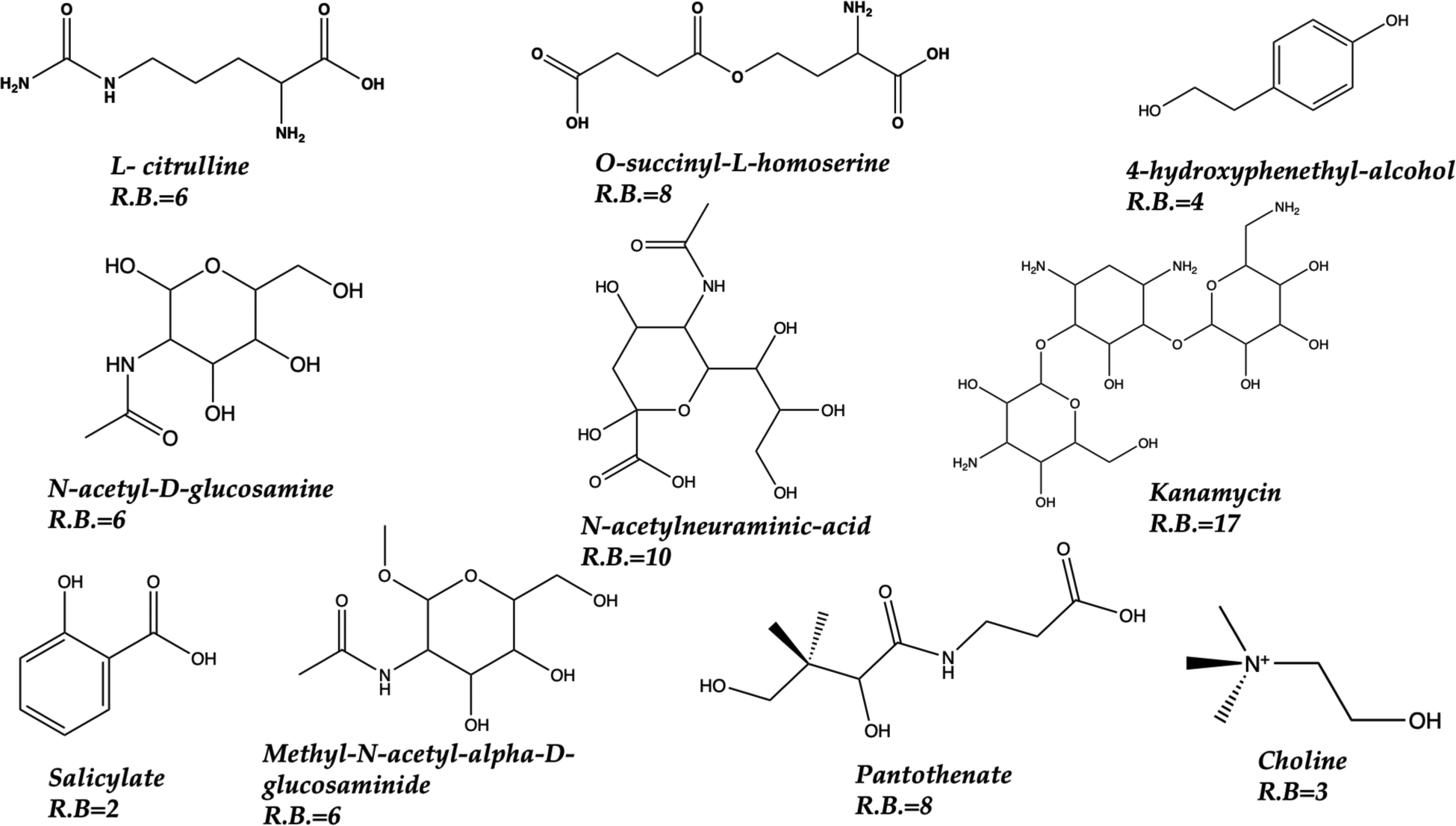
Ten metabolites explored herein. Atom counts between 20 to 65. The number of rotatable bonds (R.B) are given for each metabolite.

The total number of generated conformations for each metabolite are tabulated in Table 1. The number of conformers we obtained ranged from 2 for salicylate to 501 for O-succinyl-L-homoserine, with the latter serving as the main example we will illustrate herein (full details for the remaining 9 metabolites are given in the SI). Not surprisingly the number of conformers is approximately related to the number of rotatable bonds.

The conformers generated by MacroModel were then subjected to energy minimization by ASE_ANI. When using standard QM methods the computational expense is very high but the minimization step proved to be effective at reducing the number of observed true minima.^66,67 For example, in our work on ibuprofen seventy-four (74) conformers were generated, but after QM optimization only nine (9) true minima were observed.⁶⁸ We have observed this behavior multiple times and were expecting ASE_ANI to perform similarly.⁶⁹ However, ASE_ANI, even when using very tight optimization criteria, was unable to hone in on just the unique subset of true minima. This may be a weakness in the gradients computed using ASE_ANI and warrants further analysis. This issue can be seen again in Table 1 and using O-succinyl-L-homoserine as an example 501 MacroModel conformations are only reduced to 485 structures with slightly different geometries and energies. As a side note, ASE_ANI simply discards conformations with imaginary frequencies during geometry optimization followed by frequency calculation. The number of structurally distinct conformations for each of the metabolites is shown in the last column of Table 1.

While the ASE_ANI step greatly accelerates QM calculations, it was less satisfactory in reducing the conformational space. However, we ran clustering calculations and found that while ANI didn’t find all the unique minima cleanly it did strongly cluster structures into distinct regions as shown in Figure 4 for methyl-N-acetyl-alpha-D-glucosaminide. In this case we reduced ~100 conformers to a set of 10 unique conformers on which we could subsequently run full QM energy minimization calculations. This reduction in computational effort is very substantial making these calculations much more tractable. In each case we ran a number of clustering trials where we requested that 2–25 clusters be generated followed by a visual inspection to determine if we had generated clusters that satisfactorily binned unique conformers. While this step performed well, more automation is needed to reduce human inspection time and intrinsic bias.

From the ASE_ANI clustering we selected a representative conformer from each cluster and subjected it to full QM energy minimization and NMR chemical shift calculation. Again, using O-succinyl-L-homoserine as our example, the 485 ANI structures, yielded 25 unique clusters which gave 25 unique conformations for NMR shift calculations. The results for the remaining 9 systems can be found in Table 1.

The Boltzmann averaging computes the equilibrium mole fraction of each conformation in solution. We have computed ¹H and ¹³C NMR chemical shifts using equation 1 for all nuclei and referenced it to TMS using a linear regression method. Values of scaling parameters (slope and intercept) were taken from Tantilo et. al (see Table S1).⁵⁷ The Boltzmann averaging results for O-succinyl-L-homoserine are tabulated in Table 2, and for the remaining 9 the results are summarized in the SI (Table S2–S10). The computed ¹H and ¹³C NMR chemical shifts and the experimental values for O-succinyl-L-homoserine are reported in Tables 3 and 4. The NMR chemical shift values of the other metabolites are shown in the SI (Table S11–S28). For the Boltzmann averaging of all the unique conformations and NMR chemical shift computation for ¹H and ¹³C, we used the python-based script of Willoughby et al. which was published in 2014.³⁶ Williams et al. in 2019 published an article revealing a “bug” in the Willoughby Scripts when calculating NMR chemical shifts.⁷⁰ The authors showed that some newer personal computer operating systems may randomly sort the Gaussian optimization/frequency and NMR output files of the original protocol. Such mis-sorting would lead to inaccurate determination of the conformationally averaged (i.e., Boltzmann-weighted) shielding tensors. Following this article, in 2020, Willoughby et al. published an Addendum to ensure that the original protocol is (and remains) compatible with all operating systems and they provided an updated script.⁷¹ Before using the original Willoughby script (2014), we validated the script using cis- and trans-3-methylcyclo-hexanol by the author and confirmed that the scripts work in our hands. We subsequently validated using the new script and obtained identical results with the 2014 script. It is important to realize that scaling parameters obtained from the linear regression method are structure independent and method dependent. These values are unique to this specific functional and basis set combination, but they are independent of the structure under study. In other words, scaling parameters can be used for any of unknown metabolite to calculate NMR chemical shifts using the B3LYP/6311G+(2d, p) //M06–2X/6–31G+ (d, p) method. However, this protocol is not restricted to only using this particular DFT model. Users can calculate NMR chemical shifts using any QM method provided the reference scaling data (e.g., TMS) are obtained from the same QM method.⁷²

Table 2.

Relative energies, Boltzmann factor and Equilibrium mole fraction of all structurally distinct conformations of O-succinyl-L-homoserine.

Conf. No.	Relative energy (kcal)	Boltzmann factor	Eq. mole fraction (%)
1	1.98	0.035	1.90
2	2.25	0.022	1.21
3	2.88	0.008	0.41
4	3.15	0.005	0.26
5	3.23	0.004	0.23
6	4.93	0.000	0.01
7	4.80	0.000	0.02
8	0.00	1.000	53.84
9	1.21	0.129	6.93
10	2.48	0.015	0.82
11	1.05	0.169	9.08
12	1.93	0.039	2.08
13	3.15	0.005	0.26
14	1.63	0.064	3.45
15	1.22	0.126	6.80
16	3.82	0.002	0.08
17	3.10	0.005	0.29
18	3.31	0.004	0.20
19	2.69	0.011	0.57
20	3.91	0.001	0.07
21	2.14	0.027	1.45
22	1.03	0.175	9.41
23	3.27	0.004	0.21
24	3.69	0.002	0.11
25	3.04	0.006	0.32

Table 3.

Computed and available experimental ¹H NMR shifts for O-succinyl-L-homoserine

Atom No.	Chemical Shift (ppm)	Exp. Chemical Shift (ppm)
H16	2.739	2.611
H17	2.710	2.469
H18	2.738	2.611
H19	2.664	2.469
H20	2.135	2.240
H21	1.827	2.240
H22	3.994	4.262
H23	4.219	4.262
H24	3.606	3.842
H25	1.373	-
H26	1.237	-
H27	6.638	-
H28	6.942	-

Table 4.

Computed and available experimental ¹³C NMR chemical shifts for O-succinyl-L-homoserine.

Atom No.	Chemical Shift (ppm)	Exp. Chemical Shift (ppm)
C1	30.039	33.200
C2	31.209	34.644
C3	33.214	32.044
C4	63.174	64.459
C5	52.461	55.519
C6	173.748	-
C7	172.761	-
C8	177.029	-

To evaluate quantitively the goodness of fit of the NMR chemical shifts computed with our protocol, we have calculated mean absolute error (MAE), which is tabulated in Tables 5 and 6. MAE is the comparison of the computed and experimental data sets using equation 3.

$$MAE=\left|\Delta {\delta }_{avg}\right|=\frac{1}{N}\sum _{i=1}^N\left|{\delta }_i^{\mathit{\text{comp}}}-{\delta }_i^{exp}\right|$$ (3)

Where ${\delta }_i^{\mathit{\text{comp}}}$ is the computed NMR chemical shift of the i^th nucleus and ${\delta }_i^{exp}$ is the experimental NMR chemical shift of the same nucleus. Table 6 focusses on the ¹H and ¹³C shifts of O-succinyl-L-homo serine. This metabolite has 25 structurally distinct conformations. To identify the structure ensemble that gives the best accounting of the experimental values, we performed three sets of calculations: (1) MAE with all 25 conformers, (2) MAE with the best 5 (i.e., higher concentration in solution) conformations and (3) MAE with the one conformation with the highest mole faction (53.84%) in solution. The MAE values of the ¹H NMR chemical shifts for sets 1, 2 and 3 are 0.195, 0.209, and 0.250, respectively. Similarly, the MAE values for the ¹³C NMR chemical shift of sets 1, 2 and 3 are 2.422, 4.009 and 3.502 respectively. Set 1, including all structurally distinct conformations yields the best fit (lowest MAE) with experiment. Hence, from the MAE data, we conclude that the high energy conformations has a subtle impact on the computed NMR chemical shifts and in order to obtain high-resolution predictions the entire ensemble is essential.

Table 5.

MAE values of the ¹H and ¹³C NMR chemical shifts.

No.	Metabolites	MAE
		1H	13C
1	L- citrulline	0.139	3.889
2	O-succinyl-L-homoserine	0.195	2.422
3	4-hydroxyphenethyl-alcohol	0.060	4.190
4	N-acetyl-D-glucosamine	0.164	2.967
5	N-acetylneuraminic-acid	0.181	2.596
6	Salicylate	0.060	4.138
7	Kanamycin	0.280	3.991
8	Methyl-N-acetyl-alpha-D-glucosaminide	0.436	3.532
9	Pantothenate	0.139	2.862
10	Choline	0.241	4.080

Table 6.

MAE values of the ¹H and ¹³C NMR chemical shifts for O-succinyl-L-homoserine. MAE is calculated when different numbers of conformations are considered.

Metabolite	No. of conformation	MAE
		1H	13C
O-succinyl-L-homoserine.	25	0.195	2.422
	5	0.209	4.009
	1	0.250	3.502

Importantly, the MAE values (¹H and ¹³C) have errors within ±1 and ± 5 ppm, respectively confirming the good agreement between theory and experiment using our protocol.

Hence, one can readily calculate the NMR chemical shifts using this protocol and utilize it to assign the structure of an unknown metabolite.

We have also plotted the differences between the experimental and computed ¹H and ¹³C chemical shifts for O-succinyl-L-homoserine in Figure 5 and the remaining 9 systems in the SI (Figures S1–S9). The Δδ (ppm) values for each nucleus of a candidate metabolite indicates the agreement between theory and experiment. Overall, the agreement is excellent with no obvious trends in terms of which nuclear environments yield larger errors in our calculations.

Figure 5.

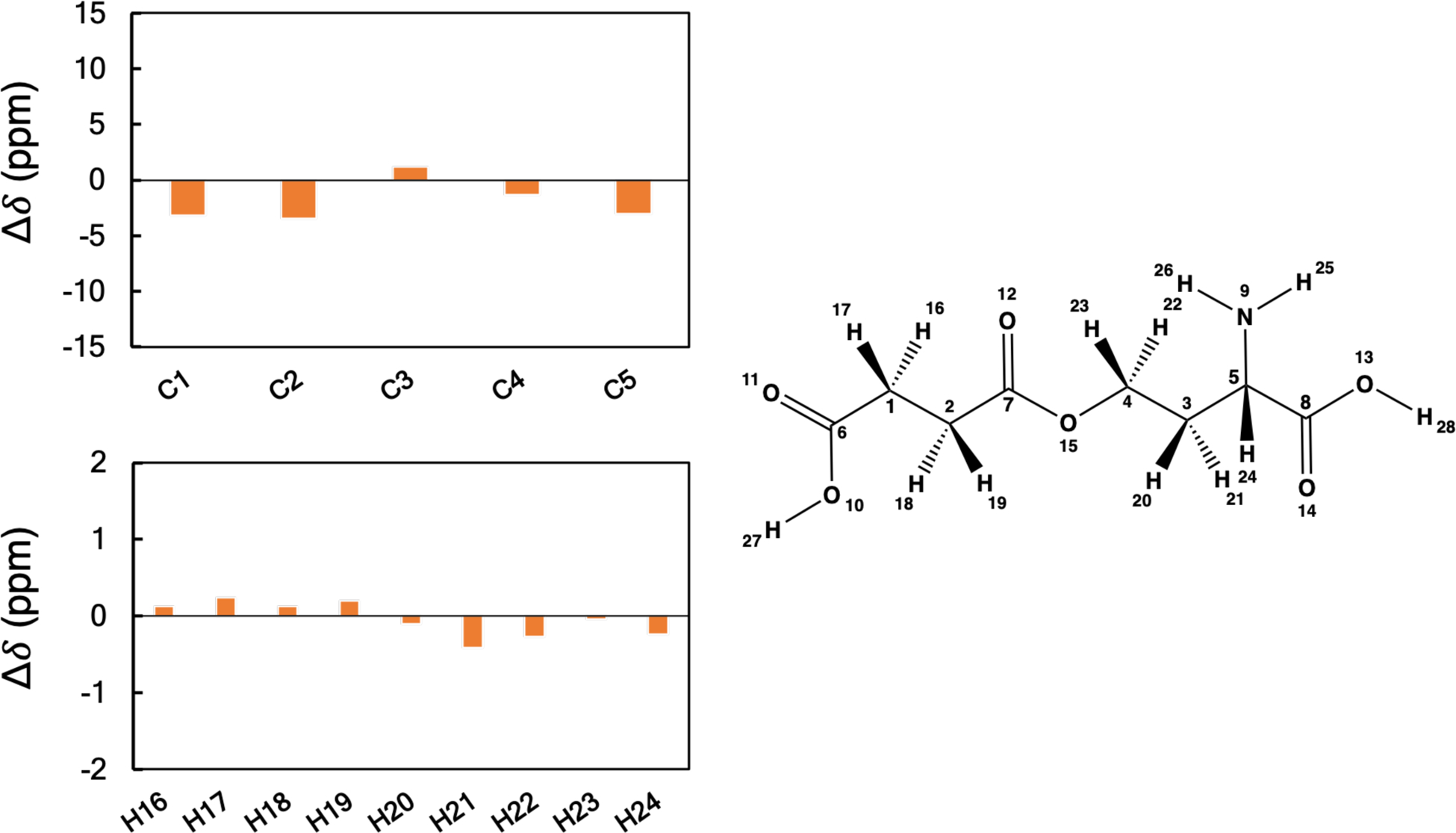
Plots of the differences between the calculated and experimental ¹H and ¹³C NMR chemical shifts of O-succinyl-L-homoserine. Shielding constants were computed at the B3LYP/6311G+(2d, p) level of theory and converted to linear scaled reference chemical shifts. Values of chemical shift differences are given in ppm.

pH effect on NMR chemical shift.

To investigate the effect of pH, we have performed NMR chemical shift calculations on the ionic states of the molecule in the solvent, D₂O. Among the 10 chosen metabolites, two metabolites (L-citrulline and O-succinyl-L-homoserine) exists in zwitterionic forms and another two metabolites (N-acetylneuraminic-acid and Salicylate) exists in anionic forms. To compute NMR chemical shifts of the ionic form of the metabolites, we have followed the same protocols as neutral metabolites. First, we use MacroMolecule to generate representative conformations followed by ASE_ANI geometry optimization and the clustering of ASE_ANI geometries (see Table S29). In the case of ionic systems, the total number of generated conformations are less than those found for the neutral systems. The reason for the reduction in the number of conformations has to do with strong intramolecular ionic interactions.⁷³ Finally, each representative geometry of the resulting clusters undergoes DFT geometry optimization followed by NMR chemical shift calculations. The results for O-succinyl-L-homoserine, L-citrulline, N-acetylneuraminic-acid and Salicylate are given in Tables S30 – S40. We have also plotted the differences between the experimental and computed ¹H and ¹³C chemical shifts (Δδ) for O-succinyl-L-homoserine ion, L-citrulline ion, N-acetylneuraminic-acid (anion) and Salicylate (anion) in Figures S10–S13, respectively.

We have further computed MAE values using eq. 3 and the results are given in Table S41. ¹H and ¹³C MAE value of O-succinyl-L-homoserine (zwitterionic form) is 0.185 and 1.997 respectively, which is lower by 0.01 and 0.425 respectively relative to its neutral state. A similar observation for L-citrulline was observed (see Tables 5 and S41). The MAE values for L-citrulline ion is lower by 0.051 and 0.265 for ¹H and ¹³C respectively. In the case of the anion of N-acetylneuraminic-acid the MAE for the ¹H chemical shift is lower by 0.014 but ¹³C values increased by 1.040 relative to the neutral state. We observed larger MAE (0.111 and 0.241 of ¹H and ¹³C respectively) values for the Salicylate ion relative to its neutral state. Overall, we can perform similar calculations on charged and neutral states of molecules, but for the molecules studied herein the effect on the computed results relative to experiment is relatively small.

CONCLUSIONS

In this work, we have developed a protocol to accurately predict NMR chemical shifts (both ¹H and ¹³C) which can then be used to assign the structure of an unknown metabolite. The pipeline of our workflow utilizes force field, machine learning QM and QM methods to achieve the best results. Including the ML QM model and the clustering method in this proposed protocol minimize the computational cost significantly and maximizes the performance. Ultimately, quantitative prediction of NMR chemical shift for any arbitrary metabolites requires high accuracy in all aspects of the underlying physics. Our effort is a step in this direction and the obtained NMR chemical shifts are very accurate with respect to experiment. Moreover, our protocol strikes an excellent balance between accuracy and computational cost. We are continuing to further explore, refine and validate our workflow to further establish its use as a structure assignment tool for unknown metabolites. Because of the computational efficiency, accuracy and reliability, we anticipate that this protocol has the potential to be applied to a large set of unknown metabolites facilitating the structural assignment of metabolites.

Figure 1.

The overall computational time to get NMR chemical shift data without using ML tools (Red) and using our protocol (Green). The bottleneck previous protocols of NMR calculation is the DFT geometry optimization of all conformations, which is significantly reduced applying the ANI QM ML model and clustering method in our protocols. O-succinyl-L-homoserine is considered as example. * No ML indicates a methodology that does not use ML approaches to accelerate the slow QM geometry optimization step.