The Implications of Using Lagged and Baseline Exposure Terms in Longitudinal Causal and Regression Models

Abstract

There are now many published applications of causal (structural) models for estimating effects of time-varying exposures in the presence of confounding by earlier exposures and confounders affected by earlier exposures. Results from these models can be highly sensitive to inclusion of lagged and baseline exposure terms for different visits. This sensitivity is often overlooked in practice; moreover, results from these models are not directly comparable to results from conventional time-dependent regression models, because the latter do not estimate the same causal parameter even when no bias is present. We thus explore the implications of including lagged and baseline exposure terms in causal and regression models, using a public data set (Caerphilly Heart Disease Study in the United Kingdom, 1979–1998) relating smoking to cardiovascular outcomes.

The aim of many longitudinal studies is the estimation of the causal effects of time-varying exposures such as treatment duration, adherence to screening programs, and smoking status. There might also be time-varying confounders that should be adjusted for in the analysis. Coefficients in conventional regression models for longitudinal data (such as time-dependent Cox regression and generalized estimating equation (GEE) regression for correlated outcomes) might fail to have a useful causal interpretation even in the absence of uncontrolled confounding by covariates if earlier exposures or outcomes confound later exposures or if there are confounders affected by earlier exposures (1–7). Several causal (structural) models are available for the estimation of the effect of time-varying exposure that can appropriately adjust for time-varying confounders (1–8), and there are now many published applications of these models (9–16).

All these models could include baseline and lagged exposure terms from different visits to capture the target effect and to adjust for early exposure. The results from these causal models in longitudinal data can be highly sensitive to inclusion of these terms, yet this sensitivity is often overlooked in practice. Moreover, the effect of switching to explicitly causal models is sometimes misstated in the specialized literature by comparing causal and conventional regression methods that estimate different effects when no bias is present. We explored the implications of including baseline and lagged exposure terms in the causal and regression models in the longitudinal data setting using a public data set relating smoking to cardiovascular outcomes.

DATA, NOTATION, CAUSAL DIAGRAM, AND MODELS

We used the public Caerphilly Heart Disease Study (United Kingdom) data set to estimate the total effect of smoking on the occurrence of either a myocardial infarction or death from coronary heart disease. Participants (all of whom were men) were recruited between 1979 and 1983 (visit 0), when they were aged 44–60 years (9). Further examinations took place during 1984–1988 (visit 1), 1989–1993 (visit 2), and 1993–1997 (visit 3). All subjects were followed until the end of 1998. To adjust for lagged confounders, a total of 1,756 subjects who had complete data at visits 0 and 1 were included in our analysis, so the baseline visit in our analysis was visit 1. For simplicity, we will ignore the slight censoring due to loss-to-follow-up and competing risks.

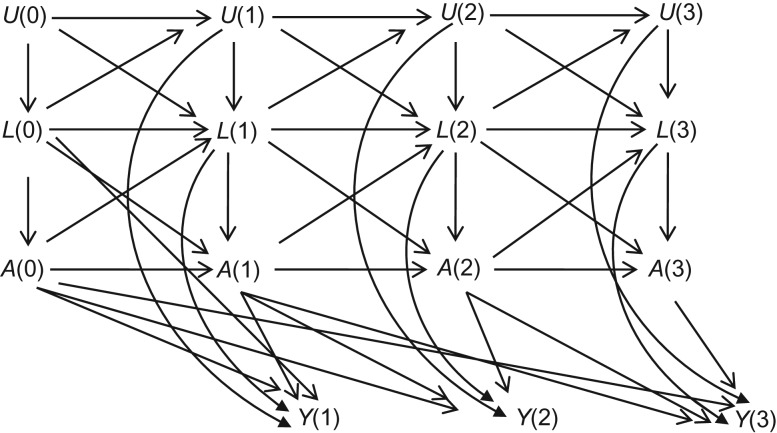
The causal diagram in Figure 1 represents the assumed causal structure for the study population (17–20). In this graph, A(k) and Y(k) denote smoking and outcome (i.e., myocardial infarction or death from coronary heart disease) at visit k. L(k) corresponds to a vector of measured time-varying potential confounders at visit k including previous reported heart attack, gout, high blood pressure, and diabetes, high fibrinogen (above the 75th percentile), high cholesterol (above the 75th percentile), high systolic blood pressure (≥140 mm Hg), high diastolic blood pressure (≥90 mm Hg), obesity (body mass index, calculated as weight (kg)/height (m)² of ≥30), and underweight (body mass index <20) indicators. L(1) includes age at visit 1 as well.

Figure 1.

Causal diagram representing the assumed causal structure for a study population: A is the exposure, L is the set of measured confounders, U is the set of unmeasured risk factors, and Y is the outcome. The numbers represent visits over time.

To simplify descriptions we will assume there are no perfect cancellations of effects or biases (“faithfulness”) (17). Then the absence of arrows from U(k) to A(k) and A(k + 1) in Figure 1 represents the (untestable) assumption of no uncontrolled confounding for exposure histories, given data on L(k). To simplify the graphs, we have omitted the arrows from L(0) to L(2), U(0) to L(2), A(0) to L(2), L(0) to A(2), L(0) to Y(2), etc. We use overbars to indicate the history of time-varying variables through visit k(e.g., $\overline{L}(k)=[L(0),L(1),\dots L(k)]$).

The arrows from L(k − 1) and L(k) to A(k) in Figure 1 suggest that {L(k), L(k − 1)} are time-varying confounders and should be adjusted for in the analysis. The standard method to adjust for time-varying confounding due to L(k) or L(k − 1) is to condition on them in a regression model. This method might lead to biased estimates: Conditioning on L(k) in Figure 1 can create biasing paths and block the targeted causal paths. For example, although conditioning on L(2) blocks the backdoor path A(2) ← L(2) → Y(2), it also introduces 2 sources of bias. First, conditioning on L(2) produces a spurious association between A(1) and Y(2), because L(2) is a collider on the path U(1) → L(2) ← A(1). This bias would occur whenever a component of time-varying confounders L(k) is affected by the exposure A(k − 1) (or shares common causes with A(k − 1)) as well as a component of unmeasured causal risk factors U(k − 1), even under the null hypothesis of no direct, indirect, or overall effect of the exposure on the outcome. Second, conditioning on L(2) creates overadjustment bias by blocking the causal path A(1) → L(2) → Y(2). This bias would occur whenever a component of time-varying confounders L(k) is affected by prior exposure A(k − 1).

We assume that the value of A(k) is determined immediately upon measuring L(k), so the visit times are the only times of potential exposure change, and A(k) represents smoking in the interval from visit k up to (but excluding at) visit k + 1. To obtain consistent effect estimates, we additionally require no measurement error for all variables in Figure 1. While likely not true in practice, we ignore measurement error to focus our arguments on issues related to lagging/modeling.

Given that the follow-up starts from visit 1, the goal of our analysis is estimating the effect of {A(1) = 1, A(2) = 1, A(3) = 1} versus {A(1) = 0, A(2) = 0, A(3) = 0}. From Figure 1, the minimally sufficient adjustment set for this effect estimation is {A(0), L(0), L(k), L(k − 1)} for k = 1, 2, 3. In particular, prebaseline treatment A(0) acts as confounder for later treatments and should be adjusted for in the analysis. Note that both A(0) and L(0) have arrows into later treatments and outcomes, but as mentioned above for visual simplicity, some of these arrows are not shown. Also Figure 1 assumes that only A(k − 1) and A(k) affects Y(k) for k = 1, 2, 3, as we will use in our causal and conventional models, but other specifications are possible.

In calculating time-specific hazard ratios as in the Cox model, the outcome at each time is conditioned on those who survived past earlier times. This can lead to bias in hazard ratios (including crossing hazard ratios), because it makes the frailty variable U in Figure 1 a confounder for the exposure effect (21). Here we might ignore this issue, as well as noncollapsibility issues for hazard ratios, as would be the case if, over the study period, U had a negligible effect on exposure or outcome, and exposure had a negligible effect on population size (22, 23).

We used 3 methods to estimate the causal effect of smoking on the occurrence of either a myocardial infarction or death from coronary heart disease: 1) stabilized inverse-probability-of-treatment weighted (SIPTW) estimation of a marginal structural model (MSM) (2, 4, 5), 2) g-estimation of a structural accelerated failure time model (SAFTM) (1), and 3) partial-likelihood estimation of a time-dependent Cox model (24), as explained below. We performed all of the statistical analyses with Stata, version 13 (StataCorp LLC, College Station, Texas), and R, version 3.5.1 (R Foundation for Statistical Computing, Vienna, Austria).

We fitted the following marginal structural Cox proportional hazards model (Cox MSM):

$$\begin{array}{c}{\mathrm{\lambda }}_{T\overline{a}}(t)={\mathrm{\lambda }}_{T\overline{0}}(t)\exp ({\mathrm{\beta }}_{1}a(k)+{\mathrm{\beta }}_{2}a(k-1)+{\mathrm{\beta }}_{3}age\hfill \\ +{\mathrm{\beta }}_{4}a(0)+{\mathrm{\beta }\prime }_{5}L(\mathrm{0})),\hfill \end{array}$$

where ${\mathrm{\lambda }}_{T\overline{a}}(t)$ denotes the hazard at time t among subjects with baseline covariates a(0) and L(0) and age in the source population had, possibly contrary to the fact, they followed the smoking history ${\overline{a}}_k=(a_1,\dots ,a_k)$ and k is the latest visit before time t. Our MSM assumes that current and lagged exposure terms a(k) and a(k − 1) are sufficient to capture the total effect of exposure. The MSM adjusts for confounding by early exposure by including baseline exposure a(0). Note that for the first visit (k = 1), lagged and baseline exposures coincide so there would be no adjustment for early confounding by the exposure in that visit.

Assuming that our MSM is correct, exp(β₁ + β₂) has a causal interpretation as the ratio of the outcome hazard rate at any time t had all subjects smoked continuously during the study follow-up compared with the hazard rate at that time had all subjects never smoked. To see the effect of confounding by baseline exposure as well as exposure lagging in defining the target effect, we also fitted 3 simpler MSMs that omit lagged exposure A(k − 1) or the baseline exposure A(0) or both from the MSM mentioned above.

To estimate the parameters of our MSM, we fit the following pooled logistic model treating each person-visit as an observation:

$$\begin{array}{c}\mathrm{logit}(\mathrm{Pr}(Y(k)=1))={\mathrm{\gamma }}_{0}t+{\mathrm{\gamma }}_{1}A(k)+{\mathrm{\gamma }}_{2}A(k-1)\hfill \\ +{\mathrm{\gamma }}_{3}age+{\mathrm{\gamma }}_{4}A(0)+{\mathrm{\gamma }\prime }_{5}L(\mathrm{0})\hfill \end{array}$$

This model was fitted using an ordinary maximum-likelihood logistic regression program with the following SIPTWs for efficiency reasons (4, 5, 13, 25):

$${SW}_i(k)=\prod _{m=1}^k\frac{\begin{array}{c}\mathrm{Pr}[A(m)=a_{i}m)|\overline{A}(m-1)\hfill \\ ={\overline{a}}_i(m-1),L(0)=l_i(0)]\hfill \end{array}}{\begin{array}{c}\mathrm{Pr}[A(m)=a_i(m)|\overline{A}(m-1)\hfill \\ ={\overline{a}}_i(m-1),\overline{L}(m)=\overline{l_i}(m)]\hfill \end{array}}.$$

Odds ratios from this weighted pooled logistic model approximate rate ratios from the Cox model within 5% or so when the risk of events is less than 10% per person-visit interval (26).

The exposure probabilities in the denominator of SW_i(k) were estimated using the following pooled logistic regression:

$$\begin{array}{c}\mathrm{logit}(\mathrm{Pr}(A(k)=1))={\mathrm{\omega }}_{0}t+{\mathrm{\omega }}_{1}A(k-1)+{\mathrm{\omega }\prime }_{2}L(k)\hfill \\ +{\mathrm{\omega }\prime }_{3}L(k-1)+{\mathrm{\omega }}_{4}age\hfill \\ +{\mathrm{\omega }}_{5}A(0)+{\mathrm{\omega }\prime }_{6}L(\mathrm{0})\hfill \end{array}$$

The exposure probabilities in the numerator of SW_i(k) were estimated by fitting the same model after dropping the time-varying covariates L(k) and L(k − 1).

Assuming a well-defined intervention, no uncontrolled confounding (as in Figure 1), positivity (27), and correct specification of the pooled logistic regression models for the denominator of SW_i(k) and for the outcome, the weighted pseudolikelihood estimates of γ₁ and γ₂ generated by using a maximum-likelihood program to fit the logistic MSM will be consistent for the causal parameters of interest β₁ and β₂ of our Cox MSM (apart from the aforementioned difference between odds and hazard ratios). Because the use of weights induces within-subject correlation, we used a sandwich variance estimator with clustering by subject to obtain conservative confidence intervals for our SIPTW estimator.

We fitted a SAFTM in which the (possibly counterfactual) survival time under no smoking during the follow-up, T_i, equals the weighted sum of time spent in a given smoking status:

$$T_i=\sum _{k=1}^3\exp [{\mathrm{\psi }}_1^{⁎}{A}_i\left(k\right)+{\mathrm{\psi }}_2^{⁎}A\left(k-1\right)]\Delta t(k),$$

where Δt(k) is the time between visit k and the earliest of the next visit, an outcome event, or the end of 1998. This sum is just the observed survival time if ψ₁* = ψ₂* = 0 or all the A_i(k) are 0. Furthermore, the model says that always smoking changes survival time by a factor of exp(−ψ₁*–ψ₂*) compared with never smoking.

The asterisk on ψ denotes that this is the true but unknown value of the effect parameter. While we do not know the true value of ψ, we do know that, in the absence of confounding, selection, and measurement bias, if we set both ψ₁ and ψ₂ to their true values, the exposure at each time will be independent of the potential outcomes. This forms the basis for g-estimation. To implement g-estimation, we define a grid of values $\{{\tilde{\mathrm{\psi }}}_1,{\tilde{\mathrm{\psi }}}_2\}\equiv \left\{\left(-1,-1\right),\left(-1,-0.975\right),\dots ,\left(0.975,1\right),(1,1)\right\}$,which we use to index a set of models

$$T_i\left(\tilde{\mathrm{\psi }}\right)=\sum _{k=1}^3\exp [{\tilde{\mathrm{\psi }}}_1{A}_i\left(k\right)+{\tilde{\mathrm{\psi }}}_2{A}_i\left(k-1\right)]\mathrm{\Delta }t(k),$$

so that by our model $T_i\left(\tilde{\mathrm{\psi }}\right)=T_i$ if $\tilde{\mathrm{\psi }}={\mathrm{\psi }}^{*}$. G-estimation searches for the value of $\tilde{\mathrm{\psi }}$ that makes the unexposed potential survival time $T_i\left(\tilde{\mathrm{\psi }}\right)$ independent of the exposure given previous treatment and covariate history (sequential exposure-assignment ignorability); this is a sufficient condition for no confounding under the above structural model. As usual in the g-estimation literature to date, the exposure-potential outcome relation is modeled with the following pooled logistic regression:

$$\begin{array}{l}\mathrm{logit}(\mathrm{Pr}(A(k)=1))={\mathrm{\alpha }}_{0}t+{\mathrm{\alpha }}_{1}A(k-1)+{\mathrm{\alpha }\prime }_{2}L(k)\\ +{\mathrm{\alpha }\prime }_{3}L(k-1)+{\mathrm{\alpha }}_{4}age\hfill \\ +{\mathrm{\alpha }}_{5}A(0)+{\mathrm{\alpha }\prime }_{6}L(\mathrm{0})+{\mathrm{\alpha }}_7{T}_i(\mathrm{\psi }).\hfill \end{array}$$

Our g-estimate ${\hat{\mathrm{\psi }}}^{*}$ of ψ* is the value of $\tilde{\mathrm{\psi }}$ for which test of hypothesis of α₇ = 0 (no association of exposure with T_i(ψ) under the model) has a 2-sided P value equal to 1. In addition to the general validity (effect identification) assumptions mentioned earlier, the procedure assumes that the structural model and the pooled logistic regression model are correct. The 95% confidence limits for ψ* are values of ψ for which the test of hypothesis of α₇ = 0 has a 2-sided P value equal to 0.05. To see the effect of confounding by baseline exposure as well as exposure lagging in defining the target effect, we also fitted 3 simpler models, which omit lagged exposure A(k − 1) from the SAFTM or the baseline exposure A(0) from the logistic exposure model or both.

To accommodate censoring of $T_i\left(\tilde{\mathrm{\psi }}\right)$ by end of follow-up, we define C as the time from the baseline visit (visit 1) to end of 1998 and replace $T_i\left(\tilde{\mathrm{\psi }}\right)$ with the following pair of variables: an observable potentially censored survival time $C_i(\tilde{\mathrm{\psi }})=C_i$ if ψ ≥ 0, and $C_i\left(\tilde{\mathrm{\psi }}\right)=C_i\mathrm{e}\mathrm{x}\mathrm{p}\tilde{\mathrm{\psi }}$ if ψ < 0, so that $C_i(\tilde{\mathrm{\psi }})=\min \{C_i,C_i\mathrm{e}\mathrm{x}\mathrm{p}\tilde{\mathrm{\psi }}\}$; and an observable censoring indicator ${\mathrm{\Delta }}_{\mathrm{i}}(\tilde{\mathrm{\psi }})=1$ if $T_i\left(\tilde{\mathrm{\psi }}\right)<C_i(\tilde{\mathrm{\psi }})$, 0 otherwise (28). To transform the estimated survival-time ratio $\exp (\hat{\mathrm{\psi }}*)$ into a hazard ratio for the exposure effect, we fitted a Weibull model to the censored data $C_i(\hat{\mathrm{\psi }}*)$, ${\mathrm{\Delta }}_i(\hat{\mathrm{\psi }}*)$, then used the fitted Weibull shape parameter s to estimate the hazard ratio as $\exp (s\hat{\mathrm{\psi }}*)$. Confidence intervals for the hazard ratios $\exp (s\underset{\_}{\mathrm{\psi }})$ computed from $\exp (s\underset{\_}{\mathrm{\psi }})$ and $\exp (s\overline{\mathrm{\psi }})$ using the limits $\underset{\_}{\mathrm{\psi }}$ and $\overline{\mathrm{\psi }}$ for ψ* are too narrow because they do not account for uncertainty in the estimated shape parameter s. In our example however s appears to have a very small standard error and so it appears safe to ignore its variability.

We specified the following conventional time-dependent Cox model for the regression of the hazard on baseline (k = 0) and subsequent exposure and confounders:

$$\begin{array}{c}{\mathrm{\lambda }}_T(t)={\mathrm{\lambda }}_0(t)\exp ({\mathrm{\theta }}_{1}A(k)+{\mathrm{\theta }}_{2}A(k-1)+{\mathrm{\theta }\prime }_{3}L(k)\hfill \\ +{\mathrm{\theta }\prime }_{4}L(k-1)+{\mathrm{\theta }}_{5}a\mathit{ge}+{\mathrm{\theta }}_{6}A(0)+{\mathrm{\theta }\prime }_{7}L(\mathrm{0})),\hfill \end{array}$$

where k is the latest visit before time t. Like our MSM, this Cox model assumes that current and lagged exposure terms A(k) and A(k − 1) are sufficient to capture the total effect of exposure and adjusts for confounding by early exposure by including prebaseline exposure A(0). Note that for the first visit (k = 1), lagged and baseline exposures and confounders coincide so there would be no adjustment for lagged confounders and early confounding by the exposure in that visit.

Under the general validity assumptions mentioned earlier, if the time-varying confounders are not affected by (or do not share causes with) previous treatment (clearly violated in Figure 1), exp(θ₁ + θ₂) is the causal hazard ratio for the outcome comparing always smoking with never smoking during the study follow-up. To see the effect of confounding by baseline exposure as well as the lagged exposure in defining the target effect, we also fitted 3 simpler time-dependent Cox models that omit lagged exposure A(k − 1) or the baseline exposure A(0) or both from the Cox model mentioned above. All Stata (StataCorp LLC) and R (R Foundation for Statistical Computing) code is provided in Web Appendix 1 (available at https://academic.oup.com/aje).

RESULTS

The baseline characteristics of participants are provided in Table 1. Of 1,756 men included in our analysis, 244 developed the outcome over follow-up, with median incidence time of 11.5 (interquartile range, 9.9–13.1) years. The censoring rate due to loss to follow-up or competing risks was 10.0% (176/1,756). The hazard ratios for smoking based on the MSM fit by SIPTW, SAFTM fit by g-estimation, and conventional time-dependent Cox regression fit by partial likelihood were 1.27 (95% confidence limit (CL): 0.80, 2.02), 1.25 (95% CL: 0.89, 1.68), and 1.49 (95% CL: 0.94, 2.34), respectively (Table 2). The mean values of the SIPTWs used for MSM fitting in the second, third, and fourth visits were 0.997 (range, 0.14, 4.19), 0.998 (range, 0.17, 4.22), and 1.001 (range, 0.10, 6.91), respectively. Correct model specification and positivity will lead to a mean SIPTW close to 1 at each study visit, so that the size of the reweighted data set (“pseudopopulation”) should approximate the size of original data set at each visit (20).

Table 1.

Baseline Characteristics of 1,756 Participants Measured at Visit 0^a, Caerphilly Heart Disease Study, United Kingdom, 1979–1998

Characteristic	No.	%
Current smoker	905	51.5
History of heart attack	113	6.4
History of gout	81	4.6
History of high blood pressure	364	20.7
History of diabetes	28	1.6
High systolic blood pressure (≥140 mm Hg)	906	51.6
High diastolic blood pressure (≥90 mm Hg)	867	49.4
Obese (BMIb ≥ 30)	196	11.2
Underweight (BMIb < 20)	61	3.5
High fibrinogen (above the 75th percentile)	263	15.0
High cholesterol (above the 75th percentile)	447	25.5
Age (years)c	57.4 (4.5)d

Abbreviation: BMI, body mass index.

^a Sterne and Tilling (9).

^b Weight (kg)/height (m)².

^c Measured at visit 1.

^d Values are expressed as mean (standard deviation).

Table 2.

Hazard Ratio for Smoking and Cardiovascular Outcomes Using 2 Longitudinal Causal Models and a Conventional Time-Dependent Cox Model With Different Exposure Terms (n = 4,621 Person-Visits), Caerphilly Heart Disease Study, United Kingdom, 1979–1998

Model	Lagged Exposure	Prebaseline Exposure Adjustment	MSM + SIPTW		SAFTM + G-Estimation		Time-Dependent Cox Model + Partial Likelihood
			HR	95% CL	HR	95% CL	HR	95% CL
1	Yes	Yes	1.27	0.80, 2.02	1.25	0.89, 1.68	1.49	0.94, 2.34
2	Yes	No	1.68	1.25, 2.26	1.63	1.13, 2.33	1.62	1.22, 2.16
3	No	Yes	1.01	0.67, 1.54	1.25	1.18, 1.40	1.23	0.87, 1.73
4	No	No	1.44	1.08, 1.93	1.26	1.18, 1.68	1.47	1.13, 1.92

Abbreviations: CL, confidence limit; HR, hazard ratio; MSM, marginal structural model; SAFTM, structural accelerated failure time model; SIPTW, stabilized inverse-probability-of-treatment weight.

Deviations of the means from 1 can arise from model misspecification, positivity violations, and random or numeric artefacts. Given that some degree of misspecification is always present along with random and numeric error, some deviation from 1 is to be expected.

As Table 2 shows, the MSM and Cox-modeling results are sensitive to covariates included in the model, including whether lagged exposure or prebaseline exposure were in the model. The SAFTM that included both A(k) and A(k − 1) varied similarly depending on whether the lagged exposure variable was adjusted for in the pooled logistic g-estimator. Nonetheless, when the lagged exposure variable was excluded in the structural model, results were insensitive to whether the prebaseline exposure was included in the pooled logistic g-estimator.

The time-dependent Cox regression with model specification 1 in Table 2 includes both current and lagged exposures (see the time-dependent Cox model above) and reports an estimated hazard ratio, exp(θ₁ + θ₂) of 1.49 (95% CL: 0.94, 2.34) for the total effect of exposure by combining the parameters of current and lagged exposure terms. Based on this model, the hazard ratio, exp(θ₁), estimate for current smoking adjusted for lagged and baseline smoking as well as covariate history is 1.06 (95% CL: 0.71, 1.58).

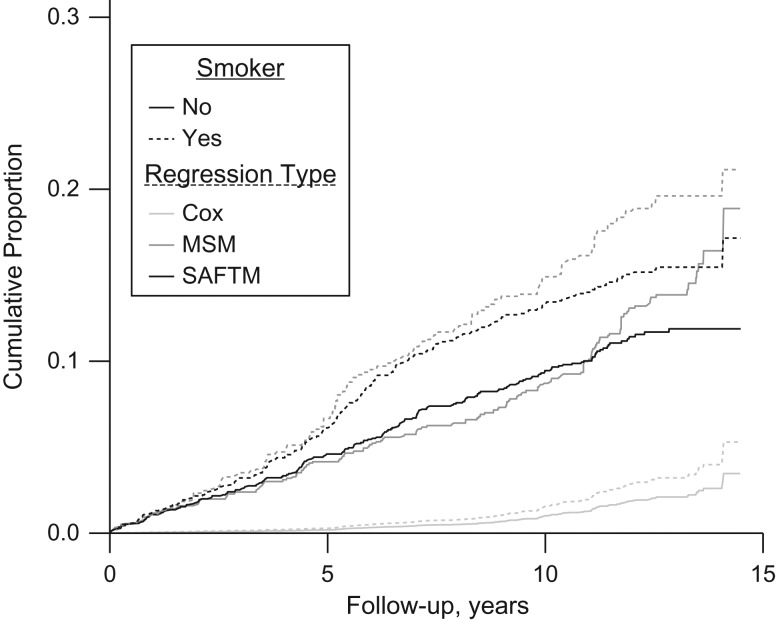
Finally, Figure 2 shows a comparison of the cumulative mortality functions under 2 scenarios (fully exposed to smoking versus fully unexposed to smoking) from the time-dependent Cox regression model, the MSM, and the SAFTM, each including current and lagged exposure when adjusted for prebaseline exposure (see the first row of Table 2). As with the results from Table 2, Figure 2 suggests similarity between the MSM and the SAFTM estimates. While the difference in the curves between fully exposed and fully unexposed to smoking from the time-dependent Cox regression model suggest a smaller effect, this is likely the result of the fact that these curves are specific to individuals with average covariate values (Figure 2).

Figure 2.

Cumulative distribution functions for mortality among 1,756 men from the Caerphilly Heart Disease Study, United Kingdom, 1979–1998, obtained from a time-dependent Cox regression model, marginal structural model (MSM), and structural nested accelerated failure time model (SAFTM), each including current and lagged exposure when prebaseline exposure is adjusted for (the first row of Table 2), under 2 exposure scenarios (exposed to smoking at all time points versus unexposed to smoking at all time points). Predicted values from the time-dependent Cox regression model were obtained by setting all covariates to their mean values.

DISCUSSION

As with conventional statistical modeling, interpreting associations from longitudinal causal models as causal effects requires validity conditions including precisely defined exposure; no uncontrolled confounding, selection bias, or measurement error; and no bias from model specification. Structural positivity (positive probability of each exposure level at each covariate level) is also often listed and is essential to basic inverse-probability-of-treatment-weight (IPTW) methods, but other assumptions might loosen this requirement by enabling projections to unobserved exposure levels (e.g., trend assumptions to interpolate between observed doses). Even with structural positivity, these assumptions become important when (as is often the case) there is random nonpositivity (i.e., no observations at some of the possible exposure-covariate combinations).

The chief advantage of longitudinal causal modeling is that it allows previous exposure to affect time-varying confounders; also, its typical implementation with inverse-probability-of-censoring weighting (IPCW) uses weaker censoring assumptions than that of random censoring implicit in conventional models and software. Nonetheless, 2 major concerns are inclusion of adequate exposure terms from different visits, so that confounding by earlier exposure is controlled, and model specification so that the desired target effect is represented by a simple transform of the exposure coefficient.

Contrasting MSM and conventional models with and without lagged exposure (models 1 vs. 3 and 2 vs. 4) in Table 2, we see how the common practice of including only the current exposure in a time-dependent model can be inadequate for capturing the causal effects of a continuous exposure. This difference highlights the importance of correct specification of the exposure in the causal models as well as for conventional time-dependent Cox models. The lagged exposure term captures the cumulative effect of smoking on myocardial infarction, and the results suggest that the duration of exposure matters. A more accurate specification would, however, use amount smoked (e.g., pack-years) during follow-up as the primary exposure.

Contrasting MSM and conventional models with and without prebaseline exposure (models 1 vs. 2 and 3 vs. 4) in Table 2 indicates that prebaseline exposure (i.e., exposure at the first visit if the analysis starts from the second visit) can act as a baseline confounder and should be adjusted for in the analysis. The results from the MSM and time-dependent Cox model are very similar, especially with no prebaseline exposure adjustment. This similarity is unsurprising, given that their model forms are similar, the degree of time-varying confounding is low (as suggested by the narrow range of SIPTWs), and time-varying confounders are not strongly affected by the previous exposure (data are not shown). The parameters they estimate are not, however, the same: MSM coefficients represent partially marginal effects (averaged over confounders in the weight function but not in the MSM), while Cox model coefficients represent fully confounder-conditional effects. Because the baseline confounders are in our MSM, that model (like the time-dependent Cox model) is conditional with respect to baseline confounders, and so our MSM effect estimates are only marginal with respect to time-varying confounders.

On the other hand, our results from g-estimation are similar to those of MSM analysis when a lagged exposure term is included, but their results diverge otherwise. The divergence can be explained by noting that g-estimation is based on a very different model, namely an SAFTM, which imposes a stronger interindividual homogeneity requirement than the MSM, which assumes only homogeneity across the levels defined by the MSM variables; in parallel, the g-estimates are conditional with respect to all of the time-varying and baseline confounders. The g-estimates in Table 2 appear to be more precise than estimates from the MSM and time-dependent Cox model, reflecting the stronger assumption, as well as the more efficient fitting method and more precise (as opposed to conservative) variance estimation available for the SAFTM.

The confidence intervals in Table 2 are wide, so it is not possible to determine whether in the example there is a practical difference from including lagged exposure terms and adjusting for baseline exposure. Under common defaults, the observed difference between the analyses could be seen as statistically important in a study in which each point estimate lies outside the other’s 95% confidence interval. Nonetheless, the differences we have emphasized concern the underlying population structure and so need to be considered regardless of the sizes of the standard errors. In particular, even with no uncontrolled confounding in either analysis, the conventional analysis does not estimate the same causal parameters as in the longitudinal causal models.

In our example, Sterne and Tilling (9) estimated a hazard ratio of 1.06 (95% CL: 0.71, 1.58) for exp(θ₁), the effect of current smoking adjusted for lagged and baseline smoking and covariate history in a conventional time-dependent Cox model, and compared it with the g-estimate of 1.38 (95% CL: 1.04, 1.60) for the total effect of smoking (using Stata’s stgest command, which we computed as 1.31 (95% CL: 0.90, 1.71) using the R code provided in the appendix). They concluded that the standard survival analysis approach to the analysis of time-varying exposures substantially underestimated the effect of smoking. They attributed the difference in estimates to the bias arising from conventional adjustment for time-varying confounders affected by the previous exposure. Nonetheless, the hazard ratio of 1.06 from conventional time-dependent Cox modeling estimates the acute effect adjusted for the previous chronic effect, which is a causal parameter different from that in the longitudinal (g-estimation) analysis. Thus the difference between the 2 estimates might be due in part to differences in their target parameters rather than more confounding in the conventional analysis. While quite imprecise on the matter, our analysis suggests that, in this example, the difference in results is more due to differences in the targeted effects than differences in confounding.

Conventional analyses assume there is no time-varying confounding affected by prior exposure, which is true when the acute effect of current exposure A(k) is the target because current exposure A(k) does not affect the time-varying confounders L(k). In particular, the path A(k − 1) → L(k) → Y(k) is assumed absent this analysis, which, if correct, prevents overadjustment bias due to conditioning on L(k). As noted earlier, in the presence of unmeasured factors U(k − 1) affecting L(k), conditioning on L(k) makes A(k − 1) a noncausal predictor of Y(k). Again there is no concern about this collider bias when the target is the effect of current exposure A(k), as if one assumes that the previous exposure does have a direct effect on the current exposure then A(k − 1) is indeed a confounder and is adjusted for in this conventional analysis. Unlike the conventional analyses presented in Table 2 for the total effect of the exposure, this analysis has causal interpretation in the absence of model misspecification and uncontrolled confounding. We note, however, that it would be necessary to include product terms between current exposure and previous exposure and covariate history; this is because, under our MSM, the acute effect of the exposure need not be constant over strata of past exposure and covariate history (2).

Residual confounding might arise even if the model is correctly specified and there are no uncontrolled confounders including early exposure. In the Caerphilly study, as in other interval cohorts, confounders are not measured at the times of exposure change and, in fact, concurrent or lagged time-varying confounders are the mismeasured versions of the true values of the confounders. Moreover, residual confounding can arise from measurement errors in confounders and prebaseline exposure. Another concern is error in smoking measurement itself and the questionable assumption that smoking reported at each visit (k) represents smoking during the ensuing interval [k, k + 1).

In sum, inclusion of correct exposure terms to account for the target effect and confounding by early exposure is crucial for longitudinal causal analysis as well as for conventional analysis, and sensitivity analysis using different specifications is often warranted. Regardless, when comparing different approaches to estimate causal effects, we should make sure that they are targeting the same causal parameter, or at least addressing the same research question.

Abbreviations

CL

confidence limit

MSM

marginal structural model

SAFTM

structural accelerated failure time model

SIPTW

stabilized inverse-probability-of-treatment weight