Improved MUSSELS Reconstruction for High-Resolution Multi-shot Diffusion Weighted Imaging

Abstract

Purpose:

MUSSELS is a one-step iterative reconstruction method for multi-shot diffusion weighted (msDW) imaging. The current work presents an efficient implementation, termed IRLS MUSSELS, that enable faster reconstruction to enhance its utility for high resolution diffusion MRI studies.

Methods:

The recently proposed MUSSELS reconstruction belongs to a new class of parallel imaging-based methods that recover artifact-free DWIs from msDW data without needing phase compensation. The reconstruction is achieved via structured low-rank matrix completion algorithms, which are computationally demanding due to the large size of the Hankel matrices and their associated computations involving singular value decompositions. Because of this, computational demands of the MUSSELS reconstruction scales as the matrix size and the number of shots increases, which hinders its practical utility for high-resolution applications. In this work, we derive a computationally efficient MUSSELS formulation by modifying the iterative reweighted least squares (IRLS) method that were proposed earlier to solve such problems. Using whole-brain in-vivo data, we show the utility of the IRLS MUSSELS for routine high-resolution studies with reduced computational burden.

Results:

IRLS MUSSELS provides about six times faster reconstruction for matrix sizes 192×192 and 256×256 compared to the earlier MUSSELS implementation. The widely employed conjugate symmetry priors can also be incorporated into IRLS MUSSELS to reduce blurring of the partial Fourier acquisitions, without incurring much computational burden.

Conclusion:

The proposed method is observed to be computationally efficient to enable routine high-resolution studies. The computational complexity matches the traditional msDWI reconstruction methods and provides improved reconstruction results with the additional constraints.

Introduction

The spatial resolution limits of diffusion weighted images (DWIs) has been traditionally set by the capabilities of single-shot echo planar imaging (ssEPI) techniques on a given set of MRI hardware. On standard clinical gradients (33mT/m gradient strength, 120T/m/s slew rate), ssEPI readouts contribute to a minimum TE of approximately 75–120 ms for a 128 × 128 imaging matrix for typical b-values of 1000–3000 s/mm². Pushing the spatial resolution of DWIs beyond the 128 × 128 matrix size results in (i) increased geometric distortions along the phase-encoding direction, (ii) reduced signal-to-noise ratio (SNR) due to the long read out time involved in sampling the center-of-k-space and (iii) increased blurring in the images due to the T₂* signal decay that accompanies the long readout duration (1). Thus, despite not being the ideal resolution to study the micro-level tissue structural properties, the characteristic resolution of standard DWI studies has largely remained at approximately 2mm isotropic. On the other hand, during a practical diffusion encode time (δ), the diffusion measurements are sensitive to length scales of the order of ∼10μm (2). However, the robust detection of subtle micro-structural changes of order ∼10μm length scale from a 2mm voxel resolution will result in significant partial volume artifacts. Thus, there is a strong biological motivation to push the spatial resolution of DWIs to sub-millimeter scales (3). Multi-shot echo-planar imaging (msEPI) readouts can enable higher spatial resolutions for DWIs on standard clinical MRI hardware. Combined with synergistic improvements offered by high field strengths, high performance gradients, and high slew rate systems, embracing msEPI methods for DWIs can set the stage to push the spatial resolution of DWIs to sub-millimeter voxel sizes.

A major concern while employing msEPI methods for diffusion studies is the fact that the reconstruction of multi-shot diffusion weighted (msDW) data is not amenable to the traditional IFFT-based reconstructions. This is because the k-space of a given DWI is sampled over multiple TRs using a msEPI scheme which contributes to a unique phase for the data corresponding to the different readouts (4, 5). Thus, the data from the k-space segments acquired across multiple TRs need to be compensated for their inconsistent phases before they can be combined. Traditionally, this phase compensated reconstruction involved a multi-stage reconstruction of the individual shot images to calibrate their phases and finally combining the images using phase compensation methods (1, 6, 7). Recently, several new strategies that can combine the k-space data from multiple shots without needing explicit phase compensation have been proposed (8–10). Such reconstructions can enable direct recovery of the DWIs from the k-space data and thus can potentially enable online reconstruction of the DWIs on the scanner. One outstanding challenge with the above iterative reconstructions compared to the IFFT-based reconstructions is the long reconstruction times involved.

In this work, we focus on the MUSSELS (Multi-shot sensitivity-encoded recovery using structured low-rank matrix completion) reconstruction (8) and identify some of its computational bottlenecks. We reformulate the MUSSELS reconstruction to enable a computationally efficient implementation to solve the matrix recovery problem embedded in the recovery scheme. The reformulation is based on the iterative re-weighted least squares (IRLS) methods that were previously proposed to address the computational complexity in similar reconstruction problems involving matrix completion (11–16). It has been shown that nuclear norm minimization involving large matrices can be efficiently solved by reformulating such problems using the IRLS formulation (17, 18). Specifically, the IRLS formulation reduces the computational complexity associated with the singular value thresholding involved in such reconstructions and also achieve faster convergence (19). The re-formulation offers the following advantages: (i) the computation time is reduced by several folds for the recovery of high-resolution data, (ii) the improved efficiency allows to accommodate additional constraints to achieve more accurate image recovery without trading off computational time. The proposed formulation is shown to provide high-quality DWI reconstruction with highly consistent image recovery from the multiple shots. We show the feasibility of whole-brain high-resolution studies using the proposed reconstruction and highlight the benefits of the higher resolution in comparison to standard 2mm isotropic dMRI data.

Theory

Review of MUSSELS

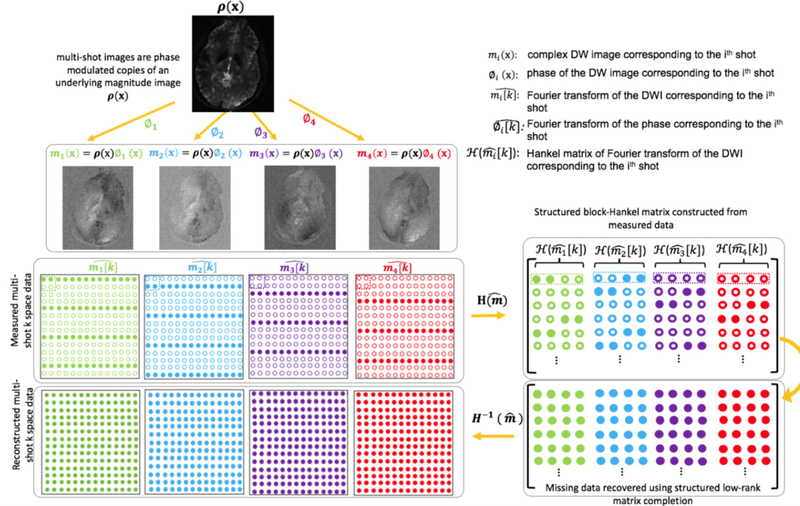
A pictorial representation of the MUSSELS reconstruction proposed in (8) is given in figure 1. This method is notably different from traditional msDW reconstruction methods that involves phase compensation (7, 20–24). Specifically, MUSSELS is an iterative reconstruction that jointly recovers the complex k-space data of all the shots by exploiting a low-rank prior as follows:

$$\widehat{\tilde{\mathbf{m}}}=\underset{\widehat{\mathbf{m}}}{\mathrm{argmin}}\underset{\text{data}\text{consistency}}{\underbrace{\Vert \mathcal{A}(\widehat{\mathbf{m}})-\widehat{\mathbf{y}}{\Vert }_{{\mathcal{l}}_2}^2}}+\lambda \underset{\text{low-rank}\text{penalty}}{\underbrace{{\Vert {\mathbf{H}}_1(\widehat{\mathbf{m}})\Vert }_{*}}},$$ [1]

where

$${\mathbf{H}}_{\mathbf{1}}(\widehat{\mathbf{m}})=\left[\mathcal{H}\left(\widehat{m_1}\right)\mathcal{H}\left(\widehat{m_2}\right)\dots \mathcal{H}\left(\widehat{m_{N_s}}\right)\right]$$ [2]

is a concatenation of the convolutional Hankel matrices, $\mathcal{H}\left(\widehat{m_i}\right)$, corresponding to the k-space data, $\widehat{m_i}$, of each shot. By enforcing a low-rank penalty on the block-Hankel matrix, ${\mathbf{H}}_{\mathbf{1}}(\widehat{\mathbf{m}})$, the reconstruction promotes the recovery of DWIs from each shot that share the same magnitude. We refer interested reader to (8) for details of the Hankel matrix construction and the derivation of the low-rank prior. Using structured low-rank matrix completion (SLRMC), the missing entries of ${\mathbf{H}}_{\mathbf{1}}(\widehat{\mathbf{m}})$, and thereby the k-space data in each of the k-space shots are recovered (figure 1).

Figure 1:

Illustration of the direct reconstruction of msDW data using MUSSELS. ρ(x) is the underlying magnitude DWI. The matrix of multi-shot k-space data is represented as $\widehat{\text{m}[\text{k}]}$. Solid and hollow circles denote respectively the measured and the missing k-space data in each shot. A block-Hankel matrix is created from the measured data whose missing samples are filled using matrix completion subject to data consistency. This, in turn, recovers the missing samples of the multi-shot k-space data.

As noted previously in (8, 25, 26), the presence of the data-consistency term guards the recovery process from converging to trivial solutions. The forward operator $\mathcal{A}$ is given by $\mathcal{M}°\mathcal{F}°\mathcal{S}°{\mathcal{F}}^{-1}$ where $\mathcal{F}$ and ${\mathcal{F}}^{-1}$ represent the Fourier transform and the inverse Fourier transform operations respectively, $\mathcal{S}$ represents multiplication by coil sensitivities, and $\mathcal{M}$ represents multiplication by the k-space sampling mask corresponding to each shot. $\widehat{\mathbf{y}}$ is the measured multi-channel k-space data and $\widehat{\mathbf{m}}$is the channel-combined matrix of k-space data from all the shots.

SLRMC Computational Complexity

SLRMC is now a widely employed MRI reconstruction technique which has been applied to solve several MR reconstruction problems (11, 15, 27–35), in addition to phase correction problems for EPI ghost correction (9, 26, 36). While SLRMC efficiently exploits the compactness in the Fourier samples to formulate novel recovery priors for several of the above-mentioned problems, the computational complexity of these methods can be challenging in some applications, especially those involving concatenated Hankel matrices (27, 37, 38).

For the iterative MUSSELS reconstruction for the recovery of msDW data involving multiple shots and large matrix sizes, the computational complexity presents a major bottleneck for whole brain studies. Here, the size of the lifted matrix ${\mathbf{H}}_{\mathbf{1}}(\widehat{m})$ is large compared to the original data $\widehat{m}$. Specifically, if the size of the DWI is given by N₁×N₂, then the size of ${\mathbf{H}}_{\mathbf{1}}(\widehat{m})$ is given by m×n where m = (N₁−r+1)×(N₂−r+1) and n = r ×r ×N_s where r is the size of the filter. In the alternating minimization schemes used to solve Eq.1, the above matrix needs to be computed and stored during each iteration. Moreover, these implementations rely on singular value shrinkage for rank minimization which involves the singular value decomposition (SVD) of ${\mathbf{H}}_{\mathbf{1}}(\widehat{m})$. Since m >> n (by ∼ 2–3 orders of magnitude), the above minimization incurs a computational complexity of O(mn²) for each iteration.

Fast algorithms proposed in the past to address the computational complexity of SLRMC include the UV factorization method (29, 38, 39) and the GIRAF algorithm (11–14). While the former method eliminated the need for SVD computation, the latter employed the IRLS formulation and exploited the convolutional structure of the lifted matrix to work in the original un-lifted domain. By exploiting a half circulant approximation of multi-level block Toeplitz/Hankel matrices, this approach reduced the computational burden. This approximation was later incorporated into the LORAKS SLRMC framework also to achieve faster implementations for concatenated Hankel matrices (15, 16). Inspired by the above works, we seek to achieve faster implementation for the iterative MUSSELS reconstruction.

Iterative Reweighted Least Squares formulation of MUSSELS

The goal of this work is to extend the fast algorithms for the SLRMC to the multi-shot diffusion weighted setting to enable high resolution studies. Unlike (15, 16) where the concatenated Hankel matrices are generated for the different coils and hence share the same sampling pattern, the concatenated Hankel matrices in MUSSELS are generated for the different shots, each with a different sampling pattern.

The iterative reweighted least squares (IRLS) method has been applied to solve nuclear norm optimization problems by several authors where the original problem of minimizing the Schatten p norm

$$\underset{\widehat{\mathbf{m}}}{\min }\Vert \mathcal{A}(\widehat{\mathbf{m}})-\widehat{\mathbf{y}}{\Vert }_{{\mathcal{l}}_2}^2+\lambda {\Vert {\mathbf{H}}_1(\widehat{\mathbf{m}})\Vert }_p^p$$ [3]

is replaced by a re-weighted formulation (17–19).

$$\underset{\widehat{\mathbf{m}}}{\min }\Vert \mathcal{A}(\widehat{\mathbf{m}})-\widehat{\mathbf{y}}{\Vert }_{{\mathcal{l}}_2}^2+\lambda {\Vert {\mathbf{H}}_1(\widehat{\mathbf{m}}){\mathbf{W}}^{1/2}\Vert }_p^p$$ [4]

where the weights, W, given by

$$\mathbf{W}={\left[{\mathbf{H}}_1^{*}(\widehat{\mathbf{m}}){\mathbf{H}}_1(\widehat{\mathbf{m}})+ϵ\mathbf{I}\right]}^{p/2-1},$$ [5]

are computed from the previous iteration and is re-weighted every iteration. Here, ϵ is a regularization parameter chosen for numerical stability and I is the identity matrix. Using the property ${\Vert {\mathbf{H}}_1(\widehat{\mathbf{m}})\Vert }_F^2\le {\Vert {\mathbf{H}}_1(\widehat{\mathbf{m}}){\mathbf{W}}^{1/2}\Vert }_{*}$, we can re-write the MUSSELS nuclear norm minimization in terms of the Frobenius norm to obtain the IRLS MUSSELS cost function :

$$C_1(\widehat{\mathbf{m}}):\widetilde{\widehat{\mathbf{m}}}=\underset{\widehat{\mathbf{m}}}{\mathrm{argmin}}\Vert \mathcal{A}(\widehat{\mathbf{m}})-\widehat{\mathbf{y}}{\Vert }_{{\mathcal{l}}_2}^2+\lambda {\Vert {\mathbf{H}}_{\mathbf{1}}(\widehat{\mathbf{m}}){\mathbf{W}}^{1/2}\Vert }_F^2,$$ [6]

where _F represents the Frobenius norm.

The computation of W involves taking the inverse of the Gram matrix ${\mathbf{H}}_1^{*}(\widehat{\mathbf{m}}){\mathbf{H}}_1(\widehat{\mathbf{m}})$ which involves computing the SVD of ${\mathbf{H}}_1^{*}{\mathbf{H}}_1$. Assume that the SVD of H₁ is given by USV^T. Then, we evoke the property that SVD of ${\mathbf{H}}_1^{*}{\mathbf{H}}_1$ has the form US²U^T. Since the size of ${\mathbf{H}}_1^{*}{\mathbf{H}}_1$ is n × n, W can be efficiently computed by order O(n³) complexity. W is updated during the outer iteration and remains the same for the inner CG updates. The pseudo-code for solving the IRLS MUSSELS optimization problem is provided in the supporting information section S1.1.

In the IRLS MUSSELS framework, each column of W is an annihilating filter for H₁. Since H₁ is a concatenation of multiple Hankel matrices, ${\mathbf{H}}_1(\widehat{\mathbf{m}})\mathbf{W}$ denotes a multi-channel convolution where each column of W is a multi-channel filter. Figure S1 in the supporting information illustrates the multi-channel convolution underlying the above computation. The term ${\mathbf{H}}_1*\left({\mathbf{H}}_1(\widehat{\mathbf{m}})\mathbf{Q}{\mathbf{Q}}^{*}\right)$ (Eq. [S2], section S1.1 in the supporting information) performs a multi-channel convolution and its adjoint in a numerically efficient manner. An equivalent formulation that achieves the convolution followed by the adjoint operation in the un-lifted domain is illustrated in Figure S1. The above computations can be implemented using FFTs and IFFTs also, the implementation details of which are provided in S1.2 in supporting information. We observe that the number of FFTs and IFFTs required for the above implementation is very high for the multi-channel case and hence results in high computation time. To overcome the high computational complexity, an approximate formulation has been pursued by (11, 16), where the valid convolution region is not enforced during the forward and adjoint convolutions. This approximation can significantly reduce the number of FFTs and IFFTs required per iteration of CG, thus bringing significant acceleration. The implementation details of this approach are provided in section S1.3 in supporting information.

Extension of MUSSELS with additional constraints

Diffusion MRI data are often collected with partial Fourier (pF) acceleration to keep the TE low. In (8), the smoothness regularization was proposed to recover such under-sampled data exploiting sparsity-like priors embedded in the structured low-rank matrix recovery. Alternatively, the conjugate symmetry (CS) property of the k-space data (40) has been exploited by several authors (10, 30, 37, 41) to recover pF data. This property can be accommodated into MUSSELS formulation by modifying ${\mathbf{H}}_1(\widehat{\mathbf{m}})$ as:

$${\mathbf{H}}_1(\widehat{\mathbf{m}})=\left[\mathcal{H}(\widehat{m_1})\mathcal{H}(\widehat{m_2})\dots \mathcal{H}(\widehat{m_{N_s}})\mathcal{H}({\widehat{m_1}}^{†})\mathcal{H}({\widehat{m_2}}^{†})\dots \mathcal{H}({\widehat{m_{N_s}}}^{†})\right],$$ [7]

where † represents the flipped conjugate of the k-space data. The additional virtual-shots are concatenated along the columns as in (15).

Note that the columns of ${\mathbf{H}}_1(\widehat{\mathbf{m}})$ are doubled when the CS property is exploited. The doubling of the shot-dimension will increase the computational complexity of MUSSELS to O(4mn²) whereas it will only change the complexity of IRLS MUSSELS to O(8n³). Thus, the IRLS MUSSELS provides a computationally efficient framework to work with higher shots and higher matrix sizes. It also offers the flexibility to incorporate additional constraints to improve the reconstruction and potentially enable online reconstruction of the high-resolution msDWIs. In the following section, we test the IRLS MUSSELS on in-vivo data and compare it to state-of-the-art reconstruction methods.

Methods

Datasets

Two high-resolution dMRI data were collected at two field strengths. The 3T dataset (GE MR750W, G_max = 33mT/m, SR_max = 120T/m/s) was acquired using a 4-shot dual-spin echo diffusion sequence at 0.82×0.82 mm in-plane resolution. With pF at 59%, the TE is 84ms for b-value of 700 s/mm². Other imaging parameters include FOV: 210×210 mm, sampling matrix: 256×152, slice thickness: 4mm and NEX=2. The 7T data (GE MR950, G_max = 50mT/m, SR_max = 200T/m/s) were collected using a 4-shot acquisition at 1.1 mm isotropic resolution with a b-value of 1000 s/mm². Since the ${\text{T}}_2^{*}$ decay is faster on 7T field strength, we employed a Stejskal-Tanner sequence to reduce the TE to 53ms with pF at 62.5%. Other imaging parameters include FOV: 210×210 mm, sampling matrix: 192×120, slice thickness of 1.1mm. 100 slices spanning the whole brain were collected in an acquisition time of 40 mins. A comparison dataset at 2mm isotropic resolution was also collected using single-shot techniques. A dielectric pad was employed to improve the signal drop off towards the inferior brain regions. Both datasets consist of 60 diffusion directions and employed a 32-channel phase array coil. All experiments were performed on healthy volunteers following the Institutional Review Board requirements at the University of Iowa and obtaining informed written consent.

Reconstruction

The datasets were preprocessed to account for EPI odd-even trajectory shifts arising from eddy currents, and ramp-sampling using standard GE preprocessing pipelines for EPI data (42). The coil sensitivity maps were estimated from the non-diffusion weighted images using a sum-of-squares reconstruction approach (8). To compare the improvements offered by the IRLS implementation, the data were reconstructed using the MUSSELS implementation in (8) without and with the CS lifting (Eq. 7) and the IRLS implementations without and with CS lifting. The MUSE reconstruction was also implemented (7, 24) to compare the computational performance of the reconstructions. All implementations were performed in Matlab (The MathWorks, Inc., Natick, MA, USA) on a high-performance computing server having 48 cores with hyper-threading enabled and 256GB memory. The reconstructed DWIs were co-registered and eddy current corrected using FSL(43). A single tensor fitting was performed to extract the primary diffusion directions for visualization of the improvement offered by the high-resolution images. The orientation distribution functions (ODF) were also computed from these datasets assuming a 3-fiber model, which helps to better visualize the improvements offered by the high-resolution images.

Results

Accelerated reconstruction

Table 1 reports the time taken to reconstruct a given DWI using various implementations for the two datasets. We note that the MUSSELS (8) without CS constraint provided robust results, however, the reconstruction time was higher than the MUSE Matlab implementation. From Table 1, it can be seen that the IRLS formulation accelerated the above reconstruction by a factor of 3 (first and third row), making it faster than MUSE Matlab implementation for both the datasets tested. Similarly, the addition of CS constraint increased the reconstruction time of the MUSSELS implementation (8) by ∼ 4.5 times. The IRLS formulation accelerated the above reconstruction by about 6 times (second and fourth row). The reconstruction time for the IRLS MUSSELS with CS constraint is only modestly longer than MUSE reconstruction, but provides improved reconstruction. For the sake of completeness, we also compare the reconstruction time to the exact and the approximate FFT-based implementations of IRLS MUSSELS. Table S1 in the supporting information reports the time for all the three IRLS implementations per iteration of CG, with the breakdown of the computation time also reported.

Table 1:

Reconstruction time in seconds per image (per slice per direction).

Case	3T dataset (256 × 256)	7T dataset (192 × 192)
MUSSELS	69	39
MUSSELS with CS	322	178
IRLS MUSSELS	22	14
IRLS MUSSELS with CS	40	24
MUSE	34	22

Equivalence of two formulations:

Figure S2 in the Supporting Information shows the individual shot images and the magnitude DWI reconstructed using MUSSELS (Eq. 1) and IRLS MUSSELS (Eq. 6) from the first dataset. As expected, the IRLS formulation with the weight term and the nuclear norm minimization generated equivalent reconstructions. The color-coded fractional anisotropy (FA) map reconstructed using both formulations also demonstrates that the accelerated IRLS MUSSELS achieves the same reconstruction quality as the original MUSSELS implementation.

Addition of conjugate symmetry:

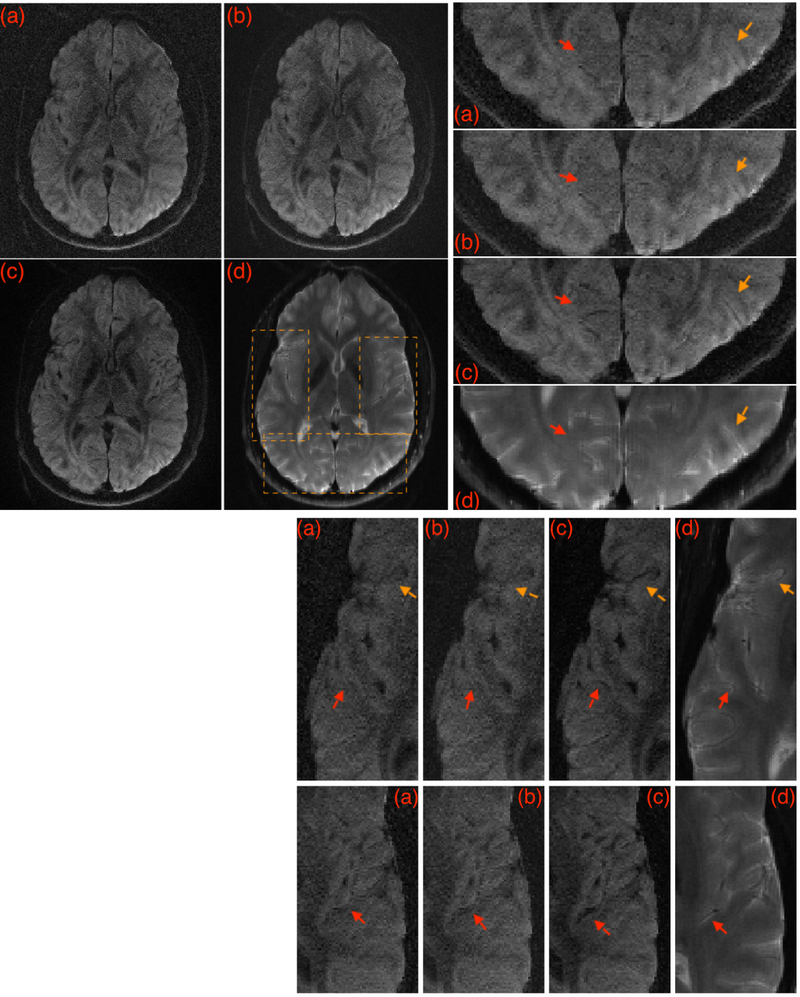
Figure 2 show the reconstructions from the IRLS MUSSELS without and with CS constraint for a given DWI. The recovery of several fine anatomical details can be observed in Fig 2c that are not visible in the reconstructions in Fig 2a–b. Such improved recovery enabled by the CS constraint has been previously reported in (26) as well. For comparison, a non-diffusion weighted image reconstructed using sum-of squares is also added that shows the corresponding anatomical details in a manner that is unaffected by the specific reconstruction method. The corresponding FA maps are provided in the figure S3 in the Supporting Information.

Figure 2:

A given DWI reconstructed using various methods. (a) shows MUSE reconstruction, (b) shows IRLS MUSSELS without CS, and (c) shows the IRLS MUSSELS with CS constraint. In (d) the sum-of-squares reconstruction of the b0 image from the same slice location is provided for comparison of the anatomical details from the slice, that is unaffected by the reconstruction method. The boxed regions are zoomed for better visualization. Arrows highlight regions with better recovery of anatomical details.

Whole brain reconstruction

The fast recovery enabled by the IRLS implementation helps to achieve whole brain high-resolution DWI reconstruction in a reasonable time. Since the data is highly parallelizable both along the diffusion directions and slices, we made use of parallel processing to reconstruct the whole brain dataset. Specifically, we parallelized the reconstruction of 6100 volumes (100 slices × 61 directions) using 48 hyper-threaded CPU cores that reconstructed the data in 1 hour.

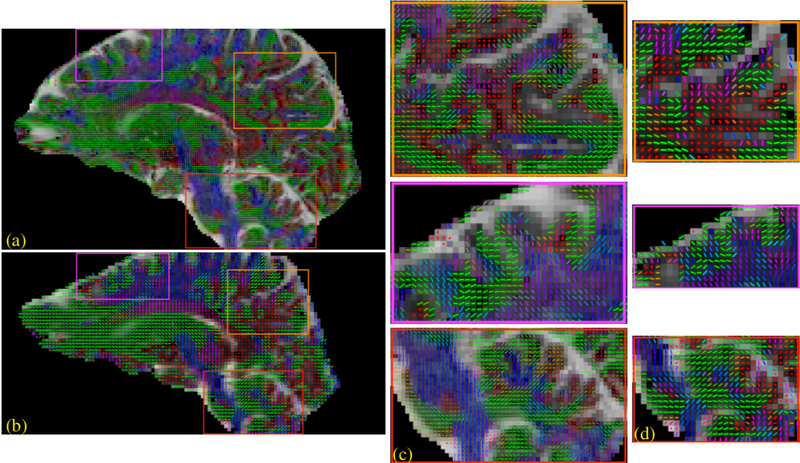
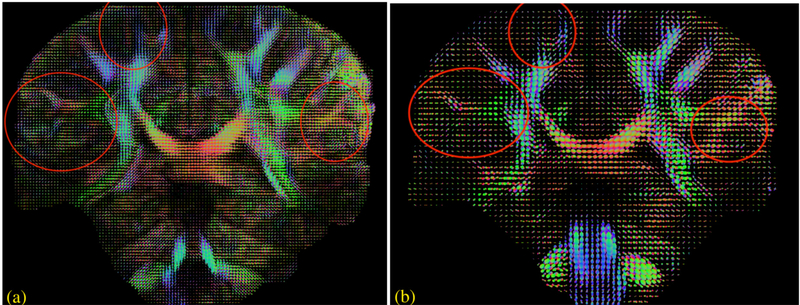
Figures 3 and 4 show the reconstruction from the 7T dataset using the IRLS MUSSELS with CS lifting. Specifically, a single tensor fit and a q-ball based ODF assuming 3 fiber peaks were fitted to this data. A comparison of similar analysis performed on the 2mm isotropic data obtained on the same subject is also shown. In figure 3, the primary diffusion direction recovered from the single tensor fit is overlaid on the apparent diffusion coefficient (ADC) map to better visualize the background contrast. This image clearly shows that the high-resolution data follows the cortical folds and better represents the anisotropy in the brain voxels. In Figure 4, the plot of the ODFs from two comparable slices also show several remarkable differences between the two resolutions as highlighted.

Figure 3:

Whole brain reconstruction of dataset 2. The IRLS with CS reconstruction was performed on the dataset and a single tensor model was fitted to the DWIs. This 1.1 mm isotropic dataset (a,c) is compared against the 2mm isotropic data (b,d) obtained from the same subject. Several regions are highlighted where the high-resolution data offers more details about the brain anatomy which is not fully captured by the low resolution data. (c) shows the zoomed view of regions highlighted in (a) and (d) shows the zoomed view of regions highlighted in (b).

Figure 4:

Whole brain reconstruction from dataset 2. The ODFs reconstructed from the 1.1mm dataset (a) is compared to that of the 2mm dataset (b). Regions where the high-resolution data offers improved details about the brain anatomy compared to the low resolution data are highlighted.

Discussion

As evident from figures 3 and 4, the high-resolution and low-resolution diffusion data are comparable in regions composed of homogeneous white matter voxels. For example, there is no notable difference within the major white matter bundles such as the corticospinal tract or the corpus callosum. The major differences, both in single tensor and the multi-compartmental representations, are in the voxels composed of multiple tissues, i.e, in voxels closer to gray/white tissue boundaries, voxels with heterogeneous fiber orientations and those in the sub-cortical regions. The differences in such regions clearly point to the inadequacy of the low resolution to feature the subtle changes resulting from neuropathologies. Thus there is a clear biological motivation to push the spatial resolution of dMRI to exploit its superior sensitivity in detecting micro-structural changes (3). Here, we compare a 2mm isotropic data with a 1.1mm isotropic data; however, the recovery of even more anatomical details can be expected from sub-millimeter voxel resolutions in the range of .8 −.6 mm isotropic resolution. The synergistic combination of improved gradient hardware (44–46) and multi-shot techniques can readily push the spatial resolution well below the standard 2mm isotropic resolution. The reduced echo-time achieved from such efforts is important not only for achieving higher spatial resolution, but also for high b-value studies (3).

The MUSSELS reconstruction provided an important step towards enabling motion-immune msDW reconstruction. In the work, we further addressed the high computational demands of MUSSELS stemming from the SLRMC, thus improving the practical utility of the method for whole brain high-resolution studies. The acceleration offered by the IRLS formulation can be attributed to several factors: i) it eliminated the computationally expensive SVD for rank minimization, ii) during each iteration, the IRLS minimization alternates between a data consistency enforcement and a projection to the signal space, orthogonal to the null-space vectors specified by W. Based on the projection to the low-dimensional subspace, the term W, can be interpreted as a denoiser that enables faster convergence. iii) the annihilating filter W can be interpreted as the k-space counterpart of the image-domain phase. Thus, without going back and forth from image-domain to frequency domain, the IRLS framework incorporates the phase estimate in the frequency domain itself in a unified framework. The implicit incorporation of the phase information accelerates the recovery problem. IRLS-based implementations were previously employed to accelerate SLRMC reconstructions (11, 15). We note that the exact implementation employing Hankel matrix multiplication is of comparable performance to the approximate FFT-based implementation. The latter may have a computational advantage when high number of iterations are needed.

Although the recovery of the missing k-space data in MUSSELS is primarily driven by the low-rank matrix recovery term, a low-rank only recovery can have multiple solutions for the under-sampled ms-DW recovery problem (8, 25, 26). In MUSSELS, the addition of the SENSE-based data-consistency term ensures the recovery to the desired solution. As a result, a limitation of the current MUSSELS formulations is that it cannot be employed for the recovery of single-channel msDW acquisitions. Since such acquisitions are becoming rare in the context of human neuroimaging DWI, we do not see this as a major limitation. Nevertheless, SLRMC enabled single-channel reconstructions have been shown before using GIRAF (11), ALOHA (36), AC-LORAKS (26) in various contexts, by formulating constraints using other priors. Single-channel phase correction in the context of EPI-ghost correction has been achieved using ALOHA and AC-LORAKS. In ALOHA, the additional constraint exploited is the sparsity of the gradient images in the Fourier domain. In AC-LORAKS, a fully sampled autocalibration region derived from a standard parallel imaging prescan(26) is exploited, from which the null space vectors are pre-computed. Hence, in contrast to MUSSELS and ALOHA(36), there is a fully sampled region of k-space that is shared by all the concatenated Hankel matrices of AC-LORAKS. This fully sampled region enables the accelerated channel-by-channel recovery in (26).

A separate aspect that needs further study is the maximum number of shots that can be recovered using MUSSELS as a function of the number of RF receive channels. Although the acceleration achievable in a traditional SENSE reconstruction is constrained by the number of channels, it has been shown that incorporating additional constraints can enable high acceleration factors (47). The addition of such priors to MUSSELS can also improve the achievable acceleration or equivalently the maximum number of shots. Using piecewise smooth signal model (48), we have shown the recovery of 8-shot data using SR-MUSSELS(8) in (9) from a 32-channel acquisition, which is also partial Fourier accelerated. The recovery of 9-shot data from a 32-channel acquisition using MUSSELS was recently shown in (49).

To overcome the slow msEPI acquisition, shot-accelerated msDWI methods can be employed. In figure S4 of supporting information, we show the results of a shot-accelerated reconstruction using IRLS MUSSELS with CS using 3 out of the 4 shots. The capability of MUSSELS to reconstruct highly (shot-) accelerated msEPI was reported in (49) also. Further, the extension of MUSSELS to incorporate slice acceleration was also demonstrated using real SMS-accelerated scans in (35) and simulations in (49). These reconstructions can also benefit from the IRLS formulation to reduce the computation time.

Conclusion:

We showed the utility of IRLS MUSSELS for fast recovery of msDW data. The scheme reduces the computation time by a factor of 6 which significantly brings down the time involved in reconstructing whole brain high-resolution msDW data to enable routine studies.