Viscoelastic properties of the human tympanic membrane studied with stroboscopic holography and finite element modeling

Abstract

A new anatomically-accurate Finite Element (FE) model of the tympanic membrane (TM) and malleus was combined with measurements of the sound-induced motion of the TM surface and the bony manubrium, in an isolated TM-malleus preparation. Using the results, we were able to address two issues related to how sound is coupled to the ossicular chain: (i) Estimate the viscous damping within the tympanic membrane itself, the presence of which may help smooth the broadband response of a potentially highly resonant TM, and (ii) Investigate the function of a peculiar feature of human middle-ear anatomy, the thin mucosal epithelial fold that couples the mid part of the human manubrium to the TM. Sound induced motions of the surface of ex vivo human eardrums and mallei were measured with stroboscopic holography, which yields maps of the amplitude and phase of the displacement of the entire membrane surface at selected frequencies. The results of these measurements were similar, but not identical to measurements made in intact ears. The holography measurements were complemented by laser-Doppler vibrometer measurements of sound-induced umbo velocity, which were made with fine-frequency resolution. Comparisons of these measurements to predictions from a new anatomically accurate FE model with varied membrane characteristics suggest the TM contains viscous elements, which provide relatively low damping, and that the epithelial fold that connects the central section of the human manubrium to the TM only loosely couples the TM to the manubrium. The laser-Doppler measurements in two preparations also suggested the presence of significant variation in the complex modulus of the TM between specimens. Some animations illustrating the model results are available at our website (www.uantwerp.be/en/rg/bimef/downloads/tympanic-membrane-motion).

1. Introduction

The natural mechanical properties of the human tympanic membrane (TM) lead to a sensitive response function over a broad frequency range. Despite several studies by different authors, there is still no consensus about which characteristics of the TM are essential for its broadly tuned response function. Proposed influential properties for the general behavior of the TM include the conical shape (Fay et al., 2006; Koike et al., 2001), the internal arrangement of collagen fibers (Fay et al., 2006), internal damping (Zhang and Gan, 2010, 2013), or some combination of these factors. The identification of the essential mechanical properties of the TM would potentially improve the treatment of a wide variety of eardrum pathologies. This paper addresses questions concerning the presence of damping within the TM by a unique combination of stroboscopic holography data of the TM surface motion, laser Doppler measurements of the umbo of the TM, and a Finite Element (FE) model of the TM structure and motion. We also address a peculiar anatomical feature of the human middle ear, the coupling of much of the length of the manubrium of the human malleus to the TM by a thin mucosal epithelial tissue layer, called the manubrial fold (Graham et al., 1978; Gulya and Schuknecht, 1995).

The chosen approach in this paper is to isolate the TM and the first ossicle, the malleus, from the rest of the middle ear and the cochlea. This preparation simplifies the system so we obtain well-defined boundary conditions of both measurement and model, and also remove any contribution of cochlear damping that may complicate estimates of damping within the TM. Experimental data is collected using stroboscopic holography, developed by the middle ear research group at Massachusetts Eye and Ear Infirmary and the Worcester Polytechnical Institute (Cheng et al., 2010, 2013). Measurements of the sound-induced motion of the complete lateral and medial surfaces of the TM are made at discrete frequencies. The medial surface measurements investigate the role of the not yet fully understood tissue fold interposed between the TM and the manubrium along much of the manubrial length (Graham et al., 1978). These surface displacement measurements are complemented by single-point vibrometry measurements that finely sample a broader stimulus frequency range, and allow better description of the frequency response of the TM and malleus. These two measurements place different constraints on our estimates of the complex modulus of the TM and the tissue fold that best fit our measurements. The experiments are described in Section 2.1. Section 2.2 presents the construction and characterization of the FE model of the TM and the malleus, followed by a description of the approaches we use to investigate each sub goal of the study. Experimental and finite element results are presented in Section 3 and are discussed in Section 4. Section 5 includes a summary of the conclusions from our work.

2. Methods

2.1. Experiments

2.1.1. Sample preparation

Measurements were performed on two fresh human temporal bones without history of otologic disease (TB1 and TB2). During temporal bone sample preparation, the bony external ear canal, cochlea, stapes, incus, stapedial and incudal ligaments and tensor tympani were removed, but the bony tympanic annulus and the anterior malleal ligament were kept intact. A photograph and line drawing of the medial surface of the isolated TM and malleus are shown in Fig. 1. For holographic experiments, the lateral (external) surface of the TM was painted with a suspension of 60 mg/ml of Zn0 (Fisher Scientific Z52-500 Zinc Oxide powder) in saline to increase the amount of light reflected from the surface. The effect of the paint on the vibration pattern of the TM has been shown to be small (Rosowski et al., 2009). We made three different functional measurements on each prepared bone: holographic measurements were made of the motion of the lateral and medial surfaces of the TM during controlled pure tone stimulation (0.5–18 kHz) of the lateral surface (Fig. 2A and B), and laser Doppler vibrometry was used to measure the broadband (70 Hz–20 kHz) sound-induced motion of the umbo of the malleus (Fig. 2C). In between experiments, the samples were stored in refrigerated saline solution to prevent dehydration and the breakdown of the ossicular ligaments and tissues of the TM.

Fig. 1.

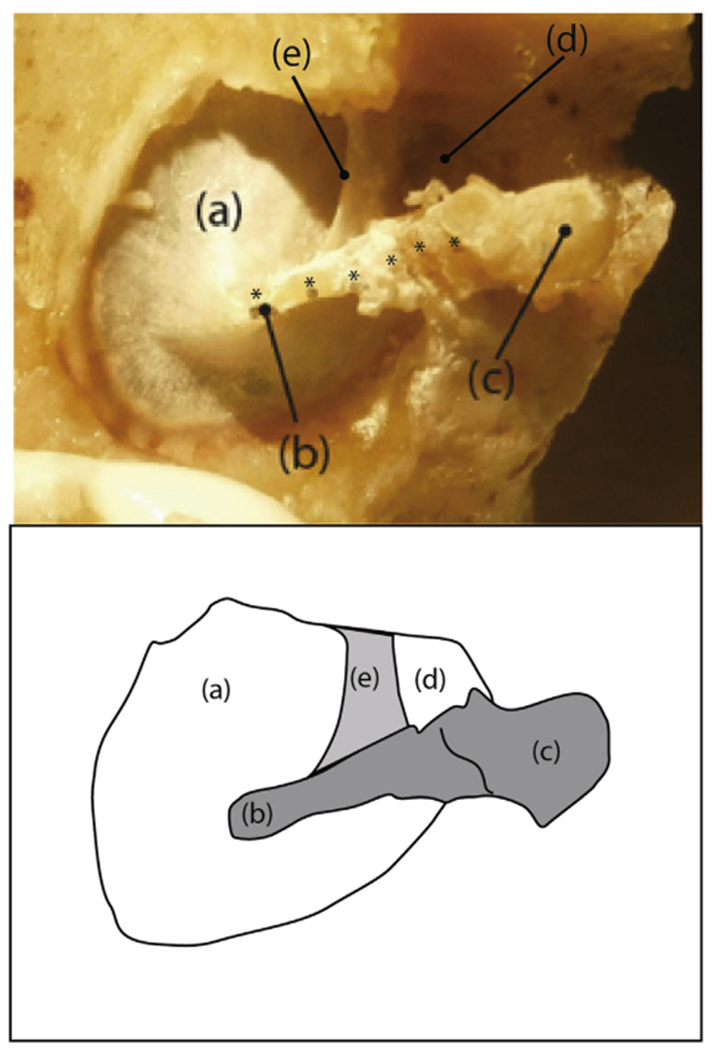
A photograph and sketch of the medial surface of a prepared sample (TB1): (a) pars tensa of the TM, (b) umbo of the malleus, (c) mallear head, (d) pars flaccida of the TM, and (e) the anterior malleal spine and fold. Six plastic reflective beads (each marked by an *) are visible along the manubrial arm and neck of the malleus. The six beads were used in measurements reported in Horwitz et al. (2012). In this report we only report measurements made at the umbo.

Fig. 2.

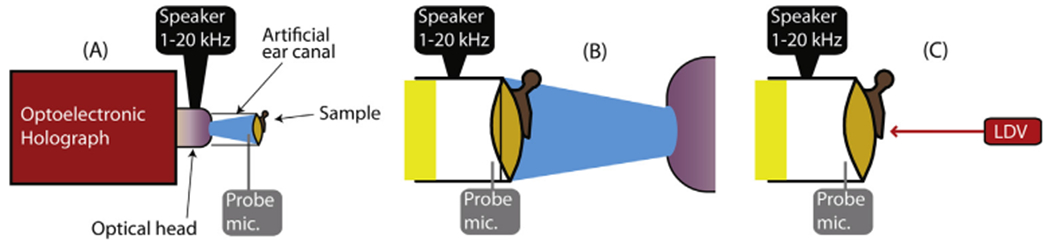
Schematics of the measurement setups. In each case a sound source is coupled to the lateral (external) surface of the TM via a clear artificial ear canal, and a probe microphone determines the sound pressure at the boney tympanic ring. (A) Holographic measurement of the lateral TM surface: The blue light is the dispersed laser illumination beam. The red Optoelectronic Holograph box contains the CCD camera and its optics. (B) Holographic measurements of the medial surface while acoustically stimulating the lateral surface. The foam yellow plug sealed the lateral end of the artificial ear canal. (C) Laser-Doppler measurements of the umbo of the malleus during sound stimulation of the TM lateral surface. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

2.1.2. Stroboscopic holography

Schematics of the holography experiments are shown on the left (A) and center (B) of Fig. 2. The painted and widely exposed TM was placed in a custom made fixture with the annular ring perpendicular to the object beam of the laser. Tonal sound pressures with 10–12 different frequencies in the range 0.5–18 kHz and sound pressure amplitudes from 80 dB SPL at low frequencies to 120 dB SPL at high frequencies were applied with a speaker connected to an artificial ear canal, and full-field measurements of the TM displacement component perpendicular to the annular ring were made. Measurements of TM surface motion were made from both the lateral (Fig. 2A) and medial (Fig. 2B) sides, while the sound excitation in both cases was presented to the lateral side. Medial measurements were required for the study of the TM-malleus connection, as explained later on in Section 2.2.5. The artificial ear canal had a long axis orthogonal to the annular ring of the TM. The actual sound pressure at the TM was measured with a probe-tube microphone (PCB Piezotronics Inc, Model 377C10) located very close to the edge of the TM surface. A series of sound pressure measurements at various probe positions suggested the sound pressure distribution on the TM was uniform in our experiments (Cheng et al., 2013). This is in contrast to natural circumstances, where the terminal portion of the ear canal is angled relative to the annular ring (Todd, 2009) and the sound field at the TM is not uniform at frequencies above 10 kHz (Stinson, 1985). The uniformity of the sound field in our measurements simplified the boundary conditions in both the measurements and the subsequent FE model.

In stroboscopic holography mode, the deformation of the TM is computed based on the optical phase difference between reconstructed holograms of the TM surface measured at two different time instants. The instants are defined by the pulsing of the ‘strobe switch’ (an opto-acoustic modulator capable of high-frequency switching) that is phase-locked to the acoustic stimulus. In this study, the sinusoidal motion of the TM driven by a continuous tone was determined from holograms that were gathered during ‘strobed’ laser pulse illumination at each of eight evenly spaced stimulus phases (ϕ = 0, π/4, π/2 … 7π/4). The membrane displacement is computed from the change in position between stimulus phase 0 (acting as a temporal reference) and the others. Each laser pulse had a duration of 5–10% of the period of the tonal stimulus. The holographic images of TM surface motions at the eight stroboscopic measurement instances (each image was 800 × 800 pixels) were used to construct full-field displacement maps as a function of time for each pixel on the TM surface. Fourier analysis of the time-dependent displacement waveforms at each measurement point yielded the magnitude and phase angle of the stimulated Fourier component at each point. For a more detailed description, see (Hernandez-Montes et al., 2009) and (Cheng et al., 2010, 2013).

2.1.3. Laser Doppler Vibrometry

A schematic of the laser Doppler vibrometry (LDV) experiment is shown in Fig. 2C. A reflective bead with a negligible mass was glued on the medial surface of the tip of the malleus (umbo) (Fig. 1). Tonal sound pressures with frequencies in the range 0.07–20 kHz and sound pressure amplitudes from 80 dB SPL to 100 dB SPL were applied. The velocity of the umbo at the bead position was measured with a laser Doppler vibrometer (Polytec OFV 501 Interferometer and OFV 2600 Laser Controller). The laser beam was focused on the bead and was approximately orthogonal to the TM surface at that point. The umbo transfer function was calculated by dividing the complex velocity, described by amplitude and phase, by the measured sound pressure and has a magnitude with units of m/s/Pa. The velocity data were also corrected for delays within the LDV velocity processor.

2.2. Finite element modeling

2.2.1. Morphology

Highly detailed morphologic data were imported from recent micro-CT measurements carried out at the University of Ghent Computer Tomography (UGCT) facility (Masschaele et al., 2007). Soft tissue structures, such as the TM, ligaments and muscles, absorb only a very limited amount of X-ray radiation under natural circumstances, in comparison to bony structures. Therefore, the samples were stained with phosphotungstic acid (PTA) (Metscher, 2009), allowing us to image both soft tissue and bony structures at the same time.

This led to a dataset of 1764 × 1775 × 1506 cubic voxels with a voxel size of 18 μm. Segmentation of the CT-slices, in which regions that represent the same material are identified, was carried out in Amira (Visage Imaging). A first distinction of separate structures was made by threshold-based region growing. However, despite the sample staining, automatic segmentation proved insufficient to detect all boundaries between components, so that significant manual input and expert knowledge of the middle ear anatomy was required in order to distinguish all structures. After segmentation, the different geometrical identities were converted to triangulated surface models and saved as ASCII .stl files (STereoLithography), which were imported in Comsol Multiphysics 4.2. The model geometry is based on a different specimen than those used in the motion measurements. Therefore this study cannot provide an exact quantitative comparison of measured and model motions, but does allow qualitative comparison. The geometric models can be downloaded freely at https://www.uantwerp.be/en/rg/bimef.

2.2.2. Boundary conditions and model description

The FE mesh that was constructed is depicted in Fig. 3 with color-coded structures. The TM has a curved (tent) shape and has a non-uniform thickness, shown in Fig. 4. Note that the precision of this thickness determination is limited by the relatively large voxel dimensions (18 μm) compared to the TM’s thickness. The thickness is calculated based on the segmented voxel data through the ‘shortest distance’ algorithm, developed and elaborated in (Van der Jeught et al., 2013).

Fig. 3.

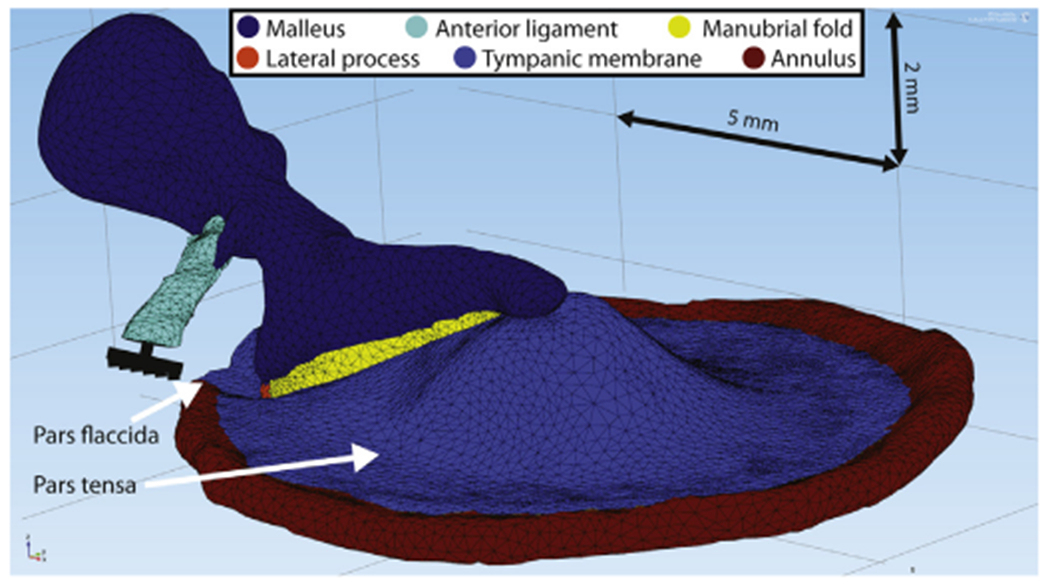
Finite element model with imported middle ear structures of a right human ear. The 5 mm and 2 mm scale bars are located in the model’s coordinate planes.

Fig. 4.

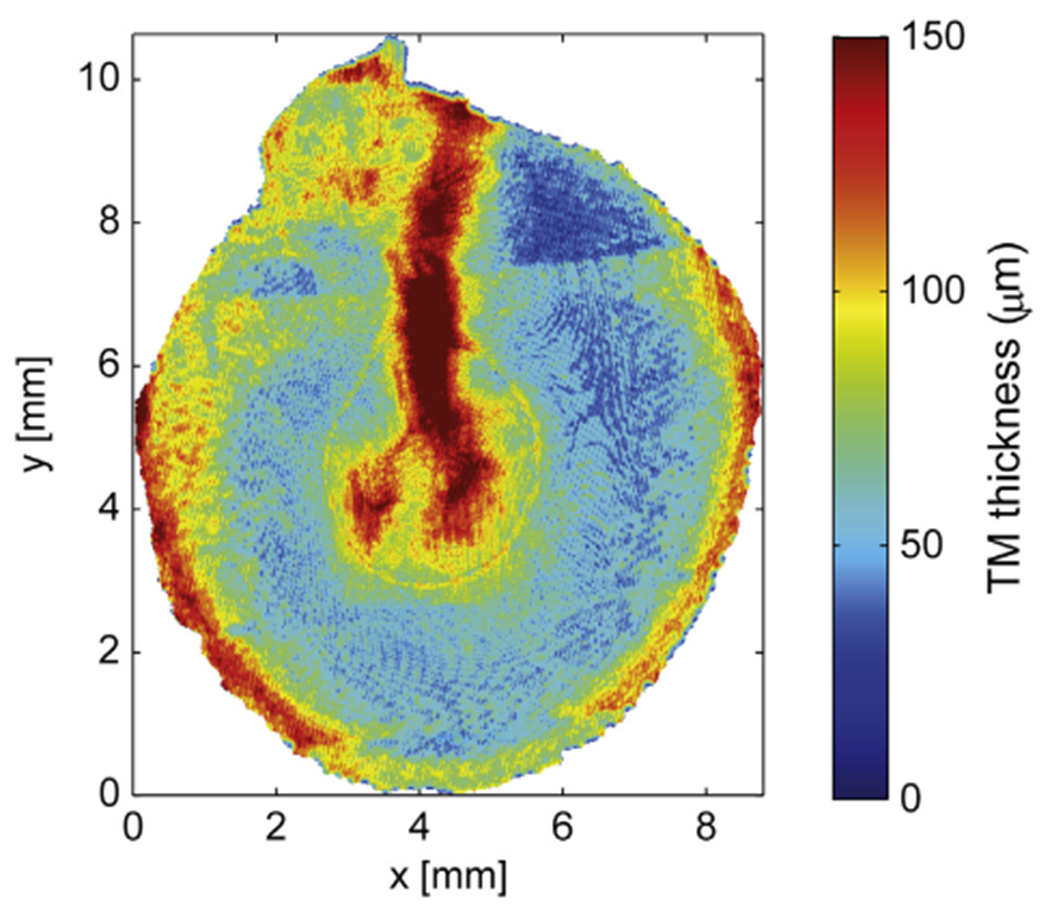
The thickness of the TM coded in the finite element model composed from segmentation of CT-images of a right human ear. The segmented TM opposite the manubrium of the malleus is significantly thicker than most other locations.

In the model, connected structures (e.g. the boundary between the annular ring and the border of the TM) share nodes at their interfaces and are inherently rigidly connected to each other so that they feature equal displacements in these shared nodes. All materials were assumed isotropic. In this study, the pars tensa and pars flaccida were given the same material properties. The bony annulus (red structure on Fig. 3) is rigidly constrained as a fixed body, is assigned the same material parameters as the malleus and the lateral process and is connected to the outer boundary of the pars tensa. Since it is fully constrained, the annulus is simply a support ring for the TM and does not absorb any computational power. The pars flaccida is not connected to the annulus at its outer rim, but has fixed boundary surfaces at its edges. The end surface of the anterior ligament was rigidly fixed as well; this ligament, along with the TM, acts to suspend the malleus.

As described by Graham et al. (1978) and Gulya and Schuknecht (1995), the connection between the TM and the manubrium is tight at the umbo (the tip of the malleus located in the center of the TM) and at the bony lateral process of the malleus (located at the rim of the TM), see the left and right sides of Fig. 5. Therefore, at these points, the model’s bony malleus and lateral process share interface nodes with the TM. In between the umbo and lateral process, the connection between the TM and manubrium is a fine fold of mucosal epithelial membrane called the manubrial fold (middle-panel of Fig. 5), which is depicted in yellow in Fig. 3.

Fig. 5.

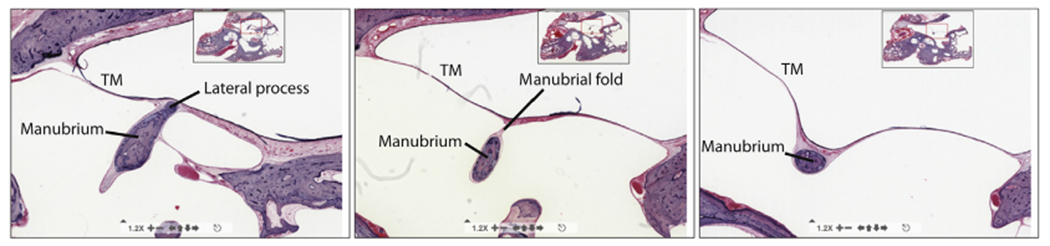
Histological sections collected from a single human right ear: at the lateral process (left), at a point midway between the lateral process and the umbo (middle), and at the umbo (right). Images from www.temporalboneconsortium.org.

Modeling was done in the frequency domain (harmonic analysis). A uniform single-frequency harmonic pressure was applied as a loading stimulus at the lateral surface of the TM, and the steady-state response of the entire geometry was calculated.

2.2.3. Damping

The soft tissues (TM, anterior ligament and manubrial fold) were treated as viscoelastic materials, while the bony structures (malleus, annulus and lateral process) were treated as purely elastic materials (i.e. a loss factor equal to 0). The stiffness and viscoelastic (damping) values of the TM and the TM-manubrium connection (manubrial fold) were investigated in this study. Other values were taken from the literature or based upon previous work that is not discussed here, see Table 1.

Table 1.

Material properties: Young’s modulus E, Poisson’s ratio v, loss factor η and density ρ. Values that are underlined are discussed in this study.

	TM	Manubrial fold	Lateral process	Anterior ligament	Malleus
E [MPa]	10–40	10% of TM	16000	21a	16000b
v	0.3c	0.49	0.3d	0.3d	0.3d
η	0.01–0.13	Same as TM	0	Same as TM	0
ρ [kg/m3]	1200d	1200d	2200e	1200d	2200e

^aA range of [2.1-21] MPa is used in the literature (Zhao et al., 2009). In our study, 21 MPa gave the best results, although this is not shown in this work.

^bThis value is based upon (Soons et al., 2010).

^cThis value is used in most of the current middle ear FE models (Zhao et al., 2009; Volandri et al., 2011), and can be seen as a compromise between an incompressible material (v = 0.5) and a material composed of parallel fibers with no lateral interaction (v = 0) (Funnell and Laszlo, 1982). We furthermore compared model outcome for this value with the nearly incompressible case (v = 0.49), which showed almost no difference.

^dThese values are used in most of the current middle ear FE models (Volandri et al., 2011).

^eThis value is based upon the reported malleus volume in (Salih et al., 2012) and the reported malleus mass in (Nummela, 1995).

Viscoelasticity was modeled by using a complex modulus in the frequency domain:

$$E^{*}(\omega )=E_1(\omega )+i{E}_2(\omega )=E_1(\omega )[1+i\eta (\omega )],$$ (1)

with ω the angular frequency, E₁(ω) the storage modulus that accounts for the elastic portion (comparable to the conventional elastic Young’s modulus), E₂(ω) the loss modulus that accounts for the viscous portion, η (ω) = E₂(ω)/E₁(ω) the loss factor and i the imaginary unit. A larger η expresses higher internal damping. Comsol uses E₁(ω) and η(ω) as input parameters. Both E₁ and E₂ are expressed in units of stress (Pascal), while η is a dimensionless scalar.

Four sets of possible damping parameters were investigated.

(Model 1) To the best of our knowledge, the only work in which the damping or viscoelastic properties of the TM are directly determined at frequencies within the hearing range is (Zhang and Gan, 2010). In that work, tones with frequencies from 0.2 to 8 kHz were used to stimulate cut-out strips of human TM, and the center displacement was measured with a laser Doppler vibrometer. The experiments were then simulated using FE modeling in which the TM was modeled with a generalized Maxwell viscoelastic model (see the Appendix). The parameters of the generalized Maxwell model were found through inverse analysis, yielding a loss factor that more or less increased logarithmically over the measured frequency range from 3.5% to 9.5%. We extrapolated these data across our measurement range, yielding a loss factor of 1% at 20 Hz that increases to 13% at 20 kHz. The definitions and values of the parameters of the generalized Maxwell models used by Zhang & Gan and in our extrapolations are provided in the Appendix

Model 1:

Loss factor, 1% at 20 Hz increasing to 13% at 20 kHz (Zhang and Gan, 2010; modified).

(Models 2 & 3) In other current middle ear FE models, damping is described in terms of Rayleigh damping instead of using a complex modulus. With Rayleigh damping, the system damping matrix is expressed as αM + βK, where M and K are the system mass and stiffness matrices and α and β the damping parameters. The relation between the loss factor and these Rayleigh parameters is frequency-dependent: η = α/ω + βω. The coefficient values of (Volandri et al., 2011), α = 260 Hz, β = 3.7 ⋅ 10⁻⁵ s (model 2) and α = 0 Hz, β = 1 ⋅ 10⁻⁴ s (model 3), are used to predict TM function. These values are not based upon experiments but they produced reasonable predictions of the TM function.

Model 2:

Rayleigh damping, α = 260 Hz, β = 3.7 ⋅ 10⁻⁵ s (Volandri et al., 2011)

Model 3:

Rayleigh damping, α = 0 Hz, β = 1 ⋅ 10⁻⁴ s (Volandri et al., 2011)

(Model 4) In a recent study (Aernouts et al., 2012), the viscoelastic properties of human TM at quasi-static frequencies (0.001–3 Hz) were investigated by applying in situ step indentations and measuring force relaxation. The relaxation curves in the time domain were transformed to complex moduli in the frequency domain. The obtained loss factor curves were more or less constant across the measured frequency range with an average value of 7.8%. In the current study, this value was extrapolated over the hearing frequency range.

Model 4:

Loss factor, 7.8% for all frequencies (Aernouts et al., 2012).

The four loss factors are plotted against frequency in Fig. 6. Note that both the horizontal and vertical axes are logarithmic. The values for the four curves are considerably different, for instance, at 20 kHz the loss factor for the extrapolated measured data of Zhang & Gan (Model 1) is 13% while the two Rayleigh damping estimates (Models 2 & 3) produces loss factors of 465% and 1257% respectively. There are also large differences between the different damping estimates at low frequencies.

Fig. 6.

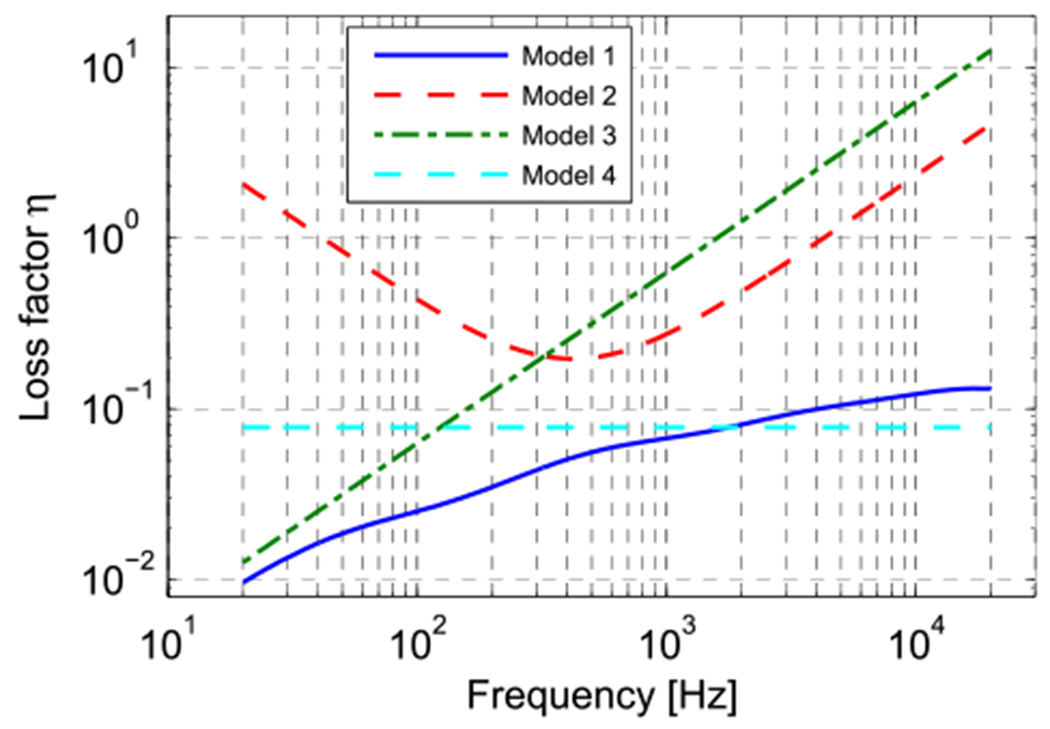
Loss factor curves of the four different damping cases, defined in Section 2.2.3.

2.2.4. Stiffness

The stiffness of the human TM has been measured in a number of studies. In a recent study, mechanical properties of human TM were investigated using in situ indentation measurements (Aernouts et al., 2012). For a quasi-static indentation frequency of 0.2 Hz, an average Young’s modulus of (2.9 ± 1.3) MPa was found. This value is considerably less than most of the values in the literature, which range from 20 MPa to 60 MPa. Aernouts et al. (2012) also report that the value for the Young’s modulus that is needed to fit model predictions to experimental data is very dependent on the thickness used in the model. Since the average TM thickness as well as the thickness distribution varies significantly across different individuals (Van der Jeught et al., 2013), it is difficult to make a quantitative analysis of TM stiffness if the model is based on a different specimen than the experimental results. The thickness distribution of the model’s TM is shown in Fig. 4 and shows that most of the TM’s thickness values in the mid part halfway between the manubrium and the annulus are in the range of 30–100 um. The thickness values of the TM close to the annulus and in the zone covering the manubrium are significantly higher, up to 240 um, although it should be noted that neither the manubrial fold nor the annulus itself were included in this thickness calculation, so the data indicate a true membrane thickening in these parts.

Since the TM should be described as a viscoelastic material, its stiffness is frequency-dependent. In this work, viscoelasticity is incorporated by a complex modulus (Equation (1)), which can be characterized by the magnitude |E*(ω)| and loss factor η(ω) as described in Section 2.2.4. We will use the loss factor described by damping model 1 from above to study the stiffness of the TM material. We will compare our measurements with model predictions made while varying the magnitude of the complex modulus: these variations were produced by multiplying the normalized spring constants of the generalized Maxwell model coefficients given in the Appendix by a variable constant to fit measurements of the umbo-velocity transfer function in two prepared specimens. The umbo LDV velocity data were used, because their low-frequency values were most affected by variations in membrane stiffness.

2.2.5. Manubrial fold

While the human TM and malleus appear tightly coupled at the umbo and lateral process, the coupling between these structures at other locations along the manubrial arm depends on the mechanical properties of the manubrial fold (Graham et al., 1978; Gulya and Schuknecht, 1995). The manubrial fold is composed of a thin singlecell layer epithelial tissue. In our model the manubrial fold was assumed to be nearly incompressible and given a Poisson’s ratio equal to 0.49, which is close to the theoretical upper limit of 0.5. Furthermore, it was assigned a complex modulus to account for viscoelasticity (eq. (1)). Since there is no literature on the viscoelastic properties of the manubrial fold, we assumed the loss factor we determined for the TM (i.e. model 1 from Section 2.2.3), and model responses were calculated for storage moduli that were 1%, 10% and 100% of the TM storage modulus that was found optimal in the study of TM stiffness (see Section 3.2.2).

3. Results

In this section, we first present the results of the experimental measurements. Then, the model outcomes for the viscoelastic properties of the TM and the manubrial fold that connects the malleus to the TM are described. For reasons of visual interpretation and to limit the number of figures, experimental and FEM data are often presented in the same figure; however, as noted above, the model predictions are all discussed in a later section of the text.

3.1. Experimental results

3.1.1. LDV

Figs. 7 and 8 illustrate experimental LDV data on TB1 (the dashed blue line in Fig. 8) and TB2 (the solid black line in Fig. 7, and the dashed red line in Fig. 8). These two figures will be used to assess the real (stiffness) and imaginary (damping) parts of the complex modulus of the model TM. Both figures show the magnitude and phase of the umbo transfer function (the complex ratio of the magnitude and phase of the umbo velocity and the stimulus sound pressure measured lateral to the TM) as a function of frequency. Each of the measurements feature a damped resonance (near 300 Hz in TB1 and 600 Hz in TB2) where the transfer function magnitude reaches a maximum and the phase angle goes through 0. The resonance in TB1 is more damped, as illustrated by its less-sharp maximum and gentler phase transition through 0. However, both of these measurements are consistent with other umbo velocities measured in humans after interrupting the ossicular chain (e.g. Rosowski et al., 2008)

Fig. 7.

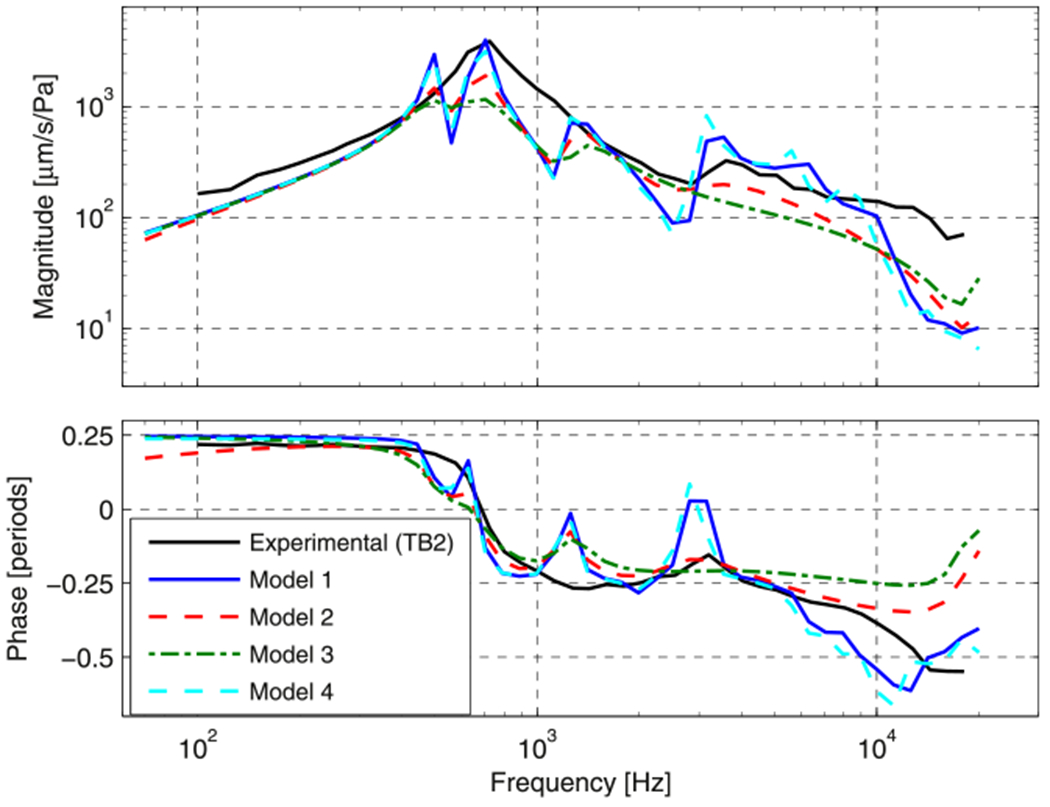
Normalized umbo velocity magnitude and angle for the four damping cases (see Section 2.2.3 and Fig. 6) and experimental data from TB2 (black line).

Fig. 8.

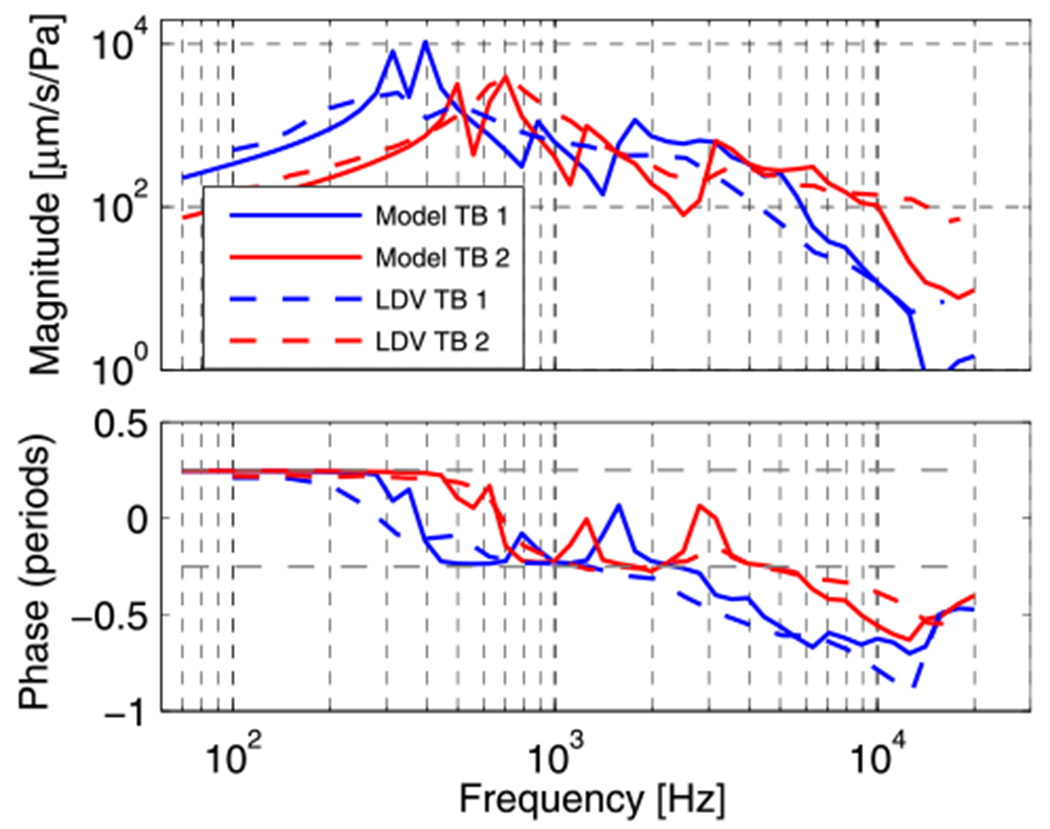
Experimental (laser Doppler Vibrometry) and model umbo velocity response for the two samples.

At frequencies below the frequency of maximal motion magnitude the umbo in TB1 and TB2 moves in phase with the pressure wave (the 0.25 period angle difference between the velocity and the stimulus pressure is consistent with an in-phase behavior of pressure and displacement), as is consistent with a stiffness dominated response. Between the frequency of maximal magnitude and 2–3 kHz, the transfer function phase becomes more negative, which is consistent with the effects of damping and an increase in reactance due to inertia. Above 2–3 kHz, the transfer function phase becomes more negative than −0.25 periods and is no longer easily explainable in terms of a simple mechanical element.

3.1.2. Digital holography

The great strength of the developed stroboscopic holographic setup is that full-field information of both amplitude and phase are determined with high spatial resolution. Experimentally derived maps (from TB1) are presented in the left-most column of Fig. 9 for frequencies 1, 7 and 16 kHz. (The illustrated results are exemplary of other measurements made at other frequencies.) The phases in each map are relative to the umbo phase. At 1 kHz, the TM in TB1 moves with one large and two smaller local areas of maximal displacements, where the two smaller areas are approximately 180° out of phase with the local maximum with the largest area. At higher frequencies, the motion becomes more complex with multiple local displacement maxima that tend to form rings around the manubrium and which show repeating phase variations that are neither continuously varying nor 180° out-of-phase. Similar results were obtained for TB2. Overall, these patterns are similar to holographic measurements made in middle ears with intact ossicular chains coupled to inner ears (Cheng et al., 2010, 2013). The location and the number of maxima and the overall magnitudes at the lowest frequencies do differ somewhat from the previous measurements. The higher frequency data show much qualitative similarity to measurements made with an intact incus, stapes and cochlea. Note the presence of graded changes in displacement phase with location, especially between the locations of the spatially small local maxima in displacement magnitude observed at 7 and 16 kHz.

Fig. 9.

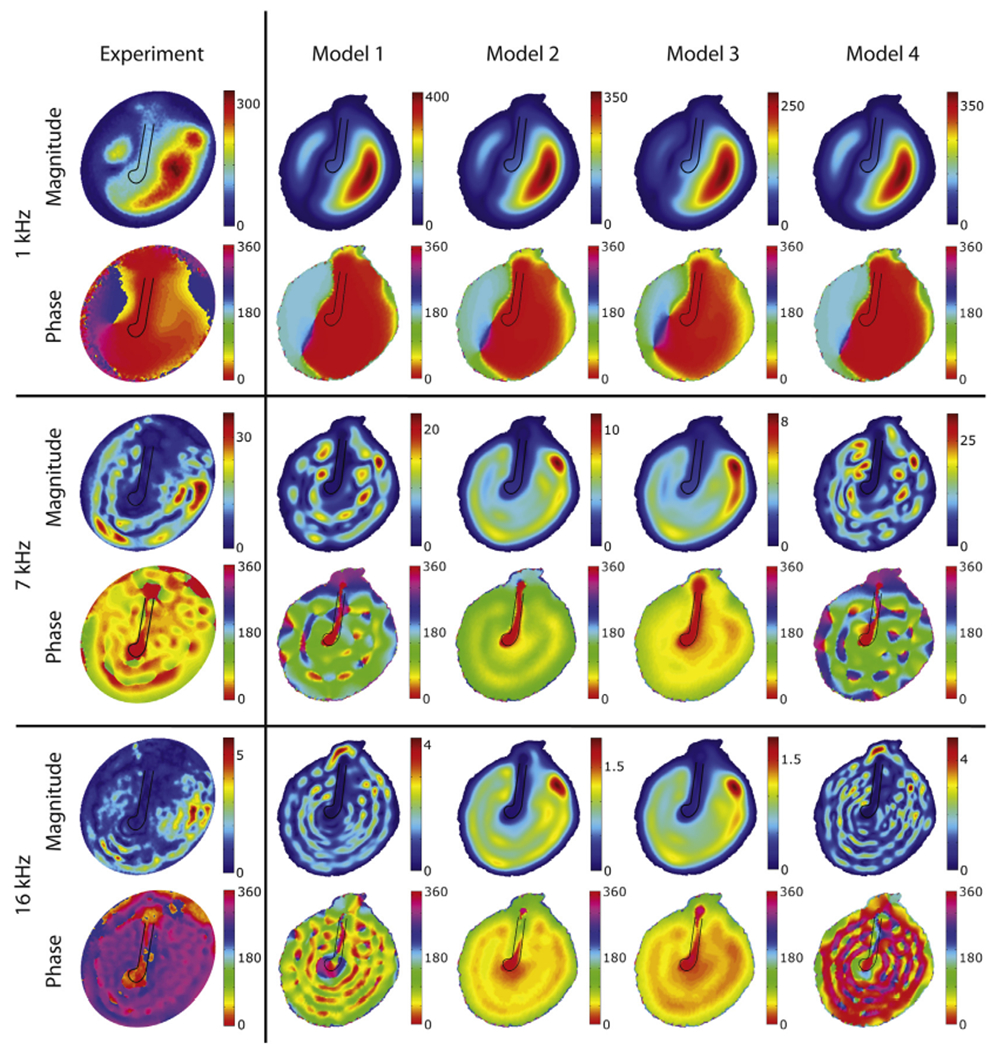
Displacement magnitudes [nm/Pa] and phase [deg] of the lateral surface of the TM for selected tonal stimuli of 1, 7 and 16 kHz (the phase is relative to the umbo position). The loss-factors used in the models are defined in Section 2.2.3 and illustrated in Fig. 6.

Fig. 10 contains holographically determined displacements of the TM lateral to the manubrium from the ear canal side in solid lines, and of the manubrium, measured from the medial side (middle ear cavity side) in dashed lines at representative stimulus frequencies of 2 kHz, 7 kHz and 13 kHz. The left column contains data from TB1, the middle column from TB2. The displayed magnitude and phase are normalized by the displacement at the umbo. The methods are schematized in the inset at the top of Fig. 10. Note that the entire lateral surface of the TM is visible from the lateral view, including the portion opposite the entire manubrium. In the medial view, however, the lateral process and other parts of the superior manubrium are blocked by the malleus neck and head. Nonetheless, our holography measurements quantify the component of the motion of the head and neck that parallels the illuminating laser beam.

Fig. 10.

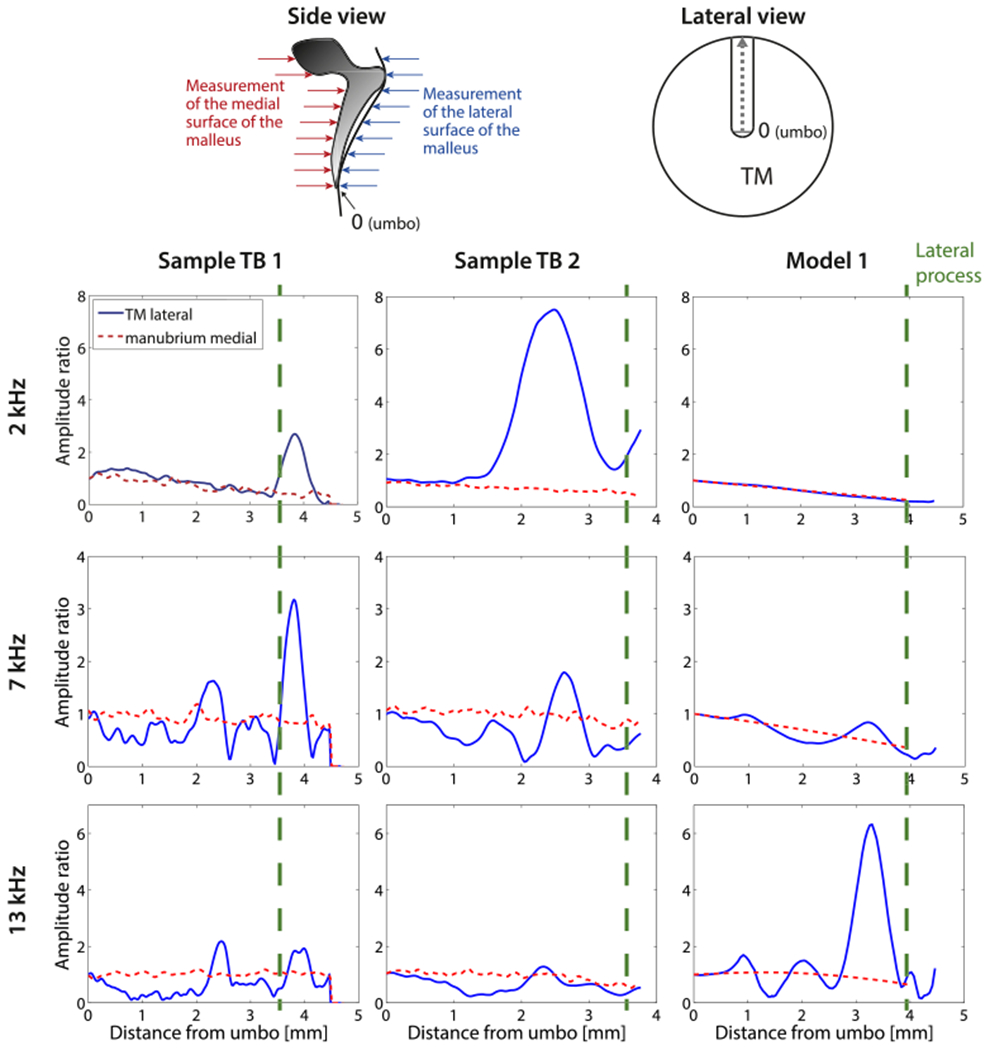
Comparison of lateral displacements of the TM along the length of its attachment to the manubrium and medial displacements of the manubrium and malleus neck and head, for frequencies of 2, 7 and 13 kHz. The schematic on the upper right represents the view of the lateral surface of the manubrium from the ear canal. The schematic on the upper left illustrates the motion components that were measured by the holography system when it viewed either the lateral or medial surface of the TM. The data are normalized to the umbo. Left and middle column: Holographically measured displacements from sample TB1 and TB2. Right column: model prediction of the motion of the lateral surface of the TM opposite to the manubrium and the medial surface of the manubrium. The vertical dashed lines on the plots indicate the location of the lateral process. Locations on the lateral surface of the ear canal superior to the lateral process represent measurements on the surface of the pars flaccida of the TM. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

The displacements measured near the umbo in the lateral (blue (in web version) solid lines) and medial (red (in web version) dashed lines) views were very similar, consistent with tight coupling of the umbo to the TM. There is also a similarity in the displacement magnitudes measured from the lateral and medial directions near the lateral process (about 3.5 mm from the umbo). In between these two locations, in the middle of the manubrial arm, there are significant differences between the displacement of the TM lateral to the manubrium and the bony medial surface of the manubrium. At certain points along the manubrial arm, the measured displacements along the lateral surface of the TM itself can be up to 5 times larger or smaller (differences of ±14 dB) than the displacement of the manubrium at that same location. These differences are consistent with the structural observations of weak coupling between the TM and manubrium in between the umbo and the lateral process (Graham et al., 1978).

While there are clear differences between TB1 and TB2 in Fig. 10, the displacement patterns are qualitatively similar. At 2 kHz the motion magnitude of the medial surface of the manubrium decreases regularly with distance from the umbo (consistent with a lever action of the manubrium), and this is matched by a decrease in the motion of the lateral TM surface with distance at locations near the umbo. However, between the umbo and the lateral process there is a significant increase in the motion of the lateral surface in TB2, which returns to near the medial displacement levels at the lateral process. At 7 and 13 kHz, the displacements along the medial surface of the manubrium become more constant – consistent with simple translation of the manubrium (Decraemer and Khanna, 2004) – or exhibit variations in the gradient of motion with position – consistent with bending of the manubrium (Decraemer and Khanna, 2004; De La Rochefoucauld and Olson, 2010). On the lateral TM surface there are a number of local maxima and minima in the motion of the TM opposite to the manubrium. These local variations in magnitude are consistent with variations in the magnitude and phase of the motion of the surface of the TM opposite the manubrium that are observed in Fig. 9, which also suggest a loose coupling of the TM to the manubrium by the fold.

3.2. Finite element modeling

In order to constrain the estimates of the damping properties of the TM, we compare our measurements to FE model predictions. The model calculates the umbo transfer function (as defined in 2.1.3) and full field TM surface motions using four different estimates of damping (Figs. 7 and 9). In performing these model evaluations, the elastic modulus of the TM, E₁(ω), was fixed at a value that produced a low-frequency model response consistent with measurements of the umbo-velocity transfer function (Fig. 8). After deciding on the best-fit model damping parameters, we use the umbo-velocity transfer function to investigate the effects of variations in the magnitude of the models complex modulus magnitude (Fig. 11). The predictions of the effects of variations in the storage modulus of the manubrial fold on the motion of the TM and malleus are compared to the results of Fig. 10.

Fig. 11.

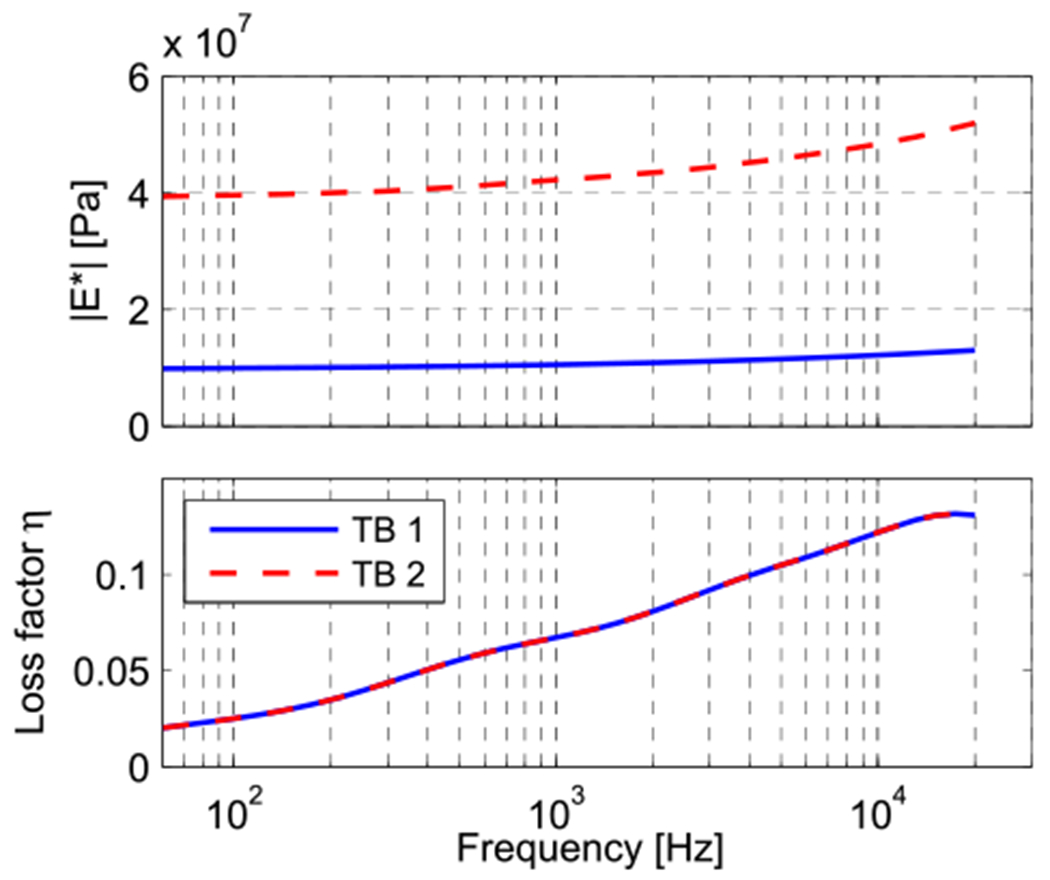
Complex modulus magnitude and phase values of the TM used for the two model data sets. Both magnitude curves differ merely by a multiplication factor, while the phase data is equal for both models and represents model 1 defined in Section 2.2.3 and depicted in Fig. 6.

3.2.1. TM damping

Fig. 7 compares predicted model umbo transfer functions (umbo velocity normalized by the stimulus sound pressure) magnitude (upper panel) and phase (lower panel) using the four different damping cases, defined in Section 2.2.3, to a measurement of this transfer function on TB2. While the phase of the measured transfer function changes relatively slowly with frequency, except near 700 Hz where there is an apparent resonance, the model predictions superimpose multiple peaks and valleys accompanied by rapid phase changes on this pattern. Generally the higher the loss factor the smoother the predicted transfer function. While all of the model predictions have some features in common with the measurement, models 1 and 4 match the peak in umbo velocity transfer function (at 0.7 kHz) and the high-frequency response better than the other models. Models 2 & 3 produce a smoother frequency response, but underestimate the measured magnitudes near 0.7 kHz and between 3 and 10 kHz.

As seen in Fig. 9, the model predictions with the four different damping parameters exhibit very similar spatial vibration patterns at 1 kHz, but the magnitude of motion varies across the four damping cases (pay attention to the color bar limits): The higher the loss factor at 1 kHz, the smaller the motion magnitude. These motion patterns are generally consistent with the displacements measured with the laser. At 7 kHz, the differences between the four predictions are larger. Models 2 and 3 have a higher loss factor at 7 kHz than the others (see Fig. 6) and produce displacement patterns with fewer local maxima. The same is true at 16 kHz. Models 1 and 4 produce motions of magnitude that are more similar to the measurements and exhibit more of the fine-scale variations in magnitude and phase measured on the surface of the experimental specimen at higher frequencies. Overall, it is clear that models 1 and 4 agree best with the experimental data. Our website (www.uantwerp.be/en/rg/bimef/downloads/tympanic-membrane-motion) and the electronic version of this paper present animated pictures of the response of model 1 at these frequencies. Videos 1, 2 and 3 and our website (www.uantwerp.be/en/rg/bimef/downloads/tympanic-membrane-motion) present animated pictures of the response of model 1 at these frequencies. We conclude that a moderate loss factor (<15%) that is either constant or increases with frequency matches the measured full field TM displacements. Very recently, new data on TM viscoelasticity was published, reporting a loss factor varying from 2% at 1 Hz to 15% at 3800 Hz (Zhang and Gan, 2013), which is very similar to our findings. These values were deduced from dynamic mechanical analysis (DMA) measurements in the frequency range of 1–40 Hz and extrapolated using frequency–temperature superposition.

Supplementary video related to this article can be found at http://dx.doi.org/10.1016/j.heares.2014.03.002.

3.2.2. TM stiffness

As explained in Section 2.2.4, in order to find the TM stiffness, we apply damping model 1 as defined in Section 2.2.3 and apply different multiplication factors to the spring constant of the generalized Maxwell model (defined in the Appendix) so that it matches optimally with the experimental umbo LDV data of both samples (Fig. 8). Aside from such differences in the complex modulus magnitude, the models fitting the two experimental results are equal. The resulting magnitudes of the complex moduli are shown in Fig. 11, together with their common loss factor. For TB1, the complex modulus had a magnitude value of 10 MPa at 70 Hz and grows to 13 MPa at 20 kHz. For TB2, the complex modulus had a magnitude value of 40 MPa at 70 Hz and 52 MPa at 20 kHz. Note that both curves differ merely by a multiplication factor of 4.

Fig. 8 contains comparisons of the experimental magnitude and phase of the umbo velocity transfer functions for the two temporal bones TB1 and TB2 (plotted as dashed lines, blue and red respectively) with model predictions, using the above described best estimates for the TM’s complex modulus in ‘model TB1’ and ‘model TB2’ respectively (following the same color code). The larger complex modulus needed to fit the TB2 data (Fig. 11) shifts the resonance frequency upwards and decreases the velocity at lower frequencies (Fig. 8). This behavior is consistent with the low-frequency behavior of a simple one-dimensional damped oscillator in which the stiffness is increased; however, the multiple peaks and stepped phase changes in the model predictions at higher frequencies are not consistent with such a simple system.

3.2.3. Manubrial fold stiffness

Model predictions with varied storage moduli of the manubrial fold were performed to investigate the consequences of this fold on the measurements in Fig. 10. A storage modulus of the fold that is 10% of that of the TM storage modulus reproduced some of the measured differences between the motion along the manubrium and the motion along the TM surface just lateral to the manubrium. Although the agreement between model and experiment is far from perfect, there are clear instances of similarity: 1) the deviations of the motion of the lateral surface of the TM from the manubrium are largest between the umbo and the lateral process; 2) the number of areas with large differences in the motion of the lateral TM and medial manubrium surface increase with frequency; 3) the lever-like linear gradient of displacement of the manubrium is observed at 2 kHz and 7 kHz; 4) both the model manubrium and the measurement in TB2 show signs of bending at 13 kHz. A significant difference is that the peak in the magnitude of the displacement of the lateral TM between the umbo and lateral process in TB2 at 2 kHz is not observed in model results. The model also does not predict the increases in motion magnitude of the lateral surface of the TM observed superior to the lateral process (distance > 3.5 mm); these peaks may indicate the presence of the more compliant pars flaccida in the two temporal bones. Differences between pars tensa and flaccida are unexpected in our model because we chose equal membrane parameters for both membrane components.

Reducing the storage modulus of the model’s manubrial fold to 1% of the TM storage modulus resulted in a significant increase in the ratio of motion of the lateral TM and the manubrium, characterized by amplitude ratios of up to 35 at 13 kHz. A storage modulus equal to the TM (100%) reduced the motion of the lateral surface of the TM by equalizing the displacements of the manubrial and TM surfaces at frequencies below 12 kHz. The significant interindividual differences in the spatial variations observed in the two cases together with the less than perfect model fits of the detailed variations is suggestive of significant mutual variations in TM and manubrial fold anatomy between the two experimental specimens and the anatomic specimen used to construct the model. Due to these differences, it is impossible to make a more precise estimation of the properties of the fold.

The manubrial fold seems to be a peculiarity of human middle ear anatomy and is not considered in most middle ear FE models. Exceptions are (Koike et al., 2002), in which the manubrial fold is modeled with a stiffness that is 1/1000 the stiffness of the TM, and (Sun et al., 2002) and (Gan et al., 2004), in which the manubrial fold and the rest of the manubrium is modeled with a stiffness that is one third the stiffness of the ossicles. Although our analysis did not yield a precise quantitative description of the modulus of the fold, our modeling results suggest that the manubrial fold should be included as a separate structure and modeled with a significantly lower stiffness than the TM (10% in our models) to account for the relatively loose coupling between the manubrium and TM motion. This loose coupling allows some independent motion of the manubrium and the lateral TM (Fig. 10), but does constrain TM motion. This constraint must be responsible for the observation of the low relative motion of the TM lateral to the manubrium compared to the rest of the TM, that is readily visible the experimental data of Fig. 9 as well as in other published measurements of TM motion in humans (Cheng et al., 2010, 2013).

4. Discussion

In this section, we discuss the significance of our experimental and modeling results.

4.1. The combination of motion measurements and FE modeling

We have combined full-field holographic and single-point laser vibrometer measurements of TM and umbo motion with an anatomically accurate FE model. The measurements were made in two cadaveric human temporal bones with greatly reduced ear canals and with the incus, stapes and inner ear removed. This preparation allowed easy access of the measurement systems to both the lateral and medial sides of the TM. It also simplified the boundary conditions on the FE model.

A limitation on our procedures is that measurements were only made in two temporal bones, and that the anatomical specimen was a third temporal bone. While our measurements and model predictions show many qualitative similarities that allowed estimation of several significant mechanical parameters of the TM, the differences between the two experimental measurements and the small anatomical differences between the anatomical and the experimental specimens prevent better quantitative assessment of these parameters. Nonetheless, our data do demonstrate significant effects of several model parameters and features, and suggest order of magnitude values for these parameters.

4.2. Internal damping smooths spatial and frequency-dependent variations in TM motion

Our measurements and model predictions suggest that a low-level of internal damping is required to smooth the frequency dependence of the umbo motion (Fig. 7), but still allow the observed small regular spatial variations in the magnitude and phase of the motions of the TM surface (Fig. 9). A too high damping reduces the peak magnitude and the high-frequency response of the umbo-velocity transfer function (Fig. 7), and also smooths away the small spatial variations in magnitude and phase seen in the model predictions of TM surface motion with lower damping.

While we show no data on this issue, we did look at model predictions when the damping was set to zero. In this case the model also failed to reproduce the multiple local spatially-graded variations in amplitude and phase that are observed in the measurements and model 1 and 4 predictions in Fig. 9. The consequences of zero damping can be understood in terms of a model of the summed modal motion of a circular plate or membrane that is stimulated harmonically and uniformly (Fletcher, 1992),

$$z(r,\varphi ;t)=\frac{p}{\rho d}\sum _{m,n}\left[\frac{{{}^{\Psi }}_{mn}(r,\varphi )\underset{S}{\int }{{}^{\Psi }}_{mn}\left(r^{\prime },{\varphi }^{\prime }\right)\mathrm{d}{S}^{\prime }}{({\omega }_{mn}^2-{\omega }^2)+2i\omega \alpha (\omega )}\right]e^{i\omega t},$$ (2)

with z describing the time dependent out-of-plane displacement in radial coordinates r and ϕ, t the time, p the input pressure, ρ the density, d a uniform thickness value, Ψ_mn the eigenmodes with radial frequency ω_mn, S the surface area of the membrane, ω the driving frequency, α(ω) a coefficient accounting for all types of damping (internal and external) and i the imaginary unit. The eigenmodes have the form:

$${{}^{\Psi }}_{mn}(r,\varphi )=[A_{mn}{J}_m(k_{mn}r)+B_{mn}{N}_m(k_{mn}r)]\cos m\varphi ,$$ (3)

where A_mn and B_mn are amplitudes of the different Bessel components, J_m(x) is the mth order Bessel function of a the first kind, N_m(x) is the mth order Neumann function and k_mn is the wavenumber of the mn mode. The term in brackets on the right side of Equation (3) describes a series of circular nodes, while the cosine function describes a set of radial nodes. When the damping is set to equal zero in Eq. (2), the predicted displacements are all either in phase with each other or completely out of phase. This result suggests, the continuous graded phases of the driven displacements that we observe in our measurements depend on non-zero damping.

The introduction of slow spatial phase gradients into model predictions by the addition of damping within the membrane is of interest. Earlier descriptions of such spatial gradients in the phase of motion on the TM surface have described them as ‘traveling-wave-like’ (Cheng et al., 2010, 2013; Rosowski et al., 2011). The model analysis here suggests that the appearance of traveling-wave-like phase gradients on the TM surface can simply be the result of uniform modal stimulation of a damped membrane.

4.3. Eardrum stiffness varies significantly between different specimens

While our estimates of the damping coefficient within the membrane reasonably fit the measurements made in both of our test specimens, it was necessary to vary the magnitude of the storage and loss moduli of the TM by a factor of 4, in order to produce reasonable fits of the low-frequency umbo motion in both preparations (Figs. 8 and 11). Considerable inter-individual variations in the stiffness-bound low-frequency motion of the human TM and middle ear are well documented. Order of magnitude variations have been reported in the low-frequency middle-ear input impedance and umbo velocity of live humans (Margolis and Hunter, 1999; Whittemore et al., 2004) and temporal bones (Rosowski et al., 1990, 2007) with intact ossicular chains and cochleae. While it has been noted above that TM stiffness depends on multiple factors, including the storage modulus of the TM material, membrane thickness, membrane shape, etc., we have no precise knowledge of how the two TMs used in our measurements varied in form or structure. Firmer tests of such relationships must await measurements of both function and precise structure in a series of individual specimens.

4.4. The eardrum and manubrium motions are not well coupled by the more compliant manubrial fold

The holographic measurements we made of the motion of the lateral and medial surface of the same TM with identical sound stimulation (Fig. 10), clearly demonstrate that the motion of the lateral surface of the TM at locations lateral to the manubrium of the malleus vary in their coupling to the manubrium. Our measurements show similar magnitudes and phase of motion between the TM and the malleus, at the umbo and the lateral process, but also show significant differences between TM motion and manubrial motion at locations between these two points. These observations are consistent with anatomical descriptions of the umbo and lateral processes embedded in the middle fibrous layer of the TM, while other points on the TM are coupled to the manubrium by a loose fold of epithelial tissue (Graham et al., 1978; Gulya and Schuknecht, 1995).

The effect of this loose coupling is directly visible in the holographic reconstruction of lateral surface motion in the measurements illustrated in the left-hand column of Fig. 9. While the motion of the TM surface just lateral to the TM is reduced in those measurements, there are visible phase and displacement variations along the manubrial arm. While the magnitude of these displacement peaks are smaller than those observed at other locations on the lateral TM surface, the density of peaks along the manubrium is similar to the density along the membrane surface. These local variations in magnitude (and phase) are not consistent with the observation of nearly rigid motion of the manubrium described by the measurements of the medial surface (Fig. 10).

The model analyses we perform varying the properties of the manubrial fold to match the magnitude of the differences between the TM and manubrial motion suggest a small but non-zero storage modulus for this structure. This is consistent with our experimental observations of low but still observable coupling between the manubrium and the TM. On the one hand, a small storage modulus is consistent with our observations of differences in motion of the manubrium and the lateral TM. On the other hand, a non-zero storage modulus is consistent with the repeated observations that the motion of the lateral surface of the human TM is smallest along the arm of the manubrium (Fig. 9 and other data illustrated in Cheng et al., 2010, 2013).

5. Conclusions

In this work, key aspects of human tympanic membrane mechanics were studied using the combination of stroboscopic holography measurements, Laser Doppler vibrometry and finite elements simulations. In the measurements and model analyses, the cochlea, stapes and incus were removed, as well as their ligaments and tendons. This allowed a more direct study of the TM with a more reliable definition of its boundary conditions.

We found that TM damping needs to be incorporated into the model to accurately model TM displacement patterns at acoustic frequencies. The experimental data was best modeled using a loss factor that increases from 1% at 20 Hz to 13% at 20 kHz (model 1) or by using a constant loss factor of 7.8% (model 4). The typically used Rayleigh damping values (models 2 and 3) are rejected since they yield too much damping, particularly at high frequencies. The best value for the complex modulus, which describes the TM stiffness, was significantly different between the two measured samples, with TB1 requiring a complex modulus of 10–13 MPa and TB2 40–52 MPa.

Holographic measurements at frequencies above 2 kHz indicate the motions of the lateral surface of the TM and the manubrium become decoupled at points in between the umbo and the lateral process of the malleus in humans. It is believed that the manubrial fold is responsible for this decoupling, and that the manubrial fold should be modeled with a lower stiffness than the TM (10% in our models).

The addition of damping to the TM in the TM-malleus model introduces spatial phase-gradients that mimic those observed in both the isolated TM and intact middle ear measurements. This suggests that a damped modal response of the TM can produce traveling-wave like phase gradients without the introduction of wave travel on the membrane surface.

In summary, we successfully investigated TM stiffness, damping and wave motion as well as its connection to the malleus. All of these aspects are essential to a realistic dynamic computer model of the entire middle ear.

Abbreviations:

TM

tympanic membrane

FE

Finite Element

Appendix

The Maxwell model is composed of a spring in series with a dashpot. The generalized Maxwell model is composed of a spring with linear spring constant R₀ in parallel with m Maxwell models with spring constants R_j and dashpot constants η_j (j = 1 … m); see Fig. 12. The complex modulus in the frequency domain is written as

$$E^{*}(\omega )=E_1(\omega )+i{E}_2(\omega ),$$

where E₁(ω) is the storage modulus and E₂(ω) the loss modulus, in this case given by

$$E_1(\omega )=R_0+{\sum }_{j=1}^m\frac{R_j{\tau }_j^2{\omega }^2}{1+{\tau }_j^2{\omega }^2},$$

$$E_2(\omega )=\sum _{j=1}^m\frac{R_j{\tau }_j\omega }{1+{\tau }_j^2{\omega }^2}.$$

with τ_j = η_j/R_j. The loss factor is defined as η(ω) = E₂(ω)/E₁(ω) so that E*(ω) = E₁(ω) [1 + iη(ω)].

Fig. 12.

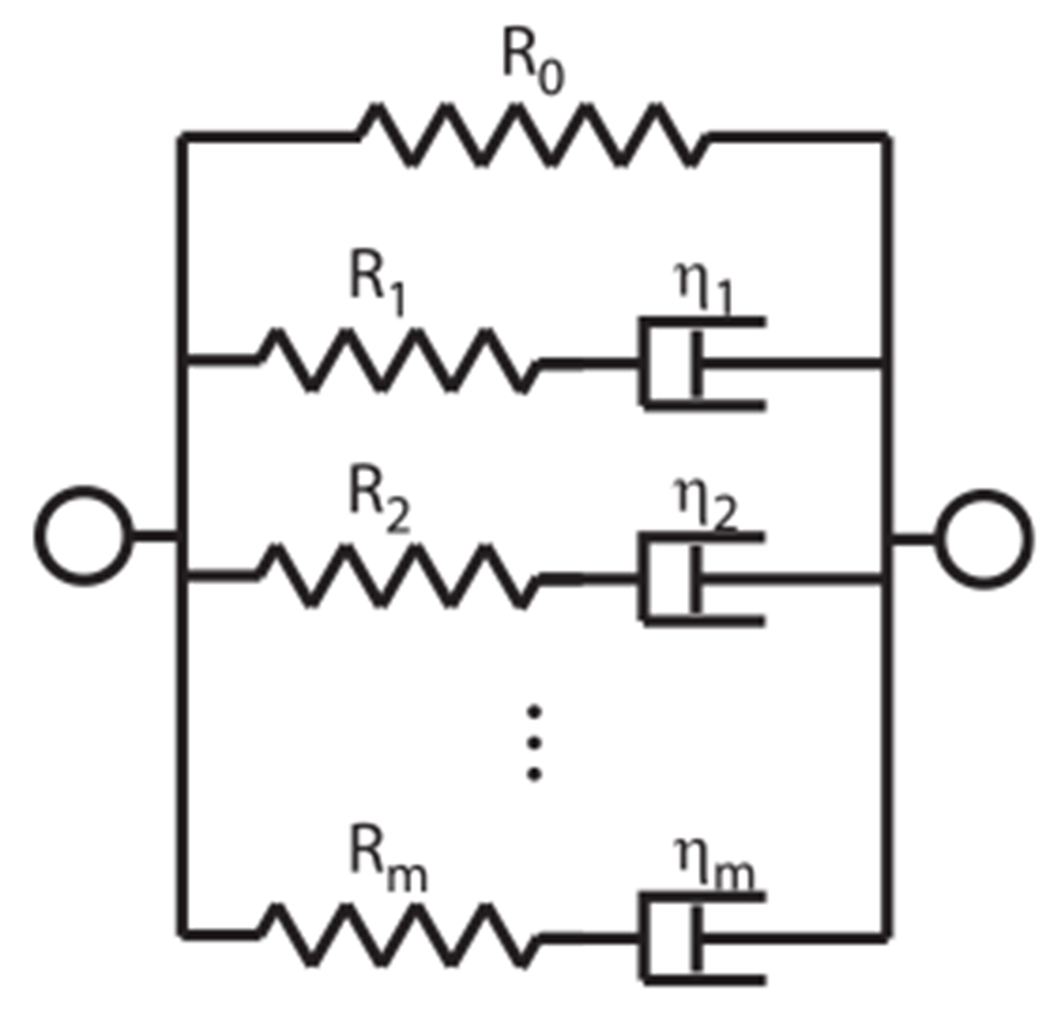
Model representation for the generalized Maxwell model.

In (Zhang and Gan, 2010), a third-order Maxwell model was used to fit viscoelastic properties in the frequency range 0.2–8 kHz. The average normalized values that were found are R₀ = 0.753 Pa, R₁ = 0.175 Pa, R₂ = 0.0559 Pa, R₃ = 0.0167 Pa, τ₁ = 2.55 ⋅ 10⁻⁵ s, τ₂ = 2.55 ⋅ 10⁻⁴ s, τ₃ = 2.5 ⋅ 10⁻³ s.

Extrapolation of this curve to the frequency range 20 Hz–20 kHz gives the solid loss factor curve (blue, in web version) in Fig. 6 (model 1), described by a fourth-order Maxwell model with coefficients: R₀ = 0.662 Pa, R₁ = 0.202 Pa, R₂ = 0.0714 Pa, R₃ = 0.0492 Pa, R₄ = 0.0147 Pa, τ₁ = 6.63 ⋅ 10⁻⁶ s, τ₂ = 3.95 ⋅ 10⁻⁵ s, τ₃ = 2.55 ⋅ 10⁻⁴ s, τ₄ = 2.50 ⋅ 10⁻³ s. These coefficients are chosen to match the third order model optimally.