Computing Proton-Coupled Redox Potentials of Fluorotyrosines in a Protein Environment

Abstract

The oxidation of tyrosine to form the neutral tyrosine radical via proton-coupled electron transfer is essential for a wide range of biological processes. The precise measurement of the proton-coupled redox potentials of tyrosine (Y) in complex protein environments is challenging mainly due to the highly oxidizing and reactive nature of the radical state. Herein a computational strategy is presented for predicting proton-coupled redox potentials in a protein environment. In this strategy, both the reduced Y-OH and oxidized Y-O^• forms of tyrosine are sampled with molecular dynamics using a molecular mechanical force field. For a large number of conformations, a quantum mechanical/molecular mechanical (QM/MM) electrostatic embedding scheme is used to compute the free energy differences between the reduced and oxidized forms, including the zero-point energy and entropic contributions as well as the impact of the protein electrostatic environment. This strategy is applied to a series of fluorinated tyrosine derivatives embedded in a de novo α-helical protein denoted α₃Y. The force fields for both the reduced and oxidized forms of these non-canonical fluorinated tyrosine residues are parameterized for general use. The calculated relative proton-coupled redox potentials agree with experimentally measured values with a mean unsigned error of 34 mV. Analysis of the simulations illustrate that hydrogen-bonding interactions between tyrosine and water increase the redox potentials by ~100–250 mV, with significant variations due to the fluctuating protein environment. This QM/MM approach enables the calculation of proton-coupled redox potentials of tyrosine and other residues such as tryptophan in a variety of protein systems.

Graphical Abstract

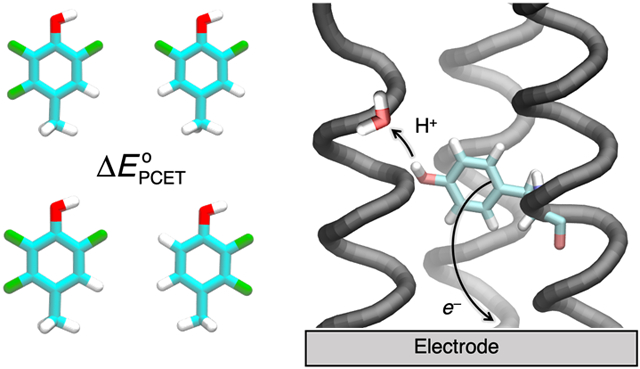
Introduction

Electron transfer (ET)^{1, 2} and proton-coupled electron transfer (PCET)^{3, 4} support the catalytic activities of a vast number of metabolic enzymes. These enzymes employ metallocofactors, organic molecules, and four types of amino acids to conduct the essential redox chemistry. In this context, tyrosine (Y), tryptophan (W), cysteine, and/or glycine protein residues serve as high potential one-electron redox mediators.^5-17 The mechanistic properties of Y and W are particularly interesting because these residues can efficiently transfer highly oxidizing equivalents over many Ångströms.^{11, 12, 17-21} These amino acid based redox reactions are difficult to characterize for a number of reasons, including the very high reduction potentials (E°) involved, the reactive nature of the oxidized (radical) state, and the weaker optical features associated with amino acid radicals. Additionally, radical formation, transfer, and decay can be coupled to protein conformational changes occurring on a broad range of timescales.^{11, 22-24} For all of these reasons, detailed mechanistic information and thermodynamic information are challenging to obtain.

Site-specific incorporation of non-canonical amino acids (ncAAs) has emerged as a technique to investigate and tune protein function.^25-27 In this technique, a protein residue of interest is replaced by a synthetic analogue with perturbed physiochemical and spectroscopic properties. Specifically, ncAAs have been employed to study catalytic mechanisms^{28, 29} and to probe mechanistically relevant redox-active tyrosines in E. coli ribonucleotide reductase,^{11, 30-36} BLUF domains,^{37, 38} and other protein systems.^39-41 Enzymatic and spectroscopic studies of these ncAA mutant proteins have provided valuable insights. However, the interpretation of these types of studies would strongly benefit from accurate thermodynamic data for the ncAAs in the protein environment.

Given the challenges associated with studying redox-active amino acids experimentally, the development of predictive computational approaches that could provide this essential information is of great interest. A variety of methods have been developed for the computational prediction of redox potentials in proteins using quantum mechanical (QM) methods,^{42, 43} molecular mechanical (MM) force fields,^44-46 or hybrid QM/MM approaches.^47-49,50 These methods are often able to obtain redox potentials within 100 – 300 mV of the experimentally measured values.⁴⁸ Recently a constant pH and redox potential molecular dynamics (MD) method was developed and used to compute proton-coupled redox potentials in several protein systems.⁵¹ This method performs conformational sampling with a MM force field and uses a Monte Carlo approach to attempt protonation and/or redox state changes while treating the solvent with a dielectric continuum model. Although the results are promising and provide useful insights, they highlight the challenges of using purely MM methods for redox potential calculations, as well as the need for careful benchmarking against experimental data.

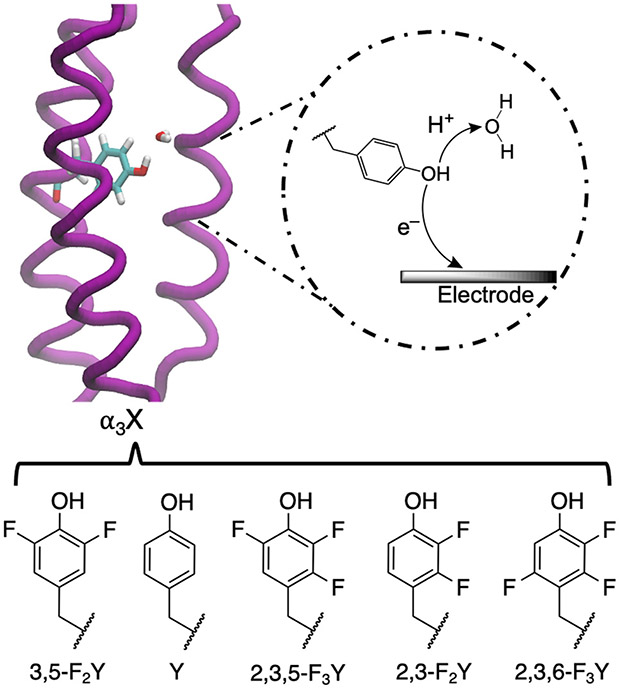
Herein, we take advantage of the structurally and mechanistically well-defined α₃X model protein system as a source of benchmarking data. The α₃X system was specifically constructed to investigate Y/W-based proton-coupled redox processes. The single-stranded model proteins consist of three alpha helices (α₃) with a single aromatic residue at interior position 32 (X32).⁵² Importantly, the α₃ scaffold remains well-structured over a broad range of experimental conditions, supports reversible oxidation-reduction of X32, and facilitates protein film voltammetry studies.^53-55 Thus, highly accurate and precise proton-coupled redox potentials (with errors ± 2-3 mV) are available for α₃Y (X32 = Y) and a series of fluorotyrosine α₃F_nY variants (X32 = F_nY where n = 2 or 3; see Figure 1). Because oxidation of tyrosine decreases its pK_a by ~12 units,⁵⁶ typically oxidation is accompanied by proton transfer from the phenol OH group to a nearby water molecule or protein residue via concerted PCET. Our previous MD simulations, combined with spectroscopic measurements, suggest that the proton acceptor for Y32 is a hydrogen-bonded water molecule, although a glutamate residue could not be ruled out.²⁴ The small size and well-defined structure of the protein,²² as well as the precisely measured redox potentials,⁵⁷ render the α₃Y protein system ideally suited for benchmarking computational methods.

Figure 1.

PCET of the oxidative process in the α₃Y protein, where the electron transfers to the electrode, and the proton acceptor is a water molecule, as suggested by prior simulations. X32 has been replaced by the depicted F_nY residues^{55, 57} in previous experiments and in the present computational work.

Herein, we present a strategy for computing proton-coupled redox potentials and apply this approach to the α₃Y protein system with the series of fluorinated tyrosines studied experimentally. Our computational strategy uses MM for conformational sampling and a QM/MM electrostatic embedding approach to compute the proton-coupled redox potentials for an ensemble of conformations. A comprehensive analysis of the results illustrates the importance of sampling hydrogen-bonding interactions between the tyrosine and water, as well as electronic effects due to the fluorine substituents. The development of a computational tool for the accurate and efficient prediction of proton-coupled redox potentials will help guide the design of new mechanistic probes or enzymes with enhanced reactivity.

Methods

Calculation of proton-coupled redox potentials

Under typical biological conditions, the oxidation of tyrosine (Y) occurs through a concerted PCET reaction, forming the neutral tyrosine radical and avoiding charged intermediates such as Y-OH^+• or Y-O⁻. The PCET reaction associated with oxidation can be described as follows:

$$\text{YOH}\to {\text{YO}}^{•}+{\mathrm{H}}^{+}+e^{-}$$ (1)

The relative proton-coupled redox potentials, ΔE°, with respect to a specified reference reaction were determined with the following expression:

$$\Delta E^{\circ }=E^{\circ }-E_{\text{ref}}^{\circ }=\frac{-\Delta G_{\mathrm{r}}^{\circ }}{F}$$ (2)

where

$$\begin{gathered} \Delta G_{\mathrm{r}}^{\circ }=\Delta G^{\circ }({\text{YO}}^{•}\to \text{YOH})-\Delta G^{\circ }({\text{YO}}^{•}\to \text{YOH}{)}_{\text{ref}} \\ =G^{\circ }(\text{YOH})-G^{\circ }({\text{YO}}^{•})-G^{\circ }(\text{YOH}{)}_{\text{ref}}+G^{\circ }({\text{YO}}^{•}{)}_{\text{ref}} \end{gathered}$$ (3)

Here ΔG° (YO^• → YOH) is the free energy change for the reduction reaction, which is the reverse of Eq. (1). Thus, E° is a reduction potential but is referred to as a redox potential to signify the reversible reduction/oxidation process. The subscript “ref” denotes the reference reaction, and the value of $E_{\text{ref}}^{\circ }$ is set to the experimentally determined value to obtain E° from Eq. (2). Using a reference reaction leads to cancellation effects that avoid introducing errors from the estimation of the solvation free energies of the proton and electron,⁵⁸ as well as the value of the standard hydrogen electrode (SHE).⁵⁹

All density functional theory (DFT) calculations in this paper were performed with the B3LYP-D3(BJ) functional^60-62 and the 6-31+G(d,p) basis set⁶³ using Q-Chem.⁶⁴ This level of theory was found to produce redox potentials in reasonable agreement with experimental values. Prior to including the protein environment, we calculated the proton-coupled redox potentials of the fluorinated tyrosine side chains in the gas phase with phenol as the reference. For calculations in the protein environment, the reference was the α₃Y protein with the unsubstituted tyrosine.

To calculate the proton-coupled redox potentials in the protein environment, we devised a QM/MM procedure with electrostatic embedding and applied it to an ensemble of conformations sampled from MD trajectories of both the reduced Y-OH and oxidized Y-O^• states. The detailed workflow is shown in Scheme 1. For each conformation, the QM/MM interface in AMBER⁶⁵ was used to automatically add a hydrogen link atom between the C_ß and C_α carbons with the default charge redistribution scheme.^{66, 67} Adding the hydrogen link atom to the QM region is necessary to satisfy the valency of the carbon atom. The resulting QM region is then optimized in the field of the partial charges corresponding to the MM system. A frequency analysis was performed on the optimized geometry to ensure that it was a minimum in the field of MM partial charges and to compute the zero-point energy and entropic contributions. For the reduced (oxidized) state conformations, the same geometry optimization procedure was followed for the oxidized (reduced) state of tyrosine in the fixed protein environment. For the reduced Y-OH conformations, Y-O^• was obtained by removing the hydrogen atom (i.e., deleting the hydroxyl proton and updating the multiplicity to reflect the loss of an electron that produces an unpaired electron). For the oxidized Y-O^• conformations, a hydrogen atom was added to generate the reduced state. For each protein conformation, the free energy difference between the reduced and oxidized states was determined to compute the proton-coupled redox potential via Eq. (2). The conformations were sampled every 100 ps from a 1 μs trajectory for the reduced state and every 10 ps from a 1 ns trajectory for the oxidized state, which required less sampling for reasons discussed below. The total proton-coupled redox potential for a given system was determined as the average value over ~10,000 conformations sampled from each of the reduced and oxidized trajectories.

Scheme 1.

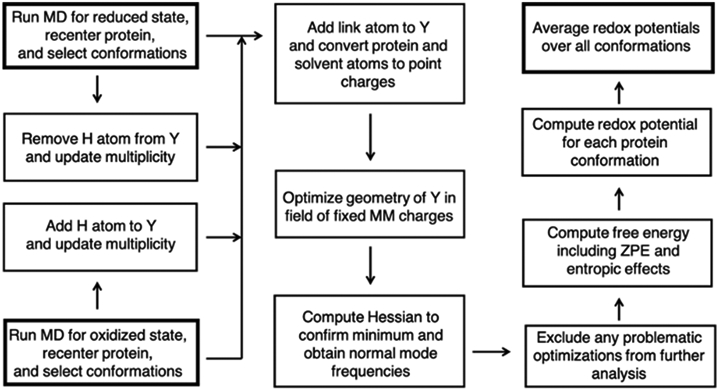
Computational workflow for calculating proton-coupled redox potentials. Bold boxes indicate the two possible starting points (left hand side) or the ending point (right hand side).

Parameterization of partial charges of fluorinated tyrosine

As the use of fluorinated and other non-canonical amino acids increases, the demand and interest in modeling systems containing these residues is rising. Unfortunately, parameters for fluorinated amino acids are not included in standard force fields. Although the Floudas group has developed FORCEFIELD_PTM⁶⁸ and FORCEFIELD_NCAA⁶⁹ to describe certain non-canonical amino acids, these parameters have not covered fluorinated amino acids. Fluoromethylated (-CF₃) derivatives of branched chain apolar amino acids and relevant force field terms have been parameterized,⁷⁰ but this effort has not been extended to tyrosine. We parameterized the non-canonical amino acids needed for this study, namely the series of fluorinated tyrosines shown in Fig. 1, in a manner that is compatible with the AMBER force field.

For each fluorinated tyrosine, a tyrosine residue was constructed with AmberTools,⁷¹ the N- and C- termini were capped, and the relevant hydrogen atoms were changed to fluorines. The atom types and parameters from the general AMBER force field (GAFF)⁷² were used for the fluorine atoms, and the standard RESP⁷³ procedure was followed to obtain the partial charges. Two conformers were generated with ϕ and ψ angles corresponding to a β-sheet and a right-handed α-helix, as given in Table II of Ref. ⁷³. These structures were optimized at the Hartree-Fock level with the 6-31G* basis set⁷⁴ to be consistent with the existing force field parameters. The atomic charges of the backbone (N, H, C, O) were fixed to the AMBER library charges for tyrosine during the multi-conformational RESP fit to be consistent with the ff14SB forcefield.⁷⁵ A constraint on the blocking N-methyl and acetyl groups was applied to ensure that the overall charge on the tyrosine residue was zero. In addition to parameterizing the standard (reduced) state of each fluorinated tyrosine (Y-OH), we parameterized the neutral radical state (Y-O^•) for each of them. The partial charges on the fluorine atoms derived within this work are comparable to the charges on the fluorine atoms parameterized for polar branched chain amino acids with CF₃ groups.⁷⁰ Additionally, these charges are similar to those found in the CHARMM cgenFF libraries.⁷⁶ Although these charges have been found to be suitable for the purpose of this paper and are presumably appropriate for other uses, they have not been rigorously validated against experimental observables except for the redox potentials discussed herein. The partial charges and associated forcefield parameters adapted from GAFF for all of these non-canonical amino acids are reported in the SI (Tables S1-S5). The partial charges for the tyrosine radical are provided in our previous work.⁷⁷

Computational details about molecular dynamics simulations

The starting structure for all of our MD simulations was the solution NMR structure for the α₃Y protein (PDB code: 2MI7).²² As the NMR ensemble includes 32 structures, the last conformer was used as the starting point for each simulation. The structures of these different conformers are extremely similar, and our previous simulations starting from different conformers yielded similar results.²⁴ Although the structures of the α₃F_nY variants have not been obtained, their global protein properties are nearly identical to those of α₃Y.^{55, 57} Typically, fluorinated proteins show enhanced thermostability and minimal structural perturbations.⁷⁸

For each α₃F_nY system studied, the non-canonical amino acid was introduced using the starting position of Y32 in the α₃Y NMR structure and converting the relevant hydrogen atoms to fluorine atoms. Each initial protein structure was solvated with explicit TIP3P⁷⁹ water in a periodic rectilinear box. The positive charge of the protein was neutralized with Cl⁻ ions, followed by adding Na⁺ and Cl⁻ ions to achieve a salt concentration of ~150 mM. The protonation states did not need to be determined, as the NMR structure contains hydrogen atoms. The MD simulations were performed using the AMBER 2018 software package⁸⁰ with the AMBER ff14SB force field.⁷⁵ The equilibration procedure and technical details are the same as those used in our previous studies of α₃Y systems,²⁴ and full details are given in the SI.

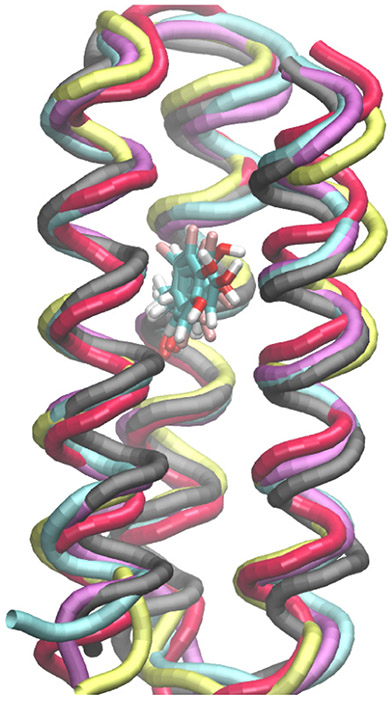
After equilibration, a trajectory was propagated for 1 μs for each reduced Y-OH system, and conformations were extracted every 100 ps over each 1 μs trajectory for computation of the proton-coupled redox potentials. Trajectories for the oxidized Y-O^• systems were propagated for 100 ns, extracting conformations every 10 ps to compute the proton-coupled redox potentials. Less conformational sampling was required for the Y-O^• systems because hydrogen-bonding interactions between the radical and water were not prevalent for any of the oxidized systems, as discussed further below. Moreover, we found that the proton-coupled redox potentials computed for the α₃(2,3,5)F₃Y-O^• and α₃(2,3,6)F₃Y-O^• systems using 10,000 conformations obtained from either the first or second 100 ns of a 200 ns trajectory are the same to within 5 mV for each of these two systems (Table S9). The simulations of the α₃F_nY proteins with the tyrosine in its standard (reduced) and neutral radical (oxidized) states were as stable as the wild-type simulations. The root-mean-square deviations (RMSDs) of the C_α atoms were ~1.1–1.8 Å for all systems studied (Table S6). Moreover, the fluorotyrosines exert minimal structural changes on the protein backbone (Figure 2).

Figure 2.

Backbones of representative equilibrated conformations of the α₃F_nY systems superimposed on a representative equilibrated conformation of the α₃Y system with the tyrosine residues depicted explicitly.

The trajectories were visualized with the VMD program⁸¹ and analyzed with the CPPTRAJ program.⁸² The hydrogen-bonding interactions, inter-residue distances, and solvent occupancy were analyzed for all trajectories. Hydrogen bonds were defined to have a heavy-atom distance less than or equal to 3.0 Å and a donor-hydrogen-acceptor angle greater than or equal to 135 degrees.

Results and Discussion

Calculation of proton-coupled redox potentials in gas phase and protein

We computed the relative proton-coupled redox potentials in the gas phase with phenol as the reference. These computed relative redox potentials agree reasonably well with the values obtained experimentally in the protein environment (Table 1, $\Delta E_{\text{gas}}^{\circ }$). The ordering of the redox potentials for the series of fluorinated tyrosines is preserved, with a mean unsigned error (MUE) of 20 mV for the series. We performed additional benchmarking with the ωB97XD⁸³ functional and various basis sets (Table S7), yielding similar results with MUEs ranging from 16–20 mV. The agreement of the gas phase results with the experimental data obtained in the protein environment indicates that the effect of the protein environment is nearly uniform for all of the fluorinated tyrosines, as it does not significantly impact the relative values. If a non-canonical amino acid caused a structural rearrangement of the protein, this agreement would break down, and a gas phase calculation would not be able to account for these effects. However, the absolute values of the redox potentials for the tyrosines in the protein environment are shifted positively for the reduced (Y-OH) systems, mainly due to hydrogen-bonding interactions, as discussed below (Table S8). It is well established that the microenvironment can modulate the redox potential of protein-associated redox cofactors.^{e.g. 84-87} Our goal is to develop a computational strategy that would be reliable in these situations, although the protein environment appears to play a relatively uniform role in our specific application.

Table 1.

Experimental and Computed Relative Proton-Coupled Redox Potentials in the Gas Phase and Protein Environment.^a

System	$\Delta E_{\text{expt}}^{\circ }$ b	$\Delta E_{\text{gas}}^{\circ }$ c	$\Delta E_{\text{prot-red}}^{\circ }$ d	$\Delta E_{\text{prot-ox}}^{\circ }$ e	$\Delta E_{\text{prot-ave}}^{\circ }$ f
α3(2,3,6)F3Y	135	142	218	130	174
α3(2,3)F2Y	70	102	183	−57	63
α3(2,3,5)F3Y	39	46	110	−124	−7
α3Y	0	0	0	0	0
α3(3,5)F2Y	−25	10	33	−77	−22
MUE		20	81	87	34

^aAll values are reported in mV relative to Y or α₃Y in the associated column. The mean unsigned error (MUE) relative to experiment is given for each method. The standard deviations of the values computed in the protein environment values are given in Table S9 and are typically ~200 mV. The proton-coupled redox potentials were computed with the B3LYP-D3(BJ) functional. The values computed for the same set of conformations with the ωb97X-D functional are very similar and are given in Table S10.

^bThe experimental values were obtained from Ref. ⁵⁷.

^cThese values were computed for the substituted tyrosine sidechains in the gas phase relative to phenol, which represents Y.

^dThese values were obtained by averaging over all conformations with Y-OH hydrogen bonded to at least one water molecule among 10,000 conformations equally distributed along the 1 μs trajectory with Y-OH for each system.

^eThese values were obtained by averaging over 10,000 conformations equally distributed along the 100 ns trajectory with Y-O^• for each system.

^fThese values were obtained by averaging the previous two columns corresponding to Y-OH and Y-O^• for each system.

The proton-coupled redox potentials were computed in the protein environment using the QM/MM approach described above. The MD conformational sampling was performed with both the reduced tyrosine (Y-OH) and the oxidized tyrosine (Y-O^•) with the corresponding relative redox potentials denoted $\Delta E_{\text{prot-red}}^{\circ }$ and $\Delta E_{\text{prot-ox}}^{\circ }$, respectively. For the calculation of $\Delta E_{\text{prot-red}}^{\circ }$ given in Table 1, only the conformations with Y-OH hydrogen bonded to at least one water molecule were included for reasons that will be discussed below. The degree of hydrogen bonding of Y-O^• to water in the trajectories used to compute $\Delta E_{\text{prot-ox}}^{\circ }$ was minimal due to the absence of the polar hydroxyl group. As shown in Table 1, $\Delta E_{\text{prot-red}}^{\circ }$ is greater than $\Delta E_{\text{prot-ox}}^{\circ }$ for the fluorinated tyrosine systems, mainly due to the more extensive hydrogen-bonding interactions with Y-OH than Y-O^• and the greater impact of hydrogen bonding on the fluorinated species than on the canonical tyrosine. The average $\Delta E_{\text{prot-avg}}^{\circ }$ of the results from sampling with Y-OH and Y-O^• to model the reversible PCET process leads to a MUE of 34 mV compared to experiment. This level of agreement is considered to be state-of-the-art among current computational methods.

A challenge that arises in this application is that the differences between the redox potentials in this series are relatively small and are difficult to capture when sampling over a large ensemble of protein conformations. To elucidate these local protein environments, we analyzed the hydrogen-bonding interactions of the tyrosine for each 1 μs trajectory used to compute the proton-coupled redox potentials $\Delta E_{\text{prot-red}}^{\circ }$ (Table 2). As shown in our previous work, the degree of hydrogen bonding of Y-OH to water and the protein is sensitive to the force field, and extensive sampling is required to converge the hydrogen-bonding percentages. ²⁴

Table 2.

Hydrogen-Bonding Interactions Involving Y for MD Trajectories of α₃Y and α₃F_nY Systems^a

System	V9:O	E13:Oε1, ε2	L58:O	L12:O	WAT:O
α3(2,3,6)F3Y	ND	<1%	28.1%	1.2%	58.2%
α3(2,3)F2Y	ND	ND	23.1%	17.9%	27.5%
α3(2,3,5)F3Y	ND	ND	26.2%	17.3%	17.4%
α3Y	54.1%	24.0%	5.12%	ND	38.2%
α3(3,5)F2Y	ND	ND	27.2%	3.1%	5.1%

^aEach value is the percentage of conformations with Y-OH hydrogen bonded to the specified atom over a 1 μs trajectory. ND denotes trajectories where this interaction was not detected. Hydrogen-bonding percentages involving water may reflect contributions from multiple water molecules and a mixture of water molecules accepting or donating a hydrogen bond to Y, with a full breakdown provided in Table S11.

The hydrogen-bonding results are only given for the trajectories with the reduced tyrosine (Y-OH) because the oxidized tyrosine (Y-O^•) did not exhibit hydrogen-bonding interactions for more than 1% of the trajectory except for α₃Y-O^•, which exhibited hydrogen-bonding interactions with water for 3% of the 100 ns trajectory. Propagation of the α₃Y-O^• system for a longer 1 μs trajectory resulted in a similar hydrogen-bonding interaction percentage of 6%. Previous experimental and computational studies have shown that the phenoxyl radical in solution is able to form a relatively strong hydrogen-bonding interaction with water.^88-90 To test our force field parameters, we simulated an individual tyrosyl radical in aqueous solution and found that such hydrogen-bonding interactions persisted for the majority of a 100 ns trajectory (see SI). This test implies that the low prevalence of hydrogen-bonding interactions in the α₃Y-O^• systems arises from the hydrophobic protein environment. As discussed for the α₃Y-OH systems, however, the α₃Y-O^• hydrogen-bonding interactions are also sensitive to the force field and degree of conformational sampling.

Although Y-OH can serve as a hydrogen bond donor or acceptor to water, typically it serves as a hydrogen bond donor in this system (Table S11). Moreover, when Y-OH serves as a hydrogen bond acceptor to water, it is almost always simultaneously serving as a hydrogen bond donor to a protein residue, such as E13. Thus, virtually all of the conformations with Y-OH hydrogen bonded to water are hydrogen bond donors. These conformations are expected to be most relevant to proton-coupled oxidation because the proton must be transferred to a molecule such as water or E13. To maintain consistency among the systems given the challenges in conformational sampling, only those conformations with Y-OH hydrogen bonded to water are included in the calculation of $\Delta E_{\text{prot-red}}^{\circ }$. The results obtained including all conformations are given in Table S9 and, as expected, do not provide quite the same level of quantitative accuracy.

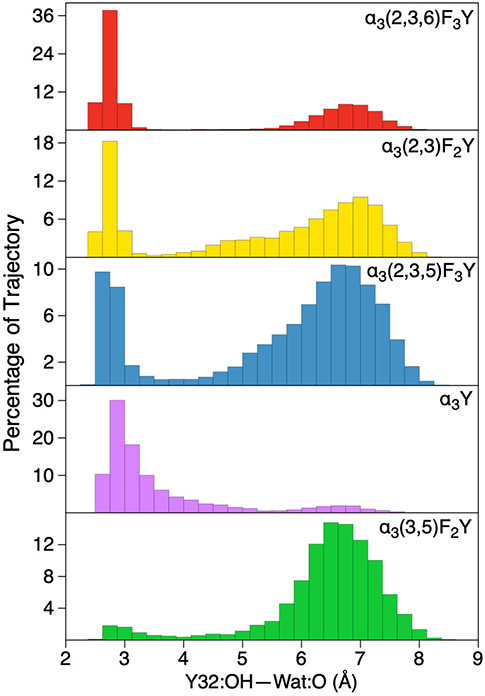
Given the impact of hydrogen-bonding interactions on the proton-coupled redox potentials, we analyzed the hydrogen-bonding interactions within the protein environment. This analysis focused on the distance between the Y32 hydroxyl oxygen and the oxygen of the closest water molecule because of the postulated role of water as the proton acceptor, the increase in the redox potential observed upon hydrogen bonding to water, and the nearly bimodal distributions of these distances (Figure 3).

Figure 3.

Distribution of hydrogen-bonding O–O distances between Y-OH and the closest water molecule in the reduced (Y-OH) trajectories for the five systems studied.

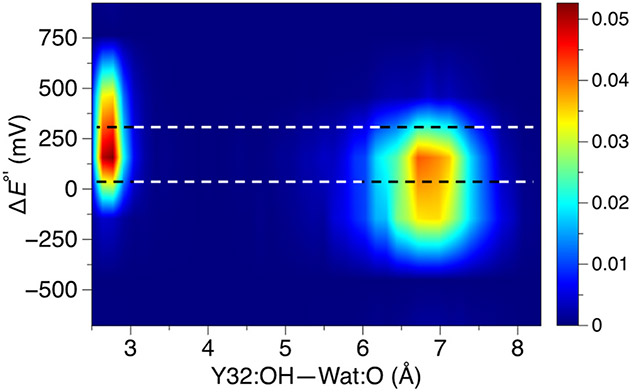
We further scrutinized the α₃(2,3,6)F₃Y system because it exhibits the greatest population of conformations with a hydrogen-bonded water molecule. Figure 4 illustrates that the population of hydrogen-bonded conformations (i.e., shorter Y-OH—OH₂ distances) exhibits proton-coupled redox potentials that are ~100–200 mV greater than those corresponding to the more diffuse population of conformations without this hydrogen-bonding interaction (i.e., larger distances). Although the fluctuations within each population are significant, this increase in the proton-coupled redox potential is consistent with the 4–6 kcal/mol interaction energy of phenol forming a hydrogen bond with water,⁸⁸ given that the Y-OH typically donates a hydrogen bond to water, and this interaction is not possible for the Y-O^• radical.

Figure 4.

Two-dimensional contour plot of the relative proton-coupled redox potential versus distance between the tyrosine hydroxyl oxygen and the closest water molecule for the α₃(2,3,6)F₃Y system. These results were obtained from the 1 μs trajectories with Y-OH, and the redox potentials are given relative to the average proton-coupled redox potential computed for α₃Y. The color bar represents density, and the bins used to generate the underlying histogram were 0.2 Å and 100 mV for distance and redox potential, respectively. The top black and white dashed line passes through the average proton-coupled redox potential for the conformations with Y-OH hydrogen bonded to at least one water molecule, while the bottom dashed line passes through the average value for the conformations without such hydrogen bonds.

This analysis indicates that the relatively large fluctuations observed in the computed proton-coupled redox potentials arise from the variations in hydrogen-bonding interactions, as well as other environmental factors within the protein. Given the sensitivity of the proton-coupled redox potential to hydrogen-bonding interactions, as well as the challenges inherent to sampling these interactions sufficiently even over 1 μs, including only the conformations with Y-OH hydrogen bonded to a water molecule ensures a degree of consistency. Furthermore, the proton-coupled oxidation of tyrosine requires proton transfer to a water molecule or other residue, suggesting that these conformations are most relevant to the experimental measurements.

Conclusions

This paper presents a QM/MM strategy for calculating proton-coupled redox potentials in proteins. This strategy entails conformational sampling of both the Y-OH and Y-O^• forms of tyrosine with a molecular mechanical force field in conjunction with a QM/MM electrostatic embedding scheme to compute the free energy differences for a large number of conformations. To allow the investigation of non-canonical tyrosine amino acids, we derived partial charges for the Y-OH and Y-O^• forms of a series of fluorinated tyrosines. The QM/MM scheme involves geometry optimizations and free energy calculations of these Y-OH and Y-O^• residues in the electrostatic field of the protein. This scheme can be used in conjunction with any QM/MM method, such as ONIOM or other embedding approaches.^{91, 92} We applied this strategy to a series of systems that each involve a tyrosine or fluorotyrosine in the α₃Y protein. Analysis of the results indicates that hydrogen-bonding interactions between tyrosine and water increase the proton-coupled redox potential by 100–250 mV, although significant fluctuations arise from the varying protein environment. This strategy produces relative proton-coupled redox potentials with a mean unsigned error of less than 40 mV relative to experimental measurements for these systems. However, the quantitative results are sensitive to the force field, conformational sampling, and the treatment of hydrogen-bonding interactions. Further benchmarking is required to determine if this accuracy will be attained for a wider range of protein systems.