Distinct error rates for reference and nonreference genotypes estimated by pedigree analysis

Abstract

Errors in genotype calling can have perverse effects on genetic analyses, confounding association studies, and obscuring rare variants. Analyses now routinely incorporate error rates to control for spurious findings. However, reliable estimates of the error rate can be difficult to obtain because of their variance between studies. Most studies also report only a single estimate of the error rate even though genotypes can be miscalled in more than one way. Here, we report a method for estimating the rates at which different types of genotyping errors occur at biallelic loci using pedigree information. Our method identifies potential genotyping errors by exploiting instances where the haplotypic phase has not been faithfully transmitted. The expected frequency of inconsistent phase depends on the combination of genotypes in a pedigree and the probability of miscalling each genotype. We develop a model that uses the differences in these frequencies to estimate rates for different types of genotype error. Simulations show that our method accurately estimates these error rates in a variety of scenarios. We apply this method to a dataset from the whole-genome sequencing of owl monkeys (Aotus nancymaae) in three-generation pedigrees. We find significant differences between estimates for different types of genotyping error, with the most common being homozygous reference sites miscalled as heterozygous and vice versa. The approach we describe is applicable to any set of genotypes where haplotypic phase can reliably be called and should prove useful in helping to control for false discoveries.

Introduction

When dealing with large sets of genotype data, such as those obtained from whole-genome sequencing, error rates that are low per site can still yield millions of miscalled genotypes. Errors can be introduced anywhere along the long process, from sampling to genotyping. The frequency of error often depends on the sequencing technology employed. With next-generation sequencing (NGS), even reads that are perfectly mapped and free of base-calling errors can lead to miscalled diploid genotypes due to the random over-sampling of one allele during amplification. Genotyping errors can profoundly hinder genetic analyses, for instance by reducing power in linkage and association studies (Abecasis et al. 2001; Gordon et al. 2002; Ahn et al. 2007). Studies interested in identifying rare variants are especially sensitive to these errors, in the context of either disease (Powers et al. 2011; Yan et al. 2016) or the rate of de novo mutation (Ségurel et al. 2014; Carlson et al. 2018). The consequences of genotyping errors for biological conclusions can often be mitigated by explicitly including the possibility of errors in genetic analyses (Sobel et al. 2002; Cartwright et al. 2007; Lebrec et al. 2008).

Methods for attenuating the effects of error often require investigators to use an estimate of error rates (Pompanon et al. 2005). While error rates can broadly be classified by the type of sequencing or genotyping technology employed, each experiment will have a different error rate. Identical pipelines for generating genotype data with NGS can lead to rates of error that vary between different samples and cohorts (Dohm et al. 2008; Huang et al. 2009). For example, the population frequency of each variant in a cohort can be used to improve the accuracy of genotype calls, as in the GenotypeGVCFs workflow (Poplin et al. 2017). While this approach increases the confidence in each genotype call, genotype error rates can become dependent on the rarity of variants at a locus.

There are several different approaches for estimating genotyping error rates in a given experiment. The most straightforward is some form of replication, where sequencing or genotyping on one or more samples is repeated—or performed at higher read-coverage with NGS—and compared to the original results (e.g., Wall et al. 2014; Pfeiffer et al. 2018; Ma et al. 2019). Aside from the potential to be cost-prohibitive, this approach generates a rate of discordance between replicates rather than a true estimate of the error rate. Robust approaches to identifying genotyping errors and estimating their rates typically leverage pedigree information. These approaches identify errors by finding discordance between the observed genotypes and those expected from the laws of Mendelian inheritance (Douglas et al. 2002; Hao et al. 2004; Saunders et al. 2007; The 1000 Genomes Project Consortium 2015).

In this study, we develop a method to estimate the rates at which different types of genotyping errors occur. Specifically, we estimate the error in genotype calling at sites that are identified to be variable in a population. We focus on errors at biallelic sites and distinguish between the errors that involve reference versus nonreference alleles. Our method is useful for establishing distinct nonreference discordance error rates for genetic analyses of rare variants, which are typically nonreference. We apply pedigree information to track the transmission of haplotypes and to identify errors by looking for sites that have genotypes that cannot be the result of a faithful transmission event. Loci that do not possess the expected phase within a haplotype block must be the result of either: a de novo mutation, a gene conversion event, or a genotyping error. Genotyping errors are by far the most common of these phenomena (Table 1). Detection of unlikely genotypes from haplotype phase has previously been used to successfully identify genotyping errors (Abecasis et al. 2002; Becker et al. 2006; O’Connell et al. 2014; Kothiyal et al. 2019). What we add here is an error model to explicitly determine the genotyping error rate, and the ability to distinguish rates for different types of errors.

Table 1.

 Approximate per-site rates for phenomena leading to phase inconsistency

NGS genotyping error	10−3
Gene conversion	10−7
Recombination	10−8
De novo mutation	10−8

References

NGS error: Nielsen et al. (2011) and Wall et al. (2014); gene conversion: Jeffreys and May (2004) and Halldorsson et al. (2016); recombination: Jensen-Seaman et al. (2004) and Coop and Przeworski (2007); de novo mutation: Kong et al. (2012), Venn et al. (2014), and Wang et al. (2020).

We apply our new method to a dataset of genotypes collected from the whole-genome sequencing of a set of owl monkey (Aotus nancymaae) pedigrees (Thomas et al. 2018). Among sites that could be phased with pedigree information, we found a significant difference in the direction in which phase errors occurred. This departure forms the signal for estimating the rate of genotyping error. Estimated error rates were significantly different among the genotypes, with the most common error being a homozygous reference site miscalled as heterozygous. The principles of our method can be applied to determine the rate of different types of genotyping error in any dataset where phase errors can be identified.

Materials and methods

We develop a method to estimate genotyping error rates from whole-genome data by examining autosomal sites that can be unambiguously phased from a three-generation pedigree. When the transmission of haplotypes can be determined according to the Mendelian laws of inheritance, we call the sites phase-informative (described below). When the genotype of the child does not match the haplotypic combination transmitted by the parents, a genotyping error is the most likely cause. The frequency of such phase violations depends on the rate of genotyping error and the relevant site frequency in the sample. The expected frequencies of different phase violations can thus be compared to the observed frequencies to estimate error rates. We focused on building an error model for three-generation pedigrees along a single line of descent (Figure 1A), though genotypes can be phased in two-generation pedigrees when there are more than two siblings (Coop et al. 2008; Fledel-Alon et al. 2009; Roach et al. 2011). We also restricted ourselves to biallelic sites, the most common form of variation across the genome. The six possible miscalls at a biallelic site are labeled in Table 2.

Figure 1.

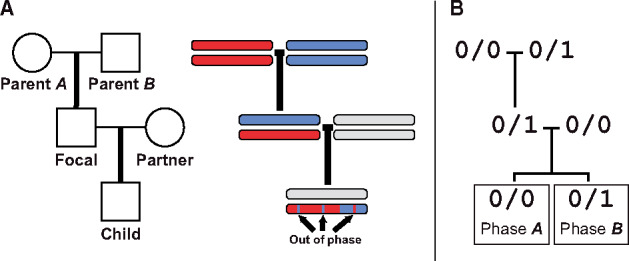
Pedigree and phase in a three-generation pedigree along a single line of descent. (A) The pedigree of five individuals and a diagram of the haplotype traced along three generations. Sites transmitted to the child can be out of phase within a haplotype block. (B) Genotypes at an example phase-informative site. The phase of the child genotype can be traced to either Parent A or Parent B.

Table 2.

 Genotyping errors at a biallelic site

Error	Truth	Observed
${\mathrm{\epsilon }}_{0>1}$	0/0	0/1
${\mathrm{\epsilon }}_{1>0}$	0/1	0/0
${\mathrm{\epsilon }}_{2>0}$	1/1	0/0
${\mathrm{\epsilon }}_{0>2}$	0/0	1/1
${\mathrm{\epsilon }}_{1>2}$	0/1	1/1
${\mathrm{\epsilon }}_{2>1}$	1/1	0/1

Reference allele represented by 0, nonreference represented by 1.

Expected number of phase violations

At phase-informative sites, the focal individual in a three-generation pedigree produces gametes with traceable phase. Within a block without crossovers, the haplotype inherited from the focal individual can be identified as being derived from either the maternally or paternally inherited chromosome of the focal individual. With a three-generation pedigree (Figure 1A), phase can only be traced for sites where the focal individual is heterozygous and the parents do not both share the same, heterozygous, genotype. Furthermore, to unambiguously track the phase to the third generation, the breeding partner of the focal individual and the child cannot both be heterozygous.

A genotyping error in any of the five individuals from the pedigree can cause an informative site to appear out-of-phase with its neighbors. For example, for a set of genotypes as in Figure 1B, a child called as heterozygous at a site in a parent A haplotype block could be an ${\mathrm{\epsilon }}_{0 > 1}$ error, a miscalled homozygous child. Similarly, a homozygous child at a site in a parent B block could be an ${\mathrm{\epsilon }}_{1 > 0}$ error. A miscalled child genotype is the most straightforward cause of a phase violation, but errors in other individuals also create apparent phase violations. Using again the genotypic combination in Figure 1B—if parent A is miscalled as homozygous alternate instead of homozygous reference (an ${\mathrm{\epsilon }}_{2 > 0}$ error; Table 2) a site in a parent A block would be expected to carry the alternate allele. When parent A is miscalled in this way, the child will be heterozygous for a site in a parent A block and would appear to be a phase violation.

The expected number of violations is the sum of potential phase violations from miscalls in all individuals across the pedigree. We estimate the number of violations for each miscall as a product of the respective genotypic combination frequencies across the genome and the corresponding error rate. We demonstrate this rationale below for the genotypic combination matching the example in Figure 1B, calculating the expected number of such phase-violating sites from phase A haplotype blocks. In this calculation, we assumed that out-of-phase-informative sites were the result of no more than one genotyping error among the sampled individuals for a given site.

Genotypic combinations are abbreviated as G_x, where x is composed of individual genotypes represented by a single digit: 0, 1, and 2 for homozygous reference, heterozygous, and homozygous alternate, respectively. These are ordered in the subscript as parent A, parent B, focal individual, partner of focal, and child.

Let n_x be the number of such genotypic combinations and ${\mathrm{\epsilon }}_{i>j}$ be the genotyping error rate as in Table 2. The genotypic combinations and possible miscalls leading to a phase violation for a site like the one depicted in Figure 1B are then:

Expected: G01100	Observed: G01101
Parent A	Observed genotype: 0/0
Possible miscall: 1/1
Focal individual inherits alternate allele from Parent A and transmits it to the child leading to apparent phase violation.
Possible miscall: 0/1
Focal individual inherits the alternate allele from Parent A, giving a 50% chance of transmission to child, leading to apparent phase violation.
Frequency: ${\mathrm{½}n}_{\mathbf{11101}}·{\mathrm{\epsilon }}_{1>0}+n_{\mathbf{21101}}·{\mathrm{\epsilon }}_{2>0}$
Parent B	Observed genotype: 0/1
Possible miscall: 0/0
Implies more than one genotyping error across pedigree.
Possible miscall: 1/1
Not detectable as phase violation, as focal individual still inherits alternate allele from Parent B haplotype block.
Focal	Observed genotype: 0/1
Any miscall would imply more than one genotyping error.
Partner	Observed genotype: 0/0
Possible miscall: 1/1
Child inherits alternate allele from the partner, which appears as a phase violation.
Possible miscall: 0/1
Child inherits alternate allele from the partner, giving a 50% chance of transmission to child, leading to apparent phase violation.
Frequency: $\mathrm{½}{n}_{01111}·{\mathrm{\epsilon }}_{1>0}+{\mathrm{ }n}_{01121}·{\mathrm{\epsilon }}_{2>0}$
Child	Observed genotype: 0/1
Possible miscall: 0/0
True genotype 0 has been miscalled as 1. Each occurrence leads to this phase violation.
Possible miscall: 1/1
Implies more than one genotyping error across pedigree.
Frequency: $n_{0110\mathbf{0}}·{\mathrm{\epsilon }}_{0>1}$

The expected number of phase violations for this genotypic combination can be written as:

$$\mathrm{E}\left[\left|A_{0110}\right|\right]=n_{01100}·{\mathrm{\epsilon }}_{0>1}+\mathrm{½}\left(n_{11101}+n_{01111}\right)·{\mathrm{\epsilon }}_{1>0}+\left(n_{21101}+n_{01121}\right)·{\mathrm{\epsilon }}_{2>0},$$ (1)

where A_y is a phase violation in the parent A haplotype block, with genotypic combination y and |A_y| is the number of such violations across the genome. Such a violation occurs when the observed genotype of the child does not match the expected genotype (see Table 3). Here, y is the abbreviated phase-informative genotypic combination, listing abbreviated genotypes for the first four individuals as ordered in x for G_x (the fifth individual in G_x is the child).

Table 3.

 Detectable phase violations in a three-generation pedigree

Parent A	Parent B	Focal	Partner	Phase violation	Child (expected)	Child (observed)	Phase violation	Child (expected)	Child (observed)
0/0	0/1	0/1	0/0	A0110	0/0	0/1	B0110	0/1	0/0
0/0	0/1	0/1	0/1	A0111	0/0; 0/1	1/1	B0111	1/1; 0/1	0/0
0/0	0/1	0/1	1/1	A0112	0/1	1/1	B0112	1/1	0/1
1/1	0/1	0/1	0/0	A2110	0/1	0/0	B2110	0/0	0/1
1/1	0/1	0/1	0/1	A2111	1/1; 0/1	0/0	B2111	0/0; 0/1	1/1
1/1	0/1	0/1	1/1	A2112	1/1	0/1	B2112	0/1	1/1
0/0	1/1	0/1	0/0	A0210	0/0	0/1	B0210	0/1	0/0
0/0	1/1	0/1	0/1	A0211	0/0; 0/1	1/1	B0211	1/1; 0/1	0/0
0/0	1/1	0/1	1/1	A0212	0/1	1/1	B0212	1/1	0/1
1/1	0/0	0/1	1/1	A2012	1/1	0/1	B2012	0/1	1/1
1/1	0/0	0/1	0/1	A2011	1/1; 0/1	0/0	B2011	0/0; 0/1	1/1
1/1	0/0	0/1	0/0	A2010	0/1	0/0	B2010	0/0	0/1
0/1	1/1	0/1	1/1	A1212	0/1	1/1	B1212	1/1	0/1
0/1	1/1	0/1	0/1	A1211	0/0; 0/1	1/1	B1211	1/1; 0/1	0/0
0/1	1/1	0/1	0/0	A1210	0/0	0/1	B1210	0/1	0/0
0/1	0/0	0/1	1/1	A1012	1/1	0/1	B1012	0/1	1/1
0/1	0/0	0/1	0/1	A1011	1/1; 0/1	0/0	B1011	0/0; 0/1	1/1
0/1	0/0	0/1	0/0	A1010	0/1	0/0	B1010	0/0	0/1

Reference allele represented by 0, nonreference allele represented by 1. Violations are mirrored in the second half of the table (Parent A and Parent B genotypes swapped, A and B violation swapped).

In pedigrees with five individuals, there are 18 genotypic combinations that are phase-informative. Table 3 lists each of these combinations and the child genotypes that indicate a phase violation. Violations at sites with the haplotype from Parent A and Parent B are labeled as A_y and B_y, respectively. Each genotypic combination can be evaluated to determine the total number of expected phase violations. Several symmetries between genotypic combinations reduce the number of unique calculations. For example, each violation has a matching pair where the phase and the genotypes of Parent A and Parent B are swapped (Supplementary Figure S1A). The frequency of each of these two classes is assumed to be equal across the genome due to independent assortment. The matching violation to A₀₁₁₀ in the example above is B₁₀₁₀, and the expected frequency can be calculated by swapping the two parental genotypes in each term as:

$$\mathrm{E}\left[\left|B_{1010}\right|\right]=n_{10100}·{\mathrm{\epsilon }}_{0>1}+\mathrm{½}\left(n_{11101}+n_{01111}\right)·{\mathrm{\epsilon }}_{1>0}+\left(n_{12101}+n_{10121}\right)·{\mathrm{\epsilon }}_{2>0}.$$ (2)

Similarly, each violation can be paired with a case in which homozygous reference and homozygous alternate genotypes are swapped. The expected frequency of violations has the same form once these genotypes and error rates are swapped. For A₀₁₁₀, the matching violation is A₂₁₁₂ (Supplementary Figure S1B) with expected frequency:

$$\mathrm{E}\left[\left|A_{2112}\right|\right]=n_{21122}·{\mathrm{\epsilon }}_{2>1}+\mathrm{½}\left(n_{11121}+n_{21111}\right)·{\mathrm{\epsilon }}_{1>2}+\left(n_{01121}+n_{21101}\right)·{\mathrm{\epsilon }}_{0>2}.$$ (3)

Derivations of the expected frequencies for the remaining set of phase violations can be found in the Supplemental Material (Appendix S1).

Estimating the error rates

Taken together, the expected number of phase violations from the genotypic combinations in Table 3 forms a linear system of equations that can be represented by a matrix equation. Let V_A be an 18 × 1 vector for the number of observed sites that violate haplotype block A across the genome, as ordered by row in Table 3; that is, ${\mathbf{V}}_{\mathbf{A}}=〈\left|A_{0110}\right|,\left|A_{0111}\right|,\left|A_{0112}\right|,\dots ,\left|A_{1011}\right|,\left|A_{1010}\right|〉$. The number of observed sites that violate block B is represented by ${\mathbf{V}}_{\mathbf{B}}$, again as ordered in Table 3. Let $\widehat{\mathbf{\epsilon }}$ be a 6 × 1 vector of estimators for each type of error rate, $\widehat{\mathbf{\epsilon }}=〈{\widehat{\mathrm{\epsilon }}}_{0 > 1},{\widehat{\mathrm{\epsilon }}}_{1 > 0},{\widehat{\mathrm{\epsilon }}}_{2 > 0},{\widehat{\mathrm{\epsilon }}}_{0 > 2},{\widehat{\mathrm{\epsilon }}}_{1 > 2},{\widehat{\mathrm{\epsilon }}}_{2 > 1}〉$. The error model can then be represented as:

$$\mathbf{M}\widehat{\mathbf{\epsilon }}=\left[\mathrm{ }\begin{array}{c}{\mathbf{V}}_{\mathit{A}}\\ {\mathbf{V}}_{\mathit{B}}\end{array}\right],$$ (4)

where the matrix M contains the coefficients of the linear equations from the expected frequencies of genotyping errors for each violation class. We can divide M into two submatrices based on the coefficients for violations in phase A and phase B as:

$$\mathbf{M}=\left[\mathrm{ }\begin{array}{c}{\mathbf{M}}_{\mathrm{A}}\\ {\mathbf{M}}_{\mathrm{B}}\end{array}\right].$$ (5)

Rows in M_A and M_B are identical for violations in phase A and phase B that share the same expected frequencies (e.g., A₀₁₁₀ and B₁₀₁₀, described in the previous section). The violations in Table 3 are ordered so that M_A and M_B can be related by an exchange matrix as:

$${\mathbf{M}}_{\mathbf{B}}={\left[\mathrm{ }\begin{array}{ccc}0& 0& 1\\ 0& ⋰& 0\\ 1& 0& 0\end{array}\mathrm{ }\right]}_{n=18}{\mathbf{M}}_{\mathbf{A}}.$$ (6)

Coefficients from equations for each of the respective expected phase A violations (see Supplementary Information) form the M_A matrix:

$${\mathbf{M}}_{\mathbf{A}}=\begin{array}{cccccc}{n}_{01100}\hfill & ½(n_{11101}+n_{01111})\hfill & n_{21101}+n_{01121}\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & ½n_{11112}\hfill & n_{21112}\hfill & n_{01110}\hfill & ½n_{01111}\hfill & 0\hfill \\ 0\hfill & ½n_{11122}\hfill & n_{21122}\hfill & 0\hfill & n_{01121}\hfill & 0\hfill \\ 0\hfill & n_{21101}\hfill & 0\hfill & n_{01100}\hfill & ½n_{11100}\hfill & 0\hfill \\ 0\hfill & ½n_{21111}\hfill & n_{21112}\hfill & n_{01110}\hfill & ½n_{11110}\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & n_{0112}+n_{21101}\hfill & ½(n_{21111}+n_{11121})\hfill & n_{21122}\hfill \\ n_{02100}\hfill & ½n_{02111}\hfill & n_{02121}\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & n_{02110}\hfill & ½n_{02111}\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & n_{02121}\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & n_{20101}\hfill & ½n_{20111}\hfill & n_{20122}\hfill \\ 0\hfill & ½n_{20111}\hfill & n_{20112}\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & n_{20101}\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & n_{10122}\hfill & n_{12121}+½n_{11122}\hfill & ½n_{12222}\hfill \\ 0\hfill & 0\hfill & 0\hfill & n_{12110}+n_{10112}\hfill & ½(n_{12111}+n_{11112})\hfill & ½n_{12212}\hfill \\ n_{12100}\hfill & ½n_{12111}\hfill & n_{12121}\hfill & n_{10101}\hfill & ½n_{11101}\hfill & ½n_{12201}\hfill \\ ½n_{10021}\hfill & ½n_{11121}\hfill & n_{12121}\hfill & n_{10101}\hfill & ½n_{10111}\hfill & n_{10122}\hfill \\ ½n_{10010}\hfill & ½(n_{11110}+n_{10111})\hfill & n_{10112}+n_{12110}\hfill & 0\hfill & 0\hfill & 0\hfill \\ ½n_{10000}\hfill & n_{10101}+½n_{11100}\hfill & n_{12100}\hfill & 0\hfill & 0\hfill & 0\hfill \end{array}$$ (7)

Equation (4) is an overdetermined linear system—there are many more equations than rates to be estimated. We can fit the model using a linear least squares approach, solving for $\widehat{\mathbf{\epsilon }}$ by taking:

$$\widehat{\mathbf{\epsilon }}=\arg \underset{\mathit{\epsilon }}{\min }{||\mathbf{V}-\mathit{M}\mathit{\epsilon }||}^2,$$ (8)

where V is the column vector of V_A and V_B, the number of observed sites violating their respective haplotype blocks as ordered in M.

Our implementation takes as initial input genotypes in the Variant Call Format (vcf) and phases for haplotype blocks in Browser Extensible Data (BED) format. We fed these data in abbreviated form into R (v. 3.5.0) and solved for the error rate estimators in Equation (8) with the linear optimization algorithm L-BFGS-B as implemented in the base stats package. The Python (v. 3.6.1) script used to abbreviate the genotype-phase combinations, and the R script applying the algorithm, is available on GitHub.

Simulating phase violations

We tested the performance of our method on simulated genotype combinations at biallelic sites from pedigrees as in Figure 1A with simulated errors. The phase at each site was assigned according to the rules of Mendelian inheritance and the simulated pattern of recombination. Genotypes in every individual each had a chance of being in error. To quickly simulate a large number of such genotypes and errors, we simulated genotypic combinations instead of individual genotypes. Our simulation approach divides the total number of simulated sites, S, into counts for each genotypic combination by progressively drawing counts from branching transmission outcomes.

We begin by dividing the number of sites among the possible genotypic combinations for the three unrelated individuals in the pedigree. We assume a neutral site frequency spectrum for each site and that the parents and partner of the focal individual were all unrelated to each other. Assuming also that the three unrelated individuals in the pedigree are from a subset of N (minimum N = 3) unrelated genotyped individuals that have S segregating sites, the probability of a given unrelated genotypic combination, U_x, can be written as:

$${\mathrm{P}(U}_x)=\sum _{i=1}^N\frac{i-1}{a_N}P\left(g_1|i\right)·P\left(g_2|i\right)·P\left(g_3|i\right),$$ (9)

where i is the allele frequency in the sample, a_N is the Watterson correction factor:

$$a_N=\sum _{i=1}^{N-1}\frac{1}{i},$$ (10)

g_n is the genotype of the nth-individual in the combination, and the conditional genotype frequency is given by:

$${P(g}_n\left|i\right)=\left\{\begin{array}{cc}{\left(1-\frac{i}{N}\right)}^2& \text{for} {\mathrm{ }g}_n=\text{homozygote} \text{reference}\\ 2\left(\frac{i}{N}\right)\left(1-\frac{i}{N}\right)& \text{for} {\mathrm{ }g}_n=\text{heterozygote}\\ {\left(\frac{i}{N}\right)}^2& \text{for} {\mathrm{ }g}_n=\text{homozygote} \text{alternate}\end{array}\right..$$ (11)

We can then divide the sites among the 27 possible genotypic combinations (3³ for a biallelic site in three individuals) by drawing from a multinomial with probabilities $〈\mathrm{P}\left(U_1\right),\dots ,\mathrm{P}\left(U_{27}\right)〉$. The counts for each of these genotypic combinations were then subdivided based on the possible genotypes inherited by the offspring (focal individual in Figure 1A) of the two parents. These counts were apportioned by drawing from a multinomial with an equal probability for each of the four possible gametic combinations from the parents. Each of the branching outcomes from different genotypes in the focal individual was in turn subdivided by the possible gametic combinations transmitted to the child from the focal and partner genotypes.

To simulate the effects of linkage and recombination, the total number of segregating sites, S, was divided into blocks each with a randomly transmitted phase,$\mathrm{ }p\mathrm{ }\sim \mathrm{ }\mathrm{Bernoulli}\mathrm{ }\left(0.5\right)$. That is, the above procedure for drawing genotype combinations was repeated for each set of sites in a phase block transmitted by the focal individual. The length of each block (in centiMorgans) was drawn from a gamma distribution, following a model for intercrossover distance in humans (Broman and Weber 2000). Blocks were drawn until their total length met the genetic map length of the genome in the simulation, L_m. Segregating sites were then assigned to each block in direct proportion to their map length relative to the total. In all simulations, we used parameters for recombination similar to those found in humans, L_m = 3500 cM and a gamma model with parameter ν  =  4.3 (Broman et al. 1998; Broman and Weber 2000). Finally, counts across all branching outcomes and all phase blocks were summed to give a total count, n_x,p, for each unique genotype-phase combination, denoted by x and p, in the pedigree.

We added errors to these counts by iterating over the genotypes, x, in each combination and drawing errors for the n_x,p sites. Let the genotype be a vector, $g=\{〈\mathrm{1,0},0〉,〈\mathrm{0,1},0〉,〈\mathrm{0,0},1〉\}$, for the homozygous reference, heterozygous, and homozygous alternate genotypes, respectively. Given a set of error probabilities, ${\epsilon }_{i>j}$, for each type of error as listed in Table 2, the probability of a genotypic transition can be written as $g·\mathbf{E}$, where

$$\mathbf{E}=\left[\mathrm{ }\begin{array}{ccc}1-{\epsilon }_{0>1}-{\epsilon }_{0>2}& {\epsilon }_{0>1}& {\epsilon }_{0>2}\\ {\epsilon }_{1>0}& 1-{\epsilon }_{1>0}-{\epsilon }_{1>2}& {\epsilon }_{1>2}\\ {\epsilon }_{2>0}& {\epsilon }_{2>1}& {1-{\epsilon }_{2>1}-\epsilon }_{2>1}\end{array}\mathrm{ }\right].$$ (12)

For each genotype at each combination, the n_x,_p counts are divided by drawing from a multinomial using the probability for genotypic transition while retaining the phase. Unique genotype and phase combinations across all branches are then summed for the final counts.

Simulations following the above strategy were implemented in Python (v. 3.6.1) with the NumPy package (v. 1.13.3).

Data availability

Raw sequence data for the owl monkey dataset are available from NCBI BioProject: PRJNA451475. Abbreviated counts of genotype-phase combinations from the owl monkey dataset are available at FigShare. Code used in analyses and simulations is publicly available on GitHub (https://github.com/Wang-RJ/genotypeErrors). Supplemental material available at figshare: https://doi.org/10.25386/genetics.13256432.

Supplementary material is available at figshare DOI: https://doi.org/10.25386/genetics.13256432.

Results

Accuracy of error estimators in simulations

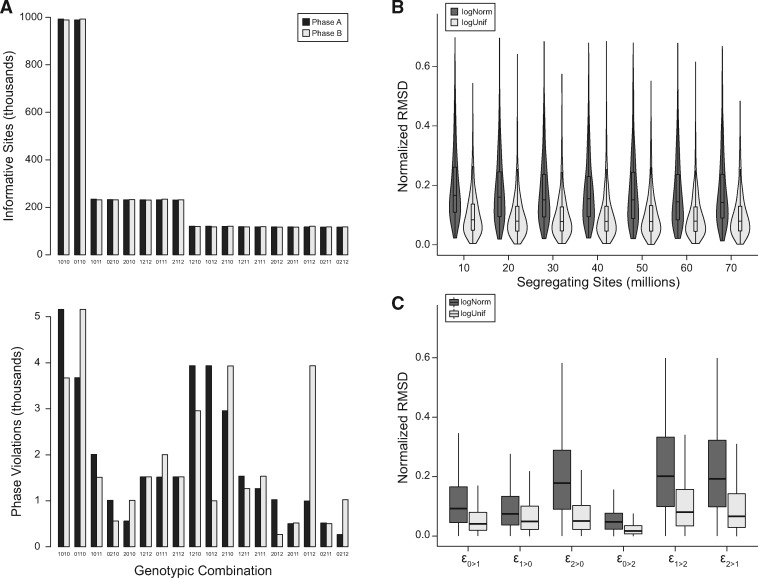
We simulated genotypes with varying error rates and numbers of segregating sites, maintaining the sample size of unrelated genotyped individuals, N = 20, and with parameters for recombination similar to those found in humans (see Materials and Methods). Simulated error rates were drawn from two distributions, a log-uniform distribution [range: (10⁻⁴, 10⁻²)] and a log-normal distribution (μ  =  10⁻³, σ  =  0.5). We simulated 1000 genotyped pedigrees of five individuals for each combination of parameters tested. In the absence of genotyping errors, the frequency of parental phases at informative sites is assumed to be equal due to independent assortment. However, genotyping errors cause apparent phase violations to occur at different frequencies based on the genotypic combination of individuals in the pedigree. Figure 2A shows an example of how the parental phase at detectable violations consistently varies from the balanced phases at informative sites. This departure is not because of different error rates in the parents, but because different errors have distinct effects on genotype-phase frequencies. The frequency of simulated genotypic combinations also reflects the neutral site frequency spectrum (see Materials and Methods).

Figure 2.

Estimating simulated genotyping error rates from phase violations. (A) Typical genotypic combinations from simulations, ordered by the expected frequency of informative sites. Phases are expected to occur at equal frequency for informative sites (top), but violations due to genotyping error do not occur equally (bottom). Depicted are the mean frequencies from 1000 simulations with error rates drawn from a log-uniform distribution. (B) Total deviation of rate estimators decreases modestly with more segregating sites in simulated samples. (C) Deviation of individual estimators from actual rates used in simulations.

We assessed the accuracy of our error rate estimation in these simulations by calculating the normalized root mean square deviation (NRMSD). The deviation between the estimators and the simulated rate was normalized by the range of error rates as:

$$\mathrm{NRMSD}=\frac{\sqrt{\sum {\left(\widehat{\mathrm{\epsilon }}-\mathrm{\epsilon }\right)}^2}}{{\mathrm{\epsilon }}_{\max }-{\mathrm{\epsilon }}_{\min }},$$ (13)

where ${\mathrm{\epsilon }}_{\max }$ and ${\mathrm{\epsilon }}_{\min }$ are the maximum and minimum error rates in each simulation.

There was little change to the estimators’ normalized deviation with an increasing number of segregating sites for simulated error rates drawn from either the log-normal or log-uniform distribution. The mean NRMSD for simulated rates drawn from the log-normal distribution was slightly higher, ranging from 17.7% to 19.9%, than from rates drawn from the log-uniform distribution, from 9.7% to 10.3%, for simulations with between 10 and 70 million segregating sites (Figure 2B). Our results indicate that this method of estimating error rates is robust across populations with different levels of nucleotide diversity and different numbers of sampled individuals (Supplementary Figure S2).

We also assessed our method’s accuracy for each estimator, normalizing the RMSD to the median difference between maximum and minimum error rates across all simulations (Figure 2C). We found ${\widehat{\mathrm{\epsilon }}}_{0 > 2}$ to be the most accurately estimated, with a mean NRMSD of 8.5% and 4.6%, for simulated errors drawn from the log-normal and log-uniform, respectively. The estimators ${\widehat{\mathrm{\epsilon }}}_{1 > 2}$ and ${\widehat{\mathrm{\epsilon }}}_{2 > 1}$ were the least accurate, with mean NRMSDs ranging from 17.1% to 34.8%. The accuracy of the estimator for error rates at the most frequent genotype, ${\widehat{\mathrm{\epsilon }}}_{0 > 1}$, was intermediate with a mean NRMSD of 15.9% and 9.6% for respective draws from the log-normal and log-uniform distributions.

This last error rate, ${\widehat{\mathrm{\epsilon }}}_{0 > 1}$, can also be estimated in trios by considering the number of Mendelian inheritance violations where both parents are homozygous reference and the child is heterozygous. Under the assumption that each such Mendelian violation is a genotyping error, the estimated error rate is simply the number of such violations divided by the number of observed sites. We estimated this error rate in our simulations, taking the focal, partner, and child as a trio from each pedigree, and calculated an NRMSD for the estimator from this approach. We found this estimator for ${\widehat{\mathrm{\epsilon }}}_{0 > 1}$ to be much less accurate, with a mean NRMSD of 34.4% (log-normal simulated) and 19.8% (log-uniform simulated).

Application to phased owl monkey genotypes

We applied the method developed here to a dataset of genotypes from the whole-genome sequencing of owl monkey (A. nancymaae). Individuals in this dataset were part of several three-generation pedigrees, allowing us to unambiguously phase focal individuals (as in Figure 1). We selected four unrelated pedigrees with genotypes from 20 total individuals for our analysis. These samples were sequenced to approximately 35× coverage on an Illumina HiSeq-X with 150-bp paired-end reads. Single nucleotide polymorphisms (SNPs) in this dataset were called with Genome Analysis Toolkit (GATK) (version 3.3.0) following best practices (Van der Auwera et al. 2013; Poplin et al. 2017), and genotypes were phased with PhaseByTransmission (Francioli et al. 2017) and assembled into haplotype blocks under the assumption that there would be at most one recombination crossover per Mb interval (Venn et al. 2014; Smeds et al. 2016). Complete details on the methods used to generate this dataset are available in Thomas et al. (2018).

We selected genotypes from biallelic SNPs on autosomes for the subsequent analyses. Based on genotypic combinations, we were able to identify approximately 5.5 million phase-informative sites in each of the pedigrees. These sites were on haplotype blocks that covered, on average, 2.46 Gb out of the 2.86 Gb genome. Among the informative sites, an average of 25,007 was out-of-phase in each family. Frequencies for the different genotypic combinations showed a similar pattern to those seen in simulations: a balanced set of phases among all informative sites and an unequal set of phases among the violations (Supplementary Figure S3). Note that an out-of-phase site does not necessarily represent a miscall in the pedigree.

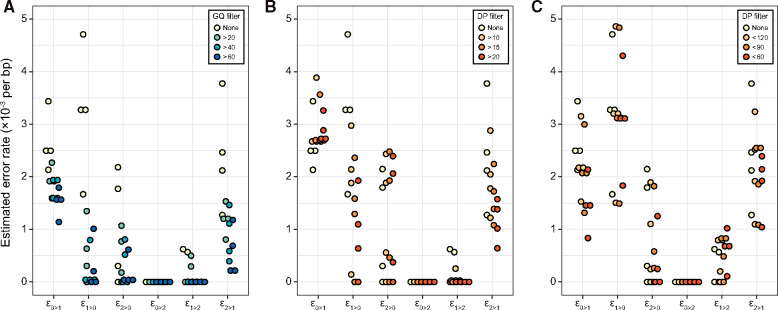
Using the frequencies of different phase violations, we estimated the genotyping error rates for each family with Equation (4). Estimates from each of the four pedigrees are depicted in Figure 3. The highest rates of error appear to be from distinguishing between homozygous reference and heterozygous genotypes, with mean rates ${\mathrm{\epsilon }}_{0 > 1}$ = 2.9 × 10⁻³ and ${\mathrm{\epsilon }}_{1 > 0}$ = 2.9 × 10⁻³ per bp. The rate at which homozygotes for the alternate allele were miscalled as heterozygotes were also appreciable, mean rate ${\mathrm{\epsilon }}_{2 > 1}$ = 2.1 × 10⁻³ per bp. In contrast, our estimate of the rate at which homozygous reference genotypes were mistaken as homozygous alternate was zero in all four pedigrees.

Figure 3.

Error rates estimated from sequencing four pedigrees of owl monkeys. Each point represents an estimate from one pedigree with genotypes filtered as described in the legend. Estimated genotyping error rates consistently decline with the stringency of the (A) minimum GQ filter and (B) minimum and (C) maximum depth filters.

We also estimated the ${\mathrm{\epsilon }}_{0 > 1}$ error rate from the number of Mendelian inheritance violations where both parents are homozygous reference and the child is heterozygous. In the focal-parent-child trios for each pedigree, we found between 59,000 and 65,000 such violations and estimated a mean ${\mathrm{\epsilon }}_{0 > 1}$ rate for the four pedigrees at 2.7 × 10⁻³ per bp.

We repeated the analysis of phase violations with genotypes that were filtered by genotype quality (GQ) as calculated in GATK and by sequencing depth (DP) in all individuals. The value of GQ is based on the difference between the probability of the called genotype and the next most likely genotype. Genotypes associated with higher GQ scores are typically interpreted as being more accurate. As expected, the estimated error rates decreased as we removed sites with more stringent GQ filters (Figure 3A; Supplementary Table S1). Filtering by GQ appears to be more effective at removing certain types of errors than others, with the most dramatic reduction in heterozygote false negatives, that is ${\mathrm{\epsilon }}_{1 > 0}$. Similarly, filtering based on DP reduced the error rate when compared to no filter (Figure 3, B and C). As we might expect, increasingly greater depth at a site reduces the estimated error rate, up to a point. The reduction in error rate observed when using a maximum DP filter is likely due to the removal of poorly mapped repetitive elements in short-read sequencing (Li 2014).

We also calculated an average error rate by weighting each estimator with the genome-wide frequency of the corresponding genotype [mean frequencies of sites across pedigrees (×10⁶), 0/0: 29.6, 0/1: 11.7, 1/1: 5.03]. As with individual estimators, increasing stringency of the GQ filter reduced the overall error rate (Supplementary Table S1). We estimated an overall error rate of 3.0 × 10⁻³ per bp, which was reduced to 1.1 × 10⁻³ per bp when genotypes were required to have a GQ > 60. Finally, we examined whether genotypes at rare variants had higher error rates by repeating the above analysis, but with sites filtered by minor allele frequency. Though we had reduced power with fewer sites, the average error rate appeared unaffected by lower allele frequencies (Supplementary Table S2).

Discussion

We have developed a method to estimate genotyping error rates for different types of errors at biallelic loci. Leveraging pedigree information, our method directly estimates underlying error rates, rather than the discordance between experiments obtained by other approaches. Our method is more robust than those that consider only Mendelian violations in a trio of individuals because of additional transmission information, reliance on multiple biological phenomena, and the ability to distinguish different types of errors.

Our estimate of the overall genotyping error rate in the owl monkey samples is comparable to estimates calculated from discordance between replicate sequencing experiments. Wall et al. (2014) inferred a genotyping error rate of 1.18 × 10⁻³ per bp on the Illumina HiSeq platform at GQ ≥ 40, remarkably similar to our overall estimate of 1.3 × 10⁻³ per bp at the same level of filtering stringency (Supplementary Table S1). Though their resequencing approach does not distinguish between all types of miscalls, they report a false-positive rate for heterozygotes (${\mathrm{\epsilon }}_{0 > 1}$) that is much higher than the false-negative rate (${\mathrm{\epsilon }}_{1 > 0}$), consistent with our findings after the application of filters on GQ.

Heterozygote false positives at homozygous reference sites occur at the highest rate among all errors, even after filtering. For a single individual in our dataset, our estimated rate at the GQ ≥ 40 level of filtering stringency implies approximately 50,000 heterozygote false-positive errors (${\mathrm{\epsilon }}_{0 > 1}$) across the genome. As the most common type of site in the genome, they are also the most common genotyping error. Homozygous alternate sites miscalled as heterozygote (${\mathrm{\epsilon }}_{2 > 1}$) are the next most numerous type of error at this level of filtering, with approximately 4000 such errors across an individual. The lowest error rates were for erroneously called nonreference homozygotes (${\mathrm{\epsilon }}_{0 > 2}$), which may have been expected. The relative rarity of the nonreference allele leads to caution in calling nonreference homozygotes by most genotyping methods. More surprising is the uneven effect of filtering across error types. Heterozygote false negatives, in particular, were dramatically reduced by both the GQ and minimum DP filters, though these filters are not independent as greater sequencing depth typically increases GQ. If the disparity between heterozygote false-positive and false-negative rates is common across NGS experiments, studies that seek rare variants may not be calibrated appropriately when assuming a single error rate. While genotyping errors for low-frequency variants may have little effect for many analyses, studies looking to identify de novo mutations in order to estimate mutation rates are very sensitive to miscalls of these variants.

The effect of genotype filters on the false-negative rate can be difficult to quantify; false positives, on the other hand, can be detected by confirming candidate sites with, for example, Sanger sequencing. We demonstrated that our method allows for an analytic estimate of the false-negative rate with varying degrees of genotype filtering. At first glance, the order of magnitude difference in heterozygote false-negative rates when filtering might suggest a corresponding difference in the number of false negatives in studies of de novo mutation. These studies, however, generally employ additional downstream filters to strictly control for the high number of false positives (Ramu et al. 2013; Wei et al. 2015). Estimates of additional filters’ effects on the de novo false-positive rate may be possible by applying our method to different filtered sets of genotypes, as we have done with GQ and DP.

Simulations demonstrated the power of our approach to estimate error rates even in samples with low levels of diversity. They also indicated differences in the accuracy of the error estimators, but these were not pronounced for the most common types of sites. One caveat to our simulations is that we did not simulate inaccuracies in phase calling. Low levels of diversity and high rates of recombination can make accurate phasing more difficult, while low rates of recombination could result in an imbalance in the proportion of phases across the genome. The assumption of at most one genotyping error among samples per site may also slightly inflate our estimates of the error rate. The potential for two or more genotyping errors is small (on the order of 10⁻⁶), and had a negligible effect in our simulations, but may be higher at sites prone to sequencing or assembly errors. These issues likely cause error rates to vary dramatically across such sites. Similarly, we ignored the effects of gene conversion and de novo mutation, as they are expected to occur at negligible rates compared to genotyping error (Table 1). Furthermore, the signal from a genotyping error and a gene conversion event is nearly identical, though careful filtering and selection of sites have been successful in identifying gene conversion events (e.g., Williams et al. 2015; Miller et al. 2016).

Finally, we note that the estimated error rates are for genotyping from a set of called variants. The heterozygote false-positive rate, ${\mathrm{\epsilon }}_{0 > 1}$, for example, does not apply to invariant reference sites. Variant discovery is an important step upstream of calling genotypes affected by reference and assembly quality (Li 2014). This is an important limitation for arriving at an overall error rate for a given site because we do not consider missed variants. Furthermore, the rarity of a variant affects its chance of being discovered. Our limited analysis of the relationship between allele frequency and genotyping error rate (Supplementary Table S2) suggests homozygous alternate genotypes may be more likely to be erroneous at sites with rare variants.

As genomic data continue to accumulate, the consideration of genotyping errors will remain an essential part of genetic analyses. Though we have focused mainly on whole-genome sequence data, our approach is generally applicable to any collection of genotype data (e.g., SNP-chips or exome sequencing) from pedigreed samples. Interest in sequencing individuals from families, as in studies seeking to identify de novo mutations (Goldmann et al. 2016; Thomas et al. 2018; Sasani et al. 2019), provides special opportunities for this method to be useful. Studies estimating de novo mutation rates may be particularly interested in distinguishing the rates for different types of genotyping errors. Differences in error rates will directly affect estimates of the false-positive and false-negative rates, and subsequent calculations of the mutation rate (Besenbacher et al. 2015; Kim et al. 2019). We have shown here that different types of errors indeed occur at different rates, necessitating their inclusion in such studies.