Dilated-DenseNet For Macromolecule Classification In Cryo-electron Tomography

Abstract

Cryo-electron tomography (cryo-ET) combined with subtomogram averaging (STA) is a unique technique in revealing macromolecule structures in their near-native state. However, due to the macromolecular structural heterogeneity, low signal-to-noise-ratio (SNR) and anisotropic resolution in the tomogram, macromolecule classification, a critical step of STA, remains a great challenge.

In this paper, we propose a novel convolution neural network, named 3D-Dilated-DenseNet, to improve the performance of macromolecule classification in STA. The proposed 3D-Dilated-DenseNet is challenged by the synthetic dataset in the SHREC contest and the experimental dataset, and compared with the SHREC-CNN (the state-of-the-art CNN model in the SHREC contest) and the baseline 3D-DenseNet. The results showed that 3D-Dilated-DenseNet significantly outperformed 3D-DenseNet but 3D-DenseNet is well above SHREC-CNN. Moreover, in order to further demonstrate the validity of dilated convolution in the classification task, we visualized the feature map of 3D-Dilated-DenseNet and 3D-DenseNet. Dilated convolution extracts a much more representative feature map.

1. Introduction

The cellular process is dominated by the interaction of groups of macromolecules. Understanding the native structures and spatial organizations of macromolecule inside single cells can help provide better insight into biological processes. To address this issue, cryo-Electron Tomography (cryo-ET), with the ability to visualize macromolecular complexes in their native state at sub-molecular resolution, has become increasingly essential for structural biology [1]. In cryo-ET, a series of two-dimensional (2D) projection images of a frozen-hydrated biological sample is collected under the electron microscopy with different tilted angles. From such a series of tilted images, a 3D cellular tomogram with sub-molecular resolution can be reconstructed [2] with a large number of macromolecules in the crowded cellular environment. To further obtain macromolecular 3D view with higher resolution, multiple copies (subtomograms) of the macromolecule of interest need to be extracted, classified, aligned [3] and averaged, which is named as subtomogram averaging (STA) [4]. However, due to the macromolecular structural heterogeneity, the anisotropic resolution caused by the missing wedge effect and the particularly poor signal-to-noise-ratio (SNR), macromolecule classification is still a great challenge in STA.

One pioneering classification method is template matching [5], where subtomograms are classified by comparing with established template images. However, the accuracy of template matching can be severely affected by the template image. Because the template image can misfit its targets when the template image and the targets are from different organisms or have different conformation. To overcome the limitations of using template images, a few template-free classification methods have been developed [6,7]. Most template-free methods use iterative clustering methods to group similar structures. Because the clustering of a large number of 3D volumes is very time-consuming and computationally intensive, template-free method is only suitable to small datasets with few structural classes.

Recently, with the blowout of deep learning, convolution neural network (CNN) has been applied to the macromolecule classification task [8, 9]. CNN classification methods recognize objects by extracting macromolecular visual shape information. Extracting discriminative features is the key to guaranteeing model classification performance. However, due to the high level of noise and complex cellular environment, it is challenging for CNN models to extract accurate visual shape information. Moreover, in traditional CNN architecture, with each convolution layer directly connected, the current convolution layer only feed in features from its adjacent previous layer. Because different depth convolution layer extracts image feature of different level, the lack of reusing features from other preceding convolution layer further limits the accuracy in macromolecule classification.

In this article, we focus on improving classification performance by designing a CNN model (Dilated-DenseNet) that highly utilizes the image multi-level features. We enhance the utilization of image multi-level features by following two ways: 1) Use dense connection to enhance feature reuse during the forward propagation. 2) Adapt dilated convolution in dense connection block to enrich feature map multi-level information. For the convenience of further discussion, here we denote this adapted block as dilated-dense block. In our dilated-dense block, with dense connection, each convolution layer accepts features extracted from all preceding convolution layers. And by gradually increasing the dilated ration of dilated convolution layers, the dilated convolution layer performs convolution with an increasingly larger gap on the image to get multi-level information.

In order to verify the effectiveness of the above two ways for classification task, we designed a 3D-DenseNet [10], a 3D-Dilated-DenseNet and compared these two models with the state-of-the-art CNN method (SHREC-CNN) of SHREC, a public macromolecule classification contest [9], on synthetic data [9] and experimental data [11,12]. Our synthetic data is SHREC dataset [9] which contains twelve macromolecular classes and is classified by SHREC into four sizes: tiny, small, medium and large. Our experimental data is extracted from EMPIAR [11,12] with seven categories of macromolecules. The results on both synthetic data and experimental data show that 3D-Dilated-DenseNet outperforms the 3D-DenseNet but 3D-DenseNet is well above SHREC-CNN. On synthetic data, 3D-Dilated-Dense network can improve the classification accuracy by an average of 2.3% for all the categories of the macromolecules. On experimental data, the 3D-Dilated-Dense network can improve the classification accuracy by an average of 2.1%. Moreover, in order to further demonstrate the validity of 3D-Dilated-DenseNet, we visualized the feature map of 3D-Dilated-DenseNet and the result shows that our model can extract more representative features.

The remaining of the paper is organized as follows. Section 2 presents the theory and implementation of our new CNN model 3D-Dilated-DenseNet. Section 3 shows dataset description, experiment details and classification performance of 3D-Dilated-DenseNet by comparing with widely used methods. Section 4 presents the conclusions.

2. Method

2.1. 3D-Dilated-DenseNet architecture

Figure 1A shows the architecture of our 3D-Dilated-DenseNet, the network mainly consists of three parts: dilated dense block (Section 2.2), transition block, and the final global average pooling (GAP) layer. Each block comprises several layers which is a composite operations such as convolution (Conv), average pooling (AvgPooling), batch normalization (BN), or rectified linear units (ReLU).

Fig. 1.

The architecture of 3D-Dilated-DenseNet. (A) The model framework of 3D-Dilated-DenseNet. (B) The composite function of each layer in dilated dense block. (C) The composite function of transition block in 3D-Dilated-DenseNet.

For a given input subtomogram, represented as a 3D array of ${\mathbb{R}}^{n\times n\times n}$, after the first shallow Conv, the extracted features are used as input for the following dilated dense block. In dilated dense block, we denote the input of block as x₀, the composite function and output of layer l (l=1,…,4) as H_l(·) and x_l. With dense shortcuts interconnect between each layer, the layer l receives the feature maps from its all preceding layers (x₁, …, x_l−1), and we denote the input of layer l as : x_l = H_l(x₀, x₁, …, x_l−1). Let each layer outputs k feature maps, so the input feature map of the current l layer is k₀ + k × (l−1) where k₀ is the number of block input feature map. Thus the whole block contains L×k₀+k×L(L−1)/2 feature maps. Such large number of feature maps can cause enormous memory consumption. In order to reduce model memory requirement, the layer is designed with a feature map compress module. So the composite function of layer (Fig. 1B) includes two consecutive convolution operations: 1) a 1x1x1 convolution operation which is used to compress the the number of input feature map, and 2) a 3x3x3 dilated convolution which is used to extract image multi-level information. The detailed information of dilated dense block which focuses on dilated convolution is shown in the next section.

Because dense connection is not available between size changed feature maps, all feature maps in dilated dense block maintain the same spatial resolution. If these high spatial resolution feature maps go through the entire network without down-sampling, the computation consumption in following block is huge. So we design a transition block between two dilated dense blocks to reduce the size of feature maps. Due to the number of input feature map of transition block is L × k₀ + k × L(L − 1)/2, the transition block is also defined with a feature map compress module. Therefore, transition block includes following operations: batch normalization (BN) followed by a 1×1×1 convolution (Conv) and average pooling layer.

After a series of convolution and down-sampling block, the given input subtomogram is represented as a patch of highly abstract feature maps for final classification. Usually, fully connection (FC) is used to map the final feature maps to a categorical vector which shows the probabilities assigned to each class. In order to increase the non-linearly, traditional CNN always contains multiple FC layers. However, FC covers most of the parameters of the network which can easily cause model overfitting. To reduce model parameter and avoid overfitting, GAP is introduced to replace the first FC layer [13]. The GAP does average pooling to the whole feature map, so all feature maps become a 1D vector. Then the last FC layer with fewer parameters maps these 1D vectors to get the category vector.

2.2. Dilated dense block

In order to obtain feature map with representative shape information from the object of interest, we introduce dilated convolution [14] in the dilated dense block. Figure 2 shows a 2D dilated convolution example. By enlarging a small k×k kernel filter to k+(k−1)(r−1) where r is dilation ratio, the size of receptive field is increase to the same size. Thus, with enlarged receptive field of the convolution layer, the model can extract multi-level information of subtomogram. And with the stack of convolution layers, the multi-level features can be integrated to present macromolecular shape with less noise.

Fig. 2.

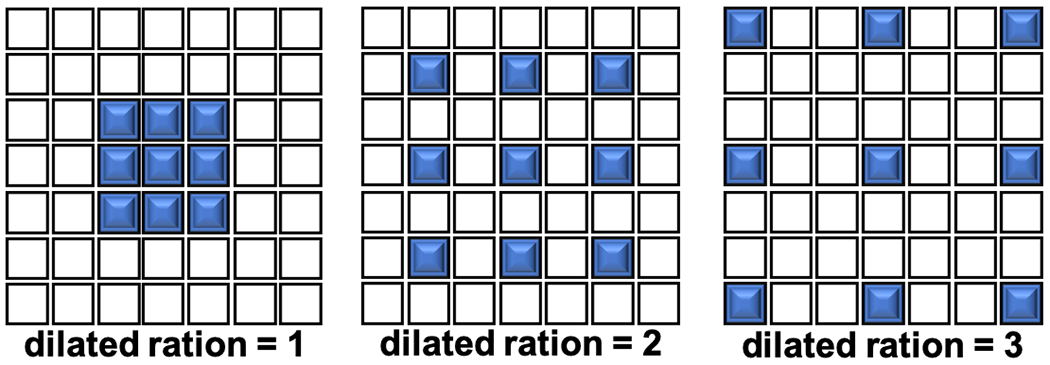
A 2D example of dilated convolution layers with 3 x 3 kernel, and the dilated ration is 1, 2, 3.

However, when stack dilated convolution layer with same dilation rate, adjacent pixels in the output feature map are computed from completely separate sets of units in the input, which can easily cause grid artifacts [15]. To solve this problem, we design our dilated convolution layers by following hybrid dilated convolution rule (HDC) [15]. First, the dilated ration of stacked dilated convolution cannot have a common divisor greater than 1. In each dilated dense block, we choose 2 and 3 as dilated ration. Second, the dilated ration should be designed as a zigzag structure such as [1, 2, 5, 1, 2, 5]. We put the dilated convolution layer at the mid of block.

2.3. Visualization of image regions responsible for classification

To prove that the dilated convolution layer can extract feature map with clearly respond regions from our interest object, we visualize the class activation mapping (CAM) [16] image by global average pooling (GAP). For GAP, the input is the feature map extracted from last convolution layer, and the output is a 1D average vector of each feature map. In a trained CNN model with GAP module followed by FC layer and softmax classification layer, the FC layer has learned a weight matrix that maps the 1D average vector to a category vector. With the computation of softmax classifier, the category vector can show the probability of the input image assigned to each class. For a predicted class that has the highest probability in the category vector, it is easy to get its corresponding weight vector from weight matrix. In the weight vector, each value represents the contribution of its corresponding feature map to classification. Therefore, we can get the class activation mapping image by using a weighted summation of feature map extracted from the last convolution layer and the weight value learned from FC layer.

Here, we denote the kth feature map of the last convolution layer as f_k(x, y, z). After f_k(x, y, z) goes through the GAP block, each f_k(x, y, z) are computed as ${\sum }_{x,y,z}{f}_k\left(x,y,z\right)$ that is denoted as F_k. From the linear layer followed by GAP, we can get a weight matrix w which shows the contribution of each feature to every category. Inputting an image, predicted with c class, we can get w^c. Each item of w^c records the contribution of last convolution feature map to c class. Then we can compute the class active mapping CAM_c by

$${\text{CAM}}_c\left(x,y,z\right)=\sum _k{w}_k^c{f}_k\left(x,y,z\right)$$ (1)

Due to the fact that CAM_c is the weighted sum of feature maps extracted from last convolution. The size of CAM_c(x, y, z) is generally smaller than origin input image. In order to conveniently observe the extracted features with the input image as a reference, we then up-sample the CAM_c(x, y, z) to get an image with same size as input data.

3. Experiments and results

3.1. Data

The synthetic subtomogram data is extracted from SHREC dataset [9], consisting of ten 512*512*512 tomograms and the corresponding ground truth tables. Each tomogram is with 1nm/1voxel resolution and contains ~2500 macromolecules of 12 categories. All macromolecules are uniformly distributed in tomograms with random rotation. And the ground truth table records the location, Euler angle and category for each macromolecule. These 12 macromolecules have various size and have been classified by SHREC to tiny, small, medium and large size. Tab. 1 shows the protein data bank (PDB) identification of the 12 macromolecules and their size category.

Table 1.

The PDB ID and corresponding size of each macromolecule in synthetic data

Macromolecule Size	PDB ID
Tiny	1s3x, 3qm1, 3gl1
Small	3d2f, 1u6g, 2cg9, 3h84
Medium	1qvr, 1bxn, 3cf3
Large	4b4t, 4d8q

According to the ground truth table, we extract subtomograms of size 32 × 32 × 32 with the macromolecules located in center. From Fig. 3A we can see the SNR of these subtomograms is low. In order to provide a noise-free subtomogram as a reference for CAM [16] images, we generated the corresponding ground truth using their PDB information. We first download each macromolecules structures from PDB, then generate a corresponding density map by IMOD [17]. Finally, we create an empty volume of 512 × 512 × 512 and put each macromolecule density map into the volume according to the location and Euler angle recorded in the ground truth table (Fig. 3B).

Fig. 3.

The example of synthetic data. (A) The middle slice of one 512 x 512 x 512 tomogram. The right 32 x 32 slices are the consecutive slices of a subtomogram with PDB ID 4d8q. The number of right corner are their slice index. (B) Ground truth corresponding to Fig.(A).

The experimental data are extracted from EMPIAR [11,12], which is a public resource for electron microscopy images. Seven cryo-ET single particle datasets are downloaded as the experiment data⁶. Each dataset on EMPIAR is an aligned 2D tilt series and only contains purified macromolecule of one category. The categories of these macromolecule are rabbit muscle aldolase, glutamate dehydrogenase, DNAB helicase-helicase, T20S proteasome, apoferritin, hemagglutinin, and insulin-bound insulin receptor. To obtain subtomograms, we first reconstruct the tilt series by IMOD and get the 3D tomogram. Then we manually picked up 400 macromolecules for each category.

3.2. Training details

In this work, our 3D-DenseNet and 3D-Dilated-DenseNet is implemented with Pytorch. During training, the weights of convolution layer and fully connected layer in both networks are initialed by the Xavier algorithm [18]. In particular, we set the parameters to random values uniformly drawn form [−a, a], where $a=\sqrt{\frac{6}{n_{in}+n_{out}}}$, n_in and n_out denotes size of input and output channel. For batch normalization layer, y is set to 1, b is set to 0, all biases are set to 0. The number of feature map output from each convolution layer in dense or dilated dense block (growth rate) is set to 12.

All our network is trained for 30 epochs on 2 GTX 1080TI GPUs with batch size of 64. With the limit memory of GPUs, our network only contains three dilated dense blocks. In fact, users can add more dilated dense blocks according to their GPU memory. According to the training experience, we used Adam [19] as the optimizer and the learning rate is set at 0.1 and scaled down by a factor of 0.1 after every 10 epochs. In order to get efficient training, we adapted various techniques mentioned in the [20] including learning rate warmup strategy, and linear scaling learning rate strategy.

3.3. The performance of 3D-Dilated-DenseNet on synthetic data

In order to compare the classification performance of 3D-DenseNet and 3D-Dilated-DenseNet with the state-of-the-art method on SHREC contest (SHREC-CNN), we chose the same test data and F1 metric as SHREC contest. The computation of F1 metric is given by Eq.2 which shows the balance of recall and precision.

$$F1=\frac{2*\mathrm{precision}*\mathrm{recall}}{\mathrm{precision}+\mathrm{recall}}=\frac{2\text{TP}}{2\text{TP}+\text{FN}+\text{FP}}$$ (2)

In Eq.2. TP means true positive, FN means false negative and FP means false positive.

Tab. 2 shows the classification performance of above three models on each macromolecule. We counted number of TP(true positive), FN(false negative) and FP(false positive) of each macromolecule and got corresponding F1 score of each category. Judging from the result, we find that the 3D-Dilated-DenseNet performs better than 3D-DenseNet, but 3D-DenseNet performs better than SHREC-CNN. Second, we find the classification performance has high relationship to macromolecule size. Here, we analyze the average F1 value of each model on macromolecules according to tiny, small, medium and large size (Fig. 4A). The F1 value in Fig. 4A and B is the average of macromolecules F1 scores from same size category. According to Fig. 4A, for all networks, the classification of large size macromolecules has the best performance. Especially, for 3D-DenseNet and 3D-Dilated-DenseNet, the F1 value is close to 1. As the size of macromolecule becomes smaller, the model gets poorer performance. This result is actually valid since that compared to smaller macromolecules larger ones can preserve more shape (or structure) information during pooling operations and get better classification results. Furthermore, with the decreasing of macromolecule size, the performance gap between 3D-DenseNet and 3D-Dilated-DenseNet becomes larger. In Tab. 2, compared with 3D-DenseNet, 3D-Dilated-DenseNet averagely increased macromolecule classification by: 3.7% on large size, 5.3% on medium size, and 6.8% on small size respectively.

Table 2.

Each macromolecule classification F1 score on SHREC

model	pdb id
	tiny			small				medium			large
	1s3x	3qm1	3gl1	3d2f	1u6g	2cg9	3h84	1qvr	1bxn	3cf3	4b4t	4d8q
SHREC	0.154	0.193	0.318	0.584	0.522	0.343	0.332	0.8	0.904	0.784	0.907	0.951
3D-DenseNet	0.522	0.519	0.644	0.712	0.580	0.504	0.563	0.795	0.958	0.807	1	0.997
3D-Dilated-DenseNet	0.684	0.485	0.675	0.778	0.652	0.565	0.635	0.855	0.971	0.846	1	0.997

Fig. 4.

Dilated-DenseNet performance on synthetic data. (A) Average F1 value on macromolecules according to different size of 3D-DenseNet and 3D-Dilated-DenseNet. (B) The relationship between F1 value and training epoch of 3D-DenseNet and 3D-Dilated-DenseNet.

Also, we test the convergence speed of 3D-DenseNet and 3D-Dilated-DenseNet, we find that dilated convolution does not affect 3D-Dilated-DenseNet convergence. Here, we analyze the performance of a series of 3D-DenseNet and 3D-Dilated-DenseNet which are trained up 30 epochs at intervals of 5. Figure 4B shows the relationship of epoch number and network performance on tiny size macromolecules. According to Fig. 4B, although in the first 13 epoch, the convergence speed of 3D-Dilated-DenseNet is slow, at epoch 15, both models reaches stability and the performance of 3D-Dilated-DenseNet is better than 3D-DenseNet.

3.4. Visualization the class active mapping of 3D-Dilated-DenseNet

In order to demonstrate the effectiveness of dilated convolution in improving classification performance, we visualize the feature map extracted from 3D-DenseNet and 3D-Dilated-DenseNet. Generally, there are two ways to assess feature map validity: 1) showing correct spatial information, in particular, the area which contains macromolecule in the tomogram, and 2) presenting object distinguishable shape information. Because the raw input image has high level noise, we further compare the CAM image of 3D-DenseNet and 3D-Dilated-DenseNet with the ground-truth. In Fig. 5, each row shows one macromolecule with the input image, ground truth, CAM image of 3D-DenseNet and 3D-Dilated-DenseNet. Because the subtomogram data is 3D, we only show the center slice. Here, we explain the image content of each data that is presented in Fig. 5. In the input image, the cluster black regions present macromolecule, and this region is located generally in the center. Oppositely, in ground truth data, the black regions represent background and white regions represent macromolecule. In the CAM image of 3D-DenseNet and 3D-Dilated-DenseNet, the response region is presented with bright pixel and the pixel value reveals the contribution of the corresponding region of input data to classification. The higher the pixel value, the more contribution to classification.

Fig. 5.

Class active mapping image of 3D-DenseNet and 3D-Dilated-DenseNet. Each row represents one macromolecule. And the column images are raw input data, ground truth, CAM image of 3D-DenseNet and CAM image of 3D-Dilated-DenseNet

Judging from Fig. 5, we can find that compared with the CAM image of 3D-DenseNet, the CAM image of 3D-Dilated-DenseNet shows more representative shape information of macromolecule. First, 3D-Dilated-DenseNet CAM shows less response to subtomogram background region. Second, the high response region of 3D-Dilated-DenseNet CAM is more consistent with the macromolecule region in input data. Moreover, the high response region of 3D-Dilated-DenseNet contains clear boundaries that can help network easily distinguish macromolecule region and background region which also arouse slight response.

3.5. The performance of 3D-Dilated-DenseNet on experimental data

We also test the classification performance of 3D-DenseNet and 3D-Dilated-DenseNet on experimental data with F1 metric (Tab. 3). Compared with synthetic data, the experimental data has higher SNR. Therefore, the classification performance on experimental data is better than that on synthetic data. Because we do not know the PDB id of each macromolecule in experimental data, we cannot compute the relationship of particle size to model performance.

Table 3.

macromolecule classification F1 score on exprimental data

Model	Particle Class
	rabbit muscle aldolase	glutamate dehydrogenase	DNAB helicase-helicase	T20S proteasome	apoferritin	hemagglutinin	insulin-bound insulin receptor
3D-DenseNet	0.9231	0.9558	1.0	0.9339	1.0	0.9569	0.9958
3D-Dilated-DenseNet	0.9915	0.9655	1.0	0.9917	1.0	0.9677	1.0

Judging from the Tab. 3, we can find that the F1 score of category DNAB helicase-helicase, apoferritin is the same, both equal to 1, which means that for these two category macromolecules, the balance between precision and recall is the same. However, for macromolecule of other categories, 3D-Dilated-DenseNet outperforms 3D-DenseNet. Overall, 3D-Dilated-DenseNet improved by 2.1% compared with 3D-DenseNet. Thus, dilated convolution do have a promotion for macromolecule classification task.

4. Conclusion

As a significant step in STA procedure, macromolecule classification is important for obtaining macromolecular structure view with sub-molecular resolution. In this work, we focus on improving classification performance of the CNN-based method (3D-Dilated-DenseNet). By adapting dense connection and dilated convolution, we enhance the ability of the network to utilize image multi-level features. In order to verify the effectiveness of dense connection and dilated convolution in improving classification, we implement 3D-DenseNet, 3D-Dilated-DenseNet and compared these two models with the SHREC-CNN (the state-of-the-art model on SHREC contest) on the SHREC dataset and the experimental dataset. The results show that 3D-Dilated-DenseNet significantly outperforms 3D-DenseNet but 3D-DenseNet is still well above the SHREC-CNN. To further demonstrate the validity of dilated convolution in the classification task, we visualized the feature map of 3D-DenseNet and 3D-Dilated-DenseNet. The results show that the dilated convolution can help network extract a much more representative feature map. Although our model has significant improvements in the macromolecule classification task. The small-sized macromolecule is still a bottleneck for our method. And due to the lack of suitable labeled experimental data, we have not fully explored the 3D-Dilated-DenseNet performance on experimental data according to macromolecule sizes. In future works, we will focus on improving classification performance on small size macromolecule and explore the method performance with abundant cryo-ET tomogram experimental data.