Abstract
In this work, we propose a theoretical framework based on maximum profile likelihood for pairwise and groupwise registration. By an asymptotic analysis, we demonstrate that maximum profile likelihood registration minimizes an upper bound on the joint entropy of the distribution that generates the joint image data. Further, we derive the congealing method for groupwise registration by optimizing the profile likelihood in closed form, and using coordinate ascent, or iterative model refinement. We also describe a method for feature based registration in the same framework and demonstrate it on groupwise tractographic registration. In the second part of the article, we propose an approach to deep metric registration that implements maximum likelihood registration using deep discriminative classifiers. We show further that this approach can be used for maximum profile likelihood registration to discharge the need for well-registered training data, using iterative model refinement. We demonstrate that the method succeeds on a challenging registration problem where the standard mutual information approach does not perform well.
Keywords: Image Registration, Deep Learning, Information Theory
1. Introduction
The maximum likelihood principle (Pawitan, 2001) is one of the most successful paradigms of probability theory. Since its popularization by Fisher in the early 20th century, it has become a primary method of statistical inference. On the theoretical side, maximum likelihood has attractive consistency and invariance properties that help to explain its empirical successes. More recently, maximum likelihood may be seen as one of the engines that drives the impressive accomplishments of Deep Learning (DL), as it is perhaps the most widely used training criteria (it is called minimum cross-entropy in that context).
Maximum likelihood has also proven to be a powerful principle for image registration – it provides a foundation for the widely-used information theoretic methods. In this article we develop a theoretical framework that is used to formulate and analyze maximum likelihood / information theoretic approaches to supervised and weakly-supervised pairwise and groupwise registration. In addition, we show how the framework can be applied to harness the power of deep discriminative methods to learn effective image agreement metrics from data.
1.1. Background on Information Theoretic Registration
Registration by maximization of mutual information and its variants have resulted in notable successes, solving many registration problems without customization of parameters (Maes et al., 1997; Pluim et al., 2003; Studholme et al., 1999; Viola and Wells III, 1997; Wells et al., 1996). The mutual information of two images is a measure of how much information is gained about one image, from observing the other one. Beyond the form of the joint distribution that characterizes the images, mutual-information-based registration does not use any specific information regarding the modalities; thus, training data is not needed for model fitting. In other words, it is unsupervised. One of the limitations of mutual-information-based registration, as conventionally formulated, is an (often implicit) assumption of pixel- or voxel-wise independence, which is clearly incorrect as nearby pixels or voxels are correlated. There are a few exceptions to this assumption (Heinrich et al., 2012; Huang et al., 2007; Yi and Soatto, 2011). For instance, Huang et al. (2007) used scale-invariant feature transform (SIFT) in a 8 × 8 pixel window, and used mixture models to approximate probability models on the high dimensional features. Despite this modeling limitation, the approach has been very successful. In fact, the reason that mutual information registration can be solved via gradient descent on the transformation parameters is precisely because the pixels are not independent, but rather spatially coherent. This coherence means that registrations that are “close” to the correct answer have scores for the estimated mutual information that are close to the optimum. This makes mutual-information-based loss suitable for gradient optimization procedures. If pixels were independent, we would expect an extremely sharp and difficult to optimize loss function, with a spike at the optimum and low values everywhere else.
Given that the principle of maximum likelihood pre-dates information theory, it is perhaps interesting that maximum likelihood registration appeared after mutual-information-based methods, in Leventon and Grimson (1998). In that work, a joint intensity model is learned from a set of registered data that characterizes the probability of observing a given intensity pair at corresponding locations in the images. Later, the spatial relationship of the images is varied to make the observed data most probable, based on the model. It is important to note that the model is application specific, for example, the model could characterize the intensities of specific MRI and CT imaging protocols.
As mentioned, in maximum likelihood registration, model parameters are derived from a set of registered data. However, they can also be estimated at registration time by joint likelihood maximization (along with the transformation parameters) (Zöllei et al., 2003), and in a conditional likelihood formulation (Roche et al., 2000). This joint maximization is called maximum profile likelihood (Pawitan, 2001). In this setting, the parametric models could be, e.g., jointly categorical or kernel densities.
Maximum likelihood formulations of image registration and their relation to entropy and mutual-information-based methods have been previously discussed. Roche et al. (2000) demonstrated that a conditional likelihood approach reduces exactly to an information theoretic criteria in the case of categorical models, though latent distributions on features and related asymptotics were not discussed. Minimum Joint Entropy (MJE) was introduced in Collignon et al. (1995) and it is the earliest reported information theoretic registration method. Empirically, the joint entropy of the intensities of a pair of images has a sharp local minimum when the images are correctly registered (a simple argument from basic principles is provided in the appendix of this article that explains this observation). Registration by MJE is closely related to registration by maximization of mutual information.
The profile likelihood can be more generally optimized by coordinate ascent, or iterated model refinement, which alternates between estimating the transformation parameters and the model parameters. In registration literature, Zöllei et al. (2003) described relations between maximum likelihood and information theoretic registration, including the possibility of modeling the joint data for all transformations (not just for registered data). They also described asymptotic analysis, though upper bound minimization was not discussed.
1.2. Background on Registration by Deep Learning
DL has revolutionized medical image analysis in the past few years, with state-of-the-art performance in many tasks such as image segmentation, classification, and registration (Balakrishnan et al., 2019; Haskins et al., 2019b; Litjens et al., 2017; Shen et al., 2017; Yang et al., 2017). Discriminative modeling (rather than generative modeling) has been the focus of DL researchers in the medical field and training is often accomplished using maximum likelihood (minimum cross-entropy). The success of deep networks is thought to be due to the automatic extraction of intermediate- and high-level features from image structures that can be effectively used for problem solving (LeCun et al., 2015).
Registration algorithms are usually characterized by an objective function that measures image agreement, an image deformation model, and an optimization method. More recently, researchers have used “unsupervised” learning to perform image registration. These methods often recast the conventional intensity-based registration into a learning problem to optimize network parameters for registration (Balakrishnan et al., 2019; de Vos et al., 2019; Krebs et al., 2019; Wolterink et al., 2017). However, the image agreement metrics that have been used are traditional ones such as normalized cross-correlation (de Vos et al., 2019), mean-squared error (Dalca et al., 2018) and LCC metric (Krebs et al., 2019). As the theoretical properties of deformation models and optimization methods are well understood, perhaps the most important limitation of registration algorithms is the image agreement functions themselves.
It may be that with enough training data, deep learning methods could learn effective measures of image agreement, perhaps superior to the engineered ones. This observation serves to motivate current research on deep metric-based registration.
Supervised (Cheng et al., 2018; Haskins et al., 2019a; Simonovsky et al., 2016), and unsupervised (Blendowski and Heinrich, 2019; Wu et al., 2015) approaches have been studied by researchers for deep metric registration. In some of these studies, deep networks are designed to classify registered and randomly unregistered patches. Cheng et al. (2018) trained a fully connected deep neural networks to recognize corresponding and non-corresponding patches. They used pre-sigmoid activation values to quantify similarity of given patches for task of 2D rigid registration on MRI and CT, and showed superior performance compared to traditional similarity metrics. In another study, Simonovsky et al. (2016) proposed an application–specific deep metric based on Convolutional Neural Network (CNN) classifiers that are trained to distinguish registered and randomly unregistered patches. In their registration framework, gradients of the deep metric were used for the optimization of the transformation parameters for image registration.
Although both studies demonstrated superior performance compared to conventional similarity metrics, the theoretical foundation, and the relationship between the derived deep metric and conventional methods were not investigated. In addition, both deep metrics require well-registered training data, which is a drawback for applications where multi-modality images cannot be obtained simultaneously (e.g., abdominal MRI and ultrasound).
1.3. Contributions
Despite the developments in registration approaches by DL, it has remained unclear if there is a connection between deep metrics and information theoretic registration. In this paper, we present a novel theoretical framework based on maximum profile likelihood for image registration which links the newly proposed classifier-based deep metrics to previous information theoretic ones. Our contributions are summarized as follows:
We establish a framework for analyzing pairwise registration methods as instances of maximum likelihood or maximum profile likelihood along with asymptotic information theoretic interpretations. We demonstrate that, asymptotically, maximizing the profile likelihood corresponds to minimizing an upper bound on the entropy of the latent distribution that governs the joint image data, and that, in the case of categorical models, the approach is exactly equivalent to registration by MJE.
Later, we extend the proposed framework to groupwise registration and show that, in a special case, maximum profile likelihood reduces exactly to the congealing method. Subsequently, we describe a method for groupwise feature-based registration that is demonstrated on tractographic data and show that it is an instance of iterative model refinement of a maximum profile likelihood criteria.
We use our framework to propose a patch-based formulation that links maximum likelihood registration and deep metric registration using discriminative binary classifiers. The patch-based formulation alleviates one of the main limitations of most entropy-based approaches, namely the strong implicit independence assumption on pixels or voxels. We also show why the sum of pre-sigmoid activations makes sense as an image registration metric in this context.
Finally, we demonstrate that maximum profile likelihood and iterative model refinement can be utilized to train a deep metric from data that is only roughly aligned; thus, enabling “weakly-supervised” registration. We explore data augmentation techniques and evaluate our proposed approach, demonstrating improved robustness in comparison to conventional mutual-information-based registration on a challenging multi-modality problem.
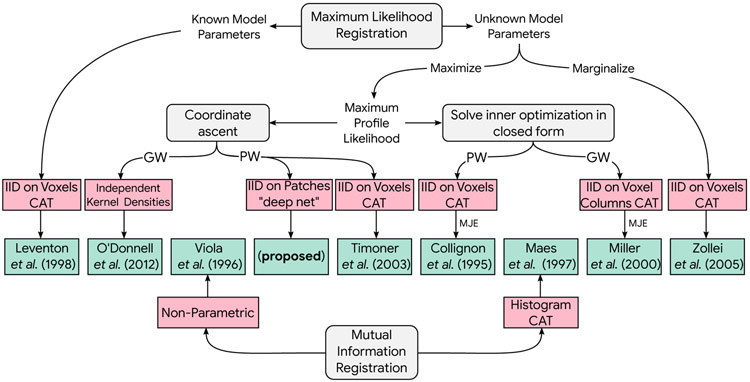
Information theoretic image registration is a substantial research area; our intention is not to provide a thorough review, but rather to provide a succinct formalism and use it to analyze a collection of registration algorithms and set the stage for new developments. The taxonomy of the discussed image registration approaches along with their modeling assumptions (in pink) and an example of each method (in green) is depicted in Fig. 1.
Fig. 1:
Taxonomy of information theoretic registration methods discussed in this article. PW: pairwise, GW: groupwise, CAT: categorical model, MJE: minimization of joint entropy, IID: independent and identically distributed.
1.4. Roadmap
The remainder of the article is structured as follows. Section 2 introduces our theoretical framework connecting maximum likelihood and information theoretic registration via asymptotic analysis and profile likelihood. It also describes a general-purpose optimization approach. We expect that this section will be of interest to experienced registration researchers who are interested in the theoretical underpinnings as well as those with a machine learning / deep learning background that are interested in learning about registration. The latter may benefit from the material in the appendix that provides some justification for the utility of entropy-based methods.
Section 3 discusses application of the theory to problems of groupwise registration, an approach that is useful for the formation of atlases, among other problems. The theoretically inclined will see a formulation using kernel density estimators that may be used in feature-based applications, a less common modeling approach in information theoretic registration. Readers with machine learning backgrounds most interested in standard pairwise registration may skip the section, as the next section does not depend on it.
Section 4 shows how maximum likelihood and minimum joint entropy registration can be approached with deep discriminative classifiers, bringing the theoretical developments to bear on registration systems that learn their image agreement metric from training data. We expect this section will be of interest to both groups of readers mentioned.
2. Pairwise Registration
The goal of pairwise registration is to find transformation parameters that bring two images into correspondence based on their contents. The development in this section will begin with a formulation of maximum likelihood registration using known modeling parameters. Alternatively, unknown modeling and transformation parameters can be jointly maximized. We show that this “profile likelihood” approach asymptotically minimizes an upper bound on the joint entropy of the distribution that governs the observed joint data under transformations. We discuss the connection to registration by maximization of mutual information and analyze a special case. We show that for discrete image intensities, the profile likelihood approach devolves exactly to registration by minimization of joint entropy. For more general cases, we describe an iterative model refinement that may be used for the joint optimization.
2.1. Maximum Likelihood Registration
Let U = {u1, u2,…} and V = {v1, v2,…} be collections of corresponding image features sampled from images and . The maximum likelihood registration approach is based on the construction of a parametric model, pR(u, v; ), that is intended to characterize pairs of corresponding image features when the two images are in registration. Here, represents estimated model parameters. The goal is to vary an offsetting transformation, β, on image features v for the highest likelihood under pR.
We assume that pairs of features are distributed independently and identically,
| (1) |
Throughout the article, we will use the concise syntactic notation βvi for the application of a transformation with parameters β to a feature. For a concrete example, let and be image intensities at a location xi ∈ R3 sampled from the space occupied by the images. The transformation notation in this case is where T(·, β) : R3 ↦ R3 is a spatial transformation parameterized by β. Note that, in this case, as β varies, βvi corresponds to intensity values from different locations in the images. In the applications studied in the article, the features will consist of pixel or voxel intensities, summaries of tractographic streamlines, or 3D patches of image intensities, and the transformations will be rigid, affine, and deformable models.
Maximum likelihood registration estimates the transformation as the one that maximizes the log-likelihood, given image data and model parameter ,
This approach was used by Leventon and Grimson (1998). In that work, the features were discretized intensities of image voxels, and the joint distribution was jointly categorical. The model parameters were estimated by histogramming from pairs of registered images.
2.2. Maximum Profile Likelihood Registration
The need for pre-registered training data for estimating the model parameters, θ, is a drawback of maximum likelihood registration methods. One way to mitigate this is to simultaneously maximize over both the transformation and model parameters,
| (2) |
In this setting, the transformation parameters, β, are of primary interest, and the model parameters θ can be viewed as nuisance parameters. “Maximizing out” the nuisance parameters is called maximum profile likelihood in the estimation literature (Cole et al., 2014; Pawitan, 2001). Bayesian methods have also been explored by Zöllei et al. (2007) that average over nuisance parameters (instead of maximizing); the resulting approach produces an approximation of registration by MJE as a special case. As we will see below, in some settings, the inner optimization of Eq. 2 may be solved in closed form.
2.2.1. Asymptotic Interpretation
To perform asymptotic analysis, we replace the sum in the maximum profile likelihood estimator of Eq. 2 with a sample average that is approximated by expectation,
Here, pD(u, v; β) is the latent distribution that generates the observed data, (ui, βvi), which is a function of β. To reiterate, the two distributions, pR(u, v; θ) and pD(u, v; β), play a major role in the rest of this article. The former is a parametric model that is designed to characterize the joint data when images are in registration. The latter is the latent (unknown) true distribution that characterizes the observed joint data. Since image V is being offset by a transformation parameterized by β in the registration setup, the latent distribution depends on β.
Re-writing the above equation,
and from Kullbac–Leibler (KL) divergence and joint entropy definitions,
Thus, maximum profile likelihood, or iterative model refinement (which we will discuss in Section 2.3), asymptotically minimizes an upper bound on the entropy of the distribution that generates the joint data. From the above equation, as β approaches the value corresponding to correct registration, then, if pR has enough capacity (parameters), the KL divergence between the estimated model and the true model could approach zero. In that case, the maximum profile likelihood will devolve to minimization of the entropy of the joint data distribution. In other related work, registration by minimization of the KL divergence between trained and empirical distributions on joint intensities was described by Chan et al. (2003).
The upper bound minimization provides traction on minimizing the joint entropy, which is otherwise difficult to perform since the latent joint distribution can not be directly accessed. A similar approach is used in the “evidence lower bound” method for marginalizing an intractable posterior probability (Blei et al., 2017).
2.2.2. Special Case: Categorical Models
We discuss next an important special case of maximum profile likelihood registration where the features are discretevalued intensities, and the model is jointly categorical, pR(u, v; θ) ≐ JCAT(u, v; θ). Here , where θjk ≥ 0 and ∑jk θjk = 1. In this formulation, and are the intensity values that ui and vi can take, and j, k represents histogram bin indices.
The model is
Maximum profile likelihood takes the form
or, summing over histogram bins rather than pixels or voxels,
| (3) |
Here Njk(β) is the joint histogram representing the number of (ui, vi) data items with intensity values equal to (, ); it varies with the transformation parameters.
In Eq. 3, the inner optimization over θ is equivalent to maximum likelihood estimation of the model parameters given data that is summarized by Njk(β). It is well-known that in the case of standard categorical models, the solution to maximum likelihood parameter estimation is the normalized histogram of the data. In more detail, using Lagrange multipliers, a closed form solution can be obtained as, where N ≐ ∑jk Njk(β).
Dividing by N, we obtain
Thus, the optimization over β has devolved exactly to registration by minimization of joint entropy; informally in words circa 1995: “adjust the registration so that the entropy of the joint histogram is minimized.” Roche et al. (2000) described a similar finding for a related conditional likelihood approach that used categorical models.
Registration by Maximization of Mutual Information.
Registration by maximization of mutual information is closely related to registration by minimization of joint entropy of the distribution on pairs of corresponding features, as . In some situations, e.g., the registration of volumetric medical images, the marginal entropy terms ( and ) may be unimportant, and neglected. In other situations that allow large scale changes in the images (e.g., perspective projection), the estimated joint entropy may approach zero as an image shrinks to one pixel in size; here the corresponding marginal entropy term is potentially useful. The utility of the marginal term is discussed in Viola and Wells III (1997).
2.3. Coordinate Ascent or Iterative Model Refinement
So far, we discussed maximum profile likelihood, its asymptotic interpretation, and a special case of categorical models in profile likelihood which we solved in closed form. If the inner optimization of maximum profile likelihood registration of Eq. 2 can not be carried out in closed form, then we may use coordinate ascent by alternating
| (4) |
| (5) |
We refer to this as iterative model refinement, which has previously been utilized in intensity-based registration by Timoner (2003) and for groupwise registration of tractography streamlines by O’Donnell et al. (2012), as we will discuss in more detail in Section 3.2.
This approach has an advantage in comparison to direct optimization of joint entropy, which is a “global” function (in the sense that changes anywhere in the image affect the joint entropy). In contrast, in the update of Eq. 4, changes in one part of the images do not affect the objective function in other parts of the images; thus, the calculations are local and can be carried out in parallel.
3. Groupwise Registration
The methods discussed so far have been examples of pairwise registration. In this section, we extend our framework to groupwise registration in which the goal is to bring a collection of images into joint registration, based on their contents. We start with the congealing method, and later we discuss an instance of feature-based registration, specifically of tractographic streamlines. We show that both applications are instances of a maximum profile likelihood formulation.
3.1. Congealing
Beyond pairwise registration, minimization of joint entropy has been also used as a measure of joint similarity for population registration via congealing (Learned-Miller et al., 2000; Learned-Miller, 2005; Zöllei et al., 2005). Learned-Miller et al. (2000) first introduced the idea of congealing for hand-written digit recognition. They used the sum of the entropy of pixel-stacks (a collection of pixels from the same location in the image set) as the measure of agreement, and minimized it by transforming each image separately. In the context of medical imaging, Zöllei et al. (2005) adopted a congealing framework to create atlases for brain MRI using entropy estimation with Empirical Entropy Manipulation Analysis (EMMA) (Viola et al., 1996) and optimization via a stochastic gradient-based approach.
Congealing registers a group of m collections of corresponding features {U1,…, Um} sampled from m images by varying a group of per-image transformations B ≐ {β1, …, βm}. Here Uj contains features {uj1,…, ujn} where uji is the intensity of the image indexed by j, sampled at location xi. The features are assumed to be independent and identically distributed within pixel/voxel locations, but with different distributions pR(u; θi) at each location, with parameters Θ ≐ {θ1, …, θn},
Then, the model takes form as
Maximum profile likelihood is
and the asymptotic form is
Learned-Miller et al. (2000) used a conventional univariate categorical distribution at each voxel location, , where are the intensity values that u can assume. Here θi are the parameters of the categorical distribution at the location indexed by i, [θi]k ≥ 0 and ∑k [θi]k = 1. The maximum profile likelihood formulation is then,
In a similar fashion to the previous case of jointly categorical distributions, the inner maximization can be solved in closed form, yielding,
| (6) |
Here, Ni(B) is the histogram of voxel intensities at voxel i. In other words, [Ni(B)]k is the number of voxels located at i that have intensity value , and Ni ≐ ∑k[Ni(B)]k is the normalizer for the histogram for voxels located at i.
Eq. 6 is equivalent to the original statement of the congealing algorithm in Learned-Miller et al. (2000). Thus, we have shown that congealing is an instance of maximum profile likelihood registration on a population of data. DL-based image alignment by congealing has also been proposed by Huang et al. (2012). In that work, unsupervised features are learned from a multilayer Boltzmann machine to find similarity transformation for alignment.
3.2. Tractographic Atlas Formation by Groupwise Registration
In the cases discussed so far, the features have been image intensities at pixels or voxels. In the following we describe a kernel-based approach that can be used with more elaborate features. In medical imaging, features can be quite varied. SIFT features (Lowe, 1999) are one example; here an image is represented by rich feature descriptors that are located at key points in images. Streamline tractograhy from diffusion MRI (Jeurissen et al., 2019) is another example. The method we describe below can be specialized to a specific problem by defining the kernel that takes a pair of features as arguments, in Eq. 12.
Streamline tractography enables in-vivo mapping of the brain’s white matter connections, or fiber tracts. Typically, the estimated fiber tracts are represented as curves (sequences of points) in 3D. These curves, often called “fibers,” have been used as image features for many proposed tractography-based registration methods (Garyfallidis et al., 2015; Leemans et al., 2006; Mayer et al., 2010; Ziyan et al., 2007), including the groupwise registration approach that we will discuss below. First, to illustrate the concept of groupwise tractography registration, we take as an example a recent work by Zhang et al. (2018), where groupwise tractography registration was employed as an initial step in creating a white matter fiber atlas (Fig. 2). The figure shows the result of whole-brain tractography registration, as well as selected individual clusters or common anatomical structures in the population. These clusters give a more fine-grained visualization of the success of the registration. The data-driven fiber cluster atlas was annotated by a neuroanatomist and enabled the first white matter parcellation across the human lifespan.
Fig. 2:
(a) Groupwise registered tractography data from 100 subjects, used to form a data-driven fiber cluster atlas. A random sample of fibers across all 100 subjects is shown. The colors are derived from the fiber similarity measure used in clustering. (b) A cluster of fibers that have a common shape and location across the population of 100 subjects. Anatomically, this cluster forms part of the arcuate fasciculus language tract. (c) An example fiber cluster that forms part of the corticospinal motor tract.
O’Donnell et al. (2012) proposed multi-subject groupwise registration of whole-brain diffusion tractography of the white matter by entropy minimization without making reference to the latent data distribution; the criteria was optimized directly. Subsequent work by Zhang et al. (2018) adopted the alternating iteration of Eqs. 15 and 16, below. We provide here a complete derivation from maximum profile likelihood in the current framework.
The features (tractographic streamlines), u, are summarized as vectors of p knot points: u[k] ∈ R3 for 1 ≤ k ≤ p, where the knot points are evenly spaced along the streamline. Each subject U, indexed by j, is represented by a collection of nj features,
| (7) |
The transformation model on features βu, is defined component-wise by βu[k] ≐ T(u[k],β) where T(·, β) : R3 ↦ R3. Previous works have used Affine (O’Donnell et al., 2012) and B-spline (O’Donnell et al., 2017; Zhang et al., 2018) transformation models.
In this setting, our model is a probability density function on features, pR(u; Θ), for a population of subjects that are in registration; so pR is a density on vectors of p points in R3. Θij are model parameters, in this case chosen to be one per feature i per subject j. pR will be described in more detail below.
We assume that the features are distributed independently and identically within and across subjects. The model for a population of subjects, offset by transformations parameters B ≐ {β1, … βm} (one per subject), and model parameters Θ, is then
| (8) |
Here, subject indexes are represented with j, and i represents indices of features within subjects.
Maximum profile likelihood registration takes the following form,
| (9) |
and the asymptotic form is
Here, pD(u; B) is the latent distribution that generates the data as the collection of transformations is varied.
Groupwise registration is accomplished using iterative model refinement (coordinate ascent),
| (10) |
| (11) |
The model for registered feature data, pR, is constructed as a sum of kernels,
| (12) |
where Θji is a vector of p points in R3 (the same representation as the features u). This is similar to a kernel density, or a mixture density. As the features u are modeled by probability density functions, arbitrary transformations, β, on the features could cause pR(βu; Θ) to not integrate to one. To avoid this, we assume that our transformations will be approximately volume preserving, i.e., the subjects’ heads do not vary in size by a large amount. Kernel densities are often described as being ‘non-parametric’, in the sense that the number of model parameters grows with the size of the data, as is the case here. Despite this terminology, the model does have parameters. We use the following kernel, where is a distance function for tracts and σ is a scale parameter.
The iteration becomes
| (13) |
| (14) |
Eq. 13 amounts to adjusting the transformations of the individuals for best registration to the most recently estimated atlas. Eq. 14 corresponds to maximum likelihood estimation of the parameters Θ of a kernel density, given a collection of data, . This can be approximated by setting the kernel density parameters to be centered on the data points (the standard way of constructing a kernel density from data). If the kernels did not overlap, the approximation would be exact. In practice, the resulting method works well. The iteration is:
| (15) |
| (16) |
Thus, groupwise registration of tractography streamlines and potentially other feature-based registration problems can be accomplished using the same maximum profile likelihood framework as used for the registration of intensity images.
4. Image Registration by Deep Classification
In the previous sections we used an information theoretic framework based on generative models on image features to construct and analyze pairwise and groupwise registration methods. In contrast, many of the successes of deep learning, e.g., in image classification, have used discriminative modeling (Huang et al., 2017; Szegedy et al., 2017). Here, we demonstrate that using discriminative models on pairs of patches, we are able to achieve a maximum-likelihood registration in the same framework. Later in Section 4.2, we show that by using iterated model refinement via Eq. 4 and Eq. 5, we can alleviate the need for accurately registered training data; thus, enabling “weakly-supervised” registration.
4.1. Maximum Likelihood Registration by Deep Classifier
We show here how to use image classifiers to construct an image agreement metric for solving maximum likelihood registration problems. Following Simonovsky et al. (2016), a binary classifier with inputs of patch pairs, (u, v), is trained to distinguish between two classes: registered pairs of patches, denoted by z = 1 and unregistered pairs of patches, denoted by z = 0.
In more detail, registered patches are cropped from the same locations in images, and unregistered patches are randomly selected from their corresponding images (in essence, for the randomly selected patches, the relationship between pairs of patches has been randomized out, in a fashion similar to permutation methods of constructing null hypothesis distributions). Thus, the ‘original’ patch data has been augmented with a collection of unregistered patches, and the corresponding indicator variables.
Similarly to Eq. 1 our joint model for the augmented data is
| (17) |
where U and V are collections of patches of image intensities sampled from the two images, Z is a collection of indicators, and pR(u, v, z; θ) is a parametric distribution that is meant to approximate the latent joint distribution that characterizes the data (both registered and unregistered). We have assumed that corresponding pairs of patches are distributed independently and identically – this assumption is substantially less severe than assuming that pairs of pixels or voxel intensities are independently distributed. The transformation model on patches is specified as follows. Let v be a collection of image intensities from locations x[k], (1 ≤ k ≤ N), in a patch, then βv contains image intensities from locations T(x[k],β)) where T(·,β): R3 ↦ R3.
Next we specify the joint model on u, v and z. Let . Also let p(u, v∣z = 1) be the latent distribution on pairs of patches that are correctly registered, and let p(u, v∣z = 0) be the latent distribution on patches that are randomly paired, i.e., unregistered. We assume that p(u, v∣z = 0) is invariant to transformations on v. In a simpler scenario involving only translations, invariance to translation corresponds to an assumption of shift invariance (or stationarity), which is natural in modeling image phenomena. This motivates, for example, the use of convolutional structures in deep image processing. Beyond translations, the invariance is a reasonable assumption if the transformations are approximately rigid, i.e., without major scale changes.
The joint model is then
| (18) |
We next construct a parametric model that is intended to approximate the true joint specified above,
| (19) |
where p(u, v) is a marginalization of the joint distribution specified above in Eq. 18, and pC(z∣u, v; θ) is a discriminative model, i.e., a classifier.
Suppose we fit the model by maximum likelihood (in practice this is done using data from multiple images, as described below),
or
| (20) |
(Here, p(ui, vi) has been dropped, as it is not a function of θ.)
If the classifier has enough capacity, then we expect it to well approximate the true conditional probability on z that is specified by the true joint,
Multiplying by p(u, v) shows that in this case, pR approximates the true latent joint,
In view of Eq. 17, maximum likelihood registration is,
| (21) |
We split the sum on cases of z,
As pR(u,βv, z = 0; ) ≈ p(u,βv, z = 0) = p(u,βv∣z = 0)p(z = 0), and, as discussed above, p(u,βv∣z = 0) is not a function of β, we drop the second term, leaving
By definition, pR(u, v, z; θ) ≐ pC(z∣u, v; θ)p(u, v); however, we do not have access to p(u, v) (it is latent), so we use the following strategy to discharge that term. We subtract a second term, that, as before, is not a function of β,
Using the following identity, that may be easily obtained from Eq. 19 by subtracting the z = 0 case from the z = 1 case (p(u, v) cancels),
we obtain,
| (22) |
where . As the sigmoid function and the logit transform are inverses, and p(z = 1∣ui,βvi; ) is typically the output of a sigmoid unit in a deep neural net, the metric is seen to be a sum of pre-sigmoid activations. Thus, their use in Cheng et al. (2018) is now justfied by our theory. This is our interpretation of ‘deep metric registration’.
A similar approach to constructing a density estimate from a discriminative classifier was used in a precursor to Generative Adversarial Networks (GANs) by Tu (2007); that work used a classifier trained to distinguish data from uniformly distributed samples.
4.2. Maximum Profile Likelihood Registration by Deep Classifier
The deep metric described above uses a classifier that was presumably trained on collections of registered images; one image pair will likely not suffice. In some applications, e.g., abdominal ultrasound and CT, it is not practical to obtain registered images for training data. In this section, we use iterative model refinement to derive a deep metric that can be trained with images that are only approximately registered; the result can be characterized as Weakly Supervised Registration by Deep Classifier.
We formulate maximum profile likelihood over a collection of pairs of images; these will serve as the source of data for training a classifier. Features (patches), are indexed by i, and image pairs are indexed by j. B ≐ {β1,…,βm} are transformation parameters, one per image pair. Following Eq. 21,
The corresponding asymptotic form is
where pD(u, v, z; B) is the latent distribution that generates the data (uji,βjvji, zji). Here, the optimization varies the transformations to minimize an upper bound on the entropy of pD.
Iterative model refinement (coordinate ascent) alternates the following optimizations,
Following Eq. 20 for the θ optimization, and Eq. 22 for the β optimization, we obtain
| (23) |
| (24) |
Eq. 24 amounts to estimating the transformation parameters (or, registering) of a collection of pairs of images using the deep metric with known model parameters, . (Note that the transform adjustment only need be applied to the patches in the ‘registered’ class.) Eq. 23 corresponds to retraining the network using patches from images that are offset by the most recently estimated transformation parameters, .
The iteration starts with Eq. 23 on the original roughly registered training data. Subsequently, the method alternates between re-aligning the data and re-estimating the deep network parameters. We envision that this iterative training needs to happen only once per application type. To perform registration on previously unseen images, the model parameters may be fixed and registration performed using Eq. 22.
4.3. Evaluation - Weakly Supervised Registration by Binary Classification
In this section, we present several experiments to demonstrate the effectiveness of our formulation of iterative model refinement (IMR) with deep probabilistic binary classifiers to perform maximum likelihood registration. We show that model parameters along with transformation parameters can be learned via IMR from a roughly aligned dataset and, unlike the work in Simonovsky et al. (2016), a completely registered dataset is not needed for training. We use the IXI Brain Development Dataset1 to demonstrate this concept with 60 subjects for training and validation and 60 subjects for testing (details follow in Data). As explained in Section 4.2, for a collection of roughly registered images (fixed and moving images in the training set), we start with Eq. 23 and train a deep binary classifier to distinguish two classes of patches: registered (z = 1) and unregistered (z = 0). Later, we switch to Eq. 24 and use the classifier’s score to derive transformation parameters for each training image pair (βj). Finally, the computed transformations are applied to the moving images. This process is iterated multiple times if needed until the training images are well registered. Throughout this section, we use IMRx notation to refer to performing IMR step x. In more detail, the first IMR, IMR1, uses Eq. 23 and Eq. 24 to register the training data. If needed, one can apply IMR2 on the outcome of IMR1 to further optimize the model and the transformation parameters and the iteration can continue. In our rigid registration experiment, we use 3 steps of IMR (IMR1 → IMR2 → IMR3) while in our affine registration experiment we use 4 steps (IMR1 → IMR2 → IMR3 → IMR4) and in our deformable registration experiments we use 2 IMR steps (IMR1 → IMR2). Finally, for registration of an unseen test case, we use the estimated model parameters at each iteration with Eq. 22 to optimize the transformation parameters. It should be noted that the test data is not used at all for training.
In order to have an end-to-end framework for registration, we use a differentiable image transformation method that is based on the Spatial Transformer Network (STN) (Jaderberg et al., 2015) to estimate transformation parameters via gradient-descent — this significantly lowers the run-time of our approach compared to non-gradient based optimizations.
Data:.
For our experiments, we use the IXI Brain Development Dataset which contains aligned T1-weighted (T1) and T2-weighted (T2) MRI image pairs from healthy brain subjects. We also generate gradient magnitude (GradMag) images from 3D T1 MRI volumes to have a multi-modal problem mimicking MRI and ultrasound registration. We choose T2 MRI as the fixed image and we register the T1 MRI (or GradMag image) to it. 60 subjects are selected for training and validation and another different 60 subjects are used for evaluation. All images are resampled to 1×1×1 mm, and their intensity is normalized to the range of [0,1]. To create a roughly aligned dataset for learning a deep metric, we apply random transformations to the moving images before each experiment. The type and parameters of each transformation are discussed in more detail in the following. We perform the same pre-processing steps on the test data. Moreover, the same distribution for transformation parameters is used to generate random misalignment on each test case in our synthetic experiments.
Patch Generation:.
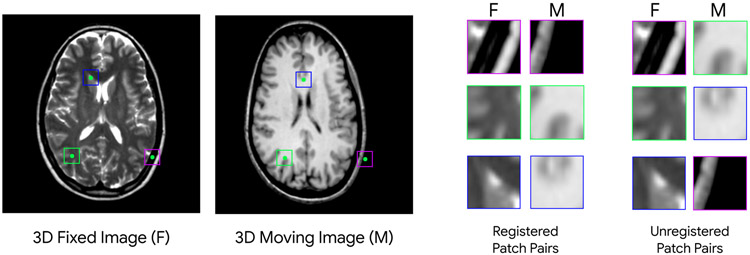
As explained in the previous section, our formulation of maximum profile likelihood based on deep classification relies on training a classifier on two classes of patches cropped from fixed and moving images. To generate these, we crop 3D patches, (ui, vi), of size 17×17×17 voxels from fixed and moving images. Our patch size is fixed for each iteration of IMR in all experiments. For the registered class (zi = 1), we crop the patches from the same physical location in the space, and for the unregistered class (zi = 0) we crop from random locations. Fig. 3 depicts a fixed and moving image in one of our experiments. As seen, for learning a deep metric, we are using images that are only approximately registered. A sample of 3 cropped patch pairs for each class is also depicted in Fig. 3. To capture large initial misregistrations, we employ a multi-resolution framework and perform initial iterations of IMR on downsampled versions of images before switching to the finer resolutions. To avoid aliasing artifact, we apply Gaussian smoothing before downsampling. Overall, 1 million patches are generated for the classifier training in each level of refinement for each experiment.
Fig. 3:
A sample of fixed (T2) and moving image (T1) in our training dataset used for deriving a deep metric for registration. The moving image is misregistered by a random affine transformation. Two classes of patches are shown on the right (we crop 3D patches; the middle cross-section of each patch is shown in 2D). The registered class (z = 1) contains patches that are cropped from the same location in the space of images, and the unregistered class patches (z = 0) are randomly picked. Fixed and moving image patches (for both classes) are concatenated in the channel dimension and used for training a deep binary classifier by minimizing the cross-entropy loss.
Network Architecture and Training:.
The architecture of our deep classifier is inspired by Densely Connected Convolutional Networks (DenseNet) (Huang et al., 2017). In more detail, we use 4 dense blocks of depth 10 with 15 filters in the first dense block and a growth rate of 12. All layers use ReLU activation functions except for the a final sigmoid layer. Therefore, the output of the network is a scalar representing the posterior probability of belonging to the registered class. For input, we concatenated patches from fixed and moving images in the channel dimension (Zagoruyko and Komodakis, 2015). We train our model by maximizing the likelihood of data under the model (this is often called cross-entropy minimisation in deep learning literature (Goodfellow et al., 2016)). During training, an initial learning rate of 10−3, batch size of 256, and ℓ2-regularization of 0.005 are used to optimize the network.
Registration:.
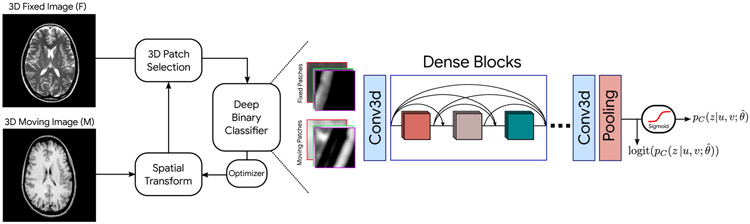
The detailed schematic of our proposed approach is depicted in Fig. 4. To register an unseen fixed and moving image pair, we sequentially use each of the binary classifiers previously trained in IMR – their aggregated pre-sigmoid activations are used for optimizing transformation parameters. In our multi-resolution framework, the resulting transformation field at the coarser level is upsampled and used for warping the original moving image (finer resolution) before starting the next iteration. In more detail, we start with the pre-trained classifier from IMR1 (with parameters θ1), and perform maximum likelihood registration with Eq. 22 using a set of 3D cropped patches with significant overlaps. Next, we use the IMR2 pre-trained classifier to perform registration on the result of the previous step; we repeat this process until registration with the last IMR pre-trained classifier. To optimize the registration parameters, we fix and freeze the classifier network’s weights, and we insert a Spatial Transformation Network (STN) before the patch selection module (as seen in Fig. 4). The transformation parameters are encoded inside the STN as learnable weights and the resulting transformation field is applied to the whole moving image. We optimize the registration network (STN) with Stochastic Gradient Descent (SGD) and Adam update rule using different learning rates for rigid (lr = 0.1), affine (lr = 0.075), and thin-plate spline (lr = 0.001 of image size).
Fig. 4:
Schematic of our proposed maximum likelihood registration with deep binary classifiers. Based on the initial misalignment in the dataset, we can perform multiple iterations to jointly learn model and transformation parameters. Our framework includes a deep binary CNN classifier, a Spatial Transform Module, and a 3D patch selector. Our classifier architecture is inspired by DenseNet. The aggregated logits signal (over a set of sampled patches) is used for the optimization of the transformation parameters.
Deep Metric Derived from Unregistered Dataset.
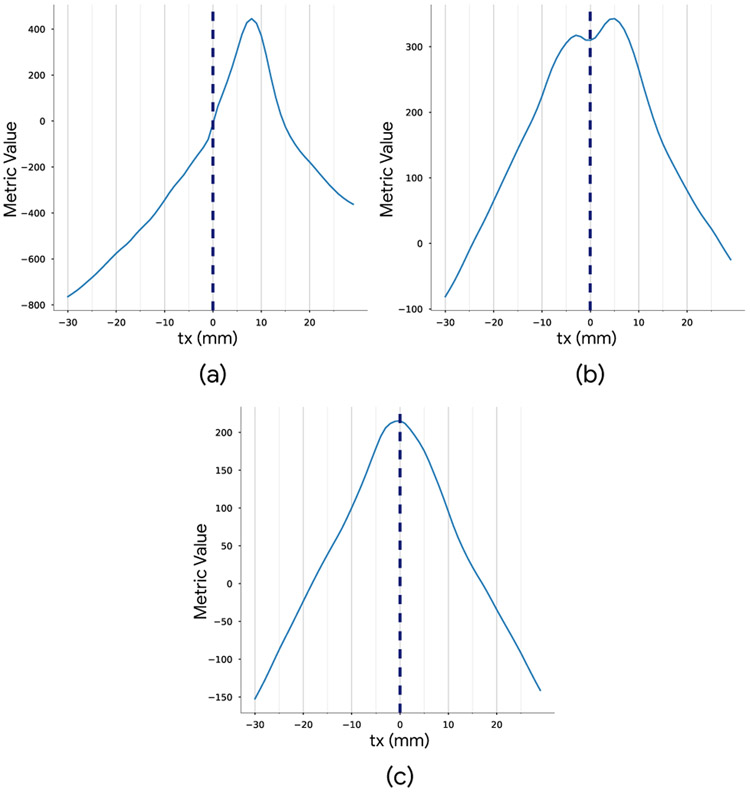
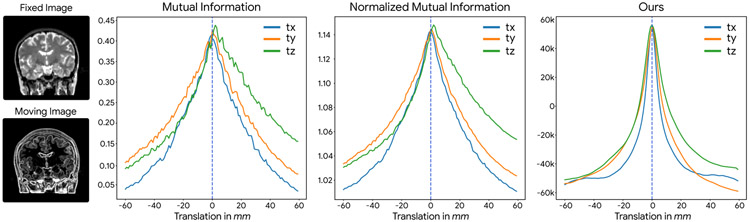
Considering the case that the deep metric is learned from a registered dataset (Eq. 22), if we observe the deep metric as a function (response function) of transformation parameters, it will have a maximum near the correct solution for registration. To illustrate, consider two registered images, the response (aggregated score from input of sampled patches) as a function of translation in x direction, will have the highest score around x = 0. However, training a deep metric on unregistered dataset can cause bias in the response function depending on the distribution of the misregistration in the data. To test this hypothesis, we generate a dataset in which moving images are all shifted in the x direction by 8 mm, and train a deep binary classifier on two classes of patches. Fig. 5(a) shows the deep metric values (the summation in Eq. 22 with i = 200) as a function of translation in the x direction for a single test case that is initially registered. As seen, it has a peak that is shifted accordingly. Therefore, the derived deep metric (from unregistered dataset) will have the highest score near the wrong solution in the transformation parameters space.
Fig. 5:
Effect of misregistered data on a deep metric derived from binary classification of patches. The training data was translated by 8 mm in the x direction. Top left: aggregated score of the deep classifier (deep metric) as a function of translation for a registered test case. Top right: aggregated deep metric from the classifier trained on patches with limited augmentation. Bottom: aggregated deep metric from the classifier trained on patches with heavy-augmentation.
We studied data augmentation with rotation and flipping as a technique to substantially reduce this bias at a cost of introducing additional variances and peaks (modes) in the response function. We performed classifier training on the augmented cropped patches from the shifted dataset. In more detail, the classifier is trained on a mixture of cropped 3D patches and randomly flipped or rotated (around z-axis) versions. As seen in Fig. 5(b), performing limited augmentation will eliminate the bias but adds another mode to the response function.
A smooth, single peak response function is preferred for effective optimization of the transformation parameters. Looking in more depth in the effect of augmentation for the response functions, we performed a heavy-augmentation (combination of rotation, and flipping in all axis) on the 3D patches for training the classifier. Fig. 5(c) depicts the result for this experiment. As can be seen, even with significant misalignment (8 mm) in the dataset, we can achieve a single-mode response function which is desirable for the optimization. In the experiments below, we demonstrate the effectiveness of the explained data augmentation technique by comparing the performance to training without data augmentation.
In the following section, we describe our image registration experiments and show the effectiveness of deep metrics, derived from training a deep binary classifier on a roughly aligned dataset. We use the described data augmentation technique on training patches for all experiments (rigid, affine and deformable) to ensure smooth and single peak response functions for optimization.
4.3.1. Experiments
We experiment with different levels of misregistration in the dataset and iterating through Eq. 23 and Eq. 24 to jointly learn the model and transformation parameters from the training data.
We report Fiducial Registration Error (FRE) for rigid/affine registration experiments calculated from 100 random sparse landmarks, and overlap scores (mean Dice Similarity Coefficient (DSC)) as a measure of agreement between Grey Matter (GM), White Matter (WM), and CerebroSpinal Fluid (CSF) which were computed by FSL FAST algorithm (Zhang et al., 2001). We use DSC because ground truth is not generally available for inter-subject registration. While DSC is not the most stringent test of registration algorithms, low scores do indicate that a method is not performing well. Our baseline for deformable registration experiments is the well-known publicly available Elastix registration package (Klein et al., 2010) with B-spline deformation model. In more detail, we used Normalized Mutual Information (NMI) with 70 histogram bins as our cost function, and we optimized it with adaptive stochastic gradient descent (Klein et al., 2009). In addition, in Elastix, the distance between control points for the finest resolution of the B-spline model was set at 16 mm. We have chosen the number of control points in our deformable experiments to obtain similar distancing between them.
Rigid Registration:.
First, we perform a rigid registration experiment where the moving images in the dataset are perturbed by applying a random rigid transformation with parameters sampled from a uniform distributions mm and radians for translation and rotation, respectively. This makes a dataset that is only approximately registered that we will use for IMR registration. We choose a non-symmetric distribution to make sure all cases in our dataset are not registered. On the training data, we perform three iterations of IMR as IMR1(×2) → IMR2(×2) → IMR3(×1). Here, IMR(×L) represents training a binary classifier on two classes of patches (Eq. 23) and performing maximum likelihood registration (Eq. 24) on the downsampled image of factor L. Later, for registering unseen test images, we use Eq. 22 with pre-trained classifiers to perform registration iteratively. We also perform an experiment in which we only utilize the last trained classifier (θ3) from IMR3 to evaluate this special case.
We also generate the GradMag images for our rigidly misaligned dataset and follow the same 3 steps IMR to perform registration. We plot the derived deep metric score (only the last stage) as a function of translation and compare it to mutual-information-based metrics.
Affine Registration:.
We also experiment with affine registration to show the capability of our proposed framework for a more general registration problem. To create a dataset that is only approximately registered, we perturb the moving images by applying random transformation with parameters sampled from , , and for translation, rotation, scale, and shear, respectively. We follow a four stage IMR as IMR1(×2) → IMR2(×2) → IMR3(×2) → IMR4(×1) for each refinement level. Similar to our rigid experiment, the trained classifiers from iterations of IMR are sequentially used for registering unseen test images. In addition, we perform an experiment by only utilizing the pre-trained classifier from the final iteration (θ4 from IMR4) to directly register the images.
Deformable Image Registrations:.
Our proposed framework is not limited by the choice of the deformation model. We also experiment with synthetic intra-subject and inter-subject deformable registrations. For our synthetic intra-subject deformable experiment, we start by artificially applying random thin-plate spline transformations with 4 × 4 × 4 control points to misregister the moving images for each subject. We perturb the location of control points with a vector drawn from a uniform distribution of . To register this dataset, we follow a 2-step IMR as IMR1(×2, (6,6,6)) → IMR2(×1.5, (7,7,7)) where IMR(×L, (nx, ny, nz)) represents performing IMR on downsampled images of factor L with thin-plate splines of (nx, ny, nz) control points in x, y, z directions, respectively. We also experiment with GradMag version of the same deformed dataset to asses the performance in a harder situation for deformable registration.
As our last experiment, we perform inter-subject T1-T2 registration. We choose 80 cases from the original dataset and create a new dataset by choosing T2 MRI from one subject and T1 MRI from another subject. We perform this twice for each subject. This will increase our dataset to 160 cases which are initially not registered (as they are from different subjects). We make sure each case is matched within its own data division (training, validation, and test). An initial Affine transformation is performed on pairs of fixed and moving images to roughly approximate the linear deformation between subjects. A 2-step IMR is employed to align the images. In more detail, we use IMR1(×2, (5,5,5)) → IMR2(×1.5, (7,7,7)). We also experiment on inter-subject T2-GradMag images by registering T2 images from one subject to GradMag images of another subject. In all deformable experiments, we only utilize the final pre-trained classifier (from the last iteration of IMR) to register the unseen test images.
5. Results and Discussion
Table 1 shows the quantitative results for the rigid and affine experiments; IMR has successfully updated model and transformation parameters jointly. We can clearly see the effect of augmentation (via rotation and flipping) on the registration performance. Although registration with binary classifiers that were trained on non-augmented patches could improve the initial results to some extent, the performance was limited due to non-smooth response functions as discussed previously. Fig. 6 demonstrates the response function of different mutual-information-based metrics compared to our derived deep metric from a binary classifier trained on a roughly aligned dataset. As a result of different contrast in images (tissue and edge contrast), artifactual characteristics appear in the MI response functions. However, our derived deep metric shows a smooth and artifact-free characterization of agreement among images.
Table 1:
Quantitative results showing the FRE for rigid and affine experiments on the unseen test data. We see that data augmentation by rotation and flipping plays a fundamental role in finding the appropriate deep metric for image registration when dealing with unregistered images. The error shown is the result of applying sequences of IMRs. Here, e.g., IMR1 → IMR4 indicates IMR1 → IMR2 → IMR3 → IMR4. Performing registration with only the initial-stage classifiers leads to significant errors. However, as we move to later stages the registration error improves. IMRfinal shows the result for using the final pre-trained classifiers directly to perform maximum likelihood registration with Eq. 22, without iteratively applying each classifier.
| Rigid |
Affine |
|||
|---|---|---|---|---|
| without Augmentation | with Augmentation | without Augmentation | with Augmentation | |
| Initial Error | 18.49 ± 3.79 | 18.49 ± 3.79 | 13.39 ± 2.40 | 13.39 ± 2.40 |
| IMR1 | 10.77 ± 1.32 | 5.31 ± 2.28 | 8.07 ± 1.00 | 2.81 ± 1.44 |
| IMR1 → IMR2 | 8.79 ± 1.64 | 2.58 ± 0.82 | 6.50 ± 0.52 | 1.38 ± 0.25 |
| IMR1 → IMR3 | 8.85 ± 2.55 | 1.37 ± 0.48 | 4.73 ± 0.47 | 1.73 ± 0.38 |
| IMR1 → IMR4 | 4.09 ± 0.37 | 1.28 ± 0.44 | ||
| IMRfinal | 0.75 ± 0.19 | 1.09 ± 0.27 | ||
Fig. 6:
Comparison of different metrics for registration of T2 and GradMag images. As seen on the left, the substantially different tissue and edge contrast between fixed and moving images make a difficult problem for registration. Our deep metric was derived from data that is only approximately registered by following a 3 step IMR. Plotting of each metric as a function of translation in x, y, z directions (tx, ty, tz) is depicted. Based on these plots, mutual-information-based metrics have a noisier response function, compared to our derived deep metric, which is smoother. The capture range of our deep metric is also comparable to mutual-information-based metrics.
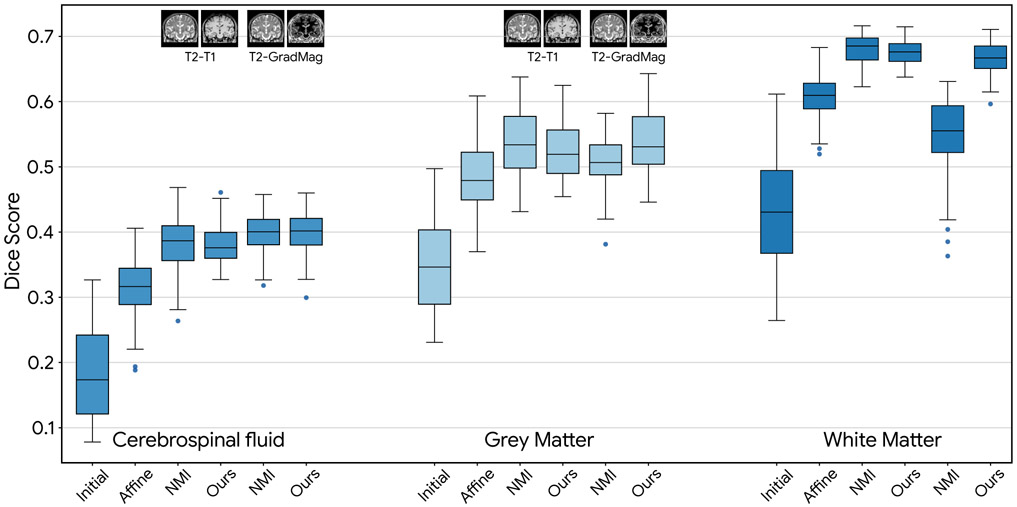
The results of the deformable intra-subject registration are shown in Table 2. As seen for T1-T2 deformable experiment, both ours and mutual-information-based methods were able to register the images successfully and improved DSC for all three areas in the brain. It should be noted that our deep metric was derived from a dataset that is only approximately registered (initial mean DSC of 0.41, 0.55 and 0.66 for CSF, GM and WM) which demonstrates the effectiveness of IMR. For the harder registration problem (T2-GradMag), we have outperformed the mutual-information-based registration significantly. Finally, Fig. 7 demonstrates the results of inter-subject registration. As seen, our method has comparable results to the mutual-information-based deformable registration while outperforming it for the harder T2-GradMag registration experiment.
Table 2:
Overlap scores (mean Dice scores) for intra-subject registration experiments. Our proposed iterative method performed comparable to mutual-information-based registration by Elastix and could outperform it in a harder registration problem on T2 and GradMag images.
| T1-T2 Deformable Experiment |
T2-GradMag Deformable Experiment |
|||||
|---|---|---|---|---|---|---|
| Initial Dice | Our method Dice | NMI Dice | Initial Dice | Our method Dice | NMI Dice | |
| CSF | 0.41 ± 0.05 | 0.63 ± 0.03 | 0.61 ± 0.04 | 0.41 ± 0.05 | 0.64 ± 0.03 | 0.49 ± 0.11 |
| Gray Matter | 0.55 ± 0.04 | 0.73 ± 0.03 | 0.71 ± 0.05 | 0.55 ± 0.04 | 0.74 ± 0.04 | 0.60 ± 0.09 |
| White Matter | 0.66 ± 0.03 | 0.84 ± 0.01 | 0.83 ± 0.03 | 0.66 ± 0.03 | 0.85 ± 0.01 | 0.69 ± 0.10 |
Fig. 7:
Inter-subject registration experiment results for both T2-T1 and T2-GradMag images chosen from different patients. The initial Dice Similarity Score (DSC) has been improved by applying an Affine transformation between images; however, further improvements are achieved with deformable transformations. In the case of T2-T1, our method can achieve comparable results to NMI, while in T2-GradMag scenario we have outperformed NMI.
Discussion:.
We used a patch size of 17×17×17 voxels as input to our CNN classifier and for capturing the large initial errors, we employed a multi-resolution pyramid scheme. At the finest resolution, 1 mm, our patch size will cover a 17 mm region in each direction. However, as can be seen in Fig. 6 our capture range can cover initial errors of up to 30 mm. In addition, our metric that was learned from roughly aligned training data has peaks closer to the correct solution, and is smoother for a wide range of displacements. Based on this, it may be that our deep metric is more amenable to optimization than MI.
We previously have studied the effect of dithering of location of the patches for smoothing the response function of deep classifier based metrics (Sedghi et al., 2019). In this article, we showed that we can achieve a single peak response function by extensively augmenting patches in training. However, the width (standard deviation) of the response function can be effectively modified with dithering which might help to increase the accuracy of the registration.
Our deformable experiments were limited to thin-plate splines due to the adaptation of the STN module (Jaderberg et al., 2015) and voxel spacing of 1.5 mm due to GPU memory limits. Extending the deformation model to B-splines and training on finer resolutions could potentially enhance the results of registration. In addition, the unregistered class patches were randomly selected from the space of images. It might be possible that with more sampling from the neighborhood of the fixed patch, we can increase the performance of our registration algorithm.
In Table 1, we showed the convergence of alignment by using a sequence of pre-trained classifiers and performing iterative registration on the test data; however, using only the final model, we were able to achieve alignment too. Based on our previous study (Sedghi et al., 2019), the initial stage models have a broader basin of attraction (response function) but are poorer models for alignment. As we move to later stages, the models get better for alignment; however, the width of the response function gets narrower. This observation has also been discussed in the congealing literature and is known as a ‘funnel’ (Huang et al., 2007). In cases where two images are far out of alignment, registering them through a sequence of models, as opposed to using the last model, may result in a better alignment.
For registration, we have used 100 iterations for rigid and affine experiments, and 200 for the deformable registration in each IMR step. An iteration refers to one step of SGD; this results in run times of in 66.60 ± 8.38, 75.61 ± 4.04, and 119.46 ± 37.02 seconds for each IMR in rigid, affine, and deformable registration, respectively. In addition, the training time for our classifier model is on average 74.33 ± 0.61 minutes for 15 epochs. All training and registration were performed using an NVIDIA TITAN RTX GPU.
In all our experiments, we started from an approximately aligned dataset and we showed that a deep metric can be successfully learned and applied on unseen test data for registration. We envision these application-specific deep metrics can be derived once per application (e.g., T1-T2) and be used for registration of future data from the same centre as well as other centers.
6. Conclusion
We presented an overview of information theoretic image registration, that began with a maximum likelihood formulation for generative models with known model parameters on joint image features. The case of unknown model parameters was treated by joint maximization, or maximum profile likelihood. We showed that, asymptotically, maximizing profile likelihood is equivalent to minimizing an upper bound on the entropy of the latent distribution that generates the data. For the case of discrete image intensities, maximum profile likelihood is equivalent to registration by minimization of joint entropy in the pairwise case and congealing in the groupwise case. In other cases, the profile likelihood criteria can be optimized by the coordinate ascent, or iterative model refinement, this approach has previously been effective for pairwise image registration and groupwise registration of tractographic streamlines.
Subsequently, we extended the formalism to discriminative models and presented a novel formulation of weakly supervised image registration that is based on deep classifiers. In our experiments, the deep learning approach had comparable results to the standard mutual information methods for registration of T1 and T2 MRI images. On a much harder registration problem with significant contrast difference, we outperformed standard mutual-information-based registration.
7. Acknowledgments
We gratefully acknowledge the funding provided by the following: Natural Sciences and Engineering Research Council of Canada (NSERC), Canadian Institutes of Health Research (CIHR), Ontario Trillium Scholarship (OTS), National Institutes of Health (NIH) grants: U01:CA199459, P41:EB015898, NIH P41:EB015898-14S3, P41:EB015902, and R01:MH119222. We also would like to thank NVIDIA for the GPU donation.
Appendix
Appendix A. Rationale for Registration by Minimization of Joint Entropy
It has been frequently observed that, empirically, the joint entropy of pixel intensities of a pair of multi-modality images has a sharp local minimum when the images are correctly registered (Collignon et al., 1995). We aim here to explain the observation using basic principles.
Suppose the images contain a collection of m discrete tissue types {}, and the intensities corresponding to the tissues in the two images are {} and {}.
If the images are correctly registered, then when intensities are sampled at corresponding locations, the observations will consist of pairs (, ) for i ∈ {1, …, m} – the intensity pairs corresponding to the same tissue.
However, if the images are not correctly registered, then we will observe, in addition, intensity pairs (, ) where i ≠ j. This happens because, in some cases, we will collect corresponding intensities that originate from different tissues, due to the misregistration. If we consider the distribution which generates the data, then in case of correct registration, the probably of observing (, ) where i ≠ j is zero. However, for case of misregistration, the probability will be nonzero for some i, j : i ≠ j (provided the tissues have distinguishing contrast in the images). The important point is that in comparison to the correctly registered case, the distribution for the misregistered cases will contain nonzero probabilities for some joint occurrences that have zero probability in the registered case. As we will see below, this corresponds to lower entropy at correct registration.
Since the intensities take on discrete values from finite collections, we use the jointly categorical model (also used above in Section 2.2.2): , where θjk ≥ 0 and ∑jk θjk = 1. The entropy of the jointly categorical distribution is: , and its partial derivative is .
Consider the case where the images are adjusted slightly away from correct registration. If the tissue structures are arranged in a piece-wise contiguous way (a reasonable assumption for many anatomical structures), then for a small perturbation away from correct registration, the probability of observing intensity pairs (, ) where j = k will not change appreciably. However, the probability of observing (, ) where i ≠ j will increase from zero. Then, the corresponding θjk parameter of the histogrammed data will increase as well. Because the partial derivative of entropy with respect to θjk diverges positive at θjk = 0, the entropy will initially strongly increase.
In summary, as the images are perturbed away from correct registration, observations that correspond to mixtures of tissues will appear, which causes an increase in entropy.
Footnotes
References
- Balakrishnan G, Zhao A, Sabuncu MR, Guttag J, Dalca AV, 2019. Voxelmorph: a learning framework for deformable medical image registration. IEEE transactions on medical imaging . [DOI] [PubMed] [Google Scholar]
- Blei DM, Kucukelbir A, McAuliffe JD, 2017. Variational inference: A review for statisticians. Journal of the American Statistical Association 112, 859–877. [Google Scholar]
- Blendowski M, Heinrich MP, 2019. Combining mrf-based deformable registration and deep binary 3d-cnn descriptors for large lung motion estimation in copd patients. International journal of computer assisted radiology and surgery 14, 43–52. [DOI] [PubMed] [Google Scholar]
- Chan HM, Chung AC, Yu SC, Norbash A, Wells W, 2003. Multimodal image registration by minimizing kullback-leibler distance between expected and observed joint class histograms, in: 2003 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2003. Proceedings., IEEE. pp. II–570. [Google Scholar]
- Cheng X, Zhang L, Zheng Y, 2018. Deep similarity learning for multimodal medical images. Computer Methods in Biomechanics and Biomedical Engineering: Imaging & Visualization 6, 248–252. [Google Scholar]
- Cole SR, Chu H, Greenland S, 2014. Maximum likelihood, profile likelihood, and penalized likelihood: a primer. American journal of epidemiology 179 2, 252–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collignon A, Vandermeulen D, Suetens P, Marchal G, 1995. 3d multimodality medical image registration using feature space clustering, in: Computer Vision, Virtual Reality and Robotics in Medicine, Springer. pp. 195–204. [Google Scholar]
- Dalca AV, Balakrishnan G, Guttag J, Sabuncu MR, 2018. Unsupervised learning for fast probabilistic diffeomorphic registration, in: International Conference on Medical Image Computing and Computer-Assisted Intervention, Springer. pp. 729–738. [Google Scholar]
- Garyfallidis E, Ocegueda O, Wassermann D, Descoteaux M, 2015. Robust and efficient linear registration of white-matter fascicles in the space of streamlines. NeuroImage 117, 124–140. [DOI] [PubMed] [Google Scholar]
- Goodfellow I, Bengio Y, Courville A, 2016. Deep Learning. MIT Press. http://www.deeplearningbook.org. [Google Scholar]
- Haskins G, Kruecker J, Kruger U, Xu S, Pinto PA, Wood BJ, Yan P, 2019a. Learning deep similarity metric for 3d mr–trus image registration. International journal of computer assisted radiology and surgery 14, 417–425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haskins G, Kruger U, Yan P, 2019b. Deep learning in medical image registration: A survey. arXiv preprint arXiv:1903.02026 . [Google Scholar]
- Heinrich MP, Jenkinson M, Brady M, Schnabel JA, 2012. Textural mutual information based on cluster trees for multimodal deformable registration, in: 2012 9th IEEE International Symposium on Biomedical Imaging (ISBI), IEEE. pp. 1471–1474. [Google Scholar]
- Huang G, Liu Z, Van Der Maaten L, Weinberger KQ, 2017. Densely connected convolutional networks, in: Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 4700–4708. [Google Scholar]
- Huang G, Mattar M, Lee H, Learned-Miller EG, 2012. Learning to align from scratch, in: Advances in neural information processing systems, pp. 764–772. [Google Scholar]
- Huang GB, Jain V, Learned-Miller E, 2007. Unsupervised joint alignment of complex images, in: 2007 IEEE 11th International Conference on Computer Vision, IEEE. pp. 1–8. [Google Scholar]
- Jaderberg M, Simonyan K, Zisserman A, et al. , 2015. Spatial transformer networks, in: Advances in neural information processing systems, pp. 2017–2025. [Google Scholar]
- Jeurissen B, Descoteaux M, Mori S, Leemans A, 2019. Diffusion mri fiber tractography of the brain. NMR in Biomedicine 32, e3785. [DOI] [PubMed] [Google Scholar]
- Klein S, Pluim JP, Staring M, Viergever MA, 2009. Adaptive stochastic gradient descent optimisation for image registration. International journal of computer vision 81, 227. [DOI] [PubMed] [Google Scholar]
- Klein S, Staring M, Murphy K, Viergever MA, Pluim JP, 2010. Elastix: a toolbox for intensity-based medical image registration. IEEE TMI 29, 196–205. [DOI] [PubMed] [Google Scholar]
- Krebs J, Delingette H, Mailhé B, Ayache N, Mansi T, 2019. Learning a probabilistic model for diffeomorphic registration. IEEE transactions on medical imaging 38, 2165–2176. [DOI] [PubMed] [Google Scholar]
- Learned-Miller EG, 2005. Data driven image models through continuous joint alignment. IEEE Transactions on Pattern Analysis and Machine Intelligence 28, 236–250. [DOI] [PubMed] [Google Scholar]
- Learned-Miller EG, Matsakis NE, Viola PA, 2000. Learning from one example through shared densities on transforms, in: Proceedings IEEE Conference on Computer Vision and Pattern Recognition. CVPR 2000 (Cat. No. PR00662), IEEE. pp. 464–471. [Google Scholar]
- LeCun Y, Bengio Y, Hinton G, 2015. Deep learning. nature 521, 436. [DOI] [PubMed] [Google Scholar]
- Leemans A, Sijbers J, De Backer S, Vandervliet E, Parizel P, 2006. Multiscale white matter fiber tract coregistration: A new feature-based approach to align diffusion tensor data. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 55, 1414–1423. [DOI] [PubMed] [Google Scholar]
- Leventon ME, Grimson WEL, 1998. Multi-modal volume registration using joint intensity distributions, in: International Conference on Medical Image Computing and Computer-Assisted Intervention, Springer. pp. 1057–1066. [Google Scholar]
- Litjens G, Kooi T, Bejnordi BE, Setio AAA, Ciompi F, Ghafoorian M, Van Der Laak JA, Van Ginneken B, Sánchez CI, 2017. A survey on deep learning in medical image analysis. Medical image analysis 42, 60–88. [DOI] [PubMed] [Google Scholar]
- Lowe DG, 1999. Object recognition from local scale-invariant features, in: Proceedings of the seventh IEEE international conference on computer vision, Ieee. pp. 1150–1157. [Google Scholar]
- Maes F, Collignon A, Vandermeulen D, Marchal G, Suetens P, 1997. Multimodality image registration by maximization of mutual information. IEEE transactions on Medical Imaging 16, 187–198. [DOI] [PubMed] [Google Scholar]
- Mayer A, Zimmerman-Moreno G, Shadmi R, Batikoff A, Greenspan H, 2010. A supervised framework for the registration and segmentation of white matter fiber tracts. IEEE Transactions on medical imaging 30, 131–145. [DOI] [PubMed] [Google Scholar]
- O’Donnell LJ, Suter Y, Rigolo L, Kahali P, Zhang F, Norton I, Albi A, Olubiyi O, Meola A, Essayed WI, Unadkat P, Ciris PA, Wells WI, Rathi Y, Westin CF, Golby AJ, 2017. Automated white matter fiber tract identification in patients with brain tumors. NeuroImage: Clinical 13, 138–153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Donnell LJ, Wells WM, Golby AJ, Westin CF, 2012. Unbiased groupwise registration of white matter tractography, in: International Conference on Medical Image Computing and Computer-Assisted Intervention, Springer. pp. 123–130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pawitan Y, 2001. In all likelihood: statistical modelling and inference using likelihood. Oxford University Press. [Google Scholar]
- Pluim JP, Maintz JA, Viergever MA, 2003. Mutual-information-based registration of medical images: a survey. IEEE transactions on medical imaging 22, 986–1004. [DOI] [PubMed] [Google Scholar]
- Roche A, Malandain G, Ayache N, 2000. Unifying maximum likelihood approaches in medical image registration. International Journal of Imaging Systems and Technology 11, 71–80. [Google Scholar]
- Sedghi A, Luo J, Mehrtash A, Pieper S, Tempany CM, Kapur T, Mousavi P, Wells III WM, 2019. Semi-supervised image registration using deep learning, in: Medical Imaging 2019: Image-Guided Procedures, Robotic Interventions, and Modeling, International Society for Optics and Photonics. p. 109511G. [Google Scholar]
- Shen D, Wu G, Suk HI, 2017. Deep learning in medical image analysis. Annual review of biomedical engineering 19, 221–248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simonovsky M, Gutiérrez-Becker B, Mateus D, Navab N, Komodakis N, 2016. A deep metric for multimodal registration, in: International Conference on Medical Image Computing and Computer-Assisted Intervention, Springer. pp. 10–18. [Google Scholar]
- Studholme C, Hill DL, Hawkes DJ, 1999. An overlap invariant entropy measure of 3d medical image alignment. Pattern recognition 32, 71–86. [Google Scholar]
- Szegedy C, Ioffe S, Vanhoucke V, Alemi AA, 2017. Inception-v4, inception-resnet and the impact of residual connections on learning, in: Thirty-First AAAI Conference on Artificial Intelligence. [Google Scholar]
- Timoner S, 2003. Compact representations for fast nonrigid registration of medical images. Technical Report. MIT Computer Science and Artificial Intelligence Laboratory. [Google Scholar]
- Tu Z, 2007. Learning generative models via discriminative approaches, in: 2007 IEEE Conference on Computer Vision and Pattern Recognition, IEEE. pp. 1–8. [Google Scholar]
- Viola P, Wells III WM, 1997. Alignment by maximization of mutual information. International journal of computer vision 24, 137–154. [Google Scholar]
- Viola PA, Schraudolph NN, Sejnowski TJ, 1996. Empirical entropy manipulation for real-world problems, in: Advances in neural information processing systems, pp. 851–857. [Google Scholar]
- de Vos BD, Berendsen FF, Viergever MA, Sokooti H, Staring M, Išgum I, 2019. A deep learning framework for unsupervised affine and deformable image registration. Medical image analysis 52, 128–143. [DOI] [PubMed] [Google Scholar]
- Wells WM, Viola P, Atsumi H, Nakajima S, Kikinis R, 1996. Multimodal volume registration by maximization of mutual information. Medical image analysis 1, 35–51. [DOI] [PubMed] [Google Scholar]
- Wolterink JM, Dinkla AM, Savenije MH, Seevinck PR, van den Berg CA, Išgum I, 2017. Deep mr to ct synthesis using unpaired data, in: International workshop on simulation and synthesis in medical imaging, Springer. pp. 14–23. [Google Scholar]
- Wu G, Kim M, Wang Q, Munsell BC, Shen D, 2015. Scalable high-performance image registration framework by unsupervised deep feature representations learning. IEEE Transactions on Biomedical Engineering 63, 1505–1516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang X, Kwitt R, Styner M, Niethammer M, 2017. Quicksilver: Fast predictive image registration–a deep learning approach. NeuroImage 158, 378–396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yi Z, Soatto S, 2011. Multimodal registration via spatial-context mutual information, in: Biennial International Conference on Information Processing in Medical Imaging, Springer. pp. 424–435. [DOI] [PubMed] [Google Scholar]
- Zagoruyko S, Komodakis N, 2015. Learning to compare image patches via convolutional neural networks. 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 4353–4361. [Google Scholar]
- Zhang F, Wu Y, Norton I, Rigolo L, Rathi Y, Makris N, O’Donnell LJ, 2018. An anatomically curated fiber clustering white matter atlas for consistent white matter tract parcellation across the lifespan. NeuroImage 179, 429–447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Brady M, Smith S, 2001. Segmentation of brain mr images through a hidden markov random field model and the expectation-maximization algorithm. IEEE TMI 20, 45–57. [DOI] [PubMed] [Google Scholar]
- Ziyan U, Sabuncu MR, O’donnell LJ, Westin CF, 2007. Nonlinear registration of diffusion mr images based on fiber bundles, in: International Conference on Medical Image Computing and Computer-Assisted Intervention, Springer. pp. 351–358. [DOI] [PubMed] [Google Scholar]
- Zöllei L, Fisher JW, Wells WM, 2003. A unified statistical and information theoretic framework for multi-modal image registration, in: International Conference on Information Processing in Medical Imaging, pp. 366–377. [DOI] [PubMed] [Google Scholar]
- Zöllei L, Jenkinson M, Timoner S, Wells W, 2007. A marginalized MAP approach and EM optimization for pair-wise registration, in: International Conference on Information Processing in Medical Imaging, pp. 662–674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zöllei L, Learned-Miller E, Grimson E, Wells W, 2005. Efficient population registration of 3d data, in: International Workshop on Computer Vision for Biomedical Image Applications, Springer. pp. 291–301. [Google Scholar]