Optical secret sharing with cascaded metasurface holography

The secret of a holographic image can be shared across two closely stacked metasurface holograms.

Abstract

Secret sharing is a well-established cryptographic primitive for storing highly sensitive information like encryption keys for encoded data. It describes the problem of splitting a secret into different shares, without revealing any information to its shareholders. Here, we demonstrate an all-optical solution for secret sharing based on metasurface holography. In our concept, metasurface holograms are used as spatially separable shares that carry encrypted messages in the form of holographic images. Two of these shares can be recombined by bringing them close together. Light passing through this stack of metasurfaces accumulates the phase shift of both holograms and optically reconstructs the secret with high fidelity. In addition, the hologram generated by each single metasurface can uniquely identify its shareholder. Furthermore, we demonstrate that the inherent translational alignment sensitivity between two stacked metasurface holograms can be used for spatial multiplexing, which can be further extended to realize optical rulers.

INTRODUCTION

Over the years, several approaches have been developed to protect data from theft and tampering. A common way to enhance data security is information encryption. Nowadays, cryptographic methods are widely used for security-related problems concerning the protection of intellectual property rights and product authentication. Invented by Adi Shamir and George Blakley (1, 2), secret sharing solves the cryptographic task of splitting a secret among multiple shareholders so that it can only be reconstructed when a sufficient number of shares are combined together. In doing so, the corruption of a single shareholder does not leak any information about the shared secret. In another type of security application, optical holography has appeared as a crucial security element against counterfeiting with several important applications in identity cards, passports, and banknotes (3–5). Among the different available holographic techniques, metaholography thrives with its inherent flexibility and compactness, which allows for dense storing and encrypting of optical information into spatially distributed phase and amplitude patterns (6, 7).

The design flexibility of metasurfaces stems from the huge variety of possible nanostructure shapes and can be used to access multiple degrees of freedom (DOFs) per pixel. For metasurface holography, these additional DOFs offer the possibility of realizing novel multiplexing schemes for improved information security, where different holographic images are encoded along multiple optical dimensions (8–16). However, so far, metasurface multiplexing frameworks were usually one-layer solutions, which only allow for the access of different information channels, but not for the physical splitting of these information channels across multiple shareholders. In this context, multilayer layouts offer an alternative as they allow for the physical separation of layers and their inherent information.

Previously, multilayer metasurface layouts were often used to achieve previously unrealized functionalities or to increase the performance of existing optical metasurface elements. This includes the demonstration of high wavelength selectivity (17, 18), multispectral (19, 20) and varifocal (21) metalenses, metasurface retroreflectors (22), holography with asymmetric transmission (23), circular polarization filters (24), multicolor holography (25, 26), image differentiation (27), and quantitative phase microscopy (28), as well as pattern recognition in an all-optical machine learning framework (29). The advantage of multilayer phase mask systems or diffractive deep neural networks is that they are highly customizable as they gradually change the state of light within each layer (29, 30). Some demonstrations based on multiple phase profiles have been proposed for watermarking and optical encryption (31–35). However, independent holographic images of each single-phase profile were not obtained. With advances in design and algorithmic techniques, these multilayer systems can be developed toward innovative holographic security features (36).

RESULTS

Here, we experimentally demonstrate a cascaded metasurface framework that can be used to split and share encrypted holographic information across multiple metasurface layers (Fig. 1). In our optical secret sharing scheme, we use a set of nanostructured optical metasurfaces as “shares.” Each of them contains an encoded phase-only Fourier hologram, which can be reconstructed in the far field upon illumination with circularly polarized light. These single-layer images serve as a unique identifier for each metasurface. Meanwhile, when the two metasurfaces are stacked 100 μm apart, the illumination of the cascaded configuration creates a new holographic image that is distinct from their two single-layer holograms. This cascaded holographic image can be used as an optical secret that is only revealed if both metasurfaces are stacked. The concept can be extended to a larger set of shares where only the combination of all of them will reveal the stored secret. To achieve this behavior, we use an iterative gradient optimization approach that uses the “automatic differentiation” feature of modern machine learning libraries (37).

Fig. 1. Conceptual illustration of the holographic secret sharing via cascaded metasurfaces.

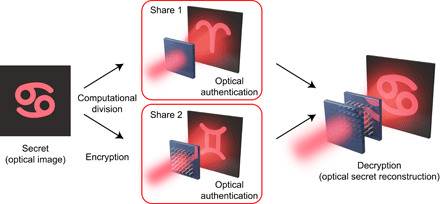
By design, both metasurfaces (shares) contain a Fourier hologram, which reconstructs an image in the visible when they are illuminated with circularly polarized light. At the same time, the illumination in the cascaded configuration creates a completely different image. While the secret of the cascaded image is shared across two metasurfaces, the single-metasurface holographic images can be used as unique identifiers for the shareholders.

In a simple picture, the cascaded hologram’s functionality can be understood as follows: Light passing through the cascaded arrangement accumulates the phase delays of both layers. In an idealized case, where both metasurfaces are virtually placed on top of each other, this would correspond to adding up both phase masks pixelwise. Considering that the same cascaded phase mask can be built up through combinations of different single phase masks, it is possible to share the “secret” of the cascaded image across two metasurface layers without revealing any information about the shared secret within the single-layer images. Meanwhile, by adding up both phase profiles pixelwise, the phase relations of the single phase masks are no longer preserved, which allows for the multiplexing of single and cascaded images.

For our demonstration, we use the concept of the Pancharatnam-Berry phase (PBP) to realize the metasurface phase masks (38, 39). Thus, the metasurfaces are made of silicon nanofin structures, which are designed as local half-wave plates. According to their individual orientation, these nanostructures introduce a spatial variant phase delay into the cross circular polarization state of the transmitted light. The PBP has not only the advantage of being quite robust with regard to fabrication and wavelength, but it also allows for filtering unwanted light through the usage of polarization optics. We fabricate two distinct metasurface holograms on one glass substrate (metasurface set A) and three additional metasurface holograms on a second glass substrate (metasurface set B). This allows for six different combinations in a cascaded configuration. Details about the design and fabrication can be found in Methods.

The experimentally reconstructed images of the encoded astrological symbols for the single metasurface holograms and their combinations are shown in Fig. 2. We observe that all five metasurface holograms reconstruct their individual single-layer image in high quality with low background noise (Fig. 2B). Meanwhile, cascading the metasurface holograms from both sets results in six reconstructed images with a similar quality compared to their single-layer counterparts (Fig. 2C). However, the cascaded image quality strongly depends on the alignment and deteriorates for small translational in-plane shifts between both metasurfaces. This behavior can be understood by considering that the appearance of the cascaded images requires correct pixel matching between both metasurfaces. Thus, we observe a breakdown of the cascaded hologram image when the translational mismatch exceeds the pixel size of 5 μm (see the Supplementary Materials).

Fig. 2. Holographic encryption scheme.

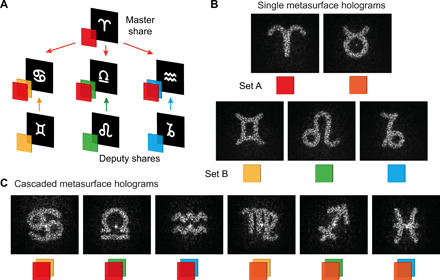
(A) Illustration of the concept using a “master share” metasurface hologram in combination with three distinct “deputy shares.” For the demonstration, we fabricate two distinct master share metasurface holograms on one substrate (set A) and three deputy share metasurface holograms on a second substrate (set B). Within every single metasurface of both sets and each stacked combination, a distinct Fourier hologram of an astrological symbol is encoded. (B) Measured single-metasurface holographic images for a wavelength of 740 nm. For better visualization, every metasurface hologram is represented by a unique color. (C) Measured cascaded metasurface holographic images for the various combinations of the metasurfaces of both sets for the same wavelength. The cascaded images nearly achieve the image quality of their single-layer counterparts.

Furthermore, all images are clearly visible without any apparent cross-talk (single metasurface images are not visible in the cascaded case). The low cross-talk can be explained by the fact that the second metasurface completely wipes out any regularities of the first metasurface’s phase profile and vice versa. In the limit of zero distance between the metasurfaces, this can be understood as follows: Because the Fourier transform of a product is the convolution of its Fourier-transformed elements, the reconstructed cascaded image is effectively the convolution of the two single images’ complex electric fields. In the vast majority of cases, this convolution operation does not preserve any visible information from the single images to the cascaded image. Therefore, we do not observe any image artifacts of the single-layer holograms within the cascaded cases. The low cross-talk is, in particular, important for optical secret sharing applications where the single metasurface hologram should not reveal any information of the secret.

In our example, we chose to use two holograms in set A and three holograms in set B. However, the concept is general, and the number of encoded images can be increased further by adding more metasurfaces to both sets or by increasing the number of sets. Note that the two sets of metaholograms (master set A and deputy set B) can be combined arbitrarily. All individual single-layer metasurface holograms and the various combinations of them carry their holographic information. With the entire series of combinations, the complete secret set can be revealed. On the basis of such scaling of information, we need to recognize that the achievable image quality is fundamentally limited by the ratio of encoded images to available phase masks. A good scaling strategy is to have a master set with a small number of shares and a deputy set with a larger number of shares. In such a scenario, the image quality primarily depends on the number of shares in the master set. Note that a decrease in image quality due to a high number of shares can be compensated by increasing the number of pixels in each hologram.

To obtain high-quality images, the design algorithm for the holograms plays an important role. Here, we treat the metasurface design process as an optimization problem in which we try to minimize the differences between the target images and the calculated images resulting from the simulated light interference. Figure 3 schematically illustrates the calculation of the total error function, which benchmarks the image qualities for a given set of metasurface phase masks. The error calculation is a two-step process, which involves both the physical recreation of the image formation for a given phase mask set and an image comparison to the target images. It is important to note that the entire forward calculation has to be explicitly performed within an automatic differentiation framework to be traced for the gradient calculation. The gradient ∇_Φα(Φ), which is the derivative of the total error α with regard to all phase mask values $\mathrm{\Phi }=\prod _{i=1,2}{\mathrm{\phi }}_{\mathrm{i}}^{(A)}\times \prod _{j=1,2,3}{\mathrm{\phi }}_{\mathrm{j}}^{(B)}$, is then used within a gradient optimization scheme, which converges toward a local optimum (for more details, see the Supplementary Materials). The actual secret splitting is achieved implicitly within the optimization framework. By providing a target for all single-layer configurations, we create an algorithmic incentive to hide the cascaded image for a single shareholder.

Fig. 3. Flow chart of the forward pass for the gradient optimization scheme.

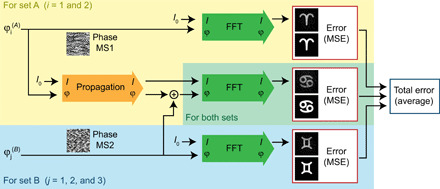
The metasurface phase masks (MS1 and MS2) used in the cascaded configuration were designed using a gradient optimization scheme. The flow chart shows the physical forward pass within the gradient optimization loop, which assigns an error or fitness value to a given set of phase masks. The algorithm performs a fast Fourier transformation (FFT) for all single and cascaded images (sets A and B) and then compares the calculated images with target images by using the mean squared error (MSE). For the light propagation between the two metasurface layers in the cascaded case, we use the angular spectrum method with zero padding. In the optimization loop, we try to find a set of phase masks that minimizes the total error α. This is accomplished by calculating its gradient ∇_Φα(Φ) with automatic differentiation and using a gradient optimizer.

Our developed algorithmic approach is an efficient and straightforward design method for the demonstrated holographic secret sharing framework. Note that the gradient optimization with regular numerical gradient calculation becomes infeasible due to the high number of DOFs. Moreover, alternative approaches based on the widely used Gerchberg-Saxton algorithm might not inherently guarantee convergence and can struggle to encode a larger number of holograms (40, 41).

To illustrate the potential of cascaded metasurface holography for optical secret sharing, we additionally introduce the concept of translational multiplexing for cascaded holograms. In the previous example, we showed that the shared secret cannot be revealed if the position of the two metasurfaces is mismatched, resulting in the precise alignment requirement. We take advantage of this feature by using the translational movement as a new multiplexing dimension (additional DOF). For that, we encode multiple images across different relative translational positions. Thus, different holographic images can be reconstructed if the metasurface holograms are slightly repositioned against each other.

As proof of principle, we demonstrate here a case where two different translational positions result in two different images for the cascaded hologram (Fig. 4). The single metasurface holograms (shares 1 and 2) contain the encoded images of the numbers “1” and “2.” At the same time, the images of the numbers “3” and “4” appear in the cascaded arrangement for two distinct overlap positions, which lie five pixels (25 μm) apart along the x axis. As the translational movement naturally changes the overlap area between both metasurfaces, we periodically expand the holographic phase mask of share 1 into a rectangular shape to ensure a square-shaped overlap in both cascaded configurations. Thus, the two cascaded images appear for the alignment of share 2 along with one of the two edges (left and right) of share 1. Because we previously observed that the cascaded holographic image quickly deteriorates for a translational movement of one pixel, we expect a negligible cross-talk here for the implemented translational shift of five pixels. This expectation is confirmed by the measurement results in Fig. 4C (for additional information, see the Supplementary Materials). In terms of practical applications, the translational multiplexing concept has the potential of being used as an optical ruler. There, cascaded images can be encoded into a discrete number of equidistant real space positions that digitally display the current overlap position as a holographic image. Here, the metasurface holograms have the advantage that micrometer pixel sizes and small spacings can be achieved, which, in turn, would allow for an optical ruler with a very high spatial resolution even below the diffraction limit of light.

Fig. 4. Translational multiplexing with cascaded holograms.

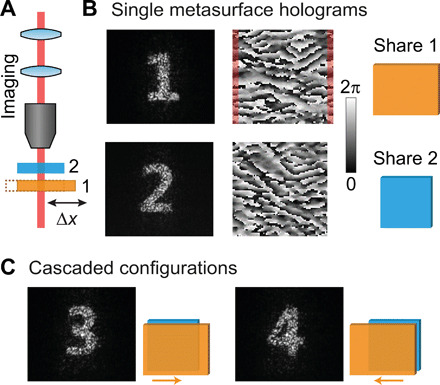
(A) Schematic view of the experiment containing both metasurface shares 1 and 2. The high alignment sensitivity for the cascaded image reconstruction allows for the implementation of translational multiplexing by shifting metasurface 1. (B) The two metasurfaces are designed and fabricated to contain one single Fourier hologram each as well as two cascaded holograms. The phase pattern of the two holograms is shown in the middle. Note that the metasurface for share 1 has been periodically expanded to ensure the same spatial overlap after the translation. (C) A spatial translation of only five pixels (25 μm) in the cascaded case results in a different holographic image reconstruction. The images with the numbers 1 to 4 show the experimentally measured Fourier images.

DISCUSSION

Our demonstrated stacking of multiple holographic metasurfaces and using them in a cascaded way allows for a unique optical secret sharing and encryption platform. The concept is scalable, both in terms of the stack size and the number of keys. It can be also altered into a (t, n)-threshold scheme, where already a subset of shareholders (t of n) can reconstruct the secret. Additional complexity and security can be added by using complex amplitude and phase holograms. Because of their compact shape and their design flexibility, metasurfaces are naturally suited for the realization of cascaded configurations. The high sensitivity for the spatial alignment is also perfectly suited for holographic seals, where two metasurfaces are slightly glued together, and the restoration of the cascaded hologram would become extremely challenging after both metasurfaces have been separated. For realizing a reprogrammable encryption scheme, one can combine a metasurface as the main share, with a spatial light modulator as the deputy share. By generating different phase patterns with the spatial light modulator and using it for the illumination of the metasurface, different holographic images can be revealed.

METHODS

Experiment and sample fabrication

All holographic images were captured by projecting the Fourier space of the metasurface plane on a complementary metal oxide semiconductor (CMOS) camera (EO USB 2.0 CMOS) with the usage of a microscope objective (Nikon S Plan Fluor ELWD 20×/0.45) and two lenses. As a light source, we use a supercontinuum laser (Fianium Whitelase WL-SC-400-2) with a tunable spectral filter (NKT Photonics SuperK VARIA) to obtain a spectral bandwidth of 10 nm. The polarization state of the light was set and after the samples filtered by pairs of a quarter-wave plate and a linear polarizer.

The silicon metasurfaces were fabricated on a glass substrate following the processes of silicon deposition, patterning, lift-off, and etching. First, through plasma-enhanced chemical vapor deposition, we prepared a 600-nm-thick amorphous silicon (a-Si) film. Following this, a poly(methyl methacrylate) resist layer was spin-coated and patterned by standard electron beam lithography. After development, a 20-nm-thick chromium layer was deposited. After a lift-off process, we used inductively coupled plasma reactive ion etching to transfer the predefined structures by the chromium mask to the silicon. Afterward, the residual chromium mask was removed using a standard wet etching process. Each metasurface hologram has a pattern size of 400 μm by 400 μm and consists of 80 × 80 pixels yielding a 5-μm pixel size. Each pixel consists of an array of silicon nanofins, which have a grid periodicity of 500 nm. Each cuboid nanostructure has a length of 190 nm and a width of 130 nm.

Metasurface design

The phase mask calculations were performed in Python v3.8 with the usage of TensorFlow v2.2 as an automatic differentiation library. For the single nanostructure design, we use rigorous coupled-wave analysis. More details can be found in the Supplementary Materials.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/16/eabf9718/DC1