Effect of mesoscale phase contrast on fatigue-delaying behavior of self-healing hydrogels

The multilevel fatigue resistance mechanism of tough and self-healing hydrogels with a hierarchical structure was revealed.

Abstract

We investigate the fatigue resistance of chemically cross-linked polyampholyte hydrogels with a hierarchical structure due to phase separation and find that the details of the structure, as characterized by SAXS, control the mechanisms of crack propagation. When gels exhibit a strong phase contrast and a low cross-linking level, the stress singularity around the crack tip is gradually eliminated with increasing fatigue cycles and this suppresses crack growth, beneficial for high fatigue resistance. On the contrary, the stress concentration persists in weakly phase-separated gels, resulting in low fatigue resistance. A material parameter, λ_tran, is identified, correlated to the onset of non-affine deformation of the mesophase structure in a hydrogel without crack, which governs the slow-to-fast transition in fatigue crack growth. The detailed role played by the mesoscale structure on fatigue resistance provides design principles for developing self-healing, tough, and fatigue-resistant soft materials.

INTRODUCTION

The soft and wet nature of hydrogels endows them with great application potentials in tissue engineering such as artificial soft tissues used for replacing damaged ones (1, 2). However, creating hydrogels with simultaneously excellent toughness, self-healing properties, and fatigue resistance that are similar to load-bearing soft biotissues remains a challenging task. Initiated by the research on double network gels (3–5), tremendous progress has been made in creating hydrogels with toughness comparable to that of cartilage by introducing covalent or noncovalent sacrificial bonds in polymer networks (6–10). However, recent studies on several synthetic tough hydrogels based on noncovalent sacrificial bonds show that these tough hydrogels exhibit a relatively poor fatigue resistance similar to that of a purely elastic network (11–13). This is in stark contrast with biological tissues that show excellent fatigue resistance along with high toughness (14, 15). These results suggest that the hierarchical structures, as seen in the biological tissues, could be beneficial for fatigue resistance. Recent studies have shown that the fatigue resistance of soft and stretchable materials is largely enhanced by embedding hard components, such as crystalline domains (16–18) and fibers (19–21). It is considered that the energy per unit area required to fracture the packed hierarchical structures is enhanced by pinning the crack tip at the hard component (22).

Recently, we found that tough and self-healing polyampholyte hydrogels (PA gels) with a hierarchical structure show a high fatigue resistance (23). The hierarchical structure of PA gels consists of reversible ionic bonds at the ~0.1-nm scale, a transient polymer network at the ~1-nm scale, a permanent polymer network at the ~10-nm scale, and a hard/soft microphase separated network at the ~100-nm scale (Fig. 1). The transient polymer network is formed by ionic bonds, and the permanent polymer network is formed by chemical cross-linking and trapped topological entanglements. The hard/soft microphase separated network consists of bicontinuous dense/sparse polymer phases in water. The polymer strands are in their collapsed globule conformation (24). The PA gels exhibit an extremely slow crack growth mode when the applied energy release rate (G) is above the fatigue threshold G₀ and that slow propagation mode is maintained until a transition point G_tran that has a value several times that of G₀, at which point a fast crack propagation mode is observed. The high fatigue resistance of the PA gels is attributed to such a multilevel fatigue behavior. This behavior of PA gels is very different from that of conventional hydrogels (13) in which the crack propagation rate increases rapidly with increasing G and only a fast crack propagation mode appears above the threshold value G₀.

Fig. 1. Illustration of the hierarchical structure of tough and self-healing PA gels.

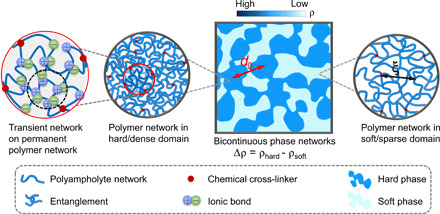
The gels contain reversible ionic bonds at the ~0.1-nm scale, a transient polymer network at the ~1-nm scale (indicated by black dotted circle), a permanent polymer network at the ~10-nm scale (indicated by red circle), and a bicontinuous hard/soft phase network at the ~100-nm scale. The polymer strands are in their globule conformation. The nanoscale mesh size of the permanent polymer network ξ depends on the effective cross-linking density of the polymer network ν_e from both chemical cross-linking and trapped topological entanglements. ξ can be tuned by the chemical cross-linker density C_MBAA and monomer concentration C_m during the synthesis of the PA gels. The characteristic length of the phase network d₀ and of the phase density contrast Δρ depend on ξ and on the dialysis temperature T_dial of the PA gels.

In this work, we intend to clarify why the slow crack propagation mode is observed for the materials with hierarchical structures and what determines the slow-to-fast propagation transition. We also intend to clarify the role of trapped topological entanglements on the intrinsic fatigue threshold G₀. We assume that the bicontinuous hard/soft phase networks play the key role in suppressing the crack growth, whereas the hard/soft phase contrast might govern such multilevel fatigue resistance behavior. To test this hypothesis, in this work, we study the effect of the phase contrast of the mesoscale networks on the fatigue resistance of PA gels. The hard/soft phase contrast in the gels was tuned by varying the effective permanent cross-linking density of the nanoscale polymer networks of the gels during the synthesis step. Combining the results of small-angle x-ray scattering (SAXS) measurements, fatigue tests, and birefringence characterization, we will discuss the inherent correlations between the characteristic mechanical fatigue parameters and the hierarchical structure parameters. We will explore, in particular, the effect of the level of contrast of the microphase separated network on the ability to blunt the crack during propagation in fatigue, the existence of a material parameter controlling the transition from slow to fast crack propagation, and the effect of trapped topological entanglements on the fatigue threshold G₀.

RESULTS

Tuning the mesoscale phase contrast

Our previous study showed that the level of phase contrast and characteristic phase length (d₀) of PA gels depend on the effective chain density of permanent polymer network ν_e and temperature (T_dial) used to dialyze the small counterions from the gels during the sample preparation (24, 25). ν_e is due to the presence of chemical cross-links and trapped topological entanglements. In polymer solutions (26), the concentration of topological entanglements between polymer chains (C_e) scales with the polymer concentration C by C_e~C^2.3. In the chemically cross-linked gels, the topological entanglements are permanently trapped and contribute to the elastic modulus similarly to the chemical cross-links (27). Accordingly, tuning the monomer concentration C_m at the gel synthesis step can change the polymer concentration and thereby the concentration of the trapped topological entanglements. In this work, we vary the chemical cross-linker density (C_MBAA) to tune chemical cross-linking density and the total monomer concentration (C_m) to tune the topological entanglement density (24, 28). Two series of samples were prepared by one-step random copolymerization of the anionic monomer sodium p-styrenesulfonate (NaSS) and the cationic monomer methyl chloride quarternized N,N-dimethylamino ethylacrylate (DMAEA-Q). The sample series PA-2.5-C_MBAA was prepared by varying C_MBAA from 0 to 1.0 mole percent (mol %) relative to C_m at fixed C_m = 2.5 M; the sample series PA-C_m-0.1 was prepared by varying C_m from 1.75 to 2.5 M at a fixed C_MBAA = 0.1 mol %. After copolymerization, the gels were immersed in deionized water until equilibrium was reached at T_dial = 30°C. During this process, the counterions were dialyzed away from the hydrogel, and the gels deswelled as a result of the Coulomb attraction between the opposite charges on polymer chains and hydrophobic interaction. The polymer volume fraction of the equilibrated PA gels after dialysis was 44.7 to 46.8 volume %, almost independent of the initial formulation, which indicates that the polymer strands are in their collapsed globule conformation (29). According to polymer theory (26, 29), for collapsed globule chains, the mesh size of the network (ξ) is related to the number of repeat units of a polymer strand between cross-linking points (N_e) through ξ ≅ bN_e^1/3, where b is the size of repeat unit. The polymer volume fraction in the gel ϕ is the ratio between the actual volume of a polymer strand and the volume it pervades. Therefore, ϕ ≅ (b³N_e)/ξ³ ~ (b³N_e)/(bN_e^1/3)³ ~ N_e⁰, independent of N_e. Therefore, in this collapsed conformation, the polymer volume fraction does not change with effective chain length. In the following experiments, the equilibrated gels were used. It is worthwhile to note that the structural and property changes of the PA gels reported in the following discussion are not due to the change in polymer volume fraction in the gel because it remains nearly the same for all the gels.

These gels show a similar dynamic modulus in the high-frequency regime from the ionic bonds, but the plateau modulus (μ) at low frequency (2 × 10⁻⁵ rad/s) increases with C_MBAA and C_m following a relation of μ ~ (C_MBAA + αC_m^2.3) for all the samples including that without chemical cross-linker (C_MBAA = 0) (fig. S1 and table S1). The scaling exponent 2.3 is consistent with polymer solution theory (26) of C_e ~ C_m^2.3, where C_e is the cross-linking concentration caused by trapped topological entanglements. This result indicates that the average number density of elastically effective chain density ν_e, which is proportional to the shear modulus, increases with increasing C_MBAA and C_m. From the dynamic mechanical spectra, the characteristic relaxation time of the ionic bonds is on the millisecond scale (fig. S1). The mesh size ξ of the permanent polymer network, estimated by the relation ν_e ≅ ξ⁻³ (24), is in the range of 4 to 9 nm (table S1).

The phase structure is tuned by the chemical formulation. As an example, Fig. 2A presents the photo images of PA-2.5-C_MBAA samples. The gels gradually change from semitransparent to transparent with increasing C_MBAA. The two-dimensional (2D) SAXS patterns of PA-2.5-C_MBAA gels are shown in Fig. 2B. For C_MBAA < 0.5 mol %, an isotropic scattering pattern with a circular scattering ring can be noticed, demonstrating the isotropic mesoscale phase network structure of the undeformed gels. The intensity of the scattering ring decreases markedly with increasing C_MBAA, and last, the ring disappears for PA-2.5-1.0, indicating that the phase contrast declines and the sample becomes homogeneous as C_MBAA increases. A periodic peak is observed for C_MBAA ≤ 0.5 mol % on azimuthally integrated 1D SAXS profiles (Fig. 2C). The peak position q_m is related to the characteristic length scale of the phase structure (d₀), by d₀ = 2π/q_m. The peak intensity of scattering I_m for a two-phase system is proportional to V₁V₂(Δρ)², where V₁ and V₂ are the volume fraction of phases 1 and 2, and Δρ is the electron density difference between them (30). In the case of PA gels, V₁, V₂, and Δρ can be considered as the volume fractions of soft and hard phases and their polymer volume density difference (also phase contrast), respectively. As the relative volume fractions of soft and hard phases weakly vary, the peak intensity I_m is proportional to the phase contrast of hard and soft domains by I_m ~ (Δρ)² (24). The values of I_m and d₀ for the sample series PA-2.5-C_MBAA and PA-C_m-0.1 dialyzed at 30°C are summarized in table S2. The remarkable decrease of I_m and d₀ with increasing C_MBAA indicates a weakened phase separation as the result of competition between the free energy gain of polyion complexation and the entropic penalty of chain elasticity that increases with cross-link density (23, 24). Similarly, for the samples PA-C_m-0.1 with different monomer concentrations C_m but a fixed chemical cross-link density C_MBAA, the peak intensity I_m and d₀ also decrease with increasing C_m (table S2), due to an increase in the topologically trapped entanglements that serve as effective permanent cross-linking density (24). For comparison, results of sample series PA-2.0-0.1 (T_dial) dialyzed at different T_dial [extracted from our previous work (25)] are also shown in table S2. A universal relation I_m ~ d₀⁴ is observed for all the samples (with values of d₀ depending on C_m, C_MBAA, and T_dial) (Fig. 2D), consistent with our previous study (24). This relationship, combining with I_m ~ (Δρ)², shows that the phase contrast Δρ and size d₀ are inherently correlated by Δρ ~ d₀² in the PA hydrogel system. This result, showing that the stronger the phase contrast, the larger the phase structure, should be attributed to the competition between the phase separations and the elasticity of the network. It is worthwhile to note that the changes of I_m, d₀, and the elasticity are not due to the change of overall polymer volume fraction in water, because it remains nearly the same for all the gels.

Fig. 2. PA gels with a tuned bicontinuous hard/soft phase network structure.

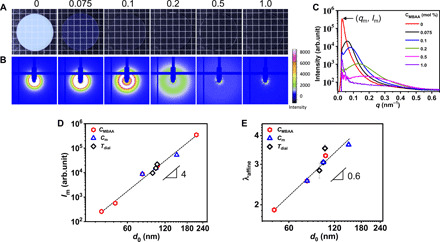
(A) Photographs of the representative gels PA-2.5-C_MBAA with different chemical cross-linker densities, and the variable C_MBAA is shown at the top of each picture. (B) Corresponding 2D SAXS patterns of (A). (C) Corresponding 1D scattering intensity profiles of (B). (D) Logarithmic plot of SAXS peak intensity I_m and characteristic length of the phase structure (d₀) estimated from q_m for three series of samples, i.e., series PA-2.5-C_MBAA and series PA-C_m-0.1 dialyzed at 30°C, and series PA-2.0-0.1(T_dial) dialyzed at different temperatures T_dial (detailed sample information can be found in tables S1 and S2) at undeformed state. (E) Logarithmic plot of maximum stretch ratio for affine deformation (λ_affine) of the phase networks in uniaxial tensile test as a function of d₀ for the three series of samples. The data of series PA-2.0-0.1(T_dial) are extracted from (25). The error bars are SEs from two to three measurements.

Tensile and fracture behaviors

We first studied the uniaxial tensile behavior and the microscopic deformation of the phase network by in situ time-resolved SAXS during the tensile test (fig. S2). The results of series PA-2.5-C_MBAA and series PA-C_m-0.1 at the stretch rate of 1 s⁻¹ are shown in fig. S3. Gels with a relatively strong and sharp phase separation (I_m > 1000 arb. unit for series PA-2.5-C_MBAA with C_MBAA = 0 to 0.1 mol % and series PA-C_m-0.1) exhibit little differences in uniaxial tensile behavior, regardless of the notably different phase contrast (fig. S3, A and E). Furthermore, the fracture behavior in pure shear geometry of these gels was also very similar (fig. S3D). Using the SAXS data, we characterized the correlation between the macroscopic deformation λ of the sample and the microscopic deformation of the phase network in the direction parallel (d_///d₀) and perpendicular (d_⊥/d₀) to the stretching direction (fig. S2). For incompressible materials, if d_///d₀ = λ and d_⊥/d₀ = λ^−1/2, the deformation is called affine. We observed that the phase network deforms affinely up to a quite large bulk stretch ratio λ. The maximum stretch ratio for affine deformation of the phase networks (λ_affine), which was interpreted as the onset of the damage of hard phase network (23), increases as I_m and d₀ increase (table S2). This result suggests that coarser structures can bear larger deformation due to larger d₀. It should be noted that the purely physical gel without chemical cross-linking, PA-2.5-0, shows the largest I_m and d₀, but we could not accurately measure λ_affine of this sample because of the detection limit of SAXS. We also could not measure λ_affine of samples PA-2.5-C_MBAA with C_MBAA = 0.5 and 1.0 mol % because of a too weak scattering intensity. From the measured results, we found that λ_affine ~ d₀^0.6 at the observing loading rate (Fig. 2E). Because the stretched length of the phase network at the maximum affine deformation (d_//,m) is expressed as λ_affine = d_//,m/d₀, we get a relation d₀ ~ d_//,m^0.6. This power law relation between the phase mesh size in its undeformed state (d₀) and in its stretched state (d_//,m) at the maximum affine deformation looks similar to the power law relationship between the end-to-end distance (ξ) and its fully stretched length (contour length L_c) of a self-avoiding polymer chain, ξ ~ L_c^3/5 (26). Accordingly, the strands of phase network could be effectively considered as self-avoiding chains and the strands of hard phase break at λ = λ_affine with the maximum stretching length d_//,m at the observation time scale.

Fatigue fracture behaviors

Fatigue experiments were carried out with prenotched samples in the pure shear geometry at a nominal loading rate 1 s⁻¹. A triangular loading profile was applied during cyclic loading. The maximum stretch ratio was kept constant at a preset value λ_max, while the minimum stretch ratio was kept at 1 (Fig. 3A). The crack propagation in fatigue test starts when λ_max reaches a threshold, denoted as λ₀. For λ_max < λ₀, no measurable crack growth was observed over 30,000 cycles. As an example, the crack propagation behaviors of samples with the high phase contrast (strongly phase-separated) PA-2.5-0.075 (I_m = 19.6k) and the low phase contrast (weakly phase-separated) PA-2.5-0.5 (I_m = 0.26k) are shown in Fig. 3 (B and C). λ₀ is found to be 1.98 for PA-2.5-0.075 and 1.2 for PA-2.5-0.5. Above λ₀, the two gels with different phase structures show notably different fatigue behaviors. For PA-2.5-0.075 with a strongly phase-separated structure, two characteristic regimes of λ_max were observed: At small λ_max > λ₀, after an initial growth over thousands of cycles, the crack length c hardly propagates with increasing cycle number N, resulting in an extremely slow crack propagation rate Δc/ΔN in steady state, and such propagation delaying phenomenon is observed below a second threshold λ_max = λ_tran(=3.14 ± 0.2). When λ_max > λ_tran, the crack length c increases rapidly with cycle number N and the whole sample ruptures quickly (Fig. 3B), resulting in a fast crack propagation rate Δc/ΔN, as observed in our previous work (25). For the weakly phase-separated PA-2.5-0.5, the crack length c always increases linearly with N for λ_max > λ₀, even at an extremely small λ_max (Fig. 3C).

Fig. 3. Crack propagation behaviors of the representative strongly and weakly phase-separated gels under fatigue test.

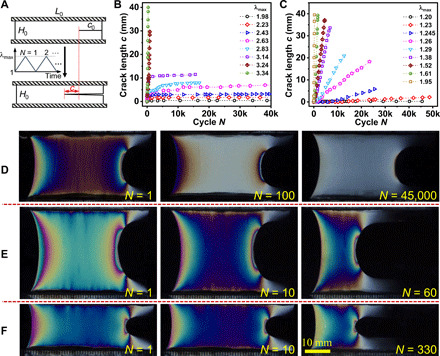
(A) Pure shear geometry (L₀ = 50 mm, H₀ = 10 mm, and c₀ = 10 mm) and loading profile for fatigue test. During cyclic loading, the length of crack propagation was recorded as c. (B and C) Crack propagation behavior at different λ_max for the strongly phase-separated gel PA-2.5-0.075 (B) and the weakly phase-separated gel PA-2.5-0.5 (C). (D and E) Typical evolutions of sample birefringence images with cycle number N for the representative strongly phase-separated gels at λ_max < λ_tran (D) and λ_max > λ_tran (E). Sample PA-2.5-0.075 at λ_max = 2.64 and at λ_max = 3.44 are taken as examples in (D) and (E), respectively. (F) Typical evolutions of sample birefringence images with cycle number N for the representative weakly phase-separated gel at a small λ_max. Sample PA-2.5-0.5 at λ_max = 1.81 is taken as an example.

Fracture mechanics theory shows that the deformation field around the crack tip is usually much larger than in the bulk far from the crack due to the presence of a singularity in both stress and strain (31–34). To observe the stress distribution around the crack tip during the fatigue test, the birefringence (circular polarization) was monitored during cyclic loading. Figure 3 (D and E) shows the birefringence patterns of a representative strongly phase-separated gel PA-2.5-0.075 at λ_max < λ_tran and λ_max > λ_tran, respectively. For λ_max < λ_tran, a blunted crack tip with an arc-shaped stress concentration zone was observed, and the distribution of birefringence colors around the crack tip became substantially weaker with increasing cycle numbers (Fig. 3D), demonstrating that the stress concentration is reduced with increasing fatigue cycles. It seems even that the singularity around the crack tip can be nearly eliminated after tens of thousands of fatigue cycles for the strongly phase-separated gels (N ~ 45,000 in Fig. 3D and movie S1), resulting in the deceleration or even arrest of crack advancement. While a severe butterfly-like stress concentration always exists around the crack tip for increasing cycle number N at λ_max > λ_tran (Fig. 3E and movie S2), which suggests that λ_tran corresponds to the critical bulk stretch above which stress concentration does not vanish under cyclic loading. This butterfly-like stress concentration is also always observed on the weak phase-separated gels PA-2.5-0.5 even at small λ_max as shown in Fig. 3F and movie S3, indicating that stress concentration around the crack tip is not alleviated with the increase in fatigue cycles even at a small λ_max for the weakly phase-separated gels. It should be noted that, regardless of whether it occurs for the strongly phase separated gels or for the weakly phase separated gels, once the butterfly-like stress concentration appears for increasing cycle numbers N, a tremendous crack extension occurs until the fracture of the whole sample (see N = 1 to N = 60 in Fig. 3E and N = 1 to N = 330 in Fig. 3F).

As a result, the crack propagation rate Δc/ΔN, obtained from the slope of the plots of crack length c versus cycle N in steady state, shows a slow mode and a fast mode for the strongly phase-separated gels, while only the fast mode is observed for the weakly phase-separated gels above the threshold value λ₀. Figure 4A shows Δc/ΔN versus λ_max for PA-2.5-C_MBAA with varying C_MBAA content. The threshold λ₀ decreases from 2.14 to 1.18 as C_MBAA increases from 0 to 1.0 mol %. For the strongly phase-separated samples (C_MBAA ≤ 0.1 mol %) at λ_max > λ₀, Δc/ΔN first increases slowly with λ_max, showing a plateau-like mode with Δc/ΔN < 0.1 μm per cycle. Then, Δc/ΔN jumps to a fast crack growth mode when λ_max > λ_tran. λ_tran shifts to a higher value, and the amplitude of the jump in Δc/ΔN increases for gels with stronger hard/soft phase contrast. The sample series PA-C_m-0.1 prepared with different monomer concentrations C_m shows a similar correlation between the microstructure and the fatigue behavior (Fig. 4B). That is, the fast crack propagation in fatigue is delayed to a larger value of λ_tran for the materials with a high hard/soft phase contrast and large d₀. Δc/ΔN at λ_max > λ_tran is orders of magnitude larger than that at λ₀ < λ_max < λ_tran, indicating that the crack propagation in cyclic fatigue is substantially suppressed at λ_max < λ_tran. However, for the weakly phase-separated gels (C_MBAA > 0.1 mol %), no slow crack propagation mode is observed, and the fast crack propagation mode occurs directly once λ_max becomes slightly larger than λ₀ (Fig. 4A). It is noticed that although the sample with C_MBAA = 0.2 mol % shows a similar fracture toughness as that of the samples with C_MBAA ≤ 0.1 mol % (fig. S3D), it only shows the fast crack propagation mode in fatigue test. This suggests that the phase network is responsible for the suppression of the fast crack growth in fatigue tests.

Fig. 4. Fatigue behavior of PA gels with different mesoscale phase contrasts.

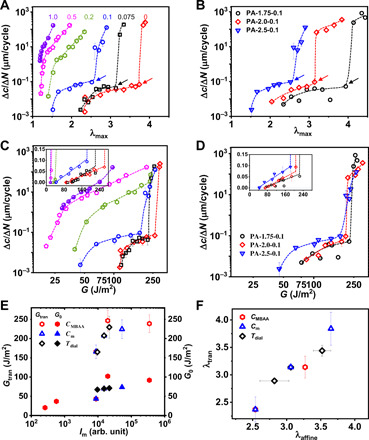
(A and B) Crack propagation rate Δc/ΔN in steady state as a function of λ_max for sample series PA-2.5-C_MBAA (A) and PA-C_m-0.1 (B). The numbers beside each curve in (A) represent C_MBAA (mol %). The dashed lines are a guide for the eyes. The arrows in (A) and (B) indicate the transition points of slow-to-fast fatigue crack growth. (C and D) Crack propagation rate Δc/ΔN as a function of energy release rate G corresponding to (A) and (B), respectively. Inset shows the initial linear regime in the linear scale. Symbols in (C) are the same as those in (A). (E) Energy release rate at transition points of slow-to-fast fatigue crack growth (G_tran) (left y axis) and the threshold G₀ (right y axis) extracted from (C) and (D) versus I_m for the three series of samples. (F) Correlation between λ_tran for slow-to-fast mode transition in the fatigue test and the maximum stretch ratio λ_affine for affine deformation of the phase structure in the tensile test for the three series of samples. The data of series PA-2.0-0.1(T_dial) are extracted from (25). The error bars are SEs from two to four measurements. Note that in these PA gels, G₀ and λ_tran are characteristic material parameters, while G_tran is geometry dependent (see Fig. 5). The measurements were performed with samples of pure shear geometry (L₀ = 50 mm, H₀ = 10 mm, and c₀ = 10 mm) and nominal strain rate 1 s⁻¹.

In fracture mechanics of soft elastic materials (35), the crack growth is considered to be driven by the release of the stored elastic energy, and crack propagation rate Δc/ΔN is a function of the energy release rate (G). The Δc/ΔN versus G profiles allow, in principle, a comparison of the fatigue behaviors between samples with different moduli and different geometries, while the Δc/ΔN versus λ_max profiles do not allow such comparisons. In the pure shear geometry, G can be calculated from G = W_el(λ_max)H₀, where W_el(λ_max) is the stored elastic energy and H₀ is the initial sample height. For purely elastic materials, W_el is equal to the input work W_ex. However, for viscoelastic PA gels containing dynamic bonds, the input work W_ex is partially dissipated during loading, and there is no well-established method to calculate G. For simplicity, we use the method presented in (33) to estimate W_el from W_ex and the mechanical hysteresis area U_hys in steady state of the fatigue test (fatigue cycle N ~ 3000 cycles), using the relation W_el = W_ex − U_hys (see the Supplementary Materials and fig. S4E).

Figure 4 (C and D) shows Δc/ΔN versus G plots of series PA-2.5-C_MBAA and PA-C_m-0.1, respectively, from which the fatigue threshold G₀ and the energy release rate G_tran, corresponding to λ₀ and λ_tran, respectively, can be obtained. G₀ and G_tran are plotted in Fig. 4E as a function of the scattering intensity I_m. Only strongly phase-separated gels (I_m > 1000 arb. unit) show values of G_tran, which are several times larger than that of G₀, while the weakly phase-separated gels (I_m < 1000 arb. unit) only show a well-defined and low value of G₀ (<50 J/m²). The series PA-2.0-0.1(T_dial) also obeys the same trend as shown in Fig. 4E. When compared at the same applied G = 150 J/m², the strongly phase-separated gels are in a slow propagation mode, while weakly phase-separated gels are in a fast mode of crack growth. Note that for all the samples, the ratio between hysteresis energy and the total input work U_hys/W_ex is approximately the same (ca. 0.4) in steady-state (accommodated) conditions (fig. S4H). This also supports the notion that the differences in crack propagation rate Δc/ΔN observed for different gels are not directly related to the viscoelastic character of the gels but rather to their differences in phase structure. It should also be noted that the fast self-recovery of large hysteresis loop during fatigue test (fig. S4), caused by the fast reforming of broken ionic bonds, enhances fatigue resistance, in comparison with purely elastic gel. As shown in fig. S5, compared with the as-prepared gel that is purely elastic in the observation time scale, the equilibrated gel with large hysteresis loop shows a larger fatigue threshold G₀ and a slower crack extension above G₀. The slowdown phenomenon of crack propagation is also observed in other self-recovery systems with noncovalent interactions, as indicated by Bai et al. (11).

Origin of the controlling structural parameter for the slow-to-fast fatigue transition

As clarified above, the two regimes (slow and fast modes) of crack propagation only occur for the PA gels with a strong phase contrast, corresponding to a high modulus contrast between the hard and soft phase networks. We hypothesize that the delayed crack growth above the threshold λ₀ is due to the weak stress concentration at the crack tip (strong crack blunting) (25). Therefore, the following two questions arise: What determines the value of λ_tran and the transition to a fast crack growth rate? Is λ_tran or the corresponding energy release rate G_tran an intrinsic material parameter determining the slow-to-fast crack transition?

λ_tran is found to be positively correlated to the limit of affine deformation of the phase networks λ_affine for the three sets of gels prepared at different C_MBAA, different C_m, or different T_dial (Fig. 4F). It suggests that the maximum bulk stretch λ_max, where crack blunting is observed during a fatigue test, is correlated to an intrinsic damage of the structure in the bulk region (away from the crack tip) during the tensile deformation. However, this is in clear contradiction with fracture mechanics theory because it suggests that the crack propagation is controlled by the stretch in the bulk and not at the crack tip. In other words, a larger pure shear sample would apply a larger G at the same bulk stretch than a smaller sample. In turn, this larger G should cause a larger local stretch at the crack tip and, hence, a larger dc/dN. To verify this, we compared the fatigue results of sample PA-2.0-0.1(T_dial = 5°C) measured with samples with a different initial height (H₀) deformed at a nominal stretch rate = 1 s⁻¹ while keeping the aspect ratios L₀/H₀ = 5 and c₀/H₀ = 1 unchanged (Fig. 5, A and B). The value of λ_tran for the two different H₀ only changes by about 3% (λ_tran = 2.79 ± 0.05 for H₀ = 15 mm and λ_tran = 2.89 ± 0.05 for H₀ = 10 mm), while the corresponding G_tran changes by about 30% (234.9 ± 6.9 J/m² for H₀ = 15 mm and 165 ± 9 J/m² for H₀ = 10 mm). On the other hand, G₀ values measured with different H₀ are almost the same (inset of Fig. 5B), confirming that G₀ is an intrinsic material parameter in this viscoelastic system. A comparison between samples with larger height differences (H₀ = 10 versus 20 mm, at a nominal stretch rate = 0.8 s⁻¹) is shown in fig. S6 using a different batch of PA-2.0-0.1 gels. In this case, λ_tran for the two different H₀ changes about 10% (λ_tran = 2.35 ± 0.05 for H₀ = 20 mm and λ_tran = 2.6 ± 0.10 for H₀ = 10 mm), while the corresponding G_tran changes by about 30% (G_tran = 202.3 ± 9.1 J/m² for H₀ = 20 mm and G_tran = 142.1 ± 15.3 J/m² for H₀ = 10 mm). Furthermore, we observed that the value of λ_tran determined from samples with a rectangular geometry (the geometry used for SAXS measurements) is very close to the value of λ_tran determined from the samples in the pure shear geometry (fig. S7). These results strongly suggest that λ_tran is a better material parameter that governs the slow-to-fast mode transition, while G_tran, showing a relatively strong geometry dependence, is not an intrinsic material parameter in this strong crack blunting system with hierarchical structures. One should be, however, a bit careful because in the limit of very large samples, G should become again a better material parameter. Our results, however, show that for reasonable laboratory-scale geometries, the blunting process at the crack tip nearly eliminates the stress concentration and effectively nearly stops crack propagation in fatigue. Only when the bulk stretch exceeds a critical value, the stress concentration persists and the crack grows.

Fig. 5. Geometry effect of fatigue behaviors.

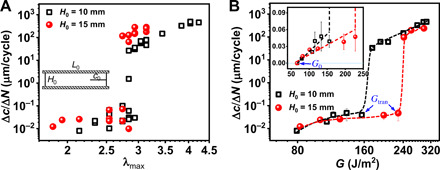
(A) Comparison of fatigue crack propagation rate Δc/ΔN in steady state versus λ_max for a sample tested at different initial height H₀ of pure shear geometry. The aspect ratios L₀/H₀ = 5 and c₀/H₀ = 1 were kept the same when changing H₀ (H₀ = 10 and 15 mm). (B) Crack propagation rate Δc/ΔN versus energy release rate G in logarithmic scale. Inset shows the initial regime in the linear scale, and the fatigue threshold G₀ (indicated by arrow) is obtained by linearly extrapolating the results to the horizontal axis. The G_tran corresponding to the energy release rate at λ_tran is also indicated by arrows. Sample PA-2.0-0.1(T_dial = 5°C) was used. The data for H₀ = 10 mm are extracted from (25). The error bars are SEs from (A).

Why does λ_tran correlate to λ_affine for the tensile behavior with no crack? We explain this result from two features of the hierarchical structure. One feature is the different force-carrying abilities of the hard and soft phase networks. At λ_max < λ_affine, the two-phase networks are maintained intact during loading in the bulk region, and the hard phase network should carry most of the stress, and the soft network should redistribute the stress homogeneously, similar to the role played by the hard and soft constituents in other fatigue resistant materials (21) or to the role played by the first network and the second network in tough double network materials (3, 4, 36–38). Another feature is the formation of an oriented structure of the phase networks due to the presence of ionic bonds. At the fast stretch rate used here (~1 s⁻¹), the deformation only partially recovers upon unloading, as seen by the large residual strain at zero stress (fig. S4C), and the phase networks in the bulk gradually adapt to form an oriented metastable structure under the cyclic loading, which is detected by SAXS (25). This orientation of the phase networks causes a blunting of the crack tip and suppresses crack advance. This explains why at the beginning of the cyclic loading, the crack tip is more highly stressed than the bulk, consistent with a relatively fast crack extension. With increasing number of cycles, the crack gradually blunts as a result of competition between high stress-induced crack growth and the formation of a highly oriented structure at the crack tip, which substantially decreases the stress concentration and results in an extremely slow crack propagation mode. At λ_max > λ_affine, the hard phase in the bulk begins to damage and the soft phase network (made from regions with a sparse polymer density) cannot bear the load to form a sufficiently strong oriented structure with cyclic loading, and the stress concentration persists at the crack tip, resulting in rapid crack growth. The shift of λ_tran to a higher value and the increase in the amplitude of the jump in Δc/ΔN for gels with a stronger hard/soft phase contrast could be explained by the intrinsic correlation I_m ~ d₀⁴ (Fig. 2D). The increase of the mesh size d₀ results in the increase of λ_affine through λ_affine ~ d₀^0.6 (Fig. 2E), and above λ_affine, the internal damage of the hard phase network results in faster crack propagation in fatigue. The increase of I_m corresponds to the increase of the relative strength of the hard and soft phase network, so crack growth per cycle is accelerated above the λ_tran threshold.

Note that although the weakly phase-separated gel PA-2.5-0.2 shows a value of λ_affine = 1.9, no slow crack propagation mode is observed. This indicates that the fatigue crack growth can only be mitigated when the hard phase is sufficiently stronger than the soft phase, i.e., when the stiffness contrast between hard and soft phase is high enough, a general design principle of crack- and fatigue-resistant materials (21, 39).

Origin of the controlling structural parameter for the fatigue threshold G₀

Last, we discuss what determines the fatigue threshold G₀ for the viscoelastic PA gels. According to the recent studies by Suo and colleagues (11, 40), G₀ of tough hydrogels containing dynamic bonds is related to the permanent polymer network that is chemically cross-linked, regardless of the transient network physically cross-linked by reversible sacrificial bonds. Here, we correlate the fatigue threshold G₀ with the mesh size ξ between effective cross-linking points of the permanent network formed by both chemical cross-links and trapped physical entanglements in PA gels. We observe that all the data from three different series of samples with varied C_MBAA, C_m, and dialysis temperature T_dial fall on the same curve, which gives a scaling relation of G₀ ~ ξ^2.7 (Fig. 6), indicating that the threshold G₀ is positively correlated to the mesh size of the permanent network, consistent with previous reports on chemically cross-linked single and double network gels without the microphase separation (41–43). From Fig. 6, we know that both the chemical cross-links and the physically trapped topological entanglements act similarly as permanent cross-links to control the fatigue threshold in our PA system. On the other hand, considering the globule conformation of the polymer strands in the PA gels, we would expect a relatively weak scaling relation of G₀ ~ ξ, using the Lake-Thomas model (see section S3) (44). The experimentally observed much stronger relation between G₀ and ξ than the scaling relation deduced from Lake-Thomas model suggests that the physical bonds might also influence G₀. As shown in fig. S4H, the dissociation and reforming times of ionic bonds for all of the strongly and weakly phase separated gels are much shorter than the observation time scale (U_hys/W_ex is ~40% in steady state for all the samples). For the PA gels with such fast ionic bond reformation, it is difficult to exclude all the contribution from ionic bonds, while in the Lake-Thomas model only chemical bonds were considered.

Fig. 6. Fatigue threshold determined by primary network structure.

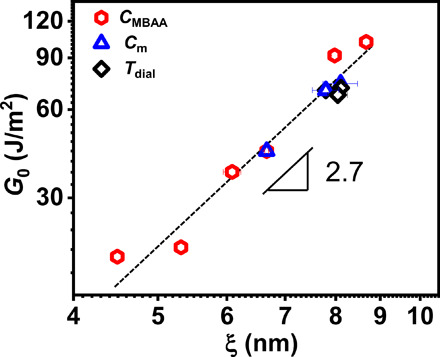
Logarithmic plot of fatigue threshold G₀ as a function of mesh size ξ between permanent cross-linking points from both chemical cross-linking and trapped topological entanglements for three series of samples. The error bars are SEs from three measurements.

Because G₀ is only related to the chemically cross-linked structure, independent of the existence of physical bonds and entanglements as suggested in the classic theory of threshold (44), a purely physically cross-linked gel would be expected not to show a finite fatigue threshold G₀ when fractured by a chain pull-out mechanism without bond scission (45). However, we also observed a multilevel fatigue resistance behavior in the physical gel PA-2.5-0 made without chemical cross-linker. This indicates that the relatively strong ionic bonds prevent chain pullout at the observation time scale, and the topologically entangled chains [~16 entanglements per chain (see section S4)] behave as being permanently cross-linked and show a finite fatigue threshold G₀ at the observation time scale.

DISCUSSION

Our study highlighted the role of multiscale structures in multimode fatigue resistance, which is reflected by two essential fatigue parameters, i.e., the threshold energy release rate G₀ and the critical stretch ratio λ_tran for the slow-to-fast crack growth transition. The nanoscale permanent polymer network structure, effectively cross-linked by both chemical cross-linking and topological entanglement, controls G₀. Above G₀, the fatigue crack growth behavior notably depends on the phase contrast of the mesoscale bicontinuous networks. When the phase contrast is sufficiently high, that is, the hard phase is sufficiently denser than the soft phase, it is presumably also stronger and better able to bear the stress and the slow mode appears at a small stretch ratio and then jumps to a fast mode at λ_max > λ_tran. Because the crack propagation rate is lower than 0.1 μm per cycle at λ_max < λ_tran, the gels have a strong fatigue resistance through a crack blunting mechanism. The jump to the fast mode for λ_max > λ_tran is directly correlated to the onset of damage of the hard phase network in the bulk of the material (λ_affine), which is itself related to the characteristic size of the phase separated network through λ_affine∝d₀^0.6. On the other hand, when the phase contrast is weak, the fast crack growth mode occurs immediately above the threshold G₀ (<50 J/m²), and the gels exhibit a poor fatigue resistance.

It is interesting to point out that for our laboratory-size macroscopic samples, λ_tran is a characteristic material parameter for the slow-to-fast crack growth mode transition and not G_tran. This is highly unusual and is a direct consequence of the ability of the material to blunt the crack and eliminate the stress concentration by local plastic strain at the crack tip. The correlation between λ_tran and the onset of deviation from affine deformation λ_affine in the PA gels without crack indicates that the bulk structure change influences the fatigue crack growth through formation of metastable oriented structure under cyclic loading by ionic bond formation. Although λ_tran and λ_affine should depend on the stretch rate due to the dynamic nature of the ionic bonds, the detailed stretch rate dependences of λ_tran and λ_affine are beyond the scope of this work and should be studied in a separate work. The mechanism for enhancing multilevel fatigue resistance of PA hydrogels in this work provides not only understanding of fatigue resistance of materials with hierarchical structures but also a promising strategy for developing highly extensible, self-healing, and fatigue-resistant soft materials with hard and soft hierarchical components.

MATERIALS AND METHODS

Materials

The anionic monomer NaSS, cationic monomer DMAEA-Q, ultraviolet (UV) initiator α-ketoglutaric acid (α-keto), and chemical cross-linker N,N-methylenebis(acrylamide) (MBAA) were purchased from Wako Pure Chemical Industries Ltd. and used as received. Deionized water was applied in all experiments.

Preparation of the PA gels

PA gels were prepared by free radical copolymerization of NaSS and DMAEA-Q with a composition around the point of charge balance in the presence of a chemical cross-linker MBAA following the procedure previously reported (7, 46). Briefly, a mixed precursor aqueous solution of NaSS, DMAEA-Q, MBAA, and UV initiator α-keto was polymerized by UV irradiation in argon atmosphere. To tune the microstructure of the gels, the total monomer concentration C_m = (NaSS) + (DMAEA-Q) was varied from 1.75 to 2.5 M, and the MBAA content was varied from 0 to 1.0 mol % (relative to C_m). After polymerization, the gels were dialyzed in 30°C deionized water for 3 weeks to remove the counterions and deswell to reach equilibrium, during which the phase separation formed (24). The equilibrated gels were used in all experiments, unless otherwise mentioned. A summary of the equilibrated gels is shown in table S1.

SAXS measurement

SAXS measurements were carried out at the Synchrotron Radiation Facility (BL19U2, Shanghai, China). The x-ray wavelength used was 1.03 Å. A 2D detector (Pilatus 1M with a resolution of 981 × 1043 pixels and pixel size of 172 μm, Dectris Co. Ltd.) was used to record data. The sample-to-detector distance was 5730 mm. To characterize the bicontinuous hard/soft phase networks of undeformed gels, the 2D SAXS patterns were acquired with an exposure time of 2 s. To detect the deformation of bicontinuous phase networks during loading, in situ time-resolved SAXS measurements were performed, and unnotched rectangular samples (7.5 mm × 16 mm × 1.65 mm, L₀ × H₀ × t₀) were applied. 2D SAXS patterns were acquired at a rate of 0.25 s per frame. The nominal loading stretch rate was 1 s⁻¹.

Rheological test

The dynamic rheological test of the PA gels was performed with an Advanced Rheometric Expansion System rheometer (Rheometric Scientific Inc.). A disk-shaped sample with diameter and thickness of 20 and ~1.65 mm, respectively, was fixed between two metal plates. To prevent water evaporating from the gel, the sample was kept surrounded by water during the whole procedure of test. A rheological frequency sweep from 0.05 to 100 Hz was performed at a shear strain of 0.1% at temperatures from 0.1 to 95°C. By following the principle of time-temperature superposition, master curves of storage modulus (G′), loss modulus (G′′), and loss factor tan δ over a wide frequency range were constructed at a reference temperature of 25°C.

Tensile and toughness test

Tensile test was performed on an Instron 5566 universal tensile tester. Unnotched rectangular sample (7.5 mm × 16 mm × 1.65 mm, L₀ × H₀ × t₀, see inset of fig. S3A) was stretched to fracture. The fracture energy of gels was obtained from a pure shear test using sample in the pure shear geometry (50 mm × 10 mm × 1.65 mm, L₀ × H₀ × t₀, the initial notch c₀ was 10 mm). During the tensile and pure shear tests, the water vapor was sustainably supplied around the gels. The experiment temperature was kept constant at 24°C, and the nominal loading stretch rate was 1 s⁻¹.

Fatigue test and birefringence test

The fatigue test was performed mainly in the pure shear geometry (50 mm × 10 mm × 1.65 mm, L₀ × H₀ × t, the initial notch c₀ was 10 mm) using a Shimadzu tensile tester (AG-X, Shimadzu Corporation) in a humidity chamber. To verify that λ_tran for slow-to-fast crack growth mode transition is geometry independent, fatigue tests have also been performed for samples with different initial height H₀, while the aspect ratios L₀/H₀ = 5 and c₀/H₀ = 1 were kept the same. The fatigue test for sample with H₀ = 10 and 15 mm was performed at a nominal strain rate of 1 s⁻¹. The fatigue test for samples with H₀ = 20 mm could only be performed at a maximal stretch rate of 0.8 s⁻¹ because of the limits of the crosshead speed of the tensile machine. Fatigue test was also performed for sample with rectangular geometry (7.5 mm × 16 mm × 1.65 mm, L₀ × H₀ × t, the initial notch c₀ was 1 mm) at a nominal strain rate of 1 s⁻¹. During the test, the temperature was kept constant at 24°C. The value of energy release rate G_tran, characterizing the energy required to cause the slow-to-fast transition of crack propagation for strongly phase separated gels, is only comparable for gels with a fixed geometry. A homemade circular polarizing optical system (47) was applied to observe the stress distribution during fatigue tests. Further details on the methods are available in the Supplementary Materials.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/16/eabe8210/DC1