Abstract
Background
An anomalous origin of the right coronary artery from the left coronary artery sinus is usually characterized by an acute take-off angle. Most affected patients have no clinical symptoms; however, some patients have decreased blood flow into the right coronary artery during exercise, which can lead to symptoms such as myocardial ischemia. Most researchers who have studied an anomalous origin of the right coronary artery from the left coronary artery sinus have done so through clinical cases. In this study, we used numerical simulation to evaluate the hemodynamics of this condition and the effect of an acute take-off angle on hemodynamic parameters. We expect that the results of this study will help in further understanding the clinical symptoms of this anomaly and the hemodynamic impact of an acute take-off angle.
Methods
Three-dimensional models were reconstructed based on the computed tomography images from 16 patients with a normal right coronary artery and 26 patients with an anomalous origin of the right coronary artery from the left coronary artery sinus. A numerical simulation of a two-way fluid-structure interaction was executed with ANSYS Workbench software. The blood was assumed to be an incompressible Newtonian fluid, and the vessel was assumed to be an isotropic, linear elastic material. Hemodynamic parameters and the effect of an acute take-off angle were statistically analyzed.
Results
During the systolic period, the wall pressure in the right coronary artery was significantly reduced in patients with an anomalous origin of the right coronary artery (t =1.32 s, P=0.0001; t =1.34–1.46 s, P<0.0001). The wall shear stress in the abnormal group was higher at the beginning of the systolic period (t =1.24 s, P=0.0473; t =1.26 s, P=0.0193; t =1.28 s, P=0.0441). The acute take-off angle was smaller in patients with clinical symptoms (27.81°±4.406°) than in patients without clinical symptoms (31.86°±2.789°; P=0.017). In the symptomatic group, pressure was negatively correlated with the acute take-off angle (P=0.0185–0.0341, r=−0.459 to −0.4167).
Conclusions
This study shows that an anomalous origin of the right coronary artery from the left coronary artery sinus causes changes in hemodynamic parameters, and that an acute take-off angle in patients with this anomaly is associated with terminal ischemia of the right coronary artery.
Keywords: Acute take-off angle, anomalous right coronary artery, fluid-structure interaction (FSI), hemodynamic parameters
Introduction
In computed tomography (CT) images, an anomalous origin of the right coronary artery (RCA) from the left coronary artery sinus (AORL) constitutes 15% of anomalous origins of the coronary artery from the opposite coronary sinus (1). Exercise can trigger fatal arrhythmias in young people with AORL (2). One of the anatomical features of AORL is an acute take-off angle, which results in reduced velocity in the RCA (3,4). The normal take-off angle is 45°–90°, and an acute take-off angle is defined as an angle of <45° (5,6). According to several studies of the common causes of sudden cardiac death due to AORL in young athletes, one of the main mechanisms is an acute take-off angle (7-9). AORL is more likely to cause sudden cardiac death when the acute take-off angle is <30°, but no relationship has been found between the interarterial course length and sudden cardiac arrest (10). Many studies have analyzed data from clinical cases and autopsy reports in order to understand the risk of AORL and propose treatment options (7,11-15). Some studies have simulated the hemodynamics of AORL through computational fluid dynamics. However, few studies have simulated the effect of an acute take-off angle on blood flow, and the sample sizes were small in those studies.
Although magnetic resonance angiography and CT angiography (CTA) can show some characteristics of blood flow, they cannot provide clear information about wall shear stress (WSS), blood flow velocity, and blood pressure (16). Therefore, the use of computational fluid dynamics to predict and diagnose cardiovascular diseases has become an important research topic. Through the analysis of the left coronary artery by computational fluid dynamics and fluid-structure interaction (FSI), researchers can study the aneurysm rupture, the effect of stent implantation, and other issues (17,18). Studying the relationship between blood flow characteristics and the development of vascular diseases has provided a deeper understanding of these diseases. Such knowledge also plays an important role in diagnoses and surgical evaluations (19-22).
Computational fluid dynamics was recently applied to an anomalous origin of the left coronary artery from the RCA sinus, and the evaluation of hemodynamic parameters confirmed that the interarterial space is compressed during exercise (23). A study involving a Newtonian model and a non-Newtonian model showed that the non-Newtonian model only affected the WSS magnitude (24). In another study, three non-Newtonian and Newtonian blood viscosity models were used to analyze the human thoracic aorta, and all of the blood viscosity models produced a consistent WSS distribution pattern (25). In many studies involving numerical simulation of human blood vessels, the blood vessels were assumed to have rigid walls (26-28). The maximum WSS in an elastic vessel is significantly lower than that in a vessel with rigid walls (29,30). By setting the blood vessel wall as elastic, not only will the simulation results be closer to the real situation in the human body, but the data will also be more accurate (31,32). In patient-specific two-way FSI analysis, the hemodynamic parameters of AORL are closer to the real physiological state in humans.
In this study, we used two-way FSI to simulate the flow of blood through human blood vessels. Hemodynamic changes caused by an acute take-off angle in AORL were analyzed. In total, 42 patient-specific models were analyzed; of these, 16 patients with a normal RCA comprised the control group. Clinicians collected CTA imaging data from hospitals, and the collected CTA images were reconstructed using modeling software to generate the three-dimensional models needed for numerical simulation. To ensure that the simulated environment was similar to the blood flow situation in humans, the entry boundary condition was set as the real pulsatile velocity, and a two-way FSI analysis was adopted. The parameters chosen for the blood vessels and blood were similar to those of the real human body. Hemodynamic parameters such as the flow rate, pressure, and WSS of all models were then collected for statistical analysis.
Methods
Data collection
CTA images from 16 patients with normal coronary arteries (7 men, 9 women; mean age, 58±8.7 years) and 26 patients with AORL (17 men, 9 women; mean age, 62±10.9 years) were collected using a 128-slice dual-source CT scanner (SOMATOM Definition Flash; Siemens, Munich, Germany) (80 kV, 140 kV). The scanning parameters were a rotation speed of 280 ms/rot and collimator of 2 mm × 128 mm × 0.6 mm. The relevant parameters of the CTA images were a slice increment of 0.50 mm, a slice thickness of 0.75 mm, and an image resolution of 512×512.
Image measurements
The acute take-off angle of the AORL was measured, as shown in Figure 1; the maximum diameter of the RCA ostium can be seen on the axial superimposed image. A black line was drawn to represent the ostial diameter, and, from the middle of this black line, a second 5-mm line was drawn along the center of the RCA. The angle between these two lines was measured as the acute take-off angle of the AORL (10,33).
Figure 1.
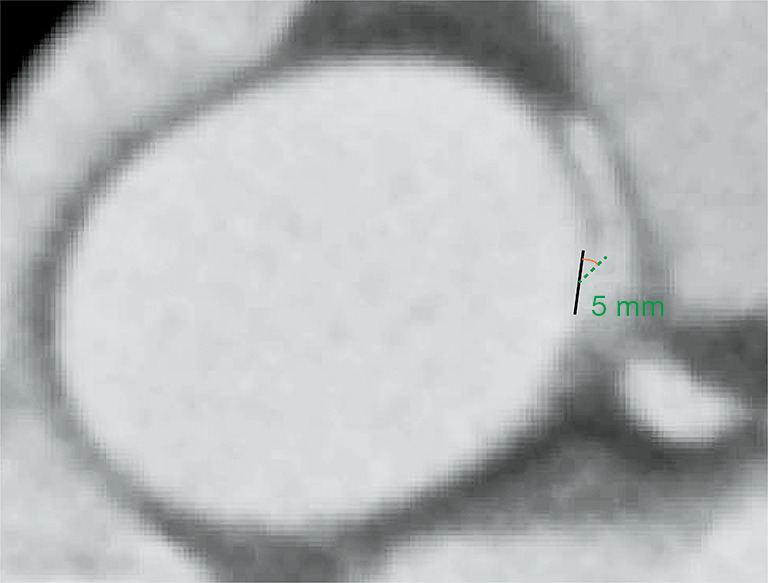
The measurement of the acute take-off angle. The black line indicates the ostium line, and the green line indicates the second 5-mm line.
Coronary artery models
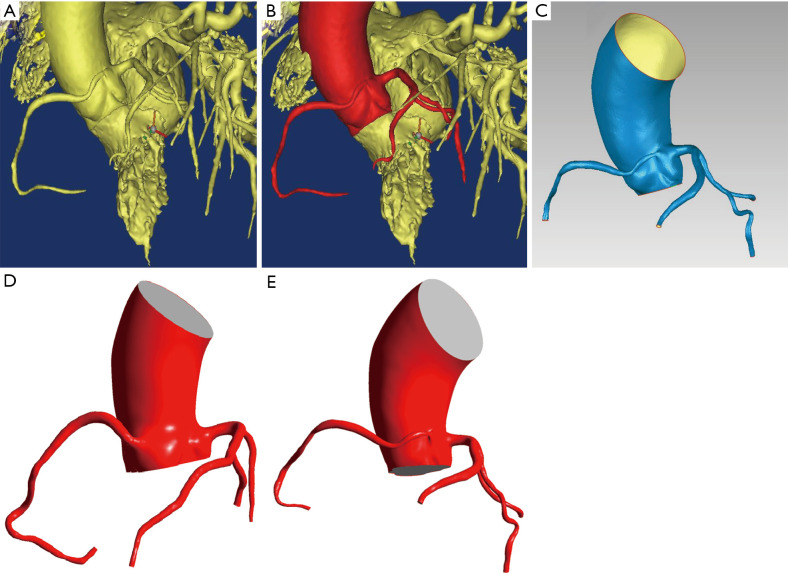
The retained part of the ascending aorta, the left coronary artery tree, and the main branch of the RCA were modeled for hemodynamic analysis. CTA images were segmented by Mimics 17.0 software (Materialise, Ann Arbor, MI, USA) using automatic and semiautomatic methods, as shown in Figures 2A,B. The red portion shown in Figure 2B is reserved for all models in order to build the FSI model used for analysis. The surface model was saved in binary stereolithography format. The surfaces of the stereolithography-format models were smoothed using Geomagic Studio 2013 software (3D Systems, Rock Hill, SC, USA). Figure 2C shows the surface solid model of the blood model. The surface of the blood-surface model was offset 0.5 mm along the normal direction to obtain the surface model of the blood vessel. Solidworks 2016 (SolidWorks Corporation, Waltham, MA, USA) was used to generate the solid filling and fluid filling models. Finally, the two models were combined to generate the vessel wall model. The blood model used in the analysis was filled and generated in the geometry module (Figure 2D,E).
Figure 2.
The process of image segmentation using automatic and semi-automatic methods. (A) Part of the coronary artery and part of the aorta structures were removed; (B) the red part is the part to be reserved; (C) the blood surface model in STL format is formed by smoothing; (D) the simulated model of the right coronary artery originating from the right coronary sinus was generated; (E) the simulated model of AORL. AORL, anomalous origin of the right coronary artery from the left coronary artery sinus.
Governing equations and boundary conditions
The main purpose of this study was to elucidate the hemodynamic differences between patients with and without AORL. Some studies have shown that Newtonian and non-Newtonian models have little impact on the hemodynamic environment (34). For the purpose of this study and for the simplicity of analysis, blood was considered to be a homogenous, incompressible, isothermal, and Newtonian fluid (35,36). Blood density and viscosity were set to be constant at 1,060 kg/m3 and 3.5×10−3 Pa∙s, respectively (31). Numerical simulation was carried out based on the continuity equation and the three-dimensional incompressible Navier-Stokes equation:
| [1] |
| [2] |
where u represents the fluid velocity vector, ρ represents the density, and σ is the stress tensor. σ is defined as follows:
| [3] |
where η and γ denote the blood viscosity and shear rate, respectively; p is the pressure; D is the rate of the deformation tensor, and is defined as follows:
| [4] |
where µ is the blood viscosity.
The vessel wall was assumed to be an isotropic, linear elastic material. The vessel wall density was 1,150 kg/m3, Young’s modulus was 5 MPa, and Poisson’s ratio was 0.45 (37). The conservation equation for the solid part was as follows:
| [5] |
where σs is the stress tensor, ρs is the density, and as is the acceleration.
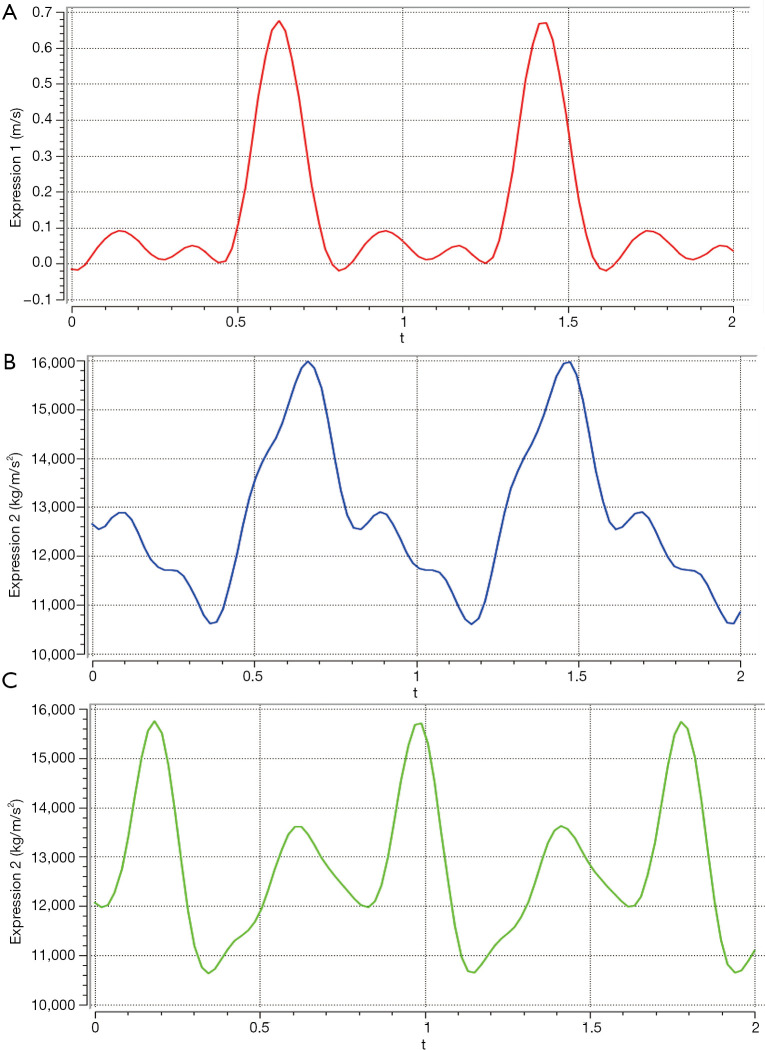
In this study, the inlet (i.e., entry) boundary condition was set as the real pulsatile velocity of the human body, and the outlet pressure condition was set to a constant value. The inlet velocity was represented by the Fourier series (Figure 3A) (38,39):
Figure 3.
The pulse curves. (A) The inlet velocity of the aorta; (B) pressure fluctuation of the aorta; (C) pressure fluctuation of the coronary artery.
| [6] |
| [7] |
where is the mean volume flow, is the angular frequency, the cardiac cycle t is 0.8 s, and is the inlet velocity. The variable A is the cross-sectional area of the inlet surface, and the value of A is the average of all the models.
The pulsation pressure was expressed by a Fourier series as follows (Figure 3B,C) (38,39):
| [8] |
where is the mean pressure.
As shown in Figure 3B,C, we calculated the mean arterial pressure difference between the ascending aorta and the coronary artery. Finally, the boundary conditions were set as follows:
At the exit of the coronary artery, the normal and tangential outlet pressures were 0 Pa (pn1 = pt1 =0 Pa).
The tangential outlet pressure of the aorta was 56 Pa, and the normal pressure was 0 Pa (pt2 =56 Pa; pn2 =0 Pa).
The wall was assumed to have no slip (vn = vt =0 m/s).
The FSI follows the most basic conservation principle. Because it was assumed that there is no heat exchange in the blood, the following equations needed to be met between the fluid and the solid:
| [9] |
| [10] |
where n is the boundary normal, σ is the stress tensor, and d is the displacement vector. The subscripts f and s represent fluids and solids, respectively.
Hemodynamic parameters
ICEM software (Ansys Inc., Canonsburg, PA, USA) was used for the mesh generation. To ensure that the grid division was reasonable, one of the models was selected for analysis, and the results are shown in Table 1. The velocity is the average velocity of the cross-sectional area at the inlet of the RCA. WSS and pressure were obtained with a five-point sampling method. The five-point sampling method was based on the region that was approximately 10–15 mm from the entrance of the RCA.
Table 1. Mesh convergence test (t =1.4 s).
| Case | The mesh size in the fluid domain (m) | Elements | The mesh size in the solid domain (m) | Elements | Velocity (m/s) | WSS (Pa) | Pressure (Pa) |
|---|---|---|---|---|---|---|---|
| 1 | 0.0007 | 486,394 | 0.0008 | 95,790 | 0.0345 | 0.43 | 687.906 |
| 2 | 0.0007 | 486,394 | 0.001 | 58,939 | 0.0346 | 0.432 | 687.889 |
| 3 | 0.0007 | 486,394 | 0.0012 | 43,145 | 0.0347 | 0.428 | 687.979 |
| 4 | 0.00075 | 423,380 | 0.0008 | 95,790 | 0.0341 | 0.439 | 683.047 |
| 5 | 0.00075 | 423,380 | 0.001 | 58,939 | 0.0394 | 0.485 | 683.442 |
| 6 | 0.00075 | 423,380 | 0.0012 | 43,145 | 0.0399 | 0.449 | 683.961 |
| 7 | 0.0008 | 373,286 | 0.0008 | 95,790 | 0.0354 | 0.417 | 681.134 |
| 8 | 0.0008 | 373,286 | 0.001 | 58,939 | 0.0356 | 0.422 | 680.96 |
| 9 | 0.0008 | 373,286 | 0.0012 | 43,145 | 0.0362 | 0.438 | 680.957 |
| 10 | 0.001 | 256,648 | 0.0008 | 95,790 | 0.0364 | 0.414 | 668.431 |
| 11 | 0.001 | 256,648 | 0.001 | 58,939 | 0.0353 | 0.412 | 668.375 |
| 12 | 0.001 | 256,648 | 0.0012 | 43,145 | 0.0362 | 0.413 | 668.306 |
WSS, wall shear stress.
The two main purposes of this study were to compare the hemodynamic differences between an AORL model and a normal model and to study the difference of numerical law, not the difference in specific values. Therefore, the mesh was set as follows: in the fluid part, the proximity size control function was used, and the maximum face size was set to 0.0008 m. The expansion layer was set as three layers, and its growth rate was 1.2. The solid part was set to proximity to control the grid resolution of the area adjacent to the mesh. The unit size was set by local grid control, and the average side length of the vessel wall was set to 0.001 m. Tetrahedral mesh was selected as the mesh type, and capture proximity was used to divide the mesh.
In this study, the FSI analysis was carried out using Ansys Workbench 19.0 (Ansys Inc.). Multiple-code coupling was used to solve the problem. A two-way FSI was adopted. Ansys mechanical and Ansys CFX 19.0 (ANSYS, Inc.) were used to solve the calculation domain of the vessel wall and blood, respectively. Fluid Flow (CFX) was adopted for the fluid portion, Transient Structural was adopted for the solid portion, and the two modules were connected by System Coupling modules. For the fluid portion, the thermodynamic state of blood was set to liquid. Heat transfer in the fluid models of the default domain was set to none, and the turbulence was also set to none according to:
| [11] |
where ρ is the density, U is the velocity, D is the diameter of the vessel, and µ is the viscosity coefficient.
The maximum blood vessel diameter and blood velocity were used in the model (Uaverage =0.18 m/s, Daverage =0.028 m, Re =1,526.4). The main purpose of this paper was to compare the different parameters of the results, which could be simplified by setting the blood to laminar flow. The material of the fluid part was set to the blood flow parameters. The minimum number of iterations was set to 1, and the maximum number of iterations was set to 20. Convergence was carried out by linear convergents, and the convergence criterion was set to 1×10−4. The inlet and outlet section of the vessel wall was set as fixed support, the inner wall of the vessel was set as a fluid-solid coupling surface, and the wall of the vessel was set to elastic support. The inner surface of the vessel wall was provided with a fluid load on the surface. The step end time was set to 2 s. Finally, the system-coupling module was used to connect the fluid part and the solid part. The total analysis time was 2 s, and the time step was 0.02 s.
Statistical analysis
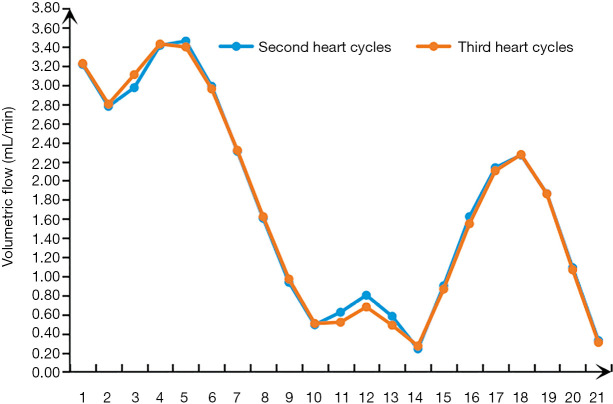
All cases were statistically analyzed to eliminate patient-specific differences. The statistical analyses were performed with GraphPad Prism 8.0 (GraphPad Software, San Diego, CA, USA), SPSS v. 22.0 (IBM Corp., Armonk, NY, USA), and MATLAB 2013b (MathWorks, Natick, MA, USA). Figure 4 shows that there is little difference between the volumetric flow of 0.8–1.2 and 1.6–2.0, and this transition is washed away. The data for t =0.8–1.6 s were collected. The pressure, WSS, and mesh deformation were collected by means of a five-point sampling method. The differences in parameters between the control group and the experimental group were analyzed by two-way repeated-measures analysis of variance in the second period. Spearman’s correlation was performed using age, sex, and cross-sectional area of the inlet as covariates to analyze the correlation between the acute take-off angle of AORL and the inlet flow, pressure, and WSS. The difference in the acute take-off angles between the asymptomatic and symptomatic AORL groups was calculated using analysis of covariance. The significance level was set at P<0.05.
Figure 4.
To prevent the numerical solution from being corrupted by the initial conditions, whether or not this transition is washed away should be determined. The volumetric flows between 0.8–1.2 s were compared with those between 1.6–2.0 s.
Results
Clinical features
In total, 42 patients were included in the study. The patients were divided into a control group (n=16) and an experimental (AORL) group (n=26). The experimental group was further divided into an asymptomatic group and symptomatic group according to the presence of clinical symptoms. The characteristics and clinical symptoms of patients are summarized in Table 2. According to the clinicians’ diagnoses, the main symptoms were chest distress and dizziness, which is consistent with AORL reported in a previous study (40).
Table 2. Patient data information.
| Group | Number | Average age | Gender | Clinical features | Number of patients with clinical symptoms |
|---|---|---|---|---|---|
| A | 16 | 56±10.0 | 7 males | – | – |
| B1 | 12 | 64±12.4 | 9 males | – | – |
| B2 | 14 | 61±10.1 | 8 males | Chest distress | 6 |
| Dizziness | 2 | ||||
| Chest distress and dizziness | 1 | ||||
| Palpitations | 1 | ||||
| Coronary disease | 4 |
Hemodynamics
The inlet flow was determined from the area and average velocity of the cross section of the inlet of the RCA. WSS and pressure were obtained by a five-point sampling method of an area approximately 10–15 mm from the inlet of the RCA.
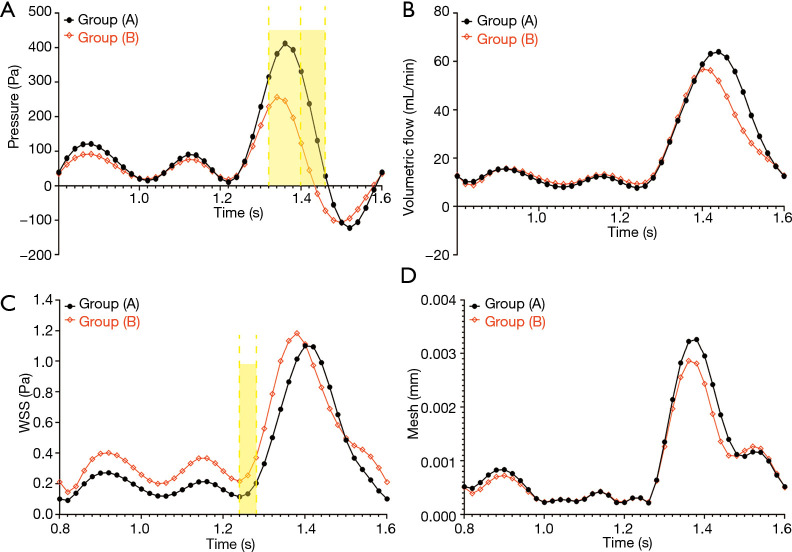
The pressure in the experimental group (−72.5 to 256.5 Pa) was significantly lower than that in the control group (28.1 to 411.9 Pa) during the time period of t =1.32–1.46 s, and the difference between the two groups was statistically significant (t =1.32 s, P=0.0001; t =1.34–1.46 s, P<0.0001) (Figure 5A). As shown in Figure 5B, the volumetric flow in the experimental group was relatively low in the time period of 1.4–1.56 s, but the difference throughout the whole period was not statistically significant (P>0.05). At 1.4–1.5 s, the WSS of the AORL group (0.216–0.370 Pa) was slightly higher than that in the control group (0.115–0.203 Pa) (Figure 5C). The statistical analysis showed a difference in the WSS between the two groups within 1.24–1.28 s (t =1.24 s, P=0.0473; t =1.26 s, P=0.0193; t =1.28 s, P=0.0441), but no significant differences were observed during the remainder of the time (P>0.05) (Figure 5C). The mesh deformation during a cardiac cycle was almost identical between the two groups, with no significant difference (P>0.05) (Figure 5D).
Figure 5.
This figure shows the comparison of the inlet cross section area, volume flow, pressure, and WSS between the abnormal group and the normal group within one period. Group (A): normal origin of the RCA. Group (B): AORL. The yellow region indicates that the hemodynamic parameters of the time region are statistically significant. WSS, wall shear stress; RCA, right coronary artery; AORL, anomalous origin of the RCA from the left coronary artery sinus.
The age and sex of the AORL patients were used as covariates, and analysis of covariance showed a significant difference between the acute take-off angle in patients without clinical symptoms (31.86°±2.789°) and patients with clinical symptoms (27.81°±4.406°) (P=0.017) (Figure 6).
Figure 6.
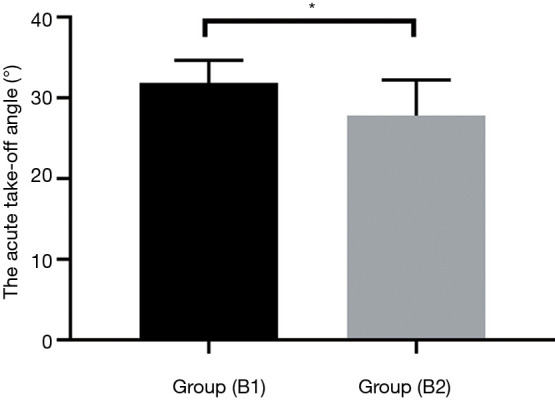
The difference in angle between group (B1) and group (B2). Group (B1) represents the acute take-off angle of an AORL patient without clinical symptoms. Group (B2) represents the acute take-off angle of an AORL patient with clinical symptoms. *, P<0.05. AORL, anomalous origin of the right coronary artery from the left coronary artery sinus.
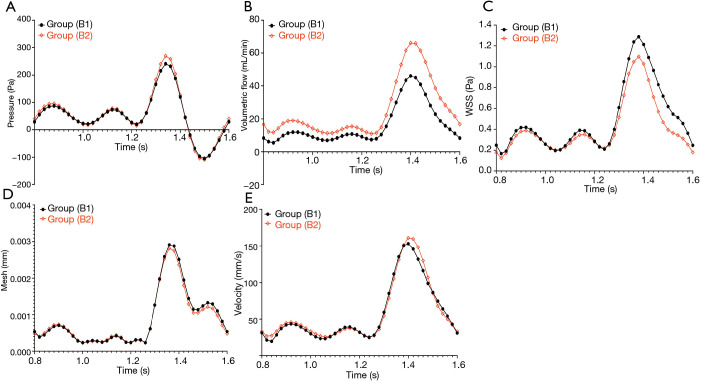
We also evaluated the differences in the hemodynamic parameters between patients with and without clinical symptoms. Figure 7A shows that the pressure in a cardiac cycle was almost identical between the two groups (P>0.05). Patients with AORL who showed clinical symptoms had a higher volume flow (Figure 7B), but the difference was not statistically significant (P>0.05). Patients with clinically symptomatic AORL had a lower WSS during systole than patients without clinical symptoms (Figure 7C); however, the difference was not statistically significant (P>0.05). There was no difference in mesh deformation between the two groups (P>0.05) (Figure 7D). As shown in Figure 7E, there was no significant difference in velocity between patients with clinical symptoms and without symptoms, but the difference was not significant (P>0.05).
Figure 7.
Differences in hemodynamic parameters between group (B1) and group (B2). Group (B1) represents the acute take-off angle of an AORL patient without clinical symptoms. Group (B2) represents the acute take-off angle of an AORL patient with clinical symptoms. AORL, anomalous origin of the right coronary artery from the left coronary artery sinus.
Spearman’s correlation was used to analyze the correlation between an acute take-off angle and the hemodynamic parameters. Using age, sex, and the cross-sectional area of the inlet as covariables, acute take-off angles were negatively correlated with pressure at 0.84–0.94 s and 1.10–1.16 s. The specific values are shown in Table 3. Throughout the cardiac cycle, the angle had no correlation with the volumetric flow, WSS, or mesh deformation (P>0.05).
Table 3. Values of P and r for statistically significant time periods.
| Time (s) | P | r |
|---|---|---|
| 0.84 | 0.0215 | −0.449 |
| 0.86 | 0.0185 | −0.459 |
| 0.88 | 0.0253 | −0.438 |
| 0.90 | 0.0279 | −0.431 |
| 0.92 | 0.0312 | −0.423 |
| 0.94 | 0.0341 | −0.4167 |
| 1.10 | 0.0256 | −0.437 |
| 1.12 | 0.0194 | −0.455 |
| 1.14 | 0.0194 | −0.455 |
| 1.16 | 0.0219 | −0.447 |
Discussion
AORL is a rare congenital anomaly that can lead to myocardial ischemia and arrhythmia, increasing the risk of sudden cardiac death (41). Risk stratification and management can reduce the risk of ischemia in patients with AORL (41). The risk of sudden death depends on several anatomical features: an intramural course, a slit-like orifice, and an acute take-off angle (8,42). These characteristics can lead to functional stenosis and, ultimately, ischemia in patients with AORL. Distention of the pulmonary artery may be the cause of RCA compression between the aorta and pulmonary root (43). Dilation of the aorta can cause an abnormal narrowing of the opening, which can reduce blood flow to the coronary arteries (44). Arterial stenosis affects the hemodynamic parameters and might lead to a series of complications such as rupture of the coronary artery (45,46).
In this study, we simulated the hemodynamics of a cardiac cycle based on CTA images and the actual fluctuating inlet flow in the human body. We investigated the correlation between an acute take-off angle in patients with AORL and various hemodynamic parameters, the hemodynamic differences between normal and abnormal groups, and the potential relationship between an acute take-off angle and clinical symptoms.
Our data showed that the volume flow in three patients in the experimental group was significantly larger (one order of magnitude) than that in the other patients. This was due to the cross-sectional area of the inlet in these patients being one order of magnitude larger than that of the other patients in the AORL group. Therefore, overall, there was no significant difference in the volume flow between the normal and abnormal groups.
Our analysis demonstrated that the experimental group (patients with an acute take-off angle) had significantly lower pressure during the systolic period. The main reason for the negative pressure is that the outlet pressure was set to 0 Pa. The main purpose of this study was not to examine the specific value, but rather the regularity of the numerical value. Therefore, the specific value of the final pressure result is not relevant to the discussion of the final result. The starting angle of a normal RCA is 45°–90°. The acute take-off angle of AORL is about 20°–40°, The acute take-off angle of AORL can cause excessive pressure loss. At the same time, the smaller cross-sectional area at the inlet of the AORL will increase the velocity of blood flow to the RCA, resulting in reduced pressure (47). If the entrance cross-sectional area of the RCA is very narrow, it reduces blood flow to the heart, especially when the heart is beating vigorously (44).
This study proved that the acute take-off angle of patients with clinical symptoms is small and that the acute take-off angle of patients with AORL is negatively correlated with pressure, indicating that patients with clinical symptoms have higher pressure at the starting position of the RCA. The main reason for this is that a small acute takeoff angle more easily produces clinical symptoms such as dizziness and chest tightness. Because of the insufficient blood supply at the RCA terminal, the heart cannot exchange nutrients, resulting in clinical symptoms. On the premise that the entrance cross-sectional area of the RCA is the same, the cause of the insufficient blood supply of the RCA is the low blood velocity entering the RCA, resulting in increased pressure (47). In the experimental group, the difference in the acute take-off angle was only about 10°, which would not cause excessive pressure loss and would eventually lead to an increase in pressure.
WSS is an effective parameter for the early diagnosis of atherosclerosis (48). Atherosclerotic plaques often occur in the bifurcation region of low WSS (49). We demonstrated that patients with AORL had a relatively large WSS at the beginning of the systolic phase, and this WSS showed no significant difference regardless of clinical symptoms. A comparison of WSS values showed that patients with AORL did not have an increased risk of atherosclerosis.
This study had some limitations. First, the number of patients in the study was so small that the differences in hemodynamic parameters were not statistically significant between the groups (i.e., volumetric flow and mesh deformation between the normal and experimental groups; and pressure, volumetric flow, WSS, and mesh deformation between the asymptomatic and symptomatic AORL groups). Second, we did not consider the effect of the pulmonary artery and heart motion on the hemodynamic environment in this study.
Conclusions
The main purpose of this study was to analyze the hemodynamics of AORL and the effect of an acute take-off angle on hemodynamics based on finite-element transient simulation. The results revealed that the pressure is lower and the WSS is higher in patients with AORL compared with those without AORL. In patients with AORL, the pressure decreases as the acute take-off angle decreases. Patients with AORL with clinical symptoms had relatively small acute take-off angles.
We can conclude that, compared with patients without AORL, patients with AORL develop greater changes in the hemodynamic environment, which may cause some clinical symptoms. Moreover, the acute takeoff angle in patients with AORL affects the hemodynamic environment. Compared with individuals without AORL, the small angle may cause insufficient blood supply to the end of the RCA during exercise. A smaller acute take-off angle is more likely to result in dizziness, vertigo, and other clinical symptoms. This study not only theoretically demonstrates the influence of AORL and an acute take-off angle on the hemodynamic environment, but also provides potential theoretical guidance for clinicians to diagnose and prevent the clinical symptoms of AORL.
Acknowledgments
Funding: This work was supported in part by the Academic Promotion Programme of Shandong First Medical University (No. 2019QL009). Jianfeng Qiu was further supported by the Taishan Scholars Program of Shandong Province (No. TS201712065).
Ethical Statement: The study was approved by Shandong the First Medical University & Shandong Academy of Medical Sciences ethics committee. Individual consent for this retrospective analysis was waived.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
Footnotes
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/qims-20-125). The authors have no conflicts of interest to declare.
References
- 1.Andreou AY, Ioannides MA, Avraamides PC, Georgiou GM. Aberrant right coronary artery origin from the left aortic sinus with interarterial course manifesting acute myocardial infarction. Exp Clin Cardiol 2009;14:50-2. [PMC free article] [PubMed] [Google Scholar]
- 2.Finocchiaro G, Behr ER, Tanzarella G, Papadakis M, Malhotra A, Dhutia H, Miles C, Diemberger I, Sharma S, Sheppard MN. Anomalous Coronary Artery Origin and Sudden Cardiac Death: Clinical and Pathological Insights From a National Pathology Registry. JACC Clin Electrophysiol 2019;5:516-22. 10.1016/j.jacep.2018.11.015 [DOI] [PubMed] [Google Scholar]
- 3.Sato Y, Matsumoto N, Komatsu S, Kunimasa T, Yoda S, Tani S, Kunimoto S, Achenbach S, Saito S. Anomalous origin of the right coronary artery: depiction at whole-heart coronary magnetic resonance angiography. Int J Cardiol 2008;127:274-5. 10.1016/j.ijcard.2007.04.180 [DOI] [PubMed] [Google Scholar]
- 4.Lee BY, Song KS, Jung SE, Jung JI, Chun HJ, Park CB, Kim CK, Cho EJ, Jin U, Jung HO. Anomalous right coronary artery originated from left coronary sinus with interarterial course: evaluation of the proximal segment on multidetector row computed tomography with clinical correlation. J Comput Assist Tomogr 2009;33:755-62. 10.1097/RCT.0b013e318190d68c [DOI] [PubMed] [Google Scholar]
- 5.Frescura C, Basso C, Thiene G, Corrado D, Pennelli T, Angelini A, Daliento L. Anomalous origin of coronary arteries and risk of sudden death: a study based on an autopsy population of congenital heart disease. Hum Pathol 1998;29:689-95. 10.1016/S0046-8177(98)90277-5 [DOI] [PubMed] [Google Scholar]
- 6.Nasis A, Machado C, Cameron JD, Troupis JM, Meredith IT, Seneviratne SK. Anatomic characteristics and outcome of adults with coronary arteries arising from an anomalous location detected with coronary computed tomography angiography. Int J Cardiovasc Imaging 2015;31:181-91. 10.1007/s10554-014-0535-4 [DOI] [PubMed] [Google Scholar]
- 7.Basso C, Maron BJ, Corrado D, Thiene G. Clinical profile of congenital coronary artery anomalies with origin from the wrong aortic sinus leading to sudden death in young competitive athletes. J Am Coll Cardiol 2000;35:1493-501. 10.1016/S0735-1097(00)00566-0 [DOI] [PubMed] [Google Scholar]
- 8.Kurosu A, Kuroyanagi K, Yamauchi S, Omura K, Saito K. Sudden Death Caused by Anomalous Origin of the Coronary Artery During Exercise. J Forensic Sci 2016;61:548-50. 10.1111/1556-4029.13004 [DOI] [PubMed] [Google Scholar]
- 9.Jacobs ML. Anomalous aortic origin of a coronary artery: The gaps and the guidelines. J Thorac Cardiovasc Surg 2017;153:1462-5. 10.1016/j.jtcvs.2016.07.058 [DOI] [PubMed] [Google Scholar]
- 10.Nagashima K, Hiro T, Fukamachi D, Okumura Y, Watanabe I, Hirayama A, Tanaka M, Tanaka T, Takamisawa I, Taguchi I, Sato A, Aonuma K, Fukamizu S, Nakada A, Watanabe A, Amioka N, Suzuki Y, Matsumoto N, Koizumi J, Kumagai K, Naya M, Higuchi Y, Naito Y, Masuyama T, Kawamura M, Tsunoda R, Suzuki S, Ishii H, Murohara T, Shimizu T, Takeishi Y, Shiina K, Yamashita J, Imamura T, Sumitomo N, Noguchi T, Aso T, Furukawa K, Yamauchi Y, Okishige K, Sakata K, Yamagishi M, Shimizu S, Ohno M, Sugano T, Matsumura K, Matsumoto K, Ozaki K, Hayashidani S, Meno H, Iwata A, Higuma T, Tomita H, Yoshino H, Taniai S, Shishido K, Murakami M, Negishi K, Nii M, Wakatsuki D, Suzuki H, Motoike Y, Ozaki Y, Nakazato J, Hayashi H, Higuchi S, Shoda M. Anomalous origin of the coronary artery coursing between the great vessels presenting with a cardiovascular event (J-CONOMALY Registry). Eur Heart J Cardiovasc Imaging 2020;21:222-30. [DOI] [PubMed] [Google Scholar]
- 11.Muñoz-Guijosa C, Permanyer E, Leta R. Anomalous origin of right coronary artery from the left coronary sinus: sudden death and successful surgical reimplantation. Eur Heart J 2012;33:1308. 10.1093/eurheartj/ehr386 [DOI] [PubMed] [Google Scholar]
- 12.Sarfaraz ZK, Siddiqi MS, Al-Kindi AH, Alameddine T. Anomalous Origin of the Right Coronary Artery from the Left Coronary Sinus: Case report. Sultan Qaboos Univ Med J 2017;17:e352-4. 10.18295/squmj.2017.17.03.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ferreira AFP, Rosemberg S, Oliveira DS, Araujo-Filho JAB, Nomura CH. Anomalous origin of coronary arteries with an interarterial course: pictorial essay. Radiol Bras 2019;52:193-7. 10.1590/0100-3984.2017.0203 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Majewski J, Shelton R, Varma M, Davis G. Anomalous origin of the right coronary artery from the left Valsalva sinus in a patient presenting with syncope, ventricular tachycardia, and electrocardiographic early repolarization pattern. Kardiol Pol 2019;77:883-5. 10.33963/KP.14909 [DOI] [PubMed] [Google Scholar]
- 15.Ibraheem WI, Abass OA, Toema AM, Yehia AM. Coronary artery bypass grafting experience in the setting of an anomalous origin of the right coronary artery from the left sinus of Valsalva: Midterm results. J Card Surg 2019;34:1162-71. 10.1111/jocs.14234 [DOI] [PubMed] [Google Scholar]
- 16.Peiffer V, Sherwin SJ, Weinberg PD. Does low and oscillatory wall shear stress correlate spatially with early atherosclerosis? A systematic review. Cardiovasc Res 2013;99:242-50. 10.1093/cvr/cvt044 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Fujimoto K, Tsukahara T, Yamada Y, Yamamoto K, Motosuke M, Tanaka K, Tahara S, Tani K, Nakamura S, Fujino Y. Valuation Of Implanted-Stent Impact On Coronary Artery Trifurcation Blood Flow By Using CFD. Annu Int Conf IEEE Eng Med Biol Soc 2018;2018:3181-4. 10.1109/EMBC.2018.8513023 [DOI] [PubMed] [Google Scholar]
- 18.Murayama Y, Fujimura S, Suzuki T, Takao H. Computational fluid dynamics as a risk assessment tool for aneurysm rupture. Neurosurg Focus 2019;47:E12. 10.3171/2019.4.FOCUS19189 [DOI] [PubMed] [Google Scholar]
- 19.Polanczyk A, Podgorski M, Polanczyk M, Veshkina N, Zbicinski I, Stefanczyk L, Neumayer C. A novel method for describing biomechanical properties of the aortic wall based on the three-dimensional fluid-structure interaction model. Interact Cardiovasc Thorac Surg 2019;28:306-15 10.1093/icvts/ivy252 [DOI] [PubMed] [Google Scholar]
- 20.Polanczyk A, Podyma M, Stefanczyk L, Szubert W, Zbicinski I. A 3D model of thrombus formation in a stent-graft after implantation in the abdominal aorta. J Biomech 2015;48:425-31. 10.1016/j.jbiomech.2014.12.033 [DOI] [PubMed] [Google Scholar]
- 21.Kafi O, Khatib NE, Tiago J, Sequeira A. Numerical simulations of a 3D fluid-structure interaction model for blood flow in an atherosclerotic artery. Math Biosci Eng 2017;14:179-93. 10.3934/mbe.2017012 [DOI] [PubMed] [Google Scholar]
- 22.Meza D, Rubenstein DA, Yin W. A comprehensive fluid-structure interaction model of the left coronary artery. J Biomech Eng 2018. [Epub ahead of print]. doi: . 10.1115/1.4040776 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Rigatelli G, Zuin M, Galasso P, Carraro M, D'Elia K, Daniela L, Roncon L, Truyen TTTT, Nguyen T. Mechanisms of Myocardial Ischemia Inducing Sudden Cardiac Death in Athletes with Anomalous Coronary Origin from the Opposite Sinus: Insights from a computational fluid dynamic study. Cardiovasc Revasc Med 2019;20:1112-6. 10.1016/j.carrev.2019.01.031 [DOI] [PubMed] [Google Scholar]
- 24.Hanafizadeh P, Mirkhani N, Davoudi MR, Masouminia M, Sadeghy K. Non-Newtonian Blood Flow Simulation of Diastolic Phase in Bileaflet Mechanical Heart Valve Implanted in a Realistic Aortic Root Containing Coronary Arteries. Artif Organs 2016;40:E179-91. 10.1111/aor.12787 [DOI] [PubMed] [Google Scholar]
- 25.Caballero AD, Laín S. Numerical simulation of non-Newtonian blood flow dynamics in human thoracic aorta. Comput Methods Biomech Biomed Engin 2015;18:1200-16. 10.1080/10255842.2014.887698 [DOI] [PubMed] [Google Scholar]
- 26.Leng X, Scalzo F, Fong AK, Johnson M, Ip HL, Soo Y, Leung T, Liu L, Feldmann E, Wong KS, Liebeskind DS. Computational fluid dynamics of computed tomography angiography to detect the hemodynamic impact of intracranial atherosclerotic stenosis. Neurovasc Imaging 2015. doi: . 10.1186/s40809-014-0001-7 [DOI] [Google Scholar]
- 27.Bongert M, Geller M, Pennekamp W, Nicolas V. Simulation of personalised haemodynamics by various mounting positions of a prosthetic valve using computational fluid dynamics. Biomed Tech (Berl) 2019;64:147-56. 10.1515/bmt-2017-0092 [DOI] [PubMed] [Google Scholar]
- 28.Xu P, Liu X, Zhang H, Ghista D, Zhang D, Shi C, Huang W. Assessment of boundary conditions for CFD simulation in human carotid artery. Biomech Model Mechanobiol 2018;17:1581-97. 10.1007/s10237-018-1045-4 [DOI] [PubMed] [Google Scholar]
- 29.Torii R, Oshima M, Kobayashi T, Takagi K, Tezduyar TE. Fluid–structure interaction modeling of blood flow and cerebral aneurysm: Significance of artery and aneurysm shapes. Comput Methods Appl Mech Eng 2009;198:3613-21. 10.1016/j.cma.2008.08.020 [DOI] [Google Scholar]
- 30.Alishahi M, Alishahi MM, Emdad H. Numerical simulation of blood flow in a flexible stenosed abdominal real aorta. Sci Iran 2011;18:1297-305. 10.1016/j.scient.2011.11.021 [DOI] [Google Scholar]
- 31.Kivi AR, Sedaghatizadeh N, Cazzolato BS, Zander AC, Arjomandi M. Hemodynamics of a stenosed aortic valve: effects of the geometry of the sinuses and the positions of the coronary ostia. Int J Mech Sci 2020;188:106015. 10.1016/j.ijmecsci.2020.106015 [DOI] [Google Scholar]
- 32.Kivi AR, Sedaghatizadeh N, Cazzolato BS, Zander AC, Roberts-Thomson R, Nelson AJ, Arjomandi M. Fluid structure interaction modelling of aortic valve stenosis: Effects of valve calcification on coronary artery flow and aortic root hemodynamics. Comput Methods Programs Biomed 2020;196:105647. 10.1016/j.cmpb.2020.105647 [DOI] [PubMed] [Google Scholar]
- 33.Cheezum MK, Ghoshhajra B, Bittencourt MS, Hulten EA, Bhatt A, Mousavi N, Shah NR, Valente AM, Rybicki FJ, Steigner M, Hainer J, MacGillivray T, Hoffmann U, Abbara S, Di Carli MF, DeFaria Yeh D, Landzberg M, Liberthson R, Blankstein R. Anomalous origin of the coronary artery arising from the opposite sinus: prevalence and outcomes in patients undergoing coronary CTA. Eur Heart J Cardiovasc Imaging 2017;18:224-35. 10.1093/ehjci/jev323 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Tian X, Sun A, Liu X, Pu F, Deng X, Kang H, Fan Y. Influence of catheter insertion on the hemodynamic environment in coronary arteries. Med Eng Phys 2016;38:946-51. 10.1016/j.medengphy.2016.06.013 [DOI] [PubMed] [Google Scholar]
- 35.Wu J, Liu G, Huang W, Ghista DN, Wong KK. Transient blood flow in elastic coronary arteries with varying degrees of stenosis and dilatations: CFD modelling and parametric study. Comput Methods Biomech Biomed Engin 2015;18:1835-45. 10.1080/10255842.2014.976812 [DOI] [PubMed] [Google Scholar]
- 36.Bahrami S, Norouzi M. A numerical study on hemodynamics in the left coronary bifurcation with normal and hypertension conditions. Biomech Model Mechanobiol 2018;17:1785-96. 10.1007/s10237-018-1056-1 [DOI] [PubMed] [Google Scholar]
- 37.Ward RC, Yambert MW, Toedte RJ, Munro NB, Easterly CE, Difilippo EP, Stallings DC. Creating a human phantom for the virtual human program. Stud Health Technol Inform 2000;70:368-74. [PubMed] [Google Scholar]
- 38.Quanyu W, Xiaojie L, Lingjiao P, Weige T, Chunqi Q. Simulation analysis of blood flow in arteries of the human arm. Biomed Eng (Singapore) 2017;29:1750031. 10.4015/S1016237217500314 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Wiwatanapataphee B, Wu YH, Siriapisith T, Nuntadilok B. Effect of branchings on blood flow in the system of human coronary arteries. Math Biosci Eng 2012;9:199-214. 10.3934/mbe.2012.9.199 [DOI] [PubMed] [Google Scholar]
- 40.Poynter JA, Williams WG, McIntyre S, Brothers JA, Jacobs ML, Congenital Heart Surgeons Society AAOCA Working Group . Anomalous aortic origin of a coronary artery: a report from the Congenital Heart Surgeons Society Registry. World J Pediatr Congenit Heart Surg 2014;5:22-30. 10.1177/2150135113516984 [DOI] [PubMed] [Google Scholar]
- 41.Singhi AK, Bari EA, Banerjee S. Anomalous origin of right coronary artery causing myocardial ischemia in a young patient. Ann Pediatr Cardiol 2017;10:212-4. 10.4103/apc.APC_151_16 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Driesen BW, Warmerdam EG, Sieswerda GT, Schoof PH, Meijboom FJ, Haas F, Stella PR, Kraaijeveld AO, Evens FCM, Doevendans PAFM, Krings GJ, van Dijk APJ, Voskuil M. Anomalous coronary artery originating from the opposite sinus of Valsalva (ACAOS), fractional flow reserve- and intravascular ultrasound-guided management in adult patients. Catheter Cardiovasc Interv 2018;92:68-75. 10.1002/ccd.27578 [DOI] [PubMed] [Google Scholar]
- 43.Cubero A, Crespo A, Hamzeh G, Cortes A, Rivas D, Aramendi JI. Anomalous Origin of Right Coronary Artery from Left Coronary Sinus-13 Cases Treated With the Reimplantation Technique. World J Pediatr Congenit Heart Surg 2017;8:315-20. 10.1177/2150135116688172 [DOI] [PubMed] [Google Scholar]
- 44.Ashrafpoor G, Danchin N, Houyel L, Ramadan R, Belli E, Paul JF. Anatomical criteria of malignancy by computed tomography angiography in patients with anomalous coronary arteries with an interarterial course. Eur Radiol 2015;25:760-6. 10.1007/s00330-014-3454-9 [DOI] [PubMed] [Google Scholar]
- 45.Kamangar S, Badruddin IA, Badarudin A, Nik-Ghazali N, Govindaraju K, Salman Ahmed NJ, Yunus Khan TM. Influence of stenosis on hemodynamic parameters in the realistic left coronary artery under hyperemic conditions. Comput Methods Biomech Biomed Engin 2017;20:365-72. 10.1080/10255842.2016.1233402 [DOI] [PubMed] [Google Scholar]
- 46.Caruso MV, De Rosa S, Indolfi C, Fragomeni G. Computational analysis of stenosis geometry effects on right coronary hemodynamics. Annu Int Conf IEEE Eng Med Biol Soc 2015;2015:981-4. 10.1109/EMBC.2015.7318528 [DOI] [PubMed] [Google Scholar]
- 47.van de Hoef TP, Nolte F, Rolandi MC, Piek JJ, van den Wijngaard JP, Spaan JA, Siebes M. Coronary pressure-flow relations as basis for the understanding of coronary physiology. J Mol Cell Cardiol 2012;52:786-93. 10.1016/j.yjmcc.2011.07.025 [DOI] [PubMed] [Google Scholar]
- 48.Zhang B, Gu J, Qian M, Niu L, Ghista D. Study of correlation between wall shear stress and elasticity in atherosclerotic carotid arteries. Biomed Eng Online 2018;17:5. 10.1186/s12938-017-0431-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Soulis JV, Farmakis TM, Giannoglou GD, Louridas GE. Wall shear stress in normal left coronary artery tree. J Biomech 2006;39:742-9. 10.1016/j.jbiomech.2004.12.026 [DOI] [PubMed] [Google Scholar]