Thermochemical Properties and Growth Mechanism of the Ag-Doped Germanium Clusters, AgGe_n^λ with n = 1–13 and λ = −1, 0, and +1

Abstract

A systematic investigation of the silver-doped germanium clusters AgGe_n with n = 1–13 in the neutral, anionic, and cationic states is performed using the unbiased global search technique combined with a double-density functional scheme. The lowest-energy minima of the clusters are identified based on calculated energies and measured photoelectron spectra (PES). Total atomization energies and thermochemical properties such as electron affinity (EA), ionization potential (IP), binding energy, hardness, and highest occupied molecular orbital-lowest unoccupied molecular orbital (HOMO-LUMO) gap are obtained and compared with those of pure germanium clusters. For neutral and anionic clusters, although the most stable structures are inconsistent when n = 7–10, their structure patterns have an exohedral structure except for n = 12, which is a highly symmetrical endohedral configuration. For the cationic state, the most stable structures are attaching structures (in which an Ag atom is adsorbed on the Ge_n cluster or a Ge atom is adsorbed on the AgGe_n–1 cluster) at n = 1–12, and when n = 13, the cage configuration is formed. The analyses of binding energy indicate that doping of an Ag atom into the neutral and charged Ge_n clusters decreases their stability. The theoretical EAs of AgGe_n clusters agree with the experimental values. The IP of neutral Ge_n clusters is decreasing when doped with an Ag atom. The chemical activity of AgGe_n is analyzed through HOMO-LUMO gaps and hardness, and the variant trend of both versus cluster size is slightly different. The accuracy of the theoretical analyses in this paper is demonstrated successfully by the agreement between simulated and experimental results such as PES, IP, EA, and binding energy.

1. Introduction

With the rapid development of nanotechnology, the research on the geometric configuration and electronic properties of clusters has become more important because clusters play a pivotal role in the transition from the molecule to the condensed phase, especially for semiconductor clusters owing to their interesting chemical structures and bonding motifs, as well as their importance in the microelectronics industry.¹⁻¹⁵ However, pure semiconductor clusters such as germanium clusters are unstable because they show only sp³ bonding characteristics.¹⁶⁻²⁰ Recently, a lot of experimental and theoretical research studies have elucidated that introducing a transition metal atom into germanium clusters can not only heighten their stability, but also deeply affect their electron properties.²¹⁻⁵⁰ Studying the structure and growth model of different transition metal (TM)-doped germanium clusters can not only find a stable cage configuration that can be used as a nanomaterial structure, but also lay a foundation for their special physical and chemical properties. To understand how these attractive physical–chemical properties attribute to the doped clusters, it is important to gain the comprehensive knowledge of the ground state and lower-lying electronic and geometric configurations of charged and neutral TM-doped Ge clusters. Therefore, Nakajima and his colleagues have first explored the electronic and geometric configurations of TMGe_n (TM = Sc, Y, Ti, Zr, Hf, V, Nb, Ta, and Lu; n = 8–20) clusters by means of dissecting their mass spectra, photoelectron spectra (PES), and reactivities to H₂O adsorption.²¹ Then Zheng and co-workers reported the electron affinities (EAs) and the electronic structures of TM_xGe_n (TM = Ag, Au, Ti, V, Co, Fe, and Cr; x ≤ 2; n ≤ 14) through recording and analyzing their PES.²²⁻³¹ Prompted by the experimental observations, some theoretical calculations and simulations of TM-doped germanium clusters have been carried out. For instance, the geometries and electronic structures of small sized clusters TiGe₂^–/0, VGe₃^–/0, CrGe_n^0/+ (n = 1–5), NbGe_n^–/0/+ (n = 1–3), and VGe_n^–/0 (n = 5–7) have been investigated through multiconfigurational methods.³²⁻³⁶ Wang et al. explored the structural evolution, stability, and electronic properties of MnGe_n (n = 2–15) by means of the Perdew–Burke–Ernzerhof (PBE) functional and found that the threshold size for the formation of caged MnGe_n and the sealed Mn-encapsulated Ge_n motif is n = 9 and 10, respectively.³⁷ Kapila et al. investigated the ground-state structures and magnetic moments of CrGe_n (n = 1–13) using the PBE functional and found that the magnetic moment in their ground-state structure is either 4 μB or 6 μB.³⁸ Bandyopadhyay and co-workers studied the evolution of configuration, electronic properties, and stability of positively charged and neutral TMGe_n clusters (TM = Mo, Nb, Ni, Sc, Ti, V, Zr, Hf, Cu, and Au; n ≤ 20) using B3LYP or B3PW91 density functional theory (DFT) and presented that the size of the smallest TM-encapsulated into Ge_n configurations was n = 8 for Nb, n = 9 for Zr, Ti, Hf, and Cu, n = 10 for Mo, and n = 11 for Au atoms.³⁹⁻⁴⁵ Rabilloud and co-workers explored the configurations, electronic properties, and magnetic moments of TMGe_n (TM = V, Nb, Ta, Pd, Pt, Cu, Ag, and Au; n ≤ 21) species using the PBE functional and reported that the smallest size of the TM-encapsulated to Ge_n cage was n = 10 for Cu and V and n = 12 for Au and Ag.¹⁷⁻²⁰ It is stated that the smallest size of the CuGe_n cluster evaluated using the PBE functional differs from that evaluated using the B3PW91 functional. For negatively charged ions, Borshch et al. evaluated the ground-state structures of TMGe_n^– (TM = Sc, Zr, Hf, Nb, and Ta; n ≤ 20), simulated their PES by employing the B3LYP functional, and found that the smallest size of TM@Ge_n^– was n = 12 for Zr, Nb, Hf, and Ta, but n = 13 for Sc atoms.⁴⁶⁻⁵⁰ Kumar and co-workers studied the equilibrium geometry and electronic structure of ZrGe_n^–/0 (n = 1–21) with the PW91 functional, compared their simulated PES with experimental ones, and found that in some cases a higher energy configuration of ZrGe_n^– species may be present in experiments, but the neutral of such an anion is often the lowest energy isomer.⁵¹ Trivedi et al. explored the structural stability and electronic and vibrational properties of M@Xn (M = Ag, Au, Co, Pd, Tc, and Zr; X = Ge and Si; n = 10, 12, and 14) with the B3LYP scheme.^52,53 Despite performing many theoretical studies on the structural evolution and electronic properties of TM-doped germanium clusters,^{17−20,32−54} this work, according to our knowledge, is the first systematic study of charged Ag-doped germanium clusters. Moreover, the lowest-energy structures for neutral AgGe_n with n = 7, 9, 10, 11, and 13 calculated in this study differ from those reported previously.¹⁹ In this work, an artificial bee colony algorithm for cluster global optimization (ABCluster)⁵⁵⁻⁵⁷ combined with a double-hybrid density functional is employed for the structure optimization of charged and neutral Ag-doped germanium clusters, AgGe_n^λ (n = 1–13; λ = −1, 0, and +1), with the goal of probing the structural evolution and stability, evaluating thermochemical parameters and electronic properties, and comparing them with charged and neutral pure Ge clusters Ge_n + 1^λ (n = 1–13; λ = −1, 0, and +1), respectively.

2. Computational Methods

The initial isomers for AgGe_n^λ (n = 1–13; λ = −1, 0, and +1) species were based on the ABCluster⁵⁵⁻⁵⁷ combined with the Gaussian 09 codes.⁵⁸ More than 400 isomers for each cluster were first optimized using the PBE0 functional⁵⁹ with the effective core potential LanL2DZ basis set⁶⁰ for Ge atoms and the cc-pVDZ-PP basis set⁶¹ for Ag atoms. Then, the lower-lying configurations were selected and reoptimized via the PBE0 functional and cc-pVTZ-PP basis set^61,62 for Ge and Ag atoms. Harmonic vibrational frequency calculations were carried out at the same level to guarantee that the configurations were true local minimal structures on the potential energy surface. After completing the initial geometrical optimization using the PBE0/cc-pVTZ-PP scheme, once again, we selected the lower-lying candidates and reoptimized them at the mPW2PLYP/cc-pVTZ-PP level⁶³ without frequency calculations. Finally, single-point energy calculations were carried out using the mPW2PLYP functional in conjunction with the aug-cc-pVTZ-PP basis set⁶¹ for Ag atoms and the all-electron aug-cc-pVTZ basis set⁶⁴ for Ge atoms to further refine the energy. At the mPW2PLYP/aug-cc-pVTZ-PP//mPW2PLYP/cc-pVTZ-PP level, the single-point energy calculations were also performed for comparison.

To check the quality of our used scheme, test calculations were previously performed using the ROCCSD(T) method for ScSi_n^0/– (n = 4–9) clusters and compared with several DFT functionals (PBE, B3LYP, TPSSh, wB97X, and mPW2PLYP).⁶⁵ The results revealed that (i) only the ground-state structure of ScSi_n^0/– (n = 4–9) clusters predicted by the mPW2PLYP functional is consistent with that calculated by the ROCCSD(T) scheme and (ii) the evaluated vertical detachment energy (VDE) by ROCCSD(T) and mPW2PLYP schemes is in good agreement with the experimental data. The mean absolute deviations of VDE from the experiment for ScSi_n (n = 4–7 and 9) are by 0.08, 0.09, 0.13, 0.19, and 0.21 eV at the ROCCSD(T), mPW2PLYP, B3LYP, TPSSh, and PBE levels, respectively. Further to check the quality of the mPW2PLYP scheme, the bond length and frequency of Ge₂ and AgGe dimers were measured using several DFT functionals (PBE0, TPSSh, B3LYP, and mPW2PLYP) combined with cc-pVTZ-PP basis sets for Ge and Ag atoms and are listed in Table 1. The bond length of Ge₂ and AgGe calculated using the mPW2PLYP scheme is 2.38 and 2.45 Å, which agrees with the experimental values of 2.368¹⁵ and 2.54 Å,⁶⁶ respectively. The frequency of Ge₂ evaluated using the mPW2PLYP scheme is 286.3 cm^–1, which is in excellent agreement with the experimental value of 287.9 cm^-1.¹⁵ The bond distance of 2.34 Å for Au-Ge predicted by the mPW2PLYP scheme is in good agreement with the experimental value of 2.38 Å.⁶⁷ Furthermore, the ABCluster’s developers presented many successful examples of ABCluster in a recent article.⁵⁷ It is proven to be a successful technique for searching the global minimal structure of atomic and molecular clusters to solve the realistic chemical problems.⁵⁷ Therefore, we believe that the results evaluated using the ABCluster global search technique and the mPW2PLYP functional should be reliable.

Table 1. Bond Length (Å) and Frequency (cm^–1) of Ge₂ and AgGe Dimers Calculated by Different Functionals Combined with the cc-pVTZ-PP Basis Set for Ge and Ag Atoms.

	Ge2		AgGe
	bond length	frequency	bond length	frequency
PBE0	2.38	290.72	2.45	203.34
TPSSh	2.39	280.94	2.44	210.83
mPW2PLYP	2.38	286.29	2.45	201.89
B3LYP	2.41	275.20	2.47	196.41
Expt.	2.368a	287.9a	2.54b

^aref (15).

^bref (66).

3. Results and Discussion

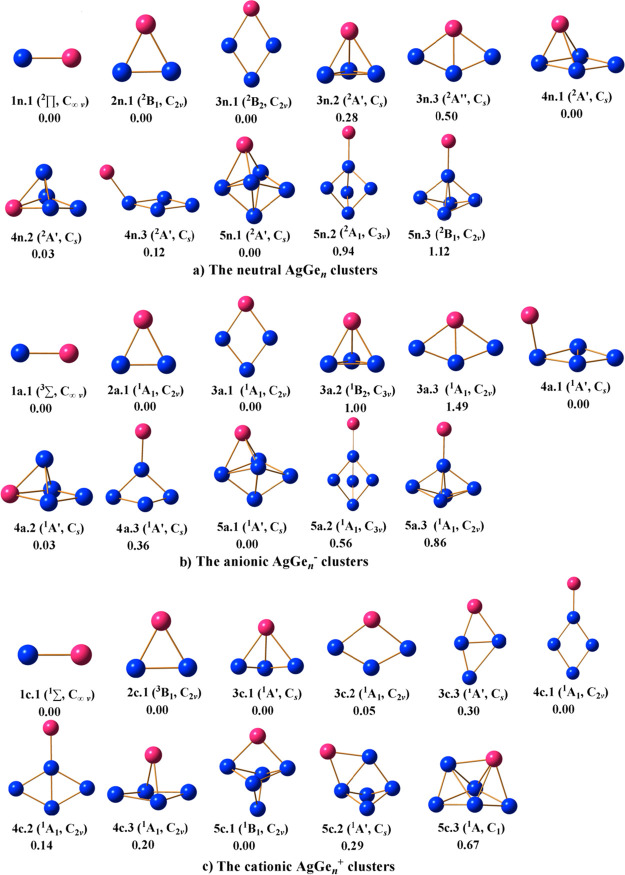
The structures of the optimized geometries of the neutral AgGe_n, cationic AgGe_n⁺, and anionic AgGe_n^– systems, their relative energies, the electronic states, and symmetries are shown in Figures 1–4. For the neutral AgGe_n (n = 1–13), all the ground states are evaluated to be a doublet; For the cationic state, its lower-lying isomers are calculated to be single except AgGe₂⁺, which is simulated to be a triplet; for the anionic state, the ground state is also simulated to be single except AgGe^–, which is simulated to be a triplet.

Figure 1.

Shapes, electron states, and relative energies (ΔE, eV) of the lower-lying isomers AgGe_n with n = 1–5 at (a) neutral, (b) anionic, and (c) cationic states.

Figure 4.

Shapes, electron states, and relative energies (ΔE, eV) of the lower-lying isomers of (a) AgGe₁₂ and (b) AgGe₁₃.

Figure 2.

Shapes, electron states, and relative energies (ΔE, eV) of the lower-lying isomers AgGe_n with n = 6–8 at (a) neutral, (b) anionic, and (c) cationic states.

Figure 3.

Shapes, electron states, and relative energies (ΔE, eV) of the lower-lying isomers AgGe_n with n = 9–11 at (a) neutral, (b) anionic, and (c) cationic states.

3.1. Lower-Lying Isomers of AgGe_n Clusters and Their Growth Mechanism

From Figures 1–4, it can be seen that the lowest structure and some of its isomers for neutral and charged AgGe_n (n = 1–13) are carefully selected. Isomers are denoted as nX.Y in which n is the size of Ge_n, X = n, c, and a stand for a neutral, cation, and anion, respectively, and Y = 1, 2, 3...is arranged in an ascending energy order of the isomers.

n = 1: AgGe, AgGe⁺, and AgGe^–. For AgGe, the ground state 1n.1 is characterized by the ²∏ electron state with [1σ²2σ²1π⁴1δ²2δ²3σ²2π¹] valence electronic configuration in which a bond distance of 2.453 Å is in good agreement with the experimental value of 2.54 Å.⁶⁵ After attaching an electron, the high spin state ³∑: [1σ²2σ²1π⁴1δ²2δ²3σ²2π²] is calculated to be the ground state of AgGe^– (1a.1). Following the detachment of one electron, the close shell electronic state ¹∑: [1σ²2σ²1π⁴1δ²2δ²3σ²] becomes the ground state of AgGe⁺ (1c.1). The bond lengths of 1a.1 and 1c.1 are calculated to be 2.465 and 2.452 Å, showing that gaining or losing an electron has little effect on the bond length of AgGe.

n = 2: AgGe₂, AgGe₂⁺, and AgGe₂^–. A triangular structure 2n.1 with C_2v symmetry is found for AgGe₂ in which the Ag atom connects with two Ge atoms. For the charged species, the structures of AgGe₂^– and AgGe₂⁺ are almost unchanged. The anion AgGe₂^– exhibits the C_2v (¹A₁) structure 2a.1 with a closed shell electronic configuration, and cation AgGe₂⁺ is found to be the ³B₁ electron state 2c.1 with C_2v symmetry.

n = 3: AgGe₃, AgGe₃⁺, and AgGe₃^–. For AgGe₃, the C_2v symmetry planar rhombus of the ²A₁ electronic state is predicted to be the ground state (3n.1). The isomer 3n.2 in the C_s point group with an ²A′ electronic state can be viewed as attaching an Ag atom to the face of the most stable Ge₃ structure,² which is less stable by 0.28 eV in energy than 3n.1. Following attachment of one electron to form the anionic species, the ground state (3a.1) shape of AgGe₃^– remains unchanged. In the cationic state, the lowest-energy structure of AgGe₃⁺ is a three-dimensional structure 3c.1 (C_s,¹A′), which corresponds to the neutral structure 3n.2. Isomer 3c.2 (C_2v,¹A₁) has a planar shape, which can be viewed as one Ge atom capped in the edge of 2c.1. Interestingly, the 3c.2 in energy is only less stable than the 3c.1 by 0.05 eV, which means that they compete for the ground state of AgGe₃⁺.

n = 4: AgGe₄, AgGe₄⁺, and AgGe₄^–. For AgGe₄, isomer 4n.1 and 4n.2 both have the C_s symmetry and ²A′ electronic state. Isomer 4n.1 can be considered as attaching an Ag atom to the face of the most stable Ge₄ structure,² and isomer 4n.2 can be considered as attaching a Ge atom to the face of the most stable AgGe₃ structure. Isomer 4n.1 is the lowest-energy isomer, being only 0.03 eV lower than 4n.2, which means both of them compete for the ground state. In the anionic state, the energy of isomer 4a.1 and 4a.2 is also degenerate with an energy gap of 0.03 eV, meaning that the potential energy surface of AgGe₄ is relatively shallow. The analysis of simulated PES (see below) indicates that both can coexist in laboratory. The structures of isomer 4a.1 and 4a.2 are both C_s symmetry and ¹A′ electronic state. For the cationic state, the C_2v symmetry plane geometry of the ¹A₁ electronic state is predicted to be the ground state (4c.1) in which an Ag atom attached on the top of the most stable rhombus Ge₄ structure.²

n = 5: AgGe₅, AgGe₅⁺, and AgGe₅^–. The AgGe₅ neutral exhibits a C_s symmetry ground state 5n.1, which can be regarded as an Ag atom capping one face of the most stable Ge_5.² After getting one extra electron, the geometry of the corresponding anion has no significant changes. The ground state 5a.1 with C_s symmetry is more stable in energy than that of isomer 5a.2 and 5a.3 by 0.56 and 0.86 eV, respectively. For the cationic state, the most stable geometry 5c.1 of AgGe₅⁺ has the C_2v symmetry with the ¹B₁ electronic state, which corresponds to the 5n.1.

n = 6: AgGe₆, AgGe₆⁺, and AgGe₆^–. AgGe₆ has a C_s (²A′) lowest-energy structure 6n.1, which can be regarded as attaching an Ag atom to the face of the ground state tetragonal bipyramid Ge_6.² The lowest stable geometries of the anion AgGe₆^– (6a.1) and cation AgGe₆⁺ (6c.1) are almost unchanged as compared to the neutral structure of 6n.1. Interestingly, the degenerate equilibrium ground states are both found in the anionic and cationic state. Energetically, isomer 6a.2 is only less stable than 6a.1 by 0.02 eV for anion AgGe₆^–, and isomer 6c.2 also is only less stable than 6c.1 by 0.06 eV for cation AgGe₆⁺. Isomer 6a.2 and 6c.2 both can be regarded as attaching an Ag atom to the edge and the top of the most stable Ge₆ structure.² The analysis of simulated PES (see below) indicates that the 6a.1 configuration is the ground-state structure.

n = 7: AgGe₇, AgGe₇⁺, and AgGe₇^–. For AgGe₇, the structure of the ground state 7n.1 (C_2v, ²B₁) and isomer 7n.2 (C_5v,²A₁) is 0.22 eV higher in energy as compared to 7n.1, and both can be considered as an Ag atom capping on the edge and the apex of Ge₇pentagonal bipyramid,² respectively. The isomer 7n.4, which is considered the most stable structure in ref (19)., is 0.45 eV higher in energy than 7n.1. Following attachment of one electron, the C_5v symmetry structure 7a.1, which corresponds to the neutral 7n.2, acts as the ground state for AgGe₇^–. For the cationic state, the geometry of the best isomer for AgGe₇⁺ is the same as that of the neutral 7n.1. The C_2v symmetry state 7c.1 (¹A₁) is more stable in energy than that of isomer 7c.2 and 7c.3 by 0.50 and 0.85 eV, respectively.

n = 8: AgGe₈, AgGe₈⁺, and AgGe₈^–. The best isomer of neutral AgGe₈ (8n.1) with C_s symmetry and ²A″ electronic state can be seen as attaching an Ag atom to the face of the capped pentagonal bipyramid Ge_8.² The next isomer 8n.2 (C_s,²A′), being 0.16 eV less stable than 8n.1, can be viewed as a distorted Ge₈quadrangular prism with a capped Ag atom on one face. Two other isomers 8n.3 (C₁,²A) and 8n.4 (C_s,²A′), which are both formed by adding one Ge atom into the pentagonal bipyramid Ge₇ and then attaching one Ag atom, are 0.19 and 0.46 eV less stable, respectively, in energy than 8n.1. For anion AgGe₈^–, the isomer 8a.1 (C_s,¹A′), corresponding to neutral 8n.1, is only 0.06 eV lower in energy than 8a.2 (corresponds to the neutral 8n.2). Although isomer 8a.1 has the lowest energy, we consider that 8a.2 is the best candidate for the ground-state structure through the comparison of the calculated and experimental PES (see below). In the cationic state, the C_s symmetry and ¹A″ electronic state 8c.1, which corresponds to neutral 8n.3, is calculated as the lowest-energy structure of AgGe₈⁺. The next isomer 8c.2 (C₁,¹A), which is a distorted form of 8n.1, is less stable in energy than the 8c.1 by 0.22 eV.

n = 9: AgGe₉, AgGe₉⁺, and AgGe₉^–. For the neutral AgGe₉, two degenerate structures, 9n.1 (C₁,²A) and 9n.2 (C_s,²A′), are found within an energy gap of 0.04 eV. Isomer 9n.1 is formed by adding one Ge atom on the face of the most stable structure AgGe₈. Isomer 9n.2 also can be viewed as attaching an Ag atom to the tricapped trigonal prism Ge_9.² The isomer 9n.3, which is reported as the most stable structure in ref (19)., is 0.37 eV higher in energy than 9n.1. For the anion, the geometries of the ground state 9a.1 for AgGe₉^– have the same structures corresponding to neutral 9n.2. The best isomer 9a.1 (C_s,¹A′) is 0.30 eV lower in energy than the isomer 9a.4 (corresponding to neutral 9n.1). In the cationic state, the most stable structure 9c.1 (C_s,¹A′), which is formed by adding an Ag atom on the edge of the most stable structure Ge9,² is 0.16 eV more stable in energy than the isomer 9c.4 (corresponding to neutral 9n.1).

n = 10: AgGe₁₀, AgGe₁₀⁺, and AgGe₁₀^–. The C_3v symmetry structure of the ²A₁ electronic state is predicted to be the ground state (10n.1) for AgGe₁₀. It is formed by either adding one Ge atom into the face of structure 9n.2 or adsorbing an Ag atom on the face of the tetracapped trigonal prism Ge_10.² The isomer 10n.3, which is predicted to be the most stable structure in ref (19)., is 0.41 eV higher in energy than 10n.1. In the anionic state, the most stable structure 10a.1 with C_s symmetry and ¹A′ electronic state is formed by adding an Ag atom on the face of bicapped tetragonal antiprism Ge₁₀. The isomer 10a.2 with C_4v symmetry and ¹A₁ electronic state can be formed by attaching an Ag atom on the vertex of the bicapped tetragonal antiprism Ge₁₀. It is only less stable than 10a.1 by 0.06 eV in energy. Simulated PES analysis shows that both isomers can exist (see below). For cationic clusters, the ground-state isomer 10c.1 with C_s symmetry (¹A′) can also be derived by adding an Ag atom on a different face of the tetracapped trigonal prism Ge₁₀.

n = 11: AgGe₁₁, AgGe₁₁⁺, and AgGe₁₁^–. For AgGe₁₁, the C₁ structure 11n.1, which can be viewed as distorted by a substitution of an Ag atom for a Ge atom of icosahedral-like Ge₁₂, is found to be the global minima of the cluster. The isomer 11n.2 with C_2v symmetry (²A₁), which is reported as the most stable structure in ref (19)., is 0.19 eV higher in energy than 11n.1. Isomer 11n.3 with C_2v symmetry (²A₁) is an Ag-encapsulated into Ge₁₁ cage, being 0.33 eV higher in energy than 11n.1. Following the attachment of one electron, the most stable structure 11a.1, corresponding to neutral 11n.1, has the C₁ symmetry and ¹A electronic state. The cage structure 11a.4 (C_2v,¹A₁) is less stable in energy than 11a.1 by 0.79 eV. For the cationic state, the ground state 11c.1 of AgGe₁₁⁺ is formed by attaching the additional Ge atom on the face of 10c.1. The structure 11c.2, which is a slightly distorted form of neutral cage structure 11n.3, is less stable in energy than 11c.1 by 0.34 eV.

n = 12: AgGe₁₂, AgGe₁₂⁺, and AgGe₁₂^–. The ground state 12n.1 of neutral AgGe₁₂ is an endohedral structure with D_2d symmetry in which an Ag atom is located inside a Ge₁₂ cage. The isomer 12n.3 is D_5d symmetric icosahedron-like in which an Ag atom is located inside a dicapped pentagonal antiprism cage. The isomer 12n.3 is 0.15 eV higher in energy relative to 12n.1. Following attachment of one electron, the ground state 12a.1 of AgGe₁₂^–, which corresponds to neutral 12n.3, has a high I_h (¹H_g) symmetric icosahedral structure. This structure is similar to that of the AuGe₁₂^– reported by Zheng in the series of studies on Au-doped Ge_n clusters.²⁶ For the cationic state, the geometry of the best isomer 12c.1 for AgGe₁₂⁺ is an exohedral structure with C_s symmetry and ¹A′ electronic state, which can be viewed as attaching an Ag atom to the face of hexcapped trigonal prism Ge_12.² Isomers 12c.2, 12c.3, and 12c.4 are all cage structures, being 0.38, 0.55, and 1.13 eV higher in energy than 12c.1, respectively.

n = 13: AgGe₁₃, AgGe₁₃⁺, and AgGe₁₃^–. The most stable structure 13n.1 of neutral AgGe₁₃ is not a cage configuration but an exohedral structure, which can be viewed as replacing a Ge atom of the most stable structure of Ge₁₄³ with an Ag atom. The best isomer 13n.1 with C₁ symmetry is more stable in energy than the cage structure 13n.2 and 13n.3 by 0.32 and 0.39 eV, respectively. Isomer 13n.4 also is a no-cage structure with C₁ symmetry, which is reported as the lowest-energy configuration in the literature,¹⁹ but here it is 0.54 eV higher than 13n.1. For AgGe₁₃^–, the ground state 13a.1 (corresponding to the neutral ground state 13n.1) with C_s symmetry and ¹A′ electronic state also is an exohedral structure. The isomer 13a.1 is more stable than the endohedral isomer 13a.2, 13a.3, and 13a.4 by 0.68, 0.70, and 0.82 eV, respectively. For AgGe₁₃⁺, the ground state 13c.1 with C_4v symmetry is calculated to be an endohedral structure, which is a capped fullerene-like cage. The next isomer 13c.2, which can be considered as the Ag-encapsulated into Ge₁₃ cage of the dimer-capped pentagonal-hexagonal prism, is less stable than 13c.1 by 0.06 eV energetically.

3.2. Growth Pattern

Based on the structural features of the determined global minimum structure, the growth mechanism for the clusters AgGe_n with n = 1–13 emerges as follows: For neutral clusters, the most stable forms of AgGe_n except the AgGe₁₂ definitely prefer an exohedral structure, which is formed by attaching an Ag atom to a Ge_n cluster or a Ge atom to an AgGe_n-1 cluster when n = 1–10, and when n = 13, it is formed by replacing a Ge atom of a Ge_n + 1 cluster with an Ag atom. For anionic states, although the lowest-energy structures of AgGe_n^– at n = 7–10 are different from the corresponding neutral clusters, the growth patterns of most stable structures are consistent. For cationic states, the global minimal structures of AgGe_n⁺ with n ranging from 1 to 12 are formed by attaching an Ag atom to the Ge_n cluster or a Ge atom to the AgGe_n–1 cluster, and the endohedral structure becomes the ground-state configuration when n = 13. The ground-state configurations of AgGe_n⁺ are different from the corresponding neutral ground-state structure when n = 3, 4, and 8–13.

3.3. Photoelectron Spectra

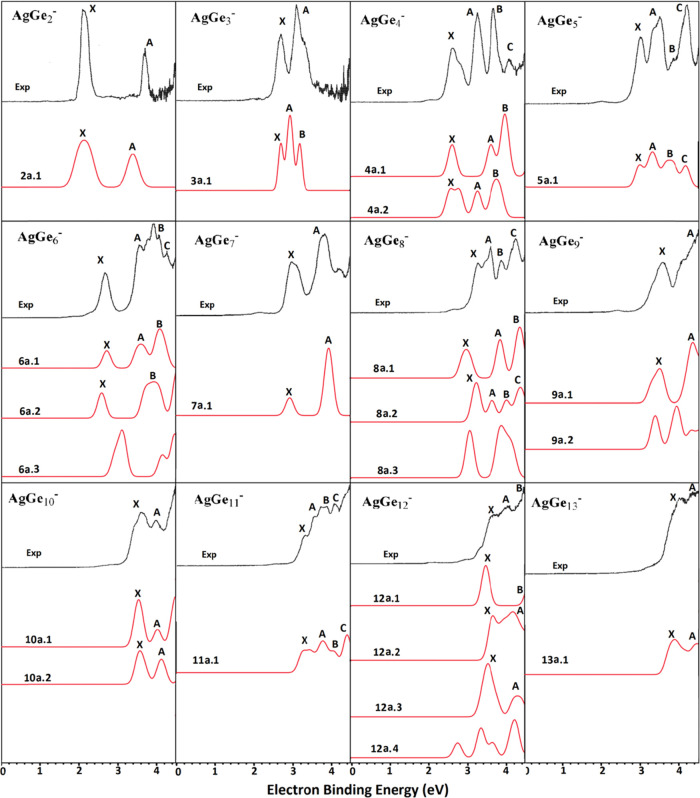
By comparing the PES obtained by theoretical calculation and experiment, it can not only verify the accuracy of the ground-state structure predicted by the theoretical calculation, but also explain the reliability of the theoretical calculation scheme. In this section, the PES of the ground-state isomers for AgGe_n^– (n = 2–13) are simulated based on the generalized Koopmans’ theorem (denoted as ΔDFT) combined with Multiwfn software⁶⁸ and compared with experimental data.²² First, the VDE which corresponds to the first peak of PES and the adiabatic electron affinity (AEA) of experiment and simulation are compared and listed in Table 2. Then, the number of other peaks and their relative locations are matched by the simulated PES and experimental one. The simulated PES of the most stable structures and experimental spectra are displayed in Figure 5.

Table 2. Theoretical and Experimental VDEs and AEAs for AgGe_n^– (n = 1–13).

	VDE		AEA
n	theor	exptla	Theor	exptla
1	1.50(1.47)		1.50(1.47)
2	2.13(2.08)	2.11 ± 0.08	2.08(2.05)	1.97 ± 0.08
3	2.71(2.65)	2.74 ± 0.08	2.55(2.51)	2.50 ± 0.08
4	2.62(2.58)	2.65 ± 0.08	2.34(2.30)	2.39 ± 0.08
5	2.98(2.93)	3.02 ± 0.08	2.62(2.58)	2.73 ± 0.08
6	2.70(2.63)	2.70 ± 0.08	2.37(2.35)	2.43 ± 0.08
7	2.93(2.87)	2.99 ± 0.08	2.45(2.37)	2.71 ± 0.08
8	3.24(3.16)	3.27 ± 0.08	2.75(2.67)	2.97 ± 0.08
9	3.47(3.40)	3.59 ± 0.08	3.07(3.02)	3.06 ± 0.08
10	3.54(3.40)	3.64 ± 0.20	2.98(2.94)	3.22 ± 0.20
11	3.32(3.27)	3.37 ± 0.20	3.05(2.99)	3.06 ± 0.20
12	3.48(3.41)	3.68 ± 0.20	3.19(3.31)	3.34 ± 0.20
13	3.86(3.74)	4.04 ± 0.20	3.56(3.48)	3.45 ± 0.20

^aFrom ref (22).; The values in parentheses are calculated at the mPW2PLYP/aug-cc-pVTZ-pp.

Figure 5.

Simulated PES spectra of the lowest-lying energy structures of AgGe_n^– (n = 2–13) clusters. Experimental PES reprinted with permission from ref (22).

As shown in Figure 5, the simulated PES of the 2a.1 have two different peaks (X and A) within ≤4.5 eV located at 2.13 and 3.39 eV, which are in concordance with the experimental data of 2.11 and 3.70 eV.²² From the PES of AgGe₃^–, it can be seen that simulated PES of the 3a.1 have three adjacent peaks (X, A, and B) located at 2.71, 2.94, and 3.19 eV. The first and third peak’s positions can be consistent with the experimental values of 2.74 and 3.13 eV. For AgGe₄^–, the simulated PES of the 4a.1 and 4a.2 have three distinct peaks (X, A, and B) situated at 2.62, 3.62, and 3.98 eV and 2.59, 3.27, and 3.76 eV, respectively. They are in concordance with the experimental data of 2.65, 3.27, and 3.68 eV, respectively. Therefore, we suggest that two energy degenerate isomers 4a.1 and 4a.2 coexist in the experiment. For the simulated PES of 5a.1, there are four peaks (X, A, B, and C) located at 2.98, 3.31, 3.74, and 4.16 eV, which is in good accordance with the experimental data of 3.02, 3.50, 3.85, and 4.22 eV,²² respectively. For AgGe₆^–, two PES are simulated. The simulated PES of the 6a.1 have three distinct peaks (X, A, and B) situated at 2.71, 3.59, and 4.08 eV, which are in excellent agreement with the experimental values of 2.70, 3.58, and 3.94 eV,²² respectively. The simulated PES of the 6a.2 have two distinct peaks (X and B) situated at 2.58 and 3.93 eV. Although they are in concordance with the experimental data of 2.70 and 3.94 eV, the number of peaks is obviously insufficient. The simulated PES of the 7a.1 have two different peaks (X and A) within ≤4.5 eV located at 2.93 and 3.93 eV, which are in concordance with the experimental data of 2.99 and 3.80 eV.²² For AgGe₈^–, there are four different peaks (X, A, B, and C) located at 3.24, 3.64, 4.02, and 4.38 eV in the simulated PES of 8a.2, which well reproduce the experimental values²² of 3.27, 3.62, 3.88, and 4.25 eV, respectively. The spectrum of isomer 8a.1 has three distinct peaks (X, A, and B) situated at 2.98, 3.86, and 4.36 eV, which can be ruled out of the most stable structure of AgGe₈^–. For AgGe₉^–, two distinct peaks located at 3.47 and 4.33 eV are obtained in the simulated PES of 9a.1, and they are in reasonable agreement with the experimental values of 3.59 and 4.38 eV.²² For AgGe₁₀^–, two distinct peaks located at 3.54 and 4.02 eV and 3.57 and 4.11 eV are obtained in the simulated PES of 10a.1 and 10a.2, respectively. They agree with the experimental values of 3.64 and 4.03 eV, respectively.²² It is to say that these two energy degenerate isomers may coexist in the experiment. Four peaks for simulated PES of 11a.1 are situated at 3.32, 3.79, 4.04, and 4.41 eV, which are in excellent agreement with the experimental data of 3.37, 3.61, 3.90, and 4.15 eV,²² respectively. Although Kong²² pointed out that the peak shape of experimental PES of AgGe₁₂^– was wide and it was difficult to observe a clear peak because of the overlap of energy levels, three peaks (X, A, and B) can be roughly assigned to 3.68, 4.11, and 4.50 eV. It is interesting that the simulated PES of 12a.1 have two resolved peaks (X and B) centered at 3.48 and 4.61 eV, which is in good accordance with the experimental data of 3.68 (X) and 4.50 (B) eV,²² while the simulated PES of 12a.2 and 12a.3 also have two distinct peaks (X and A) situated at 3.67 and 4.18 eV and 3.54 and 4.30 eV, respectively. They are in concordance with the experimental data of 3.68 (X) and 4.11 (A) eV, respectively. In this case, one cannot determine which isomer is the ground-state structure. Therefore, we highly suggest that the experimental PES of AgGe₁₂^– should be further examined. The simulated PES of 13a.1 have two major features centered at 3.86 and 4.45 eV, which are in reasonable agreement with the experimental values of 4.04 and 4.38 eV.²²

3.4. EAs and IP

From Table 2, it can be concluded that the first theoretical VDEs of AgGe_n^– (n = 2–13) show a good agreement with available experimental values.²² The average absolute deviation of them is 0.07 (0.14) eV (the value in parentheses is calculated at the mPW2PLYP/aug-cc-pVTZ-PP//mPW2PLYP/cc-pVTZ-PP level). The largest deviation is 0.20 eV for AgGe₁₂, which is within experimental errors of 0.20 eV. For the AEAs, the quantitative analysis suggests that the mean absolute deviation of simulated of AgGe_n (n = 2–13) from the experimental data is 0.11 (0.12) eV. The largest error is AgGe₇ and AgGe₁₀, which is off by 0.26 and 0.24 eV, respectively. The reason may be that their experimental PES exhibit a featureless long and very rounded tail, which means that it is difficult to determine the exact AEA value. If AgGe₇ and AgGe₁₀ are removed, the average absolute deviations are only 0.09 eV. All these show that our theoretical method is reliable and once again confirms that the ground-state configurations in this paper are accurate.

Vertical ionization potential (VIP) and adiabatic ionization potential (AIP), as important chemical and physical quantities, are discussed in this section. The VIP [defined as the difference of total energies as follows: VIP = E(cation at optimized neutral geometry) – E(optimized neutral)] and AIP [defined as the difference of total energies in following manner: VIP = E(optimized cation) – E(optimized neutral)] of neutral AgGe_n cluster and pure Ge_n + 1 clusters are calculated and listed in Table 3. No experimental IP of AgGe_n is available for comparison. Therefore, we compared the IP of AgGe_n with that of pure Ge_n clusters as shown in Figure 6. From Figure 6, it can be found that (i) The IP with two different types of VIP and AIP for AgGe_n clusters is lower than that of pure Ge_n + 1 clusters, respectively, meaning that doping an Ag atom in neutral Ge_n clusters will decrease their IP. (ii) For AgGe_n (n = 1–13) clusters, the highest VIP and AIP values are calculated to be 7.71 eV for AgGe₃ and 7.07 eV for AgGe₂, respectively. AgGe₇ and AgGe₁₀ present the minimum values of VIP and AIP by 5.91 and 5.68 eV, respectively. (iii) For Ge_n + 1 (n = 1–13) clusters, the calculated values of VIP are in good agreement with the experimental data,⁵ and their average absolute deviation is only 0.08 (0.09) eV.

Table 3. VIP and AIP of AgGe_n and Ge_n + 1 (n = 1–13) Clusters.

cluster	VIP (eV)	AIP (eV)	Cluster	VIP (eV)	expt. of VIP	AIP (eV)
AgGe	7.05 (7.02)	7.05 (7.02)	Ge2	7.57 (7.52)	7.58–7.76 (7.67)a	7.57 (7.51)
AgGe2	7.07 (7.03)	7.07 (7.03)	Ge3	8.01 (7.96)	7.97–8.09 (8.03)a	7.92 (7.87)
AgGe3	7.71 (7.67)	6.89 (6.84)	Ge4	7.80 (7.76)	7.87–7.97 (7.92)a	7.53 (7.48)
AgGe4	6.70 (6.64)	6.33 (6.32)	Ge5	7.96 (7.91)	7.87–7.97 (7.92)a	7.79 (7.75)
AgGe5	7.17 (7.11)	6.61 (6.54)	Ge6	7.76 (7.72)	7.58–7.76 (7.67)a	7.36 (7.33)
AgGe6	6.63 (6.57)	6.25 (6.23)	Ge7	7.89 (7.84)	7.58–7.76 (7.67)a	7.55 (7.51)
AgGe7	5.91 (5.88)	5.70 (5.67)	Ge8	7.01 (6.94)	6.72–6.94 (6.83)a	6.61 (6.53)
AgGe8	6.64 (6.54)	6.17 (6.09)	Ge9	7.20 (7.09)	7.06–7.24 (7.15)a	7..1 (6.94)
AgGe9	6.42 (6.34)	6.05 (5.94)	Ge10	7.55 (7.45)	7.46–7.76 (7.61)a	7.38 (7.31)
AgGe10	6.24 (6.17)	5.68 (5.60)	Ge11	6.59 (6.53)	6.55–6.72 (6.64)a	6.34 (6.28)
AgGe11	6.46 (6.39)	5.86 (5.81)	Ge12	7.10 (7.00)	6.94–7.06 (7.00)a	6.88 (6.83)
AgGe12	6.13 (6.82)	5.67 (5.81)	Ge13	7.03 (6.97)	6.94–7.06 (7.00)a	6.82 (6.71)
AgGe13	6.74 (6.65)	6.06 (5.92)	Ge14	7.14 (7.08)	7.06–7.24 (7.15)a	6.86 (6.82)

^aThe data taken from ref (5). and in parentheses are average values; the values in parentheses are calculated at the mPW2PLYP/aug-cc-pVTZ-pp level.

Figure 6.

IP of the ground-state structure of AgGe_n and Ge_n + 1 (n = 1–13) clusters.

3.5. Binding Energy and Relative Stability

The relative stabilities of the most stable structures of AgGe_n^λ (λ = −1, 0, and +1; n = 1–13) clusters are examined in terms of both binding energy per atom (E_b) and second-order difference in energy (Δ²E). E_b(AgGe_n^λ) and Δ²E(AgGe_n^λ) are defined as the following reactions:

1

2

3

4

Where E(Ag), E(Ge), E(Ge⁺), and E(Ge^–) are the total energies of the Ag atom, Ge atom and the charged Ge⁺ and Ge^–, respectively. E(AgGe_n), E(AgGe_n⁺), and E(AgGe_n^–) are the total energies of the cluster AgGe_n at neutral, cationic, and anionic states, respectively. To understand how the Ag dopant influences the stability of pure Ge_n clusters, the E_b and Δ²E of Ge_n + 1^λ (λ = −1, 0, and +1; n = 1–13) are further examined and are defined as follows:

5

6

Where E(Ge_n^λ) are the total energies of neutral, cationic, and anionic Ge_n clusters, respectively. These total energies are calculated through the mPW2PLYP scheme combined with the aug-cc-pVTZ basis set for the most stable structures of neutral and charged Ge_n clusters reported in previous studies.^2,3,9,67 The E_b values are listed in Table 4, and the plots are shown in Figures 7 and 8. The plots of Δ²E are given in Figure 9.

Table 4. Average Binding Energies (E_b, eV) of AgGe_n^λ and Ge_n + 1^λ (λ = −1, 0, and +1; n = 1–13) Clusters^a.

	Eb
n	AgGen–	AgGen	AgGen+	Gen + 1–	Gen + 1	Gen + 1+
1	1.00 (1.00)	0.87 (0.87)	1.26 (1.25)	1.79 (1.77)	1.44 (1.42)	1.57 (1.56)
2	2.00 (1.98)	1.72 (1.70)	1.97 (1.95)	2.44 (2.41)	2.14 (2.12)	2.11 (2.09)
3	2.42 (2.40)	2.09 (2.07)	2.33 (2.31)	2.79 (2.76)	2.63 (2.61)	2.71 (2.68)
4	2.57 (2.55)	2.35 (2.33)	2.65 (2.62)	3.02 (2.99)	2.82 (2.80)	2.83 (2.80)
5	2.88 (2.86)	2.66 (2.63)	2.86 (2.84)	3.11 (3.08)	3.00 (2.98)	3.08 (3.05)
6	2.91 (2.88)	2.75 (2.72)	2.97 (2.94)	3.20 (3.17)	3.11 (3.09)	3.15 (3.13)
7	2.99 (2.96)	2.84 (2.81)	3.10 (3.08)	3.14 (3.10)	3.01 (2.99)	3.17 (3.14)
8	3.03 (3.00)	2.86 (2.84)	3.05 (3.02)	3.24 (3.21)	3.11 (3.08)	3.11 (3.17)
9	3.11 (3.09)	2.93 (2.90)	3.11 (3.09)	3.31 (3.28)	3.23 (3.20)	3.27 (3.25)
10	3.18 (3.15)	3.02 (2.99)	3.22 (3.19)	3.25 (3.22)	3.15 (3.12)	3.29 (3.26)
11	3.15 (3.12)	3.00 (2.97)	3.16 (3.13)	3.23 (3.20)	3.16 (3.13)	3.24 (3.21)
12	3.17 (3.16)	3.02 (3.00)	3.18 (3.15)	3.27 (3.24)	3.16 (3.13)	3.24 (3.22)
13	3.22 (3.19)	3.05 (3.02)	3.18 (3.16)	3.28 (3.26)	3.22 (3.19)	3.29 (3.26)

^aThe values in parentheses are calculated at the mPW2PLYP/aug-cc-pVTZ-pp level.

Figure 7.

Average binding energy (E_b, eV) of AgGe_n^λ (λ = 0, +1, and −1; n = 1–13) clusters.

Figure 8.

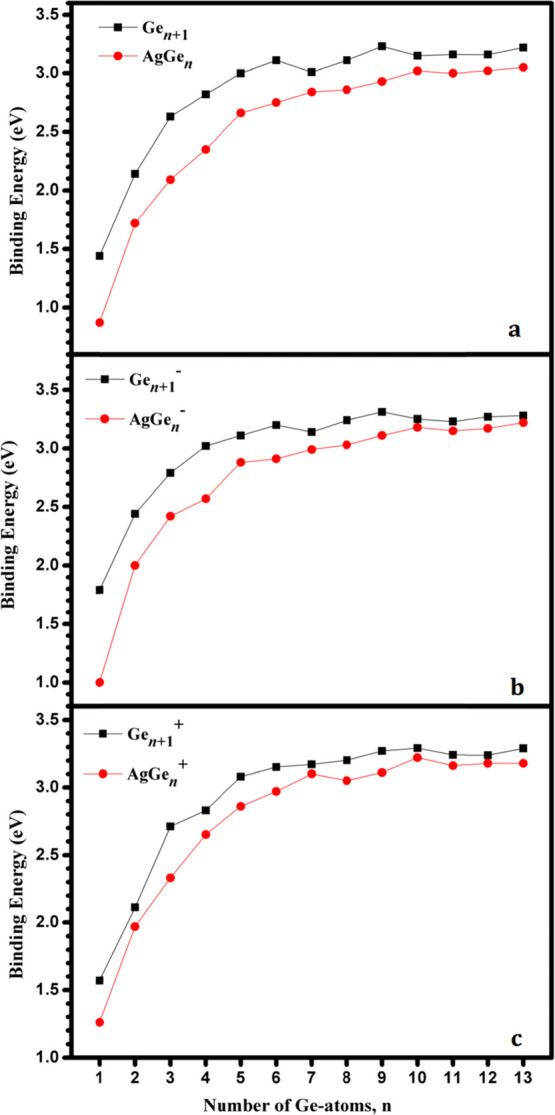
Binding energy (E_b, eV) of AgGe_n^λ and Ge_n + 1^λ (λ = 0, −1, and +1; n = 1–13) clusters at (a) neutral, (b) anionic, and (c) cationic states.

Figure 9.

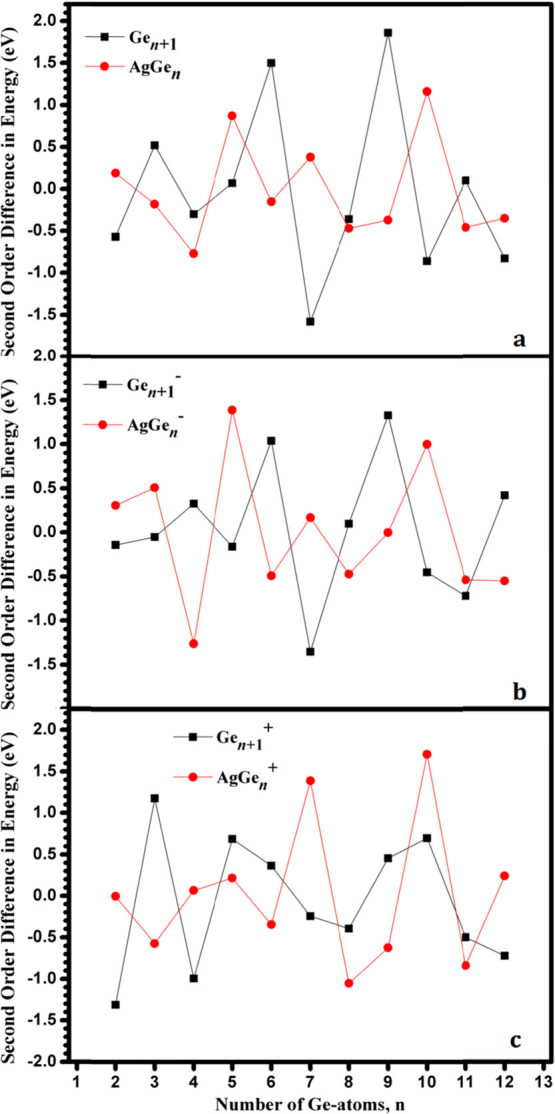
Second-order difference in energy (Δ²E, eV) of AgGe_n^λ and Ge_n + 1^λ (λ = 0, −1, and +1; n = 1–13) clusters at (a) neutral, (b) anionic, and (c) cationic states.

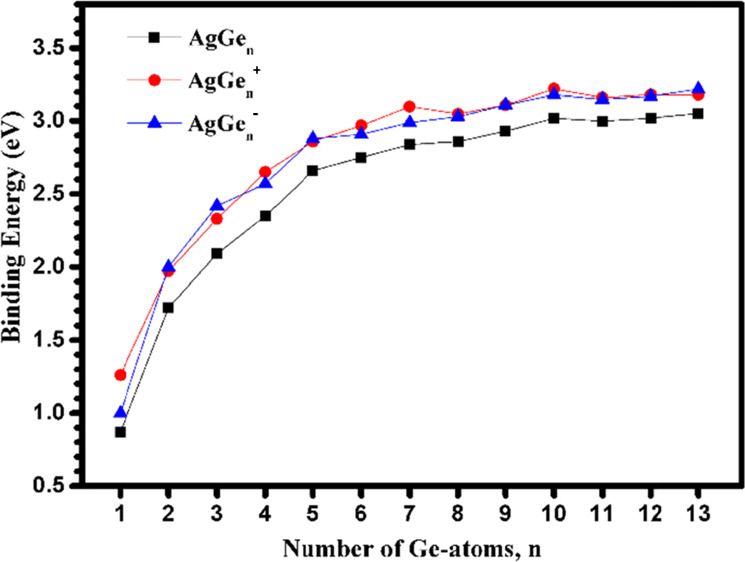
From Figures 7 and 8, it can be seen that: (i) The E_b(AgGe_n^–) and E_b(AgGe_n⁺) are larger than the corresponding E_b(AgGe_n). This is because AgGe_n clusters possess an open-shell electronic structure. When an electron is obtained or lost, AgGe_n^– (except for AgGe^–, the most stable state is a triplet) or AgGe_n⁺ (except for AgGe₂⁺, the most stable state is a triplet) clusters have the closed shell electronic structure, enhancing the stability. It should be noted that the simulated binding energy of AgGe is 0.87 eV, which is perfectly in line with the experimental value of 0.89 eV.⁶⁶ (ii) Whether it is neutral or charged AgGe_n and Ge_n + 1, the binding energy is increased with the increase of the cluster sizes. The binding energies of pure Ge_n + 1 and its charged clusters are slightly larger than those of Ag-doped germanium corresponding clusters, respectively, which indicates that doping of an Ag atom may decrease the stability of neutral and charged Ge_n + 1 clusters. (iii) The maximum values of E_b are calculated to be 3.02 eV (AgGe₁₂) and 3.05 eV (AgGe₁₃) for neutral AgGe_n clusters and 3.23 eV (Ge₁₀) and 3.22 eV (Ge₁₄) for neutral Ge_n + 1 clusters, which indicates that they show a good thermodynamic stability. At the anionic state, the value of E_b is the maximum at n = 10 (3.18 eV) and n = 13 (3.22 eV) for AgGe_n^– clusters and at n = 10 (3.31 eV) and n = 14 (3.28 eV) for Ge_n^– clusters. At the cationic state, AgGe₁₀⁺ presents the highest E_b value by 3.22 eV for AgGe_n⁺ clusters, and Ge₁₁⁺ and Ge₁₄⁺ present the highest binding energy at the same value (3.29 eV) for Ge_n⁺ clusters.

The second-order difference in energy of the nanoalloy cluster is the feature that reflects the relative stability between one cluster and its two directly adjacent clusters. The higher the value of Δ²E, the better the relative stability of the cluster. It can be observed from Figure 9 that the Δ²E for AgGe₅^0/–/+, AgGe₇^0/–/+, AgGe₁₀^0/–/+, AgGe₁₂^0/–/+, Ge₄^0/+, Ge₇^0/–, Ge₁₀^0/–, Ge₁₂, Ge₅^–, Ge₆⁺, and Ge₁₁⁺ clusters all have obvious peaks, indicating that their stability is higher than that of the adjacent clusters.

3.6. HOMO-LUMO Gap and Hardness

HOMO-LUMO energy gap (E_gap) is an electronic property of clusters, which can be used to express the performance of related chemical properties, such as photochemistry and conductivity. The value of E_gap means the minimum energy required to transfer an electron from the HOMO to the LUMO. The value of the HOMO-LUMO gap has an inverse response to the external perturbations, which means that a small value corresponds to a large response. Therefore, the E_gap of neutral and charged AgGe_n^λ (λ = 0, −1, +1; n = 1–13) clusters has been computed using the mPW2PLYP scheme and is pictured in Figure 10. It can be found that: (i) For neutral clusters, the values of E_gap range from 3.07 to 4.88 eV. The maximum value is calculated at AgGe₃, and the minimum value is calculated at AgGe₇. In anionic states, E_gap ranges from 3.16 to 4.49 eV. The maximum value is calculated at AgGe₁₂^–, and the minimum value is calculated at AgGe^– and AgGe₂^–. For cationic states, it ranges from 3.63 to 5.74 eV. The minimum value is simulated at AgGe₁₃⁺, and the maximum value is calculated at AgGe₂⁺. (ii) The E_gap of AgGe_n clusters are larger than that of AgGe_n^– clusters with the exception of n = 8 and 12, indicating that an additional electron reduces their chemical stability. Furthermore, after losing an electron, the E_gap of AgGe_n⁺ is narrower than that of AgGe_n for n = 3, 5, and 11–13 and is wider for n = 1, 2, 4, and 6–10.

Figure 10.

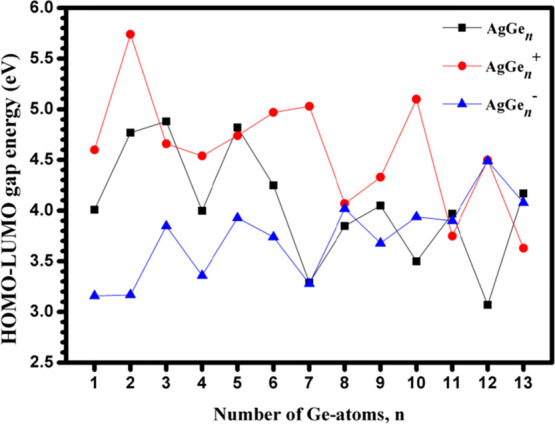
Highest occupied molecular orbital-lowest unoccupied molecular orbital (HOMO-LUMO) energy gap (E_gap, eV) of AgGe_n^λ (λ = 0, −1,+1; n = 1–13) clusters.

Hardness (η), as another important parameter reflecting the chemical properties, is calculated for AgGe_n (n = 1–3), and it can be defined as follows:

7

To facilitate comparison, hardness and HOMO-LUMO gap of AgGe_n are shown in Figure 11 as a function of cluster sizes. To better understand the relationship of changes between them, the comparison of HOMO with VIP and LUMO with VDE is also given in Figure 11. It can be seen from Figure 11 that the trend of E_gap and hardness is slightly different. For example, the hardness analysis of AgGe shows that it has a weak chemical reactivity, but HOMO-LUMO gap analysis indicates that it possesses a strong chemical activity. The reason is that the trend of HOMO and VIP is the same. However, the trend of LUMO and VDE is slightly different.

Figure 11.

Chemical hardness and HOMO-LUMO gap of AgGe_n clusters.

3.7. Charge Transfer and Partial Density of States (PDOS)

In this section, NPAs of the most stable structure for AgGe_n^λ (n = 1–13; λ = −1, 0, and +1) clusters were performed using the mPW2PLYP scheme. The results are shown in Table 5. From Table 5, it can be seen that the valence configurations of the Ag atom in AgGe_n^λ (n = 1–13; λ = −1, 0, and +1) clusters are 5s^0.36–1.224d^9.77-9895p^0.01–2.70. Regardless of being neutral or charged, the 4d electrons of Ag atoms are almost unchanged, meaning that the 4d electrons of Ag hardly participate in bonding. The calculated charges of Ag atoms in AgGe_n (n = 1–13) with the exception of n = 1 and 12 are 0.02–0.48 a.u, indicating that Ag atoms mainly act as electron donors. The charges of Ag atoms in anionic clusters are the same as those in neutral clusters, revealing that the extra electron is completely localized in the germanium clusters. Ag atoms in cationic AgGe_n⁺ (n = 1–12) clusters also act as electron donors. The charges of Ag atoms in cationic AgGe_n⁺ (n = 1–12) clusters are 0.20–0.69 a.u. which are larger by 0.14–0.47 a.u. as compared with the charges of Ag atoms in neutral clusters. That is to say the germanium clusters provide the majority of lost charges for cationic AgGe_n⁺ (n = 1–12) species. The charges of Ag atoms in the cage-like configuration of AgGe₁₂, AgGe₁₂^–, and AgGe₁₃⁺ clusters are by −1.8 a.u., indicating that Ag atoms in these clusters act as an electron acceptor.

Table 5. Natural Population Analysis (NPA) Valence Configurations and Charge of Ag Atoms (in a.u.) Calculated with the mPW2PLYP Method for the Most Stable Structure AgGe_n (n = 1–13) and Their Charged Clusters.

species	charge	electron configuration	species	charge	electron configuration	species	charge	electron configuration
AgGe	–0.05	[core]5s1.074d9.865p0.05	AgGe–	–0.05	[core]5s1.224d9.875p0.11	AgGe+	0.20	[core]5s0.844d9.855p0.05
AgGe2	0.20	[core]5s0.794d9.875p0.08	AgGe2–	0.20	[core]5s0.844d9.875p0.19	AgGe2+	0.41	[core]5s0.614d9.865p0.07
AgGe3	0.28	[core]5s0.704d9.865p0.11	AgGe3–	0.28	[core]5s0.884d9.865p0.24	AgGe3+	0.45	[core]5s0.564d9.865p0.07
AgGe4	0.32	[core]5s0.634d9.875p0.12	AgGe4–	0.32	[core]5s1.064d9.885p0.09	AgGe4+	0.68	[core]5s0.384d9.895p0.01
AgGe5	0.28	[core]5s0.594d9.865p0.22	AgGe5–	0.28	[core]5s0.694d9.865p0.29	AgGe5+	0.42	[core]5s0.504d9.855p0.18
AgGe6	0.30	[core]5s0.624d9.855p0.18	AgGe6–	0.30	[core]5s0.734d9.835p0.38	AgGe6+	0.69	[core]5s0.364d9.895p0.01
AgGe7	0.48	[core]5s0.494d9.885p0.11	AgGe7–	0.48	[core]5s1.034d9.885p0.06	AgGe7+	0.64	[core]5s0.374d9.885p0.07
AgGe8	0.16	[core]5s0.594d9.825p0.37	AgGe8–	0.16	[core]5s0.624d9.815p0.67	AgGe8+	0.37	[core]5s0.654d9.885p0.05
AgGe9	0.19	[core]5s0.604d9.845p0.31	AgGe9–	0.19	[core]5s0.614d9.875p0.22	AgGe9+	0.63	[core]5s0.404d9.875p0.05
AgGe10	0.32	[core]5s0.634d9.865p0.14	AgGe10–	0.32	[core]5s0.604d9.885p0.19	AgGe10+	0.58	[core]5s0.404d9.885p0.09
AgGe11	0.02	[core]5s0.564d9.825p0.53	AgGe11–	0.02	[core]5s0.634d9.815p0.74	AgGe11+	0.50	[core]5s0.514d9.865p0.09
AgGe12	–1.80	[core]5s0.674d9.775p2.24	AgGe12–	–1.80	[core]5s0.634d9.845p2.70	AgGe12+	0.53	[core]5s0.464d9.875p0.09
AgGe13	0.23	[core]5s0.634d9.835p0.25	AgGe13–	0.23	[core]5s0.704d9.845p0.25	AgGe13+	–1.78	[core]5s0.684d9.785p2.21

To better explore the electronic properties and HOMO-LUMO gap changes caused by the doping of Ag atoms, the detailed density of states (DOS) of AgGe₇ as an example is provided. The PDOS of pure Ge₇ and AgGe₇ is shown in Figure 12. It can be seen from Figure 12 that the position of occupied spin up and spin down states is identical for DOS of pure Ge₇. However, after the doping of Ag atoms, a new occupied spin up state in DOS is created, which causes a significant change in the HOMO-LUMO gap (from 4.86 to 3.29 eV). The electronic states of the HOMO mainly come from the 5s orbital of Ag atoms and 4s and 4p orbitals of the Ge₇ cluster because the 0.48 a.u. charge transfer from the 5s orbital of Ag atoms to the 4s4p orbital of the Ge₇ cluster as can be seen from Table 5.

Figure 12.

PDOSs for Ge₇ and AgGe₇ show a significant change in the PDOS at the Fermi level because of doping of Ag.

4. Conclusions

A systematic investigation of the silver-doped germanium clusters AgGe_n with n = 1–13 in the neutral, anionic, and cationic states is performed using the unbiased global search technique combined with the double-density functional scheme. The lowest-energy minima of the clusters are identified based on calculated energies and the measured PES. Total atomization energies and thermochemical properties such as EA, IP, binding energy, hardness, and HOMO-LUMO gap are obtained and compared with those of pure germanium clusters. The structural evolution for AgGe_n^λ (n = 1–13; λ = −1, 0, and +1) emerges as follows: For neutral and anionic clusters, although the most stable structures are inconsistent when n = 7–10, the structure patterns both are exohedral structures except for n = 12, and a highly symmetrical endohedral configuration is formed when n = 12. For the cationic state, the most stable structures are attaching structures (in which an Ag atom is adsorbed on the Ge_n cluster or a Ge atom is adsorbed on the AgGe_n–1 cluster) at n = 1–12, and when n = 13, the cage configuration is formed. The analyses of binding energy indicate that doping of an Ag atom into the neutral and charged Ge_n clusters may decrease their stability. The EAs of AgGe_n clusters including AEAs and VDEs are presented and are in perfect agreement with the experimental values. The IP including VIP and AIP of neutral Ge_n clusters is decreased when doped with an Ag atom. The HOMO-LUMO gaps of neutral AgGe_n (n = 1–13) excluded n = 8 and 12 are larger than that of anionic clusters. For cationic states, the HOMO-LUMO gaps of AgGe_n⁺ are wider than that of AgGe_n for n = 1, 2, 4, and 6–10 and are narrower for n = 3, 5, and 11–13. The variant trend of the HOMO-LUMO gap and hardness versus cluster size is slightly different. The accuracy of the theoretical analyses in this paper is demonstrated successfully by the agreement between simulated and experimental results such as PES, IP, EA, and binding energy.

The authors declare no competing financial interest.