Quantum Mechanical Methods Predict Accurate Thermodynamics of Biochemical Reactions

Abstract

Thermodynamics plays a crucial role in regulating the metabolic processes in all living organisms. Accurate determination of biochemical and biophysical properties is important to understand, analyze, and synthetically design such metabolic processes for engineered systems. In this work, we extensively performed first-principles quantum mechanical calculations to assess its accuracy in estimating free energy of biochemical reactions and developed automated quantum-chemistry (QC) pipeline (https://appdev.kbase.us/narrative/45710) for the prediction of thermodynamics parameters of biochemical reactions. We benchmark the QC methods based on density functional theory (DFT) against different basis sets, solvation models, pH, and exchange-correlation functionals using the known thermodynamic properties from the NIST database. Our results show that QC calculations when combined with simple calibration yield a mean absolute error in the range of 1.60–2.27 kcal/mol for different exchange-correlation functionals, which is comparable to the error in the experimental measurements. This accuracy over a diverse set of metabolic reactions is unprecedented and near the benchmark chemical accuracy of 1 kcal/mol that is usually desired from DFT calculations.

Introduction

Thermodynamics provides a quantitative framework for modeling metabolic processes at a fundamental level to understand design principles of natural and synthetically engineered microbial systems.¹⁻⁵ To accurately use a thermodynamic framework and to better understand microbes and microbial communities, it requires a comprehensive, precise, and accurate prediction of thermodynamic parameters for all of the relevant metabolites and metabolic reactions. Comprehensive thermodynamic data provides the foundation for the development of thermodynamically constrained flux balance analysis of metabolism⁶⁻⁸ enabling prediction of reaction rates and metabolite concentration ranges consistent with the laws of thermodynamics. Unfortunately, experimentally derived values for thermochemical parameters, such as the standard Gibbs free energy change of biochemical reactions (ΔG_r^′°), have been limited to a small number of biochemical reactions.⁹ Thus, there is currently a gap in our knowledge of thermochemical parameters for diverse biological reactions. This information gap limits our ability to rationally design and engineer microbes for various applications.

Accurate and efficient determination of thermochemical parameters of metabolites, cofactors, and metabolic reactions from first-principles quantum-chemistry method modeling and simulation is a long-standing problem with implications in drug discovery, biofuels processing, and synthetic biology.¹⁰ In the metabolic modeling community, thermodynamic parameters such as the standard Gibbs free energy of formation for metabolites (Δ_fG′) are generally estimated using empirical-component or group-contribution methods that are subsequently used to calculate standard reaction-free energies (ΔG_r^′°).¹¹⁻¹⁷ However, for some secondary metabolites and cofactors, such anempirical approach is not possible to estimate parameters due to the lack of experimental data needed to determine all required group-contribution values. These empirical methods use numerical approximations to account for crucial molecular-level information and relevant properties such as solvation effect, ionic strength, pH, and different protonation states. For many metabolites, Gibbs energy is not equal to the sum of the Gibbs energies of their constituent chemical moieties, leading to inaccurate group-contribution estimates.¹⁸ Other metabolites may share few, if any, moieties with those in the training set, so group-contribution estimates may be imprecise or impossible. All group-contribution methods are currently based on an a priori heuristic definition of each chemical moiety, but such moieties may incompletely represent the metabolites to be estimated or overestimate the number of moieties transformed by a chemical reaction leading to large uncertainties in estimates of thermodynamic parameters.

Using first-principles quantum mechanical methods for predicting thermodynamic parameters offers several advantages: they are not limited by the available experimental data, thus reducing the risk of overfitting and providing a consistent approach throughout all metabolic processes. Additionally, such methods can take advantage of an established hierarchy of increasingly accurate (yet computationally expensive) quantum chemical (QC) methods. Some effort^19,20 has been made in the past to estimate the thermodynamical parameters of biomolecules using QC calculations based on the density functional theory (DFT);^21,22 however, such studies were limited to only a small subset of reactions and ignored the challenging and more complex metabolites and reactions.^23,24 Moreover, such studies were limited only to a particular choice of DFT exchange-correlation functionals and a basis set. Jinich et al.¹⁰ calculated the thermodynamic redox potentials of bioreactions directly using the single-point energies thus ignoring the vibrational contribution to the Gibbs free energy of metabolites. An extensive benchmark study of DFT functionals for studying main group thermochemistry on GMTKN55 database was performed by Goerigk et al.,^25,26 where they proposed double-hybrid DSD-BLYP-D3(BJ) as the best performing functional. They also proposed SCAN-D3(BJ) as the best performing meta-GGA functionals among all. Extension of similar studies to modern and range of other functionals have also been reported in the literature.²⁷⁻³⁰ Other studies have used experimental data to calibrate the first-principles predicted thermodynamical parameters to improve the accuracy.¹⁰ Despite these preliminary studies, the thermodynamic properties of complex cofactors, metabolites, corresponding biochemical reactions, many of which occur in central carbon metabolism, have yet to be computed using quantum mechanics to-date.

In this study, we used a highly parallelized in-house developed computational chemistry code, NWChem,³¹ to investigate the current state-of-the-art DFT for predicting reaction-free energies, ΔG_r^′° of diverse biological reactions. In this context, we first benchmark the performance of different basis sets, solvation models, and diverse exchange-correlation functionals in current state-of-the-art DFT for predicting Gibbs free energy change (ΔG_r) over a large and diverse set of metabolic reactions with known experimental references. To understand the impact of pH for calculating ΔG_r^′° from DFT simulations, we compute and compare ΔG_r values at pH = 0 and 7. In addition, we examine the performance of DFT for different categories of biological reactions typically defined by Enzyme Commission (EC) numbers. We show that our best QC approach can predict ΔG_r^′° for diverse metabolic reactions with a mean absolute error of ∼1.50 kcal/mol. We also highlight unique challenges associated with DFT approaches and provide possible solutions to overcome those challenges. As a result, we developed a quantum-chemistry-based workflow for automatically performing nonempirical high-throughput calculations for estimating thermodynamics of metabolic reactions and metabolites and we integrated that computational workflow within DOE Systems Biology Knowledgebase (KBase).⁸

Methods

NWChem Computational Chemistry Calculations Using ModelSEED Data

All calculations were performed using the massively parallel NWChem-7.0.0³¹ quantum-chemistry code embedded within our workflow for ab initio prediction of Gibbs free energies of reactants and products in a given reaction. Our workflow starts with the SMILES strings of the metabolites from the ModelSEED database³² and uses Chemaxon³³ to generate the major microspecies of a given SMILES string at a desired pH (pH = 0 or 7). Three-dimensional molecular geometries were generated from these SMILES strings using RDkit³⁴ and then geometrically optimized using dispersion³⁵-corrected B3LYP³⁶ (B3LYP-D3) exchange-correlation functionals and 6-31G* as the basis set.^37,38 Since metabolic reactions occur in an aqueous phase (more precisely in a lipid) in biological systems, the effect of solvation (by water) was considered using an implicit solvation model called the solvation model density (SMD).³⁹ The ground state of the DFT calculations for each metabolite was confirmed by doing stability analysis on the calculated frequencies. The standard Gibbs free energy of each metabolite was calculated by taking into account the entropy (S) and enthalpy (H) contribution using the expression (G = H – TS), where T = 298.15 K. We note that vibrational frequencies calculated at B3LYP-D3/6-31G* level of theory were used to calculate the correction to the single-point electronic energy to get the standard Gibb’s free energy used for the subsequent evaluations. The standard Gibbs free energies of metabolites were stoichiometrically combined to predict the standard free energy change of reactions (ΔG_r^′°) for 300 biological reactions, which were then compared with the existing experimental references from the National Institute of Standards and Technology Thermodynamics of Enzyme-catalyzed Reactions database (NIST).⁹ For the thermal analysis, we used 1 M concentration for all of the metabolites and 55.5 M for water. The Gibbs free energy of −268.61 kcal/mol was used as the solvation energy of a proton.¹⁹ For some of the reactions, multiple experimental references exist in the NIST data. For such reactions, an average of the available ΔG_r values was used as a reference. All of the calculations were performed using Cascade supercomputer at Environmental Molecular Sciences Laboratory, DOE Office of Science User Facility sponsored by the Office of Biological and Environmental Research.

Effect of Different Exchange-Correlation Functionals and Basis Set

To understand the effect of exchange-correlation functionals for predicting ΔG_r^′°, we have used seven diverse exchange-correlation functionals from the Jacob’s Ladder shown in Figure 1 that ranges from the pure generalized gradient approximation (GGA, PBE),⁴⁰ to hybrid functionals (PBE0⁴¹ and B3LYP⁴²), to meta-GGA functionals (M06,⁴³ SCAN,⁴⁴ SCAN0⁴⁵), along with a range-separated functional (LC-ωPBE)⁴⁶ and a double hybrid (B2PLYP).⁴⁷ PBE is a pure GGA functional proposed by Perdew, Burke, and Ernzernof. PBE0 is the PBE hybrid functional with 75% of its exchange energy contributed by PBE exchange and 25% from Hartree–Fock (HF) exchange, with correlation from the PBE functional. The meta-GGA functionals M06 have a 27% HF exchange mixed with the DFT exchange. LC-ωPBE is a long-range-corrected GGA functional that partitions exchange interactions into short- and long-range terms in which short-range exchange interactions are described with a PBE exchange, while long-range interactions are treated by an HF exchange. SCAN is a recently proposed meta-GGA functional that works well with a range of properties because of its ability to satisfy most of the system constraints. SCAN0 is a hybrid of SCAN and B2PLYP is a double hybrid that uses second-order perturbation from MP2 for the correlation part of energy in combination with a GGA correlation.⁴⁷ These functionals with larger basis sets are computationally demanding for geometry optimization. To circumvent the computational cost required for optimizing the molecular geometry and subsequent frequency calculations using larger basis sets, only single-point solution-phase calculations were carried out for larger basis sets on top of the optimized geometry from B3LYP/6-31G* basis set.^37,38 The ΔG_r at larger basis sets (6-311++G**)^38,48,49 were calculated using the thermal and entropy contributions from the small basis set. To benchmark different approaches for calculating ΔG_r^′°, we performed DFT calculations of metabolites using a SMILES representation of major microspecies generated at pH = 0 and 7. We extracted the Gibbs free energies of reactions from the Gibbs free energy of metabolites directly computed at pH = 0 and 7. To measure the performance of each of the methods discussed above, we used mean absolute error (MAE) as defined by eq 1 as a metric.

1

Figure 1.

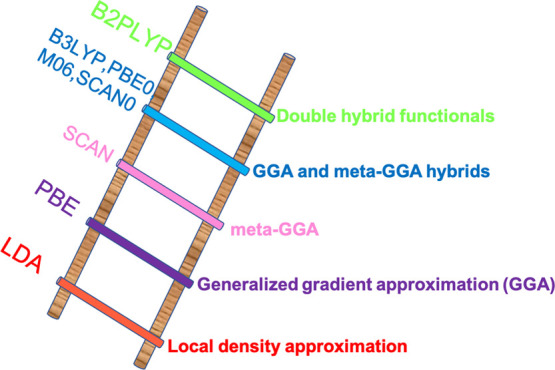
Jacob’s ladder for exchange-correlation functionals in DFT.

NIST Experimental Data

Our benchmark data set includes 300 reactions from the NIST database⁹ with known experimental references. Experimental Gibbs free energies of reactions are derived from the measured equilibrium constant (K) (using ΔG_r^′° = −nRT ln (K)). Although the NIST data set covers only a relatively a small number of the known biochemical reactions, it is diverse both qualitatively and quantitatively, with EC numbers varying from 1 to 6, where the experimental reference for ΔG_r varies from −10 to +12 kcal/mol. EC numbers are used to classify the unique metabolic reactions numerically based on the reaction they catalyze. Our benchmark data set contains 65 oxidoreductase reactions grouped in EC category 1 (EC1), 84 transferase reactions in category 2 (EC2), 37 hydrolase reactions in category 3 (EC3), 44 lyases reactions in category 4 (EC4), 66 isomerase reaction in category 5 (EC5), and four ligase reactions in category 6 (EC6). Some reactions in the NIST database have multiple experimental references measured at different experimental conditions such as pH, ionic strength, etc. For reactions with multiple references, the average of transformed ΔG_r^′° values is calculated. This introduces the noise in the experimental reference data. We minimized such condition dependence in the reference NIST data using inverse Legendre transformation.⁵⁰ We note that, although inverse Legendre transformation reduces the noise in the reference data, it cannot completely erase it (see Figure S3 for details). Such transformed ΔG_r has a mean experimental measurement error of 0.37 kcal/mol and is used as an experimental reference.

Development of KBase App

Finally, we integrated our automated pipeline to calculate metabolic ΔG_r^′° with the DOE Systems Biology Knowledgebase⁸ (KBase) module to develop a QC-based web-accessible application (App). Our narrative integrates a set of modules, each of which are self-contained and independently validated. It uses a benchmarked QC method and provides open-source access as a ThermoCalculator to calculate ΔG_r of metabolic reactions. For this, we have used snakemake⁵¹ as an underlying package for workflow management to bind together different Python-based components ensuring scalability, portability, and fault tolerance. Within the app, the ModelSEED database is used for describing the biochemical reactions that are typically utilized to construct a new genome-scale model for a given organism. Our app takes ModelSEED³² reaction IDs or a reaction as an input and generates a metabolite list of ModelSEED compounds and returns QC-predicted ΔG_r^′° as well as Δ_fG′ as an output.

This tool not only provides an accurate prediction of ΔG_r^′° but also increases access of QC methods to a community where users do not have access to the huge computational resources required for these calculations. ThermoCalculator tools like this are very critical for synthetic biology to predict the metabolic fluxes and metabolites levels as well as to determine the growth and engineering strategies for optimizing the production of biofuels and bioproduct precursors.

Results and Discussion

Assessment of the Quantum Mechanical Method

We performed the analysis by splitting our entire data set into two reaction sets (see Table 1) based on the molecular size and challenges they offer to calculations in predicting ΔG_r^′° of metabolic reactions. The first subset (hereafter called Set-1) contains 150 reactions and primarily consists of small to medium size metabolites that are more amenable for quantum mechanical calculations. Set-1 is diverse and consists of all possible EC-classes with metabolite charges varying from 0 to −4. Set-2 consists of another 150 reactions whose ΔG_r values are relatively challenging to predict accurately based on the first-principles quantum mechanical methods. This is due to the fact that Set-2 contains some relatively large, and more negatively charged metabolites, which are known to be problematic for quantum mechanical calculations because of a high computational cost associated and other reasons discussed below.¹⁹ The error in predicting Δ_fG′ of these complex metabolites is further compounded when using these values to compute ΔG_r^′° for the Set-2 reactions that often involve multiple complex metabolites. Based on our extensive reaction data analysis, this seems to be more predominant on the Set-2 reactions where each reaction generally contains more than one reactant or product. Only few reactions with a single reactant or product have such large errors associated. Part of the error originates from the huge conformational space that exists for each of the metabolites in these reactions and the fact that two very different conformers may be generated for a reactant and product in a reaction.

Table 1. Classification of Biochemical Reactions Considered in Set-1 and Set-2 into Different Categories Using EC Numbers.

	number of reactions
EC-category	Set-1	Set-2
1	32	65
2	41	84
3	14	37
4	24	44
5	37	66
6	2	4
total	150	300

As a first step, we assessed the effect of basis sets on the ΔG_r^′° of Set-1 using B3LYP as the exchange-correlation functionals with 6-31G* and 6-311++G** as the basis sets⁵² (see Table 2). These are two typical basis sets used in work reported in the literature where the latter has a high computational cost. With the 6-31G* as the basis set, we obtained an MAE of 4.69 kcal/mol when compared to experimental references, whereas the MAE was 3.69 kcal/mol when the 6-311++G** basis set was applied. A similar error of 4.18 kcal/mol was reported¹⁹ with B3LYP/6-31G* for 113 NIST reactions in EC-categories 2, 4, and 5 in earlier studies. Further increasing the size of the basis set increases the computational cost without significant improvement in the resulting ΔG_r.⁵³⁵³ Therefore, we have used 6-311++G** as the working basis set for this work. Subsequently, we analyzed the sensitivity of ΔG_r^′° on the solvation method using COSMO⁵⁴ and SMD³⁹ continuum solvation models at the B3LYP/6-311++G** level of theory.⁵² Our results show that changing the solvation model from COSMO to SMD improves the resulting ΔG_r MAE from 4.35 to 3.69 kcal/mol. Thus, for the rest of the work reported here, we used SMD as the implicit solvation model unless mentioned otherwise.

Table 2. Effects of Basis Set and the Solvation Model on ΔG_r^′° in Set-1.

	MAE (kcal/mol)
basis set
6-31G*	4.69
6-311++G**	3.69
solvation model
COSMO	4.35
SMD	3.69

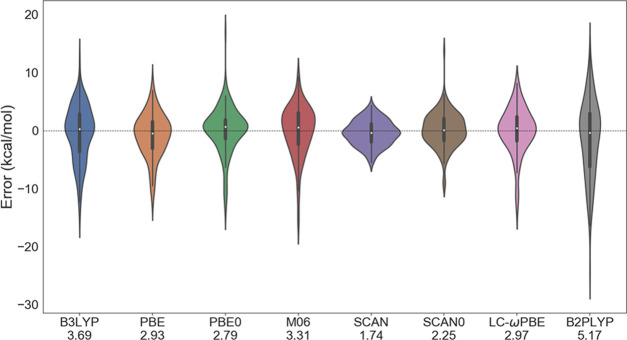
As a next step, we analyzed the performance of different exchange-correlation functionals for calculating the ΔG_r^′°. The violin plots in Figure 2 indicate that the accuracy of ΔG_r for Set-1 reactions depends strongly on the particular choice of exchange-correlation functionals. Most importantly, among all functionals studied, SCAN was the best performer with an MAE of 1.74 kcal/mol. The reason is that SCAN represents charged species more accurately with the smallest overbinding tendency of excess charge in the molecules among all approximate functionals.⁵⁵ On the other hand, the overbinding tendency is relatively large in other functionals that show detrimental effects on calculated properties including free energies of the molecules for the charged species. Moreover, SCAN is more robust by construction because it satisfies all of the constraints needed of a meta-GGA functional. The SCAN error of 1.74 kcal/mol is close to the chemical accuracy (1 kcal/mol) desired from DFT calculations and this level of accuracy from quantum chemical methods is unprecedented in such a diverse set of biological reactions.

Figure 2.

Violin plot showing an error in reaction-free energy (ΔG_r^′°) for Set-1 for different DFT exchange-correlation functionals compared to an experimental reference. The mean absolute error (MAE, kcal/mol) for each functional is shown in labels.

SCAN0 follows parent SCAN with an MAE of 2.25 kcal/mol. As shown in Figure 2, all other functionals provide relatively large error as compared to SCAN. Meta-GGA functional M06 has an MAE result almost twice that from SCAN. With parameter-free PBE functional, we get an MAE of 2.93 kcal/mol and its hybrid (PBE0) further improves the MAE to 2.79 kcal/mol. Such improvement might be the result of self-interaction error cancellation in PBE0 when compared to PBE. B3LYP, LC-ωPBE, and double-hybrid B2PLYP functionals yield relatively large error compared to the other functionals. The improvement in ΔG_r^′° is very significant (almost by 200%, 3.43 kcal/mol) as we go from B2PLYP to SCAN. The performance of double hybrid is in stark contrast with the literature,^25,26 where other variants of double hybrids yield smaller MAE for calculating reaction energies. However, we note that cited work directly calculates the reaction energies (not reaction-free energy) only from the electronic energies of single-point calculation performed in a gaseous phase, thus ignoring the correction to the electronic energies from solvation and from vibrational frequency calculations. Moreover, we take into account such correction while also considering the effect of the solvent. This could be the reason for the observed discrepancy between our work and literature. Our calculations also highlight the typical distribution of error in the data set for different functionals (Figure 2). It is important to mention that the error in ΔG_r is large for all of the functionals employed except SCAN and its hybrid. This can also be seen from the long tails in the violin plots. The predicted large error associated with such functionals is consistent with previous studies where they reported a large error of 4.18 kcal/mol using B3LYP¹⁹ for a small subset of reactions.

Effect of Metabolite Charges on Quantum-Chemistry Calculations

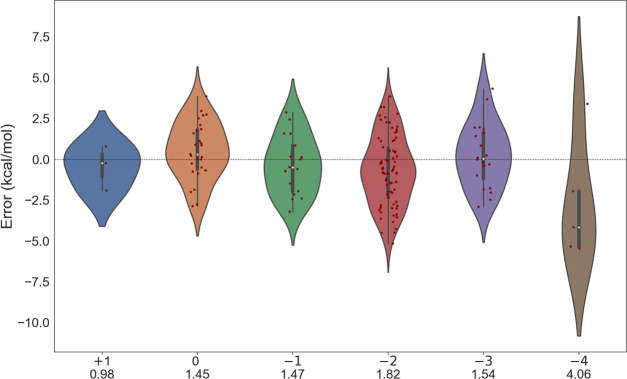
We also observed that the accuracy of DFT depends upon the charges of the metabolites involved in the reactions (see Figure 3). In general, the MAE in ΔG_r^′° with our best performing functional SCAN gradually increases as the negative charge on metabolites increases from −1 to −4 in those reactions. In general, DFT yields a relatively small error, when a particular reaction has a positive charge or a small negative charge on metabolites and the error increases if the reaction has multiple large negatively charged metabolites, as shown in Figure 3. This is to some extent, the artifact of DFT calculations and is a well-known issue in DFT-based quantum-chemistry methods.^56,57 In this context, the nonphysical self-interaction error is one of the limitations which particularly deteriorate the DFT performance for negatively charged species.^56,57 Self-interaction error is known to overbind excess electrons in negatively charged molecules, with consequences in calculated properties⁵⁵ such as the binding affinity or the ionization energy. Self-interaction-free DFT functionals have shown to improve the energy differences among negatively charged species.⁵⁸ However, these methods are computationally not possible (as of now) for large metabolites involved in our benchmark.⁵⁸ Some of the self-interaction errors can be removed using the hybrid-exchange-correlation functionals as used in our work which include a fraction of Hartree–Fock exchange that cancels self-interaction error to some extent. This is reflected in a comparative analysis of ΔG_r between PBE and PBE0 functional, where the performance improves as we move from PBE to PBE0 (Figure 2). We note that this is surprisingly not observed in the case of SCAN and where its hybrid performance slightly reduces. Such reduction in performance in the case of SCAN0 compared to SCAN has been reported for several properties⁴⁵ including isodesmic reaction energies of n-alkanes to ethane. The error with negatively charged metabolites can be eliminated or improved further using the more accurate wave-function-based methods^59,60 (such as couple-cluster singlet doublet CCSD, methods); however, the computational cost associated with those methods is huge⁶¹ with NWChem.

Figure 3.

Violin plot showing error in SCAN ΔG_r^′° (kcal/mol) for Set-1 as compared to experimental reference for different charges on metabolites. Labels display a maximum negative charge on metabolites involved in the reaction along with respective MAEs.

Reaction Associated with Metabolic Reaction Categories (Enzyme Commission, EC)

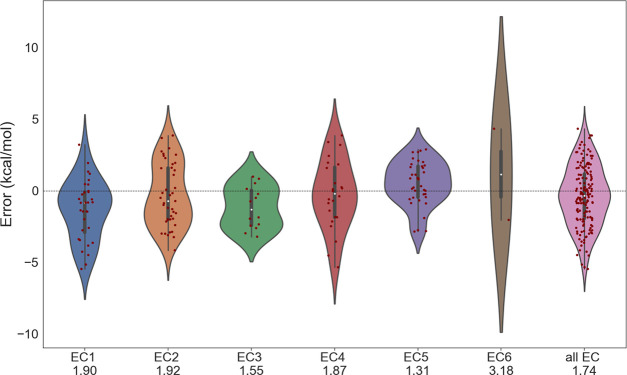
The accuracy of DFT for predicting ΔG_r^′° of metabolic reactions varies between reaction categories. Figure 4 shows the error distribution in each EC category of the Set-1 reactions with SCAN as the underlying theory. For the majority of the reactions, the errors lie within the ±4 kcal/mol. In general, EC1, EC2, and EC4 reactions are the most challenging class of metabolic reactions for accurate prediction of ΔG_r from DFT followed by EC3 and EC5. We note that these metabolic reactions are mostly reversible and any change in reaction direction will not affect the MAE presented. The smallest MAE of 1.31 kcal/mol was obtained for EC-5, which generally consists of only one reactant and product in a reaction in contrast to other EC categories where reactants and products have multiple metabolites.

Figure 4.

Violin plots showing error in SCAN ΔG_r^′° for Set-1 for different EC compared to the experimental reference. MAE values in terms of kcal/mol for each EC are shown in labels.

We also analyzed the performance of each DFT functional for each category of reactions as shown in the bar diagram (see Figure S1). SCAN consistently gives a smaller error in ΔG_r^′° between different EC-categories except for EC-6, where SCAN0 performs more accurately with an MAE of 1.37 kcal/mol. Performance of DFT in Set-1 shows that DFT can achieve close to benchmark chemical accuracy (1 kcal/mol) to predict ΔG_r for diverse biological reactions. However, this trend does not transfer to a larger set of reactions involving larger, more negatively charged metabolites for the several reasons discussed hereafter.

Then, we extended our study to the larger data set consisting of larger and more complex metabolic reactions included in Set-2. The general trend for the accuracy of different exchange-correlation functionals remains the same as we observed for Set-1. However, the error increases significantly compared to Set-1, particularly for our best performing functionals, SCAN (see Table 3). Among all of the functionals for Set-2, SCAN is best with an MAE of 3.48 kcal/mol followed by SCAN0, PBE, LC-ωPBE, M06, and PBE0 with MAE values of 4.00, 4.13, 4.42, 4.42, and 5.17 kcal/mol, respectively. B3LYP and B2PLYP give relatively large errors compared to SCAN. The poor performance of some hybrid functionals like B3LYP and B2PLYP compared to parameter-free PBE functionals shows that higher level functionals in Jacobs ladder do not necessarily improve the prediction of ΔG_r^′°. Overall, our results show that SCAN is most accurate for predicting ΔG_r for a diverse set of reactions.

Table 3. MAE (kcal/mol) for Different Exchange-Correlation Functionals on Set-2.

functionals	MAE
PBE	4.13
B3LYP	5.07
PBE0	5.17
M06	4.42
SCAN	3.48
SCAN0	4.00
LC-ωPBE	4.42
B2PLYP	6.26

In Set-2, none of the DFT functionals provided a small enough error to achieve chemical accuracy. The large error stems from many different factors that we discuss below. First and foremost, ΔG_r^′° is extremely sensitive to individual metabolites and complexity increases as we increase the number of metabolites in the reaction. This is the case observed from our work, where we see that for reactions in EC-class 5, we have generally only one metabolite in each side of the reaction and hence a small error. Our predicted ΔG_r analysis further reveals that the different converged conformers of the related metabolites can provide very different free energy of formation adding huge error in the predicted ΔG_r^′°. For the case of NAD⁺/NADH (same for ATP/ADP/AMP), if we do not generate the NAD⁺ structure from an optimized NADH structure, it can lead to significant error. In addition, to reduce the error, where ΔG_r deviates by a large number compared to the experiment, we explored the conformer space of the molecule to look for other more stable conformers of a given metabolite. When possible we used such lowest energy conformers to calculate ΔG_r^′°. This approach reduced the deviation in ΔG_r for some reactions.

Calibrated Quantum-Chemistry Calculations

The MAEs obtained for Set-2 are relatively large for DFT to be routinely and reliably used for predicting ΔG_r^′° across the range of metabolic reactions. One way to reduce the large errors is to use alternative and more accurate QC calculations such as the multireference wave functions-based methods. However, these methods are computationally very demanding/or even impossible for some of these large species. Alternatively, another way to reduce such relatively large errors without performing additional computationally expensive calculations is by calibrating DFT-predicted ΔG_r with simple linear regressions. This approach has been used in the past for reducing the large error associated with QC prediction of reduction potentials for a particular category of reductase reactions.^10,62 In that work,¹⁰ DFT-predicted reduction potentials were calibrated by fitting Alberty’s empirically predicted numbers to corresponding experimental references. In our work, we fit the SCAN-DFT calculated ΔG_r^′° values with the corresponding experimental references and extrapolate such fittings to reduce the error obtained from all functionals. We see a significant improvement in accuracy when QC-predicted ΔG_r are corrected using the equation of best fit. Calibrated QC values reduce the MAE from the range of 3.48–6.26 to 2.22–3.17 kcal/mol for different functionals, as shown in Table 4.

Table 4. MAE (kcal/mol) for Different Exchange-Correlation Functionals before and after Calibration in Set-2.

functionals	MAE before calibration	MAE after calibration	MAE EC calibrated
PBE	4.13	2.48	1.91
B3LYP	5.07	2.58	1.99
PBE0	5.17	2.65	1.76
M06	4.42	2.49	1.81
SCAN	3.48	2.22	1.64
SCAN0	4.00	2.19	1.60
LC-ωPBE	4.42	2.48	1.74
B2PLYP	6.26	3.17	2.27

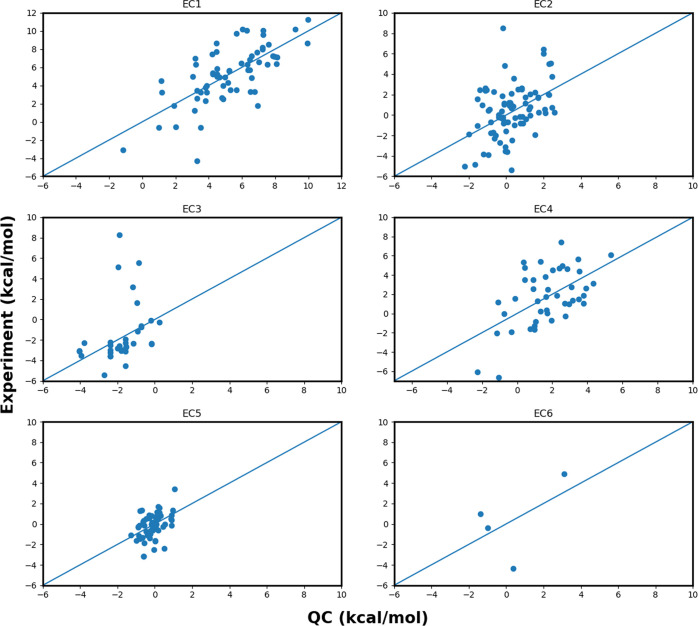
Further improvement is observed when the calibration is performed individually for each reaction category, thus reducing the MAE to the range of 1.64–2.27 kcal/mol (see Figure S2 for violin plot). The trend observed in MAEs using calibrated QC calculations is similar to the trend observed from the uncalibrated QC calculations, with SCAN/SCAN0 being the most accurate and the B2PLYP being the least accurate among all functionals employed in this study. With SCAN/SCAN0, individual calibration of the entire Set-2 reduces the MAE to 1.64/1.60 kcal/mol, which is similar to what we obtained from QC calculations without any calibration for Set-1. The scatter plots of EC-calibrated ΔG_r^′° with the corresponding experimental reference are shown in Figure 5. It shows that calibrated QC calculations provide consistent results across all EC categories, with few outliers in each EC category.

Figure 5.

Scatter plot showing the QC (SCAN) calibrated reaction-free energies and the experimental reference for each EC category of reactions. y = x line is drawn for reference.

This improvement using calibrations is consistent across all of the functionals and MAEs for all of the functionals employed before and after calibration for Set-2 (see Table 4). We observed that based on our preliminary calculations, further improvement from the use of calibrations may be realized using more advanced techniques based on machine learning. Currently, work in this direction is constrained by the limited amount of data available to train the physics-informed models. Work to create such a database from QC calculations is the primary focus of our laboratory and this benchmark work is the first step in that direction.

Protonation State of Metabolites

In the literature,^19,62 it has been discussed extensively that the issue of large error from quantum chemical calculations with negatively charged metabolites can be circumvented by performing the calculations at pH = 0.¹⁰ The major microspecies generated at pH = 0 are a protonated counterpart (highest positively charged species) of the structures generated at pH = 7. Performing calculations at pH = 0 allows us to ignore the issues of DFT associated with negatively charged species. Comparing our results at two pH levels shows that ΔG_r^′° obtained from SMILES generated at pH = 7 are most accurate over a diverse data set, with the smallest MAE being 3.48 kcal/mol. ΔG_r calculated using SMILES generated at pH = 0 have relatively large errors with MAEs of 4.72 kcal/mol. At pH = 0, EC2 is the most challenging category of reactions for which we obtained a large MAE of 6.28 kcal/mol, whereas the MAE is 4.18 kcal/mol at pH = 7 for the same set of reactions. Another category where we see large improvement is EC1, where MAE decreases from 3.99 to 2.58 kcal/mol. We observed that such a large error at pH = 0 comes mainly from the metabolites containing phosphate groups such as NAD⁺/NADP, ATP/ADP/AMP. Because metabolic processes in the human body occur at pH = 7 and our results show that ΔG_r^′° are most accurate at pH = 7, we recommend calculating ΔG_r directly using SMILES generated at pH = 7. We note that empirical transformation has been used in the literature to transform other properties calculated at pH = 0 to pH =7 using Legendre transformation.¹⁰

Thermodynamics of Metabolic Reactions Essential for the Central Metabolism

Thermodynamics plays a very important role in metabolic modeling and engineering new synthetic pathways with desired functions. With the increasing efficiency of high-performance computers and the availability of highly parallel computational chemistry code NWChem,³¹ there is an absolute need to develop nonempirical computational methods for predicting ΔG_r^′° of metabolic reactions. Empirical methods, such as component and group-contribution,¹⁸ are currently used to estimate the standard Gibbs energies of metabolites, which then are used to estimate the ΔG_r. However, for some secondary metabolites and cofactors, this empirical approach cannot be applied because of a lack of experimental data (e.g., newly designed synthetic pathways that involve uncharacterized metabolites). These empirical methods use unconventional approaches to account for crucial molecular-level effects, such as solvation effects, ionic strength, pH, conformers, and different protonation states. For example, the eQuilibrator⁶³ component-contribution method fails to predict ΔG_r^′° for reactions with molecules consisting of the functional groups which are not part of the experimental database used to build eQuilibrator. In contrast, the QC approach used here is free from such limitations and provides detailed information about the structures and thermal properties of metabolites, including energies, enthalpy, and entropy of metabolites in solution transformed into Gibbs energy at the given pH and temperature. Therefore, QC methods can consistently take into account all possible atoms and functional groups in the molecule. In eQuilibrator, ΔG_r are calculated at a constant temperature of 298.15 K. However, in the human body, metabolic reactions occur at 310.00 K. Temperature effects however can be easily addressed in DFT calculations. To study the effect of temperature on ΔG_r^′°, we performed calculations at three different temperatures: 298.15, 310.00, and 320.00 K. The results are shown in Table 5. Even though the temperature has a marginal effect on ΔG_r, a maximum change of 1.40 kcal/mol can be observed when the temperature is increased from 298.15 to 320 K with the MAE changing by 0.60 kcal/mol in the TCA/glycolysis cycle.

Table 5. SCAN ΔG_r^′° (kcal/mol) for Different Reactions in the TCA/Glycolysis Cycle with Corresponding EC Numbers^a9.

EC-numbers	CCM	expt.	DFT 298.15 K	DFT 310 K	DFT 320 K	deviation
Glycolysis
5.3.1.9	0.60	0.80	–0.82	–0.71	–0.62	–1.62
3.1.3.11	–2.72	–4.57	–1.28	–1.39	–1.49	3.29
2.7.1.11	–3.59	–2.31	–4.32	–4.42	–4.51	–2.01
4.1.2.13	4.73	3.52	–1.82	–2.49	–3.06	–5.34
5.3.1.1	–1.31	–1.88	–4.69	–4.75	–4.80	–2.81
1.2.1.12	1.86	3.21	–2.24	–1.67	–1.18	–5.45
2.7.2.3	4.42	4.80	–1.68	–1.75	–1.81	–6.48
5.4.2.12	–1.00		–6.77	–6.79	–6.80
4.2.1.11	–0.98	–0.74	1.22	0.70	0.26	1.96
2.7.1.40	6.62	6.02	7.88	7.67	7.49	1.86
1.2.1.-	–9.98b		5.43	5.94	6.37
TCA Cycle
2.3.3.1	–8.27		–7.70	–7.55	–7.42
4.2.1.3	1.98	1.88	2.13	1.60	1.15	0.25
4.2.1.3	–0.12		–3.44	–2.96	–2.55
1.1.1.41	1.29		–5.66	–6.02	–6.32
1.2.1.M9	–6.5		–0.50	–0.26	0.90
6.2.1.5	0.43	1.25	–0.36	–0.85	–1.26	–1.61
1.3.5.1	–5.41		–4.89	–5.12	–5.32
4.2.1.2	–0.84	–0.85	–1.45	–0.96	–0.55	–0.60
1.1.1.37	7.24	7.63	9.21	9.13	9.07	1.58

^aEmpirical values calculated with eQuilibrator⁶³ using the component-contribution method (CCM)¹⁵ are given, when not available the group-contribution method¹⁸ values are provided as a footnote b. Experimental values are provided as reference when available. Deviations are calculated using DFT at 298 K and corresponding experimental value.⁹

^bGCM value.

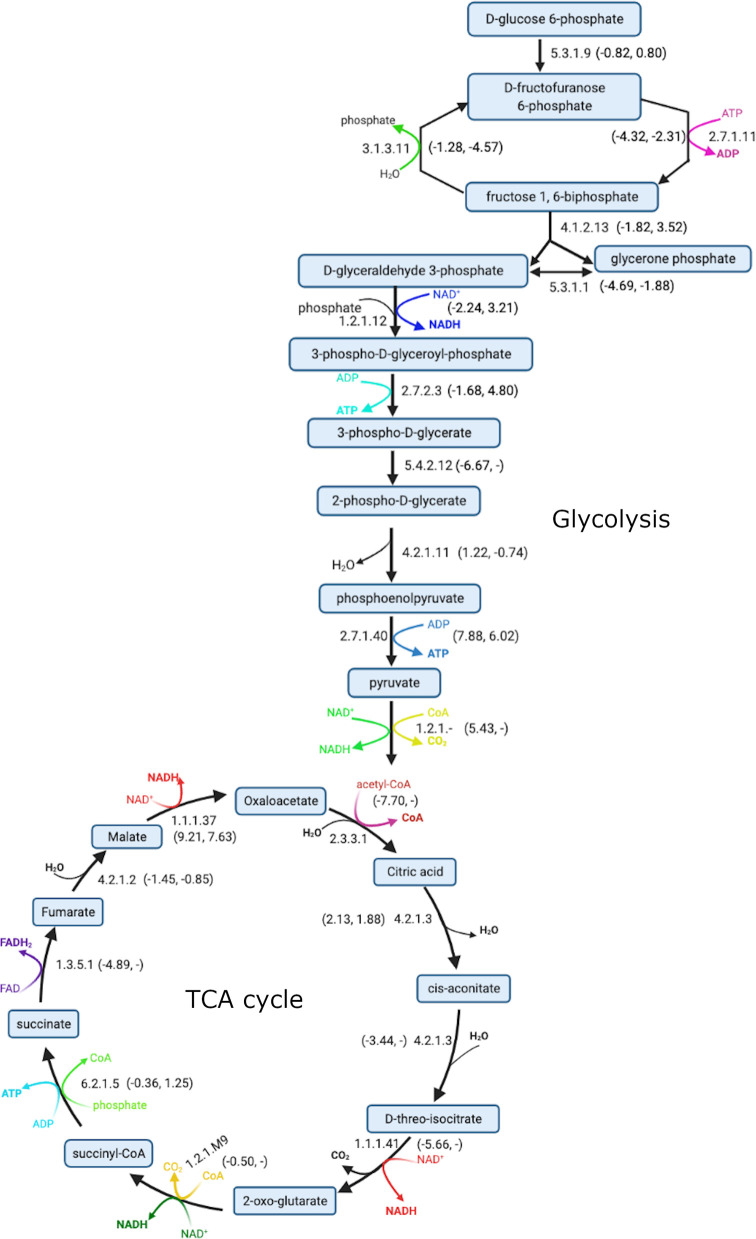
To assess the impact of QC-based methods for accurately predicting and understanding the thermodynamics of metabolic processes, we applied our QC approach to predict the free energy of reactions from the core metabolism of the eukaryotic model organism Yarrowia lipolytica.^64,65 The important metabolic reactions of the TCA/glycolysis cycle that are parts of the central metabolism are shown in Figure 6 and corresponding results in Table 5. QM predicts the citrate synthesis reaction (EC 2.3.3.1) of the TCA cycle to be favorable with a reaction energy of −7.70 kcal/mol, which is similar to the CCM value −8.27 kcal/mol. As temperature increases, ΔG_r^′° decreases to −7.55 and −7.42 kcal/mol at 310 and 320 K, respectively. The QC value at 298.15 K is the most accurate for lysase reactions (4.2.1.3) with ΔG_r value of 2.13 kcal/mol, which is close to the experimental and CCM values of 1.88 and 1.98 kcal/mol, respectively. The error for the lysase reactions increases when the temperature increases from 298.15 to 310 K. We also noticed that the effect of temperature on ΔG_r^′° is not consistent; it increases in some cases but decreases in other cases as the temperature is increased from 298.15 to 320 K. In fact for EC 1.2.1.12, error decreases as the temperature increases. For another lysase reaction (4.2.1.3), which involves a transformation from cis-aconitate to d-threo-isocitrate, CCM demonstrated this reaction to be neutral (−0.12 kcal/mol), whereas our QC calculations revealed thermodynamically favorable at all three temperatures by −3.44 to −2.55 kcal/mol, respectively. Moreover, CCM predicts an unfavorable reaction (positive value) for EC-1.1.4.11, whereas QC predicts a favorable reaction (negative value) with ΔG_r in the range of −5.66 to −6.32 kcal/mol. For the oxidoreductase reaction (1.2.1.M9), in which oxidative decarboxylation of ketoglutarate occurs to form succinyl-CoA, our QC method predicts ΔG_r^′° value of −0.50 kcal/mol whereas CCM overestimates with ΔG_r value of −6.5 kcal/mol.

Figure 6.

Different reactions studied in tricarboxylic acid cycle (TCA) and glycolysis with corresponding EC numbers. QC predicted and experimental (when exists) reaction free energies are provided in parentheses.

Similarly, for another oxidoreductase reaction (EC-1.1.1.37), the CCM, experiment, and DFT approaches all predict unfavorable (positive) ΔG_r^′° with QC overestimating experimental value with an error of 1.58 kcal/mol. For translocase reaction (6.2.1.5), we obtained an error of −1.61 kcal/mol with respect to the experimental reference. We calculated small errors in the range of 0.30 to −0.60 kcal/mol for the lysase reaction (4.2.1.2), which involves hydrolysis of fumarate to form malate.

The performance of the QC method is similar in the glycolysis cycle. The error obtained from the QC method is relatively small (≤2 kcal/mol with respect to the experiment values) for four out of nine reactions for which the experimental reference exists. These reactions correspond to glycolysis reactions EC-5.3.1.9, 2.7.1.11, 4.2.1.11, 2.7.1.40 and have an MAE of 1.89 kcal/mol. This MAE is similar to that observed for the benchmark Set-1 without calibration and Set-2 with calibration. As discussed earlier, it is difficult to accurately calculate ΔG_r^′° for reactions that primarily consist of multiple metabolites with phosphate groups (e.g., 1.2.1.12, 2.7.2.3, 4.1.2.13, 5.3.1.1) compared to other reactions in both TCA and glycolysis. For the specific case of the reaction EC 1.2.1.-, QC gives us ΔG_r in the range of 5.43–6.37 kcal/mol, whereas eQuilibrator is unable to calculate ΔG_r^′° for this reaction, so we used a less accurate group-contribution value of −9.98 kcal/mol as empirical ΔG_r value, which is quite different than our QC estimated value. In this preliminary study, we determined that a certain combination of tools and parameters can predict Gibbs free energy change of a biochemical reaction within a standard error of ∼1.5 kcal/mol, which is comparable to the error in the experimental measurements themselves. Our work will expand the coverage of thermodynamic property data in the biochemistry database of KBase, which also includes the KEGG and MetaCyc reactions and metabolites. Experimental data is currently very limited; however, less computationally expensive group-contribution methods have been applied to further expand this coverage, even these methods only cover 54% of the biochemistry database, leaving large numbers of reactions with completely unknown thermodynamic properties. Additionally, these group and component-contribution methods often carry errors far higher than 1.5 kcal/mol.

Conclusions

Computational chemistry calculations continue to make considerable progress and are approaching a state where predictions of thermochemical parameters can be obtained for metabolites and reactions of biochemical interest. With growing high-performance computing (HPC) power, electronic calculations of large biomolecular systems are more feasible today than ever before, and the computational chemistry NWChem code is capable of using a highly parallelized infrastructure for the accurate prediction of thermodynamic parameters. In this report, we assess the accuracy of the nonempirical computational methods based on quantum mechanics for predicting standard Gibbs reaction energies of metabolic reactions with the goal of developing an accurate automated quantum chemical modeling approach, which can help fill in the gaps in the existing thermodynamic databases that are typically used for constructing genome-scale metabolic models.

We have developed a software stack for ab initio quantum mechanical prediction of standard metabolite and reaction Gibbs free energies using a QC approach. Using this workflow, we have benchmarked several QC methods for predicting standard Gibbs energies for a range of biological reaction types, defined by top-level EC number, and we compared the best DFT method with experimental data in the NIST Thermodynamics of Enzyme-catalyzed Reactions database. A comparison between predictions and experimental data in the first set of diverse reactions revealed that meta-GGA SCAN, when used with 6-311++G** as the basis set and SMD as implicit solvation model, can predict the reaction-free energies with a mean absolute error of 1.74 kcal/mol on Set-1. We observed a relatively large error of 3.48 kcal/mol in Set-2 that when combined with simple calibration can be reduced to 1.64 kcal/mol, which is near the benchmark chemical accuracy of 1 kcal/mol desired from DFT calculations. We further assessed the performance of our best QC-based methods for different categories of reactions. We found that SCAN provided the most accurate results for EC3 and EC5. We show that error increases as the number of metabolites increases in reactions. Error also increases as the negative charge on metabolites increases from −1 to −4. Finally, we developed an automated pipeline to carry out the first-principles quantum mechanical calculations and integrated the workflow within the KBase module for access by the broader research community. In the future, we will be able to predict thermodynamic properties for nearly all of the biochemistry database of KBase with far greater accuracy than ever done before by applying the best quantum mechanical calculations at a large scale to compute these properties, which will subsequently enhance all metabolic models that use these properties to predict thermodynamic flux in microbes, fungi, and plants. The predcition of such biophysical and biochemical properties can be accelerated by using domain-aware machine learning models by incorporating metabolic network based knowledge and QM simulated data.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c00997.

• Analysis of the performance of DFT functionals with respect to each EC number, violin plot before and after calibration, SCAN calculated and experimental reaction-free energies, reactions in TCA/glycolysis, regression parameters for calibration, and details of inverse Legendre transformation are provided. The python scripts and metabolites data used to analyze the QC estimated biochemistry reaction data are available at https://github.com/nkkchem/CompMolNWChem_Thermo/tree/master/nwchem-scripts (PDF)

The authors declare no competing financial interest.

Notes

Project home page: The CME Modelseed narrative https://appdev.kbase.us/narrative/45710 is developed for use in explaining how to utilize the NWCHEM CompMol Thermo KBase Application. All files, source code, and narrative are provided in the https://github.com/nkkchem/CompMolNWChem_Thermo. Free academic and nonprofit research use only.