Optimized Magnesium Force Field Parameters for Biomolecular Simulations with Accurate Solvation, Ion-Binding, and Water-Exchange Properties

Abstract

Magnesium ions play an essential role in many vital processes. To correctly describe their interactions in molecular dynamics simulations, an accurate parametrization is crucial. Despite the importance and considerable scientific effort, current force fields based on the commonly used 12–6 Lennard-Jones interaction potential fail to reproduce a variety of experimental solution properties. In particular, no parametrization exists so far that simultaneously reproduces the solvation free energy and the distance to the water oxygens in the first hydration shell. Moreover, current Mg²⁺ force fields significantly underestimate the rate of water exchange leading to unrealistically slow exchange kinetics. In order to make progress in the development of improved models, we systematically optimize the Mg²⁺ parameters in combination with the TIP3P water model in a much larger parameter space than previously done. The results show that a long-ranged interaction potential and modified Lorentz–Berthelot combination rules allow us to accurately reproduce multiple experimental properties including the solvation free energy, the distances to the oxygens of the first hydration shell, the hydration number, the activity coefficient derivative in MgCl₂ solutions, the self-diffusion coefficient, and the binding affinity to the phosphate oxygen of RNA. Matching this broad range of thermodynamic properties, we present two sets of optimal parameters: MicroMg yields water exchange on the microsecond timescale in agreement with experiments. NanoMg yields water exchange on the nanosecond timescale facilitating the direct observation of ion-binding events. As shown for the example of the add A-riboswitch, the optimized parameters correctly reproduce the structure of specifically bound ions and permit the de novo prediction of Mg²⁺-binding sites in biomolecular simulations.

1. Introduction

Magnesium ions play a crucial role in a large variety of physiological processes such as ATP hydrolysis, cellular signaling, or the catalytic activity of enzymes and ribozymes.¹⁻⁴ In particular, in nucleic acid systems, Mg²⁺ ions are essential to stabilize the tertiary structure, to drive folding or to enable catalytic reactions.^3,5−11 Due to the biochemical importance of Mg²⁺, the modeling of these ions has received significant scientific attention.¹²⁻²¹ However, providing a quantitative description of their interactions and resolving their role in the folding and function of biomolecules is challenging. On the one hand, ab initio quantum mechanical approaches could provide unbiased insights but are limited to small system sizes. On the other hand, classical all-atom simulations allow us to treat much larger and biologically relevant systems but require accurate empirical force fields. Currently, in the most widely used force fields, Mg²⁺ ions are modeled as point charges and the electrostatic, dispersion, and excluded volume interactions are taken into account by a pairwise interaction potential. Hereby, the most common form of the nonelectrostatic interactions is the 12–6 Lennard-Jones (LJ) potential.²²

In order to provide accurate Mg²⁺ models, the two parameters of the LJ potential are typically adjusted to reproduce experimental solution properties such as the solvation free energy ΔG_solv,¹⁷⁻²⁰ the distance to the water oxygens in the first hydration shell R₁,^{13,14,16,18,19} and the coordination number n₁.^13,16−20 In addition to thermodynamic and structural data, including kinetic properties in the parametrization is crucial to capture dynamical processes such as water exchange, ion-binding, or ion-pairing.^16,20,23 However, including kinetic data in the optimization is quite demanding since water exchange is on the microsecond timescale^24,25 and involves the concerted motion of two exchanging water molecules.²⁶ Therefore, simple and computationally efficient methods based on transition state theory are insufficient to provide an accurate rate estimate.²⁶

Moreover, force fields optimized based on ion–water properties alone frequently fail to reproduce thermodynamic and structural properties of electrolytes at nonvanishing salt concentrations.^27,28 It is therefore essential to balance ion–water and ion–ion interactions by including experimental data for activity coefficient derivatives or osmotic pressures in the optimization.²⁸⁻³²

Finally, in order to improve the applicability of the parameters for biomolecular simulations, it has proven useful to consider the interactions between Mg²⁺ and specific ion-binding sites on RNA and proteins.^33,34

Reproducing this broad range of structural, thermodynamic, and kinetic properties by optimizing the force field parameters is tremendously challenging. Despite considerable scientific effort, none of the Mg²⁺ force fields from the literature based on the common 12–6 LJ interaction potentials is able to reproduce all properties with sufficient accuracy.²³ For example, apparently, no parameter combination of the LJ parameters exists that simultaneously reproduces ΔG_solv and R₁.^17,18,20,35 In addition, current force fields underestimate the experimental rate of water exchange by several orders of magnitude leading to unrealistically slow exchange dynamics in biomolecular simulations.^20,23,26 The too slow exchange kinetics has severe consequences since it governs any type of reaction involving the replacement of strongly bound hydration water. Therefore, important biochemical processes such as the transition from outer-to-inner sphere binding, chemical reactions in metalloenzymes or ribozymes, or the transport of ions across cell membranes^{24,25,36−39} become so rare that they cannot be simulated with sufficient statistics or, in many cases, not at all. In order to address this problem, Allnér et al. developed a set of Mg²⁺ parameters that reproduces the experimental exchange rate.¹⁶ However, similar to the ΔG_solv–R₁ parametrization problem, the authors failed to simultaneously reproduce the solvation free energy and the water exchange rate.

The aim of our current work is to provide optimized Mg²⁺ parameters in combination with the TIP3P water model that accurately reproduce all the abovementioned thermodynamic and kinetic properties. However, due to the complexity of the optimization problem, the question arises whether simple 12–6 potentials are sufficient for an accurate description or whether additional terms in the interaction potential are required. In particular, classical nonpolarizable force fields do not include many-body quantum effects explicitly. While Mg²⁺ ions themselves have a low polarizability, they polarize their environment strongly. Therefore, charge-induced dipole interactions and charge transfer can become significant, rendering the interaction between the cation and water more attractive and long-ranged compared to ions with low charge density. It therefore seems appealing to include additional parameters in the interaction potential to account for such polarization effects explicitly. For example, 12–6–4 potentials include an additional r^–4 term that mimics the charge-induced dipole interactions.¹⁹ This parametrization strategy has proven successful in simultaneously reproducing ΔG_solv, R₁, and n₁ for different metal ions.¹⁹ Another possibility is to modify the description of the electrostatic term.^40,41 For example, Jungwirth and co-workers, introduced an additional charge scaling term to reproduce structural properties of aqueous MgCl₂ from neutron-scattering experiments.¹⁵ Nevertheless, it is clear that any model with more parameters is expected to be in general more accurate if optimized properly with respect to all its parameters.

Here, we follow an alternative approach to improve the agreement with experimental properties without introducing more complex force fields. This approach is motivated by the fact that nonpolarizable force fields of the 12–6 type take polarizability into account implicitly. Therefore, instead of enlarging the parameter space of the interaction model, we explore the already existing force field parameter space in all depth. This includes an extensive optimization in an extended range of possible ion–water LJ parameters and a systematic optimization of the ion–ion and ion–RNA combination rules. Our optimization strategy is justified a posteriori by illustrating that the agreement with experimental results is similar or better compared to more complex force fields with additional terms in the interaction potential.

Our optimization procedure is done in three consecutive steps. In the first step, we optimize the ion–water interactions by selecting parameter combinations that reproduce ΔG_solv, R₁, and n₁. In the second step, we optimize the water-exchange kinetics by choosing the combination that reproduces the experimental water-exchange rate (microMg). In addition, we choose a second parameter set that yields accelerated water-exchange dynamics (nanoMg). In the last step, we optimize the ion–ion and ion–biomolecule interactions by introducing scaling factors in the combination rules.³⁰ This allows us to reproduce the activity derivative of MgCl₂ solutions over a broad concentration range. Furthermore, we balance the Mg²⁺–RNA interactions by tuning the pairwise interaction to reproduce the binding affinity toward the nonbridging oxygen atoms of the phosphate group on RNA. Finally, we test the performance of our optimized parameters for the add A-riboswitch. MicroMg leads to stable RNA structures and correctly reproduces the structure of two specifically bound ions. This parameter set is particularly suited to simulate Mg²⁺ in aqueous solutions and its interactions with biomolecules such as nucleic acids, proteins, and lipids. On the other hand, nanoMg yields accelerated water-exchange dynamics and is therefore particularly suited to investigate specific ion-binding including the de novo prediction of inner-sphere ion-binding sites on RNA.

2. Methods

2.1. Molecular Dynamics Simulations

In the following, Mg²⁺ ions are modeled as point charges and the electrostatic, dispersion, and excluded volume interactions are taken into account by a pairwise interaction potential. Hereby, the most common form of the LJ potential is used with a repulsive r^–12 and an attractive r^–6 term. Overall, the interaction potential has the following form

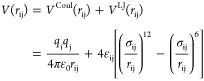1

where q_i and q_j are the charges of atoms i and j, respectively, r_ij is the distance between them, and ϵ₀ is the dielectric constant of vacuum. The parameters σ_ij and ε_ij describe the LJ diameter and interaction strength, respectively. We refrain from adjusting parameters of the Coulomb term while the two parameters of the LJ potential are free to be optimized. The Lorentz–Berthelot combination rules are used to describe the interactions between atoms i and j

2

We used the TIP3P water model⁴² with LJ parameters of σ_o = 0.315061 nm and ε_o = 0.6364 kJ/mol. This choice was motivated by the fact that this water model is frequently used in biomolecular simulations since the AMBER force fields for nucleic acids and proteins have been optimized in combination with TIP3P water.

In order to compare our newly optimized parameters (Table 1) to force fields from the literature, we performed simulations using the 12–6-based parameters by Allnér–Villa,¹⁶ Mamatkulov–Schwierz,²⁰ and Li–Merz¹⁸ (HFE set) and the 12–6–4-based parameters by Li–Merz.¹⁹ For our optimization procedure and for simulations with the Mg²⁺ parameters by Mamatkulov–Schwierz,²⁰ Cl^– parameters were taken from Mamatkulov–Schwierz.²⁰ In all other cases, the Cl^– parameters were taken from Joung–Cheatham.⁴³ The parameters of all force fields used are listed in Table S6. Simulations with force fields of the 12–6 type were performed with GROMACS⁴⁴ (versions 5.1.4, 2018, 2020). Simulations with force fields of the 12–6–4 type were performed with AMBER⁴⁵ (version 2020) since GROMACS does not support 12–6–4 interaction potentials. An overview over the various simulation setups can be found in Section S1.1 (Table S1).

Table 1. Optimized Force Field Parameters for Mg²⁺ for Simulations with the TIP3P Water Model^a.

		microMg	nanoMg
σii	[nm]	0.1019	0.1025
εii	[kJ/mol]	235.80	389.80
σio	[nm]	0.2085	0.2088
εio	[kJ/mol]	12.250	15.750
λσCl		1.8000	1.8000
λεCl		0.1000	0.1000
σMgCl	[nm]	0.4878	0.4884
εMgCl	[kJ/mol]	0.8181	1.0518
λσRNA		1.1375	1.1435
λεRNA		0.3200	0.2500
σMgOP	[nm]	0.2262	0.2277
εMgOP	[kJ/mol]	4.6061	4.6266

^aσ_ii, ε_ii, σ_io, and ε_io are the ion–ion and ion–water LJ parameters. λ_σ^X and λ_ε are the scaling factors for the Lorentz–Berthelot combination rules (eq 3) for the interaction with Cl^– or the RNA atoms, shown exemplary for the interaction between Mg²⁺ and OP. Note that the scaling factors are only valid in combination with the Cl^– parameters from ref (20) and the parmBSC0χ_OL3 RNA parameters.⁵⁰⁻⁵²

Following the work by Fyta and Netz,³⁰ we introduce adjustable scaling parameters λ_σ^X and λ_ε in the Lorentz–Berthelot combination rules to describe the Mg²⁺–Cl^– and the Mg²⁺–RNA interactions. With this, the Lorentz–Berthelot combination rules have the following form

3

where X denotes Cl^– or the atoms of the RNA. Note that these additional scaling factors leave the ion–water interaction parameters unchanged. Therefore, the solvation free energy, the structural properties of the first hydration shell, and the rate of water exchange remain unchanged.

To optimize the ion–RNA interactions, dimethylphosphate (DMP) was used similar to previous work.^16,33,46,47 The DMP molecule contains two nonbridging phosphate oxygen atoms that are considered to be the most important inner-sphere Mg²⁺-binding sites. The force field parameters for the DMP molecule are based on a parametrization with GAFF⁴⁸ (see Section S1.2).

For the add A-riboswitch (PDB ID: 1Y26(49)), the parmBSC0χ_OL3 force field⁵⁰⁻⁵² was used. Adenine was parameterized using GAFF (see Section S1.2).

The analysis was performed with the built-in GROMACS⁴⁴ code and using the MDAnalysis package^53,54 for python.

2.2. Optimization Procedure

In the first step, we optimize the ion–water interaction by performing a grid search in σ_io–ε_io space. Initially, all σ_io–ε_io parameter combinations are selected that match the experimental solvation free energy ΔG_solv, the Mg²⁺–oxygen distance in the first hydrations shell R₁, and the coordination number n₁.

In the second step, we optimize the water-exchange dynamics by calculating the rate of water exchange for the abovementioned parameter combinations. Two parameter sets were chosen: the microMg parameter set yields water exchange on the microsecond timescale and reproduces the experimental rate exactly. The nanoMg parameter set yields water exchange on the nanosecond timescale, thereby providing exchange dynamics that are 2 orders of magnitude faster while still reproducing thermodynamic and structural properties.

In the last step, we optimize the ion–ion and ion–RNA interactions by calculating activity coefficient derivatives and ion-binding affinities by performing a grid search in λ_σ^X and λ_ε parameter space (eq 3). In particular, we used Kirkwood–Buff theory⁵⁵ to calculate the activity coefficient derivatives a_cc and to select the scaling factors λ_σ^Cl and λ_ε that reproduce the experimental activity derivative over a broad range of MgCl₂ concentrations. Subsequently, alchemical transformation calculations were used to calculate the binding affinity of Mg²⁺ toward one of the nonbridging phosphate oxygens of DMP. Finally, the scaling factors λ_σ,ε^RNA that reproduce the experimental binding affinity ΔG_b and binding distance R_b toward the phosphate oxygen were selected.

2.3. Free-Energy Perturbation and Single-Ion Properties

The solvation free energy of neutral MgCl₂ ion pairs ΔG_solv was calculated following the same procedure described in our previous work.²⁰ Since the proton solvation free energy used for absolute solvation free energies can vary according to different sources, we use the more robust solvation free energy of neutral MgCl₂ ion pairs.³⁵ The parameter range used in our current study is σ_io = 0.16–0.24 nm and ε_io = 1.8–28 kJ/mol. Finite size, pressure, and surface effect corrections were applied and simulations with three different box sizes yielded the same result in agreement with previous findings.^35,56 Further details can be found in refs (20, 35) and Section S1.3.

In addition to ΔG_solv, R₁, and n₁, the self-diffusion coefficient D₀ was calculated (see Section S1.4).

2.4. Umbrella Sampling

One-dimensional free-energy profiles were calculated using umbrella sampling.^57,58 The distance between Mg²⁺ and the leaving water molecule r_MgOw1 or between Mg²⁺ and one of the two nonbridging phosphate oxygens of DMP r_MgOP was used as the umbrella coordinate. Note that parameters defining partial charge, atom type, and angle potential of the two nonbridging phosphate oxygens of the DMP were adjusted to be identical to the AMBER RNA force field parameters (parmBSC0χ_OL3,⁵⁰⁻⁵² see Section S1.2). The Mg²⁺ parameters and scaling factors are therefore directly transferable.

The two-dimensional free-energy profile was calculated as a function of the distance between Mg²⁺ and the two exchanging water molecules, r_MgOw1 and r_MgOw2. During the sampling, additional restraints have been applied (see ref (26) and Section S1.5).

2.5. Rate Constant of Water Exchange

The rate constant k of water exchange in the first hydration shell of Mg²⁺ is defined by²⁴

4

where 6 is the coordination number of the first hydration shell and [Mg(H₂O)₆²⁺] is the concentration of hexa-coordinated Mg²⁺ ions.

The most popular theory to calculate reaction rates is transition state theory (TST).^59,60 In simple systems for which the reaction coordinate is exactly known, TST gives an accurate estimate of the rate. However, in complex many-body systems as the ones presented here, TST can fail due to the violation of the non-recrossing hypothesis which forms the cornerstone of the theory. Therefore, in the following, we use TST only to compare to results from the literature or to provide an upper estimate for the rate constant (see Sections S1.6 and S2.3).

In order to provide an accurate rate estimate, we use 1 μs long trajectories of a 1 M MgCl₂ solution and calculate the rate from the number of transitions over time. Hereby, we follow each water molecule individually through the trajectory. The rate constant k is then given by

5

where N_H2O is the number of water molecules in the simulation box and N is the total number of transitions for all water molecules (counting the exchange from first to second hydration shell and the reverse transition as individual events). t_B = N_Mg × p_B × t_sim is the cumulative time the water molecule spends in the first hydration shell of any Mg²⁺ ion. N_Mg is the number of Mg²⁺ ions in the simulation box, p_B = 6/(N_H2O – 6) is the probability of water to be in the first hydration shell, and t_sim is the total simulation time. The number of transitions is calculated from an indicator function which defines the bound and unbound state using two cutoff parameters. Different values for the cutoff parameters were tested and the calculated rates were found to be insensitive to the exact definition (for further details see Section S1.7). Errors are calculated from block averaging⁶¹ by dividing the trajectory into two blocks.

2.6. Kirkwood–Buff Theory

To optimize the scaling factors for ion–ion interactions, 150 ns long simulations were performed at finite salt concentration. The parameter range investigated was λ_σ^Cl = 1–2.6 and λ_ε = 0.01–1. The activity coefficient derivatives a_cc were calculated using Kirkwood–Buff theory.⁵⁵ The optimization was done for a concentration of 0.25 M MgCl₂. Additional simulations at MgCl₂ concentrations of 0.25, 0.5, 1, and 2 M were performed for the final parameter sets. Errors were calculated from dividing the trajectories into three blocks and block averaging. Further details on the calculation of a_cc can be found in Section S1.8.

2.7. Alchemical Transformation

To optimize the scaling factors for ion–RNA interactions, the binding affinity was calculated from alchemical transformations (see Section S1.9 for simulation details). In particular, the binding affinity ΔG_b⁰ and the binding distance R_b toward one of the nonbridging phosphate oxygens of DMP were calculated for the parameter range λ_σ = 0.97–1.23 and λ_ε^RNA = 0.08–1.04. Subsequently, the scaling factors that reproduced the experimental value for ΔG_b⁶² and R_b(63) were selected. Note that in the experimental work by Sigel and Sigel,⁶² two sets of values are given for the binding affinity. The first value is the stability constant of the DMP (log K = 0.45 or equivalently ΔG_b⁰ = −1.036 k_BT). The second value (log K = 1.05 or ΔG_b = −2.418 k_BT) is the stability constant of a modular RNA model. The value takes into account the fourfold access of the phosphate oxygen-binding site on the backbone compared to the nucleobase-binding sites and is appropriate only within the context of the modular RNA model. For our simulations, hence, the first value (log K = 0.45) is appropriate and was used in the optimization.

To further validate the results from alchemical transformations, ΔG_b⁰ and R_b were calculated independently from free-energy profiles obtained for the final parameter sets (Section S1.9). Both methods yielded identical results within error (Section S2.4). Similarly, ΔG_b and R_b for the Allnér–Villa and Panteva–York m12–6–4 parameters³³ were calculated from free-energy profiles. The free-energy profiles were obtained from refs (16, 33) with permission.

Errors were calculated from block averaging by dividing the trajectory of the alchemical transformation into three blocks.

2.8. Performance of MicroMg and NanoMg for the add A-Riboswitch

To test the performance of our optimized parameter sets in a biologically relevant RNA system, the add A-riboswitch was simulated for 100 ns. The simulations included five Mg²⁺ ions positioned as observed in the X-ray structure (PDB ID: 1Y26,⁴⁹ resolution: 2.10 Å). A total of 30 additional Mg²⁺ ions were placed randomly into the simulation box to neutralize the charge of the riboswitch. The rmsd was calculated discarding the first 2 ns for equilibration.

In a second setup, used to predict inner-sphere binding sites with nanoMg, 10 replicas of 200 ns were simulated. Here, all Mg²⁺ ions were placed randomly in the simulation box.

Three-dimensional Mg²⁺ densities were obtained with GROmaρs.⁶⁴ The density was visualized with PyMOL.⁶⁵

3. Results and Discussion

In the following, we present the results from our optimization procedure. The optimization is performed in three sequential steps and is aimed to capture ion–water, ion–ion, and ion–RNA interactions. In particular, the optimization is designed to simultaneously reproduce the solvation free energy, the distance to oxygens in the first hydration shell, the hydration number, the activity coefficient derivative in MgCl₂ solutions, the self-diffusion coefficient, and the binding affinity and distance to the phosphate oxygens of RNA (Tables 2 and 3).

Table 2. Results for Single-Ion, Ion–Ion, and Ion–RNA Properties for the Optimized Parameters in Direct Comparison with Experimental Results^a.

	ΔGsolv [kJ/mol]	R1 [nm]	n1	D0 [10–5 cm2/s]	ΔGb0 [kBT]	Rb [nm]	acc
microMg	–2532.9 ± 1	0.207 ± 0.004	6	0.754 ± 0.006	–0.633 ± 0.6	0.207 ± 0.004	0.93 ± 0.01
nanoMg	–2532.0 ± 1	0.209 ± 0.004	6	0.750 ± 0.004	–0.375 ± 0.1	0.207 ± 0.004	0.97 ± 0.01
exp.	–253279	0.209 ± 0.00466	666	0.70679	–1.03662	0.206–0.20863	0.9380

^aSolvation free energy of neutral MgCl₂ ion pairs ΔG_solv, Mg²⁺–oxygen distance in the first hydration shell R₁, coordination number of the first hydration shell n₁, self-diffusion coefficient D₀, binding affinity toward the phosphate oxygen of DMP ΔG_b⁰, Mg²⁺–phosphate oxygen distance in the inner-sphere conformation R_b, and a_cc is the activity derivative of a MgCl₂ solution at 0.25 M concentration. ΔG_b is derived from the log stability constant of the DMP (log K = 0.45) given in ref (62).

Table 3. Properties of Water Exchange from Simulations and Experiments^a.

	N	k [s–1]
microMg	376 ± 56	(8.04 ± 1.20) × 105
nanoMg	52,086 ± 120	(1.11 ± 0.003) × 108
Mamatkulov–Schwierz	2 ± 2	24.0 ± 8.8 from ref (26)
Allnér–Villa	2 ± 2	<2.4 × 105
Li–Merz (12–6)	2 ± 2	<3.5 × 104
Li–Merz (12–6–4)	6720 ± 160	(1.44 ± 0.03) × 107
exp.	248,25 31424	5.3 × 105 from ref (24), 6.7 × 105 from ref (25)

^aNumber of transitions N in 1 μs for different force fields in 1 M MgCl₂ solutions. The experimental value^24,25 is obtained from eq 5. The rate constant k is calculated from the number of transitions for microMg, nanoMg, and Li–Merz (12–6–4). The value for Mamatkulov–Schwierz is taken from ref (26). For Allnér–Villa and Li–Merz (12–6), an upper estimate is given based on TST since the number of transitions is insufficient to calculate the rate from eq 5. The errors for N and k are obtained from block averaging.

Matching this broad range of structural and thermodynamic properties, we present two sets of optimal parameters: MicroMg yields water exchange on the microsecond timescale and matches the experimental exchange rate. NanoMg yields water exchange on the nanosecond timescale. Subsequently, we validate the performance of our optimized parameter sets for the example of the add A-riboswitch.

3.1. Optimization of Solvation Free Energy, Mg²⁺–Water Distance, and Coordination Number

In the first step, we optimize the ion–water interactions by adjusting the LJ parameters σ_io and ε_io to reproduce the experimental solvation free energy ΔG_solv, the distance to the oxygens in the first hydration shell R₁, and the coordination number n₁ (Figure S1). Since ΔG_solv includes the energy and entropy of ion hydration, it is considered the most important thermodynamic property in the development of accurate force field parameters.³⁵ Moreover, Mg²⁺ is coordinated by six water molecules arranged in octahedral symmetry.⁶⁶ In order to correctly capture the structure of the first hydration shell, we include R₁ and n₁ in our optimization.

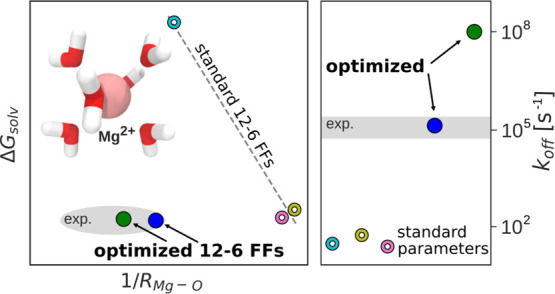
Reproducing ΔG_solv and R₁ with force fields of the 12–6 type is challenging. As illustrated in Figure 1A, in previous work, no parameter combination could be found that matches both properties simultaneously.^{16−18,20,35} In order to improve the agreement, we have considered a much larger σ_io and ε_io range in the optimization (Figure S1). As shown in Figures 1A and S1 and Table 2, this allows us to accurately reproduce ΔG_solv, R₁, and n₁. Hereby, the agreement with experimental results is comparable to 12–6–4 interaction potentials which have one additional adjustable parameter. Based on the results for ΔG_solv and R₁, we conclude that additional terms in the interaction potential that mimic polarization effects are not strictly necessary. Nevertheless, charge-induced dipole interactions and charge transfer are particularly important for Mg²⁺ ions in aqueous solutions. Both effects render the interaction potential more attractive and long-ranged compared to metal cations with lower charge density. This becomes evident from Figure 1B: the interaction potential of our optimized parameter sets microMg and nanoMg and the 12–6–4 potential by Li–Merz are similar in shape and more attractive and long-ranged compared to previous 12–6-based force fields. Capturing the long-ranged interactions is therefore crucial to correctly describe ion–water interactions in general and ΔG_solv and R₁ in particular.

Figure 1.

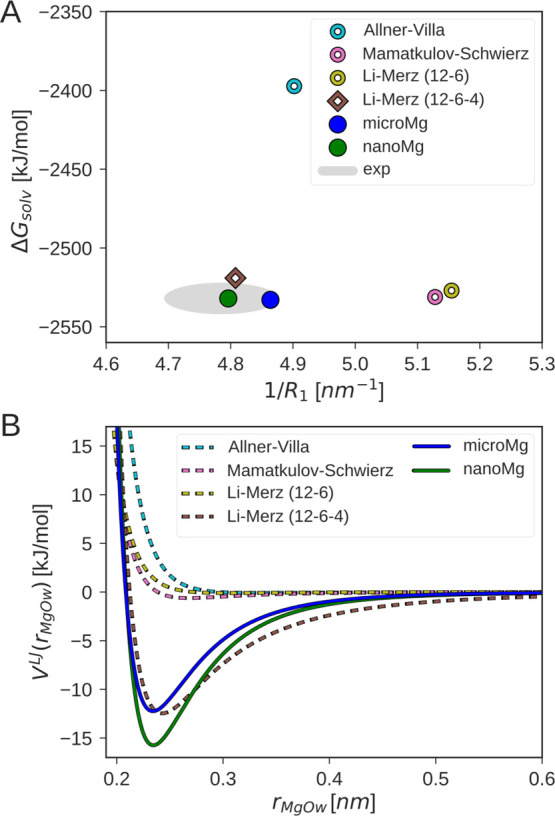
Comparison of the optimized parameter sets microMg and nanoMg with force fields from the literature^16,18−20 and experimental data. (A) Solvation free energy ΔG_solv for neutral MgCl₂ pairs in correlation with the inverse of the Mg²⁺–oxygen distance of the first hydration shell 1/R₁. The gray area indicates the experimental results from refs (66, 70). (B) Lennard-Jones interaction potential V^LJ as a function of the Mg²⁺–oxygen distance r_MgOw for different Mg²⁺ force fields and TIP3P water.

3.2. Optimization of the Water-Exchange Rate

In aqueous solutions, water molecules from the first tightly bound hydration shell around Mg²⁺ exchange with the second hydration shell on the microsecond timescale.^24,25 In the second step of our parametrization, we optimize the water-exchange dynamics by calculating the rate constant k of water exchange in the range of parameter combinations that reproduce ΔG_solv, R₁, and n₁ obtained in the previous optimization step. Hereby, special emphasis is placed on an accurate calculation of the rate constant. The reason is that the popular and frequently used transition state theory (TST) can fail due to the violation of the noncrossing hypothesis. In fact, recent work shows that for water exchange, TST based on the Mg²⁺–water distance overestimates the true rate by more than 2 orders of magnitude.²⁶ In order to provide a more accurate rate estimate, we use 1 μs long simulations of 1 M MgCl₂ solutions to calculate the rate from the number of transitions (eq 5). Based on this, two parameter combinations were selected (Table 3): the parameter set microMg yields water exchange on the microsecond timescale in agreement with experimental results.^24,25 The parameter set nanoMg yields water exchange on the nanosecond timescale. Hereby, we chose the parameter combination that leads to the fastest exchange while still matching all other experimental properties.

Figure 2A compares the number of exchanges for different force fields with the 248–314 transitions expected from experiments.^24,25 The results reveal that water exchange is several orders of magnitude too slow for the force fields by Allnér–Villa,¹⁶ Mamatkulov–Schwierz,²⁰ and Li–Merz (12–6).¹⁸ Surprisingly, the rate calculated from the Allnér–Villa parameters deviates from the experimental results despite being optimized on the exchange kinetics. The reasons are twofold: the Allnér–Villa parameters were optimized with the mTIP water model,⁶⁷ and transferring the parameters to TIP3P leads to deviations (Section S2.2). In addition, the rate used in the optimization was calculated from TST and might therefore deviate notably from the true rate as discussed above. The number of exchanges for the Li–Merz 12–6–4 parameters is significantly higher and thus the rate overestimates experiments by 1 order of magnitude (Table 3). As expected from the current optimization procedure, the number of transitions for microMg closely matches the experimental value while nanoMg yields the highest number of exchanges of all force fields considered here.

Figure 2.

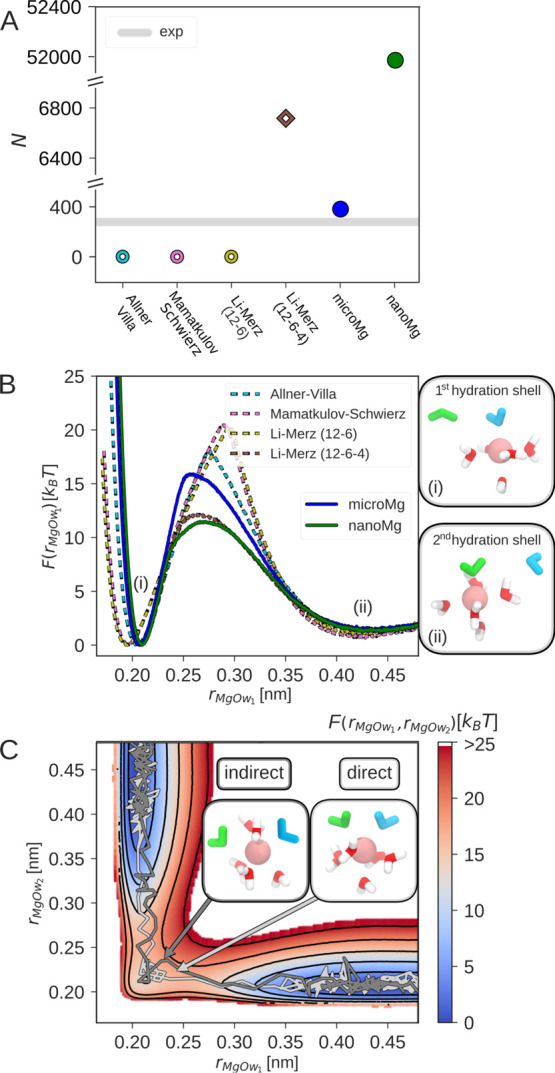
Water exchange in the first hydration shell of Mg²⁺. (A) Number of exchange events in 1 μs for different force fields in 1 M MgCl₂ solutions. The gray horizontal line indicates the experimental values^24,25 (Table 3). (B) One-dimensional free-energy profiles as a function of the distance between Mg²⁺ and the leaving water molecule r_MgOw1 for different force fields. The snapshots show representative conformations in the two stable states: (i) before exchange: leaving water (Ow₁ shown in blue) is in the first hydration shell and incoming water (Ow₂ shown in green) is in the second hydration shell. (ii) After exchange: Ow₁ is in the second and Ow₂ is in the first hydration shell. (C) Two-dimensional free-energy profile as a function of the distances between Mg²⁺ and the two exchanging waters, r_MgOw2 and r_MgOw1, obtained with the microMg parameters. The insets show representative snapshots of the transition state along the direct (dark gray) and the indirect (light gray) exchange pathway. The energy contour spacing corresponds to 5 k_BT.

Qualitative insights into the cause of the vastly different timescales of water exchange for the different force fields can be gained from the free-energy profiles along the Mg²⁺–water distance r_MgOw1 (Figure 2B). The free-energy profiles have two minima corresponding to the first and second hydration shell [shown in snapshots (i,ii) of Figure 2B]. The two minima are separated by a high free-energy barrier which corresponds to the cost of removing one water from the tightly bound first hydration shell. The height of the barriers differs by more than 10 k_BT for the different force fields. Force fields with slow exchange kinetics [Li–Merz (12–6), Mamatkulov–Schwierz, and Allnér–Villa] have high energetic barriers of 20.4, 20.7, and 18.0 k_BT. Force fields with comparatively faster exchange kinetics [microMg, Li–Merz (12–6–4), and nanoMg] have lower energetic barriers of 15.9, 12.2, and 11.5 k_BT, respectively.

Water-exchange dynamics is, however, more complex than the one-dimensional free-energy profiles might suggest. It involves the concerted motion of two exchanging water molecules in which the molecular void provoked by the leaving water is immediately filled by an entering water molecule.²⁶ In order to provide a more realistic picture, Figure 2C shows the two-dimensional free-energy profile as a function of the distance of the two exchanging waters r_MgOw1 and r_MgOw2 obtained with the microMg parameters (for nanoMg see Figure S3). Two exchange pathways are shown corresponding to a direct and indirect exchange mechanism in agreement with our previous results.²⁶

In summary, the optimized microMg parameters yield much closer agreement with experimental water exchange rates compared to force fields from the literature (Table 3). In addition, the self-diffusion coefficient D₀ matches the experimental value without further optimization (Table 2).

3.3. Optimization of Activity Derivative and Binding Affinity

In the last step of our parametrization, we sequentially optimize the ion–ion and the ion–RNA interactions. In order to correctly capture ion-pairing, a proper balance between ion–water and ion–ion interactions is required. This balance is achieved by optimizing the parameters based on experimental activity coefficients.²⁸ Following the seminal work by Fyta and Netz,³⁰ we introduce scaling parameters in the Lorentz–Berthelot combination rules (eq 3). The advantage of this approach is that it allows us to reproduce the experimental activity coefficient derivative a_cc over a broad concentration range for MgCl₂ solutions (Figure 3A) without changing ΔG_solv, R₁, n₁, D₀, or k. In fact, with the standard combination rules (eq 2), a_cc was found to be too small for all parameter combinations investigated, in agreement with previous findings.^17,20,30 Since no solid foundation for the standard combination rules exists, it is not surprising that they fail to capture cation–anion interactions. Targeting this interaction in the optimization therefore appears to be the natural choice. The resulting scaling factors (Table 1) reflect that without modifications, the Mg²⁺–Cl^– interactions are too attractive. This problem can easily be corrected by increasing the effective diameter of the outer-sphere ion pair via λ_σ^Cl and by reducing the cation–anion LJ energy via λ_ε.

Figure 3.

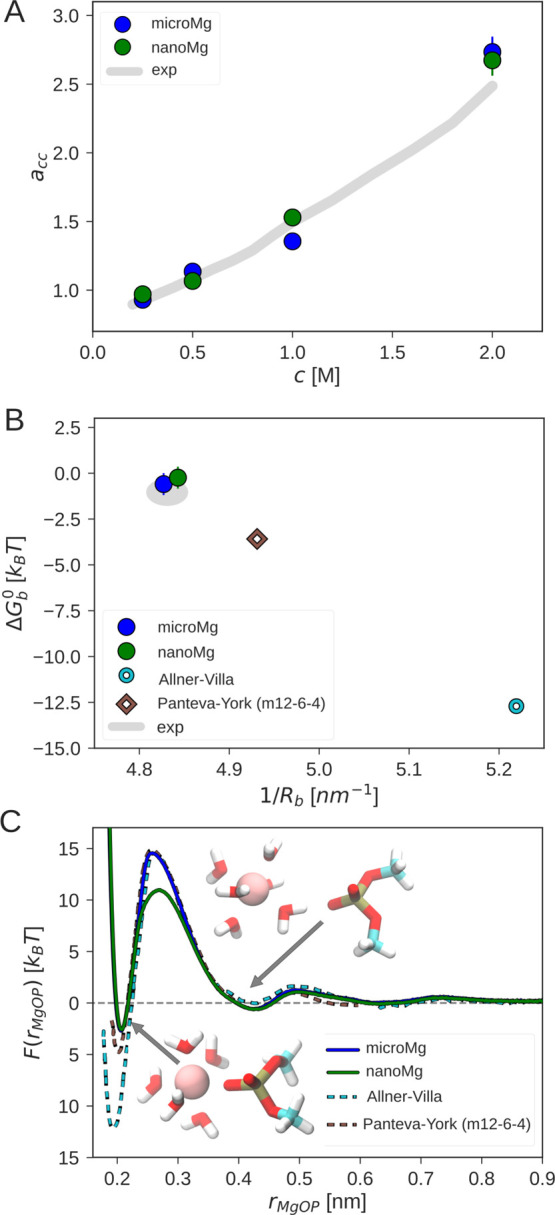
Optimization of ion–ion and the ion–RNA interactions. (A) Activity derivative a_cc as a function of the MgCl₂ salt concentration with the optimized scaling factors for microMg and nanoMg (Table 1) and from experiments.⁸⁰ (B) Binding affinity ΔG_b⁰ in correlation with inverse of the Mg²⁺–phosphate oxygen distance 1/R_b. The experimental values (gray) are taken from refs (62, 63). (C) Free-energy profiles as a function of the distance between Mg²⁺ and the phosphate oxygen of DMP, r_MgOP, for different force fields. The Allnér–Villa and Panteva–York free-energy profiles were obtained from refs (16, 33) with permission. The insets show Mg²⁺ in the inner- and outer-sphere conformation.

So far, the optimization was performed based on bulk ion properties. However, this does not guarantee that the interactions of Mg²⁺ and specific ion-binding sites on biomolecules are described correctly. For example, the 12–6–4 Li–Merz parameters significantly overestimate the Mg²⁺–RNA interactions.³³ In order to solve this problem, modified m12–6–4 parameters were developed by Panteva and co-workers to reproduce experimental site-specific binding affinities.³³

Here, we introduce ion–RNA scaling parameters in the Lorentz–Berthelot combination rules (eq 3) that are optimized based on experimental binding affinities⁶² and structural properties of the inner-sphere conformation.⁶³ Similar to previous work,^16,33,46,47 DMP was used. The DMP molecule contains two nonbridging phosphate oxygen atoms that are considered to be the most important inner-sphere Mg²⁺-binding sites on larger RNA molecules.^3,62,68,69 Similar to a_cc, the unmodified combination rules result in Mg²⁺–RNA interactions that are too attractive, possibly reflecting the small excess polarizability of Mg²⁺. Again, this can be corrected by increasing the effective diameter via λ_σ^RNA and by reducing the cation–RNA LJ energy via λ_ε (Table 1, Section S2.4).

Figure 3B summarizes the binding affinity ΔG_b⁰ and binding distance R_b for different force fields from the literature. As expected, the Allnér–Villa parameters show the largest deviations from the experimental results. The Panteva–York m12–6–4 parameters provide significant improvement. Finally, the optimized ion–RNA scaling factors for microMg and nanoMg provide the closest agreement with experimental results.

Initial insights into the process of ion-binding to RNA is obtained from the free-energy profiles as a function of the distance between Mg²⁺ and the phosphate oxygen of DMP for different force fields (Figure 3C). The free-energy profiles have two stable states corresponding to the inner-sphere and the outer-sphere conformation (inset of Figure 3C). In the inner-sphere conformation, Mg²⁺ forms a direct contact with the phosphate oxygen of the DMP. In the outer-sphere conformation, the contact is mediated by a water molecule from the first hydration shell. There are clear deviations between the free-energy profiles from different force fields. The different depths of the first minimum reflect the different binding affinities as discussed above. Consequently, force fields that overestimate the binding affinity have a higher free-energy barrier and therefore slower dissociation kinetics. Similarly, the minimum in the free-energy profile is shifted to the left for force fields that underestimate R_b.

The free-energy barrier for nanoMg is 3.5 k_BT lower compared to microMg while ΔG_b⁰ and R_b are identical. Removing a water molecule from the first hydration shell for nanoMg requires less work as reflected in the higher water-exchange rate (Table 3). Mg²⁺ association and dissociation is therefore 2–4 orders of magnitude faster compared to other force fields.

In summary, matching ΔG_b⁰, R_b, and the rate of water exchange is crucial to describe the kinetics of ion binding and the structure of specifically bound Mg²⁺ ions. In this respect, microMg is particularly suited to reproduce the distribution and exchange of Mg²⁺ as closely as possible. On the other hand, the ion-binding kinetics for nanoMg is significantly enhanced. This opens up the possibility to use nanoMg to predict inner-sphere ion-binding sites from straightforward simulations without the necessity to use enhanced sampling techniques.⁷⁰

3.4. Performance of MicroMg and NanoMg for the add A-Riboswitch

In order to evaluate the performance of the optimized parameter sets, the add A-riboswitch was simulated (Figure 4A). This riboswitch is particularly suited to validate the parameters since experimental^49,71−73 and simulation results^16,74 exist.

Figure 4.

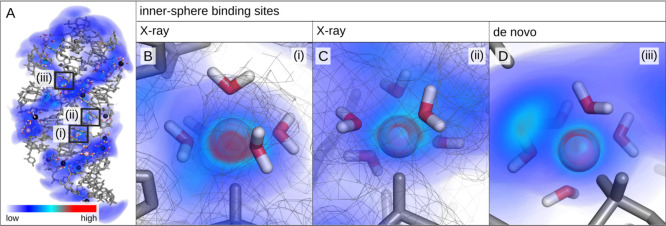
Representative snapshot of the add A-riboswitch from simulations with the nanoMg parameter set and three-dimensional Mg²⁺ probability density. The probability density is low in the blue regions (diffusive ions) and high in the red regions (specifically bound ions). Selected inner-sphere (pink) and outer-sphere (black) Mg²⁺ ions are shown including the water molecules in their first hydration shell. Snapshots (i–iii) show the most probable ion-binding sites predicted from simulations with nanoMg. Snapshots (i,ii) coincide with the two inner-sphere binding sites reported in the X-ray structure.⁴⁹ The experimental electron density is shown as gray mesh.

The experimental X-ray structure⁴⁹ includes five Mg²⁺ ions (PDB ID: 1Y26,⁴⁹ resolution: 2.10 Å). Two ions are bound in inner-sphere conformation to phosphate oxygens, two ions are involved in outer-sphere interactions, while the remaining ion is a crystallization artifact due to crystal packing.

3.4.1. Stability and Specific Ion-Binding Sites with MicroMg and NanoMg

Initially, we investigate that microMg and nanoMg do not affect the stability of the tertiary structure. In 100 ns simulations, both parameter sets yield stable structures that are close to the experimental structure with an rmsd of 0.28 (microMg) and 0.24 nm (nanoMg). Both values are slightly smaller compared to the rmsd of 0.30 nm obtained with the Allnér–Villa parameters.¹⁶

With microMg, both inner-shell ions of the X-ray structure remain bound over the duration of the simulation. The distance of Mg²⁺ to the phosphate oxygen of the first binding site (Figure 4B) is 0.208 ± 0.005 nm in close agreement with the 0.210 nm in the X-ray structure. The average distance of Mg²⁺ to the oxygen phosphate of the second binding site (Figure 4C) is 0.209 ± 0.005 nm. This value is smaller compared to the 0.244 nm in the X-ray structure. Note, however, that the experimental value is located in the exclusion range and might be over-rated as judged by the assignment criterion of 0.206–0.208 nm.⁶³ With nanoMg, the distances are similar with 0.209 ± 0.012 nm for both binding sites. Here, however, the ions exchange with bulk due to the faster exchange kinetics discussed above. After 100 ns, 9 Mg²⁺ ions are observed in inner-sphere conformation with nonbridging phosphate oxygens. No inner-sphere contacts other than with phosphate oxygens are observed in agreement with experimental results, reproducing that nucleobase nitrogens and carbonyls are weak inner-sphere Mg²⁺-binding sites.^63,75

In addition, about 20 outer-sphere contacts are formed with microMg and nanoMg, similar to the results with the Allnér–Villa parameters.¹⁶ The outer-sphere interactions are mediated by a water molecule and involve besides phosphate oxygens also the oxygen and nitrogen atoms of the nucleobases and the ribose oxygens (Section S2.5).

3.4.2. Identification and de novo Prediction of Inner-Sphere Binding Sites with NanoMg

With nanoMg, the ion-binding kinetics is 2–4 orders of magnitude faster compared to other force fields. Consequently, the formerly rare events of Mg²⁺ association and dissociation can now be observed directly in straightforward simulations. To evaluate this behavior, in a second step, all ions were placed randomly within the simulation box. Figure 4 shows the distribution of Mg²⁺ ions around the add A-riboswitch after a cumulative duration of 2 μs. The riboswitch is surrounded by highly mobile, diffusive ions leading to a low probability density (blue regions). In addition, about 16 Mg²⁺ ions bind in inner-sphere conformation leading to regions of high probability density (red regions). The three ion-binding sites with the highest probability density are shown in Figure 4B–D. Interestingly, the two most probable binding sites correspond to the two inner-sphere binding sites from the X-ray structure. Hereby, the experimental electron density is on top of the probability density calculated from the simulations (Figure 4B,C). This illustrates that the nanoMg parameters are particularly useful to predict inner-sphere binding sites. One such prediction, corresponding to the third most likely binding site, is shown in Figure 4D (see Section S2.6 for additional predictions). In addition, the simulations provide an unique atomistic description of the binding site including the exact coordination chemistry of Mg²⁺, RNA, and hydration water.

4. Conclusions

The importance of Mg²⁺ in biological systems has driven the development of force field parameters for molecular dynamics simulations. However, Mg²⁺ force fields in combination with TIP3P water have fundamental drawbacks in reproducing a broad range of structural, thermodynamic, and kinetic properties. Our current work shows that the effects of polarizability that are presumably the cause of the deviations can be included by tuning the parameters of the 12–6 Lennard-Jones potential in an enlarged parameter range and by modifying the standard combination rules. Our results show that this allows us to accurately reproduce the experimental solvation free energy, the distances to the oxygens of the first hydration shell, the hydration number, the activity derivative in MgCl₂ solutions, the self-diffusion coefficient, and the binding affinity and distance to the phosphate oxygens of RNA.

In particular, by increasing the LJ interaction strength between Mg²⁺ and water, the interaction potential becomes more attractive and long-ranged, thereby mimicking the charge-induced dipole and charge-transfer effects that Mg²⁺ ions cause in their environment. This in turn allows us to correctly describe ion–water interactions as quantified by the solvation free energy and the structure of the first hydration shell.

The activity coefficient derivative and the binding affinity to RNA reveal that the Mg²⁺–Cl^– and Mg²⁺–RNA interactions described by the standard combination rules are too attractive. The reason is that the combination rules do not reflect the law of matching water affinities according to which ions with high charge density have more tightly bound first hydration shells compared to ions with low charge density.⁷⁶ This problem can easily be solved by introducing scaling factors that reduce the LJ energy of Mg²⁺–Cl^– pairs or the Mg²⁺–RNA interactions while simultaneously increasing their effective diameters. The advantage of this approach is that it leaves the ion–water interactions unchanged and can therefore be transferred to other anions or other binding sites on biomolecules. On RNA, for instance, the nucleobase nitrogens and carbonyl atoms could be considered as additional Mg²⁺-binding sites.⁶² However, special care must be taken since the Mg²⁺ ions are unlikely to bind in the inner-sphere binding mode^63,77,78 and the binding affinity of the inner- and outer-sphere conformation can differ significantly.⁶⁹

In progressing toward improved force fields, special emphasis is placed on an accurate calculation of the water-exchange rate, circumventing the shortcomings of transition state theory.²⁶ Matching the abovementioned broad range of thermodynamic properties, we present two sets of optimal parameters: microMg which yields water exchange on the microsecond timescale in agreement with experiments and nanoMg which yields water exchange on the nanosecond timescale. As shown for the example of the add A-riboswitch, microMg yields stable RNA structures and reproduces the structure of specifically bound ions. NanoMg yields accelerated water exchange and ion-binding dynamics and is therefore particularly suited for the de novo prediction of Mg²⁺-binding sites on biomolecules.

In summary, the Mg²⁺ parameters presented here provide an efficient and highly accurate model for the simulation of Mg²⁺ ions in aqueous solutions and their distribution and exchange around biomolecules such as nucleic acids, proteins, or lipids.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.0c01281.

• Additional information regarding the methods presented in the main manuscript are presented. Additional results including a study of box size dependencies on the calculation of solvation free energies, a brief discussion of the performance of Allnér–Villa in combination with mTIP3P water, a study of the dependency of the number of transitions on calculation parameters, a comparison of the two-dimensional free-energy profiles of microMg and nanoMg, a comparison of different methods to obtain binding affinities and distances, a brief discussion of outer-sphere ion-binding sites, and additional de novo-predicted inner-sphere ion-binding sites are presented (PDF)

The authors declare no competing financial interest.

Notes

The parameter files are freely available at https://github.com/bio-phys/Magnesium-FFs.