Characterization of Groundwater Recharge and Flow in California's San Joaquin Valley From InSAR‐Observed Surface Deformation

Abstract

Surface deformation in California's Central Valley (CV) has long been linked to changes in groundwater storage. Recent advances in remote sensing have enabled the mapping of CV deformation and associated changes in groundwater resources at increasingly higher spatiotemporal resolution. Here, we use interferometric synthetic aperture radar (InSAR) from the Sentinel‐1 missions, augmented by continuous Global Positioning System (cGPS) positioning, to characterize the surface deformation of the San Joaquin Valley (SJV, southern two‐thirds of the CV) for consecutive dry (2016) and wet (2017) water years. We separate trends and seasonal oscillations in deformation time series and interpret them in the context of surface and groundwater hydrology. We find that subsidence rates in 2016 (mean −42.0 mm/yr; peak −345 mm/yr) are twice that in 2017 (mean −20.4 mm/yr; peak −177 mm/yr), consistent with increased groundwater pumping in 2016 to offset the loss of surface‐water deliveries. Locations of greatest subsidence migrated outwards from the valley axis in the wetter 2017 water year, possibly reflecting a surplus of surface‐water supplies in the lowest portions of the SJV. Patterns in the amplitude of seasonal deformation and the timing of peak seasonal uplift reveal entry points and potential pathways for groundwater recharge into the SJV and subsequent groundwater flow within the aquifer. This study provides novel insight into the SJV aquifer system that can be used to constrain groundwater flow and subsidence models, which has relevance to groundwater management in the context of California's 2014 Sustainable Groundwater Management Act (SGMA).

Key Points

• The timing, magnitude, and spatial pattern of deformation in the San Joaquin Valley changes between dry and wet water years

• Seasonal amplitudes and peak seasonal uplift timing of deformation indicate possible recharge locations and pathways for groundwater flow

• Geodetic observations have the potential to provide insight into aquifer dynamics at policy relevant scales

1. Introduction

California's Central Valley (CV) is a major agricultural production center with an economic output of tens of billions of dollars (USD) annually (Howitt et al., 2015). Because agricultural water demand exceeds supply from precipitation and surface water even in climatologically wet years (Faunt et al., 2016), groundwater is a key resource for CV water users. Periods of prolonged and intense drought threaten economic and agricultural production by limiting access to surface‐water supplies, which motivates increased reliance on groundwater (Hanson et al., 2012). This was particularly evident in the semi‐arid southern two‐thirds of the CV (the San Joaquin Valley or SJV) during the 2012–2016 drought (Lund et al., 2018). Sustained dependency on groundwater resources, such as occurs in the SJV, may jeopardize future groundwater availability if extraction persistently exceeds aquifer recharge (Scanlon et al., 2012).

The hydrological system of SJV is diverse in terms of availability, storage, and conveyance. During an average water year (WY; October 1 to September 30), the SJV receives most of its precipitation between November and April (∼85%), with half occurring between December and February (Faunt, 2009; Williamson et al., 1989). Geographically, this precipitation typically falls on the western slopes of the Sierra Nevada as rain and snow, and much of that which does not directly run off is stored in seasonal snowpack, soil moisture, and groundwater (Enzminger et al., 2019). Much of the drainage from these sources of water storage funnels into streams and rivers, with about 84% of the total unimpaired streamflow (surface‐water runoff not regulated by dams, reservoirs, or conveyance systems) entering the SJV from January to June (Williamson et al., 1989). Water is transported from north to south and from east to west via conveyance systems such as the California Aqueduct and the Friant‐Kern Canal (Figure 1). Networks of canals and artificial waterways distribute surface water from these primary diversions and natural streamflow throughout the valley for agricultural, industrial, and urban use.

Figure 1.

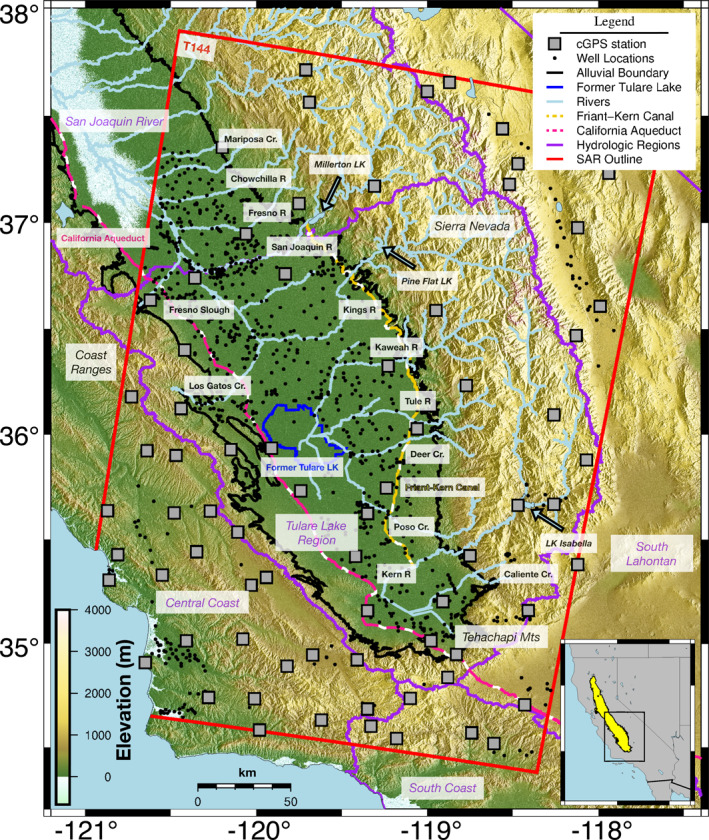
Topographic map of study region in the San Joaquin Valley (elevation data from the Satellite Radar Topography Mission). Inset (bottom right) shows the study region over California with the Central Valley (yellow). Synthetic aperture radar (SAR) data used are provided by the Sentinel‐1A/B missions, descending track 144 (red outline). A subset of continuous Global Positioning System (cGPS) station locations in the Geodesy Advancing Geosciences and EarthScope (GAGE) network (gray squares) are used to correct and reference each interferogram. We note key hydrological features such as monitoring well locations with data spanning April 2015 to October 2017 (black dots), the alluvial boundary of the valley floor (black outline), the former Tulare Lake (blue outline), rivers entering the valley (light blue lines), the Friant‐Kern Canal (dashed yellow line), the California Aqueduct (dashed pink line), and hydrologic regions as designated by the Department of Water Resources (DWR) (purple outlines).

Interannual variation in surface‐water availability, as well as within‐year differences in the timing of natural (river) and imported (state and federal project) surface water, plays an important role in SJV water use and groundwater recharge. In an average water year, surface water accounts for ∼60% of water demand with groundwater supplementing the remaining ∼40% (Faunt et al., 2016). During dry or drought years, more groundwater is typically used (some years accounting for as much as 70% of the demand) due to reduced surface‐water availability (e.g., Faunt et al., 2016). In the dry WY2016, e.g., total unimpaired and natural local inflows to the San Joaquin Valley (San Joaquin and Tulare Lake basins) totaled 7,167 thousand acre‐feet (TAF) while state and federal projects imported 3,476 TAF. This is in contrast with wet years, such as WY2017, where total natural inflows were 22,530 TAF and imports from state and federal projects were 6,431 TAF (Public Policy Institute of California, 2019). During these wet years, surface‐water use increases while groundwater use declines, with excess surface water available for groundwater banking (Scanlon et al., 2016) and natural recharge (Faunt, 2009; Meixner et al., 2016). Generally, SJV natural inflows peak in March, while project water imports peak months later in July at the height of surface‐water irrigation (U.S. Bureau of Reclamation, 2020). Thus, both the dry and wet year magnitudes of local and imported supplies, and differences in their timing, are expected to be reflected in recharge dynamics. To better understand the resiliency of groundwater reservoirs for future use, there is a great need for assessing how and where both natural and artificial aquifer recharge occurs, whether via managed recharge, return flow from irrigation, direct precipitation, or river runoff.

Directly observing the state of aquifer systems remains challenging because of the sparsity of quality in‐situ point measurements (both in time and space). However, groundwater extraction and recharge induce Earth surface displacements that can be observed using geodetic techniques. In sedimentary basins such as the SJV, surface displacements are often attributed to the expansion or compaction of the aquifer system in response to pore‐pressure variations (Poland & Davis, 1969). This poroelastic deformation is governed by the law of effective stress (Terzaghi, 1925), which is directly related to groundwater levels (hydraulic head). Furthermore, poroelastic deformation can be inelastic or elastic. Wherever the effective stress within the aquifer‐system matrix exceeds the preconsolidation stress, often taken to be the lowest previous level of hydraulic head, a new preferred grain realignment with reduced capacity for water storage may result (Leake, 1990). For fine‐grained deposits such as clay and silt, this consolidation can lead to inelastic deformation, which is manifested as permanent land subsidence (Leake, 1990). Changes in hydraulic head that do not result in irreversible realignment of grains result in elastic deformation, which includes reversible land subsidence or uplift.

The sediment‐filled trough that is the SJV aquifer system can be described as an interbedded mix of sand and gravel with finer‐grained deposits of clay and silt (Page, 1986). Deposited as coalescing alluvial fans, there are generally thicker lenses of coarser‐grained sediments at the valley margins and a higher clay content nearer the valley axis (Page, 1986). Clay and silt deposits are particularly susceptible to inelastic deformation, resulting in observed subsidence of as much as tens of centimeters annually in the SJV (e.g., Faunt et al., 2016). While the link between recent land surface subsidence and groundwater extraction in the SJV has been well documented and attributed to the inelastic aquifer‐system response to pumping (Chaussard & Farr, 2019; Farr & Liu, 2014; Faunt et al., 2016; Jeanne et al., 2019; Murray & Lohman, 2018; Ojha et al., 2018, 2019; Smith et al., 2017), the relatively subtle surface uplift response related to the recovery of local groundwater levels at subannual time scales has not been extensively studied.

In 2014, California passed the Sustainable Groundwater Management Act (SGMA) to protect its groundwater resources. To understand the evolution of groundwater resources under natural and human forcing, it is critical to characterize and monitor the aquifer‐system response to variable climatological regimes and with respect to anthropogenic management over short (<1 year) and long (≥1 year) time periods. Here, we leverage continuous Global Positioning System (cGPS) daily positions and interferometric synthetic aperture radar (InSAR) techniques (Neely et al., 2020) to evaluate the time evolution of SJV surface deformation associated with changes in groundwater levels across dry and wet water years. We present a new methodology for investigating the elastic (reversible) deformation associated with the seasonal response of the aquifer system by analyzing both the magnitude and timing of peak seasonal surface uplift at high spatial resolution (100 m). Interpreting our results in the context of relevant hydrological features and data, we provide insight into the movement of water through the SJV aquifer system, with relevance to groundwater management.

2. Data and Methods

2.1. InSAR Displacements

Our study region spans the southern Central Valley from 34.4°N to 37.9°N. For this analysis, synthetic aperture radar (SAR) scenes from the European Space Agency's Sentinel‐1A/B mission (descending track 144; Figure 1) are merged along track to construct 51 extra‐long images spanning April 1, 2015 to October 23, 2017 (Table S1). Using the GMTSAR software package (Sandwell et al., 2011; Xu et al., 2017), we generate a suite of 263 interferograms (difference in carrier signal phase between SAR images), geometrically aligned to a primary reference image on August 17, 2016. For the purpose of interferogram construction, a maximum perpendicular baseline of 250 m and a maximum 100‐days separation are imposed between SAR acquisitions (Figure S1 and Table S2). The 1 arc second digital elevation model (DEM) from the Shuttle Radar Topography Mission (SRTM) (Farr et al., 2007) is used to remove the topographic phase contribution from each interferogram. To remove observed burst discontinuities from misregistration, we used the enhanced spectral diversity (ESD) algorithm (Prats‐Iraola et al., 2012) available in GMTSAR. Finally, interferograms are unwrapped using the Snaphu algorithm (Chen & Zebker, 2000) with pixel correlation of 0.1 and subsequently converted to line‐of‐sight (LOS) displacements (∼100‐m resolution).

2.2. InSAR Correction Using cGPS

Since InSAR estimates are affected by atmospheric, orbital, and processing errors, we augment interferometric displacements with independent surface displacements from 89 cGPS stations located within the study region (Figure 1 and Table S3). We obtain daily time series of postprocessed position data for these stations from the National Science Foundation's Geodesy Advancing Geosciences and EarthScope (GAGE) facility (Herring et al., 2016), then (a) correct for offsets from equipment and other nongeophysical changes, (b) smooth using a 6‐days Gaussian filter to minimize high frequency signals that are likely due to multipath and tropospheric effects (Borsa et al., 2007), and (c) project the three components of cGPS displacements into the SAR LOS direction. For a given interferometric pair, the cGPS displacements spanning the dates of the associated SAR images are computed. We take the difference between the cGPS and InSAR displacements at each station location to create a set of residuals, to which we fit a low‐order polynominal surface (second order in longitude and fourth order in latitude, empirically selected based on strategies presented in Neely et al. (2020); Figure S2). This surface is separately calculated for and subtracted from each interferogram to correct long‐wavelength error. This methodology (GPS‐enhanced InSAR or GInSAR, Neely et al., 2020) has the additional benefit of aligning interferometric pairs to the absolute reference provided by the cGPS.

2.3. InSAR Time Series Construction

To construct the deformation time series of the SJV study area from our set of corrected interferograms, we implement a modified version of the Small Baseline Subset (SBAS) algorithm (Berardino et al., 2002). Standard SBAS requires pixels to be coherent in every interferogram, which is well suited for urban or rocky terrain where loss of coherence between SAR scenes is minimal. To improve coverage over highly decorrelated vegetated regions such as the agricultural fields in the SJV, we employ a newer algorithm (temporally Connected SBAS, or CSBAS) that estimates displacement for all pixels for which there is at least one valid displacement estimate spanning every interval of the time series (Neely et al., 2020). We apply a temporal smoother to the least‐squares CSBAS estimation via a first‐order Tikhonov regularization, with the weight of the smoothing constraint λ = 150, to minimize large changes in displacement velocity often attributed to the turbulent component of atmospheric noise (Schmidt & Bürgmann, 2003; Wang et al., 2019). Validation of the CSBAS time series with an independent set of 28 cGPS velocities and time series show good agreement (Table S4).

To isolate the vertical component of displacement, we remove LOS‐projected horizontal motion from the Southern California Earthquake Center (SCEC) Community Geodetic Model (CGM) (Sandwell et al., 2016). Inspection of the seasonal amplitudes for cGPS vertical and horizontal components projected into LOS in this region show that the horizontal amplitudes (median value 0.36 and 0.12 mm for East and North, respectively) are about an order of magnitude smaller than the vertical amplitudes (median value 3.12 mm). Thus, we consider this approach to be valid and we project the horizontal‐corrected LOS residual into the vertical component of displacement by dividing by the cosine of the radar incidence angle.

2.4. InSAR Time Series Modeling

To evaluate the annual seasonal response of surface deformation (hereafter referred to simply as “seasonal”), the displacement time series are modeled for each water year at each CSBAS pixel as a linear trend and a single sinusoid described by

$$Y(t)=vt+A\cos (2\pi (t-T))+Y_0$$ (1)

where Y(t) is our observed surface displacement (mm), t is time in fractional years, v is the linear rate of displacement (mm/yr), A is the seasonal amplitude (mm), T is the time of maximum uplift (in fractional year, where T = 0 corresponds to October 1), and Y ₀ is a constant shift in the model (mm). We solve Equation 1 using least‐squares minimization and then map A and T across our study region to investigate spatial patterns in the seasonal signal.

2.5. Spatiotemporal Evolution of Seasonal Uplift

The solution to Equation 1, offers unique insights into the timing of seasonal signals and how they vary across the SJV. For the purpose of this analysis, we assume the peak uplift time T corresponds to the time of maximum instantaneous aquifer pore pressure. By mapping T across the SJV, we are able to observe the spatial evolution of peak uplift time, and thus the temporal propagation of aquifer pressure. Additionally, the spatial gradient of T indicates the directionality of the subsurface pressure front, which can distinguish the geometry and location of focused groundwater recharge zones.

To estimate this gradient, we convert T(lat, lon) from fractional year into “day of year” relative to the start of the water year (hereafter referred to as “phase” or “p”). We then apply a 2.5‐km radius median filter on the phase, p(lat, lon), to smooth over smaller spatial scale features and capture the general behavior of phase progression. For each water year, we take the two‐dimensional numerical gradient of this filtered phase P(lat, lon):

$$\nabla P=\frac{\partial P}{\partial \text{E}}\widehat{ı}+\frac{\partial P}{\partial \text{N}}\widehat{ℐ}$$ (2)

where $\frac{\partial P}{\partial \mathrm{E}}$ is the difference in the longitudinal (East) direction, and $\frac{\partial P}{\partial \mathrm{N}}$ is the difference in the latitudinal (North) direction. We unit‐normalize ∇P, giving a vector that indicates the lateral direction of (peak) uplift over time. Following the same steps, we calculate the local topographic gradient, ∇P _topo, from the SRTM DEM (Farr et al., 2007) to determine the approximate direction of uninterrupted surface‐water drainage. For shallower groundwater systems, in particular, the water table may represent a subdued replica of topography where streams and rivers can provide locations for efficient groundwater recharge or discharge. Thus, the consideration of the topographic gradients, along with river traces, is important in the interpretation of the seasonal uplift timing progression. While recent land subsidence has modified the land surface elevation since SRTM data collection, these effects are relatively small compared to the topographic slope and gradient differences are generally confined to the valley axis (Figure S3).

2.6. Hydrological Data

While geodetic time series from cGPS and InSAR have expanded our understanding of the SJV aquifer system, they are best interpreted together with hydrological data. We use stream and river traces (average annual streamflow >0.5 m³/s) from the U.S. Geological Survey's (USGS) Elevation Derivatives for National Applications database and the outlines of the California Aqueduct and Friant‐Kern Canal (provided by the U.S. Bureau of Reclamation [USBR]) to relate natural and artificial surface‐water flow patterns to spatial features observed in the displacement data. In particular, we compare the timing of peak seasonal uplift with the surface flow paths inferred from the SRTM DEM (Farr et al., 2007) and watershed boundaries (hydrologic units code level 8 (HUC8)) from USGS. Separately, we characterize water availability by hydrologic region using summary statistics from the California Department of Water Resources (DWR: Bulletin 132, n.d.) and USBR and DWR summaries of surface‐water deliveries by water year (Lund et al., 2018). Though periodic groundwater level measurements from DWR are temporally sparse, we qualitatively compare relative changes in hydraulic head to seasonal surface displacements. Lastly, we infer the role of surface runoff (occurring as streamflow) in our estimated seasonal uplift timing using area‐normalized runoff data from USGS WaterWatch portal (U. S. Geological Survey, n.d.). The runoff information helps constrain our interpretation of the observed deformation in the SJV.

3. Results

3.1. Vertical Displacement Rates

The estimated vertical displacement rates (v in Equation 1) between April 2015 and October 2017 are dominated by two areas of high subsidence (≥100 mm/yr) inside the alluvial boundary of the SJV (V _t1 and V _t2 in Figure S4). These subsidence regions are well documented and geographically consistent with recent studies (Farr, 2018; Murray & Lohman, 2018; Ojha et al., 2019). We observe a maximum subsidence rate of ∼270 mm/yr within V _t2, similar to the 250 mm/yr maximum subsidence rate reported by Ojha et al. (2019) for January 2015 to April 2017. Much higher subsidence rates were reported by Farr (2018) (∼400 mm/yr; May 2015 to May 2017) and Murray and Lohman (2018) (∼550 mm/yr; November 2014 to September 2017). The observational time window and methodologies for estimating the vertical motion from LOS play large roles in the differences between these reported rates. Further, we show in a recent study (Neely et al., 2020) that interferogram referencing methodologies can influence peak deformation rates, which may account for some portion of these observed differences.

Importantly, subsidence rates in the SJV change throughout the year in response to water demand (Levy et al., 2020). All four of these rate estimates include data across dry and wet years. Because of this interannual variability, and to assess displacement responses to hydrological endmembers (Figure 2), we partition our data into water years and separately analyze the dry (WY2016; October 1, 2015 to September 30, 2016) and wet (WY2017; October 1, 2016 to September 30, 2017) water years. While the absolute magnitude of surface displacements can be related to groundwater changes, for this study, we focus on comparing relative displacement changes between dry and wet years.

Figure 2.

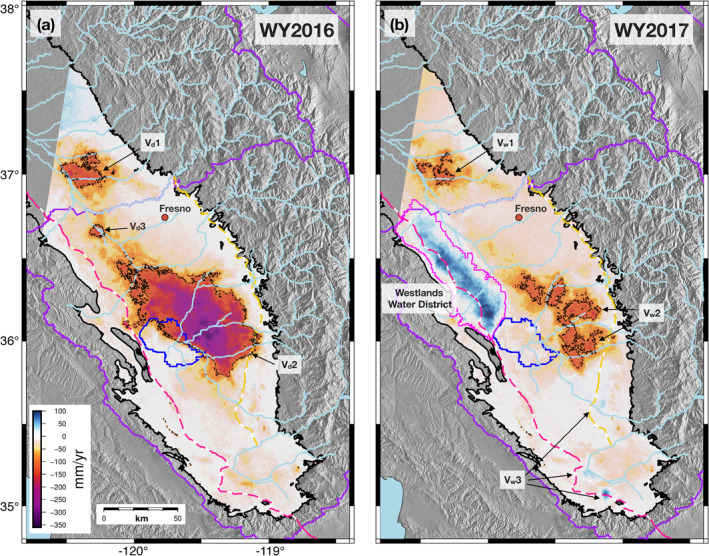
Vertical displacement rate maps (mm/yr) over the San Joaquin Valley study region for (a) WY2016 (October 1, 2015 to September 30, 2016) and (b) WY2017 (October 1, 2016 to September 30, 2017). Regions with vertical displacement rates ≤−100 mm/yr (indicating subsidence greater than or equal to 100 mm/yr; dashed black contour) are labeled V _d1–3, velocity for dry WY2016, and V _w1–2, velocity for wet WY2017. The Westlands Water District (magenta outline) exhibits relatively strong uplift in WY2017. Other smaller regions of uplift in WY2017 are noted as V _w3. The city center of Fresno, CA, is marked by a red‐orange circle. We note rivers entering the valley (light blue lines), hydrologic regions (purple outlines), the Tulare Lake (blue outline), the California Aqueduct (dashed pink line), and the Friant‐Kern Canal (dashed yellow line).

3.1.1. WY2016 (Regulatory “Dry” Year)

In WY2016, California received 104% of average precipitation, had an estimated 90% of average snowpack, and experienced 97% of average river runoff (DWR: Bulletin 132, n.d.), it also had minimal surface‐water deliveries (0–5% of requested) from the state and federal water projects and was preceded by 4 years of extreme drought (Lund et al., 2018). Thus, we characterize WY2016 as a regulatory “dry” year. High‐subsidence regions in WY2016 (V _d1–2 in Figure 2) occur in the same locations as those in our multiyear estimate (Figure S4), but WY2016 subsidence rates are greater, with the maximum exceeding 345 mm/yr. Inside the alluvial boundary of the SJV, the surface subsided at an average rate of 42.0 mm/yr (Table 1). Some uplift is observed north of V _d1 though this is likely due to residual unwrapping errors not corrected by our GPS correction (Xu et al., 2017). Outside of the SJV alluvial boundary, the average rate of displacement was near zero. There is some modest uplift (as much as 20 mm/yr) in the adjacent mountain ranges (Figure S4), which has also been observed using campaign and permanent GPS. It is attributed to the solid earth elastic rebound from loss of groundwater and surface water incurred during the 2012–2016 drought (Adusumilli et al., 2019; Argus et al., 2017; Borsa et al., 2014; Fu et al., 2015).

Table 1.

Summary Statistics for Vertical Displacements in the San Joaquin Valley

Time period	Mean rate (mm/yr)	Mean amplitude (mm)	High amplitude (% of pixels ≥ 20 mm)	Moderate amplitude (% of pixels ≥ 10 mm and < 20 mm)	Low amplitude (% of pixels < 10 mm)
April 2015 to October 2017	−35.3	7.4	5.7	16.3	78.0
WY2016 (October 2015 to September 2016)	−42.0	6.7	2.6	17.2	80.2
WY2017 (October 2016 to September 2017)	−20.4	7.1	2.6	16.8	80.6

3.1.2. WY2017 (“Wet” Year)

In the wet WY2017, average precipitation within California was ∼164% of average, mountain snowpack was ∼163% of average, statewide river runoff was ∼217% of average (DWR: Bulletin 132, n.d.), and 85–100% surface‐water delivery requests were met (Lund et al., 2018). While the regions of greatest subsidence in WY2017 (V _w1–2 in Figure 2) coincide with those of WY2016, the areal extent of subsidence and its peak magnitude are sharply reduced in the wet year. The peak subsidence rate in WY2017 is 177 mm/yr and occurs ∼25 km northeastward of the peak subsidence location in WY2016. The average vertical displacement rate inside the alluvial boundary of the SJV was −20.4 mm/yr, which was less than half the subsidence rate in WY2016. The most striking feature in the wet year displacement rate was the substantial uplift (up to 100 mm/yr; mean value of 26.4 mm/yr) across the Westlands Water District (magenta outline in Figure 2). In addition to this large area of uplift, we observe several localized uplift features in the southern SJV (V _w3 in Figure 2).

In summary, a comparison of vertical displacement rates between the dry WY2016 and the wet WY2017 shows that even with substantial increases in precipitation, runoff, and surface‐water allocations in WY2017, subsidence persisted in the two regions of greatest subsidence in WY2016. These locations feature an abundance of underlying clay and silt layers that are highly susceptible to compaction (Faunt, 2009; Williamson et al., 1989). Conversely, in regions with coarser‐grained deposits, such as the glacial fluvial fans underlying Fresno (Faunt et al., 2016; Weissmann et al., 2005), observed land subsidence is comparably subdued.

3.2. Amplitude of Seasonal Surface Deformation

Seasonal amplitudes (A in Equation 1) of the vertical displacement time series are an indicator of change in groundwater storage within each water year. Our underlying assumption is that seasonal surface deformation within the alluvial boundary of the SJV is dominated by poroelastic deformation of the aquifer system, which is driven by cyclical changes in groundwater storage (Murray & Lohman, 2018). Small seasonal amplitude values typically indicate that groundwater storage changes are noncyclic on an annual period. Examples include, but not limited to, regions with multiple intervals of groundwater extraction throughout the year or negligible seasonal groundwater recharge. Large seasonal amplitudes are consistent with significant seasonal groundwater recharge and/or highly variable pumping between seasons.

For the purpose of assigning significance to amplitude values, we bin seasonal amplitudes for each water year into three categories: low (A < 10 mm), moderate (10 mm ≤ A < 20 mm), and high (A ≥ 20 mm). We note that compared to previous InSAR studies that also examined seasonal amplitude (e.g., Colesanti et al. (2003) over portions of the Santa Clara Valley and Bell et al. (2008) over the Las Vegas Valley), our low threshold is on the high end of their maximum amplitude of 10 mm.

3.2.1. WY2016 Amplitudes

For the dry WY2016, seasonal amplitudes reach 35 mm, with an average amplitude of 6.7 mm inside the SJV alluvial boundary (Table 1) and an average of 4.3 mm outside the boundary. High‐amplitude regions are exclusively located within the SJV sedimentary basin, accounting for 2.6% of the study area. Moderate‐amplitude and low‐amplitude regions accounted for 17.2% and 80.2% of the study area, respectively. The spatial pattern of estimated seasonal amplitudes (Figure 3a) is similar to that of Murray and Lohman (2018), although their magnitudes are smaller. High‐seasonal amplitudes are generally coincident with the high‐subsidence rates in WY2016 (Figure S5a); however, the location of the highest seasonal amplitude value (A _d5) is offset ∼30 km to the southeast of the peak subsidence rate.

Figure 3.

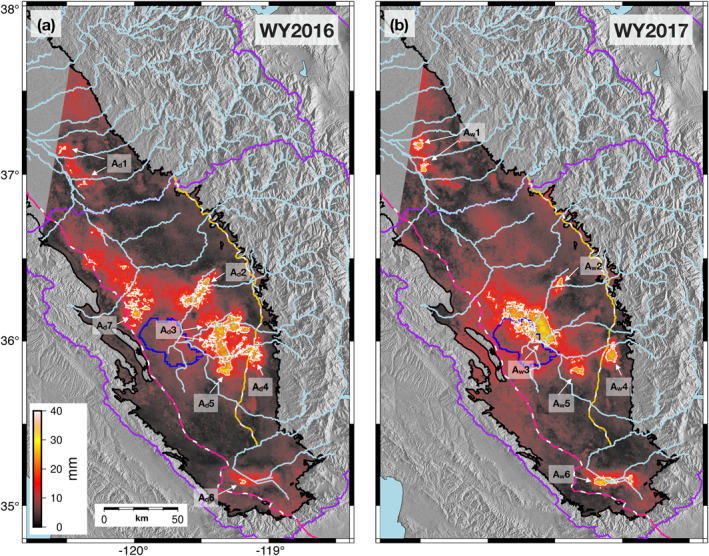
Seasonal amplitude maps (mm) over the San Joaquin Valley study region for (a) WY2016 (October 1, 2015 to September 30, 2016) and (b) WY2017 (October 1, 2016 to September 30, 2017). Regions of high‐amplitude (≥ 20 mm; white contours) are labeled A _d1–7 (amplitude for dry WY2016), and A _w1–6 (amplitude for wet WY2017). We note rivers entering the valley (light blue lines), hydrologic regions (purple outlines), the Tulare Lake (blue outline), the California Aqueduct (dashed pink line), and the Friant‐Kern Canal (dashed yellow line).

High‐amplitude to moderate‐amplitude areas are typically located along the course of rivers (perennial or ephemeral) originating in the Sierra Nevada to the east or the Coast Ranges to the west (Figure 3a). On the eastern side of the SJV, these areas are associated with (from south to north) Caliente Creek and other ephemeral streams from the Tehachapi Mountains, Deer Creek and the Tule River, the Kaweah River, and the termini of several smaller outflows (Fresno River, Chowchilla River, and Mariposa Creek) (Figure 1). On the western side of the SJV, the zone of high‐seasonal amplitude is located north of former Tulare Lake and southwest of the Fresno Slough, adjacent to the Los Gatos Creek. Not all rivers are associated with areas of high‐amplitude seasonal displacements: most notably the Kern, Kings, and San Joaquin Rivers. These perennial rivers are host to the three largest reservoirs in the southern Sierra Nevada (Isabella, Pine Flat, and Millerton) and heavily managed to support SJV irrigation in both wet and dry years. As a result, we expect groundwater recharge along these rivers to occur more continuously throughout the year, which would act to dampen or eliminate the seasonal signal.

3.2.2. WY2017 Amplitudes

Similar to WY2016, WY2017 also exhibits seasonal amplitudes of up to 35 mm, with the high‐amplitude areas located exclusively within the alluvial boundary and adjacent to rivers and creeks primarily sourced in the Sierra Nevada (Figure 3b). High‐amplitude, moderate‐amplitude, and low‐amplitude pixels account for 2.6%, 16.8%, and 80.6% of the study area within the SJV, respectively (Table 1). We observed average amplitudes of 7.1 and 6.6 mm inside and outside of the SJV, respectively. We identified six regions of high‐seasonal amplitude; the largest magnitude (A _w3) is located at the terminus of the Tule River, bordering the boundary of the former Tulare Lake. Spanning 10s of km, A _w3 is located just west of WY2017 peak subsidence and east of the uplift of the Westlands Water District, where we observe relatively little secular deformation (Figure S5b). In contrast to WY2016, many of the high‐seasonal to moderate‐seasonal amplitude regions (e.g., A _w1, A _w3–6) are not coincident with strong subsidence rates (Figure S5b).

Comparing the dry and wet years, we observed an increase in mean seasonal amplitude from 5.0 mm (WY2016, dry) to 6.7 mm (WY2017, wet) across the entire study area. Within the SJV itself, seasonal amplitude statistics are similar for both water years (Table 1), although there are differences in the spatial patterns of seasonal amplitudes and associated uncertainties (Figure S6). Specifically, in WY2017 we observe reductions in amplitude along the Kaweah River, Tule River, Deer Creek, and intervening regions relative to WY2016. Conversely, we observe an increase in seasonal amplitude near the former Tulare Lake in WY2017 at the confluence of these watercourses. Interestingly, the entire Westlands Water District exhibited moderate‐seasonal to high‐seasonal amplitude during the dry year but only the southeast portion of this region experienced appreciable seasonality during the wet year. However, for all the changes in the spatial pattern, more than half of the local maxima in amplitude are common to both years (A _d1–2 to A _w1–2 and A _d4–6 to A _w4–6) despite differences in surface‐water availability.

3.3. Timing (Phase) of Seasonal Surface Deformation

In addition to amplitude, the sinusoidal term in our model provides the temporal phase shift (T in Equation 1) associated with seasonal surface displacements. In the SJV, these surface displacements are controlled by the pore‐pressure response to changes in hydraulic head (Poland & Davis, 1969). We interpret peak subsidence to correspond to annual minima in local groundwater storage and peak uplift to correspond to annual maxima in local groundwater storage (Leake, 1990). In this study, we focus on groundwater storage maxima and use phase timing to estimate when the maximum seasonal uplift occurs for each interferometric pixel. We map the peak seasonal uplift in terms of time of year across the SJV (Figure 4) to investigate spatiotemporal patterns in seasonal groundwater storage. While we highlight higher confidence pixels (σ ≤ 31 days) in Figures 4 and 5, we consider all pixels in our analysis because of the observed spatial coherence in timing.

Figure 4.

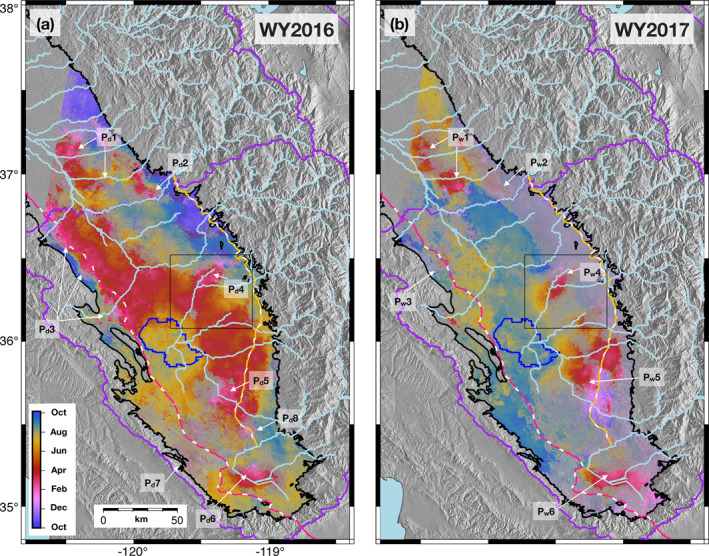
Seasonal phase maps (time of year) over the San Joaquin Valley study region for (a) WY2016 (October 1, 2015 to September 30, 2016) and (b) WY2017 (October 1, 2016 to September 30, 2017). Colors correspond to the timing of peak seasonal uplift in the valley. Regions of interest are labeled P _d1–8, phase for dry WY2016, and P _w1–6, phase for wet WY2016. We note the area around P _d4 and P _w4 shown in Figure 5 (black box). We note rivers entering the valley (light blue lines), hydrologic regions (purple outlines), the Tulare Lake (blue outline), the California Aqueduct (dashed pink line), and the Friant‐Kern Canal (dashed yellow line).

Figure 5.

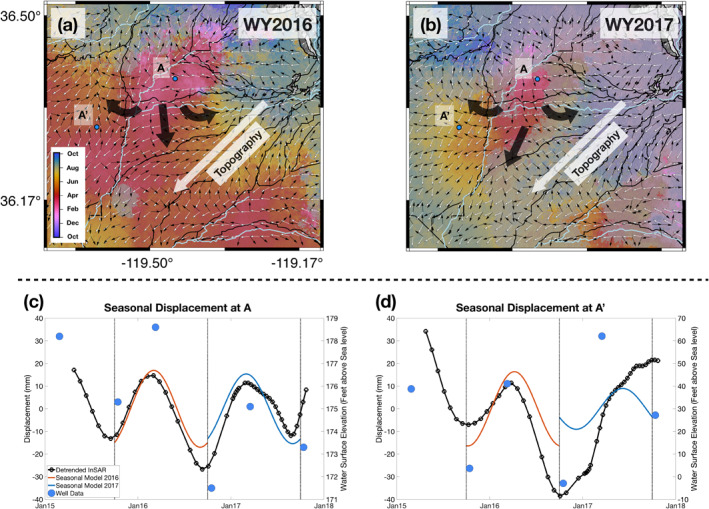
Seasonal phase (time of year) for (a) WY2016 and (b) WY2017 around P _d4 and P _w4. The topographic gradient (white arrows) shows the direction of implied natural surface‐water flow. The gradient of uplift timing (black arrows) indicates direction of phase progression. The general direction of these gradients (larger arrows) is shown in context with watershed boundaries (black outlines). A and Aʹ (blue circles) mark the locations of the seasonal displacement time series shown in (c) and (d), respectively. (c) The detrended and modeled seasonal displacement time series (mm) at A along with collocated water surface elevations (feet above sea level; blue circles) from well 327204N1168056W001 (DWR). Similarly, (d) shows the detrended and modeled seasonal displacement time series at A′ along with collocated water surface elevations (blue circles) from well 329223N1170659W001 (DWR). Water years (October 1 to September 30) are indicated by vertical dotted lines.

3.3.1. WY2016 Peak Seasonal Uplift Timing

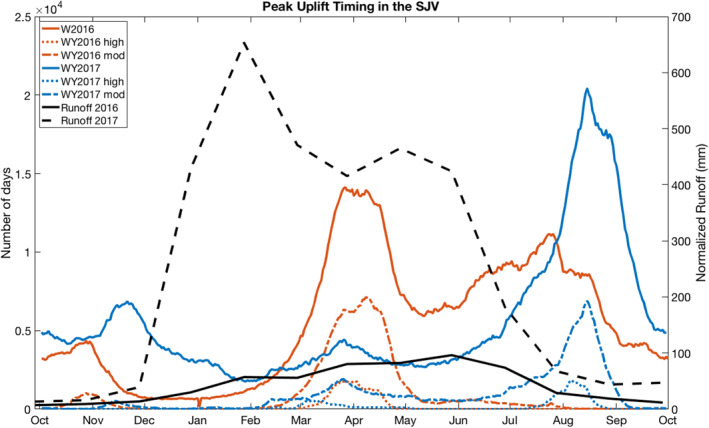
During WY2016, we observe spatially continuous patterns of uplift timing in the SJV that indicate migration of annual groundwater storage peaks across the valley. In Figure 4a, we identify uplift originating in January (pink) to early March (red) along the San Joaquin River (P _d2), the Kaweah River (P _d4), the southern end of the Friant‐Kern Canal (P _d8), the northern section of the agricultural fields south of Bakersfield (P _d6), and adjacent to the California Aqueduct along the western edge of the SJV north of the former Tulare Lake (P _d3). From these locations, peak seasonal uplift radiates outward (e.g., Figure 5a), with peak timing extending through July (yellow). Regions with uplift outside of this range (October to December and August to September) occur where there is (a) less intense agriculture, (b) coarse‐grained glaciated fluvial fan deposits (e.g., near Fresno), and/or (c) within the former Tulare Lake bed. As a whole, we observe a somewhat trimodal distribution of uplift timing across the SJV, with peaks around April, late July, and, to a lesser extent, late October with the mode of peak uplift occurring in late March (Figure 6).

Figure 6.

Histograms of the peak seasonal uplift timing in the San Joaquin Valley for WY2016 (orange) and WY2017 (blue). Contribution from moderate‐amplitude and high‐amplitude value pixels are represented by dotted‐dashed and dotted lines, respectively. The monthly area‐normalized runoff (waterwatch.usgs.gov) for hydrological unit codes (Figure S11) 18030003, 18030004, 18030005, 18030006, 18030007, 18030009, 18030012, 18040001, and 18040007 is shown for WY2016 (solid black line) and WY2017 (dashed black line).

3.3.2. WY2017 Peak Seasonal Uplift Timing

In WY2017, spatially continuous patterns of uplift timing are also observed yet differ from those described for WY2016. We observe fewer locations of winter (January to early March) peaks in uplift during the wet year than in the dry year (Figure 4). However, these regions are typically common to those in WY2016 and include P _w2 along the San Joaquin River (compare to P _d2 although with higher uncertainty), P _w4 along the Kaweah River (compare to P _d4), and P _w6 in the agricultural fields south of Bakersfield (compare to P _d6). In some cases, these peaks visually correspond to regions with high‐seasonal amplitudes (Figure S8b). An exception being the most notable high‐amplitude feature, A _w3, which coincides with a summer uplift (August) and is concurrent with the final stages of the river runoff sequence (Figure 6). Radiating outward and typically downslope from these winter uplift maxima, peak seasonal uplift in WY2017 occurs progressively later into the year toward the interior of the valley, lasting through September (Figures 4b and 5b). Compared to WY2016, the summer and autumn uplift peaks for the SJV as a whole are delayed by about a month in WY2017 (Figure 6). In a year such as WY2017, with elevated precipitation and prolonged associated runoff, we can observe peak seasonal uplift timing patterns that delineate specific surface‐water features at great detail (e.g., the Kern River west of Bakersfield; Figure S9).

For both WY2016 and WY2017, we observe winter (January to early March) peak uplift at discrete locations on the eastern side of the valley. These uplift features typically correspond to areas with high‐seasonal amplitudes and are directly adjacent to perennial rivers sourced at high elevations in the Sierra Nevada which nevertheless experience high‐seasonal variability in flow. However, seasonal displacements in the interior of the SJV during the wet year do not achieve peak seasonal uplift until September (Figure 6). This is a stark difference with the dry year, where a majority of the valley experiences peak uplift in early spring (April) or mid‐summer (July).

3.4. Phase Progression vs. Surface‐Water Flow

As detailed above (Section 3.3), we assume that the time of peak uplift at any given location indicates the time of maximum local groundwater storage. With this interpretation, we postulate that the spatial gradient peak seasonal uplift can indicate either the timing of maximum local vertical infiltration of surface water into the aquifer, the lateral flow of groundwater in response to recharge and/or redistribution resulting from changes in hydraulic gradients, or a combination of the two processes. We examine the horizontal progression of peak uplift for each year and compare it with the direction of uninterrupted surface‐water flow derived from topography in order to assess these potential mechanisms for generating observed uplift timing patterns.

Using the unit‐normalized ∇P _topo (Section 2.5), the azimuthal distribution and spatial patterns of surface‐water flow derived from topography indicate a bimodal distribution of flow in the SJV (Figure 7a), consistent with water entering the valley from the northeast near the Sierra Nevada and from the southwest near the Coast Ranges. Surface‐water flow patterns show convergence at topographic lows (rivers and streams) and divergence at topographic highs (coincident with watershed boundaries). These surface flow directions provide context for the lateral migration of peak seasonal uplift over our study period. That is, a difference between the direction of uplift progression and the topographic gradient suggests that the patterns of uplift timing are not controlled by surface‐water drainage according to elevation. Conversely, where the direction of uplift progression aligns with the topographic gradient, either vertical infiltration of surface water (moving downstream over time as the aquifer fills) or the downslope migration of groundwater can be at work.

Figure 7.

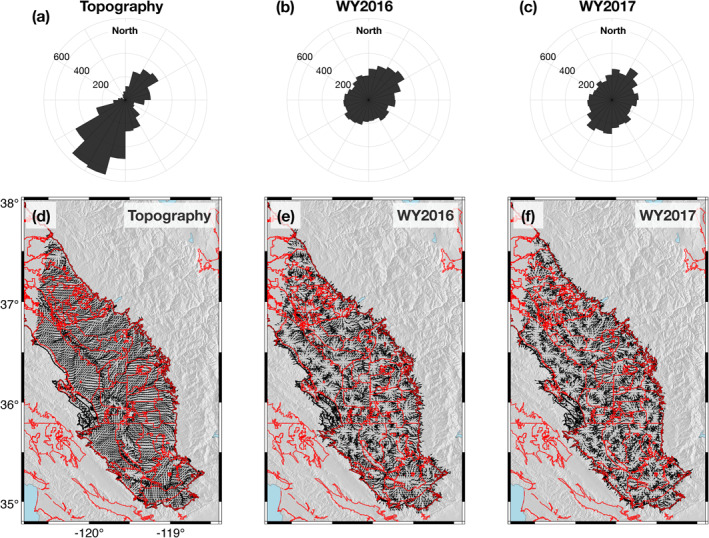
Azimuthal distribution of (a) the gradient of topographic slope, (b) the WY2016 phase progression, and (c) the WY2017 phase progression. (d), (e), and (f) show the gradient and phase progression (arrows) for topography, WY2016, and WY2017, respectively, in the context of proposed groundwater sustainability agencies (red outlines).

We find that the azimuthal directions of uplift migration in both the dry and wet water years (Figures 7b and 7c) are more uniformly distributed than the pattern of surface runoff, but are still preferentially oriented along the northeast‐southwest axis observed in the pattern of the topographic gradient (Figure 7a). While the seasonal uplift timing is broadly different between WY2016 and WY2017, the direction of the progression near noted regions of winter uplift is fairly consistent for both years (Figure S10). For example, the region focused on P _d4 in WY2016 has peak uplift timing ranging from January to June (Figure 5a), whereas in WY2017 (P _w4), the phase timing spans January to August (Figure 5b). However, despite this difference in uplift timing, the horizontal direction of uplift progression in both water years is similar (Figures 5a, 5b and 7e, 7f).

4. Discussion

4.1. Implications for Groundwater Recharge and Flow Within the SJV

In the SJV, vertical surface displacements are often attributable to changes in hydraulic head (e.g., Smith et al., 2017). A decomposition of these displacement time series into annual rates and seasonal oscillations offers unique insight into the spatiotemporal variability of groundwater resources in this region. While displacement trends can inform us of groundwater sustainability and the relative balance of groundwater recharge and extraction, the seasonal amplitudes and timing of surface displacements are suggestive of how groundwater moves through the aquifer system. Comparison of deformation observed in the SJV between dry and wet water years further illustrates the complexities and dynamic behavior of groundwater flow on short time scales. However, surface displacements can be interpreted in several ways. For example, a displacement time series reflecting only seasonal drawdowns from pumping (or conversely reflecting only seasonal recharge) separated by periods of no change may yield a similar amplitude to that from a displacement time series consisting of both seasonal pumping and recharge (Bell et al., 2008). Further, pumping and recharge can alter hydraulic head gradients on seasonal time scales, which can change the direction of groundwater flow (Fetter, 2018). Here, we use “recharge” to denote local groundwater storage increases in the aquifer system that result from either or both external sources (e.g., infiltration of water from the land surface to the aquifer system) and internal sources (e.g., redistribution of groundwater within the aquifer system to areas impacted by groundwater extraction).

Seasonal surface displacements are best understood in the context of local and regional hydrology. Conceptually, low seasonal amplitude values during a dry year suggest the region was subjected to either negligible groundwater extraction or that the extraction is noncyclic on an annual period. Conversely, high‐amplitude values in a dry year most likely result from strong seasonal groundwater extraction. Low‐amplitude values in a wet year, similar to a dry year, suggests that there was either negligible groundwater extraction/recharge or that any extraction/recharge is noncyclic on an annual period. High‐amplitude values in a wet year indicate strong seasonal groundwater extraction and/or seasonal recharge. This includes the case where there is both strong seasonal and nonseasonal groundwater extraction and/or recharge. Thus, the inclusion of in‐situ data and ancillary information is needed to constrain possible interpretations of the amplitude variations.

WY2016 was a regulatory dry year, having a total uninterrupted runoff from the Sierra Nevada into the Tulare Lake Region (TLR) of the SJV of ∼2.4 km³ (65% of average), with peak runoff in May (∼0.6 km³), and below‐average river flow for all months (DWR: Bulletin 132, n.d.). Further, water deliveries from regional, state, and federal water projects were minimal (0–5% of requested for agricultural contractors south of the Sacramento‐San Joaquin Delta) (Lund et al., 2018). In general, a reduction in available surface water often leads to an increased reliance on groundwater in order to meet the water demand of agricultural production (Hanson et al., 2012; Howitt et al., 2015). The increased pumping in WY2016, and in the preceding drought years, reduced pore pressure in the aquifer system and subsequently induced high‐subsidence rates across the SJV (e.g., Murray & Lohman, 2018; Ojha et al., 2019, Figure 2a). WY2016 vertical land surface displacements also exhibited strong seasonal amplitudes (∼35 mm; Figure 3a), despite the minimal surface water available for natural or artificial recharge. One interpretation is that seasonal groundwater pumping was a dominant driver of observed seasonal displacements, consistent with results from previous studies (e.g., Chaussard & Farr, 2019). Groundwater‐level observations show increases that are coincident with the timing of uplift (Figure 5c). These relative increases may be the result of a comparatively rapid pressure response related to groundwater pumping operations, a slower lateral redistribution of water within the aquifer system due to changes in hydraulic head gradients, or a combination of the two.

In contrast to WY2016, WY2017 was an exceptionally wet year. The SJV experienced above‐average precipitation (∼171% of average in the TLR) and river runoff into the TLR exceeded 8.9 km³ (∼223% of average; peak runoff in June with ∼1.8 km³) with above‐average river flow from January to September. Contractual surface‐water deliveries from the State Water Project and the Central Valley Project were 85–100% fulfilled statewide (Lund et al., 2018). Even when surface water is broadly available, groundwater is often still extracted to meet agricultural demand late in the growing season or in regions with minimal access to surface‐water supplies (Faunt et al., 2016). Relative to WY2016, subsidence in WY2017 was greatly diminished, with only a few regions of high (>100 mm/yr) subsidence persisting across both years (Figure 2). Part of this wet year subsidence may be explained by delayed groundwater drainage from relatively thick fine‐grained (e.g., clays and silts) sedimentary units (aquitards or interbeds) in the aquifer system (Ojha et al., 2019; Smith et al., 2017). Although large precipitation and runoff events occurred within several months of the start of WY2017, compaction of clay layers at depth (due to the previous period of low hydraulic heads) likely continued until the surface‐water influx (recharge) started raising water levels in deeper aquifers. While the deeper confined aquifer is typically conceptualized as distinct from the shallow “semi‐confined” aquifer, groundwater wells that are perforated in both aquifers can increase the exchange of groundwater between the aquifers through intraborehole flow, promoting recharge to the deeper confined aquifer (Faunt, 2009).

Some displacement patterns can be related to specific water management districts, underscoring this data set's utility for informing groundwater policy. Strikingly, the Westlands Water District exhibits elevated uplift rates in WY2017 (as much as 100 mm/yr with a mean value of 26.4 mm/yr and standard deviation of 29.5 mm/yr; Figure 2b). Historically, this region has experienced periods of uplift, with as much as 61 mm of apparent rebound observed in 1975 (Ireland et al., 1984). Available extensometer data, which measures compaction or expansion of the subsurface material over a specific depth interval, revealed ∼40 mm of expansion (from the near land surface to ∼307 m depth) in this region during WY2017 indicating that some of the observed uplift can be attributed to recharge and/or regional redistribution of groundwater in the deeper aquifer system. The remaining uplift maybe explained by additional expansion below the depth of the extensometer, a swelling of clays at the surface, or the result of a perched water table from water pooling near the surface due to poor natural drainage (A Management Plan For Agricultural Subsurface Drainage and Related Problems on the Westside San Joaquin Valley, 1990). Finally, the heterogeneity of the aquifer‐system material may result in a combination of poor drainage and local recharge that explains the pronounced but spatially localized uplift observed at several locations across the valley (V _w3; Figure 2b).

WY2017 also exhibited significant seasonal amplitudes (as much as ∼35 mm; Figure 3b). The largest amplitude area (A _w3) is associated with summer uplift and occurs near the confluence of the Kaweah and Tule Rivers (Figure S5b). This feature is absent in the dry WY2016, but there are higher amplitude‐value regions farther upstream not observed in WY2017 (compare A _w3 with A _d3). In a wet year with increased water deliveries and elevated uninterrupted streamflow, runoff originating in the Sierra Nevada commingled with canal water imports may travel the lengths of these rivers and directly recharge the central region of the SJV near the former Tulare Lake in much higher volumes than is possible in dry years. The change in uplift timing between the dry and wet years near the terminus of the Kern River (Figure S9) may support this hypothesis, although we note that this is a region with relatively large timing uncertainties. In WY2016, there is no discernible trace of the river in the uplift timing map (Figure S9b). However, in WY2017, there is a clear indication of the river trace and recharge reservoirs defined by winter uplift (Figure S9c). Runoff was relatively low during WY2016, followed by a sharp increase around January 2017 (Figure 6; waterwatch.usgs.gov). This general runoff history, taken with our seasonal uplift timing estimates, may indicate when and where water is moving vertically into the aquifer at locations of high sediment porosity and permeability (i.e., likely higher hydraulic conductivity of coarse‐grained sediments). Lateral groundwater flow from recharge areas of high hydraulic head near rivers to areas of lower hydraulic head could explain the increases in groundwater level and surface uplift observed in this region. We interpret the timing of seasonal uplift (Figure 4) to reveal the spatiotemporal evolution of this flow for a given water year.

As stated previously, there are a number of regions common to both the dry and wet water years that exhibit winter (January to early March) uplift (e.g., P _d2 vs. P _w2; P _d4 vs. P _w4; P _d6 vs. P _w6). Taking the feature originating off of the Kaweah River (P _d4 in Figure 4a; P _w4 in Figure 4b) as an example, we observe that the onset of uplift and the ensuing lateral progression of uplift are consistent between wet and dry years. While the topographic slope trends from the northeast to the southwest in this region, uplift in both years does not simply migrate along this gradient (Figures 5a and 5b), as would be expected if groundwater recharge were initiating along the SJV margin and progressing from high to low elevations through the aquifer under unstressed conditions (Williamson et al., 1989). Instead, we find the progression of surface uplift ranges across all azimuths and often crosses surface watershed boundaries indicated by topographic gradients, which implies that hydraulic head gradients must deviate substantially from uninterrupted surface flow gradients and likely are modulated by groundwater withdrawals (Williamson et al., 1989). While a hypothetical displacement time series resulting from only seasonal groundwater extraction can generate modeled (Equation 1) uplift (as the model assumes equal magnitudes for peak subsidence and uplift amplitudes), the relative increase in spring hydraulic head for both dry and wet years (e.g., Figures 5c and 5d) also supports the concept that the modeled uplift is responding to local increases in groundwater storage. Additionally, we do not observe symmetrical phase progression on either side of the Kaweah River. This indicates that the hydraulic head gradients and/or hydraulic conductivity within the aquifer system can vary over spatial scales as short as several kilometers, consistent with a high degree of heterogeneity in the aquifer system.

Attribution of these winter uplift features in WY2017 to recharge from rivers and streams sourced in the Sierra Nevada is also supported by recent studies of stable isotopes of water. As water vapor travels from the warmer coast toward cooler high elevations of the Sierra Nevada, the heavier isotopes precipitate out first, leaving relatively depleted concentrations of the heavier stable isotopes (e.g., δ ¹⁸O in the water molecule) in precipitation that falls farther inland, often referred to as the “continental effect” (Ingraham & Taylor, 1991). Water with a relatively lighter isotopic signature (depleted in the heavier isotopes) is then channeled and transported into the SJV by Sierra‐sourced rivers. Visser et al. (2018) found plumes of depleted δ ¹⁸O concentrations in groundwater samples originating near the Kings, Kaweah, Tule, and Kern Rivers (their Figure 4b), emphasizing the role that these rivers play in the recharge of the aquifer system. In fact, all winter uplift features on the eastern side of the valley (e.g., P _w2, P _w4, and P _w6) are associated with lower δ ¹⁸O concentrations. While we do not observe a similar, distinct winter uplift feature along the Kings River, the region of lowest δ ¹⁸O content in the Visser et al. (2018) study, this could be due to the perennial nature of the Kings (i.e., recharge occurring with more regularity rather than just seasonally) and that the coarser‐grain material underlying the region is less susceptible to high‐amplitude deformation related to changes in pore pressure. The agreement between these two independent data sets underscores the potential utility of these new observations of uplift timing and evolution as a tool for understanding groundwater recharge and flow.

4.2. Limitations of This Study and Implications for Other Aquifer Systems

This study investigates the use of surface displacement time series and their seasonal components for identifying and characterizing potential regions of groundwater recharge and flow in the SJV. Our approach can be applied to interferometric time series over other aquifer systems, with the caveat that any such studies consider the simplifying assumptions we have made about the SJV aquifer.

First of all, our analysis does not relate surface displacement to absolute changes in groundwater volumes. Rather, we use surface displacement estimates as a proxy for relative groundwater storage changes, where we assume that displacements are proportional to variations in pore pressure and are governed by the characteristics (e.g., compressibility, thickness, confinement) of the aquifer system. To estimate actual groundwater recharge volumes and/or flow rates would require explicitly characterizing aquifer structure and properties, which we do not do.

Second, we assume that the San Joaquin Valley aquifer system is spatially (vertically and horizontally) and temporally homogeneous, even though aquifer heterogeneity has been extensively documented (Faunt et al., 2010). As a result, a given change in groundwater volume may not translate to the same magnitude of surface displacement at different locations in the valley and vice versa. This is why we do not focus on the relative amplitudes of seasonal displacement changes between locations, but instead focus on the timing and location of peak uplift, which we interpret in the context of the spatiotemporal evolution of groundwater flow.

Additionally, while we observe seasonal uplift occurring along river channels where streamflow from the Sierra Nevada provides a potential source of groundwater recharge, there are river‐adjacent locations without measurable seasonal surface elevation change. An example is the city of Fresno, which is underlain by a coarse‐grained glacial fluvial fan deposit (Weissmann et al., 2005) that would be less compressible than finer‐grained sediments found elsewhere in the valley. Other notable examples are the large perennial Kings River and San Joaquin River systems, which are extensively managed to provide year‐round water flow. These rivers may provide nearly continuous recharge to adjacent aquifers, which would limit seasonal surface deformation.

Further, interpretations may be improved with the inclusion of mass change observations. The use of freely available satellite gravimetry from the Gravity Recovery and Climate Experiment (GRACE) and/or elastic loading estimates derived from GPS have proven effective at determining regional estimates of terrestrial water storage changes (Adusumilli et al., 2019; Argus et al., 2017; Borsa et al., 2014; Famiglietti et al., 2011; Lau et al., 2020). The addition of higher spatial resolution surface displacements from InSAR to these estimates may be helpful for constraining the areal extent of mass change concentrations and in turn help supplement water level observations in data limited regions (Castellazzi et al., 2016). Results from this study further highlight the potential of synergetic use between these data sets.

Lastly, while this study showed success in identifying potential regions of recharge over an aquifer composed of unconsolidated sediments, we might not expect our approach to be as relevant to karst aquifer systems where deformation related to fluid‐pressure changes is strongly dependent on the orientation and size of preexisting rock fractures (Serpelloni et al., 2018; Silverii et al., 2019).

4.3. Groundwater Management

With the passage of the Sustainable Groundwater Management Act (SGMA), the State of California established a framework to protect against the exploitation and degradation of its groundwater resources. Critical to this initiative was the designation of “groundwater sustainability agencies” (GSAs; see Figures 7d–7f). A GSA is established by a single agency or a combination of local agencies (Water Code sect; 10723.6) and is tasked to develop, implement, and enforce a basin's groundwater sustainability plan in accordance with SGMA (Water Code sect; 10733.4). As such, their boundaries often coincide with existing water management entities, which were typically designed around the availability and flow of surface water as well as urban development. At agency, regional, and state levels, new or independent data that have the potential to constrain groundwater flow models can lead to an improved understanding of the interconnectedness of the aquifer systems. This would aid monitoring and protection of groundwater resources efforts by informing how existing GSAs can improve their coordination in achieving sustainability goals.

Here, we offer a synoptic view of seasonal surface displacements from InSAR and cGPS over the southern San Joaquin Valley at policy relevant scales. Seasonal displacement amplitude, uplift timing, and lateral progression of timing demonstrate the complexities of deformation associated with joint surface‐water and groundwater hydrological processes in the SJV. Our results highlight where groundwater‐driven deformation deviates from natural surface‐driven processes. We infer these differences to be preferential pathways for annually averaged groundwater flow. While streams and canals define surface‐water networks for GSAs, these inferred pathways suggest potential subsurface interconnectivity (Figures 7e and 7f). Novel information such as this may help identify strategies for GSA coordination that maximize the utility of groundwater resources shared between GSAs. The striking differences in the uplift timing between a dry and wet year display the changing dynamics of the SJV aquifer system under different water availability scenarios at relatively short timescales. Further analysis comparing other water years with a range of hydrological conditions may establish a framework that groundwater managers and users can use to assess and perhaps anticipate the movement and availability of groundwater early in the water year and in time to inform critical planning decisions. These decisions may include, but are not limited to, crop selection, diversions for active conjunctive water use, and monitoring prioritization.

5. Conclusions

Leveraging the high spatial resolution of InSAR with the greater accuracy and temporal resolution of cGPS provides detailed insight into regional surface displacements. We estimated the annual rate and seasonal behavior of land surface elevation over the southern SJV for both a regulatory dry (WY2016) and wet (WY2017) water year using GPS‐enhanced InSAR. We find that subsidence in the valley was greatly diminished in WY2017 compared to WY2016, consistent with a reduction in groundwater withdrawals in the presence of increased surface‐water availability. Our characterization of the seasonal deformation reveals coherent patterns in amplitude and phase (peak uplift timing) across the SJV. While the peak seasonal amplitude was ∼35 mm for both years, regions of high amplitude in WY2017 are typically located near the confluence of rivers and downstream of their WY2016 counterparts. From the seasonal phase, we find that relative uplift generally occurs in the late winter to spring (March to May) for the dry year (WY2016) and during the summer (July to September) for the wet year (WY2017), coincident with waning river runoff volumes. We identified several regions of winter uplift common to both years which are adjacent to rivers with headwaters in the high Sierra Nevada. These regions are consistent with recent isotope studies indicating zones of possible recharge. The progression of this seasonal uplift across the valley often deviates from the topographic gradient, which suggests that the displacement signal is controlled by subsurface processes. Relative maxima in groundwater levels from well measurements (where available) are generally coincident with the timing of peak seasonal uplift, further indicating that we are able to resolve the pore‐fluid pressure response from changes in pumping activities and/or a lateral redistribution of water (groundwater flow) in the SJV aquifer system. These analyses and interpretations highlight the complexities of surface deformation related to changes in surface‐water availability, groundwater resources, and the conjunctive water use.

Supporting information

Figure S1

Figure S2

Figure S3

Figure S4

Figure S5

Figure S6

Figure S7

Figure S8

Figure S9

Figure S10

Figure S11

Table S1

Table S2

Table S3

Table S4

Neely, W. R. , Borsa, A. A. , Burney, J. A. , Levy, M. C. , Silverii, F. , & Sneed, M. (2021). Characterization of groundwater recharge and flow in California's San Joaquin Valley from InSAR‐observed surface deformation. Water Resources Research, 57, e2020WR028451. 10.1029/2020WR028451

Data Availability Statement

All raw geodetic and hydrological data are freely available from public sources (as referenced). Processed GPS‐enhanced InSAR products are available from the Zenodo repository (https://doi.org/10.5281/zenodo.3968903). We are grateful to P. Castellazzi, C. Jones, an anonymous reviewer, and D. Galloway who provided thoughtful and constructive feedback which helped improve this manuscript. Further, we thank S. Adusumilli, E. Knappe, D. Kilb, and S. Mumma for their helpful comments during the drafting of this manuscript. Analyses and visualizations were done using GMTSAR (Sandwell et al., 2011; Xu et al., 2017), Generic Mapping Tools (Wessel et al., 2013), and MATLAB. Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by the U.S. Government.