Accurate and robust whole-head segmentation from magnetic resonance images for individualized head modeling

Abstract

Transcranial brain stimulation (TBS) has been established as a method for modulating and mapping the function of the human brain, and as a potential treatment tool in several brain disorders. Typically, the stimulation is applied using a one-size-fits-all approach with predetermined locations for the electrodes, in electric stimulation (TES), or the coil, in magnetic stimulation (TMS), which disregards anatomical variability between individuals. However, the induced electric field distribution in the head largely depends on anatomical features implying the need for individually tailored stimulation protocols for focal dosing. This requires detailed models of the individual head anatomy, combined with electric field simulations, to find an optimal stimulation protocol for a given cortical target. Considering the anatomical and functional complexity of different brain disorders and pathologies, it is crucial to account for the anatomical variability in order to translate TBS from a research tool into a viable option for treatment.

In this article we present a new method, called CHARM, for automated segmentation of fifteen different head tissues from magnetic resonance (MR) scans. The new method compares favorably to two freely available software tools on a five-tissue segmentation task, while obtaining reasonable segmentation accuracy over all fifteen tissues. The method automatically adapts to variability in the input scans and can thus be directly applied to clinical or research scans acquired with different scanners, sequences or settings. We show that an increase in automated segmentation accuracy results in a lower relative error in electric field simulations when compared to anatomical head models constructed from reference segmentations. However, also the improved segmentations and, by implication, the electric field simulations are affected by systematic artifacts in the input MR scans. As long as the artifacts are unaccounted for, this can lead to local simulation differences up to 30% of the peak field strength on reference simulations. Finally, we exemplarily demonstrate the effect of including all fifteen tissue classes in the field simulations against the standard approach of using only five tissue classes and show that for specific stimulation configurations the local differences can reach 10% of the peak field strength.

1. Introduction

Transcranial brain stimulation (TBS) has been established as a method for modulating and mapping the function of the human brain, and as a potential tool for clinical intervention in major depressive disorder (MDD) (Nitsche et al., 2009; Palm et al., 2012) and rehabilitation after stroke (Baker et al., 2010; Hummel and Cohen, 2006; Schlaug et al., 2008). Currently, the most common approach for applying the stimulation is to place the electrodes, in transcranial electric stimulation (TES), or the coil, in transcranial magnetic stimulation (TMS), to predefined reference positions across all subjects in a study (Karabanov et al., 2016; Mutz et al., 2018). However, simulation studies in healthy subjects have shown that the electric field distribution in the brain is fundamentally shaped by anatomical features in both TES (Opitz et al., 2015) and TMS (Laakso et al., 2018; Thielscher et al., 2011), implying the need for individualized optimization of the stimulation protocol opposed to applying a standard protocol in all subjects. This finding is further corroborated by stimulation studies reporting large inter-subject variability in physiological responses to TES (Chew et al., 2015) and to TMS (Conde et al., 2012). Anatomically accurate individualized modeling is thus crucial, both in healthy subjects and in patient populations with brain pathologies that alter the neuroanatomy such as stroke (Datta et al., 2011; Minjoli et al., 2017) or tumors (Korshoej et al., 2017), in order to translate TBS from a research tool into a viable option for treatment. Additionally, source localization approaches in magneto- and electro-encephalography (M/EEG) also benefit from accurate models of the head anatomy (Cho et al., 2015).

As the need for individualized head models has become more widely recognized (Laakso et al., 2015; Thielscher et al., 2015; Vorwerk et al., 2014), simulation toolboxes for creating such models have been developed and made available. Many open-source toolboxes for simulation of TBS (Huang et al., 2019; Thielscher et al., 2015) and source mapping in MEG and EEG (Gramfort et al., 2013; Oostenveld et al., 2011; Tadel et al., 2011) include automated generation of individualized volume conductor models directly from structural magnetic resonance (MR) scans of the head anatomy. Most of these toolboxes rely on existing software developed for segmentation of brain tissues (Ashburner and Friston, 2005; Dahnke et al., 2013) or more fine-grained neuroanatomical structures (Cointepas et al., 2010; Fischl et al., 2002; Shattuck and Leahy, 2002). Although the field of automated segmentation of neuroanatomy is quite mature (Akkus et al., 2017; Despotovic et al., 2015; Iglesias and Sabuncu, 2015), segmenting extra-cerebral structures from MR scans has received less attention. In (Nielsen et al., 2018) the authors review the skull segmentation accuracy of open-source software tools for simulation of TES against computed tomography (CT) scans and conclude that while accurate segmentation of the skull from MR is possible to a certain extent using current tools, robustness, spatial detail, and number of extra-cerebral tissue classes are still lacking. Recently a convolutional neural network architecture was proposed for automated segmentation of multiple head tissues (Rashed et al., 2019), which obtained good agreement with semi-automated segmentations on the same data set. However, it is not clear how to generalize the segmentation performance to MR data sets acquired with scanners, scan sequences or settings that are different from those of the training data set (Rashed et al., 2019). Generalization performance and robustness are two crucial points for translating TBS to a clinical treatment tool, as the quality of clinical MR scans is limited by resolution, motion artifacts and scan time.

In this article, we present an automated segmentation approach for fifteen different tissue classes of the head from, possibly, multi-modal MR scans of a subject. The method, called Complete Head Anatomy Reconstruction Method (CHARM),¹ is based on our previous work in neuro-anatomical segmentation (Puonti et al., 2016), and is completely contrast-adaptive and thus readily generalizes to MR data from different scanners, scan-sequences, and even modalities (Agn et al., 2019). Apart from extending the segmentation method to cover extra-cerebral structures, and testing its accuracy and robustness, the article includes other novel contributions. Specifically, we study the link between segmentation accuracy and its effect on the simulated electric field distributions for TES and TMS and show that subtle differences in the input scans can lead to large effects on the electric field simulations. We also show results on the effects of including multiple tissue classes in the head model, as opposed to the five main head tissues which is the standard (Huang et al., 2019; Saturnino et al., 2018), and how this affects the simulations. The rest of the article is structured as follows: we first describe the data set used for training and testing the new method, next we give an overview of the segmentation model, then we describe the experiments and present the results, and finally conclude with a discussion.

2. Materials and methods

In this section we first detail the data set, which is used for training and validating our segmentation approach, next we describe how a probabilistic head atlas is built from the training data, and finally we give a brief overview of how the segmentation of novel, unseen, MR scans proceeds given the head atlas. The segmentation model, which includes both atlas construction (Van Leemput, 2009) and segmentation of new scans (Iglesias et al., 2015a; Puonti et al., 2016), is based on our previous work which we revisit here for completeness.

2.1. Data set

The data set consists of 20 subjects who all underwent head scanning with both MRI and CT. The subject group was evenly split in gender (10 males/10 females) and ancestry (10 Asian/10 Caucasian), with an age range from 20 to 50 years old. The data set covers a large variety of different head and neck sizes. As a proxy for the variation, we computed the body mass indexes (BMIs), which range from 18 to 33.6. The study was approved by the Ethical Committee of the Capital Region of Denmark.

We collected five different head scans for each subject with all the MR scans acquired on a 3T Philips Achieva scanner, equipped with a 32-channel receive headcoil, and the CT scans on a Siemens Biograph mCT (PET-CT). The scans, and parameters thereof, are as follows:

• T1-weighted scan (T1w): 3D Turbo Field Echo, Relaxation Time (TR) = 6 ms, Echo Time (TE) = 2.7 ms, Flip Angle (FA) = 8°, voxel size = 0.85 mm³.

• T2-weighted scan (T2w): 3D Turbo Spin Echo, TR = 2500m, TE = 272 ms, FA = 90°, voxel size = 0.85 mm³.

• mDixon scan: TR = 4.1 ms, TE1 = 1.34 ms, TE2 = 2.4 ms, FA = 9°, voxel size = 1.1 mm³.

• Venogram: TR = 18 ms, TE = 6.9 ms, FA = 8°, voxel size = 0.8 × 1.1 × 1.6 mm³.

• CT: voxel size = 0.42 × 0.42 × 0.6 mm³, tube potential = 80 keV, maximum effective dose below 0.35 mSv for all participants.

Using the complementary contrasts provided by the different sequences, the head scans were segmented into fifteen different tissues using the open-source iSEG software.² The segmentation procedure consisted of masking, connected thresholding, morphological operations and manual corrections. A list of all the tissues along with an example of a semi-automated segmentation, which we call reference segmentation from hereon, is shown in Fig. 1. Further details regarding demographics, scan parameters, data pre-processing and segmentation steps can be found in (Farcito et al., 2019). Importantly, this data set is, to the best of our knowledge, the first with detailed semi-automated segmentations of several extra-cerebral tissues, also covering the neck region, on multiple subjects, which allows us to develop an accurate automated tool for labeling new MR scans with the same spatial detail.

Fig. 1.

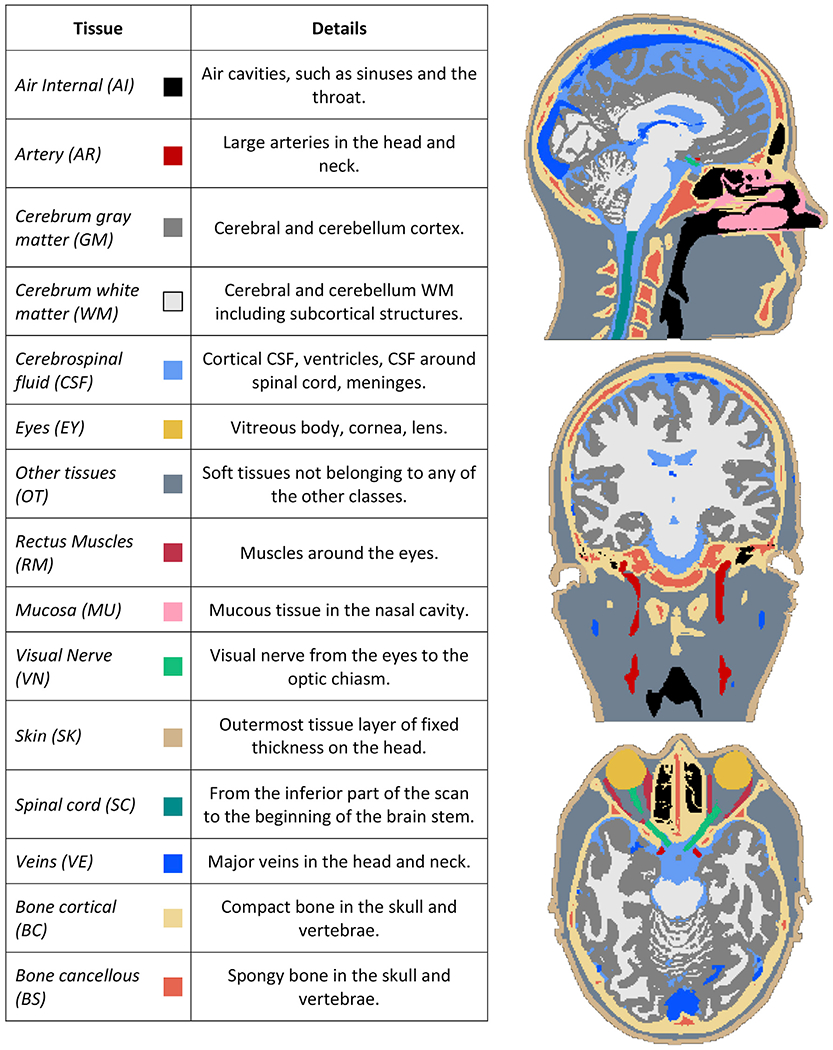
On the left: list of the different head tissues, and what they are comprised of, segmented from the imaging data. On the right: an example reference segmentation where the tissues are color-coded according to the colors in the table. Note the spatial detail of the extra-cerebral tissues, and the coverage of the neck region.

2.2. Construction of the head atlas

Given the training data our aim is to construct a representation of the average anatomy of the head, along with a deformation model capturing the anatomical variability among the subjects. Here, we rely on a mesh-based encoding of the anatomy first introduced in (Van Leemput, 2009), and subsequently applied to whole-brain segmentation (Puonti et al., 2016) , and segmenting the sub-structures of the hippocampus (Iglesias et al., 2015a), thalamus (Iglesias et al., 2018), brainstem (Iglesias et al., 2015b) and amygdala (Saygin et al., 2017). These tools are all freely available in the FreeSurfer software suite.³ The mesh-based atlas is defined through a generative model of how the discrete segmentations are formed. Specifically, we assume that a 3D segmentation l = (l₁,…,l_I), where l_i denotes the label in voxel i with a total of I voxels, is generated by the following process:

$$p\left(\mathit{l}|\mathit{\alpha },\mathit{x},\mathit{\kappa })=\prod _{i}p(l_i|\mathit{\alpha },\mathit{x},\mathit{\kappa }\right)$$ (1)

$$p\left(l_i=\kappa |\mathit{\alpha },\mathit{x},\mathit{\kappa }\right)=\sum _n{\alpha }_n^{\kappa }{\varphi }_n\left({\mathit{r}}_i\right).$$ (2)

Eq. (1) states that the segmentation labels in each of the voxels are drawn conditionally independently from each other given parameters α, x, and κ. Here x denotes the positions of the mesh nodes, α denotes the probabilities of the fifteen different head structures attached to each node, and κ is the connectivity of the mesh. Eq. (2) states that the probability of one of the fifteen possible structures, κ, to occur at voxel i depends on the probability of that structure, ${\alpha }_n^k$, summed over the mesh nodes and weighted by an interpolation function, ${\varphi }_n\left(r_i\right)$, which depends on the distance between the voxel location, r_i, and the mesh node location, x_n. In practice, the interpolation function is based on barycentric interpolation (Van Leemput, 2009). We further need to define probability distributions on these parameters. For this purpose, we assign flat priors for the structure probabilities α and mesh connectivity κ, whereas the mesh node positions x are drawn from:

$$p\left(\mathit{x}|{\mathit{x}}_{ref},\beta \right)\alpha \mathit{exp}\left(-\beta F\left(\mathit{x},{\mathit{x}}_{ref}\right)\right).$$

Here x_ref denotes the reference position of the mesh, i.e., the position of the nodes in the average anatomy given a group of subjects. β is a parameter controlling how much the sampled positions x can deform from the reference positions, which defines the stiffness of the mesh, and the function F(·) ensures that the mesh does not tear or fold onto itself (Puonti et al., 2016; Van Leemput, 2009). We fix the stiffness parameter β to 0.1, which has been shown to work well for whole-brain segmentation (Puonti et al., 2016).

The reference position and connectivity of the mesh and the structure probabilities can be learned from a set of reference segmentations using Bayesian inference as detailed in (Van Leemput, 2009). The benefit of the adopted mesh-based parameterization, combined with Bayesian modeling, is that it allows for a compact encoding of the anatomy where the local mesh resolution is automatically adjusted during learning based on the size of the training data set (Puonti et al., 2016; Van Leemput, 2009). A trained head mesh in its reference position is shown in Fig. 2.

Fig. 2.

Example slices from the trained atlas in its reference position. The trained mesh is overlaid on the rasterized color-coded tissue probabilities. The opacity is scaled according to the tissue probabilities, i.e., the blurriness illustrates areas where multiple tissues have similar probabilities.

Once the reference position, connectivity, and structure probabilities have been learned, the generative model defines a prior probability distribution of a segmentation through (Puonti et al., 2016):

$$p\left(\mathit{l}\right)=\int p\left(\mathit{l}|\mathit{x}\right)p\left(\mathit{x}\right)dx,$$ (3)

Where we have dropped the explicit dependence on the learned, or fixed, parameters $\widehat{\mathit{\alpha }}$, $\widehat{\mathit{\kappa }}$, $\widehat{\mathit{\beta }}$, and ${\widehat{x}}_{ref}$. Marginalization over the mesh node positions in eq. (3) is intractable in practice, and we rely on an approximation, see section 2.3 eq. (4), for finding a point estimate for the positions.

2.3. Segmentation of unseen MR scans

To segment a previously unseen, possibly multi-contrast, MR scan D = (d₁,…,d_I), where the vector $d_i={\left(d_i^1,\dots ,d_i^N\right)}^T$ contains the log-transformed intensities in voxel i for each of the N contrasts, we combine the segmentation prior with a likelihood distribution p(D|l). The likelihood links the segmentation labels to the scan intensities, and we can then model the unobserved segmentation given the data in terms of the posterior distribution:

$$p\left(\mathit{l}|\mathit{D}\right)\alpha p\left(\mathit{D}|\mathit{l}\right)p\left(\mathit{l}\right).$$

Before we can compute the posterior, we need to define a parametric form for the likelihood. Following the approach in (Puonti et al., 2016), we define the data likelihood for a given segmentation label to be a mixture of Gaussian distributions (GMM):

$$p\left({\mathit{d}}_i|{\mathit{l}}_i=k,\mathit{\theta })=\sum _{g=1}^{G_k}{w}_{k,g}N({\mathit{d}}_i-{\mathit{b}}_i|{\mu }_{k,g},\sum {}_{k,g}\right)$$

Here, G_k is the number of Gaussians for label k, w_k,g is the weight, μ_k,g is the mean, and Σ_k,g is the covariance matrix for Gaussian g in the mixture of label k. The well-known bias field (Van Leemput et al., 1999; Wells et al., 1995), which is a low-frequency intensity artifact inherent to MRI, is denoted as b_i and modeled as a combination of basis functions, see (Puonti et al., 2016) for details. The bias effect is multiplicative, which is the reason we work with log-transformed intensities as the estimated bias field can then be subtracted from the intensities. Assuming the intensities in the voxels are conditionally independent given the segmentation label and parameters θ, we can write the likelihood over all voxels as:

$$p\left(\mathit{D}|\mathit{l})=\underset{\theta }{\int }p(\mathit{D}|\mathit{l},\mathit{\theta }\right)p\left(\mathit{\theta }\right)d\mathit{\theta },$$

Where

$$p\left(\mathit{D}|\mathit{l},\mathit{\theta })=\prod _{i}p({\mathit{d}}_i|{\mathit{l}}_i,\mathit{\theta }\right).$$

Now, we look for the maximum-a-posteriori (MAP) segmentation given by

$$\widehat{\mathit{l}}=\mathit{arg}{\mathit{max}}_{l}p\left(\mathit{l}|\mathit{D}\right).$$

However, the integration over the model parameters x and θ is intractable. To overcome this problem, we resort to the so-called empirical Bayes method and approximate the posterior as (Puonti et al., 2016):

$$p\left(\mathit{l}|\mathit{D})={\int }_{\mathit{\theta },\mathit{x}}p(\mathit{l}|\mathit{D},\mathit{x},\mathit{\theta }\right)p\left(\mathit{x},\mathit{\theta }|\mathit{D}\right)\mathit{d}\mathit{x}\mathit{d}\mathit{\theta }\cong p\left(\mathit{l}|\mathit{D},\widehat{\mathit{x}},\widehat{\mathit{\theta }}\right),$$ (4)

where the point estimates for the parameters are given by

$$\left\{\widehat{\mathit{x}},\widehat{\mathit{\theta }}\right\}=\mathit{arg}{\mathit{max}}_{\mathit{x},\mathit{\theta }}p\left(\mathit{x},\mathit{\theta }|\mathit{D}\right).$$ (5)

The approximation in eq. (4) assumes that the posterior of the parameters is very peaked around its mode, i.e., that the variation of the parameter estimates given the data is small. Now the segmentation problem is translated into an optimization problem of finding the MAP parameter values. The expression in eq. (5) can be further expanded to obtain:

$$\begin{array}{l}\left\{\widehat{\mathit{x}},\widehat{\mathit{\theta }}\right\}=\mathit{arg}{\mathit{max}}_{\mathit{x},\mathit{\theta }}\sum _{\mathit{l}}p\left(\mathit{D}|\mathit{l},\mathit{\theta }\right)p\left(\mathit{l}|\mathit{x}\right)p\left(\mathit{x}\right)p\left(\mathit{\theta }\right),=\mathit{arg}{\mathit{max}}_{\mathit{x},\mathit{\theta }}\prod _i\\ \times \sum _{k}p\left({\mathit{d}}_i|l_i=k,\mathit{\theta }\right)p\left(l_i=k,\mathit{x}\right)p\left(\mathit{x}\right)p\left(\mathit{\theta }\right),\end{array}$$

which can be efficiently solved using a coordinate ascent approach where the mesh node positions x and likelihood parameters θ are optimized in turn until convergence. The details of the optimization approach are discussed in (Puonti et al., 2016). Once the parameter values have been found, the segmentation can be easily obtained using the approximation to the posterior in eq. (4), which factorizes over the voxels, by finding the most probable label in each voxel independently.

3. Implementation

3.1. Modeling of tissue intensities

Based on our previous work (Puonti et al., 2016), we model the tissues with similar intensity properties with the same GMM. This reduces the number of parameters, which makes the algorithm more robust as, in general, we have more data to fit the parameters compared with the case where each tissue would have its own GMM. Table 1 lists the tissues, which share their GMMs along with the number of Gaussian components. These assignments and number of components are based on pilot experiments on a separate data set. The bias field is modeled as a combination of low-frequency components of the discrete cosine transform (DCT) basis functions. The number of DCT components per scan dimension is calculated based on a user input smoothing kernel width, so that the highest frequency component matches the desired width. For unimodal segmentation, i.e., a T1-weighted scan only, we use a kernel width of 70 mm, whereas for a multimodal input, i.e., both T1-and T2-weighted scans, we use a width of 50 mm. These choices are based on pilot experiments, and fit our previous experience that multimodal inputs require more flexible bias field models (Nielsen et al., 2018).

Table 1.

Left columns shows the tissue classes that share their GMM, and the right column denotes the number of Gaussian components in each GMM.

SHARED TISSUE CLASSES	NO. OF GMM COMPONENTS
BACKGROUND	1
CEREBRUM WHITE MATTER	2
CEREBRUM GRAY MATTER	2
CEREBROSPINAL FLUID, EYES	2
VEINS	1
OTHER TISSUES, RECTUS MUSCLES, MUCOSA, SKIN, ARTERY	1
VISUAL NERVE	1
BONE CORTICAL	1
BONE CANCELLOUS	1
SPINAL CORD	1

3.2. Initialization

To initialize the segmentation algorithm, we need to affinely map the mesh-based atlas to the input scan. Here we assume that multi-modal inputs have been previously co-registered and are in the same space. The affine registration is based on a standard normalized mutual information (MI) similarity metric between the atlas and the input scan (D’Agostino et al., 2004). We also search through three scaling factors: (0.8, 0.85, 0.9), and five pitch angles, e.g., rotation around the left-right axis: (−7°, −5°,0°,5°, 7°), for initializing the transformation. The search ranges can be controlled by the user in case the initialization fails. Based on pilot experiments on a separate data set, searching through these scales and angles gave a good starting point for the affine registration. After the initial scale and rotation have been found, the affine transformation is computed by optimizing the MI metric. Given the transformation, we separately refine the deformation of the neck region, defined as the region below the most superior point of the spinal cord. This is necessary as the neck region often has a deformation in the anterior-posterior direction due to positioning in the scanner. We account for this, heuristically, by optimizing the following deformation: y(z) = y(z) + k(z₀ – z), where the displacement in the anterior-posterior direction at a given axial location, y(z), is a linear function of the distance from the top of the spinal cord z₀, and we optimize over the free parameter k using a Nelder-Mead simplex algorithm implemented in the fminsearch function in MATLAB (Release 2017b, The MathWorks, Inc., Natick, Massachusetts, United States). The idea here is that the displacement can get larger the further we move from the base of the skull, which approximates the natural motion of the neck. The affine registration and neck optimization can be interpreted as a piece-wise affine transformation, where the transformation of the atlas to the input image is first optimized over the whole head, and then separately for the neck. Finally, the transformed mesh node positions are used as initial estimates in the parameter optimization procedure.

3.3. Optimization of model parameters

The optimization proceeds in two resolution levels where in the first level the input scan(s) is downsampled to a target resolution of 2.0 × 2.0 × 2.0 mm³ and a sparse mesh atlas is used (approximately 57000 nodes), and in the second level a target resolution of 1.0 × 1.0 × 1.0 mm³ is used along with a denser mesh atlas (approximately 110000 nodes). The target resolution is used to compute a downsampling factor by dividing with the original scan resolution and rounding to the nearest integer. The final segmentation is reconstructed in the original scan resolution. The GMM and bias field parameters are optimized by a dedicated generalized expectation-maximization (GEM) algorithm, see (Puonti et al., 2016) for details, followed by the mesh deformation optimization using a limited memory Broyden-Fletcher-Goldfarb-Shanno (L-BFGS) optimizer. The GEM iterations are stopped if the relative change in the objective function, normalized with the number of voxels, falls below 10⁻⁴ or 100 iterations have been reached, whereas the L-BFGS updates are run until the mesh stops deforming or 20 iterations have been reached. The two iteration steps are repeated until the relative change in the overall objective function falls below 10⁻⁴ or 100 iterations are reached in both resolution levels.

4. Experiments

We validate CHARM in three different experiments to explore both the quality of the automated segmentations and to link the segmentation accuracy, along with the parameters of the MR scans, to electric field simulations. The first experiment concentrates on quantitative and qualitative validation of the accuracy of the anatomical segmentations. The second experiment shows how differences in the anatomical segmentations result in clear, physiologically relevant, differences in the e-field simulations, and how these segmentation differences are influenced by the MR scan settings. The third experiment shows the effect of modeling multiple tissue compartments against the standard approach of modeling the five main head tissue classes, namely: WM, GM, CSF, bone, soft tissues.

4.1. Experiment 1: segmentation accuracy

In the first experiment, we compare the segmentation accuracy of CHARM against two freely available software packages for individualized simulation of TDCS: SimNIBS 2.1 (Saturnino et al., 2018) and ROASTv2.7 (Huang et al., 2019). Both tools are widely used for electric field (e-field) simulations and have been shown to obtain reasonably good segmentation accuracies in automated skull segmentation from MR scans (Nielsen et al., 2018). The segmentations are generated either using only a T1w scan, or using both the T1w and T2w scans, to quantify the added benefit of the extra contrast provided by the T2w scan. We use two accuracy metrics to compare the automated segmentations to the reference segmentations. The first one is the well-known Dice score, which measures the spatial overlap of two binary masks:

$$D=\frac{2\left|A\cap M\right|}{\left|A\right|+\left|M\right|},$$

where A denotes a tissue mask created automatically and M denotes the reference tissue mask. The Dice score varies between zero and one, where zero corresponds to no overlap and one to perfect overlap. The second accuracy measure is the modified Hausdorff distance, which finds the maximum of two directed Hausdorff distances, h_m(A, M) and h_m(M, A):

$$H\left(A,M\right)=\mathit{max}\left\{h_m\left(A,M\right),h_m\left(M,A\right)\right\},$$

where the directed Hausdorff distance is defined as:

$$h_m\left(A,M\right)=\frac{1}{\left|A\right|}\sum _{a\epsilon A}\underset{m\in M}{\min }\left\{\mathit{d}\left(a,m\right)\right\},$$

which measures the average distance between the closest points in the two point sets (Dubuisson and Jain, 1994). For the distance measure d(a, m) we use standard Euclidean distance. While the Dice score measures the volume overlap and can be dominated by a large cluster of voxels, the modified Hausdorff distance is more sensitive to errors along the borders of the segmented structures, and thus the two accuracy measures provide complimentary information of the segmentation accuracy.

The segmentation approaches implemented in SimNIBS 2.1, termed HEADRECO from hereon, and ROAST v2.7, termed ROAST from hereon, only segment the five main head tissue classes in an MR scan. Although the eyeballs are separately segmented in the reference segmentations, and by both CHARM and HEADRECO, we added these to the CSF class in all segmentations in Experiments 1 and 2, because they are labeled as part of the CSF in the ROAST segmentation. For the comparisons, we assign the fourteen different tissues, where we exclude the air pockets in the head, in the reference segmentations to one of these five tissue classes. The tissue assignments are listed in Table 2. As the reference segmentations are also used to build the probabilistic mesh atlas used by CHARM, we use four-fold cross-validation to obtain unbiased estimates of the accuracy metrics. Specifically, the 20 reference segmentations are divided randomly to four sets of five and fifteen subjects, making sure we cycle through all the 20 subjects as test cases, where the fifteen subjects are used to build the atlas and the rest serve as test cases. Finally, all the methods are run using the standard settings without any extra tuning to optimize segmentation performance on the data set. Note that the atlas used in HEADRECO and ROAST is trained on a completely separate data set (Huang et al., 2013), and cross-validation is not needed. We also report the segmentation accuracy of CHARM, as measured by the two metrics, on all the fifteen tissue classes using the same cross-validation scheme.

Table 2.

Tissue assignments mapping the 14 different tissues in the semi-automated segmentations (right column) to the five main head tissue classes (left column).

Merged tissue class	Assigned tissues
White matter (WM)	Cerebrum white matter Spinal cord Visual nerve
Gray matter (GM)	Cerebrum gray matter
Cerebrospinal fluid (CSF)	Cerebrospinal fluid Veins Eyes
Bone	Compact bone Spongy bone
Soft tissues	Other tissues Rectus muscles Mucosa Skin

4.2. Experiment 2: accuracy of e-field simulations

In the second experiment, we first show a qualitative comparison between the two best performing methods, HEADRECO and CHARM (see Results, section 5.1 for the scores), on four subjects coming from two different data sets. These two data sets were selected based on our previous studies (Csifcsak et al., 2018; Puonti et al., 2020) in which we have observed segmentation errors due to issues with MR data quality. The four subjects were chosen so that they represent the typical segmentation errors observed in the two data sets, to demonstrate a worst-case scenario of poor segmentation accuracy on the e-field simulations. The first data set was collected as part of a functional MRI study and is freely distributed through the OpenfMRI database (https://openfmri.org/; accession number: ds000171). The two subjects chosen were the control subjects 07 (sub-control07) and 17 (sub-control17). The data set consists of T1-weighted anatomical scans, along with functional scans, acquired on a 3T Siemens Skyra scanner using a 3D MPRAGE sequence (TR = 2300 ms, TE = 2.01 ms, FA = 9, FOV = 256, matrix = 256×192, slice thickness = 1 mm). No fat suppression was used, resulting in a fat shift in the superior-inferior direction, which makes accurate segmentation of the skull difficult, see (Nielsen et al., 2018) for details. The second data set comes from a study where the authors recorded TDCS induced electric fields using intra-cranial electrodes in a group of epilepsy patients (Huang et al., 2017). Here, the chosen subjects were subjects P014 and P015. The T1-weighted scans, and field measurements, are freely downloadable after registration from https://doi.org/10.6080/K0XW4GQ1. The MR scan parameters are unfortunately not available for this data set. The two data sets, especially the latter given the challenging clinical population, are well-suited for testing the robustness of the automated segmentations to varying quality of the input data. We illustrate how segmentation differences between HEADRECO and CHARM result in clear differences in the estimated e-fields in a standard M1-SO TDCS stimulation paradigm (Nitsche and Paulus, 2000), where we placed rectangular electrodes of size 5 × 7 cm over the C3 (anode) and AF4 (cathode), see Figs. 6 and 7, and simulated a current injection of 1 mA.

Fig. 6.

Example subject from the data set described in (Huang et al., 2017). The first column shows the MR scan along with the electrode locations, the second column the segmentations and e-field simulation from HEADRECO, and the third column the segmentations and e-field simulation from CHARM. The small emblem in the lower right corner denotes that the CHARM simulations were run on a head model with the standard five tissues and not all fifteen that are segmented.

Fig. 7.

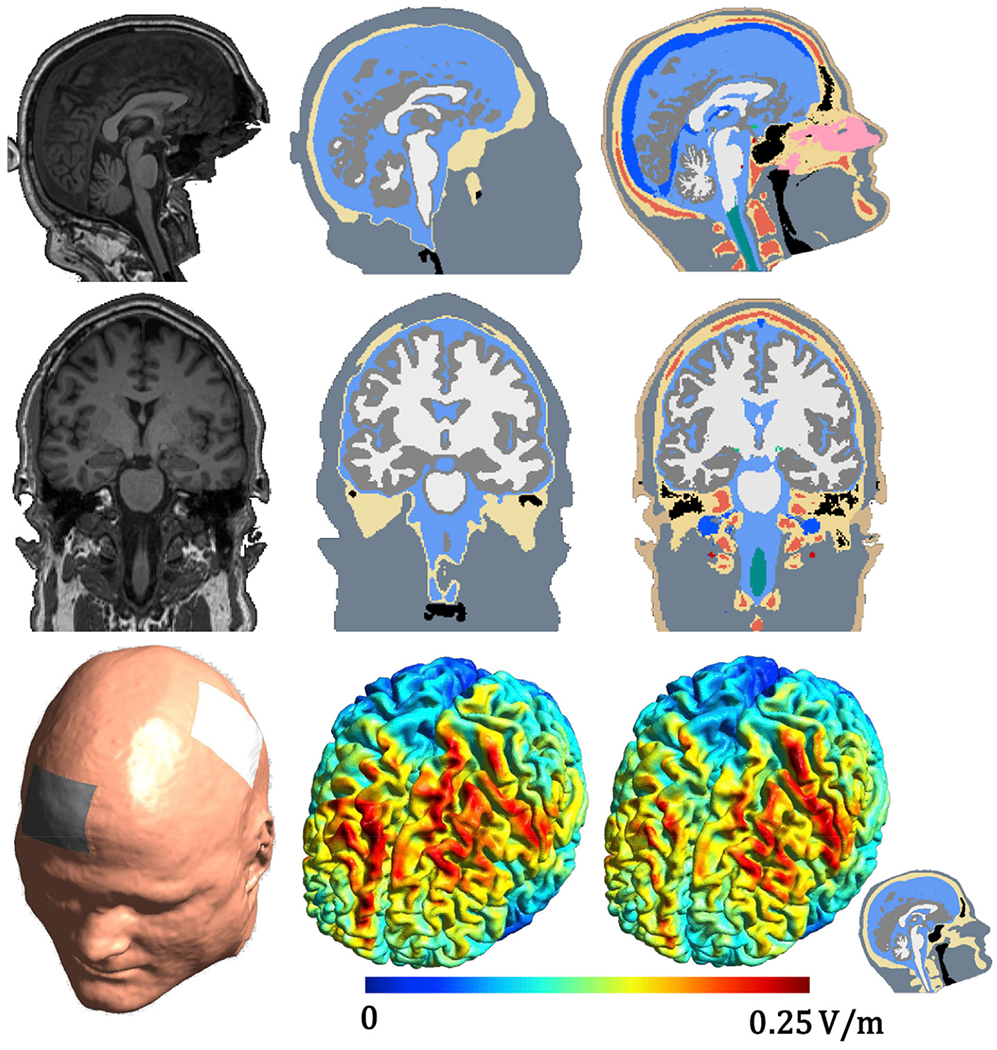
Example subject from the data set described in (Csifcsák et al., 2018). The first column shows the MR scan along with the electrode locations, the second column the segmentations and e-field simulation from HEADRECO, and the third column the segmentations and e-field simulation from CHARM. The small emblem in the lower right corner denotes that the CHARM simulations were run on a head model with the standard five tissues and not all fifteen that are segmented.

To gauge the relationship between segmentation accuracy and e-field simulations further, we compare the e-field simulations on head models constructed using either HEADRECO or CHARM segmentations to e-field simulations on head models constructed using the reference segmentations on all 20 subjects in the semi-automatically segmented data set. As in experiment 1, we use either only a T1w scan, or both T1w and T2w scans, to construct the head models. We quantify differences in the strength of the e-field over the 20 subjects in two stimulation paradigms: a standard M1-SO TDCS stimulation, as described above, and TMS over the motor cortex. For the TMS we simulated a Magstim 70 mm Figure-of-Eight coil placed at the C3 position of the EEG 10–20 system with the coil direction towards CP3 (Fitzgerald et al., 2009), see Supplementary material Figure S9. The e-field differences between the automated and reference models are measured by calculating a subject-wise normalized absolute difference, defined as:

$$e_{diff}=\frac{{\sum }_n\left|e_r^n-e_a^n\right|}{{\sum }_n{e}_r^n},$$

where $e_r^n$ denotes the simulated e-field strength, using the head model constructed from the reference segmentation, in node n of the fsaverage template, and e’a is the simulated e-field strength, constructed using a head model based on an automated segmentation, in the corresponding node on the template. The fields are mapped to the fsaverage template using SimNIBS 2.1. Furthermore, all e-field simulations are done in SimNIBS 2.1, and we use the merged five tissue segmentations, as defined in Table 2, for generating the head models from the reference and CHARM segmentations. We apply the same remaining steps of the HEADRECO pipeline to convert the voxel segmentations to tetrahedral head meshes. By that, we ensure that all segmentations are processed in the same way during the conversion. Finally, we demonstrate exemplarily on two representative subjects how the MR scan parameters, especially of the T1w scans, can adversely affect the automated segmentations, along with the e-field simulations, and how these adverse effects can be mitigated.

4.3. Experiment 3: modeling multiple tissue classes in e-field simulations

In the third experiment, we qualitatively compare how the simulated e-fields change when multiple tissue classes are included in the head model, against the established approach of using only five tissue classes. The standard head model generation pipeline in SimNIBS 2.1 does not readily support generating finite element (FEM) meshes for more than five tissue classes, and thus we used the computational geometry algorithms library (CGAL 4.13) to generate the volume meshes. Specifically, we developed an in-house implementation relying on the “Mesh_3” package in CGAL 4.13 (Rineau and Yvinec, 2007), where the mesh optimization parameters were set as follows: facet angle = 30°, facet size = 6 mm, facet distance = 0.4 mm, cell radius = 3 mm, and cell size = 8 mm. The segmentations were initially resampled to twice the resolution of the original image to avoid stair-casing effects in the mesh. Table 3 lists the tissues that were explicitly modeled, along with their assigned conductivities, together with a six-tissue class model, now including the eyes, and their conductivities.

Table 3.

Tissue conductivities for the six “standard” tissues (two leftmost columns) and for the 14 different tissues (two rightmost columns).

Tissue	Conductivity (S/m)	Tissue	Conductivity (S/m)
White matter	0.126 (Wagner et al., 2004)	Cerebrum white matter Spinal cord Visual nerve	0.126 (Wagner et al., 2004)
Gray matter	0.275 (Wagner et al., 2004)	Cerebrum gray matter	0.275 (Wagner et al., 2004)
CSF	1.654 (Wagner et al., 2004)	Cerebrospinal fluid Veins	1.654 (Wagner et al., 2004) 0.6 (Gabriel et al., 2009)
Bone	0.01 (Wagner et al., 2004)	Compact bone Spongy bone	0.008 (Opitz et al., 2015) 0.025 (Opitz et al., 2015)
Soft tissues	0.465 (Wagner et al., 2004)	Artery Other tissues Rectus muscles Mucosa Skin	0.6 (Gabriel et al., 2009) 0.465 (Wagner et al., 2004) 0.16 (Gabriel et al., 2009) 0.465 (Wagner et al., 2004) 0.465 (Wagner et al., 2004)
Eyeballs	0.5 (Opitz et al., 2015)	Eyes	0.5 (Opitz et al., 2015)

We simulated the e-fields for two stimulation set-ups: the first one is the standard M1-SO TDCS, as in the previous experiment, and the second one is TMS over the pre-supplementary motor area (pre-SMA). We again used the Magstim 70 mm Figure-of-Eight coil, but now placed it manually over the target region with the coil direction towards FC2. The target of the stimulation was intentionally chosen to highlight the effect of modeling the superior sagittal sinus. We visualize the e-fields for the six-tissue head model, the head model with multiple tissues, and their node-wise difference to demonstrate the size of the effect.

5. Results

5.1. Experiment 1: segmentation accuracy

Quantitative comparisons of the three automated segmentation pipelines are shown in Fig. 3 with the means and standard deviations listed in Table S1 in the supplementary material. The segmentation accuracies of HEADRECO and ROAST are on a similar level, which is expected as both rely heavily on SPM12 for the tissue segmentation with differences only in the post-processing of the tissue masks (Huang et al., 2019; Nielsen et al., 2018), while CHARM obtains higher accuracies in terms of both Dice scores and modified Hausdorff distances. Note that HEADRECO and ROAST both use a custom probabilistic atlas including the neck (Huang et al., 2013), and not the standard atlas in SPM12, which only covers the upper part of the head. Including a T2w scan as an input generally increases segmentation accuracy for most tissues and helps especially in the segmentation of bone and CSF. This has been observed before (Nielsen et al., 2018), and is due to the added CSF contrast in the T2w scans, which helps to pin down the skull-CSF border more accurately. We observed a single outlier in the CHARM segmentations, visible for example in the CSF and bone Dice scores, which was due to sub-optimal affine registration between the probabilistic mesh atlas and the T1w input scan. After the affine transformation was initialized differently, the segmentation improved and we recomputed the quality metrics, which are listed in the supplementary material Table S1. In all the following results we use the corrected segmentation for this single subject. We also report the Dice score and Hausdorff distance for a restricted field-of-view (FOV) including only the upper part of the head, for all methods, in the supplementary material Figure S1 and Table S3. Here the segmentations were clipped at the top of the spine (see Fig. 1). The segmentation accuracy is higher for the extra-cerebral structures in the restricted FOV for all methods indicating that the neck region is difficult to segment accurately.

Fig. 3.

Dice scores and modified Hausdorff distances (in natural log scale) for the five tissues and three methods. The filled boxes correspond to the case where only a T1w scan is used as an input, whereas the striped boxes correspond to a case where both T1w and T2w scans are used as input. On each box, the line marks the median, the box extends to lower and upper quartiles, whiskers extend up to 1.5 times the interquartile range, and data points beyond that are marked as outliers. The color coding is shown in the figure legend.

The main limitation of these comparisons is the different structural detail of the automated segmentations of HEADRECO and ROAST compared to the reference segmentations. For example, subcortical gray matter is included into the white matter class in the semi-automated segmentations (see Fig. 1). Also, the visual nerve is segmented separately in the reference segmentations and is added to white matter as listed in Table 2. The segmentations used to build the extended tissue probability maps used in HEADRECO and ROAST use different tissue class assignments (Huang et al., 2013), which likely results in under-estimation of the segmentation accuracy for the WM and GM tissues. This is one of the reasons we used the modified Hausdorff distance as a quality metric, which uses an average distance instead of the maximum and is less sensitive to outliers. Nevertheless, we consider the quantitative comparison as an indication of general segmentation performance of the methods especially in the non-brain structures.

We additionally show the segmentation performance of CHARM on all fifteen tissue classes in Fig. 4, with the means and standard deviations listed in Table S2 in the supplementary material. In general we see that the segmentation accuracy for the large tissue classes (the first nine from the left in Fig. 4) is fairly high, but drops for the small tissue classes (the last six from the left in Fig. 4), which vary more in location and shape in the MR scans. Including a T2w scan increases the segmentation accuracy for the CSF, bone compartments (spongy and compact), and veins, which is expected based on the results in Fig. 3. The veins appear dark in T2, which helps to separate them from CSF which appears bright. Fig. 4 also shows the accuracy for a restricted FOV, similar to Figure S1 in the supplementary, where the segmentations are clipped at the top of the spine. The segmentation accuracy in the restricted FOV is slightly higher, especially for CSF, spongy and compact bone, and veins, indicating that the neck is challenging to segment likely due to more variable tissue locations and lower signal in the MR scans. Finally, Fig. 5 shows reference and example segmentations for four subjects from each of the methods using T1w and T2w scans. Corresponding 3D renderings of the tissue segmentations from CHARM can be found in the Supplementary material (Figures S2–S5).

Fig. 4.

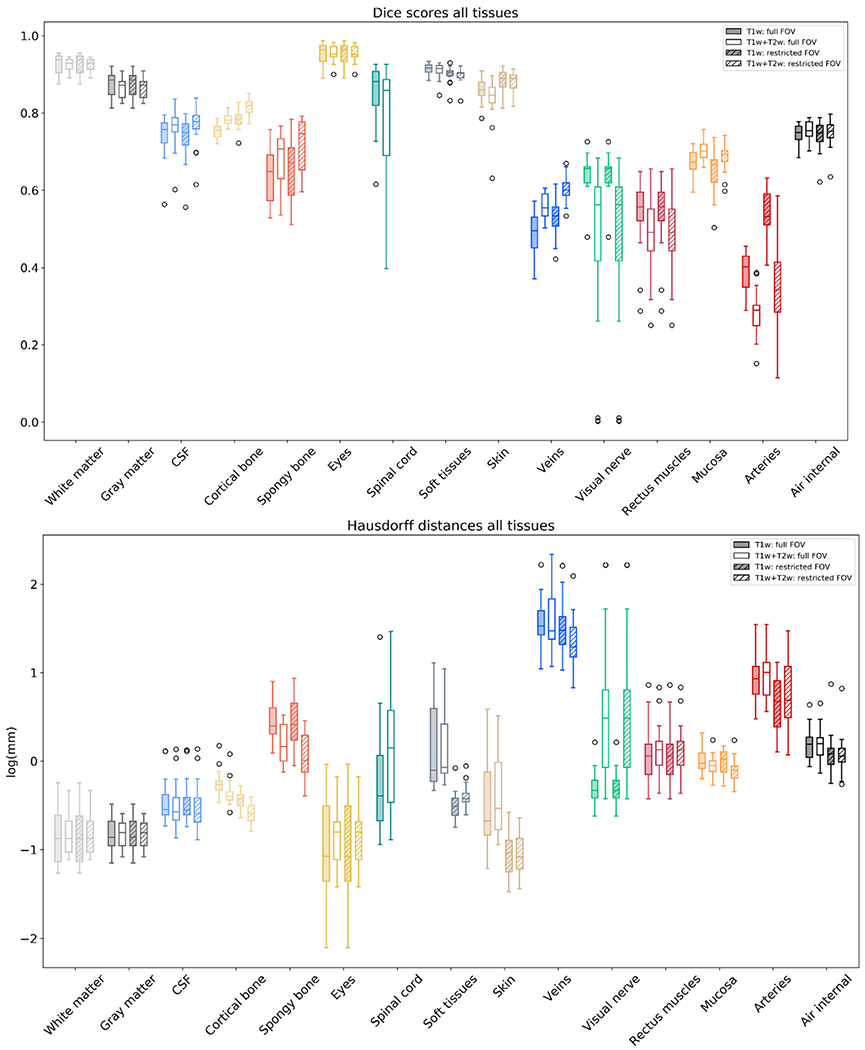
The Dice scores and modified Hausdorff distances (natural log scale) over all 15 tissue classes segmented by CHARM. The filled boxes correspond to the case where only a T1w scan is used as an input, and the non-filled boxes to a case where both T1w and T2w scans are used as inputs. The striped boxes correspond to a case where the FOV was restricted to the upper part of the head. On each box, the line marks the median, the box extends to lower and upper quartiles, whiskers extend up to 1.5 times the interquartile range, and data points beyond that are marked as outliers. The color-coding of the tissues matches the color-coding of the segmentations for example in Figs. 5 and 6.

Fig. 5.

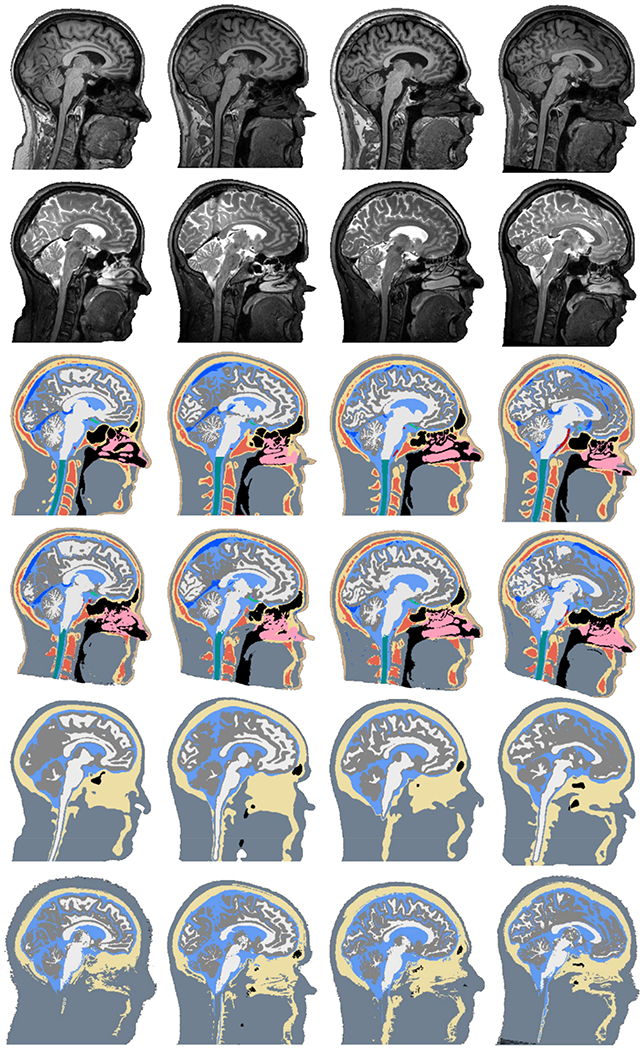
Each column shows the MR data and example segmentations for a single subject. The rows (from top to bottom) show the T1-weighted scan, T2-weighted scan, reference segmentation, CHARM segmentation, HEADRECO segmentation, and ROAST segmentation.

In the comparisons shown here, we did not optimize parameters of CHARM, e.g., the number of Gaussian distributions used to model the different tissues, specifically for this data set. For example, the eye muscles (rectus muscles) are modeled together with other soft tissues, which include muscle and fat, using a single Gaussian. This is not optimal for accurate segmentation of the eye region, which also contains fat. Further refinement of the tissue atlas, to separate muscle and fat, would likely increase the segmentation accuracy in the eye region as well as in the neck, which consists to a large extent of fat and muscle tissues. The model settings, apart from the bias field, are kept fixed when a T2w scan is added and further experimentation with the settings would probably help to increase the segmentation accuracy further in the multi-contrast case. Additionally, if the structure borders do not exactly overlap between the T1w and T2w scans, this can result in a decrease in the segmentation accuracy of the small structures. Finally, we did not postprocess the CHARM segmentations in any way, and some form of cleaning of the segmentation maps, using e.g., morphological operations or Markov random field (MRF) models, would likely benefit the segmentation accuracy and improve the head models generated from these segmentations.

5.2. Experiment 2: accuracy of e-field simulations

In Figs. 6 and 7, we show segmentations and e-field simulations on two subjects from the two clinical data sets segmented using HEADRECO and CHARM. Two additional subjects are shown in the supplementary material Figures S6 and S7. In both data sets spongy bone is clearly visible in the MR scans, which implies that no fat suppression was used, and the fat signal is shifted in the superior-inferior (SI) direction as indicated by the bright rim right above the skull. As a result, HEADRECO severely under-segments the skull in locations with spongy bone, which is also shifted in the SI direction towards the cortex. CHARM explicitly models the spongy bone tissue in the probabilistic atlas and obtains a better segmentation of the skull. The e-field simulations on an M1-SO montage demonstrate exemplarily the effect of these segmentation differences on the simulations. In the first subject (see Fig. 6) the under-segmentation of the skull, when using HEADRECO, coincides with the electrode location, and the thin skull area is surrounded by areas where the skull is correctly segmented to be thicker. The current shunts through the thinner part and the e-field strength in the cortex directly below the electrode is high. The strength is reduced in the simulation based on the CHARM segmentation where the under-segmentation does not happen. In the second subject (see Fig. 7) a similar pattern repeats but now in the anterior part of the brain under the SO electrode.

Fig. 8 shows the box plots of the normalized absolute differences, e_diff, over subjects for the TDCS simulation (top panel) and the TMS simulation (bottom panel). In the TDCS case, the difference between CHARM and the reference is significantly lower than the difference between HEADRECO and the reference both when using a T1w scan or when a T2w scan is added. Additionally, HEADRECO benefits from a T2w scan more than CHARM, obtaining a significantly lower difference compared to when a T1w scan alone is used. In the TMS case, the group-wise difference between CHARM and the reference is significantly lower than that of HEADRECO and the reference both when a T1w scan alone is used and when both T1w and T2w scans are used as inputs. Including a T2w scan results in significantly lower differences for both CHARM and HEADRECO. The average e-field, and its standard deviation, over the 20 subjects for all segmentations and simulation are visualized in the Supplementary material Figures S8 and S9. Based on visual assessment the CHARM average fields are closer to the reference than those from HEADRECO, but the variability between subjects, based on the standard deviation maps, is underestimated by both CHARM and HEADRECO.

Fig. 8.

Box plots of the normalized absolute difference of the electric field, e_diff, for TDCS (top panel) and TMS (bottom panel) for the 20 subjects in the data set. CHARM is shown in green and HEADRECO in blue. The asterisks show significant differences using a two-sided pair-wise t-test at the 0.01 (**) level. The p-values are corrected for multiple comparisons using Bonferroni correction. On each box, the line marks the median, the box extends to lower and upper quartiles, whiskers extend up to 1.5 times the interquartile range, and data points beyond that are marked as outliers.

Underestimation of the subject-to-subject variability by CHARM is somewhat unexpected as the average Dice scores for the non-brain tissues in the upper part of the head, in both the T1w and T1w + T2w cases, are over 0.85 except for CSF, see Supplementary material Table S3. Furthermore, the relative e-field differences are mostly under 0.1 as shown in Fig. 8. A possible explanation is that these are global scores, i.e., summaries of the differences over the whole volume, whereas the e-field is affected more by local differences as indicated in Figs. 6 and 7. This prompted us to check the local skull and scalp segmentation differences between the reference and CHARM segmentations in one of the subjects shown in Fig. 9. The skull and scalp segmentation from CHARM, using T1w as an input, systematically underestimates the thickness of the skull and overestimates the thickness of the scalp. This systematic error is driven by the fat-shift and results in differences up to 30% between the simulated TDCS e-fields from CHARM (T1w) and the reference. The difference in the e-fields for TMS is lower with a maximum around 10%. Adding a T2w scan helps in segmenting the skull and scalp borders more accurately and reduces the e-field differences notably. To investigate if the under-segmentation is mainly a result of the fat-shift, we also used an mDixon scan without a fat-shift as an input to CHARM. The skull-scalp border segmentations are more accurate on the mDixon than the standard T1w scan, see tissue borders in Fig. 9 last column, and the e-field differences are correspondingly smaller. Figure S10 in the supplementary material shows the same results for another subject from the data set to confirm that the effects are consistent.

Fig. 9.

Comparison between head models constructed from the reference segmentation (first column), and CHARM segmentations using a T1w (second column), a T1w and a T2w (third column) or an mDixon (fourth column) scan(s). The first row shows the segmentations, the second row the input scans and a CT scan which was used to segment the skull in the reference segmentations, the third row zoomed comparisons between the CT and input scans, the fourth row tissue border reconstructions from the reference (red) and CHARM, and the final two rows the field simulations from TDCS and TMS on the reference segmentation, and relative differences (peak strength) between the reference and automated segmentations.

5.3. Experiment 3: modeling multiple tissue classes in e-field simulations

Fig. 10 shows the comparisons between the simulated e-field strengths on a six-tissue (standard) head model, where the eyeballs are included, against a fifteen-tissue (extended) head model, along with the node-wise differences for TDCS (first row) and TMS (second row). Visual inspection of the e-fields between the standard and extended head models does not reveal large differences, although small changes in the anterior part of the brain can be observed for the TDCS case. However, the node-wise differences reach up to 10% of the maximum e-field strength both for TDCS and TMS. In the TDCS case the largest differences are in the anterior part of the brain, where the field strength in the extended head model is lower, and next to the superior sagittal sinus, where the field strength in the extended head model is higher. The lower field strength in the anterior part of the brain is explained by the splitting of the bone compartment into two sub-compartments (compact and spongy bone); when bone is modeled as single tissue the conductivity is typically set to 0.01 S/m (Wagner et al., 2004) while the conductivity of the compact bone compartment is set to 0.008 S/m (Opitz et al., 2015). As the anterior part of the skull in this subject consisted mostly of compact bone, the resulting field strength in the extended head model is lower due to the lowered conductivity. The increased field strength next to the superior sagittal sinus is explained by the difference in conductivity between the veins (0.6 S/m, Gabriel et al., 2009) and CSF (1.654 S/m, Wagner et al., 2004). Modeling the veins separately from CSF changes the current pathway, making the current shunt through the better conducting CSF next to the vein, which results in higher e-field strengths in the neighboring cortical areas. In the TMS case, where the current flows inside the skull tangentially to the plane of the coil from left to right, the effect of the vein can be clearly seen in the node-wise field differences. Here, as in the TDCS case, the conductivity difference between the vein and CSF results in higher e-field strengths in the cortex next to the superior sagittal sinus when the simulation is done on the extended head model. We note that the effects observed here might change substantially if different tissue conductivity values are used. Here we have used conductivity values reported in the literature and kept the conductivities of skin, mucosa and soft tissues identical to that of scalp. The soft tissues consist of both fat and muscle tissue, which have different conductivities. Segmenting and modeling these tissues separately would further change the spatial pattern of the e-field strength shown in the figures.

Fig. 10.

Comparison of e-field strengths between a five-and a fourteen-tissue head model for a TDCS stimulation (top row) and a TMS stimulation (bottom row). Second column shows the strength of the e-field on the extended head model, the third column on the standard head model, and the fourth column shows the node-wise relative difference (peak strength) between the two.

6. Discussion

In this article we presented a new method (CHARM) for automated segmentation of fifteen different head tissues from MR scans. CHARM compared favorably to two other freely available tools in a simplified segmentation task of the five main head tissue classes. It achieved a relatively good segmentation accuracy over all fifteen tissues, yielding a higher segmentation accuracy on the larger structures and a lower accuracy on the smaller structures, which is expected. The latter could potentially be improved by incorporating further structures into the semi-automated segmentations, including relative intensity priors on the Gaussian distribution parameters (Agn et al., 2019), and/or employing dedicated shape models as a post-processing step (Puonti et al., 2018). Critically, the segmentation performance of CHARM turned out to be robust on lower quality clinical data sets.

Our work also revealed important links between segmentation performance and electric field simulations. We showed that, at the group-level, higher Dice scores result in lower relative electric field differences, but that inter-individual variation is underestimated especially for TDCS. Furthermore, the automated segmentations, and consecutively, the electric field simulations were affected by systematic fat-shift artifacts that are usually more prominent in T1w compared to T2w structural MR images. This led to simulation errors of up to 30% for TDCS. Finally, we showed that the inclusion of multiple tissues into the simulations results in local differences in the estimated electric field of up to 10%, compared to the standard five-tissue head models.

The results highlight the importance of accurate anatomical tissue modeling for individualized simulations of the spatial distribution of electric fields in TDCS and TMS. Millimeter scale anatomical differences, which are not reflected on summary scores of segmentation accuracy, can result in notable electric field differences especially for TDCS, where the current flow is highly sensitive to local anatomical features. Gross segmentation errors can be detected by visual inspection, but the detection of small deviations can be difficult, and quickly becomes a bottleneck in large studies. While changes in the tissue conductivity values mainly affect the overall magnitude of the electric field (Saturnino et al., 2019), changes in the anatomy affect both the magnitude and the pattern as shown in Figs. 6, 7 and 9. Ensuring good MR scan quality can mitigate the segmentation errors, and future brain stimulation studies using individualized modeling should include careful consideration of the sequence parameters. Based on the results here, and in line with our previous advice (Nielsen et al., 2018; Saturnino et al., 2018), we recommend to include a T2-weighted structural MR scan acquired at a higher bandwidth to minimize fat-shift artifacts as a standard and to use fat suppression when acquiring the T1-weighted image. Alternatively, the fat-shift in the T1w image can be reduced using a high-bandwidth readout, but this will result in a lower signal-to-noise ratio. Acquiring pilot scans to determine optimal parameters before the start of the study is recommended.

Given that the MR data quality plays such a noticeable role in accurate electric field simulations, translating brain stimulation, specifically TDCS, into an individualized clinical treatment tool remains challenging. Robust segmentation of clinical data to minimize gross segmentation errors is possible with CHARM, as shown in this article, but the precision of the field simulations is in the end limited by the MR data quality that depends not only on the signal-to-noise ratio, but in particular also on systematic and motion-induced artifacts. The clinical data set consisting of epilepsy patients (Huang et al., 2017) used in Experiment 2 did not include T2-weighted scans, which is likely due to restrictions in the clinical workflow. When planning modeling studies in patient populations these restrictions need to be weighed against the requirements for accurate simulations, which puts a focus on developing and applying improved scanning sequences. Maintaining high data quality while reducing scan times could be achieved using compressed sensing methods (Jaspan et al., 2015), which have already found use in clinical pediatric body imaging (Zhang et al., 2014) where fast acquisition is necessary due to hemodynamic changes, breathing and motion. The scan time freed up by the fast acquisition could then be used to acquire additional contrasts, such as a T2-weighted scan, or to acquire multiple high-bandwidth T1w scans with reduced fat-shift for averaging. Additionally, prospective motion correction can be combined with standard sequences (Maclaren et al., 2013) or compressed sensing techniques (Usman et al., 2013) to reduce scan artifacts. Scanning protocols applying motion correction together with compressed sensing should be able to reduce scan times while ensuring that the acquired data is artifact-free. Sometimes the clinical T1w and T2w scans can have very different field-of-views. In the current implementation of CHARM, the scans are masked so that the segmentation parameters are estimated only from the overlapping region, and missing values are imputed from the prior. This could be handled in a more principled manner, given the adopted Bayesian approach, by inferring the, non-overlapping, missing values in the input scans (Brudfors et al., 2019).

Finally, including multiple tissue classes into the modeling is likely beneficial for accurate electric field simulations for TDCS and for specific cortical targets, such as the pre-SMA, for TMS. As the two skull compartments, i.e., spongy and compact bone, have quite different conductivities, MR sequences where the signal from the fatty spongy bone tissue is not suppressed are preferable, given that the fat-shift is minimized. Accurate modeling of the CSF is important for TDCS and TMS, as the amount of highly conducting CSF can result in either current distributing more evenly around the brain, due to a thick CSF layer, or in local hotspots in the cortex due to shunting where the CSF layer is thin. Modeling the superior sagittal sinus as CSF, which is currently the standard procedure (Huang et al., 2019; Saturnino et al., 2018), likely underestimates the amount of cortical hotspots for TDCS and TMS configurations where the current flows close to the midline.

The caveat to adding more tissues into the modeling is that the conductivities of even the standardly used tissue classes are not well known (Saturnino et al., 2019), and by introducing additional tissues we might unintentionally increase the uncertainty in the simulations. Here, we have applied the conductivity of scalp to skin, mucosa and soft tissues. The latter represents a mixture predominantly of muscle and fat, so that it might be beneficial to assign a conductivity that lies in between these two types or to label them separately in the reference segmentations. Also, the CSF layer could be further refined by modeling the Dura mater in addition to segmenting the large veins and arteries. Alternatively, as the Dura mater is thin and challenging to segment and mesh, strategies to account for its effects on the current flow while preventing its direct modeling could be explored. It might be advantageous to mimic its effects by a contact impedance between skull and CSF (as done in (Dannhauer et al., 2012) for the electrode-electrolyte contact). Adjusting the conductivity of CSF to a lower “effective” value that represents an average across the tissues that are commonly labeled as CSF (Dura, Arachnoid and Pia mater) might also be helpful (Jiang et al., 2020). The latter strategy comes at the disadvantages that the conductivity of larger CSF volumes such as the ventricles or within some sulci is underestimated and that the effective value will likely need readjustments in patient groups with increased CSF volumes, e.g. due to brain atrophy. The effective conductivity value suggested in (Jiang et al., 2020) was tested on a dataset that only included clinical-grade T1-weighted scans, which could have biased the results, similar to the systematic misestimations of the electric fields for T1w-based head models observed here.

In general, careful analysis of the effect of each additional tissue on the simulated electric fields, and their uncertainties, is needed in the future to fully explore the implications of the increasingly complex head models. Systematic uncertainty analyses are helpful to characterize the impact of additional tissues on the field estimates (Saturnino et al., 2019) . In addition, in-vivo measurements of the electric fields are needed, first in order to validate if the range of the simulations and measurements agree (Goksu et al., 2018; Huang et al., 2017; Opitz et al., 2017) , and, in case the quality of the measurements allows, for optimizing the modeling parameters, such as conductivities (Puonti et al., 2020) . Potentially, using innovative non-invasive measurements (Goksu et al., 2018), the parameter optimization could be done in larger groups of subjects or even on a subject-by-subject basis in the future.