Probing the Local Reaction Environment During High Turnover Carbon Dioxide Reduction with Ag‐Based Gas Diffusion Electrodes

Abstract

Discerning the influence of electrochemical reactions on the electrode microenvironment is an unavoidable topic for electrochemical reactions that involve the production of OH⁻ and the consumption of water. That is particularly true for the carbon dioxide reduction reaction (CO₂RR), which together with the competing hydrogen evolution reaction (HER) exert changes in the local OH⁻ and H₂O activity that in turn can possibly affect activity, stability, and selectivity of the CO₂RR. We determine the local OH⁻ and H₂O activity in close proximity to a CO₂‐converting Ag‐based gas diffusion electrode (GDE) with product analysis using gas chromatography. A Pt nanosensor is positioned in the vicinity of the working GDE using shear‐force‐based scanning electrochemical microscopy (SECM) approach curves, which allows monitoring changes invoked by reactions proceeding within an otherwise inaccessible porous GDE by potentiodynamic measurements at the Pt‐tip nanosensor. We show that high turnover HER/CO₂RR at a GDE lead to modulations of the alkalinity of the local electrolyte, that resemble a 16 m KOH solution, variations that are in turn linked to the reaction selectivity.

Local affection: The abundance of gas diffusion electrodes (GDE) in modern electrochemistry has grown drastically, especially with the increasing interest in electrochemical reduction of CO₂. Since several aspects of those electrodes and that reaction are not clarified yet, we herein couple assessment of the local reaction environment to the actual product distribution of the hydrogen evolution/CO₂ reduction reaction system at Ag‐based GDEs.

For the elucidation of the complex parameter interplay in front of an electrode it is imperative to not solely determine the reactions products of the investigated electrocatalytic conversion, but also to acquire knowledge about formed by‐products such as H₃O⁺ or OH⁻ which may modulate the reaction microenvironment and by this impact back on the thermodynamics and kinetics of the anticipated reactions. Particularly, industrially relevant reactions such as the hydrogen evolution reaction (HER), ^[1] the oxygen reduction reaction (ORR), ^[2] and the carbon dioxide reduction reaction (CO₂RR) ^[3] are known to exert drastic changes to the electrode surroundings. Especially for the CO₂RR, the depletion of protons and the generation of OH⁻ can be regarded as a crucial factor affecting kinetics and selectivity of the reaction ^[4] by formation of an interfacial pH gradient. Subsequent reaction steps can be altered since most reaction steps to final products are proton coupled electron transfer (PCET) reactions. ^[5]

Owing to similar overpotentials, the CO₂RR proceeds concomitantly with the parasitic HER, which leads to the interconnection of both reactions since they compete for active sites on the surface of the electrocatalyst and produce OH⁻. This competition represents one of the narrowest bottlenecks for large‐scale implementation of the CO₂RR. The inherently low faradaic efficiency (FE) for carbon products has to be overcome in order to ultimately achieve CO₂ conversion with a close to 100 % FE to unlock the electrochemical CO₂RR as potential carbon feedstock for producing value‐added hydrocarbons. Thus, besides overpotential and selectivity, the maximum achievable current densities hamper potential industrial applications.

Due to the low solubility of gaseous CO₂ in aqueous solutions (35 mm) ^[6] the substrate flux and its availability at the electrode surface is limited. This issue can be counterbalanced using gas diffusion electrodes (GDE), which allow for a significant decrease of the diffusion path length of gaseous reactants. ^[7] Ag–PTFE‐based GDEs, which are already utilized for the ORR on an industrial scale for Cl₂ production, ^[8] can sustain current densities of up to several kA m⁻². These electrodes exhibit interconnected pore channels, enabling the formation of a triple‐phase boundary between gaseous CO₂, liquid electrolyte, and solid catalyst, which lowers the diffusional mass‐transfer pathway to a thickness of roughly 50 nm. ^[9] Since the electrochemically active surface area (ECSA) is predominantly located within the electrodes and the diffusion path length for the CO₂ is also minimal there, the reaction only proceeds in significant rates within the porous system. The concentration equilibration of products as well as reactants with bulk solution is physically mitigated by the electrode itself. Intraporous electrolyte modulations in close proximity to the CO₂ conversion sites are hence highly interesting, yet experimental probing of solution species within the electrode was, to the best of our knowledge, not yet achieved. ^[10]

Probing the interfacial pH value close to an electrode has so far been addressed by a variety of theoretical ^[11] and experimental approaches.[ ² , ³ , ¹² ] For instance, nuclear magnetic resonance spectroscopy (NMR), ^[3] Raman spectroscopy, ^[12d] infrared spectroscopy, ^[13] or (rotating) ring disc electrodes ((R)RDE)[ ^12e , ¹⁴ ] have been employed. However, these techniques suffer from low spatial resolution and may not be suitable to identify changes localized at a dynamic interface. However, unambiguous identification of the local pH value, or more precisely, the activity of OH⁻ may contribute to elucidate the reaction mechanism and particularly the selectivity.

Scanning electrochemical microscopy (SECM)‐based techniques are highly suitable to determine dynamic changes at the electrode surface, invoked by different reactions rates for example, due to different current densities or different gas pressures. Nanometer‐sized tip electrodes which are positioned in close proximity to the GDE surface can be employed as local probes to determine reaction rates or analyte concentrations/activities. ^[15] We recently reported the operando determination of changes of the local pH value, respectively the modulation of OH⁻ and H₂O activities in close proximity of an operating Ag‐based GDE ^[16] reducing O₂ at high current densities. ^[2]

This was achieved by potentiodynamic cycling of the positioned Pt nanoelectrode in a potential range between Pt oxide formation and Pt oxide reduction. We demonstrated that the peak potential of the Pt oxide reduction peak is dependent on OH⁻‐ions and H₂O activities. Verification of the developed methodology was done in a subsequent theoretical study involving dynamic simulations, fully supporting the proposed approach. ^[17] Here, we adapt this strategy to a Ag‐based GDE ^[18] under CO₂RR conversion conditions in CO₂ gas breathing mode and extend it to elucidate the interdependence of the applied potential at the GDE and local pH value changes inside the GDE with the selectivity of the CO₂RR and competition with the parasitic HER.

A Pt nanoelectrode is positioned as close as 100 nm ^[19] above the GDE electrode surface using a shear‐force based positioning approach (Figures S1 and S2 in the Supporting Information). ^[20] The Pt nanoelectrodes were fabricated by laser pulling of quartz capillaries and subsequent focused ion beam milling to avoid contaminations from further polishing (see Figure S3 for details). ^[21] It is well known that several features in the voltametric response of a Pt electrode change with the local pH value. ^[22] Particularly, Pt oxide formation and Pt oxide reduction involve the consumption and release of OH⁻ and H₂O as shown in the corresponding Nernst equation [Eq. 1].

$${\displaystyle E_{\mathrm{P}\mathrm{t}\mathrm{O}/\mathrm{P}\mathrm{t}}=E^0+\frac{RT}{nF}ln\frac{a\left(\mathrm{P}\mathrm{t}\mathrm{O}\right)·a\left({\mathrm{H}}_2\mathrm{O}\right)}{a\left(\mathrm{P}\mathrm{t}\right)·a{\left(\mathrm{O}{\mathrm{H}}^{-}\right)}^2}}$$ (1)

with R = universal gas constant, T = temperature, z = number of transferred electrons and F = Faraday constant.

The activity (a) of the solids Pt and PtO can be considered to be unity, implying that the potential of Pt oxide conversion (E _Pt/PtO) solely depends on the local activities of freely diffusing OH⁻ and H₂O. Hence, the shape and the peak position of Pt oxide reduction represents the ratio of H₂O and OH⁻ activities as depicted in Figure 1.

Figure 1.

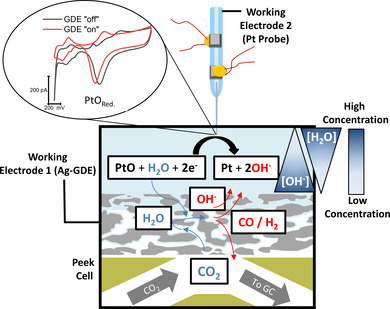
Local H₂O and OH⁻ activities modulated by the competing HER and CO₂RR are monitored using a precisely positioned Pt nanoelectrode. The PtO reduction peak potential changes with the different ion activities established inside the three‐phase boundary of the GDE at varying reaction rates.

In a first set of experiments, the pH dependence of Pt oxide reduction at the nanoelectrode was evaluated, not only to confirm the feasibility of the proposed analytical concept but also to derive the potential values for PtO reduction (E(PtO_red.)) at different ion activities. For that, Pt nanoelectrodes (average diameter 700 nm) were immersed in differently concentrated KOH solutions ranging from 1 m up to 16 m. To confirm the concentrations of the used and purified ^[23] KOH solutions despite potential CO₂ uptake and variable water contents, we titrated each solution with oxalic acid (see experimental part in the Supporting Information). Cyclic voltammograms (CVs) were recorded between +600 and −1100 mV vs. Ag/AgCl/3 m KCl (Figure 2 a), a potential window that ensures Pt oxidation, which is a prerequisite for utilizing the PtO_red. as pH‐dependent reporter reaction.

Figure 2.

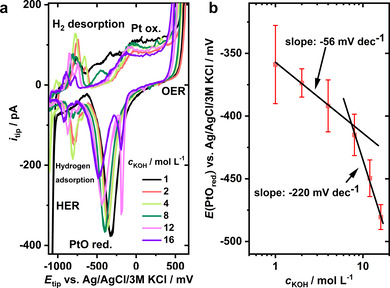
a) pH‐dependent CVs obtained using a Pt nanoelectrode (ø=700 nm) in KOH solutions with concentrations from 1 m up to 16 m. CVs (scan rate: 200 mV s⁻¹) were acquired between +600 and −1100 mV vs. Ag/AgCl/3 m KCl. b) Calibration curves derived from the PtO_red. peak position (E ${}_{\mathrm{PtO}{}_{\mathrm{red}.}}$ ) as a function of the KOH concentration. Linear fits (black lines) with different slopes (displayed in mV dec⁻¹) suggest distinct concentration dependencies between 1 and 4 mol L⁻¹ and between 8 and 16 mol L⁻¹ as suggested by the slopes of −56 mV dec⁻¹ and −220 mV dec⁻¹, respectively. Peak positions are averaged over 3 different calibration measurements as indicated by the red error bars.

The CVs in Figure 2 a show several pH‐dependent peaks, as for instance the hydrogen adsorption ^[24] peak at roughly −800 mV and the PtO_red. peak located between −350 and −500 mV. Plotting E ${}_{\mathrm{PtO}{}_{\mathrm{red}.}}$ as a function of the KOH concentration yields calibration curves with significantly different slopes corresponding to a low (1–4 mol L⁻¹) and a high (8–16 mol L⁻¹) KOH concentration regime. According to the Nernst equation, E ${}_{\mathrm{PtO}{}_{\mathrm{red}.}}$ changes depending on the ion activities, and the peak potential shift is more pronounced for larger ion activity disparities.

That can be rationalized if a water activity of about 1 is assumed for low KOH concentrations, whereas this value decreases at high ionic strength due to undercoordination and insufficient solvation of the K⁺ and OH⁻. In particular, it has been shown that on average three to four H₂O molecules are necessary for tetrahedral solvation of an OH⁻‐ion. ^[25] The Nernst equation [Eq. (1)] implies a shift of E ${}_{\mathrm{PtO}{}_{\mathrm{red}.}}$ towards more cathodic potentials. The transition of the H₂O activity deviating from 1 can be observed experimentally in a KOH concentration range between 4 and 8 mol L⁻¹ (Figure 2 b), which is close to what was observed in a similar experiment performed in highly concentrated NaOH solutions. ^[2]

At extreme OH⁻ concentrations (>8 mol L⁻¹) the decreased H₂O availability does not only hamper PtO reduction but also impacts on the CO₂RR and the competing HER.[ ² , ²⁶ ] High ion concentrations can exert changes to the water order similar to those exerted by increased external pressures, as it was shown earlier for the case of NaOH solutions. It was claimed that higher ion concentrations „pull the water molecules in“ towards the solute ions, ^[27] suggesting that water is bound more tightly to the ions at increased ion concentrations. Moreover, the interaction with interfacial water and its change of structural properties is modulated at increasing pH values and leads to shifts in the hydrogen adsorption potential, which underlines that both, H₂O and OH⁻ activities have to be considered for pH‐dependent phenomena. ^[24] Hence, for obtaining a complete picture of the reaction microenvironment during electrochemical turnover, it is not sufficient to solely determine the OH⁻ activity, since the increased abundance of OH⁻ drastically affects the water activity. Ion activities might not be an immutable feature of electrolyte solutions, but they can be altered by reactions, which involve the consumption or release of water.

Since solvation shell properties and also the abundance of reaction partners change, it can be expected that the reaction itself influences crucial parameters such as the pH value in the immediate reaction zone. We hypothesize that high reaction rates play a particularly drastic role in that scenario. Adapting laboratory‐scale technology into industrial settings, however, necessitates the opportunity to run reactions at current densities exceeding some hundreds of mA cm⁻². ^[9c] As for the case of the CO₂RR, which itself acts as a proton consuming reaction, we find that the thermodynamically favored HER (proton reduction) always competes for protons and electrons and thus can effectively hinder the conversion of CO₂ to carbon products. The reaction pathway changes upon alkalization since the decreased proton abundance favors water reduction. That distinction is especially necessary when the proton source for CO₂RR and HER is predominantly water in highly alkaline solutions. ^[28]

To elaborate on the impact of electrochemical CO₂RR and HER on the local electrolyte environment, we used Pt tip electrodes, which were approached via shear‐force SECM positioning to a distance of around 100 nm towards a CO₂ converting Ag‐based GDE. While biasing the GDE to different potentials to induce different reaction rates and hence different ion activity changes, the Pt tip electrode was cycled potentiodynamically (as depicted in Figure 2 a) in a bipotentiostatic setup (Figure 1). The Ag‐GDE potential was stepped more cathodic from −0.1 to −1.7 V vs. Ag/AgCl/3 m KCl in 50 and 100 mV steps, respectively (Figure 3). Upon increasing the overpotential at the Ag‐GDE, the voltammograms at the Pt tip shift towards more cathodic potentials (Figure 3 a).

Figure 3.

a) Pt‐tip voltammograms in the potential range between −0.8 and 0.8 V vs. Ag/AgCl/3 m KCl at a scan rate of 200 mV s⁻¹ in 1 m KOH. The Pt‐sensor is approached to a distance of approximately 100 nm over the Ag‐GDE, which is polarized to potentials between −0.1 and −1.57 V vs. Ag/AgCl/3 m KCl invoking CO₂RR and HER. b) Zoom‐in to the voltammograms displayed in (a), highlighting the shift of E ${}_{\mathrm{PtO}{}_{\mathrm{red}.}}$ in dependence of an increased cathodic potential applied to the Ag‐GDE. c) Peak potentials of E ${}_{\mathrm{PtO}{}_{\mathrm{red}.}}$ from the voltammograms in (a) as a function of applied E _Ag‐GDE. Stars refer to measurements at −0.1 V vs. Ag/AgCl/3 m KCl, the lower one directly after the measurement at −1.69 V and the higher one after further biasing the GDE for 15 min to −0.1 V.

In addition to the local ion activity changes, one also needs to consider that the predominant product of the CO₂RR at a Ag‐GDE is CO, which may poison the Pt tip surface. However, by sweeping the potential anodically, adsorbed CO is removed, which re‐establishes a clean Pt tip in each potentiodynamic cycle. ^[29] We found that ultraclean Pt tips are necessary for the anticipated measurements above CO₂‐converting electrodes, since otherwise often ambiguous Pt voltammograms are observed (Figure S3). The cathodic shift of the PtO_red. peak positions was utilized as indicator for changes in the local H₂O and OH⁻activities upon increasing the driving force for the CO₂RR at the GDE and is shown in Figure 3 b. The peak potential was extracted and plotted as a function of the GDE potential (Figure 3 c).

At E _Ag‐GDE with insignificant turnover (−0.1 V vs. Ag/AgCl/3 m KCl) in Ar‐purged 1 m KOH, values for E ${}_{\mathrm{PtO}{}_{\mathrm{red}.}}$ of roughly −50 mV are observed. This value contradicts the results from the calibration in 1 m KOH (Figure 2), where E(PtO_red.) was around −350 mV. This can be rationalized considering the GDE configuration and the CO₂ gas feed. Since CO₂ is constantly supplied from the backside for each measurement, a local acidification of the electrolyte is expected at no‐turnover potentials due to the formation of bicarbonate by reaction of CO₂ with OH⁻ , which is further neutralized to carbonate at more alkaline conditions.[ ^11a , ³⁰ ] Upon stepping the potential at the GDE more cathodically, both the GDE current and the E ${}_{\mathrm{PtO}{}_{\mathrm{red}.}}$ start to change at −1.3 V vs. Ag/AgCl/3 m KCl, which coincides with a measurable turnover of the CO₂RR and HER, respectively (Figure 4 b). As soon as substantial reductive GDE currents (denoted as i _Ag‐GDE) are observed E ${}_{\mathrm{PtO}{}_{\mathrm{red}.}}$ shifts towards cathodic potentials. Both, E ${}_{\mathrm{PtO}{}_{\mathrm{red}.}}$ and i _Ag‐GDE increase drastically beyond the −1.3 V threshold. E ${}_{\mathrm{PtO}{}_{\mathrm{red}.}}$ increases to values of up to −0.6 V at the highest applied GDE potential of −1.69 V. This value would indicate a hydroxide/water activity ratio far beyond what was measured for 16 m KOH. Considering that the observed E ${}_{\mathrm{PtO}{}_{\mathrm{red}.}}$ value resembles the conditions directly above the GDE pores, it is fair to assume that inside the GDE even higher hydroxide and lower water activity values are obtained.

Figure 4.

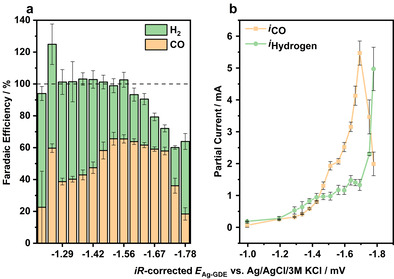
a) E _Ag‐GDE‐dependent FE displaying the formation of CO (orange) and H₂ (green) in dependence on the applied GDE potential. The individual measurements were averaged over 2 GC measurements per potential. b) Partial currents for H₂ (green) and CO (orange) formation at Ag‐GDE (0.2 cm² size) potentials between −1.0 and −1.8 V vs. Ag/AgCl/3 m KCl in 1 m KOH.

Industrial devices are usually operated with a continuous electrolyte flow , which would counterbalance the progressive increase in electrolyte pH value. Such flow‐by schemes are leading to a stagnant layer at the electrode/electrolyte interface in the case of planar electrodes; however, in the case of a GDE mass transport processes inside the pores of the GDE are predominantly governed by diffusion and, due to the potentially locally high ionic strength, by migration. We decided to perform experiments using a stagnant electrolyte, allowing (by)products to accumulate. As pointed out before, the reactions proceed within the pores, not only because the predominant amount of the electrochemically active surface area (ECSA) is located therein, but also because the necessary vicinity to the gas phase is provided there. Thus, in the case of a stagnant system a correlation with the processes inside the GDE can be obtained by determining ion activities within the diffusion zone directly adjacent to the GDE/electrolyte interface. It has been proposed theoretically that mass transport of water into the electrode and hydroxide transport out of the electrode is crucial for the performance of reduction processes inside a GDE, ^[31] and the extent of those ion fluxes is exactly what can be probed with the proposed technique.

To correlate the measured current values at the GDE beyond −1.3 V vs. Ag/AgCl/3 m KCl to the selectivity of the reaction as well as the competition between CO₂RR and HER, the gaseous reaction products were analyzed by coupling the open SECM cell to a gas chromatograph (GC) for on‐line product determination.

Ag, besides Au and Zn, ^[32] is known for producing CO with a rather high FE of over 90 % during CO₂RR, whereas it has also been reported that at higher overpotentials (−1.5 V vs. RHE) also methane can be formed if special electrode architectures are used. ^[33] As it can be inferred from the electrochemistry‐coupled GC measurements (Figure 4 a), the main products observed in the gas phase are indeed CO and H₂.

The fraction of CO formation increases at potentials more cathodic than −1.3 V vs. Ag/AgCl/3 m KCl until it reaches a maximum of around 65 % at −1.56 V vs. Ag/AgCl/3 m KCl. Beyond that point, the H₂ formation increases and a simultaneous overall decrease of the FE is observed due to the open‐cell configuration and a loss of the formed H₂, which initially dissolves in the electrolyte. At potentials beyond −1.56 V vs. Ag/AgCl/3 m KCl, a visible H₂ bubble formation is observed at the GDE. Performing the same experiment with a closed electrolyte compartment allowing to also collect the head‐space products is impossible while simultaneously positioning the Pt‐electrode in close proximity to the GDE surface. However, due to the decrease of the FE for CO formation at increasing cathodic potentials we suppose that the missing products in the FE balance accounts for H₂ escaping through the electrolyte. In a similar experiment, however, using a closed electrochemical cell, we determined the gas composition of the head space above the electrolyte at higher overpotentials (Figure S4). We found that at potentials of roughly −1.65 V vs. Ag/AgCl/3 m KCl, 25 % of the FE is due to escaping H₂ bubbles, whereas measurements at even higher cathodic potentials are distorted by H₂ bubbles blocking the electrode surface.

Figure 4 b displays the partial currents of CO and H₂ formation, respectively. Significant amounts of products are formed if E _Ag‐GDE exceeds −1.3 V vs. Ag/AgCl/3 m KCl, which is in line with the observed shift of E ${}_{\mathrm{PtO}{}_{\mathrm{red}.}}$ , which is only observed beyond this particular potential threshold. This also explains the large error bars for the determination of the FE in the bar diagram (Figure 4 a), which is due to the low product quantity at potentials up to −1.3 V. With increasing cathodic potentials applied to the GDE the partial currents for both products increase from roughly 0.5 to 6 mA, respectively, whereas the CO production is dominant until −1.7 V. A reversal of the product distribution of H₂ and CO is observed at −1.7 V, after which H₂ evolution outweighs CO formation.

This observation shows the intrinsic dilemma since it prevents the CO₂RR at maximal current density to maximize the absolute amount of carbon conversion products. However, as it is shown here and elsewhere ^[34] higher currents can steer the selectivity towards the HER. A similar observation was also made upon increasing pH values of bicarbonate solutions. ^[35] It is important to mention that increasing pH values do not favor the HER via proton reduction, since the effective proton concentration is diminished. Moreover, it has been shown that alkaline H₂O reduction may become favorable at higher hydroxide concentrations. ^[14b] It should also be mentioned that reports with contradicting results exist, in which increased HER suppression on Au‐based catalysts was linked to higher local alkalinity. ^[36] Therefore, we infer that the change of ion activities may be a factor to consider as possible explanation for the observed modulations of selectivity; however, additional parameters such as electrowetting and electrode flooding cannot be excluded to contribute to the observed trend. It can also be assumed that the wetted surface area within the electrode itself increases as a function of the applied reductive potential, which would in turn favor the HER. Even though the impact of the local pH value is not fully clear, the local pH value affects the product selectivity substantially. ^[37]

Moreover, at high current densities the available amount of CO₂ may become mass‐transport dominated and is decreased on the one hand by the CO₂RR itself and on the other hand by the increased formation of CO₃ ²⁻ at higher pH values. ^[38] Hence, in addition to coupling catalyst properties such as the material composition, its structure and selectivity to each other, we propose to pay close attention to changing reaction environments when performing CO₂RR. This is particularly important for porous/rough catalyst materials including GDEs at high current densities (>50 mA cm⁻²). By simultaneously monitoring product distribution and alterations in ion activity close to the electrode, both phenomena can possibly be linked to each other: we show that high reaction rates increase the local pH value, that is, OH⁻ ion activity, which in turn should favor alkaline water reduction, which could shift the reaction selectivity towards the HER. We have shown earlier for ORR measurements that a measured increase of electrolyte concentration in stagnant diffusion layers are in very good agreement with numerical simulations. ^[31] Similar numerical models for the more complex CO₂RR are not yet available.

In summary, we have monitored the electrochemically induced ion activity change close to a CO₂‐converting Ag‐based gas diffusion electrode (GDE), allowing to shed light into the complex interplay between the CO₂ reduction reaction (CO₂RR) and its parasitic reaction partner, the hydrogen evolution reaction (HER). The steep concentration gradients established within a GDE between the three‐phase boundary and the electrolyte results in selectivity not only being affected by the intrinsic selectivity of the active sites but also by mass transport effects and subsequently by higher local alkalinity.

By linking local pH value and H₂/CO ratio, possible interesting implications arise. While it obviously is desirable to manipulate the reaction selectivity towards CO production, it could also be desirable to modify electrolyte and process conditions so that particular ratios of H₂/CO, for example, syngas for the Fischer–Tropsch process, ^[39] are obtained.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

S. Dieckhöfer, D. Öhl, J. R. C. Junqueira, T. Quast, T. Turek, W. Schuhmann, Chem. Eur. J. 2021, 27, 5906.