Twisting versus Delocalization in CAAC‐ and NHC‐Stabilized Boron‐Based Biradicals: The Roles of Sterics and Electronics

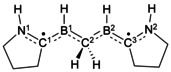
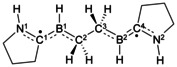
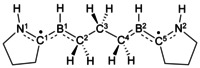
Abstract

Twisted boron‐based biradicals featuring unsaturated C₂R₂ (R=Et, Me) bridges and stabilization by cyclic (alkyl)(amino)carbenes (CAACs) were recently prepared. These species show remarkable geometrical and electronic differences with respect to their unbridged counterparts. Herein, a thorough computational investigation on the origin of their distinct electrostructural properties is performed. It is shown that steric effects are mostly responsible for the preference for twisted over planar structures. The ground‐state multiplicity of the twisted structure is modulated by the σ framework of the bridge, and different R groups lead to distinct multiplicities. In line with the experimental data, a planar structure driven by delocalization effects is observed as global minimum for R=H. The synthetic elusiveness of C₂R₂‐bridged systems featuring N‐heterocyclic carbenes (NHCs) was also investigated. These results could contribute to the engineering of novel main group biradicals.

Twist or not: A thorough computational investigation of the origin of the distinct electrostructural properties of twisted boron‐based biradicals featuring unsaturated C₂R₂ (R=Et, Me) bridges is presented. Steric effects are mostly responsible for the preference of twisted over planar structures, while the ground state multiplicity of the twisted structure is modulated by the σ framework of the bridge, with different R groups leading to distinct multiplicities.

Introduction

Among the various structural motifs adopted by boron centers, the planar, tricoordinate borane (BR₃) is one of the most studied. These compounds are characterized by having an empty p orbital on the boron atom, and several attempts to populate it by chemical reduction or with coordinating Lewis bases and anionic reagents have been made. However, radical anions obtained by addition of a single electron to boranes, which are isoelectronic to neutral, tertiary carbon radicals, are generally highly reactive species, and the synthesis of persistent boron‐containing radicals was an arduous challenge for many years. ^[1] Fortunately, recent advances in the synthesis of boron compounds have paved the way for the generation of distinct boron radicals stabilized by steric and/or electronic effects, and this has led to a flourishing and active research field. ^[2]

One of the most successful strategies for the stabilization of main‐group radical species is the use of cyclic (alkyl)(amino)carbenes (CAACs) as coordinating ligands. Since their first synthesis and isolation by Bertrand and co‐workers in 2005, ^[3] CAACs have been used for a variety of applications, including: i) the activation of small molecules and chemical bonds; ^[4] ii) the stabilization of reactive main group and transition metal species; ^[5] and iii) the development of efficient and robust catalysts for diverse applications. ^[6] The electronic properties of these singlet carbenes differ significantly from those of conventional (diamino) N‐heterocyclic carbenes (NHCs), which are also widely used. ^[7] The replacement of one of the two π‐donating amino substituents of NHCs by the relatively σ‐donating but non‐π‐donating alkyl group of CAACs leads to an increase in both the σ‐donor and π‐acceptor abilities of the carbene center. Qualitatively, their tendency to stabilize radical species is derived from the so‐called captodative effect, ^[8] wherein the unpaired electron occupies the p orbital of the sp²‐hybridized C^CAAC atom and is stabilized by an intricate push–pull mechanism involving the neighboring π‐donating N atom (also sp²‐hybridized) and an attached π‐acceptor unit (e.g., borane) bound to the carbene. In fact, all‐sp²‐hybridized N‐C‐B moieties have emerged as a promising design principle in computational searches for molecules and materials for use in photochemical and light‐harvesting applications. ^[9]

On going from compounds containing one borane radical to systems with two, the two spin centers can form a closed‐shell system if both electrons occupy a stable bonding orbital. Alternatively, they also can exist as biradicals if both electrons occupy two nearly degenerate orbitals. Two noteworthy examples of the latter are CAAC‐stabilized bis‐borane systems, a number of which consist of two directly connected (CAAC)(RE)B radical units, namely (CAAC)(RE)B−B(ER)(CAAC) (I, Scheme 1, ER=SBu, SPh, SePh), ^[10] while other reported examples contain an unsaturated −C(R)=C(R)− bridge between the boron centers: (CAAC)(Cl)B−(RC=CR)−B(Cl)(CAAC) (II; Scheme 1; R=CH₃, C₂H₅). ^[11] A further example has been published recently, namely a CAAC‐stabilized 9,10‐diboraanthracene (III, Scheme 1). ^[12] All of these examples have biradical ground states (either singlet or triplet) and adopt different geometries than their closed‐shell counterparts. In the directly connected (CAAC)(RE)B−B(ER)(CAAC) biradicals, for example, the planar (CAAC)(ER)B units are mutually orthogonal, precluding the presence of a B−B π bond. ^[10] This molecule has a triplet ground state. In the bridged biradicals (CAAC)(Cl)B−(RC=CR)−B(Cl)(CAAC), the RC=CR units are effectively orthogonal to the planar B(Cl)(CAAC) units. ^[11] Finally, CAAC‐stabilized 9,10‐diboraanthracene adopts a butterfly shape, which takes the BCN π system out of the plane of the adjacent phenylene groups. ^[12] Both last‐named systems have singlet ground states, but the triplet states are so close in energy that signals can be observed in their EPR spectra. In contrast to the CAAC systems, the corresponding NHC‐stabilized 9,10‐diboraanthracene and (NHC)(ER)B−B(ER)(NHC) compounds adopt structures that allow the formation of stabilized HOMOs. The former adopts a nearly flat structure, ^[13] while in the latter the (RE)B−B(ER) unit is planar with distinct B=B bond. The NHC moieties are twisted with respect to this plane by 90°.

Scheme 1.

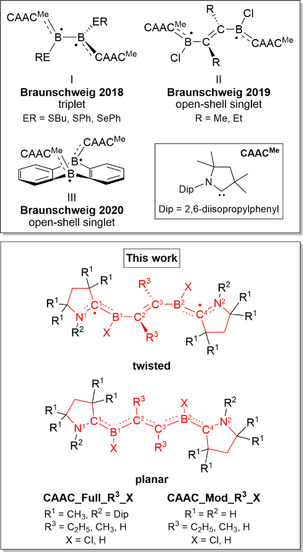
Top: experimentally realized compounds I, ^[10] II, ^[11] and III. ^[12] Bottom: structures studied herein. The combinations of substituents R¹ and R² are denoted Full (R¹=CH₃, R²=Dip) or Model (Mod; R¹=R²=H), while the substituents R³ and X are explicitly given. For example, the compound with R¹=CH₃, R²=Dip, R³=CH₃, and X=Cl is abbreviated as CAAC_Full_CH₃_Cl, while that with R¹=H, R²=H, R³=H, and X=H is labeled CAAC_Mod_H_H. In the planar geometry the dihedral angles ϕ(N¹C¹B¹C²), ϕ(C¹B¹C²C³), ϕ(B¹C²C³B²), ϕ(C²C³B²C⁴), and ϕ(C³B²C⁴N²) are equal to 180°. For the twisted geometry, the dihedral angles ϕ(N¹C¹B¹C²), ϕ(B¹C²C³B²), and ϕ(C³B²C⁴N²) are equal to 180°, while ϕ(C¹B¹C²C³)=−90° and ϕ(C²C³B²C⁴)=90°. Further geometrical data are summarized in Tables S1–S5 of the Supporting Information. The corresponding dihedral angles for the fully optimized structures are given in Table S4 of the Supporting Information. See text for more details.

While experimental work unambiguously determined the differences in structures and electronic characters between the CAAC‐ and NHC‐stabilized congeners, the reasons for the differences were unclear. This was remedied in the case of the L(RE)B−B(ER)L systems by computational comparison of the two sets of compounds, which showed that the stronger steric demands of the NHCs are important, but the lower‐lying triplet states of the CAAC congeners are an essential prerequisite for the formation of biradical ground states. ^[14]

The present study extends these investigations to the bis‐borane systems (L)(X)B−(RC=CR)−B(X)(L) in which the borane moieties are bridged by an unsaturated C₂R₂ group. Remarkably, for L=CAAC, X=Cl, and R=CH₃, C₂H₅, the central olefinic bridge is maintained perpendicular to the B–CAAC moieties, precluding the presence of π delocalization along the CBCCBC backbone and leading to biradical systems. In addition to investigations of the experimentally isolated systems,[ ¹⁰ , ¹¹ ] we used theory to investigate derivatives that are not synthetically accessible. Thereby, we performed a comprehensive exploration of the singlet and triplet states of C₂R₂‐bridged bis‐borane compounds, aiming to disentangle steric and electronic effects that drive the preference for molecular twisting over π delocalization in experimentally realized structures, and to find reasons why the nonbridged species (CAAC)(RE)B−B(ER)(CAAC) have triplet ground states, whereas the bridged species (CAAC)(Cl)B−(RC=CR)−B(Cl)(CAAC) have open‐shell singlet ground states. To obtain further insights we replaced the boron‐bound halo substituents, the alkyl groups of the bridging unit, and the bulky groups attached to the CAAC donors with hydrogen atoms. This diminishes steric effects, so that the electronic contributions come to the fore. Another elegant method to disentangle steric and electronic effects was described by Bickelhaupt et al. in 2006. ^[15] Additionally, we characterized the experimentally unknown NHC counterparts to investigate the generality of the reasons for the differences found for (L)(RE)B−B(ER)(L) and why their syntheses may have failed.

Computational Details

The geometries of the Full and Model systems were optimized by using the MN12L functional ^[16] in the spin‐unrestricted formalism in conjugation with the 6‐311G(d,p) basis set. ^[17] The computations were performed in vacuum, since the experiments were done in nonpolar solvents. ^[11] In the following discussion, geometries obtained from optimizations without restrictions are described as “fully optimized” (full‐opt). For the singlet states the broken‐symmetry method was employed. The relative energies are based on the values of the UMN12L/6‐311G(d,p) calculations as well. Such single‐reference approaches are often sufficiently accurate. ^[18] However, for biradicals with small singlet–triplet (S–T) gaps, multireference approaches are needed to obtain accurate potential‐energy surfaces (PESs), ^[19] electronically excited states, ^[20] or even properties. ^[21] Hence, the energies of the model systems were also calculated with NEVPT2 ^[22] /cc‐pVDZ, ^[23] which is based on a CASSCF(4,6) calculation. ^[24]

Tables 1 and 2 give computed ⟨S ²⟩ expectation values of the total spin (see Supporting Information Equation S1) ^[25] as they provide valuable information about the character of the states and the quality of the computations. Spin‐restricted approaches such as CASSCF or NEVPT2 give the correct ⟨S ²⟩ values of 0 for singlet states [⟨S ²⟩=S(S+1)], irrespective of whether a closed‐shell or an open‐shell state is described. In turn, ⟨S ²⟩=2 is obtained for triplet states. Since such approaches are too computationally expensive, we employed less‐expensive spin‐unrestricted (also called broken‐symmetry) one‐determinant DFT approaches for the full systems. These give ⟨S ²⟩=0 for singlet closed‐shell systems, but ⟨S ²⟩=1 for singlet open‐shell systems, because in such one‐determinant approaches an open‐shell biradical wave function represents a complete mixture of the correct singlet and triplet wave functions. For perfect biradicals the accompanying error in the energy is small because the S–T gap is small. The error can increase for open‐shell systems with larger S–T gaps. In spin‐unrestricted approaches errors often also arise from spin contamination, for which the wave function contains artificial contributions from higher spin multiplicities. Hence, the computed ⟨S ²⟩ values not only give information about the character of the state (closed versus open‐shell singlet versus triplet), but also offer insights into the quality of the computations, because deviations from the expected ⟨S ²⟩ values indicate problems in the calculations. The singlet open‐shell character y was also estimated by the Yamaguchi formula, whereby a closed‐shell singlet state is represented by y=0 and an open‐shell biradical singlet or triplet by y=1 (see Equation S1 in the Supporting Information). ^[26] For the C₂R₂‐bridged systems the adiabatic S–T gaps were calculated. For the saturated hydrocarbon‐bridged systems the calculated S–T gaps are the vertical ones (i.e., obtained by changing the spin state with a fixed geometry), and the NEVPT2/cc‐pVDZ calculations were based on a CASCI with an active space size of (2,2). The DFT calculations were carried out with Gaussian 16 ^[27] and the NEVPT2 calculations were performed with ORCA 4.1.1. ^[28]

Table 1.

UMN12L/6‐311G(d,p) relative electronic energies [kcal mol⁻¹] of the singlet (S₀) and triplet (T₀) states of the CAAC_Full_R³_X systems, where zero is defined as the S₀ state of the planar structures.^[a]

System	S0	T0	S–T gap	⟨S 2⟩ (S0)
CAAC_Full_C2H5_Cl (full‐opt)	−42.4	−42.3	0.1	1.01
CAAC_Full_C2H5_Cl (twisted)	−41.5	−41.4	0.1	1.00
CAAC_Full_C2H5_Cl (planar)	0.0	1.2	1.2	0.93
CAAC_Full_CH3_Cl (full‐opt)	−34.1	−33.5	0.6	0.97
CAAC_Full_CH3_Cl (twisted)	−32.4	−31.8	0.6	0.98
CAAC_Full_CH3_Cl (planar)	0.0	2.3	2.3	0.77
CAAC_Full_H_Cl (full‐opt)	−2.1	9.0	11.1	0.00
CAAC_Full_H_Cl (twisted)	17.7	17.7	0.0	1.01
CAAC_Full_H_Cl (planar)	0.0	11.2	11.2	0.00
CAAC_Full_C2H5_H (full‐opt)	−8.3	−7.9	0.4	0.99
CAAC_Full_C2H5_H (twisted)	−7.6	−7.4	0.2	1.01
CAAC_Full_C2H5_H (planar)	0.0	12.8	12.8	0.02
CAAC_Full_CH3_H (full‐opt)	−5.1	−4.5	0.6	0.98
CAAC_Full_CH3_H (twisted)	−4.5	−3.8	0.7	0.98
CAAC_Full_CH3_H (planar)	0.0	11.4	11.4	0.00
CAAC_Full_H_H (full‐opt)	−1.0	11.0	12.0	0.00
CAAC_Full_H_H (twisted)	23.3	23.4	0.1	1.01
CAAC_Full_H_H (planar)	0.0	12.1	12.1	0.00

[a] Planar‐to‐twisted energies ΔE _p→t can be obtained by comparing the energies of the respective planar and twisted structures. A positive value of ΔE _p→t indicates that the planar structure is more stable. S–T gaps and the ⟨S ²⟩ values (for S₀) are also shown.

Table 2.

Relative electronic energies [kcal mol⁻¹] of the singlet (S₀) and triplet (T₀) states of the CAAC_Mod_R³_X systems, where zero is defined as the S₀ state of the planar structures.^[a] ΔE _p→t, S–T gaps, y (for S₀), and the ⟨S ²⟩ values (for S₀) are also shown.

System	NEVPT2(4,6)/cc‐pVDZ				UMN12L/6‐311G(d,p)
	S0	T0	S–T gap	y (S0)	S0	T0	S–T gap	⟨S 2⟩ (S0)
CAAC_Mod_C2H5_Cl (twisted)	−3.7	−3.3	0.4	0.86	−0.9	−0.6	0.3	0.98
CAAC_Mod_C2H5_Cl (planar)	0.0	10.9	10.9	0.08	0.0	10.5	10.5	0.00
CAAC_Mod_CH3_Cl (twisted)	3.5	3.9	0.4	0.84	3.5	4.0	0.5	0.97
CAAC_Mod_CH3_Cl (planar)	0.0	10.6	10.6	0.09	0.0	10.5	10.5	0.00
CAAC_Mod_H_Cl (twisted)	22.6	22.5	−0.1	0.96	29.0	29.0	0.0	1.01
CAAC_Mod_H_Cl (planar)	0.0	11.2	11.2	0.07	0.0	13.6	13.6	0.00
CAAC_Mod_C2H5_H (twisted)	14.2	14.7	0.5	0.84	15.1	15.6	0.5	0.98
CAAC_Mod_C2H5_H (planar)	0.0	15.7	15.7	0.11	0.0	12.2	12.2	0.00
CAAC_Mod_CH3_H (twisted)	13.1	13.5	0.4	0.81	15.9	16.6	0.7	0.97
CAAC_Mod_CH3_H (planar)	0.0	14.7	14.7	0.08	0.0	11.9	11.9	0.00
CAAC_Mod_H_H (twisted)	27.2	26.9	−0.3	0.96	27.2	27.2	0.0	1.01
CAAC_Mod_H_H (planar)	0.0	11.9	11.9	0.07	0.0	13.9	13.9	0.00

Results and Discussion

The experimentally realized molecules CAAC_Full_CH₃_Cl and CAAC_Full_C₂H₅_Cl adopt twisted geometrical structures in the solid state, leading to open‐shell biradical ground states. In both cases a singlet ground state is found, while the corresponding triplet state lies slightly higher in energy. Various effects disfavor the planar arrangement, despite the fact that it would allow extended π delocalization over the C₂R₂ bridge. The twisting may result from the core of the molecule being quite sterically crowded. The underlying steric effects comprise interactions between the methyl groups of the C₂R₂ bridge and the chloro substituent or effects resulting from the CAAC substituents. Additionally, electronic effects similar to those found in the related CAAC‐ and NHC‐stabilized diborenes might contribute. ^[14] To obtain initial insights into these various effects, we replaced the alkyl substituents of the C₂R₂ bridge, the boron‐bound chloro substituents, and the peripheral CAAC substituents consecutively by hydrogen atoms and compared the computed energy differences between the planar and twisted structures (ΔE _p→t). In the planar geometry the dihedral angles ϕ(N¹C¹B¹C²), ϕ(C¹B¹C²C³), ϕ(B¹C²C³B²), ϕ(C²C³B²C⁴), and ϕ(C³B²C⁴N²) are constrained to 180° while all other geometrical parameters are optimized. Note that these restrictions enforce a planar orientation of the backbone consisting of N¹, C¹, B¹, C², C³, B², C⁴, and N², but do not force the substituents of the C₂R₂ bridge (R³=C₂H₅, CH₃, H) into the same plane. For the twisted geometry, the dihedral angles ϕ(N¹C¹B¹C²), ϕB¹C²C³B²), and ϕ(C³B²C⁴N²) are constrained to 180°, while ϕ(C¹B¹C²C³)=−90° and ϕ(C²C³B²C⁴)=90°. Again, all other geometrical parameters are optimized. The global minimum of a given compound was obtained by geometry optimization without constraints (full‐opt). The corresponding dihedral angles for these fully optimized structures are given in Table S4 of the Supporting Information. Variations in the geometrical parameters are listed in Tables S1–S3 of the Supporting Information. The energy data are summarized in Tables 1 and 2. In all cases we give the relative energy with respect to the singlet state of the planar structure to introduce a clear sign convention. For the computations we used NEVPT2/cc‐pVDZ and UMN12L/6‐311G(d,p). The former is a multireference approach and is hence able to describe open‐shell biradical structures very accurately. However, it is too demanding for the full systems, for which we had to employ DFT methods. We adopted the UMN12L functional herein to directly compare the present results with our previous works.[ ¹⁰ , ¹¹ , ¹⁴ ] The computations for the model systems (Table 2), for example, CAAC_Mod_C₂H₅_Cl or CAAC_Mod_CH₃_Cl, allow reliable comparison of the NEVPT2 and UMN12L results. We assume that calculations using NEVPT2 are more accurate, because UMN12L describes the open‐shell S₀ state of the biradical twisted structure as a complete mixture of the singlet and triplet states, as indicated by the ⟨S ²⟩ expectation value of 1.0. Furthermore, DFT tends to overestimate the contribution of π delocalization to the stability of a molecule, that is, it should prefer planar structures to some extent. ^[29] For CAAC_Mod_C₂H₅_Cl, NEVPT2 predicts that the planar structure is about 4 kcal mol⁻¹ higher in energy than the twisted one. UMN12L also computes the planar structure to be less stable than the twisted arrangement, but the difference is only about 1 kcal mol⁻¹. For all other model systems, both approaches predict planar structures. However, as anticipated, UMN12L slightly overestimates the energy differences with respect to the twisted structure, that is, slightly favors the planar arrangement. The error bars of UMN12L for the S–T gaps are smaller than those obtained for ΔE _p→t. For the twisted structure of CAAC_Mod_CH₃_Cl, NEVPT2 predicts an S–T gap of 0.4 kcal mol⁻¹, while UMN12L computes a value of 0.5 kcal mol⁻¹. This energy variation between NEVPT2 and UMN12L is very similar for the other model systems in their twisted structures. For the planar structures, deviations in the S–T gaps between the two methods are about 1–3 kcal mol⁻¹, but in these cases the S–T gaps are around 10–15 kcal mol⁻¹, and are thus considerably larger than those of the twisted structures. Taken together, these results indicate that UMN12L is qualitatively correct for all model systems studied herein. Hence, also for the full systems, UMN12L is expected to give qualitatively correct results, because the size of the effects determining the energy order of the electronic states and geometrical structures are larger than those of the model systems. Benchmark calculations with RI‐NEVPT2(4,6)/def2‐SVP additionally showed that the geometries predicted by UMN12L are sufficiently accurate. This is in line with earlier benchmark calculations. ^[30]

In agreement with the experimental results, UMN12L predicts that CAAC_Full_C₂H₅_Cl and CAAC_Full_CH₃_Cl have twisted structures and open‐shell singlet ground states (S₀). The dihedral angles of the fully optimized structure deviate by up to 6° from those of the solid‐state structure (Table S4 of the Supporting Information). Such deviations are observed because the system seems to be quite flexible despite the large, bulky substituents. This can be seen in the energy differences between the computed twisted and the fully optimized structures for both systems. Their calculated energies deviate by only 1–2 kcal mol⁻¹ despite variations of more than 10° in their dihedral angles (see Table S4 in the Supporting Information). The deviations between measured and computed bond lengths and angles are even smaller (Tables S1–S3 of the Supporting Information). The triplet T₀ state of the fully optimized structure of CAAC_Full_C₂H₅_Cl (CAAC_Full_CH₃_Cl) lies about 0.1 kcal mol⁻¹ (0.6 kcal mol⁻¹) higher in energy than the singlet state. Their multiplicities stand in contrast to the recently investigated CAAC‐stabilized diborenes.[ ¹⁰ , ¹⁴ ] These compounds are also twisted and show an open‐shell electronic structure, but have triplet ground states.

The planar structure of CAAC_Full_CH₃_Cl is about 34 kcal mol⁻¹ higher in energy than the fully optimized one. The latter resembles the twisted structure, which is less than 2 kcal mol⁻¹ higher in energy. For CAAC_Full_C₂H₅_Cl the corresponding planar structure is even higher in energy, lying 42 kcal mol⁻¹ above the fully optimized one. To investigate the underlying reasons for these energy differences the C₂H₅, CH₃, and Cl substituents and the CAAC units were consecutively replaced by hydrogen atoms (Tables 1 and 2). If we replace the CH₃ groups of the C₂R₂ bridge with hydrogen atoms (CAAC_Full_CH₃_Cl → CAAC_Full_H_Cl), the computations predict that the planar structure becomes about 18 kcal mol⁻¹ lower in energy than the twisted one. The fully optimized structure closely resembles the planar structure, which is only about 2 kcal mol⁻¹ higher in energy. This is in line with experimental X‐ray data of the corresponding molecule. ^[31] As expected, the planar and the fully optimized structure of CAAC_Full_H_Cl has a closed‐shell S₀ ground state with an S–T gap of about 11 kcal mol⁻¹ (UMN12L).

Considering that the planar structure is stabilized by delocalization over the C₂R₂ bridge, steric interactions are essentially responsible for the adoption of twisted structures in the derivatives with alkyl substituents at the C₂R₂ bridge (R³=CH₃, C₂H₅). The steric demands result from interaction between the R³ substituents on one side with the boron‐bound chlorine atoms, and with the methyl substituents of CAAC moieties (R¹=CH₃) on the other side. Additionally, interactions between R²=Dip and R³ may also contribute. Interactions between R²=Dip and X=Cl or H are also expected, but they do not change on going from the twisted to the planar structure. Hence, the preference for twisted or planar structures directly results from the interplay of the stabilization resulting from the delocalization over the planar structure and the strain effects, which decrease significantly on going from the planar to the twisted structure. This higher strain in the planar system arises from all substituents effectively lying in one plane. In contrast, for the twisted structure the distances increase because the R³ alkyl substituents stay perpendicular with respect to the other bulky groups. To quantify the various effects we used the UMN12L/6‐311G(d,p) approach, because NEVPT2 turned out to be too computationally expensive for the full systems.

The magnitude of the stabilization effects resulting from delocalization are best estimated by comparing the energy difference between the twisted and planar structures (ΔE _p→t) for CAAC_Mod_H_H, because in this truncated model, steric effects are diminished as far as possible. The difference is about 27 kcal mol⁻¹ in favor of the planar structure. For CAAC_Mod_CH₃_H and CAAC_Mod_C₂H₅_H, ΔE _p→t decreases to about 15–16 kcal mol⁻¹, that is, the steric interactions between X=H and the R³ alkyl substituents of the C₂R₂ bridge alone amount to approximately 11–12 kcal mol⁻¹. Since R¹=R²=H for Mod systems, their steric demands should be negligible. On going from X=H to X=Cl, ΔE _p→t changes to approximately +29, +4, and −1 kcal mol⁻¹ for R³=H, CH₃, and C₂H₅, respectively. This shows that alkyl groups at the C₂R₂ bridge are essential to make the twisted structure competitive. This same conclusion is reached when analyzing CAAC_Full_H_Cl, which, in contrast to the alkyl‐substituted systems CAAC_Full_CH₃_Cl and CAAC_Full_C₂H₅_Cl, adopts the planar structure.

For CAAC_Full_CH₃_Cl and CAAC_Full_C₂H₅_Cl the steric interactions are so strong that restraining ϕ(N¹C¹B¹C²), ϕ(C¹B¹C²C³), ϕ(B¹C²C³B²), ϕ(C²C³B²C⁴), and ϕ(C³B²C⁴N²) to 180° is not sufficient to enforce a completely planar structure, although it forces the backbone consisting of N¹, C¹, B¹, C², C³, B², C⁴, and N² (see Scheme 1) into a planar orientation. However, the systems use the remaining freedom to move the R³ alkyl substituents below or above this plane. For CAAC_Full_C₂H₅_Cl a value of ϕ(C¹B¹C²C^R3) of about 43° is predicted. The resulting pyramidalization of the C² and C³ centers reduces the strain because the distances between the R³ and R¹ substituents increase, as is obvious from Figure S1 of the Supporting Information, which shows the computed planar structure for CAAC_Full_CH₃_Cl. The corresponding distances are given in Table S5 of the Supporting Information. The pyramidalization should additionally destabilize the system because two sp³ carbon centers are formed, breaking the C−C double bond and allowing biradical character to emerge. The formation of two sp³ centers is proven by the sums of the bond angles around C² and C³ (Table S3 of the Supporting Information). For the fully optimized structure of CAAC_Full_C₂H₅_Cl the sum of the angles around the C² center is 359.8°, which nicely agrees with the 360° expected for a planar sp²‐hybridized carbon center. In contrast, for the planar structure the sum is only 346.6°. For CAAC_Full_CH₃_Cl similar values are found. For the planar conformer of CAAC_Full_H_Cl the sum is again 359.8°. The biradical character of the corresponding systems (Table 1, see CAAC_Full_CH₃_Cl (planar) and CAAC Full C₂H₅  Cl (planar) entries) becomes obvious from the computed ⟨S ²⟩ values (0.77 and 0.93) and the small S–T gaps (2.3 and 1.2 kcal mol⁻¹). For completely planar structures [e.g., CAAC_Mod_H_H (planar), see Table 2] the ⟨S ²⟩ values are 0, and considerably larger S–T gaps (e.g., 14 kcal mol⁻¹) are computed. By combining ΔE _p→t for CAAC_Full_C₂H₅_Cl (−42 kcal mol⁻¹) and CAAC_Full_CH₃_Cl (−32 kcal mol⁻¹) with the values estimated for the stabilization effects resulting from the delocalization (≈27 kcal mol⁻¹), the steric effects in CAAC_Full_C₂H₅_Cl (planar) and CAAC_Full_CH₃_Cl (planar) can be estimated to be at least 70 and 60 kcal mol⁻¹, respectively. These values only represent lower bounds, because they neglect effects resulting from the formation of biradical species in CAAC_Full_CH₃_Cl (planar) and CAAC_Full_C₂H₅_Cl (planar).

To summarize, the strain effects leading to the twisted structures of CAAC_Full_CH₃_Cl and CAAC_Full_C₂H₅_Cl are greater than 60 and 70 kcal mol⁻¹, respectively. Alkyl substituents at the C₂R₂ bridge are mainly responsible for the twisting, as CAAC_Full_H_Cl adopts a planar structure, which is computed to be approximately 18 kcal mol⁻¹ more stable than the twisted structure. By comparing this value with the stabilization estimated by delocalization (≈27 kcal mol⁻¹), it becomes obvious that, even for CAAC_Full_H_Cl, steric effects should play a role. Indeed, the distances between the X=Cl atom and the C₂H₂ hydrogen atoms, and between the R¹=CH₃ groups of the CAAC and the C₂H₂ hydrogen atoms, are still about 0.2 Å smaller than the van der Waals radii (Table S5, Figure S1 of the Supporting Information). Nevertheless, the resulting repulsions are overcompensated by the stabilization resulting from the delocalization. For completely planar systems with R³=alkyl, the corresponding distances would be considerably shorter than their respective van der Waals radii, so that the resulting strain cannot be overcompensated.

In contrast to the biradical congeners of CAAC‐stabilized diborenes, which have open‐shell triplet ground states,[ ¹⁰ , ¹⁴ ] CAAC_Full_C₂H₅_Cl and CAAC_Full_CH₃_Cl have open‐shell singlet ground states. ^[12] The similarities and differences of the systems are summarized in Scheme 1. The small S–T gaps of less than 1 kcal mol⁻¹ show that in both systems the interactions between the two radical centers are very weak. For the C₂R₂‐bridged boron biradicals (Scheme 1, II) the π systems of both radical centers have the same alignment, that is, their π systems could interact in principle. However, the interaction is diminished because both radical centers are separated by the twisted C₂R₂ group. For the biradical congeners of the diborenes (Scheme 1, I) the interaction between the radical centers is weak because both radical centers are twisted by 90°, so that the π systems of both radical centers are perpendicular to each other. To obtain insight into these interactions, we turn to the data computed for the twisted systems. The twisted orientation is not always the equilibrium geometry; for example, for CAAC_Mod_H_Cl the planar structure is more stable. However, by using the computed twisted structures we can extend the investigation of the S–T gaps to include different substituents at the C₂R₂ bridge. Relying on experimental data,[ ¹⁰ , ¹¹ ] we could only compare CAAC_Full_CH₃_Cl and the biradical congeners of the diborenes for which temperature‐dependent measurements were performed.[ ¹⁰ , ¹¹ ] Since the S–T gaps are quite small, we used the model systems for this analysis, as they can be characterized by high‐level multireference approaches. The computed energies are given in Table 2. The multireference calculations predict singlet ground states for the twisted structures of CAAC_Mod_C₂H₅_Cl, CAAC_Mod_C₂H₅_H, CAAC_Mod_CH₃_Cl, and CAAC_Mod_CH₃_H. On replacing the alkyl groups of the bridge with hydrogen atoms, the triplet states become the ground states of such twisted structures. The shapes and the energies of the relevant SOMOs are summarized in Figure 1, which also gives the computed S–T gaps.

Figure 1.

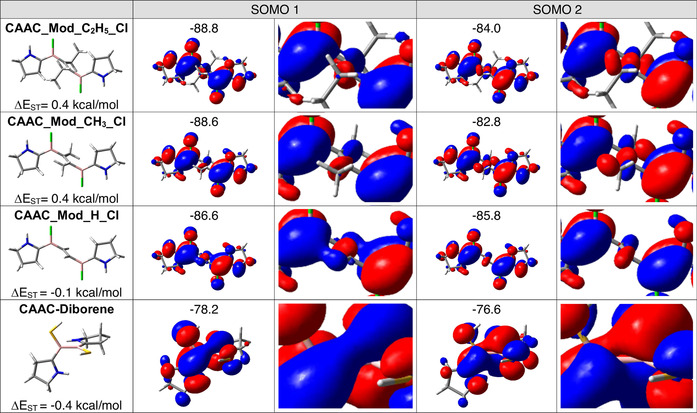
SOMOs of the twisted structures of distinct model C₂R₂‐bridged systems and those of the model diborene biradical congener. The triplet orbital energies are given in kcal mol⁻¹. The corresponding CASSCF orbitals possess virtually identical shapes and show the same energy trends (Figures S3, S4 of the Supporting Information). S–T gaps ΔE _ST obtained from NEVPT2/cc‐pVDZ computations are also given. A positive value means a singlet ground state.

According to Hund's rule, molecules in which two electrons occupy two energetically degenerate orbitals should have a triplet ground state. If the energy difference between the orbitals is small but nonzero, the situation becomes more complicated, as excellently described in the reviews of Bonačić‐Koutecký, Koutecký, and Michl. ^[32] These authors coined the expression “biradicaloids” to describe systems with two nearly degenerate orbitals whose energy splitting arises from possible interactions between both radical centers. In biradicaloids three different singlet states and one triplet state have to be considered. Here, we will only briefly reiterate the underlying aspects. More information can be taken from the Supporting Information or from the original reviews. ^[30]

For orbitals that are delocalized over both spin centers, such as those we obtained for the twisted C₂R₂‐bridged diborenes and the biradical congeners of diborene systems (Figure 1), the wave function of the lowest‐lying singlet state is dominated by the negative linear combination of the two determinants in which either SOMO1 or SOMO2 is doubly occupied (Scheme S2 of the Supporting Information). This state may be shifted below the triplet state, either due to its interaction with the other two singlet states, or because SOMO1 becomes considerably more stable than SOMO2. With increasing energy difference between the orbitals, the determinant in which SOMO1 is doubly occupied increasingly dominates the wave function of the lower singlet state. Finally, the singlet state moves below the triplet state, in which SOMO1 and SOMO2 are both singly occupied.

Indeed, Figure 1 shows that the energy differences between the SOMOs are about 5–6 kcal mol⁻¹ for the C₂Et₂‐ and the C₂Me₂‐bridged systems, while an energy difference of less than 1 kcal mol⁻¹ is predicted for the CAAC–diborene system. This explains why singlet ground states are found for the former but a triplet ground state for the latter. Experimental data for the S–T gap of the twisted structure of CAAC_Full_H_Cl are not available because its planar structure is much more stable than its twisted structure. However, theory allows inclusion of this system in the investigation. Astonishingly, NEVPT2 predicts that the twisted forms of CAAC_Mod_H_Cl and CAAC_Mod_H_H have triplet ground states (Table 2). The UMN12L computations predict negligible S–T gaps for both the model systems (Table 2) and the full systems (Table 1). The difference for the systems with alkylated C₂R₂ bridges can again be reduced to the energy difference of the two SOMOs (Figure 1). For CAAC_Mod_H_Cl it is less than 1 kcal mol⁻¹, which explains its triplet ground state.

This large variation arises because on replacing, for example, CH₃ with H, SOMO1 is destabilized, while SOMO2 is stabilized. In fact, closer inspection of the phases of the B–CAAC π system shows that they even cross (see Figure 1 and Figures S2–S4 of the Supporting Information). For all alkyl substituents the lower SOMO consists of the bonding linear combination of the π systems of the B–CAAC units, while the upper SOMO contains the antibonding combination. For SOMO1, the inner C₂(CH₃)₂ contribution represents a linear combination of two σ C−CH₃ bonds. This linear combination has the correct symmetry to interact with the π systems of the B–CAAC units and is antibonding with respect to both π systems. For SOMO2 the CH σ bonds also contribute, and clearly destabilize this orbital. For the C₂H₂ bridge this CH–σ destabilizing contribution is missing. Inspection of the phases of the π systems of the B‐CAAC units shows that the energy order of the two SOMOs is reversed and the energy difference becomes smaller. Consequently, the triplet becomes the ground state.

The substituents at both boron centers do not considerably influence the size of the S–T gap (Table 2). On replacing X=Cl with H, the computed S–T gaps remain approximately 0.4–0.5 kcal mol⁻¹. This may result because these substituents do not influence the inner part of the SOMOs (see for example Figure S2 of the Supporting Information), so that the orbital energy differences do not change strongly. Figure 1 compares the SOMOs obtained for the bridged compounds with those of the nonbridged, twisted diborane congeners. In this triplet‐ground‐state system, the interaction between the CAAC π orbitals is diminished because the B–CAAC moieties are rotated with respect to each other. Nevertheless, the energy difference between the two SOMOs is 1.6 kcal mol⁻¹. This energy gap is larger than those calculated for the C₂H₂‐bridged systems, for example, CAAC_Mod_H_Cl or CAAC_Mod_H_H.

In another picture, the interaction between the spin centers is responsible for the energy order of singlet and triplet. If the two centers cannot interact, the triplet state is the ground state. If the interaction increases, one singlet state (bonding character between both spin centers) is stabilized while the other is destabilized (antibonding character). If the interaction is sufficiently strong, the stabilized singlet state becomes more stable than the triplet. However, for the given examples this picture is misleading, because the alkylated C₂R₂ bridge likely hampers the interaction between the two spin centers more than the simple C₂H₂ bridge.

The orientation and distance between the spin centers are important structural properties that can influence the relative energy of singlet and triplet states, and thus affect the ground‐state multiplicity of the molecular system. However, the fact that a preference for triplet states is observed for twisted CAAC_Mod_H_Cl and CAAC_Mod_H_H, whereas their counterparts featuring methyl‐substituted C₂R₂ bridges have singlet states, indicates that the rules determining singlet or triplet ground states are more complicated, at least for the bridged boron systems studied herein. To shed more light on these complicated relationships, we computed molecules in which two B–CAAC spin centers are connected by the saturated hydrocarbon bridges CH₂, (CH₂)₂, and (CH₂)₃ in their staggered orientation. The computation of these systems allows insights into the role of distance and orientation, because the saturated hydrocarbon bridge cannot interact with the spin centers, regardless of their orientation. Additionally, they also provide some understanding of the special role of unsaturated bridges described above. The NEVPT2 results are summarized in Table 3.

Table 3.

NEVPT2 computations of saturated hydrocarbon‐bridged systems to investigate the influence of the relative orientation of radical centers on the multiplicity of the ground state.^[a]

bridge	CH2		C2H4		C3H6
dihedral angle	ϕ(B1C2B2C3)		ϕ(C2C3B2C4)		ϕ(C3C4B2C5)
dihedral angle	180°	90°	180°	90°	180°	90°
S–T gap	0.71	−0.21	0.22	−0.05	0.05	0.00

[a] The S–T gap [kcal mol⁻¹] is the singlet–triplet gap obtained from NEVPT2(2,2)/cc‐pVDZ calculations (for more explanation, see text or Supporting Information). Negative S–T gaps indicate that the system has a triplet ground state.

According to our calculations, for these systems the relative orientation of the B–CAAC moieties exclusively determines the preferred multiplicity. All systems in which the two B–CAAC moieties are perpendicular to each other have a triplet ground state. This even holds for the CH₂‐bridged system, in which the two boron centers are only 2.6 Å apart. In contrast, for all systems with parallel alignments the computations predict a singlet state. Even for the (CH₂)₃‐bridged system, in which the boron centers are 5.3 Å apart, our computations predict a singlet ground state. These findings underline the special role of the C₂R₂ bridge in the twisted conformers of CAAC_Mod_H_Cl and CAAC_Mod_H_H. Although the boron centers in these systems are only 4.0–4.1 Å apart, and both spin centers are oriented in a parallel fashion, the computations still predict the triplet state to be lower than the singlet state for this conformer. More information about orbital shapes and energies, as well as the relationship between the form of the MOs (localized versus delocalized) and the wave functions of the saturated hydrocarbon‐bridged molecules, are given in the Supporting Information (Sections II and III).

Differences in the properties of NHCs and CAACs, such as the tendency of CAACs to stabilize radicals and biradicals, are usually discussed in terms of their greater π‐donating and σ‐accepting properties. However, very few studies have closely examined the differences between CAACs and NHCs. ^[33] We recently contributed to this topic by comparing the properties of CAAC‐ and NHC‐stabilized diborenes ^[14] and a diboraanthracene. ^[12] As mentioned above, both showed considerable differences in their geometrical structures and electronic characters. For the diborenes, in addition to steric effects, the differences also result from the triplet states of the CAAC compounds lying considerably lower in energy than those of the corresponding NHC systems. These low‐lying triplet states result from smaller HOMO–LUMO gaps, which could be traced back to a more favorable nodal structure for the LUMO of the CAAC compounds. To investigate the generality of these trends, we attempted to synthesize NHC‐based diboron compounds with unsaturated C₂ bridges, but without success. To shed some light on this important issue we characterized the corresponding NHC compounds by means of computation. The corresponding geometrical parameters are given in Table S7–S9 of the Supporting Information. The energies are summarized in Table S10 of the Supporting Information.

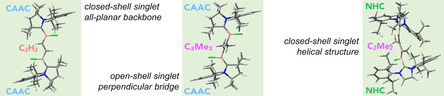
The main results are summarized in Figure 2, which reveals that the differences found for diborenes are also present in the C₂R₂‐bridged compounds. While CAAC_Full_CH₃_Cl has an open‐shell singlet ground state in which the C₂R₂ bridge is twisted with respect to the B–CAAC moieties, the analogous NHC derivative NHC_Full_CH₃_Cl has a closed‐shell singlet ground state, and the triplet state lies 8.3 kcal mol⁻¹ higher in energy (Figure 2 a). The equilibrium geometry is neither planar nor twisted. In contrast, the C^NHC‐BCCB‐C^NHC backbone adopts a helicoidal form (Figure 2 b). This geometry seems to balance the steric demands of the various bulky groups with the possibility of forming a π system that is delocalized over the whole backbone (Figure 2 c).

Figure 2.

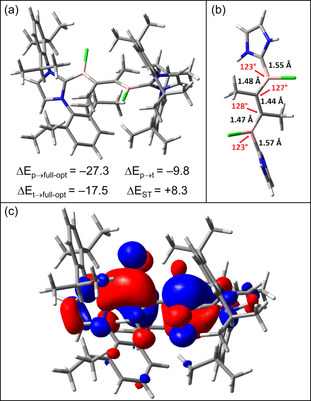
Structure and energies [UMN12L/6–311G(d,p)] of NHC_Full_CH₃_Cl. a) Full system and selected relative energies [kcal mol⁻¹]. The S–T gap ΔE _ST is the adiabatic one of the fully optimized (full‐opt) structures. b) The substituents are omitted for clarity and some geometrical parameters are indicated (bond lengths in Å). c) HOMO of NHC_Full_CH₃_Cl (full‐opt structure). For more information, see text.

The underlying reason for the different behavior of NHC_Full_CH₃_Cl in comparison to CAAC_Full_CH₃_Cl is again the higher‐lying triplet state of the NHC compounds. This becomes obvious from Table S11 of the Supporting Information, which compares ΔE _p→t and the S–T gaps of the planar model systems for which the steric effects are diminished. The corresponding orbital energies and shapes are also given. For CAAC_Mod_CH₃_Cl, the planar structure is about 4 kcal mol⁻¹ more stable than the twisted one. The triplet state of the planar structure lies approximately 11 kcal mol⁻¹ higher than the singlet.

For NHC_Mod_CH₃_Cl the S–T gap of the planar structure is approximately 22 kcal mol⁻¹, that is, about 11 kcal mol⁻¹ higher than that of CAAC_Mod_CH₃_Cl. The additional triplet‐state destabilization experienced by NHC_Mod_CH₃_Cl in comparison to its corresponding CAAC system is also reflected in its higher ΔE _p→t value, whereby the planar structure is favored by about 7 kcal mol⁻¹ (NHC: ΔE _p→t≈+11 kcal mol⁻¹) with respect to that of CAAC_Mod_CH₃_Cl (CAAC: ΔE _p→t≈+4 kcal mol⁻¹). As discussed above for diborenes, the increase in the S–T gap again seems to result from stronger destabilization of the LUMO if CAAC and NHC systems are compared. The similarities between the various systems become obvious from the shapes of HOMO−1, HOMO, and LUMO (Table S11 of the Supporting Information).

The variations in the steric demands of the C₂ bridge and the boron substituents of the full NHC systems resemble those found for CAAC systems (Tables S10 of the Supporting Information). In both cases, if the alkyl groups at the C₂R₂ bridge are replaced with hydrogen atoms, our computations predict that virtually planar structures are formed. The equilibrium geometry of NHC_Full_CH₃_H again resembles that of NHC_Full_CH₃_Cl, while that of NHC_Full_H_H is again nearly planar. This shows that—also for the NHC compounds—the methyl groups of the C₂ bridge would be mainly responsible for the distorted equilibrium geometries. More information is provided in the Supporting Information (Section IV).

As previously mentioned, attempts to synthesize the corresponding NHC‐based compounds were unsuccessful. To shed some light on the factors precluding their experimental realization, we computed the thermodynamics of the CAAC‐to‐NHC exchange reaction (Scheme 2). The computed reaction energies for the various systems are summarized in Table S12 (Supporting Information Section V). Our UMN12L/6‐311G(d,p) computations indicate that the exchange reaction energy is only about 4 kcal mol⁻¹ for X=Cl and R²=CH₃. The reaction energy is slightly lower (≈3 kcal mol⁻¹) for R²=H, while that for R²=C₂H₅ is higher (10 kcal mol⁻¹). This indicates that for R₂=CH₃ and H, the difficulties in the synthesis of the NHC compounds are mainly due to kinetic effects. In contrast, for R₂=C₂H₅ thermodynamic effects seem to be more important.

Scheme 2.

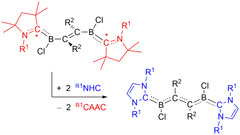
Conceptual exchange reaction of CAAC substituents with NHC substituents. R¹=Dip and R²=C₂H₅, CH₃, H.

Conclusion

We have applied DFT and high‐level multireference calculations to explore the steric and electronic effects at play in the planar and twisted structures of C₂R₂‐bridged boron‐based biradicals. The recently synthesized CAAC‐stabilized diboron compounds with alkyl‐substituted unsaturated C₂ bridges showed unexpected geometrical and electronic structures that were not fully understood at the time. Without strain effects, one would expect a planar orientation of the two B–CAAC moieties and the C₂ bridge, because it would allow a π‐delocalized system with a closed‐shell ground state. However, alkyl‐substituted C₂R₂ bridges twist by about 90° with respect to both B–CAAC units, and an open‐shell singlet ground state results. While the unusual geometrical and electronic properties of the molecules were unambiguously determined, the underlying reasons remained unclear, especially the interplay between steric effects induced by the various groups, delocalization effects through the C₂R₂ bridge, and the energy gap between open‐ and closed‐shell structures, which motivated the present work.

Our analysis shows that the steric demands of the CAAC and chloro substituents are necessary to induce the twisting of the structure in systems containing the C₂(CH₃)₂ bridge, while those containing the C₂(C₂H₅)₂ bridge twist even without the presence of substituents at CAAC. For the C₂H₂ bridge a planar structure with a closed‐shell ground state is formed even in the presence of the other bulky groups, that is, the presence of alkyl groups at the C₂ bridge is essential to induce a twisted structure. By replacing the various substituents with hydrogen atoms, we could quantify the distinct effects that contribute. Delocalization through the C₂ bridge provides a stabilization of approximately 27 kcal mol⁻¹. For alkyl‐substituted bridges this stabilizing effect is overcompensated by the much stronger influence of the steric effects induced by the substituents at CAAC and by the chlorine atoms, which amount to at least 60–70 kcal mol⁻¹. These effects are so strong that they induce sp³ hybridization of the carbon centers of the C₂R₂ bridge, imposing a biradical character on the system. On relaxing the geometry, an open‐shell singlet structure is favored, in which the C₂R₂ bridge is twisted with respect to the B–CAAC units. This clarifies that for an alkyl‐substituted C₂R₂ bridge, steric effects are the dominant player. In contrast, the significant negation of steric demands in systems with non‐alkylated C₂H₂ bridges leads to the dominance of delocalization effects, resulting in planar structures.

We also investigated the effects determining the preference for singlet or triplet multiplicities in these systems. According to our computations, the preferred open‐shell singlet multiplicity for alkyl‐substituted, twisted C₂R₂ bridges results from the energy gap between the two SOMOs. These consist of the bonding and antibonding linear combination of π orbitals of the CAAC moieties but are modulated by participation of the σ framework of the unsaturated C₂ bridge. For the alkyl substituents, this contribution increases the energy difference between the SOMOs by destabilizing the orbital comprising the antibonding combination. In contrast, for the hydrogen‐substituted C₂R₂ bridges the antibonding combination is stabilized by a contribution from the CH‐σ system, so that the bonding and antibonding orbitals cross and a small energy gap results. This ultimately leads to a triplet ground state for the compound with a twisted C₂H₂ bridge. The replacement of the unsaturated C₂R₂ bridge with saturated CH₂, (CH₂)₂, and (CH₂)₃ bridges allowed us to underline the unusual role of the former.

Finally, we investigated the thermodynamic consequences of replacing the CAAC ligands with appropriate NHCs. Our computations indicate that kinetic effects are mainly responsible for the elusiveness of the corresponding NHC‐stabilized systems with unsaturated C₂R₂ (R=H, CH₃) bridges, whereas for R=C₂H₅, thermodynamic effects also play a significant role. We believe that the findings discussed herein will contribute to the experimental development of novel boron‐based biradicals.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

P. Schmid, F. Fantuzzi, J. Klopf, N. B. Schröder, R. D. Dewhurst, H. Braunschweig, V. Engel, B. Engels, Chem. Eur. J. 2021, 27, 5160.