Complex‐Solid‐Solution Electrocatalyst Discovery by Computational Prediction and High‐Throughput Experimentation

Abstract

Complex solid solutions (“high entropy alloys”), comprising five or more principal elements, promise a paradigm change in electrocatalysis due to the availability of millions of different active sites with unique arrangements of multiple elements directly neighbouring a binding site. Thus, strong electronic and geometric effects are induced, which are known as effective tools to tune activity. With the example of the oxygen reduction reaction, we show that by utilising a data‐driven discovery cycle, the multidimensionality challenge raised by this catalyst class can be mastered. Iteratively refined computational models predict activity trends around which continuous composition‐spread thin‐film libraries are synthesised. High‐throughput characterisation datasets are then used as input for refinement of the model. The refined model correctly predicts activity maxima of the exemplary model system Ag‐Ir‐Pd‐Pt‐Ru. The method can identify optimal complex‐solid‐solution materials for electrocatalytic reactions in an unprecedented manner.

Complex solid solutions (“high‐entropy alloys”) promise a paradigm change in electrocatalysis but expose the challenge of almost unlimited options in adjusting their compositions. We propose the utilisation of computational models, combined with high‐throughput experimentation for the verification of the model assumptions, which allows for model refinement in iterative loops, understanding of binding mechanisms, and discovery of the most active composition.

Complex solid solutions (CSS), often referred to as “high entropy alloys”, were recently discovered to hold the promise of shifting the paradigm in materials design from “using materials that we have” to “engineering materials that we need”. In electrocatalysis there is an urgent need to discover new materials to catalyse the production of sustainable fuels and chemicals, needed for mitigating climate change. For many key reactions the scalability towards a global level is limited by present‐day catalysts. However, most of the plausible billions of different materials have never been synthesised and nearly all materials that have been employed up to now represent edges and corners in the vast continuum of chemical space. Exploration of the promising multidimensional chemical space of CSSs with the aim of finding previously out‐of‐reach catalysts is extremely challenging and requires an intelligent materials discovery strategy to focus on interesting regions of potential catalytic activity since neither simulation nor experiments alone can overcome serendipity in materials discovery.

The emerging paradigm change in electrocatalysis is based on the availability of millions of different active sites in the CSS atomic surface configuration. This unique arrangement of multiple elements directly neighbouring a binding site enables tuning activity by electronic and geometric effects. ^[1] Recently, we discovered a noble‐metal free CSS for the oxygen reduction reaction (ORR), ^[2] proposed a theoretical base for CSS catalysts as a discovery platform, ^[3] applied this strategy on the CO₂ and CO reduction reactions, ^[4] and described experimental challenges and concepts, ^[5] which were confirmed experimentally ^[6] and further confirmed theoretically. ^[7] Moreover, the discovery and investigation of CSS electrocatalysts is attracting a burgeoning interest. Independently, several groups have shown that CSS electrocatalysts are indeed “game‐changing” materials for a wide span of electrochemical reactions such as hydrogen and oxygen evolution reactions, ^[8] CO, ^[4] CO₂[ ⁴ , ⁹ ] and O₂[ ² , ³ , ¹⁰ ] reduction reactions as well as methanol oxidation ^[11] or ammonia synthesis and decomposition.[ ¹² , ¹³ , ¹⁴ ] Outstanding activities were reported even though in most cases only the simplest case of equiatomic CSS compositions were investigated. This success was enabled by the development of an increasing number of mostly non‐equilibrium synthesis methods comprising carbothermal shock synthesis,[ ¹² , ¹⁴ ] combinatorial co‐sputtering,[ ² , ⁶ ] solvothermal reactions, ^[15] ball milling, ^[9] dealloying, ^[10] oil phase synthesis ^[16] and laser ablation ^[17] amongst others.

Up until now selection of an elemental CSS composition is guided by chemical intuition. With the combinatorial explosion of possibilities that occurs when considering combinations and composition of constituent elements, it becomes almost impossible to discover optimal multinary electrocatalysts for specific reactions without an underlying theoretical framework. While no such framework exists for predicting the optimal set of constituent elements for a reaction, finding the most active composition of a given set is of equal importance. To accomplish this, we demonstrate a closed‐loop data‐driven high‐throughput experimentation approach that iteratively combines (i) ab‐initio simulations and modelling, (ii) combinatorial synthesis of materials libraries (MLs) and (iii) high‐throughput characterisation (see Figure 1). This starts with an initial hypothesis/prediction of a system of interest which is synthesised, in the form of thin‐film MLs, comprising large compositional ranges which allow the efficient identification of property maxima and minima. The results are used to refine the model to improve predictions in the next cycle.

Figure 1.

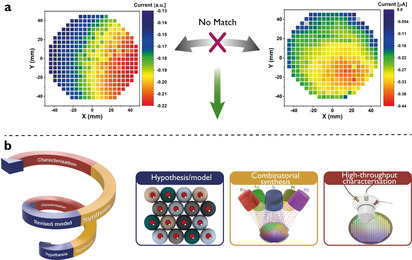
Schematic representation of the iterative materials discovery loop. a) Predicted and experimentally obtained ORR activity on ML1 using SDC measurements: the initial model does not match the experimental result. The x and y‐axis denote the dimension of the ML. b) The data‐driven discovery cycle combining prediction, combinatorial synthesis and high‐throughput characterisation.

As a testbed, noble metals as electrocatalysts for the ORR allow robust and well‐defined experimental parameters without risking material modification such as surface oxidation or dissolution. Moreover, established theoretical design principles exist for ORR performance, which have been confirmed experimentally. Theory and experiment suggest that an optimal catalyst binds *OH and *O with an adsorption energy 0.1 eV ^[18] and 0.2 eV ^[19] weaker than Pt, respectively. For comparing surfaces an estimate of the relative activity, A, is calculated from all binding energies with associated weights given by the probability of finding each type of site using Equation 1:

$${\displaystyle A=\sum _{i=1}^Z\left({\prod }_k^{\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{a}\mathrm{l}\mathrm{s}}{f}_k^{n_{ik}}\right)\exp \left(-\frac{\left|\Delta E_i-\Delta E_{\mathrm{o}\mathrm{p}\mathrm{t}}\right|}{k_{\mathrm{B}}T}\right)}$$ (1)

Per‐site activity is assumed to increase exponentially with decreasing difference between the binding energy of an intermediate on site i, ΔE_i, and the optimum given by the Sabatier principle, ΔE _opt. k _B and T are the Boltzmann constant and temperature, respectively. The per‐site activity is then multiplied by the probability of site i occurring, ${\prod }_k^{metals}{f}_k^{n_{ik}}$ , where k are constituent metals, f are the fractions of k in the overall composition, and n_ik is the number of atoms of k constituting the binding site. Finally, all per‐site activities of the Z sites included in the model (Figure S1) are summed to give the overall activity.

The computational challenge posed by CSS surfaces derives from the millions of possible local atomic arrangements, all having different binding energies defined by the composition and relative positions of atoms. A totally mixed alloy has a statistical distribution of different local atom arrangements which serve as active sites. Therefore, a fast method of calculating binding energies is needed. A DFT‐dataset of thousands of binding energies enables fitting a model to describe the remaining millions of possible arrangements. This initial model predicted CSS activities of Ir‐Pd‐Pt‐Rh‐Ru for the ORR ^[3] and Pt‐Pd‐Cu‐Ag‐Au for the CO₂ and CO reduction reactions. ^[4] Here, we focus on the system Ag‐Ir‐Pd‐Pt‐Ru, with the constituents chosen based on the likelihood of forming a stable and active CSS, and a composition predicted with the initial model. By training a linear regression model on 3317 DFT calculated *OH and *O binding energies and predicting all ΔE_i, sequential least squares programming was used to find compositions that maximise Equation (1), considering only *OH binding energies. For computational details of the DFT‐calculations and regression model, see SI and Figures S1–2. Two most active compositions were calculated in this way: Ag₅Ir₅Pt₂₀Pd₃₅Ru₃₅ and Ag₅Ir₅Pd₁₇Pt₆₈Ru₅, both assuming *OH binding as the activity descriptor. The first composition optimisation was bound to fractions between 5 % and 35 % to retain a high probability for CSS stability. The second composition was found by removing the upper bound of 35 %. Three Ag‐Ir‐Pd‐Pt‐Ru MLs (ML1, ML2 and ML3) covering different composition spaces centred around the predicted compositions were fabricated using combinatorial co‐sputtering from five elemental targets (Figures S5, 6) with composition ranges shown in Table S1 in the Supporting Information. ML1 was centred around the composition Ag₅Ir₅Pt₂₀Pd₃₅Ru₃₅ and characterised for comparison with the model described above. ML2 and ML3 were both centred around Ag₅Ir₅Pd₁₇Pt₆₈Ru₅, being fabricated for data consistency and trend reproducibility. All 342 measurement areas (MAs) on a ML are synthesised simultaneously in one experiment.

The MLs were investigated with scanning droplet cell (SDC) measurements in 0.1 M HClO₄. After rinsing with new electrolyte, the SDC head was pressed onto each MA. The wetted area served as working electrode. By measuring a linear sweep voltammogram (LSV) we evaluate the materials’ ORR activity (see SI). Mapping composition‐activity dependencies enables comparison with modelling. A homogeneous Pt thin film showed a small standard deviation with respect to the ORR activity for all MAs (Figure S8), confirming reliability. Each ML was measured a second time, being turned by 90°, to rule out systematic errors (Figure 4 e and Figure S9). Thus, fully consistent datasets unambiguously tied to the composition gradients (Figure S10) were obtained. Spatially resolved XRD and EDX data as well as results from atom probe tomography (APT) confirm the presence of a single‐phase CSS state of the samples and allow comparison of activity at each MA of the MLs with predicted data (Figure 2 and Figures S6 and S7).

Figure 4.

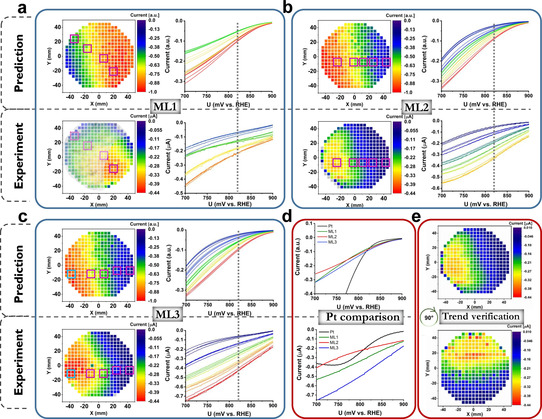
Comparison of predicted (model III) and experimental ORR activity trends for Ag‐Ir‐Pd‐Pt‐Ru MLs and Pt. a) ML1, b) ML2, and c) ML3 activity maps with individual LSVs of the selected MAs covering high to low activity (indicated by squares) are illustrated on the right. The current at 820 mV vs. RHE (dashed line) was chosen as the measure of activity. ML1 exhibits different phase regions: fcc, fcc + hcp, and hcp, (greyed areas in ML1), whereas ML2 and ML3 are all fcc. d) LSVs of Pt thin film benchmark compared to the most active compositions of the MLs. e) Repetition after 90° rotation verifying the reproducibility of the experimentally obtained trend on ML2.

Figure 2.

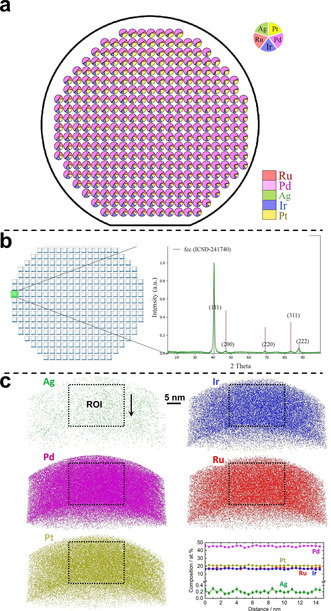
Results of spatially resolved a) EDX measurements at each MA of ML2 illustrating the continuous composition gradients; b) XRD measurements of ML2 and a selected diffraction pattern of the MA Pd₄₆Pt_19.2Ru_17.9Ir_16.8Ag_0.1; c) visualisation of APT results from a CSS thin film sputtered on a tip‐array ^[20] to confirm the single‐phase CSS state. The overall composition of this sample as determined by APT is Pd_47.1Pt_18.9Ru_17.8Ir_15.9Ag_0.3.

Initial predictions fail to anticipate activity trends satisfactorily (Figure 1 a). Whereas composition might differ from the bulk composition, due to for example, surface segregation, these effects can be neglected for the given case of a fully noble metal system, which is measured in the as‐deposited state and trends in the ML remain unaffected. We iteratively developed a series of models I, II, III built upon the initial model by additionally providing a measure of current per site, j_i, as a function of potential, U, see Equation 2. Using the local composition around each binding site, (details in Figure S1) surface binding energies are mapped. The Koutecký‐Levich equation for rotating disk electrode (RDE) experiments is used to model j_i.

$${\displaystyle \frac{1}{j_i}=\frac{1}{j_{k_i}}+\frac{1}{j_D}}$$ (2)

$${\displaystyle j_{k_i}=\mathrm{e}\mathrm{x}\mathrm{p}\left(\frac{-\left|{\Delta E}_i-{\Delta E}_{\mathrm{o}\mathrm{p}\mathrm{t}}\right|+{\Delta E}_{\mathrm{o}\mathrm{p}\mathrm{t}}-eU}{k_{\mathrm{B}}T}\right)}$$ (3)

Here e is the charge on an electron. j_i is calculated per site i, and then summed up over all sites, N, on the surface.

$${\displaystyle j_{\mathrm{t}\mathrm{o}\mathrm{t}}=\sum _i^N{j}_i=\sum _i^N\frac{1}{\frac{1}{j_{k_i}}+\frac{1}{j_D}}}$$ (4)

The magnitude of the per‐site current response diminishes exponentially with increasing distance from the ORR volcano peak, similar to the initial model. The resulting shape of the current response can be correlated to the adsorption energy distribution pattern. At low overpotentials there is little mass transport limitation (j_D, set to 1, i.e., relative currents are calculated with arbitrary units) in experiment, enabling comparison with SDC measurements.

Three models were developed with distinct binding and site interactions as illustrated in Figure 3. All models are “brute force methods” since for every composition a small section of the surface is simulated (100×100 atoms, 3 layers) with Ag, Ir, Pd, Pt, and Ru randomly populating the face centred cubic (fcc) lattice. By extracting nearest neighbour compositions around on‐top and hollow sites on this surface ≈20 000 binding energies are predicted. Model I focuses on the *OH binding energy as catalytic activity descriptor, with the optimum energy being 0.1 eV weaker than on Pt. Assuming *OH binds to on‐top sites without neighbouring site interactions (Figure 3 a left), using the surface binding energies (Figure 3 b) a measure of the current response at certain potentials (Figure 3 e) is calculated using Equation (2). In contrast, model II considers *O binding to hollow sites (Figure 3 a middle). In this case, even though neighbouring sites share an atom, no site interactions are assumed. The optimum energy is now 0.2 eV weaker than on Pt. ^[19] The binding energies (Figure 3 c) are then used to predict current (Figure 3 f) as in model I.

Figure 3.

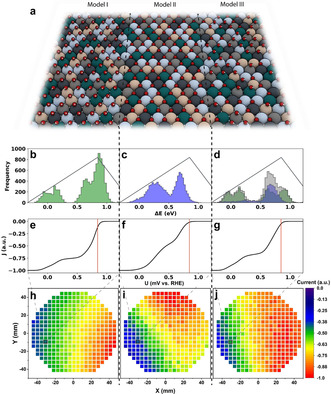
Comparisons between models I, II and III. a) Schematic representation of how the CSS surface is populated in the models. Red atoms represent oxygen, white atoms represent hydrogen, and the other colours represent the CSS surface. b–d) Histograms showing the binding energy distribution patterns of *OH (green), *O (blue), and combined (grey) on the simulated 10 000 atom surface. Volcano curves illustrate the optimum binding energy. e–g) Example polarization curves for Ag₄Ir₁₆Pd₃₀Pt₁₄Ru₃₆ plotted as a function of potential. Red lines indicate the potential 820 mV vs. RHE. h–j) Activity maps plotted using models I, II and III respectively. Current is calculated at 820 mV vs. RHE, compositions are taken from ML1. Selected compositions in (e–g) are indicated by the black box.

Applying models I and II to a single‐element surface, scaling between fcc‐hollow and on‐top sites leads to an identical activity prediction since an adsorbate sees the same surface environment regardless of the binding site. This is not the case for a CSS since adsorption energy distributions for *OH and *O have different shapes, (Figure 3 b and c), confirming that fcc‐hollow and on‐top sites do not scale on a CSS. Interaction of *OH and *O at different binding sites is important due to the complex surface arrangements. Model III includes this effect and additionally considers that on a real CSS surface some sites will prefer an *O binding to the hollow position while other sites an *OH to on‐top, and that sites can be blocked by neighbouring adsorption (Figure 3 a right). The simulated surface of 10 000 atoms is populated with *O and *OH adsorbates by filling the sites starting from the most stable on‐top and hollow sites. Once the surface is filled, only blocked sites, assumed to be inactive, remain vacant. Filled sites take part in the current calculation (Figure 3 g) as in models I and II. Since the surface is populated with neighbouring site blocking considered, the available binding energy distributions (Figure 3 d) are not simply a combination of the non‐interacting *O and *OH distributions. Moving from a pristine surface to a situation where neighbouring sites interact, the binding energy distribution is altered. We demonstrate predictions by the three models, displaying predicted activity maps (Figure 3 h–j) using composition data from ML1 (Figure S5).

Figure 4 shows the comparison of predicted (model III) and experimental activity maps as well as measured LSVs for the ORR at selected MAs from regions with different activity. All activity maps use the current (measured or calculated) at 820 mV vs. RHE as activity descriptor. Since the polarisation curves do not cross within the relevant potential range, the composition trends are not significantly affected by choosing different potentials. An already good match of predicted and measured data for ML1 is observed. XRD analysis revealed that ML1 consists of three regions with different crystal structure (Figure S7a), which can interfere with the comparison and we highlighted the fcc‐only region as the model assumes an fcc structure. We then prepared MLs that were purely fcc (Figures S7b,c). They show a very good agreement with the activity trends. The simpler models I and II yield different composition trends (Figure S3) emphasising the importance of the additional interaction used in model III. The most active CSS compositions surpass Pt activity, especially in the relevant low overpotential region. Considering the drastically reduced Pt content in the CSS, it is shown that superior activities are achieved on CSS surfaces and the importance of implementing high‐throughput iterative strategies to fully exploit their multidimensional search space is demonstrated.

To summarise, we combine simulation, machine learning, data‐guided combinatorial synthesis, and high‐throughput characterisation to identify CSS compositions with high electrocatalytic activity, particularly for but not limited to the ORR. We demonstrate that models for predicting ORR activity based on simple descriptors do not contain enough information to make predictions on a CSS surface. This provides fundamental insights, namely that it is the interaction between adsorbates and resultant blocking that creates the active surface. We find a model incorporating the simplest adsorbate‐adsorbate interactions is able to replicate experimental activity trends remarkably well. Comparison of data from over 1000 ORR activity measurements and machine learning guided predictions demonstrates an efficient methodology for high‐throughput closed‐loop materials design in the flourishing field of electrocatalysis on CSS surfaces.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

T. A. A. Batchelor, T. Löffler, B. Xiao, O. A. Krysiak, V. Strotkötter, J. K. Pedersen, C. M. Clausen, A. Savan, Y. Li, W. Schuhmann, J. Rossmeisl, A. Ludwig, Angew. Chem. Int. Ed. 2021, 60, 6932.