Polymorphs of the Gadolinite‐Type Borates ZrB₂O₅ and HfB₂O₅ Under Extreme Pressure

Abstract

Based on the results from previous high‐pressure experiments on the gadolinite‐type mineral datolite, CaBSiO₄(OH), the behavior of the isostructural borates β‐HfB₂O₅ and β‐ZrB₂O₅ have been studied by synchrotron‐based in situ high‐pressure single‐crystal X‐ray diffraction experiments. On compression to 120 GPa, both borate layer‐structures are preserved. Additionally, at ≈114 GPa, the formation of a second phase can be observed in both compounds. The new high‐pressure modification γ‐ZrB₂O₅ features a rearrangement of the corner‐sharing BO₄ tetrahedra, while still maintaining the four‐ and eight‐membered rings. The new phase γ‐HfB₂O₅ contains ten‐membered rings including the rare structural motif of edge‐sharing BO₄ tetrahedra with exceptionally short B−O and B⋅⋅⋅B distances. For both structures, unusually high coordination numbers are found for the transition metal cations, with ninefold coordinated Hf⁴⁺, and tenfold coordinated Zr⁴⁺, respectively. These findings remarkably show the potential of cold compression as a low‐energy pathway to discover metastable structures that exhibit new coordinations and structural motifs.

Push the boundaries: The behavior of β‐HfB₂O₅ and β‐ZrB₂O₅ under extreme pressure up to 120 GPa has been studied by synchrotron‐based in situ high‐pressure X‐ray diffraction in a diamond anvil cell. Both compounds remain stable to the highest applied pressure and for both experiments, a second additional phase, named γ‐HfB₂O₅ and γ‐ZrB₂O₅, respectively, was found at pressures above 114 GPa.

Introduction

Due to their exceptional physical and chemical properties, the minerals of the gadolinite supergroup ^[1] have been investigated for the past decades for potential use in the electrical engineering industry or as materials for radiation shields.[ ² , ³ , ⁴ , ⁵ , ⁶ ] In petrology and geochemistry the gadolinite group minerals also serve as markers for geological reconstructions.[ ⁷ , ⁸ , ⁹ ]

The members of the gadolinite supergroup are represented by the general chemical formula A ₂ MQ ₂ T ₂O₈ φ ₂ (A=Ca, RE, Pb, Mn, Bi; M=Fe, Vac., Mg, Mn, Zn, Cu, Al; Q=B, Be, Li; T=Si, P, As, B, Be, S; φ=O, OH, F) ^[10] and their structures feature eight‐ and four‐membered rings, made up of tetrahedra centered by the Q and T‐site atoms. Prominent representatives of the gadolinite group (space group P2₁/c) are minerals including datolite CaBSiO₄(OH),[ ¹¹ , ¹² , ¹³ , ¹⁴ ] homilite Ca₂B₂FeSi₂O₈(OH)₂, ^[15] hingganite‐(Y) Y₂Be₂Si₂O₈(OH)₂, ^[16] and hingganite‐(Yb) Yb₂Be₂Si₂O₈(OH)₂, ^[17] minasgeraisite Y₂Be₂CaSi₂O₈(OH)₂, ^[18] and gadolinite‐(Y) Y₂Be₂FeSi₂O₈O₂ itself.[ ¹⁹ , ²⁰ ] In 2007 and 2008, researchers led by Huppertz found the “simplest” structural variants of all compounds of the gadolinite supergroup, namely β‐HfB₂O₅ and β‐ZrB₂O₅.[ ²¹ , ²² ] They represent the first ternary compounds in this structure family with Hf⁴⁺ or Zr⁴⁺ on the A site and boron on the Q and T sites, corresponding to “(Hf₂/Zr₂)B₂B₂O₈O₂”→HfB₂O₅/ZrB₂O₅.

Considering the importance of the gadolinite‐supergroup minerals there is relatively little information on their behavior under high‐pressure and/or high‐temperature conditions. To the best of our knowledge, there are only such studies concerning the borosilicate datolite, CaBSiO₄(OH),[ ⁹ , ²³ , ²⁴ , ²⁵ , ²⁶ , ²⁷ , ²⁸ ] and, very recently, hingganite‐(Y). ^[29] While the crystal structure of hingganite‐(Y) is preserved up to pressures of 47 GPa, a displacive phase transition can be observed in datolite between 27 and 33 GPa. The application of such high pressures leads to the formation of solely fivefold coordinated Si atoms, resulting in the splitting of the eight‐membered rings into two five‐membered rings, separated by edge‐sharing SiO₅ trigonal bipyramids. ^[28] The present study was in part motivated by a natural desire to synthesize a compound with boron in the coordination higher than four.

To date, only a few structural studies of borates under extreme pressure conditions using diamond anvil cells were performed. For FeBO₃ and GdFe₃(BO₃)₄, optical absorption spectra were recorded up to pressures of 82 GPa and 60 GPa, respectively. Additional electrical resistance measurements for FeBO₃ were conducted up to 140 GPa. In both cases, electronic transitions were observed at 46 GPa for FeBO₃ and at 26 and 43 GPa for GdFe₃(BO₃)₄, but no additional structural information was given.[ ³⁰ , ³¹ ] In addition to these iron borates, SrB₄O₇:Sm²⁺ was studied up to 130 GPa for its potential application as an optical sensor in the diamond anvil cell.[ ³² , ³³ , ³⁴ , ³⁵ , ³⁶ ]

To expand current information from surveys into this field and in the context of the investigations into datolite, the high‐pressure behavior of the isostructural borates β‐HfB₂O₅ and β‐ZrB₂O₅ were investigated to aspire to similar structural changes as that described for datolite. The results of these high‐pressure studies up to 120 GPa are presented in the following.

Experimental Section

Single crystals of β‐ZrB₂O₅ and β‐HfB₂O₅ were synthesized under high‐pressure and high‐temperature conditions in a Walker‐type multianvil apparatus according to the procedure described by Knyrim and Huppertz.[ ²¹ , ²² ] In situ high‐pressure single‐crystal X‐ray diffraction experiments (SCXRD) were performed at the experimental station P02.2 (Extreme Conditions Beamline) at the synchrotron Petra III (Hamburg, Germany). Preselected single crystals of β‐ZrB₂O₅ and β‐HfB₂O₅ were placed inside the sample chamber of a diamond anvil cell (DAC) along with a ruby sphere for pressure estimation. The DAC was loaded with neon as pressure‐transmitting medium. The samples of β‐ZrB₂O₅ and β‐HfB₂O₅ were gradually pressurized up to 120 GPa. Neon is known to be hydrostatic up to 15 GPa ^[37] therefore most of the experiment has been performed under quasihydrostatic conditions. SCXRD data were collected at each pressure step of ≈5–10 GPa. In total, 17 high‐pressure structural refinements have been performed for each crystal. The starting crystallographic parameters for β‐ZrB₂O₅ and β‐HfB₂O₅ were taken from the structural refinements reported by Knyrim and Huppertz.[ ²¹ , ²² ] More details on the synchrotron XRD measurements and the structure refinement is provided in the Supporting Information.

Results and Discussion

β‐Phases of ZrB₂O₅ and HfB₂O₅ at 120 GPa

The crystal structure of β‐ZrB₂O₅ and β‐HfB₂O₅, synthesized at 7.5 GPa in the multianvil press, is composed of eight‐ and four‐membered rings of BO₄ tetrahedra that form layers in the bc plane. Between those layers, the Zr⁴⁺ and Hf⁴⁺ cations, respectively, are coordinated by eight oxygen atoms and form square‐antiprisms. Upon further compression up to 120 GPa, both compounds, β‐ZrB₂O₅ and β‐HfB₂O₅, preserve this structural arrangement (Figure 1). As expected, a shrinkage of the cell parameters during the compression process was observed. At 120 GPa, the highest pressure achieved, the unit cell volume decreases to 74.7 % of the ambient pressure volume in β‐ZrB₂O₅, and to 75.2 % in β‐HfB₂O₅. Also, the β angles increase for both compounds (Figure S1 in Supporting Information). A comparison of the unit cell parameters at atmospheric pressure and at nearly 120 GPa is given in Table 1. A graphical representation of the pressure dependence of the lattice parameters of β‐ZrB₂O₅ and β‐HfB₂O₅ is shown in Figure 2 and Figure 3, respectively. More detailed data for all pressure points is provided in the Supporting Information (Tables S1 and S2; for the normalized unit cell parameters see Figure S2).

Figure 1.

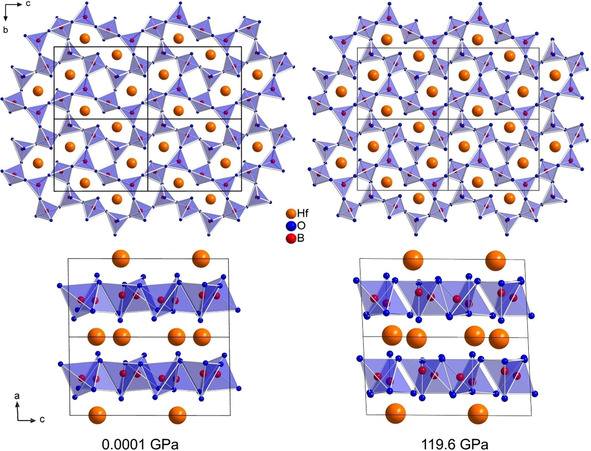
Comparison of β‐HfB₂O₅ at ambient pressure (left) and at nearly 120 GPa (right).

Table 1.

Comparison of the lattice parameters of β‐ZrB₂O₅ and β‐HfB₂O₅ at ambient pressure and at ≈120 GPa.

Compound	β‐ZrB2O5		β‐HfB2O5
Pressure [GPa]	0.0001	119.6	0.0001	119.6
Space group	P21/c		P21/c
a [Å]	4.4021(2)	3.901(2)	4.3843(3)	3.8918(7)
b [Å]	6.9315(3)	6.434(2)	6.9048(6)	6.4311(8)
c [Å]	8.9924(3)	8.11(4)	8.9727(6)	8.17(2)
β [°]	90.93(3)	92.95(8)	90.76(1)	92.90(4)
V [Å3]	272.1(2)	203.3(10)	271.6(1)	204.2(4)

Figure 2.

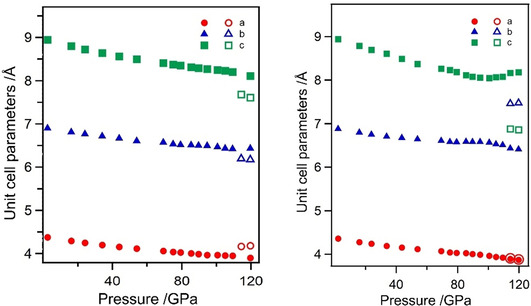
Course of the cell parameter of β‐ZrB₂O₅ (left) and β‐HfB₂O₅ (right) during the compression process. The outlined symbols indicate the simultaneous existence of the new phases γ‐ZrB₂O₅ (left) and γ‐HfB₂O₅ (right), respectively.

Figure 3.

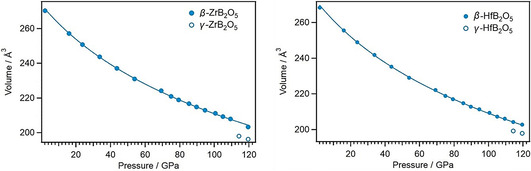
Reduction of the cell volume of β‐ZrB₂O₅ (left) and β‐HfB₂O₅ (right) with increasing pressure. The outlined symbols indicate the simultaneous existence of the new phases γ‐ZrB₂O₅ (left) and γ‐HfB₂O₅ (right), respectively.

At pressures above ≈114 GPa, the appearance of new reflections in the diffraction patterns indicated the formation of a second phase for both the zirconium and the hafnium borates (Figure 2 and 3). The structures of these new high‐pressure phases, designated as γ‐ZrB₂O₅ and γ‐HfB₂O₅, have been solved and refined. In the following, the structural transformations will be discussed, starting with the zirconium borate γ‐ZrB₂O₅.

Crystal structure of γ‐ZrB₂O₅ at 120 GPa

At approximately 114 GPa, a displacive phase transition from β‐ZrB₂O₅ to γ‐ZrB₂O₅ takes place. The wavelike arrangement of BO₄ tetrahedra (marked red in Figure S3, top left) orientate themselves in opposite directions alongside the c‐axis, counteracting the applied pressure and leading to an abrupt decline in the cell parameter values for b and more pronounced for c. In the structure of the new phase γ‐ZrB₂O₅, the eight‐ and four‐membered rings from the β‐phase are preserved (Figure 4 and Figure S3). This alignment is responsible for the tilting of the layers. In the β‐phase, the layers run parallel to the c‐axis, and in the γ‐phase, they are inclined by ≈29° (Figure 4, right). In this new arrangement at 120 GPa, the BO₄ polyhedra diverge significantly from the ideal tetrahedral arrangement, leading to B−O distances in the range of 1.333(7) to 1.440(6) Å, with an average value of ≈1.382 Å, but in about the same range of the bond lengths in the even more distorted β‐ZrB₂O₅ at 120 GPa, which lie in the range of 1.28(9)–1.72(2) Å (average=≈1.4 Å). As expected, these values are much shorter than in BO₄ tetrahedra at ambient pressure (1.476 Å[ ³⁸ , ³⁹ ]). The O‐B‐O angles also lie in a wide range between 88.1(4) and 117.6(4)°. Here, the resulting mean value of 109.25° agrees well with the ideal tetrahedral angle. All bond lengths and angles for γ‐ZrB₂O₅ are listed in Tables 2 and 3, the values for β‐ZrB₂O₅ at 120 GPa can be found in Tables S3 and S4.

Figure 4.

Layered structure of γ‐ZrB₂O₅ still containing eight‐ and four‐membered rings depicted along [$\bar{1}$  0 0] (left) along [0 $\bar{1}$  0] (right).

Table 2.

Interatomic B−O distances [Å] for γ‐ZrB₂O₅ and γ‐HfB₂O₅ at 119.6 GPa (standard deviations in parentheses).

γ‐ZrB2O5
B1	‐O4	1.354(6)	B2	‐O2	1.333(7)
	‐O5	1.363(6)		‐O3	1.380(7)
	‐O1	1.371(6)		‐O5	1.426(6)
	‐O2	1.382(6)		‐O1	1.440(6)
Ø		1.368	Ø		1.395

γ‐HfB2O5
B1	‐O5	1.26(3)	B2	‐O1	1.38(2)
	‐O2	1.40(4)		‐O4	1.39(6)
	‐O3	1.42(4)		‐O1	1.43(4)
	‐O4	1.42(5)		‐O3	1.48(3)
Ø		1.38	Ø		1.42

Table 3.

Bond angles [°] for γ‐ZrB₂O₅ and γ‐HfB₂O₅ at 119.6 GPa (standard deviations in parentheses).

γ‐ZrB2O5
O5‐B1‐O2	101.1(3)	O5‐B2‐O1	88.1(4)
O4‐B1‐O1	104.8(4)	O3‐B2‐O1	111.0(4)
O4‐B1‐O5	106.4(4)	O3‐B2‐O5	111.0(4)
O5‐B1‐O1	112.3(4)	O2‐B2‐O5	112.3(4)
O4‐B1‐O2	115.2(5)	O2‐B2‐O3	114.1(5)
O1‐B1‐O2	116.9(4)	O2‐B2‐O1	117.6(4)
Ø	109.5	Ø	109.0

γ‐HfB2O5
O3‐B1‐O4	91(2)	O4‐B2‐O3	100(2)
O2‐B1‐O4	99(2)	O1‐B2‐O1	101(2)
O2‐B1‐O4	100(4)	O1‐B2‐O3	103(3)
O5‐B1‐O2	113(2)	O1‐B2‐O3	113(2)
O5‐B1‐O4	116(2)	O1‐B2‐O4	117(4)
O5‐B1‐O3	133(5)	O4‐B2‐O1	123(2)
Ø	108.5	Ø	109.5

The tilting of the layers is also responsible for the increased coordination number of ten for the zirconium cation (Figures S3, bottom and S4). Half of the O4 atoms in the β‐phase shift in the c‐direction and the other half in the opposite direction, leading simultaneously to a displacement of the oxygen atoms O3 and O5 for the newly formed polymorph γ‐ZrB₂O₅ (Figure S3, middle). These two atoms O3 and O5 are now in closer proximity to the Zr⁴⁺ cations and account for the enlarged coordination number. To the best of our knowledge, such a high coordination was never observed for Zr⁴⁺. The Zr−O distances at 120 GPa are around the same values in γ‐ZrB₂O₅ (1.958(4)–2.377(4) Å) and β‐ZrB₂O₅ (1.93(4)–2.10(5) Å) with slightly longer distances for the increased coordination number (Table 4).

Table 4.

Interatomic Hf/Zr−O distances [Å] for γ‐ZrB₂O₅ and γ‐HfB₂O₅ at 119.6 GPa (standard deviations in parentheses).

γ‐ZrB2O5			γ‐HfB2O5
Zr	‐O4	1.958(4)	Hf	‐O5	1.95(2)
	‐O5	2.018(4)		‐O2	1.97(2)
	‐O4	2.028(4)		‐O4	2.03(2)
	‐O3	2.029(4)		‐O3	2.04(3)
	‐O1	2.110(4)		‐O5	2.09(3)
	‐O2	2.136(3)		‐O3	2.10(4)
	‐O1	2.175(4)		‐O2	2.11(2)
	‐O5	2.240(3)		‐O1	2.16(3)
	‐O3	2.243(4)		‐O4	2.27(2)
	‐O3	2.377(4)
Ø		2.131	Ø		2.08

Crystal structure of γ‐HfB₂O₅ at 120 GPa

In contrast to the phase transition from β‐ZrB₂O₅ to γ‐ZrB₂O₅ discussed before, the phase transition of β‐HfB₂O₅ at about 114 GPa is reconstructive and accompanied by a reorganization of the BO₄ tetrahedra. As a consequence of the extreme pressure applied to β‐HfB₂O₅, the bonds between B2 and O2 atoms are broken apart, thus opening the four‐ and eight‐membered rings (Figure 5). New bonds between the B2 and O1 atoms of two different BO₄ tetrahedra can now form, leading to edge‐sharing BO₄ tetrahedra (Figure 6 a), a relatively rare structural motif in the structural chemistry of borates. In comparison with other borates containing these B₂O₆ groups, the B⋅⋅⋅B distance of 1.79(6) Å at 120 GPa in γ‐HfB₂O₅ is exceptionally short. In other borates containing this structural motif, the B⋅⋅⋅B distances typically range from 2.072 Å in Dy₄B₆O₁₅ (Figure 6 b), ^[40] 2.04 Å in α‐Gd₂B₄O₉, ^[41] and 2.088 Å in HP‐NiB₂O₄, ^[42] to 2.17 Å in HP‐CsB₅O₈, ^[43] and 2.21 Å in HP‐KB₃O₅ (Figure 6 c). ^[44] The slightly longer distances in the latter two compounds originate from the oxygen atoms forming the common edge, which are coordinated by a third boron atom and not a metal cation like the aforementioned compounds. In all of the compounds with edge‐sharing BO₄ tetrahedra, the B−O bonds inside the B₂O₂ rings are longer than those outside the ring. This is not the case in the here presented γ‐HfB₂O₅, which is attributed to the high applied pressure of 120 GPa. To maximize the distance between the two boron cations located in the centers of the two edge‐sharing tetrahedra, the O‐B‐O angle inside of the B₂O₂ ring is usually very small (here: 101(2)°). In this case, the B‐O‐B angle constitutes the smallest angle inside the B₂O₂ ring, with only 79(2)°. Comparing this to all of the other known borates that contain edge‐sharing BO₄ tetrahedra, only in HP‐MB₃O₅ (M=K, Rb, Tl)[ ⁴⁴ , ⁴⁵ , ⁴⁶ ] and HP‐Cs_1−x(H₃O)_xB₃O₅ (x=0.5–0.7) ^[47] the B‐O‐B angle is the smallest angle inside the B₂O₂ ring. Within these compounds, the oxygen atoms at the common edge are coordinated by a third boron atom and not by a metal cation. Additionally, the values of these two angles inside the B₂O₂ ring in γ‐HfB₂O₅ depart considerably from all those of known compounds, causing the greatest distortion of such a B₂O₆ group compared to all borate compounds containing edge‐sharing BO₄ tetrahedra. Also, the ratio of edge‐sharing to corner sharing BO₄ tetrahedra in γ‐HfB₂O₅ is strikingly high. In this phase, this ratio is 1:1, that is, there are equal amounts of edge‐sharing and corner‐sharing BO₄ tetrahedra, which is the second largest ratio of this rare structural motif in all known borates and related compounds. Only HP‐MB₂O₄ (M=Ni, Co, Fe)[ ⁴² , ⁴⁸ , ⁴⁹ ] consists of solely edge‐sharing BO₄ tetrahedra, and therefore contains more B₂O₆ groups. Considering just compounds where corner‐sharing BO₄ tetrahedra are also present, γ‐HfB₂O₅ comprises the highest ratio of edge‐sharing to corner‐sharing tetrahedra.

Figure 5.

Layered structure of γ‐HfB₂O₅ with ten‐membered rings depicted along [$\bar{1}$  0 0] (left) and along [0 $\bar{1}$  0] (right). Corner‐sharing BO₄ tetrahedra are colored in blue, edge‐sharing BO₄ tetrahedra in red.

Figure 6.

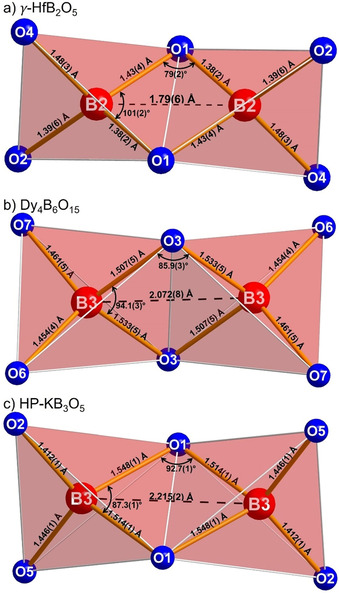
a) Edge‐sharing BO₄ tetrahedra in γ‐HfB₂O₅ in comparison to b) Dy₄B₆O₁₅ and c) HP‐KB₃O₅.

Examining all the B−O bonds in γ‐HfB₂O₅, a variation of bonding distances is found to be larger than in γ‐ZrB₂O₅. In γ‐HfB₂O₅, they vary within the range of 1.26(3) to 1.48(3) Å, with the longest distances, as expected, within the edge‐sharing tetrahedra. Similar variations of bond lengths occur in silicates at high pressure and mark the beginnings of a transition from SiO₄ to SiO₅ polyhedra, as for example in danburite, ^[50] titanite‐like silicate CaSi₂O₅, ^[51] and high‐pressure forms of enstatite. ^[52] In the present borate compound, this could designate the start of a possible transition to BO₅ polyhedra. The mean value for all the B−O distances is 1.40 Å, which is in the same range as for β‐HfB₂O₅ at 120 GPa (B−O distances from 1.35(1)–1.45(2) Å; average=≈1.38 Å). The O‐B‐O angles in γ‐HfB₂O₅ vary from 91(2) to 133(5)° with both the smallest and the widest angle inside the corner‐sharing tetrahedra, featuring, therefore, the greatest distortion. All bond distances and angles of γ‐HfB₂O₅ are listed in the Table 2, the values for β‐HfB₂O₅ at 120 GPa can be found in Tables S3 and S4.

As in the zirconium compound, the coordination of the hafnium cation by oxygen atoms in γ‐HfB₂O₅ increases from an eightfold to a ninefold coordination. The Hf−O distances range from 1.95(2) to 2.27(2) Å (Table 4), which again is in the same range as the Hf−O distances in β‐HfB₂O₅ at 120 GPa (1.96(2)–2.086(7) Å). A comparison of the coordination polyhedra is illustrated in Figure S6.

Tables 5 and 6 present all the relevant data from the crystal structure refinement, as well as the atomic coordinates for both phases γ‐ZrB₂O₅ and γ‐HfB₂O₅. ^[53] Additionally, the charge distributions for both compounds were calculated according to the CHARDI concept (∑Q)[ ⁵⁴ , ⁵⁵ ] to further verify the determined structures. All formal charges are in good agreement with the formal valence state of the cations and anions (Table S5). Only the oxygen atom O5 in γ‐HfB₂O₅ features a lower charge (−1.64) than the expected −2. This can be attributed to the fact that the O5 atom is coordinated by two hafnium cations and only one boron cation. In contrast to O3, which has a similar environment, O5 is further away and therefore receives less attraction from the boron cation.

Table 5.

Crystal data and structure refinement of γ‐ZrB₂O₅ and γ‐HfB₂O₅ at 119.6 GPa.

Empirical formula	γ‐ZrB2O5	γ‐HfB2O5
Molar mass [g mol−1]	192.84	280.11
Crystal system	monoclinic
Space group	P21/n (no. 14)	P21/c (no. 14)
T [K]	285(2)
Wavelength [Å]	0.2901
a [Å]	4.1859(7)	3.8804(13)
b [Å]	6.1734(12)	7.476(3)
c [Å]	7.6078(11)	6.86(2)
β [°]	93.343(14)	96.22(10)
V [Å3]	196.26(6)	197.9(6)
Z	4
Calculated density [g cm−3]	6.526	9.400
Max. θ [°]	18.047	12.870
Index ranges	−7≤h≤6, −10≤k≤9, −12≤l≤14	−6≤h≤6, −13≤k≤13, −5≤l≤4
Reflections collected	1017	550
Independent reflections	629 [Rint=0.0459, R sigma=0.0488]	276 [Rint=0.0185, R sigma=0.0205]
Data/ restraints/ parameters	629/0/38	276/0/38
Goodness‐of‐fit on F 2	1.063	1.169
R1/wR2 indices [I≥2σ(I)]	0.0490/0.1236	0.0565/0.1593
R1/wR2 indices (all data)	0.0504/0.1264	0.0608/0.1659
Largest diff. peak/hole [e Å−3]	3.54/−2.41	3.02/−2.99

Table 6.

Atomic coordinates, and equivalent isotropic displacement parameters U _eq [Ų] (standard deviations in parentheses) for γ‐ZrB₂O₅ and γ‐HfB₂O₅ at 119.6 GPa. All atoms are located at the Wyckoff position 4e.

γ‐ZrB2O5
Atom	x	y	z	U eq
Zr1	0.0168(3)	0.1152(2)	0.6763(6)	0.0085(6)
B1	0.511(5)	0.221(4)	0.41(2)	0.0025(5)
B2	0.443(9)	0.074(5)	1.13(2)	0.0031(6)
O1	0.794(6)	0.101(3)	0.16(1)	0.0036(5)
O2	0.311(6)	0.880(2)	0.14(1)	0.0035(5)
O3	0.277(6)	0.204(4)	0.1(1)	0.0050(7)
O4	0.278(7)	0.149(4)	0.31(1)	0.0042(5)
O5	0.747(5)	0.080(3)	0.458(9)	0.0035(5)

γ‐HfB2O5
Atom	x	y	z	U eq
Hf1	0.4392(2)	0.37445(7)	0.3009(2)	0.0126(9)
B1	0.011(5)	0.170(2)	0.125(8)	0.017(3)
B2	0.135(4)	0.077(2)	0.441(6)	0.010(2)
O1	0.229(3)	0.560(2)	0.076(5)	0.018(2)
O2	0.092(3)	0.811(2)	0.261(5)	0.018(2)
O3	0.264(3)	0.259(2)	0.032(5)	0.027(2)
O4	0.268(3)	0.089(2)	0.258(5)	0.034(2)
O5	0.0755(3)	0.071(2)	0.063(5)	0.015(2)

Comparison to gadolinite‐type minerals datolite and hingganite‐(Y)

The observed high‐pressure pathways of β‐ZrB₂O₅ and β‐HfB₂O₅ differ from the behavior recently described for the isostructural borosilicate datolite, CaBSiO₄(OH), that is built up of four‐ and eight‐membered rings of alternating SiO₄ and BO₄ tetrahedra. Datolite undergoes a displacive phase transition between 27 and 33 GPa with the formation of additional Si−O bonds across the eight‐membered rings (Figure S7, top left). In contrast, β‐ZrB₂O₅ and β‐HfB₂O₅ reveal striking sustainability up to ≈120 GPa, the highest pressure achieved in this study. The bulk moduli of β‐ZrB₂O₅ and β‐HfB₂O₅ were determined to 228(1) and 223(1) GPa, respectively. The boron‐oxygen distances at 120 GPa inside the eight‐membered rings are of 2.36 and 2.45 Å in β‐HfB₂O₅ and β‐ZrB₂O₅, respectively, and therefore too long to be considered a bonding distance (Figure S7, bottom left, and right). The new phases γ‐ZrB₂O₅ and γ‐HfB₂O₅ formed at ≈114 GPa do not feature an increased boron coordination number and possess structural motifs different from datolite‐II. Similar to β‐ZrB₂O₅ and β‐HfB₂O₅, another member of the gadolinite‐type minerals, hingganite‐(Y), Y₂□Be₂Si₂O₈(OH)₂ persists its structure up to 47 GPa at least. ^[29] Gorelova et al. have explained the increased persistence of the initial structure of hingganite‐(Y) in comparison to datolite by the nature of the interlayer cation, that is, by its size and charge. Our observations are in line with this assumption. The evolution of MO₈ (M=Ca²⁺, Y³⁺, Zr⁴⁺) polyhedral volumes in datolite, hingganite‐(Y) and β‐ZrB₂O₅ are compared in Figure S6 while their bulk moduli are given in Table S6. Due to the small size (0.83 Å) ^[56] and high charge of Zr⁴⁺, the ZrO₈ polyhedron is twice as stiff as YO₈ in hingganite‐(Y) and three times stiffer than CaO₈ in datolite (Table S6). It is likely that the compressibility of the tetrahedra also contributes to the increased persistence of the initial crystal structure. The B1O₄ and B2O₄ units show the highest stiffness among TO₄ tetrahedra in datolite, hingganite‐(Y), and β‐ZrB₂O₅ (Table S6). Accordingly, the BO₄ tetrahedra in β‐ZrB₂O₅ undergo an insignificant geometrical distortion upon compression as is evident from the evolution of quadratic elongation and bond angle variance parameters (Figure S9). ^[57] Interestingly, the pronounced increase of these parameters at ≈120 GPa likely indicates the upcoming phase transition at higher pressures, in line with previous reports on the pressure‐induced evolution of structures based on tetrahedral layers and frameworks.[ ²⁸ , ⁵⁰ , ⁵⁸ , ⁵⁹ , ⁶⁰ ] The high ratio of charge to cation size for both Zr⁴⁺ and B³⁺ results in the increased stiffness of ZrO₈ and BO₄ polyhedra and, thus, of the overall crystal structure. Indeed, the bulk modulus of β‐ZrB₂O₅ is considerably larger than those of datolite (106(4) GPa) and hingganite‐(Y) (124(1) GPa).

Conclusions

The presented study of the high‐pressure behavior of the gadolinite‐type borates β‐ZrB₂O₅ and β‐HfB₂O₅ up to 120 GPa offers new fundamental insights into the properties of borates at extreme conditions. Using synchrotron single‐crystal X‐ray diffraction in a diamond anvil cell it was shown that the structure of the two compounds was preserved up to the highest pressures achieved in this study. At pressures of about 114 GPa, a phase transition was observed in both β‐ZrB₂O₅ and β‐HfB₂O₅, which resulted in the synthesis of the previously unknown polymorphs γ‐ZrB₂O₅ and γ‐HfB₂O₅. The structure of γ‐ZrB₂O₅ features layers containing four‐ and eight‐membered rings, similar to those characteristic for β‐ZrB₂O₅, but the layers are tilted. The structure of the new hafnium borate polymorph, γ‐HfB₂O₅, features ten‐membered rings along with the relatively rare structural motif of edge‐sharing BO₄ tetrahedra, mostly occurring in high‐pressure compounds. An extreme contraction of B−O distances and distortion of O‐B‐O angles are typical for the high‐pressure borates. In both structures, the coordination number of the cations increase in comparison to that (equal to eight) in their ambient pressure counterparts: In γ‐HfB₂O₅, Hf⁴⁺ is ninefold coordinated by oxygen, while in γ‐ZrB₂O₅, Zr⁴⁺ is tenfold coordinated. In the presented work, the high‐pressure behavior of the two borates β‐HfB₂O₅ and β‐ZrB₂O₅ was found to be different to that of the isostructural silicate datolite, CaBSiO₄(OH), up to 120 GPa. Thus, subsequent experiments to at least 180 GPa are desirable to figure out if further pressure increase could promote turning boron's coordination to fivefold, analogous to that of silicon in datolite.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

A. Pakhomova, B. Fuchs, L. S. Dubrovinsky, N. Dubrovinskaia, H. Huppertz, Chem. Eur. J. 2021, 27, 6007.