Bifunctional Hydrogen Bond Donor‐Catalyzed Diels–Alder Reactions: Origin of Stereoselectivity and Rate Enhancement

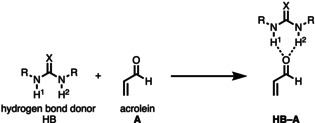
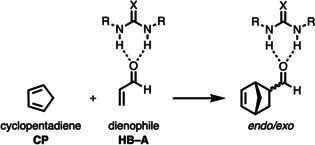
Abstract

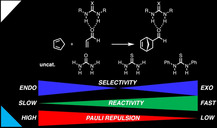
The selectivity and rate enhancement of bifunctional hydrogen bond donor‐catalyzed Diels–Alder reactions between cyclopentadiene and acrolein were quantum chemically studied using density functional theory in combination with coupled‐cluster theory. (Thio)ureas render the studied Diels–Alder cycloaddition reactions exo selective and induce a significant acceleration of this process by lowering the reaction barrier by up to 7 kcal mol⁻¹. Our activation strain and Kohn–Sham molecular orbital analyses uncover that these organocatalysts enhance the Diels–Alder reactivity by reducing the Pauli repulsion between the closed‐shell filled π‐orbitals of the diene and dienophile, by polarizing the π‐orbitals away from the reactive center and not by making the orbital interactions between the reactants stronger. In addition, we establish that the unprecedented exo selectivity of the hydrogen bond donor‐catalyzed Diels–Alder reactions is directly related to the larger degree of asynchronicity along this reaction pathway, which is manifested in a relief of destabilizing activation strain and Pauli repulsion.

Speed it up! Quantum chemical activation strain analyses reveal that (thio)urea‐derived bifunctional hydrogen bond organocatalysts accelerate the Diels–Alder reaction between cyclopentadiene and acrolein by reducing the two‐center four‐electron (steric) Pauli repulsion between the occupied π‐orbitals of the reactants and not by enhancing the donor–acceptor orbital interactions, as is traditionally considered.

Introduction

The Diels–Alder (DA) cycloaddition reaction is arguably one of the most useful processes in chemistry due to its ability to produce six‐membered rings in a single reaction step generating up to four stereocenters. ^[1] Due to the relevance of this transformation in synthesis, ^[2] an impressive number of organocatalysts have been developed not only to accelerate but also to produce highly enantioselective cycloadditions. In this regard, a wide variety of chiral amines, heterocyclic carbenes, guanidines, ureas, amidinium ions, diols, squaramides, and other Lewis acids have successfully been used to afford the corresponding cycloadduct with high enantiomeric excess.[ ³ , ⁴ ]

In particular, bifunctional hydrogen bond donor organocatalysts, i.e., molecules able to act as Lewis acid via two hydrogen bonds, have attracted considerable attention in this line of research. ^[4] For instance, the seminal works by Rawal and co‐workers ^[5] and Schreiner and co‐workers ^[6] on the use of TADDOL and thioureas, respectively, as organocatalysts for Diels–Alder reactions should be especially highlighted (Scheme 1). The catalytic activity of these species is generally ascribed to the bidentate nature of the organocatalyst–substrate binding, which favorably preorganizes and activates the substrate.[ ^3b , ⁶ , ⁷ ] In analogy with conventional Lewis acid catalysts, this type of activation is widely accepted to be the result of the lowering of the LUMO of the dienophile upon binding with the double hydrogen donor catalyst. ^[6] However, we recently demonstrated that orbital interactions are not the origin of conventional Lewis acid catalysis in Diels–Alder reactions, but, in contrast, a significant reduction of the steric (Pauli) repulsion between the occupied π‐molecular orbitals of the diene and dienophile enhances the Diels–Alder reactivity. ^[8] It would not be surprising if this Pauli‐repulsion lowering concept, which is also operative in iminium‐catalyzed Diels–Alder reactions ^[9] and dihalogen‐catalyzed aza‐Michael additions, ^[10] would be the actual driving force behind the catalysis mediated by bifunctional hydrogen bond donor species.

Scheme 1.

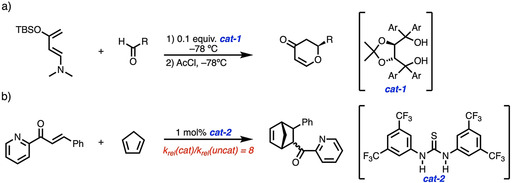
Representative organocatalyzed Diels–Alder cycloaddition reactions involving a) TADDOL and b) Schreiner's thiourea. AcCl = acetyl chloride.

To check our hypothesis and to gain detailed insight into the hitherto poorly understood mode of activation of bifunctional hydrogen bond donor (HB) species, we selected the Diels–Alder cycloaddition reaction between cyclopentadiene (CP) and acrolein (A) catalyzed by different, as Lewis acid acting, (thio)urea species analogous to the processes described by Schreiner and co‐workers (Scheme 2). ^[6a] The endo/exo selectivity as well as the origin of the rate enhancement are quantitatively explored by means of state‐of‐the‐art computational methods, namely, the activation strain model (ASM) of reactivity ^[11] in conjunction with quantitative Kohn–Sham molecular orbital theory (KS‐MO) and a matching energy decomposition analysis (EDA). ^[12] This computational approach has been chosen due to its good performance to understand not only fundamental processes in organic and organometallic chemistry ^[11] but, in particular, the mode of activation and catalysis in related transformations.[ ⁸ , ⁹ , ¹⁰ ]

Scheme 2.

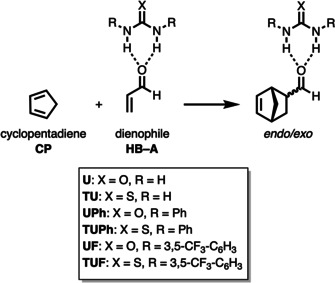
(Thio)urea‐catalyzed Diels–Alder cycloaddition reactions considered in this study.

Computational Methods

Full geometry optimization of all stationary structures and vibrational analyses were carried out at the M06‐2X/def2‐SVPP level[ ¹³ , ¹⁴ ] using the Gaussian 16 program. ^[15] The potential energy surfaces of the studied Diels–Alder reactions were obtained by performing intrinsic reaction coordinate (IRC) calculations. ^[16] The activation strain model (ASM) and energy decomposition analyses (EDA) were carried out by using the PyFrag 2019 ^[17] and ADF.2018.104 ^[18] programs using the same functional in conjunction with doubly polarized triple‐ζ quality TZ2P basis set ^[19] on the geometries optimized at M06‐2X/def2‐SVPP. The zeroth‐order regular approximation (ZORA) was used to account for scalar relativistic effects. ^[20] This level is referred to as ZORA‐M06‐2X/TZ2P//M06‐2X/def2‐SVPP and has been selected because it has been proven to provide accurate activation barriers in related reactions ^[8a– , ^10] and is well suited to capture the non‐covalent interactions relevant to reaction kinetics.[ ²¹ , ²² ] Domain‐based local pair natural orbital coupled‐cluster (DLPNO‐CCSD(T)) calculations, with default normalPNO settings, were performed using Orca 4.0.1 ^[23] using the def2‐QZVPP ^[14] basis set on the M06‐2X/def2‐SVPP optimized geometries.

Results and Discussion

We first analyzed the nature and strength of the (thio)urea‐acrolein (HB‐A) interaction, which is crucial to understand the catalysis mediated by these bifunctional organocatalysts. In all cases, the (thio)urea hydrogen bond donor (HB) catalysts form a bidentate complex via a bifurcated hydrogen bond to A. This typical stabilizing double hydrogen bond interaction can be easily visualized by means of the NCIPLOT method. ^[24] As shown in Figure 1, for the complex involving Schreiner's thiourea TUF, ^[6] there exist two clear non‐covalent attractive interactions (green surfaces) between both N−H hydrogen bond donors of TUF and the carbonyl oxygen atom of A acting as a hydrogen bond acceptor, which confirms the occurrence of both hydrogen bonds. In this particular complex, and in agreement with previous experimental findings, ^[25] there are two additional stabilizing C−H⋅⋅⋅S interactions between the Lewis basic sulfur atom and the ortho hydrogen atoms of the aryl groups as a consequence of the polarization exerted by the electron‐withdrawing CF₃ substituents on the aryl groups. The latter non‐covalent interactions are suggested to hinder the rotation of the aryl groups. ^[6a]

Figure 1.

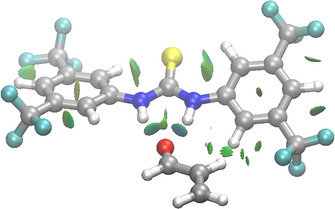
Contour plots of the reduced density gradient isosurfaces (density cutoff = 0.03 au) for the TUF‐A complex. The green surfaces indicate attractive non‐covalent interactions.

More detailed quantitative insight into the (thio)urea‐acrolein (HB‐A) complexation can be obtained by using the energy decomposition analysis (EDA) ^[12] Scheme at the ZORA‐M06‐2X/TZ2P//M06‐2X/def2‐SVPP level. This method decomposes the interaction energy (ΔE _int) between HB and A into the following three chemically meaningful energy terms: classical electrostatic interaction (ΔV _elstat), Pauli repulsion (ΔE _Pauli) between closed‐shell orbitals which is responsible for steric repulsion, and stabilizing orbital attractions (ΔE _oi) that account, among others, for HOMO–LUMO interactions. As gathered in Table 1, the interaction between the different HBs and A, derived from the double hydrogen bond, ranges from −7 to −14 kcal mol⁻¹, which, not surprisingly, is significantly weaker than the value computed for the analogous interaction involving strong Lewis acids such as BF₃ or AlCl₃ but comparable to those species involving weaker Lewis acids such as SnCl₄ or TiCl₄. ^[8a] As shown in Table 1, the ΔE _int becomes increasingly more stabilizing from U < UPh < UF and TU < TUPh < TUF, which, interestingly, follows the same trend as their experimentally determined acidities ^[26] and the observed acceleration of the Diels–Alder cycloaddition involving the analogous methyl vinyl ketone (TU < TUPh < TUF). ^[6a] The corresponding bifurcated hydrogen bond length between H¹⋅⋅⋅O=C and H²⋅⋅⋅O=C becomes steadily shorter along this series, in line with the increasing bond strength. One exception, however, is TUPh, which has a slightly longer hydrogen bond length than UPh. As expected, the interaction term is dominated by the ΔV _elstat term, confirming the electrostatic nature of this hydrogen bonding interaction. Although the ΔV _elstat term is more than twice as strong, the ΔE _oi is not negligible and also follows the same trend as ΔE _int and ΔV _elstat. As a result, the LUMO of the complex, i.e., the π*_C=C molecular orbital located on the C=C double bond of A, becomes more stabilized from U to TUF, which is consistent with the widely accepted LUMO lowering concept (vide supra). ^[6] The donor–acceptor interaction between HB and A, which transfers charges from A to HB, results in a slightly positively charged A. This positive field, in turn, lowers (i.e., stabilizes) the LUMO on A and this effect becomes more prominent as the donor‐acceptor interaction between HB and A is strengthened. Furthermore, it becomes visible that thiourea‐based HBs have, in line with their experimentally determined stronger acidity (pK _A = 21.1 and 26.9, for thiourea and urea, respectively),[ ²⁶ , ²⁷ ] a consistently more stabilizing interaction with A than their urea counterparts, which suggests that thiourea species are better catalysts than their urea analogues.

Table 1.

Energy decomposition analysis terms (in kcal mol⁻¹), LUMO (π*_C=C) energy (in eV), and H⋅⋅⋅O=C distances (in Å), computed on hydrogen bond donor–acrolein (HB‐A) complexes.^[a]

HB	ΔE int	ΔV elstat	ΔE Pauli	ΔE oi	ϵ LUMO	r(H1⋅⋅⋅O=C)	r(H2⋅⋅⋅O=C)
U	−7.1	−9.3	5.5	−3.2	−1.7	2.147	2.144
TU	−8.5	−11.0	6.6	−4.1	−1.8	2.115	2.101
UPh	−9.1	−12.0	7.6	−4.7	−1.9	2.053	2.052
TUPh	−10.4	−13.9	9.5	−6.1	−1.7	2.078	2.067
UF	−13.0	−15.3	9.0	−6.8	−2.3	2.084	1.955
TUF	−13.8	−16.3	10.2	−7.7	−2.3	2.076	1.935

[a] The hydrogen bond donor (HB) and acrolein (A) constitute the two interacting fragments. All data computed at the ZORA‐M06‐2X/TZ2P//M06‐2X/def2‐SVPP level.

After analyzing the bonding situation in the HB‐A complexes, we focused on the Diels–Alder reaction of these activated species with cyclopentadiene. The electronic reaction barriers (ΔE ^≠), reaction energies (ΔE _rxn), and HOMO_CP–LUMO_HB‐A orbital energy gaps (Δϵ _H–L) of the uncatalyzed and HB‐catalyzed Diels–Alder (DA) reaction between cyclopentadiene (CP) and HB‐acrolein complexes (HB‐A) (Scheme 2) are provided in Table 2. In agreement with previous calculations, ^[6b] all studied reactions occur in a concerted asynchronous manner through the corresponding six‐membered transition state (see Figure S1 for the optimized transition state structures).

Table 2.

Electronic reaction barriers (ΔE ^≠), reaction energies (ΔE _rxn) (in kcal mol⁻¹), and HOMO_CP–LUMO_HB‐A energy gaps (Δϵ _H–L) (in eV) for the uncatalyzed and hydrogen bond donor‐catalyzed Diels–Alder reaction between cyclopentadiene and acrolein.

HB‐A	Cycloadduct	ΔE ≠[a]	ΔE ≠[b]	ΔE rxn [a]	Δϵ H–L [a]
A	endo	13.1	14.3	−25.3	−6.6
	exo	13.6	14.8	−25.1	−6.6
U‐A	endo	9.3	11.1	−25.8	−5.9
	exo	8.9	10.4	−25.5	−5.9
TU‐A	endo	8.2	9.5	−25.9	−5.7
	exo	8.3	10.0	−25.5	−5.7
UPh‐A	endo	8.4	8.2	−27.4	−5.6
	exo	6.4	6.4	−29.0	−5.6
TUPh‐A	endo	7.5	8.9	−27.0	−5.8
	exo	6.4	8.0	−28.2	−5.8
UF‐A	endo	7.2	7.2	−27.0	−5.3
	exo	6.7	6.0	−26.8	−5.3
TUF‐A	endo	7.0	7.8	−26.9	−5.3
	exo	6.2	7.0	−27.2	−5.3

[a] Computed at the ZORA‐M06‐2X/TZ2P//M06‐2X/def2‐SVPP level. [b] Computed at the DLPNO‐CCSD(T)/def2‐QZVPP//M06‐2X/def2‐SVPP level.

According to the computed ZORA‐M06‐2X/TZ2P//M06‐2X/def2‐SVPP barrier energies, which agree well with the more accurate DLPNO‐CCSD(T)/def2‐QZVPP//M06‐2X/def2‐SVPP values, three distinct trends can be observed. In the first place, we, surprisingly, found that the endo selectivity of the widely studied uncatalyzed DA reaction between CP and A changes to exo selectivity when this reaction is catalyzed by a HB. The reaction barriers of the exo HB‐catalyzed DA reaction pathways are 0.4 to 2.1 kcal mol⁻¹ lower in energy than the corresponding endo pathways. There is, however, one exception, namely, the Diels–Alder reaction between CP and TU‐A, where the exo and endo reaction barriers are nearly identical. Secondly, the Diels–Alder reactions catalyzed by thiourea‐based HBs proceed with a lower reaction barrier than those promoted by their urea‐based analogues, which confirms the superior catalytic activity of thioureas. Their reaction energies are, on the other hand, nearly identical. Thirdly, introducing a HB catalyst significantly accelerated the DA lowering the reaction barrier 4–7 kcal mol⁻¹. This rate enhancement becomes more significant when the hydrogen atom of the parent (thio)urea (U‐A, TU‐A) is replaced by a phenyl group (UPh‐A, TUPh‐A) and even more pronounced, when the aryl groups bear the strong electron‐withdrawing CF₃ groups (UF‐A, TUF‐A), which, as commented above, follows the same trend as the computed ΔE _int of the HB‐A complexes and is consistent with the experimental findings. ^[6a] Furthermore, there is a modest linear correlation (R² = 0.88 for endo; R² = 0.83 for exo) between the computed reaction barriers (ΔE ^≠) and the corresponding HOMO_CP–LUMO_HB‐A orbital energy gaps (Δϵ _H–L, see Figure S2). This suggests that the reduced reaction barrier, upon coordination of a catalyzing HB to A, might be related to the lowering of the LUMO_HB‐A. We will show later that, similar to our previous study on Lewis acid‐catalyzed Diels–Alder reactions, ^[8] this is not the case for these hydrogen bond donor‐catalyzed Diels–Alder reactions.

endo/exo Stereoselectivity

Before exploring the factors controlling the rate enhancement induced by the organocatalysts, we first aim to understand why coordinating a HB to A significantly alters the endo/exo selectivity by applying the activation strain model (ASM) of reactivity. ^[11] This method decomposes the electronic energy (ΔE) into two terms: the strain (ΔE _strain) that results from the distortion of the individual reactants and the interaction (ΔE _int) between the deformed reactants along the reaction coordinate, defined in this case as the IRC projection onto the shorter newly forming C_CP⋅⋅⋅C_β bond. ^[28] To this end, we have analyzed the endo/exo selectivity of the process involving UPh‐A, which has the largest, and hence clearest, difference between the endo and exo reaction barriers (see Figure 2). Note that the activation strain diagrams (ASD) of all other reactions can be found in the Supporting Information (Figures S3–S6). The exo selectivity of the CP+UPh‐A cycloaddition is the result of both a less destabilizing activation strain and a more stabilizing interaction energy (Figure 2 a). Surprisingly, the stronger interaction energy computed for the exo pathway is not dictated by the electrostatic interaction (which still favors endo, just as in the case of the uncatalyzed reaction which does go via endo; see Figure S3) but by the reduction in the steric (Pauli) repulsion (Figure 2 b). The less destabilizing strain energy for the exo pathway can be ascribed to the larger degree of asynchronicity compared to endo (exo: Δr ^TS _C⋅⋅⋅C = 0.40 Å, endo: Δr ^TS _C⋅⋅⋅C = 0.35 Å, where Δr^TS _C⋅⋅⋅C is the difference between the newly forming C⋅⋅⋅C bond lengths in the TS), which leads to a lower degree of deformation of the reactants since the C_CP⋅⋅⋅C_β bond forms ahead of the C_CP⋅⋅⋅C_α bond (see Figure S1).

Figure 2.

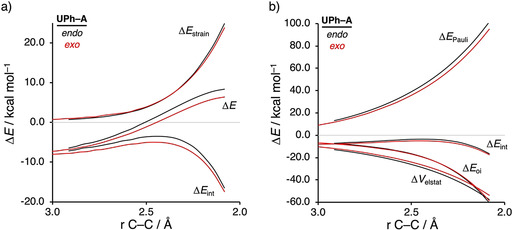
a) Activation strain analyses and b) energy decomposition analyses of the catalyzed endo (black lines) and exo (red lines) Diels–Alder reactions between CP and UPh‐A complex, where the energy values are projected onto the shorter newly forming C_CP⋅⋅⋅C_β bond between CP and the UPh‐A, computed at the ZORA‐M06‐2X/TZ2P//M06‐2X/def2‐SVPP level.

The origin of the less destabilizing Pauli repulsion for the exo Diels–Alder reaction pathway between CP and UPh‐A complex was further investigated by performing a Kohn–Sham molecular orbital (KS‐MO) analysis.[ ^12b , ²⁹ ] The occupied molecular orbitals of CP and UPh‐A, following both the endo and exo pathways, were quantified at the transition state geometries where the C_CP⋅⋅⋅C_β bond length between CP and the UPh‐A is 2.08 Å (Figure 3 a). The most important occupied MO of UPh‐A involved in the two‐center four‐electron interaction, which determines the underlying differences in Pauli repulsion between the endo and exo pathway, is the HOMO−6. This particular orbital corresponds to the π‐molecular orbital located on the reactive C=C double bond of A. The contributing occupied orbital of CP is the HOMO−6 where all 2p_π AOs and the σ_C‐H (pseudo‐π), located on the reacting C=C double bonds and the methylene bridge, respectively, are in‐phase. Along the exo pathway, the orbital overlap between HOMO−6_CP and HOMO−6_UPh‐A is smaller (S = 0.13) and, therefore, less destabilizing than along the endo pathway (S = 0.15) (see Figure S7 for the evolution of the orbital overlap along the reaction coordinate). This difference in orbital overlap is a direct consequence of the previously discussed different degrees in asynchronicity, which is, as we have previously shown in our analysis of iminium‐catalyzed Diels Alder reactions, ^[9] induced by their difference in MO coefficients of the 2p_z atomic orbital on the α‐carbon of the dienophile. The larger this MO coefficients, the larger the degree of asynchronicity. As shown in Figure 3 b, for the endo pathway the MO coefficient on the α‐carbon is 0.51, while for the exo pathway it is 0.53, resulting in a more destabilizing closed‐shell repulsion at the α‐carbon side for the latter. This effect gets compensated by the elongation of the C_CP⋅⋅⋅C_α bond distance along the exo pathway, making this reaction more asynchronous. As a result, along the more asynchronous exo pathway, the reactants have less orbital overlap at the α‐carbon of the dienophile due to a longer the C_CP⋅⋅⋅C_α bond length, manifesting in less destabilizing Pauli repulsion and a lower reaction barrier compared to the endo pathway.

Figure 3.

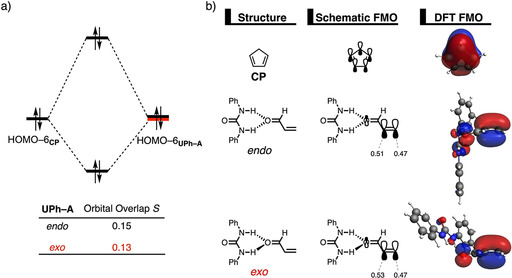
a) Molecular orbital diagram and the most significant occupied orbital overlaps of the endo and exo Diels–Alder reactions between CP and UPh‐A and b) key occupied orbitals (isovalue = 0.03 au), where the MO coefficients of the carbon 2p_z atomic orbitals, contributing to the occupied orbitals of the UPh‐A, are shown. Computed at the transition state geometries where the C_CP⋅⋅⋅C_β bond length between CP and the UPh‐A is 2.08 Å at the ZORA‐M06‐2X/TZ2P//M06‐2X/def2‐SVPP level.

One might expect that CP, along the endo pathway, also has a larger steric (Pauli) repulsion with the HB catalyst. In order to test this hypothesis, we performed a numerical experiment in which we evaluate the interaction between CP and UPh in the position they obtain in the transition state geometries used for the analysis in Figure 3 (Table S1). Surprisingly, we found a more favorable C−H⋅⋅⋅π interaction between CP and the phenyl group of UPh for the exo than for the endo pathway (ΔE _int ^endo = −2.7 kcal mol⁻¹; ΔE _int ^exo = −3.3 kcal mol⁻¹). As a result of this stronger interaction along the exo pathway, the CP and UPh distance is shorter which, as expected, also goes with a more destabilizing Pauli repulsion compared to the endo pathway (ΔE _Pauli ^endo = 1.3 kcal mol⁻¹; ΔE _Pauli ^exo = 2.1 kcal mol⁻¹). Note that this enhanced interaction for the exo pathway between CP and HB has also been observed for the other HBs, with an exception for U and TUF for which the interaction is equal or is slightly stronger along the endo pathway. Thus, these findings indicate that besides having less Pauli repulsion between CP and HB‐A along the exo pathway, the more favorable interaction between the CP and HB also induce an exo selective preference for this reaction. ^[30]

Transitioning from urea‐ to thiourea‐based hydrogen bond donor catalysts

Next, we want to establish why thiourea‐based HBs accelerate the Diels–Alder reaction between CP and A to a larger extent than urea‐based HBs. Figure 4 shows the activation strain diagrams (ASDs) from the reactants to the transition states for the exo Diels–Alder reaction between CP and A catalyzed by the parent urea (U) and thiourea (TU) HBs. The Diels–Alder reaction following the endo pathway, as well as the reactions catalyzed with the larger UPh‐A and TUPh‐A HBs show the same, albeit less pronounced, features (see Figures S8–S10). The enhanced reactivity of the Diels–Alder reaction involving TU‐A originates from both a less destabilizing strain energy (in the transition state region) and a more stabilizing interaction energy compared to the analogous process involving U‐A (Figure 4 a). The difference in strain energy can again be ascribed to the different degrees of asynchronicity of these reactions, which is the largest for TU‐A (U‐A: Δr ^TS _C⋅⋅⋅C = 0.34 Å, TU‐A: Δr ^TS _C⋅⋅⋅C = 0.41 Å), leading to less deformation of the reactants up until the transition state. The more stabilizing interaction energy computed for the TU‐A+CP cycloaddition is, according to the EDA (Figure 4 b), exclusively originating from a less destabilizing Pauli repulsion. The electrostatic and orbital interactions, on the contrary, are less stabilizing for TU‐A compared to U‐A.

Figure 4.

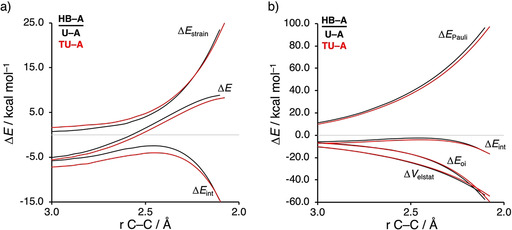
a) Activation strain analyses and b) energy decomposition analyses of the exo Diels–Alder reactions between CP and U‐A (black lines) and TU‐A (red lines), where the energy values are projected onto the shorter newly forming C_CP⋅⋅⋅C_β bond between CP and HB‐A, computed at the ZORA‐M06‐2X/TZ2P//M06‐2X/def2‐SVPP level.

The less destabilizing Pauli repulsion for the reaction involving TU‐A derives from a reduced occupied–occupied orbital overlap with the incoming CP. The occupied molecular orbitals of CP and the U‐A and TU‐A complexes were quantified at consistent geometries with a C_CP⋅⋅⋅C_β bond length between CP and HB‐A of 2.10 Å (Figure 5 a). ^[31] Analysis at a consistent geometry, instead of at the transition state, is advised when the transition states occur at different points on the reaction coordinate. A single‐point analysis on the transition state geometries result in skewed conclusions since the position of the transition state (i.e., early‐ or late‐transition state) has a significant impact on the magnitude of the energy terms. ^[11a] The occupied π‐MO of HB‐A contributing most to the trend in two‐center four‐electron (Pauli) repulsion, is the HOMO−3 of both U‐A and TU‐A, which corresponds to the π‐molecular orbital predominantly located on the reactive C=C double bond of A. Furthermore, CP has two π‐MOs that are contributing to the built‐up of Pauli repulsion, namely the HOMO−1 and HOMO−6 where, for the former, the 2p_π AOs on the reacting C=C double bonds and the σ_C‐H (pseudo‐π) on the methylene bridge are out‐of‐phase whereas, for the latter, they are in‐phase. The computed HOMO–HOMO overlaps decrease from ⟨HOMO−1_CP|HOMO−3_U‐A⟩ = 0.10 and ⟨HOMO−6_CP|HOMO−3_U‐A⟩ = 0.12 for U‐A to ⟨HOMO−1_CP|HOMO−3_TU‐A⟩ = 0.09 and ⟨HOMO−6_CP|HOMO−3_TU‐A⟩ = 0.11 for TU‐A. The differences in orbital overlap between U‐A and TU‐A can be attributed to two different phenomena: (i) the thiourea‐based HB of TU‐A is, due to its more acidic nature and, therefore, lower‐lying LUMO, ^[25] able to better polarize the π‐MO of the dienophile away from the reactive C=C double bond of A than U‐A, and (ii) the DA reaction involving TU‐A is more asynchronous than the analogous reaction with U‐A. The stronger donor–acceptor interaction between the two σ*_N‐H orbitals of the hydrogen bond donor catalyst TU and the oxygen lone pair of A (see Table 1) results in a charge transfer from A to TU which is manifested in a smaller orbital amplitude on the C=C double bond of A (see MO coefficients in Figure 5 b), compared to the interaction between U and A. We expect, based on the surmounting evidence provided by our recent work,[ ⁸ , ⁹ , ¹⁰ ] that the stronger the (Lewis) acid, the greater the catalysis will be. This is due to the relationship between the strength of the (Lewis) acid and the polarization of the orbital density away from the reactive center, which accelerates the reaction via a reduction of activation strain and steric repulsion. Furthermore, in analogy with the analysis of the exo preference of UPh‐A, the larger degree of asynchronicity for TU‐A also contributes to the reduction of destabilizing orbital overlap between the reactants.

Figure 5.

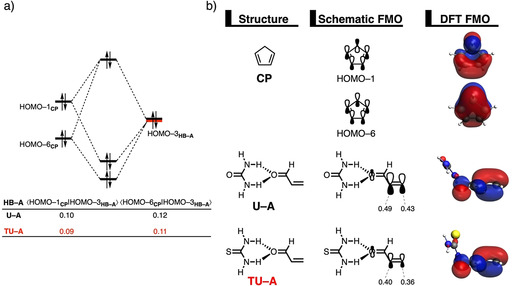
a) Molecular orbital diagram and the most significant occupied orbital overlaps of the exo Diels–Alder reactions between CP and dienophiles U‐A and TU‐A and b) key occupied orbitals (isovalue = 0.03 au), where the MO coefficients of the carbon 2p_z atomic orbitals, contributing to the occupied orbitals of HB‐A are shown. Computed at consistent geometries with a C_CP⋅⋅⋅C_β bond length between CP and HB‐A of 2.10 Å at the ZORA‐M06‐2X/TZ2P//M06‐2X/def2‐SVPP level.

Catalytic effect of hydrogen bond donor catalysts

Lastly, we examined the actual catalytic effect of the HBs, in other words, why do HBs accelerate the Diels–Alder reaction and why does this effect become more pronounced when the hydrogen atom of the parent (thio)ureas (U/TU) are replaced by aryl groups. To this end, we have analyzed and compared the uncatalyzed exo DA reaction with the HB‐catalyzed U‐A and UPh‐A DA reactions (see Figure 6). The accelerated reactivity, i.e., lower reaction barrier, for the HB‐catalyzed compared to the uncatalyzed DA reactions originates from both a less destabilizing strain energy and, to a greater extent, a more stabilizing interaction energy between the deformed reactants along the entire reaction coordinate (Figure 6 a). The endo reaction pathway as well as the series catalyzed by thiourea‐based HBs, i.e., A, TU‐A, TUPh‐A, exhibit identical reactivity trends and are provided in the Supporting Information (Figures S11–S13).

Figure 6.

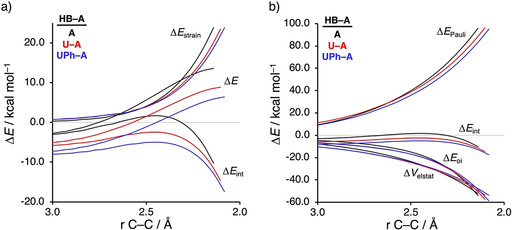
a) Activation strain analyses and b) energy decomposition analyses of the exo Diels–Alder reactions between CP and A (black lines), U‐A (red lines), and UPh‐A (blue lines), where the energy values are projected onto the shorter newly forming C_CP⋅⋅⋅C_β bond between CP and HB‐A, computed at the ZORA‐M06‐2X/TZ2P//M06‐2X/def2‐SVPP level.

The difference in strain energy can again be explained by looking at the degree of asynchronicity, which is the largest for UPh‐A (A: Δr ^TS _C⋅⋅⋅C = 0.21 Å, U‐A: Δr ^TS _C⋅⋅⋅C = 0.34 Å, UPh‐A: Δr ^TS _C⋅⋅⋅C = 0.40 Å). The higher degree of asynchronicity of UPh‐A leads to a lower degree of deformation of the reactants since the C_CP⋅⋅⋅C_α bond forms behind of the C_CP⋅⋅⋅C_β bond (see Figure S1). As previously discussed, the differences in degrees of asynchronicity are originating from the asymmetry of the π‐MO located on the reactive C=C double bond of the dienophile, which is induced by the coordination of the HB catalyst (Figure S14). The stronger the HB catalyst coordinates to A, the more significant asymmetry in the π‐MO and hence the asynchronicity of the DA reaction becomes. ^[9] To understand why the interaction energy becomes increasingly more stabilizing from A to U‐A to UPh‐A, we applied the energy decomposition analysis (EDA) (Figure 6 b). Interestingly, we find that the decrease in destabilizing ΔE _Pauli is the actor behind the more stabilizing ΔE _int when going from A to U‐A and to UPh‐A. In contrast, the ΔV _elstat and ΔE _oi terms are more stabilizing for the uncatalyzed DA reaction, because both terms are weakened by the donor–acceptor interaction between HB and A. This donor–acceptor (i.e., charge transfer) interaction results in less negative charge on the reactive C=C double bond and, therefore, a less stabilizing ΔV _elstat for the HB‐catalyzed reactions and, as we will discuss later, it also leads to a significant reduction in inverse electron demand orbital interaction (i.e. ΔE _oi). This finding confirms our initial hypothesis that, similar to Lewis acid or iminium catalysis,[ ⁸ , ⁹ ] the Pauli‐repulsion lowering rather than the LUMO lowering is the actual mechanism behind the bifunctional hydrogen bond donor catalysis in Diels–Alder reactions.

We used once again a Kohn–Sham molecular orbital (KS‐MO) analysis to rationalize why the Pauli repulsion becomes steadily less destabilizing when going from an uncatalyzed to a hydrogen bond donor‐catalyzed Diels–Alder reaction (Figure 7). The occupied molecular orbitals of CP and A, U‐A, and UPh‐A were quantified at consistent geometries with a C_CP⋅⋅⋅C_β bond length between CP and HB‐A of 2.14 Å (Figure 7 a). ^[31] The most important occupied π‐MO of the dienophile that are decisive for the trend in Pauli repulsion are the HOMO−1, HOMO−4, and HOMO−8 of A, U‐A, and UPh‐A, respectively, which are, in all cases, predominantly located on the reactive C=C double bond of A. The occupied orbital of CP involved in this interaction is the HOMO−6, where all 2p_π AOs and the σ_C‐H (pseudo‐π), located on the methylene bridge, are in‐phase. The orbital overlap between the occupied orbitals decreases from S = 0.16 for the uncatalyzed DA reaction to S = 0.10 and S = 0.07 for the reactions involving U‐A and UPh‐A, respectively (Figure 7 a). Coordination of a HB to A significantly polarizes the π‐orbital located on the C=C double bond of A towards the HB and away from the incoming CP, leading to a decreased occupied–occupied orbital overlap. The previously discussed donor–acceptor interaction between the two hydrogen bond donors of the HB and the hydrogen bond acceptor of A causes a charge transfer from A to the HB which results in less π‐orbital amplitude on the C=C double bond of A that points in the direction of the approaching CP. The replacement of the hydrogen atom of the parent urea U by a phenyl group in UPh notably increases the extent of charge transfer (from ΔE _oi = −3.2 kcal mol⁻¹ for U‐A to ΔE _oi = −4.7 kcal mol⁻¹ for UPh‐A; see Table 1) and, hence manifests in a progressively smaller π‐orbital amplitude on the C=C double bond and more orbital density on the HBs. This can clearly be seen when comparing the spatial distribution of the involved occupied orbitals in Figure 7 b. In addition, the larger degree of asynchronicity of the HB‐catalyzed DA reactions, which arises from a larger asymmetry in the π‐MO_HB‐A located on the reactive C=C double bond of the dienophile (vide supra), also plays a role in reducing the occupied–occupied orbital overlap between the reactants. As discussed above, a more asynchronous reaction has less orbital overlap at the α‐carbon of HB‐A, which, in turn, leads to less Pauli repulsion between the reactants and a lowering of the reaction barrier.

Figure 7.

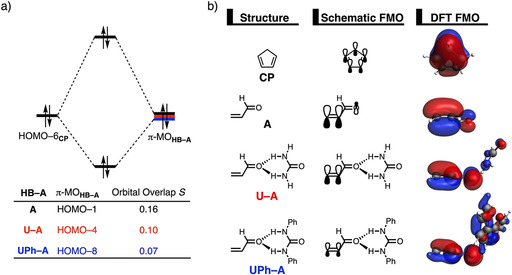
a) Molecular orbital diagram and the most significant occupied orbital overlaps of the exo Diels–Alder reactions between CP and A, U‐A, and UPh‐A and b) key occupied orbitals (isovalue = 0.03 au), computed at consistent geometries with a C_CP⋅⋅⋅C_β bond length between CP and HB‐A of 2.14 Å at the ZORA‐M06‐2X/TZ2P//M06‐2X/def2‐SVPP level.

Finally, we address why the orbital interactions for the uncatalyzed DA reaction are more stabilizing than for the HB‐catalyzed counterpart despite the latter benefits from a smaller HOMO_CP–LUMO_HB‐A gap (see Table 2). To this end, we applied the NOCV (natural orbitals for chemical valence) ^[32] extension of the EDA method for the extreme situations represented by the uncatalyzed and UPh‐catalyzed Diels–Alder reactions. This approach identifies two main molecular orbital interactions that dominate the total orbital interactions, namely, the normal electron demand (NED) HOMO_CP → LUMO_HB‐A and the inverse electron demand (IED) LUMO_CP ← HOMO_HB‐A interactions (ρ ₁ and ρ ₂, respectively; see Figure 8 a and b). As expected for a NED Diels–Alder reaction, the former interaction is much stronger than the latter in both instances (ΔE(ρ ₁) > ΔE(ρ ₂)). Interestingly, whereas the NED interaction is only slightly stronger for the UPh‐catalyzed reaction (ΔΔE(ρ ₁) = 0.8 kcal mol⁻¹), the corresponding IED interaction is significantly weaker compared to the uncatalyzed reaction (ΔΔE(ρ ₂) = −5.8 kcal mol⁻¹). As a result, the total orbital interactions are, for the hydrogen bond donor‐catalyzed Diels–Alder reaction, less stabilizing than the uncatalyzed analogue. The mechanism behind these EDA‐NOCV results can be established by performing a Kohn–Sham molecular orbital analysis.[ ^12b , ²⁸ ] In line with the original rationale behind hydrogen bond donor catalysis, ^[6] the HB catalyst decreases the NED HOMO_CP–LUMO_HB‐A orbital energy gap from 5.8 eV for the uncatalyzed to 5.0 eV for the UPh‐catalyzed reaction (Figure 8 c). This reduction in orbital energy gap is large enough to overcome the slight decrease of orbital overlap, as a result of a more asynchronous reaction mode, and, therefore, coordination of a HB leads to a stronger HOMO_CP–LUMO_HB‐A NED interaction. The IED interaction, however, is also modulated by the coordination of a HB. More specifically, the HB stabilizes all molecular orbital of HB‐A and hence also the HOMO_HB‐A, manifesting in an IED orbital energy gap that increases from 9.2 eV for the uncatalyzed to 10.0 eV for the UPh‐catalyzed reaction (Figure 8 d). This, together with a reduced orbital overlap, results in a weaker IED interaction for the HB‐catalyzed compared to the uncatalyzed DA reaction. The weakening of the IED interaction effectively overrules the more stabilizing NED interaction and, for that reason, the total orbital interaction of UPh‐catalyzed DA reaction are less stabilizing than for the uncatalyzed DA reaction.

Figure 8.

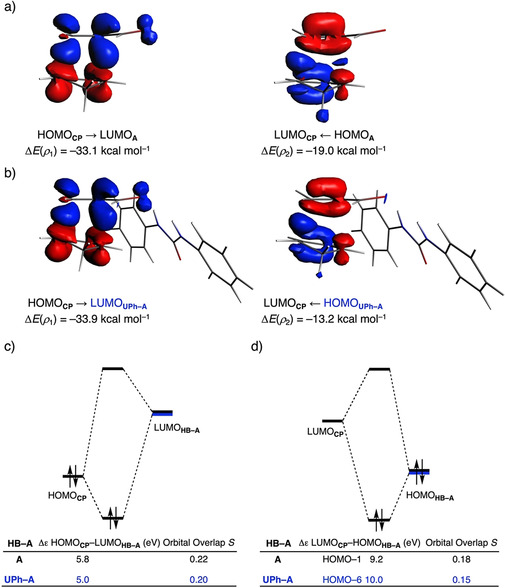
NOCV deformation densities Δρ (isovalue = 0.0015 au) and associated energies ΔE(ρ) for the normal electron demand (NED), HOMO_CP → LUMO_HB‐A, and inverse electron demand (IED), LUMO_CP ← π‐HOMO_HB‐A, where the color flow is red → blue, for the a) A, b) UPh; the Kohn–Sham molecular orbital analysis for the c) NED, and d) IED. All data computed, at consistent geometries with a C_CP⋅⋅⋅C_β bond length between CP and HB‐A of 2.14 Å, at the ZORA‐M06‐2X/TZ2P//M06‐2X/def2‐SVPP level.

Conclusions

Our theoretical study reveals that urea‐ and thiourea‐derived bifunctional hydrogen bond donating (HB) organocatalysts accelerate the Diels–Alder (DA) reaction between cyclopentadiene (CP) and acrolein (A) by coordinating to the carbonyl group of the dienophile through a double hydrogen bond and effectively lowering the reaction barrier up to 7 kcal mol⁻¹. This catalytic effect is stronger for thiourea‐based HBs compared to their urea‐based counterparts. In addition, the endo selective uncatalyzed cycloaddition reaction becomes exo selective upon coordination of the HBs.

Our activation strain and Kohn–Sham molecular orbital analyses identified that the exo selective preference for the HB‐catalyzed DA reaction originates from both a larger degree of asynchronicity, which is induced by a more asymmetric π‐MO on the reactive C=C double bond of the dienophile, as well as a stronger C−H⋅⋅⋅π interaction between CP and HB along the exo pathway. This larger asynchronicity in the new C⋅⋅⋅C bond formation between the reactants along the exo pathway leads to two stabilizing and thus barrier lowering phenomena: (i) reduced occupied–occupied orbital overlap and hence more stabilizing interaction between the CP and HB‐A; and (ii) less destabilizing activation strain, as one newly forming C⋅⋅⋅C bond forms later than the other resulting in less pressure to deform the individual reactants.

The rate enhancement provoked by the HBs is exclusively caused by a diminished two‐center four‐electron Pauli repulsion between the occupied π‐orbitals of CP and HB‐A reactants. The reason for the reduced Pauli repulsion is the donor–acceptor interaction between the HB and A, which significantly polarizes the π‐orbital away from the reactive C=C double bond of A, resulting in less occupied–occupied orbital overlap with the incoming CP. Strikingly and in sharp contrast to the widely‐accepted rationale, we observed that, in the HB‐catalyzed DA reaction, the orbital interactions become less stabilizing compared to the uncatalyzed reaction. This is mainly due to a remarkable weakening of the inverse electron demand interaction, LUMO_CP ← π‐HOMO_HB‐A, induced by the binding of the organocatalyst to the dienophile. Therefore, the results shown here demonstrate that the concept of Pauli‐repulsion lowering catalysis is a general phenomenon which is not only limited to conventional Lewis acid and iminium catalysis.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

P. Vermeeren, T. A. Hamlin, F. M. Bickelhaupt, I. Fernández, Chem. Eur. J. 2021, 27, 5180.