A new extension of state-space SIR model to account for Underreporting – An application to the COVID-19 transmission in California and Florida

Abstract

In the absence of sufficient testing capacity for COVID-19, a substantial number of infecteds are expected to remain undetected. Since the undetected cases are not quarantined, they can be expected to transmit the infection at a much higher rate than their quarantined counterparts. That is, in the absence of extensive random testing, the actual prevalence and incidence of the SARS-CoV-2 infection can be significantly higher than that being reported. Thus, it is imperative that the information on the percentage of undetected (or unreported) cases be incorporated in the mechanism for estimating the key epidemiological parameters, like rate of transmission, rate of recovery, reproduction rate, etc., and hence, for forecasting the transmission dynamics of the epidemic.

In this paper, we have developed a new dynamic version of the basic susceptible-infected-removed (SIR) compartmental model, called the susceptible-infected (quarantined/ free) - recovered- deceased [SI(Q/F)RD] model, to assimilate the impact of the time-varying proportion of undetected cases on the transmission dynamics of the epidemic. Further, we have presented a Dirichlet-Beta state-space formulation of the SI(Q/F)RD model for the estimation of its parameters using posterior realizations from the Gibbs sampling procedure.

As a demonstration, the proposed methodology has been implemented to forecast the COVID-19 transmission in California and Florida. Results suggest significant amount of underreporting of cases in both states. Further, posterior estimates obtained from the state-space SI(Q/F)RD model show that average reproduction numbers associated with the undetected infectives [California: 1.464; Florida: 1.612] are substantially higher than those associated with the quarantined infectives [California: 0.497; Florida: 0.359]. The long-term forecasts of death counts show trends similar to those of the estimates of excess deaths for the comparison period post training data timeline.

Introduction

As per the scientific brief of the World Health Organization (WHO) published on its website on 9 July 2020, transmission of SARS-CoV-2 occurs primarily between people through direct, indirect, or close contact with infected people through infected secretions such as saliva and respiratory secretions, or through their respiratory droplets, which are expelled when an infected person coughs, sneezes, talks or sings; refer to [1]. That is, in order to break the chains of transmissions of SARS-CoV-2, the objective of the preventive measures should be to minimize the contact of susceptibles with infected people. The first step towards this goal is to identify the infecteds so that they can be kept in quarantine till they are no longer infectious. However, high variability in the level and the nature of symptoms in infecteds, coupled with a significant length of incubation period, poses a difficult challenge to frame a targeted testing strategy which can serve the purpose effectively. In the presence of high proportion of asymptomatic cases, limiting testing to only symptomatic individuals will fail to serve the objective of detecting and quarantining all infecteds. Situation becomes more challenging as even asymptomatic cases are capable of transmitting infection [2], [3]. Although contact tracing can help in identifying the chains of transmission linked to detected cases, presence of a high proportion of asymptomatic cases flags concerns about the reliability of the strategy. So, apart from testing symptomatic individuals (mild or severe), and identifying and testing high risk individuals having history of contact with infected people, the situation demands aggressive random testing to isolate even the asymptomatic cases from the population. In the absence of adequate amount of random testing, a significant number of infecteds, especially asymptomatic individuals, may remain undetected (i.e., number of cases will remain significantly underreported). Since the undetected cases are not quarantined, they are expected to remain infectious in the population for a relatively much longer period as compared to those who are detected and quarantined. Lack of any visible symptom in the undetected cases increases the likelihood of susceptibles spending prolonged period in their proximity. Thus, the undetected cases can exhibit a strikingly higher reproduction rate as compared to that of their quarantined counterparts.

Despite repeated appeals and advisories to all countries from the WHO to employ extensive random testing, only few countries have shown intentions to conduct adequate number of COVID-19 tests [4]. Rate of positive tests at a place can give an indication about the adequacy, or inadequacy, of the number of tests being carried out in the region. New Zealand has set an extraordinary example in quickly containing the epidemic by efficiently adhering to the strategy of aggressive testing and isolation of infecteds to break the chains of infection. As on 25 August 2020, New Zealand had reported a total of 1690 confirmed cases of which 1539 had recovered, 129 were active and 22 had died. These are very encouraging figures, especially when compared with those of the countries like USA, Brazil, UK, India, Russia, and many others. Till 19 August 2020, the overall percentage of positive tests in New Zealand was reported to be 0.23% [5]. While in the USA, the percentage of positive tests has remained quite high since the beginning, with the overall positive percentage staring at 9%. Also, there is a lot of variation between the percentages of positive tests reported by different states in the United States- which varies between 0.53% (Vermont) to 100% (Washington) as reported on 26 August 2020 by the Johns Hopkins University [6]. As per the recommendation of the WHO, the rates of positivity in testing should remain at 5% or lower for at least 14 days at a stretch before governments decide about relaxing the containment/ lockdown measures. This advisory from the WHO is based on the rationale that very high positive rates may indicate that people with only severe symptoms are getting tested and all the asymptomatic cases, or cases with mild symptoms, are being left out. That is, a high rate of positivity may imply that the testing capacity of the state/country is insufficient to gauge the actual size of the outbreak, leading to a significant proportion of cases being unreported.

Underreporting of cases in the USA has been confirmed and reported by some published scientific studies. Wu et al. [7] have used a semi-Bayesian probabilistic bias analysis to account for incomplete testing and imperfect diagnostic accuracy. As per their estimate, there were 6,454,951 true cumulative infections compared to 721,245 confirmed cases (reported) as of 18 April 2020 in the United States. The actual number of infections was reported to be 3 to 20 times higher than the confirmed cases for different states. Lau et al. [8] used a simple intuitive method based on crude case fatality risk and adjusted case fatality risk to evaluate extent of underreporting in various COVID-19 epicentres across the world. Their study was based on early-stage data of COVID-19 and they reported severe underreporting of cases in most of the countries worldwide. For the USA, they found the estimate of actual number of infections to be around 53.8 times the reported number of confirmed cases. This extraordinarily high estimate of underreporting can be explained by the fact that their study was based on the data reported till 17 March 2020. In general, underreporting is expected to be high at the initial stage of any epidemic owing to the lack of proper system at place, and the lack of knowledge and awareness about the infection. Based on their findings, Lau et al. [8] suggested that due to limited testing capacities, mortality numbers may serve as a better indicator for COVID-19 case spread in many countries.

Accurate forecasts of the size and the progression of an epidemic would be imperative for policy makers to effectively strategize allocation of resources, implementation of interventions, and promotion of awareness among the public. However, reliable forecasting of true incidences of infections and deaths due to an epidemic becomes an arduous challenge in the presence of high percentage of undetected cases. Methodologies to estimate the true burden of an epidemic in the observed period, i.e., to estimate the level of underreporting in the observed period, exist in the literature. However, there is a dearth of research for developing models to forecast the true trajectory of an epidemic by dynamically adjusting for underreporting of cases. For example, as discussed earlier, Wu et al. and Lau et al. [7], [8] have assessed the extent of underreporting till a fixed past date, but have not presented any methodology to forecast the true number of cases in the presence of progressively changing rates of underreporting. The primary objective of this paper is to construct a robust statistical compartmental epidemic model which can forecast the true incidences of infections and deaths due to an epidemic even in the presence of time-varying proportion of undetected (or unreported) cases. The popular compartmental epidemic models used widely for forecasting number of infections and deaths, like the susceptible-infected-removed (SIR) model, the susceptible-exposed-infected-removed (SEIR) model, and their extensions, do not incorporate the impact of undetected cases on the epidemiological parameters. In this paper, we have developed a comprehensive methodology to estimate the true parameters of an epidemic and forecast its transmission dynamics in the presence of time-varying proportion of unreported cases. A new compartmentalised epidemic model, called the susceptible-infected (quarantined/ free) - recovered- deceased [SI(Q/F)RD] model, has been developed to assimilate the effects of undetected cases on the transmission dynamics of an epidemic. Further, the deterministic SI(Q/F)RD model has been adopted in a Dirichlet-Beta state-space (Bayesian hierarchical) formulation to induce stochastic uncertainties in the computations. The Bayesian hierarchical formulation has been implemented in JAGS through the R package ‘R2Jags’ to obtain posterior estimates of the unknown parameters.

To demonstrate the implementation of the methodology, we have considered the cases of two of the worst COVID-19 affected states of the USA, California, and Florida, which have very high percentages of positive tests. Since the level of testing, and protocols/ procedure of reporting of number of deaths may vary between different state jurisdictions, the level of underreporting of deaths and cases can also be expected to vary between states. This is the reason that we have performed state-wise analyses rather than analysing the combined data of USA. We have assumed that the presence of undetected cases because of insufficient testing is the sole (or at least the major) reason behind the underreporting of cases. It should be noted that the underreporting of cases can occur because of various other reasons also, like poor communication between the government administration and health centres, conscious data manipulation to conceal administrative failures, anomalies in protocols for declaring epidemic related deaths, lack of proper digital infrastructure to keep reliable records, to name a few. However, our assumption practically holds true for a developed country like the USA, where other reasons like lack of proper communication or digital infrastructure can be conveniently crossed off.

Methodology

To realize the objective of our study, we propose the following methodological framework, which has been further implemented on the COVID-19 time-series data of California and Florida in the next section.

Method to estimate time-varying proportion of unreported infecteds- a prerequisite for the proposed model

True counts of daily number of infecteds can be estimated using a reliable estimate of case fatality rate (CFR). CFR based on population level data can be alarmingly misleading if the reported data on the number of cases is expected to suffer from underreporting. If we assume that the level (or proportion) of underreporting of deaths and infecteds are same, the CFR estimated from the reported data will be a reliable estimate of the true population CFR. However, this is rarely observed, and the proportions of underreporting of deaths and infecteds usually differ considerably. In such situations, an estimate of CFR based on an individual patient level (follow-up) data is deemed as most reliable [9]. So, a simple rule of thumb to know if the levels of underreporting of deaths and infecteds can be assumed to be the same is to compare the delayed CFR obtained from the reported data with the one obtained from the individual patient level data. If they vary significantly, we can infer that the levels of underreporting are different for the number of deaths and the number of infecteds. In such a situation, it is advisable to use the CFR obtained from the individual patient level data as the best estimate for the true CFR of the epidemic. Once a reliable estimate of the CFR is obtained, it can be used to calibrate daily data for the number of true infecteds using the estimated counts of true deaths and the average delay between infection and death. That is, if the average duration between infection (or detection/ reporting of infection) and death associated with COVID-19 is known to be, say, h days, and suppose that D_t number of people have died of the infection on a particular day t, then I^C_t-h+1 = (D_t/CFR) number of new cases are expected to be infected h days prior to day t.

If daily reported data on the number of recovered cases (R_t) is available, it can be inflated relative to the estimate of the proportion of underreporting of the daily case counts as follows.

$${q_t=1-p}_t=\frac{I_t^C-I_t}{I_t^C}$$ (1)

$$R_t^C={\mathit{R}}_{\mathit{t}}/p_{t-r+1}={\mathit{R}}_{\mathit{t}}/(1-q_{t-r+1})$$ (2)

where, $q_t$ is the proportion of unreported infecteds at time t, $p_t$ is the proportion of detected (reported) cases at time t, $I_t^C$ is the estimate of true value of new infecteds at time t, $I_t$ is the reported number of new infecteds at time t, $R_t^C$ is the estimate of true count of recovered cases at time t, ${\mathit{R}}_{\mathit{t}}$ is the reported number of recovered cases at time t and r is the average duration from infection to recovery of patients. If the daily number of recovered cases is not reported, or if it is not reliable, a viable calibration can be done using r and (1- CFR) as R^C_t-r+1 = $I_t^C$(1-CFR).

Compartmental structure of the proposed SI(Q/F)RD epidemic model

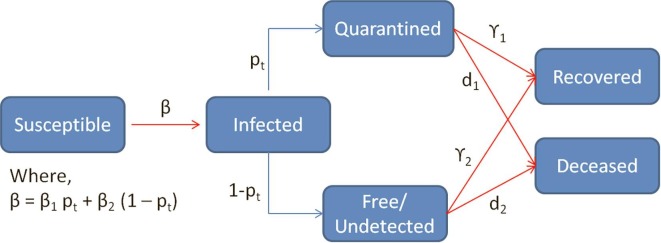
The SI(Q/F)RD compartmental epidemic model has been designed to incorporate the impact of undetected cases on the progression of the epidemic. That is, the overall compartment of infecteds is divided into two sub-compartments- ‘Detected and Quarantined’ and ‘Undetected and Free’- such that different transmission rates are associated with each sub-compartment. It is assumed that a proportion of the infecteds are detected (p) and quarantined (mostly symptomatic cases), while the rest of the infecteds (mostly asymptomatic cases) are undetected and roam freely among the susceptibles. Thus, the undetected cases can be expected to infect the susceptibles at a higher rate (β₂) than that of their quarantined counterparts (β₁). The proportion of detected cases, p, can vary with time if testing policy changes over the period of the epidemic, and can be taken as a function of time t, say, p_t. The overall compartmental structure of this model is presented in Fig. 1 . Since the quarantined infecteds consist mostly of symptomatic cases, quarantined infecteds can be expected to be at a higher risk of death on an average. Consequently, different death rates can be assumed for quarantined and undetected cases. Different recovery rates can also be assumed for quarantined and undetected cases if any scientific evidence supports such hypothesis. Otherwise, we can assume that both sub-groups of infecteds have equal average recovery rate.

Fig. 1.

SI(Q/F)RD model structure- p_t is the proportion of infecteds detected and quarantined, 1-p_t is the proportion of infecteds who are undetected and roaming freely among the susceptibles, β₁ is the transmission rate associated with quarantined infecteds and β₂ is the transmission rate associated with undetected infecteds, ϒ₁ and d₁ are the rate of recovery and the rate of death for quarantined cases and ϒ₂ and d₂ are the rate of recovery and the rate of death for undetected cases.

The set of differential equations quantifying the progressive transitions between different compartments shown in Fig. 1 can be expressed as follows.

$$\frac{d{\theta }_t^s}{\mathit{dt}}=-\left[{\beta }_1{\theta }_t^Q+{\beta }_2{\theta }_t^F\right]{\theta }_t^S$$ (3)

$$\frac{d{\theta }_t^I}{\mathit{dt}}=\left[{\beta }_1{\theta }_t^Q+{\beta }_2{\theta }_t^F\right]{\theta }_t^S-{\gamma }_1{\theta }_t^Q-{\gamma }_2{\theta }_t^F-d_1{\theta }_t^Q-d_2{\theta }_t^F$$ (4)

$$\frac{d{\theta }_t^R}{\mathit{dt}}={\gamma }_1{\theta }_t^Q+{\gamma }_2{\theta }_t^F=\gamma {\theta }_t^I(if{\gamma }_1={\gamma }_2=\gamma )$$ (5)

$$\frac{d{\theta }_t^D}{\mathit{dt}}=d_1{\theta }_t^Q+d_2{\theta }_t^F$$ (6)

$$\mathit{where},{\theta }_t^Q=p_t{\theta }_t^I,{\theta }_t^F=\left(1-p_t\right){\theta }_t^I,and{\theta }_t^S+{\theta }_t^I+{\theta }_t^R+{\theta }_t^D=1$$ (7)

Here, ${\theta }_t^S,{\theta }_t^I,{\theta }_t^Q,{\theta }_t^F,{\theta }_t^R,\mathrm{a}\mathrm{n}\mathrm{d}{\theta }_t^D$ are the true but unobserved (latent) prevalence of susceptibles, infecteds, infected & quarantined, infected & undetected (free), recovered, and deceased respectively. In other words, they are the probabilities of a person being in the respective compartments at time t. Also, let ${\mathit{\theta }}_t={\left({\theta }_t^S,{\theta }_t^I,{\theta }_t^R,{\theta }_t^D\right)}^T$ be the latent population prevalence.

Solution of this set of differential equations can be obtained using Runge-Kutta approximation. Let $f({\mathit{\theta }}_{t-1},\mathit{\beta },\mathit{\gamma },\mathit{d})$ denotes the solution of the set of differential equations for time t, where the function takes the values of the vectors ${\mathit{\theta }}_{t-1}$, $\mathit{\beta }={\left({\beta }_1,{\beta }_2\right)}^T$ , $\mathit{d}={\left(d_1,d_2\right)}^T$and $\mathit{\gamma }={\left({\gamma }_1,{\gamma }_2\right)}^T$ as the arguments. Then the fourth order Runge-Kutta approximation for the solution of these differential equations can be expressed as follows.

$$f\left({\mathit{\theta }}_{t-1},\mathit{\beta },\mathit{\gamma },\mathit{d}\right)=\left(\begin{array}{c}{\theta }_{t-1}^S+\frac{1}{6}\left[k_{t-1}^{S_1}+2k_{t-1}^{S_2}+2k_{t-1}^{S_3}+k_{t-1}^{S_4}\right]\\ {\theta }_{t-1}^I+\frac{1}{6}\left[k_{t-1}^{I_1}+2k_{t-1}^{I_2}+2k_{t-1}^{I_3}+k_{t-1}^{I_4}\right]\\ {\theta }_{t-1}^R+\frac{1}{6}\left[k_{t-1}^{R_1}+2k_{t-1}^{R_2}+2k_{t-1}^{R_3}+k_{t-1}^{R_4}\right]\\ {\theta }_{t-1}^D+\frac{1}{6}\left[k_{t-1}^{D_1}+2k_{t-1}^{D_2}+2k_{t-1}^{D_3}+k_{t-1}^{D_4}\right]\end{array}\right)$$ (8)

Complete expressions for calculating $k_t^{S_i},k_t^{I_i},k_t^{R_i},and{k}_t^{D_i}$are presented in Appendix A.

Dirichlet-Beta state-space formulation of the SI(Q/F)RD model

We have defined a flexible state-space probabilistic model based on the deterministic SI(Q/F)RD model structure to account for the uncertainties in the epidemiological parameters and the transmission dynamics of the epidemic. Osthus et al. [10] introduced a Dirichlet-Beta state-space model based on the basic SIR model. We have extended the Dirichlet-Beta state-space SIR model in conformity with the SI(Q/F)RD compartmental structure to estimate the transmission parameters, and forecast the progression of the epidemic. Let $Y_t^S,Y_t^I,Y_t^R,\mathrm{a}\mathrm{n}\mathrm{d}{Y}_t^D$ be the observed proportion of susceptibles, infecteds, recovered and deceased respectively. Then the Bayesian hierarchical state-space SI(Q/F)RD model can be defined as follows.

$$Y_t^I|{\mathit{\theta }}_{\mathit{t}},\tau ~Beta\left({\lambda }^I{\theta }_t^I,{\lambda }^I\left(1-{\theta }_t^I\right)\right)$$ (9)

$$Y_t^R|{\mathit{\theta }}_{\mathit{t}},\tau ~Beta\left({\lambda }^R{\theta }_t^R,{\lambda }^R\left(1-{\theta }_t^R\right)\right)$$ (10)

$$Y_t^D|{\mathit{\theta }}_{\mathit{t}},\tau ~Beta\left({\lambda }^D{\theta }_t^D,{\lambda }^D\left(1-{\theta }_t^D\right)\right)$$ (11)

and,

$${\mathit{\theta }}_{\mathit{t}}|{\mathit{\theta }}_{\mathit{t}-1},\tau ~Dirichlet(\kappa f\left({\mathit{\theta }}_{\mathit{t}-1},\mathit{\beta },\mathit{\gamma },\mathit{d}\right))$$ (12)

where, $\tau =\left\{{\mathit{\theta }}_0,\kappa ,\mathit{\beta },\mathit{\gamma },\mathit{d},{\lambda }^I,{\lambda }^R,{\lambda }^D\right\}$ , ${\mathit{\theta }}_0$ is the baseline value of the vector ${\mathit{\theta }}_{\mathit{t}}$, and ${\lambda }^I,{\lambda }^R,{\lambda }^D,\kappa >0$ control the variances of the distributions defined in Eqs. (9), (10), (11), and (12) respectively. All other notations have already been defined in the previous section. From equation (12), it is apparent that ${\mathit{\theta }}_{\mathit{t}},t=1,2\cdots ,T$, is a first-order markov chain. Also, the Eqs. (9), (10), (11) suggest that, for $t\ne s$, $Y_t^I$ is independent of $Y_s^I$, $Y_t^R$ is independent of $Y_s^R$, and $Y_t^D$ is independent of $Y_s^D$, given ${\theta }_t^I,{\theta }_t^R,\mathrm{a}\mathrm{n}\mathrm{d}{\theta }_t^D$ respectively.

Further, prior distributions of the model parameters can be defined as follows.

$${\theta }_0^I~Beta\left(1,{\left(Y_1^I\right)}^{-1}\right),{\theta }_0^R~Beta\left(1,{\left(Y_1^R\right)}^{-1}\right),{\theta }_0^D~Beta\left(1,{\left(Y_1^D\right)}^{-1}\right),{\theta }_0^S=1-{\theta }_0^I-{\theta }_0^R-{\theta }_0^D$$ (13)

$$R_i~LogN\left({\mu }_{r_i},{\sigma }_{r_i}^2\right),{\sigma }_{r_i}^2=ln\left(\frac{V\left(R_i\right)+{\left(E\left(R_i\right)\right)}^2}{{\left(E\left(R_i\right)\right)}^2}\right)\mathrm{a}\mathrm{n}\mathrm{d}{\mu }_{r_i}=\mathit{ln}\left(E\left(R_i\right)\right)-\frac{{\sigma }_{r_i}^2}{2},i=1,2$$ (14)

$${\gamma }_i~LogN\left({\mu }_{g_i},{\sigma }_{g_i}^2\right),{\sigma }_{g_i}^2=ln\left(\frac{V\left({\gamma }_i\right)+{\left(E\left({\gamma }_i\right)\right)}^2}{{\left(E\left({\gamma }_i\right)\right)}^2}\right)\mathrm{a}\mathrm{n}\mathrm{d}{\mu }_{g_i}=\mathit{ln}\left(E\left({\gamma }_i\right)\right)-\frac{{\sigma }_{g_i}^2}{2},i=1,2$$ (15)

$$p_t~Beta\left(a_p,b_p\right),\forall t=1,2\cdots ..T$$ (16)

R₁ and R₂ are basic (average) reproduction rates associated with quarantined (Q) and undetected (F) infecteds, respectively. That is,$R_i=\frac{{\beta }_i}{{(\gamma }_i+d_i)},i=1,2.$

$$\kappa ~Gamma\left(a_k,b_k\right),{\lambda }^I~Gamma\left(a_I,b_I\right),{\lambda }^R~Gamma\left(a_R,b_R\right),{\lambda }^D~Gamma\left(a_D,b_D\right)$$ (17)

The hyperparameters of these Gamma prior distributions can be assumed according to the size of variability to be allowed in the Beta and Dirichlet distributions defined in Eqs. (9), (10), (11), (13), (14), (15), (16), (17), (18), (19), (20), (21), (22), (23), (24), (25), (26), (27), (28), (29), (30), (31), (32), (33), (34), (35), (36), (37). The higher the values of the parameters, $\kappa ,{\lambda }^I,{\lambda }^R\mathrm{a}\mathrm{n}\mathrm{d}{\lambda }^D$, the lower will be the variance of the respective Beta and Dirichlet distributions. If limited prior information is available regarding these parameters, a relatively flat Gamma prior distribution with a high expected value and a relatively higher variability is assumed while choosing the values of the hyperparameters $a_k,b_k,a_I,b_I,a_D,\mathrm{a}\mathrm{n}\mathrm{d}{b}_D$ . Hyperparameters of the prior distribution of p_t are obtained by the method of moments using the mean and variance of the daily estimates of underreporting. Hyperparameters of the lognormal distributions defined in the expressions (14), (15) can be either based on historical knowledge on a similar epidemic, or can be estimated from the observed data. In our study, we have used a time-series SIR (TSIR) model-based technique to estimate the hyperparameter for transmission rate, $\mathit{\beta }$ [11]. The detailed methodology is described in the next sub-section. Values for the hyper parameters $\mathit{\gamma }\mathrm{a}\mathrm{n}\mathrm{d}\mathit{d}$ are calculated using required information from the published literature on COVID-19. ${\gamma }_1={\gamma }_2=\gamma \left(say\right)$ is taken as the inverse of the average recovery period. We have assumed equal recovery rates for both groups of infecteds. The components of $\mathit{d}$ , viz., d₁ and d₂ are estimated as, $d_1=\frac{\mathrm{C}\mathrm{F}\mathrm{R}}{h}\mathrm{a}\mathrm{n}\mathrm{d}{d}_2=\frac{\mathrm{I}\mathrm{F}\mathrm{R}}{h}$, where h is the average number of days from infection till death and IFR is the infection fatality rate. CFR is the ratio of the number of deaths divided by the number of confirmed cases of the disease. While, IFR is the ratio of deaths divided by the number of actual infections with SARS-CoV-2 and is generally expected to be lower than CFR.

Detailed outline for fitting the state-space SI(Q/F)RD model

Estimation of the hyperparameter $\beta$ using TSIR model

The two components of the vector $\mathit{\beta }={\left({\beta }_1,{\beta }_2\right)}^T$ must be estimated separately, such that they conform to their definitions. To do so, we have made some assumptions about the reported data, based on certain practical considerations. Generally, it is difficult to enforce adequate testing capacity, quarantine measures, and other preventive measures during the initial period of any epidemic due to the lack of resources, awareness, and preparedness. Consequently, the transmission rate observed during that period can be safely considered as an initial estimate of ${\beta }_2$ (the transmission rate due to infecteds who are not quarantined). Once the containment measures are imposed, the transmission rate based on the reported data is expected to change (reduce) and the average transmission rate observed over the entire period of reporting can be considered as an initial estimate of $\beta$ (the overall average transmission rate as a result of both quarantined and undetected infecteds). This logic can be implemented through TSIR model to estimate these hyperparameters as follows.

In TSIR model, the response, being a count variable, is assumed to follow a certain discrete count process distribution, like the Poisson distribution or the Negative Binomial distribution. The basic structure of TSIR model can be defined as follows; refer to [12], [13], [14].

$$S_{t+1}=S_t-I_t$$ (18)

$${\lambda }_{t+1}={\beta }_0\frac{S_t}{N}{I}_t^{\alpha }$$ (19)

$$log\left({\lambda }_{t+1}\right)=log{\beta }_0+\alpha log{I}_t+log\left(\frac{S_t}{N}\right)$$ (20)

where, S_t and I_t are the number of susceptibles and infecteds (or infectives) at time t, N is the population size, β₀ is the transmission rate and ${\lambda }_{t+1}$ is the expected number of new infecteds at time t + 1. New number of infecteds is assumed to follow Negative Binomial (or Poisson) distribution and a generalized Negative Binomial (or Poisson) linear model with log link is fitted with $\mathit{log}{I}_t$ as a covariate and $log\left(\frac{S_t}{N}\right)$ as an offset variable. The exponent α is expected to be just under 1 (i.e., close to 1) and is meant to account for discretizing the underlying continuous process. However, we have used an alternative interpretation of α based on the basic SIR model defined in Eq. (21). This method is drawn from our prior work where we have proposed a new method for obtaining time-varying estimates of transmission rate using TSIR model [11]. The transmission rate is assumed to be time-varying, and hence, denoted as ${\beta }_t$ in the following expressions.

$$\frac{d{\theta }_t^S}{\mathit{dt}}=-{\beta }_t{\theta }_t^I{\theta }_t^S,\frac{d{\theta }_t^I}{\mathit{dt}}={\beta }_t{\theta }_t^S{\theta }_t^I-\gamma {\theta }_t^I,and\frac{d{\theta }_t^R}{\mathit{dt}}=\gamma {\theta }_t^I$$ (21)

Using (21), the expression for expected number of new infecteds at time t + 1 (taking α = 1) with a time-varying transmission rate can be written as follows.

$${\lambda }_{t+1}={\beta }_t\frac{S_t}{N}{I}_t$$ (22)

Comparing Eqs. (19), (21), we can see that if α = 1 (or close to 1), β_t = β₀ (constant over time). However, if the value of α deviates considerably from 1, it has an impact on the effective rate of transmission and makes it time-dependent. That is, in such cases α assimilates the empirical changes in transmission rate over time. Further, using Eqs. (19), (21), we can write,

$$\widehat{{\beta }_t}={\beta }_0{I}_t^{\alpha -1}$$ (23)

Now, suppose T₁ represents the initial period of the epidemic when proper quarantine protocols were not in place, and T represents the entire period for which the reported data on the epidemic is available. The estimates of α and β₀ obtained by fitting the TSIR model shall be used in Eq. (23) to find estimates of transmission rate at each time t, $\widehat{{\beta }_t}$, t = 1,2,3…, T. Average of these estimates over a time period will give us the estimate of average transmission rate for that period. That is, the estimates of the transmission rates will be taken as, $\widehat{\beta }=\frac{1}{T}{\sum }_{t∊T}{\widehat{\beta }}_t$ and ${\widehat{\beta }}_2=\frac{1}{T_1}{\sum }_{t∊T_1}{\widehat{\beta }}_t$. Then an initial estimate of ${\beta }_1$, the transmission rate associated with quarantined infecteds, can be obtained using the relation, $\hat{\beta }={\hat{\beta }}_1\stackrel{-}{p}+{\hat{\beta }}_2\left(1-\stackrel{-}{p}\right);where,\stackrel{-}{p}=\frac{1}{T}{\sum }_1^T{p}_t$. As a simpler, but logical, alternative to this step for finding ${\widehat{\beta }}_1$ related to the COVID-19 epidemic, we can use the fact that the quarantined infecteds are expected to spread infection for approximately only one-third of the duration for which the undetected infecteds remain infectious among the susceptibles. This is because quarantined cases spread infections among the susceptibles mostly in the incubation period of around 4–5 days, prior to getting quarantined. While infecteds who are not quarantined are expected to spread infection for the entire average infectious period of 14 days. So, after estimating ${\widehat{\beta }}_2$ using the method described above, we can take ${\widehat{\beta }}_1=\frac{{\widehat{\beta }}_2}{3}$ as the initial estimate.

Estimation of parameters of the state-space SI(Q/F)RD model and forecasting

Posterior realizations on the parameters of the state-space model have been generated using Gibbs sampling MCMC approach. We have adopted the model in JAGS format and have implemented it in R using the package R2jags. Mean of posterior realizations of a parameter has been taken as its posterior estimate. Further, 0.025 and 0.975 quantiles of the posterior realizations have been taken as the limits of 95% credible intervals (CI) of the posterior estimates. Let t₀ be the time till which the observations are available, and suppose that we wish to forecast the values of the observed process $\left(Y_t^S,Y_t^I,Y_t^R,Y_t^D\right)$ from t₀ + 1 till the time T. We have followed the following iterative procedure to achieve our goal.

• a. L posterior realizations are generated on the latent prevalence process ${{\mathit{\theta }}_t}^{\left(l\right)},l=1,2\cdots ,L$ using Gibbs sampling approach, at each time point t = t₀ + 1,2…..,T. Here L is a sufficiently large number, say 1000 or more.
• b.At each t (=t₀ + 1,2…..,T), and at each posterior realization of the prevalence process ${{\mathit{\theta }}_t}^{\left(l\right)},l=1,2\cdots ,L$, values of the observed process, say $Y_t^{I\left(l\right)},Y_t^{R\left(l\right)}\mathrm{a}\mathrm{n}\mathrm{d}{Y}_t^{D\left(l\right)}$ are simulated from their conditional distributions, $\left[Y_t^I|{{\mathit{\theta }}_{\mathit{t}}}^{\left(\mathit{l}\right)},{\tau }^{\left(l\right)}\right]$, $\left[Y_t^R|{{\mathit{\theta }}_{\mathit{t}}}^{\left(\mathit{l}\right)},{\tau }^{\left(l\right)}\right]$ and $\left[Y_t^R|{{\mathit{\theta }}_{\mathit{t}}}^{\left(\mathit{l}\right)},{\tau }^{\left(l\right)}\right]$ which are defined in the Eqs. (9), (10), (11), respectively.
• c.Further, using the posterior realizations of $p_t^{\left(l\right)}$, at each l and each t, $Y_t^{Q\left(l\right)}=p_t^{\left(l\right)}.Y_t^{I\left(l\right)}$ and $Y_t^{F\left(l\right)}=Y_t^{I\left(l\right)}-Y_t^{Q\left(l\right)}$ are also obtained. At each t, mean of the L simulated values serves as the estimate (forecasted value) of the respective variable (compartment proportion). 95% credible interval of each variable, at each time t, is also obtained using the 0.025 and 0.975 quantiles of the L values.

Implementation and results

Data used for the analyses

Daily time-series data on total confirmed cases and total deaths for the states California and Florida has been obtained from the github repository of the Centre for Systems Science and Engineering (CSSE), Johns Hopkins University, Maryland, USA (https://github.com/CSSEGISandData/COVID-19). Daily time-series data till 11 July 2020 was available at the time of the procurement of data, and the same has been used for the entire analyses. Data on weekly state-wise estimates of excess deaths associated with COVID-19 till 11 July 2020, calculated as a difference between expected and reported number of deaths from all causes, has been obtained from the website of Centers for Disease Control and Prevention (CDC) [https://www.cdc.gov/nchs/nvss/vsrr/covid19/excess_deaths.html]. These weekly estimates of excess deaths have been used to calibrate daily number of true deaths. Details of the calibration procedure are provided in Appendix B. Data on the rates of positivity of COVID-19 testing for the two states, California, and Florida, was procured from the official website of Johns Hopkins University on 29 July 2020 (https://coronavirus.jhu.edu/testing/testing-positivity).

CFR and data calibration to account for underreporting

To exclude the initial period of extremely uncertain reporting due to the lack of awareness both at the governement and the public level, we have used the data from 02 March 2020 onwards for all analyses. The weekly excess death estimates have been used to reconstruct the daily time-series data of deaths using the procedure discussed in Appendix-B. According to the results reported by Verity et al. [15] based on a patient level data from the mainland China, the mean duration from the onset of symptoms to death is 17.8 days (95% credible interval 16.9–19.2). They reported the best estimate of case fatality ratio in China as 1.38% (1.23–1.53), with substantially higher CFR in older age groups (0.32% [0.27–0.38] in those aged < 60 years vs. 6.4% [5.7–7.2] in those aged ≥ 60 years, and up to 13.4% (11.2–15.9) in those aged 80 years or older). Their estimate for overall IFR in China is 0.66% [0.39–1.33], with an increasing profile with age. Yang et al. [16] reported that the median time from symptom onset to radiological confirmation of pneumonia is 5 days (interquartile range [IQR] 3–7 days); from symptom onset to intensive care unit (ICU) admission is 11 days (IQR 7–14 days); and from ICU admission to death is 7 days (IQR 3–11 days). That is, as per their findings, the estimate of median time from the onset of symptoms to death can be taken as 11 + 7 = 18 days. This estimate of time-to-event of death is consistent with the results of Verity et al. [15]. According to these results, the estimate of average duration from the onset of infection to death should be around 17.8 + 5 ≈ 23 days, where 5 days is the average incubation period. However, for estimating delayed CFR based on the reported data, and for estimating actual number of infecteds from the calibrated data on the number of deaths, we have taken average duration from infected/ reported to death as 18 days. This is because, in the absence of aggressive random testing, infecteds are generally tested on the onset of symptoms, i.e., after the incubation period.

The delayed CFR values calculated based on reported data came out to be quite high for both states. For California, the delayed CFR was 3.36%, while for Florida it came out to be 3.17% (Table 1 ). Both estimates are quite higher than 1.38%, the estimate based on individual patient data as reported by Verity et al. [15]. In fact, some other reports have suggested even lower actual CFR of COVID-19. The Centre for Evidence-Based Medicine (CEBM) at the University of Oxford currently estimates the CFR globally at 0.51%, with all the caveats pertaining thereto; refer (https://www.virology.ws/2020/04/05/infection-fatality-rate-a-critical-missing-piece-for-managing-covid-19/). We have taken 1.38% as a conservative estimate of the standard CFR due to COVID-19 as the estimate of CFR based on a follow-up data of individual patients is deemed as the most reliable, especially during the initial stages of the epidemic. Thus, the results of CFR based on the reported data indicate possibilities of significant underreporting of cases in both states. Also, significantly high rates of positivity of COVID-19 testing in the two states- 7.47% in California and 18.96% in Florida- as compared to the recommended rate of less than or equal to 5%, suggests lack of adequate testing capacity.

Table 1.

Delayed CFR estimates for the two states based on the reported data.

State	Total deaths till 16 July 2020	Total confirmed till 29 June 2020	Average Delayed CFR
California	7535	223,931	0.0336 (3.36%)
Florida	4802	151,389	0.0317 (3.17%)

Using a delay of 18 days (between detection of infection and death), and a CFR of 1.38%, we have employed the method discussed in the methodology section to estimate the true count of daily infected cases (new cases). Due to the use of an 18-day lag in the formula, number of daily infected cases could be calculated only till 24 June 2020 (18 days prior to 11 July 2020). Data on the number of recovered cases has not been reported by the two states. So, we have calibrated the data on number of recovered cases using the formula given in Eq. (24). Instead of fixing the value of ρ as (1–CFR) = 0.9862, we have generated random values for ρ uniformly between 0.975 and 0.99 to introduce stochastic uncertainty.

$${\mathit{R}}_{\mathit{t}}=I_{t-r+1}^C.\rho ,\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\rho ~Uniform\left(0.975,0.99\right)\mathrm{a}\mathrm{n}\mathrm{d}r=14$$ (24)

Here, $I_t^C$ represents the calibrated new number of infecteds at time t, and ρ is the average recovery rate. The average duration of recovery, r, is taken as 14 days based on the WHO report [17]. However, at this juncture we should also note that some other studies have reported higher average duration of recovery from COVID-19. Verity et al. [15] have estimated mean duration from onset of symptoms to hospital discharge to be 24.7 days [95% CI: 22.9–28.1]. Recovery time also varies according to the severity of symptoms. Since small recovery time implies faster recovery rate, our choice of 14-day average recovery period (from the onset of symptoms) can be called as a conservative estimate, and the forecasts of transmission dynamics based on it can also be expected to be slightly on the conservative side. Since the formula given in Eq. (24) cannot give us the estimates of the first 13 days, we have reconstructed the daily recovery data for these initial days using daily recovery rate equal to the inverse of the average duration of recovery. Again, to induce some stochastic uncertainty in the data, we have randomly generated the recovery rate, ${\phi }_t$, between 0.042 (1/24) and 0.071 (1/14), for each day. Following formula has been applied to estimate the true count of recovered cases.

$${\mathit{R}}_{\mathit{t}}=I_t^C.{\phi }_t,\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}{\phi }_t~Uniform\left(0.042,0.071\right),t<14$$ (25)

$I_t^C$ is the calibrated number of new infecteds at time t. For t < 14, the already calculated values of recovered cases at time (t + 13) using Eq. (24), R_t+13, is adjusted by subtracting R_t from it.

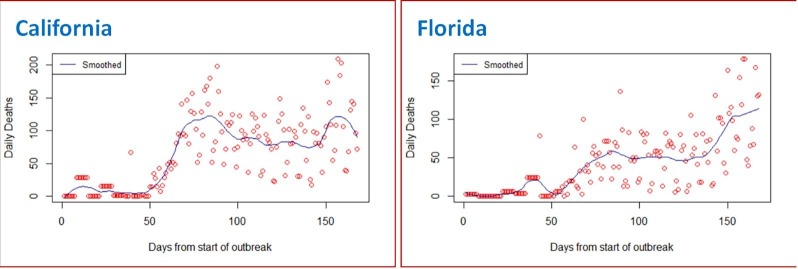
For further analyses, the reconstructed/ calibrated data on the number of cases in each compartment is treated as the true data. The ratio of reported number of infecteds and true number of infecteds on each day gives us the estimates of daily proportion of reporting p_t. Graphs of LOESS smoothed calibrated data on total number of deaths due to COVID-19 for the two states are presented in Fig. 2 . Summary statistics of p_t are provided in Table 2 .

Fig. 2.

LOESS smoothed calibrated data on total number of deaths due to COVID-19. Scattered circles represent the calibrated data points before smoothing.

Table 2.

Summary statistics of p_t, the estimated time-varying proportion of cases reported out of the actual number of cases, as obtained from the calibrated data.

Summary of estimates of pt	California		Florida
pt values/ period considered	Mean	Variance	Mean	Variance
First 30 days of the observed period	0.034 (3.4%)	0.0015	0.061 (6.1%)	0.008
Last 10 days of the observed period	0.57 (57%)	0.04	0.39 (39%)	0.007
Values lying between the first and the third sample quartiles	0.26 (26%)	0.01	0.23 (23%)	0.007

Evaluating parameters and hyperparameters of the state-space SI(Q/F)RD model

In California, the first official lockdown measure was implemented on 19 March 2020, while in Florida it was implemented from 01 April 2020. So, the period till 18 March 2020 has been considered as the initial period of transmission for California, and the period till 31 March 2020 has been taken as the initial period of transmission in Florida for obtaining the initial estimate of the transmission rate in the absence of proper quarantine measures for infecteds $\left({\widehat{\beta }}_2\right)$. TSIR model has been fitted assuming both Poisson and Negative Binomial distributions for the count process. The Negative Binomial TSIR model was chosen over the Poisson TSIR model because of lower model deviance. These models have been fitted using IBM-SPSS version 24. Estimated coefficients of the Negative Binomial TSIR models for both states are provided in Table 3 . Estimates of ${\beta }_2$ for the two states have been obtained using these coefficient estimates in Eq. (23) and taking average over respective initial periods of the COVID-19 epidemic (02 March 2020–18 March 2020 for California and 02 March 2020–31 March 2020 for Florida). Initial estimate of ${\beta }_1$ has been taken as one-third of the estimate of ${\beta }_2$. These estimates are also provided in Table 3.

Table 3.

Estimated coefficients of the TSIR models for the two states, with respective p-values of the Wald Chi-square statistic, and the resultant estimates of ${\mathit{\beta }}_2$ and ${\mathit{\beta }}_1$. Based on the p-values of the Wald-test, all coefficient estimates are significant.

State	Parameter	Estimate	Wald statistic p-value
California	loge${\beta }_0$	3.892	0.022**
	α	0.459	0.005*
	Initial period	02 March 2020–18 March 2020
	${\beta }_2$	0.319
	${\beta }_1$	0.106
Florida	loge${\beta }_0$	3.395	0.008*
	α	0.463	0.001*
	Initial period	02 March- 31 March 2020
	${\beta }_2$	0.280
	${\beta }_1$	0.093
*Significant at 1% level of significance **Significant at 5% level of significance

Using the estimates of CFR and IFR, and the average duration from the onset of symptom to death, as reported by Verity et al. [15], we get the estimates of d₁ and d₂ as ${\hat{d}}_1=\frac{0.0138}{18}=0.000767\mathrm{a}\mathrm{n}\mathrm{d}{\hat{d}}_2=\frac{0.0066}{18}=0.000367.$

The estimate of recovery rate has been taken as ${\widehat{\gamma }}_1={\widehat{\gamma }}_2=\widehat{\gamma }\left(say\right)=\frac{1}{14}=0.071$. ${\hat{d}}_1,{\hat{d}}_2,{\hat{\gamma }}_1,\mathrm{a}\mathrm{n}\mathrm{d}{\hat{\gamma }}_2$remain same for both states. So, the initial estimates of average reproduction numbers, R₁ and R₂, have been obtained as follows.

$$\mathrm{C}\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{n}\mathrm{i}\mathrm{a}:R_1=\frac{0.106}{\left(0.071+0.000767\right)}=1.477\mathrm{a}\mathrm{n}\mathrm{d}{R}_2=\frac{0.319}{\left(0.071+0.000367\right)}=4.470$$

$$\mathrm{F}\mathrm{l}\mathrm{o}\mathrm{r}\mathrm{i}\mathrm{d}\mathrm{a}:R_1=\frac{0.093}{\left(0.071+0.000767\right)}=1.296\mathrm{a}\mathrm{n}\mathrm{d}{R}_2=\frac{0.28}{\left(0.071+0.000367\right)}=3.923$$

These estimates of $\gamma$, R₁ and R₂ have been used to obtain informed hyperparameters of their prior distributions defined in Eqs. (14), (15). To decide on the hyperparameters of the Beta prior distribution of the time-varying proportion of quarantined infecteds, p_{t ,} we have used the descriptive statistics of its estimates over the observed period. Till the observed time period, the Beta prior distribution of p_t is assumed to have mean equal to ${\widehat{p}}_t$, the estimate of p_t based on the calibrated data, and variance equal to the overall variance of the estimates calculated at all time points. It was observed that after an initial period of around one month, the values of ${\widehat{p}}_t$ tend to first increase and then settle around some central value. So, for forecasting beyond the observed time period, sample mean and sample variance of the estimates corresponding to the last ten days of the observed period have been taken as the mean and variance of the Beta prior distribution of p_t. Complete list of prior distributions, along with the values of hyperparameters, used for fitting the state-space SI(Q/F)RD models for the two states is presented below.

California:

$$R_1~LogN\left(0.201,0.377\right),E\left(R_1\right)=1.477,V\left(R_1\right)=1;{\beta }_1=R_1\left(\gamma +d_1\right)$$ (26)

$$R_2~LogN\left(1.473,0.049\right),E\left(R_2\right)=4.47,V\left(R_2\right)=1;{\beta }_2=R_2\left(\gamma +d_2\right)$$ (27)

$$\gamma ~LogN\left(-2.736,0.181\right),E\left(\gamma \right)=0.071,V\left(\gamma \right)=0.001$$ (28)

$$p_t~Beta\left(a_t,b_t\right),suchthatE\left(p_t\right)={\hat{p}}_t,V\left(p_t\right)=\frac{1}{n}\sum {\left({\hat{p}}_t-\overline{{\hat{p}}_t}\right)}^2\forall t\in \mathrm{o}\mathrm{b}\mathrm{s}\mathrm{e}\mathrm{r}\mathrm{v}\mathrm{e}\mathrm{d}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{o}\mathrm{d}$$ (29)

$$p_t~Beta\left(2.89,2.21\right),E\left(p_t\right)=0.57,V\left(p_t\right)=0.04\forall t\in f\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{o}\mathrm{d}$$ (30)

Florida:

$$R_1~LogN\left(0.026,0.467\right),E\left(R_1\right)=1.296,V\left(R_1\right)=1;{\beta }_1=R_1\left(\gamma +d_1\right)$$ (31)

$$R_2~LogN\left(1.335,0.063\right),E\left(R_2\right)=3.923,V\left(R_2\right)=1;{\beta }_2=R_2\left(\gamma +d_2\right)$$ (32)

$$\gamma ~LogN\left(-2.736,0.181\right),E\left(\gamma \right)=0.071,V\left(\gamma \right)=0.001$$ (33)

$$p_t~Beta\left(a_t,b_t\right),suchthatE\left(p_t\right)={\hat{p}}_t,V\left(p_t\right)=\frac{1}{n}\sum {\left({\hat{p}}_t-\overline{{\hat{p}}_t}\right)}^2\forall t\in \mathrm{o}\mathrm{b}\mathrm{s}\mathrm{e}\mathrm{r}\mathrm{v}\mathrm{e}\mathrm{d}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{o}\mathrm{d}$$ (34)

$$p_t~Beta\left(11.79,18.38\right),E\left(p_t\right)=0.39,V\left(p_t\right)=0.007\forall t\in \mathrm{f}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{o}\mathrm{d}$$ (35)

Further, for models pertaining to both states, we assume,

$$\kappa ~Gamma\left(2,0.0001\right),{\lambda }^I~Gamma\left(2,0.0001\right)$$ (36)

$${\lambda }^R~Gamma\left(2,0.0001\right),{\lambda }^D~Gamma\left(2,0.0001\right)$$ (37)

Posterior estimates and forecasts from the state-space SI(Q/F)RD model

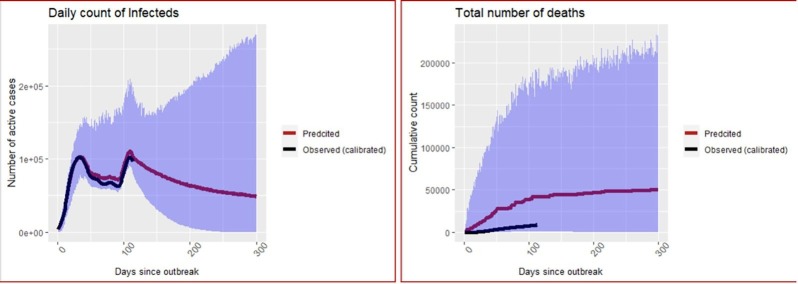
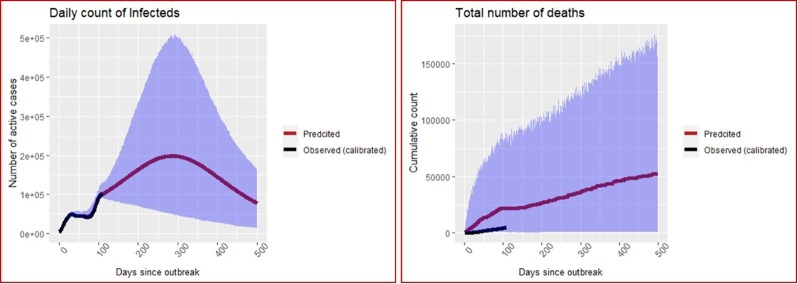
The Dirichlet-Beta state-space SI(Q/F)RD model is fitted to the calibrated data using the parameters and hyperparameters obtained in the previous sub-section. The model has been implemented in JAGS platform using R2jags package. Three parallel markov chains were run, each with 20,000 iterations of which first 10,000 were discarded. After thinning at an interval of 10, 1000 posterior simulations were saved from each chain, i.e., total 3000 posterior simulations were saved for each parameter. Posterior estimates of time-invariant parameters along with their standard deviations and 95% credible intervals for the two states are presented in the Tables 4 and 5 . Plots of the predicted values of the observed process on the number of infecteds ($Y_t^I$) and the number of deaths ($Y_t^D$), corresponding region of 95% credible intervals, and true (calibrated) counts till the observed time, are exhibited for the two states in Fig. 3, Fig. 4 . Predicted final size of the COVID-19 epidemic for each state, in terms of the total number of infections and deaths, is presented in Table 6 .

Table 4.

Posterior estimates of the parameters of the state-space SI(Q/F)RD model, along with their standard deviations and 95% credible intervals- California.

Parameter	Posterior mean	Posterior standard deviation	95% credible interval
R1	0.497	0.262	[0.068, 1.004]
R2	1.464	0.155	[1.214, 1.813]
$\mathit{\gamma }$	0.069	0.006	[0.056, 0.081]
$\mathit{\kappa }$	336063.593	47259.956	[243264.879, 431918.329]
${\mathit{\lambda }}^{\mathit{D}}$	1355.195	718.277	[397.588, 2632.883]
${\mathit{\lambda }}^{\mathit{I}}$	1012524.750	734717.729	[1349.955, 2006982.462]
${\mathit{\lambda }}^{\mathit{R}}$	1633152.503	334437.988	[1073803.103, 2360304.964]
${\widehat{\mathit{\beta }}}_1={\widehat{\mathit{R}}}_1(\widehat{\mathit{\gamma }}+{\mathit{d}}_1)$		0.035
${\widehat{\mathit{\beta }}}_2={\widehat{\mathit{R}}}_2(\widehat{\mathit{\gamma }}+{\mathit{d}}_2)$		0.102

Table 5.

Posterior estimates of the parameters of the state-space SI(Q/F)RD model, along with their standard deviations and 95% credible intervals- Florida.

Parameter	Posterior mean	Posterior standard deviation	95% credible interval
R1	0.359	0.224	[0.052, 0.880]
R2	1.612	0.097	[1.416, 1.799]
$\mathit{\gamma }$	0.063	0.004	[0.054, 0.071]
$\mathit{\kappa }$	500800.490	94547.445	[327261.995, 679843.447]
${\mathit{\lambda }}^{\mathit{D}}$	1022.341	303.916	[539.044, 1629.331]
${\mathit{\lambda }}^{\mathit{I}}$	999169.436	753473.727	[4778.595, 2403835.884]
${\mathit{\lambda }}^{\mathit{R}}$	1807366.511	365988.299	[1164580.155, 2616920.665]
${\widehat{\mathit{\beta }}}_1={\widehat{\mathit{R}}}_1(\widehat{\mathit{\gamma }}+{\mathit{d}}_1)$		0.0229
${\widehat{\mathit{\beta }}}_2={\widehat{\mathit{R}}}_2(\widehat{\mathit{\gamma }}+{\mathit{d}}_2)$		0.102

Fig. 3.

Predictions of number of infecteds and number of deaths in California. The blue shaded ribbon is the region of 95% credible intervals. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Fig. 4.

Predictions of number of infecteds and number of deaths in Florida. The blue shaded ribbon is the region of 95% credible intervals. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Table 6.

Predicted final size of the COVID-19 epidemic in the two states.

State	Total confirmed Cases	Total detected Cases (Quarantined)	Total undetected Cases (Not quarantined)	Total number of deaths
California	2,384,143	1,328,158	1,055,985	58,292
Florida	4,793,903	1,873,747	2,920,156	58,937

Discussion

Some key insights from the results

Estimates of the proportion of reported cases, p_t, based on the calibrated data impress upon the seriousness of the problem of underreporting. The first 30 days since the outbreak of the COVID-19 epidemic in the two states (i.e., for the month of March as per the timeline of this study) experienced extremely high level of underreporting, with the estimated average percentages of underreporting being 96.6% for California, and 93.9% for Florida. Similar results have been reported by Lau et al. [8]. Based on the reported data till 17 March 2020, they estimated the true number of infecteds to be 53.8 times higher than the reported number of cases in the United States- i.e., 98.1% of the total cases remained unreported. Similar situation was also reported by Wu et al. [7], and as per their findings the ratios of estimated cases to confirmed infections in California and Florida till 18 April 2020 were around 17.5 (94.3% underreported cases) and 10 (90% unreported cases), respectively. With time, the proportion of reported cases increased steadily, and after a couple of months it stabilizes around an average value of 57% for California, and 39% for Florida. That is, due to the lack of adequate testing capacity in these states, around 43% of the total infected cases in California and 61% of the total infected cases in Florida, on an average, are expected to remain unreported. These average values of p_t calculated at the later stage of the pandemic, are representative of the nature and capacity of long-term testing policy of the states. For the same reason, the hyperparameters of the prior distributions of p_t for the purpose of forecasting have been based on these later-stage averages. Such high percentages of infecteds remain undetected, are not quarantined, and remain infectious for a much longer period than their quarantined counterparts, moving freely among the susceptibles. The SI(Q/F)RD epidemic model proposed in this paper is based on this hypothesis and the hypothesis is strongly supported by the posterior estimates of the transmission parameters obtained from the Dirichlet-Beta state-space SI(Q/F)RD model. Posterior estimates of average reproduction rates associated with the quarantined infecteds are 0.497 (sd: 0.262) and 0.359 (sd: 0.224), while those associated with the undetected infecteds are 1.464 (sd: 0.155) and 1.612 (sd: 0.097), for California and Florida respectively. This clearly indicates that successful detection and quarantining of almost all infecteds would have resulted in quick decline in the number of active cases and would have drastically reduced the final size of the epidemic in both states. However, quarantining almost all infecteds in the presence of a large proportion of asymptomatic cases would require extensive amount of random testing. This is clearly missing in both states under consideration, as also suggested by the high rates of positivity of tests, and high reported CFR values for the two states.

Comparing forecasted deaths with post-analyses published estimates of excess deaths

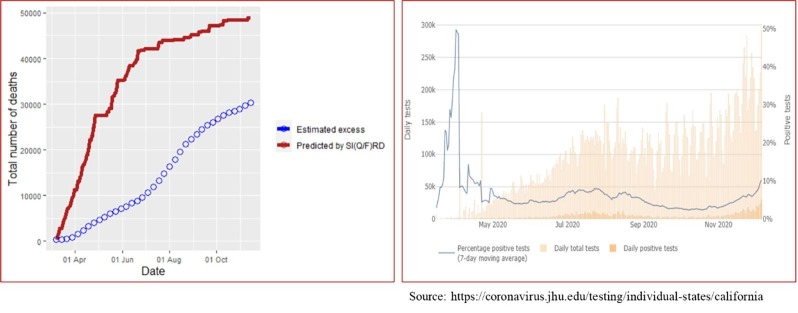
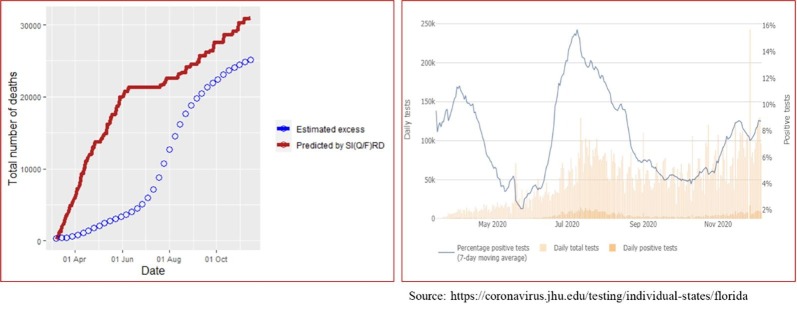
Since the true number of infecteds, detected plus undetected, remain latent in the population, it is not possible to compare forecasted values with the true values. However, comparing cumulative number of deaths forecasted by the state-space SI(Q/F)RD model with the estimated values of excess deaths can serve as a potent alternative to assess predictive efficiency of the model. Estimates of epidemiological parameters and predictions obtained from the state-space SI(Q/F)RD model in our study are based on the daily time-series data on the number of cases reported till 11 July 2020 and the weekly estimates of excess deaths available till the same date. Predictive accuracy of the model will be determined by its ability to forecast true values beyond the training period of the model. From this perspective, we have plotted the forecasted time-series of cumulative number of deaths obtained from the fitted SI(Q/F)RD model alongside the weekly estimated excess deaths due to COVID-19 till 14 November 2020. The estimates of excess deaths due to COVID-19 was retrieved from the website of CDC (https://www.cdc.gov/nchs/nvss/vsrr/covid19/ excess_deaths.html) on 4 December 2020. Striking difference in the estimated values of average reproduction numbers associated with detected (quarantined) cases and undetected cases suggest that the assumption regarding future values of proportion of detected cases plays a crucial role in ascertaining high predictive accuracy of the model. In other words, accuracy of the predictions from the proposed SI(Q/F)RD model relies greatly on the validity of the assumption regarding future testing policy in the region- i.e., on whether the testing capacity relative to the number of true cases is expected to increase, remain unchanged or decrease over time. To stress upon this argument, observed time-series of the rates of positivity of COVID-19 tests are also plotted alongside the comparative plots of the forecasted number of deaths. Figs. 5 and 6 present these plots for California and Florida, respectively. In both figures, the left panel shows the comparative trends of cumulative number of deaths (forecasted and excess), and the right panel presents the rate of positive tests over time. The trend line in blue in the right panel shows the average percentage of tests that were positive over the last seven days, i.e., a seven-day moving average of percentage of positive tests. The time-series plots of rates of positive tests for the two states were sourced from the website of Johns Hopkins University on 08 December 2020 [https://coronavirus.jhu.edu/testing/testing-positivity].

Fig. 5.

California- Left panel shows comparison of cumulative number of deaths predicted by the SI(Q/F)RD model with the estimates of excess deaths due to COVID-19. Right panel shows trend line of seven-day moving average of percentage of positive tests, along with daily total number of tests and daily total number of positive tests.

Fig. 6.

Florida- Left panel shows comparison of cumulative number of deaths predicted by the SI(Q/F)RD model with the estimates of excess deaths due to COVID-19. Right panel shows trend line of seven-day moving average of percentage of positive tests, along with daily total number of tests and daily total number of positive tests.

In case of California, there is a considerable difference between the predicted number of deaths and the estimated excess deaths due to COVID-19. However, the difference is majorly in the scale of the values, and the two trend lines look similar in shape over time. Possible reason for the difference in the scale can be explained by analysing the trend line of the rate of positive tests. The percentage of positive tests in California was extremely high during March-April, but although it started dropping exceptionally towards the end of April, it remained around 10% till July. However, September onwards, the rate of positivity came down below 5%, the WHO recommended threshold. The steep rise in the total number of tests performed daily, as shown by the pink towers in the graph, clearly explains this change. That is, California experienced a drastic change in testing capacity in the period of forecasting. Since, the hyperparameters of the model corresponding to the proportion of detected cases were defined based on the status of rate of positivity till July, the model tends to give overestimated forecasts of total number of deaths. Increasing the proportion of detected cases in the model as per the increase in testing capacity of the region would result in reduction in the total number of forecasted deaths. This is because the estimated rate of transmission for the detected (quarantined) cases is relatively much lower than that of the undetected cases.

The scenario of the rate of positive tests over time looks entirely different for Florida. Percentage of positive tests dipped below 5% for only two brief periods and it remained high for most of the time. That is, except for few short periods, the testing capacity has remained below par. Insufficient testing is also indicated by the fact that the trend line of the rate of positive tests is mostly parallel to the changes in the peaks of the total number of tests conducted per day. It suggests that the increments in the number of tests were not sufficient to reduce the rate of positivity of tests. Ideally, the rate of positivity of tests should decrease with the increase in the number of tests if the testing capacity is sufficient- as can be seen in the case of California. In other words, no significant change in the testing policy of Florida is observed in the forecasting period. This further implies that the hyperparameters defined for the proportion of detected cases in the state-space SI(Q/F)RD model remained valid for most of the forecasting period. Consequently, the forecasted values of cumulative number of deaths are much closer to the estimates of total excess deaths in case of Florida. These observations reaffirm the consequential impact of underreporting due to inadequate testing capacity on the transmission dynamics of the pandemic, which forms the conceptual backbone of the proposed state-space SI(Q/F)RD model.

Conclusion

We have provided a comprehensive framework of data calibration and flexible epidemic modelling for forecasting the transmission dynamics of epidemics in the presence of underreporting. The structure of the proposed SI(Q/F)RD model allows for adjusting the trajectory of the epidemic in terms of time-varying levels of underreporting. The Dirichlet-Beta state-space formulation of the SI(Q/F)RD model provides a dynamic approach to the estimation and prediction of both time-invariant and time-varying transmission parameters of the epidemic. Further, the proposed method based on TSIR for estimating hyperparameters of prior distributions of transmission rates (or reproduction rates) enriches the state-space model with strong prior information. Posterior estimates of the transmission parameters of the COVID-19 pandemic obtained for California and Florida exhibit the need to incorporate different transmission rates for detected (quarantined) and undetected (not quarantined) cases in epidemic models. Thus, the state-space SI(Q/F)RD model can also be used to gauge the difference in the progression and final size of an epidemic under diverse testing strategies with distinct potential for detecting cases. Since the estimates of transmission rates and reproduction numbers associated with undetected infecteds are significantly higher than those of the detected ones, adequate testing capacity for efficiently quarantining infecteds is of utmost importance in the fight against pandemics like COVID-19. The proposed methodological structure can play a pivotal role in assessing and forecasting the true burden of any epidemic, even in the presence of time-varying level of underreporting of cases. Reliable projections at the early stage of an epidemic will be indispensable to policy makers for successfully planning the allocation of resources, and implementing effective containment measures.

Limitations and further scope of research

We have taken the rate of death as a fixed (known) parameter in the state-space SI(Q/F)RD model. Obtaining its posterior estimates may improve the overall predictions from the model. Further, the model can be extended by introducing time-varying transmission rates using modifier functions [11], which will make it more flexible.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A.

Expressions for ${\mathit{k}}_{\mathit{t}}^{{\mathit{S}}_{\mathit{i}}},{\mathit{k}}_{\mathit{t}}^{{\mathit{I}}_{\mathit{i}}},{\mathit{k}}_{\mathit{t}}^{{\mathit{R}}_{\mathit{i}}},\mathit{a}\mathit{n}\mathit{d}{\mathit{k}}_{\mathit{t}}^{{\mathit{D}}_{\mathit{i}}}$

$$k_t^{S_1}=-\left[{\beta }_1{p}_t+{\beta }_2(1-p_t)\right]{\theta }_t^I{\theta }_t^S$$

$$k_t^{S_2}=-\left[{\beta }_1{p}_t+{\beta }_2\left(1-p_t\right)\right]{[\theta }_t^I+0.5k_t^{I_1}]\left[{\theta }_t^S+0.5k_t^{S_1}\right]$$

$$k_t^{S_3}=-\left[{\beta }_1{p}_t+{\beta }_2(1-p_t)\right]{[\theta }_t^I+0.5k_t^{I_2}][{\theta }_t^S+0.5k_t^{S_2}]$$

$$k_t^{S_4}=-\left[{\beta }_1{p}_t+{\beta }_2(1-p_t)\right]{[\theta }_t^I+k_t^{I_3}][{\theta }_t^S+k_t^{S_3}]$$

$$k_t^{I_1}=\left[{\beta }_1{p}_t+{\beta }_2\left(1-p_t\right)\right]{\theta }_t^I{\theta }_t^S-[{\gamma }_1{p}_t+{\gamma }_2\left(1-p_t\right){]\theta }_t^I-\left[d_1{p}_t+d_2\left(1-p_t\right)\right]{\theta }_t^I$$

$$k_t^{I_2}=\left[{\beta }_1{p}_t+{\beta }_2\left(1-p_t\right)\right]{[\theta }_t^I+0.5k_t^{I_1}]\left[{\theta }_t^S+0.5k_t^{S_1}\right]-\left[{\gamma }_1{p}_t+{\gamma }_2\left(1-p_t\right)\right]\left[{\theta }_t^I+0.5k_t^{I_1}\right]-\left[d_1{p}_t+d_2\left(1-p_t\right)\right]\left[{\theta }_t^I+0.5k_t^{I_1}\right]$$

$$k_t^{I_3}=\left[{\beta }_1{p}_t+{\beta }_2\left(1-p_t\right)\right]{[\theta }_t^I+0.5k_t^{I_2}]\left[{\theta }_t^S+0.5k_t^{S_2}\right]-\left[{\gamma }_1{p}_t+{\gamma }_2\left(1-p_t\right)\right]\left[{\theta }_t^I+0.5k_t^{I_2}\right]-\left[d_1{p}_t+d_2\left(1-p_t\right)\right]\left[{\theta }_t^I+0.5k_t^{I_2}\right]$$

$$k_t^{I_4}=\left[{\beta }_1{p}_t+{\beta }_2\left(1-p_t\right)\right]{[\theta }_t^I+k_t^{I_3}]\left[{\theta }_t^S+k_t^{S_3}\right]-\left[{\gamma }_1{p}_t+{\gamma }_2\left(1-p_t\right)\right]\left[{\theta }_t^I+k_t^{I_3}\right]-\left[d_1{p}_t+d_2\left(1-p_t\right)\right]\left[{\theta }_t^I+k_t^{I_3}\right]$$

$$k_t^{R_1}=\left[{\gamma }_1{p}_t+{\gamma }_2\left(1-p_2\right)\right]{\theta }_t^I$$

$$k_t^{R_2}=\left[{\gamma }_1{p}_t+{\gamma }_2\left(1-p_2\right)\right]{[\theta }_t^I+0.5k_t^{I_1}]$$

$$k_t^{R_3}=\left[{\gamma }_1{p}_t+{\gamma }_2\left(1-p_2\right)\right]{[\theta }_t^I+0.5k_t^{I_2}]$$

$$k_t^{R_4}=\left[{\gamma }_1{p}_t+{\gamma }_2\left(1-p_2\right)\right]{[\theta }_t^I+k_t^{I_3}]$$

$$k_t^{D_1}=\left[d_1{p}_t+d_2\left(1-p_2\right)\right]{\theta }_t^I$$

$$k_t^{D_2}=\left[d_1{p}_t+d_2\left(1-p_2\right)\right]{[\theta }_t^I+0.5k_t^{I_1}]$$

$$k_t^{D_3}=\left[d_1{p}_t+d_2\left(1-p_2\right)\right]{[\theta }_t^I+0.5k_t^{I_2}]$$

$$k_t^{D_4}=\left[d_1{p}_t+d_2\left(1-p_2\right)\right]{[\theta }_t^I+k_t^{I_3}]$$

Appendix B.

Calibrating daily number of deaths using weekly excess deaths due to COVID-19

Extent of underreporting of deaths has been estimated using the estimates of excess deaths. Excess deaths due to an epidemic (COVID-19 in our case) can be estimated as the difference between the total number of deaths reported in the period of epidemic (from all causes) and the expected number of baseline deaths due to all other causes in the absence of COVID-19. One popular method to calculate the expected number of baseline deaths in the absence of COVID-19 is to fit a Poisson regression to the time-series (weekly) data of death counts, and then projecting the baseline death counts till the required future point in time. An over-dispersed Poisson generalized linear models with spline terms is used to model trends in counts, accounting for seasonality; refer to [18], [19], [20]. The model is also adjusted for year-to-year baseline variation and any pre-existing epidemic, like influenza epidemic. In our study we have used weekly estimates of excess deaths published by the Centers for Disease Control and Prevention (CDC) for the two states under consideration for the analyses [18]. The estimated excess death counts in the presence of COVID-19 are taken as the estimates of actual (or true) number of deaths due to the pandemic. The reported daily deaths due to COVID-19 are summed over weeks to find weekly reported deaths. The difference between the weekly excess deaths and weekly reported deaths gives us the estimate of the unreported deaths due to the pandemic. For further analysis, the weekly estimate of unreported deaths due to COVID-19 is distributed among each day of the corresponding week as per the proportion of the number of pandemic related deaths reported on a day out of the total number of deaths due to the pandemic reported in that week. If all days of a week have zero reported deaths, the total number of unreported deaths is equally distributed among all seven days. Combining the additional death counts assigned to each day to the already reported death counts for the day gives us the calibrated daily time-series data on actual number of deaths due to COVID-19. The calibrated data is smoothed using the method of LOESS regression before proceeding with further analyses.