Dynein Harnesses Active Fluctuations of Microtubules for Faster Movement

Abstract

The cytoskeleton forms a dynamic network that generates fluctuations larger than thermal agitation of the cytoplasm¹. Here, we tested whether dynein, a minus-end-directed microtubule (MT) motor², can harness energy from these fluctuations using optical trapping in vitro. We show that dynein forms an asymmetric slip bond with MTs, where its detachment rate increases more slowly under hindering forces than assisting forces. This asymmetry enables dynein to generate unidirectional motility towards the minus-end from force fluctuations. Consistent with our model, oscillatory forces exerted by the trap drive dynein stepping without net force and ATP. Dynein is capable of ratcheting towards the minus-end even when the net force is in the plus-end direction. With ATP, force oscillations increase the velocity and stall force of dynein as it transports cargos and glides MTs. Therefore, dynein is a mechanical ratchet that rectifies cytoskeletal fluctuations to move faster and resists higher forces along MTs.

The cellular interior is highly dynamic and far from equilibrium. Mechanical properties of the cytoplasm are dominated by dynamics of cytoskeletal filaments, MT and actin, which harness energy from nucleotide triphosphate hydrolysis. These polar filaments rapidly polymerize and depolymerize, providing a continuous supply of mechanical energy to the cell. Molecular motors (actin-associated myosins and MT-associated kinesins and dyneins) additionally use energy from ATP hydrolysis to generate force and mechanical work along these tracks. Collectively, the cytoskeleton forms an active network. Forces generated by filament polymerization and motors control the flow of cytoplasmic streaming and drive the motion of large objects in the cytoplasm^{1, 3}. Unlike thermal agitations, the energy of these fluctuations can in principle be harnessed by molecular machines to perform mechanical work.

While the roles of molecular motors in motility, contractility, and self-organization of cytoskeletal networks are studied in detail, little is known about how active fluctuations of cytoskeleton affect the mechanics and cellular function of cytoskeletal motors and nonmotor proteins. MT-associated proteins (MAPs), such as NuMA and EB1, exhibit asymmetric friction when they crosslink a pair of actively moving MTs and this may be a viable strategy for these proteins to diffuse towards one end during MT growth and shrinkage⁴. Actin-binding proteins, vinculin, and cadherin-catenin form a force-dependent catch bond when pulled toward the pointed-end, which may reinforce cell adhesion and maintain front-rear asymmetry in migrating cells^{5, 6}. Similarly, myosin II and kinesin-8 motors diffuse at different speeds towards the plus- and minus-ends of actin and MT under load^{7, 8}.

It remains unclear whether processive motors can harness energy from cytoskeletal fluctuations for faster stepping along their tracks. Optical trapping studies revealed that dynein (Fig. 1a), a motor protein responsible for nearly all motility and force generation functions towards the MT minus-end, rapidly releases from MTs and moves faster when pulled forward, while resisting backward movement when pulled towards the plus-end^9–12. This asymmetry has been proposed to play a role in interhead coordination of dynein motility^{10, 13, 14}, as well as tight anchoring of dynein to MT under high tension¹⁵.

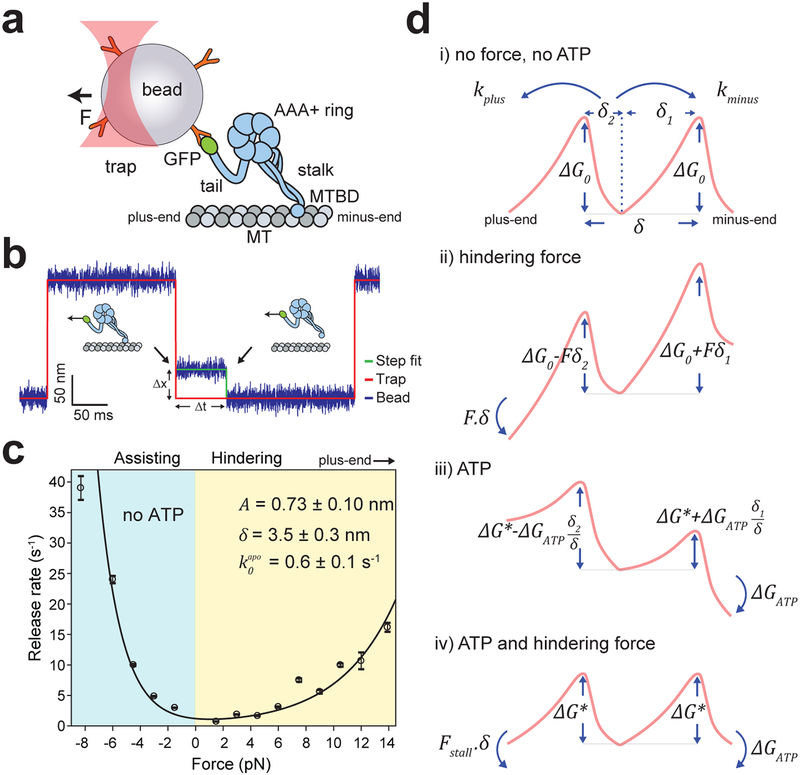
Figure 1. Dynein forms an asymmetric slip bond with an MT.

a. Schematic of a dynein motor domain. Dynein heavy chain has a catalytic AAA+ ring, which connects to an MT through a coiled-coil stalk. Dynein was attached to an 860 nm-diameter polystyrene bead from its tail using the GFP-antibody linkage and trapped with a focused laser beam (not to scale). b. Measuring the force-induced release of dynein monomers from MTs. (Inset) A trapped bead coated with monomeric dynein is oscillated between two positions 200 nm apart. When a dynein monomer binds to the MT, the bead does not follow the trap to its next position (black arrows). A constant force is applied due to trap-bead separation (Δx) until dynein releases from MT (Δt). c. The release rates of dynein monomers from MT under force are calculated from an exponential decay fit to the dwell-time histograms (± s.e.; n = 270, 243, 479, 407, 385, 354, 487, 461, 380, 260, 208, 325, 137, 325 from left to right, see Extended Data 1). The solid curve represents a fit to equation 3. Errors in derived parameters are s.e. of the fit. d. The model for the asymmetric potential landscape of dynein along an MT in the presence and absence of a nucleotide and external force (δ_1,2 = δ/2 ± A). The energy barrier in the presence of ATP (ΔG*) is lower than the apo condition (ΔG₀). Work done by hindering force (Fδ) shears the energy landscape towards the plus-end (ii), while the free energy of ATP hydrolysis (ΔG_ATP) shears it towards the minus-end (iii). At F_stall = −ΔG_ATP/δ, the motor comes to a stall because the negative work done by hindering force is equal to the positive work done by ATP hydrolysis (iv).

In order to test dynein’s ability to harness energy from cytoskeletal fluctuations, we first characterized the force-dependent kinetics of the dynein-MT bond. Previous studies proposed that dynein-MT is a slip-ideal¹², ideal¹¹ or catch¹⁵ bond, predicting that the release rate remains constant or decreases under high hindering forces (Extended Data 1a). These models could not be distinguished because of the small changes in the velocity and MT release rate of dynein under low (1–5 pN) hindering forces (Extended Data 1a). To address this, we measured the MT dwell time of single S. cerevisiae cytoplasmic dynein (“dynein” hereafter) monomers¹⁶ under a wider range (1–14 pN) of forces using an optical trap^{10, 17} (Fig. 1b, Extended Data 2). The dwell time distributions fit well to a double exponential decay. MT release rate is interpreted as the slow rate of the fit, whereas the fast rate likely represents weak interactions between dynein and MT (Extended Data 1b–d). Consistent with previous studies^{10, 12}, we observed that the release rate rapidly increases when dynein is pulled toward the MT minus-end (assisting) and release is slow at low (1–4 pN) hindering forces in the absence of ATP. However, we clearly detected an increase in MT release rate at higher hindering forces (6–14 pN), albeit less drastically than release under the forward pull of the trap (Fig. 1c). These results showed that dynein forms an asymmetric slip bond with an MT. Force-detachment kinetics of dynein from MT can be described by a model⁸ based on the Arrhenius theory (see Supplementary Notes). In the absence of force and nucleotide, forward (k_minus) and backward (k_plus) release rates are equal:

$$k_{\mathit{\text{minus}}}=k_{\mathit{\text{plus}}}=k_0^{\mathit{\text{apo}}}\propto e^{-\mathrm{\Delta }{G}_0/k_{B}T}$$ (1)

where $k_0^{\mathit{\text{apo}}}$ is the release rate and ΔG₀ is the energy barrier in the absence of force and nucleotide, k_B is the Boltzmann constant and T is the absolute temperature (Fig. 1d, i). An external force (F, positive forces are in the plus-end direction) biases the potential landscape and increases the release rate towards the direction motor is pulled from the MT (Fig. 1d, ii).

$$k_{\mathit{\text{minus}}}=k_0^{\mathit{\text{apo}}}{e}^{-F\left(\frac{\delta }{2}+A\right)/k_{B}T},k_{\mathit{\text{plus}}}=k_0^{\mathit{\text{apo}}}{e}^{F\left(\frac{\delta }{2}- A\right)/k_{B}T}$$ (2)

where A is the asymmetric distance that biases the energy barrier for the release from the MT, and δ is the barrier width (Fig. 1d, i). The total release rate (k_total) is given by:

$$k_{\mathit{\text{total}}}=k_{\mathit{\text{minus}}}+k_{\mathit{\text{plus}}}=2k_0^{\mathit{\text{apo}}}{e}^{-\frac{F A}{k_{B}T}}\mathit{\text{cosh}}\left(\frac{F\delta }{2k_{B}T}\right)$$ (3)

The fit of force-dependent release rate to equation 3 reveals that A of dynein (0.73 ± 0.10 nm, Fig. 1c) is higher than the previously reported values for kinesin-8⁸, NuMA, and EB1⁴, suggesting that dynein is a stronger ratchet than these proteins. We note that δ (3.4 ± 0.3 nm) represents the distance over which external force acts on a dynein monomer to release it from MT, and it is shorter than the distance between adjacent tubulin binding sites (8.2 nm). Due to the vertical forces inherent to the single bead trapping assay¹⁸, we anticipate that $k_0^{\mathit{\text{apo}}}$ of the motor is lower than 0.6 ± 0.1 s⁻¹ we measured and dynein exhibits even greater asymmetry in the absence of vertical forces.

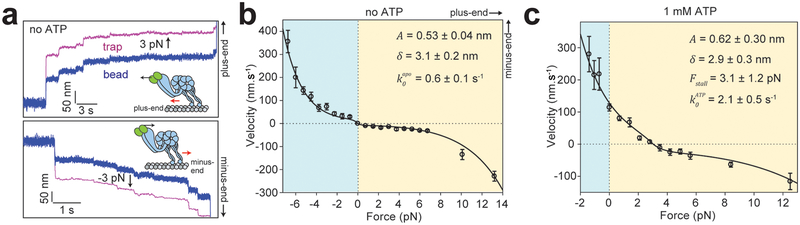
To determine how force affects the velocity of dynein dimers, we applied constant forces to beads transported by single full-length dynein¹⁶ (Fig. 2a). In the absence of ATP, dynein was immobile without force and moved processively towards the direction it was being pulled by the optical trap⁹. Consistent with its asymmetric force-dependent detachment from MT, dynein moved faster towards the minus-end compared to the plus-end under the same magnitude of force (Fig. 2b)^{9, 11, 19}. The average velocity (V, positive velocities are in the minus-end direction) at a given force is given by:

$$V\left(F\right)=k_{\mathit{\text{total}}}\left(F\right)d\left(F\right)$$ (4)

where d(F) is the average step size of dynein in the absence of ATP, measured from the step analysis of individual trajectories under constant load (Extended Data 3). The fit of experimentally measured V(F)/d(F) values to equation 3 (Extended Data 3d) revealed similar $k_0^{\mathit{\text{apo}}}$, A and δ values estimated from the force-dependent release rates of monomeric dynein (Fig. 1c).

Figure 2. Dynein responds asymmetrically to assisting and hindering forces.

a. Representative position-time graph of a dynein motor under constant 3 pN hindering (top) and assisting (bottom) force. (Insets) Dynein moves (red arrows) towards the direction of the applied force (black arrow). b. F-V relationship of dynein in the absence of ATP (mean ± s.e.m.; from left to right n = 51, 50, 59, 53, 41, 35, 48, 46, 43, 54, 62, 47, 82, 68, 56, 92, 85, 44, 45, 78 from 3 technical replicates). c. F-V relationship of dynein in 1 mM ATP (mean ± s.e.m.; from left to right n = 38, 36, 48, 78, 42, 56, 58, 47, 39, 35, 35, 48, 43, 42 from three technical replicates). In b and c, the solid curves represent a fit to equations 3 and 5, respectively (see Supplementary Notes). Errors of the derived parameters are s.e. of the fit.

We next determined how force affects dynein velocity in saturating (1 mM) ATP. Similar to Gennerich et al.⁹, we observed that dynein asymmetrically responds to load, and moves processively backward under high resistive forces (Fig. 2c)^{9, 11}. However, we observed dynein to move at higher velocities (114 ± 11 nm s⁻¹, ± s.e.m.) in unloaded conditions¹⁶ and the velocity increased rapidly under forward load. In addition, we did not see evidence of a nonadvancing stepping mode⁹, in which the motor takes consecutive forward and backward steps at the same position on an MT under load. These disparities may be related to differences in assay conditions and calibration of the force response of the optical trap.

To determine how energy from nucleotide hydrolysis biases the potential landscape towards the minus-end (Fig. 1d, iii), we fit the F-V measurements to:

$$V\left(F\right)=2d\left(F\right)k_0^{\mathit{\text{ATP}}}{e}^{-\frac{\left(F-F_{\mathit{\text{stall}}}\right) A}{k_{B}T}}\mathit{\text{cosh}}\left(\frac{\left(F-F_{\mathit{\text{stall}}}\right)\delta }{2k_{B}T}\right)$$ (5)

where $k_0^{\mathit{\text{ATP}}}$ is the release rate in the absence of force, and F_stall is the hindering force at which k_minus = k_plus (Fig. 1d, iv). The average step size in ATP at a given force (d(F)) is measured from individual trajectories under constant load (Extended Data 4). The fit revealed similar A and δ values to the no nucleotide condition (Extended Data 4d). F_stall (3.1 pN) is consistent with earlier measurements in fixed trap assays¹¹ and lower than 7 pN stall force reported by Gennerich et al⁹ (Fig. 2c). Notably, $k_0^{\mathit{\text{ATP}}}$ is ~4 fold higher than $k_0^{\mathit{\text{apo}}}$, which might result from switching of dynein from strongly-bound to weakly-bound states during the nucleotide hydrolysis cycle.

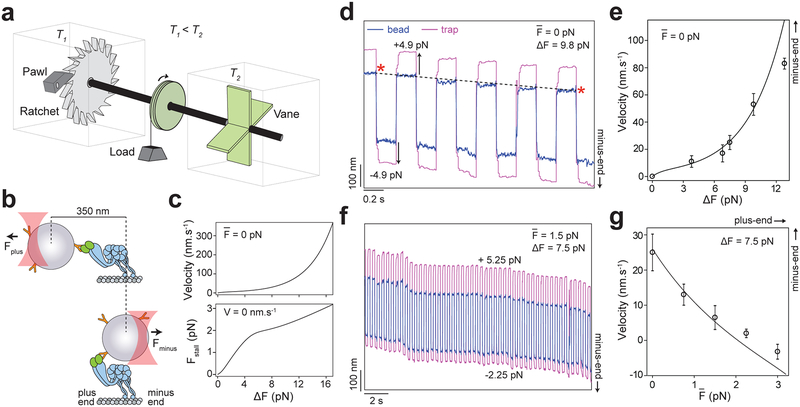
To test whether this asymmetric F-V relationship enables dynein to harness energy from cytoskeletal oscillations, we designed an experiment analogous to Feynman’s hypothetical “ratchet and pawl” device²⁰, in which a microscopic ratchet generates work from random fluctuations that occur at an effective temperature higher than the ambient temperature (Fig. 3a). We increased the effective temperature, but not the actual temperature, of a single dynein’s local environment by oscillating the optically trapped bead (Fig. 3b–c). We first checked whether force fluctuations can drive unidirectional motility without ATP and the net force on the bead $\left(\overline{F}=\left(F_{\mathit{\text{plus}}}+F_{\mathit{\text{minus}}}\right)/2\right)$. The magnitude of force oscillations (ΔF = F_plus − F_minus) was increased from 0 pN to 13 pN, while $\overline{F}$ was kept at 0 pN (Fig. 3d–e, Extended Data 5). Consistent with our prediction, dynein processively moved towards the minus-end when subjected to force oscillations in a square wave pattern and the velocity increased with ΔF (Fig. 3e). The ΔF-V relationship is consistent with the average velocities of dynein under F_plus and F_minus (Fig. 2b and 3e).

Figure 3. Force oscillations drive minus-end-directed motility of dynein without ATP.

a. Feynman’s microscopic ratchet device. Two chambers are maintained at temperatures T₁ and T₂. Thermal fluctuations in the right chamber drive the shaft. The ratchet generates net clockwise rotation and lifts the load if T₂ > T₁. b. Dynein is driven by back-and-forth oscillations of the optically trapped bead, which increase the local effective temperature above that of the environment. Due to the rotational freedom of the bead, the trap freely moves 350 nm between the assisting and hindering directions before applying a significant force on dynein. c. The estimated velocity and stall force of dynein under force oscillations are calculated from the F-V curve in Fig. 2b. d. A dynein-driven bead oscillated ±4.9 pN in a square wave pattern at 2.5 Hz exhibits motility towards the MT minus-end. Velocity is calculated from the ratio of the net displacement of the bead (black dashed line) to elapsed time (red stars). e. The minus-end-directed velocity of dynein-driven beads increases with ΔF (mean ± s.d.; from left to right n = 32, 35, 25, 39, 42 from three technical replicates). f. Example trajectory of a dynein-driven bead oscillated with 5.25 pN hindering and −2.25 pN assisting forces at 2.5 Hz. g. The velocity of dynein-driven beads decreases by the increase in the average hindering force on the bead (mean ±s.d.; from left to right n = 25, 23, 29, 28, 25 from three technical replicates). In d and f, black curves represent the estimated velocities from the F-V curve in Fig. 2b.

To test the effectiveness of dynein’s ratcheting along MTs in the absence of ATP, we biased the net force $\overline{F}$ from 0 pN to 3 pN towards the plus-end while keeping ΔF constant (7.5 pN). Remarkably, dynein was able to move towards the minus-end even though it was pulled more strongly towards the plus-end. The motor stalled at $\overline{F}=2pN$, and moved backward under higher hindering loads (Fig. 3f–g, Extended Data 5). We also observed the mammalian dynein-dynactin-BicD2N (DDB) complex²¹ to move processively towards the MT minus-end under force fluctuations in the absence of ATP and net force (Extended Data 6), suggesting that ratcheting is a general property of dynein motors.

We next tested our prediction that dynein’s ratcheting along MT increases the velocity and stall force under physiological ATP concentrations (Fig. 4a). We measured the velocity of dynein-driven beads subjected to force oscillations in 1 mM ATP (Fig. 4b). At $\overline{F}=0pN$, application of ΔF up to 4.2 pN increased the velocity by 67% (190 ± 11 nm s⁻¹, Fig. 4c), demonstrating that dynein moves faster by harnessing the energy of force fluctuations under saturating ATP.

Figure 4. Force oscillations increase cargo transport and MT gliding velocity of dynein in the presence of ATP.

a. The estimated velocity and stall force of dynein under force oscillations are calculated from the F-V curve in Fig. 2c. b. Example trajectory of a dynein-driven bead oscillated ±2.1 pN at 2.5 Hz. c. The velocity of dynein-driven beads increases by the increase in ΔF on the bead (mean ± s.d.; n = 78, 42, 35, 28, 30, 21 from left to right from three technical replicates). The black curve shows the estimated velocities in (a). d. Schematic of the optical trapping assay for the MT oscillations. Dyneins were fixed on the glass surface from their tail through a biotin-streptavidin linkage. MTs glide with their plus-end in the lead (red arrow) due to the minus-end-directed motility of surface-immobilized dyneins (blue arrow). The trapped bead was tightly attached to a gliding MT on the surface and oscillated back and forth at 1 Hz. e. Example trajectory of a gliding MT oscillated ±1.75 pN at 1 Hz in 20 μM ATP. The yellow shaded region represents duration the force-feedback is engaged for trap oscillations. f. MT gliding velocity increases by the magnitude of force fluctuations. Data at 0 pN were obtained from fluorescence experiments. The center line and edges represent mean and s.d., respectively. p values are calculated from Welch’s t-test (n = 144, 30, 16, 12 from left to right). g. Due to the asymmetric force-detachment kinetics, dynein ratchets towards the minus-end of MTs under external fluctuations.

In cells, dynein motors also anchor onto large organelles or the plasma membrane and pull the MTs. To test whether oscillations of the MT network affect the MT sliding activity by multiple dyneins, we oscillated beads attached to MTs as they are glided by surface-immobilized dyneins (Fig. 4d). In order to initiate force oscillations before the beads escape the trap, we lowered gliding velocity under no force to 23 ± 2 nm s⁻¹ (mean ± s.e.m.) by reducing ATP concentration to 20 μM. Trajectories revealed that assisting forces significantly increased the gliding velocity whereas hindering forces caused a modest slowdown of MT gliding (Fig. 4e). In the absence of net force, the application of ΔF up to 6.3 pN caused a two-fold increase in gliding speed (Fig. 4f), demonstrating that the periodic oscillation of MTs leads to faster filament sliding activity of dynein motors.

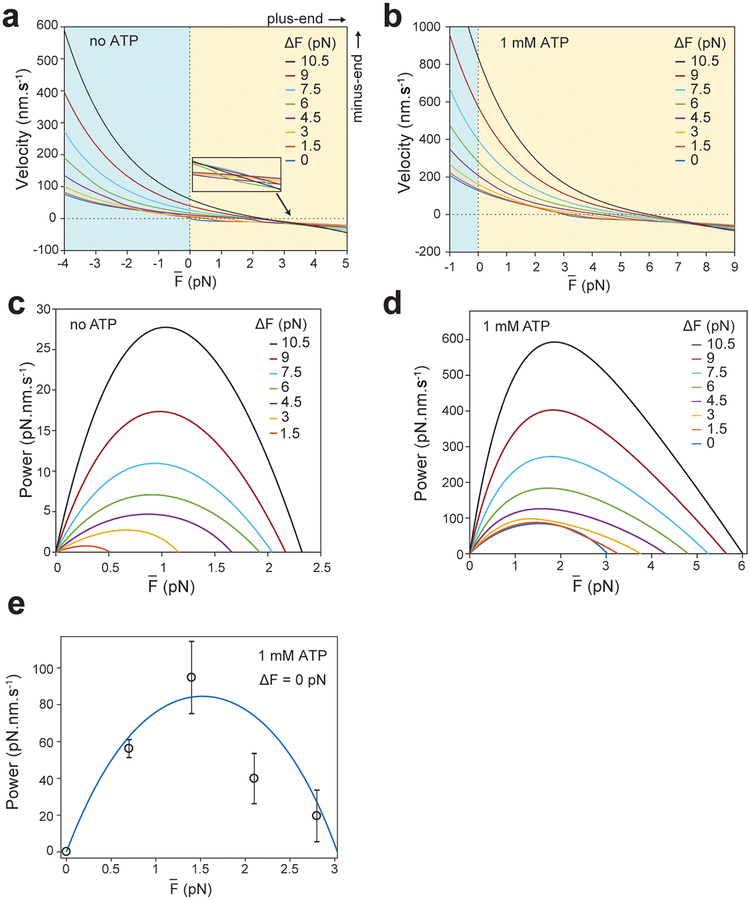
Collectively, our results show that dynein forms an asymmetric slip bond with an MT, which enables this motor to harness energy from cytoskeletal fluctuations (Fig. 4g). Unlike myosin V that functions as a reverse ratchet²², dynein is a forward ratchet that favors faster movement when pulled towards its natural direction of motion. Therefore, fluctuations increase the speed of dynein motility and the ability of the motor to resist hindering forces, resulting in higher power output (Extended Data 7).

It is possible that ratcheting along MTs may assist dynein to perform its cellular functions. Dynein carries organelles and vesicles towards the nucleus of interphase cells and drives retrograde transport towards the cell body in neurons². Dyneins also generate periodic oscillations of MTs from millisecond to minute timescales²³. During asymmetric cell division, the entire mitotic spindle undergoes periodic oscillations due to antagonistic force generation of cortical dyneins and this is attributed to force-dependent detachment of dynein from an MT^{24, 25}. Ratcheting may enable dyneins to move towards the minus-end at faster speeds and increase tension for proper positioning of the spindle²⁶. Similarly, the beating of motile cilia is powered by antagonistic forces generated by axonemal dyneins on either side of an axoneme. Active oscillations of the parallel bundle of MTs may increase the MT sliding velocity of axonemal dyneins (Fig. 4) and the frequency of ciliary beating^{27, 28}. Our oscillating trap assay can be combined with efforts on in vitro reconstitution of the mitotic spindle²⁹ and cilia-like beating of MT bundles³⁰ for testing these ideas.

Methods

Protein purification and labeling

Full-length S. cerevisiae dynein was tagged with GFP at its N-terminus and a HaloTag (DHA) at its C-terminus and expressed under the native promoter¹⁶. To construct monomeric dynein, the 5’ end of the dynein gene encoding the tail was deleted leaving amino acids 1219–4093 with a predicted molecular weight of 331 kDa. The construct was tagged with GFP at its N-terminus and DHA at its C-terminus and expressed under a galactose promoter (GFP-Dyn_331kD-DHA)¹⁶. For MT gliding assays, a GST dimer of tail truncated dynein was tagged with DHA at the N-terminus (DHA-GST-Dyn_331kD)¹⁶. These constructs were purified from S. cerevisiae cultures by incubating the cell lysate with IgG beads (GE Healthcare) and eluting the protein from beads using Zz-Tev cleavage, as described previously¹⁶. The motor was labeled with 10 μM tetramethylrhodamine (TMR)- or biotin-alkyl chloride (a HaloTag ligand) at the DHA tag for an additional 1 h at 4 °C before cleaving the protein from IgG beads. For DNA-tethered optical trapping experiments, a 74 bp double-stranded DNA tether was labeled with biotin in one end and alkyl chloride-NHS at the opposite end, and excess ligand was removed using ethanol precipitation at 4 °C, as previously described¹¹. 10 μM DNA tether was incubated with monomeric dynein for an additional 1 h at 4 °C before cleaving the protein from IgG beads.

The constructs that express a phi mutant of human dynein (SNAP-DYNC1H1_{E1518K/R1567K}) in a pACEBac1 vector backbone³¹; the pDyn2 plasmid that contains genes from IC2C, LIC2, TCTEX1, LC8, and ROBL1, and mouse BICD2–400-GFP (BicD2N-GFP) in a pOmniBac vector backbone were provided by A. P. Carter³². Human dynein and BICD2N constructs contain a 6xHis-ZZ tag followed by a TEV protease cleavage site for protein purification. The proteins were expressed using the baculovirus insect cell system, and purified using Tev cleavage from IgG beads, as described previously³³. Dynactin was purified from pig brain using the large-scale SP-Sepharose and MonoQ ion-exchange chromatography³⁴. The 6xHis-tagged GFP-SRS_85:82-MTBD construct was expressed in E. Coli and purified using NiNTA affinity purification, as previously described³⁵. Purified protein was aliquoted and flash-frozen in liquid nitrogen. Protein purity was confirmed with gel electrophoresis and the concentration was measured using the QuickStart Bradford kit (BioRad).

Coating beads with anti-GFP antibodies

Carboxyl latex beads (860 nm in diameter, Life Technologies) were coated with custom-made rabbit polyclonal anti-GFP antibodies (Covance). 200 μL of beads were resuspended three times in activation buffer (10 mM MES pH 6.0, 100 mM NaCl) after spinning down at 8,000 rpm for 3 min. 1 mg of EDC and 1 mg of S-NHS were dissolved in 1 mL and 2 mL DMF, respectively and 20 μL of dissolved EDC and 40 μL of dissolved S-NHS were added to beads. The beads were sonicated for 3 min and nutated at low speed until visible clumps disappeared. The beads were rinsed in PBS (phosphate-buffered saline, pH 7.4) buffer in 800 μL total volume and reacted with 200 μL of 0.4 mg ml⁻¹ of antibody. After shaking the mixture for 30 min, the beads were passivated by adding 10 mg ml⁻¹ BSA for 2 h, washed in PBS three times and stored in PBS supplemented with 0.1% sodium azide and 0.5 mg ml⁻¹ BSA at 4 °C.

Sample preparation

Cy5-labeled axonemes were flown into the chamber in DLB buffer (30 mM HEPES pH 7.2, 2 mM MgCl₂, 1 mM EDTA, 10% glycerol). To determine the polarity of axonemes, a TMR-labelled DHA-GST-Dyn_331kD was flown into the chamber with 1 mM ATP in DLBC buffer (DLB supplemented with 1 mg ml⁻¹ casein and 2 mM DTT). After waiting for 5 min to allow dynein to accumulate at the MT minus-end, the chamber was washed three times with 30 μl DLBC. GFP-tagged S. cerevisiae dynein was mixed with antiGFP-coated beads for 10 mins on ice. For DNA-tethered optical trapping experiments, monomeric S. cerevisiae dynein labeled with a DNA tether was incubated with streptavidin-coated polystyrene beads (860 nm in diameter, Spherotech) for 5 mins on ice. The motor-bead mixture was introduced into the chamber along with 1 mM ATP and the oxygen scavenger mixture (35 mg ml⁻¹ protocatechuic acid (PCD) and 2.5 mM protocatechuate-3,4-dioxygenase (PCA)).

For trapping experiments with mammalian dynein-dynactin, DDB complexes were assembled by mixing 1 μl of 1.2 mg ml⁻¹ dynein with 1 μl of 1.6 mg ml⁻¹ dynactin, and 1.5 μl of 3–4 mg ml⁻¹ cargo adaptor (BicD2N-GFP) in 10 μl dynein motility buffer (DMB: 30 mM HEPES pH 7.0, 5 mM MgSO₄, 1 mM EGTA, 1 mM TCEP (tris(2-carboxyethyl)phosphine) supplemented with 1 mg ml⁻¹ bovine serum albumin (BSA). The complex was incubated on ice for 10 min. The complex assembly was incubated with antiGFP-coated beads for 10 mins on ice, diluted in DMB supplemented with 1.25 mg ml⁻¹ casein (DMB-C), 5 U ml⁻¹ of apyrase, 2.5 mM PCA (protocatechuic acid) and 50 nM PCD (protocatechuate-3,4-dioxygenase), and flown into the chamber.

To ensure that more than 95% of the beads are driven by single dyneins, the motor to bead ratio was reduced until less than 30% of the beads walk along MTs in the presence of ATP. To test the motility of dynein-driven beads in the absence of nucleotide, instead of 1 mM ATP, 5 U ml⁻¹ of apyrase was added to the motor-bead mixture to deplete the residual ATP in the chamber.

MT Gliding Assays

To polymerize MTs, unlabeled and Cy5-labeled pig tubulin were mixed in BRB80 buffer (80 mM PIPES pH 6.8, 1 mM MgCl₂, 1mM EGTA, 1mM DTT) supplemented with the polymerization mixture (2 mM GTP, 20% Dimethyl sulfoxide (DMSO) in 2x BRB80). MTs were polymerized for 20 min at 37 °C. 10 μM taxol was added to the mixture and incubated for an additional 10 min at 37 °C. Excess tubulin was removed by pelleting and resuspending MTs at 20,000 g for 12 min in BRB80 supplemented with 10 μM taxol. MTs were stored at room temperature in dark.

To exert forces on MTs during gliding motility, beads were densely coated with a construct that contains dynein MTBD and part of the stalk coiled-coil fused to monomeric seryl-tRNA synthetase (GFP-SRS_85:82-MTBD)³⁰. 2 μl of 5 μM GFP-SRS_85:82-MTBD was incubated with 1 μl of 4% v/w bead solution for 5 min. Excess protein was removed by the addition of 1 ml DLB, and pelleting and resuspending the beads in 5 μl DLB. DHA-GST-Dyn_331kD was labeled with biotin at the N-terminus and fixed onto the glass surface through a BSA-biotin and streptavidin linkage. The sample was washed with DLB, and 10 μl of 0.1 mg ml⁻¹ Cy5 MTs were introduced to the chamber in the presence of 10 μM taxol. After 2 min incubation, 40 μl of 20 mg ml⁻¹ beads were introduced to the chamber in DLB supplemented with 20 μM ATP, 10 μM taxol, oxygen scavenger mixture (2.5 mM PCA and 50 nM PCD) and the ATP regeneration mixture (2 mM phosphoenolpyruvate and 0.42 mM pyruvate kinase).

Optical trapping assays

All trapping experiments were performed on a fully automated optical trap that was custom-built in an acoustically isolated and temperature-controlled (±0.1 °C) room around the body of a Nikon Ti-E inverted microscope¹¹. Beads were trapped using a 2 W 1064 nm laser (Coherent). The trapping beam was focused on the image plane using a 100 × 1.49 N.A. apochromat oil-immersion objective (Nikon). Cy5-labeled axonemes or MTs were excited using a 632 nm HeNe laser (Melles Griot) and imaged via a monochrome CCD camera (The Imaging Source). MTs were moved to the center of the field of view using a locking XY stage (M-687, Physik Instrumente). A pair of perpendicular acousto-optical deflectors (AODs, AA Optoelectronic) were placed in a plane conjugate to the back focal plane of the objective to steer the trap. The laser power was adjusted with a half-wave plate on a motorized rotary mount (New Focus). Beads were lowered on the axonemes using a piezo flexure objective scanner (P-721 PIFOC, Physik Instrumente). Bead position relative to the center of the trap was determined by imaging the back-focal plane of a 1.4 N.A. oil immersion condenser (Nikon) on a position-sensitive detector (First Sensor). Calibration of the detector response was performed by raster-scanning the laser across a trapped bead with the AOD¹². The power spectrum of a trapped bead position was fit to a Lorentzian to obtain the trap stiffness.

Freely diffusing monodisperse beads were trapped and lowered onto a surface-immobilized Cy5-labeled axoneme oriented parallel to the PSD horizontal axis. To perform constant force assays in the presence of ATP, force-feedback control was activated after the beads moved 40 nm away from the trap center. In the absence of ATP, MT polarity was determined by allowing TMR-labeled dynein to walk on axonemes for 5 min and accumulate at the minus-end before washing the assay solution and replacing it with the bead-motor mixture and apyrase. A trapped bead was lowered onto an axoneme and briefly released and trapped until it binds to an MT. Force feedback was applied in forward or backward directions. The magnitude of the applied force was adjusted by changing the laser power while keeping the bead-trap separation at 100 nm. The bead position was acquired at 5 kHz and the trap position was updated at 100 Hz to keep the bead-trap separation constant. The trap stiffness was set to 37.5 fN nm⁻¹. The thermal relaxation of the bead (300 Hz) was taken to be roughly equal to the corner frequency of the trap.

Force oscillation experiments were performed using the force-feedback controlled trap. The applied force was alternated periodically in a square wave pattern at 2.5 Hz, two order of magnitude slower than the thermal relaxation of the trapped bead (300 Hz). To enable for more rapid and accurate switching between the assisting and hindering forces, we commanded the trap to move by an experimentally estimated offset every time it switched between the forward and backward feedback setpoints. This compensated for the free rotation of the bead, which results in a movement without a net force exerted on the bead. This “dead” region corresponds to the 250–500 nm difference between bead positions under the forward and backward pull of the trap, despite the motor remains attached to the MT. For experiments with zero $\overline{F}$ on the bead, the bead-trap separation was kept constant at 100 nm and the trap stiffness was adjusted to apply desired forces on the bead. In experiments where ΔF was kept constant, force bias was provided by using different trap-bead separation distances when the bead was pulled towards the plus- and minus-ends of an MT. Over 90% of the applied force was along the long axis of the MT, whereas the short axis deviated from the trap center negligibly during data collection.

For the release rate measurements, beads were sparsely coated with tail-truncated dynein monomers (GFP-Dyn_331kD-DHA)¹⁶ were brought onto an axoneme and oscillated with a period of 0.7 s between two positions (±100 nm). MT polarity was determined using TMR-labeled dynein, as described above. The bead position was fitted to a step-finding algorithm¹² to detect individual release events. The bead to motor ratio was adjusted such that more than 80% of release events occurred in a single step. Release events occurred in more than a single step and dwells shorter than 3 ms were discarded from the analysis. Release data were sorted and binned by force. The cumulative distribution of each bin was fitted to a double exponential decay to determine fast (k₁) and slow (k₂) release rates. The double exponential decay fit was statistically justified using the F-test.

In MT gliding assays, the surface density of dynein was sufficient to glide MTs on a straight path for several microns throughout force application. Freely diffusing polystyrene beads were lowered to a gliding MT between 4 to 10 μm in length. These beads were tightly bound to the MT as soon as they were in contact with each other. After MT binding, the force-feedback controlled trap was engaged and the bead was pulled along the MT long axis back and forth at 2.5 Hz. The beads remained firmly attached to MTs during force oscillations. The external force did not alter the direction of gliding motility. The bead-trap separation was kept at 100 nm and forces on the bead were adjusted by altering the trap stiffness.

Data Analysis

Traces were recorded at 5 kHz, downsampled to 500 Hz and visualized using custom software written in MATLAB. Trajectories that contain instantaneous jumps greater than 40 nm were either excluded from the data analysis because this distance exceeds the maximum size of the steps that dynein takes. For the force-velocity measurements, the minimum accepted run time was 200 ms. The velocity was calculated by dividing the total distance traveled to the elapsed time during force application. Power was calculated by the multiplication of the average force on the bead and velocity of the motor movement. For step size analysis, trajectories were downsampled to 100 Hz, and fit to a step finding algorithm using the Schwartz Information Criterion¹¹. Step size versus force graphs in Supplementary Figs. 3c and 4c were interpolated using an exponential function. The step size was set to zero at 0 pN in no ATP, and at 3.1 pN in 1 mM ATP condition.

Data Availability

The data represented in Figures 1–4, and Extended Data 2, 3, 4, and 6 are available as source data in Supplementary Data. All other data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request. Yeast strains used in this study are available from the corresponding author upon request.

Code Availability

Software and code used in this study are available from the corresponding author upon request.

Extended Data

Extended Data Fig. 1. Force-induced release rate analysis of dynein.

a. When pulled towards the minus-end, dynein exhibits a slip bond behavior with an MT, in which the release rate increases exponentially by assisting force (black dashed curve). In the hindering direction, possible force-detachment kinetics of slip, slip-ideal, ideal and catch bond behavior are shown for comparison (solid curves). b. Cumulative distributions of dynein dwell time on an MT under a given force were fit to a double exponential decay (red curves) to calculate fast (k₁) and slow (k₂) release rates from MT. n = 504 for 1 pN and 512 for −1 pN. c. k₁ of dynein from MT (mean ± s.e.m.; n 270, 243, 479, 407, 385, 354, 487, 461, 380, 260, 208, 325, 137, 325 from left to right). This rate likely represents a weak interaction between dynein and tubulin. Similar to k₂ (Fig. 1c), k₁ increases with force in both directions. d. Comparison of the single and double exponential fit to example cumulative distributions of dynein dwell time. p values are calculated using F-test.

Extended Data Fig. 2. Measurement of force-detachment kinetics of dynein using a DNA tethered optical trap.

a. A tail truncated dynein monomer (GFP-Dyn_331kD-DHA) was labeled a 74 bp DNA tether at its C-terminal DHA tag using the HaloTag chemistry. The DNA-labeled motor was attached to a bead via a biotin-streptavidin linkage. b. MT release rates of dynein monomers pulled from the C-terminal AAA ring via a DNA tether (blue, mean ± s.e.m.; from left to right n = 534, 661, 251, 973, 1074, 1742, 3216, 1423, 1003, 984, 792, 501, 310, 240 from three technical replicates). MT release rates of dynein monomers pulled from the N-terminal linker via the GFP-antibody (red, Figure 1c) are shown for comparison.

Extended Data Fig. 3. Force-induced stepping of dynein in the absence of ATP.

a. Example trajectory of a bead driven by single full-length dynein at 4.5 pN hindering force (blue) in the absence of ATP. Red horizontal lines represent a fit with a step finding algorithm (see Methods). b. Step size distribution of dynein under assisting and hindering forces in the absence of ATP (n = 214, 207, 204, 203, 266, 316, 308, 400, 211, 233, 247, 233, 202, 204, 238, 205, 226, 203, 208, 265 steps from hindering to assisting forces). c. (Top) The average step size of dynein under different forces. Positive steps are in the minus-end direction. Error bars represent s.e.m. The red dashed curve is an interpolation of the data to an exponential function. (Bottom) The ratio of steps taken in the plus-end direction to minus-end-direction. d. The ratio of the experimentally measured velocities (Fig. 2b) to the average step size (c) in the absence of ATP. The errors represent s.e.m. of velocity measurements (Fig. 2b). The blue curve represents a fit to equation 3. The errors of the derived parameters are s.e. of the fit.

Extended Data Fig. 4. Force-induced stepping of dynein in 1 mM ATP.

a. Example trajectory of a bead driven by single full-length dynein at 5.6 pN hindering force (blue). Red horizontal lines represent a fit with a step finding algorithm. b. Step size distribution of dynein under assisting and hindering forces (n = 447, 428, 492, 430, 440, 460, 442, 291, 314, 381, 335, 298, 340 steps from hindering to assisting forces). c. (Top) The average step size of dynein under different forces. Error bars represent s.e.m. The red dashed curve is an interpolation of the data to an exponential function. (Bottom) The ratio of steps taken in the plus-end direction to minus-end-direction. d. The ratio of the experimentally measured velocities (Fig. 2c) to the average step sizes (c) in 1 mM ATP. The errors represent s.e.m. of velocity measurements (Fig. 2c). The blue curve represents a fit to equation 5. The errors of the derived parameters are s.e. of the fit.

Extended Data Fig. 5. Example traces for nucleotide-free oscillations.

a. Example trajectory of a dynein-driven bead oscillated ±4.9 pN in a square wave pattern without ATP. b. Example trajectory of a dynein-driven bead oscillated with +6 pN and −1.5 pN in a square wave pattern at 2.5 Hz. Even though dynein was pulled more strongly backward, it moved towards the MT minus-end in the absence of ATP. c. The bead position was subtracted from the trap position to determine the force exerted on the bead during force oscillations. Due to the thermal relaxation of the bead and the rotational freedom of the bead-motor linkage, the bead-trap separation reaches near zero when the bead is moved between forward and backward positions. To determine how force affects velocity, this “dead” period t₁ is omitted from total elapsed time and t₂ is taken as half period of oscillations. (Left) To change force on the bead, the trap is first moved 250 nm and then with proportional feedback-controlled increments every 10 ms until the desired force is reached. (Right) The trap is first moved 500 nm and then with feedback-controlled increments every 10 ms until the desired force is reached. An increase in this “overshoot” distance decreases t₁.

Extended Data Fig. 6. Force oscillations facilitate ratcheting of mammalian dynein-dynactin towards the minus-end of MTs in the absence of ATP.

a. The assembly of the DDB complex from human dynein, pig-brain dynactin and the N-terminal coiled-coil of mouse BicD2 (BicD2N, 1–400). BicD2N was fused with GFP at its C-terminus for attachment of the complex to antiGFP-coated beads. b. Example trajectories of DDB-driven beads pulled towards the MT plus- (left) and minus- (right) end under 1.5 pN force. The average velocities (mean ± s.e.m.) were calculated from 44 (left) and 27 (right) trajectories. c. Example trajectory of a human dynein-driven bead oscillated ±2.75 pN in a square wave pattern at 10 Hz shows processive motility towards the MT minus-end. d. The velocity of dynein-driven beads increases with ΔF in the absence of net force on the bead (mean ± s.e.m.; from left to the right n = 25, 32, 26 from three technical replicates). In comparison, DDB ratcheted faster towards the MT-minus end than S. cerevisiae dynein.

Extended Data Fig. 7. Force fluctuations increase the power output of dynein towards the minus-end.

a-b. Estimated $\overline{F}-V$ relationship under different ΔF in the absence (a) and presence (b) of 1 mM ATP. The model predicts that increasing ΔF leads to faster minus-end directed velocities at $\overline{F}=0pN$ and higher average hindering forces to stall the bead movement. The inset in (a) shows that the curves do not intersect at the same point. c-d. Force oscillations increase the power output of dynein in the absence (c) and presence (d) of 1 mM ATP. The power output of dynein at average hindering forces was calculated from the F-V relationship. e. Power output of dynein (black circles, mean ± s.e.m.; n = 42, 56, 58, 47 from left to right) in 1 mM ATP and in the absence of force fluctuations (ΔF = 0 pN). The blue curve corresponds to the 0 pN curve in d.