Concepts for design and analysis of receptor radiopharmaceuticals: The Receptor-Binding Radiotracers series of meetings provided the foundation

Abstract

A symposium at George Washington University on Receptor-Binding Radiotracers in 1980 and three follow-up meetings held at University of California, San Diego provided a forum for debating the critical concepts involved in the new field of designing and evaluating radiotracers for imaging receptors and transporters. This review is intended to educate young investigators who may be relatively new to receptor radiopharmaceutical development. Our anticipated audience includes researchers in basic pharmacology, radiochemistry, imaging technology and kinetic data analysis and how these disciplines have worked together to build our understanding of the human biology of transporters and receptor signaling in health and disease. We have chosen to focus on radiochemical design of a useful imaging agent and how design is coupled to analysis of data collected from dynamic imaging with that agent. Some pharmacology may be required for designing the imaging agent and some imaging physics may be important in optimizing the quality of data that is collected. However, the key to a successful imaging agent is matching the radiotracer to the target receptor and to analysis of the time-course data that is used to parse delivery from specific binding and subsequent metabolism or degradation. Properly designed imaging agents are providing critical information about human biology in health and disease as well as pharmacodynamic response to drug interventions.

The review emphasizes some of the ideas that were controversial at the 1980 conference and chronicles with literature examples how they have resolved over the four decades of using radiotracers to study transporters and receptors in human subjects. These examples show that there are situations where a very small K_D, i.e. high affinity, has the potential to yield an image that reflects blood flow more than receptor density. The examples also show that by combining two studies, one with high specific activity and a second with low specific activity injections one can unravel the pseudo-first order rate B′_max into the true second-order rate constant, k₃, and the unoccupied receptor density. The final section describes how mathematical methods first presented to the receptor-imaging community in 1980 are now being used to provide confidence in the analysis of kinetic biodistribution studies. Our hope is that by bringing these concepts together in a single review, the next generation of scientists developing receptor imaging agents can be much more efficient than their pioneers in developing useful imaging methods.

1. Introduction

The individual honored by this festschrift issue played an important role in many aspects of the development of radiopharmaceutical chemistry, starting with his pioneering work on technetium chemistry with Powell “Jim” Richards and Joe Steigman at Brookhaven National Lab. He was instrumental in developing the kit for labeling red blood cells with Tc-99m, as well as the “instant DTPA” kit and can rightly be called the father of instant kits for technetium. Bill co-authored with Joe Steigman the Nuclear Science Series monograph on The Chemistry of Technetium in Medicine (NAS-NS-3204). As a professor at George Washington University, his group worked on a single-photon emitter for imaging muscarinic receptors in the heart, an antagonist called 3-quinuclidinyl-[¹²³I]-4-iodobenzoate or IQNB, and that started his interest in receptor imaging, which is the theme of this review article. He also continued his work on Tc chemistry with development of a cyclic DTPA anhydride and a generic route for labeling peptides and proteins. These accomplishments have been described in JNM Newsline accounts after receiving two if the most prestigious awards of SNMMI, the Paul Aebersold Award in 1988 [1] and the de Hevesy Award in 1997 [2].

Prompted by his growing interest in receptor-based imaging agents, Professor Eckelman organized and hosted a symposium on Receptor-Binding Radiotracers in 1980, which lead to a two-volume series published by CRC Press [3]. There were many challenges that had to be overcome in order to make substantial progress in development of receptor-binding radiotracers but two decades later a few radiopharmaceuticals with this classification were being developed commercially. Research in development and clinical use of receptor-based imaging agents had grown rapidly over those decades, such that it became clear that a focused workshop would be useful to bring together thought leaders in radiochemistry, nuclear imaging and mathematical modeling of dynamic imaging studies with the goal of sharing ideas and hopefully standardizing some methods and nomenclature. In response to this need, Bill Eckelman and David Vera organized a meeting in La Jolla that included many of those who had attended the original 1980 conference and it followed a similar format. The proceedings of this meeting were published in Nuclear Medicine and Biology in 2001. That meeting had such an important impact on the conceptual evolution of receptor-targeted radiopharmaceuticals that it was followed by another Workshop on Receptor-Binding Radiotracers with the proceedings published in Nuclear Medicine and Biology in 2003. A third La Jolla meeting was called The Magic Bullet: A Century Later and contributions from that meeting were published in Nuclear Medicine and Biology in 2005. Several papers from these meetings are referenced in this review.

Our primary objective is to educate young investigators who may be relatively new to receptor radiopharmaceutical development. Our anticipated audience includes researchers in basic pharmacology, radiochemistry, imaging technology and data analysis and how these disciplines have worked together to build our understanding of the human biology of receptor signaling in health and disease. We have chosen to focus on radiochemical design of a useful imaging agent and how it couples to analysis of data collected from dynamic imaging studies. Some pharmacology may be required for designing the imaging agent and some imaging physics may be important for optimizing the quality of data that is collected. The biomedical significance of receptor imaging in health and disease will be found in other contributions in this issue.

2. Overview of concepts to be reviewed

Three broad topics are covered in this teaching review. These topics are limitations associated with receptor-radioligand affinity, the inherent second-order kinetics of ligand-receptor binding and the robustness of mathematic analysis of the kinetics of receptor imaging experiments in vivo. Each of these was part of the 1980 symposium on Receptor-Binding Radiotracers [3]. To show how these three topics interact, the issues are summarized here and then presented with more details and examples in the subsequent sections. In this presentation, we specifically start with an assumption that a receptor target has been validated. Our objective is to emphasize how a new radioligand for in vivo imaging might be conceived and developed for that target.

The first issue is related to affinity of a ligand-receptor interaction and inevitably comes down to the association (forward binding) rate constant, k_on, in Fig. 1A. Pharmacologists engaged in developing receptor-based ligands intended for an in vitro assay of receptor density in a tissue slice strive to achieve the highest k_on possible and are content with a dissociation rate, k_off, that is nearly negligible. This approach is completely acceptable for experiments where tissue slices are directly and equally exposed to a dilute radioactive ligand in buffer for sufficient time to achieve equilibrium. The unbound ligand is then washed off of the slice on a slide and the ligand bound to tissue is exposed to autoradiography for quantification. It is apparent from Fig. 1A that k_on·[L]·[R] and k_off·[LR] reach a steady state and the equilibrium constant is $\text{K}=\frac{\left[\text{LR}\right]}{\left[\text{L}\right]}\cdot \left[\text{R}\right]=\frac{{\text{k}}_{\text{on}}}{{\text{k}}_{\text{off}}}$. Written in this format, the equilibrium constant has the units of L/mol whereas the inverted equilibrium constant, commonly referred to as the equilibrium dissociation constant, K_D, has units of mol/L, a concentration unit that is more familiar to the chemist. A lower K_D implies a higher affinity so one generally aims for make radioligands for imaging where K_D is sub-μM or even sub-nM. We recommend Hulme [4] as a practical teaching review on theoretical and experimental aspects of in vitro ligand binding assays. Note that in this review a rate constant is lower case, e.g. k₁, and an equilibrium constant is upper case, e.g. K_D.

Fig. 1.

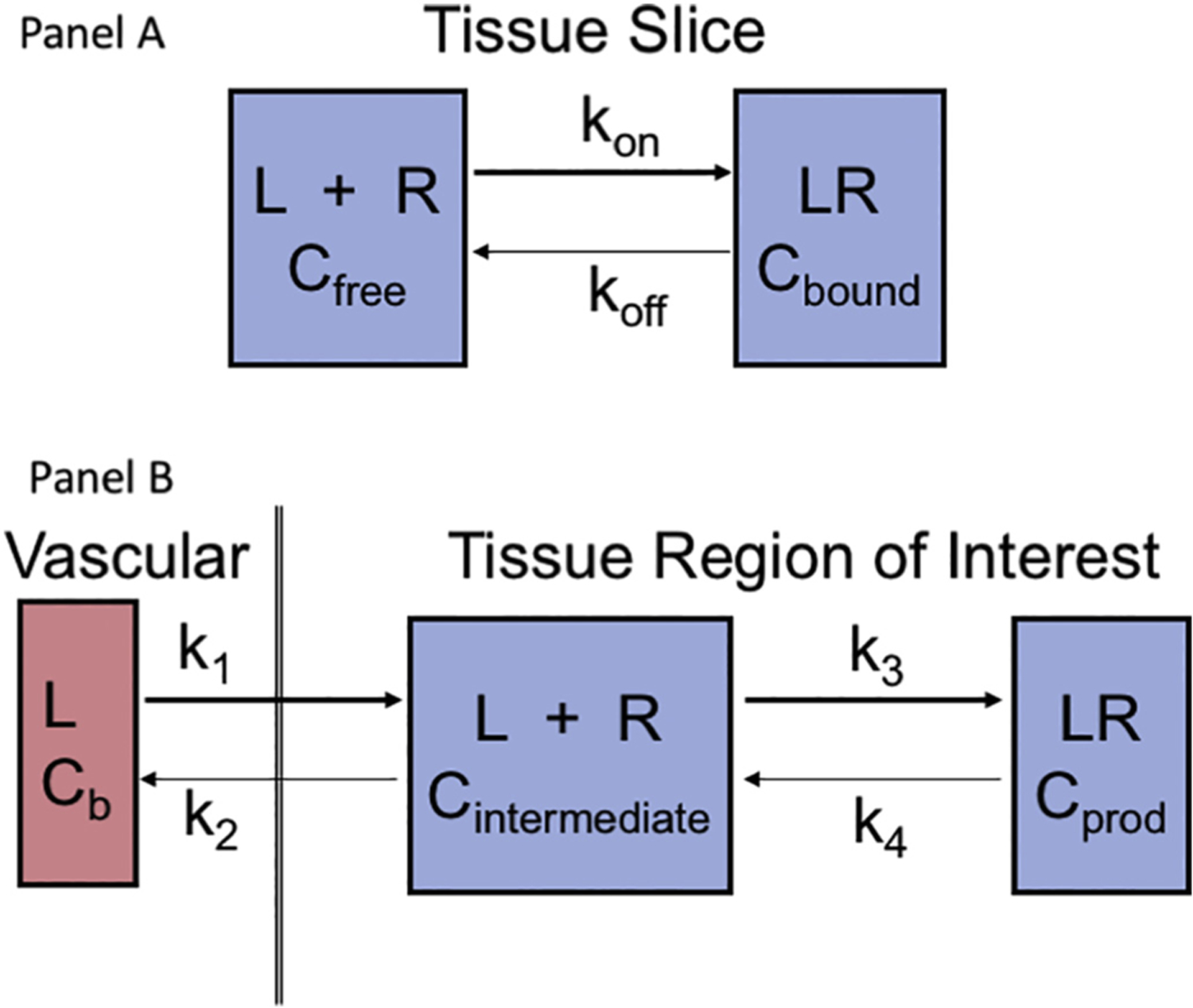
Receptor binding in vitro and in vivo. (A) The whole tissue section is exposed to a uniform level of ligand for sufficient time to achieve a steady state in the free and bound compartments. Then the medium is replaced by a ligand-free solution to wash away unbound or non-specifically bound ligand, leaving only C_bound, which can be measured by quantitative autoradiography. (B) The ligand is supplied in the vascular pool and requires transport across the capillary endothelium and a cell wall to enter the intracellular space where it then equilibrates between a bound and a free state. This is a dynamic process, so identifying a true steady-state condition is problematic.

The radiochemist engaged in developing new imaging radioligands often builds on the medicinal chemistry and pharmacology literature. However, for in vivo studies radiochemical design is faced with an additional complication, Fig. 1B. The rate of receptor binding in vivo is also coupled to delivery of the radiotracer from the vascular space to the cellular target, k₁, a factor that the pharmacologist exposing a tissue slice to a bath of radioligand and then washing off unbound material can legitimately ignore. There are now two equilibria to address; the delivery process to the cellular target where receptor resides, k₁/k₂, will result in a steady state concentration of radioligand in that extravascular pool, C_intermediate in Fig. 1B. Then equilibration between free and bound radioligand, k₃/k₄ in vivo, will be quantified by the same equilibrium K_SS described above for in vitro measurements. In fact, k₄ for dissociation of bound ligand in the in vivo situation should have the same value in vitro as assayed by a washout experiment when the imaging study cover about the same time of exposure [4]. The new constraint in vivo is that $\frac{d{\text{C}}_{\text{intermediate}}}{dt}\simeq 0$ at steady state.

It is apparent from Fig. 1B that the flux for intravascular L binding to a tissue receptor to yield C_prod is $\text{FLUX}=\frac{{\text{k}}_1\cdot {\text{k}}_3}{{\text{k}}_2+{\text{k}}_3}$. However, when k₂ is diminishingly small compared to k₃, the rate of receptor binding in vivo resolves to k₁·k₃/k₃ which is simple k₁, the delivery parameter. The consequence is that a very high affinity radioligand becomes a flow agent, an elegant “molecular microsphere.” The first broad topic for this review relates to issues of separating flow from the detailed biochemistry that is the ultimate goal of the imaging experiment, be it receptor density, antigen targeting, enzyme activity or even metabolism.

The second issue is that binding of a receptor to a radioligand is always a second-order reaction that requires consideration of the concentration of both components. Binding rate = k_on [R]·[L] is useful for measuring the initial velocity of a reaction in a test tube or cuvette. However, the in vivo world is often complicated by a mixture of high-affinity (e.g. G-protein coupled) and low affinity receptors and even non-specific binding when the receptor target is expressed on the cell membrane. Furthermore, some receptors are in the cytosol, others may be bound to mitochondria or even in the nucleus. And there will likely be non-specific binding sites, NSB, in addition to those that the radiopharmaceutical was designed to target. Often the NSB sites are orders of magnitude more abundant but with orders of magnitude lower affinity, than the targeted receptor. Quantifying [L] is also not easy, especially if there are naturally occurring ligands that compete with the injected radioligand. The experiment might be limited to measuring [L]_unoccupied. Note also that images generally report a quantity of radioactivity, Bq, in an image voxel; this corresponds to a value of L that can be quantified through the measured specific activity, Bq/nmol. Thus, it is common in the mathematical models to parse [L] into a quantity variable, L (Bq, which is converted to nmol from specific activity value, SA), and a reaction volume, V_r (mL).

The biological question becomes one of separately distinguishing the different effects of [R] and k₃ in Fig. 1B. One solution uses a combined parameter, B_max = k₃·[R], but that is not satisfying if disease might involve changes in both parameters and in an unknown way. Some have argued that association rate constants are not affected by disease; pathology only changes the rate of dissociation of the LR complex. However, we are not aware of convincing experimental evidence to support the generalization that association rates, k_on, are not influenced by pathology. The way to unambiguously separate these two variables is to carry out multiple sequential dynamic imaging experiments, the first is at high specific activity to measure k₃·[R_max] but the second is at much lower specific activity such thata significant portion of the receptor population is filled by the increased amount of ligand in the second injection. The time course of uptake can be analyzed by classical 2nd order kinetic methods. Graphically this involves plotting 1/conc of ligand added (to injection 2 minus that in injection 1) versus time t; the observed $\text{rate}=\frac{1}{\text{t}}\cdot \text{ln}\frac{{\text{C}}_0}{\text{C}}$ where C₀ is the concentration of added carrier. In this experiment we are measuring k₃·([R_max] − [R_occupied]) by manipulating [R_occupied] by the cold ligand added for the low- specific-activity second injection, effectively carrying out an in vivo Scatchard assay. This strategy deliberately reduces specific activity of a radiopharmaceutical, which goes against the instinct of any radiochemist, but may be the surest way to tease out the independent information of k₃ and [R_max].

Earlier studies of drug occupancy had used imaging with tracer amounts of an imaging agent after administering graded doses of a blocking drug. In this case the goal was to measure the mass sensitivity of a particular binding site. The NIH PET Department used this approach to test a putative M2-selective drug [5]. [¹⁸F]FE-TZTP uptake was inhibited by administration in a mass dose-dependent way of the muscarinic agonist L-687,306. In a similar study, [¹⁸F]FES-PET was used to demonstrate that the therapeutic mass of fulvestrant determined via a uterine binding assay was not sufficient to block tumor-associated estrogen receptors in vivo in breast cancer [6] (see Fig. 1 in that publication). This result led to the company increasing the recommended treatment dose. These are both examples of receptor imaging to assess the pharmacodynamics of a new treatment drug; neither was used to quantify receptor concentration, only to test whether the receptor was fully occupied.

The third issue involves mathematical analysis of the time course for in vivo biodistribution kinetics of a new radioligand. This section considers sensitivity, identifiability, quantification of the goodness of fit between experimental observations and the data analysis and the receiver operating curve for the imaging biomarker. A typical imaging experiment will provide the time course in regions that are putatively rich in target receptors and regions where there is good reason to believe that there are no target receptors although there may be NSB sites. In addition, information is collected on the plasma clearance curve, perhaps even quantification of arterial as well as venous curves, possibly with correction for metabolites if the blood is sampled and analyzed. This experimental information is described by a complement of differential equations that describe the time course of the radioactive ligand in various compartments, including delivery, uptake, any chemical modification in vivo, and washout. Vascular, interstitial and cellular compartments may be involved and the chemical form of the radioligand may be bound or free or metabolites. The extent to which these equations match the experimental observations will need to be solved simultaneously and iteratively, frequently using a Marquardt-Levenberg style solver algorithm for non-linear systems of differential equations. Clearly this process involves numerous variables, multiple data channels (e.g. uptake in organs and plasma clearance curves with metabolite correction) and an even larger number of data points that are often not evenly spaced on the time axis. One thus faces the challenge of showing that a plausible fit for these physiological variables can be determined. Mathematical simulations of the several differential equations is the first step in showing that the shape of the resulting time-activity curves changes as biologically significant variables in the model change, for example blood flow, vascular permeability and receptor density. This process is called sensitivity analysis and is a test to show that the radioactivity level at the target changes with target density, ideally in a linear way with unit slope. After studying this section, the radiochemist should be convinced that sensitivity analysis should precede any radiochemical development of a new radioligand. The basic principle is that if the imaging study cannot be interpreted, the radiotracer will never become useful.

Identifiability analysis is a more advanced concept that considers all of the factors that are important to biodistribution kinetics of an imaging agent: target organ blood flow, receptor-ligand affinity and target receptor concentration as well as potential non-specific interactions. It goes beyond showing that a plausible fit for physiological variables can be determined by testing whether or not the fit is unique. This is a more abstract analysis that considers the mathematical model as well as the imaging protocol, for example the timing requirements for the initial uptake phase, uptake parameters that can be independently measured, or the length to which the tail should be followed. It might be thought of as global sensitivity analysis for high-dimensional problems. Ordinary differential-equation models often contain a large number of parameters that must be determined from dynamic imaging measurements by parameter estimation. For the parameter estimation procedure to be useful, there must be a unique set of parameters that can produce the measured data. This is not the case when a model is not structurally identifiable with the given set of outputs selected as measurements. This analysis may combine parameters to simplify the task. For example, one common approach is to fit k₁/k₂ as a single variable, another is to estimate only the product k₃·[R_max] although this introduces the limitation described in the second issue.

Another important analysis tests for systematic errors by measuring the goodness-of-fit between the model and the data. The easiest way to evaluate this characteristic is through visual examination of a plot of the standardized residuals at each time, basically a χ² analysis for a single region. A more complicated Akaike information criteria (AIC) test should be applied if many parameters are adjusted and many regions are involved. Lastly, in order to qualify interpretation of an imaging biomarker, a receiver-operating characteristic curve should be generated to illustrate the diagnostic ability of a binary classifier system for modeled parameters as the discrimination threshold is varied. The graph is a plot of the true positive rate (sensitivity) versus the false positive rate (1-specificity) as the threshold between positive and negative interpretation of the parameter is varied.

3. The influence of physicochemical properties in radioligand design

3.1. Kinetic constraints

Building a potentially clinically useful new imaging agent involves much more that chemical synthesis. The physicochemical properties that the radiochemist needs to consider during the initial design of a new imaging agent include the equilibrium constant for ligand-receptor binding, specificity of binding, and the lipophilicity of the drug. The equilibrium constant is generally expressed as a dissociation constant, K_D, which is in molar units with a goal of K_D in the range of <10 nM. For non-specific binding sites, K_D may be in the mM range which should not be a limitation per se. The limitation comes from the fact that non-specific binding (NSB) sites frequently have a concentration in tissue that is orders of magnitude higher than the target receptor so NSB may out-compete for a radioligand based on a mass affect. Constraints for partition coefficient depend on whether the agent needs to cross the blood-brain barrier or not. Our objective in this section is to review these properties and their practical limits and to introduce some of the tools available during radiopharmaceutical design to increase the likelihood of achieving these goals.

In the 1980s, pharma often relied on in vitro tissue binding assays for initial screening of receptor-based drugs, as depicted in Fig. 1, panel A. The assay is based on equilibration of ligand with receptor mounted on a slide, followed by washing off any unbound ligand. This approach emphasized a very low K_D for the equilibrium. The initial drugs for radiolabeling with the intent of imaging receptor concentration or enzyme activity did not have sufficiently high affinity (i.e. sufficiently low K_D) to produce the high target to background ratio desirable for generating an image with acceptable signal-to-noise. Within the next two decades, that situation changed but with the consequence that when the ratio of receptor concentration to K_D became too extreme, the radiopharmaceutical uptake became dependent on flow/transport more than receptor concentration. This situation in readily apparent from analysis of the algebra associated with the simple model in Fig. 1, panel B. In this model, k₁ is the initial delivery parameter for L and is generally blood flow; k₁/k₂ is the equilibrium constant for movement between the intravascular and extravascular spaces. Immediately after administration of radioligand, L, the value of k₄ can reasonably be assumed to equal zero and be neglected in analyzing the initial observed uptake. The concentration of L in the intermediate space is not independently measured but the relative rate of egress from this tissue region of interest, ROI, involves a competition between returning to the vascular pool versus moving into the receptor-bound pool via rate k₃. Thus, the flux for tracer ligand that becomes bound is given by $\frac{{\text{k}}_1\cdot {\text{k}}_3}{{\text{k}}_2+{\text{k}}_3}$.

What happens in this equation when k₂ becomes diminishing small, k₂ ≪ k₃? Clearly k₂ drops out of the equation and k₃/k₃ = 1 so it also drops out, leaving only Flux = k₁. In simple language, the new radioligand tracer has become a blood flow tracer, a molecular microsphere. This concept was demonstrated experimentally by Bassingthwaighte’s laboratory in developing radioiodinated 2-iododesmethylimipramine (IDMI) as a freely diffusible (log P = 1.5) but highly retained (k₂ ~ 0) flow marker [7]. Desmethylimipramine is an α₂-adrenergic antagonist. In a large animal study eleven open-chest sheep were injected simultaneously but from different syringes with 16.5 μm radioactive microspheres (¹⁴¹Ce or ¹⁰³Ru labels) and [¹²⁵I or ¹³¹I]IDMI [8]. The myocardium from each of the eleven sheep was cut into 254 pieces averaging ~200 mg and regional deposition densities were calculated for each tracer. The linear regression coefficient for the two flow markers was 0.93 ± 0.050; the relative dispersion within animals for the two tracers was also remarkably similar, 33% for IDMI and 38% for microspheres. From this example, it is clear that a K_D where k₂ approaches zero will not lead to an imaging agent useful for measuring flux into the receptor-bound pool; it will not quantify receptor concentration in a tissue region. The lesson is that any impulse by a radiochemist to make a molecule with the highest possible k₃/k₂ ratio will not be rewarded. This concept was sufficiently controversial at the 1980 meeting that it was addressed in more detail with examples at the first La Jolla meeting [9]. More recent studies with neogalactoalbumin, a receptor ligand that can be synthesized with a wide range of k_on values can be pushed to a limit where it only measures blood flow.

A report at Receptors 2000 considered three biochemical reactions that are generally thought of as rapid and tested whether they were diffusion limited, i.e. reacted on every collision [9]. Superoxide dismutase contains a copper active site that degrades the oxygen radical anion with a rate constant k₃ of ~10⁹ M⁻¹ s⁻¹, compared to a maximum collision rate in solution approaching 10·10¹⁰ M⁻¹ s⁻¹, but it also has a very rapid reverse rate so is not diffusion limited. Epidermal growth factor is a 6 kD peptide that binds to a cell-surface receptor with a sub-nM K_D. However, it is not flow-limited because of a low k_off, 2·10⁻³ s⁻¹. One of the most thoroughly studied rapid reactions involves the O₂-carrying function of heme iron. The measured rate constant for collision of O₂ with myoglobin is 4·10⁸ M⁻¹ s⁻¹, which is ~40× faster than the rate at which O₂ binds to myoglobin; the critical k₃ reaction occurs inside the heme complex. These examples show that k_on was not a limitation when it was balanced by a reasonably high k_off.

3.2. Thermodynamic constraints

Lipophilicity is also measured as an equilibrium constant called the partition coefficient, P. Partition coefficients describe the equilibrium partitioning of a neutral solute between two immiscible phases. Octanol-water partition coefficients (P_OW), or their logarithms (log P), are commonly used to quantify lipophilicity in drug discovery. P_OW was originally developed for drug and pesticide development, but now it’s considered an important characteristic of any chemical because it determines that chemical’s fate in any environment, including tissues of the human body. Lipophilicity was another limitation of many of the early receptor-imaging tracers, perhaps because pharma generally favors lipid soluble molecules as they are bioavailable orally and, to the extent that they bind weakly and non-specifically to plasma proteins, they are cleared more slowly from blood and are not rapidly excreted. PET imaging was just getting started in 1980 and so most of the imaging agents were labeled with radioisotopes of iodine (¹²³I) for SPECT imaging. Iodine is nearly the same electronic diameter of a methyl group and adds to lipophilicity of a molecule. With increased availability of cyclotrons, ¹¹C and ¹⁸F became more widely available as practical labels for PET. The potential to modify lipid solubility in order to help imaging agents cross the blood-brain barrier (BBB) thus became possible. Dischino played a pivotal role in demonstrating the optimal partition coefficient for extraction of ¹¹C-labeled radiopharmaceuticals in the brain [10].

In the chemical and pharmaceutical sciences, two phases are used as solvents, one phase is water and the other is hydrophobic, typically 1-octanol. Partition coefficients are useful in estimating the distribution of drugs within the body. Drugs with high octanol/water partition coefficients are mainly distributed to hydrophobic areas such as lipid bilayers of cells. Hydrophilic drugs have low P_OW and are primarily located in aqueous regions such as serum; they are also more rapidly excreted. Partition coefficients can be measured experimentally by a simple shake-flask assay or by HPLC [10]. Alternatively, they are estimated by fragment-based or atom-based calculations [11,12]. In practice the partition coefficient is described by an equilibrium constant but the amount of solute being tested should also be specified because sometimes the equilibrium is limited by its solubility in one of the distribution phases. This is not a limitation with radiopharmaceuticals which are generally tested at mg levels or lower.

Dischino’s studies involved molecules that were not ionizable under normal aqueous conditions, aliphatic and aromatic ethers and alcohols and benzophenones [10]. The conclusion from his partition coefficient study was that when log P_OW values for molecules were between 0.9 and 2.5 they passed freely across the intact BBB at a blood flow of 100 mL/min; i.e. extraction was quantitative. As log P increased, extraction fell precipitously because of binding of radiotracer to plasma proteins. As expected, there was also a minimum lipophilicity required to cross the tight junctions of the BBB during the first pass. We are not aware of any subsequent publications that have been inconsistent with his Fig. 4 [10], which is now a classic in radiopharmaceutical chemistry. This is in spite of the fact that drugs are frequently designed with log P > 3 for optimal binding to receptors, presumably because it leads to sustained biodistribution kinetics. Regrettably, this characteristic is not an advantage for imaging studies.

Fig. 4.

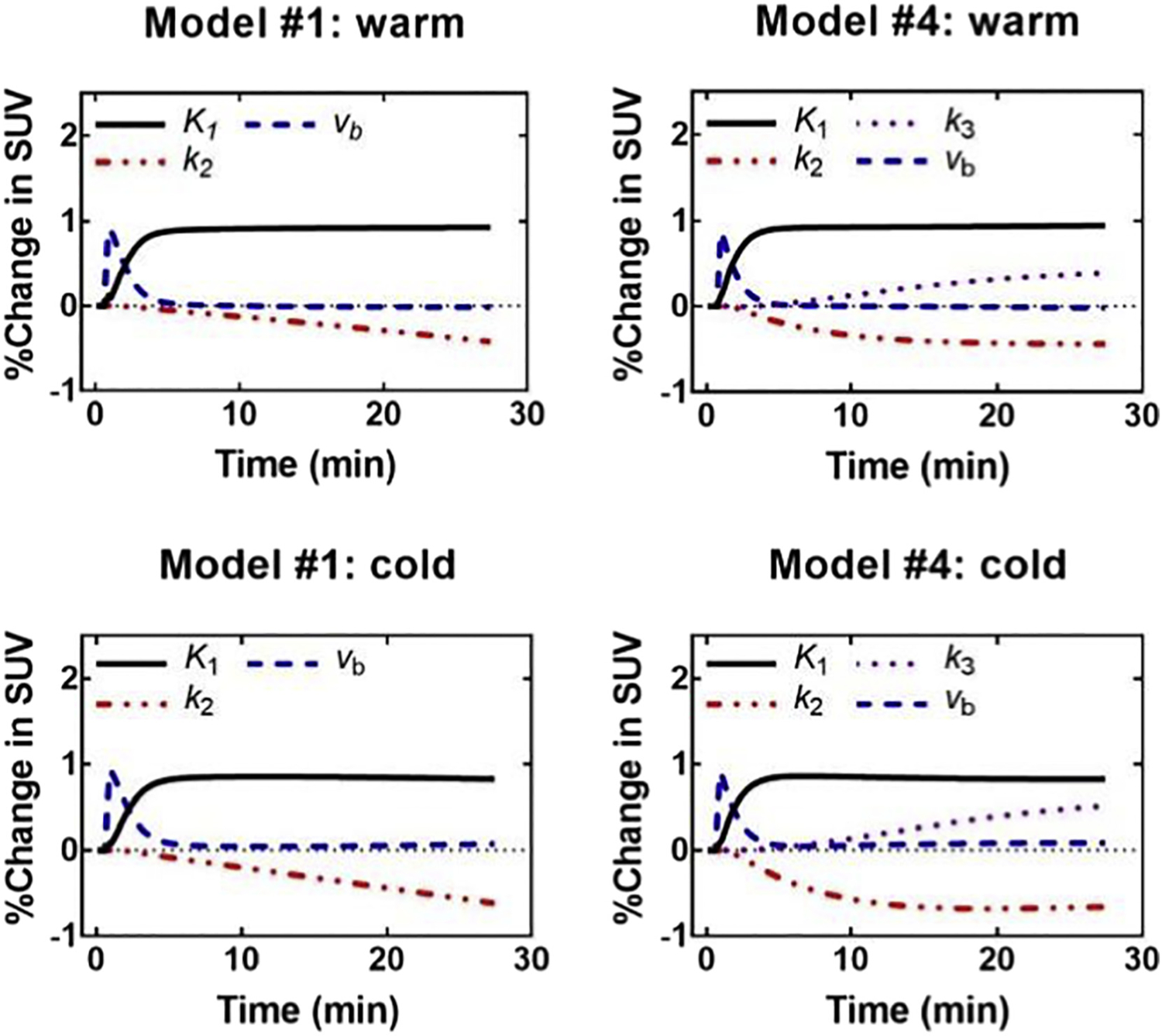
Sensitivity analysis shown as a percentage of change in SUV at different times after injection. This figure was helpful in evaluating different approaches to analysis of [¹¹C]-acetate PET in brown adipose tissue activated by cold exposure in healthy elderly men. Models with only 2 or 3 tissue compartments and four model parameters provided the best compromise between quality of fit and stability/accuracy.

Figure is reproduced from supplemental data for reference [60].

Dischino’s work showed that with log P as low as 0.1, extraction in brain was still 70%, implying that a radiopharmaceutical with a partition coefficient as low as 1 (log P_OW = 0) would equilibrate in the brain within a few minutes. This became an issue in developing alternative hypoxia imaging agents, where there are agents in the literature with log P ranging from −0.76 to +0.75, well on the hydrophilic side of Dischino’s graph. However, because there is often covariance between hypoxia and perfusion, it is important to have a hypoxia imaging agent where the equilibrium image after at least an hour is free of the influence of any perfusion limitation. Biodistribution studies with [¹⁸F] fluoromisonidazole (P_OW = 0.43) showed that the image within 5 min after administration was highly correlated with flow but the image at 60 min was uniform at a tissue/blood value of ~1 in all tissues except those involved in excretion [13]. Thus, depending on the application, log P for a useful radiopharmaceutical may be lower than 1.

Lipinski’s rule of five (RO5) for biologically active compounds goes beyond log P in characterizing a potential ligand [14]. The rule was originally based on the observation that most orally administered drugs are relatively small molecules and moderately lipophilic. In addition to log P < 5, it also recommended molecular weight < 500 and hydrogen-bonding parameters, H-bond donors <5 and H-bond acceptors <10. Note that all of these parameters are multiples of five, hence the name RO5. When one searches a structure in PubChem, as much information as is available related to RO5 parameters is provided. The RO5 has been described as one of the most influential concepts in development of bioavailable drugs. However natural selection has found structures that do not comply with the RO5 but are still useful drugs; the classical example being cyclosporine [14]. While this concept is often recited in the medicinal chemistry literature, its relevance to radiopharmaceutical development is limited because RO5 focuses on oral administration. It would be unfortunate if a potential imaging agent was ruled out of development because it violated RO5 requirements.

3.3. Structure-activity relationships and molecular modeling

Structure-activity relationships have been the method of choice for designing radiotracers with optimal properties for imaging. Often this might involve a development strategy as simple as a graduate student reviewing the medicinal chemistry literature and finding a drug structure that is in development for targeted therapy but could also become a useful imaging agent. Perhaps the molecule was too toxic at the amount required for therapy, but it could still be useful for imaging. The clever chemist can design a labeling strategy for introducing ¹¹C or ¹⁸F at a site the medicinal chemistry studies have shown is not critical to binding and is not metabolized. Alternatively, molecular mechanical modeling simulations of receptor binding pockets are becoming more readily available and docking software platforms are providing novel insight for testing initial design of new drugs and imaging agents. This provides a potential for reducing the time and resource-consuming component of radiopharmaceutical development. These studies are often called in silico design and are already being used by pharma to help screen for optimal absorption, distribution, metabolism, excretion and toxicity of potential new drugs. While the approach might appear deceptively simple at first introduction, the procedures are not simple, as demonstrated below. However, we believe they have great potential in guiding future design of receptor-binding radiotracers.

The in silico design procedure begins with as much structural information on the receptor target as possible, including X-ray structures of crystals and NMR in solution, ideally with a ligand in the binding pocket. The second requirement is similar and requires gathering structural information on a family of alternative lead compounds that interact with the receptor. While there are large libraries of small-molecule structures, the fact remains that the number of possible small molecules is unimaginably large. The number of proteins with detailed structural information is growing rapidly. The Protein Data Bank archive (PDB, www.wwpdb.org) serves as the repository for >50,000 3D structures of proteins. Structural information often requires the chemist to develop detailed information on the molecular geography of the intended binding pocket. A large protein may contain 100 or more possible pockets with a wide range of shape similarity. The larger the pocket, the more likely it is to change its shape to allow binding of multiple conformations. It must also be appreciated that the ligand can protrude into the surrounding solvent space, increasing the possible ligand structures and further complicating the search for a thermodynamic energy minimum for ligand binding. There are several software toolkits available for ligand-receptor docking studies based on molecular mechanical energy minimization. Two examples are presented in this section to show the potential value of in silico design in imaging.

The impact of molecular mechanical modeling or docking studies on design of receptor imaging agents has been modest at this point in time. David Reichert’s program at Washington University is leading the way and we present two of his findings to stimulate further research in this area. Molecular modeling has not yet been used to find new structures for novel imaging agents. It is, however, proving effective for optimizing the design of lead radiopharmaceuticals. A Comparative Molecular Field Analysis, CoMFA, docking study has been reported for 36 estrogen-receptor, ER, ligands whose experimental relative binding affinities (RBAs) were available for both of the nuclear receptors, ERα and ERβ. A PET imaging agent, 16α-[¹⁸F]-fluoro-17β-estradiol, is currently being used to assay ER density in patients with the clinical objective of selecting ER-positive breast cancer patients for hormonal therapy [6,15]. The molecular modeling study took advantage of known crystal structures for 17β-estradiol bound to ERα and genistein bound to ERβ that were modeled with SYBYL software. Docked poses of the ligand-receptor complexes were predicted and optimized using the Tripos force field. The LR complex was allowed to relax until a pre-determined stopping criterion was reached. This required adding a single water molecule in the complex. A robust correlation between experimental relative binding affinities, RBA, and calculated molecular steric and electrostatic fields was found. For ERα the R² was 0.79; for ERβ it was 0.93. The experimental subtype selectivity expressed as (RBA for ERα)/(RBA for ERβ), ranging from 0.1 to 5.3, was tested against that predicted by the models with the result that the most selective ligands were ranked correctly [16]. This publication provides a good tutorial on the input information and software required for carrying out a docking study. The result nicely illustrates the value of molecular mechanical modeling as a prescreening tool for in silico drug design of a receptor subtype-selective imaging agent.

Dopamine receptor subtype-selective molecules are an important second topic to which molecular modeling has been applied. This research was initiated with minimal X-ray diffraction structural data on these aminergic receptors. Realistic homology models were built for the D₂ and D₃ receptors complexed with haloperidol [17]. Both D₂ and D₃ share similar 3D folds and conformations although there are sequence differences for residues in both the extracellular loop and the transmembrane regions that make the D₂ binding pocket less shallow that that for D₃. A combined receptor-structure and ligand-binding computational model was developed to explore D₂/D₃ selectivity. To further refine the model, molecular dynamics simulations were done in a lipid bilayer/solvent environment. The resulting conformation of haloperidol-receptor binding was aligned with the binding conformation of other ligands and 3D quantitative structure-activity relationships (3D-QSAR) were tested by Comparative Similarity Indices Analysis (CoMSIA). This approach accommodates differences in steric and electrostatic interactions, including hydrogen-bonding and hydrophobic interactions that contribute to selectivity. The new models for D₂ and D₃ were highly predictive of subtype selectivity when tested against 162 ligands that had been built by the Washington University group [18,19] or were available from the NIDA-IRP library, with K_i values ranging over five orders of magnitude. This result validated the stereochemical quality of the receptor model to predict the equilibrium dissociation constant K_i that is calculated from measured IC₅₀ using the Cheng and Prusoff [20] correction. This corrected K_i parameter quantifies differences between a standard ligand and the experimental ligand that is being modeled. It was discussed in detail at the 2nd LaJolla meeting, including the importance of the Cheng-Prusoff correction [21].

At this point in development, molecular modeling has not addressed the extent to which the wide range in K_i is a result of changes in either k_on or k_off or both for receptor binding. This is a current limitation in the field that deserves more attention as methods develop. The rate constants that drive the equilibrium k_on parameter are k₁·k₃·[R_max]; for k_off they are k₄ ~ k₂ in the in vivo model (Fig. 1B). Additional kinetic information would be important to test whether in vivo very high affinity ligands have crossed over to where they are dominated by delivery/blood flow such that it will be hard to tease out k₁ from receptor density, k₃·[R_max], in vivo from kinetic analysis of a dynamic imaging experiment. Perhaps the observation that D₂/D₃ selectivity is retained at high affinity suggests they will not be flow-limited but more specific supporting data is needed. However, this appears to be the only radiopharmaceutical study that is sufficiently rigorous and with enough compounds to test whether a high affinity ligand in the brain might be so high that it transitions to flow domination rather than a measure of receptor density. Additionally, it might be extended to test whether it confirms the hypothesis that changes in K_i are dominated by changes in k_off, with k_on remaining relatively constant.

A similar approach has been applied to discovery of optimal β₂-adrenergic ligands where the receptor is a 7-transmembrane G-protein coupled receptor. The published crystal structure of the human β₂-adrenoceptor containing a diffusible ligand, carazolol, was used [22]. At this time molecular modeling of ligands binding to the β₂-adrenergic receptor has only been applied to potential therapeutic drugs [23,24], but the study illustrates the sophistication of targetable receptors that can be modeled in silico, studied in a somewhat realistic in vitro environment in the laboratory and compared with docking predictions. It should be helpful for studies directed toward imaging the sympathetic nervous system or adrenergic receptors in the lung.

3.4. Putting it all together

In closing this section, it is important to always remember that the time course of biodistribution of an injected imaging agent involves a delivery phase and an uptake/binding phase. It is always important to be able to analyze the data to distinguish tracer uptake rate independent of the contribution of regional blood flow [25]. This point was emphasized in a recent “Invited Perspectives” comment on a new radiopharmaceutical for imaging apoptosis [26]. In this case, k₃ for retention of the tracer in muscle was zero but k₁ was high, feigning tracer accumulation in muscle if uptake is reported as %ID/g or SUV_max.

4. On the influence of radioligand specific activity in design and modeling

4.1. Receptor binding follows second-order kinetics

The second issue and the one that probably drew the most energetic discussion at the 1980 Receptor-Binding Radiotracers meeting related to the issue of deliberately reducing the specific activity of a radioligand in order to analyze the time-activity curve using second-order kinetic models [25]. This prompted a more thorough discussion of the theoretical issues [27,28] and some practical examples [29–31] at the April 2003 La Jolla meeting, including approaches to measuring both k₃ and B_max. From Fig. 1B it is apparent that receptor binding rate = k₃ [R]·[L] is a second-order process where k₃ has units of L/mol·s (M⁻¹ s⁻¹) and the two reagents, receptor and ligand, have units of mol/L. In a typical tracer imaging experiment, the concentration of [L] is not sufficient to change [R] during the time interval when the reaction rate is observed, so analysis of the rate curve will only provide the product k₃·[R], which is often referred to in publications as B′_max, the level of unoccupied receptors.

4.2. Graphical analysis of compartmental models

The Brookhaven group quantified dopamine transporter occupancy with a graphical method using the behaviorally active (−)-[¹¹C]-cocaine as the tracer [32]. These studies nicely documented the capability of a rapidly reversible tracer with only modest affinity to measure dopamine transporter availability in the human brain. Measurement of tissue radioactivity in a region of interest and plasma radioactivity, ROI(t) and C_p(t), respectively, were analyzed graphically. These measurements were the experimental input for a graphical analysis model for the distribution volume of the ligand, DV, plus the plasma volume, V_p. Occupancy of the dopamine transporter by drugs like cocaine, whose residence time in the brain is short, could be done with tracer injections without additional carrier. The study provided important new information on the function of neurocircuitry in addiction. A publication from the first La Jolla meeting, Receptors 2000, describes the experimental methods and data analysis in detail [32].

Another presentation at the first La Jolla meeting provided a teaching review on compartmental modeling for in vivo quantification of neuroreceptors [33]. It compared and contrasted kinetic, equilibrium and graphical methods for estimating rate constants that characterize tracer transfer between plasma, brain and receptors. While it did not address the potential value of parsing receptor binding into k₃ and [R_max], it is a useful teaching review about standard modeling methods.

Radiochemists aspire to achieve the highest specific activity product as possible, intuitively justified because of the relatively few specific binding sites in receptor systems, especially for neuroreceptors. For generator-produced radionuclides such as ^99mTc and ⁶⁸Ga, specific activity approaches the theoretical limit. For cyclotron produced radionuclides such as ¹⁸F and ¹¹C, specific activity is often several orders of magnitude below the theoretical limit [34,35]. Later in this section we discuss some advantages of experiments involving deliberately reduced specific activity, called carrier-added protocols.

4.3. TcNGA is a versatile model system for testing concepts of data analysis

The receptor-binding agent we presented at Receptor-Binding Radiotracers in 1980 was labeled with ^99mTc and was a hepatocyte-specific ligand for imaging liver pathology [28]. It was called neogalactoalbumin, NGA, and it could be synthesized by coupling albumin with a ratio of reactant IME-thiogalactose varying from ten to >500. This resulted in a wide range of affinity constants for binding to membrane-bound hepatic binding protein, HBP. The experiment had several unique and advantageous features. There is no barrier between hepatic plasma and the receptor on hepatocyte plasma membrane, therefore no endothelial barrier to transit. When the ligand is degraded in vivo, the low molecular weight metabolite is rapidly excreted into urine. We could safely inject macroscopic quantities of the HBP ligand, resulting in second order kinetics for quantification of receptor density. Thus, ^99mTc-NGA provided a useful platform for testing analysis of receptor kinetics. The model was essentially the same as in Fig. 1B except that there was a degradation pathway where TcNGA bound to HBP (i.e. LR complex) decomposed to a small ^99mTc species that rapidly returned to the blood and was filtered by the kidneys. Because ^99mTc imaging involves SPECT, the image voxels are the quantity L of ^99mTc-NGA radioligand in that voxel so the equations were parameterized to L/V_vasc for flow (rather than k₁) and k₃·R/V_liver for the pseudo-first order binding constant, rather than k₃·[R]. This is frequently done because SPECT images provide the quantity of radioligand L in a volume of interest, rather than a concentration unit. The results, which will be presented in part 5 of this review, showed that rate parameters were driven by the shape of the tissue’s time-activity curve and were not highly dependent on the absolute imaging quantification of Bq/mL or, with knowledge of specific activity, in units of nmol/mL. The dose-dependent and affinity-dependent uptake of ^99mTc-NGA has been demonstrated in animals [36] and in normal human subjects [37]. With five parameters adjusted during the curve-fitting process, the human studies demonstrated simultaneous estimation of receptor quantity, binding affinity and plasma flow, along with relative standard errors of the model estimates, which were less than the relative standard deviation between subjects.

4.4. Continuing with graphical analysis for brain receptor ligands

The first publication to use PET to quantitatively characterize regional drug binding sites in the brain in vivo used [¹⁸F]spiperone, a ligand that binds almost irreversibly to dopamine D₂ receptor sites. This research introduced a mathematical model that described transport as well as specific and non-specific binding in the brain [38]. Even though [¹⁸F]spiperone has some limitations for imaging, this was the seminal work on modeling receptor kinetics and we will cover it in some detail. The student of radiopharmaceutical design will want to work through the original mathematics in detail. The basic model is the same as Fig. 1B, with two physical compartments and one chemical environment, specifically bound radioligand within the tissue space. The authors appreciated that the radiopharmaceutical’s biodistribution at any time would be influenced by the number and affinity of receptors and also by blood flow, BBB permeability and potentially nonspecific binding. They started with a presumption that repeated measures of local radioactivity could be combined with appropriate mathematics such that the investigator can quantify the sizes of individual compartments and fluxes between them. They described the flux between the intravascular and tissue space as a permeability-surface area product with a passive linear diffusion mechanism. PS (mL/s) in their model is analogous to k₁/k₂ in Fig. 1B. Only ligand in the tissue compartment is free to bind to receptor via bimolecular association and unimolecular dissociation, which correspond to k₃ and k₄, respectively in Fig. 1B. With this framework, they wrote conservation equations for each of the three compartments. In their equations, B_max is the maximum receptor concentration R_max. From their eqn set 1, the differential equation for compartment 3 translated (using the variables in Fig. 1B) to $\frac{\text{d}{\text{C}}_{\text{prod}}}{\text{dt}}={\text{k}}_3\cdot {\text{C}}_{\text{intermed}}\cdot \left({\text{R}}_{\text{max}}-{\text{C}}_{\text{prod}}\right)-{\text{k}}_3\cdot {\text{C}}_{\text{prod}}$ and can be simplified for a high specific activity tracer because ${\text{C}}_{\text{prod}}\ll {\text{R}}_{\text{max}}$. Thus, the equation simplifies to $\frac{\text{d}{\text{C}}_{\text{prod}}}{\text{dt}}={\text{k}}_3\cdot {\text{C}}_{\text{intermed}}\cdot \left({\text{R}}_{\text{max}}\right)$. In their mathematics, a variable f was introduced to correct the activity of the ligand for nonspecific binding. Mintun defined k₃·[R_max] as a combined unimolecular rate that, with only dynamic tracer data, could not be parsed into the forward finding rate constant k₃ and the maximum receptor concentration. This product, B_max/K_D, was called a binding potential (BP) because it reflects the capacity of a region of tissue for a ligand-receptor interaction. In spite of that limitation, their study was able to make several important observations. The nonspecific binding of [¹⁸F]spiperone was about 95% in baboons, a practical limitation of the tracer, and the BP of the baboon’s striatum ranged from 17.4 to 21.6. These values are within the very wide range (2–200) calculated from literature values for B_max and K_D. Because B_max and K_D are both in units of mol/L, BP is a unitless parameter. Simulations showed that BP was not critically dependent on estimates of local flow or blood volume. This probably increases the robustness of the BP parameter for this tracer. The model did not provide for possible metabolites and would not permit measuring NSB by using a wide range of substrate concentrations. NSB was measured by activity in the cerebellum, which is believed to lack specific spiperone binding sites.

The PET group at Johns Hopkins made an alternative dopamine D₂ ligand, 3-N-[¹¹C]methylspiperone, NMSP, and evaluated it for quantifying neuroreceptors in the living human brain [39,40]. The interested student is referred to the figures in these two publications to verify the following analysis based on the data presented therein. Their basic model construct was similar to Fig. 1B except they redefined k₃ as the pseudo-first order rate constant, ${\text{k}}_3={\text{k}}_{\text{on}}\cdot \frac{{\text{B}}_{\text{max}}^{\text{'}}}{{\text{V}}_{\text{d}}}$, where the parameter ${\text{B}}_{\text{max}}^{\text{'}}$, represented unoccupied (i.e. available for binding) receptors. They also added a compartment for nonspecific binding and used a brain reference region free of D₂ receptors (e.g. cerebellum) to independently determine the rate constants for NSB [39] (Fig. 3). These NSB constants were used to correct uptake in the caudate nucleus for the small fraction that was not specific to D₂ uptake, assuming NSB was constant throughout both regions. This report also emphasized the value of correcting the plasma curve for metabolites, which were measured. Because the [¹¹C]NMSP ligand is irreversibly bound, L_free and L_plasma reach a steady state during a 2-hour imaging study but L_free and L_bound do not, requiring a separate determination of k₃ in order to calculate the receptor B_max. Their main contribution in the second paper [40] was to adjust the number of available receptors with a blocking inhibitor, ingested haloperidol, administered prior to the radiotracer. They used standard models for inhibition kinetics to arrive at the equation $\frac{\frac{1}{{\text{k}}_3}\left({\text{K}}_i^{\text{'}}+{\text{C}}_i\right)\cdot {\text{V}}_{\text{d}}}{{\text{B}}_{\text{max}}\cdot {\text{k}}_{\text{off}}^{\text{'}}}$ where ${\text{k}}_{\text{off}}^{\text{'}}={\text{k}}_{\text{i}}^{\text{'}}\cdot {\text{k}}_{\text{on}}^{\text{'}}$ and the subscript i refers to inhibitor, haloperidol. In this study, ${{\text{K}}^{\prime }}_i$, the inhibition constant for haloperidol, was used for several different concentrations of inhibitor (nM) as the independent variable; measurements were done for C_i = 0 and one or more higher values. The apparent volume of distribution, (mL/g), was plotted versus normalized time integral for the arterial input function, $\frac{{\int }_0^T{C}_a\left(t\right)dt}{C_a\left(T\right)}\left(\min \right)$. This modified time ordinate for the integrated C_a(t) input function is widely accepted for analysis of dynamic PET studies [41]. The relationship between apparent V_d of [¹¹C]NMSP in caudate and cerebellum (NSB) and the normalized time integral is shown in Wong’s Fig. 3 [40] before and after ingestion of haloperidol.

Fig. 3.

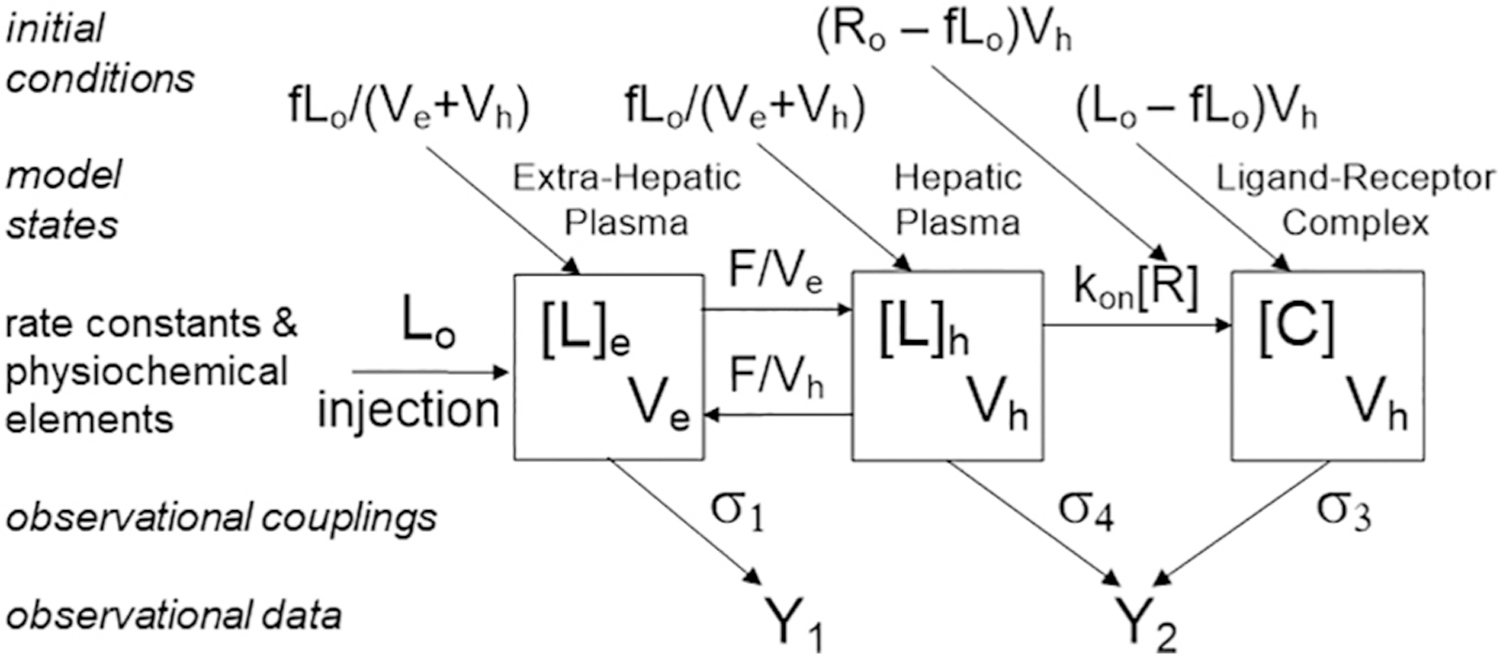
Pharmacokinetic model used for analysis of TcNGA. Note similarities to Fig. 1, panel B. The physiochemical elements F, V_e, and V_h for the rate constants that determine the transfer of radiopharmaceutical in and out of the target organ plasma, and k_on and [R] control the formation of the receptor-ligand complex C. If the amount of PR injected L_o is equal in magnitude to total amount of free receptor, the physiochemical element [R] will change in value during the imaging study. The model states, [L]_e, [L]_h, and [C] are in concentration units (mol/L). The initial conditions of the model assume an equilibrium between the [L]_e and [L]_h and conservation of mass between all compartments (model states) at the time that the plasma sampled as the fraction of the injected dose, f, at 2 min PI, which is the start of the simulation. Additionally, the k_off is 9 orders of magnitude a smaller amount of than the k_on and is not considered in the model. Additionally, metabolism of the complex is neglected. The observational data (Y₁ & Y₂) consists of a heart/lung and liver time-activity curves are coupled to the model states by the observational couplings (σ₁, σ₄ & σ₃).

The equation above for 1/k₃ (minutes) can be solved using C_i·V_d, the haloperidol concentration in the caudate per unit volume of tissue from the concentration in serum and the value for the equilibrium and k values for the inhibitor. Fig. 4 in their publication is a linear regression of 1/k₃ (min) versus brain haloperidol concentration (nM) [40]; it has a slope of $\frac{1}{{\text{k}}_{\text{off}}^{\text{'}}\cdot {\text{B}}_{\text{max}}}$ and the abscissa intercept, which has a negative value, is −K_i′⋅V_d; it was 1.4 ± 0.2 nM. The decline in k₃ with added haloperidol was used to solve for B_max, which had a mean value for NMSP of 9.5 ± 0.5 pmol/g. These studies showed that, within the time constraints of the PET study with ¹¹C (T_1/2 = 20.4 min), uptake of NMSP was irreversible, their k₃ was constant and k₄ was small compared to their pseudo-first order k₃. This does not, however, suggest that the bimolecular rate constant k₃ is a constant.

4.5. Advantages of multiple-injection protocols for graphical analysis

The group at Orsay introduced a complementary experimental protocol and mathematical analysis to measure cardiac beta-adrenergic receptor density [42]. They chose (±)[¹¹C]CGP12177, a ligand that is a potent hydrophilic antagonist for cell-surface beta receptors. In vitro assays with tritiated drug measured a K_D of 0.3 nM. Because it is metabolized, correction of the plasma input function for kinetic modeling would be difficult to measure and potentially inaccurate. Therefore, they introduced a new multiple-injection protocol that was amenable to an original graphical analysis they developed that did not require a plasma input function. The student of receptor imaging is referred to the original papers [42–46] because the mathematics is too involved to detail in this review but the concept is quite simple, Fig. 2. The protocol starts with injection of high specific activity ligand (low molar dose $D_0^{\ast }$ compared to $B_{\max }\text{'}$), which is imaged for a few minutes to measure an accurate slope for the slow-clearance phase of the tracer, S₀. Under these conditions, dissociation of bound ligand is negligible and a linear model is applicable for simulation of the slope, ${\text{B}}^{\ast }\left(\delta \right)=\frac{{\text{k}}_3\cdot {\text{B}}_{\text{max}}^{\text{'}}}{{\text{V}}_{\text{R}}}\cdot {\text{D}}_0^{\ast }\cdot {\int }_0^{\delta }{\text{F}}^{\ast }\left(\tau \right)d\tau$, where ${\text{D}}_0^{\ast }$ is the mass dose for that first injection and δ is the time for observing that injection. In this case, k₃/V_R is the bimolecular rate constant (nM⁻¹·min⁻¹) and B_max is the concentration of receptor in the region of interest, V_R. For the first injection C⁰ ≃ B^∗(δ). The slope S₀ is used to estimate ${\text{C}}_0^{\ast }$ graphically as shown in Fig. 2. Note that the vertical axis is logarithmic. After a few minutes of imaging, a second injection containing both labeled $\left({\text{D}}_1^{\ast }\right)$ and unlabeled ligand (D₁) in the same syringe is administered. This is the step where specific activity of the imaging agent is deliberately reduced with the intent that a significant fraction of receptor sites will become occupied over the course of dynamic data collection. Again, the slope is measured, S₁, and used to estimate ${\text{C}}_1^{\ast }$ graphically, correcting for the uptake curve for the first injection. Because the second injection contains carrier, the height ${\text{C}}_1^{\ast }$ will be lower than ${\text{E}}_0^{\ast }$ by an amount depending on D₁. The graphical method for estimating the receptor concentration requires five variables: ${\text{C}}_0^{\ast }$ and ${\text{C}}_1^{\ast }$ as well as ${\text{D}}_0^{\ast }$, ${\text{D}}_1^{\ast }$, and D₁, where the C and D units are nM. The nonlinear equation for graphical analysis is $C_1^{\ast }\frac{D_1}{D_1^{\ast }}=\left(1-exp\left(-\frac{C_0^{\ast }\times D_1}{B_{max}^{\text{'}}\times D_0^{\ast }}\right)\right)\times B_{max}^{\text{'}}$, and it sets up conveniently in a spreadsheet. Compare this with Eq. (18) in [42].

Fig. 2.

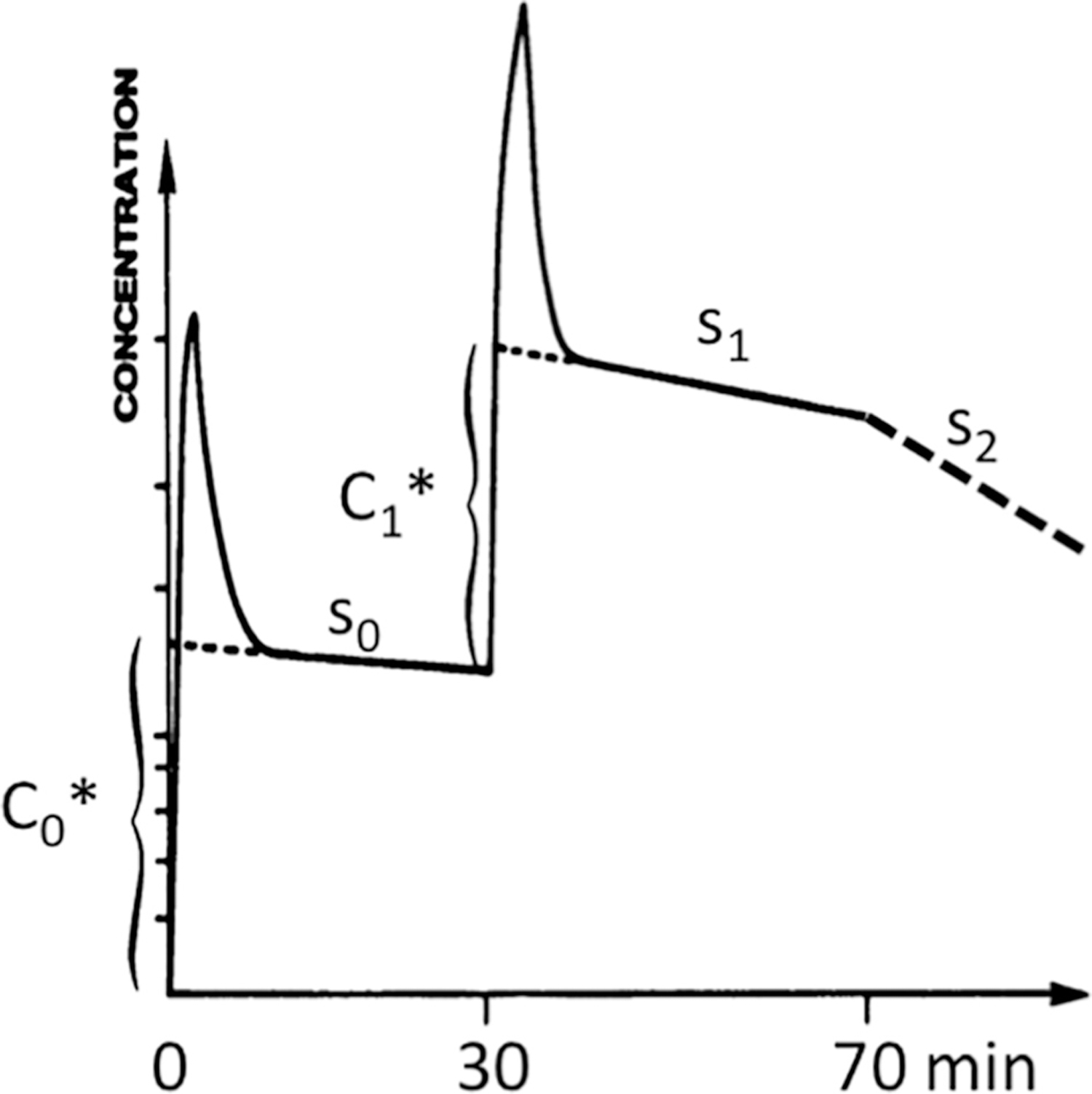
Schematic of data collection and analysis for graphical analysis of a ¹¹C-CGP-PET study. Note that the concentration axis is a logarithmic scale. Procedurally, a tracer dose D₀* is injected at time T₀ and imaged for sufficient time to accurately define the slope s₀ of the plateau phase so that its intercept, C₀*, can be estimated graphically. At approximately T₃₀ a co-injection of labeled (D₁*) and carrier CGP (D₁) is administered and a new slope s₁ is extrapolated to the time of the second injection to estimate C₁*. If desired, a massive injection of carrier CGP with no added radioactivity can then be administered to displace bound radioactivity. The slope s₂ is a measure of the unimolecular dissociation rate of the LR complex, k_off or k₄ in Fig. 1B.

The next task is to calculate k₃ from graphical analysis. This requires additional experimental information, namely the slope S₂ after a much larger mass of carrier ligand has been injected and the washout rate is observed. In this case, S₂ is a direct measure of the unimolecular dissociation rate, k₄. It also requires defining the slopes in terms of rate constants, again translating Delforge’s Eqs. (20) and (21) to our rate variables from Fig. 1B. His k is the unimolecular washout from the tissue compartment, k₂ in Fig. 1B.

$$\begin{gathered} {\text{S}}_0={\text{k}}_4\left(\frac{{\text{k}}_2}{{\text{k}}_2+{\text{k}}_3\times {\text{B}}_{\text{max}}^{\text{'}}}\right)\text{where}\hspace{0.17em}{\text{k}}_4 \\ \hspace{1em} ={\text{S}}_2\hspace{0.17em}\text{and}\hspace{0.17em}\frac{{\text{S}}_2}{{\text{S}}_0}=\frac{{\text{k}}_2+{\text{k}}_3\times {\text{B}}_{\text{max}}^{\text{'}}}{{\text{k}}_2}\text{so}\left(\frac{{\text{S}}_2}{{\text{S}}_0}-1\right)={\text{k}}_3\times {\text{B}}_{\text{max}}^{\text{'}} \end{gathered}$$

$${\text{S}}_1={\text{k}}_4\left(\frac{{\text{k}}_2}{{\text{k}}_2+{\text{k}}_3\times \left({\text{B}}_{\text{max}}^{\text{'}}-\frac{{\text{C}}_1^{\ast }\times {\text{D}}_1}{{\text{D}}_1^{\ast }}\right)}\right)\hspace{0.17em}\text{and}$$

$$\frac{{\text{S}}_2}{{\text{S}}_1}=\frac{{\text{k}}_2+{\text{k}}_3\times \left({\text{B}}_{\text{max}}^{\text{'}}-\frac{{\text{C}}_1^{\ast }\times {\text{D}}_1}{{\text{D}}_1^{\ast }}\right)}{{\text{k}}_2}\text{so}\left(\frac{{\text{S}}_2}{{\text{S}}_1}-1\right)={\text{k}}_3\times \left({\text{B}}_{\text{max}}^{\text{'}}-\frac{{\text{C}}_1^{\ast }\times {\text{D}}_1}{{\text{D}}_1^{\ast }}\right)$$

These two graphical equations combined with the measure of ${\text{B}}_{\max }^{\text{'}}$ determined above will give two somewhat independent values for k₃ in units of nM⁻¹·min⁻¹. When an analysis involves calculations based on individual slopes and their quotients, careful attention must be paid to propagation of errors. In their beagle dog study ${\text{B}}_{\max }^{\text{'}}$ was 30.9 ± 3.7 nM and 29.4 ± 3.4 nM from the two measurements; the dissociation rate constant k₄ was 0.014 ± 0.002 min⁻¹. The variability in k₃/k·V_R was larger, 0.10 ± 0.07 when slopes S₀ and S₂ were used and 0.017 ± 0.04 when S₁ and S₂ were used [42]. In a study of 8 patients with dilated cardiomyopathy, the left ventricular concentration of beta-adrenergic receptors was 6.61 ± 1.18 nM [45]. This was only a two-dose study so k₃ was not measured.

This graphical analysis of [¹¹C]CGP12177-PET was used in research presented at Receptor Radiotracers 2002 [30] and in a more recent large clinical study testing how age and exercise training caused changes in the cardiac sympathetic nervous system function in healthy male or female volunteers [47]. Post-sympathetic function was evaluated using CGP-PET with a two-injection protocol to estimate only the concentration of beta receptors. At baseline there were no age-related differences or training-related differences detected in B_max but there were changes in presynaptic function measured as a permeability-surface area product for a norepinephrine analog, [¹¹C]meta-hydroxyephedrine.

Another motivation for a more absolute approach to quantification of receptor density in vivo was the finding that receptor sites were often occupied by endogenous ligand at basal level [44]. Reports ranged as high as 25 to 40% and yet models were not taking into account the presence of endogenous ligand. Delforge and colleagues studied the bias associated with this extra level of native ligand through pharmacologic manipulation of the endogenous ligand level and found that receptor concentration was correctly estimated by the models, but the apparent affinity k₃ was biased. While this approach is too invasive for use in humans, it emphasized that k₃·B_max will be biased in the presence of competing endogenous ligand.

4.6. Multiple ligand concentration receptor assays, MLCRAs

Holden, in collaboration with colleagues at the University of British Columbia/TRIUMF PET Centre has used kinetic analysis of dynamic studies and multiple ligand concentrations to measure B_max and apparent affinity in normal and lesioned monkeys [48]. They took on the challenge of multiple ligand concentration receptor assays, MLCRAs, which have been widely used in vitro for separating receptor density and apparent affinity in postmortem preparations by classical Scatchard analysis but are much more challenging in vivo using PET data. They used [¹¹C] raclopride, a D₂ ligand, and the experimental protocol involved administering half of the test ligand by a 30-s bolus followed by constant infusion over an hour for the remaining 50%. The goal was to achieve equilibrium between bound and free concentrations of radiotracer at several carrier-added levels. There are two attractive features for this design: it avoids blood sampling and the duration of infusion to attain true equilibrium can go for as long as permitted by decay of the radionuclide. This approach built on an earlier report by Farde who advocated transient equilibrium between bound and free raclopride [49]. In the equilibrium phase, the receptor bound-to-free ratio (B/F) in target tissue becomes constant and the Logan graphical method can be applied to determine an equilibrium distribution volume DVR for reversible tracers [50].

Half of the monkeys studied at UBC were experimentally lesioned in the right striatum using MPTP, a dopaminergic neurotoxin, to induce a significant increase in the binding potential, BP, for raclopride binding to D₂ receptors [48]. A potential confounder in k₃ for receptor studies would occur if increasing antagonist concentration induced changes in endogenous ligand level, resulting in a change in apparent affinity either between experiments or over time. Studies were performed with three or four progressively increasing ligand concentrations. The question was whether this treatment was upregulating receptor density, B_max, or decreasing synaptic dopamine levels, either of which would alter the apparent affinity (expressed inversely as a dissociation constant K_D) between receptor and test ligand. The model was parameterized for B_max and K_D in four ways, two linear and two non-linear, with the resounding conclusion that this method was simple enough for routine use and was reliable for repeat studies.

Germaine to the issue of specific activity, this study was a careful search for systematic changes in affinity of the test ligand as its concentration increased because of added carrier. Increasing antagonist levels will induce changes in concentration of endogenous ligand so each study would yield a different apparent affinity. The search for this effect was one important aspect of the UBC study. The time-activity curves (TACs) reached a constant level after about 25 min in both striatum (specific binding) and cerebellum (NSB) in normal and lesioned sites. These TACs were used to estimate receptor-bound and free ligand, the B/F ratio, from the equilibrium distribution volume ratio (DVR) for this reversible tracer [50,51]. The ratio from the method was called (B/F)_g, where the subscript refers to use of Logan graphical analysis. (B/F)_g = (DVR − 1). The Logan plot was evaluated from 30 to 60 min after initiating administration of the drug. This analysis is appropriate when reverse uptake, k₂, is large enough and late-time data is available. The equilibrium B and F concentrations were derived from the radioactivity concentrations in striatum, S(t), and cerebellum, C(t) averaged over the final 30 to 60 min of imaging. The calculation uses the averages, S and C; to convert to molar units using the known specific activity at the time of injection, SA. $\frac{\text{B}=\left(\text{S}-\text{C}\right)}{\text{SA}\text{and}\hspace{0.17em}\text{F=}\frac{\text{C}}{\text{SA}}}$ are reported in nM units so B/F is unitless. At equilibrium $\text{B}=\frac{{\text{B}}_{\text{max}}\cdot \text{F}}{{\text{K}}_{\text{D}}+\text{F}}$, which can be fit directly as a non-linear equation or linearized as ${\left(\frac{\text{B}}{\text{F}}\right)}_{\text{g}}=\frac{B_{\text{max}}}{K_{\text{D}}}-\frac{1}{{\text{K}}_{\text{D}}}{\left(\frac{\text{B}}{\text{F}}\right)}_{\text{g}}\text{F}$. A linear plot of ${\left(\frac{\text{B}}{\text{F}}\right)}_{\text{g}}$ versus ${\left(\frac{\text{B}}{\text{F}}\right)}_{\text{g}}$ will have a y-intercept of BP, B_max/K_D, and a slope that is the negative inverse of the apparent K_D. While linearization is attractive, the caveat of error analysis in this situation is significant. Note that experiments can be done at several different values of SA for the test ligand in order to test the constancy of apparent K_D. In the [¹¹C]raclopride experiments, there was no evidence for a change in apparent K_D [48]. The authors recommended performing similar studies with different specific activity values with any new application of MLCRAs and emphasized the benefit of experiments where both B_max and apparent K_d can be determined. Furthermore, a measured equilibrium B/F and a BP from optimization provides the advantage, which the reader can test algebraically, that they should be equal at high specific activity. This provides a useful check on the experiment and its analysis.

In a more recent publication, the same team reported in vivo measurement of receptor density and affinity of the monoamine vesicular transporter using the MLCRA protocol. In this case, the method was applied to the vesicular monoamine transporter (VMAT2) rather than a receptor. They use [¹¹C]-(+)-α-dihydrotetrabenazine (DTBZ), another tracer with rapidly reversible binding, in a unilaterally 6-hydroxydopamine lesioned rat model of Parkinsonism [52]. This experiment involved a bolus injection rather than the bolus-infusion protocol described for the [¹¹C]raclopride experiments. The analysis invoked the assumption that B and F were equilibrated and thus followed the scheme for B as a function of B_max and K_D as described above. Linearizing as ${\left(\frac{\text{B}}{\text{F}}\right)}_{\text{g}}=\text{BP}-\frac{\text{B}}{{\text{K}}_{\text{D}}}$ provided the most robust results. B is the bound tracer concentration calculated as the striatal-cerebellar difference averaged from 30 to 60 min and converted to nM units using SA of the injected radiotracer. Thus, B is $\frac{\left(\text{S}-\text{C}\right)}{\text{SA}}$. ${\left(\frac{\text{B}}{\text{F}}\right)}_{\text{g}}$ was determined by the graphical method [50] for each SA value for the test tracer. BP is the value for ${\left(\frac{\text{B}}{\text{F}}\right)}_{\text{g}}$ extrapolated to zero transporter occupancy, i.e. the vertical intercept. B_max is the horizontal intercept on the B-axis with the linear equation above. An agreement between B/F values from graphical analysis and the measured ratio from (S-C)/C provided a test of equilibrium between compartments. Lastly, it is important to notice that the situations where B_max refers to either a receptor or a transporter have been successfully inferred from dynamic PET studies involving radioligands where k₂ is substantial. This is consistent with our arguments related to the first issue in this review.

4.7. Summary conclusions

This section emphasized that receptor density from an imaging study requires a mathematical model and a fitting procedure that invokes assumptions that are matched to the radiotracer’s characteristics for a dynamic tissue uptake protocol that often involves a measured input function to calculate useful parameters in the model equations. These issues are addressed further in the next section. We have deliberately taken our examples from the early literature using compartmental modeling of radioligands for specific receptors, both brain and body, because these reports provide detailed and stepwise development of the underlying assumptions and the mathematics. They also emphasize the complementary aspects of an experimental protocol for data collection and the mathematics involved in estimating relevant parameters for ligand-receptor kinetics in vivo. While it is regrettable that these early publications used somewhat different symbols for rate constants, variables for L and R and reaction volumes, it will be highly instructive for the novice to work through the details of each of these publications, preferably in parallel, to become confident that each is telling the same story and that the approaches ultimately resolve to the same model. Only then can one appreciate the strengths as well as the limitations of an imaging experiment and its analysis.

One parting concern regarding this topic: The simple binding potential BP has become the prevalent result that is reported for radioligand-receptor imaging studies. It has the practical appeal of simplicity and reliability and is probably robust with respect to data collection and handling. However, it reflects the density of receptors times the second-order rate constant for reaction with receptor binding. Studies have shown that endogenous ligand that partially occupies receptor sites changes the apparent k₃ and so simple visual assessment of receptor density, for example as BP or an SUV, will potentially be biased. One cannot help but worry that the receptor imaging community is missing important information by not putting more effort into measuring both k₃ and [R_max].

5. On the impact of mathematical analysis in constraining radioligand design

In a 1978 editorial Eckelman and Reba [53] predicted that receptor-binding radiopharmaceuticals would offer a “mechanistic approach” which, by defining the “precise mechanism of action studied by the radiosubstrate”, would lead to a “precise diagnostic interpretation”. This section will support that prediction by expanding on the bimolecular mechanism of receptor-ligand binding alluded to by Eckelman and Reba and continue with examples of increased diagnostic power. It follows the theme of the editorial, namely that chemical precision of receptor-binding leads to diagnostic precision. The caveat is that the radiopharmaceutical must be properly designed.

5.1. The general structure of a mathematical model

The first step toward a mathematical analysis is the design of the model’s structure. This structure will have six components. The most familiar component are the compartments (also known as the model states), which is a quantity of distinct material that is well-mixed within a defined volume. For our purposes, the material is the injected radiotracer within the various plasma and interstitial spaces, as well as the radiolabeled products resulting from receptor binding and metabolism. Examples of individual compartments include the radiopharmaceutical within the plasma, metabolites of the radiopharmaceutical within the plasma, the radiopharmaceutical within the plasma of the target tissue, the radiopharmaceutical within various interstitial spaces, the radiopharmaceutical bound to the receptor (also known as the ligand-receptor complex), and various metabolites of the radiopharmaceutical within various spaces. Compartments can have units of quantity (moles) or concentration (mol/L). It is customary to represent compartments as boxes or circles.

The second component details all of the rate constants that connect the compartments and control the magnitude of the transfer between the compartments. Graphically, rate constants are typically represented by arrows that signify the direction of the flow between two compartments. Mathematically, rate constants are usually represented by the symbol k with subscripts that further specify the process.

Rate constants can be deconstructed to specific physiochemical elements. These are the third component of a model’s structure. An example [28] includes the rate constant that controls the flow of a radiotracer from the extra-hepatic space to the hepatic space, into and out of the target organ (Fig. 3). This is a first-order process with a rate constant in units of reciprocal time. The elements of this rate constant will be the volume of the compartment from which the tracer exits and the plasma flow. Division of the volume by the flow yields a rate constant in units of volume per time. Deconstructing rate constants into specific physiologic elements is critical to validation of the model and is an important step toward clinical application.

The fourth component of the model structure are the observational couplings, σ parameters in Fig. 3. These components connect the compartments to the observational data set, the fifth component of a model’s structure. They are typically linear couplings that interconvert moles or concentration of radiopharmaceutical and counts per unit time from experimental measurements. The couplings are typically not limited to one compartment to one data set. For example, a series of plasma samples assayed by an auto-well counter Y₁ will observe two compartments: the radiopharmaceutical within the plasma as well as its metabolites. Another common example is the time-activity curve from the target organ, where the scanner Y₂ simultaneously observes two compartments, the radiopharmaceutical in the target organ plasma and the radiopharmaceutical bound to the target organ tissue. If the tracer is a radioactive ligand intended for a receptor within the target organ, the second compartment will include the ligand-receptor complex. The parameters that describe the magnitude of the observational couplings are typically the detector sensitivities in units of counts per unit time per unit volume per mole of radiotracer or its metabolite.

The sixth component of the model results from the requirement that a compartment be homogenous or “well-mixed”. When a radiopharmaceutical is administrated via intra-venous injection, the plasma compartment fails this requirement during the first several minutes. The radiopharmaceutical concentration doesn’t achieve a homogenous concentration until after several plasma recirculation times. For this reason, typical plasma clearance curves display a very rapid decline during the first 2 min when the radiopharmaceutical is “mixing” into the entire plasma volume. One solution to this requirement is to not start the model simulation until after a preset time; usually 2 min. Consequently, the sixth component of the mathematical model is a set of initial conditions that define the compartment or state quantities at the start of the simulation. Typically, a plasma sample at a preset time is used to calibrate a heart/lung time-activity curve (or a set of plasma clearance samples) to units of radiotracer quantity (moles) or concentration (mol/L). Depending on the model design, the initial conditions can employ conservation of mass.

An excellent presentation on mathematical modeling of systems studied by radioactive tracers, Compartmental Analysis in Biology and Medicine [54], is out of print but available at an academic library. It contains an excellent introduction as well as advanced topics. Most importantly it incorporates a presentation of second-order processes, such as a bimolecular chemical reaction, which is a chemical depiction of receptor-binding.

These five components are depicted graphically in Fig. 3, composed of the state variables (compartments) and rate constants that define the magnitude of the connections between the compartments. In this example, which is the simplest form for a receptor-binding model for a radiotracer, the compartments are: the concentration of radiopharmaceutical within the extra-target organ plasma [L]_ex, the concentration of radiopharmaceutical within the target organ plasma [L]_to, and the concentration of radiopharmaceutical bound to the receptor, also known as the ligand-receptor complex [C]. These states are in units of moles/L. The variables are composed of compartment volumes, plasma flow, and the chemical reaction rate constants k_on and k_off. The initial conditions use conservation of mass to define the state values at the time of the plasma sample, which is the time at which the model simulation is started. The initial conditions assume that the concentration of radiotracer sampled from the patient’s intravenous catheter is representative of the concentration throughout the extra-target organ plasma and the target organ plasma. This value will be used to scale a heart/lung time-activity curve (or other intravascular compartment such as aorta or carotid) to units of concentration. The observational couplings connect the state variable [L]_ex to the intravascular curve through a scaling factor σ₁. The observational couplings also connect the target organ time-activity curve to the model states [L]_to and [C] with equal sensitivity (σ₂ and σ₃).

In the next section we will use TcNGA as an example. Introduced [28] at the original Receptor-Binding Radiotracer conference, TcNGA was the first technetium-99m agent to enter a Phase 1 clinical trial [55]. An “instant kit” version known as TcGSA [56] was commercialized by Nihon Mediphysics in Japan [57] and is still used today to measure functional hepatic mass. TcNGA and TcGSA both share several attributes that simplify the chemical design and mathematical modeling. These include: 1) the ability to chemically alter k_on over more than an order of magnitude [58]; 2) a lack of a pharmacologic response [36]; 3) a molecular target, the asialoglycoprotein (ASGP) receptor, that reside on only one organ, namely the liver; and 4) hepatic fenestrated capillaries that permit plasma macro-molecules, such as TcNGA and TcGSA, to reach the hepatocellular surface without the impediment of an endothelial barrier. Data in support of each of these characteristics of TcNGA is included in the references cited above and has not been repeated in this review.

The last two features greatly simplify the mathematical model to the form represented in Fig. 3. The fact that the receptor is unique to a single cell type, hepatocytes, eliminates any need for the model to represent multiple target organs. Additional target organs, and hence more model states, produce a larger set of mathematical equations, which require more computational power. Additionally, more compartments necessitate more interconnections and additional parameters. The addition of parameters (especially if their value is unknown) unaccompanied by additional observational data will seriously impact identifiability or the precision of the receptor estimate.

The presence of fenestrated blood capillaries in the liver also reduces the number of compartments and rate constants. The presence of an endothelial barrier would add an interstitial space between the hepatic plasma and the cell surface where the receptor resides. Diffusion through the barrier would be governed by Fick’s law, which would assign two new physiologic elements, a permeability constant which is related to the diffusion constant of the radiopharmaceutical divided by the thickness of the endothelial barrier and the surface area of the endothelial barrier. These elements form the rate constant that governs the oneway fluxes (k_f = DA/δV_to and k_r = DA/δV_in) of the radiopharmaceutical through the barrier. Where k_f and k_r are the forward and reverse rate constants and V_ex and V_in are the volumes of the target organ plasma and the interstitial space. In radiotracer kinetic models, this is often collapsed into a permeability-surface area product, PS.

5.2. Sensitivity analysis

The importance of assigning physiochemical elements to the rate constants of the model analysis becomes evident when we analyze the model for sensitivity. Sensitivity analysis is used in many fields, ranging from economic models to weather forecasting, always with different definitions and goals [59]. The goal of sensitivity analysis in radiopharmaceutical design and analysis is to determine whether the time course of the observational data changes when an important physiochemical element of the model is altered. The observational data may be a single image, a single metric from a time-activity curve, or the entire time-activity curve data set. The most interesting physiochemical elements are, of course, receptor concentration and receptor affinity but in radiotracer design we will also be interested in the sensitivity to target organ plasma flow and plasma volume. In its simplest terms, the sensitivity of an individual parameter k_i at time t is the variation of the time-activity curve, TAC(t) or SUV(t), induced by a small variation in $k_i.\frac{\text{Sen}{\text{s}}_{k_i}\left(t\right)=\delta \text{TAC}\left(t\right)/\text{TAC}\left(t\right)}{\text{δ}{k}_i/k_i}$. Note that this definition is unitless, which reduces computational error and eases the graphical analysis. As an example of this sensitivity function, Fig. 4 shows how SUV changes with time for some rate parameters describing the uptake of [¹¹C]-acetate in brown adipose tissue, BAT, where metabolism is activated by prolonged cold [60]. Model 1 had only 2-compartments with two rate constants and volume of blood. Model 4 added an oxidative compartment and k₃.

Visual inspection of the curves shows that k_f (K₁ in the figure) can be quantified within 10 min and V_b is observable early, but the ability to separate k₂ and V_b is only possible after 20 or more minutes and is better when BAT is activated by cold, i.e. greater separation between the red and blue lines. Note that the vertical axis in this figure is not the value of the rate parameters; it is how much they change with an incremental change in time. Model 4 introduces the oxidative compartment with a rate k₃ leading to ¹¹CO₂. In this case, k₃ is the parameter that requires the longest time to become observable. This is an example where sensitivity analysis was used for selecting an appropriate model for data analysis and is a good introduction to the value of sensitivity analysis. There are other examples of sensitivity analysis used in this way. The PET group at University of Groningen used this approach to show that [¹⁸F]-fluoroethoxybenzovesamicol, FEOBV, for evaluating the vesicular acetylcholine transporter is best modeled using an irreversible 2-tissue compartmental model or Patlak graphical analysis; their results expressed reservation concerning SUV in this application [61].

When developing a new radiotracer for imaging, sensitivity analysis initiates the validation process and provides a first impression of its ability to measure a physiochemical parameter with precision. Kinetic sensitivity is a requirement, although it is not sufficient for accurate measurement of a model parameter or element. For example, if the goal of the imaging protocol is to measure plasma flow to the target organ, the accurate measurement of plasma flow will not be possible if another parameter such as plasma volume or vascular permeability changes the time-activity data in the same fashion as plasma flow. There are many approaches to analyzing the ability of a physiochemical parameter to produce changes in images or time-activity curves. Most common is the “blocking” experiment. Typically, the goal is to demonstrate changes in standardized uptake values (SUVs) after co-injection of a receptor-binding radiotracer with a “blocking” dose of cold receptor ligand. These experiments, which are usually meant to demonstrate biochemical specificity, are typically based on an image at a single time point after injection and are most convincing if they show dose-dependent blocking.

Another approach (Fig. 5) is to define a metric that summarizes the time-activity curve from the target organ or clearance from the plasma. Kudo et al. [62] used the time to reach 90% of the peak value as a metric from liver time-activity curves of human TcNGA dynamic imaging studies. Measurements of asialoglycoprotein receptor (ASGPR) density (mol per mg of biopsy weight) were obtained from Scatchard binding assays of hepatic biopsy samples. After scaling the receptor density by total liver weight, the total hepatic ASGPR quantity was plotted against the rise-time (t₉₀) of the time-activity curve. The correlation from ten subjects with liver diseases that ranged for mild to severe was 0.82.

Fig. 5.

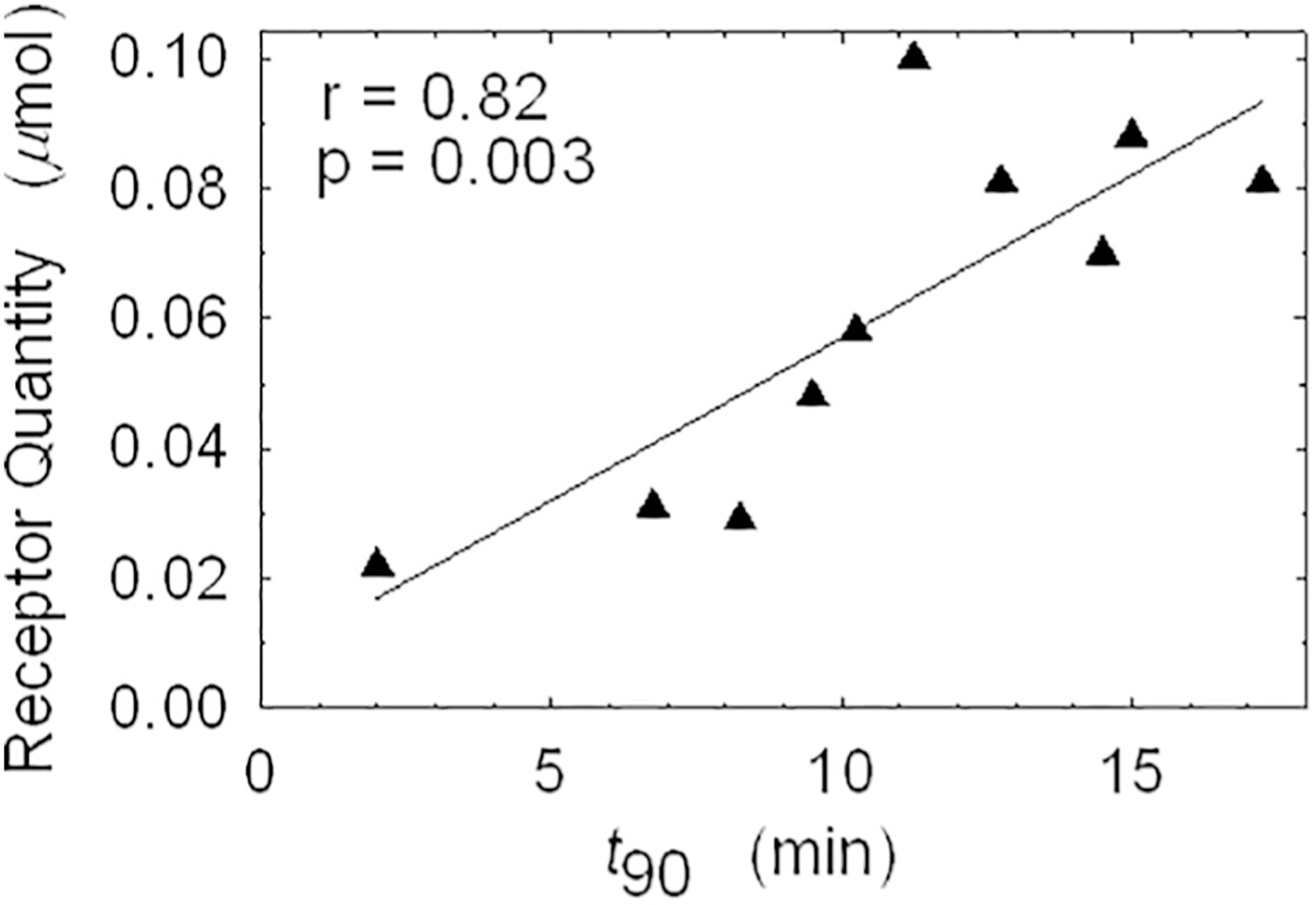
A sensitivity analysis of receptor quantity. This analysis used an in vitro measurement of receptor density from liver biopsy samples and the metric t₉₀, which represents the rate of hepatic accumulation. The statistically significant correlation demonstrates kinetic sensitivity of TcNGA time-activity date to receptor quantity [62].

Another approach is to perform the analysis under controlled conditions, where other physiochemical parameters are measured or held constant. TcNGA was studied under these conditions [63]. In this study, pigs were injected with TcNGA having different receptor affinities, specifically different values of k_on. One of the advantages of this imaging agent is that k_on can be manipulated by changing the number of galactose residues on the substrate [58]. These studies also varied hepatic plasma flows and used different molar doses of TcNGA. A hepatic vein catheter was installed and an infusion of ICG was started prior to each dynamic imaging study to independently measure its hepatic extraction and calculate hepatic plasma flow (F) based on the Fick Principle. The [¹²⁵I]-albumin plasma volume (V_t) was also measured independently. These additional measurements permitted the calculation of the delivery rate constant F/V_ex. These measurements along with control of the radiopharmaceutical’s affinity for the ASGP receptor and the amount of TcNGA administered are an important and often neglected aspect of a properly designed sensitivity analysis. Many sensitivity analyses are conducted without accounting for all of the parameters [59].

As shown in Fig. 6, three different scaled molar doses (1.2, 12.0, and 110 nmol per kg of body weight) produced three time-activity curves with qualitatively different shapes. The “tracer” dose (1.2 nmol/kg) rose to an early peak and plateaued before the intermediate scaled dose (12 nmol/kg) reached its peak. The scaled hepatic plasma flow (F/V_e) for both pigs was similar: 47 min⁻¹ for the tracer study and 58 min⁻¹ for the 12 nmol/kg study. The times-to-peak were 5.6, 11.2, and >20 min, respectively; the t₉₀ values were 2.4, 3.4, and >20 min, respectively. Note the almost linear curve of the 110 nmol/kg dose; this a hallmark of a second-order receptor-binding process when stoichiometry is sufficient to change the amount of unoccupied receptor during the time course of the experiment. First-order processes are linear only when plotted as a semi-log graph. The time-activity curve from the “tracer” dose study, despite the lower scaled hepatic plasma flow, exhibited a faster time-to-peak and faster rise-time (t₉₀) than the 12 nmol/kg study. All three studies used an NGA preparation with a k_on of 12.5 μM⁻¹ min⁻¹.

Fig. 6.

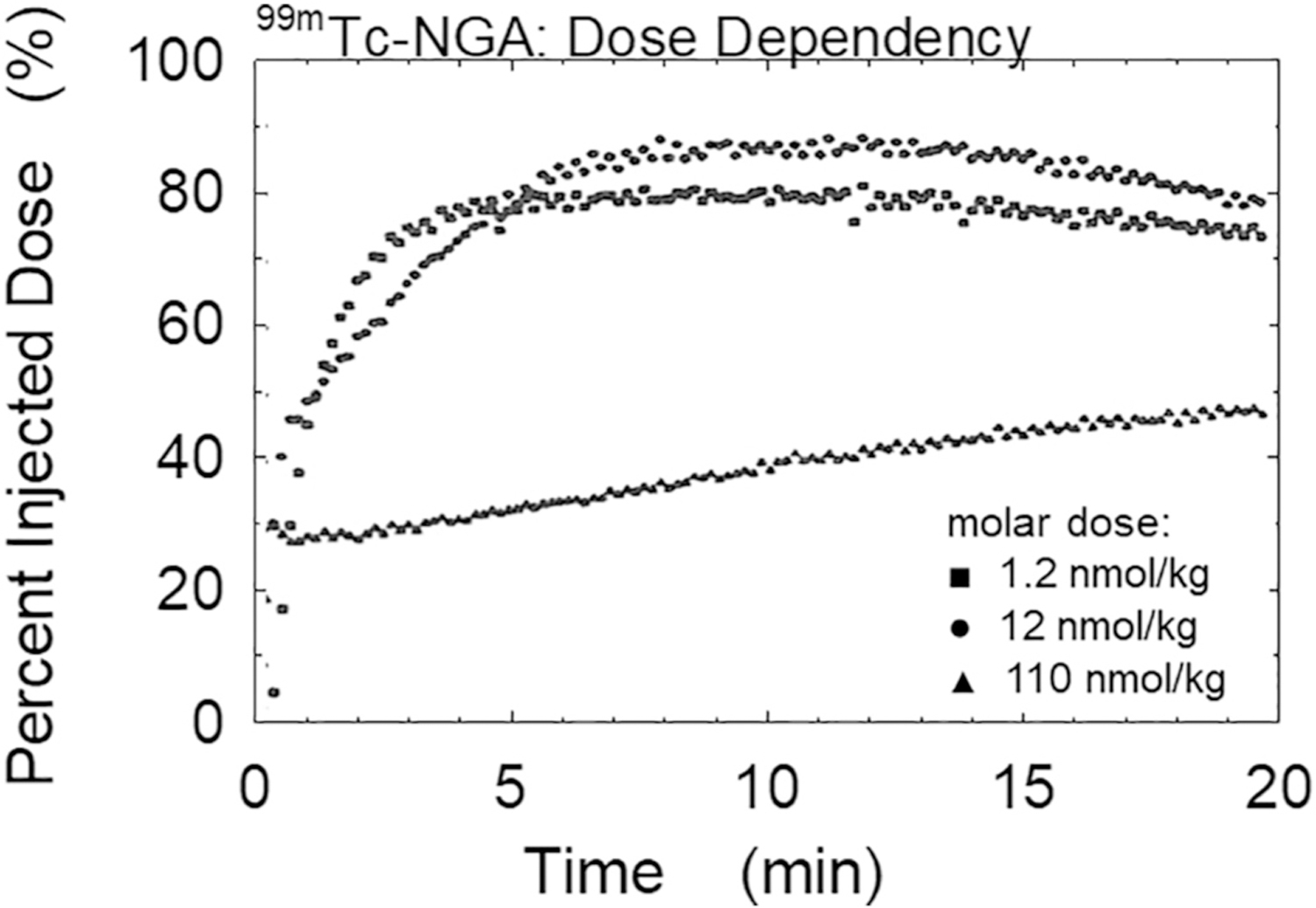
A sensitivity analysis of scaled molar dose. This analysis was performed in pigs using increasing molar doses of the radiopharmaceutical (RP). Measurements during the 20-minute dynamic study provided the calculation of F/V_e, the rate constant for RP delivery via hepatic plasma flow. Three different scaled molar doses (1.2, 12, & 110 nmol per kg of body weight) produced three time-activity curves with vastly different shapes, time-to-peak, and t₉₀ values. Note the almost linear curve of the 110 nmol/kg dose- a hallmark of a second-order process.

This study, which demonstrated kinetic sensitivity to scaled molar dose, implies that a properly designed TcNGA imaging protocol could detect changes in receptor concentration. If, for example, a scaled molar dose of 12 nmol per kg of body weight was employed, a healthy subject would produce a time-activity curve with a shape similar to that of the pig study. If the same scaled molar dose was used to image a patient with sufficiently severe liver damage, e.g. ASGP receptor concentration reduced by a factor of ten, the resulting time-activity time would resemble the pig study with the linear curve.

A sensitivity analysis that provides observational data in the form of a time-series with many data points and data channels, such as target organ and blood clearance curves, is optimal, even if the clinical protocol will use images at only two time points. Time-activity data not only provides information regarding the optimal times for static imaging, a continuous plot of the target organ accumulation and plasma clearance provides a graphic depiction of how each physiochemical parameter effects the biodistribution. As depicted in Fig. 6, the shape of the time-activity curves contains the information pertaining to the magnitude of the model parameters. The model parameters that produce time-activity curves with unique shapes will be the parameters that can be estimated with highest precision. As stated in the beginning of this section, a properly designed sensitivity analysis provides a preliminary assessment of precision of the imaging protocol. We present in a later section the concept that the parameter with the highest sensitivity will form the physiochemical basis for interpretation of the imaging study.

Another approach to studying the sensitivities of the observational data to the model parameters is to simulate the mathematical model in a computer. Fig. 7 is an example of a simulated sensitivity analysis of the TcNGA system using human values for the physiochemical elements. The simulations where performed at two different scaled molar does of NGA. Panel A uses a “tracer” dose where the ratio of L_o (the amount of TcNGA administered) to R_o (the amount of receptor) is low (0.01) and Panel B where L_o/R_o is 0.5, a “non-tracer” dose. Using a “tracer” dose the physiochemical element with the highest sensitivity is the extra-hepatic plasma volume, V_e. Hepatic plasma flow, F, is higher than the initial receptor concentration, R_o/V_r, which is similar in magnitude as k_on and the hepatic plasma volume, V_h. The fact that the R_o/V_r and k_on, curves have different shapes is an indication of good identifiability. Similar shapes to the R_o/V_r and F curves are an indication that an attempt to simultaneously estimate both parameters will yield high relative uncertainties (i.e. poor identifiability). When L_o/R_o is high (0.5), the parameter with the highest sensitivity is the initial receptor concentration, R_o/V_r. The sensitivity to flow, F, is significantly lower compared to the low dose scenario. The large difference in sensitivity predicts estimates of high precision for R_o/V_r but high uncertainty for F. Both sensitivity curves were generated with a ligand-receptor affinity k_on/V_r of 0.5 μmol⁻¹ s⁻¹. The authors recommend any one of the excellent texts from the “Numerical Recipes” series [64] for the theory and algorithms for simulation and regression (curve-fitting) analysis.

Fig. 7.

Sensitivity analysis of the TcNGA system at “tracer” and “non-tracer” doses. (A) When the ratio of L_o to R_o is 0.01, the physiochemical element with the highest sensitivity is V_e. Hepatic flow, F, is higher than R_o/V_r, which is similar in magnitude as k_on and V_h. The fact that the R_o/V_r and k_on, curves have different shapes indicates good identifiability. Similar shapes to the R_o/V_r and F curves are an indication that an attempt to simultaneously estimate both parameters will yield high relative uncertainties. (B) When the ratio of L_o/R_o is 0.5, the parameter with the highest sensitivity is R_o/V_r. The sensitivity to F is significantly lower compared to the “tracer” dose scenario. The large difference in sensitivity predicts estimates of high precision for R_o/V_r and high uncertainty for F.

The potential to provide simultaneous independent data that complements pharmacokinetic images of a radiotracer is especially powerful and should become more common as PET/MR technology becomes more widely used so that hemodynamic parameters from MR can be quantified simultaneously with collection of the PET emission study. For example, a recent report used MRI information from arterial spin labeling, a perfusion parameter, in a model of [¹⁸F]-florbetapir PET for quantification of amyloid-β [65].

5.3. Curve-fitting & goodness-of-fit

After the sensitivities are studied, it is time to parameterize the kinetic model and study the potential of various curve-fitting procedures. A literature example of this process [37] converted the compartmental model of Fig. 3 into a set of differential equations with four states, [L]_e, [L]_h, [R], and [C]. This set of equations contains a second-order process (Fig. 1A) by which L_h binds to R to form C. This results in non-linear differential equations, which will complicate the simulation and curve-fitting in two ways that are unique to receptor-binding radiopharmaceuticals. First, the bi-molecular reaction, which is responsible for the non-linearity, produces a set of differential equations that cannot be solved analytically. Unlike the Bateman equations [66], which provides an analytical solution to the differential equations that describe a radioactive decay series, a receptor-binding model operated in a second-order mode (L_o/R_o > 0.1) must be solved using numerical integration. Fig. 6 provides a visual appreciation, where increasing scaled molar doses create curves that slow their uptake progress as a significant portion of free receptor becomes occupied and unavailable for binding. The resulting set of equations do not have an analytical solution, hence the need for a numerical solution using numerical integration.

A second problem becomes pertinent to curve-fitting and goodness-of-fit. Second-order kinetic systems, when not operated in a “bi-molecular” mode, produce difficult curve-fitting issues. Fig. 8 illustrates the issues regarding curve-fitting and goodness- of-fit by comparing two TcNGA scenarios: L_o/R_o = 0.01 (a system not operating in “bi-molecular” mode) and L_o/R_o = 0.5 (a system operating in “bi-molecular” mode). The figure consists of two contour plots of the Reduced Chi-Squared (RCS) space generated by changes in receptor concentration and hepatic plasma flow. The red lines represent the reduced Chi-square contours from curve-fits to a data set resulting from a “tracer” (L_o/R_o = 0.01) injection of TcNGA. The blue lines represent the reduced Chi-square contours for a data set resulting from a non-tracer (L_o/R_o = 0.5) injection of TcNGA. The numbers represent the RCS for each contour. The black dot at the center of the plot is the lowest Chi-square, where the curve-fitting algorithm will converge if it is properly controlled. Note the elongated contours of the red plot, which can become a source of bias in the R_o/V_r estimate if the curve-fitting algorithm does not stop appropriately; it may settle along the narrow valley defined by the RCS = 2 contour. Errors in parameter estimates are higher in narrow valleys. Errors are lowest and curve-fitting efficiency is highest when the slope of the contour is high. The sensitivity curves responsible for producing this space can be viewed in Fig. 7 and the identifiability plots (next section) that result for these contours can be viewed in Fig. 9.

Fig. 8.

A graphical depiction of goodness-of-fit. Two contour plots of the Reduced Chi-Squared (RCS) space generated by changes in receptor concentration and hepatic plasma flow. The red lines represent the reduced Chi-square contours from curve-fits to a data set resulting from a “tracer” (L_o/R_o = 0.01) injection of TcNGA. The blue lines represent the reduced Chi-square contours for a data set resulting from a “non-tracer” (L_o/R_o = 0.5) injection of TcNGA. The numbers represent the RCS for each contour. The black dot at the center of the plot is the lowest Chi-square, where the curve-fitting algorithm will converge if it is properly controlled.

Fig. 9.

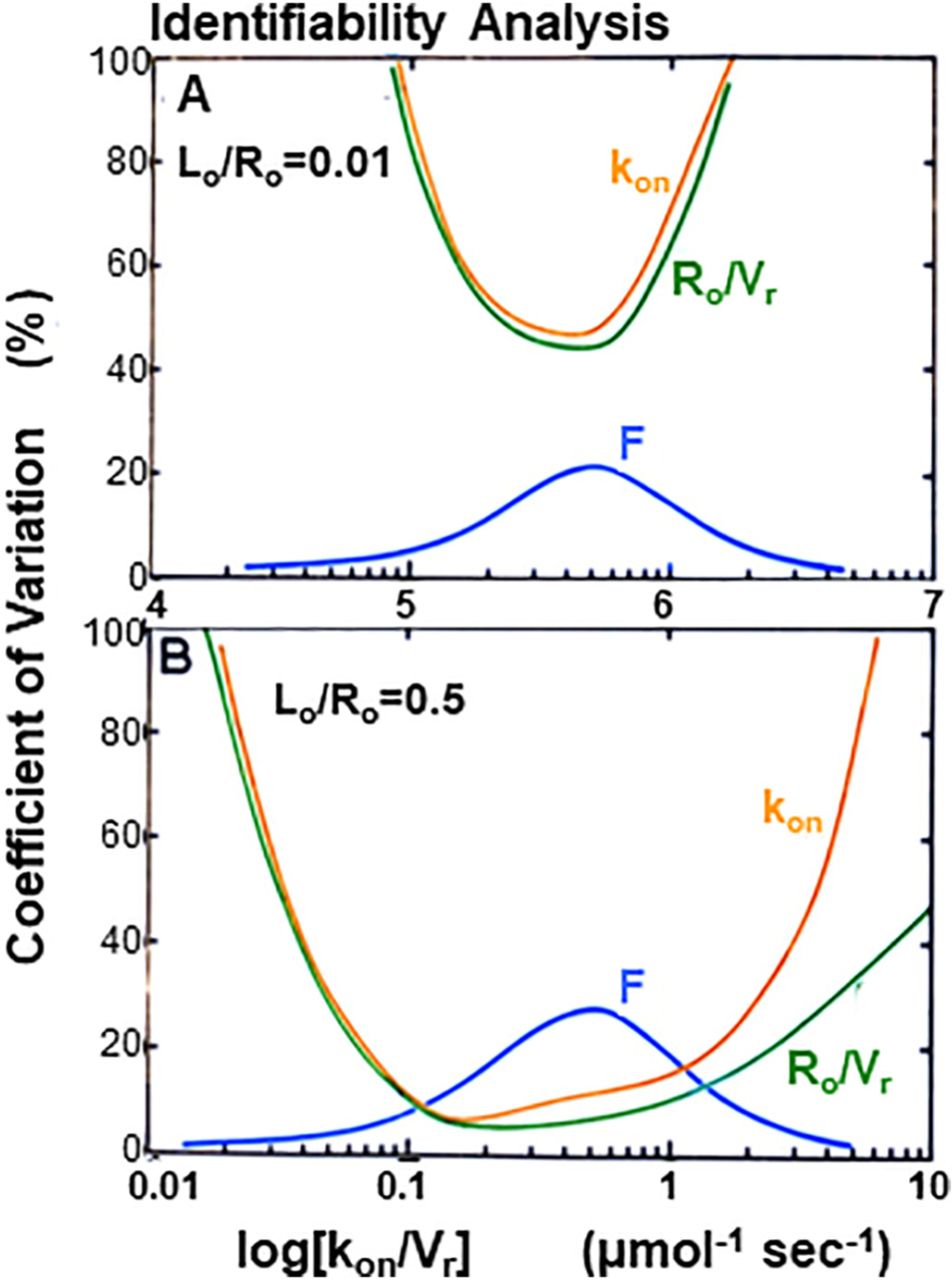
Local parameter identifiability analysis at “tracer” and “non-tracer” doses. Both panels provide the coefficient of variation (CV) for three model parameters: receptor concentration R_o/V_r, forward binding rate constant k_on, and hepatic plasma flow F. (Panel A) At “tracer” doses it is not possible to simultaneously estimate k_on & R_o/V_r; the orange and green curves in panel A do not fall below CVs of 40%. It is possible to estimate hepatic plasma flow F with uncertainties <25%. At both very low and very k_on/V_r it is possible to estimate F to a relative uncertainty of <10%; at low and high affinities the blue line falls below CVs of <10%. (Panel B) At a “non-tracer” dose (L_o/R_o = 0.5), it will be possible to simultaneously estimate F, k_on & R_o/V_r; this was predicted by the sensitivity analysis (Fig. 7B) where the “nontracer” dose produced F, k_on & R_o/V_r curves of somewhat different shapes and vastly different magnitudes.

5.4. Identifiability analysis

The common objective of a receptor-based radiotracer imaging experiment is to determine from imaging data both the ligand affinity for receptor and the concentration of receptor sites in a ROI and also delivery of the tracer to each ROI. These parameters are not directly observable; they must be “identified” through a mathematical model that simulates the measured imaging data. Models range from simple to highly complex so the researcher may make independent measurements for some variables, most commonly hemodynamic variables. But even with this additional information, a question remains of how many different variables can be adjusted during simulations and still arrive at a unique solution for the most biologically relevant parameters. Identifiability analysis is a formal analysis to determine how many and which parameters are uniquely identifiable. It assists radiotracer design by testing questions such as whether reversible or irreversible binding will be better, how limitations to k_on impact the ability to distinguish flow and vascular volumes from initial binding kinetics, and what level of NSB can be accommodated. The challenge is daunting because a full model often contains over ten parameters for rates and volumes yet, from a practical perspective, only 4 or 5 can be identified from a single TAC. As more parameters are added to a model, the likelihood of finding several different combinations of parameters that give an equally good simulation (Reduced Chi-Square) of the experimental data is high. The goal in this section is to match the radiotracer design and the model to arrive at a single unique parameter set to characterize the in vivo biology.

5.4.1. Identifiability of radiopharmaceuticals using “non-tracer” doses

Local parameter identifiability analysis is an engineering technique that predicts the uncertainty of parameter estimates resulting from the regression of a mathematical model to observation data. At the 1980 Receptor-Binding Radiotracer Workshop, Scheibe and Thomas [25] used the TcNGA kinetic system to illustrate the use of local identifiability analysis. Their objective was to determine whether imaging with a receptor-binding radiotracer could differentiate abnormal receptor concentration from variations in blood flow. A more detailed analysis [67] predicted the ability to estimate the initial receptor amount R_o and plasma flow F to within a relative uncertainty of 10%, if the affinity of the receptor was of a moderate value and if the amount of radiotracer injected was >10% of the amount of receptor within the target organ. The conclusion was that in vivo measurements of receptor biochemistry (k_on or [R]_o) required a change away from the concept of a radiopharmaceutical as a tracer. A “tracer” dose implies that the administered amount of radioactive compound will not perturb the biochemical pathway being studied. The early identifiability analyses of the TcNGA system predicted that a tracer dose of high affinity TcNGA could only measure hepatic plasma flow.

Fig. 9 illustrates the local identifiability of the TcNGA kinetic model using human physiochemical values. Both panels of Fig. 8 provide the coefficient of variation (CV) for three model parameters: receptor concentration R_o/V_r, forward binding rate constant k_on, and hepatic plasma flow F. The TcNGA kinetic model (Fig. 3) was simulated using two observers, time-activity curves from a region-of-interest (ROI) placed over the heart and lungs, and a ROI placed over the liver. Multiple identifiability calculations were performed with different values of receptor-ligand affinity k_on/V_r. These calculations generated two sets of CV curves, one set for L_o/R_o = 0.01 (panel A) and another set for L_o/R_o = 0.5 (panel B). In both scenarios, the analysis assumed that: 1) parameter f, the fraction-of-injected dose per gram of plasma in the plasma at the start of the model simulation would be measured; 2) the three model states conserved mass at the time of the plasma samples, 3) the observational coupling σ₁ could be calculated by dividing Y₁ at the time of the plasma sample by NGA plasma concentration at the time that the plasma was sampled fL_o, and 4) the regression of the observational data to the model simulation (the goodness-of-fit) would equal a reduced Chi-square of 1.0, indicating a “mean” fit.

Comparison of Panels A and B of Fig. 9 provides an interpretation of the analysis. Panel A of Fig. 8 is a simulation using a “tracer” dose. The three CV curves indicate that at tracer doses it is not possible to simultaneously estimate the two biochemical elements (k_on and R_o/V_r); the orange and green curves in Panel A do not fall below CVs of 40%. It is possible to estimate hepatic plasma flow F with uncertainties <25%. This was predicted by sensitivity analysis (Fig. 7A) where the tracer dose produced k_on and R_o/V_r curves of similar shape and magnitude. At both very low and very high receptor-ligand affinities (k_on/V_r) it is possible to estimate hepatic plasma F to a relative uncertainty of <10%; at low and high affinities the blue line falls below CVs < 10%. This graphical response on the right side of Panel A is consistent with the concept of a chemical microsphere, where a “tracer” dose of an extremely high affinity probe is used to measure tissue blood flow. In Panel B the two CV curves for the biochemical parameters are shifted down toward more favorable relative uncertainties. At a “non-tracer” dose (L_o/R_o = 0.5), it will be possible to simultaneously estimate F, k_on, and R_o/V_r. This was predicted by the sensitivity analysis (Fig. 7B) where the nontracer dose produced F, k_on, and R_o/V_r curves of somewhat different shapes and vastly different magnitudes.

5.4.2. Identifiability of radiopharmaceuticals using multiple tracer inputs

The liver presents modeling challenges when using plasma data as an input function to “drive” hepatic accumulation. Identifiability analysis was used to determine optimal solutions in view of the liver’s dual blood supply and used it to evaluate solutions to FDG-PET/CT for evaluating human liver inflammation via the blood-to-tissue rate constant k₁. In this case the input function is complicated by a dual blood input function, hepatic artery and portal vein. Static FDG scans do not show a potential for quantifying liver inflammation. This problem was recently addressed by local identifiability analysis using computer simulation of imaging data from fourteen patients [68]. Wang and co-workers [69] had used an optimization-derived approach to jointly estimate the dual-blood input function and liver FDG kinetics without invasive blood sampling. Zuo’s approach used the Laplace transform to assess structural identifiability as an indication of accuracy and precision for this kinetic modeling problem. The model was similar to that in Fig. 1, panel B, but it added a fractional blood volume, V_b, and two parameters for the dual input, the rate at which FDG flows through the GI system, k_a, and the fractional hepatic artery contribution to liver blood flow, f_A. The publication provided graphs of sensitivity versus scan time for k₁, k₂, k₃, k₄ as well as V_b, k_a and f_A, a total of seven parameters. As expected for this model structure, sensitivity for k₁ and k₂ was greatest at early times and k₃ and k₄ at later times. The sensitivity curves for V_b and f_A were overlapping but sufficiently different from the shape of K₁ so should have a minimal effect on this important parameter. Practical identifiability was quantified by presenting graphs of percentage bias (and standard deviation) in K₁ for each patient. The conclusion was that the net FDG influx rate from the model correlated with liver inflammation score better than an SUV.

5.4.3. Identifiability of radiopharmaceuticals using multiple injections

Jacques Delforge and colleagues have considered from first principles the identifiability problem with different ligand-receptor imaging protocols [43]. Their report was built on measurements in the dog heart with the radiotracer methyl-quinuclidinyl benzilate, [¹¹C]-MQNB. This is a non-metabolized hydrophilic antagonist for the muscarinic acetylcholine receptor. Their publication follows the model shown in Fig. 1, panel B, although their parameters are labeled differently. Identification of the model parameters required measurement of the arterial blood TAC with 5-s temporal resolution for early times. This publication provides a valuable learning exercise for investigators planning to develop a receptor-based imaging agent. The didactic value is that it compared 3 experimental protocols to evaluate the trade-offs between the data that is collected and the identifiability of important parameters.

Identification of model parameters from a single tracer injection was described as disappointing, important parameters were not uniquely determined. Three different simulations with widely varying parameters all gave indistinguishable simulated curves that matched the measured data. The next step investigated the possibility of improving parameter estimation by the administration of unlabeled ligand 20 minutes after the tracer injection. This led to an increased association with unoccupied receptors and marked washout of the labeled [¹¹C]-MQNB. Model parameters were estimated by minimization of a least-square error function weighted by the magnitude of the decay-corrected measurements. It was disappointing to find that, depending on starting conditions, an equally good fit could be obtained with two very different solutions. B′_max was 15.8 ± 1.3 nM for the first solution and 49.1 ± 1.9 nM for the second. The parameter uncertainties were calculated from the covariance matrix as described in the original report. Differences of the same magnitude were found for k₃ (k₊₁/V_R in their nomenclature) although now the first solution was higher. The solutions for flow were much closer because the arterial input had been measured independently. The third approach was a 3-injection protocol intended to allow determination of which of the two solutions from the second approach was valid. It started with two consecutive injections but was then followed by a third injection where labeled and 4-times more unlabeled MQNB were mixed before injection at 40 min after the first [¹¹C]MQNB dose. Now the solutions for the two simulations were qualitatively different and the simulation from the second starting condition was very close to the experimental data. The result was a unique set of parameters; the protocol was identifiable under reasonable noise conditions. This was confirmed by a Monte Carlo procedure with a simulated noise-free theoretical curve generated with a 4th-order Runge-Kutta method. The authors concluded that, in a routine imaging examination, co-injection at 40 min will not always be necessary but they did not test whether an equally unique parameter set would result from only the simultaneous injection described at 40 min.

5.5. Diagnostic power

As any new radiopharmaceutical progresses through early clinical studies, the imaging community will demand evidence that it provides clinically relevant information. One way to demonstrate this characteristic is through a receiver-operating-characteristic curve, a plot of the false-positive rate, FP, versus the true-positive rate, TP. The plot is called ROC analysis and is constructed from analysis of different cut-off points between positive and negative groups as evaluated by the new imaging test. A simple coin toss would give a straight-line correlation. A useful test would have a consistently higher TP than FP.

Different combinations of model estimates provide different levels of diagnostic accuracy. When a kinetic model has multiple parameters, the last step in the design is to select the measurement or combination of measurements that will provide the clinician with the most powerful metric by which to interpret the study results and management of a patient’s disease. Fig. 10 illustrates our investigation [70] of this issue. The metric with the largest area-under curve (AUC) was k_on[R]_o[R]_o/tbw (A_z = 0.985 ± 0.011). This metric is known in the hepatology literature as the maximum transport rate and is used as a metric for many classic liver function tests [71], such as the ICG clearance test. The R_o/V_r metric produced an AUC (A_z = 0.974 ± 0.018) that was not statistically different (P = 0.188) than k_on[R]_o[R]_o/tbw. The ABT metric from the aminopyrine breath test [72], an excellent but logistically challenged liver function test, yielded a high AUC (A_z = 0.939 ± 0.030). When the total amount of receptor R_o was tested, the AUC was 0.875 ± 0.042, which differed significantly (P < 0.005) from k_on[R]_o[R]_o/tbw. Other metrics of interest, but not shown in Fig. 10, are the pseudo-first order rate constant k_b[R]_o, which performed favorably (Az = 0.941 ± 0.026) and the scaled plasma flow F/V_e, which performed poorly (Az = 0.643 ± 0.066). Poor diagnostic accuracy from the flow parameter was expected for two reasons. First, the TcNGA system was optimized for high sensitivity to receptor concentration [55]; we employed an NGA of moderate affinity and an injected dose that would occupy a high percentage of hepatic receptors within healthy liver. Consequently, the relative errors were high for the scaled plasma flow estimates from the TcNGA functional imaging studies: 50 to 90% [37]. Second, it is well known that plasma flow measurements are poor diagnostic metrics of organ function. This is especially the case for the liver, which during exercise or a meal can significantly alter its plasma flow. We concluded from this analysis that intensive variables such as k_on[R]_o[R]_o/tbw and [R]_o, which equals R_o/V_r, provide the best diagnostic metrics. Such variables are independent of size. The extensive metric R_o yielded a poor AUC because it can change depending on the patient’s body weight and gender.

Fig. 10.

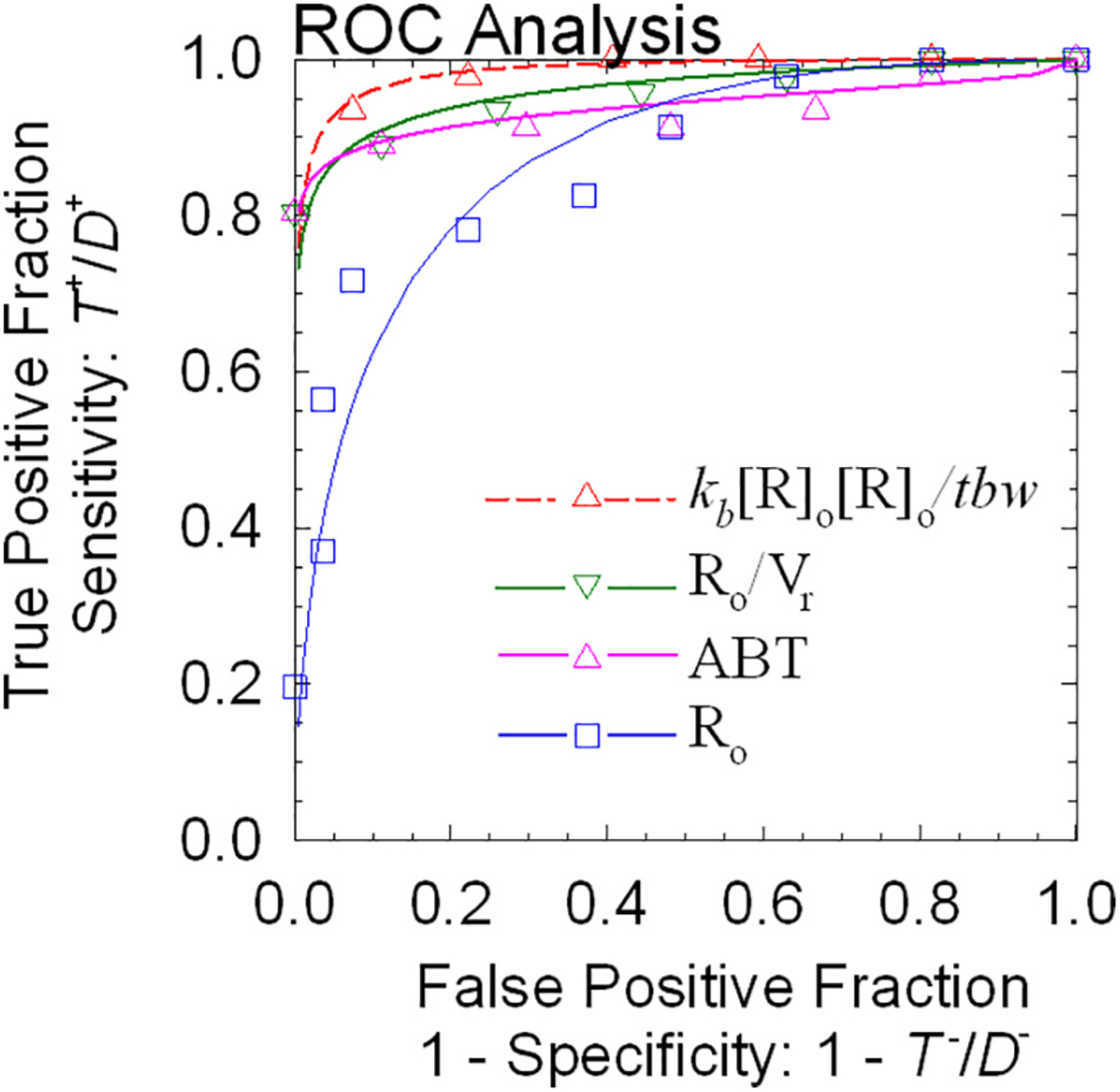
Analysis of diagnostic accuracy. Different combinations of model estimates provide different levels of diagnostic accuracy. The metric with the largest area-under curve (AUC) was k_on{R]_o{R]_o/tbw (A_z = 0.985 ± 0.011). The R_o/V_r metric produced an AUC (A_z = 0.974 ± 0.018) that was not statistically different (P = 0.188) than k_on{R]_o{R]_o/tbw. The ABT metric yielded a high AUC (A_z = 0.939 ± 0.030). When the total amount of receptor R_o was tested, the AUC was 0.875 ± 0.042, which differed significantly (P < 0.005) from k_on{R]_o{R]_o/tbw. We concluded from this analysis that intensive variables such as k_on{R]_o{R]_o/tbw, [R]_o, which equals Ro/V_r, provide the best diagnostic metrics. Such variables are independent of size. The extensive metric R_o yielded a poor AUC because it can change depending on the patient’s body weight and gender.

The literature provided another example of ROC applied to hypoxia imaging. Without duplicating the background for hypoxia imaging [73], the fact is that hypoxia has a negative prognostic role in many situations. In cancer it leads to genomic changes that make the disease resistant to radiotherapy and chemotherapy. Imaging should be a useful way to select patients with more hypoxic disease and predict that they would benefit from more aggressive therapy. The practical question is what metric of hypoxia imaging best separates those patients with sufficient hypoxia to warrant additional treatment. Tachibana [74] approached this question in patients with a variety of tumors and generated the ROC curve in Fig. 11. The interpretation of this figure is that hypoxia can be distinguished from normoxia equally well with the maximum tumor-to-muscle ratio or the hypoxic volume or even the SUV_max.

Fig. 11.

An ROC analysis of three hypoxia imaging metrics. Hypoxia can be distinguished from normoxia equally well with the maximum tumor-to-muscle ratio (T/M) or the hypoxic volume (HV) or even the SUV_max.

The ROC analyses provide evidence to confirm the prediction of Eckelman and Reba [53] that radiopharmaceuticals that bind to a specific molecule within a biochemical pathway would lead to a “more precise diagnostic interpretation”. As we stated at the beginning of this article, receptor-binding radiopharmaceuticals provide a more precise understanding of the process by which the nuclear images are formed. Knowledge of the second-order nature of ligand-receptor binding permits mathematical modeling with specific chemical properties that can be measured and tested in vitro, as well as in vivo. These properties can be used to optimize the performance of the radiopharmaceutical.

6. Conclusion

We hope that this educational review will find value for young scientists embarking on a career developing new radiotracers, whether or not they are for quantifying receptor binding with a new radioligand. A beginning student might survey the pharmacology and medicinal chemistry regularly and will soon compile a list of candidate molecules that could be labeled with ¹⁸F or ¹¹C using minor modification to standard methods. But this is the time to step back and ask whether, if this radiopharmaceutical performed as well as anticipated, a physician might be convinced that the resulting information would have practical diagnostic or prognostic value. With an affirmative response from one or more physicians, the student should next benefit from considering the numerous challenges to radiopharmaceutical design discussed in this article.