The role of the bubble–bubble interaction on radial pulsations of bubbles

Highlights

• •Bubble–bubble interaction can suppress or enlarge the radial pulsations of bubbles.
• •The suppression or enlargement depends on the ultrasound parameters, the radii, the distances and the bubble number.
• •The frequency response curve of expansion ratio decreases and shifts to left due to bubble–bubble interaction.
• •The larger the coupling strength is, the more the left-shifting is.

Abstract

Using a model that with or without considering the interaction between bubbles through the radiated pressure waves, numerical simulations of cavitation bubbles have been performed in order to study the effect of the bubble–bubble interaction on radial pulsations of bubbles. Comparing the results obtained by with or without considering the bubble–bubble interaction, it is suggested that the suppression or enlargement property of expansion ratios of bubbles due to the bubble–bubble interaction largely depends on the ultrasound parameters, the ambient bubble radii, the distances between bubbles and the number of bubbles (in multi-bubble environment, the last two aspects can be expressed using the coupling strength). The frequency response curve of expansion ratio decreases and shifts to left due to the bubble–bubble interaction and the larger the coupling strength is, the more the left-shifting is.

1. Introduction

When intense ultrasound irradiates into liquid such as water, many tiny gas/vapor bubbles appear and these bubbles experience wildly nonlinear oscillations, which is known as acoustic cavitation [1]. As the acoustical energy is continuously localized to the oscillating bubbles, the bubbles will repeatedly released secondary radiation pressure waves to surrounding liquid which, in turn, act on the neighboring bubbles as an additional driving pressure [2]. This phenomenon is called the bubble–bubble interaction which has been extensively studied by many researchers to gain a deep understanding of the physical features between bubbles. Most of these researches focused on the direction and magnitude of the bubble–bubble interaction or translational motions of bubbles [3], [4], [5], [6], [7], [8], [9], [10], [11], [12], however the bubble–bubble interaction affects not only translational motions but also radial pulsations. Ida showed that the maximum radius of a small bubble is reduced or suppressed by an injected large bubble when the ultrasound parameters and the distances between two bubbles are appropriately set, but that of the injected (big) bubble remains almost constant [13]. Yasui obtained a similar result through numerical simulations of radial pulsations in multi-bubble environment by assuming that the ambient radius of each bubble is the same for all the bubbles and by introducing a new variable named the coupling strengths ($S={\sum }_{i}1/r_i$, where $r_i$ is the distance from the bubble numbered i) [14], [15], [16], [17]. Wang formulated an interacting equation of multi-bubble motion for a system of a single bubble and a spherical bubble cluster, and found that the maximum radius of a bubble is suppressed and the suppression is enhanced as the bubble density increases [18], which confirmed the result achieved by Yasui. The numerical simulation obtained by An suggested that the interaction between bubbles suppresses bubble expansion and the violent extent of the bubble collapse by analyzing the characteristics of cavitation in acoustic standing waves [19]. Aside from these, Jiang numerically investigated the dynamics of two bubbles at high frequency acoustic fields, and found that the suppression gradually enhances by decreasing the distance between two bubbles [20]. To the best of our knowledge, all of these results showed that the interaction between bubbles influences the evolution of bubbles: it partly reduces or dramatically suppresses expansion ratio of the small bubble, and has less reduction in that of the big one, which is the common viewpoint about the effect of the bubble–bubble interaction on radial pulsations of bubbles.

In the present study, the dynamics of multi-bubble system are performed to study the role of the bubble–bubble interaction on radial pulsations of bubbles with different ambient radii under different driving frequencies, different number of bubbles and different distances between bubbles. The attention is mainly focused on the effect of the bubble–bubble interaction on radial pulsations of bubbles rather than the translational motions whose contribution to radial pulsations is a higher-order correction. In order to reduce the computational complexity, the distance between bubbles in this work is set to a fixed value (not as a function of time).

2. Model equations

The Keller Miksis equation [21], [22], a variant of Rayleigh-Plesset equation, is used to study the radial pulsation of an isolated spherical bubble in liquid:

$$\left(1-\frac{\dot{R}}{c}\right)R\ddot{R}+\frac{3}{2}\left(1-\frac{\dot{R}}{3c}\right)=\frac{1}{\rho }\left(1+\frac{\dot{R}}{c}\right)p_s+\frac{R}{\rho c}\frac{\mathrm{d}{p}_s}{\mathrm{d}t},$$ (1)

where $·$ is the time derivative, R is the time-dependent radius of the bubble, c is the sound speed in liquid, $\rho$ is the liquid density, $p_s$ is the pressure on the bubble wall:

$$p_s=\left(p_0+\frac{2\sigma }{R_0}\right){\left(\frac{R_0^3-h^3}{R^3-h^3}\right)}^{\gamma }-\frac{2\sigma }{R}-\frac{4\mu \dot{R}}{R}-p_A\sin (2\pi \mathit{ft})-p_0,$$ (2)

where $p_0$ is the atmospheric pressure, $\sigma$ is the surface tension of the liquid, $R_0$ is the ambient radius, h is the van der Wall’s hard-core [23], $\mu$ is the viscosity of liquid, $\gamma$ is the specific heat ratio of the gas inside the bubble, $p_A$ and f are the amplitude and frequency of the driving pressure acting on the bubble, respectively.

The radiated pressure (p) from this bubble can be expressed by the following equation:

$$p=\frac{\rho \left(R^2\ddot{R}+2R{\dot{R}}^2\right)}{r}\text{.}$$ (3)

where r is the distance from the center of the bubble.

Assuming there are some gas bubbles in a liquid driven by a stationary sound field, and the distance between (centers of) two bubbles (named i and j) is fixed to $d_{\mathit{ij}}$. The wave length is in magnitude of centimeter in this work which is much larger than the distances d, so it is safely assumed that bubbles experience an equal driving amplitude. And the distances between bubbles are always large enough to make the bubbles remain spherical [4], [13]. The bubble–bubble interaction, the influence of acoustic wave radiated by the other bubbles, should be considered in the calculations of radial pulsations in order to study its effect on radial pulsations of bubbles. Thus, the modified equation of bubble i:

$$\left(1-\frac{{\dot{R}}_i}{c}\right)R_i{\ddot{R}}_i+\frac{3}{2}\left(1-\frac{{\dot{R}}_i}{3c}\right){\dot{R}}_i^2=\frac{1}{\rho }\left(1+\frac{{\dot{R}}_i}{c}\right)p_{s,i}+\frac{R_i}{\rho c}\frac{\mathrm{d}{p}_{s,i}}{\mathrm{d}t}-{\displaystyle \sum _{j=1,j\ne i}^N}\frac{1}{d_{\mathit{ij}}}\left(2R_j{\dot{R}}_j^2+R_j^2{\ddot{R}}_j\right),$$ (4)

where N is the number of the bubbles, $i=1\cdots N$. And the pressure on the wall of bubble i:

$$p_{s,i}=p_{g,i}-\frac{2\sigma }{R_i}-\frac{4\mu {\dot{R}}_i}{R_i}-p_A\sin (2\pi \mathit{ft})-p_0,$$ (5)

The pressure inside the bubble, $p_{g,i}$, is assumed to obey the van der Waals equation [24], [23], [25]:

$$p_{g,i}=\left(P_0+\frac{2\sigma }{R_{i0}}\right){\left(\frac{R_{i0}^3-h_i^3}{R_i^3-h_i^3}\right)}^{\gamma }$$ (6)

where the $R_{i0}$ is the ambient radius of the bubble $i,h_i$ is the van der Waals hard-core radius [23] for bubble i which represents the volume excluded by the total volume of gas molecules as hard spheres.

3. The effect on radial pulsation in two-bubble system

The calculations are carried out for two bubbles ($N=2$) in liquid (water) under atmospheric pressure $p_0=1\mathrm{atm}$ to compare the dynamics of two bubbles with or without (the distance between two bubbles is set to $\infty$) considering the bubble–bubble interaction. The parameters of liquid (water) and gas inside the bubbles are set to c = 1481 m/s, $\rho =998.2{\text{Kg/m}}^3\text{, }\mathit{\text{σ}}=\text{72.75 mN/m,}\mathit{\text{μ}}=\text{0.001 Pa·s}$ and $\gamma =1.33$. The driving pressure is a sine wave and it is assumed that there is no initial phase difference between two bubbles. The ambient bubble radii of two bubbles, the driving frequency and amplitude will be given for different cases within each subsection. For all of the figures in this section, in the left sub-figure, the red (blue) solid-line and red (blue) dash-line are the dynamics of the bubble with ambient radius $R_{10}$ ($R_{20}$) without and with considering the bubble–bubble interaction as a function of time, respectively. In the right sub-figure, the red (blue) solid-line and red (blue) dash-line are expansion ratios ($R_{\mathit{max}}/R_0$) of the bubble with ambient radius $R_{10}$ ($R_{20}$) for different distances between two bubbles without and with considering the bubble–bubble interaction, respectively. In the legends, the ‘0’ after the ‘–’ means the results without considering the bubble–bubble interaction and the ‘1’ after the ‘–’ means the results with considering the bubble–bubble interaction. All the figures are plotted after two bubbles stabilize. Table 1 displays different cases of the effect of the bubble–bubble interaction on expansion ratios of two bubbles which will be discussed. In this table, ‘$\uparrow$’ stands for the increase of expansion ratio when considering the bubble–bubble interaction, ‘$\downarrow$’ stands for the decease of expansion ratio when considering the bubble–bubble interaction, ‘–’ means that the change of expansion ratio of the bubble remains constant or within a really small range.

Table 1.

Different cases of two bubbles.

$R_{\mathit{max}}/R_0$	Case 1	Case 2	Case 3	Case 4	Case 5
Big Bubble	–	$\downarrow$	$\uparrow$	$\downarrow$	$\uparrow$
Small Bubble	$\downarrow$	$\downarrow$	$\downarrow$	$\uparrow$	$\uparrow$

3.1. Suppression of the bubbles

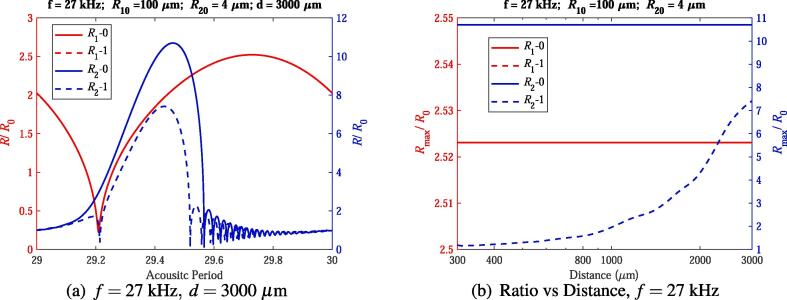
In this subsection, we will first introduce that the bubble–bubble interaction suppresses the radial pulsation (expansion ratio) of the bubbles, which corresponds to cases 1–2. In case 1, expansion ratio of the big bubble is not sensitive to the bubble–bubble interaction but that of the small bubble is suppressed. The dynamics of two bubbles with the ambient radii ($R_{10}=100\mu \mathrm{m}$ and $R_{20}=4\mu \mathrm{m}$) are shown in Fig. 1(a), where the driving frequency is 27 kHz and the distance between two bubbles is $3000\mathrm{\mu }\mathrm{m}$. It can be seen that the bubble–bubble interaction has a much larger effect to the dynamic of the small bubble than that of the big one (in this case, the red solid-line and the red dash-line overlap).

Fig. 1.

Radius-time curves and expansion ratio of two bubbles ($R_{10}=100\mathrm{\mu }\mathrm{m},R_{20}=4\mathrm{\mu }\mathrm{m}$).

Expansion ratios of two bubbles are plotted in Fig. 1(b) as function of distances between two bubbles. One can find from Fig. 1(b) that expansion ratios of the big bubble remain no change, but that of the small bubble decrease due to the bubble–bubble interaction, and expansion ratios of the small bubble decrease with the decrease of the distance between two bubbles, which agree with the results shown in reference [20]. When the distance between two bubbles is sufficiently short, the small bubble can be completely suppressed (expansion ratio of the small bubble is close to one), which is similar to the results shown in reference [13].

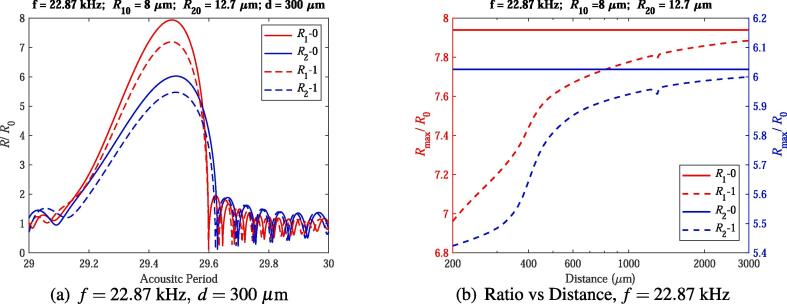
In case 2, we show that both expansion ratios of two bubbles decrease due to the bubble–bubble interaction. The ambient radii of two bubbles are $R_{10}=8\mathrm{\mu }\mathrm{m},R_{20}=12.7\mathrm{\mu }\mathrm{m}$, and the driving frequency is 22.87 kHz. In Fig. 2(a), the dynamics of two bubbles are shown where the distance between two bubbles is 300 $\mathrm{\mu }\mathrm{m}$. It can be seen that both expansion ratios of two bubbles decrease due to the present of the other bubble. In Fig. 2(b), expansion ratios of two bubbles are shown as a function of the distances between two bubbles. It can be seen that expansion ratios of both bubbles is suppressed due to the bubble–bubble interaction.

Fig. 2.

Radius-time curves and expansion ratios of two bubbles ($R_{10}=8\mathrm{\mu }\mathrm{m},R_{20}=12.7\mathrm{\mu }\mathrm{m}$).

3.2. One suppression one enlargement

In this subsection, the cases that expansion ratio of one bubble is suppressed but that of the other one is enlarged are introduced, which correspond to cases 3–4.

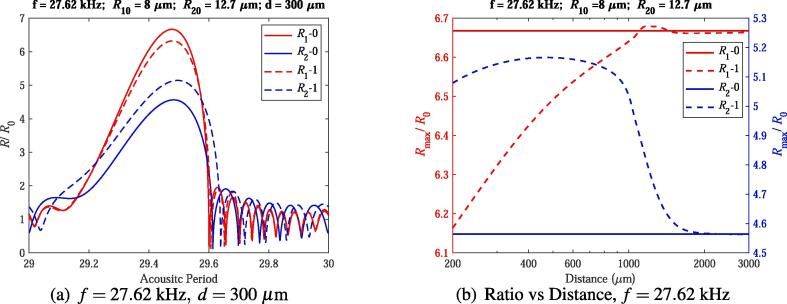
In case 3, we introduce that expansion ratio of the big bubble is enlarged but that of the small one is suppressed. The dynamics of two bubbles for ambient radii $R_{10}=8\mu \mathrm{m}$ and $R_{20}=12.7\mu \mathrm{m}$ at driving frequency $f=27.62$ kHz and the distance $d=300\mathrm{\mu }\mathrm{m}$ are shown in Fig. 3(a). It is shown that the bubble–bubble interaction enlarges expansion ratio of the big bubble $R_{20}$ rather than that of the small one $R_{10}$. The expansion ratios of two bubbles under different distances between two bubbles are shown in Fig. 3(b). One can find that expansion ratios of the small bubble $R_{10}$ is always suppressed by the bubble–bubble interaction and the suppression generally disappears with the increase of the distance; on the contrary, the bubble–bubble interaction always enlarges expansion ratios of the big bubble $R_{20}$ until $d=2000\mathrm{\mu }\mathrm{m}$.

Fig. 3.

Radius-time curves and expansion ratios of two bubbles ($R_{10}=8\mathrm{\mu }\mathrm{m},R_{20}=12.7\mathrm{\mu }\mathrm{m}$).

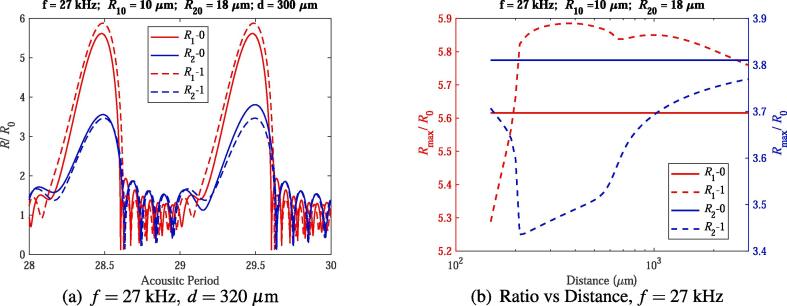
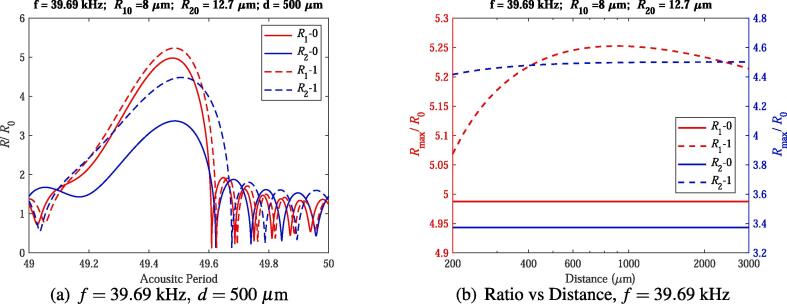
In case 4, expansion ratio of the big bubble is suppressed but that of the small one is enlarged. The dynamics of two bubbles for ambient radii $R_{10}=10\mu \mathrm{m}$ and $R_{20}=18\mu \mathrm{m}$ at driving frequency $f=27$ kHz and the distance $d=320\mathrm{\mu }\mathrm{m}$ are shown in Fig. 4(a). In this figure, one can find that expansion ratio of the small bubble ($R_{10}$) increases due to the bubble–bubble interaction, however, expansion ratio of the big bubble decreases. In Fig. 4(b), expansion ratios of two bubbles under different distances are shown. One can find that when the distance between two bubbles is smaller than 200 $\mathrm{\mu }\mathrm{m}$, the small bubble expands to a lower maximum radius; on the contrary, at distance ranging from 200 to 3000 $\mathrm{\mu }\mathrm{m}$, the small bubble can reach a higher expansion ratio due to the bubble–bubble interaction and expansion ratios hit its peak point ($R_{\mathit{max}}/R_0=5.89$) at $d=380\mu \mathrm{m}$, which is in conflict with the results in the reference [20]. But the big bubble is always suppressed by the bubble–bubble interaction for the whole distance range considered here.

Fig. 4.

Radius-time curves and expansion ratios of two bubbles ($R_{10}=10\mathrm{\mu }\mathrm{m},R_{20}=18\mathrm{\mu }\mathrm{m}$).

3.3. Enlargement of the bubbles

In this subsection, we then introduce that the bubble–bubble interaction enlarges expansion ratio of the bubbles, which corresponds to case 5.

The dynamics of two bubbles for ambient radii $R_{10}=8\mathrm{\mu }\mathrm{m}$ and $R_{20}=12.7\mathrm{\mu }\mathrm{m}$ at driving frequency $f=39.69$ kHz and the distance $d=500\mathrm{\mu }\mathrm{m}$ are shown in Fig. 5(a). It can be seen that expansion ratios of two bubbles when considering the bubble–bubble interaction are larger than that when without considering the bubble–bubble interaction, and the enlargement of expansion ratio of the big bubble is larger than that of expansion ratio of the small one. In Fig. 5(b), expansion ratios are shown under different distances between two bubbles. For the distance range (from $200\mathrm{\mu }\mathrm{m}$ to $3000\mathrm{\mu }\mathrm{m}$) considered here, expansion ratios of both bubbles is always enlarged by the bubble–bubble interaction.

Fig. 5.

Radius-time curves and expansion ratios of two bubbles ($R_{10}=8\mathrm{\mu }\mathrm{m},R_{20}=12.7\mathrm{\mu }\mathrm{m}$).

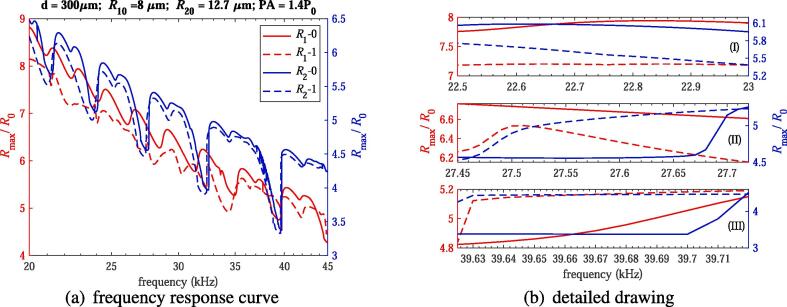
In this section, five cases are introduced to display different suppression or enlargement properties of expansion ratios of two bubbles under different parameters. In cases 2, 3, 5, the bubble ambient radii used are $R_{10}=8\mathrm{\mu }\mathrm{m}$ and $R_{20}=12.7\mathrm{\mu }\mathrm{m}$, but the frequencies are different (22.87, 27.62 and 39.69 kHz, respectively). From these three cases, the suppression or enlargement properties of bubbles due to the bubble–bubble interaction are totally different. Fig. 6(a) shows expansion ratios of two bubbles under the driving frequencies ranging from 20 kHz to 45 kHz and Fig. 6(b) shows a corresponding detailed drawing where the frequencies are around the three frequencies mentioned above. It can be seen from Fig. 6(a) that the frequency response curve shift a little to left, which results that the bubble–bubble interaction can cause expansion ratio to increase or decrease when using a suitable frequency. Fig. 6(b) suggests that around the frequencies mentioned above, the effects of the bubble–bubble interaction are similar to cases 2, 3, 5, respectively. It should be noted that the two-bubble system in this work is not a energy conversation system because the total energies of the two bubbles acquired from the driving sound wave are different when comparing the results obtained by with or without considering the bubble–bubble interaction.

Fig. 6.

The expansion ratios of two bubbles under different frequencies ($R_{10}=8\mathrm{\mu }\mathrm{m},R_{20}=12.7\mathrm{\mu }\mathrm{m}$).

4. The effect on radial pulsation in multi-bubble system

In this section, we consider a multi-bubble environment to study the effect of the bubble–bubble interaction on radial pulsations of bubbles. Assuming that the number density of the bubbles is n, that the ambient radius of each bubble is the same for all the bubbles, and that the distribution of the bubbles is uniform in space [15]. Then, the last term in Section 3

$$-{\displaystyle \sum _{j=1,j\ne i}^N}\frac{1}{d_{\mathit{ij}}}\left(2R_j{\dot{R}}_j^2+R_j^2{\ddot{R}}_j\right)$$

can be rewritten as [14]

$$-S\left(2R_j{\dot{R}}_j^2+R_j^2{\ddot{R}}_j\right)$$ (7)

where

$$S={\displaystyle \sum _i}\frac{1}{r_i}={\int }_{l_{\min }}^{l_{\max }}\frac{4\pi r^{2}n}{r}\mathrm{d}r=2\pi n\left(l_{\max }^2-l_{\min }^2\right)\approx 2\pi {\mathit{nl}}_{\max }^2\text{.}$$

where $l_{\mathit{max}}$ is the radius of the bubble cloud which contains all the bubbles, $l_{\mathit{min}}$ is the distance between a bubble and a nearest bubble, $l_{\mathit{max}}⩾l_{\mathit{min}}$ is also assumed in the last term. The factor S is called the coupling strength of the bubble–bubble interaction [14], [26], [27], [17], [28].

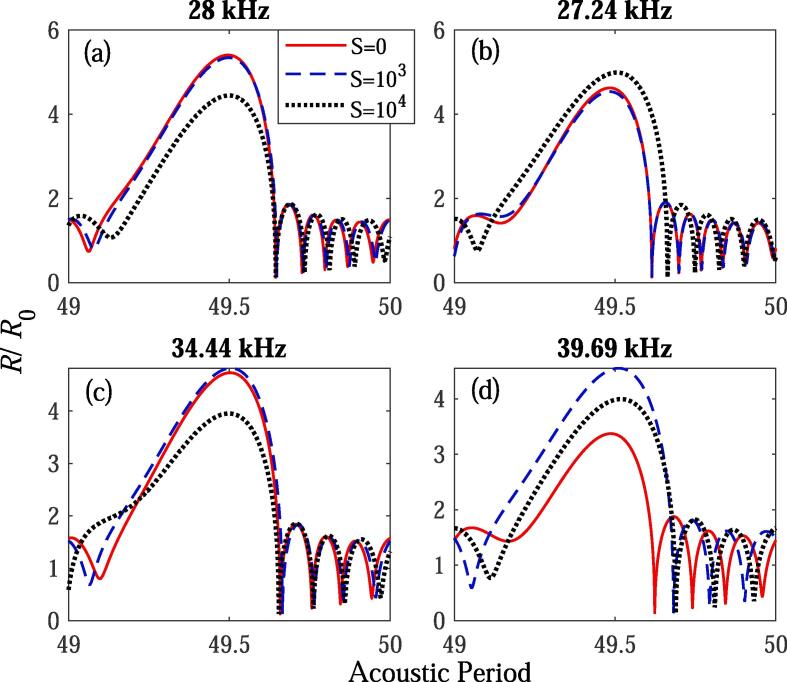
The dynamics of the bubble ($R_0=12.7\mathrm{\mu }\mathrm{m}$) are shown in Fig. 7 for various coupling strengths (S) of the bubble–bubble interaction. The ultrasound frequencies are $28,27.24,34.44$ and $39.69$ kHz, respectively. The other parameters are the same as the Section 3. The coupling strengths (S) are chose to be ${10}^3$ and ${10}^4{\mathrm{m}}^{-1}$. It can be seen that from Fig. 7(a) that expansion ratio is more strongly suppressed as the coupling strength increases [27] when the ultrasound frequency is 28 kHz; in Fig. 7(b), expansion ratio is suppressed when the coupling strength is ${10}^3{\mathrm{m}}^{-1}$ and enlarged when the coupling strength is ${10}^4{\mathrm{m}}^{-1}$ when the ultrasound frequency is 27.24 kHz; in Fig. 7(c), expansion ratio is enlarged when the coupling strength is ${10}^3{\mathrm{m}}^{-1}$ and suppressed when the coupling strength is ${10}^4{\mathrm{m}}^{-1}$ when the ultrasound frequency is 34.44 kHz; and in Fig. 7(d), expansion ratio is enlarged for both the coupling strengths when the frequency of ultrasound is 39.69 kHz. Thus, it is suggested from Fig. 7 that the suppression or enlargement properties of expansion ratios are different when using the ultrasound frequencies.

Fig. 7.

Radius-time curves of the bubble for various coupling strengths (S), ($R_0=12.7\mathrm{\mu }\mathrm{m}$).

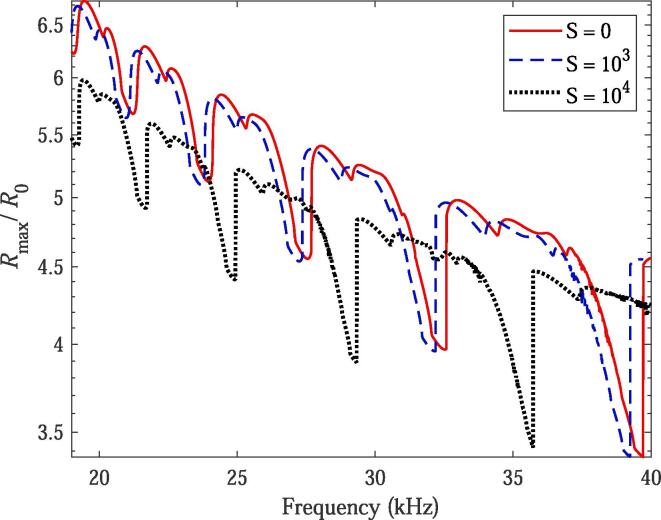
The expansion ratios of bubble under different coupling strengths and different ultrasound frequencies are shown in Fig. 8. It can be seen that the frequency response curve of expansion ratio decreases and shifts to left due to the bubble–bubble interaction and the larger the coupling strength is, the more the left-shifting is. The reason is that the resonance frequency (Eq. (8)) of a bubble decreases as the coupling strength (S) increases [15].

$${\omega }_0=\sqrt{\frac{3\gamma p_0+(3\gamma -1)2\sigma /R_0}{\rho R_0\left(R_0+{\mathit{SR}}_0^2+4\mu /c\rho \right)}}$$ (8)

Fig. 8.

The expansion ratios of bubble for various coupling strength (S) of the bubble–bubble interaction under different ultrasound frequencies. The ambient radius is $12.7\mathrm{\mu }\mathrm{m}$.

Because of the nonmonotonicity of frequency response curve of expansion ratio, thus, expansion ratio of one bubble could be enlarged because of the bubble–bubble interaction when the ultrasound frequency is suitable (see Fig. 8).

5. Conclusion

In this work, the dynamics of bubbles are investigated to study the effect of the bubble–bubble interaction on radial pulsations of bubbles under different driving frequencies, different ambient radii, different distances between two bubbles and different number of bubbles (coupling strength). The results suggest that the bubble–bubble interaction, the radiated pressure waves, not only can decrease or suppress expansion ratios of bubbles, but also can enlarge that of bubbles. The suppression or enlargement property of expansion ratio of one bubble due to the bubble–bubble interaction is because of the driving frequency, the ambient radii of bubbles, the distances between bubbles and the number of bubbles (maybe also the driving pressure amplitudes and liquid parameters, but this is beyond the scope of this work). The frequency response curve of expansion ratio decreases and shifts to left due to the bubble–bubble interaction. Besides that, in multi-bubble environment, the larger the coupling strength is, the more the left-shifting is.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.