Abstract
In order to reduce the radar cross section (RCS) of the unmanned aircraft while suppressing its infrared signature, a comprehensive design method (CDM) based on sorting factor Pareto solution is presented. The physical optics and physical diffraction theory are used to evaluate the electromagnetic scattering characteristics of the aircraft, and the Monte Carlo and ray tracing method are used to evaluate the infrared radiation intensity of the exhaust system. CDM is used to evaluate and screen each individual in each offspring, and the design parameters and sub-models of the aircraft exhaust system are continuously improved. The results show that the exhaust port model, lower baffle and nozzle height are the main factors affecting the RCS indicators, nozzle stages, exhaust port model, lower baffle and outer width make the main contribution to infrared radiation suppression. The presented CDM is efficient and effective in enhancing the radar/infrared integrated stealth performance of the aircraft.
Subject terms: Aerospace engineering, Electrical and electronic engineering, Optical physics
Introduction
The exhaust system of an unmanned fighter not only affects its aerodynamic characteristics and infrared (IR) signature, but also affects the electromagnetic scattering characteristics of its tail and sides1–3. Studying the comprehensive design of the exhaust system is of great significance to the infrared/radar stealth performance of the aircraft.
Future fighters and bombers are inclined to ultra-flat fuselage layout, which also brings certain challenges to the design of their intake and exhaust systems, while the balance and restriction between multiple performances is also the key concern of interdisciplinary4,5. Computational fluid dynamics (CFD), physical optics (PO), radial basis functions and sequential quadratic programming are integrated to optimize the aerodynamic/stealth characteristics of the flying wing aircraft, and good design variables and strategies are obtained6. Diverter less technology and tail nozzle baffles are often used on stealth fighters to improve the aerodynamic and stealth characteristics of these aircraft7,8. Compared with the traditional layout, the flying wing layout has the advantages of high aerodynamic efficiency, stealth and internal space utilization9,10, which makes the design of its exhaust system must take into account the low radar cross-section (RCS) and infrared radiation. Surface pixel method, PO and equivalent electromagnetic flow method are used to solve the RCS of three-wing fighter and stealth fighter11,12. Based on the existing aerodynamic design concepts and RCS analysis methods, the stealth development of the unmanned fighter exhaust system will pay more attention to infrared radiation suppression and radar/infrared integrated stealth.
The rapid development of high-sensitivity, high-resolution infrared imaging detection technology has made the survivability of fighters with radar stealth design also challenged13,14. Replace the axisymmetric nozzle with a binary non-axisymmetric nozzle with larger width and height to obtain better infrared radiation suppression. Combining the exponential broad band model and the radiation transfer equation (RTE), an infrared radiation characteristic estimation method was developed to evaluate the infrared signature of the engine exhaust system15. Using the CFD method, the temperature field of the unmanned combat aircraft in the non-forced state is obtained, and the numerical calculation of infrared radiation is performed16,17. Ray tracing method is used to solve the infrared signature of high temperature exhaust gas from different nozzles18. The serpentine nozzle can effectively suppress the infrared radiation characteristics while enhancing the radar stealth characteristics of military aircraft19. With the rise of comprehensive stealth research20, the design and optimization of unmanned combat aircraft are more inclined to consider multiple performance21,22. The gray correlation model can effectively evaluate the aerodynamic characteristics, RCS and IR signatures of the aircraft22–24. The comprehensive optimization method based on Pareto solution can also give a better solution to the needs of many aspects of stealth25,26. The continuous development of various technologies of unmanned bombers27 has also prompted its radar stealth design and infrared radiation suppression to achieve a better balance.
Previous research on the exhaust system of unmanned combat aircraft has mostly focused on aerodynamic shape improvement and infrared radiation characteristic calculation. With the continuous development and joint search of radar and infrared detectors, unilateral reduction of RCS or IR signatures has been unable to counter the threat of multiphysics. In view of the mutual constraints of aerodynamics, radar stealth and infrared radiation suppression when designing the unmanned aircraft exhaust system, this paper attempts to establish a hybrid design approach to establish a comprehensive stealth scheme that takes into account aerodynamic characteristics. This is of guiding significance and engineering value for improving the survivability and integrated combat effectiveness of unmanned fighters.
In this manuscript, the comprehensive design method (CDM) is presented in Sect. 2. Models of unmanned aircraft and exhaust system are built in Sect. 3. The results of RCS and IR signatures are provided and discussed in detail in Sect. 4. Finally, the full article is summarized in Sect. 5.
Comprehensive design method
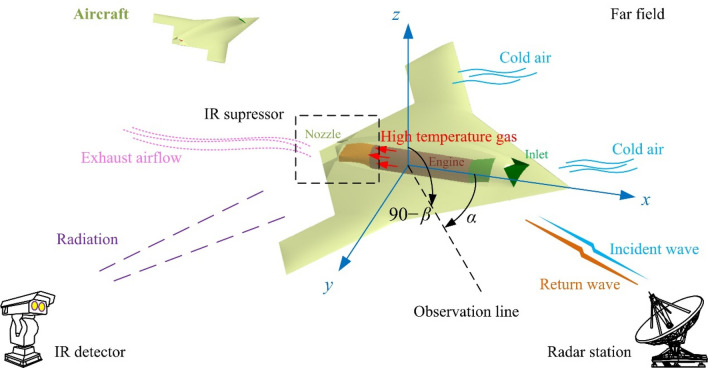
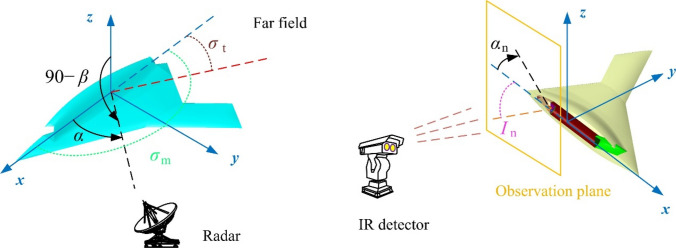
The analysis of the threat of unmanned aircraft from radar and infrared detectors is shown in Fig. 1, where α is the azimuth between the radar station and the aircraft, β is the elevation angle between the radar station and the aircraft. The comprehensive design method is used to reduce the electromagnetic scattering level of the aircraft exhaust system while suppressing its infrared radiation.
Figure 1.
Schematic diagram of radar/infrared integrated stealth design of aircraft exhaust system, drawn using Microsoft Visio 2007.
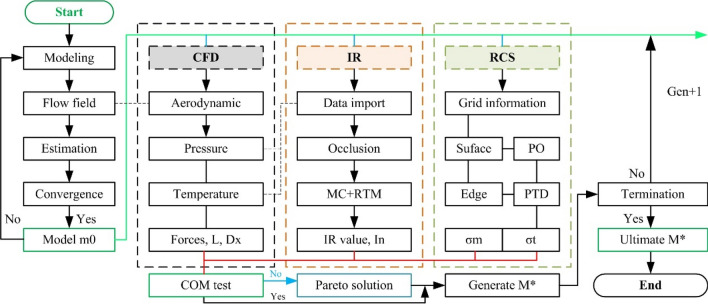
The entire design process includes three parts as shown in Fig. 2: the establishment of the initial model (m0), the calculation of performance indicators and the cycle judgment module. The first part emphasizes that both the flow field calculation and the grid need to converge to ensure that the subsequent calculations are comparable. The middle module performs aerodynamic, IR and RCS evaluation on each individual in each offspring, and comprehensively evaluates the optimal solution (M*). The third part judges the termination of the obtained M* to see if the next generation (Gen) design is needed.
Figure 2.
Flow chart of the comprehensive design method, drawn using Microsoft Visio 2007.
RCS calculation
PO and physical theory of diffraction (PTD) are used to solve the electromagnetic scattering characteristics of each individual in each offspring3. According to the magnetic vector position caused by the induced current on the surface of the target model, the electric field and magnetic field can be obtained as follows:
| 1 |
| 2 |
where r is the coordinate vector of the field point, ω is the electromagnetic wave angular frequency, k is the wave number in free space, R is the distance vector between the field point and the source point, r′ refers to the coordinate vector of the source point, ε is the dielectric permittivity28–30, Js represents the induced current on the target surface. When calculating RCS, the integral surface of the model is treated as an ideal conductor.
According to the assumption of PO, there is current in the illuminated area of the target surface, but no current in the dark area:
| 3 |
where ZI refers to the illuminated area, ZD is the dark area, and n represents the unit normal vector of the outer normal direction of r' at the surface of the scatterer. Therefore, the electric field formula can be changed to
| 4 |
where k means wave vector, λ represents the wavelength in free space, r refers to the distance from the field point to the origin of coordinates. The integral term can be calculated separately, so there is the following expression:
| 5 |
Therefore, the RCS of the surface can be determined as
| 6 |
In fact, the aircraft model has many edges and split angles, and these geometric features will also produce diffraction effects on electromagnetic waves. Here, PTD is used to solve the edge diffraction. 20 The total RCS can be expressed as the joint contribution of PO and PTD:
| 7 |
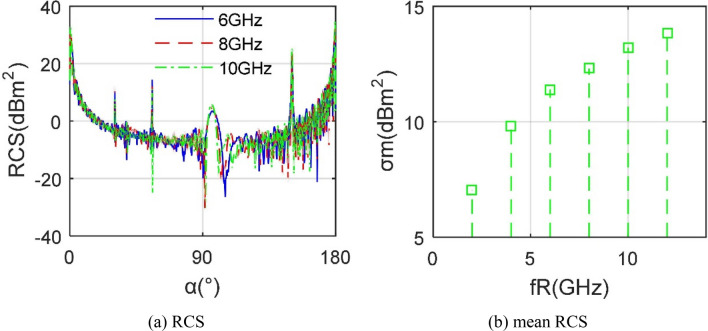
where NF refers to the number of facets and NE represents the number of edges. The presented RCS calculation method is verified by PO + MOM (Method of Moment)/MLFMM (Multi-Level Fast Multipole Method) in FEKO (FEldberechnung bei Korpern mit beliebiger Oberflache) as shown in Fig. 3, where fR is the radar wave frequency and the radar wave uses horizontal polarization. It can be seen that the two RCS curves are roughly coincident, and the result calculated by FEKO is slightly larger than the other, where the mean of the RCS curve of PO + PTD is smaller than that of FEKO by 0.3909 dBm2. This is because the two use different grid processing methods and different RCS algorithms. These results indicate that the RCS algorithm presented in this paper is accurate to deal with the electromagnetic scattering characteristics of the aircraft model.
Figure 3.
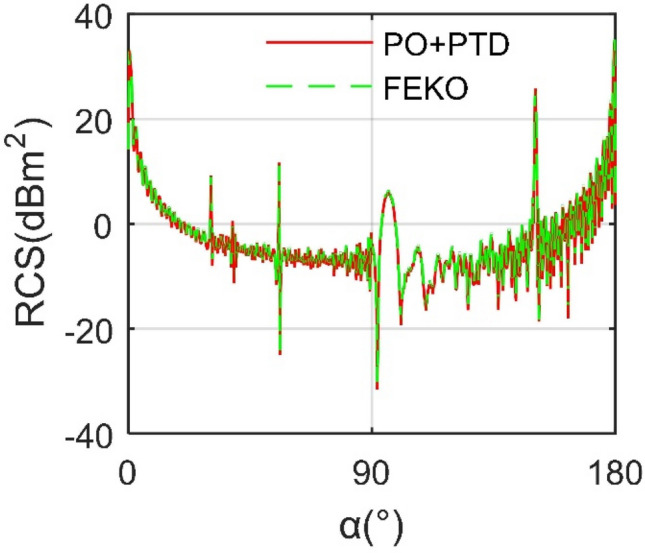
Verification of RCS calculation method on m0, β = 0°, fR = 10 GHz.
IR signature evaluation
Monte Carlo (MC) and ray tracing method (RTM) are used to solve the infrared signature of aircraft exhaust system3. Consider the absorption and emission in the RTE, without considering the scattering of the medium, so that the refractive index is always equal to 1, then RTE can be described as:
| 8 |
where r refers to the position vector, s is the direction vector, s represents the length along the path, a is the absorption coefficient, L is the radiance, σ refers to the Stefan-Boltzmann constant, T is the local temperature.
Using discrete coordinate model to calculate thermal radiation, RTE can be transformed into:
| 9 |
According to MC + RTM, the spectral radiance reaching the receiving point of the detector can be expressed as:
| 10 |
where refers to spectral radiance of wall reverse rays, means spectral radiance, τiσ represents i-th layer spectral transmittance.
On this basis, the irradiance reaching the receiving point of the detector can be calculated as:
| 11 |
where E means the radiant illumination, Nb refers to the total number of wave bands, N represents the total number of rays contributing to the measurement point, θ jrefers to the angle between the center of the j-th solid angle and the surface normal of its measuring point, ΔΩ jmeans the j-th solid angle, Δσi is the width of the i-th wave band.
At this time, the radiation intensity can be determined as:
| 12 |
where I is the radiation intensity and R refers to the linear distance between the aircraft and the IR detector.
For the infrared radiation of the exhaust pipe, regarding the exhaust pipe as a gray body, the total radiation and total radiation intensity can be expressed as:
| 13 |
| 14 |
where λ is the wavelength, represents the radiation emission degree of the black body between the bands λ1 ~ λ2. ε is the emissivity of the exhaust pipe, which is set to 0.9. ΔA is the area of the nozzle bin, Mλ means the spectral radiation emission degree of the black body.
Noting the Planck's formula:
| 15 |
Thus the radiation emittance of blackbody in λ1 ~ λ2 band could be calculated as:
| 16 |
The radiation constants have the following relationship:
| 17 |
where h refers to the Planck constant, h = 6.626176 × 10-34 J·s, k = 1.38 × 10-23 J/K, c is the speed of light. The IR signature calculation method presented here is verified as shown in Fig. 4, where the calculation results presented here are basically consistent with the known data in the literature26. The mean of the red data is 1.67 W/sr smaller than that of the green data. These results indicate that the IR calculations in this paper are feasible and accurate for evaluating the infrared radiation characteristics of this aircraft exhaust system.
Figure 4.
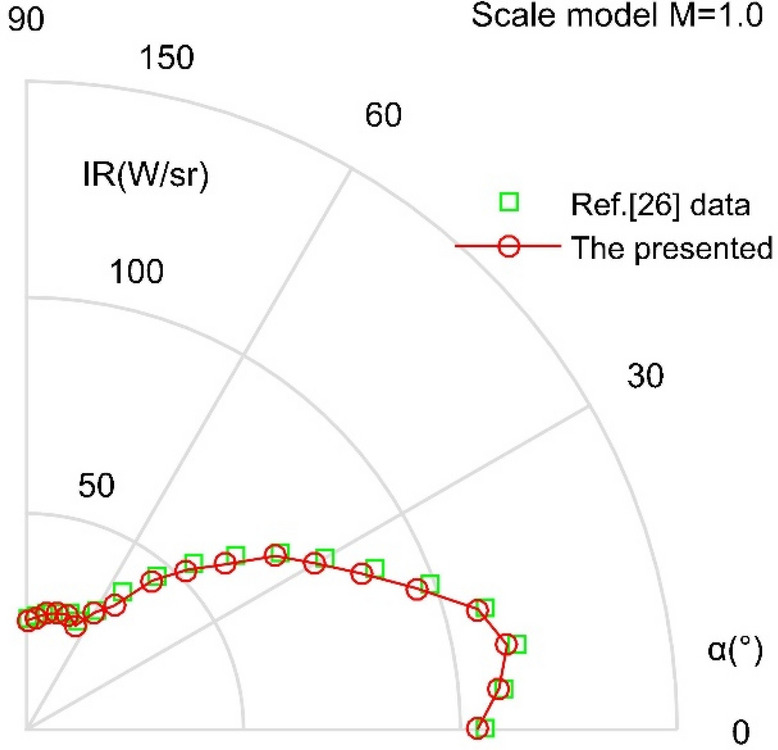
Verification of IR signature calculation method, 3–5 μm wavelength band.
Comprehensive stealth design
In order to improve the radar/infrared stealth performance of this aircraft, the objective function is defined as follows:
| 18 |
where iind is the serial number, m is the individual of the aircraft model, M is the collection of descendants20,25, noting that this expression implies that the objective function pursues the minimum of these three indicators. The comprehensive stealth indicators are:
| 19 |
where HH represents that the radar wave is horizontally polarized, αn means the observation angle in the normal observation field, σm is the mean RCS indicator, σt is the tail RCS indicator, In is the infrared radiation intensity indicator in the normal observation field.
Throughout the overall design process, equation constraints are expressed as follows:
| 20 |
where Wf is the width of the aircraft fuselage, Din is the diameter of the end of the intake pipe, Le is the length of the engine compartment, Lin represents the length of the air intake, Xn means the x coordinate of the front face of the nozzle, Xin refers to the x coordinate of the end face of the intake pipe, and k is the number of generations.
The inequality equality constraints can be expressed as:
| 21 |
where Lf refers to the length of the fuslage, Lex is the length of the exhaust pipe, Lf,max, and Lex,max are the limit values, Dx is the drag indicator, Tn is the temperature indicator of nozzle face.
When there are optimal solutions for the stealth indicators, the following relationship (COM test20,25) should be satisfied:
| 22 |
When the optimal solution does not exist, that is, these stealth indicators cannot reach the minimum at the same time, then the Pareto solution needs to be applied:
| 23 |
In order to establish individuals with better stealth performance, a ranking factor can be defined here to distinguish these feasible solutions in each generation:
| 24 |
| 25 |
where fs(jie, iind) represents the sorting factor of the iind-th stealth indicator of the jie-th individual, Nind is the number of individuals in the current offspring, rind(jie, iind) indicates the ascending ranking of the iind -th indicator of the jie -th individual, fr is the ranking factor, Nindc is the number of stealth indicators.
At this time, the optimal solution can be expressed as the individual with the smallest fr:
| 26 |
If the above ranking factor Pareto section is still not unique, the priority is defined to continue to distinguish these individuals:
| 27 |
where pindc is the priority of individual stealth indicator. At this time, priority is given to the individual whose RCS mean indicator performs better.
Model
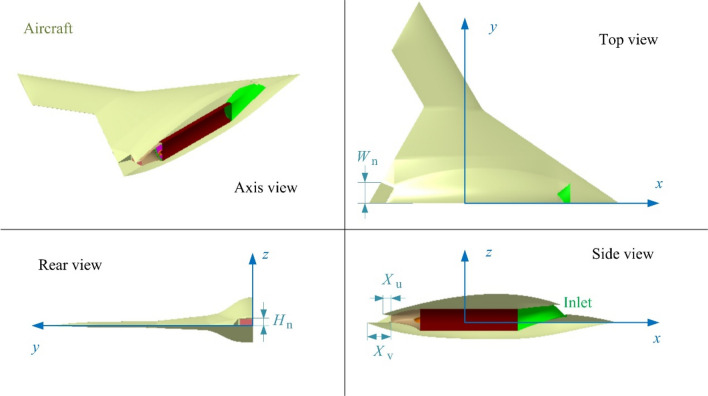
The outline design of the aircraft symmetry plane is shown in Fig. 5, where Mex represents the model of the exhaust port, Bd is the nozzle model with downward blocking, Ns refers to the number of nozzle stages, Bu is a nozzle model with upward blocking, Hn is the height of the nozzle.
Figure 5.
Aircraft design draft and parameter variables, drawn using Microsoft Visio 2007.
The model of the unmanned aircraft was built as shown in Fig. 6, where Wn is a custom parameter used to determine the nozzle width, Xv is a custom length parameter used to determine the size of Bd, noting that the outer edge of Bd is parallel to the tail edge of the aircraft. Xu is the size parameter of Bu. The main geometric size data of m0 is shown in Table 1, where Hf is the height of the fuselage, Wb is wingspan, Asl is the sweep angle of wing leading edge, Asn is the sweep angle of nose, Aft is forward sweep angle of the trailing edge of the fuselage. When the parameters of the exhaust system change, the aircraft model also changes, and the aircraft model here can be represented by the following parameters or sub-models:
| 28 |
Figure 6.
Three-view display of aircraft geometric model, drawn using Microsoft Visio 2007 and CATIA V5R20.
Table 1.
The main geometric size data of m0.
| Parameter | Lf (m) | Xn (m) | Asl (°) | Hf (m) | Wb (m) |
|---|---|---|---|---|---|
| Value | 11.041 | -2 | 30.518 | 2.082 | 18.5 |
| Parameter | Wn (m) | Din (m) | Xin (m) | Asn (°) | Aft (°) |
| Value | 0.8 | 0.5 | 2.5 | 55.717 | 29.938 |
where the parameters in Eq. (28) are set as variable parameters, the parameters in Eq. (20) are restricted to constant parameters.
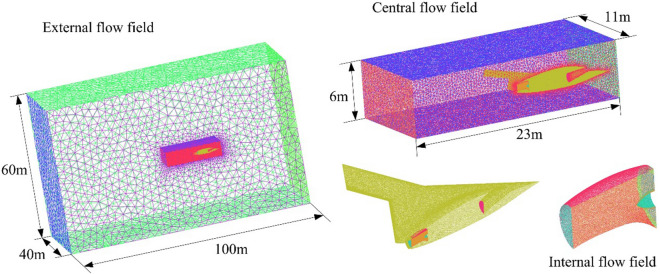
The flow field of the aircraft exhaust system is established as shown in Fig. 7, where high-precision unstructured grid technology is used to divide the external, central and internal flow field areas. Mesh encryption is added to surfaces and edges with small dimensions or large curvature changes, including air intakes, exhaust ports, center body, nozzle pipe, leading and trailing edges of wings. The velocity of the incoming flow in the far front of the aircraft is set to 85 m/s with the temperature 300 K, while the high-temperature airflow at the nozzle inlet is set at 870 K. The standard k-ε model is used to solve the Navier-Stocks equation of the exhaust system flow field. Momentum, density, turbulent kinetic energy, energy and turbulent dissipation rate are discretized using a second-order upwind scheme.
Figure 7.
Aircraft exhaust system flow field construction and grid division, drawn using Microsoft Visio 2007 and ANSYS ICEM 16.0.
In order to evaluate the changes in stealth characteristics brought to the aircraft during the design of the exhaust system, the radar and infrared observation fields are set as shown in Fig. 8, where σm is equal to the mean RCS in the range of 0° ≤ α ≤ 180°, σt is equal to mean RCS in the range of 150° ≤ α ≤ 180°, In is equal to the mean value of the IR radiation intensity in the range of –30° ≤ αn ≤ 30°.
Figure 8.
Observation field setting of aircraft radar cross section and IR signature, β = 0°, drawn using Microsoft Visio 2007 and CATIA V5R20.
Results and discussion
Figure 9 presents that the aircraft's RCS and RCS mean indicators show great differences under different radar wave frequencies. When fR is increased from 6 to 10 GHz, the RCS curve is generally consistent, but the local amplitude slightly increases, which is very obvious in the peaks of the head, side and tail. The increasing speed of the RCS mean index gradually decreases with the increase of the radar wave frequency. The σm at 2 GHz is only around 7 dBm2, and the index at 12 GHz reaches 13.8551 dBm2. In order to make the calculation results of the electromagnetic scattering level of the aircraft comparable in the design process, the radar wave frequency here is set to 10 GHz.
Figure 9.
RCS of aircraft model under different radar wave frequencies, β = 0°.
Effects of Mex and Ns
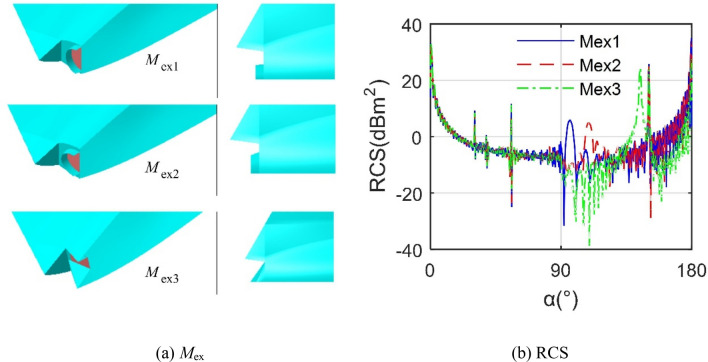
Figure 10 provides that these three exhaust port models have a great influence on the RCS of the aircraft, where Mex1 uses a simple round pipe, Mex2 uses an oval design, and Mex3 uses a rectangular nozzle with a triangular upper and lower baffle. It can be seen that the RCS level of Mex3 is lower than the other two, but it produces a peak of 24.41 dBm2 at 144.5° because Mex3 does not use the arc design of the first two, but accepts a more concise triangle + large acute angle nozzle, this measure can effectively deflect most radar waves to non-threatening azimuth. The RCS curves of Mex1 and Mex2 are generally similar, but the peaks and fluctuations in the lateral 92.25° ~ 116.5° are different, where the average RCS of Mex2 curve is 13.1265 dBm2, and that of Mex3 is 11.6694 dBm2. These results show that the reasonable design of the nozzle can effectively reduce the average RCS of the aircraft and the peak RCS of certain azimuths.
Figure 10.
RCS of aircraft under different exhaust port models, fR = 10 GHz, β = 0°, drawn using Microsoft Visio 2007 and CATIA V5R20.
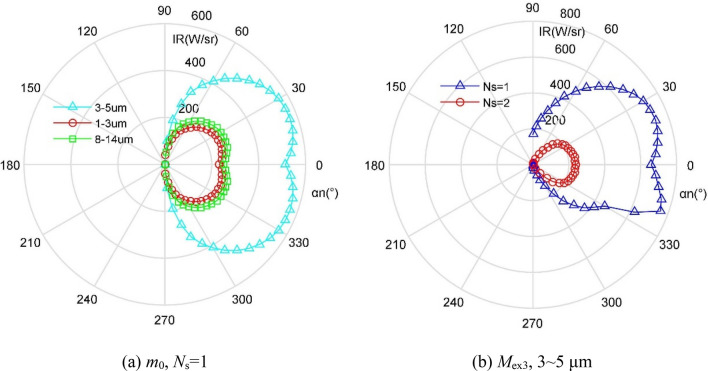
Figure 11 shows that the IR signatures of aircraft in different bands are very different, and the radiation intensity in the 3 ~ 5 μm band is significantly higher than the other two bands. In order to make the infrared radiation index results in the entire comprehensive design process comparable, the following IR calculations are performed in the 3 ~ 5 μm band. For the Mex3, the IR value in the positive observation angle range is significantly larger than that in the negative observation angle range, because the size of the upper baffle of the nozzle is smaller than that of the lower baffle, and the effect of blocking the heat source is small. The maximum IR value when Ns = 1 reaches 756.41 W/sr, while the IR curve at Ns = 2 as a whole is much smaller than the IR curve at Ns = 1, because at this time the introduction of circular cold air can better surround the high-temperature heat flow and form a certain isolation and protection, these combined effects greatly reduce the IR performance. These results show that the nozzle based on the principle of two-stage ejection can significantly improve the infrared radiation characteristics of the aircraft.
Figure 11.
Aircraft IR signature under different wave bands and Ns.
Effects of Bd and Hn
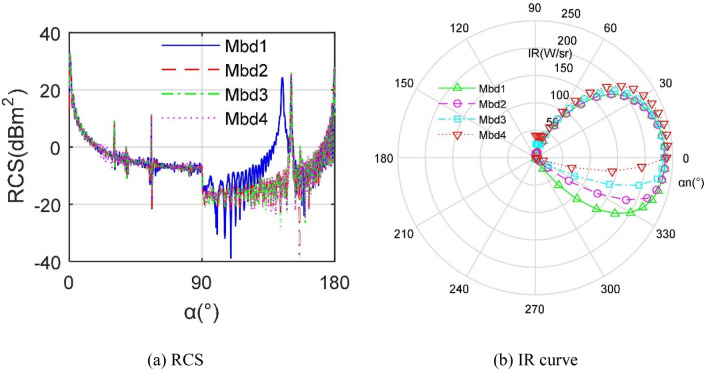
Figure 12 provides that the effect of different Mbd models on the stealth performance of the aircraft is obvious. As the value of Xv increases, the size of the lower baffle of the nozzle becomes larger and gradually integrates with the aircraft. This design results in a more concise shape of the entire aircraft and a stable deflection effect on electromagnetic waves, thus the RCS curves of Mbd2, Mbd3, and Mbd4 are very similar. The RCS curve of Mbd1 has a peak of 24.41 dBm2 at 144.5°, and the last three RCS curves have peaks at 150.5°. For the IR curves, the IR curve clearly shows an upward contraction trend with the increase of Xv, this is because the outward extension of the lower baffle effectively blocks the radiation characteristics in the negative observation angle. As shown in Table 2, the difference between the radar stealth indicators under these four Mbd models is relatively small, but the IR indicator has a significant decreasing trend with a reduction of 65.5709 W/sr. These results indicate that the design of Mbd contributes more to the infrared stealth of the aircraft.
Figure 12.
Comparison of stealth characteristics of aircraft under different Mbd models.
Table 2.
Comparison of stealth indicators of aircraft under different Mbd models.
| Mbd | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Xv (mm) | 500 | 650 | 850 | 1150 |
| σm (dBm2) | 11.6694 | 11.0772 | 11.1147 | 11.0857 |
| σt (dBm2) | 12.3457 | 12.6437 | 12.5575 | 12.5467 |
| In (W/sr) | 223.7332 | 212.3998 | 187.0830 | 158.1623 |
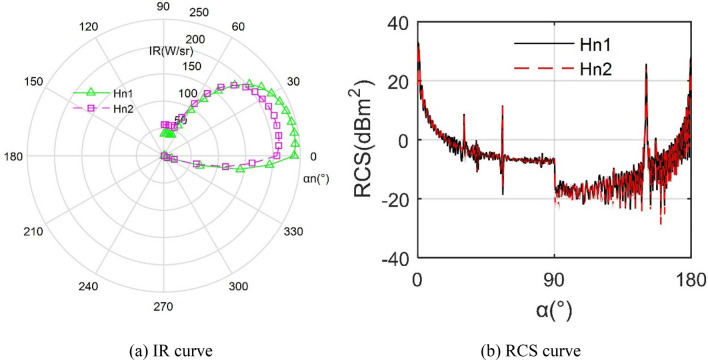
Figure 13 indicates that the height of the exhaust port will also have a more obvious impact on the stealth performance of the aircraft, where Hn1 = 330 mm, Hn2 = 300 mm. For the IR curves, the IR value of Hn1 is obviously greater than the value of Hn2 except the observation angle is greater than 45°, because reducing the height of the nozzle can increase the mixing intensity of the hot and cold air flow, which results in the normal infrared radiation effect of the nozzle being suppressed, but the blocking effect of the upper baffle on the nozzle is slightly weakened, thus the infrared radiation of the nozzle didn't weaken much when the observation angle increases positively. Note that the IR indicator at Hn1 is around 158 W/sr, while that at Hn2 is reduced to 140.0023 W/sr. The RCS curves under the two Hn are very similar, where the mean indicator here differs by only 0.1285 dBm2. These results indicate that choosing a suitable nozzle height is beneficial to improve the radar/infrared performance of the aircraft.
Figure 13.
Effect of exhaust port height on aircraft stealth performance.
Effects of Wn and Bu
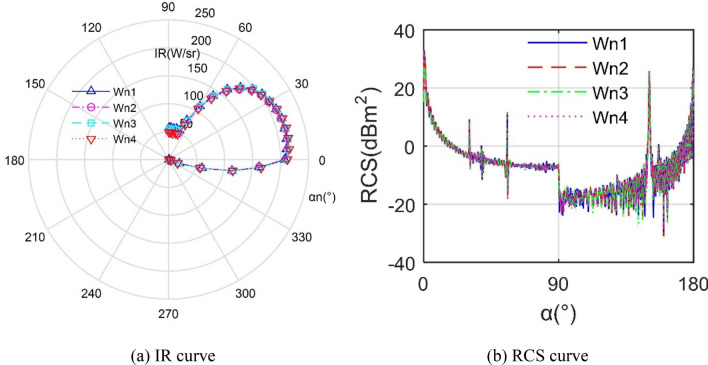
Figure 14 manifests that the difference between RCS and IR curves of aircraft under different Wn is small. For the IR curves, the values of the four curves are relatively large in the range of 0° ~ 35°, exceeding 165.7 W/sr. At this time, the IR of Wn1 and Wn2 is slightly smaller than the other two. Overall, the IR radiation characteristics at these four Wn values are similar, because the opening width of the nozzle is defined on the edge of the tail of the aircraft. For the heat flow that is about to leave the tail of the aircraft, the mixing effect brought by Wn will have little effect on the wall near the outer baffle. For the RCS results, the four curves are very similar, including shape, maximum value, peak size, peak position and number of fluctuations. In the range of 90.75° ~ 108.8°, the difference between the four curves is somewhat obvious, because the increase of Wn reduces the surface area and average height of the side baffle outside the spout, which brings changes to the lateral electromagnetic scattering characteristics of the aircraft. As shown in Table 3, the results of the various stealth indicators under different Wn values are very similar, where the maximum difference of the RCS tail indicator is only 0.051 dBm2. These also show that the impact of Wn on the overall stealth performance of the aircraft is very limited within the given range.
Figure 14.
Comparison of stealth characteristics of aircraft under different Wn.
Table 3.
Comparison of stealth indicators of aircraft under different Wn.
| Wn number | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Wn (mm) | 800 | 850 | 900 | 950 |
| σm (dBm2) | 10.9572 | 10.9806 | 10.9583 | 10.9544 |
| σt (dBm2) | 12.0435 | 12.0527 | 12.0426 | 12.0017 |
| In (W/sr) | 140.0023 | 139.8559 | 141.4906 | 141.2781 |
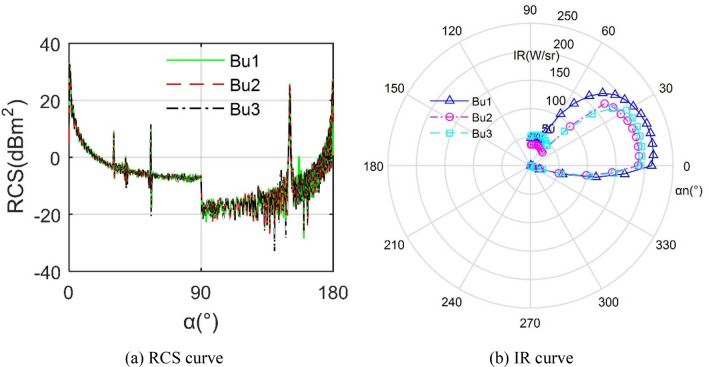
Figure 15 investigates that different Bu parameters will affect the radar and infrared stealth characteristics of the aircraft, and the impact on the latter is more obvious, where Xu1 = 300 mm, Xu2 = 400 mm and Xu3 = 500 mm. For the RCS results, the three curves are very similar in shape, and all produce large peaks at 0.25°, 150.5° and 179.8° with the maximum peak reaching 33.04 dBm2. For infrared radiation characteristics, the IR curve of Bu1 is obviously larger than that of the other two. The IR values of Bu1 and Bu2 are almost equal in the negative observation angle range, and the IR result of Bu3 in the positive observation angle range is larger than that of Bu2, because the size of the upper baffle outside the nozzle increases and extends outward with the increase of Xu, which is helpful to induce the airflow at the back of the fuselage to flow behind the center of the tail flame. This is conducive to the mixing of hot and cold airflow to a certain extent, but it also affects the radiation angle of the tail nozzle. These results indicate that Bu is a non-negligible factor affecting the performance of aircraft radar and infrared stealth performance.
Figure 15.
Radar/infrared stealth characteristics of aircraft under different Bu.
Comprehensive results discussion
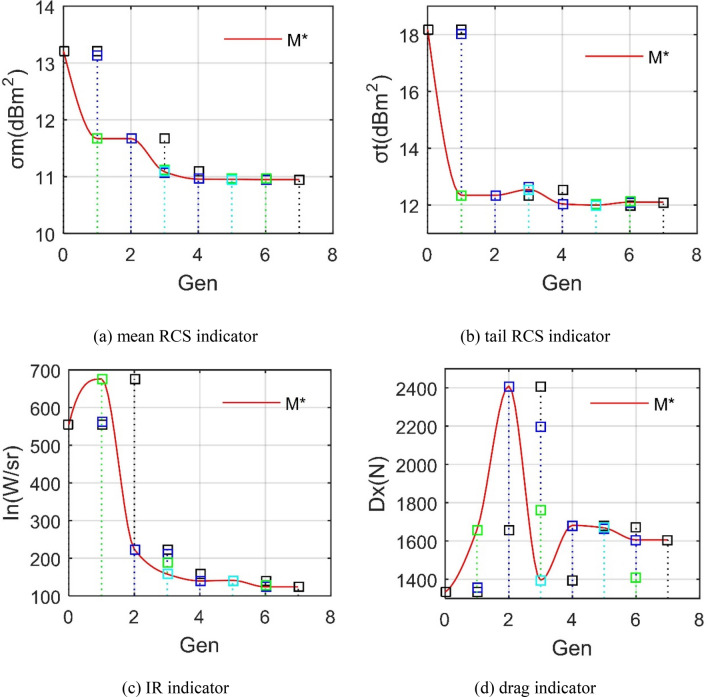
Figure 16 supports that the three stealth indicators have been improved overall, and the aerodynamic indicator has made a little sacrifice. For the mean RCS of M*, σm generally maintains a steady downward trend because both ranking factors and priorities are beneficial to this radar stealth indicator. The tail RCS indicator has been greatly reduced, which is conducive to the rearward stealth of the exhaust system. As shown in Table 4, σt is reduced from greater than 18 dBm2 to 12.1045 dBm2, the reduction is 6.0763 dBm2. This is mainly because of the reasonable choice of exhaust port model and the optimization of nozzle height. The infrared signature indicator of M* shows a trend of increasing first and then decreasing sharply. Many factors contributed to this process, including the exhaust port model, nozzle series and lower baffle, where In indicator has been reduced by 430.2313 W/sr. The drag performance of the individual fluctuated greatly throughout the process with a maximum difference of 1076.172 N, while the Dx indicator of M*increased by 272.9023 N from 1332.9243 N. Overall, a little drag sacrifice here is also acceptable. These results indicate that CDM is satisfactory for improving the radar/infrared stealth characteristics of the aircraft's exhaust system.
Figure 16.
History chart of various performance indicators.
Table 4.
Aircraft main performance comparison before and after CDM.
| σm (dBm2) | σt (dBm2) | In (W/sr) | Dx(N) | |
|---|---|---|---|---|
| m0 | 13.2120 | 18.1808 | 554.3546 | 1332.9243 |
| M* | 10.9492 | 12.1045 | 124.1233 | 1605.8266 |
The changes in the design parameters or sub-models of the exhaust system are shown in Table 5, where all the design factors here have been improved under the comprehensive evaluation of CDM. The exhaust port model changed from a simple round tube to a rectangular design with upper and lower triangular baffles. The nozzle of the exhaust system was upgraded from single-stage injection to two-stage injection. The size of the upper and lower baffles, the height and width of the nozzle have also changed. These results indicate that CDM is clearly effective for the overall design of this aircraft exhaust system.
Table 5.
Comparison of main design parameters or sub-models of aircraft before and after CDM.
| Mex | Ns | Bd(mm) | Hn(mm) | Wn(mm) | Bu(mm) | |
|---|---|---|---|---|---|---|
| m0 | Mex1 | 1 | Xv = 500 | 330 | 800 | Xu = 300 |
| M* | Mex3 | 2 | Xv = 1150 | 300 | 950 | Xu = 400 |
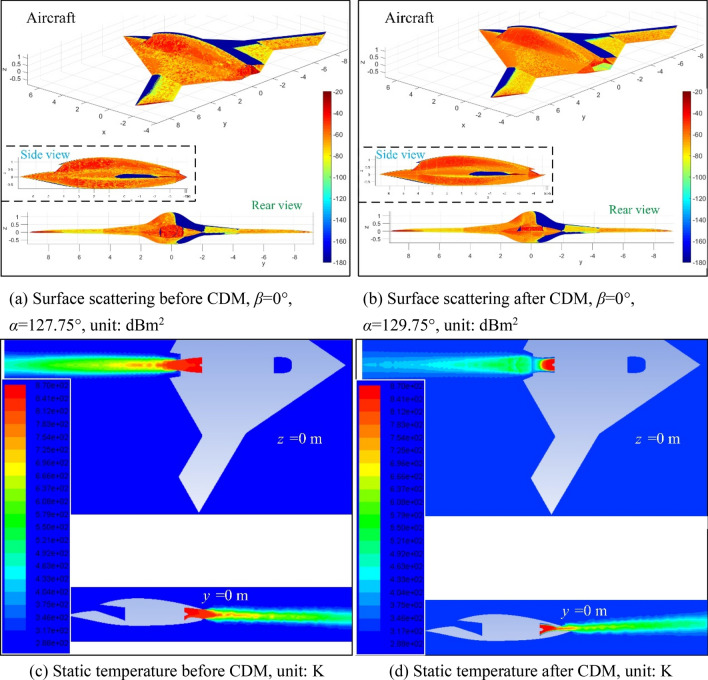
Figure 17 presents that the optimized aircraft model has made significant improvements in surface electromagnetic scattering characteristics and plume temperature field. For the Fig. 17a, the cut surface at the tip of the wing, the wall near the tail nozzle and the upper middle part of the fuselage show the most obvious red under the current incident wave, because at this time, the angle between the radar wave and the normal direction of the wing tip is very small, so that the surface here does not have a good ability to deflect the radar wave. The tail nozzle adopts a conventional round tube design, and the nearby end face and baffle form a strong scattering source, that is, a right-angle dihedral angle, which leads to a high RCS level here. For the Fig. 17b, at this time, the incident azimuth angle of the radar wave has increased by 2°, and the distribution of strong scattering sources on the surface of the aircraft is still similar compared with the initial model, while the performance of RCS near the tail nozzle has been obviously changed, because the lower baffle of the nozzle of the optimized model adopts a shielding design that blends with the curve of the fuselage tail, the baffle on the side of the nozzle does not form a right-angle dihedral angle with the nozzle end surface, the upper baffle is extended from the surface of the fuselage and cut off with a triangular outer contour, the combined effect of these measures makes the optimized aircraft model have a good low electromagnetic scattering level. For the Fig. 17c, it can be found that there is a large-area high-temperature core zone with a temperature range of 696 K ~ 841 K in the tail flame outside the nozzle of the initial model, where the static temperature of the space in the exhaust nozzle pipe is basically above 812 K, because the exhaust system at this time uses a single-stage ejection method, which makes the high-temperature wake jet from the center cone unable to be directly cooled until it reaches the edge of the nozzle. For the Fig. 17d, it can be noticed that the core area of the plume whose static temperature exceeds 801 K is confined in the space of the jet pipe, where the static temperature of the tail flame outside the baffle under the nozzle is basically below 648 K, because the optimized exhaust system has a design based on the principle of secondary ejection, coupled with the combined effect of nozzle height, outer width, and upper and lower baffles, the temperature field of the entire aircraft's tail flame is very popular. These results show that the CDM based on the Pareto solution of the ranking factor is feasible and effective to improve the electromagnetic scattering and infrared radiation of this aircraft.
Figure 17.
Performance comparison of the aircraft before and after CDM, drawn using Microsoft Visio 2007 and MATLAB 2015A.
Conclusions
By studying the radar cross-section and infrared radiation characteristics of this aircraft exhaust system, the relevant parameters and sub-models are fully designed, and the following conclusions can be obtained:
The exhaust port model, lower baffle and nozzle height are the main factors affecting the two RCS indicators of this aircraft model. The design of the upper baffle has a greater impact on the drag indicator than on the other three indicators.
The order that has the greatest influence on the infrared radiation indicator is the nozzle stages, the exhaust port model, the lower baffle, the nozzle outer width and the nozzle height. For the drag indicator, the order is the lower baffle, nozzle stages, exhaust port model, nozzle height and nozzle outer width.
CDM can effectively improve the radar/infrared stealth performance of the aircraft exhaust system while sacrificing some aerodynamic drag. This mainly benefits from the Pareto solution based on ranking factors and priority comparison.
The main contribution of this paper is the presentation of CDM and ranking factors. The former is to improve the target’s aerodynamic/stealth comprehensive performance, and the latter is to establish relatively good individuals in the Pareto solution.
Author contributions
Z.Z. and J.H. conceived the idea; Z.Z. designed the study and carried out the computational simulations; Z.Z. and J.H. analyzed the data; Z.Z. wrote the manuscript. All authors reviewed the complete manuscript.
Funding
This work was supported by the project funded by the China Postdoctoral Science Foundation (Grant No. BX20200035, 2020M680005).
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Lozano F, Paniagua G. Airfoil leading edge blowing to control bow shock waves. Sci. Rep. 2020;10(1):1–18. doi: 10.1038/s41598-019-56847-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Chen WJ, Fan W, Zhang Q, et al. Experimental investigation of nozzle effects on thrust and inlet pressure of an air-breathing pulse detonation engine. Chin. J. Aeronaut. 2012;25(3):381–387. doi: 10.1016/S1000-9361(11)60399-3. [DOI] [Google Scholar]
- 3.Zhou Z, Huang J, Wang J. Radar/infrared integrated stealth optimization design of helicopter engine intake and exhaust system. . Aerosp. Sci. Technol. 2019;95:105483. doi: 10.1016/j.ast.2019.105483. [DOI] [Google Scholar]
- 4.Yan XJ, Yang T, Yao HH. Conceptual scheme and key technologies of sixth generation fighters abroad. Aeronaut. Sci. Technol. 2018;29(4):18–26. [Google Scholar]
- 5.Li C, Dong H, Zhao K. A balance between aerodynamic and olfactory performance during flight in Drosophila. Nat. Commun. 2018;9(1):1–8. doi: 10.1038/s41467-017-02088-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Li M, Bai J, Li L, et al. A gradient-based aero-stealth optimization design method for flying wing aircraft. Aerosp. Sci. Technol. 2019;92:156–169. doi: 10.1016/j.ast.2019.05.067. [DOI] [Google Scholar]
- 7.Tan HJ, Guo RW. Design and wind tunnel study of a top-mounted diverterless inlet. Chin. J. Aeronaut. 2004;17(2):72–78. doi: 10.1016/S1000-9361(11)60217-3. [DOI] [Google Scholar]
- 8.Jiang H, Ang HS. The Analysis of Aerodynamic and Stealth Characteristic of F-35 Fighter. Aircr. Des. 2010;30(6):1–10. [Google Scholar]
- 9.Mirkovic D, Stepanian PM, Kelly JF, et al. Electromagnetic model reliably predicts radar scattering characteristics of airborne organisms. Sci. Rep. 2016;6:35637. doi: 10.1038/srep35637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ma Y, Pan ZX, Luo L. X-47B flying wing aerodynamic configuration analysis. Aeronaut. Sci. Technol. 2014;25(12):1–4. [Google Scholar]
- 11.Murfitt SL, Allan BM, Bellgrove A, et al. Applications of unmanned aerial vehicles in intertidal reef monitoring. Sci. Rep. 2017;7(1):1–11. doi: 10.1038/s41598-017-10818-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Yue K, Liu W, Li G, et al. Numerical simulation of RCS for carrier electronic warfare airplanes. Chin. J. Aeronaut. 2015;28(2):545–555. doi: 10.1016/j.cja.2015.01.004. [DOI] [Google Scholar]
- 13.Huang Z, Jiang W, Zhang Y. Brief introduction to infrared stealth and detection technology of aircraft. Infrared. 2017;38(8):1–7. [Google Scholar]
- 14.Qu ZJ, Zhang EL, Zhou FF. Modeling infrared radiation characteristics for F35 stealth fighter. Infrared Technol. 2014;36(11):920–925. [Google Scholar]
- 15.Ma GJ, Zhang YF, Lai DX. Numerical research on infrared radiation of engine exhaust system. Aricraft Des. 2015;35(1):30–34. [Google Scholar]
- 16.Zhang Y, Chen J, Shen L. Real-time trajectory planning for UCAV air-to-surface attack using inverse dynamics optimization method and receding horizon control. Chin. J. Aeronaut. 2013;26(4):1038–1056. doi: 10.1016/j.cja.2013.04.040. [DOI] [Google Scholar]
- 17.Jia QL. Numerical calculation of IR radiation for unmanned aerial vehicle. Laser Optoelectron. Prog. 2014;51:071201. doi: 10.3788/LOP51.071201. [DOI] [Google Scholar]
- 18.Li X, Yang QZ, Chen LH, et al. Numerical simulation of infrared characteristics of aero-engine exhaust nozzle. Adv. Aeronaut. Sci. Eng. 2013;4(1):126–133. [Google Scholar]
- 19.Cheng W, Wang W, Zhou L, et al. Infrared signature of serpentine nozzle with engine swirl. Aerosp. Sci. Technol. 2019;86:794–804. doi: 10.1016/j.ast.2019.01.057. [DOI] [Google Scholar]
- 20.Zhou ZY, Huang J, Yi MX. Comprehensive optimization of aerodynamic noise and radar stealth for helicopter rotor based on Pareto solution. Aerosp. Sci. Technol. 2018;82:607–619. doi: 10.1016/j.ast.2018.09.030. [DOI] [Google Scholar]
- 21.Cheng X, Sun M. Wing-kinematics measurement and aerodynamics in a small insect in hovering flight. Sci. Rep. 2016;6:25706. doi: 10.1038/srep25706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Sun ZJ, Liu L, Li H, et al. Analysis on aerodynamic / stealth synthetical performance of flying wing UAV. Flight Dyn. 2018;36(3):15–18. [Google Scholar]
- 23.Wang B, Cong W, Wang CZ, et al. Infrared radiation characteristics calculation and infrared stealth effect analysis of stealth fighter. Trans. Beijing Inst. Technol. 2019;39(4):365–371. [Google Scholar]
- 24.Han JS, Han JH. A contralateral wing stabilizes a hovering hawkmoth under a lateral gust. Sci. Rep. 2019;9(1):1–13. doi: 10.1038/s41598-019-53625-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zhou ZY, Huang J, Wu NN. Acoustic and radar integrated stealth design for ducted tail rotor based on comprehensive optimization method. Aerosp. Sci. Technol. 2019;92:244–257. doi: 10.1016/j.ast.2019.06.003. [DOI] [Google Scholar]
- 26.Anagnostopoulos KA, Charalambopoulos A, Fotiadis DI. Scattering of electromagnetic spherical waves by a buried spheroidal perfect conductor. Int. J. Eng. Sci. 2003;41(11):1239–1266. doi: 10.1016/S0020-7225(03)00006-5. [DOI] [Google Scholar]
- 27.Zhen ZY, Zhu P, Xue YX, et al. Distributed intelligent self-organized mission planning of multi-UAV for dynamic targets cooperative search-attack. Chin. J. Aeronaut. 2019;32(12):2706–2716. doi: 10.1016/j.cja.2019.05.012. [DOI] [Google Scholar]
- 28.Liu J, Yue H, Lin J, et al. A simulation method of aircraft infrared signature measurement with subscale models. Procedia Comput. Sci. 2019;147:2–16. doi: 10.1016/j.procs.2019.01.177. [DOI] [Google Scholar]
- 29.Iemma U, Palma G. Design of metacontinua in the aeroacoustic spacetime. Sci. Rep. 2020;10(1):18192. doi: 10.1038/s41598-020-74304-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Zhu HJ, Meng XG, Sun M. Forward flight stability in a drone-fly. Sci. Rep. 2020;10(1):1975. doi: 10.1038/s41598-020-58762-5. [DOI] [PMC free article] [PubMed] [Google Scholar]