A mechanical model of early somite segmentation

Summary

Somitogenesis is often described using the clock-and-wavefront (CW) model, which does not explain how molecular signaling rearranges the pre-somitic mesoderm (PSM) cells into somites. Our scanning electron microscopy analysis of chicken embryos reveals a caudally-progressing epithelialization front in the dorsal PSM that precedes somite formation. Signs of apical constriction and tissue segmentation appear in this layer 3-4 somite lengths caudal to the last-formed somite. We propose a mechanical instability model in which a steady increase of apical contractility leads to periodic failure of adhesion junctions within the dorsal PSM and positions the future inter-somite boundaries. This model produces spatially periodic segments whose size depends on the speed of the activation front of contraction (F), and the buildup rate of contractility (Λ). The Λ/F ratio determines whether this mechanism produces spatially and temporally regular or irregular segments, and whether segment size increases with the front speed.

Graphical abstract

Highlights

• •Dorsal pre-somitic mesoderm of chicken embryos epithelializes before somite formation
• •Dorsal epithelium shows signs of apical constriction and early segmentation
• •A mechanical instability model can reproduce sequential segmentation
• •A single ratio describes spatial and temporal patterns of segmentation

Poultry Embryology; Mechanical Modeling; Developmental Biology

Introduction

Somitogenesis in vertebrate development sequentially and periodically creates metameric epithelial balls (somites) along the elongating embryo body from bilateral rods of loosely connected mesenchymal cells called pre-somitic mesoderm (PSM). As cells leave the rostral/anterior (head) end of the PSM to form each somite, new cells continuously move from the tail bud to join the PSM at the caudal/posterior (tail) end of the embryo (Pourquié, 2001). At any given rostral-caudal position, a pair of nearly equal-sized somites form simultaneously on both sides of the neural tube, between the ectoderm and the endoderm. These transient structures are the precursors of vertebrae, ribs, and many skeletal muscles; many birth defects arise from a failure in one or more steps of these developmental steps (Christ and Ordahl, 1995).

Somitogenesis is strikingly robust to perturbations (both spatial and temporal). Changes in the total number of embryonic cells or in the rate of new cell addition at the caudal end of the PSM lead to compensating changes in the size and timing of somite formation so that the embryo eventually produces the same final number of somites as in normal development (Cooke, 1975; Snow and Tam, 1979). A linear increase (scaling) of the somite size with the speed of the caudal-moving position of the determination front (Cooke and Zeeman, 1976; Dubrulle et al., 2001) or with the rate at which cells join the caudal end of the PSM can result in this number conservation.

Models seeking to explain somite formation include the “cell-cycle model”, which couples the timing of segmentation to the progression of cells through the cell-cycle and a cell-intrinsic gating mechanism (Stern et al., 1988; Primmett et al., 1989; Collier et al., 2000) and reaction-diffusion models (Meinhardt, 1982; Cotterell et al., 2015). Currently, the most widely accepted family of models employ a “clock-and-wavefront” (CW) mechanism, which combines caudally progressing fronts of determination and differentiation with an intracellular oscillator which determines cell fate based on its phase at the moment of determination (Cooke and Zeeman, 1976). Following the identification of the first oscillating transcripts (hairy1 and hairy2) in the PSM (Palmeirim et al., 1997), many computer simulations of varying complexity have implemented different CW models. Most CW models reproduce the experimentally-observed scaling of somite size with clock period, front speed and rate of elongation of the PSM (Hester et al., 2011; Tiedemann et al., 2012; Baker et al., 2006).

Recent experiments have shown that somite-like structures can form without either a clock or a progressing determination front (Cotterell et al., 2015; Dias et al., 2014). The ability of somites to form without either a clock or a front suggests that we should consider other mechanisms that could lead to spatially and temporally periodic sequential division of the PSM into regular segments. Recent experiments by Nelemans et al. showed that applied tension along the rostral-caudal axis can induce the formation of intersomitic boundaries in locations not specified by CW signaling (Nelemans et al., 2020), suggesting that mechanical mechanisms may be important in generating intersomitic boundaries. Truskinovsky et al. explored how mechanical instabilities could result in vertebrate segmentation (Truskinovsky et al., 2014). Assuming relaxation of junctional adhesion sites as the PSM elongates, their pre-patterning mechanism generates a number of somites independent of the final segmentation mechanism. Their model, however, does not consider the sequential development of the boundaries nor any active processes within the tissue.

In 2009, Martins et al. imaged the morphology of cells during chicken somitogenesis in vivo, showing that cells elongate, crawl, and align with each other as they form a somite (Martins et al., 2009). They found that cells epithelialize gradually during somite formation, with epithelialization beginning before segments separate from each other. Their finding is consistent with other reports showing that PSM cells gradually increase their density of cell-cell adhesion molecules (Duband et al., 1987) and decrease their motility (Bénazéraf et al., 2010; Mongera et al., 2018) as they approach the time of the physical reorganization associated with somite formation. Several decades ago, scanning electron microscopy (SEM) observations of the PSM in a variety of species led to the suggestion that “pre-somite”-like structures, named “somitomeres”, precede the condensation of cells into somites by at least 2-3 somite lengths (Meier, 1979; Tam et al. 1982). However, these observations in randomly fractured fixed embryos could not reveal the detailed progression of somitogenesis.

Here we investigated this early organization in more detail. Our observations showed that dorsal PSM cells undergo early maturation, forming an epithelial monolayer along the ectoderm boundary, beginning long before somite formation. This pre-somitic epithelium also shows signs of pre-segmentation, with clusters of cells forming arched tissue segments roughly the length of a somite diameter.

These observations suggest that periodic tissue segmentation and somite boundary positioning could result from a mechanical instability, similar to periodic cracking of materials subjected to stress. We developed a model of the dorsal epithelial monolayer where the observed boundaries between dorsal segments arise from the loss of contact between neighboring cells due to increased apical tension between cells. We simulated this scenario with a 2D computational model of a cross-section of the epithelial monolayer and showed that a simple mechanical model without a clock can explain the spatial periodicity in segment sizes. We also showed that this model can produce either roughly constant-size segments or segments whose size increases (scales) with activation-front speed and inverse rate of increase of apical contractility. A critical threshold for the ratio of the buildup rate of apical contractility to the activation-front speed defines the boundary between these two domains. A second threshold for this ratio predicts whether this mechanism produces spatially and temporally regular segments or irregular segments.

Results

Early signs of boundary specification

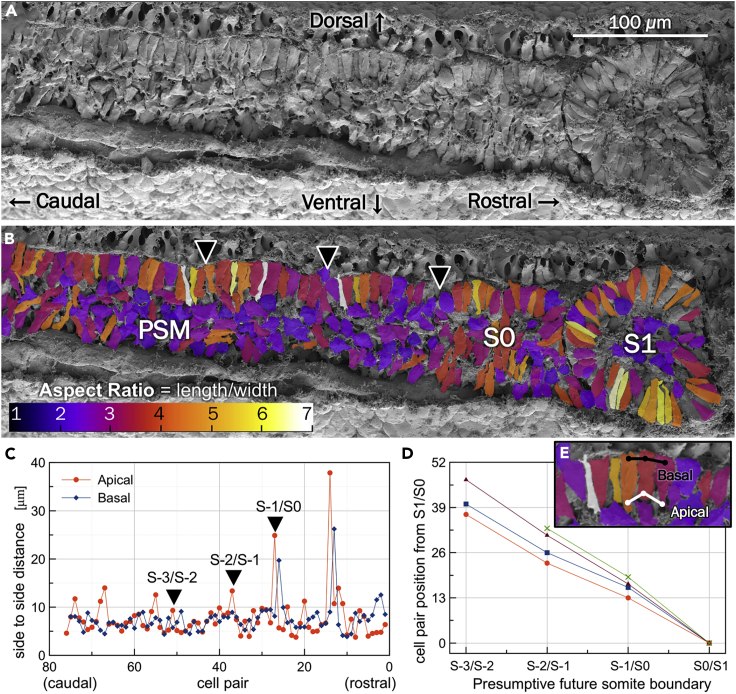
To investigate the beginning of epithelialization, we performed 3D SEM of chick embryos fixed at various Hamburger-Hamilton stages of somitogenesis, fractured as precisely as possible along parasagittal or transverse planes (Stern and Piatkowska, 2015). We then manually defined the contour of each individual PSM cell and calculated its aspect ratios (Figures 1A and 1B).

Figure 1.

Early signs of pre-somitic epithelium segmentation

(A) SEM images of para-sagittally sectioned chicken embryos show the epithelialization of dorsal PSM cells at least 3 somite lengths caudal (left) to the S1 somite.

(B) Scale bar is 100 μm. Cells are colored according to their aspect ratio in (B).

(C) Quantification of side-to-side distances of adjacent cell pairs near the dorsal surface. The black arrowheads in (B) mark cell pairs with increased apical-apical distances.

(D) Location of the apical peaks for four different embryo, indicating the number of cell pairs in each segment. The red line is for the sample shown in A–C.

(E) Inset showing the side-to-side distance quantification metric.

Our observations show that a dorsal layer of PSM cells begins to epithelialize at least as early as 4-5 somite lengths caudal to the most recently formed somite (S1). Cells within this dorsal epithelium form a series of clusters, arched groups of cells, at least 3-4 somite lengths caudal to the forming somite (Figure 1A). Cells near the dorsal surface in these clusters are usually wedged shaped, with their apical (ventral-facing) sides more constricted than their basal (dorsal-facing) sides. Estimates of side-to-side cell distances along the dorsal surface (Figure 1E), beginning with the rostral-most pair of S1, show instances of increased apical-side separation (Figure 1C). These peaks (black arrows in Figure 1B) roughly correspond to the cluster boundaries. The number of adjacent cell pairs (Figures 1C and S1A–S1C) within each peak is 14.27 ± 2.72, excluding the already formed caudal boundary of S0/S1. This value is similar to the rostral-caudal length of the future somites, calculated from measurements of dorsal cell pairs within the already formed somite (S1) of 12.25 ± 2.22 (Figure 1D). Fewer peaks along the basal sides indicate that the cells start their separation from the apical side (Figures S1A–S1C).

A mechanical model of dorsal PSM pre-patterning of segmentation

Our experimental results point to the formation of a continuous dorsal epithelium and the appearance of a series of clusters before the formation of intersomitic boundaries. Based on these observations, we hypothesize that these structures arise from a pre-patterning of the future boundaries and we propose a model for segmenting the dorsal epithelium.

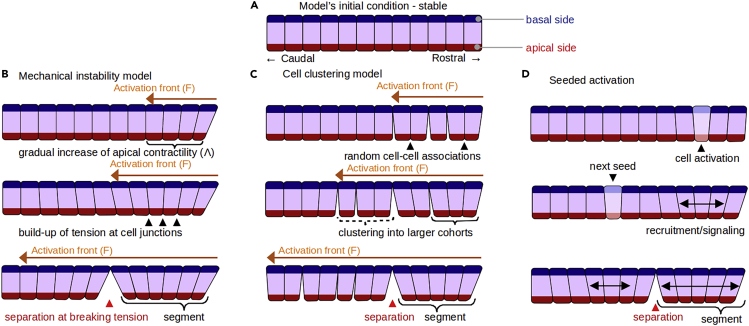
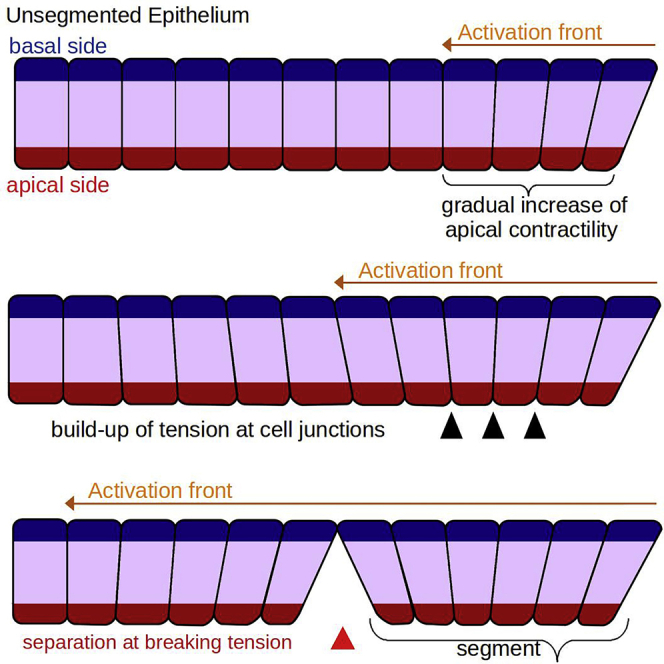
Here, we take the convergence of the cells' apical sides within the cluster as an indication that cells are apically constricting as the PSM matures. Apical constriction results from contractile forces generated by myosin activity at the cells' apical side, which often brings neighboring cells together and gives them a wedge shape (Baker and Schroeder, 1967; Pilot and Lecuit, 2005; Martin and Goldstein, 2014; Sawyer et al., 2010; Pearl et al., 2017). Excessive apical contractile forces on junctional adhesion sites can cause junctions to fail and the tissue to tear, as observed in Drosophila embryos (Martin et al., 2010; Manning et al., 2019). We postulate that such a mechanical instability may create the pre-segmentation pattern we observe: a caudally traveling activation-front induces apical constriction in the maturing PSM cells, leading to a buildup of cell-cell apical tension that eventually subdivides the monolayer into regularly-sized segments (Figure 2B). Figures 2C-D illustrate some other possible mechanistic models that could also lead to segment formation, including a cell-clustering model with a continuously caudally-progressing front (Figure 2C), and models where changes in cell behaviors do not progress caudally (Figure 2D).

Figure 2.

Proposed models of segment formation

(A) Epithelialized cells, with defined apical (red) and basal (blue) sides form a rostral (right)-caudal (left) monolayer along the dorsal side of the PSM.

(B) Mechanical instability model: a caudally-progressing front of myosin activation (orange arrows) initiates apical constriction of the cells in the monolayer eventually leading to the periodic segmentation of the tissue.

(C) Cell condensation model: a caudally-progressing maturation front (orange arrows) initiates random cell-cell groupings that eventually organizes the tissue into regularly-sized clusters.

(D) Seeded activation model: instead of a continuously progressing front, small groups of cells activate and rearrange neighboring cells into a segment.

Our mechanical instability model has three main parameters (F, Λ and Γ_Break): the speed at which this caudally-traveling activation-front (which we will refer to simply as the front for compatness) passes through the tissue (F), the rate (Λ, which we will refer to as the buildup rate of contractility) at which each pair of activated cells increases its apical contractility (the variable λ_A), and the maximum tension the link between adjacent apical domains of neighboring cells can sustain before the cells lose their connection with each other (${\text{Γ}}_{\mathrm{Break}}$).

A Cellular Potts implementation of the mechanical instability model

We implemented a stochastic Cellular Potts/Glazier-Graner-Hogeweg (CP/GGH) model version of dorsal tissue segmentation (Graner and Glazier, 1992; Swat et al., 2012) (for more details see transparent methods). In this model, the cells are spatially extended objects similar to the schematic cells in Figures 2A–2D, with a width and height; apical, basal and core domains; and elastic connections between neighboring apical domains representing apical junctional adhesion domains (Dias et al., 2014; Belmonte et al., 2016a, 2016b) (Table S1). We first characterize the model behavior for different fixed values of λ_A and then for simultaneous increase of λ_A in all cells at a rate Λ, before exploring the effect of a gradual, caudally-progressing front (F) of apical constriction activation.

Tension profiles as a function of number of cells and constriction strength

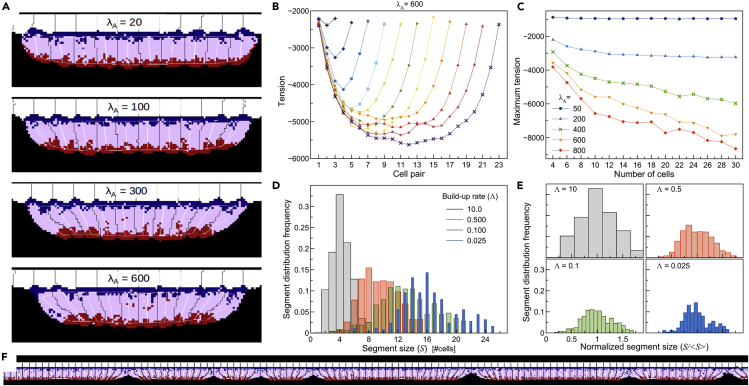
We first tested our model by creating small epithelial monolayers of fixed aspect ratio AR = 2 (Figure 3A). We increased the strength of apical contractility of all cell pairs simultaneously at a fixed buildup rate $\Lambda =0.05$, from λ_A = 0 up to a maximum value of λ_A ranging from 20 to 600, without allowing apical links to break. We then observed the shape of the tissue and the average cell-pair tension (Equation 7) over 20,000 simulation time units (defined in terms of Monte Carlo Steps [MCSs]), after λ_A reached its maximum value (Videos S1-S4). As the number of cells in the monolayer increases, cell-pairs in the middle of the segment experience higher tension than cell-pairs near the periphery (Figures 3B and 3C). This dependence of tension on position within a segment forms the premise of our model—as the tissue becomes larger, tension between cell pairs increases. Since the junctional bonds between cells have a defined breaking tension, higher local tensions predispose the tissue to break into smaller segments.

Figure 3.

Tension and segment-size distributions for fixed tissue sizes and simultaneous increase in contractility

(A) Snapshots of 4 simulations of 10 cells with different levels of maximal apical contractility strength. The tissue becomes more constricted for larger values of λ_A. (White – ectodermal tissue; black – core PSM; cells domain colors as in Figures 2A–2D; vertical white lines – internal distance constraints between domains in a single cell (Equation 3); horizontal white lines – distance constraints between domains in neighboring cells (Equation 5)).

(B) Plot of average apical tension (Equation 7) between cell pairs at the end of multiple simulations with different numbers of cells (from 4 to 24). In all simulations λ_A= 600.

(C) Maximum cell-pair tension versus the number of cells in the tissue for different maximal values of λ_A.

(D and E) Histogram of distribution of segment sizes (D) and normalized segment sizes (E) for different rates of simultaneous buildup of apical contractility.

(F) Snapshot of a simulation with Λ = 0.05 showing a wide distribution of segment sizes.

Simultaneous activation of apical contractility leads to irregularly-sized segments

Next, we combine simultaneous activation of contraction with the breaking of the apical links between neighboring cells at breaking tension ${\text{Γ}}_{\mathrm{Break}}=-7500$. In these simulations, the strength of apical contractility increases linearly from λ_A = 20 to a maximum of λ_A = 600 with different buildup rates of apical contractility ($\mathrm{\Lambda }=d{\mathrm{\lambda }}_{\mathrm{A}}/dt$). Since all cell-cell links have the same breaking tension, and the link tension is initially uniform with small fluctuations, the position of the first break is random. This break relieves tension nearby, but the tension far from the break remains roughly uniform with small fluctuations, so the next breaks can occur in a wide variety of locations, provided they are distant from the first break. As this process of tension build-up and release of tension by breakage continues we obtain a broad distribution of segment sizes (Figures 3D–3F), with the average segment size increasing as the buildup rate decreases (Figure 3D). The shape of the distribution, however, is similar for all values of Λ below 10 (Figure 3E). For Λ>10, the apical links between most cell pairs break. The data in Figures 3D–3F are from simulations with periodic boundary conditions with the rostral- and caudal-most cells connected to each other through basal and apical links identical to the links between the other cells (Video S5), but the results are qualitatively the same for simulations with many cells (N > 400) and fixed boundaries (Figure S2, Video S6). We conclude that a simultaneous activation of constriction activity is insufficient to produce a regular pattern of pre-segments like those seen in our SEM observations of embryos (Figures 1A and 1B).

Caudally-progressing activation of apical contractility leads to roughly periodic tissue segmentation

Next, we investigated whether caudally-progressing activation of apical constriction can generate regularly-sized segments. From now on, all simulations include a large number of cells fixed between two immobile cells, and a caudally-moving front that sequentially initiates a gradual and linear increase in the strength of apical contractility of cell pairs. We vary the front speed F and buildup rate of apical contractility Λ systematically around their reference values (see Table S2 in transparent methods). In addition, apical links between neighboring cell pairs will have a breaking tension ${\text{Γ}}_{\mathrm{Break}}$, allowing for tears between apical domains of neighboring cells. We quantify the positions of these tears. We do not impose additional tension loads between the basal domains. The basal domains only separate if these domains lose contact and separate by a distance more than three times the width of the cell. We selected the reference values so each segment's caudal boundary tear forms approximately three segment lengths rostral to the progressing front (Dubrulle et al., 2001) and produces segments of size 11-13 cells, corresponsind to the size of formed somites in our experimnents (Figure 1D).

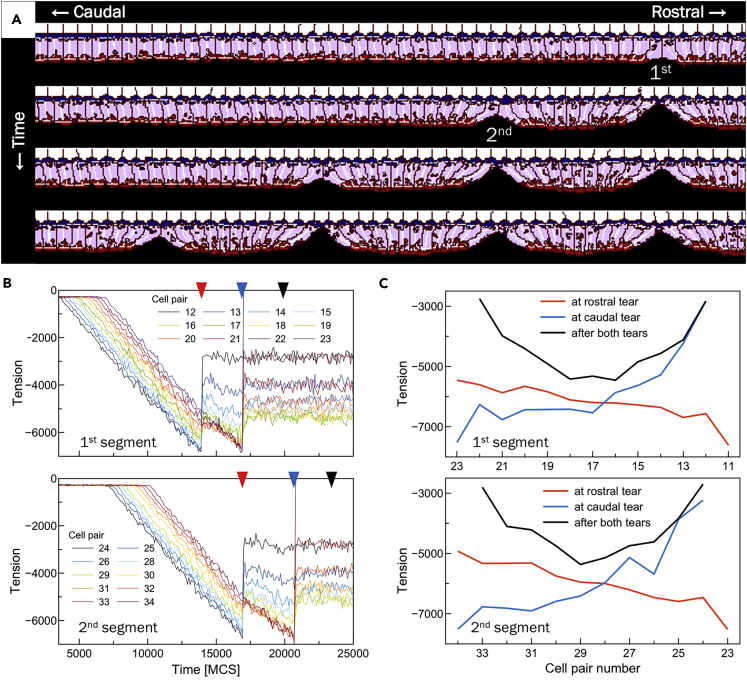
Figure 4A shows a detail of a time series of a simulation with 115 cells in which 5 tissue segments form. Neglecting the outermost segments next to the immobile fixed cells, all segments are of similar size ($⟨S⟩=11.36+/-1.45$) and segmentation occurs at similar time intervals ($⟨\tau ⟩=3442.37+/-587.87$) for our reference parameter (see Table S2, Video S7). We also looked at the evolution of the tension profile in two sequential segments. After the activation front passes, the tension between cell pairs gradually increases, with the rostral-most pair having highest tension (Figure 4B and red lines in Figure 4C). After the formation of the rostral-most boundary/tear, the pattern inverts, with the rostral-most cell pairs now more relaxed and the caudal-most pairs now under highest tension (compare red and blue lines in Figure 4C). Formation of the caudal-most boundary relaxes the tension of these pairs and the segment tension profile is now symmetrically convex, with a lower average tension than in the intermediate steps (black lines in Figure 4C). Subsequent segments form similarly.

Figure 4.

Tissue segmentation from a caudally-propagating activation-front initiating apical constriction

(A) Time series of a simulation showing the sequential segmentation of a tissue due to a linear increase of λ_A as cells progressively activate from rostral (right) to caudal (left). Colors as in Figure 2A and parameters from Table S2. Snapshots taken at the approximate moment separation occurs (17000, 21,000, 24,000, and 28,000 MCS).

(B) Time evolution of cell-pair tensions in two consecutive segments. Colors code different cell-pairs, beginning with the rostral-most pair for each segment and ending with the caudal-most pair. When the links break the pairwise tension goes to 0.

(C) The line of a given color corresponds to the arrowheads of the same color in (B). The colors denote: (red) time of formation of the rostral segment boundary; (blue) time of formation of the caudal segment boundary; and a time after caudal boundary formation when the forces in the segment have reached mechanical equilibrium (black).

Segment size scaling with activation-front speed and rate of apical constriction

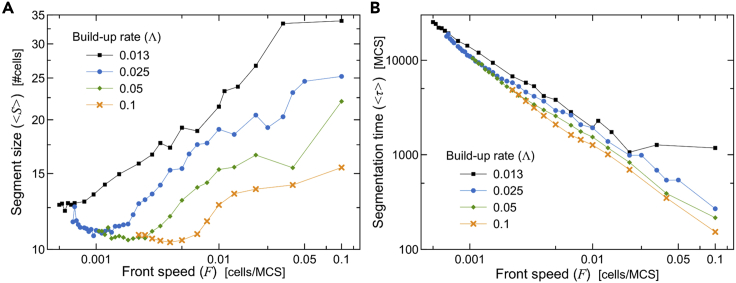
The CW model can explain how somite size adjusts to variations of embryo size (Cooke and Zeeman, 1976): all else being equal, a faster clock produces smaller somites, while a faster wavefront generates larger somites. We now investigate if our mechanical model of segmentation has the same scaling features: does a faster activation front (F) lead to larger segments? How does average segment size change with different buildup rates of apical contractility (Λ)? In the results that follow, we systematically varied both parameters, averaging all metrics over 5 simulation replicas.

We first fixed the buildup rate of apical contractility Λ and varied the activation-front speed F. We observe two regimes for the average segment size $⟨S⟩$ with respect to the front speed. For front speeds below a critical value (<F^∗), average segment size $⟨S^{\ast }⟩$ was nearly constant. For faster front speeds (>F^∗) average segment size increased as a power law of F with exponents close to ¼ (Figure 5A). The critical value of the front speed F^∗ and average segment size $⟨S^{\ast }⟩$ for the change from nearly constant segment size to the scaling regime depends on the buildup rate Λ (Figure S3A). These results suggest that the spatial compartmentalization of the tissue into cells imposes a lower limit on segment size as a function of Λ (Figure S3A). Our simulations with simultaneous contraction indicated that the maximum tension between cell pairs increases with the number of cells within a forming segment (Figure 3B), so slow fronts should lead to tears at regular size intervals.

Figure 5.

Segmentation as a function of activation-front speed

(A) Average segment size $⟨S⟩$ as a function of front speed F. For slower speeds, segments are of roughly constant size. For faster speeds segment size increases as a power of the speed.

(B) Average segmentation time $⟨\tau ⟩$ decreases as a power law with F^{−0.80±0.008}. (A and B) Each line shows a similar behavior for different base values of the buildup rate of apical contractility (Λ).

The average time interval between the formation of successive tears/boundaries $⟨\tau ⟩$ depends strongly on F, and very weakly on Λ, with faster activation-front speeds decreasing the segmentation time as a power law with exponent −0.80 ± 0.008 (Figure 5B).

Next, we fixed the activation-front speed F and varied the buildup rate of apical contractility Λ. Average segment sizes $⟨S⟩$ decrease logarithmically with higher buildup rates, but became roughly constant for $\Lambda$ above ${\Lambda }^{\ast }$ (Figures S3B and S3C). As before, mean segment size outside the scaling regime ($⟨S^{\ast }⟩$) depends on the front speed F (Figure S3C). We can understand these results from the way cell-pair tension increases with segment size (Figure 3B). For slow buildup rates ($<{\Lambda }^{\ast }$), the sole factor determining segment size is the front speed, with faster speeds adding more cells to the forming segment before boundary formation (Figure 5A). For higher buildup rates ($>{\Lambda }^{\ast }$), however, segment size is nearly independent of F and primarily determined by the dependence of the shape of the tension profile as a function of number of cells (Figure 3B).

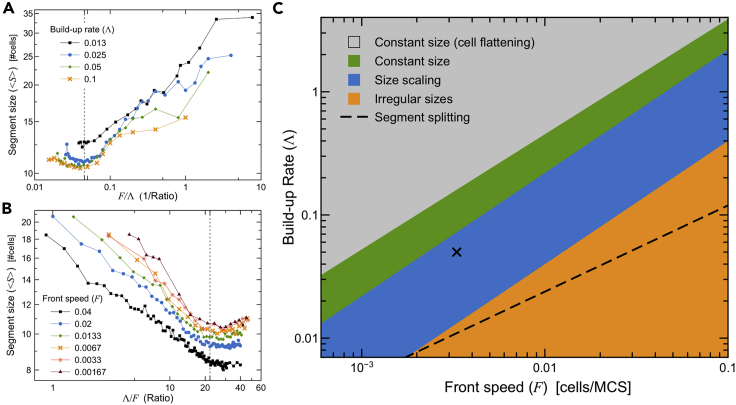
Ratio of buildup rate to activation-front speed sets the transition of scaling regimes

The critical values for the activation-front speed F^∗ and buildup rate of apical contractility Λ^∗ for the transition between the nearly constant segment size and scaling regimes shown in Figures S3A and S3C are related. Rescaling the horizontal axis in Figures 5A and S3B for each curve by its corresponding value of Λ and F, respectively, shows that in both cases, the transition occurs near the same ratio of Λ/F = 22 MCS²/cell (Figures 6A and 6B). This critical ratio allows us to define a boundary in parameter space that separates regions where segment sizes change with either Λ or F from regions where the segment sizes remain nearly constant with changes in one of these parameters (Figure 6C, blue and green regions, respectively). Note that we use the word constant in contrast to the size scaling of the segments with respect to either Λ or F; segment sizes change gradually within the green region in Figure 6C (see Figures S4A and S4B).

Figure 6.

Λ/F defines the boundaries between segmentation regimes

(A and B) Rescaled version of Figure 5A and S3B, showing average segment size $⟨S⟩$ as a function of (A) activation-front speed over buildup rate, and (B) its inverse. Vertical dashed line at Λ/F = 22 indicates the transition threshold between near-constant-size and scaling-size segments.

(C) Parameter space diagram showing regions where the combination of the parameters Λ and F leads to nearlyconstant segment sizes (green), nearly constant segment sizes with flattened cells (gray), scaling segment sizes (blue), or irregularly-sized segments (orange). Black dashed line shows transition from stable to splitting segments. The point marked X indicates the reference simulation parameters (see Table S2).

The parameter space in Figure 6C also contains a gray region where the combinations of Λ and F lead to flattening of the cells as the rate of contractility becomes too large for a particular front speed (Video S8). Segment sizes in this region still saturate (Figure S5C) as in the nearly-constant-size regime, but the simulated cells “flatten” and decrease their height by around 10%, while neighboring apical compartments separate from each other without breaking their apical links (compare Figures S5A and S5B to Figure 4A). Since these changes in cell shape do not occur in experiment, we did not explore this regime in detail. We discuss the orange region and dashed boundary line below.

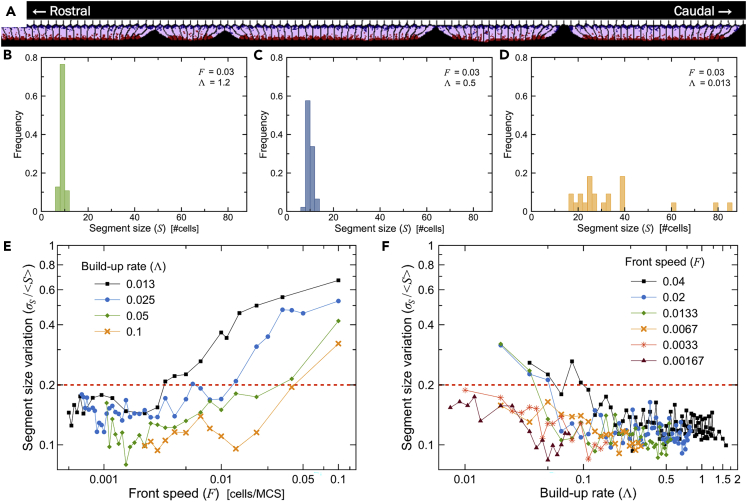
Segment sizes become irregular for low ratios of buildup rate to activation-front speed

While average segment size increases with higher activation-front speeds (F) or lower buildup rates of apical contractility (Λ), segment size distribution becomes irregular for lower ratios of Λ/F (Figures 7A–7D), as seen from the coefficient of variation, the ratio of the standard deviation (σ_s) to the mean ($⟨S⟩$) (Figures 7E and 7F). We classify segments as irregular when σ_s/$⟨S⟩$ > 0.2.

Figure 7.

Segment size variation

(A) Typical simulation showing a wide range of segment sizes for a simulation with parameters in the irregular regime (orange) of the parameter space in Figure 6C (F = 0.03, Λ = 0.013).

(B–D) Histogram of segment sizes for combinations of Λ and F in the nearly constant-size regime (B), scaling regime (C), and irregular regime (D), of the parameter space for 5 replicas each.

(E) Coefficient of variation as a function of front speed F for different buildup rates of apical contractility, Λ.

(F) Coefficient of variation as a function of Λ for different front speeds F. (E and F) Dashed red lines at ${\sigma }_s/⟨S⟩=0.2$ indicate the threshold defining irregular segment sizes in Figure 6C.

When the activation-front speed is much faster than the buildup rate ($F\gg \Lambda$), a large group of cells starts to constrict at about the same time. In this situation, the effect on the tension profile in the tissue of the position of the last-formed boundary is weak, and new tissue tears can appear anywhere in the tissue (Video S9). In our parameter space diagram, the uniform segments occur for ratios of Λ/F ≤ 4 and non-uniform segments for Λ/F > 4. The variance of the segmentation time (${\sigma }_{\tau }/⟨\tau ⟩$), measures the uniformity of the time between consecutive boundary formations (see Figure S6). ids ${\sigma }_{\tau }/⟨\tau ⟩$<0.33 for Λ/F ≤ 4 and >0.33 for Λ/F > 4. This variability in segmentation time makes sense , since the time between tears is an emergent property in our mechanical model, not determined by the oscillation period of the clock as in the CW model.

Buildup rate and front speed limit larger segment sizes

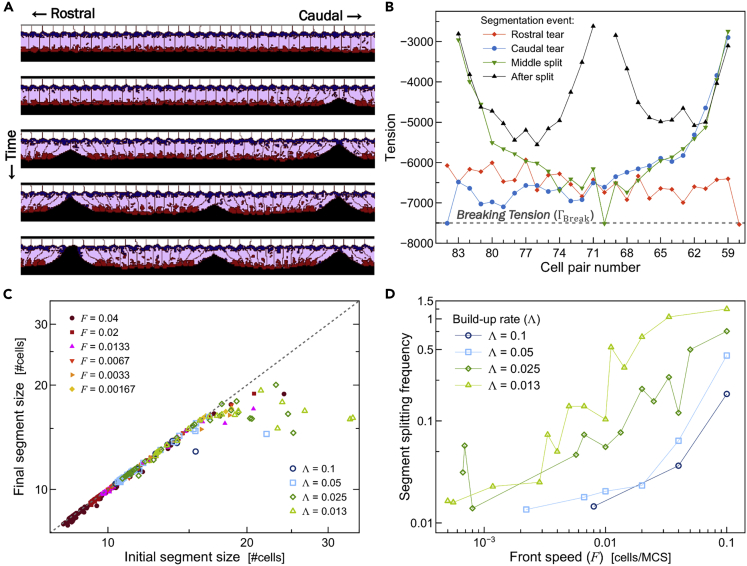
The above results show that initial segment sizes increase with faster front speeds (F) (Figure 5A) and slower buildup rates of apical contractility (Λ) (Figure S3B). However, splitting of segments limits the maximum segment size. After their initial formation, larger segments are prone to split as the cells within them continue to increase λ_A until the tension within the segment, which is maximal near its center, crosses the breaking threshold and the segment splits in two near its middle (Figures 8A and 8B, Video S10).

Figure 8.

Splitting of Large Segments

(A) Simulation snapshots showing the splitting of a large segment for Λ = 0.013, F = 0.005 (times, from top to bottom: 47,000, 49,000, 52,000, 54,000, and 56,500 MCS).

(B) Evolution of the tension profile for the splitting segment shown in (A).

(C) Plot of final versus initial segment sizes. Data points below the diagonal dashed line indicate splitting.

(D) Splitting frequency as a function of front speed F.

While the rate of occurrence of a splitting increases with the initial segment size (Figures 8C and S4), the front speed F has a more direct effect on the frequency of splitting, with higher buildup rates only delaying the appearance of splits (Figure 8D). The breaking tension in our model sets a maximal segment size, which also depends on the speed of the front with respect to the buildup rate of apical contractility (Figures 8C and 8D). A best fit through parameters with a higher frequency (>0.1) of splitting defined a boundary given by Λ = 0.6F^0.7 between the regimes with stable and splitting segments (dashed line in Figure 6C).

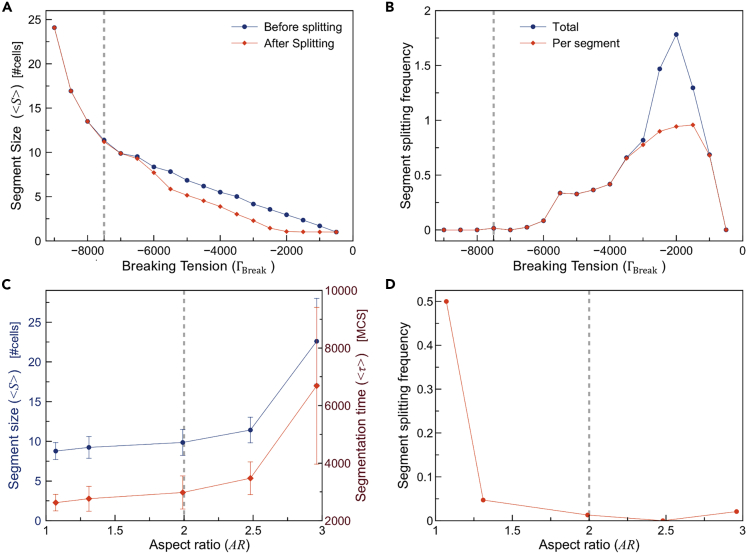
Segment size and splitting dependence on breaking tension

So far, we used a fixed breaking tension of Γ_Break = −7500 for the breaking of junctional links between apical regions of neighboring cells. We now test the effects of varying the breaking tension. For breaking tension near zero, the average segment contains only one cell. Conversely, for values of breaking tension higher than $\left|{\text{Γ}}_{\mathrm{Break}}\right|=9500$, no breaks occur and the tissue never segments. As the breaking tension increases between these limits, the average segment size also increases, as expected (Figure 9A). The splitting frequency is higher for lower breaking tensions, and zero for higher breaking tensions, with segments breaking in more than once breaking tensions below around Γ_Break = −2000 (Figure 9B).

Figure 9.

Influence of breaking tension and cell aspect ratio on segmentation

(A) Average segment size $⟨S⟩$ as a function of the breaking tension (Γ_Break). Blue lines are initial segment sizes, red lines are segments sizes after splitting.

(B) Average number of splits per segment as a function of the breaking tension (Γ_Break).

(C) Average segment size $⟨S⟩$ (blue) and average segmentation time $⟨\tau ⟩$ (red) as functions of cell aspect ratio AR.

(D) Frequency of segment splitting (red) as a function of cell aspect ratio AR. Dashed lines show reference simulation values for breaking tension (Γ_Break=-7500) and aspect ratio (AR=2).

Segmentation dependence on cell aspect ratio

In the pre-somitic tissue, cells elongate dynamically prior to and during boundary formation. We kept the length of the cell fixed in our previous simulations. Now we explore how segment size depends on the aspect ratio of the cell (AR = height/width). Figure 9C shows the average segment size $⟨S⟩$ as a function of cell aspect ratio. Figure 9D shows that the segment splitting frequency (red line) is higher for lower cell aspect ratios, which we can understand as a result of the packing constraints that increase the accumulation of tension between apical cell pairs and make them more prone to splitting.

Discussion

Experimental observations of cell rearrangements during somite formation (Martins et al., 2009), observations with somitomeres (Meier, 1979; Tam et al. 1982) and our own SEM images (Figure 1), suggest that segmentation begins dorsally in the PSM at least 4 somite lengths caudal to the position of the last-formed somite. We interpreted the spatial segmentation of the dorsal epithelium into similarly-sized clusters of cells as the result of a caudally progressing activation front of apical constriction, which yields an increased longitudinal (rostral-caudal) tension between the cells. This increasing tension coupled with a breaking tension between neighboring cells' apical domains sets the position of future somite boundaries.

Gradual contraction leading to increasing stress eventually relieved by fracture, leads to periodic cracks on non-biological thin films subjected to tensile stress, e.g., due to cooling or drying (Thouless, 1990; Thouless et al., 2011). Analysis of these films shows that the spacing between these cracks depends on the stress, thickness, and toughness of the film. Models of cracking usually assume the stress to be uniform, non-time varying, and applied externally to the material. In other studies, Yuse and Sano applied a time-varying inhomogeneous thermal stress to a plate moving at constant speed between two reservoirs (Yuse and Sano, 1993; Yuse, and Sano, 1997). The velocity of the plate and the temperature difference between the two reservoirs acted as control parameters and defined a phase space with regimes with straight, spatially-periodic and other crack morphologies. Cohesive granular materials subject to stress can develop periodic crack fracture patterns of ofabove a critical applied strain (Alarcón et al., 2010).

In biology, fibroblasts generate mechanical forces which assist in the remodeling of the external collagen matrix to form self-organized tissue structures (Stopak and Harris, 1982). TStretched fibroblasts suspended in collagen and restrained by a glass mesh generate tensile stresses which can aggregate cells. The self-organization of cells into clusters in the absence of chemical signals led Harris et al. to suggest that mechanical instabilities could provide positional information instead of diffusible factors like morphogens (Harris et al., 1984). Mechanics may play a role in forming alligator scales, here fast growth of the underlying skeleton generates stresses which cracks the brittle keratinized facial skin (Milinkovitch et al., 2012).

Analysis of our model of epithelial segmentation identified four key parameters: the speed of the front (F), the buildup rate of apical contractility (Λ), the breaking tension between apical cell-cell junctions (Γ_Break), and the aspect ratio of the cells (AR) (Table S2). We chose our reference parameters to reproduce the segment sizes seen in embryonic chick. However, in our experiments the aspect ratio of the PSM cells in the dorsal region could be as high as 7, while our simulated aspect ratio before contraction was around 2. To simulate cells with these higher aspect ratios would require simulations with a greater spatial resolution.

We considered a conceptual cell-clustering model (Figure 2C) in which the dorsal cells are initially confluent, but their apical domains are not tightly connected. Behind a caudally-progressing maturation front, cells start to connect with their neighbors and condense, initially into small groups, later clustering into larger, more tightly connected clusters that eventually pattern the dorsal tissue into distinct tissue segments. We also considered a conceptual model in which small groups of cells at the center of each future segment initiate apical constriction and cell clustering, eventually recruiting and/or activating their neighbors (Figure 2D). This mechanism requires some mechanism to identify the positions of the future somite centers, e.g., a molecular clock, which is necessary for the molecular patterning of the somites into caudal and rostral identities (Dias et al., 2014). All these models define an initial segmentation prepattern that could later guide the formation of the full somites as epithelialization spreads to the ventral, medial and lateral sides of each forming epithelial sphere.

Our purely mechanical model (Figure 2B) can produce spatially and temporally regular segments. Similar to the CW models, segment sizes increase with front speed, as seen in many species (Figure 5A). However, unlike in the CW model, tsegment size does not increase linearly with front speed. As we see in Figure 6C for low ratios (Λ/F < 4), mechanical instabilities cause large segment to split, so the final segment sizes are smaller than the scaling relation would predict; for high ratios (Λ/F > 22), segment sizes are almost independent of front speeds (F). These phenomena are absent in CW models and could explain the splitting of large somites in some perturbation experiments (Stern and Bellairs, 1984; Cooke, 1978). Segmentation time in our model is not imposed but results from the time the tension between neighbors takes to exceed the breaking tension for two successive intersomitic boundaries. This time decreases with increasing front speed and is insensitive to the buildup rate of apical contractility (Figure 5B).

While our mechanical model lacks the molecular clock central to CW models, it does include a caudally-traveling front, which may not be the same as the determination front postulated in CW models. TLater in segmentation, we see a gradual mesenchymal to epithelial transition progressing caudally along the PSM (Figure 1). During axis elongation and segmentation, the PSM becomes stiffer with a caudal-to-rostral stiffness gradient (Marrese et al., 2020) which is associated with increasing cell polarity and expression of adhesion molecules like cadherins (Duband et al., 1987), which are sufficient to reproduce boundary formation in models of somite formation (Glazier et al., 2008). Higher cadherin density corresponds to faster actin reassembly (Yonemura et al., 1995) and myosin enrichment in epithelial cells (Maddugoda et al., 2007), since faster actin turnover and higher levels of myosin correlate with greater apical contractility, these patterns are compatible with a model in which contractility gradually builds up with a caudal-rostral gradient along the PSM.

Our model predicts that disruptions to levels of molecules (e.g., myosin, actin) that control apical contractility in PSM cells should change segment sizes. Increasing the levels of these molecules should effectively increase λ_A (Figure 3C), leading to smaller segments. However since the segment size in our model also depends on the rate of progression of the rostral-caudal activation of these molecules, we expect cases in which, for a fixed tension load, segment sizes could become independent of the protein levels (similar to the nearly constant segment sizes in Figure 6C). Reducing the strength of the adhesion junctions between the PSM cells (equivalent to lowering the breaking tension in our model) will also lead to smaller segments.

Our model considers a 2D sagittal section of the dorsal monolayer and aims to reproduce segmentation prior to the formation of a full somite. In chicken (Martins et al., 2009) different regions of the PSM epithelialize at different times and dorsally propagating signals cause the caudal edge of the forming somite to epithelialize before the rostral edge (Nakaya et al., 2004; Sato and Takahashi, 2005). These observations suggest that mechanics and molecular oscillatory signaling, including expression-control of EphA4-EphrinB2 (Watanabe et al., 2009), Lunatic fringe and Notch (Sato et al., 2002), work together to yield a robust morphological outcome. We hope to explore the implications of these observations in an augmented model combining mechanical instability with a molecular clock to propagate somite boundaries in the dorso-ventral and medio-lateral directions.

Limitations of the study

Our experiments used 2D sagittal sections of fixed tissues to estimate side-to-side distances in the dorsal layer of cells in the PSM. These observations do not provide complete cell shapes or reveal changes in cell shape in time and give only rough estimates of cells’ aspect ratios and of the side-to-side distance. However, our measurements of the side-to-side cell distances are consistent and suffice to indicate the approximate periodicity and locations of maximal apical separation between the epithelial cells along the rostral-caudal axis.

Segment formation times in our model have higher variance (coefficient of variation of 0.17) than in experiments (coefficient of variation of 0.03) (Schröter et al., 2008). In vivo, epithelialization along the dorsal surface occurs in a plane that also extends along the medio-lateral direction. Extending our model to 3D would likely reduce variation in the segmentation time.

Resource availability

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by the lead contact, Julio M. Belmonte (jbelmon2@ncsu.edu)

Materials availability

This study did not generate any new materials.

Data and code availability

All data are available from authors upon request. The simulation files are available at https://compucell3d.org/SomiteMechanicalModel.

Methods

All methods can be found in the accompanying Transparent Methods supplemental file.

Published: April 23, 2021