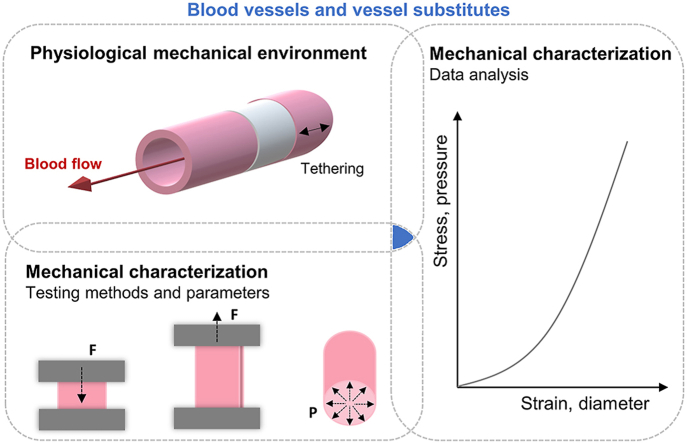
Abstract
During the last 50 years, novel biomaterials and tissue engineering techniques have been investigated to produce alternative vascular substitutes that recapitulate the unique elastic mechanical features of blood vessels. A large variation in mechanical characterization, including the test type, protocol, and data analysis, is present in literature which complicates the comparison among studies and prevents the blooming and the advancement of this field. In addition, a limited mechanical assessment of the substitute for the intended application is often provided. In this light, this review presents the mechanical environment of blood vessels, discusses their mechanical behavior responsible for the suited blood flow into the body (non-linearity, anisotropy, hysteresis, and compliance), and compares the mechanical properties reported in literature (obtained with compression, tensile, stress-relaxation, creep, dynamic mechanical analysis, burst pressure, and dynamic compliance tests). This perspective highlights that the mechanical properties extracted through conventional tests are not always suitable indicators of the mechanical performance during the working life of a vascular substitute. The available tests can be then strategically used at different stages of the substitute development, prioritizing the simplicity of the method at early stages, and the physiological pertinence at later stages, following as much as possible ISO standards in the field. A consistent mechanical characterization focused on the behavior to which they will be subdued during real life is one key and missing element in the quest for physiological-like mechanical performance of vascular substitutes.
Keywords: Mechanical testing, Mechanical properties, Vascular substitutes, Viscoelasticity, Vascular tissue engineering, Young modulus, Compliance, Burst pressure, Strength at break, Elongation, Creep, Tensile, Compression, Stress-relaxation
Graphical abstract
1. Introduction
The vascular system has the noble role to nourish all other tissues and organs in the human body. Composed of impressive 19 000 km of interconnecting vessels, oxygen-rich blood flows in their hollow structure from the heart through large arteries which progressively divide into smaller vessels until the capillaries of all other tissues. The blood then delivers nutrients and oxygen, removes metabolic by-products, and continues through veins back to the heart to be resaturated with oxygen in the pulmonary circuit [1]. The complex structure and composition of the vascular wall impart unique mechanical features for the blood flow propagation and any disturbance on its physiology can significantly compromise its circulation. Indeed, vascular pathologies such as atherosclerosis have been the leading cause of death worldwide [2] and the total replacement of the diseased tissue must be applied in a number of cases [3,4].
The first publication on vascular replacement surgery was in 1906, in which a segment of vein from the own patient was used to replace a diseased vessel [5]. Their unsatisfactory long-term results led to the investigation of techniques for collection, processing, and storage of grafts and to the exploration of synthetic prostheses [6]. Currently, polyethylene terephthalate (PET, Dacron®) and expanded polytetrafluoroethylene (PTFE, Teflon®) conduits have been applied for high flow state in large-diameter vessels (>6 mm). For small-diameter vessels (<6 mm), autografts (AG) such as the saphenous vein, internal mammary artery, and radial artery remain still the gold standard because the effects of the compliance mismatch between the synthetic material and native vessels and their thrombogenic surface are amplified in low-flow states [7]. However, donor site morbidity, prior harvesting, and the need for an additional surgery prevent the use of autologous vessels in one third of the patients [8,9].
The limitations of AG and synthetic prosthesis (SP) motivated the development of alternative conduits using less-stiff materials (e.g. polyurethane) or tissue engineering approaches to construct responsive vascular substitutes [10]. Vascular tissue engineering strategies involve the use of cells with or without tubular supports (known as scaffolds) composed of natural (e.g. collagen, chitosan, fibrin, decellularized matrices) or synthetic (e.g. polycaprolactone [PCL], polyglycolide, polylactic acid) biopolymers. The construct is cultured under optimal conditions for cell proliferation and for their de novo expression of extracellular matrix proteins allowing the (re)generation of a vascular tissue-like conduit. This approach significantly contributes to the biological properties of the implant; however, the mechanical mismatch has still been reported to be an issue [11].
For all types of substitutes, SP, AG, and tissue-engineered vessels (TEV), their mechanical characterization is then extremely important to foresee whether the construct is able to withstand the mechanical loading of the intended application and to provide a feedback and guidelines for their improvement. Conventional mechanical tests for vascular substitutes include but are not limited to compression, tensile, tensile stress-relaxation, creep, dynamic mechanical analysis (DMA), burst pressure, and dynamic compliance. Their main difference relies on the nature of the applied loading or deformation, i.e. compressive, or tensile; constant, or incremental or cyclic; uniaxial or pressure based. In addition, further variations in the mechanical testing apparatus, grips configuration, geometry of the specimen, direction and rate of load or deformation, and data analysis are found.
In this light, the purpose of this work is twofold: (1) to review the mechanical environment of human blood vessels and their unique mechanical behavior resulted from its structure and composition; and (2) to provide a comprehensive overview and a critical analysis of the conventional mechanical tests (compression, tensile, stress-relaxation, creep, dynamic mechanical analysis, burst pressure, and dynamic compliance) found in literature for the characterization of blood vessels and their substitutes. Finally, a strategic plan for their mechanical characterization will be proposed for a more structured and profound evaluation of potential vascular substitutes.
2. Structure and mechanics of blood vessels
2.1. Structure and composition of blood vessel walls
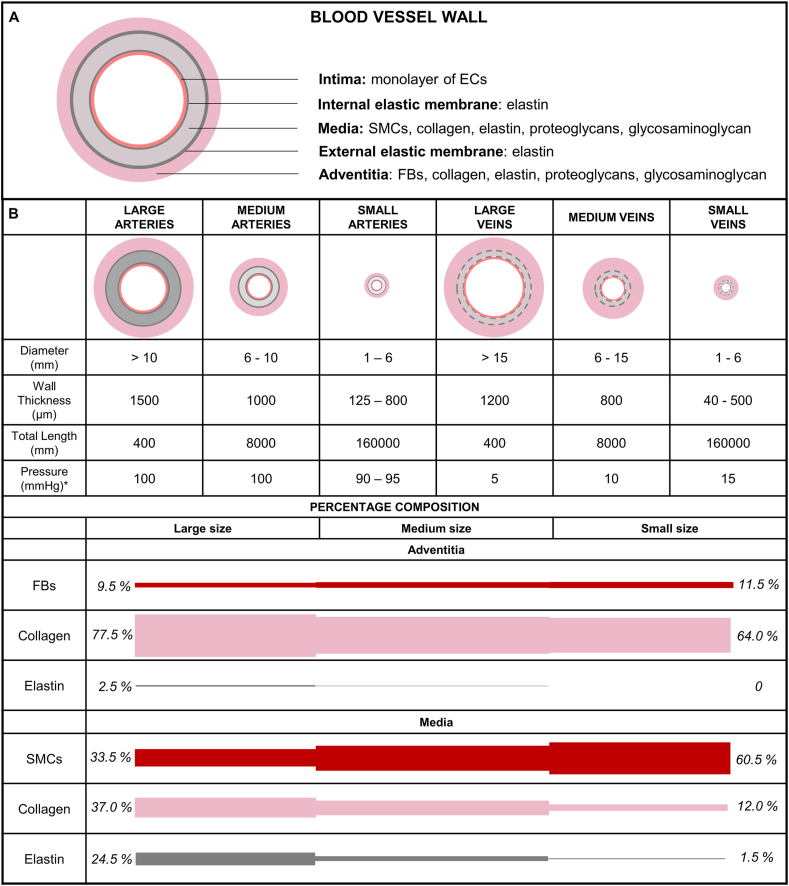
Approximately 70% of the vascular wall is composed of water and 30% consists in dry mass including collagen, elastic, proteoglycans, and vascular cells. Fig. 1A schematizes the basic structure and composition of the vascular wall organized in three layers known as tunica intima, tunica media, and tunica adventitia intercalated by elastic membranes. The innermost layer is composed of endothelial cells covering all the luminal surface of blood vessels. The tunica media is composed of circumferentially aligned smooth muscle cells (SMCs), elastin, and collagen fibers. The outer layer comprises fibroblasts, some elastin but mainly collagen fibers oriented longitudinally as wavy bundles [12]. The wall thickness and the proportion of the structural components in each layer vary among large, medium, and small-caliber arteries and veins (Fig. 1B) which in turn vary with the distance from the heart. The systemic vascular system starts with a single large artery (the aorta) and progressively divides increasing the number of smaller vessels to reach more organs and tissues. In the capillary beds, the vessels progressively merge, decreasing the number of vessels ending the network with two large veins (inferior and superior vena cava) connecting it back to the heart. The pressure in the arterial system (90–100 mmHg) is much higher than that in veins (5–15 mmHg) because arteries receive the blood directly from the heart. In each cardiac cycle, the heart acts as a pump giving to the blood the required energy to achieve all the extremities by increasing the output pressure. Large arteries contain more elastin than collagen (~1.5x) tissue to stretch and recoil during the systole and diastole thereby propelling blood forward. Medium and small vessels contain more SMCs, less elastic tissue and stretch relatively little. The SMCs control the vessel caliber by contracting (vasoconstriction) or relaxing (vasodilatation) maintaining the proper blood pressure. Veins have a similar structure, however, with a relative lower wall thickness especially for the media layer. Therefore, veins contain little elastic tissue and relatively high amount of collagen (~0.3x) [1,13,14].
Fig. 1.
Structure and composition of blood vessel walls. A) The blood vessel wall is composed of three main layers: tunica intima, tunica media, and tunica adventitia. Elastic membranes are found in their interfaces. B) The thickness and the composition of each layer vary according to the vessel type (artery or vein) and diameter. Large arteries contain a thick media layer and higher amount of elastin. The amount of elastin decreases in small arteries which in turn contain more smooth muscle cells. Veins contain a thinner media layer and less amount of elastic tissue. Physical quantities for the human circulatory system from Ref. [1]. Percentage composition is an example for large, medium, and small arteries based on the data from Ref. [13]. The complementary percentages are ground substances such as glycosaminoglycan and proteoglycans. ∗Normal pressure values for the systemic vascular system.
2.2. Physiological forces acting on blood vessels
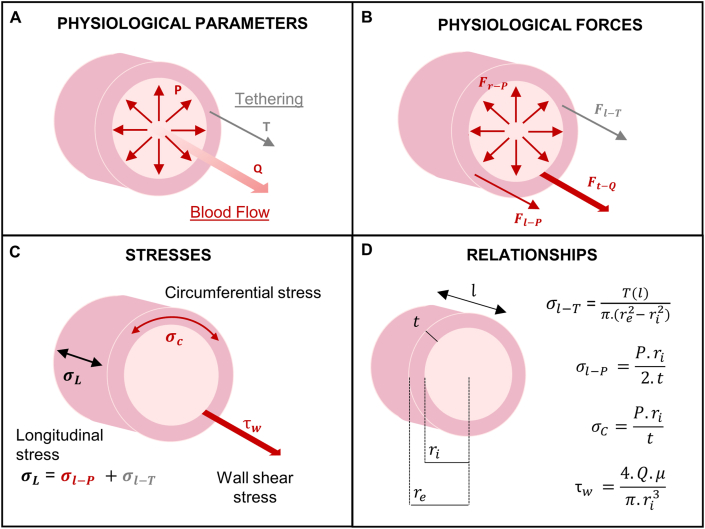
The blood vessel wall structure is built to withstand and propagate the forces applied by the blood flow and pressure, and the surrounding tissues. Blood pressure (P) is a measure of the tensile cyclic forces acting radially and longitudinally on the vascular wall. The tensile radial force due to pressure produces an internal circumferential (or hoop) stress in the vessel wall. Similarly, the distending force in the longitudinal direction produces an internal longitudinal stress . In addition, a second tensile force is present in the latter direction due to the tethering of the vessel with the surrounding tissue at the ends and at several locations along its length. This force is responsible for the longitudinal stress due to tethering . The blood flow also imparts a shear stress parallel to the lumen of the vessel (tangential to the axis of the flow). Fig. 2A–C summarizes the physiological parameters, the physiological forces and the corresponding stresses present in the vascular wall. Stresses and strains can be calculated from in vitro experiments where forces and loaded dimensions are measured. The calculations include some assumptions such as incompressibility (constant volume during deformation) and uniform strain across the vessel wall (Fig. 2D) [[15], [16], [17]].
Fig. 2.
Physiological forces acting on blood vessels. A) Physiological parameters involved in the forces and stresses acting on the vascular wall. In red, blood flow parameters: pressure (P) and volumetric flow (Q). In gray, the longitudinal tissue tethering (T); B) Physiological forces acting on blood vessels resulted from the blood pressure and flow, and surrounding tissues: radial force resulted from the blood pressure (, tensile and cyclic), longitudinal force resulted from the blood pressure (, tensile and cyclic), tangential force resulted from the blood flow (, shear and constant), longitudinal force resulted from the tethering (, tensile, constant); C) Stresses generated in the vascular wall from the physiological forces: circumferential stress , longitudinal stress and shear stress . Longitudinal stress is composed by a stress due to pressure and a stress due to tethering ; D) Stresses relationships assuming incompressibility and uniform strain across the vascular wall [15,17,70]. Blood viscosity (μ) is required for the shear stress calculation. The vascular wall dimensions are inner radius , external radius , length (l), and wall thickness (t).
2.3. Physiological mechanical behavior of blood vessels
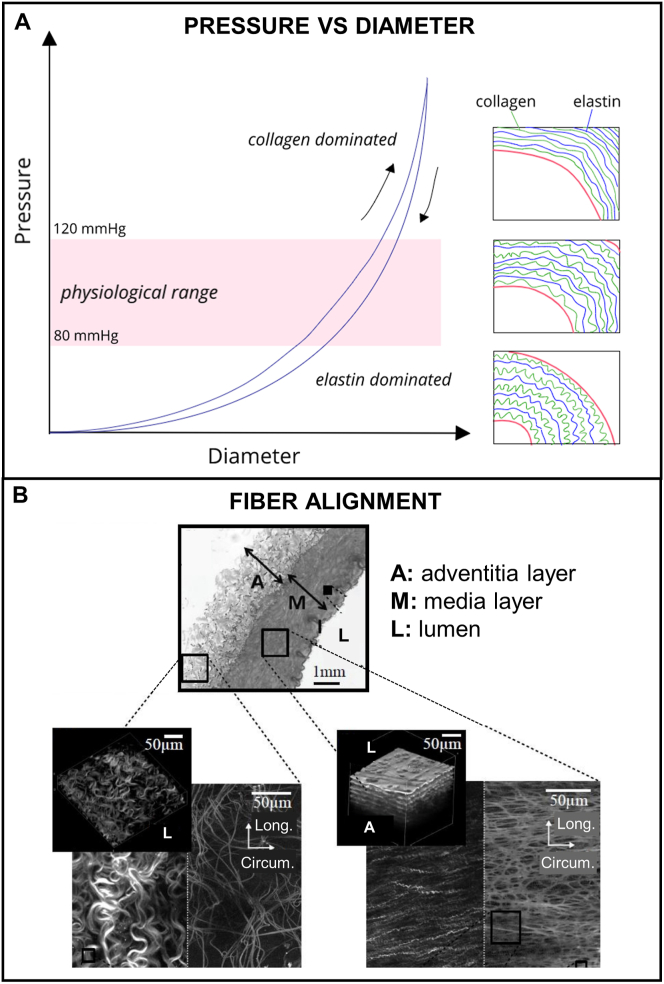
The composite characteristics of the vascular wall impart unique mechanical features in response to the physiological forces such as i) non-linearity, ii) anisotropy, iii) viscoelasticity, and iv) compliance. Fig. 3 illustrates the non-linearity (i) in the pressure-diameter curve of an artery which is a result of the wavy and disorganized configuration of elastin and collagen fibers when unpressurized (Fig. 3A, right bottom rectangle). As the pressure increases, the fibers start to gradually straighten. At the lower value of the physiological pressure (80 mmHg), elastin fibers become nearly straight (Fig. 3A, right middle rectangle). An increase in pressure results in the stretching of elastin fibers and the continuous straighten of collagen fibers up to the upper limit of physiological pressure (120 mmHg, Fig. 3A, right top rectangle). After that, collagen and elastin fibers are fully stretched. Therefore, at lower pressures the mechanical behavior is dominated by the elastic components which are less stiff and more elastic chains (Table 1). In the physiological range of pressure, the load transits between the elastin and collagen fibers. Finally, at high pressures, the mechanical behavior is dominated by the rigid collagen fibers, where greater amount of load is necessary for a change in the diameter. The stiffer collagen fibers prevent the damage and/or rupture of blood vessels when the pressure is increased [12]. The non-linearity is important to the formation of solitary waves (solitons) in arterial pulse [18].
Fig. 3.
Physiological mechanical behavior of blood vessels. A) Pressure-diameter behavior of an artery: Soft elastin fibers dominate the response under low pressure states (<80 mmHg) while stiff collagen fibers dominate the response beyond the physiological range avoiding vessel damage. Loading and unloading curves represents the hysteresis phenomena; B) Microstructure of the vessel wall highlighting the specific alignment of the fibrous components responsible for the anisotropy behavior: in the media layer fibers are circumferentially aligned while in the adventitia layer fibers are less dense and organized [[71], [72], [73]]. Reproduced from Ref. [71] with permission from Elsevier.
Table 1.
Mechanical properties of ECM components, smooth muscle cells, blood vessels, and commercial vascular prosthesis in terms of young's modulus (MPa), stress at break (MPa) and/or burst pressure (mmHg), strain at break (%) and compliance (%/100 mmHg).
| Human vascular tissue and substitutes | Young's modulus (MPa) | Stress at break (MPa) and/or BP (mmHg) | Strain at break (%) | Compliance (%/100 mmHg) |
|---|---|---|---|---|
| Elastin | 0.3–1 [1,23] | 1–2 MPa [23] | 100–150% [23] | NA |
| Collagen | 100 [1] 1000 [13,23] |
120 MPa [23] 50–100 MPa [13] |
13% [23] | NA |
| SMCs | 0.1–2 [1] | NA | NA | NA |
| Human femoral artery | 9-12 (circ) [24] | 1–2 MPa (circ) [24] | 63-76 (circ) [24] 155 (circ) [25] 120 (long) [25] |
5.9 [26] |
| Internal mammary artery | 8.0 (circ) [27] 16.8 (long) [27] |
4.1 MPa (circ) [27] 4.3 MPa (long) [27] 2000 mmHg [27] 3196 mmHg [28] |
134 (circ) [27] 59 (long) [27] |
11.5 [28] |
| Saphenous vein | 4.2 (circ) [27] 23.7 (long) [27] |
1.8 MPa (circ) [27] 6.3 MPa (long) [27] 1680–3900 mmHg [27] 1600 mmHg [28] |
242 (circ) [27] 83 (long) [27] |
4.4 [26] |
| Dacron | 800-900 [12] 14 000 [29] |
170–180 MPa [29] | 5-20 (circ) [25] 60-130 (long) [25] |
1.9 [26] |
| Teflon | 500 [29] | 14 MPa [29] 600 mmHg [30] |
5-25 (circ) [25] 100-140 (long) [25] |
1.6 [26] |
Circ: circumferential; long, longitudinal; ECM, extracellular matrix; SMCs, smooth muscle cells.
The geometrical arrangement of the fibrous components into the circumferential direction specially in the media layer (Fig. 3B) leads to the anisotropic behavior (ii). Blood vessels are usually much stronger in fiber direction than perpendicular to it [19]. The viscoelasticity property (iii) is also another important component contributing to the blood hemodynamics. When the tissue is stretched and the strain is maintained constant, the induced stress decreases with time, a phenomenon known as stress relaxation. Inversely, if a stress is applied and maintained constant, the tissue continues to deform, a feature known as creep. During the cyclic inflation-deflation stresses, the stress-strain curve in the loading process is different from the unloading process due to this delayed response leading to a phenomenon known as hysteresis (Fig. 3A). The area of the loop is equal to the energy dissipated at each cycle and it corresponds to around 15–20% of the total strain energy. This means that a major component of the strain energy is recovered elastically each time the wall is distended. The lost energy helps to attenuate pressure pulses that propagate along arteries [20].
The compliance (iv) of blood vessels is defined by the percentage increase in diameter at a given increase in pressure and it has a key role in propagating the pulsatile blood flow. The Windkessel model was proposed to describe this phenomenon that relates how reservoirs can affect the pulsatile nature of a fluid flow. During the systole, the heart pumps blood into the aorta (reservoir) which stores around 70% (in volume) by a local wall distension (elastic stretching) with the rest resulting in forward flow. In the diastole, the blood stored is released forward in the vascular network to regions of lower pressure because the aortic valve blocks the return to the heart. In this way, the pressure wave or the circumferential wall distension is propagated into the downstream vessels. The property of compliance is a measure of the storage capacity of arteries and represents their buffering action to convert the pulsatile flow at the level of the aorta to continuous flow in the capillaries [21,22].
Those unique mechanical features are difficult to recapitulate in blood vessel substitutes specially in synthetic prothesis. Table 1 contains some mechanical properties found in literature for the main components of the vascular wall (i.e. collagen, elastin, and SMCs), native tissues and synthetic substitutes. The discrepancy between blood vessels and the synthetic conduits is evident for all values. During the last 50 years, novel biomaterials and tissue engineering techniques have been investigated to produce alternative vascular substitutes that mirror the mechanical attributes of blood vessels. It is then reasonable to expect that a detailed mechanical characterization has a key role on the design and development of successful vascular substitutes. In this light, the international standard for the mechanical evaluation of vascular prosthesis will be recapitulated in the next section followed by a comprehensive overview on the conventional mechanical tests most applied and reported in literature.
3. Mechanical characterization of blood vessels and their substitutes
Vascular prosthesis as any other medical device needs to be evaluated as per consensus standards recognized by federal agencies (such as the U.S. Food and Drug Administration) before they are approved for market entry. Recognized standards are developed in an open and transparent process such as those developed by American National Standards Institute (ANSI)-accredited standards developing organizations as well as the International Organization for Standardization (ISO) and the International Electrotechnical Commission. A good conduct in research for the characterization of new technologies is to base the corresponding methodology on these standards because they are carefully elaborated for the technology's final application. This section will start by presenting the ANSI/ISO 7198:2016 for tubular vascular grafts and vascular patches with a special focus on the suggested mechanical testing methods. An overview of the conventional mechanical testing found in literature will compose the second part of this section, which will detail their respective protocols and variations with respect to the ANSI/ISO and among literature.
3.1. ANSI/ISO 7198:2016 cardiovascular implants and extracorporeal systems—vascular prostheses—tubular vascular grafts and vascular patches
The ANSI/ISO 7198:2016 standard for ‘Cardiovascular implants and extracorporeal systems—Vascular prostheses—Tubular vascular grafts and vascular patches’ includes the requirements for the evaluation of tubular vascular substitutes implanted by direct visualization surgical techniques intended to replace, bypass, or form shunts between segments of the vascular system in humans [31]. This international standard is considered as a supplement to ISO 14630:2012 (level 1 standards), which specifies general requirements for the performance of non-active surgical implants. Vascular substitutes made of synthetic textile materials, synthetic non-textile materials and non-viable biological materials (e.g. tissue engineered vascular grafts) are within the scope of this international standard. General requirements of configuration, size, and materials designation, intended performance, design attributes, and design evaluation of tubular vascular prostheses are included in the document.
Concerning the mechanical properties, the compliance, and the strength in terms of tensile strength, burst strength and, if applicable, factory anastomotic strength of the vascular prosthesis are recommended to be evaluated. The methods proposed to evaluate those properties are dynamic radial compliance test, circumferential tensile strength, diaphragm pressurized burst strength, longitudinal tensile strength, pressurized burst strength, and probe burst strength. Suture retention strength and kink diameter/radius are also recommended tests to determine the force required pulling a suture through the wall of a graft and the radius of curvature required to kink a vascular graft, respectively. For tubular prosthesis used as vascular access, the strength after repeated puncture should be also measured. The characterization methods proposed by the ISO are summarized in Table 2. The ISO 7198:2016 recognizes that not all the tests mentioned are applicable for each type of tubular vascular substitute. It might be required modification to the existing test methods or additional test methods. In this case, attention should be made to physiological conditions in the vasculature. Because the test methods should be adapted for each case, they are not complete in the international standard. The ISO recommends the researchers to design test methods based on the steps and concepts outlined in the document to enhance consistency in the testing of devices. If alternative methods are used, they should be justified.
Table 2.
Design evaluation of mechanical properties for tubular vascular substitutes in accordance with ANSI/ISO 7198:2016.
| Testing method | Mechanical descriptors | Units | Sample geometry | Testing equipment | Procedure |
|---|---|---|---|---|---|
| CTS | Circumferential tensile strength | kN/mm | Tubular | Tensile testing machine with appropriately sized pins and holders over which the sample is placed | Length of the sample not less than the nominal relaxed internal diameter. Place the sample over the two pins; stretch at a steady rate between 50 and 200 mm/min (until the break point) |
| LTS | Longitudinal tensile strength | kN | Tubular | Tensile testing machine with suitable jaws to hold the sample firmly without damaging its structure | Place the ends of the sample in the jaws (initial separation between 50 and 150 mm); stretch at a steady rate between 50 and 200 mm/min (until the break point) |
| DPBSt | Burst strength | kPa | Flat | Bursting pressure tester with a clamping ring; Diaphragm able to extend beyond the failure deflection of the sample at 120 mmHg | Cut the sample longitudinally. Place the sample over the orifice of the baseplate; secure the clamping ring; increase the pressure at a uniform rate between 10 and 70 kPa/s |
| PBST | Pressurized burst pressure | kPa | Tubular | System capable of measuring and recording pressure; Apparatus capable of applying a steadily increasing rate of fluid or gas pressure to the inside of the sample; If applicable, an elastic, non-permeable liner distension apparatus of greater burst pressure than the sample | Feed fluid or gas to produce a steady rise in pressure at a controlled rate between 10 and 70 kPa/s. Measure and record the pressure inside the sample. |
| ProbeBS | Burst Pressure of an area of the sample | kN | Flat | Tensile testing machine capable of operation in the compression mode or fitted with a suitable compression cage; Sample holder with a clamping ring and a traversing probe | Cut the sample longitudinally; place the sample over the orifice of the baseplate; secure the clamping ring; align the baseplate and the probe to be concentric; traverse the probe through the sample at a constant rate of 50–200 mm/min until it bursts |
| DRC | Dynamic radial compliance | %/100 mmHg | Tubular | Machine capable of applying a dynamic pressure to the inside of a sample under constant tension or at a fixed length at 37 °C; pressure and diameter measuring device; If applicable, an elastic, non-permeable liner with diameter at 16 kPa (120 mmHg) greater than the nominal pressurized diameter of the sample | Length of the sample at least 10 times its diameter. Pressurize the sample in a cyclic fashion at a rate of 60 beats/min. To assess non-linear behavior, the tests should be conducted at 50–90 mmHg, 80–120 mmHg, and 110–150 mmHg |
| SRS | Suture retention strength | G | Flat | Tensile testing machine with a sensitive load cell (accuracy of ±5% of the measured value) and appropriate grips; A suture normally used for tubular vascular grafts | Cut the sample longitudinally, or at 45° to the long axis; Insert the suture 2 mm from the end of the stretched sample forming a half loop; pull the suture at the rate of 50 mm/min to 200 mm/min; record the force required to pull the suture and the suture size |
| SRP | Strength after repeated puncture | kPa or kN/mm | Tubular | 16-gauge dialysis needle and a tensile testing instrument or a system capable of applying a steadily increasing rate of fluid or gas pressure to the inside of the sample | Puncture 24 times per cm2 the external surface area of the sample (limited to one-third of the sample circumference); test the sample for PBSt or CTS |
| k | Kink diameter/radius | Mm | Tubular | Templates of known radii1 or cylindrical mandrels of known diameter2 |
1Place the sample in a radius template; decreases the template radius until kinking of the graft and record this radius 2Form a loop out of the test sample and pulls the ends of the sample in opposite direction until kink is observed; Measure and record the kink diameter with the appropriate mandrel |
CTS, circumferential tensile strength; LTS, longitudinal tensile strength; DPBSt, diaphragm pressurized burst strength; PBSt, pressurized burst strength; ProbeBS, probe burst strength; DRC, dynamic radial compliance; SRS, suture retention strength; SRP, strength after repeated puncture; K, kink diameter/radius.
3.2. Conventional mechanical tests in literature
The most common tests in literature for the mechanical characterization of vascular tissues and their substitutes are compression, tensile, tensile stress-relaxation, creep, DMA, burst pressure, and compliance. Table 3 summarizes the possibilities or range for each parameter of these testing methods that have been applied in the field. Following the table, each testing method will be schematically described and exemplified.
Table 3.
Conventional mechanical testing methods for the characterization of blood vessel substitutes, main parameters, manipulated variables, and the responding mechanical properties.
| Testing method | Sample geometry | Test direction | Deformation rate range | Strain/pressure rangea | Mechanical properties | References |
|---|---|---|---|---|---|---|
| Compression | Cylindrical/Ring | Longitudinal | 0.01–0.2 mm/min | YM: 0–30% | SB, EB, YM | [32,33] |
| Rectangular | Radial | [34] | ||||
| Tensile | Rectangular | Longitudinal | 1–50 mm/min | YM: 0–30% | SB, EB, YM | [35,36] |
| Circumferential | ||||||
| Dogbone | Longitudinal | [37,38] | ||||
| Circumferential | ||||||
| Ring | Circumferential | SB, EB YM, BP, C | [[39], [40], [41], [42], [43], [44], [45]] | |||
| Tensile stress-relaxation | Ring | Longitudinal | 1–50 mm/min | YM: 10–70% | SB, EB IEM, EEM BP, C | [46] |
| Circumferential | [41,[46], [47], [48], [49], [50], [51], [52], [53]] | |||||
| Creep | Rectangular | Circumferential | 1.6 mm/s | 30–50% of SB | CP | [54] |
| Ring | [42,50,55] | |||||
| Burst pressure | Tubular | Circumferential | 0.1–100 mL/min | 0 until rupture | BP | [35,[37], [38], [39],[42], [43], [44],55,56] |
| Compliance | Tubular | Circumferential | 4–100 mL/min | 50–180 mmHg | C | [35,38,39,43,49,55,56] |
| DMA | Rectangular | Longitudinal | 0.1–10 Hz | 5–16% | E′, E″, tanδ | [57] |
| Ring | Circumferential | [33,58] |
DMA, dynamic mechanical analysis; SB, strength at break; EB, elongation at break; YM, Young elastic modulus; IEM, initial elastic modulus; EEM, equilibrium elastic modulus; CP, creep profile; BP, burst pressure; C, compliance; E′, storage modulus; E′′, loss modulus; tanδ, damping factor.
Strain/pressure range used for the calculation of the mechanical properties.
3.2.1. Incremental uniaxial loading tests
Compression, tensile, tensile stress-relaxation, and creep tests are used to obtain YM, SB, EB, and creep profiles. The main difference in these methods is related to the application of force or deformation in the sample illustrated in Fig. 4. In most cases, compression and tensile tests consist in applying an incremental strain at a constant rate in opposite directions. Stress-relaxation and creep tests consist in sustaining a specific strain and force, respectively, during a period. The stress or strain response can be then measured. A preconditioning treatment is often applied to the sample before the test composed of some loading cycles. This provides a consistent loading history to the specimens to ensure that they are at a repeatable reference state reducing experimental variability [59]. The incremental uniaxial loading tests and further variations within each one will be presented.
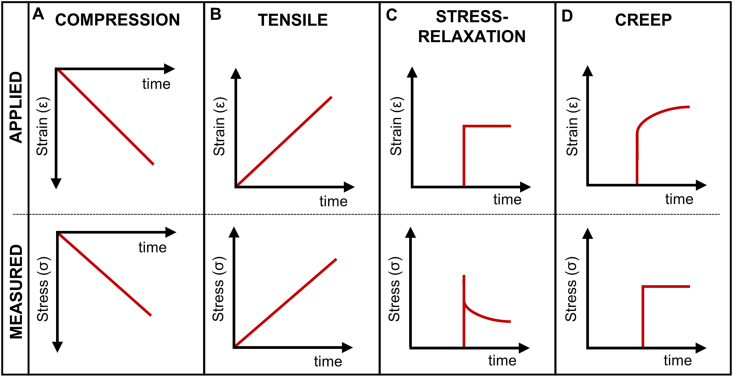
Fig. 4.
Stress and strain curves in function of time for (A) compression, (B) tensile, (C) tensile stress-relaxation, and (D) creep tests. First row represents the applied strain or stress, and the second row represents the corresponding strain or stress response measured.
3.2.1.1. Compression stress-strain testing
In the compression testing, the specimen is placed between two plates where a compressive load is applied by moving one crosshead in direction to the stationary base (Fig. 5A). Rectangular or cylindrical samples have been tested, and the test has been carried out in air or aqueous environment. The deformation of the sample and the applied load is usually recorded. Engineering stress is defined as the force divided by the initial cross-sectional area of the sample (Eq. (1)) and engineering strain as the variation of the distance between the plates per initial distance (Eq. (2)), as follows:
| (1) |
| (2) |
where σ is the stress (Pa), F is the load at a given moment (N), is the initial cross-sectional area, ε is the strain, is the distance between the plates at a given moment, and is the initial distance. The generated data have been used to determine the SB and EB, in the point which a strong decrease in stress is observed and the YM by the slope or linear regression of the stress-strain curve at a specific strain range.
Fig. 5.
Incremental uniaxial loading tests. Compression tests: A) Mach-1 micromechanical tester (Biomomentum Inc.) used for testing cylindrical collagen-based samples in compression [74]. Tensile, stress relaxation, and creep tests: B) Cellularized collagen gels were tested in the longitudinal direction using a tubular specimen attached in cylindrical grips [75]; C) Tensile tester (Instron E-1000) adapted for testing a ring specimen produced by the self-assembled method [60]; D) Carotid artery rings were cut radially and tested circumferentially in tension, initial failure occurred in the media layer followed by the adventitia [76]; E) Cellularized collagen-fibrin hydrogel were radially and longitudinally tested using ring specimens, samples were approximately 5 times stronger in the radial direction [77]; F) Tensile tester (MTS Insight®) coupled with a Laser Speckle extensometer connected to a PC video processor that measures the movement of the sample via two video-cameras. The instrument was used for testing samples from porcine carotid and thoracic arteries [78]. Reproduced from the indicated references with permission from the publishers.
Although relatively simple compared with other tests, variations in the compression testing protocols can be found among studies in literature. Borschel et al. [34] tested rectangular (2 × 2 × 0.15 mm) specimens of acellularized and fresh iliac rat artery at a constant strain rate of 0.01/s to a maximum strain of 0.3. The YM was calculated at the nominal strain of 0.275, where the maximum slope of the stress-strain response was obtained. Liu and Chan-Park [33] performed compression testing in cylindrical dextran and gelatin scaffolds (D = 12 mm, thickness = 3 mm). The elastic modulus was obtained by the slope of the stress-strain curve over the strain range of 0–20%, achieved by a strain rate of 0.1 mm/min. The SB and EB were also reported. Achilli M. and Mantovani [32] tested cylindrical collagen scaffolds (height = 5.5 mm, D = 11 mm) in compression mode at a strain rate of 0.2 mm/s after three cycles of preconditioning (0–2%). The compressive modulus was obtained in the strain range of 15–30%. The authors well stated that the direct comparison of the obtained modulus with other works is not always possible; however, conclusions regarding the different conditions within the work could be made. The compressive strain energy was also calculated by the integral of the curve between 0 and 40% of strain.
3.2.1.2. Tensile stress-strain testing
The tensile stress-strain testing is the most reported method for the mechanical characterization of vascular constructs in literature. However, there is a great variety on how the test is performed (protocols) and how the final values are calculated (data analysis). The test consists in applying a tensile deformation on the sample at a constant strain rate, until failure or until a specific strain value. The first common difference is the sample geometry. Tubular specimens have been open longitudinally, laid flat, and cut with a die cutter in the circumferential and/or longitudinal direction to obtain dogbone-shaped or rectangular samples. They are then mounted on high-friction grips by their extremities in the testing apparatus. There are also ring-shaped samples, and in this case, the experimental setup is adapted with hooks (or pins) to serve as grips (Fig. 5, Fig. 6). Samples have been tested dried or rehydrated or the test is performed directly in a phosphate-buffered saline (PBS) bath, at room temperature or 37 °C. Furthermore, cycles of preconditioning are occasionally applied before the test.
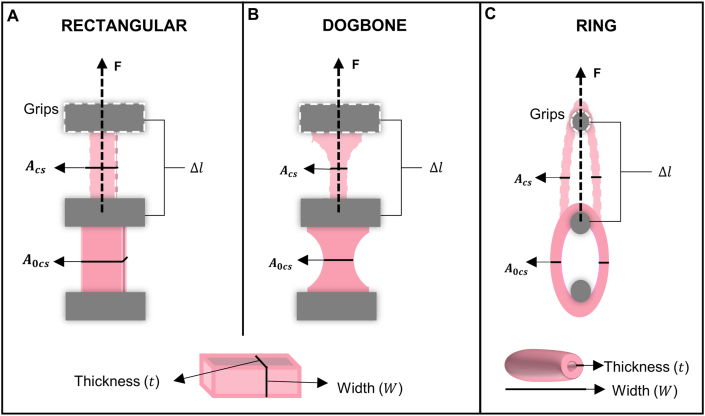
Fig. 6.
Specimen geometries used in tensile mechanical tests: (A) rectangular, (B) dogbone, and (C) ring. The dimensions used in the calculation of engineered or true stress and strain are represented: initial cross-sectional area (A0cs), actual cross-sectional area (Acs), initial distance between the grips (l0) actual distance between the grips (l0).
Force and displacement values are continuously recorded, and engineering stress and strain are obtained using Eq. (1) and Eq. (2), respectively. For ring samples, the initial cross-sectional area perpendicular to the applied force is given by Eq. (3), where W is the sample width and t is the sample thickness. In addition, some authors include the changes in the cross-sectional area during deformation assuming no change in volume to obtain the true stress (Eq. (4)), where λ is defined as the sample length divided to initial length. The elastic modulus is calculated by the slope or the linear regression of the engineering stress or true stress-strain curves at a given strain range. The SB and EB are considered as the maximum engineering or true stress and strain values before failure, respectively.
Compliance measurements have also been obtained for ring-shaped samples using the stress and strain data between a specific range of pressure with their corresponding diameter, which will be better described in Section 3.2.3.2. In addition, the BP has been estimated from the results of ring specimens using Laplace's law (Eq. (5)) which is commonly used in physiology to describe the behavior of thin-walled cavities under pressure. In Eq. (5), F is the load measured at the rupture of the sample, W the sample width, and the internal diameter. For the latter parameter, the unloaded (initial) and the failure diameter is found to be applied. Although challenging to measure, the failure diameter has been reported to lead an accurate estimation of the BP when compared to measurements with the direct method (burst pressure testing, Section 3.2.3.1) [60].
| (3) |
| (4) |
| (5) |
The ISO 7198 proposes the tensile testing in the circumferential and longitudinal directions to obtain the tensile strength. According to the ISO, ring specimens should have the length not less than the nominal relaxed internal diameter and rectangular specimens should have the length of 50–150 mm. In both cases, the specimen should be stretched at a steady rate of 50–200 mm/min. In literature, these parameters often differ from the ISO. Stankus et al. [39] performed the tensile testing on ring samples (4.7 mm diameter and 1–2 mm length) of an elastomeric poly(ester urethane) urea (PEUU) electrospun scaffolds cellularized with SMCs. The samples were preconditioned (5% strain) and deformed at a rate of 10 mm/min until failure. Load-displacement data were recorded, and stress-strain relationships were calculated using Eqs. (1), (2), (3), (4). The elastic modulus was calculated by the slope of stress-strain curves at stretch values corresponding to that recorded during inflations under physiological pulsatile conditions in the compliance tests. Soletti et al. [35] used rectangular strips (2 mm width and 15 mm length) cut from tubular PEUU scaffolds both in the circumferential and longitudinal directions to perform the tensile testing at a rate of 10 mm/min until the rupture after a preconditioning of 20% strain. Stress-strain relationships were obtained based on the assumption of incompressibility (Eq. (4)). Elastic modulus in the circumferential direction was obtained similarly to the previous work. Stoiber et al. [40] tested small-diameter rat aorta rings (0.7 mm diameter and 2 mm length). Specimens were placed on loading pins and continuously deformed at a strain rate of 1.14 mm/min until sample rupture. SB (N) and stiffness (N/m) were obtained. The authors reported the tensile forces instead of true stresses because the determination of the exact wall thickness is challenging for soft tissues and a potential source of errors. Overall, the length of the specimen and the stretch rate are usually lower presumably because of the time-consuming process of sample fabrication and its soft nature, respectively. In addition to that, variations in the preconditioning step and data analysis were exemplified.
3.2.1.3. Tensile stress-relaxation testing
Tensile stress-relaxation testing is a more complete test to describe the mechanical behavior of vascular constructs because it can provide information about the viscoelasticity of the material. As mentioned in Section 2, the vascular tissue exhibits a viscoelastic deformation when undergoing deformation and many vascular substitutes such as tissue-engineered vessels have been developed to reproduce this behavior. In this test, the load is recorded while a tensile deformation is applied and during a period which a fixed value of constraint is maintained. The load measured tends to decrease during the relaxation time due to molecular rearrangement within the construct. In this case, the initial elastic modulus (IEM) corresponds to the response of the construct immediately after the application of the strain and the relaxed (or equilibrium) elastic modulus (EEM) corresponds to the end of the relaxation period. The variability on the sample geometry, direction of the load, and calculations of the stress-strain curves are similar to the tensile testing. Samples have been tested dried or rehydrated or the test is performed directly in a PBS bath, with or without temperature control. Cycles of preconditioning are occasionally applied before the test. In addition, for the calculation of the IEM and EEM, simple linear regressions of stress-strain relationships are found, or the time course of stress can also be compared with mathematical models for viscoelastic materials with the aid of data analysis software such as MATLAB.
The general Maxwell (or Maxwell-Wiechert) model is the most general form of linear viscoelasticity and commonly applied to analyze the stress relaxation response of soft tissues and its components [13,[61], [62], [63], [64], [65]]. The model is composed of one spring in parallel with several spring-dashpot (Maxwell) elements (a spring with modulus Ei and a dashpot with viscosity ƞi in series). The Maxwell elements are used to describe the relaxation process within the construct because it does not occur at a single time but in a set of times due to the presence of different molecular segments. The general Maxwell-Wiechert equation can be represented by Eq. (6) [66].
| (6) |
Stress relaxation tests introduce even more possibilities of variation for data analysis when compared with the compression and tensile testing. Seifu et al. [49] investigated the viscoelastic properties of ring specimens (4.7 mm diameter and 10 mm length) composed of one, two, or three layers of collagen gel cellularized with SMCs. The stress-relation test consisted of incremental steps of 10% strain at 5%/s strain rate and 600 s relaxation until failure. The true (or total) stress represented the combination of the elastic and viscous components of the construct, calculated immediately after each incremental step. The elastic stress was determined for each incremental strain after the equilibrium force was reached (time-independent value). The time-dependent viscous component was calculated by subtracting the elastic stress from the total stress. The viscous and elastic stress-strain curves showed linear regions where the viscous and elastic moduli were respectively obtained using the least square method in the slope of the curves. Berglund et al. [50] applied the stress-relaxation method on ring samples (3 mm diameter and 5 mm length) based on fibroblasts and collagen, which consisted in 6 incremental step displacements of 15% strain for 360 s each. Stress-strain data were fit to a mathematical model for viscoelastic materials composed of an elastic element connected in series with a Voigt unit (a spring with modulus Ei and a dashpot with viscosity ƞi in parallel). The fitting was applied by minimizing the sum of the square of the errors between experimental data and the model prediction using an add-in of Microsoft Excel. The initial and relaxed elastic modulus were obtained. Camasão et al. [51] performed the test to evaluate the viscoelasticity of ring collagen gels (3.8 mm diameter and 5 mm length) cellularized with different SMCs density. The samples were preconditioned with a 5% strain and the test consisted of 5 progressive stress-relaxation cycles each consisting of 10% strain ramps (5%/s strain rate) and 600s of relaxation at constant strain, achieving a final deformation of 55%. The data were adjusted to the Maxwell-Wiechert model with 3 Mx elements using MATLAB to obtain the initial and equilibrium elastic modulus and relaxation time constants.
3.2.1.4. Creep testing
Contrary to the tensile stress-relaxation, the creep test consists in applying a constant load into the specimen that is maintained fixed during a period. The time-dependent change in strain with the fixed load is recorded to obtain the creep profile. The variability on the sample geometry, direction of the load, calculations of the strain curves are similar to the tensile testing. Samples have also been used dried or rehydrated or the test is done directly in a PBS bath, with or without temperature control. Furthermore, cycles of preconditioning are occasionally applied before the test. For soft tissues and delicate samples, the strain is commonly measured with high-definition images taken during the test. Although mathematical models for viscoelastic materials can also be used for fitting experimental data [67], creep profiles (strain vs. time curves) are usually reported and compared within the work.
Data acquisition is a major source of variation for this type of test because it usually relies on measurements from pictures (similar to Fig. 5F) and the results can be mainly compared within the work. Berglund et al. [50] also conducted creep testing on the ring samples (cellularized collagen-based) by applying loading levels equivalent to 33% of the sample SB for 20 min periods. The constructs were stretched at 1.6 mm/s until target stresses were reached. Images series were collected throughout the tests (4 frames/s from 0 to 4 min; 0.2 frames/s from 4 to 20 min) to determine strain as function of time. The creep profiles were compared among the different samples and a native artery. Soffer et al. [42] applied the test on silk-based electrospun tubular scaffolds (3.8 mm diameter and 5 mm length) after three loading and unloading cycles to precondition the material. The samples were stretched to reach 33% of the SB and maintained constant for 10 min. The authors observed that after 10 min the strain rate remained constant and did not increase to indicate any potential material failure. However, the test did not provide conclusive evidence of the long-term creep response, including fatigue and creep. Levesque et al. [55] developed a computer-controlled testing apparatus for the mechanical characterization of tissue-engineered vascular constructs produced by the self-assembly approach. The test initiated with a motor rotation to compress the syringe at a rate of 2 mL/min until the nominal test pressure was reached (200 mmHg). The motor was controlled through a closed loop to maintain this pressure. Images of the construct were taken at a fixed rate and saved as a sequential set of pictures during the test to determine diameter variations as function of time. The diameter variation among the samples was compared.
3.2.2. Cyclic uniaxial loading tests
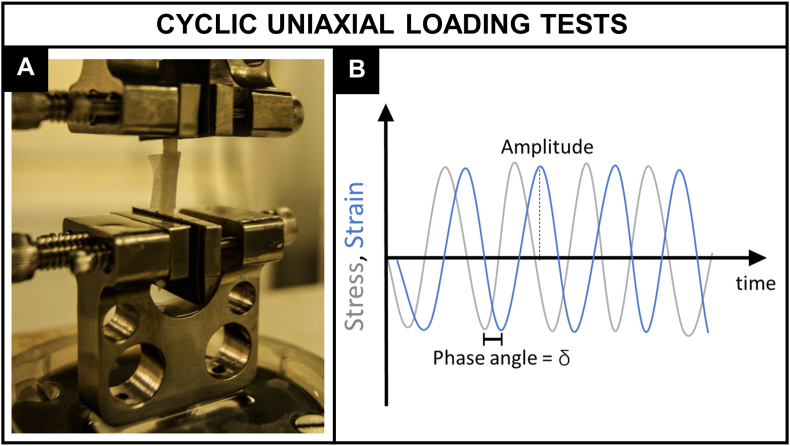
DMA is a powerful technique to evaluate the viscoelastic behavior of polymers as a function of temperature or frequency. Although less often found for the characterization of vascular tissue and substitutes, the method has been becoming more popular lately (Fig. 7A). The technique is very sensitive to the motions of the polymer chains and widely applied for determining its glass transition temperature (Tg) [68]. The instrument consists in a drive motor which generates a dynamic force or displacement that acts on the sample. The sample holder is located inside a furnace allowing the temperature control and/or variation during the test. Force, displacement, and temperature sensors are installed for the measurements. Solid samples can be rectangular or cylindrical shaped. For a stress applied sinusoidally with time at a frequency (Eq. (7)), a viscoelastic material will show a sinusoidal strain response out of phase, by the phase angle (Eq. (8)) illustrated in Fig. 7B. This phase lag is related to the excess time necessary for molecular motions and relaxation and its tangent is referred as the damping factor (tan ).
Fig. 7.
Cyclic uniaxial loading tests. A) Bose ElectroForce 3200 (Bose Corporation) used to perform DMA on left anterior descending coronary arteries. Reproduced from Ref. [79] with permission from Springer Nature. B) Schematic illustration of the cyclic forces applied to a viscoelastic material and the ‘out of phase’ response in terms of deformation.
Using the symbols E′ and E″ for the in-phase (real) and out-of-phase (imaginary) components (Eqs. (9), (10)) respectively), the applied stress can be rewritten as Eq. (11). The storage (E′) modulus describes the ability of a material to store energy and release it on deformation. The loss (E″) modulus refer to the energy dissipated in the form of heat upon deformation. Both moduli are collectively represented as the complex modulus (E∗) of a material, a measure of its resistance to deformation encompassing the elastic and viscous responses (Eq. (14)). The phase angle is given by Eq. (15).
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
The DMA test has less variability in terms of data acquisition and analysis because the mechanical information is mostly generated by the apparatus. One limitation is that the specimen geometry used in this test is normally rectangular and cylindrical hampering the assessment of the mechanical properties in the circumferential direction. To address this issue, Khosravi et al. [57] tested segments of saphenous vein and internal thoracic artery (5–7 cm length) which was transversely cut open with a scalpel and positioned in the equipment at 45° angle to determine the materials properties in the circumferential and axial directions. A sinusoidal dynamic force with a base static force and a peak dynamic force were applied to the specimens under varying frequencies from 1 to 2 Hz. Graphs of storage and loss modulus in function of time and average values of tan were compared. On the other hand, some groups reported that ring specimens were tested suggesting that adaptations in the grips configuration have been done. Nguyen et al. [58] applied the DMA in ring specimens of elastin-containing bilayered collagen scaffolds (3 mm diameter and 4 mm length). Oscillatory time sweeps at a constant strain (8%) and frequency (1 Hz) were applied for a total of six sweeps with five oscillation cycles per sweep. The effect of the elastin incorporation on the cyclic properties of the scaffolds was analyzed by comparing the storage and loss modulus as function of the number of cycles. Liu et al. [33] evaluated the dynamic mechanical properties of tubular gels composed of dextran and gelatin (12 mm diameter). Mechanical spectrometry was applied in ring specimens using dynamic frequency sweep with frequencies ranging from 0.1 Hz to 10 Hz at 37 °C, and with strain amplitude of 5%. The force varied from 0.001 N to 0.2 N and the maximum strain was set at 10%. The storage and loss modulus and tan graphs in function of frequency were compared.
3.2.3. Pressure-based tests
Pressure-based tests for the mechanical characterization of blood vessels and their substitutes resemble the hydrostatic tests used for evaluating the strength and leaks of vessels such as pipelines, plumbing, and gas cylinders. For the latter case, the tests involve the filling of the vessel with a liquid which may contain a dye for leak visualization until a specified pressure level. For vascular applications, pressure-based tests are particularly valuable for reproducing the mechanical forces generated by the blood pressure. They are recommended by the ISO to evaluate the burst pressure and the compliance of tubular substitutes which will be detailed in this section.
3.2.3.1. Burst pressure testing
The burst pressure testing is a direct form of obtaining the burst pressure of tubular constructs and native vessels. Briefly, a saline solution or water is infused at a constant rate inside the tubular sample until the failure occurs. The system (sample and the tubing) must be hermetically sealed, and the pressure is continuously monitored by an inline pressure transducer and recorded in a data acquisition program (Fig. 8A, C, E). There is less variability in terms of sample geometry (tubular), direction of load (circumferential), and external conditions (aqueous environment). On the other hand, depending on the porosity and permeability of the sample, the ANSI/ISO 7198:2016 recommends the use of an elastic, non-permeable sleeve of greater BP to be placed in the lumen of the sample. The samples were also reported to be immersed in a high viscous solution for filling the pores. Diameter of the sample under pressure has been measured by a laser micrometer and pressure vs. diameter curves are obtained and compared within the work.
Fig. 8.
Pressure-based tests. A) Custom-made system for the burst pressure testing of constructs produced by the self-assembly method [60]; B) System used to apply a pulsatile flow (Bose Corporation) for the compliance testing of PLA-PCL tubular constructs [43]; C) Polyurethane-based nanocomposite vascular prosthesis coupled in a high-pressure syringe pump (Harvard apparatus PHD 2000 Programmable) and a pressure transducer for the burst pressure testing [80]; D) Bioreactor system with a laser scanning and pressure transducer used for the compliance testing of cellularized collagen gels [49]; E) Burst strength device used for testing tubular constructs made of Tecoflex®, point of burst showed in the right [81]; F) Elastingraft composed of elastin-like recombinamers in a bioreactor system for assessing compliance [82]. Reproduced from the indicated references with permission from the publishers.
The major variability of pressure-based test relies on the ad hoc testing systems. Drilling et al. [37] evaluated the burst pressure of tubular electrospun PCL scaffolds. An angioplasty balloon with the same diameter was inserted into the scaffolds and filled with water at a rate of 20 mL/min. The scaffold was allowed to lengthen freely until burst occurred. The balloon + scaffold diameter was measured using a laser micrometer and the pressure was recorded with a transducer during the filling. The burst pressure was defined as the highest pressure reached before failure. McKenna et al. [38] used this method to calculate the burst pressure of an electrospun scaffold of human recombinant tropoelastin. The samples were rehydrated in PBS and a saline solution at a rate of 100 mL/min was inserted in its lumen until failure. The samples were previously loaded with high-viscosity freezing medium to clog the pores avoiding transluminal flow for a more accurate reading. The pressure in mmHg was continuously monitored. Laterreur et al. [60] used this direct method to assess the BP of tissue engineered vascular constructs produced by the self-assembly method. A custom-made system composed of a syringe coupled to a pump activated by a stepper motor was used to fill the sample with PBS. The sample was cannulated at both ends by silk sutures to prevent leakages and the tip of the syringe was connected to one cannula. The constructs were pressurized, and the applied pressure and external diameter were continuously recorded until the failure of the sample. After bursting, the longitudinal failure rather than failure at the sutures was checked to validate the test.
3.2.3.2. Dynamic compliance testing
The compliance of tubular samples has been investigated with a similar procedure as for the burst pressure by using a perfusion system that provides a circulation of a saline solution or water in the lumen of the tubular sample. Briefly, a centrifugal pump within a closed perfusion loop connected to a testing chamber produce a sinusoidal pulsatile pressure with the flow consistent with physiological values (Fig. 8B, D, F). There are also less variations with respect to sample geometry (tubular), the direction of load (circumferential), and external environment (aqueous). The external diameter has been measured with a laser micrometer. The compliance (C) has been determined by the following equation:
| (16) |
where is the internal diameter corresponding to the higher-pressure value, is the internal diameter corresponding to the lower pressure value, and the difference between the higher and lower pressure. The internal diameter has been estimated on the assumption of incompressibility from the cross-sectional area (A) of the scaffold previously measured and the external diameter () by Eq. (17). Similarly to the burst pressure testing, the ANSI/ISO 7198:2016 recommends the use of an elastic, non-permeable sleeve of greater BP to be placed in the lumen of the sample if needed.
| (17) |
The ISO recommends pressurizing the sample in a cyclic fashion at a rate of 60 beats/min (1 Hz) and in three pressure ranges (50–90 mmHg, 80–120 mmHg, and 110–150 mmHg) to assess the non-linearity. Shen et al. [69] compared the radial compliance of three kinds of vascular prostheses (PET knitted, PET woven, and expanded PTFE) and a porcine carotid artery. A highly deformable latex tube was used to prevent leakage at high pressures. Sinusoidal wave form was applied in a commercial dynamic-simulated system at a frequency of 1 Hz. Four pressure phase groups (50–90 mmHg, 80–120 mmHg, 110–150 mmHg and 140–180 mmHg) were selected to calculate the compliance as per Eq. (16). Li et al. [43] developed a composite vascular substitute combining PLA knitted fabric with soft PCL and measured its dynamic compliance. A commercial pulsatile flow system was filled with deionized water with a flow rate of 100 mL/min and 1 Hz. The pulsatile intraluminal pressure was set at three different levels (50–90 mmHg, 80–120 mmHg, and 110–150 mmHg) to evaluate the construct performance at a low, medium, and high pressure. The compliance was calculated using Eq. (16). Soletti et al. [35] tested tubular PEUU scaffolds in a vascular perfusion system with a slightly different procedure. The circuit was filled with a saline solution at 37 °C and a physiological arterial pulsatile intraluminal pressure (120/80 mmHg) and flow (100 mL/min) were applied. Two pressure transducers were placed equidistant upstream and downstream of the vessel center and the average of them was considered the intraluminal pressure. The values of pressure and diameter were recorded at 30 Hz for 1 min every hour over one day. The compliance was finally obtained through Eq. (16).
4. Critical summary
4.1. Mechanical assessment of vascular substitutes: ISO, literature, and variations
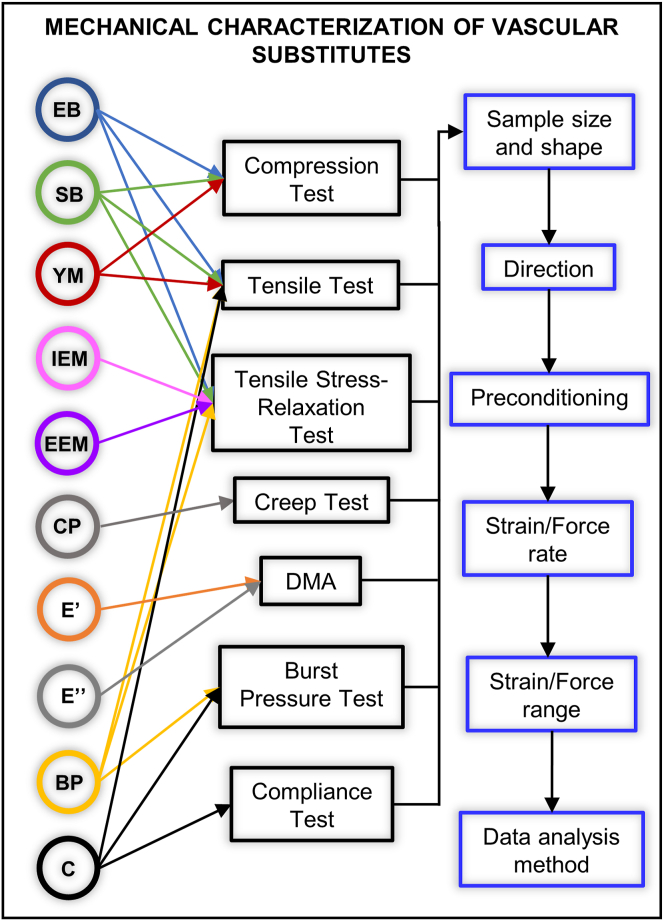
Although the international standard discussed in Section 3.1 provides relevant mechanical testing methods in which potential vascular substitutes would be subjected to evaluation, it also states that modifications or additional tests can be necessary due to the different nature of the constructs. Possible causes for the large variability in the methods and protocols reported in literature include but are not limited to the real necessity to adapt the ISO methods, the lack of knowledge of the ISOs for vascular substitutes and the familiarity with other protocols for synthetic polymers or metallic materials. Fig. 9 summarizes the main mechanical properties reported in literature (colored circles), the different mechanical tests in which they are obtained (black rectangles) and the variable parameters of their protocols (blue rectangles). Variations within a testing method include the custom-made apparatus itself, the grips configuration, the geometry (rectangular, dogbone-shaped, rings) and cut of the specimen, the direction (longitudinal, radial, circumferential) and rate of the applied load or deformation, the preconditioning, the strain or pressure range, and the data analysis.
Fig. 9.
Main mechanical properties reported in literature for vascular substitutes (colored circles), the corresponding mechanical testing methods in which they can be obtained (black rectangles), and the main variable parameters of their protocols (blue rectangle). In each blue rectangle (right), two or more options are available as detailed in section 3. EB, elongation at break; SB, strength at break; YM, Young elastic modulus; IEM, initial elastic modulus; EEM, equilibrium elastic modulus; CP, creep profile; E′, storage modulus; E′′, loss modulus; BP, burst pressure; C, compliance.
As per Fig. 9, the first obstacle when comparing the mechanical properties of vessel substitutes in literature is that they can be obtained by different tests. For e.g. Young's modulus can be obtained by compression or tensile test, and the mechanical response of a polymeric material is often different under these types of load. The burst pressure can be estimated from Laplace's law using the tensile test or directly measured with the BP testing, which influences the value obtained [60]. Therefore, the direct comparison of the same mechanical property obtained by different tests should be avoided or carefully analyzed. Furthermore, at least three possibilities or range of each parameter are found within each test. This can be exemplified in Table 4, which contains the mechanical properties of vascular substitutes reported in some of the references mentioned in Section 3 (one condition per study) and the parameters applied in their test with as much information available.
Table 4.
Examples of mechanical properties and testing parameters reported on blood vessel substitutes studies.
| Testing method | Sample type, geometry | Preconditioning | Deformation rate | Data analysis methoda | Elastic modulus (MPa) | SB or BP | EB | C (%/100 mmHg) | Ref |
|---|---|---|---|---|---|---|---|---|---|
| 1. Natural biomaterials | |||||||||
| CS | Collagen gel, cylindrical | Three cycles: 0–2% strain | 0.2 mm/s | 15–30% strain, linear regression | 0.010 | – | – | – | [32] |
| T | Square-section toroidal | 0.040 | 0.005 MPa | – | – | ||||
| T | Collagen gel, ring | Ten cycles: 0–5% strain at 1%/s | 5%/s | Slope of stress-strain linear region curve before break | IEM: 0.043 EEM: 0.012 |
– | – | – | [41] |
| SR | 1 step of 10% strain, 2.5 min relax. | Viscoelastic mathematical models | 0.046 | – | – | – | |||
| T | Collagen gel with SMCs, ring | Three cycles: 0–20% of EB | 0.2 mm/s | 10–20% strain, slope | 0.142 | 0.058 MPa | ~50% | [45] | |
| T | Collagen gel with FBs, ring | Three cycles: 0–20% of EB | 0.2 mm/s | 25–75% of the SB, best fit regression | 0.018 | 0.0053 MPa | – | – | [50] |
| SR | – | 6 steps of 15% EB, 6 min relax. | Viscoelastic mathematical models | IEM: 0.0097 EEM: 0.00166 |
– | – | – | ||
| SR | Collagen gel with SMCs, ring | Stretched to a preload of 30 mN | 5%/s, 6 steps of 10% strain, 10 min relax. | Slope (least-square method) of the stress-strain curve linear region | IEM: 0.030 EEM: 0.012 |
– | – | – | [49] |
| C | Tubular | – | 20 mL/min, 20–120 mmHg, 1 Hz | Eq. (16) | – | – | – | 19 | |
| SR | Collagen gel and recombinant elastin with FBs, ring | Stretched to 5% strain | 5%/s | 25% strain, viscoelastic mathematical models | IEM: 0.056 EEM: 0.024 |
0.026 | 70% | – | [52] |
| T | Electrospun recombinant elastin, dogbone | – | 2 mm/s | 10–30%, linear regression | 0.15 (long) 0.15 (circ) |
0.38 MPa (long) 0.34 MPa (circ) |
75% (long) 79% (circ) |
20.2 | [38] |
| BP | Tubular | – | 100 mL/min | Burst point | – | 485 mmHg | – | – | |
| CS | Dextran and gelatin gel, cylindrical | – | 0.1 mm/min | 0–20% strain, slope | 0.051 | 0.031 | 47% | – | [33] |
| DMA | ring | – | 5% strain amplitude, 0.1–10 Hz | – | E′: 0.040 E′′: 0.004 |
– | – | – | |
| T | Electrospun silk, ring | – | Three incremental cycles at 0.2 mm/s | 25–75% of the yield stress | 2.45 | 2.42 MPa | – | – | [42] |
| BP | Tubular | – | Burst point | – | 811 mmHg | – | – | ||
| BP | Self-assembled construct, tubular | – | 4 mL/min, 80–120 mmHg | Burst point | – | 1075 mmHg | – | – | [55] |
| C | – | Eq. (16) | – | – | – | 4.6 | |||
| 2. Synthetic biomaterials | |||||||||
| T | PEUU scaffold, rectangular | 10 cycles: 0–20% strain | 10 mm/min | Strain level at physiological pressure | 1.8 (long) 1.4 (circ) |
21.1 MPa (long) 8.3 MPa (circ) |
5.6 (long) 5.3 (circ) |
– | [35] |
| BP | Tubular | – | 100 mL/min | Burst point | – | 2300 mmHg | – | ||
| C | 100 mL/min, 80–120 mmHg | Eq. (16) | – | – | – | 4.6 | |||
| T | Electrospun PEUU | – | 10 mm/min | – | 2.5 | 8.5 MPa | 280% | – | [36] |
| T | PLA/PCL tube, tubular and ring | Pretension of 0.5 N | 50 mm/min | 0–5%, slope | 59.6 (long) 46.4 (circ) |
21.3 MPa (long) 11.8 MPa (circ) |
28.0% (long) 212.6% (circ) |
– | [43] |
| BP | Rectangular | Preload of 0.1 N | Burst point | – | 37 038 mmHg | – | – | ||
| C | Tubular | – | 100 mL/min, 1 Hz, (50–90, 80–120, 110–150) mmHg | Eq. (16) | – | – | – | 1.70 | |
| T | Electrospun PCL, dogbone | – | 5 mm/min | 0–10% strain | 3.49 (long) 3.95 (tang) |
1.25 MPa (long) 1.63 MPa (tang) |
– | – | [37] |
| BP | Tubular | 20 mL/min | Burst point | – | 500–1800 mmHg | – | – | ||
| T | Electrospun PCL, tubular | – | 10 mm/min | – | – | 4.1 MPa | 1092% | – | [44] |
| BP | – | 0.1 mL/min | Burst point | – | 3280 mmHg | – | – | ||
| BP | Electrospun PCL, tubular | – | According to ISO 7198 | Burst point | – | 684 mmHg | – | – | [56] |
| C | – | 80–120 mmHg | – | – | – | 5.3 | |||
CS, compression testing; T, tensile testing; SR, tensile stress relaxation testing; IEM, initial elastic modulus; EEM, equilibrium elastic modulus; ES–TIPS, electrospinning–thermally induced phase separation; tang, tangential; SMCs, smooth muscle cells.
Data analysis method includes the strain range used and the method for calculation of the mechanical properties.
The first section of Table 4 shows constructs based on natural biomaterials, whereas the second section contains synthetic substitutes. Owing to the inherent features of these types of biomaterials, it is expected a lower mechanical strength for natural-based constructs than synthetic substitutes. However, even within the sections, the values can vary from one to three orders of magnitude. This variation is predominantly related to the material used, sample preparation and maturation time, but the different testing parameters can also contribute to this discrepancy. The lack of a standard procedure for the preconditioning of the samples may not ensure a steady-state response of the materials prior to experimentation. The behavior of these biomaterials significantly changes depending on the direction of the applied load or deformation with respect to the orientation direction of the polymeric chains. For e.g. Li et al. [43] reported an elongation at break of 28.0% in the longitudinal direction and 212.6% in the circumferential direction for the same PLA/PCL composite vascular graft. Similarly, the mechanical properties vary with the rate of loading or deformation. Elastic modulus and SB increase with the increasing strain rate, and this can be accompanied by a decrease in the EB. Low strain rates favor the viscous or energy-damping aspects of material behavior [70]. Finally, the data analysis method is an additional source of result variation.
The testing parameters affect the final results, and their effects should be considered if a comparison is made. The last obstacle relies on the fact that not all parameters are always specified, and they are not expressed in an easy comparable manner. For e.g. the strain rate in Table 4 is expressed as percentage (5%/s) or absolute values (0.2 mm/s). The strain/stress range at which the elastic modulus was obtained is expressed as strain percentage, or percentage of EB, or percentage of the yield stress. Overall, the several testing methods, the different possibilities of their parameters, and the lack of consistency in their reporting prevent a direct comparison of the mechanical properties in literature which can interfere in the development of promising vascular substitutes. A simple way to prevent misinterpretation and facilitate comparison is to clearly specify the test type and all the parameters applied (in percentage and absolute values when applicable) in the study and in the work of comparison (when present).
Another important point is that elastic modulus, SB, BP, or EB alone are not the most suitable indicators of the mechanical performance of the substitute in the physiological environment. These properties can be used to select superior conditions within a project at early stages of development; however, as far as progress has been done, a more profound mechanical analysis should be applied. The ISO itself recognizes that a group of tests is necessary to mechanically evaluate vascular conduits before they are approved for market entry. A group of complementary tests applied at the level of research and development with a critical analysis is also valuable for generating successful substitutes. The next section will summarize the physiological pertinent features of the conventional tests to present in the last session a strategic plan for the mechanical characterization of vascular substitutes.
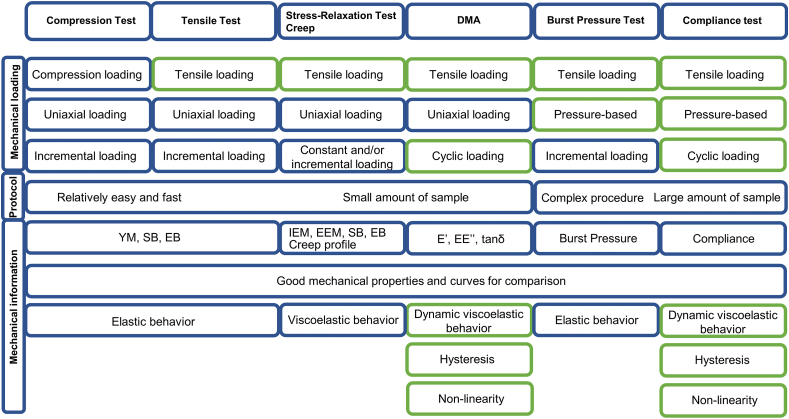
4.2. Conventional mechanical testing of vascular substitutes: strengths, weakness, and physiological pertinence
Fig. 10 summarizes the conventional testing methods in the perspective of vascular applications. The incremental uniaxial loading tests (compression, tensile, tensile stress-relaxation, and creep) are the most popular in literature specially because they have been largely used in materials science research. Their main advantages rely on the relative simplicity of their protocols, and the low amount of sample required for the test. The compression test is the farthest to reproduce the mechanical environment of blood vessels since physiological loads are rather tensile. The tensile test is recommended for obtaining YM, SB, and EB, but they do not provide information about the viscoelastic properties of the specimen. Blood vessels, most polymers, and TEV respond to the applied force in two ways: with a viscous response that decreases during time by dissipating the mechanical energy through internal motion (time-dependent response) and an elastic response important for the partial recovery of the mechanical energy (time-independent response). In this light, stress-relaxation and creep tests can provide a more complete characterization of the construct by evaluating its mechanical response in function of time. The IEM and the EEM can be extracted from the generated curves which show the contribution of the viscous and the elastic attributes to the mechanical behavior, respectively. A balance between these two features is important for the propagation of the blood flow into all tissues. Furthermore, the creep test can give important information about whether the material tends to move or deform permanently under the long-term exposure to stress which is particularly valuable for the long-term patency of a vascular substitute. In sum, these tests can be used to determine the mentioned mechanical properties at specific conditions, but they cannot be directly used to predict the performance of a vascular substitute in the hemodynamic environment.
Fig. 10.
Summary of the conventional mechanical tests used in the characterization of blood vessels and their substitutes in terms of nature of the applied load (compression vs. tensile, uniaxial vs. pressure-based, constant vs. incremental vs. cyclic), complexity of the method and the mechanical information obtained by them. The green rectangles correspond to the mechanical aspects that are physiologically pertinent for vascular substitutes.
The mechanical behavior of a vascular substitute should match the one of the vascular tissue during the whole period of vessel wall distension and recoil and not just at a specific time point of this process. In this regard, the cyclic uniaxial loading test (DMA) goes a step further toward reproducing the physiological environment because sinusoidal cycles of deformation can be applied at a physiologic frequency (1 Hz) and temperature (37 °C). The technique is very sensitive to the motions of the protein chains under conditions of low mechanical force which is valuable for analyzing the viscoelasticity of the construct in a more physiological range of strain when compared with stress relaxation and creep tests. Another strong advantage is that the instrument directly generates the graphs of E′, E″, and tan with time eliminating the variations in data processing. One limitation of the technique so far relies on the sample geometry (rectangular or cylindrical).
The tests that most match the hemodynamic forces acting on blood vessels are the pressure-based tests because they reproduce the radial forces applied in the entire inner surface of the vessel due to the pressure. The value of burst pressure and compliance obtained in this case is likely to be closer to the physiological one when compared with the estimations of the previous testing methods. Furthermore, dynamic compliance is a measure of the storage capacity of blood vessels and represent their buffering action to convert the pulsatile flow at the level of the aorta to continuous flow in the capillaries; thus it is a pertinent parameter to evaluate the quality of a vascular substitute. The latter test also allows assessing the non-linearity and hysteresis phenomena by the analysis of the inflation and deflation curves. The current limitations of these tests include the non-standard protocols and the custom-made apparatus imparting extra variation in the results. In addition, the need for a long specimen reduces the use of pressure-based tests in the field.
4.3. Recommendations for mechanical testing
The conventional mechanical tests for the in vitro characterization of blood vessels and their substitutes do not always reproduce the physiological forces generated by the blood pressure and flow as shown in Fig. 2. This is mainly because most of the mechanical testing was adapted from other applications. In any case, they are important for a simple and fast mechanical comparison among the conditions within the study and with respect to the native tissue. Furthermore, most of the conventional tests can be performed using a reduced volume of specimen which is an important aspect in the field considering the laborious preparation of the samples. As summarized in Fig. 10, compliance and burst pressure tests assemble more physiological features, but they are also the more complex procedures.
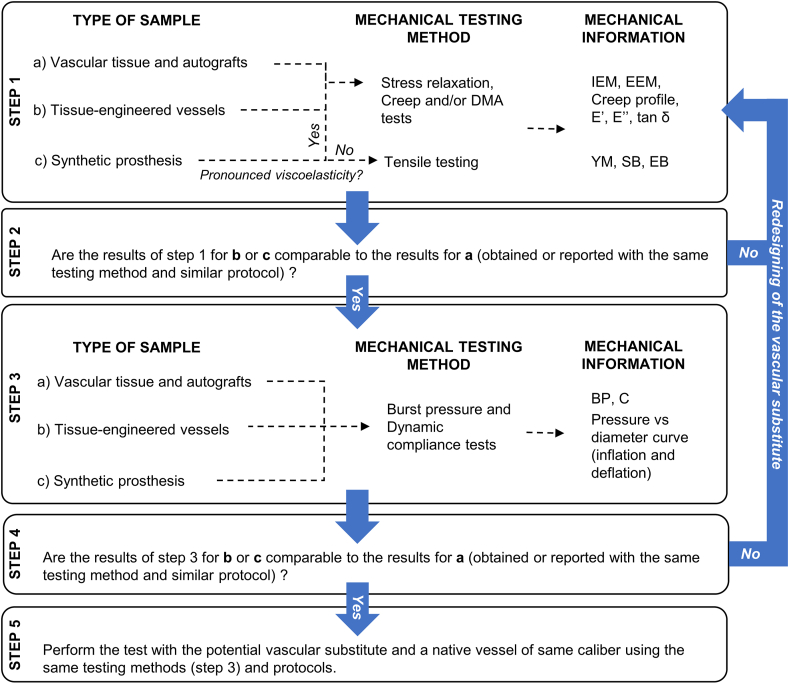
In this light, Fig. 11 proposes a strategic plan for assessing the mechanical properties of vascular substitutes considering the strengths of each method and the specimen in question. At early stages of the substitute development, incremental and cyclic uniaxial loading tests can be applied for the initial assessment of their mechanical properties (step 1). The lower amount of sample required and the relatively simplicity and availability of these tests can accelerate the detection of superior conditions within a study. For e.g. if the YM obtained is much higher than 100 MPa or the EB is much lower than 50%, the construct will probably not show a suitable performance under physiological levels of mechanical loading. The redesigning of the substitute can then be considered (step 2). Pressure-based tests are recommended to be applied once step 2 is succeeded. The later tests are important to evaluate the mechanical performance of the substitutes in a more physiological condition (step 3). The redesigning of the substitute can also be done if the mechanical response differs significantly from the physiological behavior (step 4). Once step 4 is succeeded, it is recommended to apply the same pressure-based tests (same protocol and parameters) in a native vessel of a similar caliber with respect to the potential vascular substitute. The redesigning of the substitute can also be envisaged to fine-tune its mechanical performance.
Fig. 11.
Strategic plan for the mechanical characterization of potential vascular substitutes. At early stages of the substitute development, incremental and cyclic uniaxial loading tests can be applied for the initial assessment of the mechanical properties because they require lower amount of sample and they have a relatively simple protocol (step 1). The redesigning of the substitute can be considered if the mechanical information obtained are orders of magnitude different from the physiological values (step 2). Pressure-based tests are recommended to be applied once step 2 is succeeded. The latter tests are important to evaluate the mechanical performance of the substitutes in a more physiological condition (step 3). The redesigning of the substitute can also be done if the mechanical response differs significantly from the physiological behavior (step 4). Once step 4 is succeeded, it is recommended to apply the same pressure-based tests (same protocol and parameters) in a native vessel of a similar caliber with respect to the potential vascular substitute. The redesigning of the substitute can also be envisaged to fine tune its mechanical performance.
As much as possible, the testing protocols should follow the recommendations of the ISO summarized in Table 2 (Section 3.1) and tested in both directions (longitudinal and circumferential). Section 3.2 can be used to guide the application of the test and to understand all the involved parameters and data analysis. Sections 2, 4 can assist in the interpretation of the results by the researcher in the perspective of the desirable behavior for a vascular application. These sections can also guide the (re)designing of the construct aiming the improvement of its mechanical properties. Overall, this review recommends to progressively apply the more complex procedures along with the development of the vascular substitute. At later stages, pressure-based tests should be performed before in vivo studies to evaluate its performance under more physiological loading conditions. The continuous quest for a vascular substitute with superior mechanical performance may just be hindered by the lack of a physiological-relevant analysis of their mechanical properties.
5. Conclusions
Intensive efforts have been devoted by research groups worldwide to overcome the limitations of AG and commercial SP, especially for small diameter vessels. The large number of different materials and fabrication techniques investigated to develop a vascular substitute can explain the need for particular modifications in their characterization techniques. This review attempted to provide a comprehensive overview and a critical analysis of the conventional mechanical tests and protocols applied in blood vessels and their substitutes with their main variations. Considering their expressive variability, the conventional mechanical characterization can be efficient to compare the different conditions within a study but less reliable among the research groups. To improve this issue, the recommendations of the ISO 7198:2016 should be followed as much as possible and all the testing parameters should be rigorously specified when reporting the results. Concerning the mechanical information obtained by the conventional tests, the common mechanical properties reported (such as strength at break, strain at break, and elastic modulus) are important parameters, but they offer a limited mechanical description for the intended application. For these reasons, a strategic plan for their mechanical characterization was proposed considering the type of specimen and the development stage of the vascular substitute. Incremental and cyclic uniaxial loading tests (compression, tensile, tensile stress-relaxation, creep, and DMA) should be applied at early stages for a faster screen of superior conditions within a study because they are relatively simple and require a low amount of sample. Pressure-based tests (burst pressure and compliance) could be applied in more advanced substitutes to simulate the physiological forces and evaluate its mechanical response in this condition. In addition to BP and C, inflation and deflation curves can be obtained to evaluate the non-linearity and hysteresis phenomena which are important mechanical features of blood vessels. Promising tubular constructs closely mimicking the structural and compositional properties of vascular tissues have been already developed and a consistent and profound mechanical evaluation is one key element to assist in their evolution toward an ideal vascular substitute.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this article.
Acknowledgments
This work was partially supported by the Natural Sciences and Engineering Research Council of Canada (NSERC), the NSERC Create Program in Regenerative Medicine, the Canadian Foundation for the Innovation, and the Fonds de Recherche du Québec (Nature et Technologies, and Santé). The authors would like to acknowledge Bernard Drouin for his valuable help and guidance.
References
- 1.Herman I. second ed. Springer Science & Business Media; Switzerland: 2016. Physics of the Human Body. [Google Scholar]
- 2.Mathers C.D., Loncar D. Projections of global mortality and burden of disease from 2002 to 2030. PLoS Med. 2006;3:e442. doi: 10.1371/journal.pmed.0030442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Melly L., Torregrossa G., Lee T., Jansens J.-L., Puskas J.D. Fifty years of coronary artery bypass grafting. J. Thorac. Dis. 2018;10:1960. doi: 10.21037/jtd.2018.02.43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Spadaccio C., Nappi F., Al-Attar N., Sutherland F.W., Acar C., Nenna A., Trombetta M., Chello M., Rainer A. Old myths, new concerns: the long-term effects of ascending aorta replacement with dacron grafts. Not all that glitters is gold. J. Cardiovasc. Transl. Res. 2016;9:334–342. doi: 10.1007/s12265-016-9699-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Vaquero F., Claral A. 2006. Tratado de las enfermedades vasculares, Madrid, Viguera; pp. 855–864. [Google Scholar]
- 6.Guevara-Noriega K.A., Martinez-Toiran A., Alvarez-Concejo B., Pomar J.L. Historical overview of vascular allografts transplantation. Vasc. Endovasc. Rev. 2019;2:19–22. doi: 10.15420/ver.2018.15.1. [DOI] [Google Scholar]
- 7.Seifu D.G., Purnama A., Mequanint K., Mantovani D. Small-diameter vascular tissue engineering. Nat. Rev. Cardiol. 2013;10:410–421. doi: 10.1038/nrcardio.2013.77. [DOI] [PubMed] [Google Scholar]
- 8.Kannan R.Y., Salacinski H.J., Butler P.E., Hamilton G., Seifalian A.M. Current status of prosthetic bypass grafts: a review. J. Biomed. Mater. Res. Part B. 2005;74B:570–581. doi: 10.1002/jbm.b.30247. [DOI] [PubMed] [Google Scholar]
- 9.Desai M., Seifalian A.M., Hamilton G. Role of prosthetic conduits in coronary artery bypass grafting. Eur. J. Cardio. Thorac. Surg. 2011;40:394–398. doi: 10.1016/j.ejcts.2010.11.050. [DOI] [PubMed] [Google Scholar]
- 10.Cleary M.A., Geiger E., Grady C., Best C., Naito Y., Breuer C. Vascular tissue engineering: the next generation. Trends Mol. Med. 2012;18:394–404. doi: 10.1016/j.molmed.2012.04.013. [DOI] [PubMed] [Google Scholar]
- 11.Pashneh-Tala S., MacNeil S., Claeyssens F. The tissue-engineered vascular graft—past, present, and future. Tissue Eng. B Rev. 2016;22:68–100. doi: 10.1089/ten.teb.2015.0100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Singh C., Wong C.S., Wang X. Medical textiles as vascular implants and their success to mimic natural arteries. J. Funct. Biomater. 2015;6:500–525. doi: 10.3390/jfb6030500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Fung Y.-c. second ed. Springer Science & Business Media; New York: 2013. Biomechanics: Mechanical Properties of Living Tissues. [Google Scholar]
- 14.Hoskins P.R., Lawford P.V., Doyle B.J. Springer; Switzerland: 2017. Cardiovascular Biomechanics. [Google Scholar]
- 15.Wagenseil J.E., Mecham R.P. Vascular extracellular matrix and arterial mechanics. Physiol. Rev. 2009;89:957–989. doi: 10.1152/physrev.00041.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Lee R.T., Kamm R.D. Vascular mechanics for the cardiologist. J. Am. Coll. Cardiol. 1994;23:1289–1295. doi: 10.1016/0735-1097(94)90369-7. [DOI] [PubMed] [Google Scholar]
- 17.Thubrikar M.J. Springer; New York: 2007. Vascular Mechanics and Pathology. [Google Scholar]
- 18.Zhou J., Fung Y. The degree of nonlinearity and anisotropy of blood vessel elasticity. Proc. Natl. Acad. Sci. Unit. States Am. 1997;94:14255–14260. doi: 10.1073/pnas.94.26.14255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Fratzl P. Springer; Collagen: 2008. Collagen: Structure and Mechanics, an Introduction; pp. 1–13. [Google Scholar]
- 20.Shadwick R.E. Elasticity in Arteries: a similar combination of rubbery and stiff materials creates common mechanical properties in blood vessels of vertebrates and some invertebrates. Am. Sci. 1998;86:535–541. https://www.jstor.org/stable/i27857121 URL: [Google Scholar]
- 21.Ethier C.R., Simmons C.A. Cambridge University Press; New York: 2007. Introductory Biomechanics: from Cells to Organisms. [Google Scholar]
- 22.Glasser S.P., Arnett D.K., McVeigh G.E., Finkelstein S.M., Bank A.J., Morgan D.J., Cohn J.N. Vascular compliance and cardiovascular disease: a risk factor or a marker? Am. J. Hypertens. 1997;10:1175–1189. doi: 10.1016/S0895-7061(97)00311-7. [DOI] [PubMed] [Google Scholar]
- 23.Muiznieks L.D., Keeley F.W. Molecular assembly and mechanical properties of the extracellular matrix: a fibrous protein perspective. Biochim. Biophys. Acta (BBA) - Mol. Basis Dis. 2013;1832:866–875. doi: 10.1016/j.bbadis.2012.11.022. [DOI] [PubMed] [Google Scholar]
- 24.Hasan A., Memic A., Annabi N., Hossain M., Paul A., Dokmeci M.R., Dehghani F., Khademhosseini A. Electrospun scaffolds for tissue engineering of vascular grafts. Acta Biomater. 2014;10:11–25. doi: 10.1016/j.actbio.2013.08.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hasegawa M., Azuma T. Mechanical properties of synthetic arterial grafts. J. Biomech. 1979;12:509–517. doi: 10.1016/0021-9290(79)90039-3. [DOI] [PubMed] [Google Scholar]
- 26.Walden R., Gilbert J., Megerman J., Abbott W.M. Matched elastic properties and successful arterial grafting. Arch. Surg. 1980;115:1166–1169. doi: 10.1001/archsurg.1980.01380100018004. [DOI] [PubMed] [Google Scholar]
- 27.Stekelenburg M., Rutten M.C., Snoeckx L.H., Baaijens F.P. Dynamic straining combined with fibrin gel cell seeding improves strength of tissue-engineered small-diameter vascular grafts. Tissue Eng. 2009;15:1081–1089. doi: 10.1089/ten.tea.2008.0183. [DOI] [PubMed] [Google Scholar]
- 28.Konig G., McAllister T.N., Dusserre N., Garrido S.A., Iyican C., Marini A., Fiorillo A., Avila H., Wystrychowski W., Zagalski K. Mechanical properties of completely autologous human tissue engineered blood vessels compared to human saphenous vein and mammary artery. Biomaterials. 2009;30:1542–1550. doi: 10.1016/j.biomaterials.2008.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Salacinski H.J., Goldner S., Giudiceandrea A., Hamilton G., Seifalian A.M., Edwards A., Carson R.J. The mechanical behavior of vascular grafts: a review. J. Biomater. Appl. 2001;15:241–278. doi: 10.1106/NA5T-J57A-JTDD-FD04. [DOI] [PubMed] [Google Scholar]
- 30.Campbell C., Brooks D., Webster M., Diamond D., Peel R., Bahnson H. Expanded microporous polytetrafluoroethylene as a vascular substitute: a two year follow-up. Surgery. 1979;85:177–183. doi: 10.5555/uri:pii:0039606079903015. [DOI] [PubMed] [Google Scholar]
- 31.Cardiovascular Implants and Extracorporeal Systems – Vascular Prostheses – Tubular Vascular Grafts and Vascular Patches. ANSI/ISO 7198; 2016. [Google Scholar]
- 32.Achilli M., Mantovani D. Tailoring mechanical properties of collagen-based scaffolds for vascular tissue engineering: the effects of pH, temperature and ionic strength on gelation. Polymers. 2010;2:664–680. doi: 10.3390/polym2040664. [DOI] [Google Scholar]
- 33.Liu Y., Chan-Park M.B. Hydrogel based on interpenetrating polymer networks of dextran and gelatin for vascular tissue engineering. Biomaterials. 2009;30:196–207. doi: 10.1016/j.biomaterials.2008.09.041. [DOI] [PubMed] [Google Scholar]
- 34.Borschel G.H., Huang Y.-C., Calve S., Arruda E.M., Lynch J.B., Dow D.E., Kuzon W.M., Dennis R.G., Brown D.L. Tissue engineering of recellularized small-diameter vascular grafts. Tissue Eng. 2005;11:778–786. doi: 10.1089/ten.2005.11.778. [DOI] [PubMed] [Google Scholar]
- 35.Soletti L., Hong Y., Guan J., Stankus J.J., El-Kurdi M.S., Wagner W.R., Vorp D.A. A bilayered elastomeric scaffold for tissue engineering of small diameter vascular grafts. Acta Biomater. 2010;6:110–122. doi: 10.1016/j.actbio.2009.06.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Stankus J.J., Guan J., Fujimoto K., Wagner W.R. Microintegrating smooth muscle cells into a biodegradable, elastomeric fiber matrix. Biomaterials. 2006;27:735–744. doi: 10.1016/j.biomaterials.2005.06.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Drilling S., Gaumer J., Lannutti J. Fabrication of burst pressure competent vascular grafts via electrospinning: effects of microstructure. J. Biomed. Mater. Res. A. 2009;88A:923–934. doi: 10.1002/jbm.a.31926. [DOI] [PubMed] [Google Scholar]
- 38.McKenna K.A., Hinds M.T., Sarao R.C., Wu P.-C., Maslen C.L., Glanville R.W., Babcock D., Gregory K.W. Mechanical property characterization of electrospun recombinant human tropoelastin for vascular graft biomaterials. Acta Biomater. 2012;8:225–233. doi: 10.1016/j.actbio.2011.08.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Stankus J.J., Soletti L., Fujimoto K., Hong Y., Vorp D.A., Wagner W.R. Fabrication of cell microintegrated blood vessel constructs through electrohydrodynamic atomization. Biomaterials. 2007;28:2738–2746. doi: 10.1016/j.biomaterials.2007.02.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Stoiber M., Messner B., Grasl C., Gschlad V., Bergmeister H., Bernhard D., Schima H. A method for mechanical characterization of small blood vessels and vascular grafts. Exp. Mech. 2015;55:1591–1595. doi: 10.1007/s11340-015-0053-x. [DOI] [Google Scholar]
- 41.Meghezi S., Couet F., Chevallier P., Mantovani D. Effects of a pseudophysiological environment on the elastic and viscoelastic properties of collagen gels. Int. J. Biomater. 2012;2012 doi: 10.1155/2012/319290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Soffer L., Wang X., Zhang X., Kluge J., Dorfmann L., Kaplan D.L., Leisk G. Silk-based electrospun tubular scaffolds for tissue-engineered vascular grafts. J. Biomater. Sci. Polym. Ed. 2008;19:653–664. doi: 10.1163/156856208784089607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Li C., Wang F., Douglas G., Zhang Z., Guidoin R., Wang L. Comprehensive mechanical characterization of PLA fabric combined with PCL to form a composite structure vascular graft. J. Mech. Behav. Biomed. Mater. 2017;69:39–49. doi: 10.1016/j.jmbbm.2016.11.005. [DOI] [PubMed] [Google Scholar]
- 44.de Valence S., Tille J.-C., Mugnai D., Mrowczynski W., Gurny R., Möller M., Walpoth B.H. Long term performance of polycaprolactone vascular grafts in a rat abdominal aorta replacement model. Biomaterials. 2012;33:38–47. doi: 10.1016/j.biomaterials.2011.09.024. [DOI] [PubMed] [Google Scholar]
- 45.Seliktar D., Black R.A., Vito R.P., Nerem R.M. Dynamic mechanical conditioning of collagen-gel blood vessel constructs induces remodeling in vitro. Ann. Biomed. Eng. 2000;28:351–362. doi: 10.1114/1.275. [DOI] [PubMed] [Google Scholar]
- 46.Rios J.L.J., Steif P.S., Rabin Y. Stress-strain measurements and viscoelastic response of blood vessels cryopreserved by vitrification. Ann. Biomed. Eng. 2007;35:2077–2086. doi: 10.1007/s10439-007-9372-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Bono N., Meghezi S., Soncini M., Piola M., Mantovani D., Fiore G.B. A dual-mode bioreactor system for tissue engineered vascular models. Ann. Biomed. Eng. 2017;45:1496–1510. doi: 10.1007/s10439-017-1813-9. [DOI] [PubMed] [Google Scholar]
- 48.Loy C., Pezzoli D., Candiani G., Mantovani D. A cost-effective culture system for the in vitro assembly, maturation, and stimulation of advanced multilayered multiculture tubular tissue models. Biotechnol. J. 2018;13:1700359. doi: 10.1002/biot.201700359. [DOI] [PubMed] [Google Scholar]
- 49.Seifu D.G., Meghezi S., Unsworth L., Mequanint K., Mantovani D. Viscoelastic properties of multi-layered cellularized vascular tissues fabricated from collagen gel. J. Mech. Behav. Biomed. Mater. 2018;80:155–163. doi: 10.1016/j.jmbbm.2018.01.021. [DOI] [PubMed] [Google Scholar]
- 50.Berglund J.D., Nerem R.M., Sambanis A. Viscoelastic testing methodologies for tissue engineered blood vessels. J. Biomech. Eng. 2005;127:1176–1184. doi: 10.1115/1.2073487. [DOI] [PubMed] [Google Scholar]
- 51.Camasão D.B., Pezzoli D., Loy C., Kumra H., Levesque L., Reinhardt D.P., Candiani G., Mantovani D. Increasing cell seeding density improves elastin expression and mechanical properties in collagen gel-based scaffolds cellularized with smooth muscle cells. Biotechnol. J. 2018;14:1700768. doi: 10.1002/biot.201700768. [DOI] [PubMed] [Google Scholar]
- 52.Camasão D.B., Pérez M.G., Palladino S., Alonso M., Rodriguez-Cabello J.C., Mantovani D. Elastin-like recombinamers in collagen-based tubular gels improve cell-mediated remodeling and viscoelastic properties. Biomater. Sci. 2020;8(12):3536–3548. doi: 10.1039/d0bm00292e. [DOI] [PubMed] [Google Scholar]
- 53.Bombaldi de Souza F.C., Camasão D.B., Bombaldi de Souza R.F., Drouin B., Mantovani D., Moraes Â.M. A simple and effective approach to produce tubular polysaccharide-based hydrogel scaffolds. J. Appl. Polym. Sci. 2020;137:48510. doi: 10.1002/app.48510. [DOI] [Google Scholar]
- 54.Song Y., Kamphuis M., Zhang Z., Sterk L.T., Vermes I., Poot A., Feijen J., Grijpma D. Flexible and elastic porous poly (trimethylene carbonate) structures for use in vascular tissue engineering. Acta Biomater. 2010;6:1269–1277. doi: 10.1016/j.actbio.2009.10.002. [DOI] [PubMed] [Google Scholar]
- 55.Levesque P., Gauvin R., Larouche D., Auger F.A., Germain L. A computer-controlled apparatus for the characterization of mechanical and viscoelastic properties of tissue-engineered vascular constructs. Cardiovasc. Eng. Technol. 2011;2:24–34. doi: 10.1007/s13239-011-0033-y. [DOI] [Google Scholar]
- 56.Madhavan K., Elliott W.H., Bonani W., Monnet E., Tan W. Mechanical and biocompatible characterizations of a readily available multilayer vascular graft. J. Biomed. Mater. Res. B Appl. Biomater. 2013;101:506–519. doi: 10.1002/jbm.b.32851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Khosravi A., Bani M.S., Bahreinizad H., Karimi A. Viscoelastic properties of the autologous bypass grafts: a comparative study among the small saphenous vein and internal thoracic artery. Artery Res. 2017;19:65–71. doi: 10.1016/j.artres.2017.06.007. [DOI] [Google Scholar]
- 58.Nguyen T.-U., Shojaee M., Bashur C.A., Kishore V. Electrochemical fabrication of a biomimetic elastin-containing bi-layered scaffold for vascular tissue engineering. Biofabrication. 2018;11 doi: 10.1088/1758-5090/aaeab0. [DOI] [PubMed] [Google Scholar]
- 59.Nava A., Mazza E., Haefner O., Bajka M. Springer; 2004. International Symposium on Medical Simulation; pp. 1–8. [Google Scholar]
- 60.Laterreur V., Ruel J., Auger F.A., Vallières K., Tremblay C., Lacroix D., Tondreau M., Bourget J.-M., Germain L. Comparison of the direct burst pressure and the ring tensile test methods for mechanical characterization of tissue-engineered vascular substitutes. J. Mech. Behav. Biomed. Mater. 2014;34:253–263. doi: 10.1016/j.jmbbm.2014.02.017. [DOI] [PubMed] [Google Scholar]
- 61.Shen Z.L., Kahn H., Ballarini R., Eppell S.J. Viscoelastic properties of isolated collagen fibrils. Biophys. J. 2011;100:3008–3015. doi: 10.1016/j.bpj.2011.04.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Wagenseil J.E., Wakatsuki T., Okamoto R.J., Zahalak G.I., Elson E.L. One-dimensional viscoelastic behavior of fibroblast populated collagen matrices. J. Biomech. Eng. 2003;125:719–725. doi: 10.1115/1.1614818. https://doi-org.acces.bibl.ulaval.ca/10.1115/1.1614818 [DOI] [PubMed] [Google Scholar]
- 63.Holzapfel G.A., Gasser T.C., Stadler M. A structural model for the viscoelastic behavior of arterial walls: continuum formulation and finite element analysis. Eur. J. Mech. Solid. 2002;21:441–463. doi: 10.1016/S0997-7538(01)01206-2. [DOI] [Google Scholar]
- 64.Gupta H., Seto J., Krauss S., Boesecke P., Screen H. In situ multi-level analysis of viscoelastic deformation mechanisms in tendon collagen. J. Struct. Biol. 2010;169:183–191. doi: 10.1016/j.jsb.2009.10.002. [DOI] [PubMed] [Google Scholar]
- 65.Haslach H.W. Nonlinear viscoelastic, thermodynamically consistent, models for biological soft tissue. Biomech. Model. Mechanobiol. 2005;3:172–189. doi: 10.1007/s10237-004-0055-6. [DOI] [PubMed] [Google Scholar]
- 66.Roylance D. Department of Materials Science and Engineering–Massachusetts Institute of Technology; Cambridge MA 2139: 2001. Engineering Viscoelasticity; pp. 1–37. [Google Scholar]
- 67.Brown E.E., Laborie M.-P.G., Zhang J. Glutaraldehyde treatment of bacterial cellulose/fibrin composites: impact on morphology, tensile and viscoelastic properties. Cellulose. 2012;19:127–137. doi: 10.1007/s10570-011-9617-9. [DOI] [Google Scholar]
- 68.Menard K.P., Menard N. Theory and Instrumentation; 2006. Dynamic Mechanical Analysis, Encyclopedia of Analytical Chemistry: Applications; pp. 1–25. [DOI] [Google Scholar]
- 69.Shen G., Lin J., Zhang H., Wang L. Springer; 2013. World Congress on Medical Physics and Biomedical Engineering May 26-31, 2012, Beijing, China; pp. 176–179. [Google Scholar]
- 70.Cheng J.K., Wagenseil J.E. Extracellular matrix and the mechanics of large artery development. Biomech. Model. Mechanobiol. 2012;11:1169–1186. doi: 10.1007/s10237-012-0405-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Morin C., Krasny W., Avril S. 2019. Multiscale Mechanical Behavior of Large Arteries. arXiv preprint arXiv:1912.06052. [DOI] [Google Scholar]
- 72.Ushiki T. Collagen fibers, reticular fibers and elastic fibers. A comprehensive understanding from a morphological viewpoint. Arch. Histol. Cytol. 2002;65:109–126. doi: 10.1679/aohc.65.109. [DOI] [PubMed] [Google Scholar]
- 73.Ratz P.H. Mechanics of vascular smooth muscle. Compr. Physiol. 2011;6:111–168. doi: 10.1002/cphy.c140072. [DOI] [PubMed] [Google Scholar]
- 74.Meghezi S., Drouin B., Mantovani D. Elsevier; 2017. Collagen Hydrogel-Based Scaffolds for Vascular Tissue Regeneration: Mechanical and Viscoelastic Characterization, Characterization of Polymeric Biomaterials; pp. 397–439. [Google Scholar]
- 75.Meghezi S., Seifu D.G., Bono N., Unsworth L., Mequanint K., Mantovani D. Engineering 3D cellularized collagen gels for vascular tissue regeneration. JoVE (J. Visual. Exp.) 2015 doi: 10.3791/52812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Teng Z., Tang D., Zheng J., Woodard P.K., Hoffman A.H. An experimental study on the ultimate strength of the adventitia and media of human atherosclerotic carotid arteries in circumferential and axial directions. J. Biomech. 2009;42:2535–2539. doi: 10.1016/j.jbiomech.2009.07.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Patel B., Xu Z., Pinnock C.B., Kabbani L.S., Lam M.T. Self-assembled collagen-fibrin hydrogel reinforces tissue engineered adventitia vessels seeded with human fibroblasts. Sci. Rep. 2018;8:1–13. doi: 10.1038/s41598-018-21681-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Chirita M., Ionescu C. On Biomimetics; 2011. Models of Biomimetic Tissues for Vascular Grafts; p. 43. [Google Scholar]
- 79.Burton H.E., Freij J.M., Espino D.M. Dynamic viscoelasticity and surface properties of porcine left anterior descending coronary arteries. Cardiovasc. Eng. Technol. 2017;8:41–56. doi: 10.1007/s13239-016-0288-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Sarkar S., Hillery C., Seifalian A., Hamilton G. Critical parameter of burst pressure measurement in development of bypass grafts is highly dependent on methodology used. J. Vasc. Surg. 2006;44:846–852. doi: 10.1016/j.jvs.2006.07.023. [DOI] [PubMed] [Google Scholar]
- 81.Castillo-Cruz O., Pérez-Aranda C., Gamboa F., Cauich-Rodríguez J., Mantovani D., Avilés F. Prediction of circumferential compliance and burst strength of polymeric vascular grafts. J. Mech. Behav. Biomed. Mater. 2018;79:332–340. doi: 10.1016/j.jmbbm.2017.12.031. [DOI] [PubMed] [Google Scholar]
- 82.Fernández-Colino A., Wolf F., Rütten S., Schmitz-Rode T., Rodríguez-Cabello J.C., Jockenhoevel S., Mela P. Small caliber compliant vascular grafts based on elastin-like recombinamers for in situ tissue engineering. Front. Bioeng. Biotechnol. 2019;7:340. doi: 10.3389/fbioe.2019.00340. [DOI] [PMC free article] [PubMed] [Google Scholar]