The genetic architecture of variation in the sexually selected sword ornament and its evolution in hybrid populations

Summary

Biologists since Darwin have been fascinated by the evolution of sexually selected ornaments, particularly those that reduce viability. Uncovering the genetic architecture of these traits is key to understanding how they evolve and are maintained. Here, we investigate the genetic architecture and evolutionary loss of a sexually selected ornament, the “sword” fin extension that characterizes many species of swordtail fish (Xiphophorus). Using sworded and swordless sister species of Xiphophorus, we generated a mapping population and show that the sword ornament is polygenic – with ancestry across the genome explaining substantial variation in the trait. After accounting for the impacts of genome-wide ancestry, we identify one major effect QTL that explains ~5% of the overall variation in the trait. Using a series of approaches, we narrow this large QTL interval to several likely candidate genes, including genes involved in fin regeneration and growth. Furthermore, we find evidence of selection on ancestry at one of these candidates in four natural hybrid populations, consistent with selection against the sword in these populations.

eTOC blurb

The sword ornament is a sexually selected trait that evolved in Xiphophorus fish and has fascinated biologists since Darwin. Several Xiphophorus species have lost the sword, allowing Powell et al. to identify regions of the genome that underlie variation in this trait and characterize selection on one such region in hybrid populations.

Introduction

The diversity generated by sexual selection poses an evolutionary puzzle. Why are courtship traits so different from one species to the next? Theoretical models suggest that much of the answer may hinge on the genetic architecture underlying sexual communication (1,2). With the genomic revolution, we have made massive progress in understanding the genetic architecture of complex traits, particularly in humans. On the whole, this research has revealed that many traits, even those formerly assumed to have a simple genetic basis (3), are in fact highly polygenic, with hundreds to thousands of sites contributing to trait variation (4).

By contrast, we know far less about the genetic architecture of adaptive traits like sexual signals that arise over evolutionary timescales. Previous work has hinted at a simpler genetic basis for adaptive traits (5–7), including traits under sexual selection (8–10), however it is often challenging to disentangle variation in genetic architecture from variation in power to map traits of interest (11). Moreover, statistical challenges like the winner’s curse (12) make it difficult to interpret the distribution of effect sizes in such studies.

Here, we investigate the genetic architecture and trace the evolutionary history of variation in a well-studied sexually-selected trait in swordtail fish (Xiphophorus). The sword is a male-specific ornament generated by an elongation of the lower caudal fin rays (Figure 1A-E). The sword ornament likely evolved in the last 3–5 million years (13,14) as a result of preexisting female mating preferences for the trait (15,16). However, contemporary species vary widely in their expression of the ornament. The length of the sword ranges from complete absence to swords exceeding male body length (Figure 1A-D; (17). In turn, female preference for swords varies across species, from strong preference to antipathy towards swords (16,18), but is also impacted by social learning (19–21). How the sword is predicted to evolve in response to female preferences depends in part on its underlying genetic architecture (2,22).

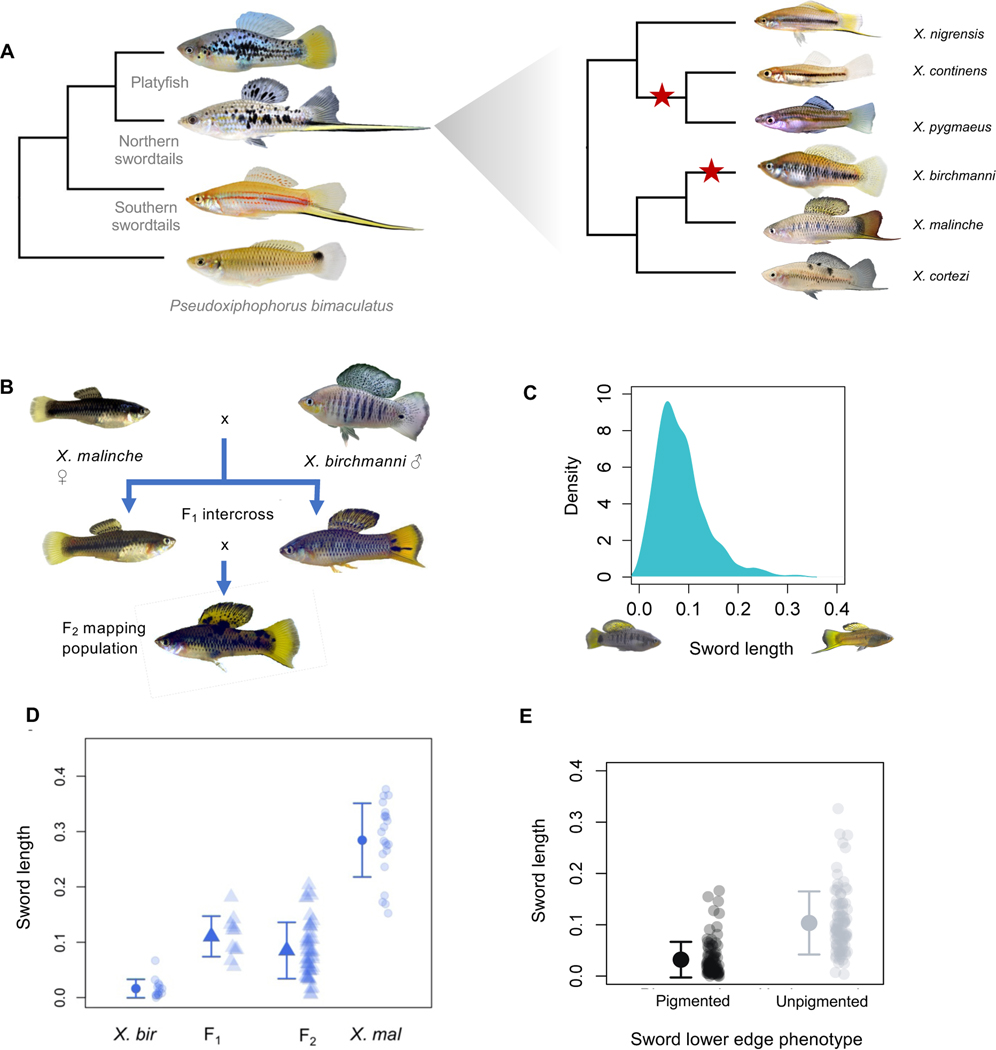
Figure 1. Evolutionary history of the sword, observed phenotypic patterns, and study design.

A. Left - Phylogenetic relationships between platyfish, northern swordtails, and southern swordtails. The sword ornament was lost in the common ancestor of all platyfish. Right - Phylogenetic relationships among northern swordtails highlights at least two losses of the sword within this clade (red stars). B. Cross design used in this study involved crosses between X. malinche females and X. birchmanni males, followed by intercrosses between F₁ hybrids (Figure S1-S2). C. Distribution of normalized sword length in individuals within the hybrid mapping population. Photographs on the x-axis show an example of a hybrid individual with a normalized sword length of zero and an example of a hybrid individual with a normalized sword length of 0.35. D. Distribution of normalized sword length phenotypes in F₁ and F₂ hybrids between X. birchmanni and X. malinche and within each of these species. These distributions allow us to estimate broad sense heritability for sword length (see also Figure S3). E. In addition to sword length, F₂ hybrids differ in their sword pigmentation phenotype (Figure S2). The sword is a composite phenotype that includes a pigmented edge. Sword length is not strongly correlated with the presence of the lower edge pigmentation, suggesting a more complex genetic basis of the composite trait than indicated by analyses of sword length.

The complete loss of the sword in some Xiphophorus species affords the opportunity to characterize the regions of the genome underlying the presence or absence of this sexually selected trait. In Xiphophorus birchmanni, males lack swords and females show a strong preference for swordless males (23). The absence of the sword in X. birchmanni is due to a recent loss of the trait, sometime after it diverged from its sister lineage, X. malinche, approximately 200,000 generations ago (or 100,000 years assuming two generations per year; (14,24). In X. malinche, males have a pronounced sword ornament, but females paradoxically appear to prefer X. birchmanni visual phenotypes (20).

Like several pairs of species in the genus, X. birchmanni and X. malinche naturally hybridize (25,26). Natural and artificial hybrid males vary in their sword phenotype, from swordless to swords as long as those of X. malinche (Figure 1B-D). Given the importance of this trait in sexual selection theory, we sought to identify regions of the genome associated with the variation in the sword and understand their evolutionary history.

Results

Estimating the heritability of sword length in hybrids

Due to the fixed differences in sword phenotype between X. birchmanni and X. malinche and variable sword length in hybrids (Figure 1D; mean sword length to body length ratio birchmanni = 0.016, malinche = 0.28), we knew that the sword was heritable. However, we wanted to quantify how much of the variation in sword length in hybrids could be attributed to genetic factors when individuals were raised in controlled conditions. To do so, we took advantage of a quantitative genetics based method for inferring the broad sense heritability of sword length by comparing phenotypic variance in F₁ hybrids, where all individuals are genetically identical with respect to ancestry, to phenotypic variance in F₂ hybrids (27) Figure 1D). We note that this approach assumes that all phenotypic variance in the parental species is due to environmental effects (see STAR Methods section Estimates of heritability). This approach resulted in an estimate of 0.48 for broad sense heritability of sword length.

Mapping the genetic basis of the sword phenotype

Although we have access to naturally occurring hybrids (28), we focused our mapping on artificial hybrids reared in common conditions (Materials & Methods), given that rearing condition can affect sword length (29). We phenotyped 536 adult male F₂ hybrids and collected low-coverage whole-genome sequence data (~0.2X coverage; Materials & Methods). Using a pipeline we previously developed (30), we inferred local ancestry of each individual along the 24 swordtail chromosomes using a hidden Markov model (Figure S1A). Although average coverage is lower than appropriate for variant calling, such data can be used with high accuracy to infer ancestry. Past work has demonstrated that this reference-panel based approach has extremely high accuracy for early generation hybrids where ancestry tracts are long (31,32). Consistent with previous work, our simulations indicated that we expect this approach to have high accuracy given our cross design (Figure S1B; see STAR Methods section Local ancestry inference).

We thinned our initial dataset of 623,053 ancestry informative sites by physical distance to retain one marker per 50 kb for mapping. Ancestry linkage disequilibrium in lab-generated swordtail hybrids extends over several megabases. This resulted in 12,794 markers that were approximately evenly distributed along the genome (95% quantile of inter-marker distance, 60 kb; 98% of markers present in all individuals). Using the scanone function in R/qtl (33), we recovered one significant QTL for sword length on chromosome 13 at the 16.7 Mb position (LOD score = 5.54; 1.5 LOD interval = 13.3–17.3 Mb; Figure 2A). As expected, individuals that harbored X. malinche ancestry in this region of chromosome 13 had longer swords on average, and the effects of the QTL appear to be additive (Figure 2B). Bootstrapping and joint analysis with another study allowed us to narrow this interval to 1.2 Mb (34).

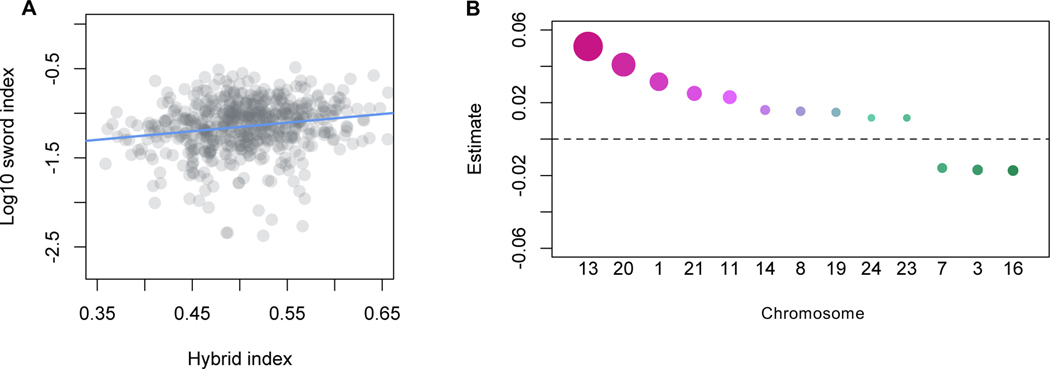
Figure 2. Chromosome 13 contains a major effect QTL that contributes to sword length.

A. Manhattan plot of QTL mapping results for sword length reveals a single genome-wide significant QTL (see also Figure S4). Red line indicates the genome-wide significant threshold determined by permutation; LOD – logarithm of odds. B. Sword length as a function of ancestry at the QTL peak. Small semi-transparent points show the raw data and large points and whiskers show the mean ± two standard errors of the mean. BB (red) - homozygous X. birchmanni, MB (light blue) - heterozygous, MM (dark blue) - homozygous X. malinche. C. Posterior distribution of ABC simulations to estimate the proportion of phenotypic variance explained by the sword length QTL on chromosome 13. The red line indicates the maximum a posteriori estimate of 0.055. This analysis indicates that the chromosome 13 QTL explains a substantial proportion of the heritable variation in sword length (~11%) but suggests the presence of other QTL underlying the sword (see Figure S3 for examination of heritability assumptions). D. MUMmer alignment of chromosome 13. This alignment, generated from the X. birchmanni and X. malinche de novo assemblies, indicates that there are no structural rearrangements between species in the QTL region. The approximate location of the QTL region is indicated by the gray box. Red dots indicate co-linear alignments, blue dots indicate inverted alignments.

Estimated effect sizes from QTL mapping studies are often inflated in cases where the experiment has low statistical power (12). Aware of such issues, we used an approximate Bayesian computation (ABC) approach to estimate the range of effect sizes for the chromosome 13 QTL consistent with our data (see STAR Methods section Effect size of the chromosome 13 QTL and expected power). Based on this analysis, we estimate that X. malinche ancestry at the QTL peak on chromosome 13 explains 5.5% of the total variation in sword length (Figure 2C; 95% confidence intervals: 1–22%) or approximately 11% of the heritable variation. We found that the QTL region was syntenic between X. birchmanni and X. malinche, with no evidence for inversions, insertions, or deletions between the species (Figure 2D).

Despite finding only a single significant genome-wide association with the sword, multiple lines of evidence indicate that the genetic architecture of the sword is more complex. Genome-wide ancestry is associated with sword length (Spearman’s ρ = 0.2, p<4×10⁻⁶), and as expected individuals with a greater proportion of their genome derived from X. malinche tended to have longer swords (Figure 3A). This association remains even after accounting for an individual’s ancestry within the QTL region of chromosome 13, indicating that it is not driven by the contribution of the QTL region to genome-wide ancestry variation (Spearman’s ρ = 0.18, p<4×10⁻⁵; Figure 3A).

Figure 3. Evidence for polygenic basis of the sword ornament.

A. Sword length is associated with genome-wide ancestry. Sword length is associated with genome-wide ancestry in early generation hybrids between X. birchmanni and X. malinche (Spearman’s ρ = 0.2, p<4×10⁻⁶). The correlation between sword length and genome-wide ancestry remains even after accounting for ancestry on chromosome 13 (Spearman’s ρ = 0.18, p<4×10⁻⁵). B. Estimated effect sizes of ancestry on each chromosome using a model selection approach to select the minimal set of chromosomes that explain sword length. Point size corresponds to the -Log₁₀ of the p-value, such that more significant associations are represented as large points. Points are colored such that warmer colors represent more positive associations with X. malinche ancestry. See also Figure S4.

We next asked whether overall ancestry on particular chromosomes explained more of the variance in sword phenotype than ancestry on chromosome 13 or genome-wide ancestry (STAR Methods). Based on a regression approach analyzing correlations between chromosome level ancestry and sword length, we found that X. malinche ancestry on chromosomes 1, 11, 20 and 21 (the putative sex chromosome) was significantly associated with variation in sword length, and together with chromosome 13 explained an estimated 27% of the heritable variation in the trait. We did not find a significant correlation between chromosome length and estimated effect size (R=−0.09, p=0.66). After accounting for ancestry on chromosomes 1, 11, 13, 20 and 21, X. malinche ancestry elsewhere in the genome was no longer significantly predictive of sword length in a partial correlation analysis. However, an AIC-based model selection approach retained thirteen chromosomes (54% of the genome) in the final model describing sword length as a function of chromosome level ancestry (Figure 3B). QTL analysis including chromosome-level ancestry of each of the thirteen chromosomes retained in the AIC model as covariates yielded similar results (peak on chromosome 13 at 16.7 Mb; peak LOD score = 7.1). Surprisingly, although X. malinche ancestry was positively associated with sword length in most cases, X. birchmanni ancestry on three chromosomes was positively associated with sword length (Figure 3B). Although these results suggest a lower bound for the number of regions underlying the sword phenotype, given our modest sample size of F₂ hybrids the true number of causal loci could be much larger.

Moreover, in addition to the genetic architecture of sword length, the sword itself is a composite trait (35). The sword phenotype found in natural populations of Xiphophorus includes both the fin extension and a pigmented upper and lower margin (Figure 1A,E). We found that these traits can become decoupled in hybrids (Figure S2A). Although sword length and upper sword edge are strongly correlated in hybrids (R=0.48, p<10⁻³²), we detected a weaker correlation between the presence of the lower sword edge and sword length in hybrids (R= 0.19, p<10⁻⁵), even though both traits are always observed in X. malinche (see STAR Methods section QTL analysis). Mapping attempts for the lower sword edge were unsuccessful. Specifically, no significant QTL peaks were identified, genome-wide ancestry was not strongly correlated with lower sword edge presence (R=0.05, p=0.25), and only ancestry on chromosome 11 was significantly associated with the lower sword edge (general linear model t=2.4, p=0.02).

Substitution, expression, and chromatin accessibility data are consistent with several candidate genes within the chromosome 13 QTL

The sword normally develops during the course of sexual maturation in X. malinche and hybrid males. To evaluate evidence for possible candidates associated with sword length within the QTL region, we took advantage of the fact that adult male X. malinche will regenerate a complete sword if the sword tissue is amputated (Figure S2B; see STAR Methods section Sword regeneration experiments). We also found that the sword will regrow in F₁ hybrids, where all individuals have short swords (Figure S2B), but in X. birchmanni we simply observe regrowth of the normal caudal fin.

We reasoned that since the sword phenotype is recovered through the regrowth process (36,37), genes important in patterning and length should be expressed in the early stages of regrowth, and may be differentially expressed between X. birchmanni, X. malinche, and hybrids. Based on our RNA sequencing dataset (see STAR Methods section Differential expression analysis; Data S1A), a large number of genes were differentially expressed between regenerating tissue in X. birchmanni and X. malinche (Figures 4A-B,D and S5). These differentially expressed genes were enriched for gene ontology categories including cell adhesion, cell cycle pathways, extracellular matrix-receptor interactions, and ribosome biogenesis (see STAR Methods section Pathway and functional category enrichment analysis). The first three pathways encompass a substantial number of genes with significant expression differences. Only two KEGG pathways were enriched, both for higher expression in X. birchmanni - ECM-receptor interaction and focal adhesion (FDR adjusted p-value of 0.004 and 0.0002, respectively). Many of the expression differences we observe during regeneration appear to be consistent with evolved changes in expression (i.e. allele-specific expression; see STAR Methods section Allele-specific expression analysis).

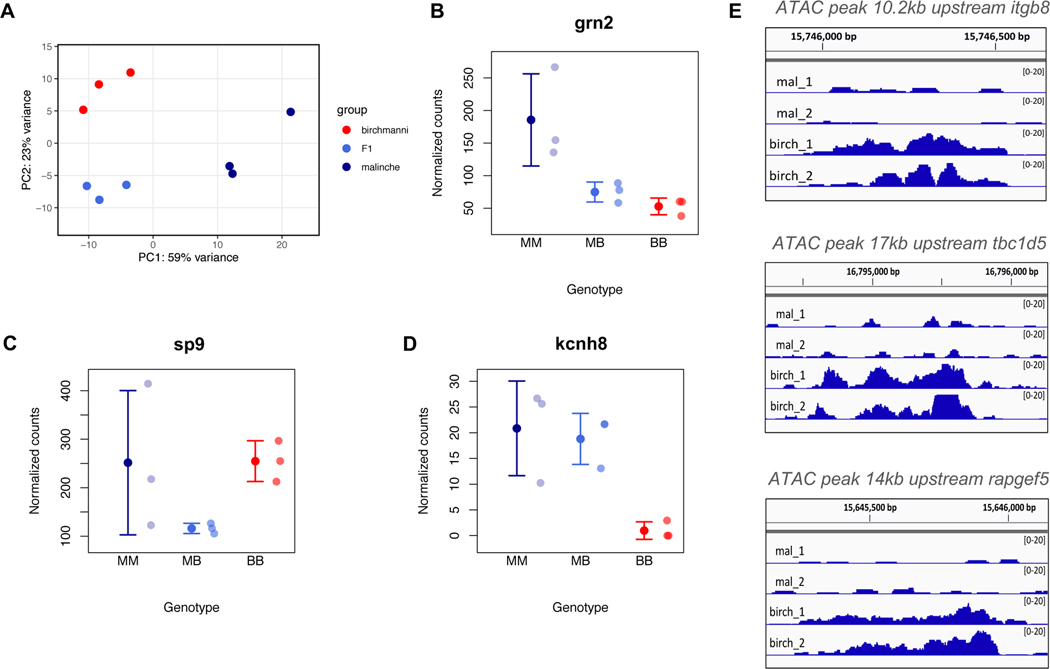
Figure 4. Expression data highlight candidate genes that may contribute to variation in sword length.

A. Principal component analysis of RNAseq data from regenerating caudal fin tissue, which will become sword tissue in X. malinche and F₁s (see also Figure S5). B. Expression patterns of a candidate gene within the QTL region, grn2, that is differentially expressed between X. birchmanni and X. malinche in the regenerating sword and shows expression patterns consistent with predicted phenotypes. We note that grn2 is not differentially expressed between regenerating sword and regenerating non-sword caudal tissue (Figure S6A). BB - X. birchmanni, MB - F₁ hybrids, MM - X. malinche. Small semi-transparent points show the raw data and solid points and whiskers show the mean ± one standard deviation. C. Expression patterns of sp9, a close functional partner of sp8, in regenerating caudal tissue. Semi-transparent points show normalized counts for each individual and solid points and whiskers show the mean ± one standard deviation. Expression in F₁s is significantly lower than either X. birchmanni or X. malinche (p=0.008 and 0.006, respectively), suggestive of expression divergence between species in this pathway. D. Expression of kcnh8 in regenerating caudal tissue in X. malinche, X. birchmanni, and F₁ hybrids. kcnh8 is a gene that falls outside of our QTL interval but was identified as a likely candidate in a companion manuscript by Schartl et al (34). Semi-transparent points show normalized counts for each individual and solid points and whiskers show the mean ± one standard deviation. The log fold change between X. birchmanni and X. malinche for kcnh8 estimated by DESeq2 was 3.54 (p< 1⁻⁴). E. ATAC-seq revealed that regenerating X. birchmanni fin tissue has significantly greater chromatin accessibility in several regions within the chromosome 13 QTL than X. malinche. The closest genes to each differential accessibility peak are noted above each plot. Peak images adapted from Integrative Genomics Viewer (39).

Although there is evidence from ancestry and expression data that the production of the sword involves genetic differences on many chromosomes and substantial differences in expression response between species, we were interested in narrowing down likely candidates associated with sword length within the QTL region of chromosome 13. Of 52 genes in this region (Data S1B), 16 had annotations associated with growth, skeletal, muscle, or limb development phenotypes. We also included genes that were annotated as involved in bioelectric signaling (GO:0005216), since these have been identified as important in zebrafish fin modifications (39). We further evaluated these candidates using a combination of differential expression, chromatin accessibility, and sequence analysis approaches, ultimately narrowing to a set of genes most likely to drive variation in sword length due to their expression or substitution patterns (see STAR Methods; Data S1C).

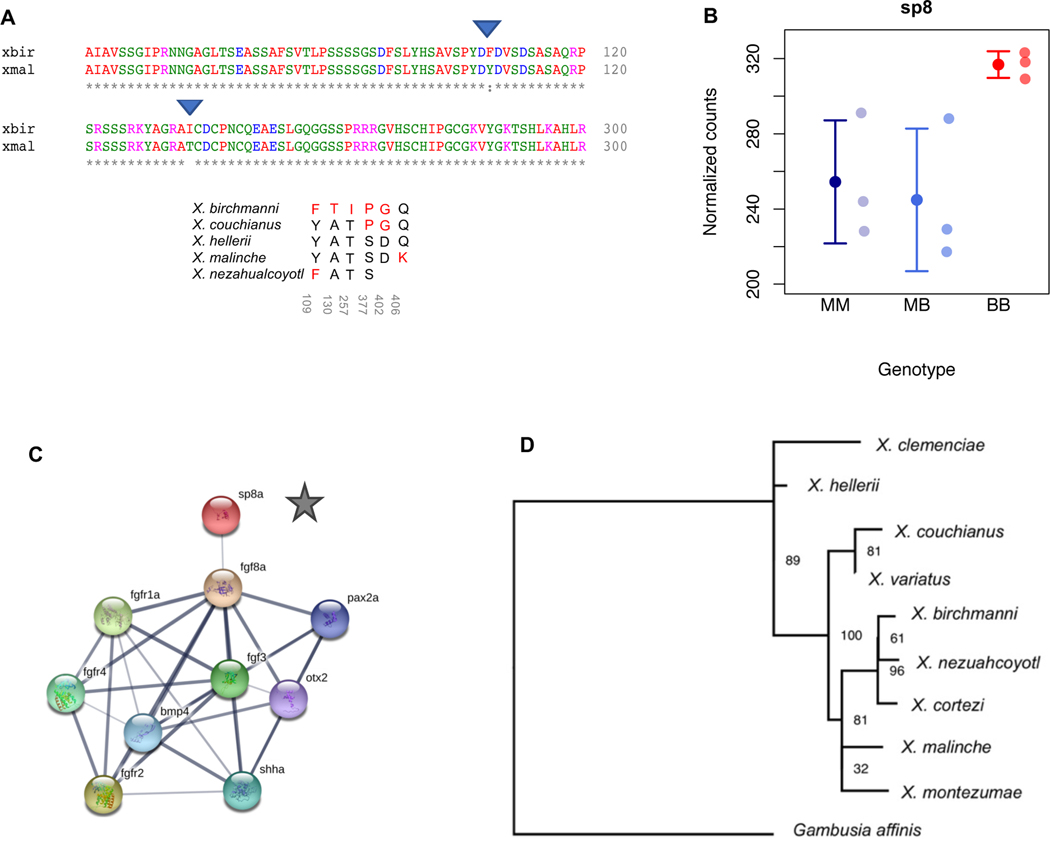
Of these genes, we highlight several of the most compelling candidates, while stressing that our mapping data lacks the resolution to zero in on any particular causal locus. sp8, which is a zinc-finger transcription factor that impacts limb and fin differentiation (40,41), has five derived nonsynonymous substitutions in X. birchmanni (Figure 5A-C) and an overall rapid rate of protein evolution between X. birchmanni and X. malinche (dN/dS = 0.78; upper 3% genome-wide; Table 1) (34). Although sp8 harbors a large number of substitutions derived in X. birchmanni (Figure 5A), we did not find strong evidence for a different substitution rate along the X. birchmanni branch based on PAML analysis (χ²=3, p=0.08; Figure 5D). We also analyzed and found no evidence for substitutions in conserved non-coding elements within 1 kb upstream or downstream of the sp8 coding sequence, or evidence of expression or chromatin accessibility differences between species (Figure 5B). However, two of the substitutions derived in X. birchmanni are predicted to affect protein function based on analysis with the program SIFT (Figure 5A, Materials & Methods, 42; see Table 1 for metrics for this and other genes in the region). Interestingly, the predicted binding sites of sp8 have also diverged somewhat between species (see STAR Methods section Predicted binding sites of candidate gene sp8), which is especially notable given recent work suggesting that sp8’s effects are dependent on its co-expression with other genes and binding site availability (43). Interestingly, we find evidence that a close function partner of sp8, sp9, is misexpressed in F₁ hybrids, hinting at additional divergence in this regulatory pathway (Figure 4C).

Figure 5. Substitution, expression, and phylogenetic data for sp8, one of several candidate genes within the QTL interval.

A. Clustal alignment of a section of the X. birchmanni and X. malinche sp8, which is found within the chromosome 13 QTL peak. Derived substitutions in X. birchmanni that are predicted to not be tolerated in a SIFT analysis are indicated by the blue triangles. Asterisks indicate identical amino acid sequences, colors indicate amino acid properties; blanks, colons and periods indicate substitutions. Below the alignment is a table of amino acid state at all sites that are variable in at least one of the species analyzed. Black indicates amino acids that follow the inferred ancestral state and red indicate amino acids that are derived. Gray numbers below amino acid states indicate the position of the amino acid in X. hellerii coordinate space. B. Expression of sp8 in regenerating caudal tissue in X. malinche (MM), X. birchmanni (BB), and F₁ hybrids (MB). Semi-transparent points show normalized counts for each individual and solid points and whiskers show the mean ± one standard deviation. The log fold change between X. birchmanni and X. malinche for sp8 estimated by DESeq2 was 0.17 (p=0.22). C. STRING network for the ortholog of Xiphophorus sp8 in zebrafish (sp8a) shows that this gene regulates a number of fibroblast growth factor and fibroblast growth factor receptor genes (fgf and fgfr genes). These genes have been implicated in fin growth in zebrafish (41), limb development in other species (40), and were previously identified as likely candidates underlying sword regeneration in southern swordtails (36). Chromosomes harboring genes known to interact with sp8 (4, 15, 19, 21 – 23) do not have a higher likelihood of impacting sword length than expected by chance. D. Local phylogeny of the sp8 region generated with RAxML with the GTR+GAMMA model is not suggestive of introgression of this gene between X. birchmanni and X. variatus. Node labels show bootstrap support based on 100 rapid bootstraps. See also Figures S6 and S7.

Table 1. Summary of ancestry changes and substitution patterns for top candidates within the chromosome 13 QTL region.

This table reports the results of SIFT analysis of aligned protein sequences, ancestry quantile analysis across X. birchmanni and X. malinche hybrid populations, rates of nonsynonymous substitutions between X. birchmanni and X. malinche, and ancestry change over time in Acuapa time series data analysis (see also Data S1 and Table S1-S4). Joint ancestry analysis was conducted using four hybrid populations and comparing observed X. malinche ancestry across populations to that expected from randomly sampling windows for each population. We also include the major candidate gene identified in a companion study by Schartl et. al ((34); kcnh8). Overall, ancestry shifted 1% towards X. birchmanni genome-wide in the Acuapa over this time period.

Candidate gene	Start position	Stop position	Joint ancestry simulation p-value	dN/dS	SIFT derived in birchmanni	X. malinche ancestry change (Acuapa)
sp4	15692146	15703983	0.04	NA (dS=0)	One substitution predicted tolerated One substitution predicted not tolerated: G710S	−0.17
sp8	15715073	15716620	0.002	0.78	Three substitutions predicted tolerated Two substitutions predicted not tolerated: Y109F, T225I	−0.17
itgb8	15720494	15738202				−0.17
twistnb	15774748	15777863	0.007	0.48	No derived substitutions	−0.17
btd	15837770	15841935	0.08	3.76	Two substitutions predicted tolerated	−0.10
grn	15874280	15877603	0.095	0	Not applicable	0.01
cdk6	15892602	15930545	0.02	0.53	One substitution predicted tolerated	−0.07
calcr	16100007	16130977	0.004	0.064	One substitution predicted tolerated	−0.02
col1a2	16245414	16260600	0.004	0.60	Two substitutions predicted tolerated	−0.02
dync1i1	16368810	16428301	0.71	0.12	One substitution predicted not tolerated: V526I	−0.10
kcnh8	16700194	16759979				−0.01

Another gene in this region, grn2, is differentially expressed in regenerating caudal tissue, and its expression patterns mirror predicted phenotypic differences between X. birchmanni and X. malinche (Figure 4B). grn2 is strongly upregulated in regenerating X. malinche fin tissue and belongs to a family of progranulin growth factors which are implicated in regulating cell growth, proliferation, and regeneration (44). Although rt-qPCR confirmed differential expression of grn2, we note that blastemas of regenerating non-sword tissue exhibited similar expression patterns (Figure S6A; see STAR Methods section Investigation of differentially expressed genes with rt-qPCR).

Finally, we identify five peaks within the QTL region of differential chromatin accessibility between species. These putative regulatory regions may provide hints into evolved differences in gene regulatory programs between the species. For example. X. birchmanni has higher chromatin accessibility at a putative enhancer ~10.2kb upstream of itgb8, which promotes wound healing and cell proliferation (Figure 4E) (45). In addition to itgb8, genes near two of the other four peaks of differential chromatin accessibility were identified as candidate genes based on their annotations (Figure 4E; Data S1C).

Sword QTL in hybrid populations

Given the importance of the sword as a sexually selected signal, we predicted that regions underlying variation in this phenotype may have unusual patterns of ancestry in natural hybrid populations formed between X. birchmanni and X. malinche. Behavioral research has indicated that in addition to males having lost the sword phenotype, female X. birchmanni prefer swordless males (23). Although X. malinche males are sworded, females of this species appear indifferent to the sword and generally prefer X. birchmanni visual phenotypes (20,46). Thus, we may expect that genomic regions underlying the sword would be selected against in hybrid populations, if swordless males, on average, have a mating advantage over sworded males.

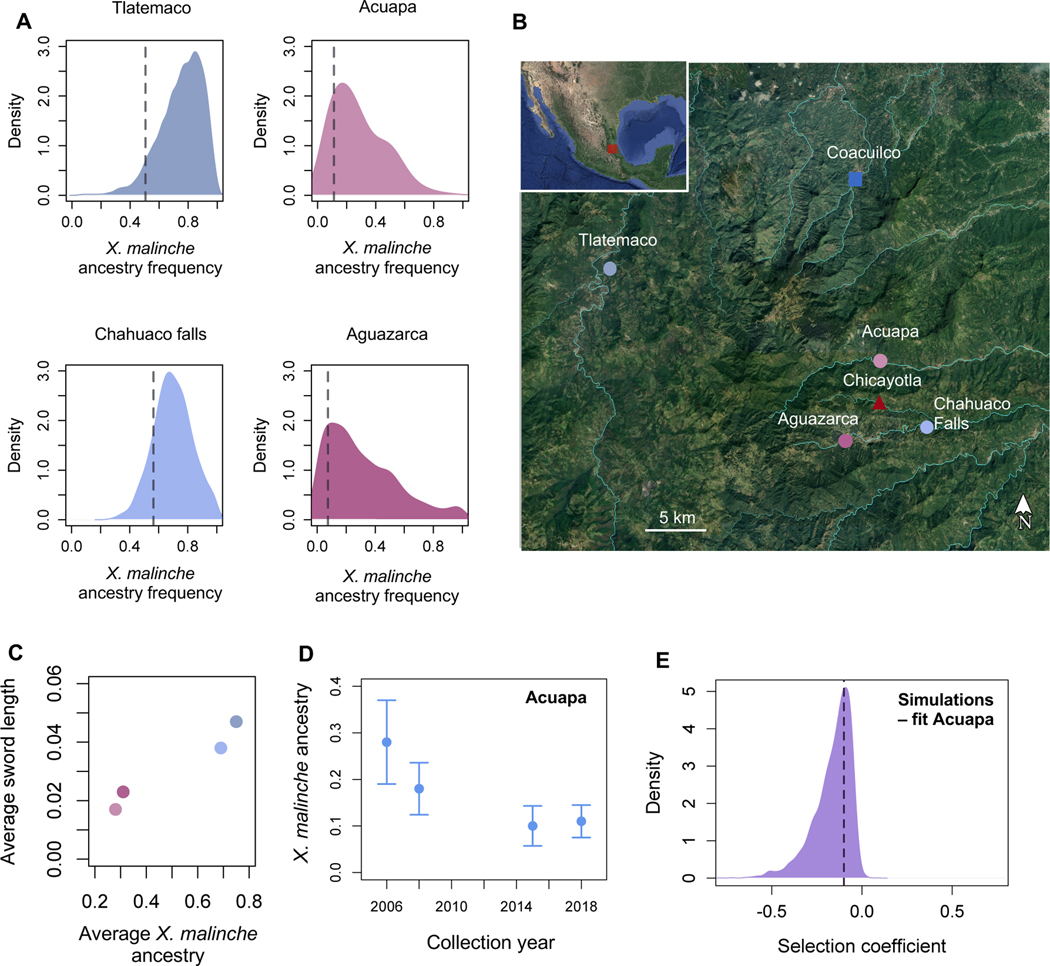
We examined local ancestry around the chromosome 13 QTL in four hybrid populations using a combination of previously collected data and new data (24,47). Two of these populations (Acuapa and Aguazarca) derive the majority of their genomes from the X. birchmanni parental species and two populations (Tlatemaco and Chahuaco falls) derive the majority of their genomes from the X. malinche parental species. Newly collected data for the Acuapa population is available through the NCBI sequence read archive (SUB8614498, pending).

Overall, X. birchmanni × X. malinche hybrid populations do not show unusual ancestry in the chromosome 13 sword QTL region as a whole. However, given the size of the QTL, there is substantial heterogeneity in ancestry within the QTL region in natural hybrid populations where ancestry linkage disequilibrium decays over ~1 Mb (24,47). Interestingly, X. malinche ancestry is lower than expected across four independent hybrid populations around the gene sp8 and genes closely linked to it (p=0.002 by simulation; Figure 6A, STAR Methods; Table 1). This is notable because sp8 was identified as a promising candidate within the chromosome 13 QTL region based on its phenotypic effects on fin and limb growth and the presence of amino acid substitutions likely to impact protein function between X. birchmanni and X. malinche (Figure 5A,C; Data S1C). If the causal locus within the QTL region is sp8 or a closely linked gene, low X. malinche ancestry could be consistent with selection against the sword in hybrid populations.

Figure 6. Patterns of ancestry at sp8 are consistent with selection against X. malinche ancestry in this region.

A. Genome-wide ancestry distribution in naturally occurring hybrid populations versus ancestry at sp8 (dotted line). Across hybrid populations, ancestry at sp8 and closely linked genes falls in the lower tail of the X. malinche ancestry distribution. Ancestry is summarized genome wide and at sp8 in 50 kb windows. The range of colors for hybrid populations represents average genome-wide ancestry in those populations. B. Sampling locations for pure X. birchmanni (blue square), pure X. malinche (red triangle), and natural hybrid populations (circles) shown in panel A. Light blue lines indicate major waterways. Images adapted from Google Earth. C. Overall, observed sword length correlates with genome-wide ancestry across hybrid populations (Pearson’s R=0.98, p=0.03). Plotted phenotypes are based on 48–193 individuals per population. We caution that this analysis does not control for potential differences in environmental effects across populations. D. X. malinche ancestry decreases over time at sp8 in a hybrid population where time series data is available (the Acuapa population). E. This decrease is consistent with moderate to strong selection against X. malinche ancestry at the sp8 region in this population. Shown here is the posterior distribution of accepted parameters from ABC simulations. Dashed line shows the maximum a posteriori estimate.

We combined local ancestry analyses in population samples with time series data, which can also be used to identify selection on ancestry. For one of the hybrid populations studied above (Acuapa) we were able to develop a time-transect dataset, spanning an estimated 24 generations of hybrid population evolution (from 2006 to 2018; see STAR Methods section Inference of selection on sp8 region in time transect data). Although we do not see evidence for unusual changes in ancestry in the QTL region as a whole, we observe a decline in X. malinche ancestry over time within the Acuapa population at sp8 (Figure 6D), consistent with moderate selection against X. malinche ancestry in this region (maximum a posteriori estimate: −0.1, 95% confidence intervals: −0.44 to −0.03; Figure 6D). This direction of change in ancestry is opposite what would be expected due to population demography, given that the Acuapa population receives X. malinche but not X. birchmanni migrants (28). Other candidate genes in this region do not change significantly in ancestry over this time period, apart from genes with the strongest physical linkage to sp8 (sp4 −11 kb away, itgb8 - 3 kb away, and twistnb - 60 kb away; Table 1).

Evolutionary patterns associated with the sword QTL

The distribution of the sword trait among Xiphophorus species indicates that there have been multiple losses of the trait (13,14). Most species lacking a sword fall within the platyfish clade, representing an ancient loss of the trait (Figure 1A). By contrast, the loss of the sword in X. birchmanni occurred since its divergence with X. malinche, an estimated 200,000 generations ago (24).

Given the distinct timescales and independence of these losses, we were surprised to find that a sword QTL on chromosome 13 was also identified in an independent study (34) using crosses between the southern swordtail species X. hellerii and the platyfish species X. maculatus, largely overlapping with our signal (see STAR Methods section Narrowing the QTL interval). Because of extensive hybridization in the group, this led us to ask whether there was evidence of introgression of genes associated with the absence of the sword.

The ranges of X. birchmanni and X. birchmanni × X. malinche hybrids overlap with a single platyfish species, X. variatus (17,25). Like other platyfish, X. variatus lacks the sword. We recently detected evidence of introgression from the lineage leading to X. variatus into X. birchmanni and X. malinche (24). We asked whether X. birchmanni harbored platyfish derived ancestry tracts that coincided with the chromosome 13 sword QTL, and were not found in X. malinche. We used the program PhyloNet-HMM to identify such regions (48). Based on simulations, we predicted that this approach will have good power to detect fixed ancestry tracts, likely due to the large sequence divergence between the groups (Figure S7; see STAR Methods section Phylogenetic approaches). Notably, we do not detect any such tracts in the QTL peak near sp8 or unusual phylogenetic relationships in this region (Figure 5D). We confirmed this result with an F₄ ratio-based approach which may be more robust to short ancestry tracts (49).

Together, this implies that introgression from X. variatus at the chromosome 13 QTL is not responsible for the loss of the sword in X. birchmanni. We caution, however, that we have not excluded a role for introgression at other, as of yet unknown regions, as a contributor to recent sword loss in the X. birchmanni lineage.

Discussion

Using a combination of approaches, we identified a major effect locus contributing to phenotypic variation in the length of the sword, a sexually selected trait that evolved in the common ancestor of Xiphophorus fish. First highlighted by Darwin, this trait has long served as a classic example in sexual selection theory of the role of female preferences in driving the evolution of male ornamentation (50). We focus our analyses on a major effect QTL on chromosome 13, containing nearly a dozen genes that could plausibly impact the sword ornament (Data S1C; Table 1). Among several intriguing candidates, ancestry patterns at the transcription factor sp8 are suggestive of selection on this region in hybrid populations (Table 1). In vertebrates, knockouts of sp8 have truncated limb phenotypes (40,51,52), and its downstream targets (41; Figure 5C) have previously been implicated in fin growth in general (41,53) and sword growth in particular (36). Moreover, a number of predicted sp8 binding sites differ between species, including those nearby canonical targets of sp8. We note, however, that contrary to expectations sp8 has similar expression levels between species and in non-regenerating caudal tissue (Figure S6B; but see 44).

Intriguingly, a companion study in two distantly related sworded and swordless Xiphophorus species, X. hellerii and X. maculatus, also maps a major effect QTL to an overlapping region on chromosome 13. The observed overlap in the QTL regions is unexpected by chance, further underscoring the importance of the chromosome 13 region in sword length throughout the clade. Using approaches grounded in developmental genetics, the authors highlight a different set of candidates associated with the sword, including the gene kcnh8, a potassium voltage-gated channel, which is uniquely upregulated in regenerating sword tissue (34). Notably, we replicate the expression patterns observed by Schartl et al. (34) at kcnh8 in X. birchmanni, X. malinche, and F₁ hybrids (Figure 4D).

Although both our study and that of Schartl et al. (34) highlight possible genes underlying variation in the length or development of the sword, our results do not allow us to reject the hypothesis that there may be multiple associated genes in the chromosome 13 interval. Indeed, theory predicts that selection can favor the evolution of linkage between co-adapted gene complexes over evolutionary timescales (54). Addressing this question empirically and narrowing in on causal genes may be difficult since this will require a high density of recombination events in a ~2 Mb region. Lab-raised natural hybrids between X. birchmanni and X. malinche could provide a solution in this regard since they harbor smaller ancestry tracts from historical recombination events.

Notwithstanding a broad interest in the community in identifying specific genes that generate variation in adaptive traits, it is important to note that the chromosome 13 QTL explains only ~11% of the heritable variation in sword length. Thus, quests to narrow in on individual causal genes may miss important features of the genetic architecture of phenotypic variation. In addition to chromosome 13, we find that ancestry throughout the rest of the genome contributes to variation in sword length. Model selection suggests that sword length is explained by ancestry proportions on as many as 13 of 24 chromosomes (Figure 3B). These results echo broader challenges in the community, that are especially difficult to tackle in non-model organisms. Massive progress in understanding the genetic architecture of complex traits in humans has indicated that although large effect variants (such as the chromosome 13 QTL we identify) exist, most phenotypic variation is explained by numerous sites spread throughout the genome. These studies have also highlighted the difficulties of disentangling the functional links between these suites of small-effect variants and the trait of interest.

Surprisingly, we also observe that X. birchmanni ancestry on several chromosomes is positively correlated with sword length. This result is puzzling since X. birchmanni males lack a sword and thus X. birchmanni ancestry should not contribute to longer swords in hybrids. Simulations suggest that these results are not expected to be an artifact of our analysis approach (see STAR Methods section Simulations of polygenic traits and QTL analysis). Instead we speculate that they could be explained by the predictions of Fisher’s geometric model (55,56), where different phenotypic optima in the two species (i.e. sworded and swordless males) result in fixation of different suites of genetic variants, whose combinatorial effects are uncovered in hybrids (57). These observations highlight a general problem for QTL mapping approaches using interspecific hybrids, where the phenotypic variance observed in hybrids is not necessarily generated by the same set of loci responsible for trait differences between the parental populations (26,58).

Our results here also serve to underscore an important finding from previous work that has been largely overlooked in the recent mapping literature (59). Without accounting for variation in genome-wide ancestry in hybrids, we originally detected three genome-wide significant QTLs (Figure S4A). Examination of two of these associations, revealed relatively flat peaks spanning most of the chromosome (Figure S4A). After accounting for genome-wide ancestry, both signals fell below our genome-wide significance threshold (Figures 2A and S4A). Our simulations suggest that when traits are polygenic ignoring genome-wide ancestry in hybrids can result in inflated QTL peaks (see STAR Methods section Simulations of polygenic traits and QTL analysis). This phenomenon was explored in earlier theoretical work from Visscher & Haley (59). The underlying biological issue is that although individuals generated by artificial crosses have a certain proportion of their genome derived from each parental species (i.e. 50% in our study, Figure 2C), substantial variation in genome-wide ancestry is generated by recombination. The technical issues that arise from this variance are analogous to those long-appreciated in the admixture mapping literature (60). Here, we emphasize again this important issue.

Results from natural populations suggest that there may be selection against the sword in hybrid zones formed between X. birchmanni and X. malinche. Female X. birchmanni prefer swordless males and female X. malinche appear to be indifferent to the sword (20,23). Moreover, natural selection is expected to act in concert against sworded males, as they are more visually obvious to potential predators (61). This leads to the expectation that there may be selection against X. malinche ancestry in regions associated with the sword. Interestingly, one of the candidate genes we identified, sp8, and genes closely linked to it, has lower than expected X. malinche ancestry across hybrid populations and have decreased in X. malinche ancestry over time in one hybrid population (Figure 6A,E; Table 1). This decrease is consistent with moderate selection against X. malinche ancestry in this region (Figure 6E). However, we caution that ancestry at the chromosome 13 QTL explains only a fraction of the overall trait variation; ancestry changes at other underlying loci may support different patterns of selection and trait evolution in hybrid populations.

The causes of variability in sexual ornamentation within and between species remains a source of controversy. Theory and empirical evidence suggest a modest role for so-called “good genes” selection, where ornaments predict offspring success (62). By contrast, ornaments can rapidly evolve simply because they are attractive, if they exploit a preexisting bias or coevolve with female preferences (63,64). While the predictions of the good genes model are not strongly dependent on genetic architecture, the dynamics of coevolutionary models depend critically on the underlying genetic architecture (64). For example, theory predicts that only traits with a polygenic basis are likely to be driven to extreme exaggeration through so-called “runaway” sexual selection (1,2,22). To date, however, most genetic studies of sexual ornaments have identified single loci of large effect on sex chromosomes (8–10).

Our results support a polygenic architecture underlying variation in the sword ornament, consistent with a number of evolutionary mechanisms that have been proposed to explain the evolution of extraordinary diversity in sword phenotypes across Xiphophorus. These findings contrast with some previous observations that identified a simpler genetic architecture for several sexually selected ornaments (8–10), highlighting the challenges ahead in understanding the genetic basis of many evolutionarily important traits.

STAR Methods

Resource availability

Lead Contact

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Molly Schumer (28).

Materials availability

This study did not generate any unique reagents.

Data and Code availability

All code generated from this project is available on github (https://github.com/Schumerlab).

Sequence data has been deposited on NCBI’s sequence read archive.

Experimental model and subject details

For QTL mapping we generated a mapping population by intercrossing F₁ hybrids. We crossed X. malinche (female) × X. birchmanni (male) to produce an F₁ generation; previous attempts to produce viable offspring from the reciprocal cross were largely unsuccessful. We reared virgin X. malinche (n = 24) born to females collected at the Chicayotla locality on the Río Xontla (20°55’27.23”N 98°34’34.12”W) using baited minnow traps. Wild X. birchmanni sires (n = 10) were collected from the Coacuilco locality on the Río Coacuilco (21°5’51.16”N 98°35’20.10”W). The resulting F₁ offspring from this cross were reared to maturity. Based on past experience, we knew that it would be difficult to generate large numbers of early-generation hybrids in the lab. As a result, in June of 2016 we seeded each of 29 mesocosm tanks with F₁ hybrids (n = 21 per tank). These mesocosm tanks are 2000 L outdoor tanks kept in semi-natural conditions but protected from predators and fed once daily.

We sampled the mesocosms in January and May of both 2017 and 2018, at which time all adult males were anesthetized with tricaine methanesulfonate (Texas A&M IACUC protocol #2016–0190), marked individually with color-coded elastomer tags for future identification (Northwest Marine Technologies), photographed for phenotyping, and fin-clipped for genotyping before returning them to mesocosm tanks. In total we genotyped and phenotyped 536 adult early generation hybrid males. Analysis of crossover numbers indicate that the majority of these individuals are F₂ hybrids, and we found that our results are robust to excluding individuals that are likely to be later generation hybrids (see STAR Methods section QTL analysis).

We also used lab-raised X. malinche, X. birchmanni, and F₁ individuals for gene expression and chromatin accessibility analyses (see STAR Methods section Sword regeneration experiments). Fish for these experiments were individually housed at Texas A&M University in 40 liter tanks at 22 °C and were kept on a 12/12 light dark cycle for the duration of the experiment (Texas A&M IACUC protocol #2016–0190). Ten individuals of each genotype were pooled to generate a total of three replicates per genotype for gene expression analysis and two pools were generated for ATAC-seq libraries to compare chromatin accessibility in regenerating caudal blastemas (see STAR Methods Analysis of chromatin accessibility).

All other individuals used in our analyses were wild-caught hybrids from the Acuapa, Tlatemaco, Chahuaco falls, and Aguazarca hybrid populations in Hidalgo, Mexico.

Method Details

Phenotyping approaches

We measured standard length (distance from the tip of the mandible to the midpoint of the distal edge of the caudal peduncle), sword extension (distance from the edge of the caudal fin to the tip of the sword; (65) from photographs of adult males using the ImageJ software package (66). For analysis, sword extension was standardized by dividing by standard length and is referred to as sword length throughout the manuscript. We note that sword length is usually referred to as the distance from the caudal fin base to the sword tip, which differs from our terminology here for convenience.

Males were considered adults based on mature gonopodium development, but were not measured at a standardized timepoint. Because swords can continue to grow throughout a male’s adult life, and in response to androgen treatment (36), this choice could introduce higher phenotypic variance due to environmental and measurement sources. However, we emphasize that noise in phenotypic measurement acts to reduce power to detect QTL and underestimate effect sizes, and thus does not pose a methodological problem for our mapping approaches described below.

Low coverage whole genome sequencing

We used the Agencourt bead-based protocol (Beckman Coulter, Brea, California) to extract DNA from fin clips. We followed the manufacturer’s instructions for the extractions except that we used half reactions. DNA was diluted to 10 ng/μl and 5 μl of sample was mixed with Tn5 transposase enzyme pre-charged with adapters. This mixture was incubated at 55 °C for 7 minutes to enzymatically shear DNA and the reaction was stopped by adding 2.5 μl of 0.2% SDS and incubating at 55 °C for another 7 minutes. Three microliters of each sample were combined with a plate-level i5 index and one of 96 i7 indices in an individual PCR reaction using OneTaq HS Quick Load mastermix. After amplification, 5 μl of each library were pooled and the pool was purified using Agencourt AMPpure XP purification beads. Libraries were quantified using a Qubit fluorimeter (Thermo Scientific, Wilmington, DE). Libraries were evaluated for size distribution and quality using a Bioanalyzer 1000 (Agilent, Santa Clara, California). Libraries were sequenced on the Illumina HiSeq 4000 at Weill Cornell Medical Center across three lanes to collect paired-end 100 nucleotide reads. This data has been deposited on the NCBI sequence read archive (SUB8614498, pending).

Local ancestry inference

To infer local ancestry, we used a pipeline we previously developed called ancestryinfer (30,67). Briefly, for each individual Illumina reads were mapped to both the X. birchmanni and X. malinche reference genomes; uniquely mapping reads were retained and counts for each allele were tabulated at each ancestry informative site. A hidden Markov model (67) was applied to these counts to generate posterior probabilities of each ancestry state (homozygous birchmanni, heterozygous, and homozygous malinche) at ancestry informative sites throughout the genome. This resulted in posterior probabilities at 623,053 sites genome-wide in our dataset.

For downstream analyses, we converted these posterior probabilities to hard calls. If an individual had a posterior probability greater than 0.9 for any ancestry state, they were assigned that ancestry state at the focal marker. On average artificial hybrids derived 50% of their genomes from each parental species, as expected from the cross design (Figure 2C). Local ancestry also mirrored expected patterns for early generation hybrids (Figure S1A).

We also performed simulations using the mixnmatch pipeline (30) to evaluate the expected accuracy of local ancestry inference for F₂ hybrids between X. birchmanni and X. malinche. mixnmatch simulates admixed genomes and outputs a table of ancestry tracts for each individual as well as simulated Illumina reads. For the purposes of these simulations we provided sequence information and the local recombination map from chromosome 1 of X. birchmanni. As in the real data we modeled two generations of admixture, 0.2X coverage, and simulated cross-well contamination rates of 2% (30) and inferred local ancestry using the ancestryinfer pipeline (30). We summarized accuracy by comparing the true simulated ancestry to the inferred ancestry state, using a threshold of 0.9 to convert posterior probabilities to hard-calls. Results of these simulations indicate that we expect local ancestry calls for F₂ hybrids to be highly accurate (Figure S1), with estimated per-site error rates of <0.2%.

Estimates of heritability

To estimate the broad sense heritability of the sword length trait, we took advantage of phenotypic data from F₁ and F₂ hybrids raised in common conditions (68). We calculated the variance in normalized sword length contributed by environmental factors (V_E) as the trait variance in F₁ hybrids, where all individuals have identical ancestry states throughout the genome. We calculated the combined impacts of environment and genetic variance (V_G) using phenotypic variance (V_P) in F₂ hybrids. This allowed us to solve for V_G and estimate broad sense heritability using the relationship h²_broad = V_G/V_P (see (68).

We note that the approach that we use to estimate heritability was designed for inbred lines and assumes that phenotypic variation within the parental species is due to environmental variation. While this is likely a valid assumption for X. birchmanni (mean sword length normalized by body length = 0.016 ± 0.02), it may not be the case in X malinche where we observe greater variation in sword length (mean sword length normalized by body length = 0.28 ± 0.07). Thus, we evaluated possible impacts of genetic variation for sword length within X. malinche on heritability inference using simulations. To do so, we used a simulation approach. We did not attempt to mimic exact parameters from our system, as many of these values are unknown, but rather asked whether adding additional genetic variation in one of the parental populations generally biased estimates of trait heritability as a function of ancestry.

We used the admixture simulator admix’em (69) to simulate genotypes and phenotypes for two parental populations, F₁ and F₂ hybrids. We simulated 10 chromosomes each with a randomly placed QTL contributing to trait variation. Each QTL explained 10% of the heritable variation in the trait generated by ancestry from the simulated X. malinche parental population. We also varied the amount of environmental variation by adding values from a random uniform distribution such that broad sense heritability due to ancestry was 0.2, 0.4, and 0.6 in three sets of simulations. For each heritability value, we performed two types of simulations. In the first, all heritability was attributable to X. malinche ancestry. In the second, segregating polymorphisms at the QTL (implemented in admix’em as loci 1 bp away) could also increase simulated sword length. Allele frequencies for these loci within the simulated X. malinche population were drawn from a random exponential distribution. We arbitrarily assigned these loci 1% of the effect size of the QTL they were linked to, but relax this assumption below.

For each value of broad sense heritability, we performed 100 replicate simulations with and without additional phenotypic variation attributable to segregating loci within the simulated X. malinche population. Based on these simulations, additional phenotypic variation from X. malinche did not appear to impact the accuracy of estimates of ancestry heritability using methods intended for inbred lines. Simulations with and without segregating variation in X. malinche resulted in overlapping estimates for heritability attributable to ancestry variation (Figure S3A). Moreover, this observation held when we increased the effect size of the loci segregating in X. malinche from 1% of the QTL effect size to 5 and 10% (Figure S3B). We hypothesize that this observation is due to the fact that loci segregating within X. malinche contribute to phenotypic variance in both F₁ and F₂ hybrids, and thus this variance tends to be absorbed in the environmental effect term, resulting in an accurate estimate for the heritability attributable to ancestry variation.

We also note that although F₁ and F₂ fish were grown in common conditions and phenotyped as adults, conditions such as age, population density, and hormone status were not tightly controlled. If these conditions systematically differed between F₁ and F₂ fish, despite attempts to keep them in similar conditions, this could result in under or overestimates of heritability.

QTL analysis

For QTL analysis, the data were thinned to retain one marker per 50 kb; this resulted in 12,794 markers spread approximately evenly across the genome (95% of intermarker distances were less than 60 kb). This thinning is necessary due to the computational intensity of analysis using the R/qtl software. We used the scanone function of R/qtl to perform single QTL model standard interval mapping using the EM algorithm (33). Recombination fraction was estimated using the est.rf() function and markers missing genotype data were excluded using the drop.nullmarker() function. Since genome-wide hybrid index was significantly correlated with sword length (ρ = 0.20, p < 4×10⁻⁶) we included it as a covariate during mapping (see also Figure S4A; STAR Methods section Simulations of polygenic traits and QTL analysis). We also repeated mapping analysis including ancestry on each chromosome retained in AIC model selection as a covariate. Rearing tank and tank location were omitted as covariates because they did not significantly affect phenotype distribution. The threshold for genome-wide logarithm of odds (LOD) at a false discovery rate of 5% was determined based on 1,000 permutations of sword phenotype onto observed genotypes. For the identified QTL, the region that fell within 1.5 LOD of the peak LOD value was treated as the associated interval for downstream analyses. For each chromosome containing a significant QTL, we aligned that chromosome from the X. birchmanni and X. malinche assemblies (47) using the program MUMmer (70). We found no evidence of structural rearrangements or deletions between the two species in this region (Figure 2D).

After identifying a significant QTL in our initial scan, we performed a two-dimensional QTL scan for sword length, with hybrid index as a covariate using the scantwo function in R/qtl and the EM algorithm. We did not identify a two-locus model with a significantly better fit to the data than a one-locus model even at a 10% false discovery rate.

We also phenotyped artificial hybrids for two other traits related to the sword phenotype: the upper pigmented sword margin, and the lower pigmented sword margin (Figure S2C; Materials & Methods). We used a partial correlation approach to test the extent to which these traits were correlated with each other in our mapping panel. We found that the sword upper edge phenotype was strongly correlated with sword length (R=0.48, p<10⁻³²), and thus chose not to map this as a separate trait. By contrast, sword lower edge was not as strongly predictive of sword length (R= 0.19, p<10⁻⁵). We thus performed QTL mapping for the sword lower edge as described above except that we modeled a binary trait. Surprisingly, we did not find evidence for any genome-wide significant QTL associated with the sword lower margin nor a clear association with genome-wide ancestry (R=0.05, p=0.26).

Because we used large mesocosm tanks seeded with F₁ hybrids to raise a sufficiently large mapping population, there is a small possibility that some of the individuals used in our mapping panel were F₃ hybrids based on variation in generation and maturation times. We decided to evaluate this based on comparisons of the number of observed crossovers in sampled individuals to the number expected in F₂ hybrids. From previous work we had access to local ancestry data from 139 F₂ hybrids generated in the lab (30). We compared the distribution of ancestry transitions, reflecting observed recombination events, between known F₂ hybrids and the individuals from our mapping populations. The median number of crossovers per chromosome was slightly higher in our mapping population (1.3 crossovers/chromosome) than expected from known F₂s (1.2 crossovers/chromosome), but the distribution suggests that few F₃ or later individuals were included in our mapping population. Out of an abundance of caution, we re-ran R/qtl excluding five individuals with numbers of crossovers outside of the range of the distribution of crossovers observed in known F₂s. Reassuringly, excluding these individuals had no effect on our results.

Narrowing the QTL interval

Because this project relied on a mapping population of early generation hybrids, the 1.5 LOD interval associated with the sword QTL on chromosome 13 was large, spanning 4.1 Mb and containing 186 genes (13.2 to 17.3 Mb). We evaluated whether there was sufficient information to narrow this region further by bootstrapping our data. Because we found R/qtl to be prohibitively slow for use in simulations, even when analyzing a single chromosome, we first verified that results were qualitatively identical using a linear-model based approach and then proceeded using this approach in simulations.

We subsampled our dataset to 75% the total number of individuals in 1,000 replicate simulations. For each simulation we recorded the location of the peak associated marker on chromosome 13. This allowed us to evaluate the extent to which we expect the QTL peak to move as a result of sampling noise in the data. The 95% confidence intervals of these locations (15.3–16.9 Mb) yielded a 1.7 Mb region at the center of the QTL we had initially identified.

While analyzing our results, we discovered that another research group had independently conducted an experiment to map the genetic basis of sword length by crossing sworded (X. hellerii) and swordless (X. maculatus) species (71,72). These two species are deeply diverged from X. birchmanni and X. malinche (1.6–2% sequence divergence), and from each other (~2% sequence divergence). This study identified a QTL overlapping with the region we identified on chromosome 13, with the 1.5 LOD interval matching the region from 14.3 to 16.5 Mb in the X. birchmanni assembly (34). At first glance, this suggests that the genetic architecture of the sword phenotype is shared in these two species pairs and that comparisons between studies could be used to further narrow the region of interest.

However, since QTL intervals identified by the two studies were relatively large, we wanted to evaluate the probability that both studies would have identified the same region by chance. To do so, we permuted a 2.2 Mb region onto the genome 1,000 times and asked how frequently it overlapped by chance with the QTL interval that we identified by bootstrapping. We found that overlap of the two QTL was unexpected by chance (p-value by permutation 0.004). This suggests that the overlap of the two QTL is not coincidental and that we can use the joint signal in our efforts to identify causal genes within the QTL region. Thus, in subsequent analyses we focus on the narrower region identified from both mapping studies, the interval from 15.3 to 16.5 Mb on chromosome 13.

The 1.2 Mb region identified by the analyses discussed above contained a total of 52 genes. From this subset of 52 genes, we first asked which had annotations known to be associated with limb or tail phenotypes, growth phenotypes, bioelectric signaling, or skeletal phenotypes based on aggregated data in the GeneCards database (73), narrowing our focal gene list to sixteen (Data S1C). Next, we asked which genes were expressed in regenerating sword tissue in X. malinche and F₁ hybrids (see STAR Methods section Sword regeneration experiments). We reasoned that genes that are not expressed during sword regeneration are unlikely to be involved in the sword length trait, leaving us with fourteen focal genes (Data S1C).

Of this subset of 14 genes, we predicted that to drive the QTL signal, they should be responsible for an effect in cis. This could be accomplished either by an amino acid difference between X. birchmanni and X. malinche that underlies the morphological difference between species, differences in expression between the two species, or some combination of the two. We thus evaluated which of these genes had nonsynonymous amino acid changes between species and which had expression differences in regenerating caudal fin tissue between X. malinche and X. birchmanni. This analysis led to a set of eight possible candidates which are listed along with their annotation information and sequence and expression results in Data S1C.

In addition to protein coding genes, we explored the possibility that our QTL region contained miRNAs. Using the X. maculatus reference genome in which miRNAs have been annotated, we identified miRNAs that were homologous to our QTL region in X. birchmanni. This analysis revealed that one annotated miRNA fell within our QTL region (ensembl gene id: ENSXMAG00000020740). We next extracted and compared X. birchmanni and X. malinche orthologs of this miRNA. These orthologs had identical sequences between the two species. We used the program RNA22 (74) to search for potential targets of this miRNA. We identified nearly 900 potential targets with greater than 30% binding probability genome-wide, which are listed in Table S3.

Effect size of the chromosome 13 QTL and expected power

We wanted to know how much of the variation in sword length is explained by the significant QTL we detect on chromosome 13. Based on the coefficient in a linear model, we estimated that the chromosome 13 QTL explains approximately 5% of the total variation in sword length, or ~10% of the heritable variation in length. However, we knew that it was possible that this effect size was an overestimate due to a well-known statistical phenomenon where effect sizes for QTL detected in studies with low power are often inflated (known as the Beavis effect or the winner’s curse, (12).

The inflated effect size estimates associated with the winner’s curse are the result of enforcing genome-wide significance thresholds in scenarios in which there is low power to detect the true signal at that threshold. Regions of the genome where noise in the data matches the direction of the underlying signal are more likely to pass the significance threshold. We thus sought to infer the likely effect size of the chromosome 13 QTL, using an approximate Bayesian approach. Importantly, by implementing the same genome-wide significance threshold as used with our real data in simulations we should capture the impacts of effect size inflation due to the winner’s curse, allowing us to more accurately estimate effect size of the chromosome 13 QTL region. We extracted the observed genotypes for each individual at the QTL peak, generated simulated phenotypes, and performed mapping analysis. We used the following steps to do so in simulations:

1. We drew the proportion of phenotypic variance explained by the chromosome 13 QTL (chr13_effect) from a uniform prior that ranged from zero to our empirical heritability estimate for sword length (0.48).

   1. Using these values and the average sword phenotype in our mapping population, we partitioned the phenotypic variance contributed by chromosome 13 (pheno_chr13) and the variance contributed by the rest of the genome and by environmental factors (pheno_other).
2. We next generated simulated sword phenotypes for each individual.

   1. Based on an individual’s genotype at the QTL peak on chromosome 13, we performed the following steps:

      1. If an individual was homozygous X. malinche, we assigned that individual a phenotype value of pheno_chr13.
      2. If an individual was heterozygous, we assigned that individual a phenotype of half of pheno_chr13.
      3. If an individual was homozygous X. birchmanni we assigned that individual zero for pheno_chr13.
   2. We next added trait variation to mimic variation explained by the rest of the genome and environmental sources.

      1. We drew from a normal distribution with mean equal to pheno_other, and variance equal to the observed variance in sword length in F₂ hybrids.
      2. We added pheno_chr13 to pheno_other to generate a simulated sword length for each individual.

3. We performed a linear regression analysis as we had done for the real data and determined the p-value for the association between chromosome 13 and simulated sword length, as well as the proportion of the phenotypic variance explained by the chromosome 13 QTL. We performed rejection sampling based on the observed p-value in the real data, using a tolerance of 5%.

4. This procedure was repeated until 5,000 simulations had been selected.

These simulations resulted in a well-resolved posterior distribution of possible effect sizes for the chromosome 13 QTL (Figure 2C). Surprisingly, we found the maximum a posteriori estimate of effect size was not lower than our initial estimate of effect size for this QTL (5.5% compared to point estimate of 5%; 95 % CIs: 0.05–0.12). This suggests that the QTL on chromosome 13 falls within the range of effect sizes that we have power to detect in our study.

We see ample evidence that there are other loci contributing to variation in sword length (see next section) and inferring the likely effect size at which we have power to detect QTL gives us some information about the QTL we were unable to map. Using a similar procedure, we estimated the threshold at which we have power to detect QTL in our study. We simulated genotypes and phenotypes as above except that instead of using an ABC framework, we performed a grid search to ask how frequently simulated QTL of a given effect size were detected. The effect sizes in the grid ranged from 0–50% of the phenotypic variance explained in increments of 5%. For each effect size we performed 1,000 simulations and recorded the proportion of simulations in which the simulated QTL was detected.

The results of these simulations suggest that we have power to detect QTL that explain ~5% of the heritable variation in about 50% of simulations (75) and QTL that explain ~10% of the heritable variation in 90% of simulations. QTL that explain a smaller degree of trait variation (~1%) are rarely detected.

Genetic architecture of the sword

In addition to QTL mapping, we asked about genome-wide associations between sword length and ancestry. We summarized ancestry per chromosome and genome-wide and used a partial correlation approach with the ppcor method in R to identify chromosomes in which ancestry was significantly associated with sword length, after accounting for ancestry on chromosome 13. We adjusted p-values with a bonferroni correction for the number of chromosomes. Finally, we evaluated associations between ancestry and sword length using an AIC model selection approach. We input a model in which ancestry on all chromosomes was included as independent variables and used the step function in R to select the minimal model of sword length as a function of chromosome level ancestry.

We also evaluated whether features such as chromosome length and the number of genes per chromosome correlated with the estimated effect sizes of the 24 chromosomes. We did not see a correlation between the number of annotated genes per chromosome and the estimated effect size of that chromosome, whether we included all chromosomes (Spearman’s ρ = 0.1, p = 0.6) or only those retained during model selection (Spearman’s ρ=0.57, p = 0.1), although the trend observed for the latter is suggestive.

Given that thousands of genes are differentially expressed between X. birchmanni and X. malinche in regenerating caudal fin tissue (see below, Figure 3A, Figure 5A), we asked whether there was a relationship when limiting to differentially expressed genes. Specifically, we asked whether chromosomes with larger estimated effects on sword length had a greater number (or proportion) of differentially expressed genes. We did not detect a relationship between the estimated chromosome-level effect sizes and number (or proportion) of differentially expressed genes, regardless of whether we performed the analysis based on all differentially expressed genes, or those with X. malinche or X. birchmanni biased expression (all comparisons p > 0.26).

Simulations of polygenic traits and QTL analysis

In R/qtl analysis, we performed mapping with and without genome-wide ancestry included as a covariate. Because we found that excluding genome-wide ancestry as a covariate resulted in two additional QTLs passing our genome-wide significance threshold, we were interested in evaluating the impact of model choice further. Since R/qtl is prohibitively slow for use in even a moderate number of simulations, we instead compared results of linear models performed in R, after first confirming that in the empirical data these approaches produced nearly identical results (Figure S4B).

To explore the expected impact of including or excluding genome-wide ancestry in the case of moderately to highly polygenic traits, we performed simulations. For each simulation, we used the observed genotypes from our 536 early generation hybrids and simulated phenotypes based on ancestry at 50 underlying loci. To generate simulated phenotypes, we used the following procedure:

1. First, we partitioned the expected trait variance in hybrids into the environmental and genetic components. We randomly selected 50 sites and treated these as causal loci underlying variation in sword length.

   1. For each individual, to specify the environmental variation in the trait, we drew from a random normal distribution with a mean equal to the trait mean in F₁s and variance set to the trait variance observed in F₁s.
2. Next, we divided the heritable variation equally among all 50 loci contributing to genetic variation in sword length F₂s and generated phenotypes based on simulated genotypes at those loci.

   1. If an individual was homozygous for X. malinche ancestry at that locus, we added the full effect of that locus to the individual’s quantitative phenotype.
   2. If an individual was heterozygous at that locus, we added half of the effect of that locus to the individual’s quantitative phenotype.
   3. If an individual was homozygous X. birchmanni at that locus we did not change the phenotype.
   4. We repeated this for all 50 loci, generating a polygenic trait for mapping in simulations.

3. We scanned for associations between genotype at each ancestry informative site and simulated phenotype using a linear model, with or without genome-wide ancestry included as a covariate.

4. We performed 100 replicates of these simulations.

Even in simulations with only 50 causal loci, we expect to have very low power to detect individual QTL with our sample of 536 individuals (Figure S3C; see STAR Methods section Effect size of the chromosome 13 QTL and expected power). We compared p-value distributions for simulated markers in a model that included genome-wide ancestry as a covariate and one that did not. We found that in analyses excluding genome-wide ancestry as a covariate, median (KS test p-value 10⁻⁹; Figure S4C) and minimum p-values were consistently lower (KS test p-value p<0.001), contributing to the appearance of peaks of association in some simulations (Figure S4D). We repeated the simulations as described above but split the genetic effects over 500 loci and replicated these results (KS test p-value 10⁻⁷; Figure S4E). In the uncorrected simulations we continue to see qualitative results similar to the broader peaks observed in the uncorrected analysis of the real data (Figure S4F). This suggests that mapping experiments that do not include genome-wide ancestry as a covariate may have a higher false positive rate when traits are highly polygenic, as has been reported previously (59).

We also used these simulations as an opportunity to investigate whether the negative correlations we observe between sword length and X. malinche ancestry on a chromosomal level are expected by chance. Specifically, we applied the same model selection approach we used in analyzing the real data and asked whether X. birchmanni ancestry was retained in the final model as a predictor of simulated sword length. While our simulations only used X. malinche ancestry to generate the simulated sword phenotype, we found that in 40% of simulations X. birchmanni ancestry was retained as predictive in the final model on at least one chromosome. However, fewer chromosomes contributed to this pattern than in the real data (p<0.01 by simulation), and effect sizes estimated for X. birchmanni ancestry were uniformly stronger in the real data than any observed in simulations (p<0.01 by simulation).

Sword regeneration experiments

In order to compare gene expression patterns in developing caudal tissue of X. birchmanni, X. malinche, and their F₁ hybrids, we took tissue samples after ten days of regeneration from three pools of ten individual males for each genotype class (90 fish in total) following Offen et al. (36). Samples had to be pooled due to the expectation of low RNA yield from individual samples [Manfred Schartl, personal communication]. Briefly, to begin the experiment we anesthetized each fish in MS-222 and amputated the distal 1/4 of the caudal fin, which includes the sword in X. malinche and F₁ hybrids, using a sterile razorblade. After recovery from anesthesia, each fish was housed individually in 11-liter aquaria and fins were allowed to regenerate for ten days at 22°C. After ten days, each fish was once again anesthetized and the regenerating blastema was removed. The dissected tissue was divided into three sections, with the most ventral section corresponding to regenerated sword tissue in X. malinche and F₁ hybrids. The ventral tissue sections were then pooled in groups of ten according to genotype and replicate for RNA extraction. We generated a total of three pools (30 males) for each biological condition: X. birchmanni, X. malinche and F₁ hybrids. RNA was extracted from the pooled tissue using a Trizol based protocol followed by on-column DNAse treatment and purification using the Qiagen RNeasy Mini Kit (Qiagen, Valencia, CA). RNAseq libraries were prepared in a single batch by the Bauer Core at Harvard using the KAPA mRNA HyperPrep Kit (Roche, Palo Alto, CA) with 300–500 nanograms of input RNA. Samples were sequenced across two HiSeq 2000 lanes at Harvard’s Bauer Core (Data S1D,E)and yielded 150bp paired-end reads.

Differential expression analysis

We tested for differential expression between X. birchmanni and X. malinche in the libraries described above. We used the Cutadapt and FastQC wrapper tool Trim Galore! to trim reads with low quality bases (Phred score < 30) and Illumina adapter sequences (76). We used kallisto (77) to pseudoalign reads to the X. birchmanni reference transcriptome and imported raw counts for differential gene expression analysis into the R package DESeq2 (77). Briefly, we created a DESeqDataSet object using the tximport package, setting X. birchmanni as the reference group. We performed log-fold change shrinkage using an adaptive shrinkage estimator with a fitted mixture of normal distributions as a prior, derived from the ‘ashr’ package (78). Counts were normalized to plot expression profiles using DESeq’s internal normalization method. Genes with zero counts, extreme outliers (using a Cook’s distance cutoff of 0.99), or low mean normalized counts (default) were removed from analysis.

To check for potential bias in the pseudoalignment step, we also pseudoaligned trimmed reads against the X. malinche reference transcriptome, repeated all analyses, and obtained qualitatively identical results. Briefly, log fold change values were strongly correlated across analyses using the two different reference sequences, with an adjusted R² of 0.92 (based on a linear model in R). Moreover, of 3,333 and 3,374 significantly differentially expressed genes identified using the X. birchmanni and X. malinche references, respectively, 3,190 genes were identified in both analyses. Results of downstream analyses were also similar. GO enrichment yielded 227 significantly overrepresented terms for the analysis using the X. birchmanni reference, and 214 terms for the analysis using the X. malinche reference, with 202 terms identified in both analyses. KEGG enrichment results were identical between analyses.

Investigation of differentially expressed genes with rt-qPCR

Using the methods described above (see STAR Methods section Sword regeneration experiments), we generated tissue from additional individuals for rt-qPCR based verification of genes of interest. We extracted total RNA using the methods described above from the most dorsal and most ventral sections of regenerating blastema tissue ten days after caudal fin amputation from X. birchmanni and X. malinche individuals. We used the GoScript Reverse Transcription System kit (according to the manufacturer’s specifications with the volume of the initial reaction doubled) to generate cDNA from total RNA (Promega, Madison, WI). We designed primers based on exon regions of our genes of interest from the X. birchmanni reference genome. We confirmed that all primers amplified fragments of the expected length prior to qPCR analysis. We prepared 10ul rt-qPCR reactions using iQ SYBR Green Supermix according to the manufacturer’s specifications in 384 well plates (Bio-Rad, Hercules, CA). For each biological replicate and gene of interest, we quantified expression of a housekeeping gene (efa1) on the same plate. We ran all reactions in triplicate and included negative controls in each plate. We quantified expression using the CFX384 Touch Real-Time PCR Detection System to run two step amplification for 45 cycles at primer-specific annealing temperatures that yielded 96–110% qPCR efficiency (Bio-Rad, Hercules, CA).

We confirmed that the standard deviations of the Ct values from the triplicate reactions were less than 0.2 or removed the outlier value before taking the mean Ct value of each technical replicate for a given sample. We calculated −ΔCt as −1 × (gene of interest Ct – housekeeping gene Ct) and used Welch’s two-sample t-tests to compare expression between the most dorsal and most ventral sections of the regenerating blastema tissue within each species.

Our RNAseq data collection focused on only the regenerating ventral blastema of the caudal fin, and one might expect different local expression patterns of genes important for sword formation in the dorsal blastema, since it does not differentiate into a sword following regrowth. Surprisingly, we do not observe lower expression of our focal genes in regenerating X. malinche dorsal blastemas compared to ventral blastemas (Figure S6A,B). Such results could indicate that these genes are important in fin regeneration but not in sword production per se, or that they may interact with other genetic factors to produce this polygenic trait.

Allele-specific expression analysis

We used a modified version of the program WASP (79) to test for evidence for allele-specific expression of genes differentially expressed between X. birchmanni and X. malinche in the regenerating caudal tissue of F₁ hybrids (https://github.com/TheFraserLab/Hornet). WASP corrects for mapping biases that can impact analyses of allele-specific expression by identifying reads that overlap SNPs and removing reads that show evidence of mapping biases. This resulted in counts for the X. birchmanni and X. malinche alleles at each ancestry informative SNP in F₁ hybrids. DESeq2 (77) was used to analyze this count data. Counts were imported into a DESeq object as a matrix with the design ~ individual + allele. All size factors were set to one to avoid size factor normalization, and the model was fit with parametric dispersion.

Although we only identified two genes with significant allele specific expression out of the 3,926 that passed our quality thresholds, we evaluated whether there was evidence for similar patterns in the allele specific and differential expression datasets. For all genes that were differentially expressed between X. birchmanni and X. malinche in regenerating sword tissue and present in our allele specific expression data, we evaluated whether there was concordance between allelic expression ratios in F₁s and the overall direction of expression level differences between species.

We extracted genes that were differentially expressed between X. birchmanni and X. malinche at a corrected p-value threshold of 0.05 and their log fold changes. For these genes, we extracted estimated fold changes in expression of the X. birchmanni and X. malinche alleles in F₁s, generated from WASP and DEseq2 (79); 724 genes present in both datasets). We asked, using a paired sign test, whether the allelic expression ratios were enriched for the observed direction of expression differences between species. We found evidence of substantial enrichment (S=503, p<10⁻¹⁶). In addition, we found a moderate correlation in the fold change estimated for differential expression and allelic ratio using this approach (ρ= 0.24, p=10⁻¹⁰).

Analysis of chromatin accessibility

We repeated the procedures described above to generate tissue for ATAC-seq library preparation. We performed two biological replicates per genotype (X. birchmanni, X. malinche and F₁ hybrids). We dissociated lower caudal blastemas into single cells with papain for 40 minutes at 37°C according to the Worthington Papain Dissociation System, following manufacturer’s instructions. Cells were then washed 2x with cold PBS, resuspended in cold sort media (PBS, 2% FBS, 500 ng/mL DAPI), passed through a 40-um strainer and sorted on BD Aria II to collect live cells. Sorted cells were spun down at 500 ×g for 5 min at 4°C and used for ATAC-seq, as described in Buenrostro, et al., 2015 (80), with inputs ranging from 17,000–50,000 cells. Cells were gently resuspended in 50 μL of cold lysis buffer (10 mM Tris-HCl, pH 7.4, 10 mM NaCl, 3 mM MgCl2, 0.1% IGEPAL CA-630) and nuclei were immediately pelleted at 1000 ×g for 10 min at 4°C. Nuclei were then resuspended in transposition mixture prepared from Illumina Nextera reagents (for 50 μL: 22.5 μL water, 25 μL 2xTD buffer, 2.5 μL Tn5 Transposase). We used 50 μL transposition mixture for inputs of 50,000 cells and scaled down the volume for fewer cells. The transposition reaction was incubated at 37°C for 30 min, then the DNA was purified with Qiagen MinElute Kit. Libraries were prepared by amplifying the transposed DNA using barcoded primers with NEBNext High Fidelity 2x PCR Master Mix (NEB). Amplified libraries were cleaned up with Ampure XP beads (Beckman Coulter) following manufacturer’s instructions, using 1.6 volumes beads per 1 volume library. The size distribution of each library was evaluated on Bioanalyzer 2100 using a high sensitivity DNA kit (Agilent) and the library concentration was determined with the KAPA library quantification kit (KAPA Biosystems). ATAC-seq libraries were multiplexed and sequenced to collect 75 bp paired-end reads on a Nextseq 550.

Reads were mapped to the X. birchmanni reference genome with bowtie and sorted, indexed, filtered to remove reads with mapping quality less than 30, and de-duplicated with samtools (81,82). Peak calling was performed using the findPeaks function in HOMER (83), using an FDR threshold of 0.001, on the two replicates of X. birchmanni and X. malinche tissue. The output was converted to a BED file, and subset to only include peaks under the putative QTL. Data was read into a DBA object with the R package DiffBind (84) to measure differential accessibility at promoters and enhancers under the QTL region. Briefly, reads were counted and normalized by library size, a consensus peak set was generated, and differential accessibility analysis was performed in DESeq2.

We found five differential peaks between X. birchmanni and X. malinche that fell underneath the joint QTL region (Table S3). These were directly upstream of four genes (rapgef5a, itgb8, btd, and slc25a13). However, none of these genes were significantly differentially expressed between regenerating caudal tissue in X. birchmanni and X. malinche (Table S3).

We also explored the possibility that long-range enhancers within the QTL may regulate genes that fall outside of it. Notably, all differential ATAC-seq peaks identified occur at least 500 kb downstream from the 5’ edge of the QTL region. We thus consider it unlikely that an enhancer within the region targets a gene falling outside the QTL to the 5’ edge (85). However, we identified two differential peaks within 60 kb of the 3’ edge of the QTL region. As a result, we evaluated whether there was evidence for differential expression of genes up to 500 kb away from this peak in the 3’ direction. We found six genes within this interval with differential expression (dlx5a, ago2, igf2bp3, gpnmb, wipf3, fkbp14; out of 16 annotated genes in this interval). All of these genes, with the exception of gpnmb, were more highly expressed in X. birchmanni, concordant with the direction of the chromatin accessibility peak. We note that the 3’ interval containing these genes also contains its own differential ATAC-seq peaks (Table S3).

Pathway and functional category enrichment analysis in regenerating sword tissue

We investigated evidence for functional enrichment among differentially expressed genes using Gene Ontology and KEGG pathway analysis. For KEGG pathway enrichment, we used X. birchmanni vs X. malinche regenerating fin log fold changes calculated for DESeq2 differential expression analysis. Gene IDs were mapped to Entrez IDs from the X. maculatus Ensembl database (version 99) and KEGG pathway gene sets were generated with the kegg.gsets function from X. maculatus KEGG IDs. Both databases were downloaded between 30 March 2020 and 2 April 2020. Enriched gene sets were inferred with the R package gage (86) for both single and dual directionality. For GO enrichment, we used BioMart to extract X. maculatus Ensembl IDs and generated a gene universe using all genes included in X. birchmanni vs X. malinche day 10 regeneration DESeq2 analysis. We used a hypergeometric test (hyperGTest in R) to obtain a set of overrepresented GO biological pathway terms in the significantly differentially expressed (FDR adjusted p-value < 0.1) gene set.

Substitution and tolerance predictions at candidate sword genes within the QTL region

For each of the candidates in the associated sword QTL region (Data S1C), we generated predicted cDNA alignments based on the X. birchmanni and X. malinche genomes and available genome sequences for other species (72,87,88) and quantified rates of amino acid evolution using PAML (89). Using the known phylogenetic relationships between species (14) we identified derived substitutions in these genes, with a focus on derived substitutions in X. birchmanni. We similarly used PAML to test for evidence of differences in evolutionary rates on the branch leading to X. birchmanni.

We also compared individual substitutions in X. birchmanni and X. malinche sequences in detail using SIFT (42). Using the X. malinche, X. cortezi, X. montezumae, X. nezahualcoyotl, and X. hellerii (outgroup) sequences, we identified derived amino acid changes in X. birchmanni. We then extracted all protein sequences for bony fish from NCBI’s protein database and aligned them with clustal omega (90). We evaluated this alignment with SIFT and asked whether derived substitutions in X. birchmanni were predicted to change protein function.

Predicted binding sites of candidate gene sp8

Sp8, one of the identified candidate genes in our QTL interval, is a zinc finger transcription factor, raising the possibility that motifs it recognizes may differ between species and in part mediate its effects. Research has shown that the action of sp8 may be dependent on other sp genes with which it dimerizes, as well as its interaction with dlx family genes (43).

Given a number of observed substitutions in the X. birchmanni ortholog of sp8, we were curious if this translated into any predicted differences in binding affinity in sp8’s targets. Using zinc finger binding prediction software available at zf.princeton.edu and the Polynomial SVM model, we were able to determine that the predicted binding motif is conserved for both X. birchmanni and X. malinche orthologs, with identical position weight matrices predicted (91). However, conservation of the position weight matrix does not mean that sp8 binding sites are conserved between species. We next used the software FIMO to search for binding sites using this position weight matrix in the X. birchmanni and X. malinche genomes (92) with a p-value threshold of 0.00001. Although the majority of identified binding sites were shared between species (81%), a subset were unique, with 1,418 predicted binding sites unique to X. malinche. We identified genes that fell within 10 kb of these X. malinche-specific binding sites. These genes are reported in Table S4 and notably include bmp, bmpr2, fgfr3, fgf6, fgf12, fgf14, wnt2, and wnt4.

Ancestry near the chromosome 13 QTL in natural hybrid populations

To ask whether patterns of X. malinche ancestry in natural hybrid populations were unusual in our QTL as a whole and at candidate genes inside the QTL region, we generated joint null distributions for each population (Figure 6B). For each hybrid population for which we had previously inferred local ancestry (24,28,47), we generated summaries of average ancestry in 1 Mb and 50 kb windows across the 24 swordtail chromosomes. Next, we generated expected null distributions for ancestry across the four focal populations. We randomly drew a window from each population and recorded the ancestry. For each population, we determined whether the randomly drawn value had equivalent or lower X. malinche ancestry than observed in the focal QTL region for that population. We repeated this procedure 5,000 times and asked how frequently randomly drawn ancestry from all four populations was equal to or lower than true X. malinche ancestry.

Inference of selection on sp8 region in time transect data

In one population where we have access to time series data (the Acuapa population), we observe a significant decrease in X. malinche ancestry over time at the sp8 gene (Figure 6D; two proportions z-test of 2018 versus 2006 – p = 0.007). This decrease in X. malinche ancestry over time could be driven by selection or by genetic drift. To explore whether the decline in X. malinche ancestry at sp8 in this time series data was consistent with selection we used an approximate Bayesian approach.

For each simulation, we drew parameters and performed simulations using the following procedure:

1. First, we determined starting parameters for each simulation

   1. We drew a starting ancestry frequency, f_m, for 2006 from a uniform distribution. We defined this uniform distribution as ranging from 0.19 to 0.37 X. malinche ancestry. This range represents the observed X. malinche ancestry at sp8 in our 2006 sample from Acuapa, plus or minus the standard error of that estimate.
   2. We drew a selection coefficient, s, from a uniform distribution ranging from 0.5 to −0.5.
   3. We drew dominance of the X. malinche allele, h, from a uniform distribution ranging from zero to one.
   4. The number of generations of selection, g, was drawn from a uniform distribution ranging from 12 to 36 generations. This is equivalent to the lower and upper bound of the plausible number of generations that could have elapsed during the 12 year sampling period (93).
   5. We drew the diploid hybrid population size, n, from a uniform distribution ranging from 200 to 10,000.
2. For each set of parameters, we iterated through g generations of selection

   1. We calculated the predicted X. malinche allele frequency in the next generation with selection using the general selection model.
   2. We simulated genetic drift by sampling 2*n alleles from a binomial distribution with the probability set to the X. malinche frequency in the next generation predicted by the general selection model.

3. We accepted simulations where the final ancestry fell within one standard error of the average ancestry at sp8 observed in 2018. We repeated simulations until 1,000 parameter sets were accepted.

These simulations resulted in a well-resolved posterior distribution of the strength of selection against X. malinche ancestry at sp8 with a maximum a posteriori (MAP) estimate of −0.1 (95% confidence intervals: −0.44 – −0.03). Estimates of the dominance coefficient, h, were skewed towards zero (MAP – 0.01) but 95% confidence intervals were broad (0.007 – 0.94). Posterior distributions for the remaining parameters mirrored the prior distribution.

Another possible cause for reduced X. malinche ancestry not captured in the simulations described above is migration from a population with greater X. birchmanni ancestry. Several lines of evidence argue against this. First, we do not observe a significant shift in genome-wide ancestry from 2006–2018 (p=0.1, average malinche ancestry 2006=0.26, average malinche ancestry 2018=0.29). Second, of 346 individuals sampled from Acuapa over this time period, we did not detect a single ancestry outlier for X. birchmanni-like ancestry, but sampled three outliers for X. malinche-like ancestry, suggesting that if migration is occurring, it would drive in the opposite direction of our signal.

Phylogenetic approaches

For phylogenetic analyses, we needed sequences from each species of interest aligned to the same coordinate system (Data S1E). To generate these sequences, we mapped reads from each species to the X. birchmanni reference genome (47) using bwa (94). Next, we removed duplicates with picard tools, realigned indels, called variants using GATK (95), and filtered variants as previously described (24). We used these variant sites to generate alignments of phylogenetically informative sites for each species on chromosome 13 (https://github.com/Schumerlab/Lab_shared_scripts).

For each gene of interest within the QTL peak, we extracted the alignment, which included both exons and introns, and ran the program RAxML (96) with 100 rapid bootstraps. Following this step, we used RAxML to infer maximum likelihood phylogenies for these regions using the General Reversible Time substitution model. We examined the output for evidence of regions with unusual topologies that received high bootstrap support, which may indicate the presence of incomplete lineage sorting (ILS) or gene flow.

We were also interested in inferring phylogenetic evidence for gene flow between X. variatus and X. birchmanni and X. malinche using this dataset. We used the program PhyloNet-HMM (48) which uses pre-defined hybridization topologies and gene trees to infer local ancestry in the presence of ILS. Specifically, we evaluated whether there were regions within the QTL interval on chromosome 13 that supported gene flow from X. variatus into X. birchmanni but not from X. variatus into X. malinche, using a posterior probability threshold of 0.9.

Past work has shown the PhyloNet-HMM approach to have a relatively low false-switching rate in the presence of ILS and good power to detect introgressed segments (88). We evaluated this further using simulations. Because of the deep evolutionary divergence between X. birchmanni and the platyfish clade (Figure 1A; 1.6% pairwise sequence divergence), we predicted that we might have power to identify introgression along the genome, even for ancient hybridization events.

To evaluate our power to detect local introgression from a platyfish species into X. birchmanni, we simulated divergence and admixture using SLiM (97), decoded ancestry and genotypes at ancestry informative sites using the tree sequence recording functions in SLiM and pySLiM. We used a burn-in of 90,000 generations and simulated four populations with split times equivalent to estimated split times between X. hellerii, X. variatus, X. birchmanni, and X. malinche, assuming a historical effective population size of 25,000 (24). We simulated a contribution of 4% of the genome from the lineage leading to X. variatus and 96% from the lineage leading to X. birchmanni (24). We assumed that a pulse of admixture occurred immediately after the split between X. birchmanni and X. malinche. This assumption is conservative because ancient gene flow will result in small ancestry tracts that are more difficult to detect using HMM-based methods.

We simulated 5 Mb sequences using the recombination map from the first 5 Mb of X. birchmanni chromosome 2. We sampled a single individual from each population, converted vcf files generated by SLiM to phylip files using the tool vcf2phylip, filtered ambiguous sites, and ran the PhyloNet-HMM program (48). We selected sites that had greater than 0.9 posterior probability support for a given ancestry state and determined whether PhyloNet-HMM inferred the correct ancestry state in that region. We also asked about the false negative rate (i.e. the rate with which tracts are missed). This procedure was repeated 50 times.

The results of these simulations suggest that even in this scenario of ancient admixture we expect to have relatively good power to detect introgressed tracts. Across simulations, the accuracy per ancestry informative site was 96% and we detected 97.5% of introgressed tracts (Figure S7). As a secondary approach, we also calculated the F₄ ratio statistic (49) in 1,000 SNP windows. Because the F₄ ratio statistic simply relies on site counts it may be more sensitive to short ancestry tracts that are too small to be detected by HMM-based approaches. We used the configuration X. maculatus X. hellerii : X. birchmanni X. malinche :: X. maculatus X. hellerii X. variatus X. malinche implemented through the admixtools program (49). We again did not find evidence for higher X. variatus contribution to the X. birchmanni genome near the chromosome 13 QTL peak.

Quantification and Statistical Analysis

QTL analysis on 536 adult males was performed with the software R/qtl (33). We used the scanone function and the EM algorithm to perform this analysis, as described in the STAR Methods section QTL analysis. Significance was determined using 1,000 permutations of sword phenotype onto observed genotypes to estimate the LOD threshold equivalent to a 5% false discovery rate for our dataset (LOD threshold = 4). Correlation analyses between different hybrid phenotypes were conducted in R using the cor.test function. Bootstrapping and permutation analyses described in the STAR Methods section Narrowing the QTL interval were performed in R. We performed Approximate Bayesian Computation simulations implemented in R to estimate the effect size of the chromosome 13 QTL and our power to detect QTL of varying effect sizes. In addition to QTL mapping, we asked about ancestry effects in aggregate on each of the 24 Xiphophorus chromosomes using the ppcor package in R with a Bonferroni correction for the number of chromosomes and an AIC model selection approach using the step function in R. We performed simulations of polygenic traits using both the hybrid population simulator admix’em as well as in R (see Simulations of polygenic traits and QTL analysis and Estimates of heritability); we compared distributions from simulations using Kolmogorov–Smirnov tests. Gene expression analysis was performed using the R package DESeq2 (77) with an adjusted p-value threshold of 0.1; allele-specific expression analysis was performed with WASP (79) and DESeq2 (77), also with an adjusted p-value threshold of 0.1. All RNAseq analyses relied on three pools of biological replicates. We performed gene-enrichment analysis on differentially expressed genes using the GOstats, GSEABase, bioMart, and GAGE packages in R. The statistical test used to evaluate enrichment was the hypergeometric test (“hyperGTest”) with a p-value threshold of 0.05. A subset of genes identified from gene expression analysis were verified with qPCR; t.tests were performed to compare −ΔCt values between groups. At least six biological replicates were included for qPCR verification. Differential chromatin accessibility analysis was quantified using the R package DiffBind (84) and statistical analysis was again performed with DESeq2 (77) with a p-value threshold of 0.05; two pools of biological replicates for each species were used. Ancestry analysis of the QTL region and inference of ancestry change over time in the Acuapa population were implemented in R as described in the STAR Methods sections Ancestry near the chromosome 13 QTL in natural hybrid populations and Inference of selection on sp8 region in time transect data. Error bars in Figures 1D-E, 2B, 4A-D, 5B, 6D, S3, and S6 indicate the mean ± one standard deviation. Figures were prepared in R and Microsoft Powerpoint.

Supplementary Material

1

Data S1. Compilation of data used for several analyses, relates to Table 1 and STAR Methods. A) Genes differentially expressed in regenerated sword tissue. Information on 3,333 significantly differentially expressed genes between X. birchmanni and X. malinche in the regenerating caudal fin. B) All genes that overlap with the joint QTL region. Genes that fall within the narrowest joint QTL interval on chromosome 13. C) Summary of expression, annotation, and substitution evidence for candidate genes in the QTL interval. Evidence associated with the strongest candidates within the QTL region on chromosome 13, those associated with fin or limb phenotypes, growth, skeletal or muscle phenotypes. D) Number of reads collected per individual included in RNAseq-based analysis of sword regeneration. E) SRA accessions for previously published datasets used in phylogenetic analysis. Average per basepair coverage when mapped to the X. birchmanni reference genome is listed.

3

Table S1. Overrepresented Gene Ontology terms in the significantly differentially expressed genes between X. malinche vs X. birchmanni regenerating fin tissue, relates to Table 1. Of 3368 GO terms tested, 216 terms were found to be significantly overrepresented with a p-value < 0.05. This analysis included all genes at FDR adjusted p-value < 0.1.

4

Table S2. Possible targets of the miRNA found in our QTL region, relates to Table 1. miRNA target search was performed with the program RNA22. Targets with binding probability scores greater than 0.3 are listed (upper 10% of binding probability scores for this miRNA genome wide).

5

Table S4. Predicted binding sites of sp8 identified in the X. malinche but not X. birchmanni genome, relates to Table 1. Predicted locations of sp8 zinc finger binding motifs that are unique to X. malinche. The position weight matrix for sp8 was generated using the computational tool at zf.princeton.edu and the program FIMO was used to search for motifs.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited Data
NCBI Sequence Read Archive: RNAseq data, ATACseq data, low coverage fastq files, ACUA time series fastq files	This paper	SUB8614498 (pending)
Dryad: qPCR data, local ancestry calls, phenotype data	This paper	doi:10.5061/dryad.c2fqz616p (pending)
Experimental Models: Organisms/Strains
Artificial crosses	Offspring generated from wild caught parental species	N/A
Hybrid population data	Wild caught samples	N/A
Oligonucleotides
Primer: sp8_for: ACACTTGAGGACGCACAGTT sp8_rev: CTGTTTTTCCGCCGGTCTCT	This paper	N/A
Primer: grn2_for: GGGAAGTGGGAACCTTGTG grn2_rev: CACAGCCACACAGTCATCCT	This paper	N/A
Software and Algorithms
Admix’em	69	https://github.com/melop/admixem
R/qtl	33	https://rqtl.org
ImageJ	66	https://imagej.nih.gov/ij/download.html
ancestryinfer	30	https://github.com/Schumerlab/ancestryinfer
mixnmatch	30	https://github.com/Schumerlab/mixnmatch
MUMmer	70	https://github.com/mummer4/mummer
TrimGalore!	76	https://github.com/FelixKrueger/TrimGalore
DESeq2	77	https://bioconductor.org/packages/release/bioc/html/DESeq2.html
‘ashr’	78	https://github.com/stephens999/ashr
WASP	79	https://github.com/bmvdgeijn/WASP
bowtie	82	http://bowtie-bio.sourceforge.net/index.shtml
samtools	81	http://www.htslib.org/download/
HOMER	83	http://homer.ucsd.edu/homer/
DiffBind	84	https://bioconductor.org/packages/release/bioc/html/DiffBind.html
PAML	89	http://abacus.gene.ucl.ac.uk/software/paml.html
SIFT	42	https://sift.bii.a-star.edu.sg
bwa	94	http://bio-bwa.sourceforge.net
GATK	95	https://gatk.broadinstitute.org/hc/en-us
RAxML	96	https://github.com/stamatak/standard-RAxML
FIMO	92	http://meme-suite.org/doc/fimo.html
PhyloNet-HMM	48	https://bioinfocs.rice.edu/software/phmm
SLiM	97	https://messerlab.org/slim/

Highlights.

• The sword ornament is a sexually selected trait lost three times in swordtail fish

• Using QTL mapping we identify a major effect QTL for sword ornament length

• In addition to major QTL, results indicate that sword length has a polygenic basis

• Patterns of ancestry in hybrid populations hint at selection against the sword