Time and laser ranging: a window of opportunity for geodesy, navigation and metrology

Abstract

Recent progress in the domain of time and frequency (T/F) standards requires important improvements of existing time distribution links. Among these, the accuracy of time transfer is actually an important part of the concerns in order to establish and maintain time & space references from ground and/or space facilities. Several time transfers by laser link projects have been carried out over the past 10 years with numerous scientific and metrological objectives. Satellite Laser ranging (SLR) has proven to be a fundamental tool, offering a straightforward, conceptually simple, highly accurate and unambiguous observable. Depending on the mission, LR is used to transmit time over two-way or one-way distances from 500 to several millions of km. The following missions and their objectives employed this technique: European Laser Timing (ELT) at 450 km, Time Transfer by Laser Link (T2L2) at 1,336 km, Laser Time Transfer (LTT) at 36,000 km, Lunar Reconnaissance Orbiter (LRO) at 350,000 km, and MErcury Surface, Space ENvironment, GEochemistry, and Ranging (MESSENGER) at tens of million km.

This article describes the synergy between SLR and T/F technologies developed on the ground and in space and as well as the state of the art of their exploitation. The performance and sources of limitation of such space missions are analyzed. It shows that current and future challenges lie in the improvement of the time accuracy and stability of the time for ground geodetic observatories. The role of the next generation of SLR systems is emphasized both in space and at ground level, from the point of view of GGOS and valuable exploitation of the synergy between time synchronization, ranging and data transfer.

1. Introduction

Early ideas about the time transfer by laser ranging technique gave opportunities to enhance the synergy between both laser ranging and time and frequency technologies. The optical time transfer as a specific space technique is motivated primarily by challenges of fundamental physics and inter-planetary navigation. This technique further provides insights into the time and frequency metrology and space geodesy such as the calibration and validation of microwave systems, the understanding of the clock behavior, the comparison of clocks in remote observatories, the monitoring of high quality space oscillators, the precise orbit determination (POD), etc. (Smith and Zuber 2016).

Some of these topics have been recently tested and studied by several space missions, where two-way and/or one-way laser ranging measurements were obtained. First, some time transfer experiments used both two-way and one-way laser ranging (with a Laser Retroreflector Array, LRA) at the same time being on Earth orbits such as: the Laser Time Transfer (LTT) project on Beidou at 36,000 km (Meng et al. 2013a), the Time Transfer by Laser Link (T2L2) experiment on Jason-2 at 1,336 km (Samain et al. 2008) and the European Laser Timing (ELT) instrument at 450 km to be launched in 2020 on the international space station (Hess et al. 2011) Second, the one-way laser ranging experiment to the Lunar Reconnaissance Orbiter (LRO) spacecraft at lunar distance proved to be an essential tool to improve the orbit determination, despite the issues that have been raised by the instability of the onboard quartz crystal oscillator (Mao et al. 2017). Finally, an original two-way experiment has been performed to the MErcury Surface, Space ENvironment, GEochemistry, and Ranging (MESSENGER) planetary mission, as an asynchronous laser transponder technique using the proper laser altimeter of the mission instead of LRA due to the huge distance (Smith et al. 2006). See the list of the missions, periods and corresponding references on Table 1.

Table 1:

Space oscillators onboard planetary [with a laser altimeter] and Earth observation missions: the Mars Global Surveyor (MGS) mission (Albee et al. 1998) [Mars Orbiter Laser Altimeter (MOLA) (Abshire et al. 2000)]; the Mercury Surface, Space Environment, Geochemistry, and Ranging (MESSENGER) mission (Solomon et al. 2007) [Mercury Laser Altimeter (MLA) (Cavanaugh et al. 2007)]; the Lunar Reconnaissance Orbiter (LRO) mission (Tooley et al. 2002) [Lunar Orbiter Laser Altimeter (LOLA) (Smith et al. 2010)]; the ICASat mission (Schutz et al. 2005) [Geoscience Laser Altimeter System (GLAS) (Abshire et al. 2005)]; the Jason-2 mission and the Time Transfer by Laser Link (T2L2) instrument (Samain et al. 2008); the Laser Time Transfer (LTT) instrument on Beidou (Meng et al. 2013a); The European Laser Timing (ELT) instrument on the ISS (Prochazka et al. 2016).

Mission	Period	Oscillator & reference	stability	τ (s)
MGS	1996–2006	USO, (Norton and Cloeren 1996)
MOLA		OCXO, (Bloch et al. 2008)
MESSENGER	2004–2015	OCXO
MLA
LRO	2009–2014	OCXO, (Weaver et al. 2004)	7.10−14	40
			2.10−13	10,000
ICESat	2003–2010	OCXO, monitored by onboard GPS
GLAS
T2L2 /Jason-2	2008-	OCXO, (Auriol and Tourain 2010)	2.10−13	10–100
LTT /Beidou	2007-	Rubidium	3.10−13	100
ELT /ISS	2020-	ACES/Pharao, (Laurent et al. 2015)	3.10−16	1 day
		ACES/H-maser	1.510−15	10,000

The need for laser ranging station development and adaptation is an enduring challenge in view of making time transfer by laser at 1-nanosecond (ns) of accuracy and less. In all of the above-cited missions, a given laser ranging station has been chosen as a primary station to conduct tests, campaigns and routine operations; in each case a number of technological time and frequency developments have been carried out. As a result, the time transfer technique has achieved a few picosecond (ps) stability at 1000 s and tens of ps accuracy (Samain et al. 2015), (Prochazka et al. 2016). Here, we specify the particular issues on which performance are thereby ensured such as the stability of the local distribution of time metrology signals, the accuracy of the time calibration at the primary station, the free-running stability of the oscillator and the long-term stability and accuracy of the local time with respect to UTC (Sun et al. 2013).

In addition to the time and frequency technologies developed at ground stations, highly stable oscillators are flown in space for a variety of different science and programmatic missions; e.g. the Cesium and Rubidium oscillators onboard the global navigation satellite systems (GNSS), or the ultra-stable-oscillators (USO) used primarily as time generators in planetary and Earth space missions. The onboard oscillators are selected by taking into account some criteria related to the required quality and durability in space conditions depending on the mission objectives, cost and the typical timespan for which they are used. Among these objectives, it is essential to maintain a short-term stability of $\frac{\delta f}{f}<{10}^{-13}$ between 1 and 100 seconds, and to reduce the systematic change in frequency with time of such free-running oscillators as much as possible, i.e. $\frac{\delta f}{f}<{10}^{-11}$. day⁻¹ (Cash et al. 2008), (Auriol and Tourain 2010); see also the Deep Space Atomic Clock which will fly soon (JPL-DSAC 2017).

The goal of this article is to highlight the different parts of the technological developments that made the success of some recent optical time transfer ranging experiments both in space and on the ground, and to extrapolate the necessary improvements to achieve future scientific goals in terms of fundamental physics, navigation, and chronometric geodesy (Lisdat et al. 2016). Section 2 is dedicated to time and frequency technologies that have been developed for ground stations, whereas section 3 describes the characteristics of space oscillators used to time tag the received laser pulses. Sections 4 and 5 describe the time transfer experiments that use both one-way and two-way laser ranging measurements, which are based on retroreflectors or transponders (laser altimeters), respectively. Finally, we discuss the next generation of optical time transfer techniques and consider the necessary future improvements to reach a better accuracy in Section 6.

2. Time and Frequency on the Ground

2.1. Timing electronics

The timing electronics at the ground stations have to time tag the transmitted and the received laser pulses to the precision and accuracy required by the laser time transfer. They usually consist of a counter or timer clocked by a stable oscillator and a register that record the timer reading when triggered by an external event. The timer reading has to be referenced to a standard time, such as the Universal Coordinated Time (UTC) or the Global Position System (GPS) time.

The timer can be a time interval analyzer (TIA) that measures the time from a periodic time mark, such as the GPS 1 pulse per second (1 PPS) tick and reset at these time marks. Another type of timer is an event timer (ET) that continuously record the time, also known as continuous time interval analyzer, which records the times of external events as well as standard time marks. The underlining clock to either a TIA or an ET is usually free running to achieve the highest clock stability. The clock frequency can be calibrated by recorded times of the standard time marks such as the GPS 1 PPS ticks.

Early TIAs were made of simple counters driven by a clock oscillator. The timing resolution was equal to the clock period. Time to digital converters (TDC) were later used to improve the timing resolution to a small fraction of the clock period by delaying the signal through a series of logic gates and use digital logics to determine the time of the signal arrival from the previous clock edge (Paschalidis et al. 2002) (Kalisz 2004). The propagation delays of the logic gates are kept constant with respect to the reference clock time with the use of a delay lock loop. TDCs achieve fine time interval measurements without the need for a high-speed clock. They use ordinary silicon integrated circuit technology to achieve picosecond timing at the same electrical power consumption as ordinary complementary metal-oxide-semiconductor (CMOS) devices. TDC can be implemented in field programmable gate array (FPGA) or application specific integrated circuit (ASIC). Nowadays TDC can achieve 1 ps precision at a standard external clock frequency of 5 or 10 MHz. TDCs have been used in both ground stations and laser timing instruments in space, see e.g. (Kalisz 2004).

2.2. Compensation of local delays

Optical time transfer from ground to space and from ground via space to ground requires a continuous control over all acting system delays between the respective clocks (Samain et al. 2015), (Schreiber and Kodet 2017). Unlike for laser ranging applications, where the estimation of the epoch of the laser fire event does not require a resolution higher than 1 ns, accurate time transfer demands a resolution of a few ps. The same stringent requirements apply for the local system delays.

Time on an observatory in practice is defined as a fast rising leading edge 1 PPS signal at a specific output port of a high quality local clock, for example a hydrogen maser (H-maser), which ideally is referenced to UTC. In order to compare this clock to an orbiting clock in space, one has to establish the time it takes for this 1 PPS signal to propagate from the reference clock to the laser ranging system timer. In addition to that the actual laser pulses used for the time transfer have to be accurately related to the reference point of the laser ranging system with respect to their time delay. Again, a meaningful measurement resolution of about 1 ps is desirable in order to make the local clock error small compared to the time transfer error.

Unlike the transfer of reference frequencies operating a clock, the transfer of time requires a very wide bandwidth in order to generate a steep leading edge slope for the time tagging process. On top of that, there must be provisions in place that keep this system delay stable. Temperature related variations of the transfer time of the 1 PPS signal through electronic circuitry, thermal expansion in electrical transmission lines and variations in the electric ground potential may cause fluctuations of the time delay in the order of roughly 30 ps. In the case of serious problems the experienced delay changes may easily exceed 100 ps.

One possible way of controlling the local system delay sufficiently, is the application mode-locked fs-pulse (femto) lasers. They have ultra low noise properties in the optical as well as in the microwave regime. When the time markers are carried from the clock to the ranging facility by the ultra-short laser pulses in a two-way approach, temperature or strain induced length variations of the connecting optical fiber can be compensated. For this purpose the reference frequency from the local clock is used to determine and fix the repetition rate of the mode-locked pulse laser. The pulses are then traveling through the fiber. A combination of two types of fibers, of which one is the conjugate of the other, compensates the effects of dispersion and ensures that the laser pulses remain short. At the end of the fiber near the timer of the laser ranging facility the pulses are reflected by a semi-transparent mirror and traveling back to the source. At the source the outgoing laser pulses are correlated with the returning signal and a variable delay line at the beginning of the transmission line is adjusted in a closed loop configuration to a constant path delay. Figure 1 illustrates this procedure in a simplified block diagram.

Figure 1:

Block diagram of the delay compensation circuit. Over several hundred meters the coherence of the time could be stabilized to within 1 ps.

A prototype of this time distribution system has been set up at the Geodetic Observatory in Wettzell (Germany) in preparation of the optical time transfer for the Atomic Clock Ensemble in Space (ACES). Currently it achieves a stability for the phase of the transferred time of 1 ps over several days. When the time distribution system is fully integrated to the laser ranging facility it should be possible to relate the ground clock to the ACES clock with an accuracy smaller than 25 ps for a single shot measurement.

2.3. Accuracy of the ground station clocks

Since the frequencies of oscillators drift over time, ground station timing accuracy degrade over time and links to the standard time − i.e. UTC, GPS time or TAI (Temps Atomique International) − have to be performed periodically. In order to maintain a uniform time frame on the long-term, this issue is of particular importance especially when a network of stations is needed. We learned from both the LRO and T2L2 time transfer experiments that some ground station clocks may have time offsets of hundreds of ns and even more, despite the International Laser Ranging Service (ILRS) recommendations of δt < 100 ns (Pearlman et al. 2009), (Exertier et al. 2017).

The easiest method to maintain a ground station time to within a few ns to the standard time is to reference it to the GPS time from a nearby receiver; see e.g. (Ray and Senior 2005). However, the GPS time from a generic GPS receiver is affected by some delays, as internal (including receiver and ground cables) and external (atmosphere), of the microwave signal (Lombardi 2008). It is thus necessary to carry out a time calibration of the equipment by itself and to use e.g. Common-View (CV) or All-In-View GPS receivers in order to link the ground station time scale to a standard in avoiding common effects as demonstrated by (Lee et al. 2008).

The NASA Goddard Space Flight Center (GSFC) has calibrated its H-maser to the master clock and hence TAI at the nearby United State Naval Observatory (USNO). An All-In-View GPS receiver (DiCOM GTR50) was used to monitor the time offset between the 1 PPS signal of the H-maser to the GPS time over a 20-month period thus achieving a long-term accuracy of 1 ns (Sun et al. 2013). The Grasse laser ranging station has time calibrated its laser system achieving an accuracy better that 0.1 ns (Samain et al. 2015). See details per primary station on Table 2.

Table 2:

Ground laser (532 nm) ranging stations used as primary station; (Sun et al. 2013)⁽¹⁾, (Abshire et al. 2007)⁽²⁾, (Samain et al. 2015)⁽³⁾, (Schreiber and Kodet 2017)⁽⁴⁾. These SLR stations use a H-maser clock and picosecond resolution and precision event timer. For the GGAO site, we separated the different experiments that were conducted since 2005 on MLA (MESSENGER), MOLA (MGS) and LRO equipped with a 1-way uplink.

Station	Laser	Calib.	Link to Std time	Std Time / Accur.
	(Hz / mJ / ps)	(ns)		(ns)
GGAO, NASA		1 (1)	All-View GPS	USNO / 1 ns
MLA	240 / 14 / –			MET / 1 ns
MOLA	49 / 11 / –	(2)		MET / 130 ms
LRO				MET / 10–20 ns
Grasse, France	10 / 100 / 10–200	< 0.100 (3)	CV GPS	UTC(OP) / 1–2 ns
SHAO, China	20 / 150 / 250		id.
Wettzell, Germany		< 0.025 (4)	id.

3. Oscillators in Space

Most spacecrafts carry quartz crystal oscillators as the clock sources for time keeping. The oscillator and clock are reset shortly before launch. A counter is used to count the clock cycles and uses it to define the mission elapse time (MET). Ideally, the spacecraft should carry an USO as the time base for the MET and distribute the time to the payload instruments. The on-board clock time is periodically compared against a common time standard, such as UTC, via a special time keeping procedure between a ground station and the spacecraft. The on-board clock frequency and drift rate are estimated by comparing the MET and UTC over a given period of time. Therefore the time keeping procedure between the ground station and the spacecraft have to be performed frequent enough to guarantee the clock frequency of such free-running oscillators (USO) can be modeled and predicted to the required precision.

For precision geodetic instruments such as a laser altimeter, a very stable and precise clock oscillator is needed. The clock oscillator has to have a short-time stability of < 10⁻¹³ so that the clock frequency drift during the laser time of flight time is negligible. A temperature compensated crystal oscillator (TCXO) or an oven-controlled crystal oscillator (OCXO) have to be used to meet these requirements (Weaver et al. 2004).

For precision radio frequency tracking and Doppler shift measurement of a spacecraft, a USO with even more stringent requirements must be used, as it is the case with the Doppler Orbitography and Radiopositioning Integrated by Satellite (DORIS) tracking technique (Auriol and Tourain 2010).

The planetary and Earth Observation missions, which are described in Section 4 and 5, generally use a highly stable OCXO oscillator with a short-term stability of a few 10⁻¹⁴ to 3–5.10⁻¹³ between 10 and 100 seconds (see Table 1). LRO has a one-way laser ranging system that requires the OCXO to be stable to a few ns over the two-hour LRO orbit period (Cash et al. 2008). NASA Jet Propulsion Laboratory will soon launch its Deep Space Atomic Clock (DSAC) in space as a technology demonstration which will greatly enhances the performance of current space clock designs and virtually eliminate spacecraft clock errors to benefit future navigation and radio science (JPL-DSAC 2017).

4. Time Transfer Experiments with Laser Retroreflectors

4.1. LTT

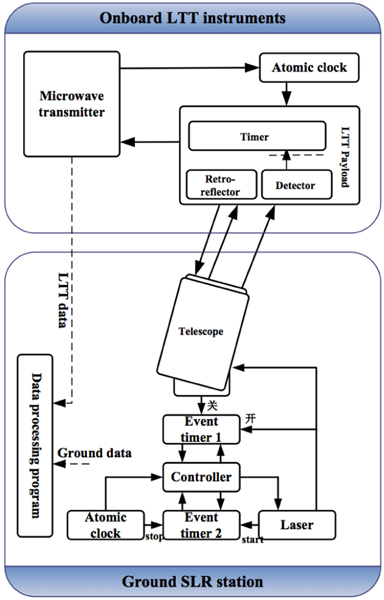
Laser Time Transfer is the first ground and satellite time synchronization system by laser ranging to navigation satellites. The whole system including the onboard instruments and ground SLR station was designed by the Shanghai Astronomical Observatory (SHAO); see the block diagram on figure 2 and the retroreflectors on figure 3. Because of the limited geographical area of the ground network of stations, high precision time synchronization is required between BeiDou satellites and ground stations. The mainly time synchronization of BDS is using a microwave system, but LTT was installed as a test experiment of the whole laser link, and for better time measurement precision and accuracy.

Figure 2:

Block diagram of LTT experiment, from ground to space clocks.

Figure 3:

Laser Retroreflector Arrays on Beidou, MEO and GEO/IGSO; the LRA includes 42 corner cubes and has a weight of 2.45 kg; but for IGSO and GESO, the LRA includes 90 corner cubes of 4.85 kg (down); see (up) the detector and event timer.

The ground station includes the normal laser ranging instruments, an additional timer and a laser emitting control system. The characteristics of the ground laser station and onboard equipment are given in Table 2 and Table 3, respectively. The onboard laser detector adopts a 25 μm active area Si Single Photon Avalanched Diode (SPAD) produced by Czech Technical University with a quantum efficiency of about 20%. This type of device has been passed through the radiation resistance test made by CNES (the French space agency) and proved to be sunlight resistant. When the very weak laser signal arrived at the detector, it must run at single photon mode. The detector is doubled for backup. To reduce the noise from Earth, of a big FOV (for elevation > 30°, 23° for MEO, 15° for IGSO) and a small one (for elevation > 50°, 17° for MEO, and 11° for IGSO). Additional solar optics and narrower band width filters are also adopted in order to reduce photon noises. Another consideration for single photon detector is a gate signal like the one for laser ranging systems, which is synchronized with onboard 1 PPS. This also leads to a clock prediction requirement and a ground laser emitting time control system. The onboard timer receives the 1 PPS and 10MHz from the satellite, generates 20 PPS gate signals. Because of the limited capability of the navigation channel, one value is selected over twenty per second. The onboard timer achieves 100 ps single shot precision.

Table 3:

Time transfer by laser ranging; characteristics of onboard instruments.

Instrument	Accuracy (ps)	Detector (photon, ps)	Timer (ps)	Stability (ps)		Link
				1-shot	NP
MLA			200	500		1-way downlink
LRO				360	165 / 5 s	1-way uplink
T2L2	< 100	multiple, 70	3	45–50	3–4 / 30 s	2-way (LRA)
LTT		single, <150	<100	260	20 /500 s	id.
ELT	25	id.	<1	10	3 /300 s	id.
GPS (CV)	1–2 ns			5 ns (15 min)	1 ns /1 day	1-way

The LTT payloads were installed on Beidou MEO/IGSO satellites, and were launched on April 2007, August 2010, April 2011 and April 2012. All four LTT experiments were carried out successfully, and the ground and satellite time difference results have the same trend compared to microwave method, but with different precision and system delay. All the measurement of LTT experiments have a single shot precision of around 300 ps, stability for a single session of 500 s duration of 20 ps at 5 (figure 4 and Table 3). The gate-mode LTT payload and FOV contribute to the noise resistance. A comparison of the different LTT payloads with different FOV and gate modes showed a much better detection rate when satellites are outside the Earth’s shadow thus confirming that the Earth’s shadow reduces the detection rate. After modifying the rate of the ground laser ranging system to 1kHz, a new Chinese Laser Timing (CLT) project is under development which will be based on a similar structure to the LTT system.

Figure 4:

Timing stability of LTT time transfer on MEO satellite.

4.2. T2L2

T2L2 is based on a ground segment materialized by a ground station network issued from the ILRS network of stations (Pearlman et al. 2009), and a dedicated space instrument which was launched as a passenger experiment on the Jason 2 satellite in June 2008 (Samain et al. 2008); see figure 5. The elementary time transfer which benefits from both one-way (ground-to-space) and two-way (range; see LRA on figure 6) links is provided by a ground laser station firing the space segment over a typical pass of 1000 s; the resulting observable is called a ”triplet“. The time transfer between two remote ground clocks is calculated from several independent elementary links, the space segment being a relay; in the common view mode (the onboard field of view is of 55°) ground stations are firing T2L2 together, whereas in the non common view mode (over intercontinental distances > 4000 km) the ground-to-space passes are separated by the time of flight of the satellite between the SLR stations.

Figure 5:

Block diagram of the T2L2 space segment.

Figure 6:

Laser Reflector Array and T2L2 optics (detectors) onboard the Jason-2 satellite.

The T2L2 experiment was designed to realize time transfers with a stability better than 1 ps over 1000 s and an accuracy better than 100 ps (Samain et al. 2014); see on Table 3. The objectives are essentially of metrological nature, especially with the common view ground-to-ground time transfer, where the deviations of the on-board clock can be reduced almost entirely. This clock is based on the reference oscillator of the DORIS tracking technique which contributes, in addition to the LRA, to the precise orbit determination of the Jason-2 satellite (Table 1). Supplementary objectives of the mission are dedicated to space geodesy and fundamental physics. On the one hand, the stability of the T2L2 ground-to-space time transfer can be used to accurately determine the frequency bias of the USO over a laser station equipped with an highly stable atomic clock (e.g. a H-maser). On the other, T2L2 provides some opportunity to make a test of the isotropy of the speed of light by cumulating several ground-to-space passes; this test depends, however, on the capability to follow both the measured range together with the difference of clocks at the same precision level on a variety of space orientations (from the satellite rise to the set).

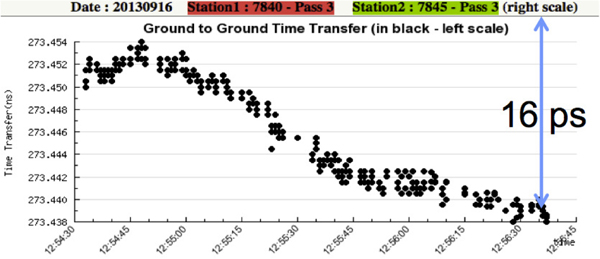
Several field campaigns were carried out between 2012 and 2016, both at the primary laser station of T2L2 (Grasse) and at the international level. First, the ground-to-ground time transfer between remote H-masers in common view (in Europe) demonstrated a very good stability over days (of tens of ps, see figure 7) in addition to an accuracy of 150 ps which was confirmed by GPS(CV) links (Exertier et al. 2016). Additionally, we are currently testing the stability of ground-to-ground links now using GPS(iPPP) solutions against T2L2 over three baselines (between three SLR stations) in Europe; early results show a standard deviation below 100 ps (Leute et al. 2018). Second, concerning space geodesy, we have demonstrated the ability of the T2L2 ground-to-space time transfer to directly ”read“ the frequency bias of the DORIS USO at a few parts in 10⁻¹³. It has allowed us to monitor the frequency changes of the oscillator over time and thus to establish a frequency model of physical nature (Belli et al. 2015). As a result, the integration of this model allowed us to calculate an on-board time scale between 1200 and 15,000 seconds regularly. This integration was applied to determine the ground-to-ground time transfer from the Grasse laser ranging station (as primary station permanently linked to GPS time with 1–2 ns accuracy) to almost all clocks of the ILRS stations during 8 years (Exertier et al. 2017).

Figure 7:

Ground-to-ground time transfer via T2L2/Jason-2 between Herstmonceux (UK) and Grasse (F) SLR stations (with H-masers); September 16, 2013.

Due to its presence in space for years, T2L2 being accessible to many SLR stations has permitted to monitor each clock from a unique time standard. As a result, we demonstrated that most of the SLR station reference clocks have a UTC shift higher than 100 ns, some times hundreds of ns and even of a few μseconds (Belli et al. 2017).

4.3. ELT/ACES

The European Laser Timing experiment will perform optical time transfer to the Atomic Clock Ensemble in Space (ACES). ACES is an ESA mission in fundamental physics which will bring atomic clocks of unprecedented stability into space (Cacciapuoti and Salomon 2009). Mounted on the International Space Station (ISS) at the nadir pointing platform of the Columbus module, it will establish a time scale built upon an active hydrogen maser for short time stability and a laser cooled Cs clock, called PHARAO (Laurent et al. 2015), for longtime accuracy (Table 1). The common time scale will have a stability of 10⁻¹⁶.

The hardware in space consists of a retro-reflector of CHAMP type, a Single Photon Avalanche Diode (SPAD) detector for the conversion of photons into an electrical signal, and a timer time tagging the events in the ACES time scale. To allow one-way and two-way laser ranging at the same time an attenuation of the incoming laser pulse at the ISS by a factor of ~106 depending on the angle of incidence has to be guaranteed. This attenuation is achieved by a diffuser plate in combination with a field stop in the shape of a snowflake (Prochazka et al. 2016). The large field of view of ±5° … 60° will allow a tracking from ground from elevation of 30 degrees. Near zenith the snowflake will limit the tracking to 85 degrees elevation. The experiment will use the single photon method. Due to the high stability of the on-board time scale, not only common view time transfer between ground stations is possible, but also non-common view. The targeted accuracy is 25 ps and precision of 3 ps at 300 s of integration time (see Table 3).

The time transfer in single photon mode is the difference from T2L2 and is in common with LTT. This method prevents systematic effects which can occur by electronically compensating time walk effects for varying laser pulse lengths and energies. The complexity of the measurement is transferred to the station operation and keeps the space segment simple. The greatest improvement is the stability of the space clock. In T2L2 time transfer precision is limited by the USO, in ELT time transfer will be limited by the method itself not by the clock.

In addition to the optical time transfer, clock comparison can be performed on a frequency basis by GNSS when the on-board GNSS receiver is connected to the ACES frequency. The main clock comparison method is a microwave link (MWL) which will be operated at time laboratories in Europe, the US and Japan. This instrument uses modulated frequencies in the Ku- and S-band with a modulation frequency in Ku of 100 MHz. MWL and ELT will share a common timer, tightly connecting these two methods. So in total two time comparison and one frequency comparison methods are available and can be compared at the collocation site Wettzell GOW, Germany) operating both techniques.

The advantage of the MWL is due to the high modulation frequency which will allow a time comparison space to ground of 0.3 ps precision in 300 s integration time with an accuracy of 100 ps. In contrast the optical link with a laser repetition rate of 1 kHz and a pulse length of 10 ps will reach a precision of 3 ps. Optical links can be calibrated in the near field with high accuracy so the accuracy of the calibrated time transfer can be as good as 25 ps space to ground. The objectives of ELT are to show the capability of single photon time transfer in the discussed accuracy and precision, to exploit the capability to calibrate the MWL, and to study the tropospheric delays in the microwave regime.

Many aspects make the ELT experiment very challenging. Some of them are related to the single photon method in combination with the low orbit of the ISS, others come along with the fact that the ISS is a manned space station. SLR stations participating in ELT have to meet safety requirements, like hardware control of laser power and handling a go/nogo-flag controlled by the mission operators (Schreiber et al. 2014) (Schlicht et al. 2012). Concerning the orbit, predictions every 90 min have to be handled. The laser power has to be controlled to measure in the single photon mode. The detector on-board will open the gate every 1–10 ms (station dependent) in ACES time. The offset of ACES time to UTC will be known to better than 50 ns and will be communicated by the ELT data center (Marz et al. 2016) via the prediction file. The biggest challenge for the station will be the fact that at daytime the detector has to be hit by the laser pulse within 100 ns after gate opening, making a strict time keeping to UTC and controlling laser fire time within some nanoseconds necessary. A real-time determination of time bias and correction of the predictions to this value will help to get along with this challenge.

The accuracy of the trajectory of the clock is the biggest uncertainty contribution in the transformation of proper time to coordinate time. The clock prediction is therefore limited by the accuracy of the orbit and attitude prediction of the ISS. To analyze our prediction procedure we compared the time transformation of a hypothetical clock based on predicted orbits with the one based on real orbits. For this analysis orbits together with their predictions were calculated by DLR on the basis of a SIGI data receiver mounted on the ISS. Each file contains 12 hours of the calculated orbit and 12 hours of prediction. Every 3 hours a new file was generated. Based on these orbits the difference between the predicted clock and the true clock is shown in figure 8. The maximum difference observed for 18 orbits was 14 picoseconds for a 12 hour prediction.

Figure 8:

Difference between true and predicted clock behavior.

To offer the laser ranging stations a handsome way of handling the ACES clock offset to UTC only the linear drifting part of the ACES time scale is communicated. So additional to the error due to predicted orbit, the variability of the clock along the orbit is neglected. The calculated clock correction without drift is of 2 ns peak-to-peak over 24 hours; the linear drift is accurate within 1.5 ns.

5. Time Transfer Experiments with Laser Altimeters in Space

NASA GSFC has built several space-borne laser altimeters over the past 25 years which provided a unique opportunity to demonstrate laser time transfer from ground stations to the spacecrafts at interplanetary distance. In-orbit calibrations were conducted in which the spacecraft point the laser altimeter at Earth and scanned the instrument bore sight about the ground station in a raster pattern. Laser pulses were transmitted simultaneously between the laser altimeter in space and ground station. The times of the transmitted and the received laser pulses were recorded at both terminals. The laser pulse arrival times and spacecraft pointing data were used to estimate the laser pointing angle with respect to the spacecraft coordinate system, the receiver bore sight, and co-alignment with the camera. The relative clock offset and drift rate with respect to ground time were estimated as well.

5.1. Time transfer to MESSENGER via two-way laser ranging

In May 2005, a two-way laser ranging test was conducted between the 1.2-m telescope facility at the Goddard Geophysical and Astronomical Observatory (GGAO) and the Mercury Laser Altimeter (MLA) following its second Earth flyby, at a distance of nearly 24 million km (Smith et al. 2006) (Zuber et al. 2006) (Neumann et al. 2014). The primary objective of the test was to calibrate the MLA ranging function and instrument bore sight. It also demonstrated a precision laser time transfer over the longest distance in space to date. The test setup was that of an asynchronous laser transponder (Degnan 2002). The one-way light time from the ground to the laser pulse arrivals at MLA were captured as well as the downlink light times of MLA laser pulses to the ground station, over a span of half an hour. The unknown variables included the motion of the spacecraft during the time of the laser pulse arrivals from Earth, and the USO-driven MET clock used to time the laser pulses received and emitted by MLA. The spacecraft trajectory was also estimated independently to a high precision from RF tracking, and the clock parameters were adjusted daily by the MESSENGER Project, allowing an overall comparison.

The MLA timing electronics not only measured the time interval of its laser time of flight to the Mercury surface, it could also be configured as an event timer to record the times of the laser emission and detection on a common time base at about 0.2 ns resolution for the nearly three-minute round trip light time. The laser time transfer precision was only limited by the MLA timing electronics and the receiver signal to noise ratios (SNR), to 10–20 cm rms. Finally, MLA shared the clock signal from the MESSENGER spacecraft and was synchronous with MET to within a fraction of 1 ns.

Laser ranging tests between MLA and GGAO were successfully conducted on May 25 and 31, 2005. Uplink and downlink are detailed in Tables 2 & 3. The ground station detected 14 and 24 laser pulses from MLA over periods spanning 2 and 3 s on the first and second occasions, respectively, chiefly limited by the brief time period when MLA and the ground station formed direct line of sight during the raster scan. MLA detected more than 100 laser pulses from GGAO over a 30 minutes period on both occasions. The precision achieved from a total of 90 uplink and 15 downlink pulses was 0.2 m in range and 0.66 ns in time, in spite of a very weak uplink detection (Smith et al. 2006).

The MESSENGER spacecraft USO stability during the test period was comparable to the resolution of the MLA timing electronics, with an unknown system offset of a few microseconds between MLA and the radio subsystem time. Since the tests were conducted during solar system cruise and the Earth’s motion is known, the instantaneous one-way light time from GGAO to MESSENGER and the frequency offset of the on-board clock oscillator could be solved via simple regression to the observations. The range measured by the laser pulses was 23,964,675,408.4 ±0.2 m, after accounting for a 486.6 m additional range due to the relativistic effect. The difference between the laser measurement and the predicted spacecraft ephemeris was 27.1 m, which could be from the uncertainty in the ground station time delay in various subsystems. Finally, the time differences between the laser measurement and the spacecraft MET estimated from the RF tracking data were 0.35 ms and 0.14 ms on the two successful days, which was well within the accuracy and resolution of the MET model for navigation and science operation.

5.2. One-way uplink time transfer experiment to MOLA in Mars orbit

A one-way laser transmission experiment was successfully conducted from GGAO to MOLA on the MGS spacecraft in Mars orbit over 81 million km on September 28, 2005 (Abshire et al. 2007). It was near the end of the MGS mission and the MOLA clock oscillator had ceased to operate (see Tables 2 and 3). The timing resolution of MOLA was degraded to the 0.125 s intervals during which the spacecraft acquired data from MOLA. The major uncertainty of the epoch time on MOLA was the delay from the MGS MET to MOLA through the software. The MET on MGS spacecraft was assumed accurate for this test.

The MGS spacecraft scanned the MOLA laser at GGAO on Earth two times during a 40-minute period. The laser pulses rate was set to 49 Hz to avoid being a multiple and consequently synchronous with the MOLA 8 Hz measurement window. For the second raster scan, the laser pulses were shuttered on and off at 1.22-second interval (6 pulses of the 49 Hz laser). There were several hundreds of laser pulses detected at MGS/MOLA during both the scans. By correlating the transmitted and the received laser pulse train patterns from the second raster scan, the time delay from the spacecraft clock time to the MOLA clock time was solved to be 137 ms at the maximum correlation. This was consistent with the time delay solved from radio frequency tracking of the spacecraft and the MOLA ground track matching, 114 ms (Rowlands et al. 1999), considering the tolerance of the epoch time in orbit determination. Despite the coarse timing resolution, this GGAO to MGS/MOLA test remained to be the longest distance and truly interplanetary laser link experiment to date.

5.3. One-way downlink time transfer from GLAS/ICESat to GSFC

A one-way laser downlink time transfer experiment was successfully conducted on November 3, 2006 from the Geoscience Laser Altimeter System (GLAS) on the ICESat spacecraft to NASA GSFC during a routine ICESat-GSFC overpass operations. The primary purpose of the overpass was to compare the atmospheric backscatter profile measurement from GLAS in nadir direction and those from ground based lidar at GSFC in zenith direction. It also provided a unique opportunity to demonstrate laser time transfer from an orbiting laser altimeter. A GLAS flight spare detector was placed along the ground track of ICESat overpass. An oscilloscope and an event timer were used to record the waveforms and the time of the received laser pulses with respect to UTC.

A total of 28 laser pulses from GLAS were recorded over a 1.1 second time period, including pulses before and after the direct line of sight during the overpass. The GLAS laser pulses forward scattered by atmosphere were strong enough to be detected by the ground detector located a few km from the actual laser footprint. Since GLAS measured the laser time-of-flight (i.e. light time) during the overpass, one could solve for the time offset of GLAS by pairing up the transmitted and the received laser pulses and calculate the differences. The measured and predicted times differed by 3.43μs. The time offset obtained from the special GLAS timing calibration operation at the White Sand was 3 ± 1μs (Magruder et al. 2005). The measurement precision and accuracy were limited by the GPS receiver time accuracy, uncertainty in the system delay, and pulse waveform saturation, which could all be improved.

5.4. Laser time transfer with the one-way Laser Ranging receiver on LRO

The LRO mission carries a one-way laser ranging system to complement the RF tracking for precision orbit determination (Zuber et al. 2010). It has a small telescope co-bore-sighted with the high gain antenna (HGA), which can receive laser pulses from Earth while LRO is in view from the ground station. The laser ranging receiver field of view is wide enough to cover the entire Earth so that laser ranging stations at different parts of the world can range to LRO simultaneously as long as the moon is in view. The signals detected by LRO are transmitted to one of the receiver channel of the Lunar Orbiter Laser Altimeter (LOLA) over an optical fiber bundle. The laser pulse emission and detection times are recorded by both LOLA with respect to the spacecraft MET and the ground station with respect to UTC. The time bases at LRO are sufficiently stable that the relative time drift during each laser ranging pass (1 hour) were only a few ns. The ground station clock at the primary ground station at NASA GSFC was based on a Cesium frequency standard from 2009 to 2011 and later switched to a H-maser clock source. As mentioned earlier, the frequency and the epoch time of the clock was monitored against the USNO master clock to within 1-ns rms using an All-In-view GPS receiver. The difference between the laser pulse event times at LRO and the ground station gave an so one-way time-of-flight measurement, which include the spacecraft orbit movement plus a nearly constant offset. The offset was a slow varying variable and could be solved from other orbital informations.

The LRO laser ranging system operated continuously from LRO launch in June 2009 to the end of the first extended science mission in September 2014. The laser ranging measurements also provided a direct monitor of the spacecraft time to tens of ns, and the LRO clock time predicted to within a few μs for months (Mao et al. 2017).

Since LRO system could detect and record laser pulses from multiple ground stations simultaneously (Mao et al. 2011), the results of these simultaneous laser ranging measurements could be used to compare the ground station clocks, or transfer times using the light times from RF tracking. The accuracy of the time transfer depended only on the difference of the light times from the ground stations to a large tolerate in light time measurement accuracy. For an LRO orbit position uncertainty of 100 m (10 m typical) in radial direction, the time transfer accuracy limited by the light time accuracy was <0.1 ns. A detailed analysis of the clock monitoring can be found in (Sun et al. 2013).

The concept of LRO time transfer was first verified on ground between NGSLR and the nearby MOBile LAser System (MOBLAS-7) at NASA GSFC (50 m from each other and they shared the same clock source) by ranging to a corner cube target. The laser pulse arrival times at the target from both NGSLR and MOBLAS-7 were recorded with a photodetector and an event timer. The target was precisely surveyed to within 1 cm. That measurement configuration was the same as LRO laser ranging but to a stationary and known target. The measurements were performed for one hour on each target. The time offsets solved from these one-way laser ranging tests differed by 0.3 ns, which was within the measurement error of our timing equipment and the uncertainty in the time delay from the photodiode that detect the laser emission to the invariant point of the telescope.

Laser time transfer between NGSLR and MOBLAS-7 to LRO was then conducted a number of times over a 20-month period from 2013 to 2014. The results show a time transfer accuracy of about 1 ns over many months (Mao et al. 2014). Laser time transfer tests were also conducted between NGSLR at Greenbelt, Maryland and the McDonald Laser Ranging System (MLRS) at Fort Davis, Texas over a 6-month period. However, MLRS did not have access to a nearby master clock site that published All-In-View GPD data. Instead, the All-In-View GPD data from USNO at Washington DC were used. As a result, the timing accuracy at MLRS was not as accurate as NGSLR and MOBLAS-7. There were some systematic trends in the time between stations, up to 45 ns peak to peak and 10–20 ns on average.

NASA GSFC also conducted a series of LOLA in orbit calibration by pointing the LRO instrument deck and consequently LOLA laser beam at GGAO and transmitting and detecting laser pulses in both directions (Smith et al. 2017), similar to the MESSENGER to GGAO tests. These tests also provided two-way laser time transfer between GGAO to LRO to within a few nanoseconds (Mao et al. 2017).

6. Next generation and future requirements

6.1. Laser ranging and planetary navigation

Several space missions have been and will be proposed with a laser link. Some of them use a coherent laser link, which is well suited for frequency transfer or measurements of position variation. Others use a propagation of laser pulses, which are most suited to meet the needs of absolute localization or time transfer.

For space missions which are at the scale of the Solar System, the distances are thus in the range of several billion kilometers. Such distances cannot be measured through a classical passive two-way laser ranging scheme. The Earth-Moon distance is now considered as a maximum with a link budget in the ratio of 1/10²⁰. To go further, it is necessary to use a one-way scheme (uplink or up- and downlink). With a payload instrument based on optics having an aperture of 100 mm, a beacon divergence of 5 arc seconds, 300mJ per pulse and a distance of 400 million km, we might have a link budget of around 1 electron. The MESSENGER and MGS experiments opened the door to future laser one-way downlinks. But for planetary missions unable to provide such an on-board equipment, progress into the on-board oscillator in terms of long-term stability and reduced sensitivities to temperature and radiation might be very fruitful. The future NASA/JPL’s Deep Space Atomic Clock (DSAC) represents an enormous advance towards improving deep-space navigation. The mission is developing a small mercury ion atomic clock with Allan deviation of less than 10⁻¹⁴ at one day (current estimates ~ 3.10⁻¹⁵) for a yearlong space demonstration in 2018 (JPL-DSAC 2017). DSAC’s stability yields one-way radiometric tracking data with better accuracy than current two-way tracking data and enables transitioning to more efficient and flexible one-way deep space navigation.

6.2. Laser ranging, time transfer and metrology

What is the perspective of time transfer? The recent experiments of time transfer by laser ranging around the Earth, such as LTT (Beidou), T2L2 (Jason-2) and ELT (ISS) between 36,000 and 500 km, proved the possibility to establish time links into space or ground links via a space equipment with an unprecedented stability (1 to a few ps over thousands of seconds) and accuracy (100 ps, currently and 25 ps expected at GOW, Germany with ELT/ACES), even on a operational basis. To achieve this performance, the primary stations behind these experiments have played on important role in maintaining a high stability of the 1 PPS distribution signals on the long-term and in accurately calibrating most of the equipment, as geodetic and time and frequency.

Currently there is a significant effort in process towards linking major National Metrology Institutions together by optical clocks over compensated fiber networks (Lisdat et al. 2016). This allows accurate frequency comparisons over long distances, already achieving around 10⁻¹⁸ over 1000 km in Europe (Germany, France and United Kingdom), which level corresponds to around 1 cm high on the geoid. Adding space optical time transfer, especially on intercontinental distances, would be an important step towards using time as an observable in space geodesy and cutting edge metrology.

6.3. Laser ranging and GNSS

Communication links between GNSS satellites are available on GPS since a long time (Rajan et al. 2003), but only recently such links are also used for ranging and time transfer on GLONASS satellites (Shargorodsky et al. 2013). Galileo will also get inter-satellite links with the second generation, as their benefit was shown in many studies (Wolf 2000), (Sanchez et al. 2008), (Fernandez et al. 2010), (Fernandez 2011). These links will make use of the whole synergy provided by the exchange of electromagnetic signals between two satellites, namely data transfer, the capability to synchronize clocks and the measurement of distances. This will increase the autonomy of the space segment, reduce the time to alert and lead to better orbits and synchronization of the space clocks.

Doing a combined Optical time transfer and ranging together with GNSS is the best technology for decoupling of these parameters (see figure 9). The troposphere is decorrelated as the optical wavelength do not suffer much from a highly variable wet delay. The clock is decoupled due to time transfer with a system that can be calibrated to a high extend. The capability of calibrating optical links with high accuracy is the reason why the collocation of GNSS receivers with SLR will allow the calibration of the collocated receiver as well as evaluating its systematic errors, like multipath. At the same time, it requires not only local survey to determine the local ties, but also the calibration of timing links. Although optical links can be calibrated to a high extend − ELT aims at 25 ps − it is not enough for a GNSS phase measurement, where about 3 ps are necessary. Therefore, the parameters have to be extracted by a common estimation for periods during which the phase coherence between clock and SLR timer can be kept. Kinematic positioning would benefit the most by clock synchronization. As SLR cannot be easily transported a reference station would be required with the capability of locally distributing the clock information.

Figure 9:

Constellation for a common ranging and time transfer in optical two-way (laser ranging) and GNSS tracking, to separate the contribution of troposphere, clock and station height in a common parameter estimation.

There are two major applications of GNSS tracking in geodesy: The determination of station positions using precise point positioning (PPP) and the realization of reference frames. In both cases not all three components of the position can be determined with the same accuracy. Whereas horizontal position in a weekly IGS solution has an accuracy of about 4 mm, the height is with 8 mm less accurately determined (Kouba 2015). This fact is caused by the high correlation between three parameters, namely station height, station clock, and atmospheric delays. In addition, systematic errors, like multipath and phase center offset and its variations contribute to the error budget of the station height component. For PPP, it is already known that additional information helps to decorrelate these parameters. It was e.g. shown by (Weinbach and Schön 2011) and (Wang and Rotacher 2013) that modeling of ground clocks can improve the kinematic precise point positioning height solution by a factor of 2–3. Surely the PPP solution will also benefit from better reference frames. The important parameters in this task are the modeling of satellite clocks and orbits in the presents of the already mentioned systematic errors. With inter-satellite links, we will have very precise relative orbits with degrees of freedom in rotation and translation. These degrees of freedom can be fixed by a combination of SLR and GNSS (Sosnica et al. 2015) (Thaller et al. 2011) (Urschl et al. 2007). The difficulties the combination has to face lies in the systematic errors of both systems.

(Sosnica et al. 2015) have pointed out, that SLR observations to GNSS satellites provide a precise link in space between these two techniques. A high consistency and strong connection between these techniques will allow to derive a more consistent international terrestrial reference frame (ITRF) in the future. This statement holds even more, when the connectivity is further strengthened by additionally connecting these techniques in time transfer.

For tying the orbit system to Earth not many stations are needed, but the ones used should be equipped with highly stable clocks. A subset of SLR stations with collocated GNSS receivers and a precise timing system synchronized to the GNSS space segment would fulfil this task perfectly as their systematic behavior can be studied, as elucidated already in the discussion of PPP. In such a system biases can be estimated and monitored and systematic effects detected. Common view analyses will help separating modeling errors from other systematics. In order to overcome the weather dependence of the optical link the ground station clocks should be synchronized by fiber links. In this case the synchronization of the ground time scale and the GNSS time scale can be performed by any station without clouds, at least for periods during which phase coherence can be kept. Non collocated ITRF sites will benefit from fixed orbits and monitored biases. They may be calibrated and their multipath analyzed by transportable SLR stations.