Computational and Neurobiological Substrates of Cost-Benefit Integration in Altruistic Helping Decision

Although altruistic behaviors, e.g., sacrificing one's own interests to alleviate others' suffering, are widely observed in human society, altruism varies greatly across individuals. Such individual differences in altruistic preference have been hypothesized to arise from both individuals' dispositional empathic concern for others' welfare and context-specific cost-benefit integration processes.

Abstract

Although altruistic behaviors, e.g., sacrificing one's own interests to alleviate others' suffering, are widely observed in human society, altruism varies greatly across individuals. Such individual differences in altruistic preference have been hypothesized to arise from both individuals' dispositional empathic concern for others' welfare and context-specific cost-benefit integration processes. However, how cost-benefit integration is implemented in the brain and how it is linked to empathy remain unclear. Here, we combine a novel paradigm with the model-based functional magnetic resonance imaging (fMRI) approach to examine the neurocomputational basis of altruistic behaviors. Thirty-seven adults (16 females) were tested. Modeling analyses suggest that individuals are likely to integrate their own monetary costs with nonlinearly transformed recipients' benefits. Neuroimaging results demonstrate the involvement of an extended common currency system during decision-making by showing that selfish and other-regarding motives were processed in dorsal anterior cingulate cortex (ACC) and right inferior parietal lobe in a domain-general manner. Importantly, a functional dissociation of adjacent but different subregions within anterior insular cortex (aINS) was observed for different subprocesses underlying altruistic behaviors. While dorsal aINS (daINS) and inferior frontal gyrus (IFG) were involved in valuation of benefactors' costs, ventral aINS and middle INS (vaINS/mINS), as empathy-related regions, reflected individual variations in valuating recipients' benefits. Multivariate analyses further suggest that both vaINS/mINS and dorsolateral prefrontal cortex (DLPFC) reflect individual variations in general altruistic preferences which account for both dispositional empathy and context-specific other-regarding tendency. Together, these findings provide valuable insights into our understanding of psychological and neurobiological basis of altruistic behaviors.

SIGNIFICANCE STATEMENT Altruistic behaviors play a crucial role in facilitating solidarity and development of human society, but the mechanisms of the cost-benefit integration underlying these behaviors are still unclear. Using model-based neuroimaging approaches, we clarify that people integrate personal costs and non-linearly transformed other's benefits during altruistic decision-making and the implementations of the integration processes are supported by an extended common currency neural network. Importantly, multivariate analyses reveal that both empathy-related and cognitive control-related brain regions are involved in modulating individual variations of altruistic preference, which implicate complex psychological and computational processes. Our results provide a neurocomputational account of how people weigh between different attributes to make altruistic decisions and why altruistic preference varies to a great extent across individuals.

Introduction

Altruistic helping behavior, i.e., sacrificing ones' own interests to boost others' welfare, is a fundamental type of social behaviors in animal and human societies (Heinsohn and Legge, 1999; Warneken et al., 2007). It is widely seen in interpersonal interactions even in situations without any opportunities for reciprocity between strangers (Batson and Shaw, 1991; Marsh et al., 2014). However, it is also found that people are not always willing to help others at their own costs (Bode et al., 2015).

On the one hand, as illustrated by the cost-reward model, people deliberately weigh between the benefit and the cost when deciding whether to behave altruistically (Penner et al., 2005), and variations in such weighing processes (i.e., other-regarding preferences) across contexts, tasks, and individuals further lead to great variations in altruistic behaviors (Morishima et al., 2012; Crockett et al., 2017). On the other hand, the empathy-altruism hypothesis emphasizes that individuals with stronger empathic concern disposition are willing to incur higher costs to help others (Batson et al., 2007; FeldmanHall et al., 2015). Recent neuroimaging studies adopting various paradigms have provided key evidence reflecting these cognitive/affective components in the brain (Moll et al., 2006; Hare et al., 2010; FeldmanHall et al., 2013, 2015). They identified a large neural network, including value-related and reward-related regions, such as orbitofrontal cortex (OFC) and ventromedial prefrontal cortex (VMPFC), and empathy/mentalizing regions, such as temporoparietal junction (TPJ), and anterior insular cortex (aINS), that are critically involved in altruistic decision-making. However, because of the lack of quantitative investigation of the underlying neural substrates, it is still unclear how individuals make altruistic or selfish decisions involving the trade-off between self-interest and other-interest, how such decision processes are implemented in the brain, and whether and how the cost-benefit integration (i.e., the task-specific other-regarding preference) is linked to individuals' dispositional personality (i.e., empathy concern).

Here, we combine a novel interpersonal helping task with computational modeling and functional magnetic resonance imaging (fMRI) to address these issues. First, we formally tested whether people integrate personal costs and other's benefits in a simple linear fashion (Crockett et al., 2017; Gao et al., 2018) or in a nonlinear manner suggested by studies in which participants evaluate subjective values (SVs) of options leading to not only monetary consequences but also other types of outcomes (e.g., effort and emotion; Charpentier et al., 2016; Lockwood et al., 2017).

Second, we tested how human brain encodes personal costs and others' benefits. Relevant previous studies focused mainly on the neural implementations of monetary cost-benefit calculations; the roles of these regions in encoding self-interest versus other-interest could have been confused with their roles in processing monetary gain/loss. For instance, aINS is suggested to be an empathy-related region to modulate altruistic behaviors (Hein et al., 2010; Tusche et al., 2016), but the same region and its adjacent areas are also implicated in representing monetary cost in economic decision-making (Knutson et al., 2007; Engelmann et al., 2017) or in representing both self-interest and other-interest (Qu et al., 2019). It is elusive whether those identified regions (e.g., aINS) are associated with self-regarding versus other-regarding motives or are just recruited in monetary gain/loss processing. The current paradigm allowed us to investigate not only the neural implementation of the cross-modality (i.e., monetary and physical suffering) cost-benefit calculations but also the roles of close but different (sub)regions in processing self-interest and/or other-interest in interpersonal interaction by parametrically manipulating participants' own monetary costs and others' physical benefits.

Third, we also examined whether and how individual differences from distinct sources jointly affect altruistic behaviors. We employed univariate mediation analysis to establish the relationship between the dispositional empathy and the task-specific other-regarding preferences, and used multivariate intersubject representational similarity analysis (IS-RSA) to further explore the neural activity patterns underlying the joint modulations of these two distinct individual variation sources on altruistic decision-making (Jordan et al., 2016).

Materials and Methods

Participants

Sample size were determined by an a priori power analysis using G*Power which suggested that 34 participants would be required in multiple regression analyses if we achieve 80% power to detect a “medium” to “large” effect size of f² = 0.25 at α = 0.05 (two-tailed). Therefore, 37 right-handed undergraduate and graduate students from Tongji University were recruited in the experiment. Four participants were excluded because of excessive head movement (>±3 mm in translation and/or >±3° in rotation), leaving 33 participants for data analyses (mean age= 21.27 ± 1.48, ranging from 19 to 24 years; 16 females). Participants reported no history of psychiatric, neurologic, or cognitive disorders. Informed written consent was obtained from each participant before the experiment. The study was conducted in accordance with the Declaration of Helsinski and was approved by the Ethics Committee of the School of Psychological and Cognitive Sciences, Peking University.

Design and procedures

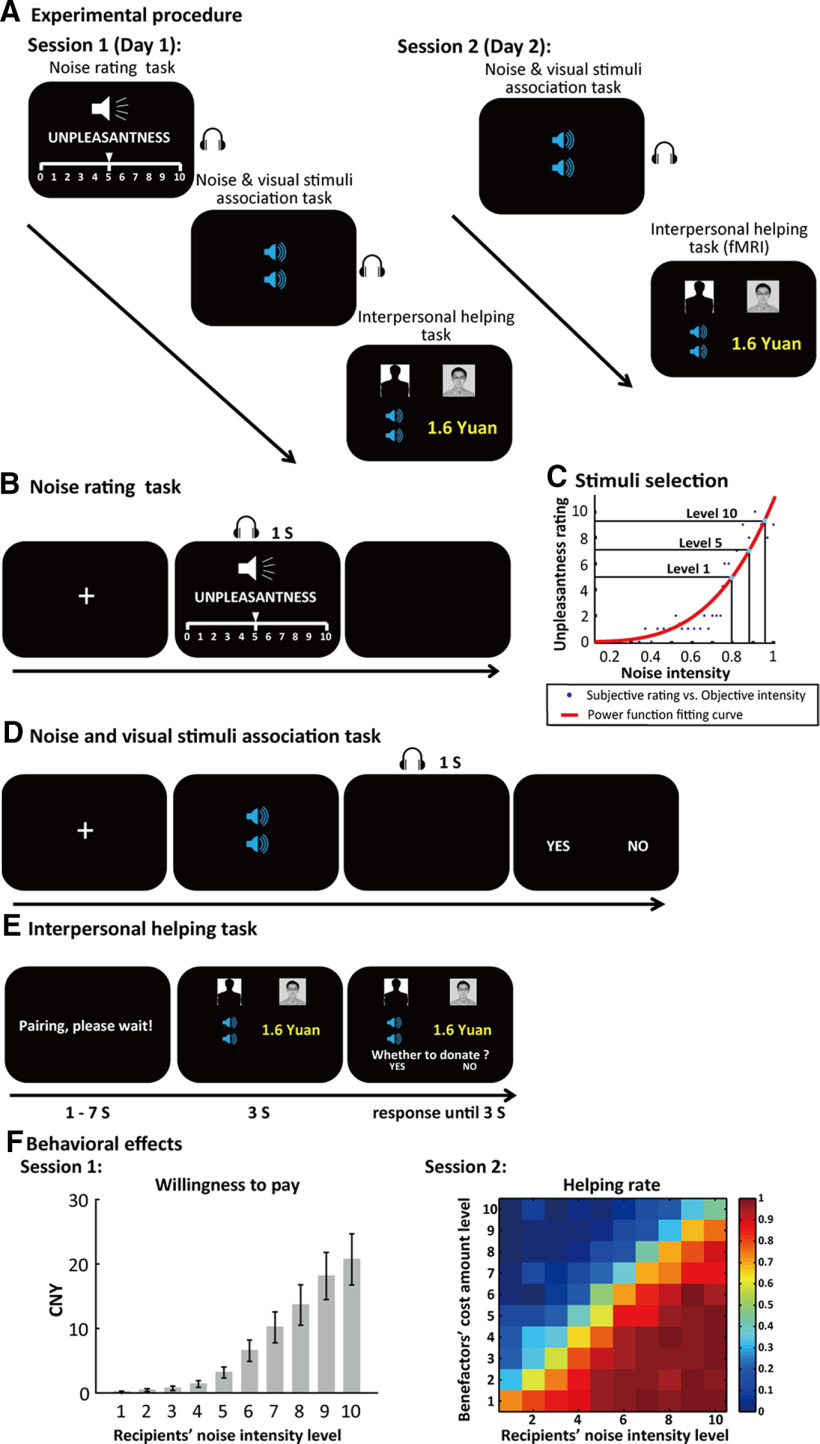
The current study included two sessions on two separate days. On the first day (session 1), participants came to a behavioral laboratory to complete three tasks sequentially: noise rating task, noise and visual stimuli association task and interpersonal helping task (Fig. 1A). First, participants performed the noise rating task in which they rated unpleasantness level for a series of noise stimuli with different intensity (Fig. 1B). Since participants would virtually not hear any noise stimuli during the interpersonal helping task, we asked them to perform a noise and visual stimuli association task (Fig. 1D) to associate different levels of noise stimuli with different visual cues before the interpersonal helping task. These cues were supposed to activate the representation of and emotional responses to the noise stimuli when shown in the helping task. In the interpersonal helping task, we measured participants' altruistic behaviors by asking them to decide whether or not to forgo a certain amount of money from their participation payments to prevent a stranger from hearing unpleasant noise stimuli (Fig. 1E). In this task, we employed a staircase procedure to measure each participant's altruistic behavior and calculate his/her willingness to pay (WTP) to help others for each level of noise stimuli. Details of this staircase procedure are described in the later design optimization section.

Figure 1.

Experimental design and behavioral results. A, The procedure of the experiment. Participants performed the tasks in two sessions on two separate days. In session 1, participants performed the noise rating task, noise and visual stimuli association task, and interpersonal helping task outside fMRI scanner. In session 2, participants performed the noise and visual stimuli association task again outside scanner and the interpersonal helping task in the scanner. B, The procedure of noise rating task. Participants rated unpleasantness for noise stimuli with different levels of intensity on a VAS. C, We estimated a power function (red curve) with individual's unpleasantness rating data, and then selected 10 levels of noise stimuli specific for each participant from mild to extremely unpleasant with equal interval of subjective unpleasantness difference between adjacent levels. D, The procedure of noise and visual stimuli association task. Each of the 10 selected noise stimuli was associated with each of 10 different visual cues (i.e., blue trumpets). Visual stimuli with more trumpets correspond to noise stimuli with higher unpleasantness score. E, The procedure of interpersonal helping task. In each trial, participants decided whether or not to forgo a certain amount of money to prevent the partner from receiving a clip of noise stimuli with a certain level of unpleasantness. Each trial began with a sentence “Pairing, please wait!” on the screen for 1–7 s. Then, the participant's own portrait and a faceless silhouette representing the partner, together with participants' cost amount and a visual cue representing the noise unpleasantness level the partner will receive were presented on the screen for 3 s. Then, the question “Whether to donate?,” together with “yes” and “no” options, was presented in the lower part of the screen. The participant had to make his/her choice within 3-s time limitation. F, Behavioral results in interpersonal helping task for both sessions. Left panel, WTP is depicted as a function of recipients' (partners') noise unpleasantness level in session 1. Error bars indicate SEM, CNY, Chinese Yuan. Right panel, Helping rate is depicted as a function of benefactors' (participants') cost amount level and recipients' (partners') noise unpleasantness level across all the trials over all participants in session 2. Each cell represents one specific cost amount level-noise unpleasantness level pairing condition.

Three to five days after session 1, participants came to the laboratory again (session 2) to complete in sequence the noise and visual stimuli association task again outside the fMRI scanner and the interpersonal helping task in the scanner. The first task aimed to let participants re-experience and re-memorize all the noise stimuli at the beginning of session 2. For each participant, we recorded the participant's blood oxygenation level-dependent (BOLD) signals while he/she was performing the interpersonal helping task with a fixed, specific set of monetary cost amount-noise unpleasantness level pairs. Here, we assumed that the participant would equate others' unpleasant feelings with his/her own feelings for the noise stimuli with certain physical intensity. A total of 160 trials were included in the fMRI version of the interpersonal helping task. Detailed descriptions of each task are presented in the following sections.

Noise rating task

In session 1, on arriving at the laboratory and before any instructions about the study were given, participants completed a noise rating task in which they heard 30 clips of 1-s noise with different levels of volume in randomized order and rated the unpleasantness for each clip on a visual analog scale (VAS; Price et al., 1994). The maximum intensity of the noise stimuli would generate a sound around 100 dB, and the 30 clips were controlled by an attenuation parameter [$\mathrm{\theta }$; $\mathrm{v}\mathrm{o}\mathrm{l}\mathrm{u}\mathrm{m}\mathrm{e}=\left(1-\mathrm{\theta }\right)\times 100\mathrm{d}\mathrm{B}$], which ranged from 0 to 0.97 with an incremental step of 0.033. When $\mathrm{\theta }=0$, there was no attenuation, and the stimuli would be delivered with the maximum intensity; when $\mathrm{\theta }=1$, the sound would be attenuated by 100 dB, which resulted in silence. The VAS ranged from 0 (not unpleasant at all) to 10 (extremely unpleasant; Fig. 1B). For each participant, we used a power function to fit the relationships between subjective unpleasant ratings and objective noise intensity, and defined 10 different levels of intensity from weakest to strongest with equal subjective unpleasantness intervals (Fig. 1C). Specifically, the noise stimuli ranged from the objective intensity which was subjectively rated as 5 (level 1) to 9.5 (level 10) with an incremental step of 0.5. Therefore, although participants' subjective unpleasantness feelings about the noise stimuli may increase nonlinearly (exponentially) with objective noise intensity, their subjective unpleasantness feelings about the 10 selected noise stimuli would increase linearly from level 1 to level 10. The 10 selected noise stimuli would be used in the following tasks. Notably, participants did not know any information about upcoming tasks before they finished the noise rating task. Thus, their subjective feelings about the noise stimuli would not be biased by other irrelevant information or motives. Noise stimuli were delivered by AKG K271 MKII headphones, and controlled by software Presentation (Neurobehavioral System Inc.).

Noise and visual stimuli association task

Since participants would virtually not hear any noise stimuli during the interpersonal helping task, we asked them to perform a noise and visual stimuli association task to associate different levels of noise stimuli with different visual cues before the helping task. In this way, we could use the conditioned visual cues to denote different selected noise stimuli in the interpersonal helping task. As individuals' subjective perceptions of unpleasantness for the same noise stimuli could vary from person to person, we defined 10 levels of noise stimuli for each participant based on his/her own ratings to make sure that different participants have the same subjective feelings of unpleasantness for the same level of noise stimuli. We used a classical conditioning procedure to associate the set of 10 noise stimuli selected in noise rating task specifically to each participant with 10 visual cues (Fig. 1D). The associated visual stimuli were pictures with different numbers of blue trumpet icons. Participants were explicitly informed that a larger number of trumpets (ranging from 1 to 10) indicate a noise stimulus with greater volume. The purpose of this association was to activate participants' experience of the noise stimulus when they saw a visual cue in the later interpersonal helping task. In each trial, a visual cue associated with a specific noise unpleasantness level was presented for one second. One second delay after that, the corresponding noise stimulus was presented to the participant in 80% trials (paired trials), and no stimulus was presented in the remaining 20% trials (unpaired trials). Then the participant indicated whether he/she had heard the noise stimulus in that trial by selecting “yes” or “no” within 3 s. Each pair of association repeated ten times. All the participants performed with high accuracy in identifying paired/unpaired trials in this task (accuracy: mean = 0.99, SE = 0.004).

Interpersonal helping task

In each trial of the interpersonal helping task, the participant decided whether or not to forgo a certain amount of money from the participation payments to help one of the three anonymous partners avoid a 30-s clip of noise stimulus. Specifically, each trial began with a warning cue to indicate that the computer was pairing the participant with one partner, which lasted for a randomly jittered interval (1–7 s). Then the decision-relevant information was presented on the screen for 3 s, including the financial cost of the participant to forgo (e.g., 1.4 CNY, with 1 CNY ≈ 0.16 USD), the benefit for the partner (i.e., the level of noise that would be exempted, indexed by a certain number of trumpets; ranging from 1 to 10), as well as the visual cues indicating the identities of both parties (i.e., a portrait for the participant and a faceless silhouette for the partner; see Fig. 1E). The participant was explicitly informed that his/her subjective unpleasant feelings about the same noise stimulus (represented by the number of trumpets) were the same as the matched partner, but the objective intensity of the noise stimulus associated with the same number of trumpets could vary across individuals. Next, the participant decided within 3 s whether to donate to his/her partner by pressing the corresponding button with the right index or middle finger. If the participant selected “yes”, he/she had decided to donate (forgo) the amount of money as indicated in the trial so that the partner could be free from receiving any noise stimulus. If the participant selected “no”, he/she would keep the amount of money but the partner could be exposed to the noise stimulus as indicated in the trial. In other words, in each trial the participant had to weigh between his/her own monetary costs and the partner's physical benefits when deciding whether to help the other. Once the participant pressed the corresponding button, the chosen option was highlighted by a white box and this screen would last for the remainder of the 3 s. Then the next trial began. Across different trials, both the positions of the facial portrait/silhouette figures and the positions of the “yes” and “no” options were randomly predetermined by computer (Fig. 1E).

To ensure the anonymity of the task and to prevent any confounding effects because of reputation concerns, participants were told that their personal information (e.g., facial portraits) and decisions in each trial (i.e., help or not to help) would not be revealed to their partners, and that they could be paired with anyone of the three partners in each trial without knowing the partner's identity. To encourage participants to treat each trial independently and seriously, they were also told that after fMRI scanning, the computer would select 20 trials randomly from all the decisions they had made in both behavioral and fMRI tasks to calculate the average amount of money, which would be deducted from their participation payments (i.e., 150 CNY). In addition, another trial would be randomly drawn to determine whether and at what unpleasantness level the paired partner would receive the noise stimulus according to the participant's decision. They were also told that the paired partner was one of the future participants in the experiment; every participant, as a partner for previous participants, would potentially receive a clip of noise stimulus determined in a trial randomly selected from previous participants' decision pool. Since we conducted this noise stimulus selection and delivery after participants had completed the whole experiment, they were aware of this procedure but did not know whether or not the previous participant had helped them avoid the noise stimulation or which noise stimulus they would receive until the very end of the experiment. Thus, participants' own decisions of whether to help future participants would not be affected by whether or not they had been helped by previous participants.

Design optimization

To optimize the choice options to efficiently estimate each participant's other-regarding preference, participants were required to perform the interpersonal helping task in both sessions. In the first session (day 1), participants performed the task in a behavioral laboratory. The amount of money for each noise unpleasantness level was generated online by a one-up-one-down staircase procedure which has been widely used in psychophysics studies to detect individuals' discrimination thresholds for stimuli (García-Pérez, 1998). Specifically, each of the 10 noise unpleasantness levels repeated 16 times so that the task included 160 trials in total. If the participant was willing to pay a certain amount of money for a certain noise unpleasantness level on trial n, the amount of money in trial n + 1 with the same unpleasantness level was increased by one step (i.e., k times the amount of money in trial n if the participant did donate on trial n-1 or k times the amount difference between trial n and n-1 at the same unpleasantness level if the participant did not donate on trial n-1; k = 0.8 for the first 10 trials, and k = 0.5 for the last 6 trials); if the participant was unwilling to donate on trial n, the amount of money in trial n + 1 with the same unpleasantness level was reduced by one step (i.e., k times the amount of money in trial n if the participant did not donate on trial n-1 or k times the amount difference between trial n and n-1 at the same unpleasantness level if the participant did donate on trial n-1; k = 0.8 for the first 10 trials, and k = 0.5 for the last 6 trials). We performed logistic analyses and calculated the amount of money the participant would donate with a probability of 0.5 for each noise unpleasantness level, which was referred to as his/her WTP for each noise unpleasantness level. Then we paired each participant's WTPs for the 10 unpleasantness levels with each of the 10 unpleasantness levels to generate 100 choice events for the fMRI task in session 2. Therefore, in session 2 in the fMRI scanner, participants performed the interpersonal helping task with a fixed set of monetary cost amount-noise unpleasantness level pairs, in which their behavior would not influence their subsequent options. For the fMRI task, the cost amounts were the WTPs for the 10 unpleasantness levels based on each participant's own decisions in session 1. As participants usually show stronger behavioral bias and smaller variances for the WTPs of extremely low (i.e., 1 and 2) and high (i.e., 9 and 10) noise unpleasantness levels, compared with the other levels, we included fewer trials with WTPs for 1, 2, 9, and 10 noise unpleasantness levels to shorten fMRI scanning. Thus, the trials pairing each noise unpleasantness level with WTPs for noise unpleasantness levels 1, 2, 9, and 10 were presented once (40 trials in total), and the trials pairing each noise unpleasantness level with WTPs for unpleasantness levels 3–8 were presented twice (120 trials in total). By having such orthogonal manipulations of participants' cost amounts and partners' noise unpleasantness levels, we could examine the behavioral and neural effects of benefactors' costs and recipients' benefits on benefactors' altruistic behaviors parametrically. Participants underwent the task in two functional scanning sessions, with each session including 80 trials and lasting around 15 min.

Other details of procedure

After fMRI scanning, participants filled out postexperiment questionnaires and the balanced emotional empathy scale (BEES), which measures individuals' dispositional empathy for others (Mehrabian, 1997). Higher BEES score reflects a stronger trait empathic concern for others.

Behavioral data analysis

Model-free behavioral data analysis

For altruistic behaviors in the interpersonal helping task in session 1, we first calculated each participant's WTP for each noise unpleasantness level, and then tested the effect of noise unpleasantness level on WTPs by performing a linear mixed-effects model with WTPs as the dependent variable and noise unpleasantness level as the independent variable. Regarding the interpersonal helping task in session 2, we performed generalized mixed-effects analyses to test the effects of cost amount level and noise unpleasantness level on individuals' choices. Specifically, we took participants' helping decisions as the dependent variable (help = 1; no help = 0), and the cost amount level (10 levels of WTP corresponding to 10 noise unpleasantness levels), noise unpleasantness level, and the interaction between cost amount level and noise unpleasantness level as predictors in the model. All the predictors were standardized before being entered into the model. We considered participants as a random-effect intercept term in all regression models above. We performed linear mixed-effects analyses using the nlme and lme4 packages in R.

Model-based behavioral data analysis

To formally examine how people weigh between costs and benefits to make altruistic decisions, we established 15 models in three model families (F1–F3), assuming that participants contingently (F1.1–F1.5) or independently (F2.1–F2.5 and F3.1–F3.5) weighed their own costs and recipients' benefits, either in a linear or a nonlinear manner. In model family F1, we assumed that the sum of weights on costs and benefits equaled to 1. In model family F2, we assumed that two independently weighting parameters modulated costs and benefits. In model family F3, we assumed that, in addition to costs and benefits, people also considered interaction between costs and benefits, and three independently weighting parameters modulated the three components. The models are listed below:

Model family F1 (interdependent models):

F1.1 (linear):

$$U\left(M,N\right)=-\kappa ·N-\left(1-\kappa \right)·M(0<\kappa <1).$$

F1.2 (nonlinear weighting on benefits):

$$U\left(M,N\right)=-\kappa ·N^{\alpha }-\left(1-\kappa \right)·M(0<\kappa <1).$$

F1.3 (nonlinear weighting on costs):

$$U\left(M,N\right)=-\kappa ·N-\left(1-\kappa \right)·M^{\beta }(0<\kappa <1).$$

F1.4 (same nonlinear transformation on both benefits and costs):

$$U\left(M,N\right)=-\kappa ·N^{\alpha }-\left(1-\kappa \right)·M^{\alpha }(0<\kappa <1).$$

F1.5 (different nonlinear transformations on benefits and costs):

$$U\left(M,N\right)=-\kappa ·N^{\alpha }-\left(1-\kappa \right)·M^{\beta }(0<\kappa <1).$$

Model family F2 (independent models):

F2.1 (linear):

$$U(M,N)=-\kappa ·N-m·M.$$

F2.2 (nonlinear weighting on benefits):

$$U(M,N)=-\kappa ·N^{\alpha }-m·M.$$

F2.3 (nonlinear weighting on costs):

$$U(M,N)=-\kappa ·N-m·M^{\beta }.$$

F2.4 (same nonlinear transformation on both benefits and costs):

$$U(M,N)=-\kappa ·N^{\alpha }-m·M^{\alpha }.$$

F2.5 (different nonlinear transformations on benefits and costs):

$$U(M,N)=-\kappa ·N^{\alpha }-m·M^{\beta }.$$

Model family F3 (independent and interactive models):

F3.1 (linear):

$$U\left(M,N\right)=-\kappa ·N-m·M-p·\mathrm{N}·\mathrm{M}.$$

F3.2 (nonlinear weighting on benefits):

$$U\left(M,N\right)=-\kappa ·N^{\alpha }-m·M-p·N^{\alpha }·M.$$

F3.3 (nonlinear weighting on costs):

$$U\left(M,N\right)=-\kappa ·N-m·M^{\beta }-p·N·M^{\beta }.$$

F3.4 (same nonlinear transformation on both benefits and costs):

$$U\left(M,N\right)=-\kappa ·N^{\alpha }-m·M^{\alpha }-p·N^{\alpha }·M^{\alpha }.$$

F3.5 (different nonlinear transformations on benefits and costs):

$$U\left(M,N\right)=-\kappa ·N^{\alpha }-m·M^{\beta }-p·N^{\alpha }·M^{\beta },$$

where $M$ is the amount of monetary costs for the participant, $N$ is the noise unpleasantness level the partner was going to receive, and $U(M,N)$ is the SV for each choice. $N$ = 0 had the participants made the altruistic choice, whereas $M$ = 0 had they made the selfish choice. Regarding the free parameters, $\kappa$ represents a participant's weight on others' benefits (i.e., noise unpleasantness level), $m$ in the model families F2 and F3 represents participant's weight on his/her own costs, and $p$ in the model family F3 represents participant's weight on the interaction between costs and benefits. Note, we incorporated $\alpha$ and $\beta$ in nonlinear models to characterize the nonlinearity of the value function for benefits and costs, respectively, where $\alpha /\mathrm{\beta }$ equals 1 when it is a linear function, $\alpha /\mathrm{\beta }$ falls between 0 and 1 when it is a convex function, and $\alpha /\mathrm{\beta }$ is larger than 1 when it is a concave function (Charpentier et al., 2016). In models F1.4, F2.4, and F3.4, we assumed that the same nonlinear transformation (i.e., $\alpha$) applied to costs and benefits; and in models F1.5, F2.5, and F3.5, we assumed different nonlinear transformations (i.e., $\alpha$ and $\beta$) for costs and benefits.

The SV difference ($\Delta U$) between altruistic and selfish choices in each trial was entered into a softmax function to compute the probability of choosing the altruistic choice:

$$P\left(\mathrm{help}\right)=\frac{1}{1+e^{-\lambda \Delta U}},$$

where $\lambda$ is a free temperature parameter reflecting to what extent an individual's decisions depend on $\Delta U$.

For each model, we estimated the parameters for each participant separately by using the MATLAB VBA-toolbox (available at http://mbb-team.github.io/VBA-toolbox/), which employed a Variational Bayesian analytical approach (Daunizeau et al., 2009, 2014). This iterative algorithm estimates the marginal likelihood or log-evidence of the models by using free energy as an approximation, and accounts for model complexity (e.g., the number of model parameters) when evaluating the likelihood of observing the participants' choice given each model (Friston et al., 2007; Penny, 2012). The prior distributions for $k$ and $\mathrm{m}$ were $N(0.5,2)$, and for $\alpha$, $\beta$, and $\lambda$ were $N(1.5,3)$.

To select the best model in explaining altruistic helping behaviors, we estimated individuals' response data across all the trials with the 15 models and inserted the log-evidence of each model for each participant into a group-level random-effect Bayesian model analysis (RFX-BMS; Stephan et al., 2009). We had 15 × 33 = 495 model evidences (15 models, 33 participants) in total. The RFX-BMS analysis estimates exceedance probability (xp) for each model, which quantifies the probability of a certain model that is more likely implemented than all the other models based on posterior probability (i.e., expected frequency) of each model within the model space (Rigoux et al., 2014).

We also performed cross-validation prediction analyses and model parameter recovery to validate the winning model. To assess the predictive accuracy of the models, we divided all the trials into even-numbered and odd-numbered trials to implement cross-validation prediction analyses. Specifically, for each participant, we first used even-numbered trials to estimate model parameters, and simulated 100 sets of response data with the estimated model parameters for the odd-numbered trials. We measured the predictive accuracy by calculating the proportion of simulated decisions that correctly predicted the observed decision for each trial. Then, we repeated this process by estimating parameters with odd-numbered trials and calculating the predictive accuracy for even-numbered trials. We computed the overall predictive accuracy by averaging the two predictive accuracy values.

In the fMRI experiment, participants went through different individual-specific sets of monetary cost amount–noise unpleasantness level pairings. To confirm that the winning model could reliably estimate parameters given different sets of choice, we performed parameter recovery analysis for the winning model with each participant's dataset separately. Specifically, we first used each participant's estimated parameter values (κ, α, and λ) in the winning model as true values and his/her own cost amount-noise unpleasantness level pairing dataset to simulate 100 sets of response data (i.e., choice). We then estimated all the parameters for the simulated response data with the winning model, and checked the means of the estimated values and the true values for each parameter.

fMRI data acquisition and preprocessing

We collected T2*-weighted echoplanar images (EPIs) using a GE-MR750 3.0 T scanner with a standard head coil at Tongji University, Shanghai, China. The images were acquired in 40 axial slices parallel to the AC-PC line in an interleaved order, with an in-plane resolution of 3 mm × 3 mm, a slice thickness of 4 mm, an interslice gap of 4 mm, a repetition time (TR) of 2000 ms, an echo time (TE) of 30 ms, a flip angle of 90°, and a field of view (FOV) of 200 × 200 mm. We used Statistical Parametric Mapping software SPM12 (Wellcome Trust Department of Cognitive Neurology, London, United Kingdom), which was run through MATLAB (MathWorks) to preprocess the fMRI images. For each session, the first five volumes were discarded to allow for stabilization of magnetization. For the remaining images, we first performed slice-time correction to the middle slice, then realigned the images to account for head movement, spatially re-sampled the images to 3 × 3 × 3 isotropic voxel, normalized them to standard Montreal Neurologic Institute (MNI) template space, and finally spatially smoothed the images using an 8-mm full-width at half-maximal Gaussian kernel. Data were filtered using a high-pass filter with 1/128-Hz cutoff frequency.

Overview of neuroimaging analyses

With neuroimaging analyses, we aimed to answer the questions of how cost-benefit computation for altruistic behaviors is implemented in the human brain, and how individual variations in altruistic behaviors arise from the underlying neural processes. To clarify the neural mechanisms underlying the helping behavior, we first performed general linear model (GLM) analyses to reveal brain regions representing SV of benefactors' costs (${\mathrm{SV}}_{\mathrm{cost}}$), recipients' benefits (${\mathrm{SV}}_{\mathrm{benefit}}$), and decision utility. To explore how individual variations in altruistic preference originate from neural implementations of the cost-benefit computation, we correlated neural responses of ${\mathrm{SV}}_{\mathrm{cost}}$/${\mathrm{SV}}_{\mathrm{benefit}}$ with the model derived parameter of other-regarding preference ($\mathrm{\kappa }$) and performed mediation analyses to further examine the relationship between dispositional empathy, model-based other-regarding preference, and neural responses of ${\mathrm{SV}}_{\mathrm{cost}}$/${\mathrm{SV}}_{\mathrm{benefit}}$. Since in the above analyses, we revealed close but different regions implicated in different subprocesses underlying the helping behavior, we conducted formal analyses to test the dissociations of these regions. In the end, to provide more comprehensive evidence for the neural underpinnings of individual differences in altruistic preference, we employed multivariate analyses (i.e., IS-RSA) to test the neural substrates of general altruistic preference which accounts for both dispositional empathy and model-based other-regarding preference. In the following sections, we provide more details for each analysis.

GLM analyses

We built GLM 1 to identify brain regions responding to the SV of benefactors' costs (${\mathrm{SV}}_{\mathrm{cost}}$) and recipients' benefits (${\mathrm{SV}}_{\mathrm{benefit}}$) and GLM 2 to identify brain regions whose activities were associated with decision utility.

GLM 1

GLM 1 was built to identify brain regions representing the SV of benefactors' costs (${\mathrm{SV}}_{\mathrm{cost}}$) and recipients' benefits (${\mathrm{SV}}_{\mathrm{benefit}}$). Specifically, we derived and standardized the ${\mathrm{SV}}_{\mathrm{cost}}$ and ${\mathrm{SV}}_{\mathrm{benefit}}$ from the winning model (i.e., model F1.2) based on behavioral model comparison results. Then, we regressed BOLD signal onto GLMs which included the regressors corresponding to the onsets of the offer presentation (i.e., cost amount and noise unpleasantness level). These onsets were modulated by two parametric regressors: the ${\mathrm{SV}}_{\mathrm{cost}}$ and ${\mathrm{SV}}_{\mathrm{benefit}}$. We turned off orthogonalization when estimating the model and allowed the two parametric modulators to compete for variance. The duration for this event was equal to the time form onsets of offer presentation to the time point at which the participant pressed the button. GLM 1 also had three regressors of no interest: the onsets corresponding to the fixation screen in each trial, to left button responses, and to right button responses. These events were modeled with a duration of 0 s.

GLM 2

GLM 2 was built to identify brain regions whose activities were associated with decision utility. We regressed BOLD signal onto GLMs containing regressors corresponding to the onsets of offer presentation. These onsets were modulated by a parametric regressor: the utility difference between the chosen choice and the unchosen choice. This event was modeled with a duration equal to the time from onset of offer presentation to the time point at which the participant pressed the button. GLM 2 also had three regressors of no interest: the onsets corresponding to the fixation screen in each trial, to left button responses, and to right button responses.

For both GLM 1 and GLM 2, regressors of interest and no interest were convolved with a canonical hemodynamics response function (HRF). Six rigid body parameters were also modeled as regressors of no interest to account for head motion artifacts.

At the second level, we employed one-sample two-tail t tests to assess the neural estimates of the SV of benefactors' costs (in GLM 1), recipients' benefits (in GLM 1), and decision utility (in GLM 2), respectively. For all GLMs, we adopted a whole-brain corrected threshold [i.e., a combined threshold of voxel-level p < 0.001 uncorrected and cluster-level p < 0.05 family-wise error (FWE) correction] unless a special note. For GLM 1, we also fed contrast images for ${\mathrm{SV}}_{\mathrm{cost}}$ and ${\mathrm{SV}}_{\mathrm{benefit}}$ into a second-level one-way ANOVA design to perform conjunction analysis to assess shared neural regions in representing the two dimensions of SV. As we were interested in regions [i.e., anterior cingulate cortex (ACC), INS, and right TPJ], which had been implicated in altruistic behaviors in prior studies, we performed region of interest (ROI) conjunction analysis and reported the results with a threshold of p < 0.05 small volume correction (SVC) at the voxel level within ROI masks for ACC, INS, or right TPJ, respectively. We used WFU PickAtlas toolbox which is implemented in SPM 12 to generate the ROI masks (Maldjian et al., 2003, 2004). ACC mask included bilateral anterior cingulum regions in AAL atlas, INS mask included bilateral insular and bilateral inferior frontal operculum regions in AAL atlas, and right TPJ mask included right inferior parietal, supramarginal, and superior temporal regions in AAL atlas (Tzourio-Mazoyer et al., 2002).

Mediation analysis

Following the procedure recommended by Preacher and Hayes (2004), we extracted average parametric estimates of ${\mathrm{SV}}_{\mathrm{benefit}}$ within a 3-mm edge cube around the peak voxel of vaINS/mINS for each participant, and constructed a model which took the parametric estimates in vaINS/mINS as a mediator variable, BEES scores as the predictor variable, and other-regarding preference ($\kappa$) as the outcome variable (MM 1). We performed statistical analyses by using a bootstrapping procedure to test the mediation effect in small samples (Preacher and Hayes, 2004).

Analyses for dissociative functions between insular subregions

To formally test functional dissociation between close but distinct regions in aINS [i.e., vaINS/mINS and dorsal aINS/inferior frontal gyrus (daINS/IFG)], we separately extracted parametric estimates of ${\mathrm{SV}}_{\mathrm{cost}}$ and ${\mathrm{SV}}_{\mathrm{benefit}}$ from right vaINS/mINS and right daINS/IFG by calculating average parametric estimates of ${\mathrm{SV}}_{\mathrm{cost}}$ and ${\mathrm{SV}}_{\mathrm{benefit}}$within the right daINS/IFG mask (i.e., dorsal anterior insular cluster in Kelly et al. (2012)' template combined with IFG in AAL template) and the right vaINS/mINS mask (i.e., middle insular cluster in Kelly and colleagues' template) for each participant. Repeated-measures ANOVA were performed to test the effects in parametric estimates of ${\mathrm{SV}}_{\mathrm{cost}}$ and ${\mathrm{SV}}_{\mathrm{benefit}}$ between daINS/IFG and vaINS/mINS. We calculated the correlations between other-regarding preferences and (1) parametric estimates of ${\mathrm{SV}}_{\mathrm{cost}}$ in vaINS/mINS and in daINS/IFG, and (2) parametric estimates of ${\mathrm{SV}}_{\mathrm{benefit}}$ in vaINS/mINS and in daINS/IFG, respectively. Correlations were compared using two-tail correlation comparison analysis (Steiger, 1980; Diedenhofen and Musch, 2015).

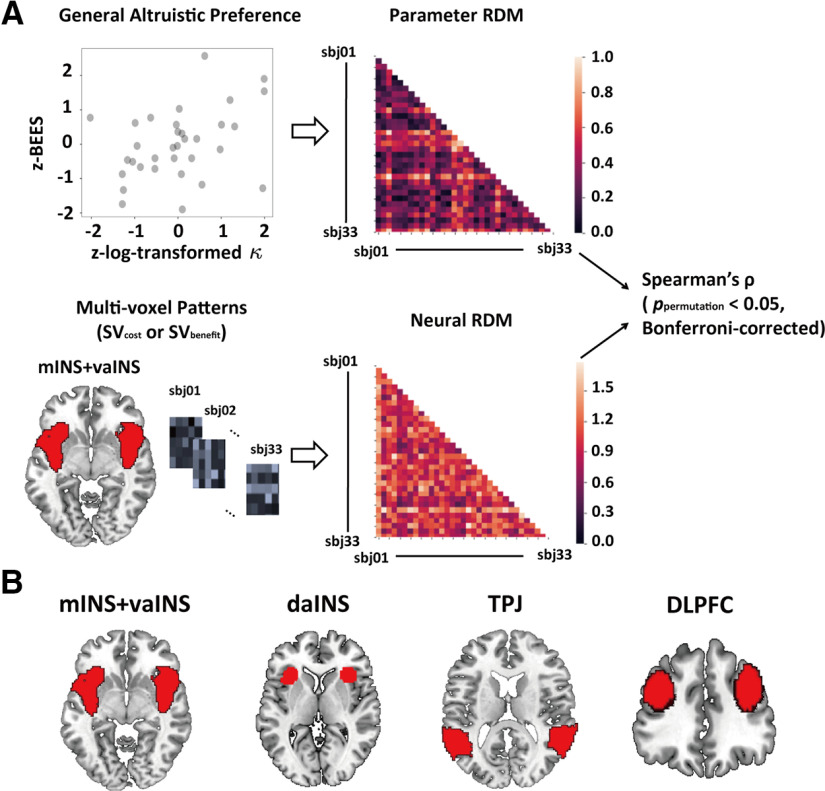
IS-RSA

We performed an IS-RSA using the NLTools package (http://github.com/ljchang/nltools). As a multivariate-based analytical approach, IS-RSA has been demonstrated to be a powerful tool in detecting brain responses associated with individual variations in complex psychological processes encompassing multidimensional features (van Baar et al., 2019). Here, IS-RSA allowed us to examine neural basis of individual variations in general altruistic preference that accounted for both measures of dispositional empathy and task-specific other-regarding preferences simultaneously. We first created a two-dimension general altruistic preference space which consists of z-scored BEES score (i.e., a measure of dispositional empathy) and z-scored log-transformed $\kappa$ (i.e., a measure of task-specific other-regarding preferences), and established a parameter representational dissimilarity matrix (RDM) of the general altruistic preference by calculating the Euclidean distance in this space across all pairs of participants. Next, we obtained the parametric contrast maps of ${\mathrm{SV}}_{\mathrm{cost}}$ and ${\mathrm{SV}}_{\mathrm{benefit}}$ in GLM 1 for each participant, and extracted the multivoxel patterns from each contrast map within the four hypothesis-driven ROIs [i.e., bilateral ventral aINS (vaINS) adjacent to middle INS (mINS), daINS, TPJ, and dorsolateral PFC (DLPFC)] based on a 50-parcel whole-brain parcellation from Neurosynth database (http://neurovault.org/collections/2099/). Given the results of univariate mediation analysis, we combined the vaINS with mINS region in the parcellation template for the first ROI. With the two different masks in INS (i.e., vaINS/mINS vs daINS), we tested whether the functional dissociation in INS identified in univariate analyses can be confirmed by multivariate analyses. Although in our univariate analyses, we only observed a significant effect in the dorsal part of TPJ [i.e., right inferior parietal lobe (rIPL)] and we did not observe any significant effect in DLPFC, these two regions have been repeatedly implicated in altruistic behavior in previous studies (Morishima et al., 2012; Hutcherson et al., 2015; Tusche et al., 2016; Crockett et al., 2017). Therefore, we also included bilateral TPJ and bilateral DLPFC in the IS-RSA analyses to explore their roles in altruistic preferences with multivariate analyses. Then, we created a neural RDM by calculating the pairwise correlation dissimilarity of these neural patterns between each pair of participants. Finally, we calculated Spearman rank correlations between the parameter RDM and the neural RDM for each ROI, respectively. Statistical significance was obtained via the permutation test (i.e., 5000 times of permutation) with Bonferroni corrections accounting for the number of ROIs.

Data and code availability

The data required to reproduce the results, the thresholded statistical parametric maps, and the custom code to implement analyses in this paper are available at https://osf.io/h75cd.

Results

Altruistic helping decreases with benefactors' costs and increases with recipients' benefits

Our model-free analyses of both sessions consistently suggested that individuals' altruistic behaviors decreased with benefactors' own costs and increased with recipients' benefits. Specifically, to test the effects of recipients' benefits on benefactors' WTPs to help recipients in session 1, we performed linear mixed-effects modeling with participants' WTPs for each noise unpleasantness level as a dependent variable, noise unpleasantness levels as a predictor. The linear mixed-effects regression revealed a strong fixed effect of noise unpleasantness level on participants' WTPs (β = 7.02, SE = 0.54, df = 296, t = 12.81, p < 0.001), suggesting that participants' WTPs increased with the level of noise intensity (Fig. 1F, left panel).

For the behavioral data in session 2, we performed a generalized mixed-effect analysis to test the effects of cost amount level (i.e., 10 levels of WTP corresponding to 10 noise unpleasantness levels based on each participant's decisions in session 1) and noise unpleasantness level on participants' altruistic behaviors in session 2 (i.e., 1 = help; 0 = not help). Results showed that participants were more likely to help when the noise inflicted on the recipient became more unpleasant, ORE (odds ratio estimate) = 2.51, 95% confidence interval (CI) [2.25,2.80], whereas they were less likely to help while the cost amount increased, ORE = 0.08, 95% CI [0.06,0.11] (Table 1; Fig. 1F, right panel). The analysis did not yield a statistically significant effect for the interaction between the two predictors on the choice behaviors, ORE = 0.87, 95% CI [0.61,1.23].

Table 1.

Mixed-effects model results of behavioral data in fMRI interpersonal helping task in session 2

Variable	Logistic model
	B (SE)	ORE (95% CI)	p value
Cost amount level (D)	−2.49 (0.14)	0.08 (0.06, 0.11)	<0.001
Noise unpleasantness level (N)	0.92 (0.06)	2.51 (2.25, 2.80)	<0.001
Interaction D*N	−0.14 (0.18)	0.87 (0.61, 1.23)	0.42
Intercept	−4.51 (0.34)	0.01 (0.01, 0.02)	<0.001
LL	−1636
BIC	3314
Marginal R2	0.72

ORE, odds ratio estimate; LL, log-likelihood; BIC, Bayesian information criterion.

Integration of benefactors' costs with nonlinearly transformed recipients' benefits

We performed model-based analyses to formally examine how the participants evaluated and weighed between their own monetary costs and others' potentially physical benefits in making their final decisions. The analyses suggested that people integrate their personal monetary costs with nonlinearly transformed recipients' benefits; this finding addressed the first question of the current study regarding whether people apply a nonlinear algorithm to make altruistic decisions especially when costs and benefits are in different modalities.

Specifically, we constructed 15 models in three model families. The 15 models assumed that participants contingently (F1.1–F1.5) or independently (F2.1–F2.5 and F3.1–F3.5) weighed their own costs and recipients' benefits, either in a linear or a nonlinear manner. The winning model was the model (model F1.2) which assumed that individuals would contingently integrate their own costs and others' benefits with nonlinear weighting on others' benefits:

$$U\left(M,N\right)=-\kappa ·N^{\alpha }-\left(1-\kappa \right)·M(0<\kappa <1),$$

where $M$ is the amount of monetary cost for the participant, and $N$ is the noise unpleasantness level the partner is going to receive, $U(M,N)$ is the SV for each choice.

Bayesian model comparison showed that the winning model (model F1.2) has the highest exceedance probability (xp = 0.71; Fig. 2A). The model F1.2 is more likely implemented than all the other models with a probability of 71%. Consistently, model comparisons with Bayesian information criterion (BIC), which punish model complexity to avoid overfitting also favored this model over other models (Table 2). The exceedance probabilities of all the models are listed in Table 2. Given that both our model-free and model-based analyses suggested that including interaction between costs and benefits did not improve model performance in explaining the helping behavior, we did not include the interaction term between cost amount and noise unpleasantness level in GLMs for the following fMRI analyses.

Figure 2.

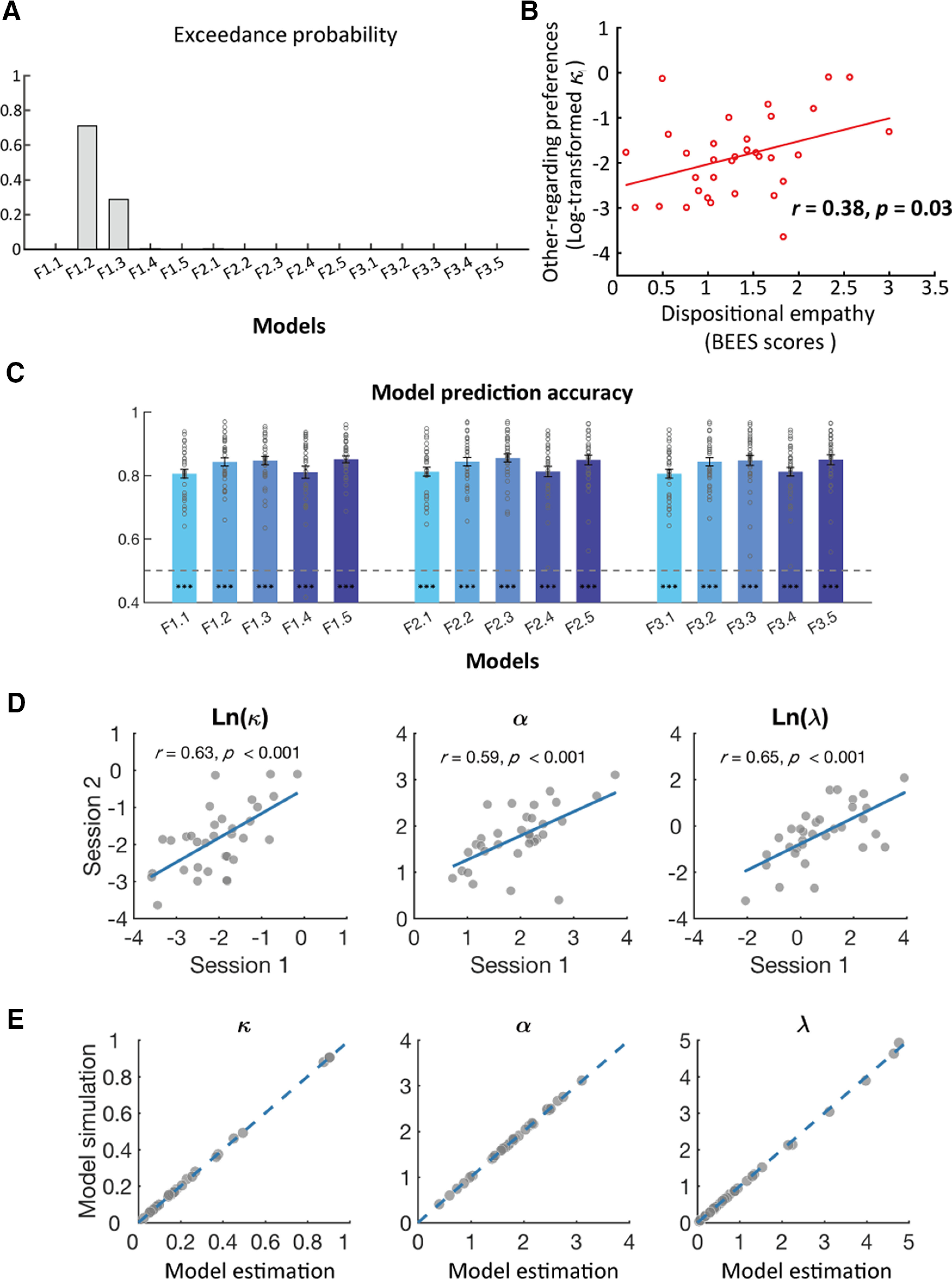
Computational modeling results. A, Model comparison results. Model F1.2 (interdependent-and-nonlinear weight of recipients' benefits model) outperforms than all the other models in the RFX-BMS analysis. Model F1.2 has the highest exceedance probability (xp = 0.71), suggesting that the probability that model F1.2 is more likely implemented than all the other models is 71%. B, Correlation between BEES score (dispositional empathy) and log-transformed κ in model F1.2 (other-regarding preferences). C, Bar plots show that cross-validation prediction accuracies are significantly higher than chance level (i.e., 0.5) for all the 15 models of interest. Error bars indicate SEM. D, Scatter plots for correlations between estimated parameters with model F1.2 in the two sessions. E, Model parameters recovered from simulated response data for each participant; 100 sets of response data were simulated with model F1.2, each participant's specific cost amount–noise unpleasantness level pairing choice set, and his/her own best-fitting parameters. Then, model parameters in model F1.2 were estimated with these 100 sets of response data for each participant's cost amount–noise unpleasantness level pairing choice set, and averaged across the 100 sets of simulated parameters. Scatter plots show the association between the averaged simulated parameters (y-axis) and the estimated parameters fitted by observed behavioral data (x-axis) across all the participants. Dashed blue lines are the diagonal lines. Each dot represents one participant; ***p < 0.001.

Table 2.

Quality of model fits for computational models of altruistic decision-making in sessions 1 and 2

Model	Description	Parameters per subject	Exceedance probability (session 2)	BIC (session 2)	BIC (session 1)
F1.1	$\kappa$,$\lambda$	2	0	3708	7697
F1.2	$\kappa$, $\alpha$, $\lambda$	3	0.71	3223	6690
F1.3	$\kappa$, $\beta$, $\lambda$	3	0.29	5269	6892
F1.4	$\kappa$, $\alpha$,$\lambda$	3	0.0007	8470	14,367
F1.5	$\kappa$, $\alpha$, $\beta$, $\lambda$	4	0	4328	8090
F2.1	$\kappa$, $m$,$\lambda$	3	0.0005	4456	7843
F2.2	$\kappa$, $m$, $\alpha$, $\lambda$	4	0	3369	7719
F2.3	$\kappa$, $m$, $\beta$, $\lambda$	4	0.0001	5140	11,841
F2.4	$\kappa$, $m$, $\alpha$, $\lambda$	4	0	6211	12,620
F2.5	$\kappa$, $m$, $\alpha$, $\beta$, $\lambda$	5	0	5802	11,881
F3.1	$\kappa$, $m$, $p$, $\lambda$	4	0	4042	7076
F3.2	$\kappa$, $m$, $p$, $\alpha$, $\lambda$	5	0	3537	6971
F3.3	$\kappa$, $m$, $p$, $\beta$, $\lambda$	5	0.0001	5307	12,009
F3.4	$\kappa$, $m$, $p$, $\alpha$, $\lambda$	5	0	6379	12,788
F3.5	$\kappa$, $m$, $p$, $\alpha$, $\beta$, $\lambda$	6	0	5970	12,049

BIC, Bayesian information criterion. BIC scores are summed across subjects. Model F1.2 was favored across both sessions. All models have an inverse temperature parameter $\mathrm{\lambda }$. κ, relative weighting parameter for others' benefits (altruistic preference) in models F1.1– F1.5; κ, weighting parameter for others' benefits in models F2.1–F2.5 and F3.1–F3.5; $m$, weighting parameter for one's own costs in models F2.1–F2.5 and F3.1–F3.5; $p$, weighting parameter for interaction between benefit and cost in models F3.1–F3.5; $\alpha$, power exponent which modulates the nonlinearity of others' benefits; $\beta$, power exponent which modulates the nonlinearity of one's own costs.

To test the relationship between participants' other-regarding preferences and their dispositional empathy, we calculated each participant's BEES score as a measure of dispositional empathy. We derived the weighting parameter (i.e., $\kappa$) which captures participants' task-specific other-regarding preferences from the winning model (model F1.2). Since the distribution of $\kappa$ was positively skewed (skewness = 1.97), we used log-transformed $\kappa$, which was normally distributed (skewness = 0.30), as the measure of task-specific other-regarding preferences in the following analyses. Pearson correlation analysis revealed a significant correlation between log-transformed $\kappa$ and BEES score across participants (r = 0.38, df = 32, p = 0.03; Fig. 2B). Since the Pearson correlation between $\kappa$ and BEES score was also significant (r = 0.37, df = 32, p = 0.04), the log transformation of $\kappa$ did not change the significance of our results. Given that individuals with greater $\kappa$ value will concern more about others' benefits (i.e., higher weight), these findings provide evidence that greater computational weighting on others' benefits may be driven by stronger dispositional empathy.

Furthermore, we performed a series of additional analyses to validate our model performance. First, to test predictive accuracy of the winning model (model F1.2), we performed cross-validation prediction analyses by estimating model parameters with each participant's behaviors in half trials and predicting his/her behaviors in the other half. Two-tail one sample t test revealed that the predictive accuracy of this model (mean ± SE, 0.843 ± 0.013) was significantly higher than chance level (i.e., 0.5, t₍₃₂₎ = 26.14, p < 0.001).

We also applied the same analyses to other models. One sample t tests revealed that predictive accuracies for all the remaining models were higher than chance level (ps < 0.001; Fig. 2C). As the predictive accuracy for each model conformed to normal distribution (Kolmogorov–Smirnov tests of predictive accuracy, p values for all models > 0.1), we performed a 5 (nonlinearity: linear vs nonlinearity on benefits vs nonlinearity on costs vs same nonlinearity on benefits and costs vs different nonlinearity on benefits and costs) × 3 (model families: F1 vs F2 vs F3) ANOVA on model predictive accuracy. We only revealed a significant main effect of nonlinearity (F_(4,128) = 12.99, p < 0.001, η²_partial = 0.29). Post hoc analyses suggested that predictive accuracy of models with nonlinearly transformed benefit (mean ± SE, 0.843 ± 0.013), models with nonlinearly transformed cost (0.850 ± 0.013), and models with different nonlinearly transformed benefit and cost (0.850 ± 0.013) were significantly higher in predictive accuracy than linear models (0.808 ± 0.014, ps < 0.001) and models with the same nonlinearly transformed benefit and cost (0.812 ± 0.017, ps < 0.01), but there was no significant difference between models with nonlinearly transformed benefit, models with nonlinearly transformed cost, and models with different nonlinearly transformed benefit and cost (ps > 0.1). Although these three types of nonlinear models predicted choice behavior equally well, only the nonlinear model with single weighting parameter and nonlinearly weighting on others' benefits (model F1.2) outperformed all the other models in model comparison analyses (i.e., exceedance probability and BIC). These findings provide evidence suggesting that when benefactors decide whether to carry out costly helping behaviors to others, they will integrate their monetary costs with nonlinearly transformed recipients' physical benefits.

Second, we applied the same models in behavioral analyses of session 2 to participants' altruistic behaviors in session 1 to examine the test-retest reliability of the interpersonal helping task. The findings that model comparisons with BIC favoring model F1.2 over the other models for data in session 1 (Table 2) and the estimated parameters of model F1.2 in session 1 and session 2 were significantly correlated with each other (Fig. 2D) demonstrated the consistency of behaviors across sessions. Third, to confirm that the winning model could reliably estimate parameters given different individual-specific datasets, we performed parameter recovery analysis for the winning model with each participant's dataset separately. The results suggested that the parameters in model F1.2 could be recovered reliably with individual-specific datasets in the current study (Fig. 2E).

Together, computational modeling results suggested that participants were more likely to integrate their own monetary costs with nonlinearly transformed others' physical benefits in the altruistic helping situation.

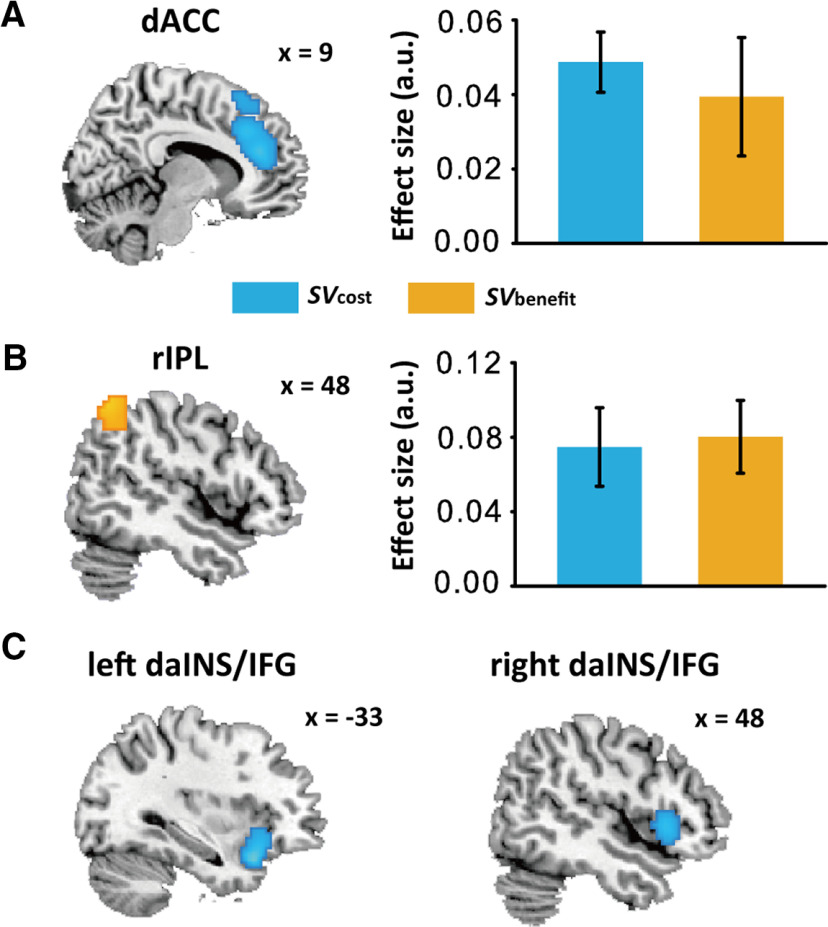
Neural valuations of benefactors' costs and recipients' benefits

To answer the question how human brain implements the computation of costs and benefits to make the help decision, we constructed GLM 1 to test brain regions associated with cost and benefit valuation, and GLM 2 to test brain regions associated with decision utility underlying the helping behavior. The analyses of GLM 1 first suggested that dorsal ACC (dACC) and rIPL are involved in representing self-interest and other-interest in an abstract manner. In search of regions involved in the valuation of benefactors' costs and recipients' benefits, we calculated SV of benefactors' cost and recipients' benefit for each trial based on the winning model (model F1.2) as follows:

$${\mathrm{SV}}_{\mathrm{cost}}=(1-\kappa )·M$$

$${\mathrm{SV}}_{\mathrm{benefit}}=\kappa ·N^{\alpha }.$$

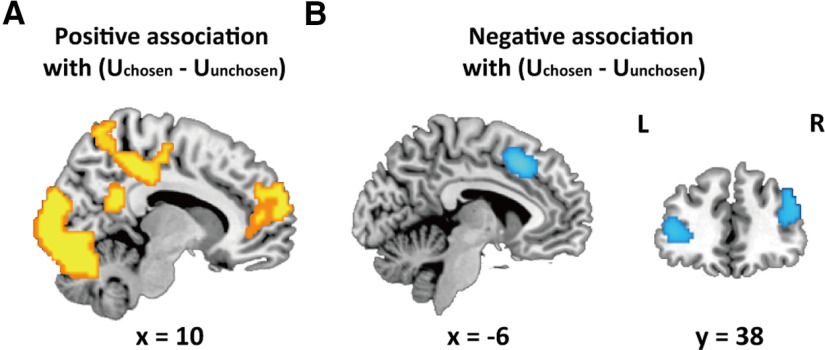
Correlating these SVs with BOLD signals in GLM 1, we found that the neural activity in dACC, and bilateral daINS/IFG were positively associated with ${\mathrm{SV}}_{\mathrm{cost}}$, whereas the neural activity in rIPL was positively associated with ${\mathrm{SV}}_{\mathrm{benefit}}$ (Fig. 3; Table 3). All these results above and hereafter were reported using a whole-brain corrected threshold (i.e., a combined threshold of voxel-level p < 0.001 uncorrected and cluster-level p < 0.05 FWE correction) unless specifically noted. No region showed significant negative association with ${\mathrm{SV}}_{\mathrm{cost}}$ or ${\mathrm{SV}}_{\mathrm{benefit}}$.

Figure 3.

Parametric analysis results in GLM 1. dACC (A) showed positive associations with ${\mathrm{SV}}_{\mathrm{cost}}$ (blue region), and rIPL (B) showed positive associations with ${\mathrm{SV}}_{\mathrm{benefit}}$ (orange region). ROI conjunction analysis revealed that part of dACC and rIPL are associated with both ${\mathrm{SV}}_{\mathrm{cost}}$ and ${\mathrm{SV}}_{\mathrm{benefit}}$. Parametric estimate values corresponding to each of the two modulators (${\mathrm{SV}}_{\mathrm{cost}}$ and ${\mathrm{SV}}_{\mathrm{benefit}}$) were extracted from dACC (A, right panel) and rIPL (B, right panel) identified in GLM 1 conjunction analysis. The parametric estimate values were the averaged values across the voxels in a within 3-mm edge cube and centered at the peak coordinate of each region (ACC: 9, 38, 19; rIPL: 54, −58, 49). C, Bilateral daINS/IFG showed positive associations with ${\mathrm{SV}}_{\mathrm{cost}}$. Neural results were thresholded at voxel- wise p < 0.001 uncorrected and cluster-wise FWE corrected p < 0.05. Error bars indicate SEM.

Table 3.

Results of whole-brain parametric analysis of fMRI data in GLM 1 and GLM 2

	Regions	Laterality	Peak MNI coordinates			Max T value	Cluster size (k)
			x	y	z
GLM 1: positive association with ${\mathrm{SV}}_{\mathrm{cost}}$
	dACC	R	9	38	22	6.57	633
	daINS/IFG	R	48	17	1	5.68	286
		L	−33	17	−23	9.48	233
Positive association with ${\mathrm{SV}}_{\mathrm{benefit}}$
	rIPL	R	48	−58	55	5.90	245
	MOG	R	18	−103	−5	8.77	445
		L	−24	−97	−2	5.62	234
GLM 2: positive association with decision utility: $U_{\mathrm{chosen}}$ - $U_{\mathrm{unchosen}}$
	MPFC	L	−12	47	34	6.63	1289
	MTG	L	−57	−40	−11	7.95	772
	Angular gyrus	L	−60	−58	25	8.16	676
	SOG	R	21	−97	7	8.20	5165
Negative association with decision utility: $U_{\mathrm{chosen}}$ - $U_{\mathrm{unchosen}}$
	MCC/SMA	L	−6	17	46	7.58	283
	IFG	L	−45	44	4	6.58	297
	DLPFC	R	48	35	31	5.75	137
	Angular gyrus	L	−33	−58	37	5.33	145

dACC, dorsal anterior cingulate cortex; daINS, dorsal anterior insular; IFG, inferior frontal gyrus; rIPL, right inferior parietal lobe; MOG, middle occipital gyrus; MPFC, medial prefrontal cortex; MTG, middle temporal gyrus; SOG, superior occipital gyrus; MCC, middle cingulate cortex; SMA, supplementary motor area; DLPFC, dorsolateral prefrontal cortex. Results are thresholded with voxel-level p < 0.001 uncorrected and cluster-level whole-brain p < 0.05 FWE correction.

Then, we performed a conjunction analysis to assess regions whose activity were engaged in evaluating both ${\mathrm{SV}}_{\mathrm{cost}}$ and ${\mathrm{SV}}_{\mathrm{benefit}}$. We observed that dACC [peak MNI: 9, 38, 19; T = 3.31, k = 2, p(SVC-FWE) = 0.013, SVC] and rIPL [peak MNI: 54, −58, 49; T = 4.15, k = 20, p(SVC-FWE) = 0.001, SVC] showed significant overlaps in neural valuation of ${\mathrm{SV}}_{\mathrm{cost}}$ and ${\mathrm{SV}}_{\mathrm{benefit}}$ (Fig. 3A,B, right panels). Contrasts of “${\mathrm{SV}}_{\mathrm{cost}}$ > ${\mathrm{SV}}_{\mathrm{benefit}}$” and “${\mathrm{SV}}_{\mathrm{benefit}}$ > ${\mathrm{SV}}_{\mathrm{cost}}$” did not reveal any region surviving a whole-brain corrected threshold or SVC.

Neural substrates of decision utility and decision difficulty underlying altruistic helping behaviors

In GLM 2, we identified regions encoding decision utility ($U_{\mathrm{chosen}}$ - $U_{\mathrm{unchosen}}$), which underlies the helping decision. Whole-brain analysis revealed that activations in MPFC, left middle temporal gyrus (MTG), left angular gyrus and superior occipital gyrus (SOG) were positively associated with the decision utility, and that activations in middle cingulate cortex/supplementary motor area (MCC/SMA), left IFG, right DLPFC, and left angular gyrus were negatively associated with decision utility (Fig. 4; Table 3).

Figure 4.

Parametric analysis results in GLM 2. A, MPFC, including VMPFC, showed positive associations with utility difference between chosen and unchosen choice. B, MCC/SMA, left IFG and right DLPFC showed negative associations with utility difference between chosen and unchosen choice. Neural results were thresholded at voxel-wise p < 0.001 uncorrected and cluster-wise FWE corrected p < 0.05.

Consistent with prior studies, the finding that the activation in MPFC, especially VMPFC, was positively associated with decision utility confirmed the role of VMPFC in representing SV of decision (Levy and Glimcher, 2012; Bartra et al., 2013; Clithero and Rangel, 2014). Given that smaller decision utility increases decision difficulty, the findings that activations in cognitive control-related regions, including MCC, IFC, and DLPFC, were negatively associated with decision utility was also in line with previous studies suggesting that more extensive cognitive resources are recruited in more difficult decisions to resolve conflicts between choices with smaller utility differences (Zaki et al., 2010; Watanabe et al., 2014).

It is plausible that the regions identified in GLM 1 were also associated with decision utility or decision difficulty, but we did not observe any significant effect of decision utility or decision difficulty on dACC, rIPL as well daINS/IFG [all ps(FWE-SVC) > 0.05]. Therefore, we suggested that dACC, rIPL, and daINS/IFG identified in the previous GLM analyses were not involved in representing decision utility or difficulty.

Valuation of others' benefits in INS mediates the effect of dispositional empathy on task-specific other-regarding preferences

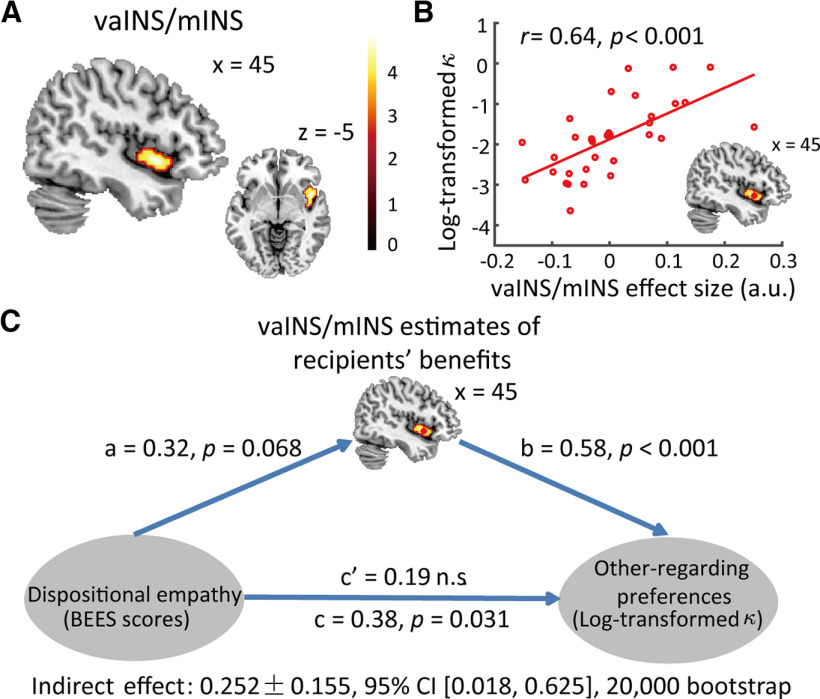
The next question we are interested in is how individual differences in altruistic preference arise from neural processing of different attributes in helping decisions. We first examined whether and how neural valuations of personal costs and other's benefits were related to dispositional empathy and model-based other-regarding preference. Mediation analyses revealed that vaINS/mINS mediated the effect of dispositional empathy on cost-benefit calculation during altruistic decision-making. Specifically, we first investigated the relationship between participants' task-specific other-regarding preferences (log-transformed $\kappa$ derived from the winning model) with neural responses of ${\mathrm{SV}}_{\mathrm{cost}}$ and ${\mathrm{SV}}_{\mathrm{benefit}}$ in three hypothesis-driven ROIs (i.e., bilateral INS, TPJ, and DLPFC) based on a 50-parcel whole-brain parcellation from Neurosynth database (http://neurovault.org/collections/2099/). We combined vaINS with daINS and mINS region in the parcellation template to form a mask covering the whole INS. Only neural responses of ${\mathrm{SV}}_{\mathrm{benefit}}$ in right vaINS/mINS [peak MNI: 45, 8, −5, p(SVC-FWE) < 0.05] were correlated with participants' other-regarding preferences. Whole-brain analyses further confirmed stronger signal of ${\mathrm{SV}}_{\mathrm{benefit}}$ in right vaINS/mINS (peak MNI: 45, 8, −5, T = 4.87, cluster size = 108) in participants weighing more on other's benefits (i.e., with stronger other-regarding preferences, voxel-level p < 0.001 uncorrected and cluster-level p = 0.078 FWE correction; Fig. 5A,B).

Figure 5.

Mediation analysis results. A, Whole-brain analyses showed the association between neural representation of recipients' benefits in vaINS/mINS with log-transformed κ in model F1.2 (other-regarding preferences). B, Scatter plot for the correlation between parametric estimates of recipients' benefits in vaINS/mINS and log-transformed κ. Parametric estimates in vaINS/mINS was averaged values across the voxels in a region within 3-mm edge cube and centered at the peak coordinates (45, 8, −5). C, Path diagram shows the mediation pathway. The predictor variable (BEES scores) shown on the left predicts neural representation of recipients' benefits in vaINS/mINS (path a for the mediator variable). The mediator variable (vaINS/mINS) predicts individuals' other-regarding preferences (log-transformed κ) after controlling for individuals' empathy disposition (path b). The effect of dispositional empathy on other-regarding preferences after controlling for the mediator variable (path c') is not significant any more, suggesting that neural estimates of vaINS/mINS fully mediate the effect of dispositional empathy on other-regarding preferences. Path coefficients are labeled on the lines. Bootstrapping analysis suggested that this indirect effect is significant after 20,000 bootstraps.

Given that our behavioral findings have revealed an association between dispositional empathy and other-regarding preferences, we further examined whether vaINS/mINS served as a neural underpinning of the effect of dispositional empathy on other-regarding preferences. Regressional analyses revealed a significant path c of 0.38 (p = 0.031), a significant path b of 0.58 (p < 0.001), and a marginally significant path a of 0.32 (p = 0.068; Fig. 5C). Since the path a was only marginally significant, we used a bootstrapping procedure to test the significance of the indirect effect (i.e., $a\times b$), which is widely used for testing indirect effect when any path in the mediation model (MM) is not significant (Preacher and Kelley, 2011; Rucker et al., 2011; Hayes, 2017). The bootstrapping procedure showed a significant indirect effect $a\times b$ (indirect effect: 0.252, 95% CI [0.018,0.625], with 20,000 bootstrapping; Preacher and Hayes, 2004). Given that path c' was no longer significant (c' = 0.19, p > 0.1) after the mediation of activity in vaINS/mINS, the positive relationship between dispositional empathy and task-specific other-regarding preferences was fully mediated by the neural signals of ${\mathrm{SV}}_{\mathrm{benefit}}$in vaINS/mINS (Fig. 5C; Table 4). In addition, we built up five control MMs (MM 2–6) to test other possibilities of mediation pathways between these three variables, and found that none of the indirect effects in these models was significant (Table 4). Taken together, these findings suggested that vaINS/mINS is a critical region linking dispositional empathy with cost-benefit integration during altruistic decision-making.

Table 4.

Mediation pathways construction and mediation analysis results for MM 1–6

	Independent variable	Mediator variable	Outcome variable	95% CI indirect effect
MM 1	BEES score	vaINS/mINS estimates of ${\mathit{S}\mathit{V}}_{\mathit{b}\mathit{e}\mathit{n}\mathit{e}\mathit{f}\mathit{i}\mathit{t}}$	Other-regarding preferences	0.018 to 0.625
MM 2	BEES score	Other-regarding preferences	vaINS/mINS estimates of ${\mathrm{SV}}_{\mathrm{benefit}}$	−0.001 to 0.083
MM 3	Other-regarding preferences	BEES score	vaINS/mINS estimates of ${\mathrm{SV}}_{\mathrm{benefit}}$	−0.006 to 0.018
MM 4	Other-regarding preferences	vaINS/mINS estimates of ${\mathrm{SV}}_{\mathrm{benefit}}$	BEES score	−0.002 to 0.083
MM 5	vaINS/mINS estimates of ${\mathrm{SV}}_{\mathrm{benefit}}$	Other-regarding preferences	BEES score	−1.073 to 4.610
MM 6	vaINS/mINS estimates of ${\mathrm{SV}}_{\mathrm{benefit}}$	BEES score	Other-regarding preferences	−0.277 to 2.664

The significant mediation model is highlighted in bold font.

Functional dissociation of vaINS/mINS and daINS/IFG in altruistic decision-making

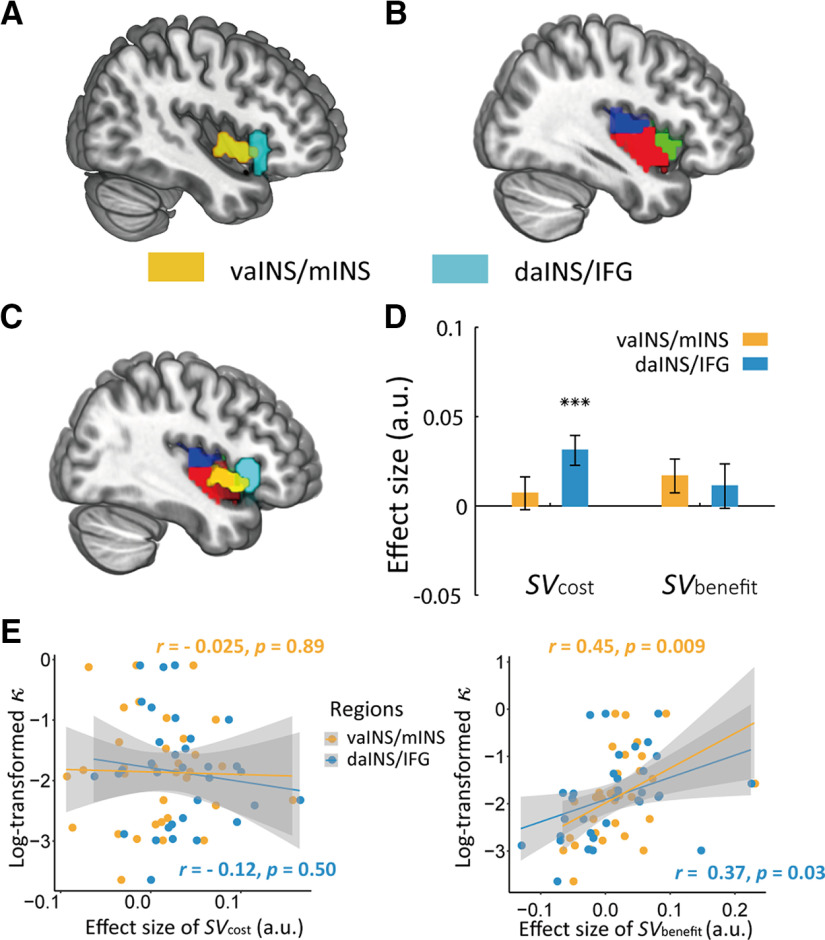
Findings above strongly indicated that the two adjacent but different regions in INS are involved in distinct functions underlying the altruistic helping behavior. In particular, right vaINS/mINS signals of ${\mathrm{SV}}_{\mathrm{benefit}}$ was associated with other-regarding preferences across individuals, while bilateral daINS/IFG were more engaged in encoding ${\mathrm{SV}}_{\mathrm{cost}}$. By mapping both subregions (Fig. 6A) to a template that disentangles insular subregions (k = 3 solutions; Fig. 6B; Kelly et al., 2012), we showed that right vaINS/mINS was mainly located in the ventral anterior and middle subregion of the insular template, whereas right daINS/IFG was partly located in the dorsal anterior subregion of the insular template and extended to IFG (Fig. 6C).

Figure 6.

Differentiation between right vaINS/mINS and daINS/IFG. A, Neural representations of recipients' benefits in vaINS/mINS (yellow) mediate the effect of dispositional empathy on other-regarding preferences, and activity in daINS/IFG (cyan) is associated with ${\mathrm{S}\mathrm{V}}_{\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{t}}$. B, Insular subregions template (k = 3 solutions) from Kelly et al. (2012): dorsal anterior insular (green), ventral anterior and middle insular (red), and posterior insular (blue). C, Mapping vaINS/mINS (yellow) and daINS/IFG (cyan) onto Kelly's insular subregions template suggests that vaINS/mINS is mainly located in the vaINS and mINS, and daINS/IFG is mainly located in the dorsal anterior part of insular and IFG. D, Activity in daINS/IFG showed significant associations with ${\mathrm{S}\mathrm{V}}_{\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{t}}$; and, none of activity of ${\mathrm{S}\mathrm{V}}_{\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{t}}$ in vaINS/mINS, activity of ${\mathrm{S}\mathrm{V}}_{\mathrm{b}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{f}\mathrm{i}\mathrm{t}}$ in daINS/IFG or in vaINS/mINS was significant from 0, ***p < 0.001. E, Scatter plots for the correlations between log-transformed κ and parametric estimates of ${\mathrm{S}\mathrm{V}}_{\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{t}}$ in vaINS/mINS and daINS/IFG (left panel), and scatter plots for the correlations between log-transformed κ and parametric estimates of ${\mathrm{S}\mathrm{V}}_{\mathrm{b}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{f}\mathrm{i}\mathrm{t}}$ in vaINS/mINS and daINS/IFG (right panel). The correlation coefficient of ${\mathrm{S}\mathrm{V}}_{\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{t}}$ was not significant for both vaINS/mINS and daINS/IFG (left panel), and the correlation coefficient of ${\mathrm{S}\mathrm{V}}_{\mathrm{b}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{f}\mathrm{i}\mathrm{t}}$ was significant for vaINS/mINS but not for daINS/IFG (right panel). The parametric estimate values for vaINS/mINS were the averaged values across the mINS template in Kelly et al. (2012); and the parametric estimate values for daINS/IFG were the averaged values across a cluster combining the anterior dorsal INS in Kelly et al. (2012) and the IFG in AAL templates. If parametric estimates of ${\mathrm{S}\mathrm{V}}_{\mathrm{b}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{f}\mathrm{i}\mathrm{t}}$ were extracted from the peak coordinates of right daINS/IFG (MNI coordinates: 48, 17, 1) and right vaINS/mINS (MNI coordinates: 45, 8, −5) identified in previous analyses, the correlation coefficient between other-regarding preferences (i.e., log-transformed $\mathrm{\kappa }$) and ${\mathrm{S}\mathrm{V}}_{\mathrm{b}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{f}\mathrm{i}\mathrm{t}}$ signal was significantly stronger in vaINS/mINS (r = 0.64, p < 0.001) than in daINS/IFG (r = 0.41, p = 0.02; Z = 2.27, p = 0.023). Whole-brain neural results were thresholded at voxel-wise p < 0.001 uncorrected and cluster-wise FWE corrected p < 0.05. Error bars indicate SEM.

We performed the following two post hoc analyses to formally test the functional dissociation between the two subregions of INS. To this end, we extracted parametric estimates of ${\mathrm{SV}}_{\mathrm{cost}}$ and ${\mathrm{SV}}_{\mathrm{benefit}}$ separately from right daINS/IFG and right vaINS/mINS for each participant. We used the middle insular cluster in Kelly et al. (2012)' template as the mask for vaINS/mINS, and combined the dorsal anterior insular cluster in Kelly et al. (2012)' template with IFG in AAL template as the mask for daINS/IFG. For the first analysis (i.e., parametric analysis), we showed a significant region-by-SV interaction in the parametric effects (F_(1,32) = 5.61, p = 0.02, η²_partial = 0.15); while the parametric estimates of ${\mathrm{SV}}_{\mathrm{cost}}$ were significantly higher in right daINS/IFG (0.031 ± 0.008) than in right vaINS/mINS (0.007 ± 0.009, p < 0.001), the parametric estimates of ${\mathrm{SV}}_{\mathrm{benefit}}$ in right daINS/IFG (0.011 ± 0.012) were not different from those in right vaINS/mINS (0.017 ± 0.010, p = 0.55; Fig. 6D). This interaction effect was further supported by post hoc analyses showing that only the parametric estimates of ${\mathrm{SV}}_{\mathrm{cost}}$ in right daINS/IFG was significantly higher than 0 (0.031 ± 0.008, 95% CI [0.014,0.048], t₍₃₂₎ = 3.71, p < 0.001), which was not the case in right vaINS/mINS (0.007 ± 0.009, 95% CI [–0.012,0.026], t₍₃₂₎ = 0.77, p = 0.45). Neither parametric of ${\mathrm{SV}}_{\mathrm{benefit}}$ in right daINS/IFG (0.011 ± 0.012, 95% CI [–0.014,0.036], t₍₃₂₎ = 0.89, p = 0.38) nor parametric of ${\mathrm{SV}}_{\mathrm{benefit}}$ in vaINS/mINS (0.017 ± 0.010, 95% CI [–0.003,0.036], t₍₃₂₎ = 1.76, p = 0.09) was different from 0.

Concerning the second analysis (i.e., correlation analysis), although the correlation comparison suggested that the difference between the correlation of other-regarding preferences (i.e., log-transformed $\mathrm{\kappa }$) with ${\mathrm{SV}}_{\mathrm{benefit}}$ signal in vaINS/mINS and that in daINS/IFG did not reach significance (Z = 0.60, p = 0.273; Steiger, 1980; Diedenhofen and Musch, 2015), the value of the correlation coefficient between other-regarding preferences (i.e., log-transformed $\mathrm{\kappa }$) and ${\mathrm{SV}}_{\mathrm{benefit}}$ signal in vaINS/mINS (r = 0.45, p = 0.009) was higher than that in daINS/IFG (r = 0.37, p = 0.03, not significant if Bonferroni multiple comparison correction was applied; see Fig. 6E, right panel). On the other hand, if parametric estimates of ${\mathrm{SV}}_{\mathrm{benefit}}$ were extracted from the peak coordinates of right daINS/IFG (MNI coordinates: 48, 17, 1) and right vaINS/mINS (MNI coordinates: 45, 8, −5) identified in previous analyses, the correlation between other-regarding preferences (i.e., log-transformed $\mathrm{\kappa }$) and ${\mathrm{SV}}_{\mathrm{benefit}}$ signal was significantly stronger in vaINS/mINS (r = 0.64, p < 0.001) than in daINS/IFG (r = 0.41, p = 0.02; Z = 2.27, p = 0.023), which confirmed the functional dissociation of daINS/IFG and vaINS/mINS in processing benefits. These results also suggested that the null neural effect of ${\mathrm{SV}}_{\mathrm{benefit}}$ in vaINS/mINS at group level was because of the modulation of other-regarding preference across different participants. In other words, people who are more altruistic will show a more positive neural effect of ${\mathrm{SV}}_{\mathrm{benefit}}$ in vaINS/mINS. In addition, other-regarding preferences was not correlated with parametric estimates of ${\mathrm{SV}}_{\mathrm{cost}}$ in vaINS/mINS (r = −0.025, p = 0.89) or in daINS/IFG (r = –0.12, p = 0.50; Fig. 6E, left panel). Together, these findings provided convergent evidence for the functional dissociation of vaINS/mINS and daINS/IFG in altruistic decision-making.

Brain activity patterns reflect individual variations in general altruistic preference

Furthermore, in addition to univariate mediation analyses, we employed multivariate analyses (i.e., IS-RSA) to explore the relationship between neural encodings of cost and benefit and individual differences in altruistic preference. To account for individual differences in both dispositional empathy and context-specific other-regarding tendency, we constructed a two-dimension general altruistic preference space with normalized BEES score and normalized log-transformed $\kappa$, and tested whether or not multivariate neural activity patterns of ${\mathrm{SV}}_{\mathrm{cost}}$ and ${\mathrm{SV}}_{\mathrm{benefit}}$ in candidate regions (i.e., bilateral vaINS/mINS, daINS, TPJ, and DLPFC) were involved in representing individual variations of this general altruistic preference. Here, we consider the general altruistic preference as a more comprehensive measure of altruistic preferences than each single measure, as it encompasses altruistic preference strength information from both long-term personality traits and task-specific preferences, and also reflects the relationship between these two measures across individuals. For instance, task-specific other-regarding preferences are more closely related to dispositional empathy for individuals whose positions are closer to the diagonal line in the general altruistic preference space than those who are farther away to the diagonal line. We implemented IS-RSA in the following procedure. First, we generated a parameter RDM by calculating the Euclidean distance in this general altruistic preference space across all pairs of participants. This parameter RDM could be taken as a measure of similarity in general altruistic preference between different individuals. Next, we created, respectively, a neural RDM with respect to target regions by calculating the correlation between multivoxel patterns of ${\mathrm{SV}}_{\mathrm{cost}}$ and ${\mathrm{SV}}_{\mathrm{benefit}}$ across all pairs of participants. Finally, we performed a Spearman rank correlation between these two RDMs (Fig. 7).

Figure 7.

Illustration of the IS-RSA. A, Procedure of performing IS-RSA. First, we created a parameter RDM, which measured the dissimilarity across participants in general altruistic preference that was calculated by the Euclidean distance between each pair of participants in z-scored BEES (a measure of dispositional empathy) and z-scored log-transformed κ (a measure of task-specific altruistic preference) driven from the winning model (also see the scatter plot showing the relationship between the two measures; each dot represents the data of a single participant). Next, we built a neural RDM for each of the hypothesized ROIs (here we used bilateral vaINS extending to mINS as an example), which was measured by the correlation distance between the multivoxel patterns in each ROI of SV_cost (or SV_benefit) of each pair of participants. Last, we calculated the Spearman rank-order correlation between these two RDMs and implemented a permutation test with Bonferroni correction to confirm the statistical significance. Notably, neural RDMs shown here were based on parametric contrasts map of SV_cost. Multivoxel patterns (heatmaps in gray scale) shown here were only for illustration. B, ROIs used in IS-RSA. ROI masks were defined based on a whole-brain parcellation given a meta-analytic functional coactivation map of the Neurosynth database (http://neurovault.org/collections/2099/). RDM, representational dissimilarity matrix; SV, subjective value; sbj, subject; BEES, balanced emotional empathy scale; daINS, dorsal anterior insular; mINS, middle insular; vaINS, ventral anterior insular; TPJ, temporoparietal junction; DLPFC, dorsolateral prefrontal cortex.

Results revealed significant intersubject similarity effects in bilateral vaINS extending to mINS for processing recipients' benefits (Spearman's ρ = 0.183; p_permutation = 0.007) and in DLPFC for processing benefactors' costs (Spearman's ρ = 0.175; p_permutation = 0.008), both regions survived Bonferroni correction (Fig. 7; Table 5). None of these effects were significant in daINS or TPJ (p_permutation > 0.1). On the one hand, these findings were consistent with our univariate analyses which suggested that responses to recipients' benefits in vaINS/mINS, but not responses to recipients' benefits/benefactors' costs in daINS/IFG, were associated with dispositional empathy and model-based other-regarding preference. On the other hand, these findings extended univariate analyses by showing responses to benefactors' costs in DLPFC was also critical for the altruistic preference.

Table 5.

Results of ROI-based IS-RSA

Hemisphere	ROI	Spearman's rho (ppermutation)
		SVcost	SVbenefit
Bilateral	vaINS + mINS	−0.025 (0.777)	0.183 (0.007)*
	daINS	−0.002 (0.989)	0.026 (0.603)
	TPJ	−0.001 (0.988)	0.057 (0.199)
	DLPFC	0.175 (0.008)*	0.032 (0.499)

ROI masks were defined based on a whole-brain parcellation given a meta-analytic functional coactivation map of the Neurosynth database (http://neurovault.org/collections/2099/). ROI, region of interest; SV, subjective value; vaINS, ventral anterior insular; mINS, middle insular; daINS, dorsal anterior insular; TPJ, temporoparietal junction; DLPFC, dorsolateral prefrontal cortex.

*Regions which survived Bonferroni-correction (i.e., p_permutation < 0.013), and the corresponding statistic information are in bold font.

To test potential hemispheric effects for the regions which had survived Bonferroni correction, we reproduced the analysis by applying the same procedure on the left or right part of vaINS/mINS and DLPFC. We found that the effects of recipients' benefits in both left (Spearman's ρ = 0.155; p_permutation = 0.007) and right vaINS/mINS (Spearman's ρ = 0.172; p_permutation = 0.018) were significant, and that the effect of benefactors' costs was significant only in right DLPFC (Spearman's ρ = 0.162; p_permutation = 0.006), not in left DLPFC (Spearman's ρ = 0.052; p_permutation = 0.41). Taken together, these findings confirmed the functional dissociation between different subregions in INS with multivariate analyses, and indicated that neural activity patterns of ${\mathrm{SV}}_{\mathrm{cost}}$ in right DLPFC and activity patterns of ${\mathrm{SV}}_{\mathrm{benefit}}$ in bilateral vaINS/mINS were more similar between individuals who exhibited similar general altruistic preference than those who differed in general altruistic preference.

Discussion

In this study, we provide a neurocomputational account of how benefactors weigh different attributes (i.e., one's own costs and others' benefits) to make altruistic decisions. Combining a novel task with model-based fMRI analyses, we clarify the algorithms of cost-benefit calculation underlying altruistic behaviors, the neural implementations of such calculation, and the neural basis of individual variations in altruistic preferences. Our findings implicate critical roles of a wide range of brain regions in altruistic decision-making and address how personality traits (i.e., dispositional empathy) and cognitive processes (i.e., cost-benefit calculation) interact to contribute to altruistic behaviors.

Our study generalizes the integration with nonlinear transformations in non-social decision-making (Park et al., 2011; Charpentier et al., 2016; Chong et al., 2017) to social decision-making and extends algorithms of altruistic decision-making from linear integration (Morishima et al., 2012; Crockett et al., 2014; Hutcherson et al., 2015) to integration with nonlinear transformations. Our findings contribute to our understandings of altruistic behaviors in at least following three ways. First, in previous studies which employed similar paradigms and the modeling approach (Crockett et al., 2014, 2017), participants were confronted with traded-offs between how much reward they gained and how much pain others received (i.e., a self-gain framework). However, in real-life situations, people often weigh between how much the personal costs to take and how much benefits others get when making altruistic decisions (i.e., a self-loss framework). In the current study, we set up a self-loss context (i.e., benefactors bear costs to benefit others) to minimize the discrepancy between laboratory manipulations and real-life problems. Second, previous studies either focused on linear models (Crockett et al., 2014, 2017) or held an assumption that all the participants integrate costs and benefits in a parabolic discounting model (Lockwood et al., 2017), ignoring the variability in the nonlinearity of the integration mechanisms across individuals. Here, we freely estimate the nonlinearity of weighting on benefactors' costs and/or recipients' benefits to allow for variations in these parameters across individuals. Third, although both empathy concern and computational processes are suggested to be crucial to altruistic behaviors (Hein et al., 2010; Hutcherson et al., 2015), previous studies did not provide direct evidence concerning how empathy concern influences valuations and cost-benefit computations (Crockett et al., 2014, 2017; Lockwood et al., 2017). In the current study, we fill in this gap by demonstrating the contribution of trait empathy to altruistic preferences and by clarifying the potential neural pathways underlying this effect with both univariate and multivariate fMRI analyses.

In the current study, we consider the weighting parameter (i.e., $\kappa$) as the measure of altruistic preferences in a similar way as previous studies (Crockett et al., 2014, 2017; Lockwood et al., 2017), with greater $\kappa$ reflecting stronger concerns for others' welfare. The power exponent (i.e., $\alpha$) further differentiates individuals based on the magnitude of marginal utility of altruistic behaviors. Such a differentiation provides us with a new way to examine individuals' altruistic preferences. One might argue that biased perceptions of noise stimuli (Shepard, 1978) and monetary magnitude (Namboodiri et al., 2014; Pardo-Vazquez et al., 2019) will render the observed integration of nonlinearly transformed attributes unreliable, and these confounding effects may not be easily addressed by our current design. Nevertheless, our findings highlight the importance of employing a nonlinear algorithm to examine cost-benefit integration of different dimensions of information underlying social decision-making.

Our model-based neuroimaging analyses further contribute to our understandings of neurocomputational basis underlying altruistic behaviors. First, our results suggest critical roles of dACC and rIPL in representing self-interest motives and other-regarding motives across different modalities. Second, univariate mediation analyses and multivariate IS-RSA provide convergent evidence for differentiating the roles of close but different subregions in INS underlying the helping behavior. Third, the IS-RSA further extend univariate analyses by revealing the role of DLPFC in altruistic preference and reconciling conflicts regarding the role of DLPFC in empathy-driven altruistic behaviors. We discuss these aspects in more detail in following sections.

First, the engagement of dACC and rIPL in evaluating benefactors' costs and recipients' benefits largely replicate our previous findings that dorsal part of MPFC encodes self-interest motives and rIPL encodes other-regarding motives when participants making altruistic decisions under a risk-taking context (Hu et al., 2017). Importantly, conjunction results in the current study suggest domain-general roles of dACC and rIPL in encoding both self-regarding and other-regarding motives. These findings are consistent with several lines of research which suggest a domain-general role of dACC in commonly encoding information of risk (Xue et al., 2009; Hu et al., 2017), reward (Lockwood et al., 2016), and pain (Singer and Lamm, 2009; Lamm et al., 2011; Engen and Singer, 2013) for both oneself and others. As rIPL is involved in a variety of non-social and social cognitive functions, including mathematical calculation, salience processing, perspective taking, and empathy (Pinel et al., 2004; Kahnt et al., 2014; Tusche et al., 2016; Igelström and Graziano, 2017), the findings here about rIPL can be explained by its role in mathematical calculation or salience processing for encoding personal costs (Pinel et al., 2004; Kahnt and Tobler, 2013) and in representing vicarious mental states for other's benefits (Lamm et al., 2011; Tusche et al., 2016). It is highly likely that dACC and rIPL work in the common currency neural system which implicates identical neural valuation processes across social and non-social decisions (Ruff and Fehr, 2014).

Second, both univariate mediation analyses and multivariate IS-RSA clarify the critical role of vaINS/mINS in linking different sources of altruistic preferences (e.g., task-specific other-regarding preferences and dispositional empathy concern). These observations are in line with the view that middle and ventral anterior insular is a well-suited interface between direct and vicarious experiences (Craig, 2008) and supports the empathic responses for others and other social-emotional processing during interpersonal interactions (Chang et al., 2013; Gao et al., 2018). On the contrary to vaINS/mINS, daINS/IFG, an adjacent but different subregion of aINS, is found to be involved in evaluating personal costs, rather than reflecting individual variations in altruistic preferences as vaINS/mINS. This observation indicates the role of daINS/IFG in goal-directed cognition and self-interests representations (Dosenbach et al., 2006; Knutson et al., 2007; Eckert et al., 2009; Engelmann et al., 2017). Increasing potential loss may enhance daINS/IFG activity to recruit more attention resources (Nelson et al., 2010; Chang et al., 2013) to process individuals' own interests (Droutman et al., 2015; Engelmann et al., 2017). Our paradigm allows us to clearly differentiate the roles of adjacent but different subregions of INS in distinct cognitive/affective subfunctions, and reconcile previous mixed evidence about the role of aINS underlying complex social behaviors.

Last but not least, IS-RSA analyses suggest that neural activity patterns of personal costs in DLPFC reflect individual variations in general altruistic preference. Given the assumption that participants in similar positions of the general altruistic preference space evaluate personal costs or others' benefits in similar ways, regions (i.e., vaINS/mINS and DLPFC) showing similar activity patterns are engaged in these processes. Recent studies suggest that DLPFC, as a cognitive control region (Miller and Cohen, 2001; Buckholtz and Marois, 2012), serves to modulate selfish motives and other-regarding motives (Knoch et al., 2006; Ruff et al., 2013; Zhu et al., 2014; Nihonsugi et al., 2015), and to construct moral values in interpersonal interactions (Crockett et al., 2017). However, it is still controversial as to what extent DLPFC is engaged in empathy-driven altruistic behaviors given that previous univariate findings were inconsistent regarding the association between DLPFC activity in altruistic behaviors and dispositional empathy (FeldmanHall et al., 2015; Crockett et al., 2017). Our multivariate analyses add new evidence to clarify the role of DLPFC in altruistic behaviors by highlighting that individuals with similar neural activity patterns representing benefactors' costs in this region exhibit similar general altruistic preference. These findings not only elucidate the critical role of DLPFC in modulating selfish and altruistic motives in altruistic decision-making, but also demonstrate the strength of multivariate analysis in clarifying the neural basis of individual variations in complex psychological and computational processes that cannot be identified by univariate analyses.

In summary, combining a novel experimental paradigm with computational modeling, our study sheds new light on the understanding of altruistic decision-making by providing a neurocomputational account of how different attributes are integrated to support altruistic helping behaviors. Our findings demonstrate the strength of introducing nonlinear algorithms into the investigation of social decision-making which involves integration of different dimensions of information. Moreover, neuroimaging results provide a comprehensive explanation for the underlying neural implementations by showing that dACC and rIPL function in an extended common currency system to subserve cost-benefit integration during altruistic decision-making. We reconcile some conflicting suggestions concerning the functions of aINS by revealing different roles in adjacent but distinct subregions within INS. Furthermore, multivariate fMRI analyses help to elucidate the crucial roles of DLPFC in general altruistic preference which accounts for both psychological (e.g., dispositional empathy) and cognitive processes (e.g., other-regarding preferences). These findings have important implications for future investigations of psychological and neurobiological bases underlying complex interpersonal interactive behaviors.