7T MR Thermometry technique for validation of system-predicted SAR with a home-built radiofrequency wrist coil

Abstract

Purpose

A 7T magnetic resonance thermometry (MRT) technique was developed to validate the conversion factor between the system-measured transmitted radiofrequency (RF) power into a home-built RF wrist coil with the system-predicted SAR value. The conversion factor for a new RF coil developed for ultra high magnetic field MRI systems is used to ensure that regulatory limits on RF energy deposition in tissue, specifically the local 10g-averaged specific absorption rate (SAR_10g), are not exceeded. MRT can be used to validate this factor by ensuring that MRT-measured SAR values do not exceed those predicted by the system.

Methods

A 14 cm diameter high-pass birdcage RF coil was built to image the wrist at 7T. A high spatial and temporal resolution dual-echo gradient echo MRT technique, incorporating quasi-simultaneous RF-induced heating and temperature change measurements using the proton resonance frequency method, was developed. The technique allowed for high temperature resolution measurements (~ ± 0.1°C) to be performed every 20 s over a 4 minute heating period, with high spatial resolution (2.56 mm³ voxel size) and avoiding phase discontinuities arising from severe magnetic susceptibility-induced B₀ inhomogeneities. MRT was performed on a phantom made from polyvinylpyrrolidone to mimic the dielectric properties of muscle tissue at 297.2 MHz. Temperature changes measured with MRT and four fiber optic temperature sensors embedded in the phantom were compared. Electromagnetic simulations of the coil and phantom were developed and validated via comparison of simulated and measured B₁⁺ maps in the phantom. The position of maximum SAR within the coil was determined from simulations, and MRT was performed within a wrist-sized piece of meat positioned at that SAR hotspot location. MRT-measured and system-predicted SAR values for the phantom and meat were compared.

Results

Temperature change measurements from MRT matched closely to those from the fiber optic temperature sensors. The simulations were validated via close correlation between the simulated and MRT-measured B₁⁺ and SAR maps. Using a coil conversion factor of 2 kg⁻¹, MRT-measured point-SAR values did not exceed the system predicted SAR_10g in either the uniform phantom or in the piece of meat mimicking the wrist located at the SAR hotspot location.

Conclusions

A highly accurate MRT technique with high spatial and temporal resolution was developed. This technique can be used to ensure that system-predicted SAR values are not exceeded in practice, thereby providing independent validation of SAR levels delivered by a newly-built RF wrist coil. The MRT technique is readily generalizable to perform safety evaluations for other RF coils at 7T.

Introduction

The arrival of MR Imaging at 7T into the clinical domain was greatly facilitated by the regulatory clearance in Europe and USA of a first 7T system in 2017. This clearance was obtained for imaging the head and knee only, due to the lack of radiofrequency (RF) coils suitable for imaging larger body areas. There is a clear need for developments in RF coil technology to bridge this gap, and many exciting new developments have appeared in recent years¹. An essential part of the safety validation for any RF coil is to ensure the specific absorption rate (SAR) does not exceed regulatory limits set by the International Electrotechnical Commission (IEC)². At 3T and lower, whole- or partial- body averaged SAR values can be determined in calorimetry phantom experiments³ and in patients via real-time measurements of reflected power from the RF coil during imaging. At 7T, however, the local SAR averaged over smaller tissue volumes must also be controlled because localized SAR hotspots can be generated within the region of the body exposed to the 300 MHz RF energy⁴. Such hotspots arise from the interaction of this RF energy with the heterogeneous distribution of dielectric properties within the body, which results in areas of constructive and destructive interference of the B₁⁺ fields. The IEC defined limits for local SAR averaged over 10 g of tissue (SAR_10g)² and this value is controlled on 7T systems in addition to the body averaged SAR values.

The local SAR_10g cannot, however, be measured directly during imaging. Rather, the 7T system predicts the SAR_10g value during imaging by measuring in real-time the RF power transmitted by the coil and converting this to SAR_10g using a coil-specific conversion factor such that:

$${\text{SAR}}_{10\text{g}}=\text{Conversion}\_\text{Factor }.\text{ Trasmitted}\_\text{RF}\_\text{Power}$$

The conversion factor (with units [kg⁻¹]) is established using electromagnetic simulations which solve Maxwell’s equations for that particular RF coil loaded with anatomically realistic virtual body models representative of the patient population^5,6. These numerical simulations are used to determine a worst-case peak SAR_10g (per unit transmitted RF power) across many different body models and from this the conversion factor for the coil is derived. In this way, the predicted SAR_10g can be kept within regulatory limits by limiting the RF power transmitted by the coil.

Because the conversion factor for single-Tx coils is derived from a worst-case scenario for a particular RF coil, the predicted SAR_10g value displayed on the console should always be greater than the actual SAR delivered to the patient (the situation is more complicated for parallel-Tx systems where the spatial distribution of the SAR can vary^7,8). This should be verified independently as part of the safety evaluation of a newly-built RF coil, by comparing the system’s predicted value with that derived from experimentally accessible data^9–11. However, recommended testing procedures are only valid for volume coils at low fields, i.e. where a uniform RF transmit field can be produced¹². At 7T, MR thermometry (MRT) can be used for this purpose: the temperature change in a phantom before and after a period of RF-induced heating provides a measure of SAR_10g, which can then be directly compared to the system’s predicted value.

The proton resonance frequency (PRF) shift method for MRT¹³ is based on a well-defined linear relationship between the phase of the measured MR signal in a material and the material’s temperature. This approach has found widespread use at 1.5T and 3T for applications such as MR-guided focused ultrasound¹⁴, microwave ablation¹⁵ and thermal therapy^16,17. For such applications, large temperature changes are typically involved, and hence sub-°C temperature resolution is not of paramount importance. However, adapting this technique to RF coil safety evaluations at 7T presents several challenges. For example, the MRT technique must be capable of measuring very small temperature changes (< ~ 1–2 °C) over a short timeframe (~ few minutes). This arises due to two factors: (i) RF-induced temperature changes are relatively low compared to temperature changes typically encountered in thermal therapies, and (ii) to accurately identify localized SAR hotspots in a phantom, the MRT technique must be capable of measuring such low temperature changes in a timescale which avoids heat convection effects in the phantom material¹⁸. A further challenge arises due to increased magnetic susceptibility effects at 7T¹⁹, which introduce significant phase dispersion and signal drop-out even over modest sequence evolution times. Additional factors common to MRT at lower field strengths, such as B₀ field drifts and gradient coil heating, further compound the challenges of measuring such small temperature changes.

To measure SAR, separate data acquisition sequences are typically used for the before/after MRT measurements and the RF-induced heating phase^20–22. A disadvantage of this approach is that the SAR must be calculated from a 2-point fit to the data at each pixel, since only two timepoints are measured. The large phase differences between the before and after MRT measurements also lead to significant phase wrap problems, particularly at 7T. The aim of this study was to develop a quasi-simultaneous RF-heating and MRT technique based on the PRF method, wherein the same sequence was used to heat the sample and perform the temperature measurement. The technique thus performed dynamic temperature measurements as a function of time, thereby allowing for a more accurate measure of the temperature change via a least squared fitting of the data at each pixel across multiple time points. This technique was used to establish the safe operation of a home-built wrist RF coil at 7T by verifying that the measured peak SAR_10g in a phantom was less than the predicted SAR_10g displayed on the system’s console.

Materials and Methods

All experiments were carried out on a 7T system (Magnetom Terra, Siemens Healthcare, Germany) with a home-built radiofrequency coil (14 cm inner diameter, 20 cm long high-pass quadrature birdcage design) designed for imaging the wrist. A conversion factor of 2 kg⁻¹ was used for the coil. A cylindrical phantom (68 mm diameter, length 160 mm) was constructed containing a uniform tissue-mimicking material with dielectric properties matching muscle tissue. The phantom material was composed of 31 wt.% polyvinylpyrrolidone (PVP K30, AppiChem GmbH, Germany) dissolved in deionized water, with 1 wt.% NaCl (S7653, Sigma Aldrich, St. Louis, MO) to achieve the dielectric properties of muscle tissue²³, using a recipe based on²⁴ but adjusted to take into account a different molecular weight PVP powder. The material was gelled by adding 1.7 wt.% agar (A6013, Sigma Aldrich, St. Louis, MO), with gelling occurring by heating the mixture to > 90°C for one hour and controlling the rate of cooling to avoid formation of air bubbles. The material’s T₁ and T₂* values were measured using standard techniques on the 7T system, while the dielectric properties were measured using a dielectric probe kit (DAK-12, SPEAG, Switzerland).

Temperature measurements were performed using the proton resonant frequency (PRF) method. The PRF method relies on the linear relationship between the phase in a gradient-recalled echo image data and the temperature of the phantom material. The large phase shifts at high fields make the PRF method well suited to MR thermometry measurements at 7T. The temperature change (ΔT) can be calculated from a measured change in phase before and after a period of heating, using:

$$\Delta T=\Delta \phi /\gamma B_{0}TE\alpha$$ Equation 1

where Δφ is the change in phase caused by a temperature change in the phantom, and α is the PRF change coefficient (0.0106 ppm/°C for the current phantom material²⁴). The SAR can then be calculated at each voxel using:

$$SAR=C.\Delta T/\tau$$ Equation 2

where C is the specific heat capacity of the phantom material (3601 J.kg⁻¹.K⁻¹) and τ is the time duration of the heating period.

A 2D dual-echo gradient-recalled echo sequence was adapted to deposit RF energy in the phantom at a uniform rate during the course of the experiment while quasi-simultaneously measuring the temperature increase via the change in phase. The dual-echo approach corrects for temperature-dependent changes in tissue’s electrical properties (conductivity, and to a lesser extent permittivity), which otherwise introduce additional phase shifts independent of TE²⁵. The acquisition parameter values were: voxel size = 0.8 × 0.8 × 4 mm³; 1 slice; FoV = 200 × 144 mm²; TE_1,2 = 2, 10ms; TR = 47 ms, flip angle = 40°; BW_r = 1385 Hz/pixel; NSA = 3, 20 s dynamic image time; 4 minute total acquisition time.

The RF energy deposition was achieved using a series of saturation RF pulses applied > 1 kHz off-resonance to avoid any influence on the imaged field of view. To achieve the maximum temperature increase in each experiment, the predicted SAR was maximized up to the regulatory limit that the system would deliver (20 W/kg local SAR averaged over 10g ²) by changing the peak voltage amplitude of the saturation pulses. For the specific phantom set-up and RF coil loading, 5 saturation pulses with peak amplitudes of 130–145 V (empirically adjusted to maximize the predicted SAR) were used, followed by the imaging period with a TR of 47 ms. A single slice of image data thus required 6.8 s, with an NSA of three used to improve SNR for a total acquisition time of 20 s. This was repeated 12 times, resulting in 12 temperature measurements over 4 minutes. Beyond 4 minutes, heat convection effects within the phantom material were found to introduce inaccuracies into the resultant temperature (and hence SAR) maps. With this approach, RF energy was delivered in an approximately uniform manner throughout the experiment. The ‘SAR override’ research functionality on the 7T system was not used since, when it was activated, the system no longer displayed the predicted SAR nor stored this value in the log file.

The SAR maps derived from the MRT data was validated by direct comparison to temperature measurements performed using a fluoroptic thermometry system (Luxtron M3300, Lumasense Technologies, CA). Four fiber-optic (FO) sensors were positioned within the cylindrical phantom in a coronal plane, each parallel to B₀ and located at the mid-point of the phantom: two positioned on the right and left sides approx. 2 mm from the phantom’s walls, one approx. 17 mm from the right wall, and the fourth in the center. The FO sensor tips were identified in the magnitude reconstructed images for the TE₁ data, and four small (< 1 mm²) regions of interest (ROIs) were placed at a distance of approx. 2 mm from each tip to avoid magnetic susceptibility-induced phase changes near the tips.

To avoid Gibbs ringing artifacts impinging on the small field of view (200 × 144 mm²), an in-plane spatial resolution of 0.8 × 0.8 mm² was used, with a 4 mm slice thickness. The highest achievable receiver bandwidth of 1385 Hz/pixel was used to minimize magnetic susceptibility-induced phase wrapping, and signal drop-out at the edge of the phantom and close to the FO sensor tips. This is particularly important, considering that the maximum SAR values for a birdcage coil are expected towards the edges of the phantom parallel to B₀ and hence it was desirable to obtain good data in these regions, and also to obtain good data in the area immediately adjacent to the FO sensors. Echo times of TE_1,2 = 2, 10 ms were used: the former was the minimum achievable given the sequence’s acquisition parameters, while the latter represented a compromise between the sequence’s temperature measurement sensitivity and susceptibility-induced phase wrapping and signal drop-out effects. For an SPGR-based MRT technique, the greatest sensitivity occurs when TE (in a single-echo experiment) or ΔTE (in a dual-echo experiment) equals the T₂* of the material¹⁶. The gradients were run in ‘whisper’ mode, to minimize any effects from eddy currents and gradient heating on the phase measurements. B₀ shimming (using the system’s default third order shim functionality) was performed over the imaged FOV.

Reference vials containing oil (cylinder of 20 mm diameter, 70 mm high; Marcol 82, ExonMobil, USA) were used to perform bias field correction for phase changes unrelated to changes in temperature, arising from drift of the main B₀ field and heating from the gradient coils. Four vials were positioned at each corner of the FOV, with a 5 mm gap between the vial and the phantom to minimize disturbance in B₀ which otherwise would introduce significant phase wraps in the phantom, particularly for the long TE data. The oil has two resonant peaks separated by 0.422 ppm (127 Hz at 7T), and hence it was important to avoid TE values where both components were out-of-phase (i.e. every 3.95 ms), as an out-of-phase acquisition resulted in an approx. 62% reduction in SNR in the oil reference. Since the phase of the oil reference ROIs are subtracted from that in the phantom, any loss in SNR in the oil ROI impacts directly on the SNR in the temperature maps. The need to maintain high SNR in the oil ROIs imposed a further limitation on the choice of TE₂, i.e. to avoid out-of-phase TE values. The SNR in the oil ROIs was further maximized by using a flip angle of 40° in the MRT sequence, slightly larger than the Ernst angle for the phantom material (22°); this only effected a ~10% decrease in SNR in the phantom.

Data processing of the raw k-space data was performed using code developed in Matlab (The Mathworks, Natick, MA). The average phase in each oil reference vial was fitted to a first order polynomial and extrapolated over the phantom FOV for each dynamic. Complex subtraction of phase data was performed in the following order:

• - TE₁ phase from TE₂ phase data

• - extrapolated oil reference phase from phantom phase data for each dynamic

• - a running subtraction between successive dynamics

This order of subtraction served to avoid phase discontinuities despite the presence of significant phase wraps in individual images, particularly for the TE₂ data, by ensuring that phase differences between successive dynamics did not exceed 2π. The cumulative phase changes for each successive dynamic at each pixel were computed, and a pixelwise least square fitting of the temperature change as a function of time was used to calculate the SAR at each timepoint, effectively replacing ΔT/τ in Equation 2 with the slope dT/dt. Final maps of SAR were thus generated after 4 minutes of heating. To compare the dT/dt slopes between the FO sensor and MR Thermometry at a given position, we computed difference estimates and corresponding 95% Welch-Satterthwaite confidence intervals (CI’s) of the difference based on the results of the independently fit simple linear regressions. Slopes were considered significantly different if the 95% CI did not overlap zero, equivalent to a two-sided test at the alpha level of 0.05. Analyses were performed using the R statistical computing software v4.0.2 (R Core Team, Vienna, Austria).

SAR maps derived from the MRT experiments were compared to those obtained from numerical simulations performed on models of the RF coil and phantom using commercial electromagnetic simulation software (Sim4Life, ZMT, Switzerland). The simulations were performed on a variable density grid of 101.16 MCells, with a geometric resolution of 0.1 mm over the phantom. The RF power in the simulations was scaled to match that in the MRI phantom experiments. The simulations were executed on a GPU (Tesla V100, NVIDIA, USA), taking approximately 3.5 hours to run. The coil and phantom simulation model was validated by comparing measured to simulated B₁⁺ maps. The 7T system’s default B₁⁺ mapping routine was used, with a spatial resolution of 1 × 1 × 4 mm³.

The validated simulations were used to identify areas of elevated SAR within the volume of the RF coil by moving the cylindrical phantom to different axial and radial positions. MRT experiments were performed on a piece of meat containing primarily bone, fat and muscle, placed at the location of the maximum SAR, with a gap of 20 mm radially from the conductive elements of the coil to the sample.

Results

The phantom’s relaxometry and dielectric properties were measured at: T₁ = 680 ms, T₂* = 35 ms, ε_r = 54.6, σ = 0.74 S m⁻¹. The relaxation values are well suited for MR measurements at 7T, while the dielectric properties closely matched muscle tissue and loaded the RF coil similar to a wrist. Figure 1 shows phase reconstructed images of the phantom surrounded by the four oil reference vials, acquired at several TE values (8 – 26 ms), to illustrate the significant susceptibility-induced phase wrapping at 7T. The maximum temperature measurement sensitivity for the MRT sequence with the phantom material would be obtained with a TE of 35 ms (i.e. same as the T₂* of the material). However, it is clear that significant phase wraps and signal drop-out make such long TE values unfeasible, and in the current study a TE₂ value of 10 ms was used which produced high temperature measurement sensitivity in the phantom material and the SNR in the oil reference ROIs (and hence high SNR in the temperature maps), while avoiding severe phase wraps between successive dynamics.

Figure 1:

Phase reconstructed images of the phantom and four reference oil vials (at the corners) acquired at TE values of (a) 8, (b) 16 and (c) 26 ms, demonstrating the significant phase wraps and signal drop-out which occurred as the TE increased. (d) Magnitude reconstructed image showing the position of the four fiber optic temperature sensors (numbered 1 – 4) and the horizontal support bars for the sensors within the phantom.

The effects of correcting for unwanted contributions to the phase changes during the MRT experiment are demonstrated in Figure 2. The graph in Figure 2(a) shows the measured change in temperature as a function of time in ROI 1 at the edge of the phantom, with and without the bias field correction. The temperature measured using only one TE value (10 ms) is compared to the dual-echo approach in Figure 2(b) for ROIs 1 and 3 (i.e. ROIs at edge and center of phantom), demonstrating the increased effect of temperature-related changes to the phantom material’s dielectric properties with increasing depth in the phantom.

Figure 2:

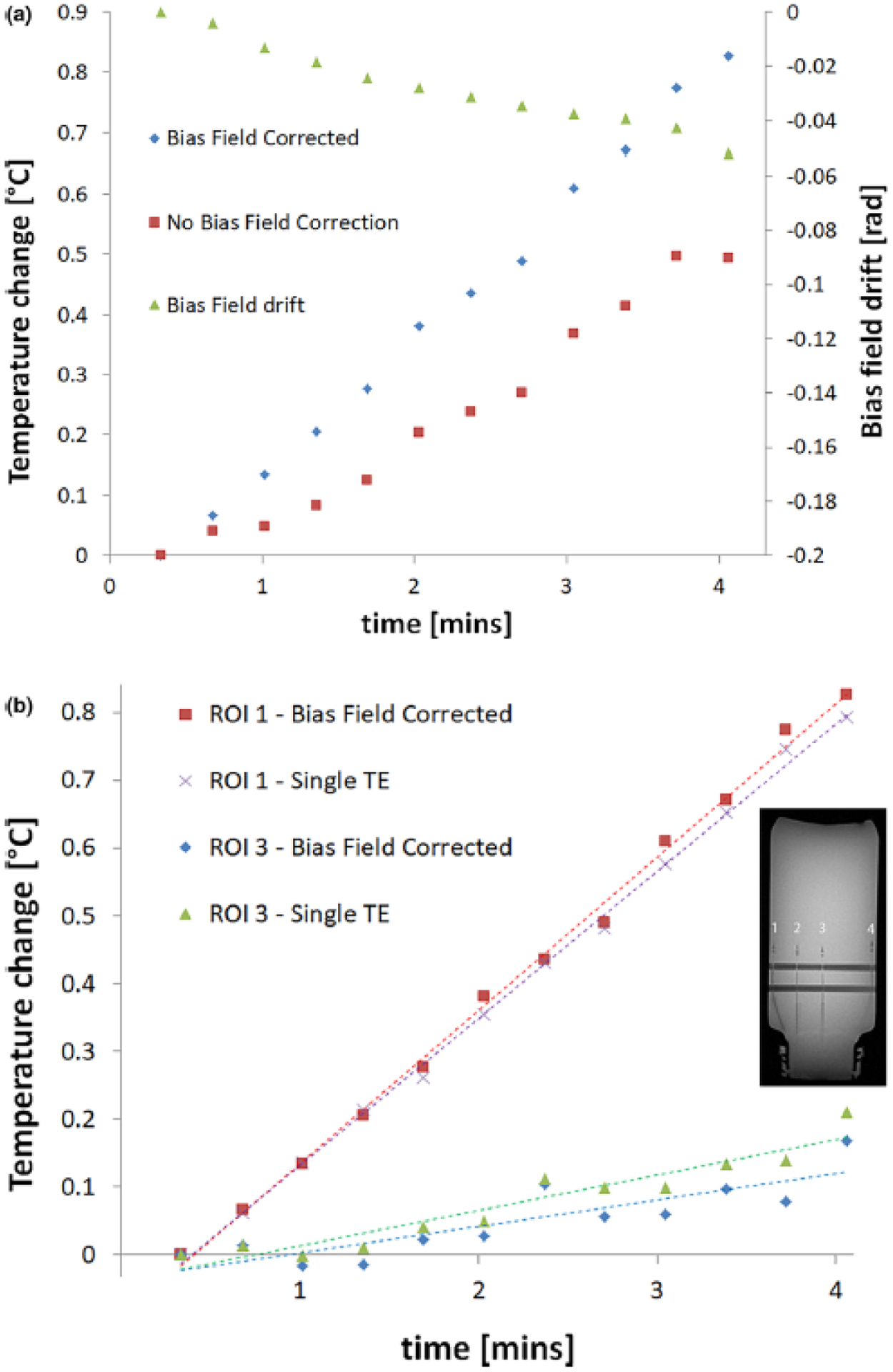
Graphs showing the change in temperature as a function of time as measured via MRT in: (a) ROI 1 placed at the edge of the phantom, with and without the bias field correction applied, and (b) ROIs 1 and 3, placed at the edge and center of the phantom respectively (indicated in the image insert), with bias field correction applied in both cases but without correcting for temperature-dependent changes in tissue’s electrical properties (i.e. with a single-echo acquisition, TE = 10 ms). This correction has little effect close to the phantom’s surface (‘ROI at edge’), and only becomes important at increasing depths as illustrated by the least square fit to the data in each case.

Figure 3 compares the temperature changes measured with the FO sensors and the bias-field corrected dual-echo MRT technique for two sensors/ROIs (located at the edge and in the center of phantom). The slope of the regression line for each data series in indicated in the graph. Statistical comparisons of the dT/dt slopes from FO sensors and MRT indicated significant differences only for two of the four sensor positions (2 and 3). However, examination of these differences and corresponding 95% CI’s indicated these were fairly modest (Table 1). The SAR calculated from this data, averaged over each ROI for the MRT data, is presented in Table 1. In all cases, the measured SAR values were less than the system-displayed predicted SAR_10g of 19.9 W/kg. SAR maps generated from the bias field corrected and uncorrected MRT data are presented in Figure 4, demonstrating the effects of the phase correction schemes. The lower SNR in the bias-field corrected map generated from the single-echo (TE = 2 ms) data (Figure 4(b)) results from the lack of temperature measurement sensitivity of the PRF experiment with such a low echo time. On the other hand, the map generated from the single-echo (TE = 10 ms) data (Figure 4(c) has higher SNR than the dual-echo map in (d), due to one less complex phase subtraction step, but slightly skews the SAR distribution (underestimates at edges and overestimates at center).

Figure 3:

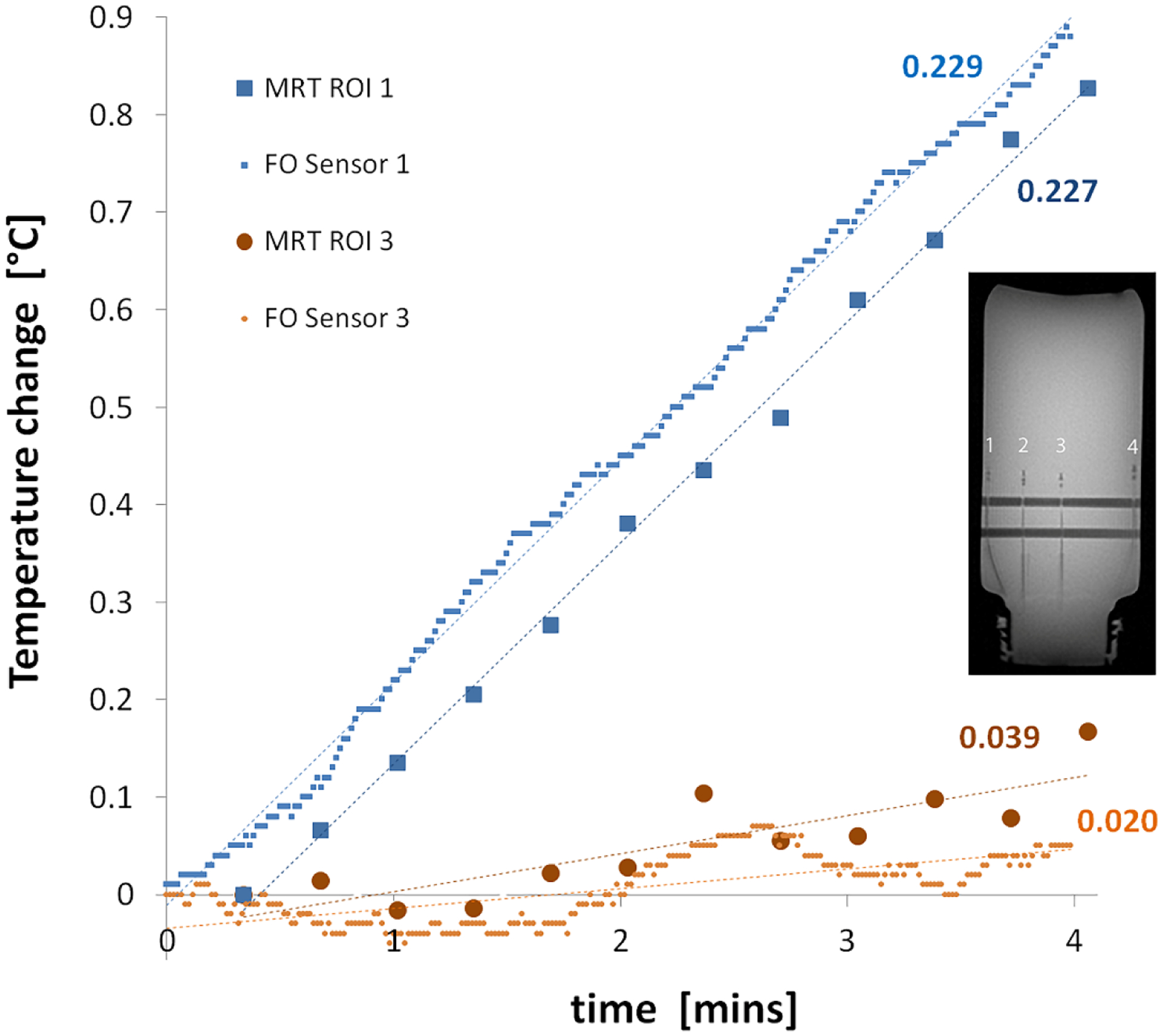
Graph comparing the temperature changes as measured by the FO sensors and the bias-field corrected dual-echo MRT at the position of the center and edge ROIs in the phantom (measurement locations 1 and 3 indicated in the image insert). The numbers beside each dataset indicated the slope of the least-square fitted line for each dataset. The temporal offset of the MRT data reflects the subtraction of phase between subsequent acquisitions.

Table 1:

Comparison of the temperature changes measured using FO sensor and MRT, and the corresponding SAR values calculated from these. The SAR values calculated from the MRT measurements were averaged over ROIs placed 2 mm from the tip of the FO sensors, rather than averaged over 10 g of phantom material. The SAR_10g predicted by the 7T system and displayed on the console was 19.9 W/kg.

FO Sensor / ROI number	FiberOptic sensor measurement		MR Thermometry measurement		Difference in dT/dt (FO sensor vs. MRT)
	dT/dt [°C/min]	SAR [W/kg]	dT/dt [°C/min]	SAR [W/kg]	°C/min [95% CI]
1	0.237	14.22	0.252	15.12	−0.015 [−0.045, 0.016]
2	0.118	7.08	0.164	9.84	−0.046 [−0.056, −0.036]
3	0.020	1.20	0.039	2.34	−0.019 [−0.035, −0.003]
4	0.229	13.74	0.227	13.62	0.002 [−0.007, 0.011]

Figure 4:

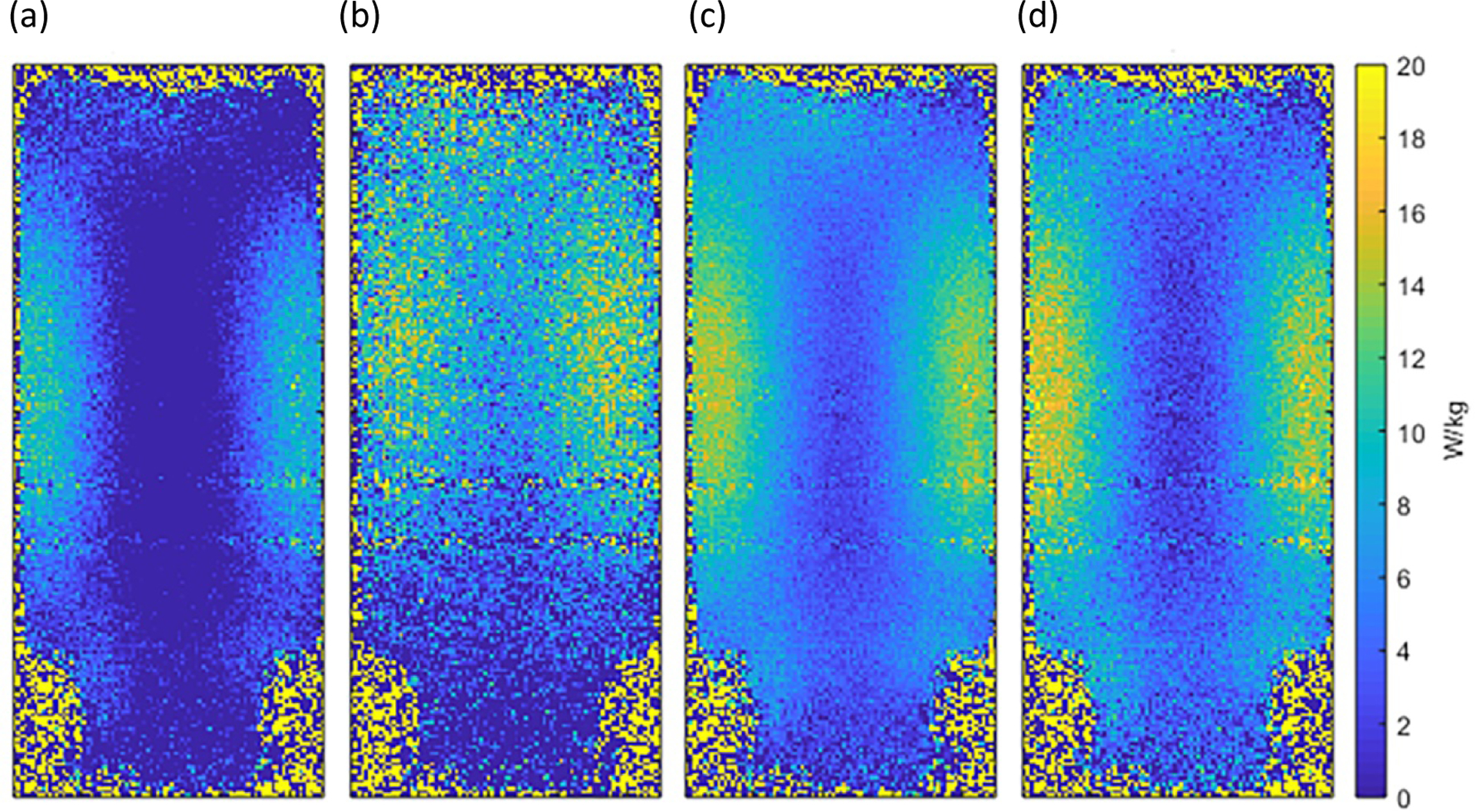
SAR maps generated from the MRT data following 4 minutes of heating are shown for: (a) dual-echo with no bias field correction; single-echo acquisition with bias field correction for TE (b) 2 ms, and (c) 10 ms; and (d) dual-echo acquisition (ΔTE= 8 ms) with bias field correction applied. The predicted SAR_10g that was displayed on the system was 19.9 W/kg; the MRT-measured point-SAR did not exceed this value at any point within the phantom.

The validation of the simulation model is presented in Figure 5, which shows the close agreement achieved in both spatial distribution and magnitude of the simulated and measured B₁⁺ fields and SAR values in the phantom. The location of the maximum simulated SAR for the cylindrical phantom was found within an oblique sagittal slice, approximately 20 mm from the end ring with the two quadrature drive ports. This position was found by repeating the simulations with the phantom repositioned within the free volume of the coil at a minimum 20 mm radial distance from the nearest electrically conductive surface of the coil. Magnitude reconstructed image and MRT-measured SAR maps of the piece of meat positioned at this location are shown in Figure 6(a) and (b). Here again, the measured SAR remained below the system predicted and displayed value of 19.9 W/kg.

Figure 5:

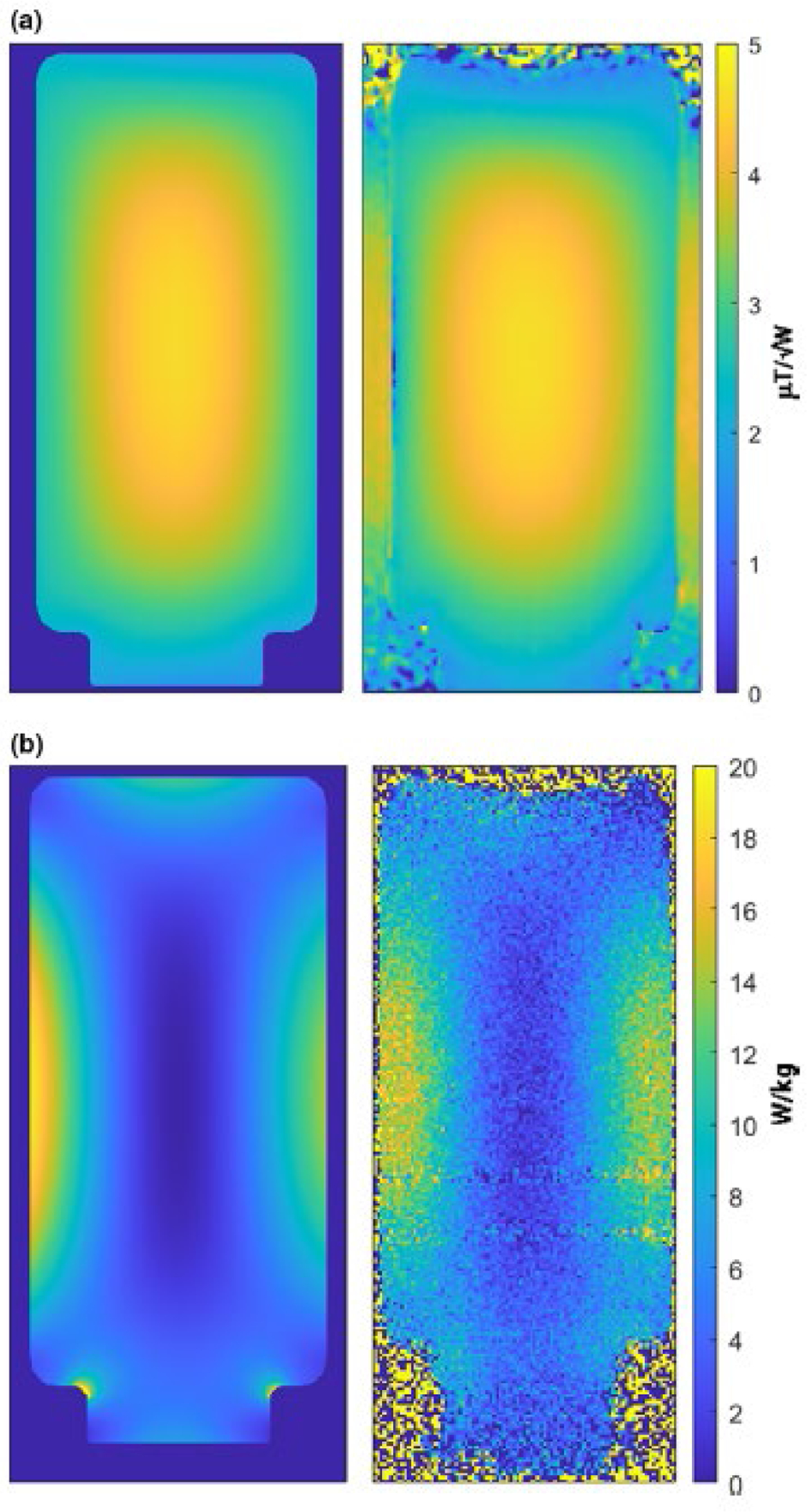
Comparison of the simulated (left) and measured (right) B₁⁺ fields (top row), and SAR maps (lower row). The close agreement in both absolute values and spatial distribution of both the B₁⁺ fields and SAR values validates the simulated RF coil and phantom model. Note the loss of SAR data in the MRT-measured maps in areas of large magnetic susceptibility mismatch, particularly at either end of the phantom and at the neck of the phantom container.

Figure 6:

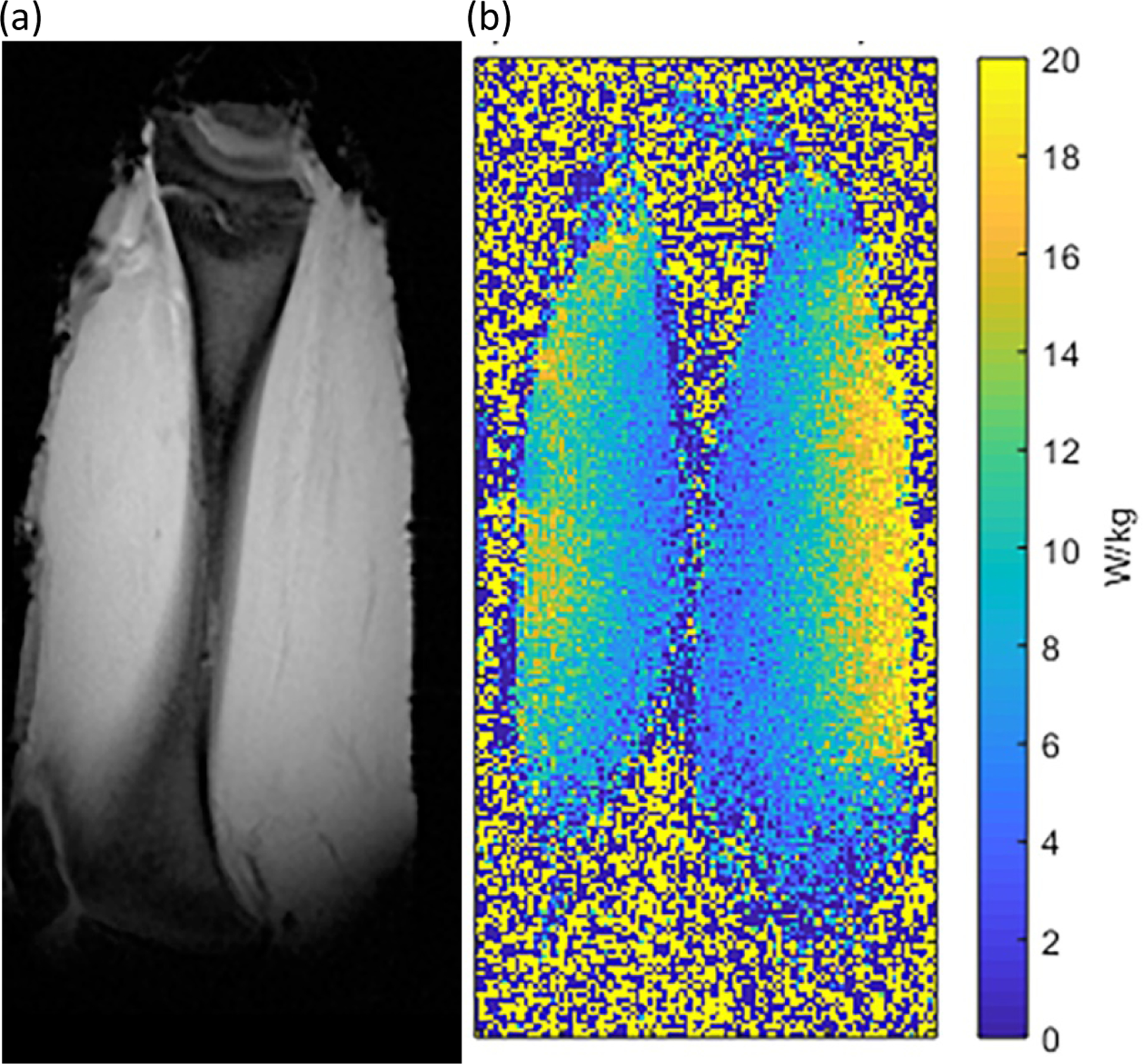
(a) Magnitude reconstructed image (acquired at TE = 2 ms) and (b) MRT-measured SAR map from a piece of ex vivo meat mimicking the wrist, positioned within the RF coil at the SAR hotspot location. The point-SAR did not exceed the system-displayed SAR_10g of 19.9 W/kg.

Discussion

The MRT method described herein allowed for the uniform deposition of RF energy into a phantom and the quasi-simultaneous measurement of temperature changes in the sub-°C range with fast acquisition times and high spatial resolution at 7T. The significant effects on the measurement accuracy of bias field-induced phase changes (B₀ field drift and gradient heating) and temperature-dependent changes in the dielectric properties of the phantom material, were also demonstrated, emphasizing the need to correct for these effects.

The MRT-measured SAR data presented herein were consistently lower than the system-predicted SAR values displayed on the system console (and stored in the system log file), validating the choice of conversion factor for the RF coil. It should be noted, however, that the maximum SAR that the system would deliver was 20 W/kg in First Level RF mode, half of the IEC limit of 40 W/kg for extremities such as the wrist. As such, a conversion factor of 2 kg⁻¹ for this coil effectively incorporates a safety factor of two into the RF energy (and hence SAR) that the coil can deliver. The use of a safety margin of this typical magnitude has been recommended to take into account inaccuracies in RF power and voltage measurements, inaccuracies with the numerical simulations, and variability in actual human subjects (e.g. shape, position, dielectric properties) not covered by the simulation models¹⁰.

A further safety margin is incorporated in the choice of coil conversion factor, considering that the simulated and MRT-measured SAR data presented herein are point-SAR values and are not averaged over 10g of the phantom material. Peak SAR_10g values, as displayed on the system’s console, are invariably lower than peak point-SAR values due to the highly localized nature of the peak SAR distribution, particularly at high fields. Such partial volume effects are not restricted to high fields, since body-averaged SAR values are known to underestimate point and 10 g local-averaged SAR values even at lower field strengths^26,27. Indeed, the use of local SAR values averaged over 1 g of tissue has been suggested as a more representative indicator of likely tissue temperature increases adjacent to electrically-conductive implants²⁸. The supervision of SAR_1g may be more appropriate for scenarios such as the highly heterogeneous SAR distribution within the small imaging field of view of the coil/phantom set-up in the current study. The absence of blood perfusion effects in the phantom and meat experiments introduces a further safety margin when comparing measured to displayed SAR values.

The choice of materials to use for phantom MRT experiments at 7T is an important consideration to maximize measurement accuracy while minimizing signal dropout due to magnetic susceptibility effects. As at lower fields, the ideal material should mimic the dielectric properties of the tissue of interest and, with suitable physical dimensions, load the RF coil appropriately. It should have a linear relationship between signal phase and temperature change, with a low heat conductivity and diffusivity to allow for localized (i.e. voxel-wise) measurements of temperature changes. At lower field strengths, phantoms comprised of gelled polyacrylic acid (PAA) or hydroxyethylcellulose (HEC) are recommended by the ASTM²⁹. However, PAA phantoms suffer from large variability in bulk electrical and thermal properties which limit their use for spatial mapping of subtle temperature changes as required at 7T. PAA formulations invariably contain many small air bubbles which, at 7T, create significant localized susceptibility-induced phase changes and signal drop-out. Air bubbles are also problematic with HEC, and it is very sensitive to local viscosity-related variations in temperature which make it difficult to accurately measure small temperature changes. Formulations composed of sucrose to achieve the desired dielectric properties have also been suggested²³, but the presence of several spectral components adds complexity to the temperature model. PVP, with agar as a gelling agent, can be produced with very homogeneous dielectric and thermal properties with no air bubbles and with relaxation values suitable for MRT experiments at 7T. This material has been suggested for use in quality control phantoms³⁰ and for MRT experiments at 7T^24,31.

MRT at 7T presents additional challenges compared to lower fields, particularly considering the small temperature changes that need to be measured over the necessarily short timescales involved. The significant magnetic susceptibility effects at 7T result in significant signal dropout and image geometric distortions in areas of large susceptibility changes. Very high receiver bandwidths were thus required, with a consequent effect on the SNR, to enable accurate temperature measurements near the edges of the phantom and close to the fiber optic temperature sensors. A further difficulty caused by the severe susceptibility effects is severe phase wrapping even for data acquired with modest TE values. In the current study, this necessitated the use of a sub-optimal (from the perspective of maximizing the temperature measurement sensitivity) TE₂ value, significantly lower than the T₂* of the phantom material. This was mitigated by the use of the dynamic MRT technique, which allowed for a longer TE₂ value than otherwise possible by enabling the calculation of a dynamic change in phase every 20 s during the experiment while ensuring that the phase change between dynamics did not exceed 2π, even in the small oil reference vials located in air outside the phantom. A recent study by Brink et al described a similar PRF-based MRT technique with quasi-simultaneous RF-induced heating and temperature measurement³¹. However, this method used a single-echo approach with a relatively long dynamic acquisition time (60 s), and hence is prone to errors in the measurement of small temperature changes with high spatial variability. The measurement of dynamic phase changes in the current study further allowed for a more accurate fit to the temperature change data across the 4 minute experiment duration, compared to methods which only acquire temperature measurements before and after a period of heating. The dual-echo approach described herein further eliminates phase-shift errors arising from the temperature-dependent changes in a material’s dielectric properties, which alter the phase propagation speed and hence induce changes in the transmit (B₁⁺) and receive (B₁⁻) phase 25. This effect becomes more pronounced with increasing depth into a sample due to phase retardation effects, and as such the MRT technique described herein is suitable for use in investigations of larger RF coils with corresponding larger sample volumes.

The temperatures measured by MR-compatible FO sensors are highly localized to the area immediately in front of the tip, and comparisons with MRT should ideally be performed with ROIs placed very close to the FO sensor tips³². This is difficult to achieve at 7T, due to phase distortions close to the tips caused by magnetic susceptibility differences between the FO sensors and the phantom material. In the current study, the error deriving from this was minimized by positioning the FO sensor tips and hence the MRT ROIs at the mid-point of the cylindrical phantom in the z-direction, where the longitudinal variation of SAR did not change much in the few mm in front of the FO sensor tips. Another source of error for MRT experiments aimed at measuring point-SAR values arises from heat convection effects within the phantom material, which during the MRT experiment alter the spatial distribution of temperature changes that one wishes to measure and would result in an underestimation of the maximum point SAR. To minimize this effect, a gelling agent is typically added to the phantom material to minimize convection effects, although short measurement times are still mandated. In the current study, no smearing of temperature changes was noted in MRT experiments up to 4 minutes, but was manifest beyond that timeframe. A final limitation of the current study relates to the PRF method, where errors of up to 10% may occur due to the non-zero magnetic susceptibility of pure water (0.0026 ppm/K).

Conclusions

An MR thermometry method suitable for validating the choice of conversion factor for a home-built RF wrist coil at 7T was described. The method corrects for phase changes arising from bias field and temperature-dependent changes in tissue dielectric properties, and avoids phase wrap problems due to local B₀ inhomogeneities. Regions of elevated SAR were identified from simulations, and the MRT-measured point-SAR values remained consistently below the system predicted SAR_10g values for both a uniform phantom and a piece of meat.