Hyperspectral interference tomography of nacre

Significance

We invented an optical technique—hyperspectral interference tomography—that rapidly and nondestructively extracts nanoscale structural information across large samples of nacre (mother-of-pearl) and other layered materials by combining multiangle and polarization-resolved hyperspectral imaging with optical-interference modeling. We investigated nacre in mollusk shells from two different species, red abalone and rainbow abalone, and discovered a previously unknown relationship between the age of the mollusk and the thickness of aragonite tablets in nacre. Hyperspectral interference tomography will have applications in climate science, since nacre tablet thickness in fossil shells is a proxy for ancient seawater temperature, and in bioinspired mechanics, because the layered structure of nacre inspires engineered materials with exceptional strength and toughness.

Abstract

Structural characterization of biologically formed materials is essential for understanding biological phenomena and their enviro-nment, and for generating new bio-inspired engineering concepts. For example, nacre—the inner lining of some mollusk shells—encodes local environmental conditions throughout its formation and has exceptional strength due to its nanoscale brick-and-mortar structure. This layered structure, comprising alternating transparent aragonite (CaCO₃) tablets and thinner organic polymer layers, also results in stunning interference colors. Existing methods of structural characterization of nacre rely on some form of cross-sectional analysis, such as scanning or transmission electron microscopy or polarization-dependent imaging contrast (PIC) mapping. However, these techniques are destructive and too time- and resource-intensive to analyze large sample areas. Here, we present an all-optical, rapid, and nondestructive imaging technique—hyperspectral interference tomography (HIT)—to spatially map the structural parameters of nacre and other disordered layered materials. We combined hyperspectral imaging with optical-interference modeling to infer the mean tablet thickness and its disorder in nacre across entire mollusk shells from red and rainbow abalone (Haliotis rufescens and Haliotis iris) at various stages of development. We observed that in red abalone, unexpectedly, nacre tablet thickness decreases with age of the mollusk, despite roughly similar appearance of nacre at all ages and positions in the shell. Our rapid, inexpensive, and nondestructive method can be readily applied to in-field studies.

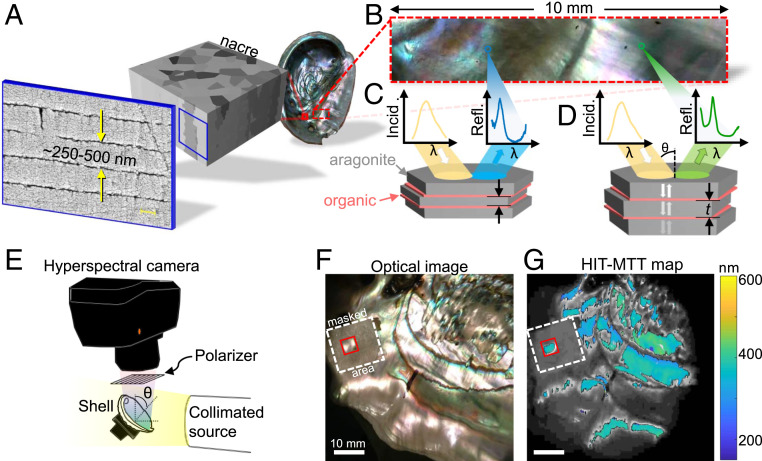
Complex optical phenomena can emerge from a variety of biological or bio-inspired processes, from arrays of colors in peacocks (1) and other birds (2), butterflies (3), and opals (4), to the metal-like sheen of herring (5) and unique polarization-dependent properties of jewel beetles (6) and Pollia fruit (7). Nacre, or mother-of-pearl, is a prominent biologically formed mineral structure found throughout our oceans. It lines the inside of the shells formed by many mollusks, including bivalves, cephalopods, and gastropods. It features brilliant iridescent colors (Fig. 1) and is studied and emulated in part because of its outstanding mechanical performance (8, 9). The striking, colorful appearance of nacre has been a source of scientific curiosity since the days of Brewster (10), Rayleigh (11), and Raman (12, 13), and is the product of optical interference resulting from multiple interface reflections as light propagates through its stratified structure comprising stacks of transparent polygonal aragonite tablets (CaCO₃) interspersed with organic polymer (chitin and proteins) layers (14–16) (Fig. 1A). Nacre is one of seven mollusk shell structures (17). In the nacre structure, the aragonite tablets are typically 5 to 10 μm in diameter and hundreds of nanometers thick [200 to 1,100 nm across all shells, and 250 to 500 nm in red abalone (18)], while the organic sheets are an order of magnitude thinner (14, 16, 19). In columnar nacre formed by gastropods like abalone and snails (Fig. 1), co-oriented tablets are stacked on top of one another, while in sheet nacre formed by bivalves like pearl oysters and pen shells, co-oriented tablets are staggered diagonally (18) (see Movie S1 for an animation showing how co-oriented tablets are stacked in columnar nacre). Despite the significant structural and formation–mechanism differences, the thicknesses of tablets and organic layers are similar in columnar and sheet nacre, and so are the optical and mechanical behavior (20). The resulting palette of colors is primarily dependent on the nacre tablet thickness and the viewing angle, and the optical response that yields these colors can be understood as that of a Bragg reflector (21) with disorder in the layer thicknesses, where the optical band gaps are determined by the thicknesses of the transparent layers (5, 22, 23). Thus, the spectrum of light reflected from a nacre surface encodes information about its physical structure (Fig. 1 B–D).

Fig. 1.

(A) Nacre, the colorful iridescent inner lining of some mollusk shells. Here, the red abalone, or H. rufescens, shell features columnar nacre, which comprises thousands of layers of polygonal aragonite tablets interspersed with organic sheets. (B) A close-up photograph of the nacre surface shows a variety of colors and nonuniformities. (C and D) Given a broadband white light source illuminating nacre at a fixed angle of incidence, variations in color are observed due to the difference in average thickness of aragonite tablets comprising nacre. (E) Hyperspectral interference tomography (HIT) setup: A hyperspectral camera collects predominantly specular reflectance data across a sample illuminated by a collimated source at a fixed angle of incidence from the normal to the sample $\left(\theta \right)$. The reflected light is polarized using a wire-grid polarizer. (F) A color photograph of a region of nacre that was analyzed. (G) Map of the mean tablet thickness (MTT) obtained using HIT, overlaid on a grayscale rendering of the photograph in F. Highlighted in red is a 5 × 5-mm region used to analyze the ontogeny of nacre in Fig. 4. The region around this area was masked off using opaque tape, which is highlighted with the dashed white box.

Understanding and characterizing the structure of nacre and other biomaterials have deep and surprising implications. For example, the average thickness of the tablets comprising ancient nacre can be used as a proxy for local ocean temperatures at the time of nacre formation, enabling paleoclimatology spanning hundreds of millions of years (18, 24, 25). The structure of nacre is also an inspiration for engineered materials thousands of times stronger than the constituent materials (15, 26, 27). To that end, new techniques have been developed to probe and understand the structure of nacre, such as polarization-dependent imaging contrast (PIC) mapping using X-ray absorption near-edge structure spectroscopy combined with photoemission electron spectromicroscopy (18, 28, 29), or X-ray nanotomography (30). However, these characterization techniques such as cross-sectional electron microscopy result in the destruction of the sample and are time-consuming and costly.

Here, we present a method for rapid, nondestructive, and large-scale structural characterization of disordered and nonuniform stratified thin-film materials and apply it to the analysis of nacre. Our all-optical method employs hyperspectral imaging combined with thin-film modeling to extract nacre mean tablet thicknesses (MTTs) and tablet degree of disorder $\left(\sigma \right)$—defined as the standard deviation of the thicknesses—across large areas (Fig. 1 E–G). This characterization method is designated as hyperspectral interference tomography (HIT). We used HIT to map the structure of mollusk shell nacre across many stages of development and identified a previously unexplored relationship between the age of the organism and the structure of the nacre layer. We investigated two particular species of nacre-forming mollusks, Haliotis rufescens (red abalone) and Haliotis iris (paua, or rainbow abalone; data only in SI Appendix), for which the aragonite tablet thicknesses lie within a range of 250 to 500 nm (18, 31); however, the method is applicable to any other transparent layered structure of animal, plant, geologic, or synthetic origin.

Nacre as an Optical Material

The lateral gaps between the abutting tablets in nacre are on the order of single nanometers (16)—much smaller than the wavelength of visible light—and therefore the aragonite/organic structure behaves largely like a thin-film assembly (22), with the color at any point along the surface of a shell attributed primarily to thin-film interference effects (21, 32) (Fig. 1 B–D) (SI Appendix, section 1). However, nacre is far from uniform in terms of both the tablet thicknesses in each tablet stack and the surface topography, which gives nacre its unique colorful appearance.

HIT simultaneously acquires the angle-dependent reflectance spectra from many areas across the shell using a hyperspectral camera and then infers the physical Bragg-like structure from these measurements (Fig. 1E and Methods). In HIT, a collimated broadband light source is used to capture predominantly specularly reflected light, discarding light that is scattered or reflected by inhomogeneities on the surface. A linear polarizer is positioned in front of the camera to independently capture s- and p-polarized reflectance.

The resulting measured spectra (one spectrum per pixel, per incidence angle, per linear polarization state) can then be modeled using well-understood thin-film optical techniques, obviating the need to model the much more complex scattering processes.

Fitting Structural Parameters to Spectra.

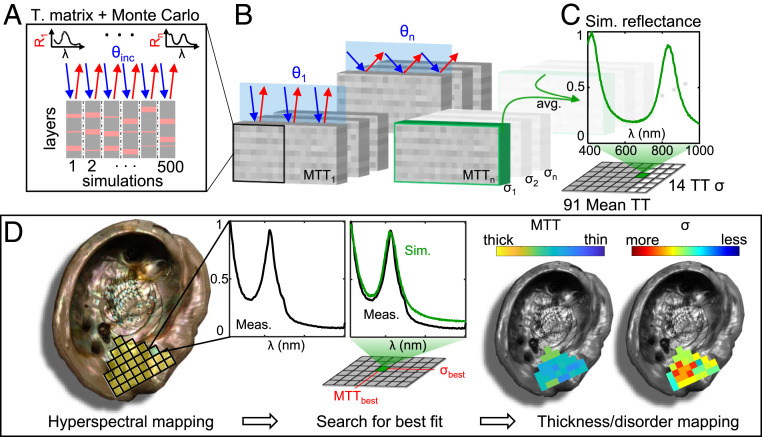
At each point on the shell, the nacre tablet thicknesses are unknown but are expected to be normally distributed around some mean value (SI Appendix, section 4). Also, the spectral reflectance measured at each pixel using HIT is a macroscopic response encompassing many stacks of nacre tablets, because a single tablet stack area (<50 μm²) is much smaller than the area measured in each pixel (∼10,000 μm²). To simulate this measurement, we performed Monte Carlo-type calculations using the transfer-matrix method (33), which simulates the reflectance spectra of a thin-film assembly. We used the refractive-index values for aragonite (34) and the organic layers (35) from literature. The combined calculation yields a simulated reflectance spectrum of nacre given input variables of MTT and degree of disorder in tablet thickness, which is the standard deviation, σ (Fig. 2 A–C and Methods) (36, 37).

Fig. 2.

(A–C) Generating simulated reflectance spectra for a given mean tablet thickness (MTT) and tablet degree of disorder (σ). To generate a single simulated spectrum for a particular MTT and TT σ, shown in C, a Monte Carlo method was used. (A and B) We calculated the reflectance of hundreds of randomly generated thin-film assemblies representing potential nacre layer configurations using the transfer-matrix method at various angles of incidence (θ) present within the acceptance angle of our camera. Thousands of simulation results were averaged to produce a single reflectance spectrum, with the peak value normalized to unity. The MTT in our simulation ranged from 150 to 600 nm, with σ ranging from 5 to 70 nm. (D) A pictorial overview of the fitting method to extract tablet thickness and σ from measured data. Left to Right: Hyperspectral mapping is performed over a large region of the shell using the setup described in Fig. 1. Each pixel of the spectral map, exaggerated as yellow squares overlaid on the left image, contains a full reflectance spectrum spanning 400 to 1,000 nm, here normalized to unity. Measured data at each pixel were then compared to every simulated spectrum generated from C until the lowest mean-squared-error (MSE) was found. Each pixel was then assigned the best-fit tablet thickness (MTT_best) and disorder (σ_best) to generate maps of nacre tablet thickness across the entire analyzed region. Note that the maps in D are schematics and do not represent a physical measurement.

For a given value of MTT and σ, we generated an ensemble of thin-film simulations, each comprising alternating aragonite/organic layers with thicknesses chosen stochastically from a normal distribution (Fig. 2A). We calculated the reflectance spectra for each simulation, accounting for the angular distribution of the collection optics of the hyperspectral camera (Fig. 2B). The resulting generated ensemble spectrum is the average of all simulations for a particular value of MTT and $\sigma$. We generated ensemble spectra for every combination of 91 values of MTT from 150 to 600 nm, and 14 values of $\sigma$ from 5 to 70 nm (a total of 3,185,000 individual spectra were calculated for the analysis in this paper; see Methods for further details).

The fitting of mapped hyperspectral data to the simulated data were done pixel by pixel, as shown in Fig. 2D. Since our measurement does not capture most of the light scattered by inhomogeneities or reflected out of the acceptance cone by surface topography, the magnitude of the absolute reflectance cannot be utilized in our fitting. Similarly, since we assume a fixed number of layers in our simulations, the amplitude of the Bragg-like reflectance peaks from the simulated data cannot reliably represent the measured data. Therefore, we normalized both sets of data to their peak values. The critical spectral features are preserved, where the band peaks correspond to the MTT and the band broadening corresponds to σ (22). A mean-squared-error (MSE) calculation was used to determine the best fit of the simulated spectrum to the measured data at each pixel (Fig. 2 D, Center) (SI Appendix, section 5 for details). The associated best-fit MTT and σ are then assigned to the pixel and two maps of the shell are generated (Fig. 2 D, Right).

Although tablet-thickness disorder (encoded in σ) is presumed to be the primary cause of broadening of the peaks of the measured reflectance spectra, other physical factors may also be captured within this metric. Any optical losses through the material or defects within nacre would also manifest as a broadening of the Bragg peaks, but these effects are not captured in our model. Thus, we believe our extracted values of σ to be less-reliable absolute quantities compared to MTT, which is not influenced significantly by optical losses. Nevertheless, relative values of σ can be used to observe trends in tablet thickness inhomogeneity within and between measured samples.

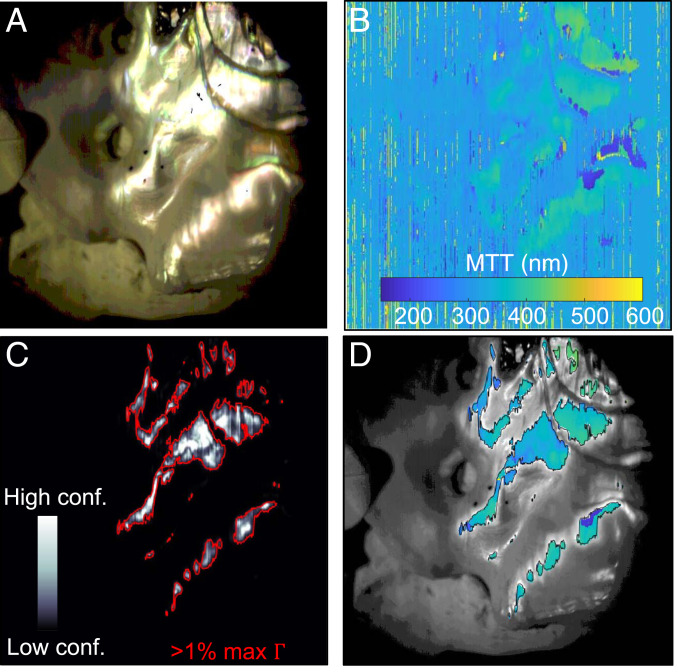
Due to surface curvature, topography, and scattering, only a subset of the shell can be reliably analyzed from any single measurement. This is shown in Fig. 3 A and B, where only the regions with the most specularly reflected light results in high-quality fits of MTT (Fig. 3B). To identify regions with trusted fits, we defined a confidence figure of merit (Γ = peak measured spectral intensity divided by the MSE). A high peak value of the raw spectral intensity indicates strong specular reflection, while a low MSE indicates that significant spectral features associated with the Bragg-like response of nacre are fit well. A map of $\text{Γ}$ is shown in Fig. 3C.

Fig. 3.

Interpretation of tablet thickness maps. (A) Color rendering of the hyperspectral data from a scan of a 135-mm-long red abalone shell. (B) After each pixel is fit to an MTT using the method described in Fig. 2, a full thickness map is generated. (C) Our confidence figure of merit, $\text{Γ}$, is used to identify regions of reliable data. To scrub unreliable data, we set a minimum threshold of $\text{Γ}$. (D) An overlay of our high-confidence MTT data and a grayscale image of the measured area.

Setting the Γ threshold to 1% of the maximum Γ was enough to eliminate the most unreliable data, e.g., shadows, nonnacre regions, such as myostracum or gill holes, and nonspecular regions (Fig. 3D). The same method can be applied to the tablet thickness disorder (σ) maps (SI Appendix, section 6). By readjusting the sample orientation and repeating the measurements, reliable data can be captured from the nacre surface. The expected systematic error of HIT mapping was found to be at most ∼25 nm in thickness at a given angle of incidence due to uncertainty in the refractive index of aragonite (SI Appendix, section 2). We validated the accuracy of HIT via scanning electron microscopy (SEM) measurements made on nacre cross-sections at several locations on one of the shells. The SEM and hyperspectral measurements agreed to within ∼15 nm for the MTT and less than 5 nm for σ (SI Appendix, section 7).

Using HIT to Investigate Nacre Formation

HIT enables rapid, nondestructive characterization of spatially resolved structural parameters of nacre or any other layered material across large areas. We used HIT to investigate whether there is a relationship between mollusk developmental stage and the structural parameters of the nacre formed by the animal.

We purchased 11 pairs of live red abalone at different developmental stages—from 1 to 6 years of age—corresponding to shell lengths between 20 and 140 mm (SI Appendix, section 9). The samples were all grown in the same environment by the Monterey Abalone Company, in cages suspended under the Monterey Wharf and thus exposed to natural ocean water composition and temperatures. All live animals were collected on August 6, 2019. Therefore, the nacre surfaces across all samples were formed at the same time and at the same temperatures.

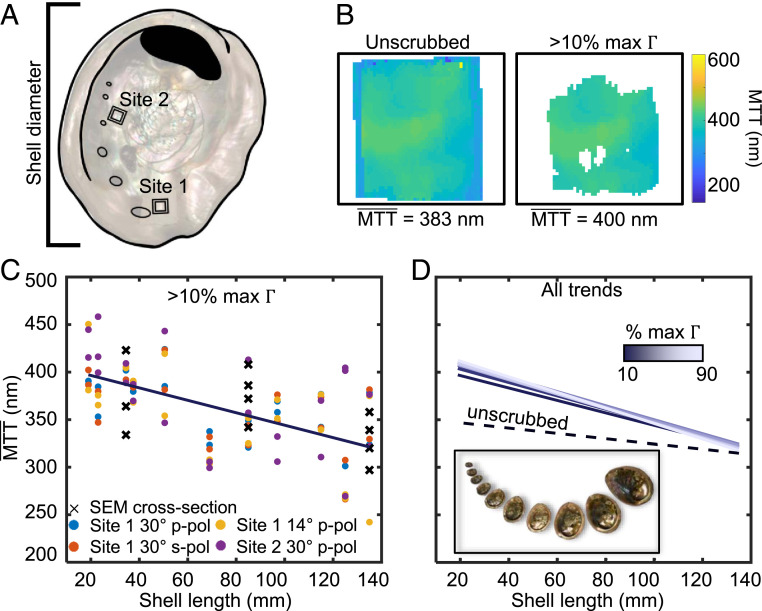
For each of the 22 red abalone samples, we defined two square regions (5 × 5 mm): site 1 near the outermost complete gill hole and site 2 near the fourth gill hole away from site 1 (Fig. 4A). As the animal grows older—and therefore larger—new nacre is continuously deposited across the entire inner surface. Thus, for every sample, site 1 contains nacre formed when the mollusk was at its oldest prior to harvesting, while site 2 contains nacre formed both when the mollusk was younger (31). Several spectral maps were taken for each site. The MTT values for all pixels in a site map were averaged to yield a single value, e.g., $\overline{MTT}=400\hspace{0.17em}\mathrm{nm}$ in Fig. 4B (Methods).

Fig. 4.

Ontogenetic dependence of red abalone nacre. (A) Two square measurement sites were defined on each of the 22 shells (11 pairs), each 5 × 5 mm. Site 1 was near the outermost complete gill hole in each shell and contains nacre predominantly formed when the mollusk is older. Site 2 was near the fourth gill hole inward from site 1 and contains nacre formed both when the mollusk was younger and older. (B) Mean tablet thickness (MTT) maps representing a single site on one of the shells. This region is a subset of the full $512\times 512$ pixel map. (C) Plots of all site averages vs. shell lengths, with the $\text{Γ}$ threshold set at 10%. Each pair of shells with the same shell length has eight thickness measurements in total, with different polarizations and incidence angles, as described in the legend at the Bottom of the plot. The dark line is a linear fit to all data points. (D) Plots of linear-fit trends obtained selecting different scrubbing thresholds, with the dashed line representing unscrubbed data, dark-light purple representing scrubbed data with the $\text{Γ}$ threshold set to 10 to 90% of the maximum $\text{Γ}$ for each map.

The data in Fig. 4C show an inverse relationship between $\overline{MTT}$ from all sites and shell length, and therefore shell age. This trend persists for all levels of data scrubbing (Fig. 4D), indicating that younger abalone grow thicker nacre tablets compared to older abalone (SI Appendix, section 9), an observation that has not been previously reported in this or any other nacre-forming mollusk genera or species. In fact, because it appears to the naked eye to be mostly similar in shells of different sizes and ages, nacre has always been assumed to have the same structure, and specifically MTT at all developmental stages (17, 18, 38). We observed, instead, in Fig. 4C that the MTT decreases with age. A similar trend was also noted in the tablet thickness disorder $\sigma$, with younger abalone producing more disordered nacre compared to more mature abalone (SI Appendix, section 8). The generality of the MTT vs. age relationship to other nacre-forming mollusks, or to other layered biominerals, including Bouligand structures in bone, shrimp clubs, fish scales, or insect cuticles (39–42), remains to be tested. Using HIT, such experimental analysis is straightforward and relatively inexpensive; thus, it can be done on a vast scale by many research groups.

Conclusion

In conclusion, we demonstrated an all-optical, rapid, and nondestructive characterization technique—hyperspectral interference tomography (HIT)—for extracting structural information from disordered and nonuniform layered materials such as nacre and other biomaterials. The accuracy of HIT in determining the thickness and disorder of aragonite tablets comprising nacre formed by red abalone (H. rufescens) and rainbow abalone (H. iris) was confirmed by electron microscopy of nacre cross-sections.

By performing large-area HIT analysis of red abalone shells at different developmental stages, we observed a previously unknown dependence of nacre tablet thickness on the age of the animal or the size of the shell. The HIT technique can be easily exported to other laboratories, or deployed to the field to study large areas of biologically formed, layered optical materials, even when these are delicate, contoured, and nonuniform in topography.

Methods

HIT Measurement Setup.

We used a hyperspectral camera (Specim IQ; Specim), rotation stage, and a collimated broadband halogen light source (40 W, reflector-type) with a beam divergence $\sim 2.4\mathrm{°}$ to illuminate and measure reflectance spectra across large areas of nacre (Fig. 1E). The spectra were all normalized to reflectance from an aluminum mirror under the same illumination conditions. The spatial resolution of our setup is 512 × 512 pixels, with each pixel containing a full reflectance spectrum from 400 to 1,000 nm with 204 spectral bands. A linear polarizer was placed in front of the camera lens to enable s- and p-polarized reflectance measurements. Due to the positioning of the hyperspectral camera, here the spatial resolution of the HIT image is ∼100 µm. The approximate acceptance angle of light captured from each point on the surface of the nacre was ±9°. The use of collimated incident light and a relatively small acceptance angle was deliberate to capture predominantly specular reflected light, and discard light that is scattered or reflected by inhomogeneities on the surface.

Transfer-Matrix Method Combined with Monte Carlo Simulations.

A transfer-matrix method calculation requires several inputs to calculate a spectrum: the refractive indices and thicknesses for every layer and the angle of incidence, polarization, and wavelength of the incident light. The optical properties of nacre’s constituent components, aragonite and the organic sheets, are approximately known. Aragonite is a biaxial birefringent material with refractive index of 1.681, 1.686, and 1.530 along the a, b, and c axes of the crystal at λ = 589 nm, respectively (34). To our knowledge, the dispersion of aragonite has not been fully characterized in literature; however, we assumed it to be dispersionless (and lossless) across the visible and near-infrared wavelengths, as is the case for calcite (43). Since the crystal a- and b-axis orientations of the nacre tablets can vary by ±90° from one layer to the next, and the c-axis orientation can vary by ±30° from the normal to the nacre layers (18, 44), we selected a refractive index value of 1.63, which is the arithmetic mean of the three values. The refractive index of the organic sheets ranges between ∼1.4 and 1.73 across different species (45). We selected a constant refractive index of 1.43 (35), noting that the results are minimally impacted for different refractive index values within the known range for the organic sheets (SI Appendix, section 2). The fitted results for s- and p-polarized measurements shown in Fig. 4C are very similar, affirming that although aragonite is biaxially birefringent (34), the wide variation in crystal orientations throughout the nacre averages all polarization-dependent effects and therefore can be reasonably treated as a single isotropic refractive index.

Although nacre can be thousands of layers thick (19, 24), we found the sampling depth to be ∼350 layers for H. rufescens and 150 layers for H. iris, likely due to absorption of the polymer layers, which are darker in color in H. iris nacre than for H. rufescens nacre (46), and thus prevented deeper penetration of light. Our model assumes a thin-film assembly of 200 layers, which is well within the range of layers that provides good fits (SI Appendix, section 3). Furthermore, the thicknesses of the organic sheets were not used as fitting variables and were fixed at 25 nm (14). We set reasonable bounds for the expected MTT between 150 and 600 nm, as well as σ between 5 and 70 nm. Monte Carlo-type calculations were performed to determine the expected ensemble spectral response of nacre from each pixel in a HIT map. For a given value of MTT and σ, 500 thin-film simulations were generated, each comprising 200 alternating layers with assigned thicknesses chosen stochastically from a normal distribution centered at the mean with a standard deviation equivalent to the tablet degree of disorder, σ (Fig. 2A). We calculated the reflectance spectra of all 500 simulations, accounting for the angular distribution of the collection optics by averaging calculated spectra over five angles spanning the acceptance angle of the camera at a single angle of incidence, e.g., 30° ± 9° (Fig. 2B). The single ensemble spectrum generated is the average of all 2,500 simulations (Fig. 2C). In total, 91 × 14 ensemble spectra were calculated spanning the thickness and disorder bounds that we defined (a total of 3,185,000 spectra).

Red Abalone Ontogeny Measurements.

Twenty-two living red abalone at different developmental stages—from 1 to 6 years of age—corresponding to shell lengths between 20 and 140 mm were measured. The samples were all grown in the same environment by the Monterey Abalone Company, in cages suspended under the Monterey Wharf and thus exposed to natural ocean water composition and temperatures. All live animals were collected on August 6, 2019. Site 1, located near the outermost valve (Fig. 4A), for all shells was measured with the following conditions: p- and s-polarized reflectance at a 30° incidence angle and p-polarized reflectance at 14° incidence. Site 2, located near the fourth valve from site 1 (Fig. 4A), for all shells was measured with p-polarized reflectance at a 30° incidence angle. The $\overline{MTT}$ was calculated for each shell as the Γ threshold was increased from 0 to 90% of the maximum. In Fig. 4C, we plotted the $\overline{MTT}$for all shells vs. the shell length with the minimum Γ threshold set to 10% of the maximum.

SEM Cross-Sectional Validation of Nacre Formation.

We cut the shells in the measured locations labeled site 1 and site 2 (Fig. 4A), embedded and ground them to expose the shell cross-sections at both sites (SI Appendix, section 7), polished and coated them, and finally used SEM to measure the tablet thicknesses directly.

The SEM measurements are reported in Fig. 4C, and in SI Appendix. The SEM data confirm that MTT decrease with shell size, making this a robust observation and validating our HIT results. We note that SEM only provides a highly localized measurement of the nacre structure, and is invasive, destructive, and time-consuming because of the sample preparation required. Thus, a limited number of samples (135-, 85-, and 34.5-mm lengths) were prepared and analyzed with SEM (11 datapoints in Fig. 4C). All SEM data points are in excellent agreement with the trend observed with the larger-area, noninvasive, and nondestructive HIT technique.

Data Availability

Data used in the analysis of nacre are available in the supporting information and upon request from the corresponding author. Codes used to analyze hyperspectral data cubes, generate simulated spectral responses, and perform nacre structural fitting data have been deposited in GitHub (https://github.com/katsgroup/PNAS_Nacre).