Human hand as a powerless and multiplexed infrared light source for information decryption and complex signal generation

Significance

The utilization of electricity-powered light sources as external stimuli is limited by the cost and energy loss. Here we demonstrate that the human hand can be used as a natural IR light source without the need of external power. As each finger can serve as an independent light source, the hand can also be utilized as a multiplexed IR light source. This work provides a different insight on using the hand in a functional system, such as the information encryption and complex signal generation systems demonstrated here, which will help move forward the effort in the integration of human components into various systems to increase the level of intelligence and achieve ultimate control of these systems.

Abstract

With the increasing pursuit of intelligent systems, the integration of human components into functional systems provides a promising route to the ultimate human-compatible intelligent systems. In this work, we explored the integration of the human hand as the powerless and multiplexed infrared (IR) light source in different functional systems. With the spontaneous IR radiation, the human hand provides a different option as an IR light source. Compared to engineered IR light sources, the human hand brings sustainability with no need of external power and also additional level of controllability to the functional systems. Besides the whole hand, each finger of the hand can also independently provide IR radiation, and the IR radiation from each finger can be selectively diffracted by specific gratings, which helps the hand serve as a multiplexed IR light source. Considering these advantages, we show that the human hand can be integrated into various engineered functional systems. The integration of hand in an encryption/decryption system enables both unclonable and multilevel information encryption/decryption. We also demonstrate the use of the hand in complex signal generation systems and its potential application in sign language recognition, which shows a simplified recognition process with a high level of accuracy and robustness. The use of the human hand as the IR light source provides an alternative sustainable solution that will not only reduce the power used but also help move forward the effort in the integration of human components into functional systems to increase the level of intelligence and achieve ultimate control of these systems.

Light sources, which emit an electromagnetic (EM) wave with specific wavelength range, play an indispensable role in the evolution of biological systems and human society (1, 2). For example, light sources help us visualize targets through the interaction between the EM waves emitted from them and the targets (3). Most of light sources used in daily life are engineered or man-made light sources, including the incandescent lamp invented more than 100 y ago (4), the fluorescent lamp emerged in 1930s (5), the lasers invented in the 1960s (6), and the light-emitting diode (LED) lamp (7) that becomes the widespread option in household and working places. The invention and commercialization of these engineered light sources did bring light into many different places in space, both in physical space and in time space, and help propel the forward development of human society. Most of these engineered light sources, however, require the use of external energy, such as electricity, for their proper operation (8). Such needs not only bring additional energy consumption into the systems but also limit the use of these light sources to places with access to electricity. Besides engineered light sources, we are also surrounded by natural light sources. One of the most used natural light sources is the sun, which helps us see things during the day. Moon is another natural light source that helps us see things during the night. Compared to the engineered light sources, these natural light sources consume zero electricity and bring sustainability to the system.

Among light sources with different wavelengths, infrared (IR) light sources represent one of the major categories of light sources, which frequently find the use in various applications including molecular sensing (9), motion detection (10), security and defense (11), energy conversion (12), and free space communication (13). To satisfy the needs of these applications, many different engineered IR light sources have been developed, such as IR lasers (14–16), IR LEDs (17, 18), and various types of thermal emitters (19–21). Similar to visible light sources, there are also natural IR light sources, which include the sun and the natural fire (22, 23). Among all the natural light sources, biological systems emit IR radiation spontaneously (24) and represent an interesting class of natural IR light sources. Recently, several studies are reported on the IR radiation from biological systems, such as the effective thermal management of various insects [butterflies (25, 26), ants (27), and beetles (28)] through the regulation of IR radiation emitted from these biological systems. Compared to engineered light sources or other nonbiological natural light sources, biological light sources can bring the advantages associated with the biological systems into engineered systems: chemical sustainability, structural multifunctionality, and intelligent controllability (29–31). The integration of biological components, especially human components, as light sources into engineered functional systems, however, is much less studied. The current usages of human components as light sources most of the time are limited on the visualization and regulation of body temperature (32–35). As a natural IR light source, human components do offer an additional level of controllability and flexibility. The use of human components as IR light sources may provide a promising way to increase the controllability and flexibility of the engineered systems.

In this work, we demonstrate that the human hand is not just a natural and powerless IR light source, but also a multiplexed light source with each finger serving as an independent light source. The relative position and number of light sources are controllable and adjustable at will by changing the hand gestures. Based on this mechanism, we show that the human hand can be integrated into various engineered functional systems. The whole hand can be integrated into an encryption/decryption system for reflection-based multilevel and unclonable information encryption/decryption. Gestures composed of different fingers can be integrated into a signal system for diffraction-based complex signal generation. The generated signals in turn can be used for sign language recognition and other applications that involve complex signal recognition. The integration of the human hand into these engineered functional systems can not only enhance sustainability but also increase the level of intelligence and controllability of these systems due to the direct involvement of human brains in the systems. The findings in this work will be of interest to communities of IR radiation related to biological systems, information decryption, human computer interface, and also the integration of biological components into functional systems (28, 36–38).

Results

The Hand as an IR Light Source.

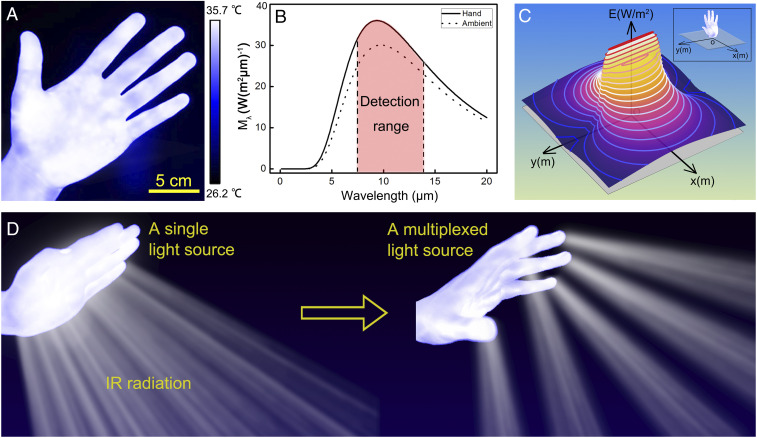
The human hand is a natural IR emitter due to the thermal emission from the hand (Fig. 1A) (33). Based on Planck distribution function (22), we calculated and plotted the intensity distribution of the thermal radiation from a typical human hand (emissivity of ∼0.98) (39) at the normal body temperature of 310 K (Fig. 1B and SI Appendix, section 1). The IR radiation peak of the human hand is well within the atmospheric transmission window (∼7.5 μm to 14.0 μm) as well as the detection range of the IR detector (FLIR T620) used in this work. For comparison, we also plotted the intensity distribution of the thermal radiation from background at the ambient temperature of 298 K in Fig. 1B. Fig. 1C shows the two-dimensional (2D) mapping of the irradiance (E), which is the radiant power received by a unit area of surface (W/m²), within the horizontal plane that is perpendicular to the human hand (SI Appendix, section 2). Similar to the axial symmetry of the human hand, the irradiance mapping also displays an axial symmetry. Fig. 1C also shows that the human hand is an incoherent light source with omnidirectional radiation to the surroundings, similar to the common IR lamps or LED light sources, all of which are different from coherent light sources such as IR lasers with unidirectional radiation.

Fig. 1.

Human hand as a natural and multiplexed IR light source. (A) An IR image of a human hand. (B) Radiation spectra of a human hand at the temperature of 310 K and the ambient at the temperature of 298 K. (C) The simulated mapping of the irradiance (W/m²) in the plane perpendicular to the human hand. (D) Schematic illustration of using human hand as a single light source (Left) and a multiplexed light source (Right).

Compared to conventional IR light sources, the human hand can serve as a single integrated and powerless IR light source with added controllability. In this work, we demonstrated the use of hand as a single integrated and powerless IR light source (Fig. 1D, Left) in an encryption/decryption system for reflection-based information encryption/decryption. The human hand not only can serve as a single integrated IR light source but also can serve as a multiplexed IR light source due to its unique composition. Each hand consists of five fingers, each of which can serve as an independent IR light source and can be controlled and grouped at will. With such integrated and relatively independent components, the human hand can also serve as a flexible and multiplexed IR light source (Fig. 1D, Right). In this work, we further took advantage of such flexibility and demonstrated the use of the human hand as a multiplexed IR light source in a complex signal generation system.

The Human Hand as a Powerless Light Source for IR-Based Decryption.

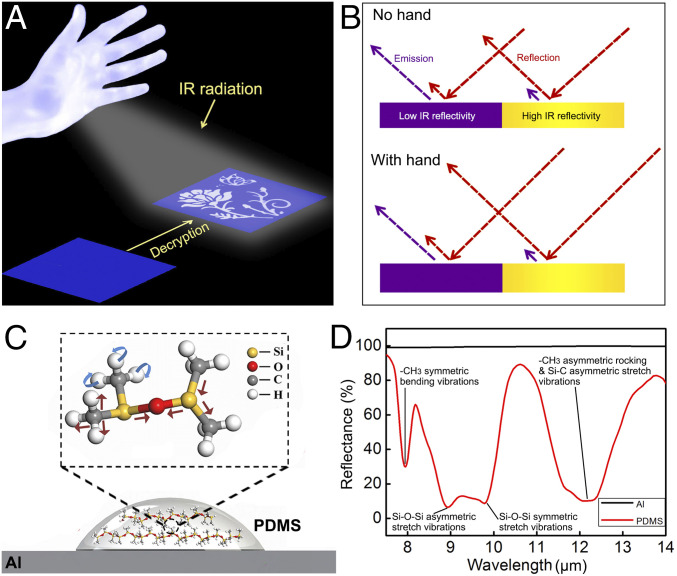
In this work, a decryption mechanism that relies on IR reflection is established to demonstrate the use of the human hand as a powerless light source. The invisible pattern composed of materials with different IR reflectivity becomes visible under the IR illumination with the hand as the single IR light source (Fig. 2A). The differences of the IR emissions between the human hand and the background play a key role in the IR reflection–based decryption process. In the decryption process, the IR detector captures the IR radiance from the sample. The IR radiance includes both the IR emission (purple arrow in Fig. 2B) and IR reflection (red arrow in Fig. 2B) from the specific region of the sample. The differences between the IR radiances from different regions of the sample provide the contrast between those regions. When there is no hand, the coding pattern, including both the region of low IR reflectivity and region of high IR reflectivity, is in temperature equilibrium with the background, so the IR radiances from different regions are the same and there is no contrast between different regions of the sample in the IR image captured by the IR detector (Fig. 2B, Top and SI Appendix, section 3). The coding pattern is therefore not shown up in the IR image. When the human hand is used as the light source, the IR emission from the hand is reflected by all the regions, and thus, the region of high IR reflectivity has a higher increase of IR radiance than that of low IR reflectivity, which leads to the differentiation of IR radiances and enables the decryption process (Fig. 2B, Bottom and SI Appendix, section 3).

Fig. 2.

Using human hand as the IR light source for information decryption. (A) Schematic illustration of using human hand as an IR light source for reflection-based decryption. (B) Mechanism of IR reflection–based decryption. (C) Schematic of molecular structure of PDMS patterned on Al substrate. (D) Reflectance spectra of Al and PDMS on Al substrate.

In the experiment, we deposited polydimethylsiloxane (PDMS), which has a low IR reflectivity, on the surface of aluminum (Al), which has a high IR reflectivity, to form the coding pattern (Fig. 2C). PDMS was diluted in hexane and sprayed through a stencil to generate the coding pattern (SI Appendix, Fig. S1). Fig. 2D shows the reflectance spectra of the bare Al sheet (∼1 mm in thickness) and PDMS film (∼3 μm in thickness) deposited on the Al substrate in the long wavelength IR range from 7.5 μm to 14.0 μm. In this region, the Al sheet shows relatively uniform reflectance of ∼99%, while the sample of PDMS coated on Al shows a wavelength-dependent reflectance due to the IR absorption from the various chemical bonds within PDMS (40). These chemical bonds are always in motion with different quantized energy levels, such as the symmetric bending vibration of CH₃. When the broadband IR radiation interacts with the PDMS, chemical bonds in different motion modes will absorb IR radiation with specific wavelengths for energy transition from a lower energy level to a higher energy level. For example, the symmetric bending vibration of CH₃ absorbs IR radiation of ∼7.9 μm for such transition. The symmetric stretch vibration of Si-O-Si absorbs IR radiation of ∼9.8 μm for the transition. The absorption of IR radiation by PDMS leads to the pattern-dependent reflectance. The measured average reflectance for the PDMS layer coated on Al sheet is ∼41.2% in this IR wavelength region. Such reflection is the combination of both the reflection at the PDMS surface and also the reflection from the underlying Al substrate. The measured reflectance of the PDMS layer coated on Al is lower than that of the Al, and such difference provides the possibility of pattern differentiation in the IR reflection–based decryption process.

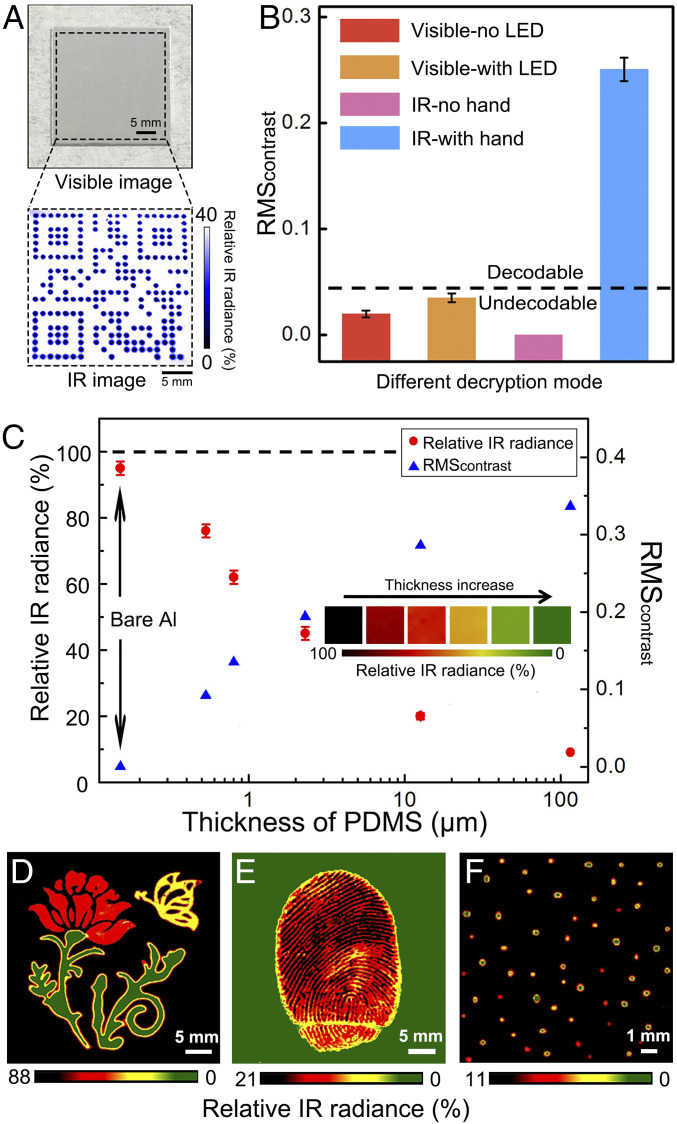
Fig. 3A shows the decryption of a PDMS pattern (a Quick Response Code). The experimental setup is shown in SI Appendix, section 4 and Fig. S2. Under the normal ambient light, the PDMS pattern on Al surface is invisible in the image captured by the visible camera (Fig. 3A, Top). The pattern, on the other hand, can be decoded under the IR detector when a human hand is used as the IR light source (Fig. 3A, Bottom). In the IR image (Fig. 3A, Bottom), we used the relative IR radiance to show the differences of received IR radiance by the IR detector between different areas (SI Appendix, section 3). Without using the hand, the pattern is also invisible in the image captured by the IR detector (Movie S1). We further used root-mean-square contrast (RMS_contrast) (41) to quantitatively compare the image contrasts recorded under different decryption approaches (SI Appendix, sections 5 and 6 and Fig. S3). These different decryption approaches were all carried out under the same ambient light. All the images were converted into grayscale images first, and then we calculated RMS_contrast for all the grayscale images. The detailed calculation process is shown in SI Appendix, section 6. As shown in Fig. 3B, the RMS_contrast for the visible image without using the LED light source (SI Appendix, Fig. S4A) is ∼0.020, indicating that the coding pattern is hardly recognizable. For the visible image using the LED light source (SI Appendix, Fig. S4B), the RMS_contrast increases to ∼0.035, which is nearly 2× the RMS_contrast of image without the LED light, but it is still quite low to make the pattern decodable. The low RMS_contrast of visible images with or without LED light is due to the high transparency of PDMS in the visible range (SI Appendix, Fig. S5), which generates nondecodable difference between the visible signals from the patterned and nonpatterned areas of Al substrate. When the human hand is used as the IR light source, the RMS_contrast for the obtained IR image increases to 0.251, which enables the clear recognition of the image and the decryption of the information embedded within the image (Fig. 3B). The decryption process can be carried out under different ambient temperatures (SI Appendix, Fig. S6).

Fig. 3.

Experimental demonstration of information encryption/decryption. (A) The visible image of the coding pattern under the ambient light and the IR image of the coding pattern with human hand as the IR light source. (B) Comparison of RMS_contrast of images under different decryption conditions. Error bars represent the SD of the mean (n = 5). (C) Effect of the PDMS thickness on the RMS_contrast of IR images; Inset shows the corresponding colors generated by PDMS with different thicknesses. Error bars represent SD of the mean (n = 5). (D) Multilevel coding with patterns of different colors. (E) Unclonable coding in fingerprint. (F) Random patterns for multilevel unclonable coding.

The Human Hand as a Powerless Light Source for Multilevel and Unclonable Information Encryption/Decryption.

In the experiment, we also found that the thickness of the PDMS pattern showed a profound impact on the image contrast (Fig. 3C). When IR radiation propagates in the PDMS, the IR radiation will be absorbed by chemical bonds in PDMS. There will be more absorption within thicker PDMS, which in general will lead to smaller reflection of the IR radiation from the PDMS surface. According to the discussion in Fig. 2B, without using the hand as the light source, the difference of IR reflection caused by the thickness difference of PDMS has no effect on IR radiance captured by the IR detector, and thus, the variation of thickness of PDMS cannot be decrypted as color contrast by the IR detector. When the hand is used as the light source, the IR radiance from the area with high IR reflection, that is, the area of thin PDMS, is higher than that from the area of thick PDMS. The pattern composed of PDMS with different thickness can thus be decrypted by the IR detector due to the difference in IR radiance, which can be shown as the color contrast in the IR image. As shown in Fig. 3C, when the thickness of the PDMS increases from 0 μm to 115 μm, the relative IR radiance decreases. With the decrease of relative IR radiance, the RMS_contrast of the PDMS pattern on Al surface increases (SI Appendix, Fig. S7). As shown in Fig. 3C, the RMS_contrast increases from 0 to 0.337 as the thickness of PDMS increases from 0 μm to 115 μm.

Such thickness-dependent contrast provides opportunity for multilevel coding as the change of relative IR radiance can be shown with color distribution under IR detection (Fig. 3C, Inset). Fig. 3D shows the potential in multilevel information coding with patterns of different colors. In this image, the thickness of PDMS in the yellow butterfly was ∼2.71 μm, in the red flower was ∼0.68 μm, and in the green leaves was ∼54.90 μm. Such capability in multicolor coding provides additional levels of information encryption/decryption and makes unauthorized decoding even more challenging than the single-color coding.

Besides multilevel information encryption/decryption, this process can also enable unclonable coding, for example, an unclonable coding in the complex pattern template such as the patterns in fingerprints (Fig. 3E). In this demonstration, a thin film of PDMS (with thickness of ∼7.37 μm) was coated onto an Al substrate through spin-coating and subsequent curing. A thumb was lightly pressed onto the PDMS film before it was fully cured to generate the fingerprint pattern. The fingerprint pattern formed on the PDMS surface had local variation in the thickness (SI Appendix, Fig. S8). The differences in the IR reflectance between the regions with varied PDMS thicknesses provided the image contrast and decoded the complex pattern printed on the surface by using the fingerprint as a template, as shown in Fig. 3E. This demonstration provides an alternative approach for unclonable encryption/decryption process. In practical applications, some edible polymers (42) represent other options for this finger-related encryption/decryption process. Besides using fingerprint as template for unclonable coding, unique random patterns with physical unclonable functions can also be integrated into coding tags for unbreakable encryption (43–45). Here we demonstrated multilevel unclonable coding using randomly deposited PDMS patterns with multicolor designs. Fig. 3F shows one example of such random patterns. Such random patterns were generated through a spray-coating process with rapid evaporation of solvent. The randomness in the distance between the dots provides one level of unclonable feature. The randomness in the size and shape of the dots provides another level of unclonable feature. With the multicolor coding capability, the randomness in the color coding also added additional level of unclonable feature (Fig. 3F). We also observed the coffee ring effect for some of the dots formed during the evaporation of the solvent, which may bring further variances into the thickness and shape of the dots, and thus will enhance the unclonability of the patterns. With the further manipulation of the composition and microstructures of the coding patterns, the unclonable features can be further enhanced.

Selective Interaction between Fingers and IR Gratings.

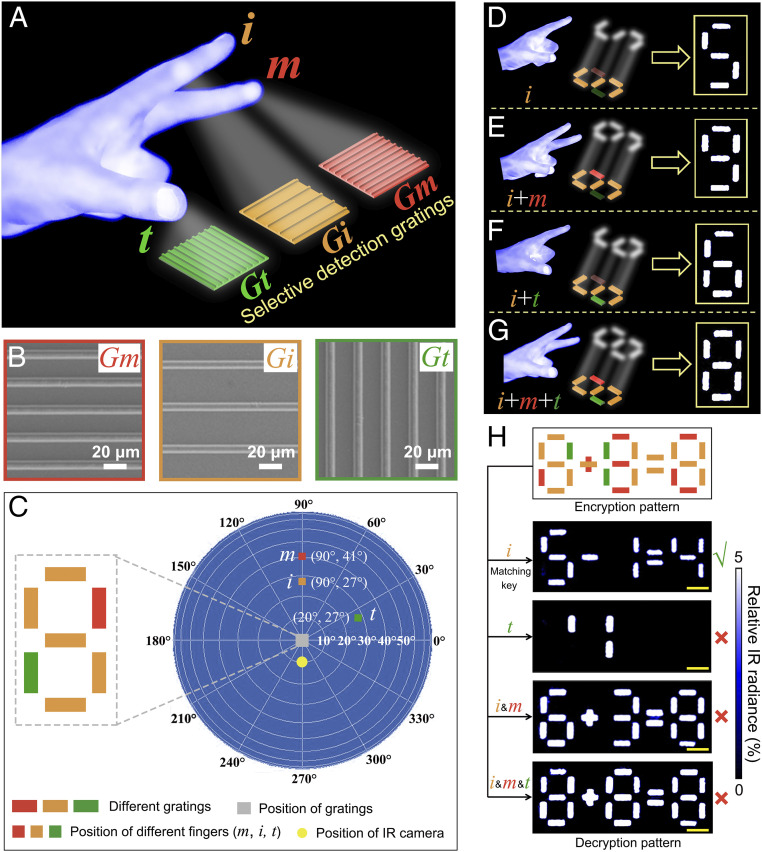
The hand not only can serve as an integrated single IR light source but also can serve as a multiplexed IR light source with each finger of the hand serving as an independent IR light source. Here, we demonstrated the use of the hand as a multiplexed IR light source based on the selective interaction between fingers and IR gratings. The diffraction grating used here is a collection of grooves separated by a distance (period) comparable to the wavelength of the light. When a beam of light is incident on a grating surface, the light is diffracted by the periodic grating grooves. These grooves act as small sources of diffracted light. When the diffracted light from a groove is in phase with the light diffracted from other grooves, these light beams are of constructive interference and the corresponding direction is the diffraction angle of the light. The incident light is diffracted into discrete directions with specific diffraction angles. With proper design of the structural parameters (periods and orientations) of the gratings, the IR radiation from each finger at specific positions can be selectively diffracted by different gratings. For example, the IR radiation from the thumb (“t”) can only be primarily diffracted by the grating shown in green (“Gt”), from the index finger (“i”) can only be primarily diffracted by the grating shown in brown (“Gi”), and from the middle finger (“m”) can only be primarily diffracted by the grating shown in red (“Gm”) in Fig. 4A. Gratings coated with metallic film can strongly diffract the IR radiation from the individual finger. The diffracted IR radiance can also be captured by an IR detector (SI Appendix, Fig. S9) and visualized, same as the reflected IR radiance discussed above. With the fixed position and angle of the IR detector, only the diffracted radiation with specific direction can be captured by the IR detector, so the detectable diffraction angle θ_d (SI Appendix, Fig. S9) is fixed as well. With each specific θ_d, there is a corresponding incident angle θ_in, and θ_in strongly depends on the structural parameters (grating period and orientation) of the gratings and the wavelength of incident light. In the three-dimensional (3D) space, the position of θ_in or θ_d is simultaneously determined by the polar angle (θ) and azimuthal angle (φ) in the spherical coordinate system (46). The spherical coordinate system can be converted into a 3D map to show the position of different angles. The relationship between the spherical coordinate system and 3D map is shown in SI Appendix, Fig. S10.

Fig. 4.

Selective interaction between fingers and metallic gratings for information encryption/decryption. (A) Schematic illustration of the selective interaction between fingers and IR diffraction gratings. Thumb (t), index finger (i), and middle finger (m) are used as IR light sources for the interaction with different gratings. (B) SEM images of different gratings (Gm, Gi, and Gt). (C) The base pattern of gratings that form number “8” and the typical positions of three fingers to illuminate the corresponding gratings. (D–G) Generating IR diffraction patterns by different gestures. (H) Decryption results with different hand gestures (scale bar: 2 mm).

In this demonstration, Al gratings were used to diffract IR radiation from hand (SI Appendix, Fig. S11). To demonstrate the selective interaction between fingers and IR gratings, first we used the finite–difference time–domain approach (47) to simulate the θ_in range of three different gratings (Gt, Gi, and Gm) in Fig. 4A for first-order diffraction at θ_d (φ = 270°, θ = 10°) (SI Appendix, section 7). The period of Gm is 25 μm, and the period of Gi is 40 μm (Fig. 4B). The period of Gt is equal to that of Gm while their orientations are orthogonal. The incident light wavelength is in the range between 7.5 μm and 14 μm. The simulated θ_in ranges in 3D space for these three gratings are marked in the 3D map (SI Appendix, Fig. S12). As shown in SI Appendix, Fig. S12, for this specific θ_d, the θ_in ranges are dependent on grating periods and orientations. We used these three gratings to generate a base pattern of number “8” for testing the recognition effect by the index finger, the middle finger, and the thumb (Fig. 4C). Here we used patterns of numbers for the purpose of demonstration. Many other patterns, such as +, −, =, etc., can also be used for the demonstration of the selective interaction between individual fingers and the specific gratings. The Fig. 4C is in the scale of the 2D projection of the spherical coordinate system. It characterizes the angles of the IR detector and fingers relative to the center of sphere (the gratings). The brown, red, and green squares in Fig. 4C represent the typical positions of the index finger, the middle finger, and the thumb that can selectively “illuminate” corresponding gratings (Gi/Gm/Gt). With the change of hand gestures, different IR diffraction patterns can be visualized from the same sample (Fig. 4 D–G). For example, when the index finger i was placed in the θ_in range of Gi (SI Appendix, Fig. S12B), it would selectively “illuminate” Gi, and number “5” was detected by the IR detector (Fig. 4D). When the combination of the index finger i with the middle finger m or with the thumb t was used, gratings “Gi + Gm” or “Gi + Gt” were “illuminated,” and “9” or “6” showed up in the IR image (Fig. 4 E and F). When all three fingers were used, number “8” was detected (Fig. 4G). Here, we used the specific combination of gratings for the demonstration of the selective response from the different combinations of fingers. The observed patterns (numbers) can vary with the change of the design and the arrangement of the gratings. All these demonstrations show that one specific gesture can generate one specific IR diffraction pattern. With this mechanism, another different decryption approach can be demonstrated as well. Compared to the decryption using the whole hand as the single light source, the freedom of using any of the five fingers of the hand will offer much more space in information encryption/decryption, and only a specific gesture can serve as the matching key to unlock the encrypted information (Fig. 4H). In the top image of Fig. 4H, there are three different patterns of number “8.” In the first number “8” from left, we used five Gi gratings (brown) to form number “5” first and then used one Gm grating (red) in the bottom left and one Gt grating (green) in the top right to combine with the five Gi gratings to form the number “8.” We used different arrangements of the three gratings to form the number “8” in the middle and right of the equation as well. We used one Gi grating and one Gm grating to form the symbol of “+” and used two Gi gratings to form the symbol of “=.” When only the index finger was used to illuminate the pattern, only Gi gratings were illuminated, which showed “5−1 = 4” (the second image from top in Fig. 4H). When the combination of index finger and middle finger was used, both Gi gratings and Gm gratings were illuminated, which showed “6+3 = 8.” Only the gesture with the index finger “i” can decrypt the right information “5−1 = 4,” while other gestures would all lead to the wrong decryption. Apart from the grating period and grating orientation, the duty ratio (ratio of line width to grating period) can also be modulated for the information encryption/decryption (SI Appendix, Fig. S13).

Finger–Grating Interaction for Sign Language Recognition.

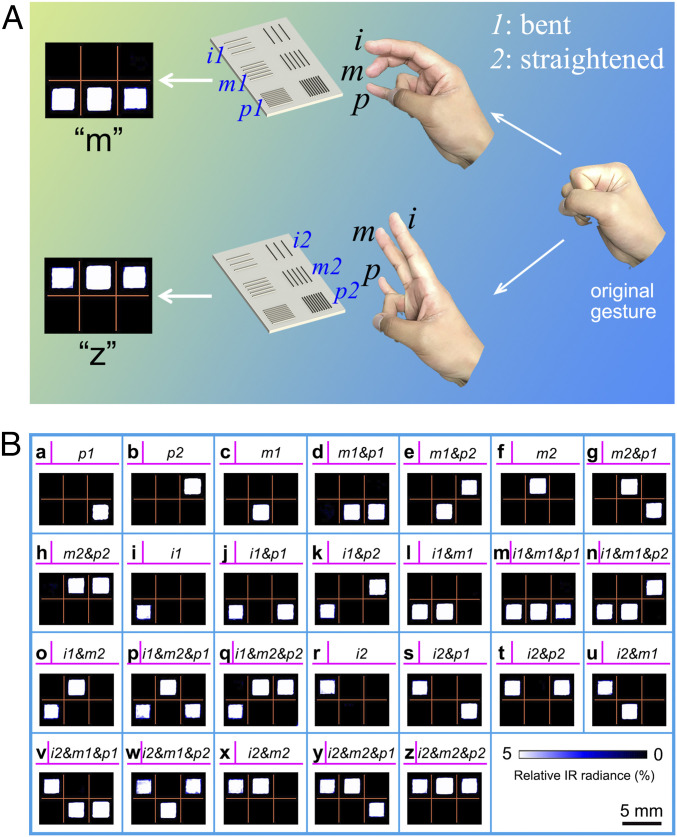
The selective interaction between fingers of hand and the diffraction gratings not only can be used for information decryption but also can be used for complex signal generation and recognition. In this work, we further demonstrate the use of the human hand as a multiplexed IR light source for the potential application in sign language recognition. Vision or IR-based sign language recognition by direct analysis of visual or IR images of hand gestures is a natural and convenient approach for sign language recognition. Some challenges, however, still remain for this approach. In sign language recognition using visible and near-IR light, the quality of captured visible or near-IR images is sensitive to ambient lighting conditions and complex background, which leads to the difficulty in the accurate and robust segmentation of gestures from captured images. Apart from these external factors, the occlusion of joints and finger segments also hinders the detection of hand configuration in the visible and near-IR imaging process, as the hand is a complex articulated object with more than 20 degrees of freedom (48). Direct capture and recognition of gestures by thermal or IR camera can minimize the effect of ambient lighting conditions and complex background. There are, however, still challenges with the occlusion of joints and finger segments that hinder the detection of hand configuration in the direct IR imaging process. To avoid the occlusion of hand in the images, an alternative approach to the direct analysis of the IR images of hand gestures may provide a different path to the effective and accurate sign language recognition. Based on the selective interaction between fingers and gratings, we demonstrate that the complex gestures can be converted into easily recognizable signal patterns. As shown in Fig. 5A, we used three fingers (index finger [i], middle finger [m], and pinkie [p]) as three independent IR light sources. Depending on the position of the fingers (bent or straightened), each finger can selectively “illuminate” one of the two orthogonal gratings. When the finger is in bent position, the grating on the left is “illuminated.” When the finger is in straightened position, the grating on the right is “illuminated.” When the finger is in a closed fist, neither grating is “illuminated.” The SEM images of designed gratings and the positions of fingers for illuminating each grating are shown in SI Appendix, Figs. S14 and S15, respectively. In the demonstration with the use of three fingers, there are 26 different gestures (3*3*3−1), which lead to 26 different IR diffraction patterns. We denote each pattern as one letter in the alphabet table. The generated IR patterns by different gestures and corresponding letters are shown in Fig. 5B. The alphabet table generated through this approach is named as IR alphabet based on hand–grating interaction (IA-HG) in this work. This IA-HG represents an alternative to the American manual alphabet (AMA).

Fig. 5.

IR alphabet based on hand-grating interaction (IA-HG). (A) Interaction of gratings and different hand gestures leads to different IR diffraction patterns. (B) The different combinations of three fingers, the corresponding IR patterns and alphabet letters.

Compared to AMA that involves hand gestures with five fingers, the alphabet that involves 26 hand gestures with three fingers can also be named as “three-finger alphabet” (TFA). Both AMA and TFA can be recorded as visible images and IR images. In this work, we named IA-HG derived from TFA as IA-HG (TFA), visible mode of TFA as Vis (TFA), IR mode of TFA as IR (TFA), visible mode of AMA as Vis (AMA), and IR mode of AMA as IR (AMA), respectively. Compared with AMA that uses five fingers with as much as nine states for one finger (34 states in total), TFA only needs three fingers, and each finger only has three different states (wrapped, bent, and straightened), as shown in SI Appendix, Table S1.

Comparison between IA-HG (TFA) and Other Sign Language Recognition Systems.

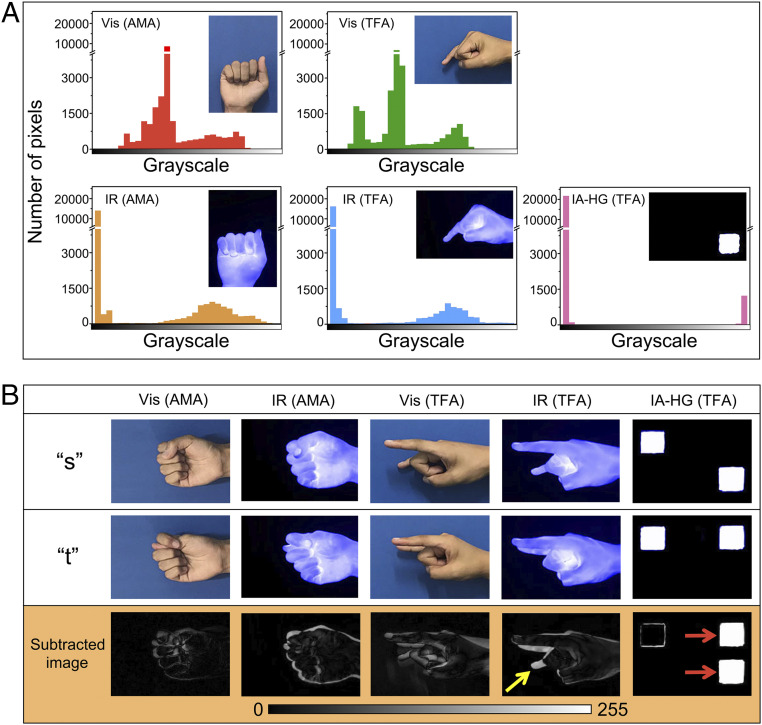
Vision-based sign language recognition can be divided into three stages: hand segmentation, feature extraction, and gesture recognition (48). Based on the three stages, we compare the performance of IA-HG (TFA) with visible mode and IR mode of AMA and TFA. The experimental setup for the visible mode and IR mode of AMA and TFA is shown in SI Appendix, section 4 and Fig. S16. Visible images and IR images of AMA and TFA are shown in SI Appendix, Figs. S17–S20. For AMA, only 24 letters are shown in SI Appendix, Figs. S17 and S18, and the gestures of letter “j” and letter “z” are dynamic gestures. In the sign language recognition process, the gesture should be segmented from the background first. For vision-based sign language recognition, accurate segmentation of hand from the background remains a challenge. We calculated grayscale distribution of gestures for letter “a” in different recognition systems: Vis (AMA), IR (AMA), Vis (TFA), IR (TFA), and IA-HG (TFA) (Fig. 6A). For both Vis (AMA) and Vis (TFA), the grayscale distribution is continuous, which shows that the hand and the background do not have explicit boundaries. It is thus challenging to accurately segment the hand from the background (Fig. 6A, Top). In contrast, grayscale distribution in IR systems (IR [AMA] and IR [TFA]) is discontinuous, in which the aggregated data on the left side are from the background and on the right side are from the hand (Fig. 6A, Bottom). It is thus easier to segment the hand from the background using IR images than using visible images. Compared with IR (AMA) and IR (TFA), the segregation of grayscale distribution of IA-HG (TFA) is further enhanced, which enables a much better segmentation of the hand from the background for IA-HG (TFA) than for IR (AMA) and IR (TFA). The clear segregation also shows that less data are produced by IA-HG (TFA) than by AMA and TFA, which may further save processing time for real-time feature extraction and gesture recognition.

Fig. 6.

Qualitative comparison between IA-HG (TFA) and other sign language recognition systems. (A) Grayscale distribution of gesture “a” in different sign language recognition systems. All the gesture images were converted into grayscale images first. The x-axis is the grayscale from black (pixel value = 0) to white (pixel value = 255). (B) Subtracted image obtained by image subtraction of gesture “s” and gesture “t” in different recognition systems. All the gesture images were converted into grayscale images first. The yellow arrow points to the main difference between gesture “s” and “t” in IR (TFA). The red arrows point to the main difference between gesture “s” and “t” in IA-HG (TFA).

To recognize different gestures accurately, each gesture should have its unique features that can differentiate itself from other gestures. Actually, in AMA, there are many gestures that are similar to each other, such as “s” and “t” (Fig. 6B). Image subtraction is a common method to detect differences between two images (49). Here, we used image subtraction to characterize the differences between gesture “s” and “t” (SI Appendix, section 8) and named the image after subtraction as the subtracted image (Fig. 6B). For the subtracted image, if the resulting pixel is black (pixel value = 0), the corresponding pixels in gesture “s” and “t” are the same, which means that the corresponding pixels in gesture “s” and “t” are indistinguishable. If the resulting pixel in the subtracted image is white (pixel value = 255), the corresponding pixels in gesture “s” and “t” then have the largest difference, which means that this resulting pixel in the subtracted image is a distinct feature to differentiate the two images. As shown in Fig. 6B, for AMA and TFA in visible condition and IR condition, the subtracted images did not show clearly features to distinguish these two gestures, which is the result of self-occlusion of the hand (48). For example, in TFA, the pinkie is bent in gesture “s” while the pinkie is straightened in gesture “t”. Thus, the feature to distinguish “s” from “t” is the bending of the pinkie. In the subtracted image of gesture “s” and “t” in IR (TFA), however, only the feature of the tip of the pinkie is shown (the yellow arrow in Fig. 6B) while the other part of the pinkie is hidden. Such an indistinct or nonoptimal feature limits the accurate and robust differentiation of these two gestures. In comparison, for IA-HG (TFA), the subtracted image shows distinct features for “s” and “t” (red arrows in Fig. 6B), which help clearly differentiate these two gestures.

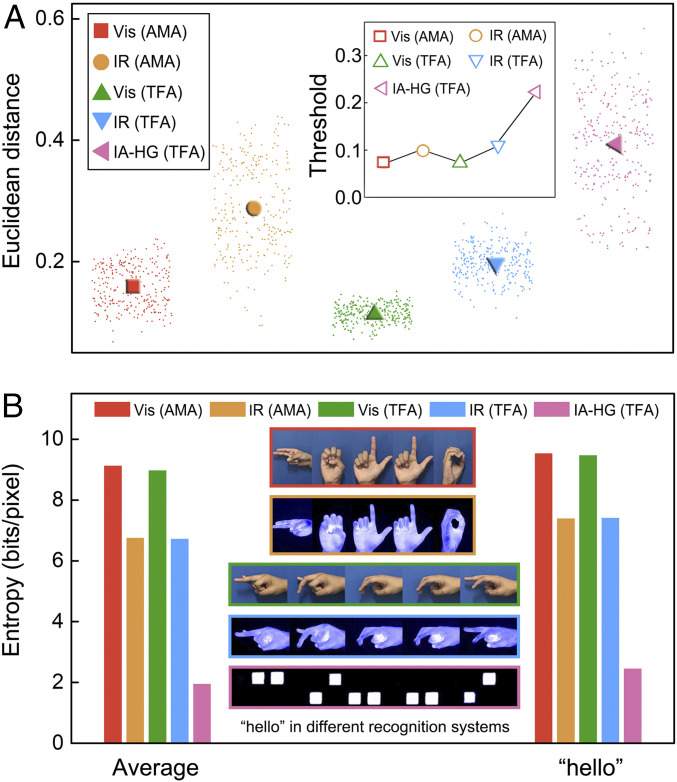
We further used Euclidean distance, which defines the distance between two points in the m-dimensional space and is often used in template matching for sign language recognition (50), to quantitatively characterize the differences between two images (SI Appendix, section 9). If Euclidean distance is 0, the two images are the same. Larger Euclidean distance means larger differences between the two images. In this comparison, we calculate the Euclidean distance between every two different gestures in different recognition systems (Fig. 7A). The solid patterns in Fig. 7A represent the average Euclidean distances for each system, and the dots around the solid patterns represent the calculated Euclidean distances for individual pairs of gestures. The inset of Fig. 7A shows the shortest Euclidean distance (distance between the two most similar images) in each recognition system, which is the threshold to recognize all gestures of this system. A larger threshold means that gestures of this system are easier to recognize with simpler algorithm. In general, IR-based recognition systems have larger average Euclidean distance than the corresponding visible light-based recognition systems. IA-HG (TFA) shows the largest average Euclidean distance among all the systems, which demonstrated the superior differentiation capability of IA-HG (TFA). Moreover, the threshold of IA-HG (TFA) is at least twice as high as those of other systems, which also shows that in general, the difference between gestures in IA-HG (TFA) is larger than those in other systems, and thus, the recognition of IA-HG (TFA) is easier than other systems, which will also help save processing time for feature extraction and gesture recognition.

Fig. 7.

Quantitative comparison between IA-HG (TFA) and other sign language recognition systems. (A) Euclidean distance of every two gesture images (the dots) and the average Euclidean distance of different sign language recognition systems (the solid patterns); Inset is the threshold for different sign language recognition systems, which is the minimum Euclidean distance in each recognition system. (B) Average entropy of gesture images in different sign language recognition systems and the entropy of word “hello” in different recognition systems.

In sign language recognition, real-time recognition is usually difficult as a large amount of image data is produced in the process, and the processing of these data is time consuming (48). Decreasing the amount of image data is thus meaningful for real-time recognition. To characterize the amount of image data for the recognition system, information entropy is often used, which is the average amount of information produced by a source of data (51). Here, we also calculated the entropy of each gesture image in different recognition systems and the average entropy (Fig. 7B, Left and SI Appendix, section 10 and Fig. S21). Besides, we used different gestures to form a word “hello” and calculate the entropy for this word (Fig. 7B, Right). Gestures in IR-based systems in general have less entropy than that in visible light-based systems. IA-HG (TFA) has the least entropy, which means that for the same sign language, IA-HG (TFA) produces the least amount of image information among all the systems. The processing of data generated in IA-HG (TFA) thus requires less time than in other recognition systems.

IA-HG (TFA) also shows strong robustness in real-time sign language recognition. The approach can be applied in poor light condition and in the dark as visible light has little effect on IR thermal imaging (SI Appendix, Fig. S22). The high differential capability of designed IR diffraction patterns also enables the high recognition accuracy even with incomplete information or extra distracting information (SI Appendix, Fig. S23). We calculated the accuracy of recognizing 260 (10 repeats of 26 alphabets) different IR patterns, and the recognition accuracy is 99.6%. The recognition of IA-HG (TFA) is also independent of the size of the hands (SI Appendix, Fig. S24), which demonstrates the robustness of this approach for practical application for different users.

Proof-of-Concept Demonstration of IA-HG (TFA) for Real-Time Sign Language Recognition.

To demonstrate the real-time sign language recognition by IA-HG (TFA), we generated a graphical user interface using Matlab for real-time input and recognition of IR patterns (SI Appendix, section 11 and Fig. S25). As illustrated in SI Appendix, Fig. S26, Mike and Amy met in a dancing party, and Mike wanted to invite Amy for a dance. He, however, cannot communicate with Amy normally as he has hearing disability. Visible light–based sign language recognition was also not suitable for this environment with dim light. They thus tried to use IA-HG (TFA) for communication, and at the end, Amy happily accepted Mike’s invitation.

Discussion

In summary, this work demonstrates that the human hand is not just a natural and powerless IR light source but also a multiplexed IR light source. As a natural and powerless IR light source, the human hand emits IR radiation constantly, and it can be integrated into a reflection-based encryption/decryption system. In this system, the difference in the IR radiation between the hand and the background enables the decryption process. Both the multilevel information encryption/decryption using multicolor coding patterns and also the unclonable coding using fingerprints and random patterns are demonstrated in this study. As a multiplexed IR light source, each finger can serve as an independent light source. The relative position and number of light sources are controllable and adjustable at will by changing the hand gestures. Metallic reflection gratings with different periods and orientations can selectively diffract IR radiation from each finger of the hand with specific configurations. The specific gesture composed of different fingers can thus be used as the matching key for information decryption as well, which increases the level of security in comparison to the use of the whole hand as the light source. The selective interaction between the fingers of the hand and the diffraction gratings can be used for complex signal generation and recognition as well. In this direction, we further demonstrated the use of human hand as a multiplexed IR light source for the potential application in sign language recognition or gesture recognition. Complex gestures are transformed into easily recognizable IR diffraction patterns. The established IR diffraction–based sign language recognition system exhibits a simplified recognition process with a high level of accuracy and robustness and minimizes the disturbance of illumination condition, complex background, and the self-occlusion of hands. In this work, the temperature difference between hand and ambient plays the key role for the generation of different patterns. When the ambient temperature gets close to the hand temperature, the IR radiance contrast will decrease. One possible way to increase the contrast is to temporarily increase the temperature of the hand by rubbing it with the other hand. A quick rubbing of the hand can increase the hand temperature up to 41 °C, which is more than enough to increase the contrast of IR radiance for the decoding. The approach can thus be applied in different ambient temperatures (SI Appendix, Fig. S6). In demonstrating the selective interaction between fingers and gratings, a relatively good alignment of the fingers to specific positions is required. Such a requirement is not only to serve the purpose of generating the selective interaction, but it actually also helps minimize the interference of IR radiation from other parts of the body that is not in the specific location of the finger. In the future, the detector and gratings can possibly be integrated into a wearable device and worn on the wrist to fix the position between gratings and the hand and enhance the accuracy of finger positioning relative to the gratings. The integration of the human hand into these engineered functional systems can not only enhance sustainability, but also increase the level of intelligence and controllability of these systems due to the direct involvement of human brains in the systems. The findings may also help further open up the possibility of using not only the human hand but also potentially other human components into functional systems and processes.

Materials and Methods

Fabrication of PDMS Patterns on Al Sheet.

The PDMS precursor was prepared by mixing the prepolymer (Sylgard 184A, Dow Corning Corporation) and the crosslinker (Sylgard 184B, Dow Corning Corporation) at the mass ratio of 10:1. The PDMS precursor was then diluted with hexane at the mass ratio of 1:3 for the spray process. A deposition mask with the coding pattern was placed on an Al sheet (3 cm × 3 cm × 1 mm), and an air brush (RH-C, Prona Corporation, Taiwan) was used to spray PDMS/hexane solution onto the Al sheet. The sample was cured at 100 °C for 10 min after the spray process. For multicolor coding, a piece of glass was laser engraved to generate the pattern of flower and butterfly with the depth of ∼60 μm. Al film ∼200 nm thick was then deposited on the sample by vacuum thermal evaporation apparatus (JSD400, Jiashuo Vacuum Technology Co., Ltd, China). The PDMS precursor solution in hexane with different mass ratios (1:1, 1:20, and 1:50) was injected into the grooves of the leaves, butterfly, and flower, respectively, to generate pattern with different thickness of PDMS in different areas. The sample was then cured at 100 °C for 10 min.

Generation of Fingerprint Pattern and Random Pattern on the Al Sheet.

The PDMS precursor (∼1 mL) was spin-coated on an Al sheet using a spin coater (KW-4A, Institute of Microelectronics of the Chinese Academy of Sciences). A thumb was pressed on the PDMS film (∼7.37 μm) before it was fully cured to form the pattern of the fingerprint. The sample was then heated up to 100 °C for 10 min to fully cure the PDMS film. For the random PDMS pattern, PDMS precursor solution in hexane (mass ratio = 1:3) was sprayed onto the Al sheet to generate random dots. The sample was then cured at 100 °C for 10 min after the spray process.

Fabrication of Gratings.

Gratings with different periods and orientations were fabricated on silicon (Si) wafer by photolithography. One milliliter of photoresist (RZJ-304, Suzhou Ruihong Electronic Chemical Co., Ltd.) was dropped on a piece of Si wafer (2 cm × 2 cm). The photoresist was then spin-coated at the speed of 1,000 r/min for 1 min and cured at 100 °C for 4 min. A photomask with designed gratings was placed on the cured photoresist, and the photoresist was exposed to ultraviolet (UV) light for 15 s using a Mask Aligner (URE-2000/35, Institute of Optics and Electronics, Chinese Academy of Sciences). After exposure, the sample was developed using a positive developer (RZJ-3038, Suzhou Ruihong Electronic Chemical Co., Ltd.) for 15 s. Al film with thickness of 200 nm was then deposited on the sample.

Measurement of Reflectance Spectra.

The IR reflectance spectra of the patterned samples were measured by a Fourier Transform Microscopic Infrared Spectrometer (NicoletiN10 MX). A cover glass coated with gold (Au) film (∼100 nm in thickness) was used as the reference sample (100% reflectance). The measurement spot size was set to be 100 μm × 100 μm. The reflectance spectra of the samples at visible range were measured by a Lambda 750S ultraviolet/visible/near-infrared (UV/VIS/NIR) spectrophotometer (PerkinElmer, Inc.).

Measurement of the Thickness of the Patterns.

The thickness of patterned samples was measured by the surface profilometer (KLA-Tencor P7). For each pattern, the thickness at five different locations was measured and averaged.

Data Availability

All study data are included in the article and/or supporting information.