Instantaneous Whole-Brain Strain Estimation in Dynamic Head Impact

Abstract

Head injury models are notoriously time consuming and resource demanding in simulations, which prevents routine application. Here, we extend a convolutional neural network (CNN) to instantly estimate element-wise distribution of peak maximum principal strain (MPS) of the entire brain (>36 k speedup accomplished on a low-end computing platform). To achieve this, head impact rotational velocity and acceleration temporal profiles are combined into two-dimensional images to serve as CNN input for training and prediction of MPS. Compared with the directly simulated counterparts, the CNN-estimated responses (magnitude and distribution) are sufficiently accurate for 92.1% of the cases via 10-fold cross-validation using impacts drawn from the real world (n = 5661; range of peak rotational velocity in augmented data extended to 2–40 rad/sec). The success rate further improves to 97.1% for “in-range” impacts (n = 4298). When using the same CNN architecture to train (n = 3064) and test on an independent, reconstructed National Football League (NFL) impact dataset (n = 53; 20 concussions and 33 non-injuries), 51 out of 53, or 96.2% of the cases, are sufficiently accurate. The estimated responses also achieve virtually identical concussion prediction performances relative to the directly simulated counterparts, and they often outperform peak MPS of the whole brain (e.g., accuracy of 0.83 vs. 0.77 via leave-one-out cross-validation). These findings support the use of CNN for accurate and efficient estimation of spatially detailed brain strains across the vast majority of head impacts in contact sports. Our technique may hold the potential to transform traumatic brain injury (TBI) research and the design and testing standards of head protective gears by facilitating the transition from acceleration-based approximation to strain-based design and analysis. This would have broad implications in the TBI biomechanics field to accelerate new scientific discoveries. The pre-trained CNN is freely available online at https://github.com/Jilab-biomechanics/CNN-brain-strains.

Introduction

Traumatic brain injury (TBI) remains a leading cause of morbidity throughout the world.^1,2 This type of injury is the result of a sudden mechanical load to the head that is further transmitted into the brain across length scales leading to tissue damage. Over the years, numerous impact kinematic variables and their variants have been proposed to quantify the severity of head impact and to assess the risk and extent of brain injury. The most fundamental kinematic variables are peak linear and rotational accelerations as well as peak rotational velocity. Some more sophisticated forms are also developed, such as head injury criterion (HIC)³ and brain injury criterion (BrIC),⁴ which consider the acceleration temporal profile shapes. To date, virtually all kinematics-based injury metrics are scalars that is, they use a single number to represent the global mechanical response status of the entire head or brain. A notable limitation is that they lack specificity in characterizing mechanical responses in specific regions of the brain. Therefore, they are oversimplified and insufficient to provide tissue-level insight into TBI biomechanisms.⁵

To translate global head impact kinematics into spatially detailed brain mechanical responses, computational head injury models are playing an increasingly important role.⁶ Obviously, these models have to be sufficiently biofidelic in order for the simulation results to be trustworthy. Efforts to improve model biofidelity and sophistication have been ongoing for almost half a century now.^7,8 Some recent advancements include the integration of white matter anisotropic material models,^9–12 more realistic brain anatomies,^13–15 much higher mesh resolutions,^16–19 and the incorporation of more realistic brain–skull boundary conditions.^20,21 In addition, experimental data for model validation have also been expanded from high-rate cadaveric head impacts^22,23 to mid-rate pure rotations simulating head impacts in contact sports^24,25 and in vivo loading conditions.^26–28 Together, these valuable experimental data allow for model biofidelity evaluations across a wide range of blunt conditions at both injury and sub-concussive levels.²⁹

However, the increase in model sophistication almost always comes with a substantial toll on computational efficiency, which has received little attention in model development at best. Simulating a single head impact typically requires hours^18,19,30 or even days^15,27 on a modern, high-end computing platform. The notoriously poor simulation efficiency and demand in computing resources make head injury models infeasible for any real-world, practical application such as immediate injury risk assessment on the sports field, large-scale model-based injury studies, or iterative design of head protective gears.

The need to substantially increase model simulation efficiency has been recognized.³¹ One strategy to mitigate the model simulation efficiency to some degree is to embed critical parameters drawn from impact simulations into a “hybrid” injury metric to better infer brain strain. The embedded parameters are determined offline by regressing the injury metric values against peak maximum principal strain (MPS) of the whole brain obtained from impact simulations using an actual head injury model.^32,33 Once determined, computing a hybrid injury metric becomes instantaneous, as no online model simulation is necessary. Because of the advantage of incorporating response feedback, hybrid injury metrics have shown promise over other conventional injury metrics when correlating against peak MPS of the whole brain.³³ However, similar to their conventional counterparts, hybrid injury metrics remain scalars that do not and cannot inform specific regions where peak MPS occurs. In addition, much simpler peak acceleration could outperform peak MPS in injury prediction,^34–36 which would defeat the utility of adopting a more complex, but potentially less effective, hybrid injury metric.

The ability to instantly compute element-wise, whole-brain MPS (vs. peak MPS alone) can be achieved via a pre-computation technique.³⁷ This approach discretizes head impact characteristic parameters such as rotational velocity/acceleration peak value and the azimuth and elevation angles to pre-compute a large library of brain strains using idealized kinematic profiles. For an arbitrary impact, MPS distribution is determined instantly via interpolation/extrapolation. The estimation achieved sufficient accuracy for impacts with one major rotational velocity peak based on dummy head impacts simulating American football.³⁸ For more complex rotational kinematics such as those with rotational motion reversal, however, significant underestimation occurred because the idealized impacts consist only of rotational acceleration but not deceleration.

The pre-computation concept was lately extended to a deep learning approach.³⁹ This approach conceptualizes an impact rotational velocity temporal profile as a two-dimensional (2D) image to allow for training a convolutional neural network (CNN) for response regression. Rather than explicitly simplifying a head injury model itself^32,33 or impact kinematic profiles,³⁷ the CNN implicitly learns the non-linear, high-dimensional but smooth and continuous relationship between impact rotational kinematics and brain strain.⁴⁰ Sufficient estimation accuracy was achieved based on several real-world data sets, including head impacts measured on the sports field^41,42 and those reconstructed.⁴³ Nevertheless, the accuracy evaluation was limited to peak MPS of the whole brain and corpus callosum and peak fiber strain of the corpus callosum, but not detailed strain distribution. In addition, the earlier study focused on more “severe” impacts but did not consider “milder” sub-concussive impacts, which are potentially important to the onset of concussion as well.^44–46

In this study, we extend the CNN technique to instantly estimate detailed MPS distribution of the entire brain and further expand the training data set to include milder impacts so as to maximize its potential utility. Reproducing element-wise strain distribution rather than peak magnitude alone³⁹ is vital to preserving the rich information about spatially detailed brain strains after long hours of impact simulation: a unique capability and utility of a head injury model in the first place. Preserving brain strain distribution also enables feature-based machine learning for injury prediction, which could potentially outperform commonly used logistical regression relying on a single feature such as peak MPS.^35,47

There are two main objectives of the study. First, we optimize a CNN architecture and evaluate its estimation accuracy via 10-fold cross-validation using impacts from a large range of severities. Second, to illustrate potential application, the CNN is used to estimate whole-brain MPS for reconstructed head impacts from the National Football League⁴³ (NFL) (n = 53, 20 concussions and 33 non-injury cases). The latter injury data set allows evaluating any degradation in injury prediction performance when using the efficient, but potentially less accurate, CNN-estimated brain strains (vs. the more accurate, but much less efficient responses from direct simulation). Scrutinizing injury prediction performance using an actual injury data set is critical for establishing confidence in the CNN technique for future practical applications. If the technique instantly estimates strain distribution with sufficient accuracy and injury prediction capability, it could unleash the full potential of a sophisticated head injury model for routine and diverse real-world applications in the future. This would have broad implications in shifting TBI biomechanics from relying on accelerations to focusing on spatially detailed brain strains.

Methods

Anisotropic Worcester Head Injury Model (WHIM) V1.0

The anisotropic version of the WHIM V1.0^12,29 (Fig. 1) was used to generate brain strain response samples.³⁹ This model was developed using high-resolution neuroimages of an athlete to create brain anatomical geometry and mesh, which contains 55 k hexahedral elements for the brain.⁴⁸ It incorporates white matter (WM) anisotropy based on whole-brain tractography and was validated against six cadaveric impacts in terms of relative brain–skull displacements.¹² The model's strain responses were recently further validated against 19 experimental data sets across a large range of blunt conditions,²⁹ including eight high-rate^22,23 and seven mid-rate^24,25 cadaveric head impacts as well as four in-vivo head rotation/extension tests.^26–28,49 Based on results from 12 cadaveric impacts, WHIM V1.0 achieves an average peak strain magnitude ratio of 0.94 ± 0.3 relative to the experimental counterparts derived from embedded markers.²⁹

FIG. 1.

The anisotropic Worcester Head Injury Model (WHIM) V1.0, showing the head exterior (a), intracranial components (b), the 50 deep white matter regions (c), and a subset of whole-brain tractography color-coded by fractional anisotropy (d). The model was recently validated in terms of brain strain across a wide range of blunt conditions.²⁹ Color image is available online.

CNN training data

A previous study reports details of generating impact-response samples for 3069 head impacts drawn from the real world using the anisotropic WHIM V1.0.³⁹ The samples included 110 head impacts measured in a variety of contact sports at Stanford University (SF)⁴¹ and their two batches of augmented data sets (n = 1320, 110 × 6 × 2), 53 head impacts reconstructed from the NFL⁴³ and their four batches of augmented data sets (n = 1272, 53 × 6 × 4), and 314 impacts recorded in American high-school football (HF).⁴² Data augmentation was introduced by permuting $v_{rot}$ components about the three anatomical directions ($3!=6$) with further random perturbation of the rotational axis and random scaling of $v_{rot}$ peak magnitude (to a range of 21.9–40 rad/sec; that is, more “severe” impacts⁵⁰). It was designed to increase the number of training samples with enhanced input feature variations, which was necessary to ensure CNN training convergence and to improve performance.³⁹ The HF data set was not augmented, as it served as an independent testing data set to evaluate CNN performance using training data generated exclusively from other sources (SF and NFL).

Rotational velocity ($v_{rot}$) profiles were available for the SF and NFL data sets. The HF data set was given in terms of rotational acceleration ($a_{rot}$) profiles, which were integrated into $v_{rot}$ by assuming a zero initial $v_{rot}$ value. The combined data set (n = 3069) was used to optimize the CNN architecture in this study.

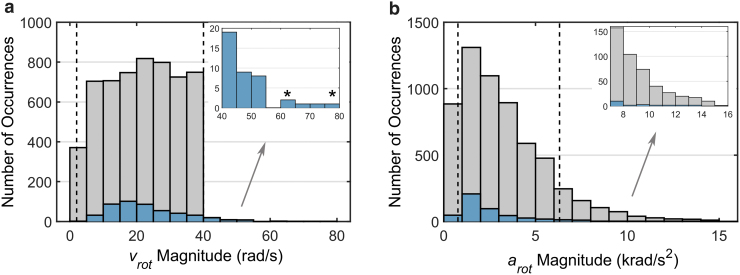
To further account for “milder” impacts relevant to sub-concussion, two additional batches of SF and four additional batches of NFL data sets were generated by targeting $v_{rot}$ peak magnitude to a range of 2.0–21.9 rad/sec. The lower bound was sufficient to cover the 25th sub-concussive impact (of 2.4 rad/sec), while the upper bound corresponded to the 50th concussive impact.⁵⁰ This led to 2592 (110 × 6 × 2 + 53 × 6 × 4) additional training samples. Combining with earlier data sets, this study employed a total of 5661 (3069 + 2592) impacts with the peak $v_{rot}$ of the augmented data targeted to a range of 2–40 rad/sec. Figure 2 summarizes peak resultant $v_{rot}$ and $a_{rot}$ magnitudes of the combined training samples.

FIG. 2. .

Histograms of peak resultant rotational velocity (a; $v_{rot}$) and acceleration (b; $a_{rot}$) for the entire training sample (n = 5661). The real-world impacts are overlaid. Regions between the two vertical lines are considered “in range.” The identified two cases (stars) are further illustrated in Figure 9. Color image is available online.

Data pre-processing

Using $v_{rot}$ profiles alone was sufficient to train/predict peak MPS of the whole brain with sufficient accuracy.³⁹ However, training MPS distribution was notably more challenging, not only because of the much larger number of response values to predict (n = 55 k brain elements vs. 1 for peak MPS of the whole brain), but also because the earlier peak MPS does not need to specify the location of occurrence, whereas MPS distribution does not have such an advantage. With trial and error, we discovered that combining both $v_{rot}$ and the corresponding $a_{rot}$ profiles as CNN input was important to maximize input features and to improve the estimation performance (further discussed subsequently).

Similar preprocessing was conducted on $v_{rot}$ and $a_{rot}$ profiles in the WHIM global coordinate system.³⁹ This included transforming the profiles using the “conjugate rotational axis”, $\Omega \left({180}^0-\theta ,-\alpha \right)$, for impacts with $\left|\right|\theta \left|\right|>90^0$, where $\theta$ and $\alpha$ are the azimuth and elevation angles characterizing the rotational axis, $\Omega \left(\theta ,\alpha \right)$, determined when the resultant $v_{rot}$ reached its peak. Essentially, this was to negate both the x- and z-components of the $v_{rot}$ and $a_{rot}$ profiles, when $\left|\right|\theta \left|\right|>90^0$,³⁷ to generate mirrored responses about the mid-sagittal plane.^37,38 The $v_{rot}$ and $a_{rot}$ profiles were then synchronously repositioned so that the $v_{rot}$ peak occurred at a fixed 100 ms. Replicated padding with zero acceleration was added to both sides of the profiles so as to reformat them into a fixed size of 3 × 201. The two dimensions corresponded to the three anatomical directions and a fixed temporal length of 200 ms at a resolution of 1 ms, respectively.

Data in $v_{rot}$ and $a_{rot}$ profiles did not have the same range. According to on-field measurements, generally, they are on the order of 0–100 rad/sec versus 0–10,000 rad/sec² respectively.⁵⁰ To ensure the same data range (of 0–100) to improve performance,⁵¹ $a_{rot}$ values were uniformly scaled to 1%. Finally, $v_{rot}$ and the scaled $a_{rot}$ profiles (3 × 201 each) were combined into a 2D image at a size of 6 × 201 to serve as CNN input (Fig. 3).

FIG. 3.

Flow chart showing preprocessing of a head impact kinematic profile (top) and an empirically optimized convolutional neural network (CNN) architecture (bottom) to predict the distribution of peak maximum principal strain (MPS) of the entire brain. The pre-processed $v_{rot}$ profile (after transforming to its “conjugate rotational axis,” and if needed, shifting, and padding³⁹) is combined with the corresponding pre-processed and scaled $a_{rot}$ profile (effectively, with a unit of 100 rad/sec² after scaling). The resulting two-dimensional [2D] image representation serves as the CNN input. Color image is available online.

CNN architecture

The previous CNN architecture³⁹ was further empirically optimized to estimate element-wise peak MPS (regardless of the time of occurrence), by minimizing a weighted loss function (described subsequently) in a 10-fold cross validation using the entire training data set (n = 3069). Compared with the previous architecture, the updated network consists of three convolutional layers, with 64, 64, and 32 filters, each with sizes of $3\times 30$, $1\times 3$, $1\times 3$, and stride sizes of $1\times 2$, $1\times 2$, $1\times 1$, respectively (Fig. 3). They are followed by a pooling layer of a size of $1\times 2$ with a stride size of $1\times 2$, a flattening layer (with a dropout rate of 0.2), and three fully connected layers with sizes of 200, 100, and 55 k (the last of which corresponds to the number of brain elements to predict responses). The pooling layer and the first fully connected layer (of a size of 200) adopted a rectified linear unit (ReLU) activation function, while all other layers used a linear activation function. A batch size of 256 was chosen with the number of epochs set to 400. An early stopping criterion was used to avoid overfitting. The CNN architecture was implemented using Keras library (Version 2.2.4) with Tensorflow (Version 1.11.0) backend.

MPS responses do not have the same variance across the brain among head impacts, as previously shown for the NFL impacts.⁵² This implies a graded estimation uncertainty across brain regions. Intuitively, if we penalize more for elements with larger variations across the impacts, it would likely improve estimation accuracy. Therefore, a weighted loss function was designed:

$$loss=\frac{1}{p}{\sum }_{i=1}^p\left(\frac{1}{q}{\sum }_{j=1}^q\left({\sigma }_i\times {\left(x_{ij}-y_{ij}\right)}^2\right)\right)\times 100,$$ (1)

where $x_{ij}$ and $y_{ij}$ are the estimated and directly simulated MPS values for the i^th brain element in the j^th training sample impact, respectively; p is the number of the brain elements in the anisotropic WHIM V1.0, q is the number of the training samples (e.g., 90% of the 3069), and ${\sigma }_i$ is the standard deviation of the i^th brain element among the q training samples. An additional scaling factor of 100 was used to mitigate the loss of data precision resulting from round-off errors during the iterative training process, as values of $x_{ij}$, $y_{ij}$, and ${\sigma }_i$ were typically small. This was important as the internal CNN architecture uses 32-bit single-precision floating numbers.⁵³

CNN estimation performance

For the entire data set (n = 5661), a 10-fold cross-validation would ensure each sample to be tested once. For each testing sample, we assessed the CNN estimation accuracy by comparing the predicted MPS distribution with the directly simulated responses in terms of element-wise linear regression slope, k, and Pearson correlation coefficient, $r.$¹⁹ For impacts that used a “conjugate rotational axis,” the estimated MPS distribution was further mirrored about the mid-sagittal plane prior to assessing estimation accuracy. When element-wise MPS estimation was identical to the directly simulated, both k and r would be 1.0. Therefore, an estimation was considered “sufficiently accurate” when k and r satisfied: $0.9<k<1.1$ and $r>0.9$. The percentage of head impacts that had sufficiently accurate estimation was referred to as “success rate.”

The majority of training impacts had a peak $v_{rot}$ within the targeted range (2–40 rad/sec; Fig. 2a). However, they did not have a uniform distribution of peak rotational acceleration, $a_{rot}$ (Fig. 2b), which was not controlled in data augmentation. In addition, we found that a significant number of impacts had a large non-zero initial $v_{rot}$ value augmented from the SF data set because the impacts were given in terms of $v_{rot}$ profiles (the ratio to the peak $v_{rot}$ magnitude of 18.1 ± 22.2% for the given data set, range 0–100%). The initial non-zero $v_{rot}$ values could be further amplified because of random perturbation and scaling during data augmentation. For these impacts, even when their peak $v_{rot}$ values were within the targeted range, a large initial $v_{rot}$ value after augmentation would effectively reduce the change in $v_{rot}$ peak values and make them “outliers.”

In order to assess the CNN estimation accuracy more conservatively with a minimum number of “outliers,” impacts with peak $v_{rot}$ outside the targeted range (1.5% of the cases), with peak $a_{rot}$ below the 10th or above the 90th percentile (20.0% of the cases), or with the ratio between the initial and peak $v_{rot}$ values >10% (11.0% of the cases), were empirically removed. This led to a total of 4298, or 75.9% “in-range” impacts remaining (a given impact may be an “outlier” in multiple categories). A separate 10-fold cross-validation was conducted once again to report the CNN estimation accuracy.

Injury prediction performance

CNN estimation may degrade accuracy, which necessitates the investigation into its significance and implication on injury prediction. To achieve this goal, we used a subset of training samples by excluding the NFL and the associated augmented impacts (n = 3064 impacts remained; 5661–53 × 6 × 8–53) to train the CNN again with the same optimized architecture. The data exclusion and retraining ensured an objective performance measure on the independent NFL head impacts (i.e., without contaminating the training data by information from the testing data set). The resulting distributions of peak $v_{rot}$ and $a_{rot}$ values for the reduced training data set are in Figure 4a and b, respectively. Estimation accuracy was similarly assessed in terms of k and r.

FIG. 4.

Histograms of peak resultant rotational velocity (a; $v_{rot}$) and acceleration (b; $a_{rot}$) for a subset of data (n = 3064) used to train and test on an independent National Football League (NFL) data set (n = 53), which is overlaid (number of occurrences multiplied by 10 to improve visualization). Color image is available online.

MPS distribution effectively represented a “feature” at every element location of the brain. Therefore, it allowed feature-based machine learning algorithms such as support vector machine (SVM)⁵⁴ and random forest (RF)⁵⁵ to classify injury versus non-injury.⁴⁷ Both CNN-estimated MPS distribution and the directly simulated responses were used for classification or injury prediction. Similarly to a previous study,⁴⁷ two feature selection methods using either F-score⁵⁴ or RF “gini” importance ranking⁵⁵ were separately applied. Injury prediction using peak MPS of the whole brain via logistical regression served as a reference for comparison in terms of accuracy, sensitivity, specificity, and area under the receiver operator's curve (AUC). All injury prediction performances were measured via leave-one-out cross-validation.^35,36

Parameters associated with SVM and RF were determined empirically to maximize injury prediction accuracy following the previous study.⁴⁷ When using F-score for feature selection, the top 4% were used. When using SVM for classification, a linear kernel was used. For RF, the number of trees and the depth of trees depended on whether it was used for feature selection or classification, as specified in Table 1.

Table 1.

The Number and the Depth of Trees, (N, D), Used in RF Depended on Whether RF Was Used for Feature Selection (FS) or Classification (CL), as Shown

	SVM (CL)	RF (CL)
RF (“gini” importance ranking), FS	(10, 2): FS	(100, 2): FS (1000, 2): CL
F-score, FS	N/A	(50, 2): CL

RF, random forest; SVM, support vector machine.

Data analysis

All head impacts were simulated using the anisotropic WHIM V1.0, which took ∼30 min for one impact of ∼100 ms duration (double precision with 15 central processing units [CPUs] and graphics processing unit [GPU] acceleration; Intel Xeon E5-2698 with 256 GB memory, and 4 NVidia Tesla K80 GPUs with 12 GB memory). Another 30 min was necessary to extract peak MPS distribution across the impact duration. In total, this study required ∼8 months of nonstop computations to generate the data, which was mitigated by concurrent running of 5–10 jobs. Each CNN training took ∼9 min per fold for the entire data set on an NVIDIA Titan X Pascal GPU with 12 GB memory. Predicting the response distribution for a testing profile was instant (<0.1 sec) on a low-end laptop.

All data analyses were conducted using MATLAB (R2019b; MathWorks, Natick, MA). Student's t tests were used to compare the injury prediction performances. Statistical significance was reached when the p value was <0.05.

Results

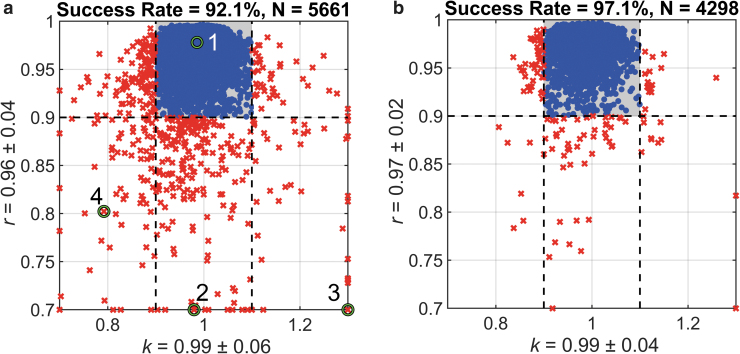
Figure 5a summarizes the linear regression slopes and Pearson correlation coefficients (k and r, respectively) for the 10 folds of testing data sets (each impact occurred once). On average, they had a value of 0.99 ± 0.06 and 0.96 ± 0.04, respectively, with 92.1% of the cases achieving sufficient accuracy. Figure 6 illustrates $v_{rot}$ and $a_{rot}$ profiles together with the estimated and directly simulated MPS distributions for a representative “successful” case (Fig. 6a) and three “failed” cases caused by: (1) out-of-range $v_{rot}$ peak magnitude (Fig. 6b); (2) out-of-range $a_{rot}$ peak magnitude which also had a large initial $v_{rot}$ value (Fig. 6c); and (3) large initial $v_{rot}$ value (Fig. 6d). After removing outliers specified in the three categories and retraining the same CNN architecture, the success rate improved to 97.1% for “in-range” impacts via 10-fold cross validation (Fig. 5b).

FIG. 5.

Summary of k and r when comparing convolutional neural network (CNN)-estimated and directly simulated maximum principal strain (MPS) distributions using a 10-fold cross-validation, using either the entire (a) or a subset of (b) the impact data set focusing on “in-range” impacts (after removing “outliers”). The shaded area represents impact cases of sufficient accuracy (i.e., $0.9<k<1.1$ and $r>0.9$). The k and r axes are capped to improve visualization. The identified four cases in (a) are further illustrated in Figure 6. Color image is available online.

FIG. 6.

Representative impact cases showing impact $v_{rot}$ and $a_{rot}$ profiles with the convolutional neural network (CNN)-estimated (${\varepsilon }_{est}$) and directly simulated (${\varepsilon }_{sim}$) maximum principal strain (MPS) distributions for a successful prediction (a) or “failed” cases resulting from (1) out-of-range $v_{rot}$ peak magnitude (b); (2) out-of-range $a_{rot}$ peak magnitude together with a large initial $v_{rot}$ value (c); and (3) a large initial $v_{rot}$ value (d). The four cases correspond to cases 1–4 identified in Figure 5. Color image is available online.

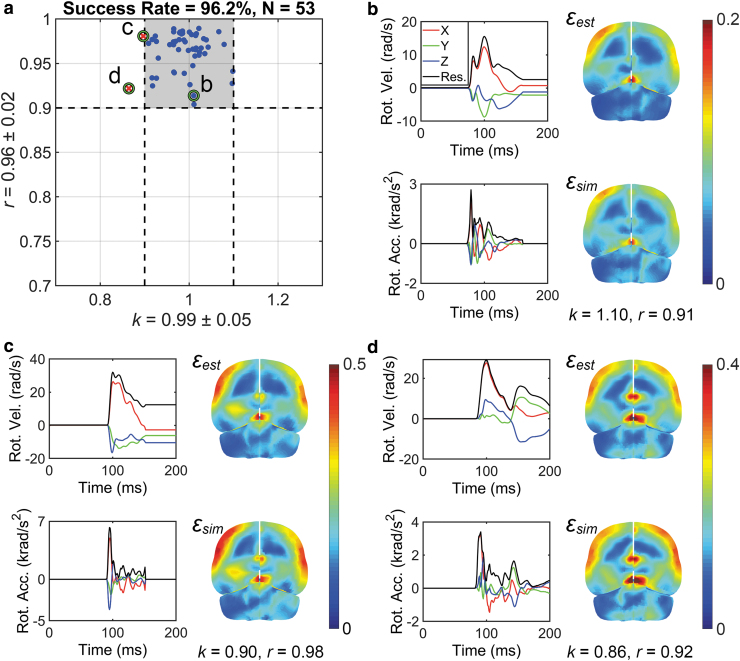
Figure 7a summarizes the k and r (0.99 ± 0.05 and 0.96 ± 0.02, respectively) performances for the NFL data set, where 51 out of the 53 cases (96.2%) were sufficiently accurate. Illustration for a representative successful case and the two “failed” cases are also shown (Fig. 7b–d), which were “almost successful.”

FIG. 7.

Summary of k and r for convolutional neural network (CNN)-estimated (${\varepsilon }_{est}$) and directly simulated (${\varepsilon }_{sim}$) maximum principal strain (MPS) distribution for an independent National Football League (NFL) impact data set (a; shaded area represents impacts of sufficient estimation accuracy, i.e., $0.9<k<1.1$ and $r>0.9$). Three representative impacts are selected to show a successful estimation (b; purposefully chosen to represent an r toward the threshold value for success) and two “failed” cases (c and d). The latter two cases only failed “marginally”; that is, their corresponding k and r were rather close to their success threshold values. Color image is available online.

Table 2 summarizes injury prediction performances using the CNN-estimated and directly simulated MPS distributions, in comparison with that from the baseline using peak MPS of the whole brain. For all performance categories, the CNN-estimated and directly simulated MPS distributions had statistically comparable performances (p > 0.05), regardless of the injury prediction algorithm or feature selection method. Compared with the baseline, machine learning methods often improved performance (p < 0.05).

Table 2.

Summary of Injury Prediction Performances in Terms of Accuracy, Sensitivity, Specificity, and AUC Using CNN-Estimated (“CNN”) or Directly Simulated (“WHIM”) MPS Distributions

Performance category	Accuracy	Sensitivity	Specificity	AUC
SVM (F-Score)
CNN	0.79	0.65	0.88	0.84
WHIM	0.79	0.65	0.88	0.82
SVM (“gini”)
CNN	0.83 ± 0.02	0.62±0.06	0.96 ± 0.03	0.88 ± 0.01
WHIM	0.83 ± 0.02	0.63±0.04	0.94 ± 0.03	0.87 ± 0.01
RF (F-Score)
CNN	0.81 ± 0.01	0.74 ± 0.02	0.85± 0.01	0.79±0.01
WHIM	0.78 ± 0.01	0.66 ± 0.02	0.85±0.004	0.80±0.01
RF (“gini”)
CNN	0.83 ± 0.02	0.71 ± 0.03	0.90 ± 0.03	0.87 ± 0.01
WHIM	0.83 ± 0.02	0.71 ± 0.03	0.90 ± 0.03	0.87 ± 0.01
Peak MPS
WHIM	0.77	0.65	0.85	0.86

Injuries are predicted using either SVM or RF with feature selection (specified in parenthesis) based on either F-score or RF “gini” importance ranking.⁴⁷ For comparison, baseline performances using peak MPS of the whole brain and logistical regression are also reported. All performances are evaluated via leave-one-out cross-validation for objective comparison. Using RF either for injury prediction or feature selection, 50 trials are used to account for the random initialization. Performances that are higher than the baseline are in bold (p < 0.05; where appropriate).

AUC, area under the curve; CNN, convolutional neural network; WHIM, Worcester Head Injury Model; MPS, maximum principal strain; SVM, support vector machine; RF, random forest.

Discussion

Injury-relevant brain strains can only be estimated via impact simulation, at least at present. However, current head injury models are notoriously time consuming and resource demanding in impact simulation. They are infeasible for any real-world practical application. In this study, we further developed a CNN to dramatically increase the efficiency in brain strain estimation—typically from hours on a high-end, modern computing platform to a fraction of a second. This led to an approximate speedup of ∼36 k, accomplished even on a low-end laptop. The speedup would likely be even higher when the technique is applied to other head injury models, because they typically take longer than WHIM for a head impact simulation (∼ 1 h vs. hours^18,30 or days^15,27). The current study significantly enhances the previous work focusing on a single response value,³⁹ as the trained CNN quickly estimates spatially detailed brain strains across the entire brain, and with sufficient accuracy for the majority of cases in both magnitude and distribution, using impacts drawn from the real world.

Further, the CNN-estimated brain strains also preserved the same injury prediction performances relative to the directly simulated (in some cases, the performances could be even better; Table 2). This finding is important, as it inspires some initial confidence with regard to adopting the much more efficient, but potentially less accurate, brain strain estimation in future applications. With feature-based machine learning, MPS distribution often outperformed peak MPS of the whole brain, relying on a single feature and the commonly used logistical regression. The random forest (RF) classification technique using the “gini” importance ranking for feature selection consistently had the best performance across almost all categories. Collectively, these findings support the use of CNN to instantly estimate spatially detailed brain strains for real-world applications in the future.

Implications and potential applications

Our technique may hold the potential to transform TBI research and the design and testing standards of head protective gears by facilitating the transition from acceleration-based approximation to strain-based design and analysis. This would have broad implications in TBI biomechanics in general. Although there is consensus that brain strains are more relevant to studying TBI biomechanics,⁵ state-of-the-art investigations continue to rely on impact accelerations to measure impact severity and exposure and to correlate with subsequent neuroimaging alterations^56–58 and clinical presentations.^44,59–61 Our pre-trained CNN model based on real-world impacts of a wide range of severities may fill a critical gap in the need to quickly reproduce detailed brain strains with sufficient accuracy, thus allowing the development of a strain-based cumulative injury risk metric. This may be an improvement over those solely based on kinematics at present (e.g., Risk Weighted cumulative Exposure [RWE].^62,63 Cumulative Head Impact Index [CHII],⁴⁴ and impact density⁶⁴) that do not directly inform brain strain.

In fact, the effort to establish a cumulative injury metric using model estimated strains has already started,⁶⁵ but it was limited to peak MPS of the whole brain from a subset of impacts. In contrast, our pre-trained CNN could enable efficient translation of all head impacts for every participant and from all sports teams into detailed and region-specific brain strains. Therefore, it has the potential to enable correlation between region-specific, cumulative strain exposure and the corresponding localized brain injury findings, either individually or on a groupwise basis. This may improve neural health monitoring and is a significant advantage over other “hybrid” injury metrics aimed at quickly inferring peak MPS of the whole brain, but not the anatomical location of occurrence or distribution.^32,33 Injury predictors based on region-specific brain strains, which have shown to improve injury prediction performance over peak MPS of the whole brain, do exist. However, they do not yet account for cumulative effects from repeated head blows.^10,66

The pre-trained CNN model could also enable other applications; for example, to improve the design of head protective gears through iterative strain-based feedback or to assess the quality of wearable impact sensors in terms of brain strains.⁶⁷ By quickly pinpointing specific regions experiencing large strains for a given head impact, a targeted multi-scale modeling could also be launched.⁶⁸ This would facilitate the understanding of how external impact energy is transmitted into the brain through the length scales leading to axonal undulation, swelling, and microtube breakage,^69–71 which are characteristic of diffuse axonal injury.⁷² These applications could accelerate new scientific discoveries of TBI biomechanics.

Limitations and further development

Explorations of these potential applications are outside the scope of the current study. It is also important to note the limitations of our study and recognize that further technique development is necessary. First, perhaps a less recognized limitation, which not only applies to our own work but also to TBI modeling in general, is that only peak, positive strain such as MPS or peak fiber strain is considered. In effect, this practice discards information on negative strain or tissue compression that also causes injury.⁷³ More broadly within the research community, our current understanding about injury mechanism relies on a “static picture” of tissue mechanical responses. Although expanding from a scalar value to a spatially detailed strain “map” is a significant improvement,³⁵ it does not account for the temporal history of tissue strain/strain rate during the rapid impact, which could be important as well. This is analogous to the temporal profile of dynamic head impact kinematics itself, which has shaped numerous injury metrics and is also the driver for any impact simulation. Rapidly reproducing the spatiotemporal details of brain strain (vs. spatial distribution alone) is yet another exciting milestone very well worth exploration in the future.

Second, although MPS distribution generally outperformed peak MPS in injury prediction (Table 2), peak rotational acceleration ($a_{rot}$) had an even better performance for this NFL injury data set (e.g., sensitivity of 0.80 for peak $a_{rot}$³⁵ vs. 0.71 using RF for both classification and feature selection based on MPS distribution, or 0.65 based on peak MPS via logistical regression). This was similarly observed with the Global Human Body Models Consortium (GHBMC) model when compared with peak MPS.³⁶ However, the NFL injury data set is known to contain reconstruction errors,⁴³ and the under-sampled non-injury cases may have significant implications in injury prediction as well.¹⁰ In addition, no cumulative effects from repeated sub-concussive impacts were considered, which is now thought to be important to the onset of concussion.^44–46 Therefore, it warrants further testing on other, perhaps more realistic, injury data sets.

On the other hand, a recent network-based injury metric consistently outperformed peak $a_{rot}$ across all five performance categories evaluated (e.g., sensitivity of 0.85 vs. 0.80 for peak $a_{rot}$³⁵). The network-based “response feature matrix” encodes peak MPS in gray matter regions as well as injury susceptibility of white matter fiber tracts between pairs of gray matter regions, the latter of which are lacking in MPS distribution employed in this study. This suggests the need to further develop the CNN model to estimate white matter injury risks that could improve the performance of injury prediction even further.^10,66 The earlier success in predicting peak fiber strain in the corpus callosum³⁹ provides some initial confidence along this line for further development.

Finally, for the different machine learning techniques and feature selection methods, we have observed some differences in their injury prediction performances (Table 2). The SVM and RF parameters were chosen to maximize accuracy; nevertheless, we did not further optimize them to maximize every performance category.³⁵ It merits further exploration into their respective advantages to better understand their utility in concussion prediction. This is outside the scope of our current study whose purpose is to investigate any difference in injury prediction, rather than to further maximize injury prediction performance. This was justified, given that significantly higher injury prediction performances were achieved after incorporating white matter injury risk,³⁵ but that was lacking in this study.

CNN architecture and estimation performance

The CNN architecture was empirically optimized for the best estimation performance using the previous training data set (n = 3069).³⁹ Although the earlier architecture was effective in predicting peak MPS of the whole brain,³⁹ it did not perform well when predicting the distribution. For example, when using $v_{rot}$ profile alone as input, it had a success rate of 67.2% (Fig. 8a; with the size of the last layer changed to match the number of brain elements for response prediction). We suspected that the penultimate layer size (of 10) was too small. Replacing it with two fully connected layers of sizes 200 and 100, respectively, significantly increased the success rate to 83.2% (similarly, using $v_{rot}$ alone as input; Fig. 8b) and with a faster convergence rate (Fig. 8c). It was possible to use a single fully connected layer of an even larger size (e.g., 500) to achieve a comparable success rate, but the convergence rate dropped (not shown).

FIG. 8.

Comparison of estimation performance using the previous convolutional neural network (CNN) architecture (a; with the size of the last output layer changed to 55 k to match the number of brain elements for response prediction³⁹) and the one updated in this study (b). Their convergence behaviors in terms of root mean squared error (RMSE) between the two distributions versus epochs are also compared (c). All performance measures reported here are based on the previous impact data set (n = 3069) using $v_{rot}$ profiles alone as CNN input, without the addition of $a_{rot}$ profiles. Color image is available online.

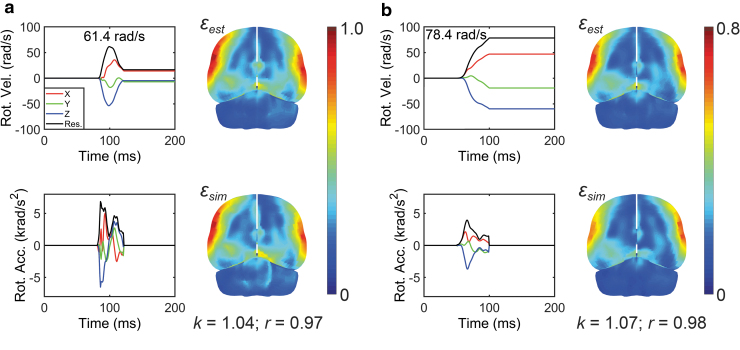
Nevertheless, further adjusting the fully connected layers did not increase the performance any further, and we discovered that the inclusion of $a_{rot}$ profile as additional input signals/features further significantly improved the success rate (from 83.2% to 92.9% for n = 3069, which was 92.1% for the entire data set of n = 5661; Fig. 5a). This led to our final architectural design and the adoption of both $v_{rot}$ and $a_{rot}$ profiles as CNN input for training (Fig. 3). The CNN estimation appeared sufficiently accurate, especially for “in-range” testing impacts where even the “unsuccessful” cases only failed marginally (i.e., k and r not too far from their respective success thresholds; Fig. 6b). For real-world impacts whose $v_{rot}$ peak magnitudes were outside of the targeted range (> 40 rad/sec; Fig. 2a), 65 out of 73 cases or 89% were successful, with two impacts illustrated in Figure 9 (correspond to those identified in Fig. 2a). These results highlight the robustness of the technique and suggest the feasibility of applying our pre-trained CNN to the vast majority of head impacts in contact sports.

FIG. 9.

Illustration of a National Football League (NFL) concussive head impact (a; Case125HD02⁴³) and another head impact from the HF data set (b; no injury diagnosis available). Even though their $v_{rot}$ peak magnitudes are significantly larger than the targeted range (61.4 rad/sec and 78.4 rad/sec, respectively, vs. 40 rad/sec as the upper bound of the targeted range; corresponding to the two cases identified in Fig. 2a), the convolutional neural network (CNN)-estimated strains were sufficiently accurate. Note, strain in (a) is higher than that in (b), even though its $v_{rot}$ peak magnitude is lower, because of its significant deceleration, which is lacking in the recorded profile in (b). Color image is available online.

Conceptually, both $v_{rot}$ and $a_{rot}$ profiles contain the same physical information in describing head motion kinematics (with the caveat of an undetermined initial $v_{rot}$ value for $a_{rot}$ profiles). Nevertheless, it was necessary to combine them as CNN input. This suggests that some higher-order information from $a_{rot}$ features were not derived from or well-represented by $v_{rot}$ profiles with the current CNN architecture (note that $a_{rot}$ is the temporal derivative of $v_{rot}$; i.e., one order “higher”). This intuition from human domain knowledge improved the CNN performance. It is also worth noting that a technique already exists to identify “important features” that are causal to the observed response; for example, through “attention mechanism.”⁷⁴ This “inverse” approach based on thousands of real-world impact-response samples would likely far exceed the ability of a conventional “forward” strategy with limited few dozens of impact data,⁵² and is worthy of exploration as well in the future.

Incorporating MPS variance as a weighting factor into the loss function (Eqn. 1) only slightly improved the estimation success rate over when that was not done (∼1%). We did not include MPS magnitude as an additional weighting factor because the linear regression slope and Pearson correlation we adopted for accuracy assessment do not discriminate the absolute response magnitude in their calculations. Nevertheless, it is straightforward to apply this additional weighting factor to focus more on higher strain regions that are likely more injury relevant, if needed. Compared with the previous CNN architecture where ReLU activation functions were used in all layers,³⁹ the new architecture also adopted linear activation functions in some layers. This improved the success rate by ∼1.3% in the 10-fold cross-validation, and also increased the convergence rate.

Finally, the zero versus non-zero initial $v_{rot}$ values seemed to have an influence on the CNN estimation performance. From a biomechanical perspective, one could, in fact, force a zero initial $v_{rot}$ value by shifting the profile along the y-axis without inducing any significant change in strain (verified but not shown). Therefore, this additional universal data pre-processing applied to all impacts could eliminate a potential confounder for the CNN, which is expected to improve the estimation performance. Although this is straightforward from the modeling perspective, the very existence of a large non-zero initial $v_{rot}$, itself in a real-world impact may indicate that the head impact sensor did not capture the entire head impact event. This is beyond the scope of any modeling effort.

These empirical observations enrich the knowledgebase of the CNN behaviors in the context of TBI biomechanics, which may facilitate future, continual development to further improve performance. To better serve the research community and the general public at large, we have made the pretrained CNN model publicly available at https://github.com/Jilab-biomechanics/CNN-brain-strains. It is anticipated that the link will be updated as needed in the future.

Conclusion

Efforts to develop head injury models have so far focused on improving model sophistication and biofidelity. However, how best to maximize the model utility in real-world applications has received little attention. This study further develops a convolutional neural network (CNN) to train offline so as to enable real-time online applications. The pre-trained CNN instantly estimates whole-brain strain distribution on a low-end computing platform with sufficient accuracy across the vast majority of head impacts in contact sports. Such a capability may have broad implications in studying the mechanisms of TBI for its ultimate detection, mitigation, and prevention.

Funding Information

Funding was provided by the National Institutes of Health (NIH) Grant R01 NS092853 and the Ford University Research Program.

Author Disclosure Statement

No competing financial interests exist.