Report on G4–Med, a Geant4 benchmarking system for medical physics applications developed by the Geant4 Medical Simulation Benchmarking Group

Abstract

Geant4 is a Monte Carlo code extensively used in medical physics for a wide range of applications, such as dosimetry, micro- and nano- dosimetry, imaging, radiation protection and nuclear medicine. Geant4 is continuously evolving, so it is crucial to have a system that benchmarks this Monte Carlo code for medical physics against reference data and to perform regression testing. To respond to these needs, we developed G4-Med, a benchmarking and regression testing system of Geant4 for medical physics, that currently includes 18 tests. They range from the benchmarking of fundamental physics quantities to the testing of Monte Carlo simulation setups typical of medical physics applications. Both electromagnetic and hadronic physics processes and models within the pre-built, Geant4 physics lists are tested. The tests included in G4-Med are executed on the CERN computing infrastructure via the use of the geant-val web application, developed at CERN for Geant4 testing. The physical observables can be compared to reference data for benchmarking and to results of previous Geant4 versions for regression testing purposes. This paper describes the tests included in G4-Med and shows the results derived from the benchmarking of Geant4 10.5 against reference data. The results presented and discussed in this paper will aid users in tailoring physics lists to their particular application.

I. INTRODUCTION

Geant4 (Agostinelli et al 2003 [1], Allison et al 2006 [2], Allison et al 2016 [3]) is a Monte Carlo (MC) toolkit describing particle transport and interactions in matter. Originally developed for high energy physics, it was later extended to the low energy domain (down to the eV scale) for medical physics and space science applications. Today Geant4 is widely used in medical physics in critical applications such as verification of radiotherapy treatment planning systems, and the design of equipment for radiotherapy and nuclear medicine. It is also used in medical imaging for dosimetry, to improve detectors and reconstruction algorithms, and for radiation protection assessments (Guatelli et al 2017 [4], Archambault et al 2003 [5]). In the medical physics domain, Geant4 can be used in stand-alone applications or via software tools like GAMOS (Arce et al 2014 [6]), GATE (Jan et al 2011 [7]), PTSim (Akagi et al 2011 [8], Akagi et al 2014 [9]) and TOPAS (Perl et al 2012 [10]). Given the extensive use of Geant4 in medical physics, a systematic benchmarking of the accuracy of the Geant4 physics models in this domain is paramount. This is crucial in a field where Monte Carlo simulations are often regarded as a gold standard.

In this work, we describe G4-Med, a group of currently 18 tests, executed on the CERN computing infrastructure to benchmark and to perform regression tests of new development tags and public releases of Geant4.

The tests are contributed by the members of the Geant4 Medical Simulation Benchmarking Group [11] to benchmark Geant4 for medical physics applications. They range from the benchmarking of fundamental physics quantities to more complex simulations typical of medical physics applications. We show the results of the tests obtained for Geant4 version 10.5 and report on their benchmarking against reference data. For the sake of brevity, we show only a sub-set of the results. The full results can be downloaded using the geant-val web interface [12].

G4-Med has been set up with the aim to assess the appropriateness of any Geant4 release in the medical domain and to monitor the impact of software development, including physics refinements, on physical quantities and applications of interest for medical physics. The results of the benchmarking are also intended to provide recommendations on the most appropriate physics configuration provided by Geant4 with the pre-built physics constructors and physics lists (Allison et al 2016 [3]) to adopt in specific user applications. The project documentation can be found at the G4-Med web page [11].

Section II describes the general method adopted in this study. This is then followed by sections that describe tests devoted to benchmarking electromagnetic physics (10 tests, Section III), hadronic physics (3 tests, Section IV), and testing both these physics sets together (5 tests, Section V). For clarity, Table I lists the tests of G4-Med, their name in the geant-val interface [12] and corresponding subsections. The subsections briefly describe the tests and their results. This Table also reports the source of the tests. We conclude our report with a summary of our findings in Section VI.

TABLE I.

Tests of G4-Med with their name in the geant-val interface and the subsections of this report with their description and results.

Test	Name in geant-val interface [12]	Source	Subsection
Photon attenuation	PhotonAttenuation	Amako et al 2005 [15]	III A
Electron electronic stopping power	ElectDEDX	*	III B
Electron backscattering	ElectBackScat	Dondero et al 2018 [17]	III C
Electron forward scatter from foils at 13 and 20 MeV	ElecForwScat	Faddegon et al 2009 [18]	III D
Bremsstrahlung from thick targets	Bremsstrahlung	Faddegon et al 2008 [19]	III E
Fano Cavity	FanoCavity	**	III F
Low energy electron Dose Point Kernels	LowEElectDPK	**	III G
Microdosimetry	microyz	** Kyriakou et al 2017 [20]	III H
Brachytherapy	Brachy-Ir	***	III I
Monoenergetic x-ray internal breast dosimetry	Mammo	Fedon et al 2018a[21] and 2018b[22]	III J
Nucleus-Nucleus hadronic inelastic scattering cross sections	NucNucInelXS	NA	IV A
62 MeV/u 12C fragmentation	LowEC12Frag	Mancini et al 2018 [23]	IV B
Charge-changing cross section for 300 MeV/u carbon ions	C12FragCC	Toshito et al 2007 [24]	IV C
67.5 MeV proton Bragg curves in water	LowEProtonBraggBeak	Faddegon et al 2015 [25]	V A
Light ion Bragg Peak curves	LightIonBraggPeak	NA	V B
Neutron yield of protons with energy 113 MeV and 256 MeV and 290 MeV/u carbon ions	ProtonC12NeutronYield	NA	V C
Fragmentation of a 400 MeV/u12 C ion beam in water	FragTest	Bolst et al 2017 [26]	V D
Test on cell survival modelling for proton therapy	Hadrontherapy	***, Petringa et al 2019 [27]	V E

^*:tests already executed by Geant4 developers for regression testing purposes;

^**:tests released as Geant4 extended examples;

^***:tests released as Geant4 advanced examples.

This report has gone through the peer review and approval processes of the Geant4 Editorial Board, which reviews all scientific papers emerging from the Geant4 Collaboration (Geant4 Collaboration website [13]).

II. METHODOLOGY

All tests included in G4-Med have been integrated into the geant-val environment (Freyermuth et al 2019 [14]), developed at CERN to perform Geant4 benchmarking and regression testing. The geant-val system provides a convenient web-based validation tool for Geant4 developers. It allows for storage of the Geant4 tests results in analysis objects, such as histograms and scatter plots, together with meta information, such as: Geant4 version, name of the test, energy and momentum of the incident particle, name of the target/detector and physics list used in the simulation. The main web interface [12] allows for visual and statistical comparison among results produced using different versions of Geant4, or a comparison with reference experimental results. In addition, users can download plots or data in various formats. The tests are executed automatically for all the global development tags and public releases of Geant4 at the CERN computing facility. All results derived from the benchmarking and regression testing, including plots and statistical analysis, are generated automatically and are accessible through the web interface [12].

In general, the tests use the same set of electromagnetic (EM) and hadronic physics constructors, with exceptions for tests aimed at validating the Geant4 EM multiple and single scattering models and specific hadronic cross sections and models. Simulation parameters, such as the secondary particles production threshold (cut) or the maximum step size, were appropriately set for each simulation scenario and are included in the description of each test.

In all the tests, the % difference between the results of the Geant4 simulations and reference data was calculated, then compared to the 1 σ uncertainty affecting the reference data (called σ_ref in the following sections). If the difference was smaller than σ_ref the agreement was considered satisfactory.

III. ELECTROMAGNETIC PHYSICS BENCHMARKING TESTS

This section describes the 10 tests in G4-Med where only the Geant4 EM physics component is activated and all the other processes are disabled. The tested Geant4 EM physics constructors are briefly described here as released within Geant4 10.5.

In all the EM constructors under investigation the set of EM processes are the same. Photon interactions include the photoelectric effect, Compton and Rayleigh scattering, and pair/triplet production (gamma conversion). Electron and positron interactions are ionization, bremsstrahlung and elastic scattering. Positrons can also annihilate at rest and in flight. Protons and heavier ions have ionization, elastic scattering and nuclear stopping.

G4EmStandardPhysics, G4EmLivermorePhysics, G4EmPenelopePhysics, G4EmStandardPhysics_option3 and G4EmStandardPhysics_option4 EM constructors, called here Opt0, Livermore, Penelope, Opt3 and Opt4, respectively, were considered in this work and correspond to different combinations of models deriving from either Geant4 Standard, Livermore or Penelope packages. The EM physics constructors and models, reported briefly in Table II, are described in detail in the Geant4 Physics Reference Manual [28].

TABLE II.

Geant4 physics models to describe EM physics processes in Geant4 EM constructors under investigation.

Geant4	Opt0	Opt3	Opt4	Livermore	Penelope
Rayleigh scattering and photoelectric effect	Livermore				PENELOPE
Compton scattering	Standard	G4KleinNishinaModel	G4LowEPComptonModel for E < 20 MeV* Brown et al 2014 [36]	Livermore for E <1 GeV*	PENELOPE for E < 1 GeV*
Gamma conversion	Standard	Standard	PENELOPE for E < 20 MeV Standard for E > 20 MeV	G4BetheHeitler,5DModel for E < 1 GeV, Standard for E > 1 GeV Bernard et al 2013 [37]	PENELOPE for E< 1 GeV, Standard for E > 1 GeV
e− and e+ ionisation	Standard	Standard	Livermore for e− for E < 100 keV, PENELOPE for e+ for E < 100 keV, Standard for E > 100 keV	Livermore for E < 100 keV Standard for E > 100 keV	PENELOPE
e− and e+ bremsstrahlung	Standard	G4SeltzerBergerModel for E < 1 GeV, G4eBremsstrahlungRelModel for E > 1 GeV			PENELOPE
e+ annihilation	Standard				PENELOPE
e− and e+ multiple scattering	Urban model for E < 100 MeV (Ivanchenko et al 2010 [39]), Wentzel model for E > 100 MeV	Urban model	Goudsmit-Saunderson model (Incerti et al 2018a [38]) for E < 100 MeV Wentzel model for E > 100 MeV
Coulomb scattering	on	off	on
Bremsstrahlung angular distribution	ModifiedTsai	2BS			PENELOPE

^*:G4KleinNishinaModel for higher energies. Geant4 10.5 is considered. For details on the models the reader should refer to the Geant4 Physics Reference Manual [28].

The Standard sub-library describes electromagnetic interactions in the range between 1 keV to 10 PeV, and is focused on high energy physics applications such as the simulation of LHC experiments (Apostolakis et al 2009 [29], Allison et al 2016 [3]). The Livermore models provide a more accurate description of EM physics processes in the low energy domain. They are based on the Livermore Evaluated Data libraries and are documented in Ivanchenko et al 2014 [30], Allison et al 2012 [31] and Chauvie et al 2004 [32]. Penelope features the specific low-energy models for electrons, positrons and photons, originally developed for the PENELOPE Monte Carlo code (Baro et al 1995 [33]) and then implemented in Geant4. They can describe particle interactions down to 100 eV.

The Opt4 constructor contains a combination of models for each EM physics process deemed to offer the best performance in term of precision at the cost of CPU efficiency (Ivanchenko et al 2019 [34]). The benchmark results of the current paper will also be used to discuss the expected better physical accuracy of Opt4 against the other EM constructors under investigation. Opt4 uses the G4GoudsmitSoundersonMscModel to describe multiple scattering for e^± below 100 MeV and the ICRU73 stopping power data for ions heavier than helium (ICRU report No.73 [35]).

In all the EM constructors, the multiple scattering of protons, muons and other hadrons is modelled with the Wentzel model and the Single Scattering. In the case of ions the Urban model is used for all energies.

Opt3, Livermore and Penelope constructors are considered as relatively accurate but less CPU demanding for medical applications. We therefore expect the Opt4 constructor to perform best overall in our benchmarking system, but we nevertheless study Opt3 and Livermore constructors, given their appeal in terms of computational efficiency.

For electron scattering and Fano cavity tests additional EM physics constructors are used, the G4EmStandardPhysicsSS, G4EmStandardPhysicsGS, G4EmStandardPhysicsWVI, called here SS, GS and WVI, respectively. They have the same physics parameters of Opt0, apart from different modelling of either the Coulomb scattering or the multiple scattering. In SS, the Single Scattering model is used for the Coulomb scattering. GS and WVI adopt the Goudsmit Saunderson and the Wentzel models, respectively, for multiple scattering. These physics constructors are mainly for Geant4 internal tests allowing study of various EM models alone, and are not meant for production physics configurations.

For completeness, Table III shows the values of EM parameters relevant for medical physics applications, listed for each of the EM constructors under investigation. The minimum energy is the minimum kinetic energy used to build the EM physics tables. The lowest electron energy parameter defines tracking cut for electrons and positrons. If after a step in a material the particle energy is below this cut, this energy is added to the energy deposition and this particle is stopped. This parameter may be changed by the user and can be set to zero. The number of bins per decade is the number of bins per decade to be used when building the physics tables. The angular generator parameter activates the angular generator interface of the ionisation process. The Mott corrections activate the Mott corrections in the electron multiple scattering. dRoverRange and finalRange are parameters of the method SetStepFunction used in the modelling of the multiple scattering. The lateral displacement due to multiple scattering is enabled by default for electrons and positrons, while it is set up differently in the EM constructors for muons and hadrons (see the Lateral displacement parameter in Table III). The Skin and Range factor parameters are used to limit the step in multiple scattering of electrons and positrons. The Theta parameter is the angular limit between single and multiple scattering. The last two rows of Table III report if the atomic de-excitation, including fluorescence X-ray and Auger electrons emission, is active in the EM constructors.

TABLE III.

Geant4 EM parameters of the EM constructors under investigation. Geant4 10.5 is considered.

Geant4 EM parameter	Opt0	Opt3	Opt4 Livermore Penelope	SS	GS	WVI
Minimum energy (eV)	100.	10.	10.	100.	100.	10.
Lowest electron energy (keV)	1.	0.1	0.1	0.01	1.	0.01
Number of bins per decade	7	20	20	7	7	20
Angular generator	false	true	true	false	false	true
Mott corrections	false	true	true	false	false	true
dRoverRange for e− and e+	0.2	0.2	0.2	0.2	0.2	0.2
finalRange for e− and e+ (mm)	1.	0.1	0.1	1.	1.	0.1
dRoverRange for muons and hadrons	0.1	0.05	0.05	0.1	0.1	0.05
Lateral displacement for muons and hadrons	false	true	true	false	false	true
Skin	1	1	3	1	1	0
Range factor	0.04	0.04	0.08	0.04	0.06	0.04
Theta (rad)	π	π	π	0.	π	0.15
Fluorescence	off	on	on	on	off	on
Auger electrons and PIXE modelling	off	off	off	on	off	off

All model parameters are unchanged with respect to their defaults, that is, no fine tuning or optimization is performed within the constructor.

A. Photon attenuation test

1. Simulation setup

The Photon Attenuation test, described and published in Amako et al 2005 [15], has the name of PhotonAttenuation in the geant-val web interface [12]. This Geant4 application calculates the attenuation coefficients of photons with energy between 1 keV and 1 GeV striking a water target with normal incidence. The number of incident photons N emerging without interacting in the target is counted and then the attenuation coefficient is calculated as $\frac{\mu }{\rho }=-\frac{1}{\rho d}\mathit{\text{ln}}\left(\frac{N}{N_0}\right)$, where ρ is the target density, d the target thickness and N₀ the number of incident photons.

The test calculates the photon attenuation coefficient in water of individual photon processes: Rayleigh scattering, photoelectric effect, Compton scattering and gamma conversion, as well as the total one. The photon attenuation coefficients are calculated in water, modelled as Geant4 NIST material G4_WATER (documented in the Geant4 Application Developer Manual [40]).

We compare the results of the Geant4 simulations to reference data of the United States National Institute of Standards and Technologies (NIST), included in the NIST XCOM database available online (Berger et al 1987 [41]). The NIST XCOM database was chosen as it is often used as a reference in medical radiation physics. It provides photon attenuation coefficients between 1 keV and 100 GeV for all the elements of the periodic table, calculated with a theoretical approach based on Hubbell et al 1980 [42]. The quoted uncertainty for the reference data is about 1% for high energies and away from the atomic edges, while it can be substantially larger, up to 10–20%, for energies close to the atomic absorption edges (Cirrone et al 2010 [43]). From here it was decided to adopt an uncertainty (σ_ref) of up to 10% and 1% for energies below and above 100 keV, respectively.

The number of histories (photon events) in the simulations is adjusted depending on the energy at which the attenuation coefficients are calculated in order to obtain simulation statistical uncertainties below 1%.

2. Results and discussion

Figure 1 shows the results concerning the total attenuation coefficient of photons in water, while Figure 2 shows the attenuation coefficients for each individual photon process. The agreement between the Geant4 EM constructors and the reference data is summarized in Table IV.

FIG. 1.

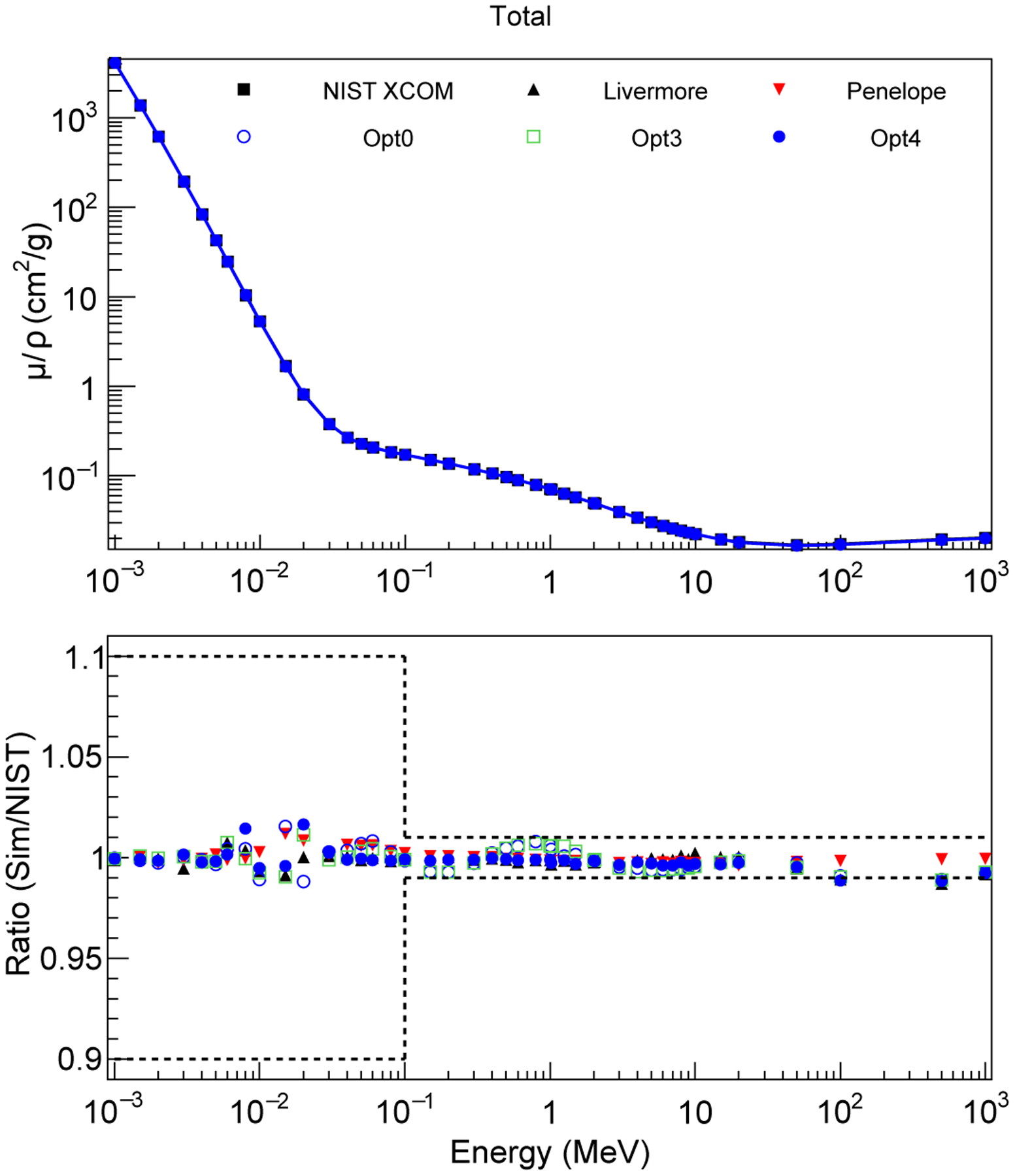
Top plot: Total attenuation coefficient in water with respect to the photon energy. Bottom plot: Ratio of the results obtained with Geant4 and the NIST XCOM reference data. The black dashed lines in the bottom plot represent the uncertainties of the NIST XCOM data (σ_ref). The statistical uncertainty affecting the Geant4 simulation results is below 1%.

FIG. 2.

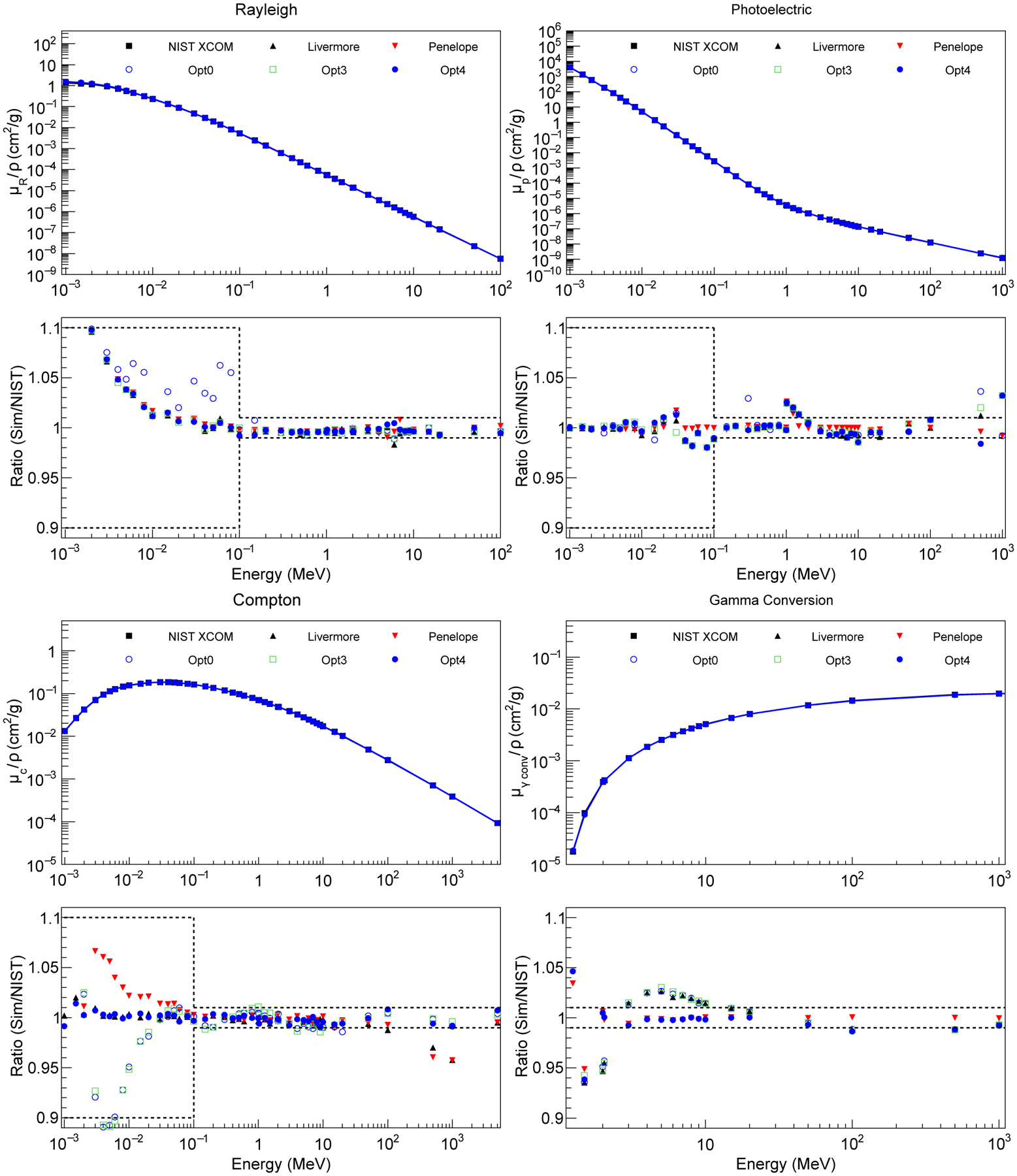
Comparison of the attenuation coefficients for each individual photon process: Rayleigh scattering (top left), photoelectric effect (top right), Compton scattering (bottom left), gamma conversion (bottom right). The plots show the attenuation coefficients as calculated using Geant4 against the NIST XCOM data; the ratio of Geant4 results and the reference data is shown as well. The black dashed lines in the lower plot represent the uncertainties of the NIST XCOM data (σ_ref). The statistical uncertainty affecting the Geant4 simulation results is below 1%.

TABLE IV.

Difference between Geant4 simulation results and NIST XCOM. σ_ref is the 1 σ uncertainty of the reference data. Ray: Rayleigh scattering; Photo: photoelectric effect; Comp: Compton scattering; Conv: pair and triplet production.

Test	Difference with respect to the reference data
	Opt0	Opt3	Opt4	Livermore	Penelope
Total	≤ 1 σref
Ray	< 1 σref, in particular: < 10% for E < 10 keV, ≤ 5% for 10 keV < E < 100 keV, < 1% for E > 100 keV	< 1 σref in particular: < 10% for E ≤ 3 keV, ≤ 5% for 3 keV < E< 10 keV, < 1% for E > 10 keV
Photo	< 1 σref with exceptions at 1 MeV-2 MeV and E ≥ 500 MeV
Comp	≤ 1 σref in particular: > 5% for E < 10 keV, ≤ 5% for 10 keV < E < 20 keV, ≤ 1% for E > 20 keV		< 1 σref	≤ 1 σref	≤ 1 σref, in particular: > 5% for E < 6 keV, ≤ 5% for 6 keV < E < 60 keV ≤ 1% for E > 60 keV
Conv	≤ 5% for 2 MeV, ≤ 3% for 3 MeV < E < 10 MeV, ≤ 1% for E > 10 MeV		≤ 1% for E ≥ 2 MeV (< 1 σref)	≤ 5% for 2 MeV, ≤ 3% for 3 MeV < E < 10 MeV ≤ 1% for E > 10 MeV	≤ 1% for E ≥ 2 MeV (≤ 1 σref)

For the total attenuation coefficient, all the Geant4 EM constructors agree with the reference data within the uncertainty of the NIST XCOM in the entire energy range under study (up to 1 GeV). The 2% local difference at 20 keV (see Figure 2) is due to differences in the photoelectric and Compton cross sections with respect to the NIST XCOM data. This is the point where we have the transition from photoelectric effect to Compton scattering as dominant process.

The results show a maximum difference of approximately 10% in the case of Rayleigh scattering for energies below few keV (see Table IV for more details). Then such differences decrease to less than 1% for higher energies. This is due to different modelling of this process in the Livermore Evaluated libraries and NIST, highlighted in Amako et al 2005 [15] and Cirrone et al 2010 [43]. Among the EM constructors considered Opt0 is the one showing the biggest differences with respect to the reference data.

In the case of photoelectric effect attenuation coefficient all the EM constructors agree with the reference data within 1 σ_ref (1 σ uncertainty of the reference data), with the exception at around 1 MeV-2 MeV, where the photoelectric attenuation coefficient changes significantly in slope and at high energies (above 500 MeV) where the photoelectric effect is not important anymore. There is a local difference of about 2% at 20 keV between the Geant4 EM constructors and the reference data, which contributes to the difference at this energy in the case of the total attenuation coefficient.

In the case of Compton scattering, an agreement within 1 σ_ref was observed for the entire energy range under investigation for Opt4, with maximum differences of less than 1.5%. Opt0, Opt3 and Penelope show differences above 5% at low energies (still within 1 σ_ref, see details in Table IV). Livermore and Penelope show local differences of a few percent at around 500 MeV – 1 GeV, however here the Compton cross section is one order of magnitude lower than the gamma conversion cross section.

The gamma conversion attenuation coefficient vanishes below the pair production threshold of 1.022 MeV, as expected. In this case, we observed differences equal or above 5% close to the threshold energy for all the EM constructors. Opt0, Opt3 and Livermore have differences up to 3% in the energy range between 3 MeV and 10 MeV and up to 1% for higher energies.

In general Opt3, Opt4, Livermore and Penelope have a good agreement with the reference data. The results are material dependent, but in water, all models are consistent with each other and with NIST XCOM within a few percent. A slightly overall better agreement with the reference data was found when considering Opt4. Nevertheless, it is important to note that the Geant4 EM physics constructors were compared here to theoretical data with modelling limitations. Therefore, this test should be extended in the future to include comparisons to available experimental measurements and other data libraries.

The results of this test are in agreement with those reported in Cirrone et al 2010 [43] and Amako et al [15]. The readers should consult these publications for results of this test when considering other target materials.

B. Electron electronic stopping power test

In this test the electron electronic stopping power is calculated in a set of target materials and compared to the ESTAR collision stopping power data, that is available online in the NIST Reference Database [44]. Electronic and collision stopping powers are the same physical quantity, however the ICRU Report No. 85 [45] recommends the use of the specific term electronic. From this observation, the term electronic was adopted here.

This technical test was developed for the regression testing of Geant4 for both low energy and high energy physics applications to demonstrate the level of agreement between available models of electron stopping powers.

Here details of the simulation, results and discussion are provided for electrons with an incident energy between 10 keV and 10 GeV. In the geant-val web interface [12], the test has the name ElectDEDX.

1. Simulation setup

Monoenergetic electrons originate in the center of a target. The simulation tests only the ionisation processes of the Opt0, Penelope, Livermore, Opt3 and Opt4 EM constructors, in the case of no energy loss fluctuations and no generation of secondary particles.

Assuming small energy losses, the stopping power is calculated as the energy deposited in the first step of the track, divided by the true step length, which takes into account multiple scattering correction.

The electronic stopping power is calculated for targets made of Al, Ar, Cu, Au, Pb, in order to represent a range of atomic numbers. Water is considered as a target as well because it is of interest for medical physics. The target materials are modelled from the Geant4 NIST material database, described in the Geant4 Application Developer Manual [40].

The ESTAR electronic stopping power values are calculated based on Bethe theory, with a density-effect correction evaluated according to Sternheimer, as described in the documentation of the NIST Standard Reference Database [44]. The uncertainties of the ESTAR electronic stopping powers for electrons are estimated to be 1% to 2% above 100 keV, 2% to 3% in low atomic number materials, and 5% to 10% in high atomic number materials between 10 and 100 keV. At energies below 10 keV the stopping powers from ESTAR are expected to be too large due to the omission of shell corrections and are recognised not to be accurate (Sakata et al 2016 [46]). Therefore we do not report data below 10 keV.

2. Results and Discussion

Figure 3 shows the electronic stopping power and ratio of the simulation results with respect to the ESTAR data libraries, in the case of water, Al and Au. These two elements have been chosen as they represent low and high atomic numbers, respectively. The simulation results do not have any statistical uncertainty because there is no multiple scattering, no energy loss fluctuations and no secondary particles generation.

FIG. 3.

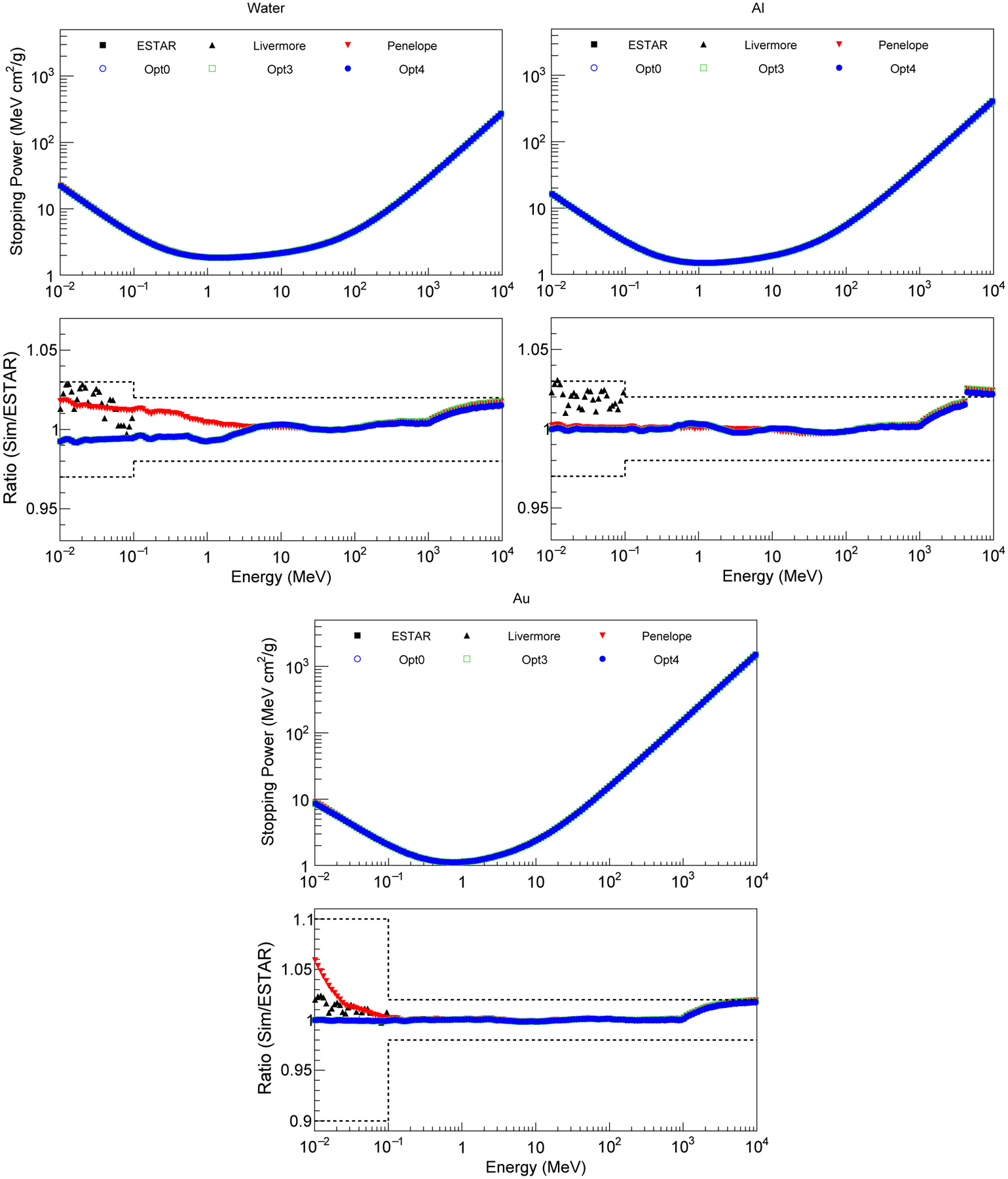
Electron electronic stopping power calculated by means of different Geant4 EM physics constructors, compared to the ESTAR reference data. The lower plots show the ratio of the Geant4 simulation results and ESTAR data. The dashed lines represent the uncertainty of the reference data σ_ref. The simulation results do not have any statistical uncertainty because there is no multiple scattering, no energy loss fluctuations and no secondary particles generation.

The agreement between the simulation results and ESTAR data is within the uncertainty of the reference data for all target materials. Between 100 keV and 1 GeV the difference between Geant4 simulation results and ESTAR data is less than 1%, below 100 keV the difference is within 3% for all models except for Penelope in Au, which is within a 5% agreement (still within the uncertainty of the reference data σ_ref). Above 1 GeV the difference increases due to different bremsstrahlung models in Geant4 and ESTAR computations. The results also indicate some interpolation problems in Livermore stopping powers below 100 keV, which is however within the model uncertainty.

C. Electron backscattering test

Electron backscattering is an important process in several physics applications including medical physics. It occurs when electrons, incident on a target, are scattered in the backward direction. The capability of properly reproducing this complex interaction in Geant4 has considerably improved in the last years, reaching a satisfactory agreement with experimental measurements published in the literature, performed in different periods and using different techniques (Dondero et al 2018 [17]). This work considers the wide selection of the available experimental data that is documented in Dondero et al 2018 [17], where a detailed description of each experimental technique used in the reported experiments can be found. This selection includes all the datasets known to the authors that respects basic quality criteria, as discussed in the reference article. This test is named ElectBackScat in the geant-val web interface [12].

1. Simulation setup

The Geant4 simulation used in this test models a simplified geometry, with an ideal mono-energetic electron beam impinging on a circular metallic target in vacuum. Several energy values, ranging from 50 eV to 1 MeV, and several incidence angles, from 0 to 75°, were simulated for the electron beam. Different target materials have also been tested. The complete list of these parameters is reported in Table V. All the possible combinations of the reported values have been simulated, in order to reproduce the experimental conditions of the reference data.

TABLE V.

Electron beam energies, incidence angle and target materials used in the Geant4 simulations. All the combinations are subject of the test.

Case study	Incidence angle (°)	Electron energies (MeV)	Target materials
Angular dependence	0, 60	1.033, 0.521, 0.314, 0.109, 0.084, 0.058, 0.032	Al
Energy dependence	0	From 50 eV to 1.033 MeV	Au, Si

The backscattering coefficient, η, is defined as follows:

$$\eta =\frac{e_{\text{back}}}{e_{\text{tot}}},$$ (1)

where e_back is the number of backscattered electrons and e_tot is the total number of incident electrons. For each simulation, the backscattering coefficient was calculated. The backscattered electrons can be either primary or secondary particles. Two case studies are addressed. The first considers the angular dependence of η, varying the incidence angle and the electron energies. The second case focuses on the energy dependence at low energies, only when the electrons are normally incident on the target.

For the reported simulations, the following Geant4 EM physics constructors have been used: Opt0, Opt3, Opt4, SS, GS, Livermore and Penelope.

All the EM constructors have been used with the default parameters apart from the electron minimum energy (see Table III), that was reduced with respect to the default value (from 100 eV to 50 eV) to reach the lowest energies available in experimental data. The simulation results have a statistical uncertainty below 1%.

2. Results and Discussion

Figure 4 shows backscattering coefficients as a function of the electron beam incident energy for an Al target for normal incidence and for 60° incidence angle. The average number of backscattered electrons increases for larger incidence angles. Above 0.2 MeV there is an agreement within 3 σ_ref between experimental data and simulation results, for all the considered EM physics constructors except GS.

FIG. 4.

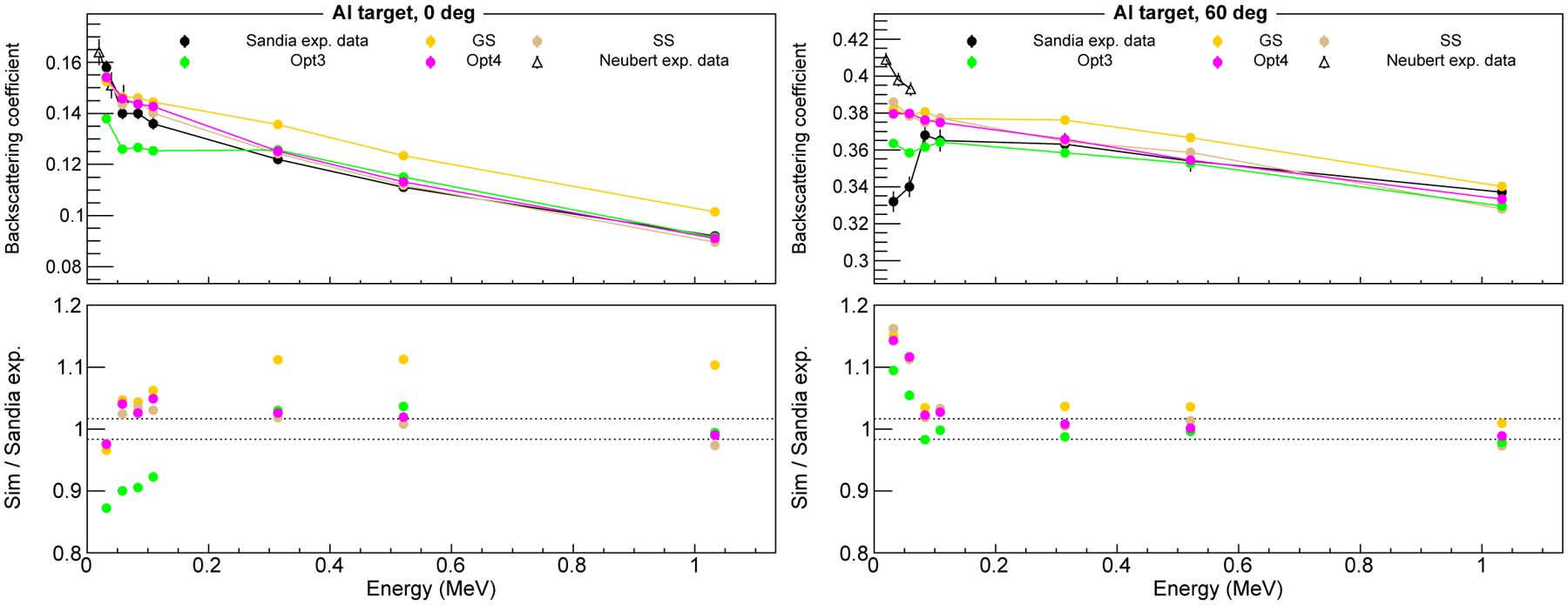
Backscattering coefficient as a function of the electron beam energies for an aluminium target, in the case when the electron beam is incident normally on the target (left plot) and with an angle of 60° (right plot). Coloured symbols are the simulated coefficient for some of the EM constructors considered. Experimental results from two different research groups are also reported. The lower plots show the ratio between the simulations and Sandia experimental data. The black dashed lines represent 1 σ experimental error (1 σ_ref). The simulation results have a statistical uncertainty below 1%.

At lower energies the considered experimental data show significant differences as reported in Figure 4, with a dependence on the beam incidence angle. For normal incidence, Opt4 and SS show an agreement within 5% with the Sandia experimental data, while Opt3 seems to underestimate the low energy backscattered electrons. GS is comparable to Opt4 below 100 keV but then it seems to overestimate η.

In the case of a 60° incidence, all EM constructors show significant differences (within 15%) below 100 keV. After that energy, there is an agreement between all the EM constructors and Sandia experimental data within 1–2 σ_ref. It is important to note that the comparison between experiments and simulations can’t be quantitatively reliable below 0.2 MeV because of the differences found in the experimental data sets themselves.

The energy-dependence results for silicon and gold targets are reported in Figure 5. Large discrepancy among the experimental data is shown, due to different experimental conditions and measurement thresholds applied to the scattered electrons. In general, SS, GS, Opt4, and Livermore produce results at lower energies with similar trend to the experimental data. In particular for high Z targets the agreement with some physics constructors results can be rather poor for energies below 10 keV. The calculation of η is influenced in the simulations, across the low energy region, by the electron minimum energy parameter applied. This parameter is related to the physical cut-off on the electron energy used in the experiments, that is observed to have an impact in the lowest energy η distribution profile. Usually this cut-off ranges between 50 eV and 100 eV, due to the use of polarized grids or polarized targets, depending on the particular experimental technique of each experiment. In Dondero et al 2018 [17] a more detailed description of the experimental setups used in these electron backscattering measurements is reported. This cut-off starts to influence the electron behaviour below 10 keV.

FIG. 5.

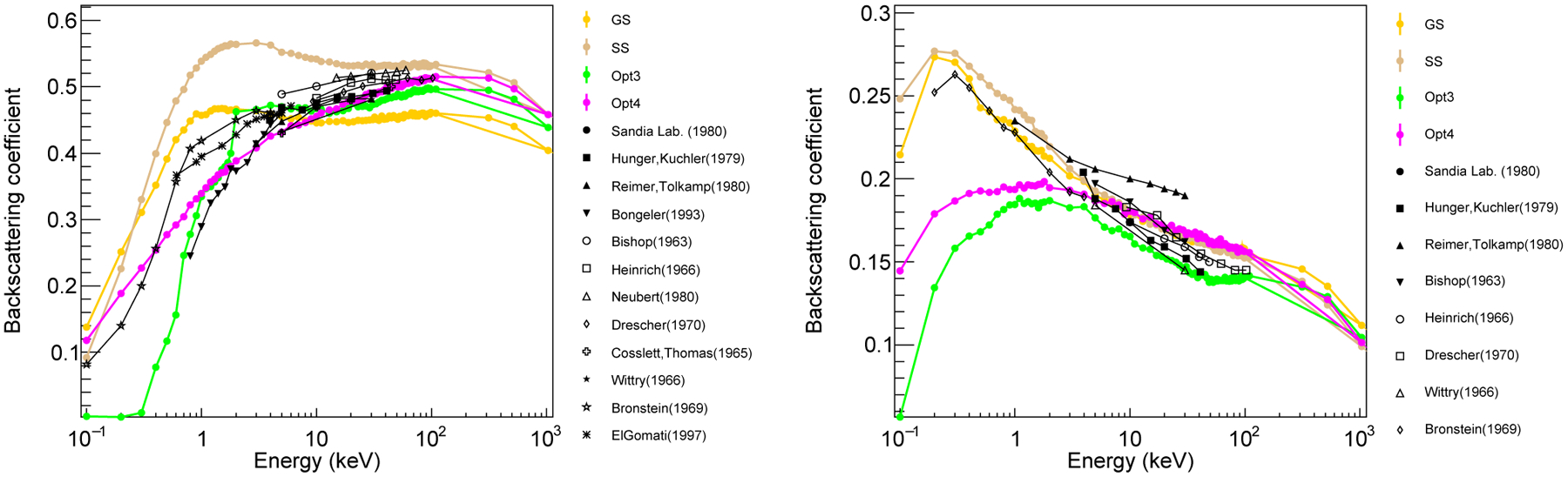
Comparison among electron backscattering coefficients simulated using various Geant4 EM physics constructors (colored symbols) and a selection of experimental data (black and white symbols), see Table VI for the complete list of references. Results for gold (right plot) and silicon (left plot) are reported. The simulation results have a statistical uncertainty below 1%.

For clarity, Figures 4 and 5 show the results for a subset of tested Geant4 EM constructors. The results obtained with Opt0 are very close to the ones generated with Opt3 as both constructors use the Urban multiple scattering model (Ivanchenko et al 2010 [39]) in the electron energy range under study. Penelope and Livermore agree very well with Opt4 as they use the Goudsmit-Saunderson model to simulate multiple scattering (see Section III).

In conclusion, SS, GS, Livermore, Penelope and Opt4 EM constructors show the best agreement with experimental results. The agreement above 0.2 MeV is within 3 σ_ref and between 5 keV and 0.2 MeV is within 15%. The agreement between simulation and experimental data below about 5 keV is, in general, worse than at higher energies due to differences of up to 40% for certain datasets. As discussed above, in this region the simulation results are particularly sensitive to experiment-related parameters, like the measurement thresholds applied to the detection of scattered electrons. Also for this reason, further investigation is still needed for electron backscattering simulation in Geant4. When this process is important, caution should be used in the meantime, even using the suggested EM physics constructors.

D. Electron forward scatter from foils at 13 and 20 MeV

The main physical processes in the transport of electrons at clinical energies are bremsstrahlung, collisional energy loss and scattering. The components of the treatment head of a linear accelerator used for electron therapy are intentionally thin in order to minimize energy loss and the generation of x-rays, which contaminate the treatment beam. In this case, accurate simulation of electron scattering is paramount.

An experimental benchmark of the scatter of electrons (13 MeV and 20 MeV) is available that represents the higher range of energies generally available in the clinic (5–25 MeV) for a comprehensive set of scattering materials (Be, C, Al, Ti, Cu, Ta, Au) for thicknesses that result in a characteristic angle (or root mean square scattering angle) of 2–8° (Ross et al 2008 [61]). The test is called ElecForwScat in geant-val.

The benchmark gives the characteristic angle for each energy, material and thickness and the angular distribution of fluence out to 0.9–2.5 times the characteristic angle, limited by the lateral extent of the helium bag that was placed between the scattering foil and detector. This helium bag was used to minimize scatter of the electron beam as it passed through this intervening space. The published measurements include a rigorous uncertainty analysis. Previously, the Monte Carlo systems (in alphabetic order) EGS, Geant, Geant4 and PENELOPE have been benchmarked against these measurements (Faddegon et al 2009 [18], Vilches et al 2009 [62]). It was found that the characteristic angle alone was insufficient to quantify the discrepancy between the measurement and simulation. Thus, both the characteristic angle and the angular distribution at points near or beyond the characteristic angle are shown. The comparison is limited to a single, representative foil thickness, chosen to illustrate the characteristic angle closest to 5°, and to the more commonly used lower energy of 13 MeV. This is justified since any discrepancy between measurement and calculation is expected to appear at all foil thicknesses and at both tested energies. The comparison for the angular distribution was for representative results from a select set of scattering foils.

1. Simulation setup

A mono-energetic electron beam of 13 MeV and Gaussian circular spot of 0.1 cm FWHM was normally incident on the exit window, a scattering foil, a monitor chamber, and mylar slabs on either side of a region filled with helium. The foils were 0.926 g/cm² Be, 0.546 g/cm² C, 0.14 g/cm² Al, 0.0910 g/cm² Ti, 0.0864 g/cm² Cu, 0.443 g/cm² Ta, and 0.0312 g/cm² Au. The scoring plane was perpendicular to the beam axis and located 1.182 m from the exit window. Details of the geometry along with the various scattering foil materials and thicknesses are the same as those used in Faddegon et al 2009 [18]. The fluence of electrons was scored in radial spatial bins of 1 mm width. A two parameter Gaussian function was fitted to the angular distribution of fluence to calculate the characteristic angle, limited to the region with the fluence greater than 1/3 of the maximum value, out to a radius of 18 cm on the scoring plane as done previously in Faddegon et al 2009 [18]. The physics constructors were Livermore, Penelope, Opt0, Opt3 and Opt4. A global production cut of 0.01 mm for secondary particles was used.

2. Results and Discussion

The characteristic angle from the benchmark measurement is compared with that from Geant4 in Figure 6 for all scattering foil materials. In the top left panel, the simulation with Opt0 agrees with the measured benchmarks to within 1 standard deviation (which is 1.0%) of the experimental uncertainty for all materials except carbon. Note that this reasonable agreement was not seen in the fluence distributions of all the other panels, where fluence at angles larger than the characteristic angle are shown. All the other constructors significantly underestimated the characteristic angle of most of the foils, by up to 3% for some foils. Results for the characteristic angle calculated with 10.5 version of Geant4 are comparable to those calculated with Geant4 9.2 (Faddegon et al 2009 [18]).

FIG. 6.

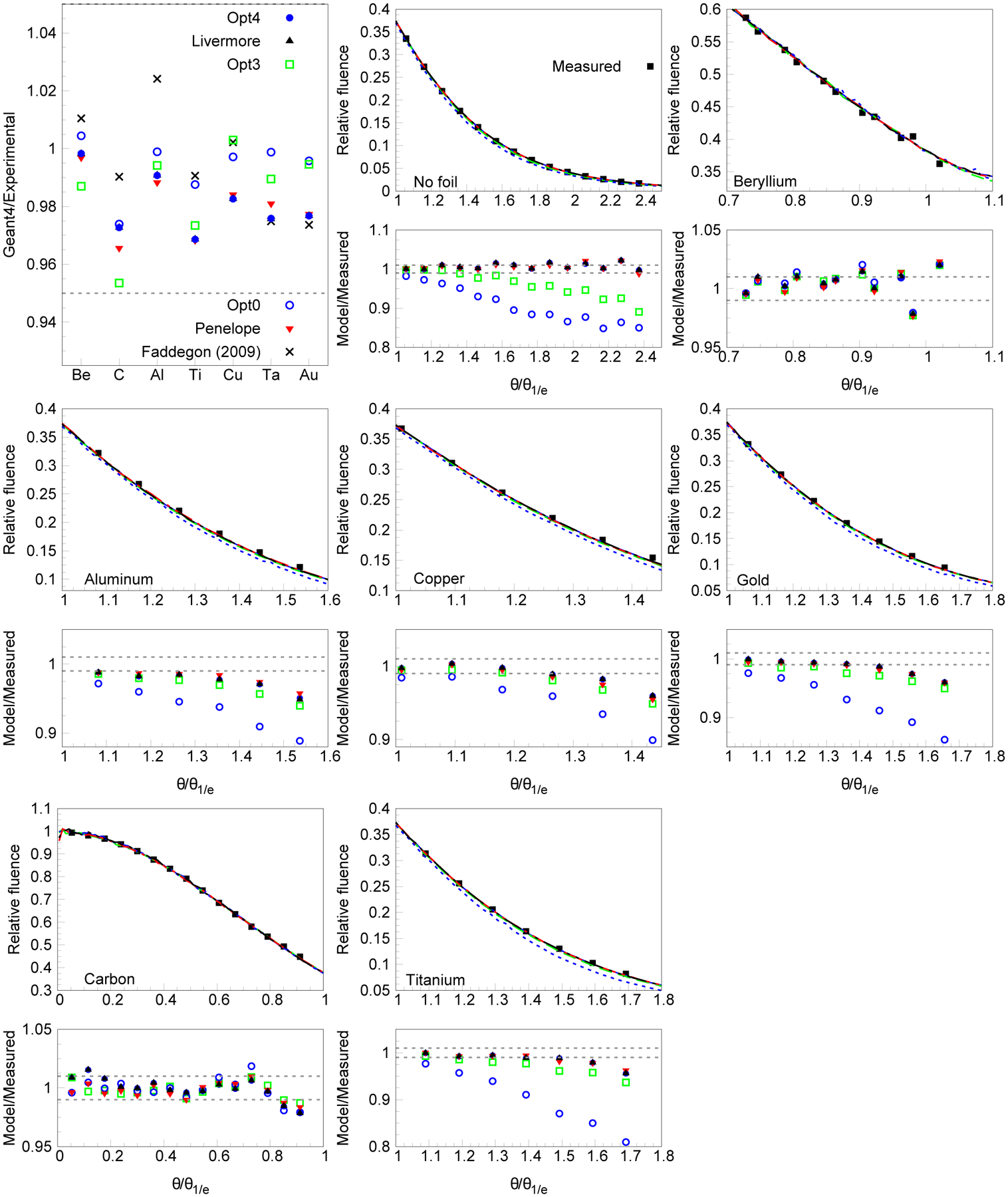
Ratio of calculated characteristic angle to that measured by Ross et al. 2008 [61] for all foil materials (top left), the calculated data from (Faddegon et al 2009 [18]) were obtained with Geant4 9.2. The measured angular distribution normalized to unity on the beam axis for select foils at points near or beyond the characteristic angle θ_1/e are also shown (symbols) compared to calculated results (lines). The gray dashed lines in the plot represent the experimental uncertainties, 1 standard deviation (σ_ref). The statistical uncertainties of the simulations are within 1%.

The angular distribution beyond the characteristic angle (below for the carbon foil) is shown in Figure 6 for all the foils. Opt3 and Opt4 for Geant4 10.5 show a comparable acceptable match to the measured angular distributions and to those calculated with the other Monte Carlo codes than past comparisons with Geant4 9.2 (Faddegon et al 2009 [18]). In general, Opt4 systematically underestimates forward-scattered electron fluence by up to 2–5% in the MeV range. The mitigation of these differences remains as an open problem.

E. Bremsstrahlung from thick targets

The measured yield of bremsstrahlung from electrons normally incident on thick targets at radiotherapy energies as a function of target material, electron energy, and angle provides a key benchmark for the modelling of linear accelerator treatment heads since this requires accurate simulation of both electron scatter and bremsstrahlung within the target.

The benchmark reference dataset are the measured photon fluence per incident electron and differential in energy: 1) along the axis for 10–30 MV x-ray beams from thick targets of aluminum and lead, and 2) from 0–90° of 15 MV beams from thick targets of beryllium, aluminum and lead. Photon fluence per unit energy per incident electron, and total photon fluence, integrated over energy, per incident electron was experimentally determined at 1 m from the target. Bremsstrahlung yield from 0.22 MeV to the incident electron energy was measured on the axis of 10.09, 15.18, 20.28, 25.38, and 30.45 MeV electron beams (Faddegon et al 1990 [63]). In a separate experiment, bremsstrahlung yield down to 0.145 MeV was measured at angles out to 90° for 15.18 MeV electrons (Faddegon et al 1991 [64]). The published measurements include a rigorous uncertainty analysis. Several Monte Carlo systems have been previously benchmarked against these measurements (Faddegon et al 2008 [19]). This benchmark is available in the geant-val web interface [12] with the name Bremsstrahlung.

1. Simulation setup

The sources in the simulation were mono-energetic, normally incident 0.35 cm diameter beams of constant fluence with energies of 10, 15, 20, 25 and 30 MeV. The beam first impinges on a titanium exit window, followed by a silicon transmission current monitor, then a pure target encased in a steel target chamber. Separate simulations were done for the 15.18 MeV beam with and without the target chamber, as the chamber was not included in measurements for angles over 10°. Details of the simulation geometry are described in Faddegon et al 2008 [19]. Photon fluence was scored on the surface of several concentric spherical rings in a sphere of 1 m radius centered at the intersection of the beam axis with the upstream face of the target. The rings covered 1° in the polar angle and the full 0° − 360° in the zenithal angle. Photons with energies larger than 0.22 MeV for the forward-directed benchmarks and 0.145 MeV for the angular distribution benchmarks were scored in 100 log spaced bins and compared with the published experimental benchmarks (Faddegon et al 1990 [63], Faddegon et al 1991 [64]).

The tested physics constructors were Penelope, Livermore, Opt0 and Opt4. A global production cut of 0.01 mm for secondary particles was used.

2. Results and Discussion

Figure 7 shows selected results of the angular and spectrum distributions for beryllium (top), aluminum (middle) and lead (bottom) for all Geant4 EM physics constructors. These results, obtained with Geant4 10.5, are in better agreement with measurement than Geant4 9.0 patch01, where some yields were well outside 1 standard deviation of experimental uncertainty (see results reported in Faddegon et al 2008[19]). In particular, the results obtained with Opt3 and Opt4 agree within 1 standard deviation experimental uncertainties for all energies and all angles below 60° with the exception of the 10 MeV yield for Opt4 on the beam axis, which is just outside 1 standard deviation. At 90° for the Al and Pb targets and 60° for the Pb target, the simulated results exceed the measurement by 1–2 standard deviations for all options, a larger discrepancy than found previously, but in better agreement with EGSnrc and PENELOPE. The energy spectra are within 1–2 standard deviations as shown in Figure 7 except at low energy fluence where contributions of experimental artifacts to the uncertainty may be underestimated.

FIG. 7.

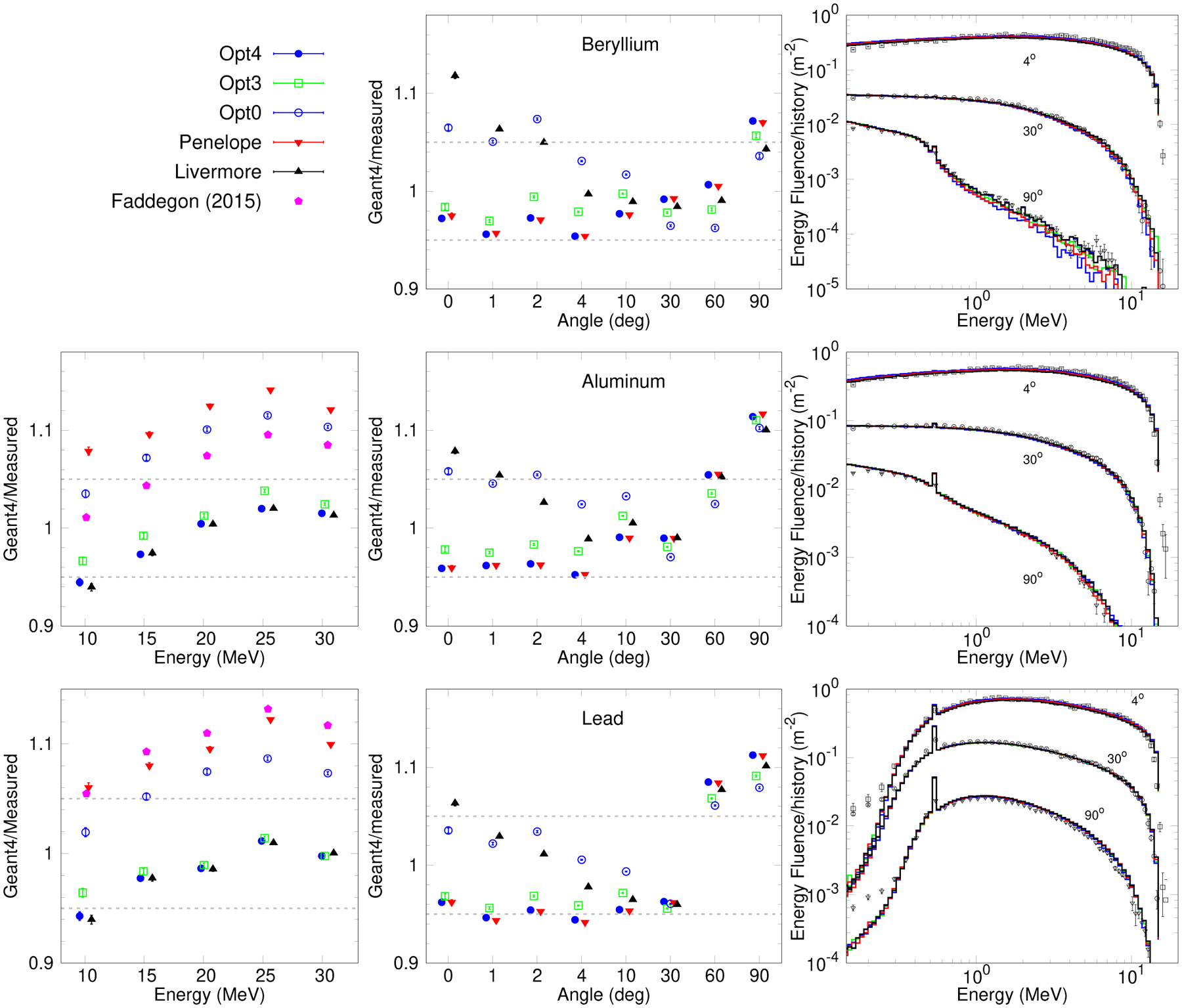
Bremsstrahlung from thick targets of beryllium (top), aluminum (middle) and lead (bottom). Ratio of simulated to measured 10–30 MeV bremsstrahlung yield on the beam axis (left) for aluminum and lead targets, including published results (Faddegon et al 2008 [19]) from an earlier version of Geant4 (left), ratio of simulated to measured 15.18 MeV bremsstrahlung yield from 0–90° (center) and spectral distributions of energy fluence at 15.18 MeV and representative beam angles of 4°, 30° and 90° (right). The measured spectra are shown with markers. Ratios are displayed at slightly shifted energy and angle for clarity. Associated error bars, in most of the cases smaller than the symbols, represent calculated statistical uncertainties, 1 standard deviation. The gray dashed lines in the plot represent the experimental uncertainties, 1 standard deviation (σ_ref).

F. Fano Cavity test to verify the multiple scattering and boundary crossing algorithm

This test is released as an extended example of Geant4 with the name FanoCavity. It is based on Poon et al 2005 [65] and Kawrakow 2000 [66]. It was designed to check the accuracy of the condensed history electron transport, especially the stability of the related stepping algorithms with respect to increasing values of the maximum allowed energy loss along an individual electron step. In case of Geant4, the corresponding continuous step limit parameter is the dRoverRange which is the maximum allowed step length in units of fraction of the (charged) particle range. This test is available under the name FanoCavity in the geant-val web interface [12].

1. Simulation setup

The different factors involved in the electron transport, i.e., the step limitation, effects of energy loss, modelling of multiple Coulomb scattering, are tested using the Fano cavity principle described in Fano 1954 [67].

The model of ionization chamber used is the one described in Poon et al 2005 [65]: a cylinder made of 5 mm water (G4_WATER) walls and a 2 mm cavity filled with steam (G4_WATER with a density of 1.0 mg/cm³). A beam of 1.25 MeV gamma rays parallel to the cylinder axis traverses it. With this setup, under idealized conditions, the ratio of the dose deposited divided by the beam energy fluence must be equal to the mass-energy transfer coefficient of the wall material.

The needed equilibrium condition for charged particles is realized using the beam regeneration after each Compton interaction: the scattered photon is reset to its initial state, energy and direction after the Compton process. Consequently, interactions are uniformly distributed within the wall material.

It is important to mention, that unlike the other tests used in this benchmark, the Fano cavity test requires its special physics modelling conditions. Therefore, the test fully relies on custom, local to the test EM physics constructors with special models for ionization and Compton scattering. Ionization is simulated using a model similar to the standard G4MollerBhabha (see the Geant4 Physics Reference Manual [28] for details) with the density dependent correction term of the corresponding stopping power removed. Moreover, in order to have the same stopping power both in the wall and cavity, the bremsstrahlung process is not modelled. The special model for Compton scattering guarantees the conservation of the charged particle fluence by utilising the above mentioned beam regeneration.

To speed up the simulation it is possible to increase the Compton cross section and the secondary particles that have no chance of reaching the cavity (when the range is smaller than 0.8 times the distance to the cavity) are killed.

To prevent the generation of δ-rays, the global production cut is set to 10 km, in order to be in the Continuous Slowing Down Approximation. On top of these options, the finalRange (see Table III) of the energy loss is set to 10 μm, which corresponds to a kinetic energy of 20 keV in water.

As it was already mentioned, this test was designed to check the accuracy of the condensed history electron transport. Therefore, five different local physics lists were used in the benchmark all with exactly the same special description of the physics interactions except the Coulomb scattering. The Coulomb scattering was modelled exactly as in the Opt0, GS, Opt3, Opt4 and WVI constructors in case of Opt0*, GS*, Opt3*, Opt4* and WVI*, respectively. The * is used in the notations in order to clearly indicate that the physics constructors used in this test are not identical to the corresponding Geant4 EM physics constructors except the modelling of the electron Coulomb scattering and the corresponding stepping algorithm.

2. Results and Discussion

Figure 8 shows the dependency of the ratio of the simulated dose and the theoretical one as a function of the dRoverRange parameter value for different physics constructors discussed in the previous section.

FIG. 8.

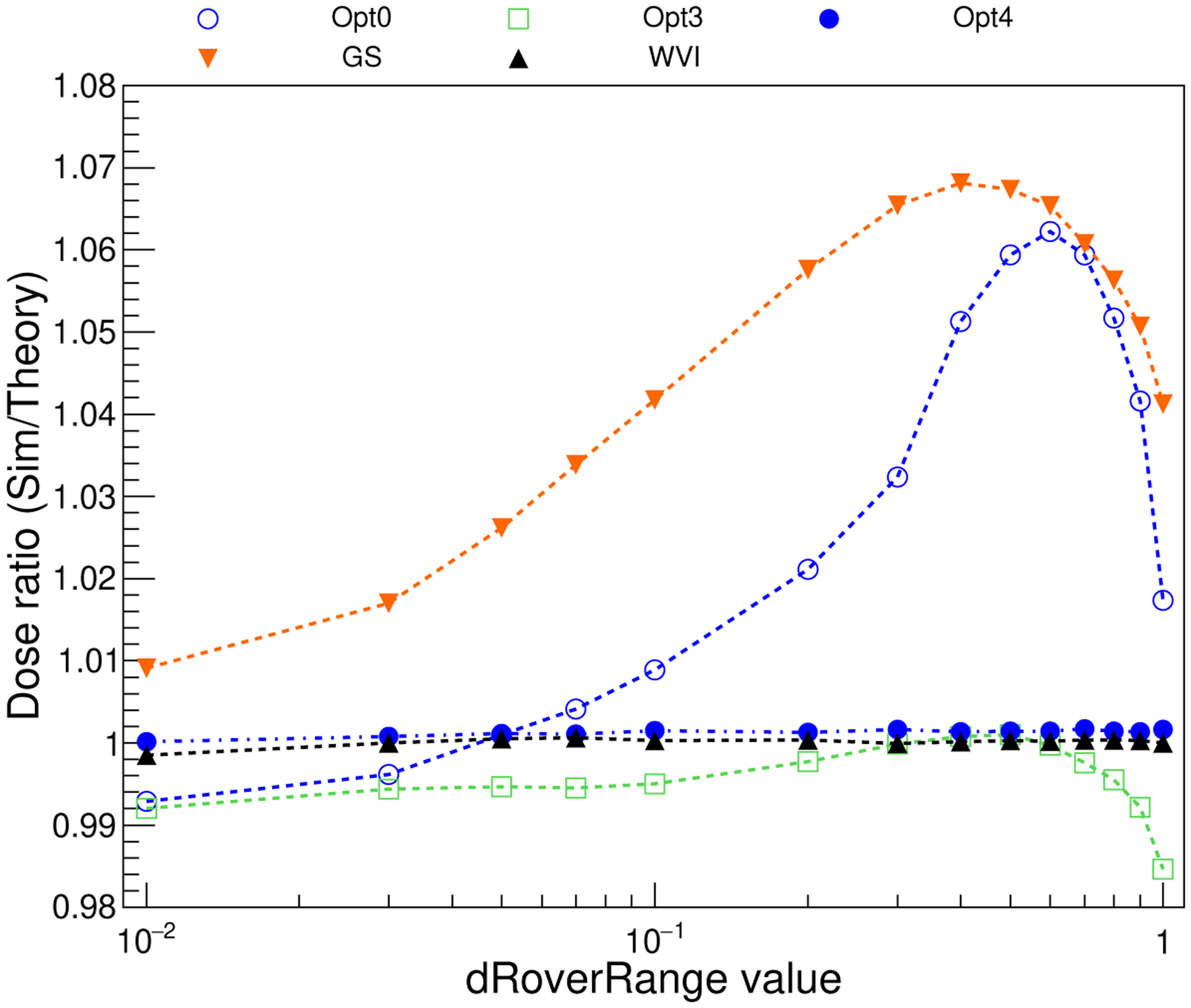
Dependency of the ratio of the simulated dose and the theoretical one as a function of the dRoverRange for different EM physics constructors. The statistical error bars affecting the simulation results are smaller than the symbols.

Opt0 and GS constructors utilise the Urban (Ivanchenko et al 2010 [39]) and the Goudsmit-Saunderson (Incerti et al 2018 [38]) models, respectively, to simulate multiple Coulomb scattering of electrons (below 100 MeV) with their special settings recommended for high energy physics (HEP) simulation applications. The corresponding settings include looser stepping algorithms since HEP applications, in general, are more tolerant of mistakes in the electron stepping especially when it comes with a significantly increased computing performance. As it is expected, both local physics constructors Opt0* and GS* show a strong dependence on the dRoverRange. Opt0* and GS* show a deviation from the theoretical data values between approximately 1% and 7%, depending on the value of the dRoverRange. The same two multiple scattering models are used to describe the Coulomb scattering in Opt3* (Urban) and Opt4* (Goudsmit-Saunderson) but with their more accurate settings, including the stepping algorithm, that are recommended for precision in critical applications. Accordingly, both multiple scattering models show significantly better stability under these settings. Opt3* shows an agreement between 1% and 2%, depending on the value of the dRoverRange. For the default value of the dRoverRange (0.2) (see dRoverRange for electrons and positrons in Table III), the agreement is approximately 0.3%. Opt4* provides a remarkably small (< 0.2%) deviation from the theoretical dose value practically independently from the dRoverRange parameter value. In addition to Opt4*, that contains the Goudsmit-Saunderson multiple scattering model with its most accurate configuration (Incerti et al 2018 [38]), the WVI* constructor, that utilises the so called mixed-simulation description of Coulomb scattering, also provides a high level of accuracy and stability (< 0.2%). These results are in a perfect agreement with the findings described in a recent study (Simiele et al 2018 [68]), in which a maximum deviation from the theoretical dose values of 0.16% was reported when the Goudsmit-Saunderson model with its Opt4* settings were used. Therefore, this test shows that Geant4 can transport electrons accurately without the need of applying significant step-size reduction, and irrespective of dRoverRange when using the Opt4 constructor, in the geometrical set-up considered (Simiele et al 2018 [68]). The Fano test subject of this section could be repeated by including photon transport and secondary particle production for completeness. It is recommended to repeat the test in the user’s geometry of interest.

G. Low energy electron Dose Point Kernels

The simulation of radial energy deposition profiles from isotropic sources of electrons has proven to be a useful method of evaluating the performance of Monte Carlo codes used in medical physics, in particular for the usage of radionuclides in targeted cancer therapy (Prestwich et al 1989 [69], Simpkin et al 1990 [70]). Although experimental data on electron Dose Point Kernels (DPK) in liquid water - the main component of biological medium - currently do not exist, preventing a full validation, we propose a benchmark comparing Geant4 performance to the EGSnrc Monte Carlo code. This application code can be found in Geant4 as the TestEm12 extended electromagnetic example. The test has the name LowEElectDPK in the geant-val web interface [12].

1. Simulation setup

In this setup electrons are emitted isotropically into a 4π solid angle from a point source placed in a spherical liquid water (defined as G4_WATER) volume. In this work, results are presented for 10, 15, 100 and 1000 keV incident monoenergetic electrons. At each simulation step, the energy deposition is randomly distributed along the step; the radial distribution of energy deposition from the emission point is then recorded in a histogram with a weight equal to the energy deposition value collected in the step. Radius values are scaled to the Continuous Slowing Down Approximation (CSDA) range (r₀) of the electron at the selected incident energy (E₀). The DPK distribution is then normalized to the number of incident electrons, to the selected histogram bin width and to the incident kinetic energy value. Results are presented for 10⁵ incident electrons. The simulation results have a statistical uncertainty lower than 3%. Opt0, Opt3, Opt4, Livermore and Penelope have been adopted to describe the EM physics interactions. In addition, a maximum step size equal to the bin width of the histogram is applied to control the spatial accuracy of the energy deposition.

2. Results and Discussion

Figure 9 presents the scaled DPK distributions obtained for each incident electron energy using the Geant4 electromagnetic physics constructors. The curve obtained with Opt0 is not shown as this constructor produces the same results of Opt3. These profiles are compared to EGSnrc predictions (Mainegra-Hing et al 2005 [71], computed as described in the PhD thesis of Perrot [72]). In this comparison with EGSnrc, energy loss fluctuations have not been considered in the simulations. All Geant4 EM physics constructors produce similar profiles as a function of scaled radius and incident energy. Opt3 shows lower maxima at 10, 15 and 100 keV and larger profiles below about (r/r₀) = 0.4 than the EGSnrc simulation data.

FIG. 9.

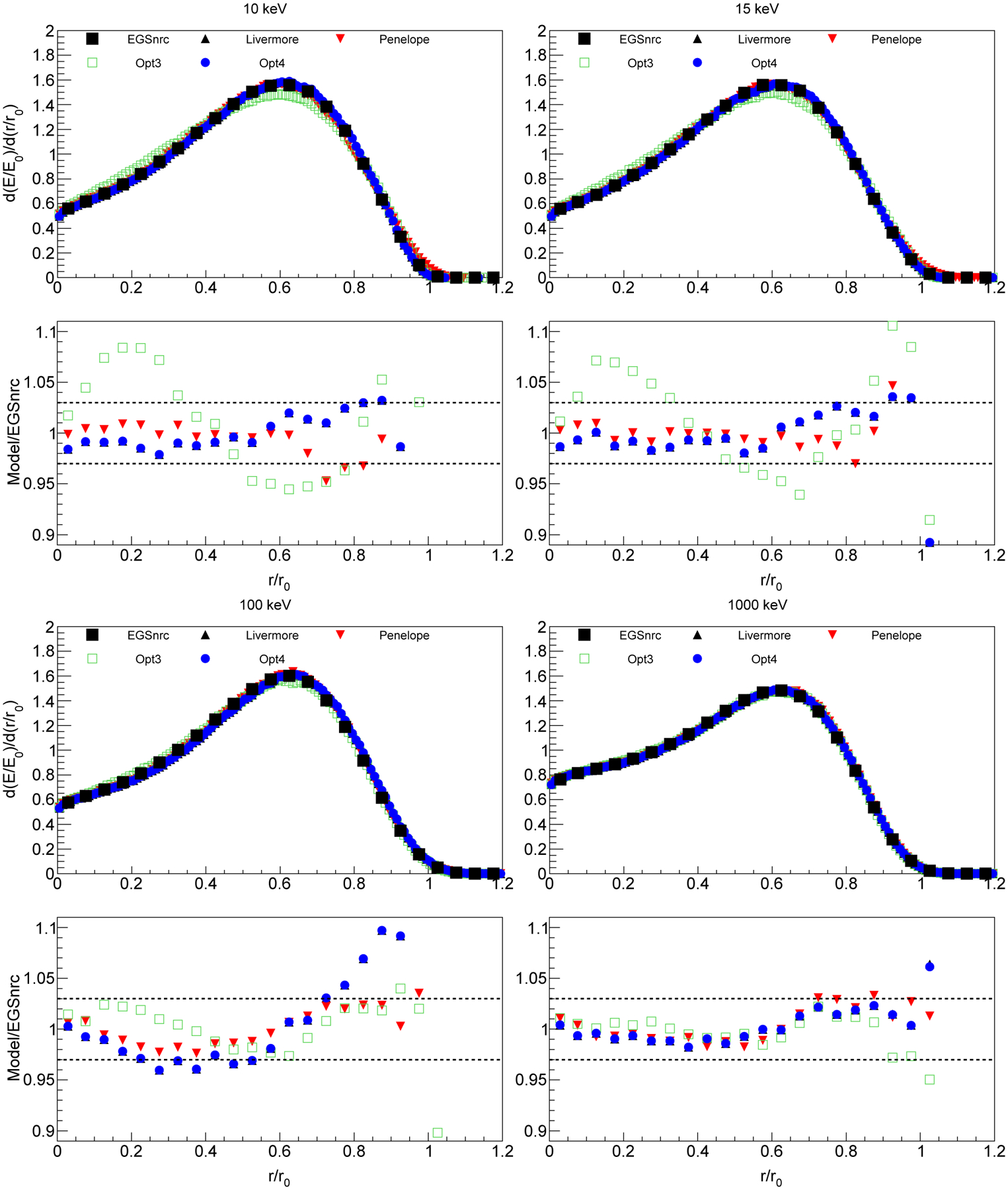
Scaled DPK distributions for incident electrons of 10, 15, 100 and 1000 keV in liquid water, simulated using the five Geant4 EM physics constructors. Ratios of Geant4 and EGSnrc results are reported as well. Dashed lines indicate an agreement of 3%, which corresponds to the statistical uncertainty affecting the Geant4 Monte Carlo simulation results.

In the case of Opt4, Livermore and Penelope constructors, one can observe a better agreement (within approximately 3%, corresponding to the statistical uncertaity of the Geant4 simulation results) with EGSnrc simulation data at all incident energies, thanks to the Goudsmit-Saunderson (GS) multiple scattering model (Incerti et al 2018a [38]), which has been recently introduced in those three physics constructors (in Geant4 version 10.5, as the best alternative to the G4UrbanMscModel). This agreement is obtained under the condition that energy loss fluctuations are ignored in Geant4. Indeed, EGSnrc simulation data do not take into account these fluctuations. Such agreement is not observed when energy loss fluctuations are taken into account in the Geant4 simulations (data not shown). This underlines that, under this condition, the GS model used in the three above constructors is able to perform as EGSnrc and can provide more accurate simulation data. It remains however impossible to fully validate such simulations in the absence of experimental data in liquid water in this energy range. At higher incident electron energies, effects of energy loss fluctuations are not important and Geant4 Opt4 with GS model and EGSnrc results agree well, so it is possible to conclude that both simulation tools (on the one hand Geant4 Opt4 constructor with GS model, and EGSnrc on the other hand) can be regarded as a gold standard for such simulations.

We show in this study the full benefit of the newly implemented GS model for the simulation of electron multiple scattering in liquid water, when compared to EGSnrc Monte Carlo code.

H. Microdosimetry test

1. Introduction

Microdosimetric spectra of lineal energy (or specific energy) are historically being used for describing radiation quality (see ICRU Reports 40 [73] and 36 [74]), and many theoretical estimates of the Relative Biological Effectiveness (RBE) of therapeutic beams are based on such calculations (Amols et al 1986 [75], Lindborg et al 2013 [76]).

The use of the Monte Carlo method for the calculation of stochastic energy deposition in an irradiated volume is facilitated by the use of condensed-history models in order to reduce simulation time, especially when we are dealing with radiotherapeutic energies. A dedicated example available in the Geant4 extended examples, called microyz, offers a way to calculate microdosimetric spectra in liquid water target spheres.

Systematic studies of the microdosimetric performance of the low-energy condensed-history models available in Geant4 (i.e., Livermore and Penelope) and the track structure models available in Geant4-DNA ( Incerti et al 2018b [77], Bernal et al 2015 [78], Incerti et al 2010a [79], Incerti et al 2010b [80]) have been recently carried out for submicron volumes for the energy range 50 eV—10 keV (Kyriakou et al 2017 [20], Lazarakis et al 2018 [81], Kyriakou et al 2019 [82]). Here we investigate the microdosimetric performance of the Opt4 constructor at energies of radiotherapeutic interest (10 keV – 1 MeV) in terms of calculating the frequency-mean lineal energy in liquid water spheres with a diameter of 1 μm (ICRU sphere). This test has been included in the G4-Med benchmarking system for regression testing purposes only. The test has the name microyz in the geant-val web interface [12].

2. Simulation setup

The extended example microyz was used to calculate the probability density function of lineal energy by scoring the energy deposited by monoenergetic electrons within target spheres of liquid water (1 μm diameter) randomly overlapping their track. The procedure of scoring the energy deposition is provided in detail in Kyriakou et al 2017 [20]. For all simulations the global production cut was set equal to the tracking cut.

The effect of the step-size limit and tracking cut is also investigated. To obtain a statistical uncertainty below 1–2% the number of electron tracks simulated was 10⁶ for electron energies up to 100 keV and 10⁵ above 100 keV.

3. Results and Discussion

Figure 10 presents the frequency-mean lineal energy as a function of incident energy for 10, 50, 100, 500 and 1000 keV electrons using two different values for the tracking cut, 100 eV and the commonly used value in condensed-history simulations of 1 keV.

FIG. 10.

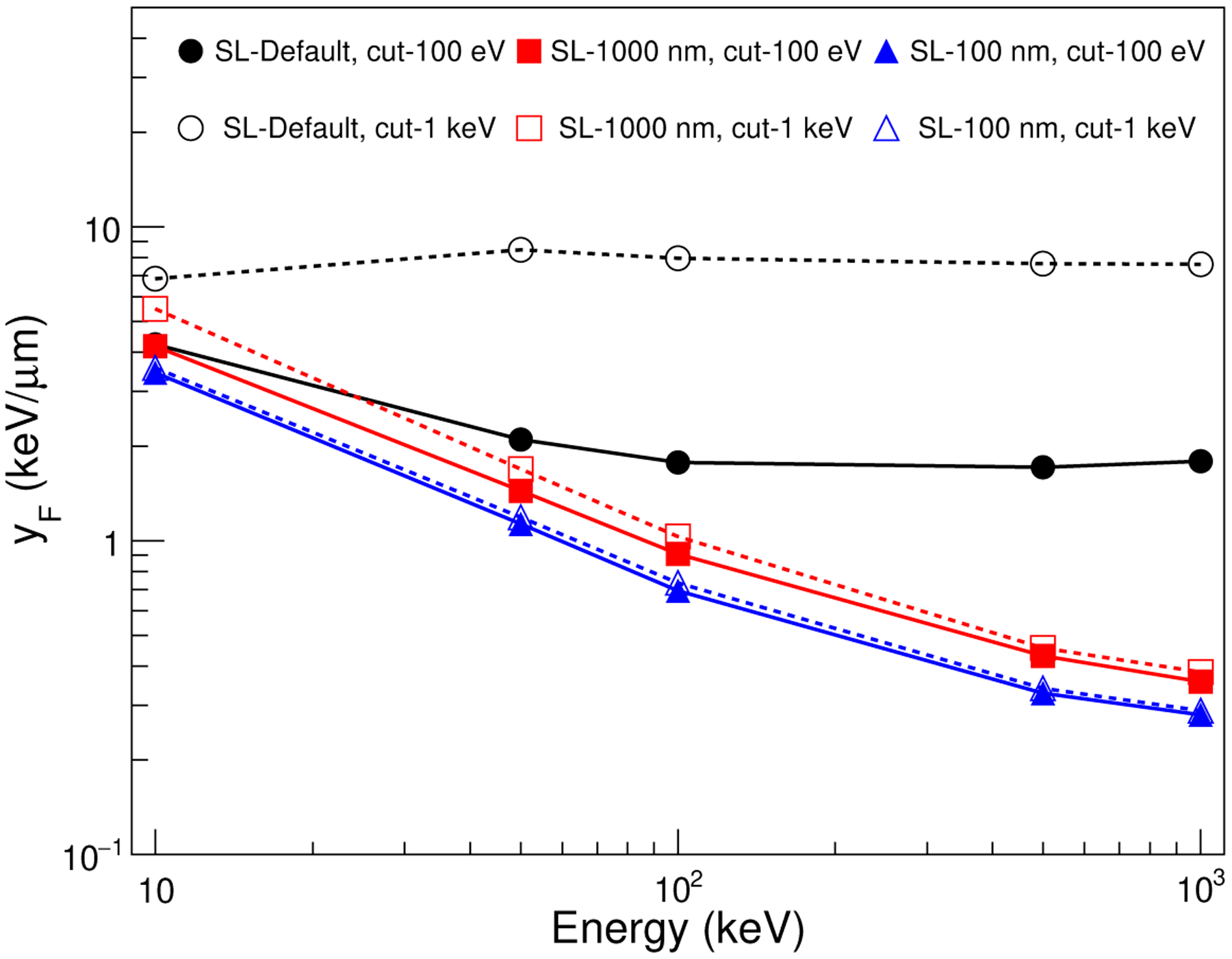
Frequency-mean lineal energy as a function of the incident electron energy, using two different values for the tracking cut 100 eV and 1 keV. SL is the step-size limit. SL was set equal to 1 mm (default value for this test), 1 μm and 100 nm. Error bars are not included since they are smaller than the symbols. The plot demonstrates that SL should be substantially less than the size of scoring volume.

Results are presented for three different step-size limits (called SL in the Figure), the default step-size limit which for this test is equal to 1 mm, a step-size limit equal to the sphere diameter (1 μm), and a small step-size limit equal to 1/10 the sphere diameter (100 nm).

We observe that for both values of the tracking cut (1 keV and 100 eV), the default step-size limit (equal to 1 mm in the present energy range) results in a significant overestimation that increases with electron energy (at 1 MeV incident electron energy it reaches a factor of 6 for the 100 eV cut, and a factor of 26 for the 1 keV cut). A step-size limit equal to the sphere diameter (1 μm) also results in sizeable overestimation (20–30% for 100 eV cut and 30–50% for 1 keV cut) compared to the small step-size limit. The influence of the tracking cut is reduced when smaller step-size limits are chosen. For example, with the small step-size limit examined (100 nm), decreasing the tracking cut from 1 keV to 100 eV affects the frequency-mean lineal energy by less than 7%.

The test microyz assumes by design discrete simulation, that is, each individual interaction leading to any modification of the particle trajectory (energy, direction) is modelled explicitly as point-like interaction and is recorded during the simulation. This assumption is broken when employing the Condensed History (CH) simulation technique which leads to the observed sensitivity to the CH step size. The extent of this artificial step size dependence is determined by the relation of the step size distribution to the size of the target sphere. Reducing this step size dependence requires that several steps are done by electrons inside the scoring sphere which may be achieved by defining a step-size limit less than the scoring sphere diamensions. For the commonly used tracking cuts studied in the present work (100 eV to 1 keV), a safe value for the step-size limit is equal to the 1/10 of sphere diameter.

I. Brachytherapy test

The Brachytherapy Geant4 advanced example is used to calculate the dose rate distribution of a high dose rate brachytherapy ¹⁹²Ir source in water. We compared the results of the simulation to the reference data published in Granero et al 2006 [83], which were obtained with Geant4 version 7.1. Therefore, the test has a regression testing focus and is available in the geant-val interface [12] with the name Brachy-Ir.

1. Simulation setup

The ¹⁹²Ir Flexisource, described in Granero et al 2006 [83], has been modelled in the center of a water box (modelled as G4_WATER) with 30 cm size. The photon radiation field, detailed in Granero et al 2006 [83], is emitted from the iridium radioactive core. Opt0, Opt3, Opt4, Livermore and Penelope have been tested. A global production cut was fixed equal to 0.05 mm. A Geant4 scoring mesh was defined to calculate the energy deposition in the plane containing the source. The plane is subdivided in voxels with size equal to 0.25 mm along x, y and z. 10⁹ histories were simulated to obtain a statistical uncertainty of 1.5% in the results. The same statistical uncertainty affects the reference data (Granero et al 2006 [83]).

2. Results and Discussion

Figure 11 shows the radial dose rate distribution about an ¹⁹²Ir brachytherapy source, as a measure of the energy deposition per unit of mass, along the transverse axis of the source, 90° from the source axis.

FIG. 11.

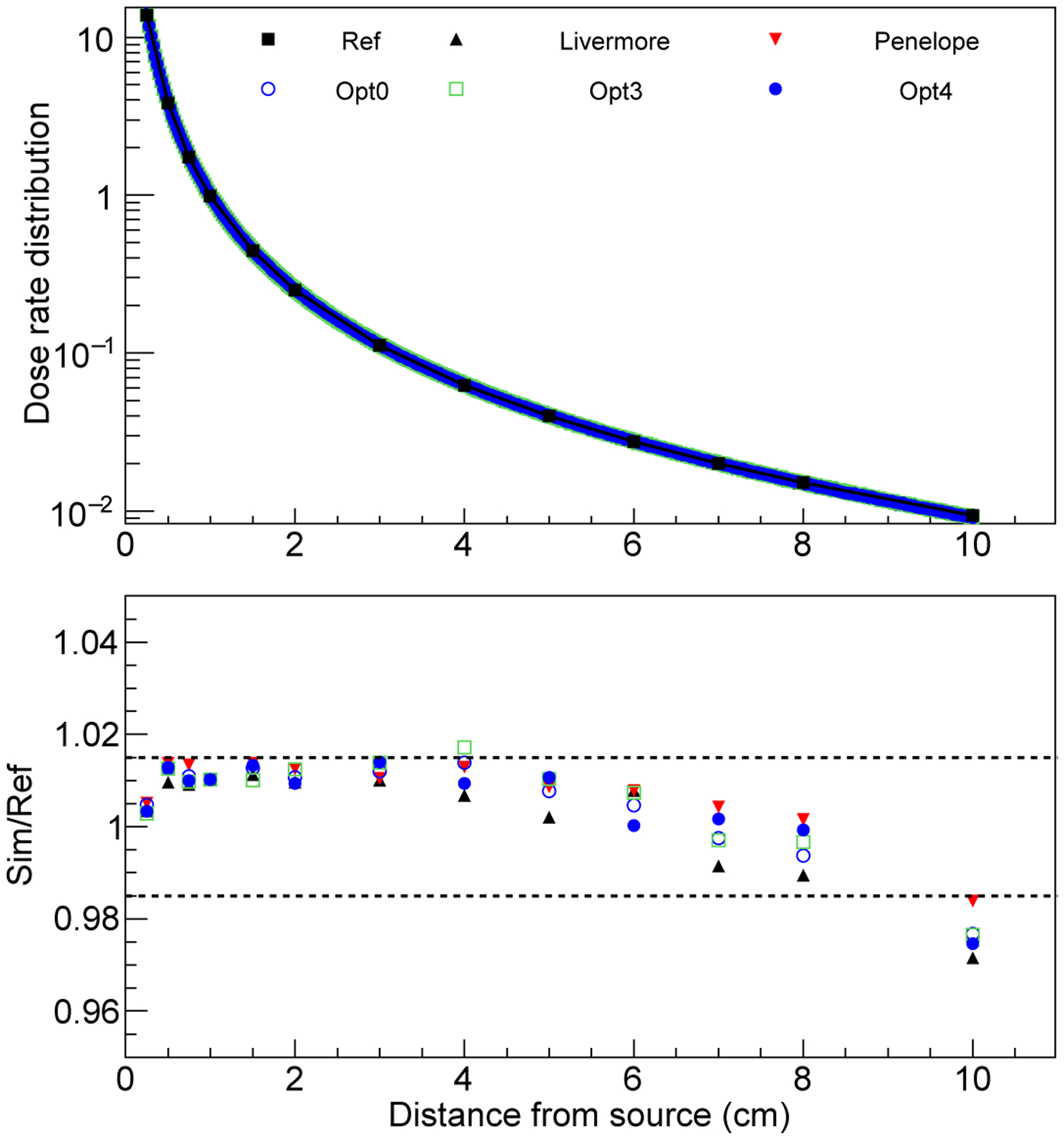
Radial dose rate distribution with respect to r, distance from the center of the ¹⁹²Ir brachytherapy source. The radial dose distribution is normalised at r=1 cm. Black squares in the top figure represent the reference data (from Granero et al 2006 [83]), the statistical uncertainties of the data are within the symbols. The bottom plot shows the ratio of the Geant4 simulation results and the reference data. The dashed lines indicate the statistical uncertainty affecting both the simulation results obtained with Geant4 10.5 and the reference data published in Granero et al 2006 [83], obtained with Geant4 7.1.

As it can be observed in Figure 11, the simulation results obtained with any Geant4 EM constructor agree with the reference within the uncertainty of the simulation data σ_ref (1.5%), for almost all points, up to a distance of 8 cm from the radioactive core. At 10 cm depth the agreement between Geant4 results and the reference data is within 3% (corresponding to 2 σ_ref) for all the EM constructors. No recommendation to use any of the EM constructors can be done at this stage with this test, because the reference data are derived from Geant4 as well (Geant4 7.1).

J. Monoenergetic x-ray internal breast dosimetry test

An accurate and controlled evaluation of the radiation dose delivered during x-ray-based breast imaging is part of quality control procedures (Perry et al 2006 [84]) and necessary for risk estimation (Dance et al 2016 [85]). This simulation aims to compare the radiation dose predicted by means of Geant4 and experimental measurements performed at the SYRMEP beamline of the ELETTRA synchrotron light source (Trieste, Italy). Dose measurements were performed using thermoluminescent dosimeters, TLD-100H (ThermoFisher Scientific, Waltham, MA, USA), in absolute terms and down to the local deposition level, in a mammographic acquisition setup installed at the SYRMEP beamline (see Castelli et al 2011 [86]). The test has the name Mammo in the geant-val interface [12]. Details about the test and the experimental procedure can be found in Fedon et al 2018a [21] and 2018b [22].

1. Simulation setup

The geometry implemented in the simulation is shown in Figure 12. A homogeneous semi-cylindrical breast phantom (with the dimensions of 18 cm × 10 cm) consisting of four 1 cm-thick slabs was positioned within the plates of the compression system. The phantom (CIRS Inc.,Norfolk, VA, USA) reproduces the x-ray attenuation property of a breast with a 50% adipose and 50% fibroglandular tissue composition. Monoenergetic, parallel 20 keV photons are emitted from a rectangular, planar x-ray source (20 cm × 12 cm) towards the breast phantom. This source geometry models the monoenergetic nature of the SYRMEP beamline of the ELETTRA synchrotron when the double-crystal Si monochromator is set to 20 keV. The scored physical quantity in the simulation was the dose deposited in thirty sensitive volumes (i.e. each TLD) positioned on the xy phantom plane at four different phantom depths (i.e. the scoring planes shown in Figure 12). The TLDs were modeled in terms of physical dimensions (i.e. 3.2 mm × 3.2 mm × 0.38 mm) and relative chemical composition (99.5% LiF, 0.2% Mg, 0.004% Cu and 0.296% P) according to the manufacturer. For each simulation, 2 × 10⁹ photons were simulated to obtain a statistical uncertainty lower than 1% in all the scored quantities, estimated using the method of Sempau et al 2001 [87]. The experimental TLD procedure and the uncertainty analysis is described in detail in Fedon et al 2018a [21]. To normalize the photon fluence in the simulation to that used in the experiments, a scale factor was used, defined as the ratio between the experimentally kinetic energy released per unit mass in air (kerma) and the simulated air kerma, analytically evaluated in the Monte Carlo simulation. The constructors Opt0, Opt3, Opt4, Livermore and Penelope were tested. A global production cut of 0.7 mm was adopted.

FIG. 12.

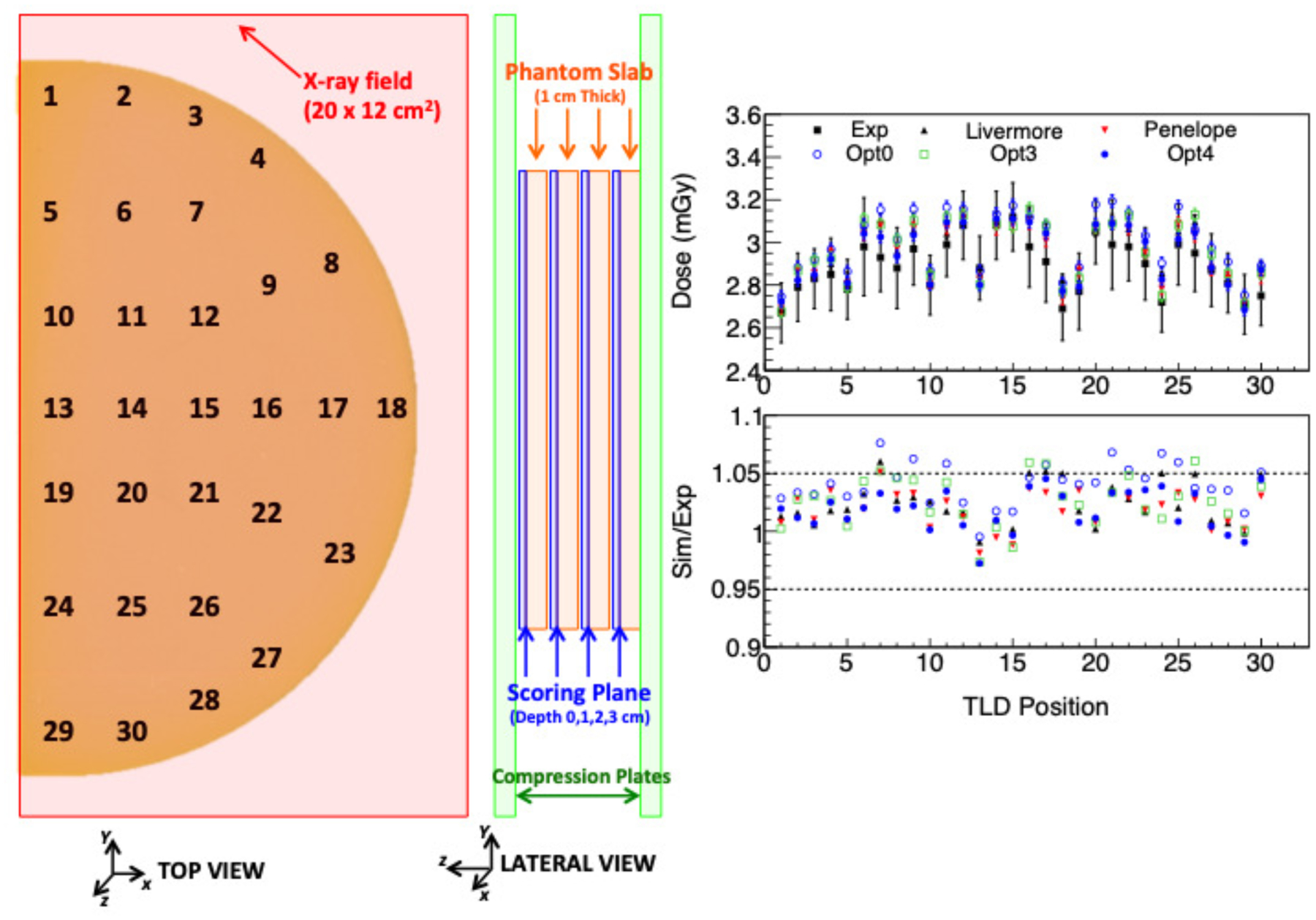
Left and center: Dosimeter placement and irradiation geometry modelled in the test. Drawings are not to scale. Right: Dose comparison between experimental data (black symbols) and the five Geant4 EM physics constructors for the depth of 3 cm. All the other depths are available in the geant-val interface. The black error bars represent the combined standard experimental uncertainty (with a coverage factor, k=1), while the color ones are referred to the simulations data. The bottom plot shows the ratio between Geant4 and experimental data. The black dashed lines represent the 5% accuracy, a typical threshold accuracy considered in breast dosimetry.

2. Results and Discussion

Dose comparison results for the depth of 3 cm are presented on the right side of Figure 12. Data for the other depths can be found on the geant-val web interface [12]. In general, all physics constructors produce results that agree with each other within the combined experimental uncertainty. The mean combined uncertainty for the depth of 3 cm is 5.7% (uncertainty range from 5% to 7.7%)(Fedon et al 2018a [21]). It should be pointed out that a systematic bias appears to be present, since the MC data results consistently overestimated the experimental data. This overestimation is, however, within the combined experimental uncertainty. Among the Livermore, Penelope, Opt3 and Opt4 constructors, no clear trend is observed that can suggest the use of one over the others, since the results are within an accuracy of 5% with only few exceptions for Opt3 (ratio plot in Figure 12). However, we noticed that the performance of Opt0 worsens with increasing depth, confirming previously observed trend (Fedon et al 2015 [88]). A maximum relative difference of 7.7% is observed at 3 cm depth when using this constructor (position 7 in Figure 12), whereas with the other EM constructors there is a better agreement with a largest difference of 6%. An accuracy of 5% might be considered large for a MC benchmark. However, in the case of breast dosimetry, this is a remarkable results considering the difficulties and inherent uncertainty in these types of measurements, where the recommended uncertainty range ±12.5% (Fedon et al 2018a [21]). Thus, these results, within the experimental uncertainty, can be considered a valid benchmark for this specific application.

IV. HADRONIC PHYSICS BENCHMARKING TESTS

Hadronic interactions are paramount in hadron therapy. In proton therapy incident protons generate a secondary neutron field which scatters in the patient producing recoil protons, which will then deposit energy in the patient outside the target tumor and potientally in organs at risk (Paganetti 2002 [89]). In addition, it recently became evident that the few fragments generated in proton-tissue interactions cannot be neglected (Tommasino et al 2015 [90]) because they can affect the average Linear Energy Transfer (LET) values, thus changing the biological outcome. Such fragments are mainly produced at the entrance in the patient where the energy of the protons is higher (Tommasino et al 2015 [90]).

In carbon ion therapy, a beam with an initial energy of 400 MeV/u, will have approximately 70% of the initial carbon ion beam undergo fragmentation before reaching the tumor target. Such fragments contribute to the dose in-field and are responsible for the dose delivered out-of-field, i.e. laterally to the beam and beyond the Bragg peak (Böhlen et al 2010 [91]). The total contribution to the dose is approximately 30% for a carbon ion spread out Bragg peak with a maximum energy of 290 MeV/u. It is therefore crucial to benchmark the hadronic physics component of Geant4, which is often used as Monte Carlo code for hadron therapy. An accurate description of the same physical interactions is important for radiation protection studies as well.

This section describes tests in G4-Med where only hadronic physics processes and models are tested and the electromagnetic physics is not considered in the simulation (Section V is dedicated instead to tests which activate both the electromagnetic and the hadronic physics). The tests described in both sections (here and Section V) were performed in the energy range of interest for hadron therapy.

The test of section IV A benchmarks the total hadronic inelastic cross section, which is described with the Glauber-Gribov model in Geant4 (see the Geant4 Physics Reference Manual [28]) against experimental measurements.

The tests subject of sections IV B and IV C benchmark different hadronic ion inelastic scattering constructors G4IonBinaryCascade, G4IonQMDPhysics and G4IonINCLXXPhysics, to describe the final state of carbon ion hadronic inelastic interactions. Table VII summarises the main features of the three constructors modelling ion fragmentation under study. It is important to note that the constructors adopt the same total inelastic cross section based on the Glauber-Gribov model, while providing different descriptions of the final state of the interactions (yield, energy and angular distributions of the secondary particles). The three constructors handle the interactions of deuteron, triton, alpha particle, ³He and heavier nuclei.

TABLE VII.

Physics models activated in the ion hadronic inelastic scattering constructors under investigation.

Constructor	Physics models
G4IonBinaryCascade	G4BinaryLightIonReaction* for E < 4 GeV/u		FTF for E > 2 GeV/u
G4IonQMDPhysics	G4BinaryLightIonReaction* for E < 110 MeV/u	QMD for 100 MeV/u < E < 10 GeV/u	FTF for E > 1 GeV/u
G4IonINCLXXPhysics	INCL for E < 3 GeV/u		FTF for E > 2.9 GeV/u

^*:the G4BinaryLightIonReaction activates the Geant4 Precompound Model (G4PreCompoundModel, Geant4 Physics Reference Manual [28]).

G4IonBinaryCascade (BIC) activates the LightIonBinaryCascade, which describes the interaction between a projectile and a single nucleon of the target nucleus interacting in the overlap region as Gaussian wave functions (Folger et al 2004 [92]).

G4IonQMDPhysics activates the Quantum Molecular Dynamics (QMD) model. In this case all nucleons of the target and projectile have their own wave function (Koi et al 2010 [93]).

G4IonINCLXXPhysics uses the approach of the Liège intranuclear-cascade model called here INCL (Boudard et al 2013 [94], Mancusi et al 2014 [95]). The target nucleons are treated as a free Fermi gas in a static potential well, whereas the projectile is modelled without Fermi motion. As result of this asymmetric treatment, the projectiles which can be modelled with INCL are limited to mass numbers less than A=19; otherwise, when the target mass is below A=19, target and projectile are interchanged internally and when both mass numbers are above A=19, the fragmentation interaction is modelled with BIC.

In the high energy range, all the ion hadronic inelastic scattering constructors adopt the Fritiof parton string model (FTF) (Yarba et al 2012 [96]). In the energy overlap region (see Table VII), an interpolation between the two models is done.

A. Test of Nucleus-Nucleus hadronic inelastic scattering cross sections

This test calculates the total cross section of hadron-nucleus and nucleus-nucleus collisions. The cross sections are then compared to reference experimental measurements publicly available in the Experimental Nuclear Reaction Data (EXFOR) database (Zerkin et al 2018 [97]). EXFOR provides libraries containing an extensive compilation of experimental nuclear reaction data.

The total inelastic scattering hadronic cross sections are calculated for incident protons and carbon nuclei. The test was named NucNucInelXS in the geant-val web interface [12].

1. Simulation setup

The benchmark test retrieves the total hadron-nucleus and nucleus-nucleus inelastic cross sections, which are stored in a data table via the use of the class G4HadronicProcessStore in the initialisation phase of the simulation. The data table is then compared to the reference data. Only the Geant4 prebuilt physics list QGSP_BIC was benchmarked in this test as the total inelastic hadronic cross section in all the hadronic physics constructors, used in any prebuild Geant4 physics list, are based on the Glauber representation with the Gribov screening correction on inelastic screening (GG model) (Kopeliovich 2003 [98], Fesefeldt 1985 [99], Grichine 2010 [100]).

The total inelastic scattering cross sections of $\text{p}{+}_6^{12}\text{C}$, $\text{p}{+}_8^{16}\text{O}$, $\text{p}{+}_{13}^{27}\text{Al}$, $\text{p}{+}_{20}^{40}\text{Ca}$, ${}_6^{12}\text{C}{+}_6^{12}\text{C}$, and ${}_6^{12}\text{C}{+}_{13}^{27}\text{Al}$ are compared with the experimental data available in EXFOR. Such reactions were selected because of relevance for hadron therapy and because EXFOR provided an adequate number of reference experimental data.

2. Results and Discussion

Figure 13 shows the total inelastic cross sections calculated by means of the QGSP_BIC, as a function of the kinetic energy of the projectile, compared to the experimental data of the EXFOR database. Overall, for both incident protons and carbon ions, an agreement within 10% was observed for most of the incident projectile energies. Significant differences (20%−40%) were found for proton energies below 2 MeV in the case of a carbon target. These differences are caused by the large variations in the experimental inelastic cross sections for p+¹²C, likely due to resonances that enhance the cross section, particularly near 10.5 MeV proton energy (e.g. Dyer et al 1981 [101], Davids et al 1971 [102]). These variations will tend to arise for low energy proton induced reactions, particularly for light targets where the density of states is low. In the case of ¹²C+²⁷Al, the data were consistently overestimated of about 10%. This reaction should be further investigated.

FIG. 13.

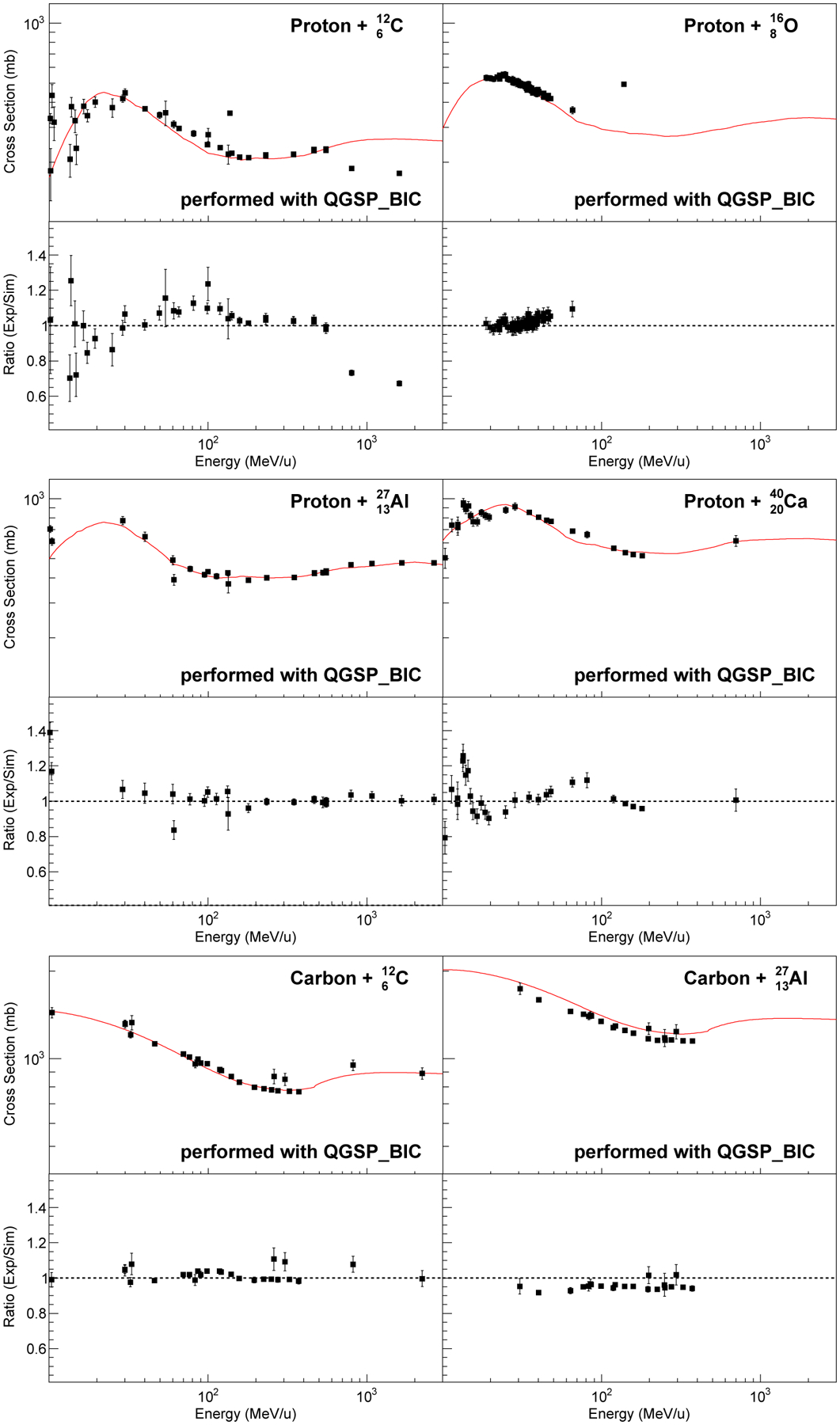
Total hadronic inelastic scattering cross sections as a function of the kinetic energy of the projectile, calculated by means of the QGSP_BIC physics list. To note, differently from the other figures depicting the results of the tests of G4-Med, in the bottom plot ratios of reference data and Geant4 simulation results (and not the other way round) have been plotted for clarity reasons. Red curve: Geant4 cross section; data points: EXFOR reference experimental data.

B. 62 MeV/u ¹²C fragmentation test

This test concerns the nuclear interaction models available in Geant4 for low energy carbon ions. The name of the test is LowEC12Frag in the geant-val web interface [12]. The models were benchmarked against double-differential cross sections of the secondary fragments produced in the ¹²C fragmentation at 62 MeV/u on a thin carbon target. This dataset has been acquired from De Napoli et al 2012 [103].

1. Simulation setup

As described before, the two models available in Geant4 at low energy are the Binary Light Ions Cascade (BIC) (Folger et al 2004 [92]) and the Liege Intranuclear Cascade (INCL) (Boudard et al 2013 [94], Mancusi et al 2014 [95]). There is a third model available in Geant4 to simulate the first part of a nuclear interaction, namely, the Quantum Molecular Dynamics (QMD) (Koi et al 2010 [93]). However, QMD has, in its default physics constructor class (G4IonQMDPhysics), a lower energy threshold at 100 MeV/u. Below this threshold it uses BIC. Therefore, in this test, we decided not to benchmark the QMD model. This selfsame benchmark with QMD included, performed with Geant4 9.4.p01, can be found in Mancini et al 2018 [23].

In order to reduce the computation time, all interactions but the hadronic inelastic ones have been switched off. All secondaries are discarded after being produced and the target is much longer than the hadronic inelastic interaction length. In this way, all primaries undergo an inelastic interaction, which is also the only process simulated. Secondaries are saved immediately after being produced and the event interrupted. Data are selected to match the geometrical acceptance and the energy resolution of the experiment. The obtained spectra are scaled by the total inelastic cross section.

2. Results and discussion

Figure 14 shows the comparison of the double-differential cross sections of α-particles production at different emission angles.

FIG. 14.

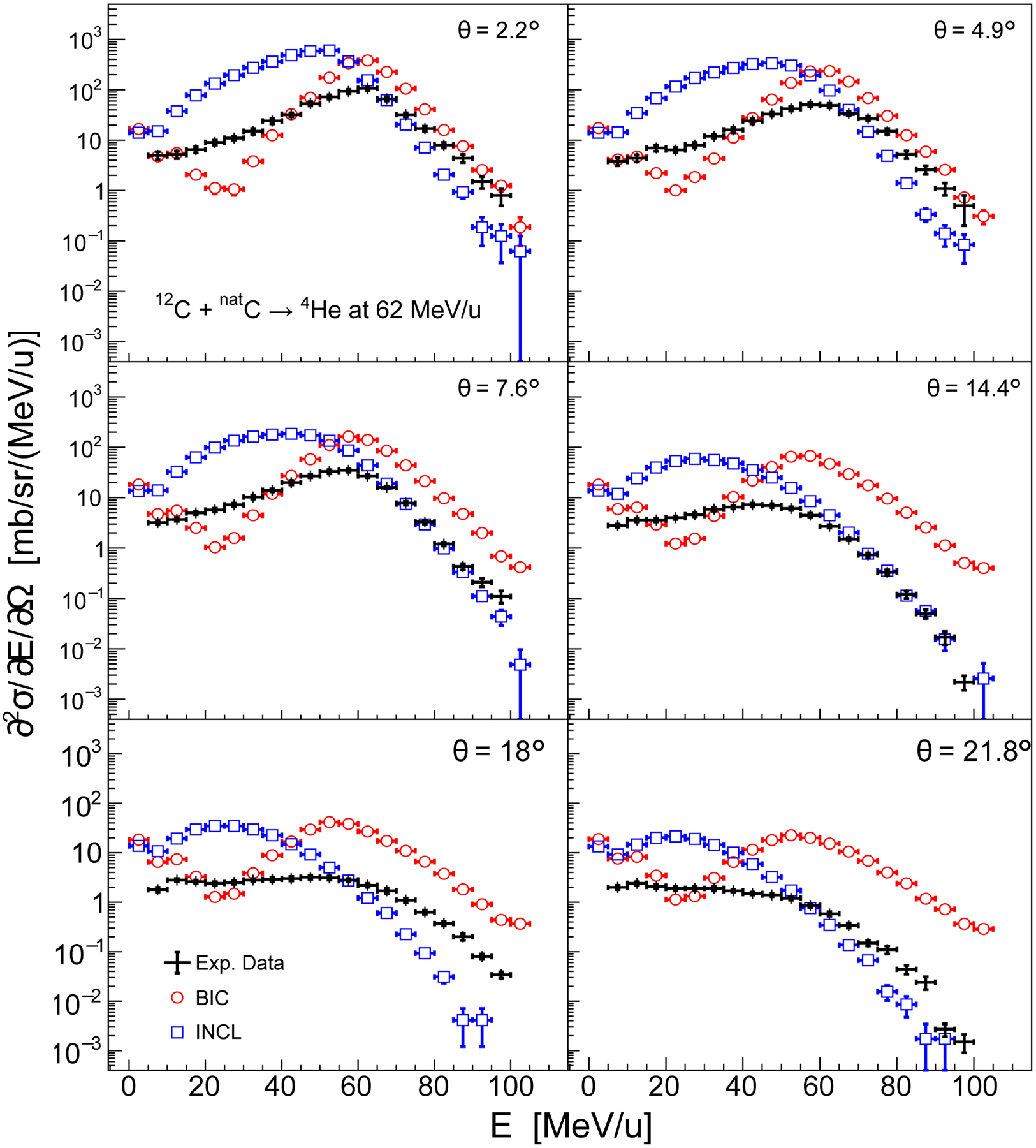
Double-differential cross sections measured at different angles of α-particle production in the ¹²C interaction with a thin C target at 62 MeV/u as a function of the α-particle kinetic energy. Experimental data from De Napoli et al 2012 [103] (in black) are compared with the two models available in Geant4 for ion interactions at this energy, namely INCL (in blue) and BIC (in red).

BIC shows a doubly peaked structure. The one at higher energy is due to the fragment produced in the statistical de-excitation of the projectile remnant, while the lower energy one comes from the de-excitation of the target. BIC underestimates the formation of fragments in the mid-rapidity region, here at roughly 30 MeV/u of kinetic energy of the emitted fragment, by up to one order of magnitude at small angles. Its minimum is approximately two decades smaller than the two neighbours regions at all angles, while the projectile-like and target-like fragments formation is overestimated for all angles. A possible explanation could be that BIC approach is based on a time-invariant optical potential and this leads to an underestimation of the formation of a neck fragmentation events (Colonna et al 1995 [104], Toro et al 2006 [105]) in the overlapping region, roughly at mid-rapidity in semi-central reactions. On the contrary, INCL shows a single distribution peaked at lower energy, with respect to the experimental peak. The INCL predictions overestimate by around a factor ten the production of α-particles below 62 MeV/u but are compatible with the experimental data for particles produced with higher kinetic energy. This could be due to its complete-fusion model.

Here we show only the plot with the comparison of the α-particle production. All other plots, with the different fragments, can be found at the geant-val web interface [12].

In conclusion, the results show that both of the tested models, BIC and INCL, exhibit limitations in reproducing doubly differential cross sections of fragments produced in the interaction of ¹²C with a thin carbon target. Efforts are underway to interface new models to Geant4 dedicated to nuclear interactions below 100 MeV/u (Mancini et al. 2019 [106] and Ciardiello et al. 2020 [107]).

C. 300 MeV/u ¹²C ion charge-changing cross section test

The goal of this test is to validate the partial and total charge-changing cross sections of ¹²C ions with energy 300 MeV/u as simulated by Geant4 against experimental data published in the literature by Toshito et al 2007 [24], obtained with an emulsion plate in the NIRS P152 experiment. The test is named C12FragCC in the geant-val web interface [12].

The partial charge-changing cross section to B, Be and Li fragments is about (428±21) mb, while the total is (1183±52) mb (including the production of B, Be, H, He, Li, N, O, α, deuteron, proton, neutron and triton), accounting for approximately 36% with respect to the other ion species in the experiment. Therefore, a correct modelling of the carbon charge-changing process is needed for an accurate calculation of the dose in carbon ion therapy, especially out-of-field where organs at risk may be located, the LET and the radiobiological effectiveness (RBE).

1. Simulation setup

In this simulation, all electromagnetic processes and decay physics are switched off and only hadron and ion transport processes are used to retrieve the carbon ion charge-changing cross section. The target geometry is a cubic water phantom with a 10 m length. The water is defined as G4 WATER in the Geant4 simulation. Carbon ions are irradiated from the surface of the phantom.

Only projectile-like fragments were considered in this work. Target-like fragments are also important to the dose, however it is difficult to measure their cross section in an experiment. When an interaction occurs in the simulation, the distance from the initial point to the interaction point is summed up as the track length only for projectile-like fragments which can be identified as they travel to the forward region (momentum along the initiated direction > 600 MeV/c/u).

The partial cross sections of B, Be and Li isotopes were calculated by means of the simulation. This choice was dictated by the availability of experimental data in Toshito et al 2007 [24].

2. Results and Discussion

The results of the test are shown in Figure 15 and summarised in Table VIII. The partial cross sections calculated by means of the G4IonQMDPhysics of B, Be and Li isotopes are 144.1, 77.90 and 97.66 mb, respectively. An agreement within the uncertainty of the reference data was observed for the total ¹²C charge-changing cross section and for the Li isotope partial cross section. Differences of approximately 18% and 34% were found for the production of Be and B isotopes, respectively. The isotope production cross sections have a similar trend when substituting QMD with either BIC or INCL. The total fragmentation cross section is almost the same for all the ion physics constructors.

FIG. 15.

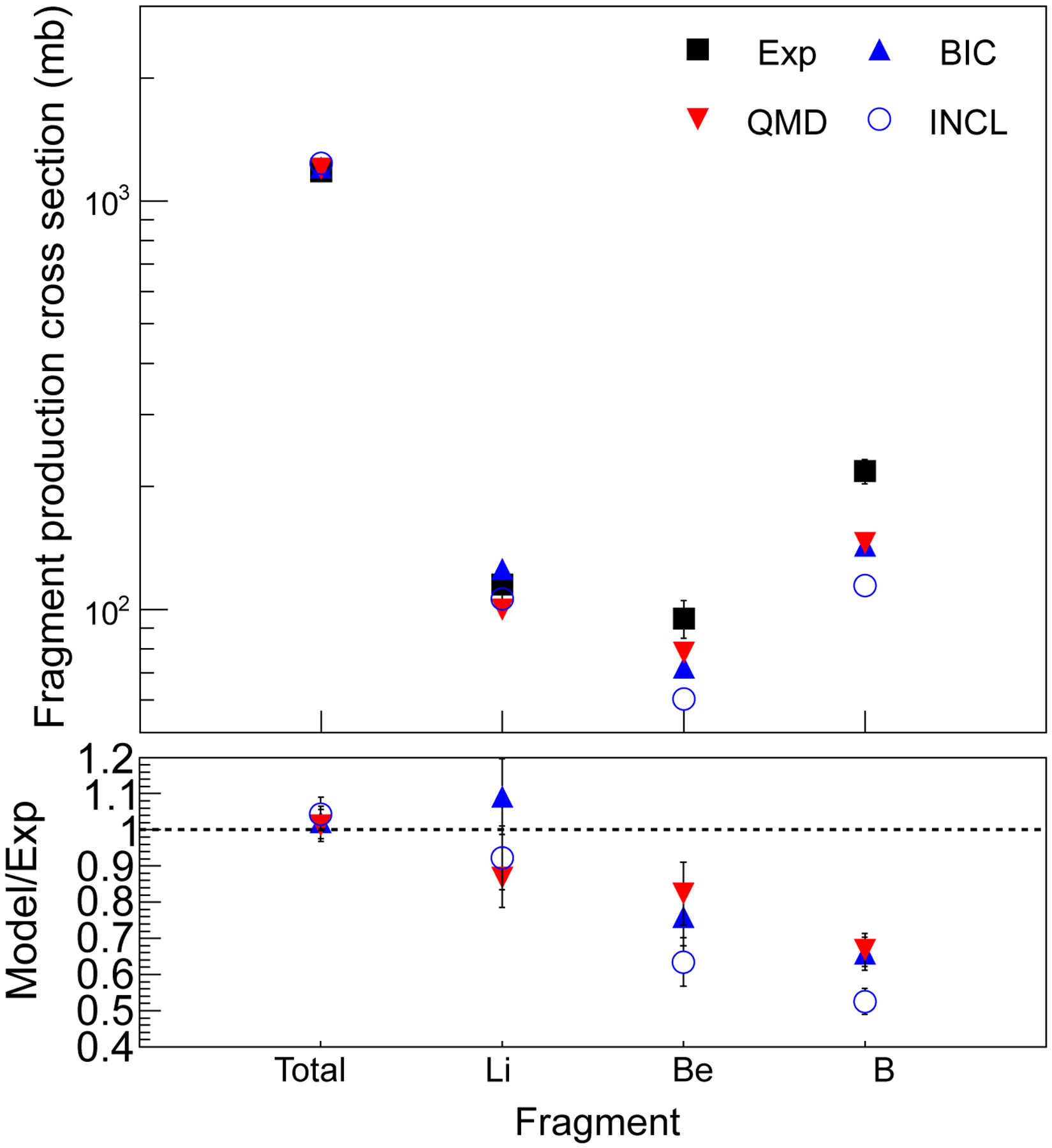
Comparison of Geant4 against experimental data for ¹²C total and partical charge-changing cross sections. The total charge-changing cross-section includes the production of B, Be, H, He, Li, N, O, α, deuteron, proton, neutron and triton. The energy of the incident ¹²C ion beam is 300 MeV/u.

TABLE VIII.

Differences between Geant4 simulation results and the reference experimental data published in Toshito et al 2007 [24]. σ_ref represents the uncertainty of the experimental measurements.

Charge-changing cross section	Geant4 ion fragmentation model
	QMD	BIC	INCL
Total	<1 σref	<1 σref	<1 σref
Li partial cross section	<1 σref	<1 σref	<1 σref
Be partial cross section	18%	26%	38%
B partial cross section	34%	36%	48%

V. ELECTROMAGNETIC AND HADRONIC PHYSICS BENCHMARKING TESTS

The tests included in this section activate both electromagnetic and hadronic physics processes, using pre-built Geant4 physics lists. QGSP_BIC_HP, QGSP_BERT_HP and QGSP_BIC_EMY were tested for the application of Geant4 in proton therapy. Details of those physics lists are reported below in the energy range of interest for proton therapy and summarised in Table IX.

TABLE IX.

Table summarising the main features of the Geant4 pre-built physics lists under investigation. In the case of HP on, the hadronic inelastic scattering of neutrons is described by means of the HP data libraries below 20 MeV (Allison et al 2016 [3]).

Physics List	QGSP_BIC_HP	QGSP_BIC_EMY	QGSP_BERT_HP
EM constructor	Opt4	Opt3	Opt0
Hadron elastic scattering	HadronElasticPhysics
Hadron inelastic scattering	BIC < 9.9 GeV		BERT < 9.9 GeV
Ion elastic scattering	Active		Not active
Ion inelastic scattering	G4BinaryLightIonReaction for E < 4 GeV
HP data libraries	on	off	on
Radioactive decay	on	on	off

In HadronElasticPhysics elastic hadronic scattering of protons and neutrons is modelled by means of the CHIPS model (Kossov et al 2002 [108]). Below an energy of 20 MeV, the High Precision (HP) data libraries are used to model the neutron elastic scattering. For deuteron, triton and α particles the elastic scattering model is based on the Geant3/GHEISHA approach (Fesefeldt 1985 [99]). In both QGSP_BIC_HP and QGSP_BIC_EMY the ion elastic scattering is modelled. The cross section is calculated with the Glauber-Gribov model while the diffuse model describes the final state (documented in Grichine 2010 [109]).

In QGSP_BIC_HP and QGSP_BIC_EMY the hadronic inelastic scattering of incident neutrons and protons on nucleons of the target nuclei is described by means of the Binary Intranuclear Cascade (BIC in Table IX) model, below approximately 10 GeV (Folger et al 2004 [92]). The BIC is followed by the Geant4 Precompound model describing the de-excitation of the remnant nucleus (Allison et al 2016 [3]). This is followed in turn by the evaporation of particles until the nucleus is fully de-excited (see the Geant4 Physics Reference Manual [28]). In QGSP_BERT_HP the proton and neutron inelastic scattering is described with the Bertini model (Wright et al 2015 [110]), which has its own precompound and evaporation models.

In all the investigated physics lists, the LightIonBinaryCascade describes the intranuclear cascade of deuteron, triton, He isotopes and heavier nuclei (Allison et al 2016 [3]). Also in this case the cascade is followed by the de-excitation of the remnant nucleus via the Precompound model and the nuclear evaporation (Allison et al 2016 [3]). HP (see Table IX) means that neutron inelastic scattering, capture and fission are modelled using the HP data libraries below 20 MeV. Particle decay is modelled in the physics lists under study. The radioactive decay is activated by default in the QGSP_BIC_HP and QGSP_BIC_EMY, while it is not included in the QGSP_BERT_HP.

A. 67.5 MeV Proton Bragg curves in water

The accurate calculation of the proton range is essential in Monte Carlo calculations for proton therapy. While submillimeter accuracy in-depth penetration can be achieved by fine tuning of the proton energy, depth-dose curves measured from a proton beam with an energy accurately known are desirable for benchmarking purposes. In this test, the setup for comparing Monte Carlo calculated Bragg peaks with experimental data of submillimeter (< 0.2 mm) uncertainty is described. The test is available in the geant-val web interface [12] with the name LowEProtonBraggBeak.

1. Simulation setup

A 67.5 MeV proton beam with a Gaussian energy spread of 0.4 MeV, and a uniform 5 mm × 10 mm oval spot travels through a tantalum (Ta) foil of either 101.6 μm or 381 μm thickness. The geometry up to and including the water phantom is described in detail in Faddegon et al 2015 [25]. The sensitive region in the water phantom is 5 × 5 × 50 mm³ divided into 1000 slices. The depth-dose curves in water (density = 0.998 g/cm³ and ionization potential I=78 eV [111], see Faggedon et al 2015 [25]) are calculated and then fitted with an analytical expression for the Bragg curve described in Bortfield 1997 [112]. The fitting parameters range, R₀, and spread, s, are compared against the corresponding experimental parameters from depth-dose measurement from Faddegon et al 2015 [25]. The range, R₀, is the depth at 80% distal falloff of the Bragg curve, whereas s is the spread of a Gaussian describing the width of the Bragg peak according to Bortfeld et al 1997 [112].

The physics list included alternatively Livermore, Penelope, Opt3 and Opt4. This test calculates the proton range which depends on the EM physics processes only. Therefore, the hadronic physics component was modelled only by means of the QGSP_BIC_HP as described in Testa et al 2013 [113], where a comprehensive validation of the Geant4 physics list for proton therapy was performed. A global production cut for secondary electrons of 50 μm was used everywhere with exception of the beam plug region. In there, a production cut of 20 μm was used. Simulations using the Bertini hadronic model gave the same results for the four tested EM physics constructors within statistical uncertainty.

2. Results and Discussion

The left side of Figure 16 shows the depth-dose distributions in water for simulated (lines) data and measured data (symbols). In the right side of Figure 16, the differences in Bragg peak spread (s) and range (R₀) are shown in the top and bottom of the figure, respectively. Differences in R₀ were within 2 standard deviations whereas (σ) for the s were within 1 σ_ref, for all the EM constructors. The uncertainties shown in the figure include experimental, fitting and statistical uncertainties from the Monte Carlo simulations. As depicted, the Monte Carlo calculation underestimates R₀ within 0.5 mm, and overestimates s within 0.05 mm.

FIG. 16.

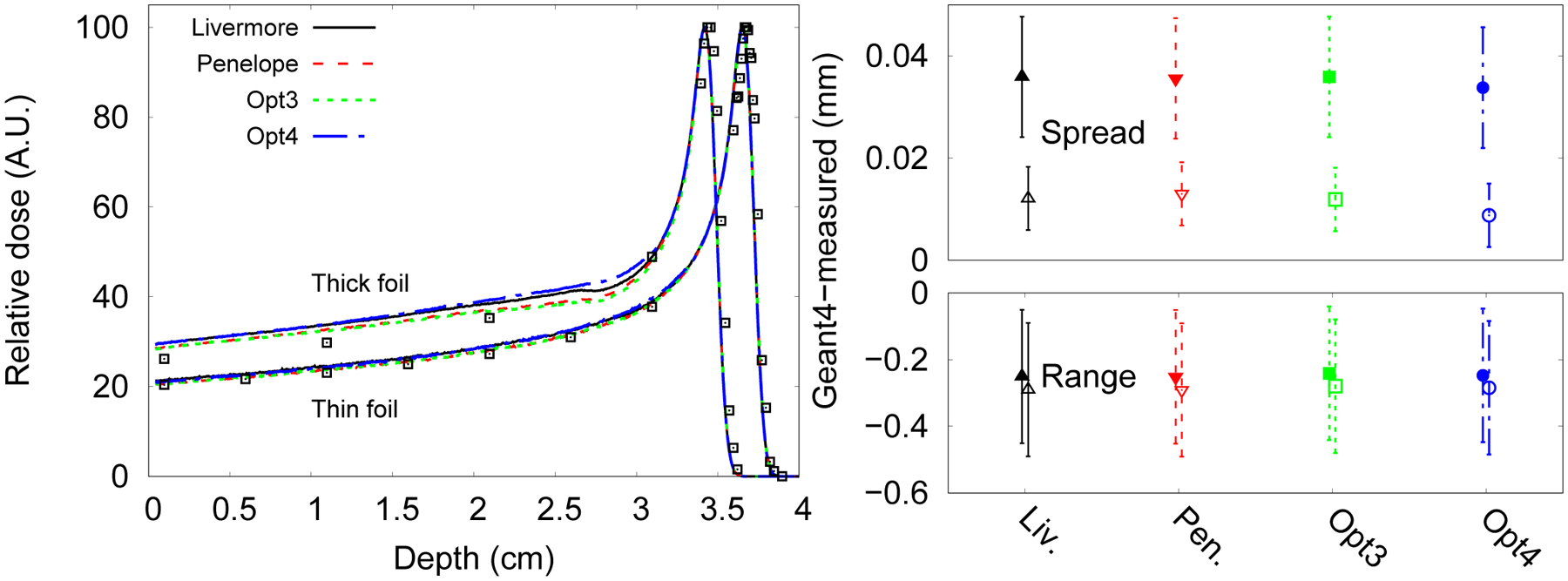
Left: Depth-dose distributions in water for protons scattered with a Ta thin foil and a Ta thick foil calculated with four EM physics constructors, while keeping the hadronic physics modelled by means of the QGSP_BIC_HP. Experimental data is shown with empty squares. Right: Differences between calculated to experimental parameters spread s (top) and range R₀ (bottom) for the thin (empty markers) and thick (filled markers) foils. Errors and error bars represent 1σ and include experimental and Monte Carlo uncertainties.

In the end, the proton range and Bragg curve spread calculated with Geant4 10.05 were in acceptable agreement with the measured depth-dose curves within better than 0.5 mm.

B. Light ion Bragg Peak curves

The accurate modeling of Bragg curves of proton and light ion beams in water is of key importance to ensure code reliability for applications in hadron therapy. In this test, we compare our Geant4 calculations against mean range values estimated experimentally at GSI (Schardt et al 2007 [114]) for proton and ¹²C beams at energies of interest in particle therapy. The test is available in the geant-val web interface [12] under the name LightIonBraggPeak.

1. Simulation setup

The Bragg curve measurements were carried out by means of a water tank, whose thickness could be varied with micrometric accuracy, and two ionization chambers (IC) placed upstream (IC1) and downstream (IC2) in the tank. These measurements were carried out for protons and ¹²C ions, among other beam species, at various nominal energies to provide range-in-water values roughly from 3 to 30 cm. The ratio between the ionization registered by IC2 over that registered by IC1 was used to estimate the mean energy deposition at each depth with respect to the energy deposited at the entrance. According to a previous work (Bichsel et al 2000 [115]), the mean range of the beam was estimated to be at the depth where the distal edge of the Bragg curve was equal to 82% of the peak value, R_d82. More details of the experimental setup can be found in Schardt et al 2007 [114].

For our calculations with Geant4, the geometry consisted of a simple water tank, modelled using G4_WATER material with density corrected according to room temperature (24° C, 0.997 g/cm³). The energy deposition was scored by means of cylindrical volumes with a radius of 28 mm (equal to the radius of the ICs) and a thickness of 50 μm (similar to the water equivalent thickness of both ICs). Pencil beams were defined in our calculations with a mean energy equal to the reported nominal energy; the energy distribution was Gaussian, whose spread was estimated by fitting the width of the experimental distal fall-off, defined from the 90% and 10% of the peak value. For each type of beam, all EM models matched experimental data with the same energy spread, which FWHM was of the order of, or below, 0.2% of the nominal energy in all cases. We tested the electromagnetic physics constructors: Opt0, Opt3, Opt4, Livermore and Penelope; the hadronic physics was activated as defined in QGSP_BIC_HP physics list. Consistent with the experimental data, we calculated the depth, at distal edge, where the energy deposition was equal to the 82% of the maximum; this value was compared with those obtained from the experiments.

2. Results and discussion

Figure 17 shows the absolute differences obtained in the value of R_d82 between measurements (suffix “exp”) and Geant4 calculations (“G4”) as a function of depth in water for protons (125–200 MeV/u) and ¹²C beams (100–400 MeV/u), respectively. In all cases, dose was calculated with statistical uncertainty below 1% (1σ) at the scoring volumes around the peak of the Bragg curve to ensure a small propagation to the calculated R_d82; thus, the uncertainty of R_d82 was estimated to be equal to the scoring volume thickness (50 μm). As for proton beams, the agreement was better than 0.2 mm (≲0.1%) in all cases, which is considered remarkable, given that (1) the precision of the algorithm itself is within 2% and (2) particle therapy calculations require a precision of about 1 mm. As for ¹²C beams, on one hand we could observe that Opt0 showed range deviations of about 1.2%–2.5%, i.e. similar to the precision of the Bethe-Bloch model used. On the other hand, the other EM physics constructors showed deviations about three times smaller, with a maximum absolute difference about 0.8 mm (0.3%) for the largest energy (400 MeV/u), and maximum relative difference of 1.1% for the smaller energy (100 MeV/u). This can be explained by the fact that the ion stopping is calculated in Opt0 by means of an algorithm based on Bethe-Bloch formula, whereas in the other constructors a more precise method is implemented, based on a parameterization of stopping power values published by the ICRU (Sigmund et al 2009 [35]) for some ions and materials, as described in Lechner et al 2010 [116].

FIG. 17.

Absolute differences obtained between the depth at which the energy deposited was 82% of peak, at distal Bragg Peak, calculated with Geant4 (R_d82,G4) and obtained experimentally (R_d82,exp), represented as function of the reported range in water for each beam. Left: Results for proton beams at 125, 150, 175 and 200 MeV/u; right: Results for ¹²C beams at 100, 200 and 400 MeV/u; here, Livermore, Penelope, Opt3 and Opt4 symbols exactly overlap. The estimated uncertainty of R_d82,G4, represented with error bars, was 50 μm in all cases (see main text for details); for ¹²C, symbols were larger than the error bars.

In summary, all electromagnetic physics constructors are able to successfully model the stopping of protons in water, whereas for ¹²C beams only Opt3, Opt4, Livermore and Penelope are recommended.

C. Neutron yield of protons with energies 113 MeV and 256 MeV and carbon ions at 290 MeV/u

Absolute neutron yields from protons and carbon ions at therapeutic energies interacting in targets of materials of interest for medical physics are presented. This benchmark shows the current status of two of the main Geant4 physics lists for hadronic physics used by the community in medical applications. For protons, two energies (113 MeV and 256 MeV) have been selected, as they are important in clinical applications. The proton beams are incident on one of three targets made of aluminum, carbon and iron, with thickness large enough to fully stop the beam. For carbon ions of 290 MeV/u, the beam is incident on a water (G4_WATER material) phantom of 18 cm thickness.

The results of the test are available in the geant-val web interface under the name of ProtonC12NeutronYield [12].

1. Simulation setup

Experimental neutron yields from thick targets of different materials bombarded by protons of energies below 256 MeV were obtained from Meier et al 1989 [117] and 1990 [118]; for carbon ions interacting in water the data was obtained from Satoh et al 2016 [119]. For protons, the Monte Carlo simulations modelled a cylindrical target irradiated with a uniformly distributed, zero divergence, monoenergetic (113 MeV or 256 MeV) proton beam with a radius equal to the radius of the target. The beam was located upstream of the target. The radius, thickness and material of each target are shown in Table X.

TABLE X.

Target dimensions, material and density for each proton energy and carbon ion beam configuration.

Material	Radius (cm)	Thickness (cm)			Density (g/cm3)
		protons
	113 MeV	256 MeV	113 MeV	256 MeV
Aluminum	3.65	8.0	4.00	20.0	2.699
Carbon	3.65	8.0	5.83	30.0	1.867
Iron	3.65	8.0	1.57	8.0	7.867
Carbon ions (290 MeV/u)
G4_WATER	-	-		18.0	1.0

Secondary neutrons produced in the inelastic nuclear interactions within the targets and escaped were scored at the surface of spherical rings (radius of 90 m) that covered specific angular bins of 4° of thickness. For carbon ions, a monoenergetic carbon ion beam of 0.25 cm radius, 290 MeV/u energy and zero divergence was simulated. The target was a water phantom 18 cm thick. Detailed dimensions are shown in Satoh et al 2016 [119]. The neutron yield per incident primary particle per steradian per energy (equally spaced logarithmic energy intervals) was scored at specific angular bins. For proton beams, the neutron yield was scored at 7.5°, 30°, 60° and 150° for 113 MeV and at 30°, 60°, 120° and 150° for 256 MeV. For carbon ions, the neutron yield was scored from 15°−90° at 15° angular steps.

The physics lists under study included alternatively QGSP_BIC_HP and QGSP_BERT_HP_EMZ. Both adopt the EM constructor Opt4 (indicated with the suffix EMZ in the pre-built Geant4 physics lists). A global production cut of 0.05 mm was used.

2. Results and Discussion

In Figure 18, top left, representative results are shown for the absolute neutron yield for protons (incident on aluminum) and carbon ions (on water) for several angles. Experimental data are shown with empty circles. In the figure, the ratio between the calculated to experimental integrated yields is shown for several angles and materials. For the carbon ion case, the yields were integrated from 2 MeV as reported in Satoh et al 2016 [119]. As shown, for protons there exists an overall better agreement (within 2 standard deviations) between QGSP_BIC_HP and the experimental yield for all the angles and materials compared to QGSP_BERT_HP_EMZ. However, the largest differences between the two physics lists were found at larger angles for the aluminum target. For water material, there was not significant difference between the two physics list for all the angles. In that scenario the yields were overestimated by up to 50%. As a comparative with other Monte Carlo engines, results from Satoh et al 2016 [119] using PHITS are shown and they agreed with Geant4 calculation within 1 standard deviation.

FIG. 18.

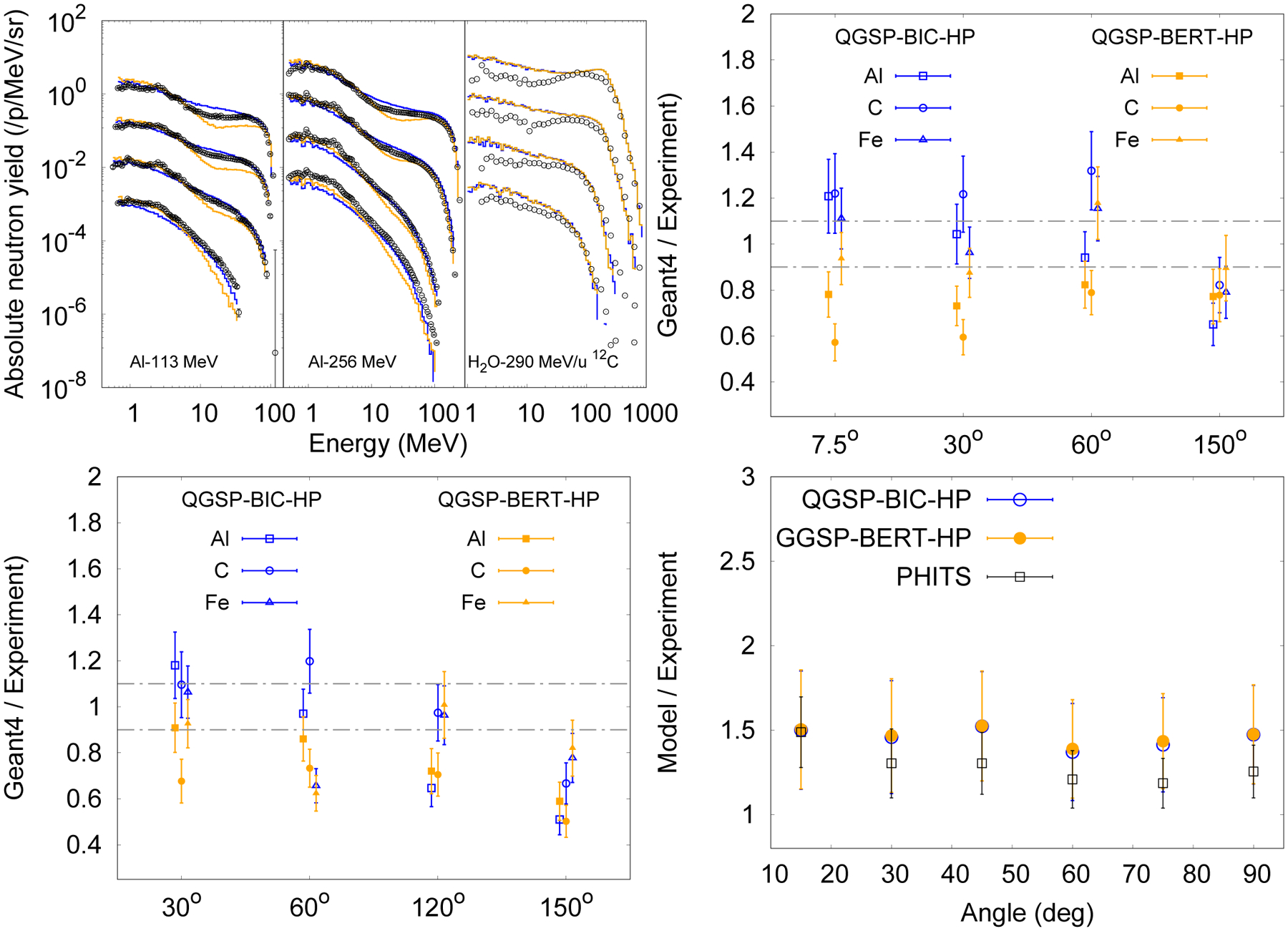
Absolute neutron yield (top left) for protons of 113 MeV and 256 MeV impinging an aluminum target and 290 MeV/u carbon ions in a water phantom. Geant4 calculation using QGSP_BIC_HP is shown with blue solid line whereas results with QGSP_BERT_HP is shown with orange solid lines. Experimental data are shown with empty markers. Ratio between calculated to experimental integrated neutron yield for 113 MeV protons (top right), 256 MeV protons (bottom left) and 290 MeV/u carbon ions (bottom right). The gray dashed line represents the experimental uncertainty, one standard deviation (σ_ref). Error bars represent one standard deviation.

In summary, a marginally closer agreement with measured data was achieved with QGSP_BIC_HP physics list for high Z materials using the proton beams. For carbon ions, no statistically significant difference was found between the two hadronic physics lists used, because they both use the same physics models to describe the hadronic interactions of heavier ions. For the case involving carbon ions, the neutron yields were underestimated compared with experimental data by 50% on average, and by 11% compared with published data calculated with the PHITS code.

D. Fragmentation of a 400 MeV/u ¹²C ion beam in water

This test, published in Bolst et al 2017 [26], benchmarks Geant4’s modelling of the fragmentation process against experimental measurements of a ¹²C ion beam incident upon a water target performed at GSI (Haettner et al 2013 [120]). The measured data includes fragment yields from hydrogen to boron for different thicknesses of water irradiated by a mono-energetic 400 MeV/u ¹²C ion pencil beam, as well as the fragment’s angular and energy distributions. The full results of the test can be downloaded from the geant-val web interface [12]. The name of the test is FragTest.

1. Simulation setup

The simulation consists of a mono-energetic ¹²C ion pencil beam with an initial energy of 400 MeV/u and energy σ of 0.15%, with a FWHM of 5 mm. The beam is incident upon a variable thickness of water with an area of 50 × 50 cm² and thicknesses of: 59 mm, 159 mm, 258 mm, 279 mm, 288 mm, 312 mm and 347 mm. Fragments were collected in a 2.94 m radius hemisphere centered on the water slab. For fragment yields, fragments were scored in a 10° cone from the center of the hemisphere. Fragment’s angular distributions were scored in arcs on the hemisphere with angles of 0.4°, corresponding to the size of the detector used in the experiment. The energy distributions of fragments were calculated based on the time of flight of fragments scored in the 0.4° arcs.

Electromagnetic interactions were modelled using Opt4, with a global production cut of 10 mm for electrons, the production cut was set this high since the electron production did not affect the production of fragments. The QGSP_BIC_HP hadronic physics component was used with alternative physics models describing the hadronic inelastic scattering of heavy ions: G4IonBinaryCascadePhysics (BIC), G4IonQMDPhysics (QMD) and G4IonINCLXXPhysics (INCL). All default configurations were used for all models investigated in this work.

2. Results and discussion

Fragment yields scored within a 10° cone are shown in Figure 19. It can be seen that the yield varies significantly between the fragmentation models, up to ~20% for particular fragment species. For the lighter fragments H and He, which represent the most abundant fragments, all alternative models agreed within ~20% of experimental measurements. For this particular version of Geant4 (10.5), INCL gives the best agreement with experiment for H fragments while QMD agrees the best for the yield of He fragment. Sample angular and energy distributions are shown in Figure 20, the simulation distributions shown here are normalised to the same area under the curve as the experiment. This is done to compare just the distributions produced by the simulation against the experimental data. INCL was seen to reproduce experimental angular distributions better than the other two models with the exception of H, where QMD reproduced the best. For kinetic energy distributions, INCL was seen to perform the poorest of the three models, with its energy distributions systematically being shifted ~10% to lower energies compared to the other models for most measurements. BIC and QMD were seen to perform very similarly to one another for both the angular and energy distributions, with QMD performing slightly better out of the two. Due to different fragmentation models giving better agreement with experimental measurements for angular and energy distributions of fragments, the user should carefully consider their needs when selecting a model for fragmentation. The simulations were also performed with the Geant4 EM constructor Opt3, however no significant differences were found between the two compared to Opt4.

FIG. 19.

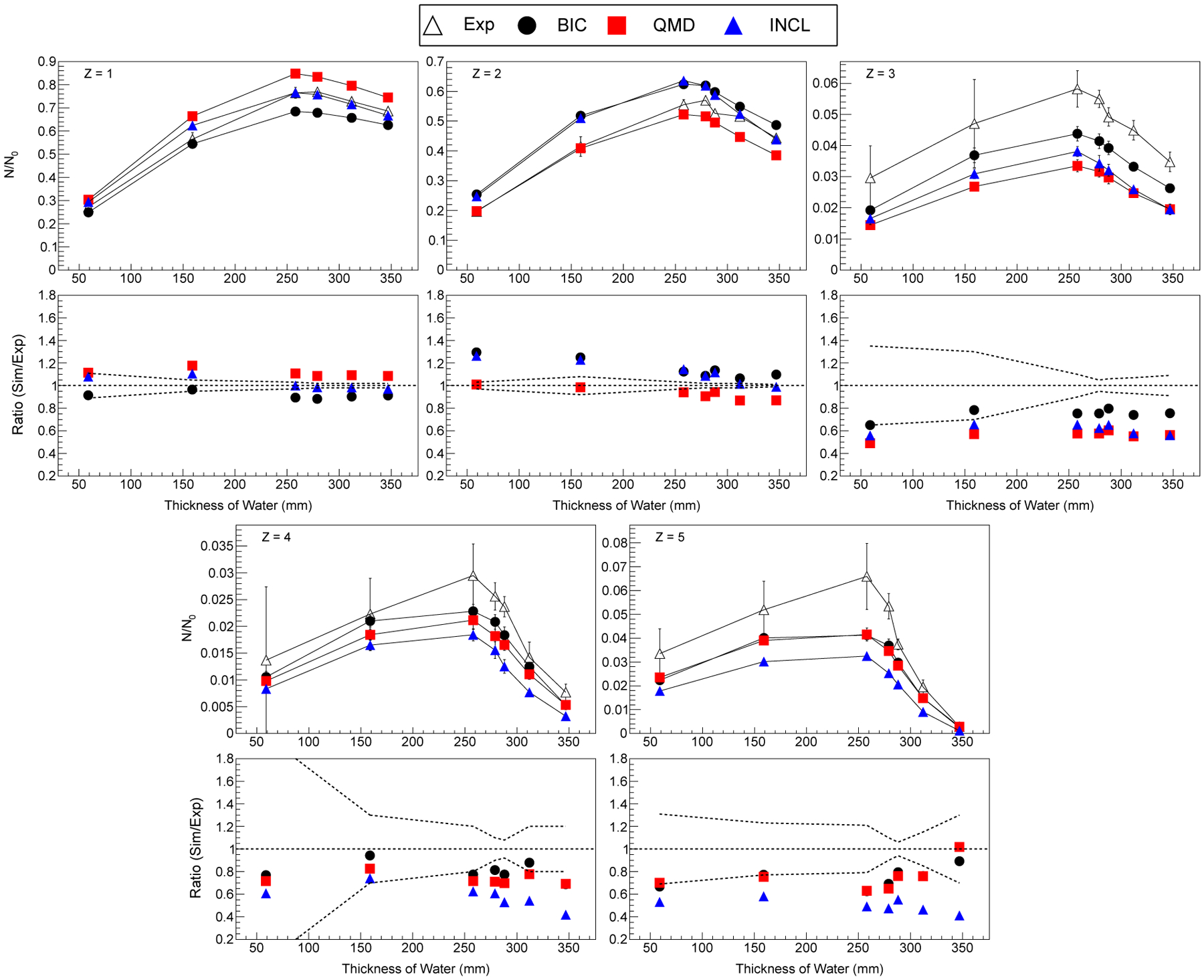
The fragment yields, N, produced from N₀ mono-energetic 400 MeV/u ¹²C ions incident upon different thicknesses of water. The fragments were scored within a forward angle of 10° from the centre of the water targets. Experimental measurements of fragments with different atomic number ranging from 1 to 5 are compared against alternative models available in Geant4. The dashed lines on the bottom ratio plots indicate the experimental uncertainty σ_ref.

FIG. 20.

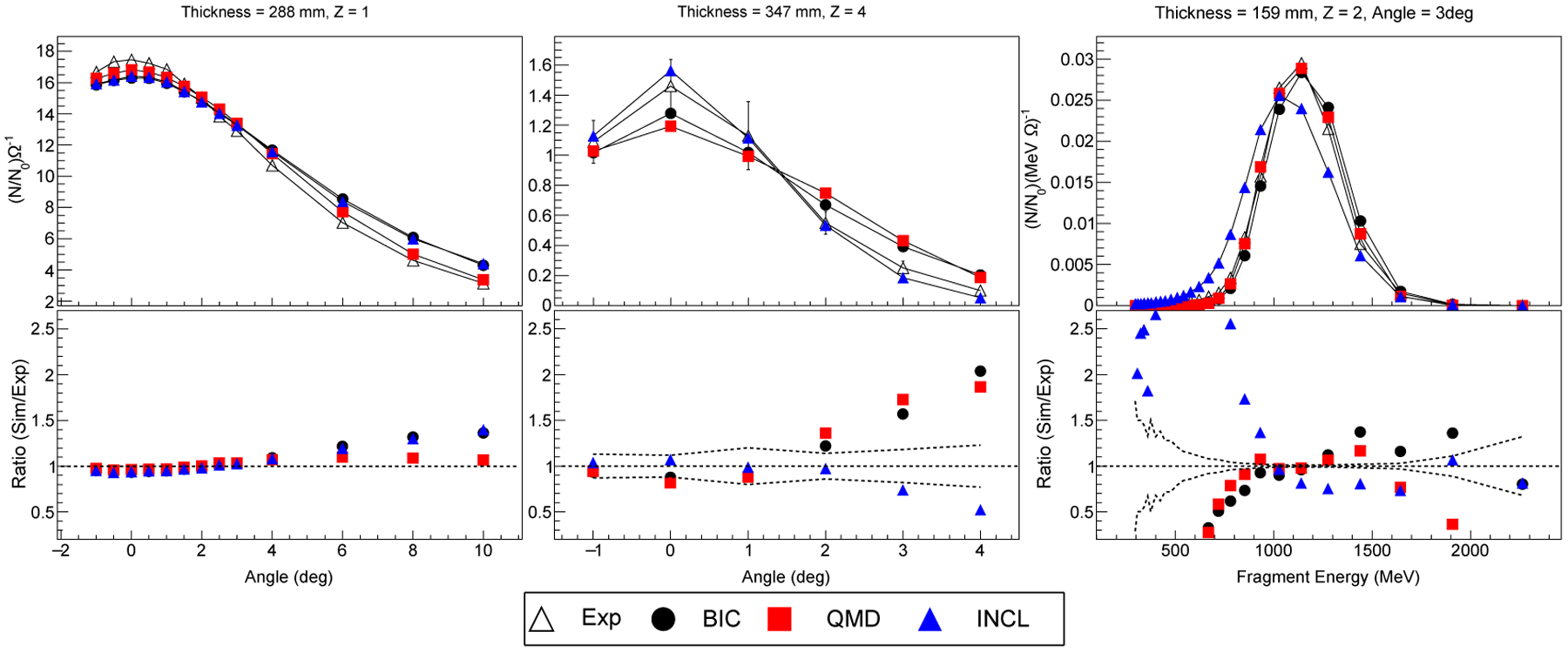
Example angular and energy fragment distributions comparing experimental measurements against alternative models available in Geant4 for a 400 MeV/u mono-energetic ¹²C ion incident upon water. Left and Middle: Angular distribution of H (left) and Be (middle) produced with a water thickness of 288 mm and 347 mm, respectively. Right: An example energy distribution of He fragments recorded at an angle of 3° from the centre of the ¹²C ion beam when incident upon 159 mm of water. The dashed lines on the bottom ratio plots indicate the experimental uncertainty σ_ref.

E. Test on cell survival curve modelling for proton therapy

This test is focused on evaluating the capability of Geant4 to reproduce in-vitro cell survival curves, also referred to as surviving fraction (SF), against experimental measurements (Chaudary et al 2014 [121]), performed at the CATANA facility radiating the radio-responsive prostate DU145 cells and breast cancer cell line MDA-MB-231 (Petringa et al 2019 [27]), at 20 mm depth in water, corresponding to the mid of a clinical 62 MeV modulated clinical proton beam. The test is called Hadrontherapy in the geant-val web interface [12].

The SF is calculated with the Linear Quadratic Model:

$$SF(D)=e^{-\left(\alpha D+\beta D^2\right)},$$ (2)

where SF(D) is the fraction of cells surviving when delivering a dose D; α and β are constants describing the linear and quadratic components of cell killing, respectively.

Precompiled Look-up Tables (LUTs) contain the values of α_i and β_i for a set of monoenergetic ions (with Z spanning from 1 to 8). α_i and β_i are calculated with the the Local Effect Model, LEM (Elsässer et al 2010 [122], Friedrich et al 2012 [123]) and are tabulated as a function of the ion kinetic energy E_i and delivered dose D_i in a specific voxel of the simulated material. E_i and D_i can be derived from the Geant4 simulations and then used as input of an algorithm able to compute the average values of 〈α〉 and 〈β〉 in a mixed radiation field, interpolating the best α_i and β_i and using the following weighted formulas:

$$\langle \alpha \rangle =\frac{\sum _i{\alpha }_i\cdot D_i}{\sum _i{D}_i},$$ (3)

$$\langle \beta \rangle ={\left(\frac{\sum _i\sqrt{{\beta }_i}\cdot D_i}{\sum _i{D}_i}\right)}^2,$$ (4)

where the index i refers to the different incident ions interacting in the voxel. This method is referred here as LEM III-weighted method. The LUTs are created taking into account the total LET at the corresponding position of the cell layer irradiation [124]. The input parameters of the LEM models were optimized referring to the radiobiological results. The threshold dose was fixed to 5 and 9 Gy for the MDA-MB-231 and DU-145 respectively, the nucleus radius was 4 μm in both cases.

1. Simulation setup

The experimental setup (transport beamline elements, detectors, irradiation device, etc.) used for cells irradiation has been modelled in detail using the Hadrontherapy advanced example (Cirrone et al 2017 [125]). The source consists of a 62 MeV proton beam characterized by a gaussian energy and angular distribution with a standard deviation of 0.3 MeV and 0.028°, respectively. The beam spot size was circular, with a gaussian spatial distribution (standard deviation of 3 mm). A plastic rotating modulator wheel (Jia et al 2016 [126]) routinely used for real treatments was simulated for the correct reconstruction of the modulated beam (clinical Spread Out Bragg Peak or SOBP). A total of 3.6 · 10⁸ histories were simulated in each simulation. Dose as a function of depth is calculated in a voxelised water phantom positioned at the end of the beam line. The water tank was divided into 400 × 400 × 0.01 mm³ segments to reproduce the real experimental conditions. The water material is modelled with G4_WATER NIST. Dose, fluence, dose-averaged Linear Energy Transfer (LET) of the primary proton beam and generated secondaries were calculated in the simulations; α and β values were determined using equations 3 and 4, along with the LUTs. The QGSP_BIC_HP physics list was used. The dose-averaged LET at the cells was 4.5 keV/mum. The global production cut was set to 0.01 mm.

2. Results and Discussion

Figure 21 shows the SF curves as derived from the experimental measurements and the Geant4 simulation.

FIG. 21.

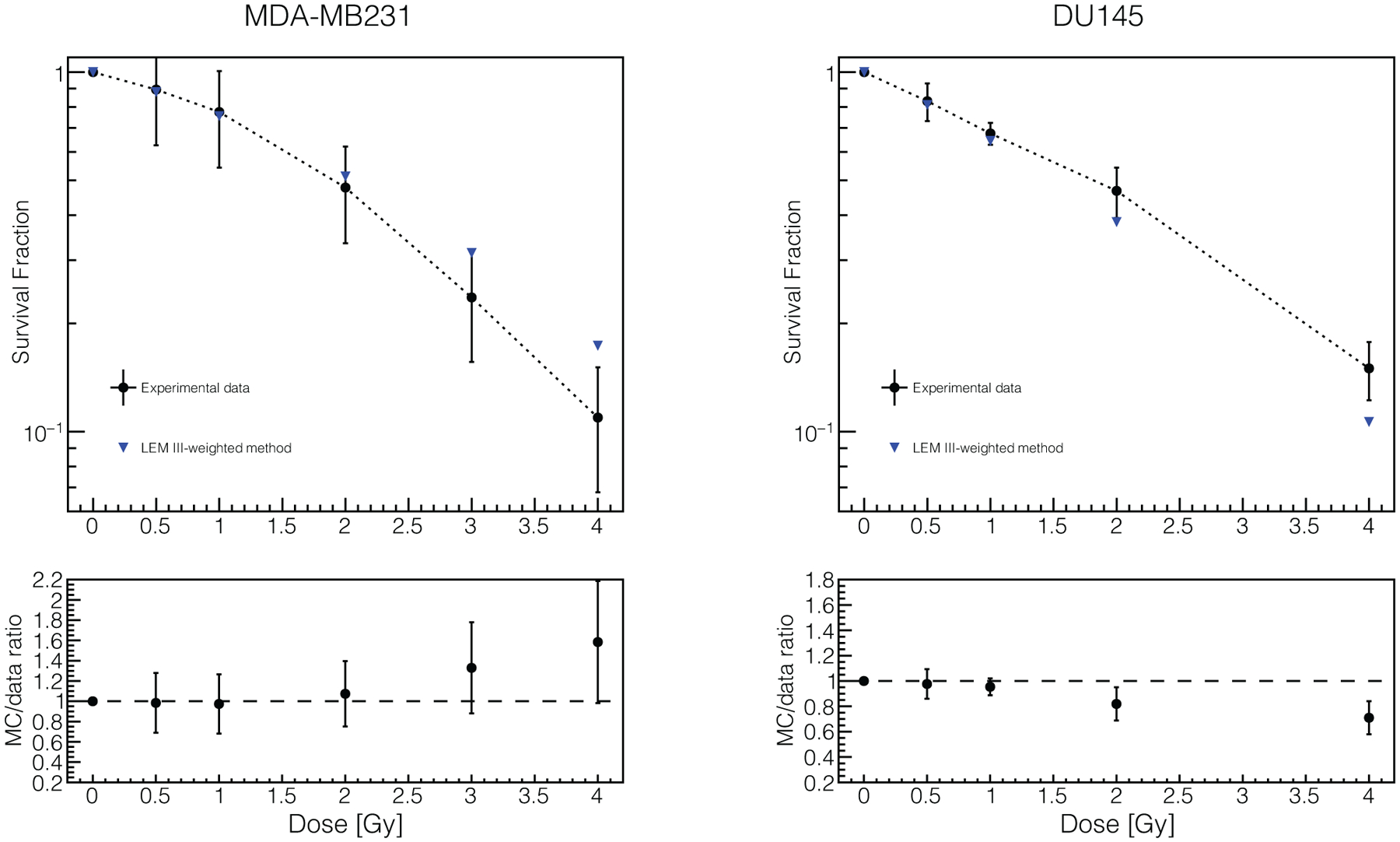
Experimental cell Surviving Fraction (SF) measured irradiating DU145 cells and MDA-MB231 (dotted points) and the corresponding curves calculated with the LEM III-weighted method (triangles). Ratios of Geant4 simulations to experimental data are also plotted.

The agreement between experimental data and Geant4 simulations data was evaluated applying the χ² test in the case of two independent distributions.

We obtained a χ² value of 4.23 and 3.64 for the DU145 and MDA cell lines, respectively.

The χ² test confirmed the good agreement between the two distributions even if, as expected, at doses greater than 3 Gy the differences become more evident (well above the 20%)[27].

VI. SUMMARY AND CONCLUSIONS

G4-Med is a group of currently 18 tests, regularly executed on the CERN computing infrastructure via the geant-val platform, to benchmark Geant4 against reference data for medical physics applications. G4-Med can also be used for regression testing purposes of Geant4. The results of the tests are provided to the Geant4 user community on-line via the geant-val web interface [12].

This work was focused on the description of the tests of G4-Med and on the results of the benchmarking of Geant4 10.5 against reference data.

Table XI is intended to provide a summary of the main results of the electromagnetic physics tests, subject of Section III. We encourage the readers to refer to the specific tests of interest, for a more detailed analysis of the results in specific scenarios of application of Geant4.

TABLE XI.

Summary of the results of the electromagnetic physics tests of Section III. The second column reports the type of reference data, either from Monte Carlo simulations, theoretical or experimental (Exp) data. σ_ref is the uncertainty of the reference data.

Test	Reference	Difference with reference data
Photon Attenuation	NIST XCOM (Berger et al 1987 [41])	≤ 1 σref for the total μ/p, more details in Table IV
ElectDEDX	ESTAR (Berger et al 1984 [127])	< 1 σref
ElectBackScat	Exp data in Table V	< 3 σref (< 5%) for $E_{e^{-}}>0.2$ MeV < 15% for 5 keV $<{\text{E}}_{e^{-}}<0.2$ MeV and < 40% for E < 5 keV for Opt0 and Opt3, < 30% for E < 5 keV for Opt4, Penelope and Livermore
ElecForwScat	Ross et al 2008 [61] Exp data	Characteristic angle ≤ 3% for Be, Al, Cu, Ta and Au foils, 3%−5% for Ti and C foils, for all EM constructors
Bremsstrahlung	Faddegon et al 1990 [63] Exp data	< 2 σref for Opt0, Penelope and Livermore < 1 σref for emission angles < 60° for Opt3 and Opt4 < 2 σref for emission angles > 60° for Opt3 and Opt4
Fano Cavity	NA	< 2% for Opt0, 0.03% for Opt3, 0.02% for Opt4 for dRoverRange equal to 0.2 (default value, see Table III)
LowEElecDPK	EGSnrc	< 10% for Opt3 (same for Opt0) < 3% for Opt4, Livermore and Penelope
Brachy-Ir	Granero et al 2006 [83], Geant4 7.1	< 1 σref
Mammo	Fedon et al 2018a [21], 2018b [22] Exp data	< 7.7% for Opt0 and < 6% (σref =5.7%) for the other EM constructors

The agreement is defined based on the discussion of the results of each individual test in Section III. SS and GS are not included in the Table as they have been used in a very limited set of tests.

In the case of the test concerning photon attenuation coefficients in water (PhotonAttenuation), slightly better agreement with respect to reference data was found for Opt4. The test includes one material only at this stage and we will expand it to other materials in the near future. We will also consider to extend the comparison of Geant4 to other reference data.

The electronic stopping power test (ElectDEDX) showed an agreement with ESTAR within the reference data uncertainty (1 σ_ref). This test is useful for regression testing purposes as it monitors a physical quantity important for the calculation of energy deposition in a target.

The electron backscattering test shows an agreement with respect to the available experimental data that clearly depends on the electron energy range and the Geant4 EM physics constructor. In particular below 5 keV the results should be taken with caution for any constructor, including the suggested ones. The best EM physics constructors to model the electron backscattering were found to be Opt4, SS, Livermore and Penelope.

For electron forward scatter, the angular distribution of electron fluence at 1.18 m calculated with Opt4 was significantly underestimated (> 1 standard deviation) in comparison to experimental data for foils of higher Z than Be by 2–5%, with calculated results comparable to or better than the comparison with the other physics constructors. For bremsstrahlung from thick Be, Al and Pb targets at radiotherapy energies, bremsstrahlung yields (≤ 1–2 standard deviations) were in better agreement with experimental data when using Opt3 and Opt4. For these constructors, the differences were significant (> 1 standard deviation) at larger angles for the higher-Z targets (≥ 60°).

The Fano cavity test (FanoCavity) was designed specifically to check the accuracy of the condensed history electron transport and this test demonstrates that the Goudsmit-Saunderson (GS) multiple scattering model (included in Opt4, Livermore and Penelope) provides a high level of accuracy and stability. Similar results were obtained for the WVI* constructor.

The Dose Point Kernel test (LowEElecDPK) demonstrates that the Opt4 constructor provides the best agreement with the selected standard (EGSnrc). This test is currently used as a regression testing benchmark for Geant4 allowing to verify the stability of DPK profiles along with Geant4 updates, especially when electron multiple scattering models undergo changes or updates. It remains impossible to validate Geant4 in terms of DPK in the absence of experimental data in water in the low electron energy range.

The results of the microdosimetry test (microyz) demonstrate that, when using Geant4 condensed history approach in EM simulations of electron transport in microdosimetric applications, it is important to limit the step size. It is shown that 1/10 of the sensitive volume diameter is adequate.

The Brachytherapy test (Brachy-Ir) has a regression testing purpose. Geant4 is compared against previous simulation results in calculating the radial dose rate distribution of a ¹⁹²Ir source. This test is of interest to monitor the evolution of Geant4 and will be extended in the near future to other brachytherapy sources. We intend also to compare the results of the simulation to dosimetric experimental measurements available in the literature.

The test on monoenergetic x-ray internal breast dosimetry (Mammo) showed an agreement between Geant4 and experimental data within the experimental uncertainty. It was observed that Opt0 provided the worst performance among the EM constructors under study.

In summary, the EM tests showed that Opt0 in general is the constructor with the least agreement with respect to the reference data. For the other physics constructors, the results of the tests should support users to select the appropriate EM physics constructor for their medical physics application. It was observed that Opt4 had good agreement with the reference data for all the tests. This result was expected as this constructor was developed to provide the most accurate Geant4 physics models, irrespective of CPU performance.

Table XII summarises the results obtained for the hadronic tests subject of section IV.

TABLE XII.

Summary of the results of the hadronic physics tests of Section IV. The second column reports the reference data, which are all experimental and published in the literature. σ_ref is the uncertainty of the reference data.

Test	Reference	Difference with reference data
NucNucInelXS	Zerkin et al 2018 [97]	< 10% overall
C12FragCC	Toshito et al 2007 [24]	< 1 σref for total and Li cross sections 18% for Be isotopes, 34% for B isotopes for QMD 26% for Be isotopes, 36% for B isotopes for BIC 38% for Be isotopes, 48% for B isotopes for INCL

The test of Nucleus-Nucleus hadronic inelastic scattering cross sections (NucNucInelXS) considered a limited number of projectiles of interest for hadron therapy (protons and ¹²C ions), incident on a limited number of targets. The choice of targets was performed based on the availability of experimental measurements in the EXFOR data library (Zerkin et al 2018 [97]). In general, an agreement within approximately 10% was found between Geant4 and the experimental data for the cases under study. The next step of this test is to find more reference experimental measurements to be able to benchmark the Geant4 inelastic scattering cross sections for more targets of interest for medical physics applications.

The 62 MeV/u ¹²C fragmentation test (LowEC12Frag) showed that both the Geant4 Ion Binary Cascade and the INCL models have limitations in reproducing doubly differential cross sections of fragments produced in the interaction of ¹²C with a thin carbon target. The results of this test show a possible domain of improvement of Geant4 of interest for carbon ion therapy.

The test on the 300 MeV/u ¹²C ion charge-changing cross section (C12FragCC) demonstrated that all hadronic ion fragmentation models, G4IonQMDPhysics (QMD), G4IonBinaryCascade(BIC) and G4IonINCLXXPhysics(INCL), reproduce the total and Li partial charge-changing cross sections. However, they all underestimate the reference experimental data for Be and B fragments.

Table XIII summarises the results obtained for the hadronic tests subject of section V, where the EM constructor is varied while keeping the hadronic physics component modelled with QGSP_BIC_HP.

TABLE XIII.

Summary of the results of the hadronic physics tests of Section V. The EM constructor is tested (Opt0, Opt3, Opt4, Livermore and Penelope) while keeping the same hadronic physics component (QGSP_BIC_HP). All the reference data are experimental measurements. σ_ref is the uncertainty of the reference data.

Test	Reference	Physical Quantity	Difference with reference data
LowEProtonBraggPeak	Faddegon et al 2015 [25]	67.5 MeV proton Bragg Peak
		Spread	< 1 σref (within 0.5 mm)
		Range	< 2 σref (within 0.5 mm) for all EM constructors
LightIonBraggPeak	Schardt et al 2007 [114]	125–200 MeV/u protons, Rd82 100–400 MeV/u 12C, Rd82	< 0.1% (< 0.2 mm) < 1.1% (< 0.8 mm) for all cases apart from Opt0

The test modelling a 67.5 MeV proton Bragg Peak in water (LowEProtonBraggPeak) showed that Geant4 can reproduce the Bragg peak spread within the uncertainty of the experimental measurements and the range within 0.5 mm accuracy. This result was confirmed for higher proton energies (125–200 MeV/u) by the Light Ion Bragg Curve test (LightIonBraggPeak). In this case an agreement within 0.1% (< 0.2 mm) was observed for R_d82. In the case of incident 100–400 MeV/u ¹²C ions, an agreement within 1.1% was found for all EM constructors apart from Opt0.

Table XIV summarises the results obtained for the hadronic tests subject of section V, where the EM constructor is kept constant while changing the hadronic physics component.

TABLE XIV.

Summary of the results of the hadronic physics tests of Section V. The EM constructor is kept constant (Opt4) while changing the hadronic physics component. All reference data are experimental. σ_ref is the uncertainty of the reference data.

Test	Reference	Physical Quantity	Difference with respect to reference data
ProtonC12 NeutronYield	Meier et al 1989 [117] Meier et al 1990 [118]	Neutron yield of 113 MeV and 256 MeV p	< 2 σref for QGSP_BIC_HP, < 4 σref for QGSP_BERT_HP
ProtonC12 NeutronYield	Satoh et al 2016 [119]	Neutron yield 290 MeV/u 12C	< 11% against PHITS < 50% against exp data for both for QGSP_BI_CHP and QGSP_BERT_HP
FragTest	Haettner et al 2013 [120]	400 MeV/u 12C fragmentation yield	QGSP_BIC_HP for hadrons BIC and QMD: < 25% , INCL:< 40%
Hadrontherapy	Petringa et al 2019 [27]	Cell survival test 62 MeV proton beam	QGSP_BIC_HP < 20% for DU145 > 20% for MDA-MB-231

The neutron yield produced by 113 MeV and 256 MeV protons showed a a marginally closer agreement when using QGSP_BIC_HP rather than QGSP_BERT_HP.

The 400 MeV/u ¹²C ion fragmentation test (FragTest) showed that BIC and QMD produce similar yields of light fragments (Z=1–5), with similar kinetic energy and angular distribution. Worst agreement in terms of fragments yield was observed for INCL, however this model produces the best description in terms of angular distributions of the fragments. The results of this test are consistent with the outcome of the charge-changing cross section test which demonstrated a better agreement between BIC and QMD to the reference data than INCL.

The test on the cell survival curves (Hadrontherapy), of interest for ion therapy, is intended to validate Geant4 against in-vitro radiobiological measurements. In particular, surviving fraction curves calculated with Hadrontherapy were compared with experimental data for different cell lines. A good agreement was found for low doses (up to 3 Gy), while significant discrepancies were evident at higher delivered doses. Provided the current stage of research in in-silico radiobiological modelling (e.g. Abolfath et al 2017 [128]), the overall agreement was deemed satisfactory.

For hadron therapy, it is recommended not to use the EM constructor Opt0. The hadronic tests showed that QGSP_BIC_HP physics list (which models EM interactions with Opt4 in Geant4 10.5) provides an overall adequate description of the physics involved in hadron therapy, including proton and carbon ion therapy. However, it should be noted that only few physical quantities (position and spread of the Bragg Peak, neutron yields, fragment yields) have been subject of testing. New tests should be included in the next stage of the project to validate Geant4 in terms of dosimetry against experimental measurements.

Concerning the carbon ion fragmentation tests, the results show a slightly better performance when using QMD and BIC ion fragmentation models. The charge-changing cross section and fragmentation tests show that ion fragmentation modelling is a domain of possible improvement of Geant4.

In conclusion, we encourage Geant4 users to use benchmarked Geant4 physics constructors and lists. The results presented and discussed in this paper will aid users tailoring physics lists to their particular application.

The next phase of the project will proceed in two main directions. The first one is the benchmarking of the computing performance of the pre-built Geant4 physics constructors and lists. We will use the regression testing to investigate the evolution of the Geant4 physics component for medical applications in terms of both accuracy and computing performance. The second main direction will be to extend the current tests and include new ones to cover domains which are currently not tested, e.g. x-ray radiotherapy and nuclear medicine.

TABLE VI.

References for the experimental datasets used in the electron backscattering test with the energy range and the target material. The first column reports the dataset names used in Figures 4 and 5.

Dataset name	Reference	Material	Energy range
Sandia Lab. (1980)	[47, 48]	Al, Au, Si	0.032 MeV - 1.033 MeV
Reimer, Tollkamp (1980)	[49]	Au, Si	1 keV - 30 keV
Hunger, Kuchler (1979)	[50]	Au, Si	4 keV - 40 keV
Cosslett, Thomas (1965)	[51]	Si	5 keV - 45 keV
Bongeler (1993)	[53]	Si	1 keV - 10 keV
Bishop (1963)	[54]	Au, Si	5 keV - 30 keV
Heinrich (1966)	[55]	Au, Si	30 keV
Neubert (1980)	[56]	Al, Si	15 keV - 60 keV
Drescher (1970)	[57]	Au, Si	10 keV - 100 keV
Wittry (1966)	[58]	Au, Si	5 keV, 30 keV
Bronstein (1969)	[59]	Au, Si	0.1 keV - 4 keV
El Gomati (1997)	[60]	Si	0.6 keV - 6 keV